Đề thi học sinh giỏi Toán 10 năm 2021 – 2022 cụm trường THPT – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KÌ THI CHỌN HỌC SINH GIỎI CỤM LỚP 10 CỤM TRƯỜNG THPT
NĂM HỌC 2021 - 2022 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
Bài I (4,0 điểm) Cho Parabol P y  2 ( ) :
x  2x  3 .
1) Lập bảng biến thiên và vẽ đồ thị (P ) .
2) Tìm tọa độ điểm M thuộc (P ) sao cho khoảng cách từ M đến đường thẳng y  4x  7
đạt giá trị nhỏ nhất.
Bài II (6,0 điểm)  2 x  2 y  xy  1
1) Giải hệ phương trình 
x  y  xy  .  3
2) Giải phương trình sau: a) 2
2x  3x  5  x  1 ; b) 2
x  3x  2  6  2 x  1  3 x  2.
Bài III (4,0 điểm) Cho ba số dương a, ,
b c thỏa mãn a  b  c  3 . 3 3 a b 1) Chứng minh   a  b. 2 2 b a 3 3 3 a b c
2) Tìm giá trị nhỏ nhất của biểu thức P    . 2 2 2 b c a
Bài IV (3,0 điểm) Cho tam giác đều A BC có cạnh bằng a . Gọi G là trọng tâm tam giác, M là
một điểm thỏa mãn MA  2MB  3MC  0.
1) Chứng minh: 6GM  A C .
2) Gọi D, E , F là hình chiếu của M lên các cạnh BC, ,
CA AB. Tính MD  ME  MF theo a.
Bài V (3,0 điểm) Trong mặt phẳng tọa độ Oxy , cho tam giác A BC có các đường cao A , D BE,CF.
Biết điểm E(5, 4), điểm F(1, 2) và phương trình đường thẳng BC là y  1.
1) Viết phương trình đường thẳng EF và tìm tọa độ trung điểm của B C .
2) Tính diện tích tam giác DEF .
- - - - - - - - - - Hết - - - - - - - - -
Họ và tên thí sinh:....................................................
Số báo danh:............................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
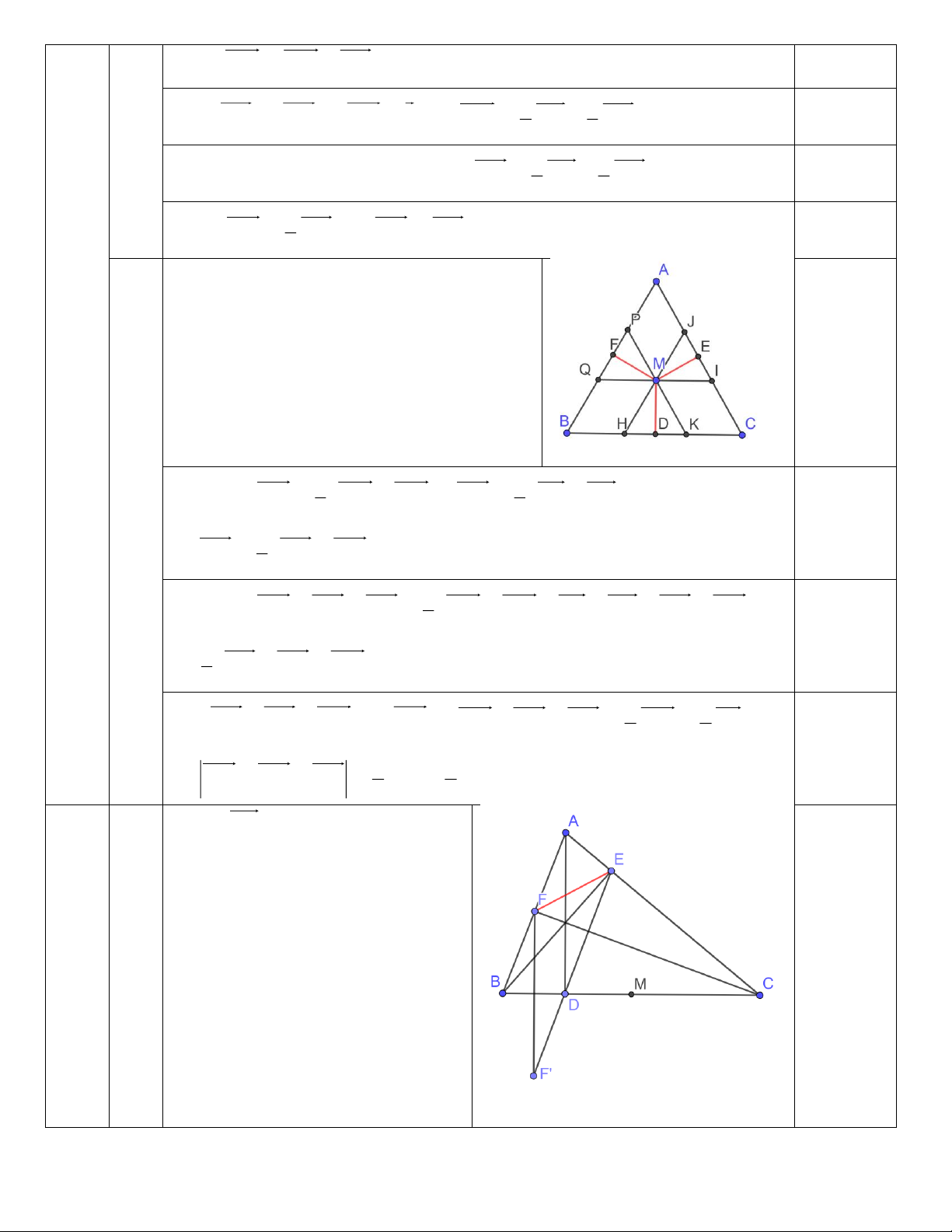
KÌ THI CHỌN HỌC SINH GIỎI CỤM LỚP 10 CỤM TRƯỜNG THPT NĂM HỌC 2021 - 2022 Môn thi: TOÁN HƯỚNG DẪN CHẤM Bài Câu Nội dung điểm 1 1 TXĐ: 0,25 (4,0đ) Đỉnh I  1  ; 4   0,25 Bảng biến thiên: x  -1    y 0,5 -4 Đồ thị: 0,25
(P) Giao với trục Ox : 3  ;0;1;0 0,25
(P) Giao với trục Oy :0;  3 Vẽ đồ thị hàm số 0,5
(Chú ý: học sinh biểu diễn tọa độ các điểm trên hình
vẽ vẫn được điểm tối đa) 2 Gọi M  ,
x yP suy ra 2
y  x  2x  3 0,25 2     y 4x 7 x 2x 4
Khi đó d M,d    0,5 17 17
Ta có: x  x   x  2 2 2 4 1  3  3 0,5
Suy ra d M d  3 17 ,  . 17
Suy ra giá trị nhỏ nhất của d M d  3 17 ,  . 17 0,5
Dấu bằng xảy ra khi x  1, y  0. Vậy M 1,0. 0,25 2 1  2 x  2 y  xy   x  2 1 ( y)  3xy  1 (6,0đ)   
x  y  xy  3
x  y  xy    3 0,25
x  y  S Đặt  xy  P 0,25
Hệ phương trình trở thành  2 S  3P  1  2
S  3S  10  0
S  2, P  1      0,5 S  P  3 P  3  S
S  5, P     8
Với S  5, P  8 suy ra x, y là nghiệm của phương trình 0,5 2
X  5X  8  0 ( vô nghiệm)
Với S  2, P  1 suy ra x, y là nghiệm của phương trình 2
X  2X  1  0  X  1 suy ra x  y  1 0,5
Vậy hệ có nghiệm là x,y   1;1 2a x  1   x  1 2
2x  3x  5  x  1  
2x  3x  5  2  2 2  x     1
x  x  6   0 1,0 x  1   
 x  2(l) . Vậy phương trình có nghiệm là:x  3  1,0  x    3(tm ) 2b
 x 1  a
Điều kiện x  2. Đặt  0,5
 x  2  b a  3
Phương trình trở thành ab  6  2a  3b  (a  3)(b  2)  0   0,5 b   2
Với a  3  x  10(t ) m
Với b  2  x  6(t ) m 1,0
Vậy tập nghiệm của phương trình là S  {6;10}. 3 1 Biến đổi : (4,0đ) 3 3
a  b  a b  5 a  5 b  3 2 a b  2 3 a b  3 a  2 a  2 b   3 b  2 a  2 b 0 1,0 2 2   b a 2   2 a  2 b   3 a  3
b    a  b a  b  2 a  ab  2 0 b   0 1,0 2 3 a
Áp dụng bđt Cauchy ta có:
 b  b  3a 2 b 3 3 1,0 b  c
c  c  3b ;
 a  a  3c 2 c 2 a Suy ra 3 3 3 3 3 3
a  b  c  a b c
2(a  b  c)  3(a  b  c)   
 a  b  c  3 2 2 2 2 2 2 b c a b c a 1,0
Dấu bằng xảy ra khi a =b= c =1
Vậy giá trị nhỏ nhất của P bằng 3 khi a =b = c =1. 4 1 GM A M A G (3,0đ) Ta có:   0,25 1 1
Ta có MA  2MB  3MC  0  A M  A B  A C 0,25 3 2 1 1
Ta có G là trọng tâm tam giác ABC  A G  A B  A C 0,25 3 3 1 Suy ra GM 
A C  6GM  A C 0,25 6 2
Từ M kẻ các đường thẳng song song với 3 cạnh
của tam giác, cắt các cạnh này tại P,Q,H,K,I,J.
Suy ra D,E,F là trung điểm các cạnh HK, IJ, PQ. 0,5 1 1 Suy ra  MD 
MH MK  ; ME  MI MJ ; 2 2 0,5
 MF  1 MP  MQ 2 1
Suy ra  MD  ME  MF 
MH MK MI MJ MP MQ 2 1 0,5 
MA MB MC 2 3 1
Mà MA  MB  MC   3MG  MD  ME  MF  MG  CA 2 4 0,5     1  a MD ME MF A C 4 4 5 1 (3,0đ)
Ta có: EF(4, 2) / / (2, 1) 0,25
Suy ra pt đường thẳng EF là:
x  2y  3  0 0,25
Gọi M là trung điểm BC suy ra M (x,1). 0,25
Chứng minh ME  MF  1 ( BC ) 0,5 2 2 2 2 2
Suy ra x  5  1  4  x  1  1  2  8x  32  0  x  4 0,5
Vậy tọa độ trung điểm BC là: M (4,1). 0,25 2
Gọi F’ đối xứng với F qua BC suy ra F '(1, 0). 0,25
Chứng minh DA là phân giác của góc EDF suy ra F’, D, E thẳng hàng 0,25
Pt EF’: x  y  1  0 Suy ra tọa độ điểm 0,25 D(2, 1). 2  2.1  3 1 1 Suy ra S
 d(D, EF ).EF  .2 5  3 0,25 DEF 2 2 5