Đề thi HSG tỉnh Toán 10 THPT năm 2018 – 2019 sở GD&ĐT Hải Dương

SỞ GD&ĐT QUẢNG TRỊ KỲ THI CHỌN HSG VĂN HÓA LỚP 10, 11
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Khóa thi ngày 03 tháng 4 năm 2019 Môn thi: Toán lớp 10
ĐỀ THI CHÍNH THỨC (Đề có 01 trang)
Thời gian làm bài: 180 phút, không kể thời gian giao đề
Câu I. (5,0 điểm) Cho Parabol (P): 2
y  x  bx  c .  1 5 
1) Tìm b,c để Parabol (P) có đỉnh S  ;   .  2 4 
2) Với b,c tìm được ở câu 1. Tìm m để đường thẳng  : y  2
 x  m cắt Parabol (P) tại hai điểm phân biệt ,
A B sao cho tam giác OAB vuông tại O (với O là gốc tọa độ).
Câu II. (6,0 điểm)
1) Tìm m để bất phương trình: 2
mx  2m  3 x  2m 14  0 vô nghiệm trên tập số thực.
2) Giải bất phương trình sau trên tập số thực:  2
x   x   2 2 4 2
x  5x  6  0. 2 3 2
x  x y  xy  xy  y 1
3) Giải hệ phương trình sau trên tập số thực :  4 2
x  y  xy  2x  1 1
Câu III. (6,0 điểm)
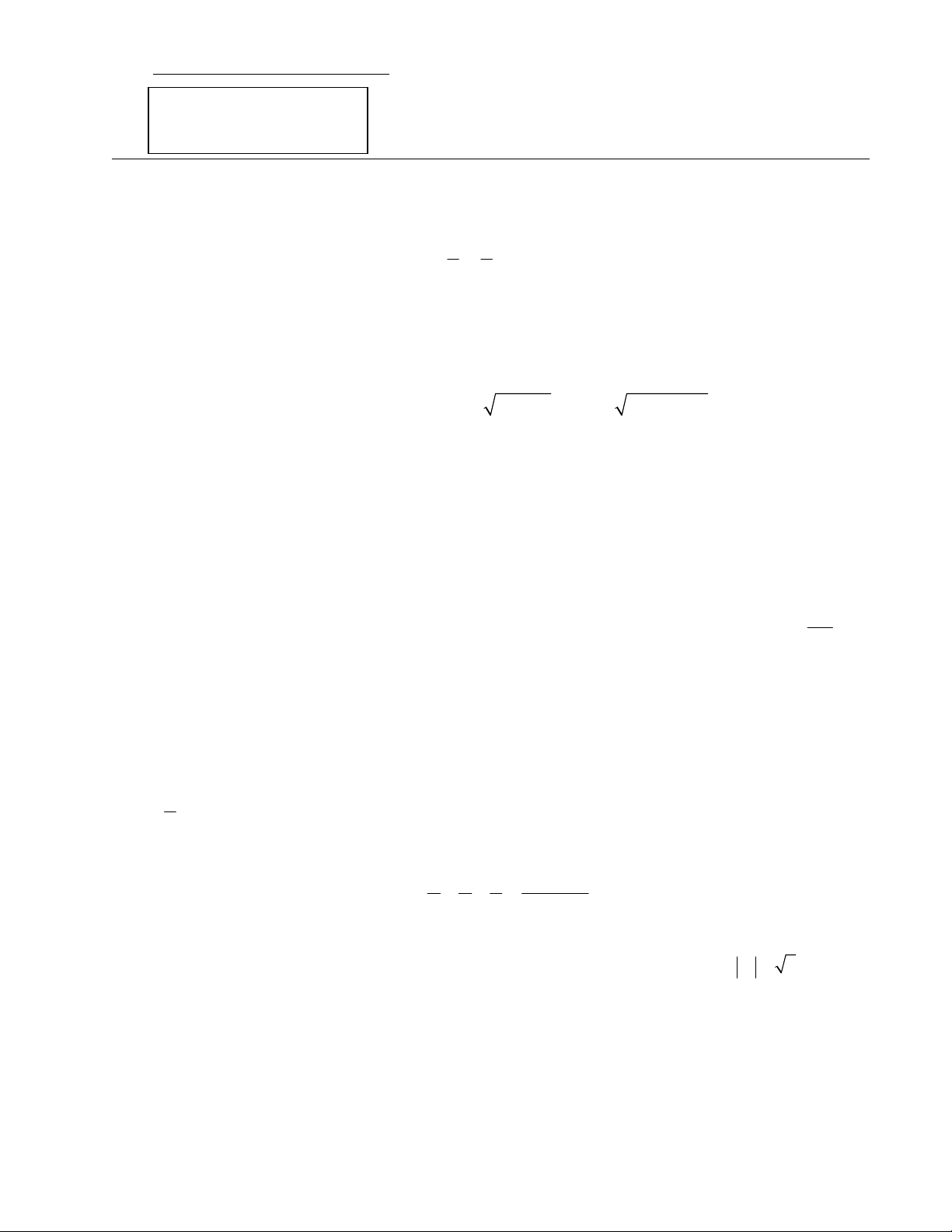
1) Cho tam giác ABC đều có độ dài cạnh bằng 3. Trên các cạnh BC, CA lần lượt lấy các điểm
N, M sao cho BN  1, CM  2.   
a) Phân tích véc tơ AN theo hai vectơ AB, AC. AP
b) Trên cạnh AB lấy điểm P, P  ,
A P  B sao cho AN vuông góc với PM. Tính tỉ số . AB
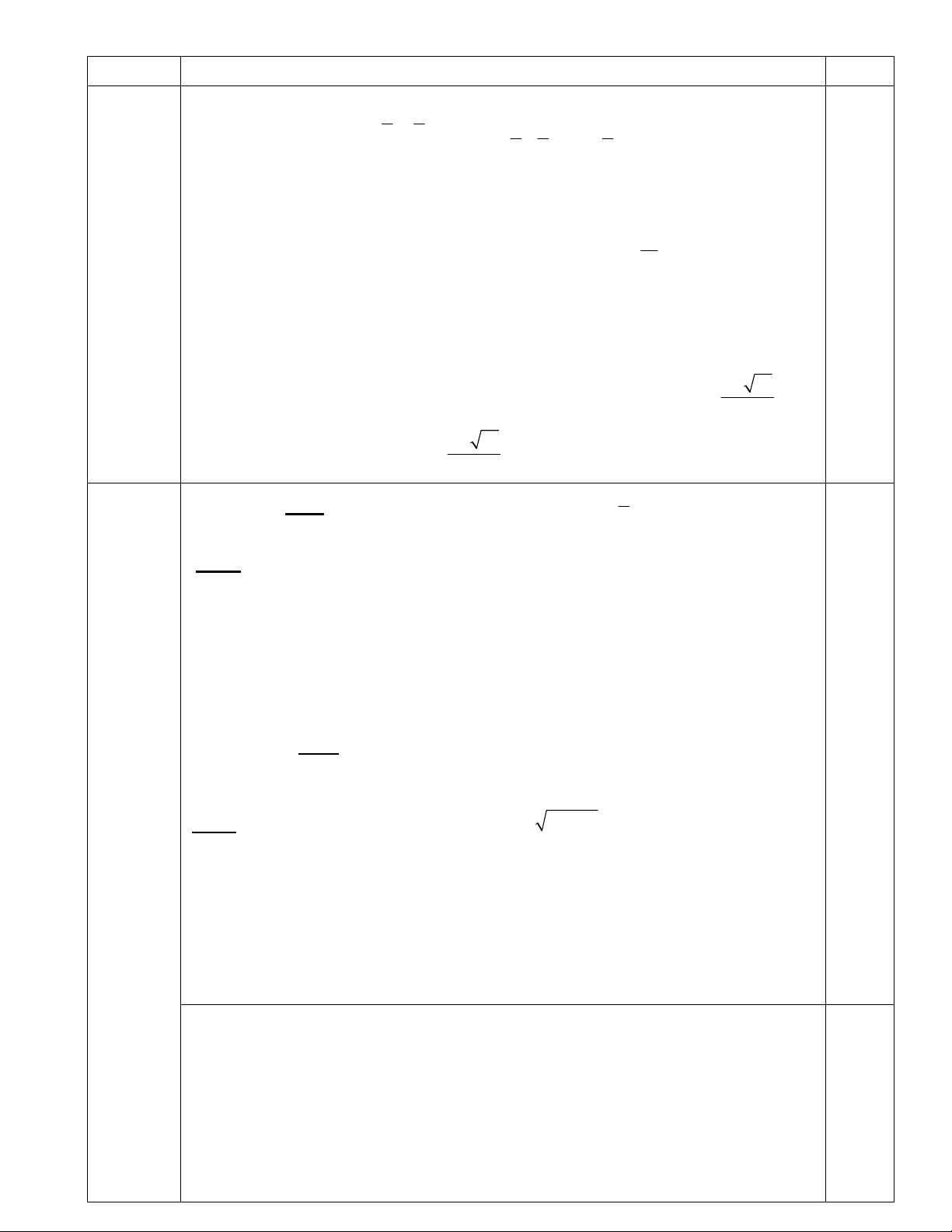
2) Trong mặt phẳng tọa độ Oxy , cho hình thang cân ABCD có hai đáy là AD, BC và AD  BC ,
biết rằng AB  BC, AD  7.Đường chéo AC có phương trình là x  3y  3  0 , điểm M  2;  5  
thuộc đường thẳng A .
D Tìm tọa độ đỉnh D biết đỉnh B 1;  1 .
Câu IV. (3,0 điểm)
1 ) Cho tam giác ABC có diện tích S và bán kính của đường tròn ngoại tiếp R thỏa mãn hệ thức 2 2 S = R  3 3 3
sin A  sin B  sin C . Chứng minh tam giác ABC là tam giác đều. 3
2) Cho x, y, z là các số thực dương thỏa mãn điều kiện 2 2 2
x  y  z  3. Chứng minh rằng x y z 9    . y z x
x  y  z
3) Cho đa thức   2018 2016 P x  x  mx
 m trong đó m là tham số thực. Biết rằng Px có 2018
nghiệm thực. Chứng minh rằng tồn tại một nghiệm thực x của P x thỏa mãn x  2. 0 0
---------------------HẾT---------------------
Thí sinh không được sử dụng tài liệu và MTCT.
Giám thị không giải thích gì thêm.
Họ và tên thí sinh:……………………………….Số báo danh:……………….
HƯỚNG DẪN CHẤM HSG 10 NĂM HỌC 2018-2019. CÂU NỘI DUNG ĐIỂM  b  / 2  1  / 2  1 5   b   1 2
1) (2,0 điểm). Đỉnh S  ; (P)    1 b 5    2 4    c    c  1   4 2 4
2) (3,0 điểm). Pt hoành độ giao điểm của (P) và  : 0,5 2 2
x  x 1  2
 x  m  x  3x  m 1  0 (*).  cắt (P) tại hai điểm phân biệt  PT(*) có hai nghiệm phân biệt 13
x , x    0  13  4m  0  m  ** 1 2 0,5 Câu I 4 (5,0 điểm) x  x  3 
Giả sử Ax ; 2
 x  m ; B x ; 2
 x  m theo Viet ta có 1 2 . 1 1   2 2  x x  m1 0,5  1 2
Ta có tam giác OAB vuông tại   1 21 O  .
OA OB  0  5x x  2m x  x  2 2
 m  0  m  m  5  0  m  . 0,5 1 2 1 2 2 1 21
Đối chiếu đk (**) ta có đáp số m  . 1 2 7
1) (2,0 điểm) TH 1: m  0 , bpt trở thành 6
 x 14  0  x  (không thỏa ycbt). 3 0,5
TH 2: m  0 , 2
mx  2m  3 x  2m 14  0 VN 2
 mx  2m  3 x  2m 14  0 CN 0,5 m  0 m  0 m  0 x           m  9.  2  '  0
m 8m  9  0 m  9  hoac m  1 1 Vậy m  9.  x  2
2) (2,0 điểm). TH1: 2
x  5x  6  0   0,5 x  3 x  2  0 x  2  Câu II TH 2: 2
x  5x  6  0   . Khi đó, bpt 2
 2x  4  x  2  x  2  0  0,5 x  3   (6,0 điểm) 2x  4   x  22 2 x  2  x  2    x  0  x  2   x  2   0,5    .   x  4 2
x 4x  0  x
  4  x  0 0,5
Vậy tập nghiệm bất phương trình S   ;0  2,  3 4; 2  
x  y  xy
x  x y  xy  xy  y    2 2 3 2
x  y  xy 1 1
3) (2,0 điểm) Hpt:    4 2 0,5
x  y  xy  2x   1  1  2  x  y  2  xy 1 Đặt 2
a  x  y,b  xy hệ thành 3 2
a  ab  b 1
a  a  2a  0
a  0 a 1 a  2           . 2 2 a  b 1 b  1 a b   1 b   0 b   3  0,5 a  0 2 x  y  0 +) Với  ta có 
 x  y  1. b   1 xy  1 a  1 2 x  y 1 +) Với  ta có    ; x y   0; 1,1;0, 1  ;0. b   0 xy   0 0,5  3 a  2  2 x  y  2 y     x  1  +) Với  ta có   x    . b   3  xy  3      x   y 1 
 2x  x3 3  0
Vậy hệ có 5 nghiệm  ; x y 
 1; 1,0; 1,1;0, 1  ;0, 1  ;3. 0,5   
 1   2  1 
1) (4,0 điểm) a) AN = AB  BN = AB   AC  AB  AB + AC 2,0 3 3 3    1  x 
b) Đặt AP  x,0  x  3 . Ta có PM = PA  AM  AC - AB 0,5 3 3   
2  1    1  x  
AN  PM  AN.PM  0  AB  AC . AC  AB  0      3 3   3 3  0,5
2   2x 2 x   1 2  A . B AC  AB  .
AB AC  AC  0 9 9 9 9 x 4
 1 2x  1  0  x  2 5 0,5 Vậy AP 4  . AB 15 0,5
2) (2,0 điểm). Do ABCD là hình thang cân
nên ABCD là hình thang nội tiếp đường tròn
tâm O.Do AB  BC  CD  AC là đường Câu III
phân giác trong góc BAD  . Gọi E là
(6,0 điểm) điểm đối xứng của B qua AC, khi đó
E thuộc AD. Ta có BE  AC
và BE qua B 1;  1 nên phương trình
BE: 3x  y  4  0 . 0,5
Gọi F  AC  BE  tọa độ F là nghiệm của
x  3y  3  0  3 1 Hệ    F ;
. Do F là trung điểm 3  x y 4 0       2 2 
Của BE  E 2; 2  . Do M  2;  5
  AD  phương trình AD: 3x  4y 14  0.
x  3y  3  0 0,5
Do A  AD  AC  tọa độ A là nghiệm của hệ   A6;  1 . 3
 x  4y 14  0
Do D  AD  D 2  4t;2  3t và  12   58 26  t  D ;      
AD  7  4t  42  3t  32 5 5 5  49     0,5 2     2 16 t   D ;   5     5 5 
Do B,D nằm khác phía với đường thẳng AC nên kiểm tra vị trí tương đối của điểm
B và hai điểm D ta có đáp số  2 16  D ;    5 5  0,5 3 3 3
1) (1,0điểm). Theo định lí sin ta có : a B c 3 3 3 sin A  ; sin B  ;sin C  3 3 3 8R 8R 8R 3 3 3 3 3 3 2  a b
c  a  b  c 2 VT = R      0,5 3 3 3 3  8R 8R 8R  12R
Áp dụng bắt đẳng thức cô – si ta có: 3 3 3
a  b  c  3abc  abc VT  4R abc Mà S 
, dấu “ =” xảy ra khi và chỉ khi a = b = c  ABC đều 4R 0,5 x y z x y z
x  y  z2 2 2 2
2) (1,0 điểm). Ta có       . y z x xy yz zx
xy  yz  zx
x  y  z2 9 Câu IV Ta cần chứng minh: 
 x  y  z3  9xy  yz  zx *. 0,5
xy  yz  zx
x  y  z (3,0 t  điểm).
Đặt t  x  y  z   t   2 3 , 3
3  xy  yz  zx  . BĐT * thành 2 9 2t 3 0,5 t   t  32 3
2t 3  0 (luôn đúng). 2
3) (1,0 điểm). Ta có P   1  1, P  
1  1. Giả sử các nghiệm thực của P  x là
a , a ,..., a
, tức là P x  x  a x  a ... x  a . 1   2   2018  1 2 2018 Khi đó, P  
1  1 a 1 a ... 1 a  1, 1   2   2018  0,5 P  
1  1 a 1 a ... 1   a  1 hay P  
1  1 a 1 a ... 1 a  1 1   2   2018  1   2   2018  Suy ra P   1 .P   1   2 1 a  2 1 a ... 2 1 a
1. Suy ra tồn tại k 1,2,...,  2018 1 2 2018  0,5 sao cho 2
a 1  1  a  2. Hay tồn tại nghiệm x : a thỏa mãn điều kiện k k 0 k x  2. 0
HƯỚNG DẪN CHẤM HSG 10 NĂM HỌC 2017-2018. CÂU NỘI DUNG ĐIỂM Câu I  b  a  a  2
1. Đỉnh S    / 2 2 1 2; 1  (P)    
4a  2b  3  1  b   4  5,0 điểm
2 . Pt hoành độ giao điểm của (P) và  : 2 2
x  4x  3  kx  4  x  k  4 x 1  0 (*). PT(*) có ac  1  nên k
 pt luôn có hai nghiệm phân biệt x , x và theo Viet ta có 1 2
x  x  k  4 . Khi đó tọa độ M, N là M  x ;kx  4 , N x ;kx  4 . 1 1   2 2  1 2
 x  x k(x  x )
Gọi I là trung điểm MN ta có tọa độ  1 2 1 2 I ;  4   hay  2 2  2
 k  4 k  4k  8  I  ; . Theo ycbt ta có: 2 2   2
 k  4 k  4k  8  2 I  ;
 d  k  3k  4  0  k 1 k  4  . 2 2   2 2 2 2 Câu II
1. Bpt: x  2m  
1 x  2  2m  0 VN  x  2m  
1 x  2  2m  0 có
6,0 điểm nghiệm x
      0 (vì a=-1<0) 2
 m  2m  3  0  m  1
  m  3. 2
x  2x  0
x  0  x  2 x  0  2. Bpt  2  x 4x 3 2 2 x 2x 0    
  x  2x  0
 x  0  x  2  x  2.     2
x  4x  3  0
x 1 x  3 x  3 
Vậy tập nghiệm bpt S   ;0    2 3:  . 2
x y  2y  x  4xy  3. Hệ phương trình  1 1 x    3  2  x xy y
Điều kiện x  0, y  0 . 2 1
Chia hai vế của (1) cho xy ta có phương trình x    4 . x y 1 1 x 1  1 1  x 1  1 1   1 1     3     3    x   4 2       x xy y
x  x y  y x  x y   y x   1  1 1   x    4     x  y x   2 1  1   1 1   1 x    4   x     4     x   2 x y   x  x y      x Ta có hệ       1   1 1  1 1   1  1 1  x    4    2    x    4  x   y x            x y x  y x   1 2 x   2
x  2x 1  0  x  x  1    1 1  1 1    2     y  1 2  x y  x y Câu III 1a.
   
3AG  AN  AM  AB 
      6,5 điểm 1 1
 AD   AD  AC  5 1
 AB  AD  AC  AB A B 3 2 6 2 N
5  1     
 AD   AB  AD  3 4
 AB  AB  AD G 6 2 2 3 K D  M C
1  4 
 AG  AB  AD 2 9  
      
1b. Đặt BK  xBC  AK  AB  BK  AB  xBC  AB  x AD Ba điểm ,
A G, K thẳng hàng nên    
 1  4    
m  4m 
AK  mAG  AB  x AD  m
AB  AD  AB  x AD  AB  AD    2 9  2 9  m 1  m  2  2      8 4m x  x    9  9  8  BK 8
 BK  BC   9 BC 9
x  y  4  0 2. Pt MN:  5 3 
x  y  4  0. Tọa độ P là nghiệm của hệ:   P ; . x y 1 0       2 2 
Vì AM song song với DC và các điểm A,B,M,N cùng thuộc một đường tròn nên ta có: P  AM  PCD   A  BD   . AMP Suy ra PA = PM
Vì A AC : x  y 1  0 nên A ; a a   1 , a  2. Ta B có: M 2 2 2 2  5   5   5   5  a  0 N a   a      A0;          1.  2   2   2   2  a  5 A P C
Đt BD đi qua N và vuông góc với AN nên có pt:
2x  3y 10  0 . Đt BC đi qua M và vuông góc với D
2x  3y 10  0
AM nên có pt: y  4  0 . Tọa độ B là nghiệm của hệ:   B  1  ;4 y  4  0 . Câu IV 1a. 1 1 1 1 1 1 1 1 1
x  y  z  xyz     1 (1)       1 yz xz xy 2 2 2 x y z xy yz xz     2,5 điểm          1 1 1 1 1 1
1b. P= x 1 y 1 y 1 z 1 z 1 x 1   -      (3 ) 2 2 2     y z x 2 2 2
 x y z   x y z 
x 1  y 1
y 1  z 1 z 1  x 1   2 2 2 Ta có: y z x  1 1   1 1   1 1  = x   1   y 1   z 1   2 2    2 2    2 2   x y   y z   x z 
 x   2   y   2  z   2 1 1 1 (4) xy yz xz 1 1 1 1 1 1  1 1 1 
Từ ( 3) và (4) suy ra P        2   (5) 2 2 2   x y z x y z  xy yz zx  2  1 1 1   1 1 1  1 1 1    3       3     (6)  x y z   xy yz zx  x y z
Từ (1), (2), (5) và ( 6)  P  3 1 . Dấu bằng xảy ra khi x  y  z  3 .
Vậy giá trị nhỏ nhất của P bằng 3 1 .
2. Gọi x là nghiệm của phương trình x  0 0 0 1 1 4 3 2 2
x  ax  bx  cx  1  0  b  x   ax  c . 0 0 0 0 0 2 0 x x 0 0 2  1  1  1       1  2 2 2
a  b  c  2 2 2 2 2  x 
1  a  c  x   ax  c    x  1 0  2 0 2 0 0 2 x  x x  x  0   0 0   0    2 2  1 1 1   1  2 2
 ax  c  x   ax  c    x  0 0  2 0 0 2 x x x x  0 0 0   0  2   2 1  x     x   t 2 2 2 1
a  b  c  0 2 2 0   , với 2 t  x   2 0 2 2 1 t 1 x  1 x0 0 2 x0 2 t 4 Mặt khác 2
  3t  4t  4  0  t  23t  2  0 Vì t  2 nên t 1 3
t  23t  2  0  Vậy 4 2 2 2
a  b  c  , dấu bằng xảy ra khi 2
a  b  c 
( ứng với x 1 ) hoặc 3 3 0 2 2
a  c  ,b   ( ứng với x  1  ). 3 3 0