Đề thi HSG Toán 10 lần 2 năm 2020 – 2021 trường THPT Đồng Đậu – Vĩnh Phúc

TRƯỜNG THPT ĐỒNG ĐẬU
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG LẦN 2 NĂM HỌC: 2020 - 2021 Số báo danh
Môn thi: TOÁN - Lớp 10 THPT ………………………
Thời gian: 180 phút (không kể thời gian giao đề)
Đề thi có 01 trang - gồm 10 câu 10  x 1
Câu 1. Tìm tập xác địnhcủa hàm số y   5  x 2 2
Câu 2. Cho phương trình  2 x  ax    a 2 1 x  ax   1 1  0   1 với a là tham số.
a. Giải phương trình với a  2  b. Khi phương trình  
1 có nghiệm thực duy nhất. Chứng minh rằng a  2 .
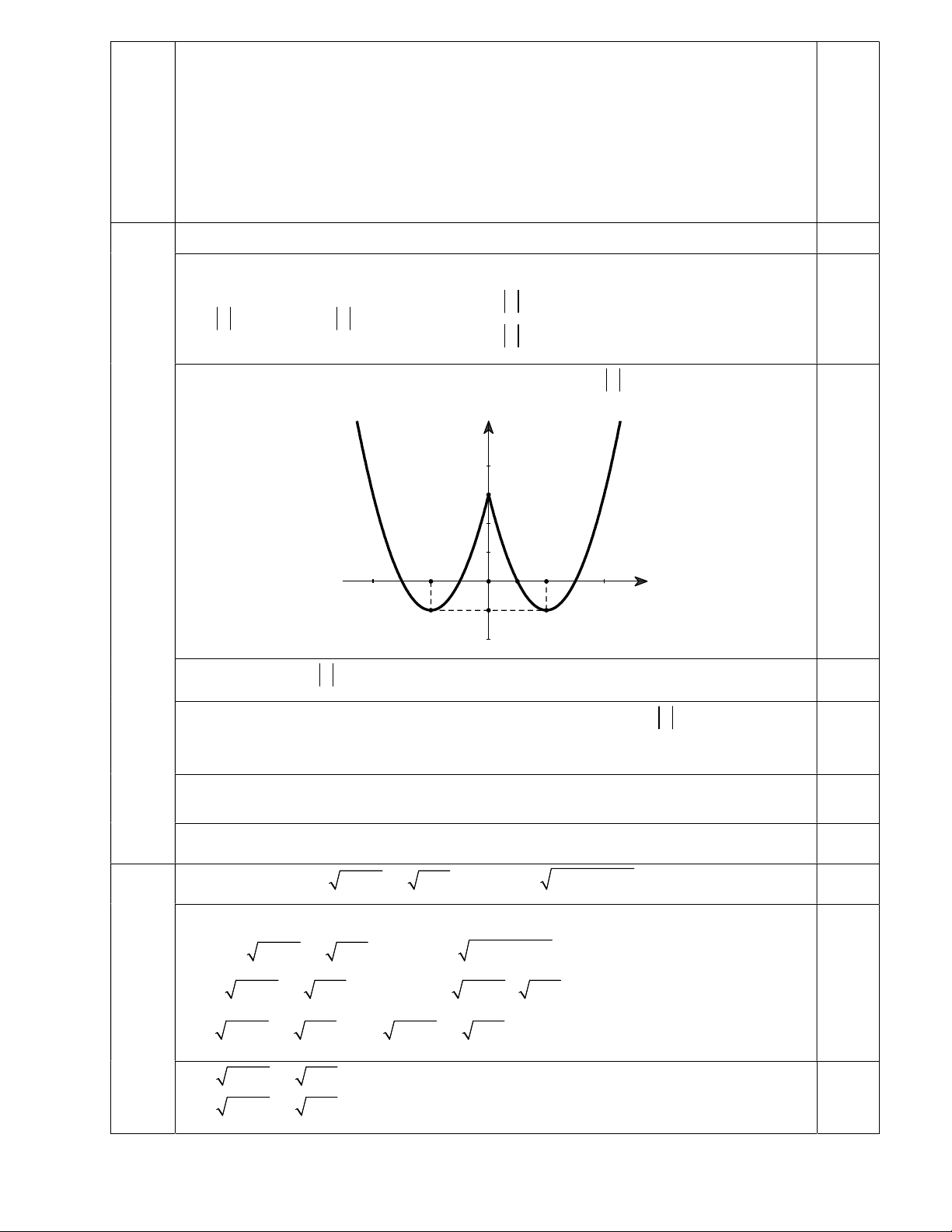
Câu 3. Cho hàm số    2 y
f x  ax  bx  c có đồ thị như hình vẽ bên. y
Tìm các giá trị nguyên của tham số m để phương trình 2
f  x   m  2 f  x   m  3  0 3 có 6 nghiệm phân biệt
Câu 4. Giải phương trình 2 3 O 1 2
3 3x  2  6 x 1  7x 10  4 3x  5x  2  0 x -1
Câu 5. Giải bất phương trình x  2  2  2x  5  x 1. 2 2 3
5x y  4xy  3y  2(x  y)  0
Câu 6. Giải hệ phương trình:  2 2 x  y  2
Câu 7. Cho hình chữ nhật ABCD có AB  2AD , BC  a . Tính giá trị nhỏ nhất của độ dài vectơ    
u  MA  2MB  3MC , trong đó M là điểm thay đổi trên đường thẳng BC .
Câu 8. Cho tam giác ABC vuông tại A , G là trọng tâm tam giác ABC . Tính độ dài cạnh AB biết cạnh  
AC  a , và góc giữa hai véc tơ GB và GC là nhỏ nhất.
Câu 9. Cho tam giác ABC cân tại A , nội tiếp đường tròn tâm O . Gọi D là trung điểm của AB , E là
trọng tâm tam giác ADC . Chứng minh rằng OE  CD . 1 x(1 1 x) 5 Câu 10. Với x  0; 
1 , hãy tìm giá trị nhỏ nhất của biểu thức P   . x 1 x
---------------------Hết------------------
Thí sinh không được sử dụng máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm. SỞ GD&ĐT VĨNH PHÚC
ĐÁP ÁN ĐỀ THI HSG LẦN 2 CẤP TRƯỜNG
TRƯỜNG THPT ĐỒNG ĐẬU
NĂM HỌC 2020-2021 MÔN TOÁN 10 Có 06 trang Câu Nội dung Điểm 10  x 1
Tìm tập xác địnhcủa hàm số y   2,0 5  x 2 10  x 1
Hàm số xác định khi và chỉ khi   0 5  x 2 0,5 10  x 1 1    0 Hoặc  5  x 2 x  5  0 20  2x  5  x 3(5  x) 
 5  x5  x  0   0   0   . 0,5 2(5  x) 2(5  x) x  5  0  5   x  5 0,5
Vậy tập xác định của hàm số là D  ( 5  ;5]. 0,5 2 Cho phương trình  2 x  ax    a 2 1 x  ax   1 1  0   1 với a là tham số.
a, Giải phương trình với a  2  2,0 b, Khi phương trình  
1 có nghiệm thực duy nhất. Chứng minh rằng a  2 . a, với a  2  phương trình   1 thành x 2x 2 2 1  2 2 x  2x   1 1  0 0,5  x  4 1  2 x  2 1 1  0  x  2 1  1 2 x  0 0,5  x  2 2 b, Xét phương trình  2 x  ax    a 2 1 x  ax   1 1  0   1 Đặt 2
t  x  ax 1, khi đó 2
x  ax 1 t  0 2 và phương trình đã cho trở thành: 2 t  at 1  0 3. 0,5 Phương trình  
1 có nghiệm khi a và t thỏa mãn: 2 a  4  0 và 2 a  4  4t  0 . 2
a  4  0  a  2 hay a  2 . Nếu a  2
 thì 3 có nghiệm t  0, khi đó 2
a  4  4t  0, suy ra 2 có hai nghiệm
phân biệt, mâu thuẫn với giả thiết   1 có nghiệm duy nhất.
Nếu a  2 thì phương trình 3 có nghiệm t  1, khi đó điều kiện 2 a  4  4t  0 không 0,5 được thỏa mãn. Vậy a  2 . 2,0 Ta có:  f  x   1 0,5 2
f  x   m  2 f  x   m  3  0   .  f   x   3  m
Từ đồ thị hàm số y  f  x ta suy ra đồ thị hàm số y  f  x  như sau: y 3 0,5 3 x O 1 -1
+ Phương trình f  x   1
 có hai nghiệm phân biệt 0,25
Để phương trình đã cho có 6 nghiệm phân biệt thì phương trình f  x   3  m phải có 0,25 4 nghiệm phân biệt  1
  3  m  3  0  m  4. 0,25
Kết hợp m là số nguyên nên m 1;2;  3 . 0,25 Giải phương trình: 2
3 3x  2  6 x 1  7x 10  4 3x  5x  2  0 2,0 ĐKXĐ: x  1 Ta có: 2
3 3x  2  6 x 1  7x 10  4 3x  5x  2  0 0,5 4
 3 3x  2  2 x 1  3x  2 2. 3x  2.2 x 1  4x   1  4  0
  3x  2  2 x 12  3 3x  2  2 x 1  4  0  3x  2  2 x 1 1   0,5
 3x  2  2 x 1  4 (VN)
 3x  2  2 x 1  1 3 x   1   2 x 1  0 3x  2 1 0,5  3 x 1   x 1  2  0   1  3x 2 1      3 x 1 Vì
 2  0  x 1 nên  
1  x 1  0  x  1 (thỏa mãn). 3x  2 1 0,5
Vậy phương trình đã cho có nghiệm duy nhất x  1 .
Giải bất phương trình x  2  2  2x  5  x 1. 2,0 5
Điều kiện xác định: x  . 2 0,5
Bất phương trình tương đương: x 2  x 1  2x5  2.
 2x12 (x2)(x 1)  2x 1  4 2x5. 0,5 5 x  6 2
 x 9x 18  0   .  0,5 x  3  x  6 2
 x 9x 18  0   .  x  3  0,5 5
Vậy nghiệm của bất phương trình là x  6 hoặc  x  3. 2 2 2 3
5x y  4xy  3y  2(x  y)  0
Giải hệ phương trình:  2,0 2 2 x  y  2  2 3 2 2 5
 x y  4xy  3y  (x  y )(x  y)  0 Hệ đã cho   0,25 2 2 x  y  2  2 3 3
4x y  5xy  2y  x  0 (*)   2 2 x  y  2 6 0,25 y
Ta thấy x = 0 không là nghiệm của hệ nên từ PT (*) đặt: t  ta được PT: x t 1 3 2 2t 5t 4t 1 0       1  0,25 t   2 y  x x 1 x  1 Khi t = 1 ta có:      0,5 2 2 x  y  2 y 1  y  1  2 2  2 2  1 x  x   1  y  x  5  5 Khi t  ta có:  2     0,5 2 2 2   2  2 x  y  2 y  y    5    5      
Vậy hệ đã cho có 4 nghiệm  x; y là      2 2 2 2 2 2 1;1 ; 1; 1 ; ; ; ;  0,25 5 5 5 5    
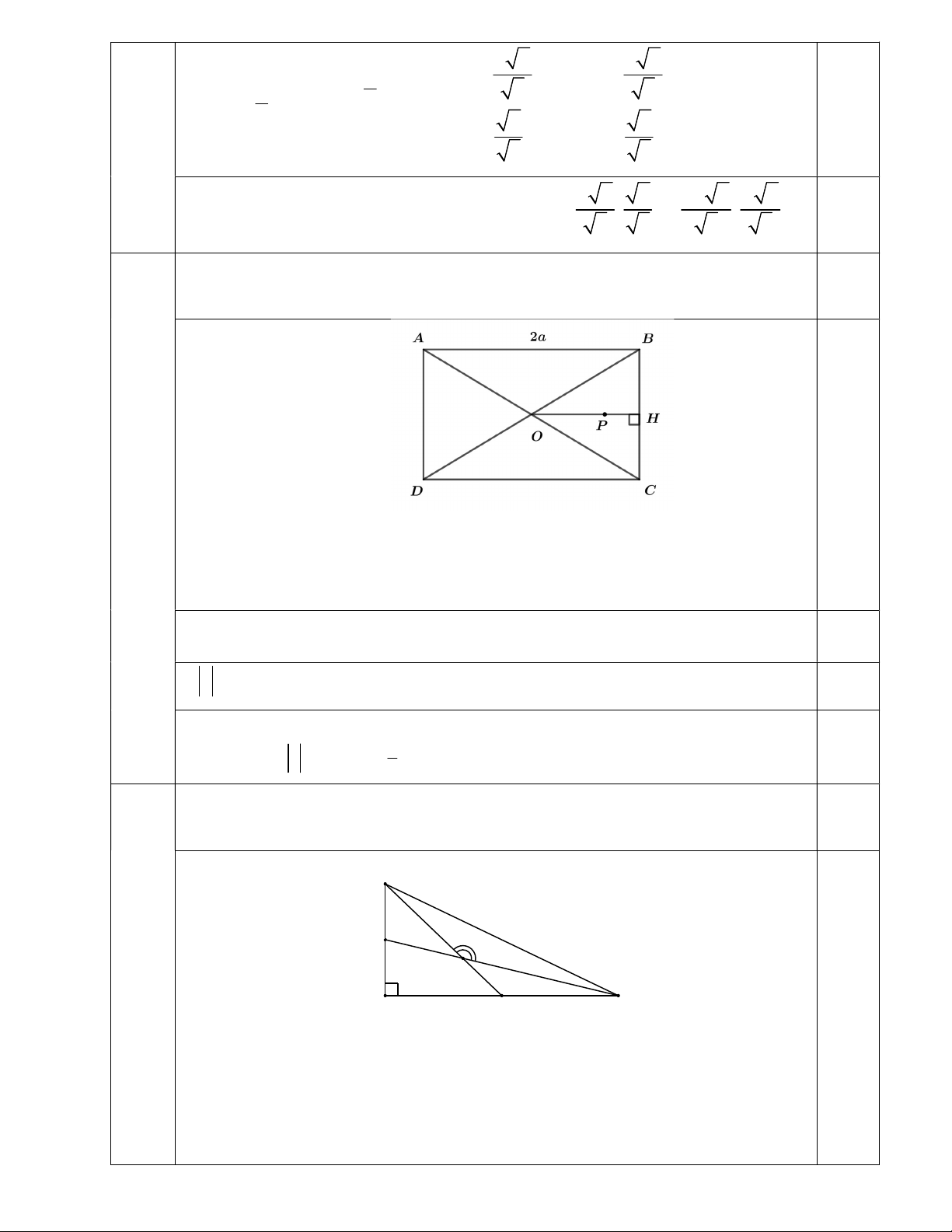
Cho hình chữ nhật ABCD có AB  2AD , BC  a . Tính giá trị nhỏ nhất của độ dài     2,0
vectơ u  MA  2MB  3MC , trong đó M là điểm thay đổi trên đường thẳng BC . 0,5 7 AB  2 AD  2BC  2a .
AC  BD  0 (trung điểm của AC , BD ).  
     
u  MA  2MB  3MC  MA  MC  2MB  2MC
   
 2MD  2MB  2MC  6MP (với P là trọng tâm OBC ). 0,5
u 6MP PM BC tại M . min 0,5 min
Vì OBC cân tại O , nên P thuộc trung tuyến OH và  1 0,5
min u  6PH  6. OH  2Oh  2a (Khi M  H ). 3
Cho tam giác ABC vuông tại A , G là trọng tâm tam giác ABC . Tính độ dài cạnh AB   2,0
biết cạnh AC  a , và góc giữa hai véc tơ GB và GC là nhỏ nhất. B K α 8 G A C 0,5 D
Gọi K, D lần lượt là trung điểm A , B AC .  
Gọi  là góc giữa hai véc tơ GB và GC .     Ta có: cos  cosG , B GC  cosD , B KC . .
   
    BA  BCCA  CB DB KC BD CK     D . B KC B . D CK 4B . D CK
      0,5 B . A CA  B . C CA  BA 2  BC 2 BC    ( Do BA  CA ) 4B . D CK 2B . D CK 1     B .
D CK  BD  CK  BA  BC2 1 2  CA  CB2 2 2 4 4 1     2 2 2
  AB  AC  2BC  2B . A BC  2C . A CB 4   0,5 1 2 2 2 2 2
  AB  AC  2BC  2BA  2CA  4 
 (Theo công thức hình chiếu véc tơ) 5 2  BC . 4 4
Suy ra cos   . Dấu bằng xảy ra khi BD  CK  AB  AC  a . 5 0,5 4
Ta có góc  nhỏ nhất khi cos lớn nhất bằng  . Khi đó AB  a . 5
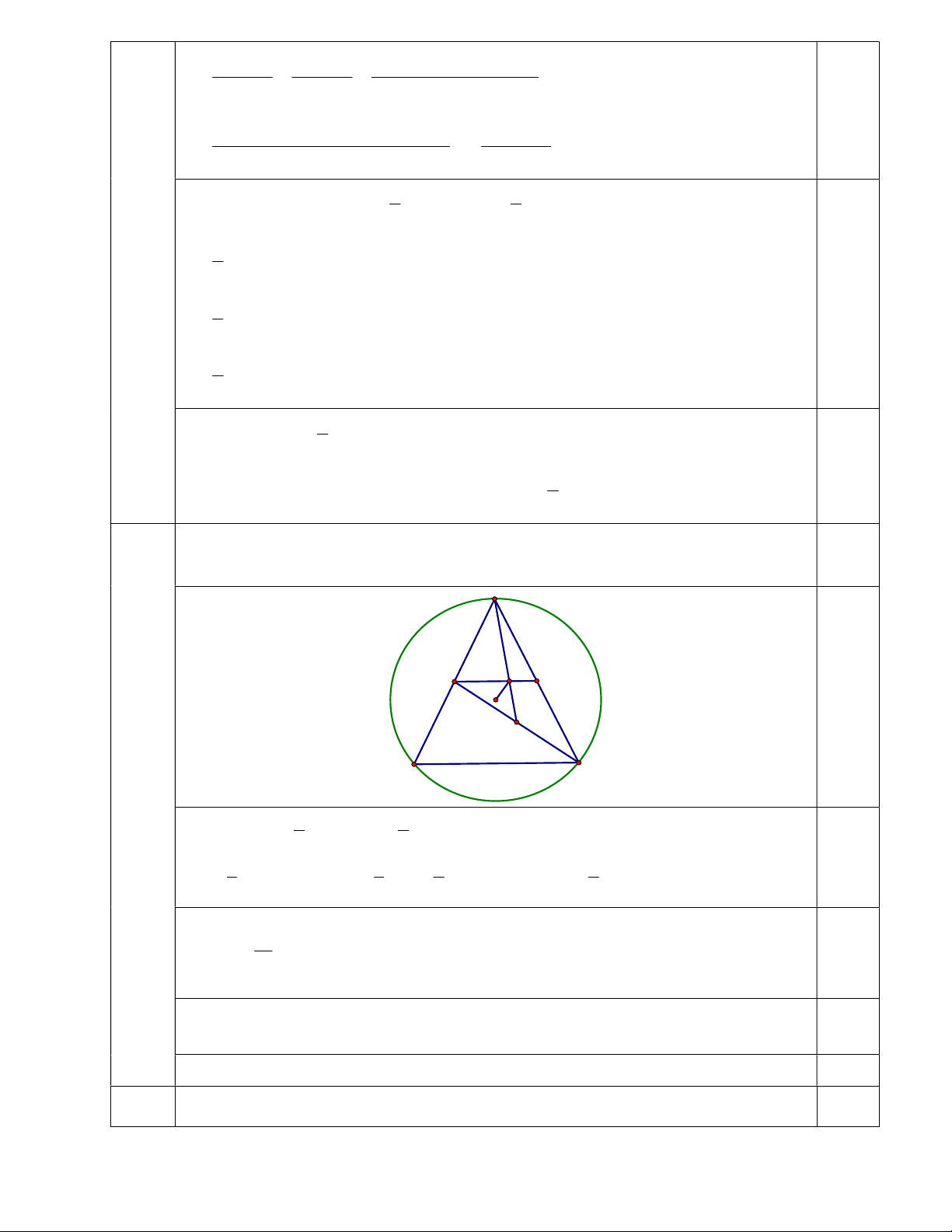
Cho tam giác ABC cân tại A , nội tiếp đường tròn tâm O . Gọi D là trung điểm của AB 2,0
, E là trọng tâm tam giác ADC . Chứng minh rằng OE  CD A E D O B C 9
 1   1   
Ta có: CD  CA  CB  OA  OB  2OC 2 2  0,5
1     
       OE  OA OD  OC 1 1  OA   OAOB 1  OC   3OAOB2OC 3 3  2  6 Do đó:
  1       C . D OE 
OAOB2OC.3OAOB2OC 0,5 12  
    2 2 2  12C .
D OE  3OA  OB  4OC  4O . A OB  4O . A OC  
      12C .
D OE  4.OAOB OC  4.O . A CB  0 0,5 (Vì A
 BC cân tại A có O là tâm đường tròn ngoại tiếp nên OA  BC )   Do đó C .
D OE  0  CD  OE (điều phải chứng minh) 0,5 10 Với x  0; 
1 , hãy tìm giá trị nhỏ nhất của biểu thức 2,0 1 x(1 1 x) 5 P   . x 1 x t 5 t 51 t
Đặt t  1 x , 0  t  1 ta được P      5 0,5 1 t t 1 t t t 51 t
Áp dụng BĐT Cô si, ta có P    5  2 5  5 . 0,5 1 t t 5  5
Dấu “=” xảy ra khi và chỉ khi t  . 0,5 4 7  5 5
Vậy MinP  2 5  5 khi x  0,5 0;  1 8
---------------------Hết------------------