Đề thi HSG Toán 6 vòng 2 năm 2023 – 2024 trường THCS Trần Mai Ninh – Thanh Hóa

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 6 đề thi học sinh giỏi cấp trường môn Toán 6 vòng 2 năm học 2023 – 2024 trường THCS Trần Mai Ninh, tỉnh Thanh Hóa; đề thi có đáp án và hướng dẫn chấm điểm.

71 36 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 6

Môn: Toán 6

Thông tin:

4 trang 6 tháng trước

Tác giả:

Profile M. Hậu
1
UBND TP THANH HOÁ
TRƯỜNG THCS TRẦN MAI NINH
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
TOÁN 6 VÒNG II NĂM HỌC 2023 - 2024
Ngày thi 29 tháng 03 năm 2024
Thời gian làm bài 120 phút (không kể thời gian giao đề)
Đề thi có 01 trang
Câu 1. (4,0 điểm):
1. Tính bằng cách hợp lí: a)
( 1011) 1,04 20,22.( 48)A
=− ⋅+ −
b)
15 6 4 20 7
10 18 29 9
5.4 27 4 3 8
15.2 6 7.2 9
B
⋅ −⋅ ⋅
=
⋅− ⋅
2. So sánh: 71
130
và 37
175
Câu 2. (4,0 điểm): Tìm x biết:
1)
5 9 44 44 44
4
44 44 5
12 20 30 44 6
x. .
1 2514

+ ++++ =−


2)
x137x137
chia hết cho 13
Câu 3. (4,0 điểm):
1. Tìm hai số tự nhiên có bội chung nhỏ nhất của hai số đó bằng 432 và ước
chung lớn nhất của chúng bằng 6.
2. Một hộp có 30 quả bóng xanh, 50 quả bóng đỏ và một số quả bóng vàng,
các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong
hộp thì cơ hội xuất hiện quả bóng vàng là
3
11
. Tính số quả bóng vàng.
Câu 4. (6,0 điểm):
1. Có 50 điểm phân biệt trong đó có đúng 10 điểm thẳng hàng. Vẽ được bao
nhiêu đường thẳng đi qua hai trong 50 điểm đó.
2. Cho đoạn thẳng DH = 10cm. Vẽ điểm C thuộc đoạn thẳng DH sao cho
CH = 4cm. Gọi M, N lần lượt là trung điểm của DC và CH.
Câu 5. (2,0 điểm): Cho các số nguyên dương a, b, c thỏa mãn
và
2
2( )a bc= +
. Tính giá trị của biểu thức T = a
3
+ b
2023
+ c
2024
--------------- Hết ---------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh …………………………………….Số báo danh………
a) Tính độ dài đoạn thẳng MN.
b) Vẽ các hình vuông CDAB và CHGE.
Tính diện tích tam giác DBG.
G
E
B
A
N
M
D
C
H
ĐỀ CHÍNH THỨC
2
UBND TP THANH HOÁ
TRƯỜNG THCS TRẦN MAI NINH
HƯỚNG DẪN CHẤM THI
HỌC SINH GIỎI CẤP TRƯỜNG TOÁN 6 VÒNG II
NĂM HỌC 2023 – 2024
Câu
Hướng dẫn chấm
Điểm
1
(4,0đ)
1. Tính bằng cách hợp lí: a)
( 1011) 1,04 20,22.( 48)A =− ⋅+ −
b)
15 6 4 20 7
10 18 29 9
5.4 27 4 3 8
15.2 6 7.2 9
B
⋅ −⋅ ⋅
=
⋅− ⋅
2,5
1.a)
( 1011) 1,04 20,22.( 48)A
=− ⋅+ −
( 1011) 1,04 ( 2022).0,48=− ⋅ +−
( 1011) 1,04 1011.( 0,96)=− ⋅+ −
( )
( 1011) 1,04 0,96=−⋅+
( 1011) 2=−⋅
2022= −
0,5
0,5
15 6 4 20 7
10 18 29 9
30 18 8 20 21
10 18 18 29 18
29 18
28 19
5.4 27 4 3 8
)
15.2 6 7.2 9
5.2 .3 2 .3 .2
3.5.2 .2 .3 7.3.2 .3
2 .3 (10 9)
2
2 .3 (15 14)
bB
⋅ −⋅ ⋅
=
⋅− ⋅
−
=
−
−
= =
−
0,75
0,75
2. So sánh: 71
130
và 37
175
1,5
2) Ta có:
130 130
130 390 260 350 260 40
175 175
175 350 350 350 260 90
90 40 175 175 130 130
71 72
72 2 .3 2 .3 .2
37 36
36 2 .3 2 .3 .3
3 2 37 36 72 71Vì nên
<
= =
>
= =
> >>>
Vậy 71
130
< 37
175
0,5
0,5
0,5
2
(4,0đ)
1. Tìm x biết:
5 9 44 44 44
4
44 44 5
12 20 30 44 6
x. .
1 2514

+ ++++ =−


2,0
Ta có:
4
5 9 11111 5
44.
12 20 3 6
..
14
214 04 5

+ ++++ =−


x
4
55
..
14 14 4
..
1
9 1111111111
44.
3445566778
5 9 11 5
4
4 14 4
. ..
14 14 2
9
4.
38
5 55
44
4

+ −+−+−+−+− =−



+ −=−


+=−
x
x
x
8
.
14 4
.
1
5 165 5
28
5 35 165
824 2
+=−
=−−
x
x
5
: 20
1
10
14 4
0
=−=−x
. Vậy x = - 20
0,25
0,25
0,25
0,25
0,25
0,25
0,25
3
2. Tìm x biết:
x137x137
chia hết cho 13.
2.0
6 4 2 62
137 137 13.10 7 .10 13.10 7 13.(10 10 ) 7 .10001B xx x x x= = + + += + +
10001 không chia hết cho 13 => B
13 Khi
x7
13
=> x = 8
Vậy x = 8
1.0
0,75
0,25
3
(4,0đ)
1. Tìm hai số tự nhiên có bội chung nhỏ nhất của hai số đó bằng 72 và
ước chung lớn nhất của chúng bằng 6.
2,0
Gọi hai số cần tìm là a, b
( )
ab≤
Ta có: ab = ƯCLN(a, b); BCNN(a, b) nên ab= 2592.
Đặt
6, 6
a mb n= =
với ƯCLN(m, n) = 1 và
( ;, )m n mn N≤∈
36 2592 72mn mn⇒ = ⇒=
Mà m, n nguyên tố cùng nhau nên
Ta được:
m
n
a
B
1
72
6
432
8
9
48
54
Vậy hai số cần tìm là (6; 432) và (48; 54)
0,5
0,5
0,25
0,5
0,25
2. Một hộp có 30 quả bóng xanh, 50 quả bóng đỏ và một số quả bóng
vàng; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu
nhiên một quả bóng trong hộp thì cơ hội xuất hiện quả bóng vàng là
3
11
. Tính số quả bóng vàng.
2,0
Tổng số quả bóng xanh, đỏ chiếm
3
1
11 11
8
−=
(tổng số bóng).
Số bóng trong hộp là
( )
0
8
30 50 : 11
11
+=
(quả).
Số bóng vàng là
3
110 30
11
⋅=
(quả).
0,5
0,75
0,75
1. Có 50 điểm phân biệt trong đó có đúng 10 điểm thẳng hàng. Vẽ được
bao nhiêu đường thẳng đi qua hai trong 50 điểm đó.
2,0
Với 50 điểm mà không có 3 điểm nào ta vữ được số đường thẳng là:
(50 1).50
1225
2
−
=
(đường thẳng)
Vì có 10 điểm thẳng hàng nên qua 10 điểm đó ta chỉ vẽ được 1 đường
thẳng và số đường thẳng giảm đi là :
(10 1).10
1 44
2
−
−=
(đường thẳng)
Vậy với
50 điểm trong đó có đúng 10 điểm thẳng hàng là
1225 – 44 = 1181 (đường thẳng)
0,75
0,75
0,5
2. Cho đoạn thẳng DH = 10cm. Vẽ điểm C thuộc đoạn thẳng DH sao
cho CH = 4cm. Gọi M, N lần lượt là trung điểm của DC và CH.
a) Tính độ dài đoạn thẳng MN.
b) Vẽ các hình vuông CDAB và CHGE.
4,0
4
Tính diện tích tam giác DBG.
4
(6,0đ)
Vì C nằm giữa M và N nên MC +CN = MN
Thay CM = 3cm, CN = 2cm ta có MN = 3 + 2 = 5(cm)
Vậy MN = 5 cm
a) Vì C nằm giữa D và H nên
CD +CH = DH
Mà DH = 10cm, CH = 4cm
nên DC = DH – CH = 10 – 4 = 6(cm)
Vì M là trung điểm của CD nên
11
.6 3 ( )
22
CM CD cm= = =
Vì M là trung điểm của CH nên
11
.4 2 ( )
22
CN CH cm= = =
G
E
B
A
N
M
D
C
H
0,5
0,5
0,5
0,5
b) Vì ABCD và CHGE là các hình vuông nên BC = DC = 6cm;
CE = CH = 4cm
BE = BC – CE = 6 – 4 = 2cm.
2
2
2
2
11
. .6.6 18 ( )
22
11
( ). .(6 4).4 20 ( )
22
11
. .10.4 20 ( )
22
18 20 20 18 ( )
BDC
BCHG
DGH
BDG BDHG DGH
BDC BDHG DGH
S BC DC cm
S BC GH CH cm
S DH GH cm
SS S
S S S cm
= = =
= + = +=
= = =
= −=
+ − =+−=
0,5
0,25
0,25
0,25
0,25
0,5
5
(2,0đ)
Cho các số nguyên dương
,,abc
thỏa mãn
333
a b c abc−−=
và
2
2( )
a bc= +
. Tính giá trị của biểu thức T = a
3
+ b
2023
+ c
2024
2,0
Vì
2
2( )a bc
= +
nên
a
là số nguyên dương chẵn.
Mà
333
;
a b c abc a b a c
− − = ⇒> >
nên
2 4 2( )abc a bc>+⇒ > +
2
44
aa a⇒ > ⇒<
mà
a
là số chẵn mà
a
nguyên dương nên
2a =
=>
2
bc+=
. Do b, c nguyên dương nên
1bc= =
Với
2; 1a bc= = =
thì
3 3 3 333
211 6abc− − = −−=
333
2Mà abc nêna b c abc= −−≠
Nên không có a, b, c thỏa mãn bài toán => Không có giá trị của T.
0,5
0,5
0,5
0,5
---------------------- Hết ----------------------
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

UBND TP THANH HOÁ
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THCS TRẦN MAI NINH
TOÁN 6 VÒNG II NĂM HỌC 2023 - 2024
Ngày thi 29 tháng 03 năm 2024 ĐỀ CHÍ NH T
HỨC Thời gian làm bài 120 phút (không kể thời gian giao đề)
Đề thi có 01 trang
Câu 1. (4,0 điểm):
1. Tính bằng cách hợp lí: a) A = (−1011)⋅1,04+20,22.(−48) 15 6 4 20 7 b) 5.4 27 4 3 8 B ⋅ − ⋅ ⋅ = 10 18 29 9 15.2 ⋅6 −7.2 ⋅9 2. So sánh: 71130 và 37175
Câu 2. (4,0 điểm): Tìm x biết: 1) 5 9  44 44 44 44 44  5 x. + . + + + + = − 14 14  12 20 30 42 6 5    4 2) 137 137 x x chia hết cho 13
Câu 3. (4,0 điểm):
1. Tìm hai số tự nhiên có bội chung nhỏ nhất của hai số đó bằng 432 và ước
chung lớn nhất của chúng bằng 6.
2. Một hộp có 30 quả bóng xanh, 50 quả bóng đỏ và một số quả bóng vàng,
các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên một quả bóng trong
hộp thì cơ hội xuất hiện quả bóng vàng là 3 . Tính số quả bóng vàng. 11
Câu 4. (6,0 điểm):
1. Có 50 điểm phân biệt trong đó có đúng 10 điểm thẳng hàng. Vẽ được bao
nhiêu đường thẳng đi qua hai trong 50 điểm đó.
2. Cho đoạn thẳng DH = 10cm. Vẽ điểm C thuộc đoạn thẳng DH sao cho
CH = 4cm. Gọi M, N lần lượt là trung điểm của DC và CH. A B
a) Tính độ dài đoạn thẳng MN.
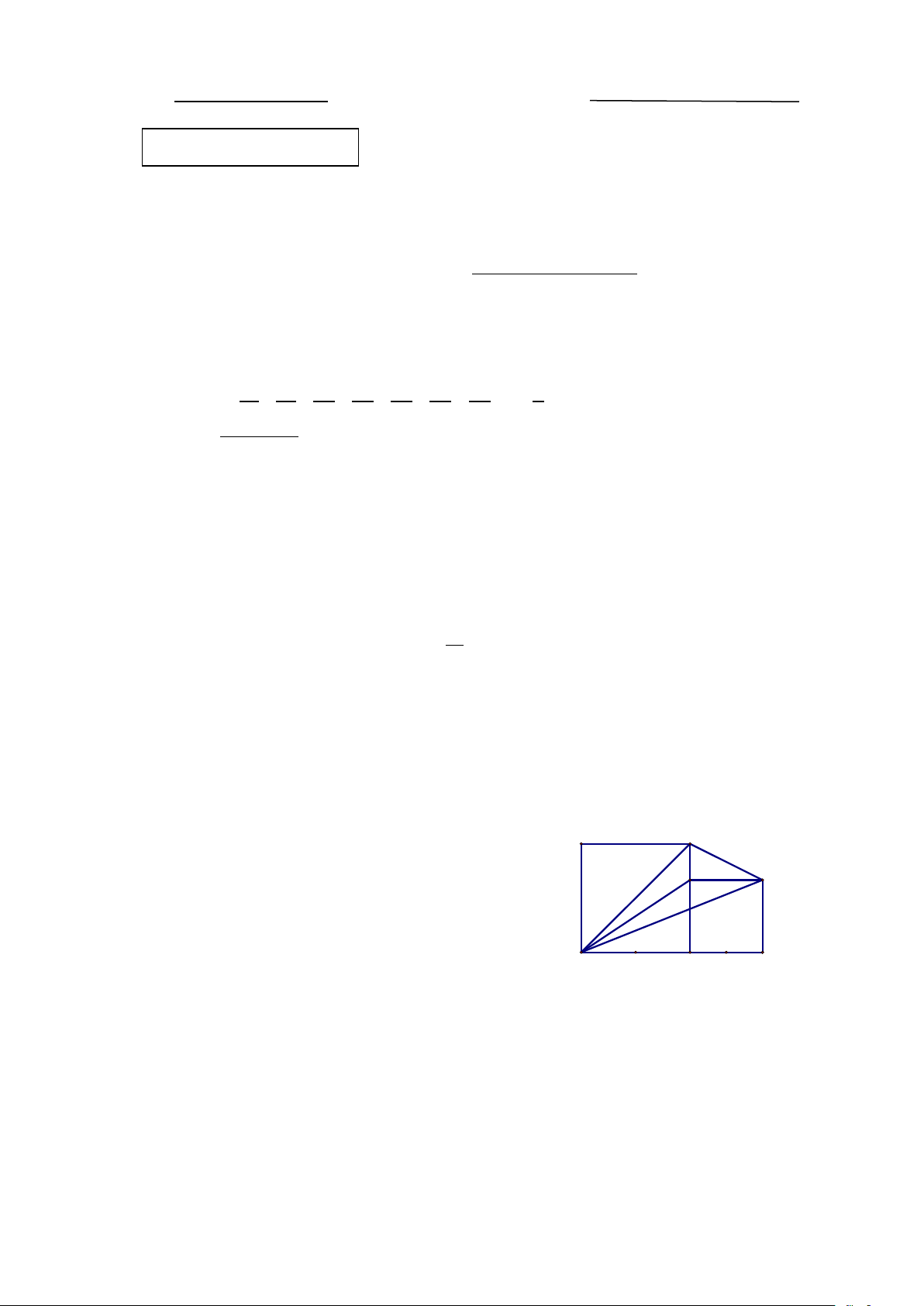
b) Vẽ các hình vuông CDAB và CHGE. G E
Tính diện tích tam giác DBG. D M C N H
Câu 5. (2,0 điểm): Cho các số nguyên dương a, b, c thỏa mãn 3 3 3
a − b − c = abc và 2
a = 2(b + c) . Tính giá trị của biểu thức T = a3 + b2023 + c2024
--------------- Hết ---------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh …………………………………….Số báo danh……… 1 UBND TP THANH HOÁ
HƯỚNG DẪN CHẤM THI
TRƯỜNG THCS TRẦN MAI NINH
HỌC SINH GIỎI CẤP TRƯỜNG TOÁN 6 VÒNG II
NĂM HỌC 2023 – 2024 Câu Hướng dẫn chấm Điểm
1. Tính bằng cách hợp lí: a) A = (−1011)⋅1,04+20,22.(−48) 15 6 4 20 7 b) 5.4 27 4 3 8 B ⋅ − ⋅ ⋅ = 2,5 10 18 29 9 15.2 ⋅6 −7.2 ⋅9 1.a) A = ( 1011 − )⋅1,04 + 20,22.( 48 − ) = ( 1011 − )⋅1,04 + ( 2022) − .0,48 0,5 = ( 1011 − )⋅1,04 +1011.( 0 − ,96) = ( 1011 − )⋅(1,04 + 0,96) = ( 1011 − )⋅2 = 2022 − 0,5 15 6 4 20 7 5.4 27 4 3 8 b) B ⋅ − ⋅ ⋅ = 10 18 29 9 15.2 ⋅6 − 7.2 ⋅9 30 18 8 20 21 5.2 .3 − 2 .3 .2 0,75 = 10 18 18 29 18 3.5.2 .2 .3 − 7.3.2 .3 29 18 2 .3 (10 − 9) 1 = = 2 0,75 28 19 (4,0đ) 2 .3 (15 −14)
2. So sánh: 71130 và 37175 1,5 2) Ta có: 130 130 71 < 72 0,5 130 390 260 350 260 40 72 = 2 .3 = 2 .3 .2 175 175 37 > 36 0,5 175 350 350 350 260 90 36 = 2 .3 = 2 .3 .3 90 40 175 175 130 130
Vì 3 > 2 nên 37 > 36 > 72 > 71 0,5 Vậy 71130 < 37175
1. Tìm x biết: 5 9  44 44 44 44 44  5 x. + . + + + + = − 14 4 1  12 20 30 42 56  2,0   4 Ta có: 5 9  1 1 1 1 1  5 .x + 44. . + + + + = − 14 14 12 20 30 2 4 6 5    4 0,25 5 9  1 1 1 1 1 1 1 1 1 1  5
.x + .44. − + − + − + − + − = − 14 14  3 4 4 5 5 6 6 7 7 8   4 0,25 5 . 9 x + .  1 1  5 44. − = − 0,25 2 14 14  3 8   4 (4,0đ) 5 . 9 x + . . 5 5 44 = − 0,25 14 14 24 4 5 . 165 5 x + = − 0,25 14 28 4 5 . 35 165 x = − − 0,25 14 28 8 2 100 5 x = − : = − 20 . Vậy x = - 20 0,25 14 14 2
2. Tìm x biết: 137 137 x
x chia hết cho 13. 2.0 6 4 2 6 2 B =137 137 x x =13.10 + 7 .10 x
+13.10 + 7x =13.(10 +10 ) + 7 .10001 x 1.0
10001 không chia hết cho 13 => B13 Khi 7x 13 0,75 => x = 8 Vậy x = 8 0,25
1. Tìm hai số tự nhiên có bội chung nhỏ nhất của hai số đó bằng 72 và
ước chung lớn nhất của chúng bằng 6. 2,0
Gọi hai số cần tìm là a, b (a ≤ b) 0,5
Ta có: ab = ƯCLN(a, b); BCNN(a, b) nên ab= 2592. Đặt a = 6 ,
m b = 6n với ƯCLN(m, n) = 1 và (m ≤ ;n , m n ∈ N) 0,5
⇒ 36mn = 2592 ⇒ mn = 72 0,25
Mà m, n nguyên tố cùng nhau nên Ta được: m n a B 0,5 3 1 72 6 432 (4,0đ) 8 9 48 54
Vậy hai số cần tìm là (6; 432) và (48; 54) 0,25
2. Một hộp có 30 quả bóng xanh, 50 quả bóng đỏ và một số quả bóng
vàng; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu
nhiên một quả bóng trong hộp thì cơ hội xuất hiện quả bóng vàng là 2,0
3 . Tính số quả bóng vàng. 11
Tổng số quả bóng xanh, đỏ chiếm 3 1 8 − = (tổng số bóng). 0,5 11 11
Số bóng trong hộp là ( + ) 8 30 50 : = 0 11 (quả). 0,75 11 Số bóng vàng là 3 110⋅ = 30 (quả). 11 0,75
1. Có 50 điểm phân biệt trong đó có đúng 10 điểm thẳng hàng. Vẽ được
bao nhiêu đường thẳng đi qua hai trong 50 điểm đó. 2,0
Với 50 điểm mà không có 3 điểm nào ta vữ được số đường thẳng là: 0,75
(50 −1).50 =1225 (đường thẳng) 2
Vì có 10 điểm thẳng hàng nên qua 10 điểm đó ta chỉ vẽ được 1 đường 0,75
thẳng và số đường thẳng giảm đi là : (10 −1).10 −1=44 2 (đường thẳng)
Vậy với 50 điểm trong đó có đúng 10 điểm thẳng hàng là 0,5
1225 – 44 = 1181 (đường thẳng)
2. Cho đoạn thẳng DH = 10cm. Vẽ điểm C thuộc đoạn thẳng DH sao
cho CH = 4cm. Gọi M, N lần lượt là trung điểm của DC và CH.
a) Tính độ dài đoạn thẳng MN. 4,0
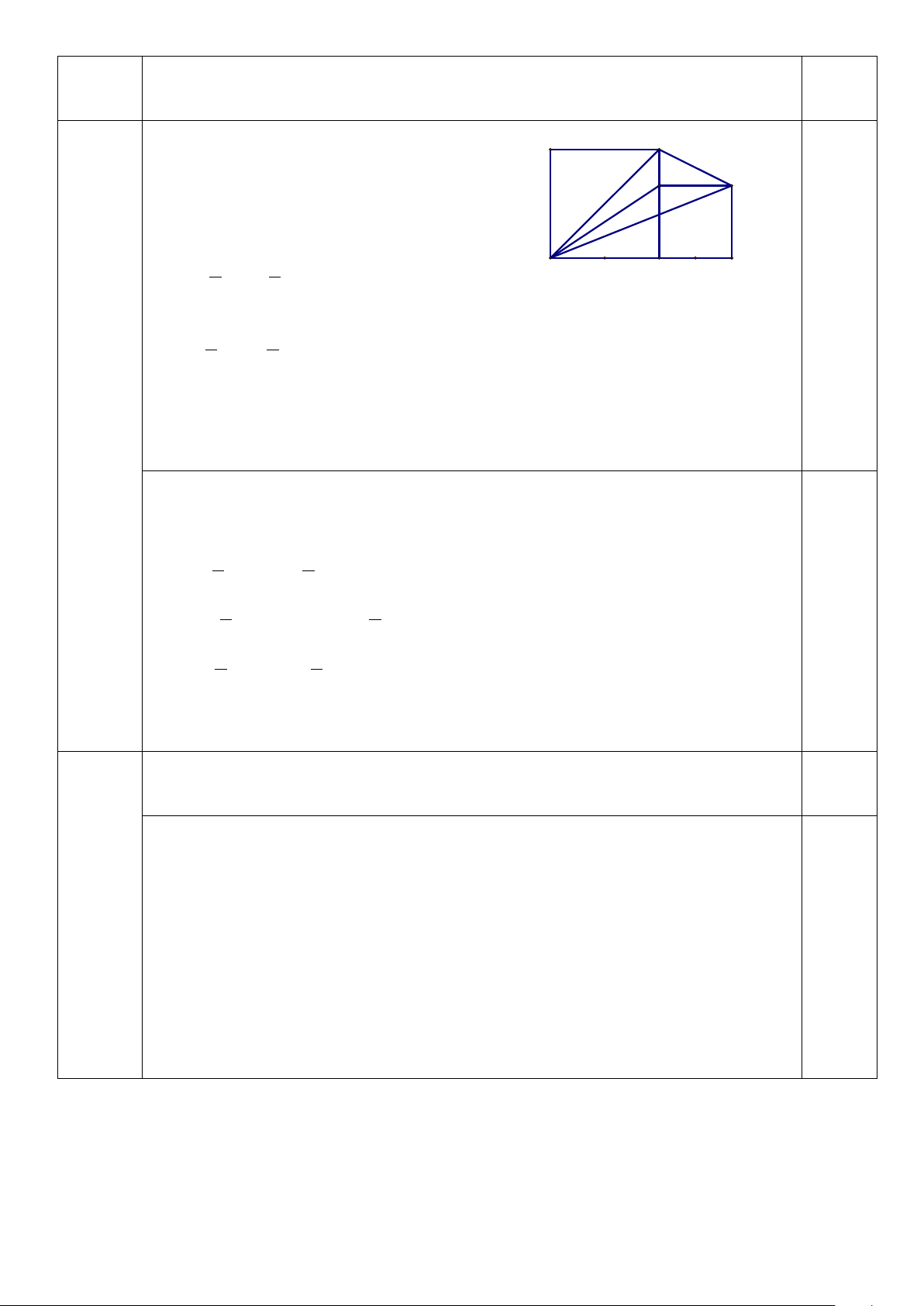
b) Vẽ các hình vuông CDAB và CHGE. 3
Tính diện tích tam giác DBG.
a) Vì C nằm giữa D và H nên A B 0,5 CD +CH = DH Mà DH = 10cm, CH = 4cm G E
nên DC = DH – CH = 10 – 4 = 6(cm)
Vì M là trung điểm của CD nên 0,5 1 1
CM = CD = .6 = 3 (cm) D M C N H 2 2
Vì M là trung điểm của CH nên 0,5 1 1
CN = CH = .4 = 2 (cm) 2 2 4
Vì C nằm giữa M và N nên MC +CN = MN
(6,0đ) Thay CM = 3cm, CN = 2cm ta có MN = 3 + 2 = 5(cm) 0,5 Vậy MN = 5 cm
b) Vì ABCD và CHGE là các hình vuông nên BC = DC = 6cm; CE = CH = 4cm 0,5
BE = BC – CE = 6 – 4 = 2cm. 1 1 2 S = BC DC = = cm BDC . .6.6 18 ( ) 2 2 0,25 1 1 2 S = BC + GH CH = + = cm 0,25 BCHG ( ). .(6 4).4 20 ( ) 2 2 0,25 1 1 2 S = DH GH = = cm DGH . .10.4 20 ( ) 2 2 0,25 S = S − S = BDG BDHG DGH 2 0,5 S + S − S = + − = cm BDC BDHG DGH 18 20 20 18 ( )
Cho các số nguyên dương a,b,c thỏa mãn 3 3 3
a − b − c = abc và 2 a 2,0
= 2(b + c) . Tính giá trị của biểu thức T = a3 + b2023 + c2024 Vì 2
a = 2(b + c) nên a là số nguyên dương chẵn. Mà 3 3 3
a − b − c = abc ⇒ a > ;
b a > c nên 2a > b + c ⇒ 4a > 2(b + c) 0,5 5 2
⇒ 4a > a ⇒ a < 4 mà a là số chẵn mà a nguyên dương nên 0,5
(2,0đ) a = 2=>b+c = 2. Do b, c nguyên dương nên b = c =1
Với a = 2;b = c =1 thì 3 3 3 3 3 3
a − b − c = 2 −1 −1 = 6 0,5 3 3 3
Mà abc = 2nên a − b − c ≠ abc
Nên không có a, b, c thỏa mãn bài toán => Không có giá trị của T. 0,5
---------------------- Hết ---------------------- 4