Đề thi HSG Toán 9 năm 2024 – 2025 các thị xã, thành phố và huyện tỉnh Lào Cai
Tài liệu gồm 92 trang, được biên soạn bởi tác giả Trần Tiến Đạt, tuyển tập đề thi học sinh giỏi môn Toán 9 năm học 2024 – 2025 của các thị xã, thành phố và huyện thuộc tỉnh Lào Cai, có đáp án và lời giải chi tiết.
Chủ đề: Đề HSG Toán 9 563 tài liệu
Môn: Toán 9 3.6 K tài liệu
Tác giả:
Preview text:
TRẦN TIẾN ĐẠT TUYỂN TẬP ĐỀ THI HỌC SINH GIỎI
CÁC THỊ XÃ, THÀNH PHỐ VÀ HUYỆN TỈNH LÀO CAI MÔN TOÁN 9 NĂM HỌC 2024-2025 LỜI NÓI ĐẦU
Chào các bạn. Trước mắt các bạn là file tài liệu Tuyển tập các đề thi Học sinh
giỏi môn Toán tỉnh Lào Cai năm học 2024-2025. Không biết phải nói sao nữa
nhỉ??? Mình cũng chỉ là một học sinh lớp 9 bình thường, “ngựa ngựa” lên đây
sưu tầm đề và làm hướng dẫn giải. Đây là sự khởi đầu nên mình sẽ chọn đề ở nơi
quê hương mình sinh ra, nơi mà mình hiểu nhất. Tất cả đề thi đều được mình
đánh lại và có lời giải chi tiết. Đồng thời, mình cũng muốn có một vài lưu ý khi đọc file này:
Thứ nhất, vốn dĩ chỉ là sự khởi đầu nên mình… không biết Latex. Bản thân
trong tài liệu này mình cũng chỉ viết chữ font Time New Roman, công thức thì sẽ
đánh bằng Microsoft Equation 3.0 hoặc Equation, hình bằng Geogebra – nói
chung là không được xuất sắc nên mong các bạn thông cảm và chờ ngày mình biết Latex nhé!
Thứ hai, vì chỉ có một mình làm cộng thêm hiểu biết chưa nhiều, lỗi đánh
máy,.. và có nhiều sai sót, mong bạn đọc hãy hoan hỉ cho qua và gửi lỗi sai qua
email của mình là dat21122010@gmail.com nhé!
Cuối cùng, hãy lan toả những giá trị tích cực nhé !
Bản quyền hình ảnh bìa thuộc về VTMO. Cảm ơn vì đã đọc! HÀNH TRÌNH KHÁM PHÁ
TRẠM: MƯỜNG KHƯƠNG TRẠM: SI MA CAI Bắt đầu: km 66
Hãy nắm rõ hành trình để có một chuyến đi vui vẻ nhé! Bắt đầu: km 73 Kết thúc: km 72 Kết thúc: km 81 TRẠM: BÁT XÁT Bắt đầu: km 13 Kết thúc: km 23 TRẠM: BẮC HÀ Bắt đầu: km 3 Kết thúc: km 12 TRẠM: TP LÀO CAI Bắt đầu: km 24 Kết thúc: km 34 TRẠM: BẢO YÊN Bắt đầu: km 35 Kết thúc: km 46 TRẠM: SAPA Bắt đầu: km 56 Kết thúc: km 65 TRẠM: VĂN BÀN Bắt đầu: km 82 Kết thúc: km 91 T r a n g | 3 UBND HUYỆN BẮC HÀ
KỲ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN LỚP 9 PHÒNG GD&ĐT
NĂM HỌC: 2024 - 2025 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Đề thi gồm 01 trang, 6 câu Câu 1 (4,0 điểm): 2 1 1
xy(x + y) − xy
1.1: Cho biểu thức M = + + . (Với x , 0 y 0 ) xy x y x x + y y
a) Rút gọn biểu thức M .
b) Biết x + y = 4 . Tìm giá trị nhỏ nhất của biểu thức M .
1.2: Cho các số dương a, b thoả mãn ab + a + b =1. a b ab + 1 Chứng minh: + = 2 a + 1 2 b + 1 ( 2 2 a + )( 1 2 b + ) 1
Câu 2 (2,0 điểm): Cho tập hợp A = {0,1,2,3,4,5,6}. Gọi S là tập hợp các số có
3 chữ số khác nhau được lập thành từ các chữ số của tập hợp A. Chọn ngẫu nhiên
một số từ S, tính xác suất để số được chọn có chữ số cuối gấp đôi chữ số đầu.
Câu 3 (2,0 điểm): Kết thúc năm học 2023-2024, Bình hỏi Tuấn: “Bạn có bao
nhiêu bài kiểm tra đạt điểm 8 và điểm 9 vậy?”. Tuấn trả lời: “Số bài kiểm tra đạt
điểm 8, điểm 9 của tớ nhiều hơn 21 và tổng số điểm của các bài kiểm tra đó là
183”. Em hãy tính giúp Bình xem Tuấn có bao nhiêu bài kiểm tra đạt điểm 8 và
bao nhiêu bài kiểm tra đạt điểm 9 nhé.
Câu 4 (2,0 điểm): Cho x, y là các số thực dương thay đổi và thoả mãn (2x + 9 y)3 4 2 x + 9 2 y = . 10 Chứng minh rằng: . 20 ( 4 2 2
x + y ) − 4x − 8y + 55 Câu 5 (4,0 điểm):
a) Cho n là số nguyên dương và d là ước dương của 2
2n , chứng minh n2 + d
không phải là số chính phương.
b) Tìm nghiệm nguyên dương của phương trình: ( 5 2 2
x + xy + y ) = ( 7 x + 2 y).
Câu 6 (6,0 điểm): Cho O là trung điểm của đoạn thẳng MN. Trên cùng một
nửa mặt phẳng có bờ là đường thẳng MN vẽ tia Mx, Ny cùng vuông góc với
MN. Trên tia Mx lấy điểm P (điểm P khác M), qua O kẻ đường vuông góc với
OP cắt Ny tại Q. Kẻ OA ⊥ PA tại A. Gọi E là giao điểm của AM và OP, F là giao điểm của AN và OQ. 2 MN
a) Chứng minh: MPO ~ NOQ và MP.NQ = 4
b) Chứng minh tứ giác EAFO là hình chữ nhật.
c) Từ A, kẻ AH ⊥ MN tại H. Gọi K là giao điểm của AH và NP. Chứng minh rằng: E,F,K thẳng hàng.
----------------HẾT----------------
(Cán bộ coi thi không giải thích gì thêm) T r a n g | 4
HƯỚNG DẪN GIẢI ĐỀ HUYỆN BẮC HÀ Câu 1: 2 1 1
xy(x + y) − xy
1.1: Cho biểu thức M = + + . (Với x , 0 y 0 ) xy x y x x + y y
a) Rút gọn biểu thức M .
b) Biết x + y = 4 . Tìm giá trị nhỏ nhất của biểu thức M . Hướng dẫn: a) Ta có: 2 1 1
√𝑥𝑦(𝑥 + 𝑦 − √𝑥𝑦) 𝑀 = ( + + ) . 3 √𝑥𝑦 𝑥 𝑦 3 √𝑥 + √𝑦 𝑥 + 𝑦 + 2√𝑥𝑦
√𝑥𝑦(𝑥 + 𝑦 − √𝑥𝑦) 𝑀 = . 𝑥𝑦
(√𝑥 + √𝑦)(𝑥 − √𝑥𝑦 + 𝑦) 2 (√𝑥 + √𝑦)
√𝑥𝑦(𝑥 + 𝑦 − √𝑥𝑦) 𝑀 = . 𝑥𝑦
(√𝑥 + √𝑦)(𝑥 − √𝑥𝑦 + 𝑦) √𝑥 + √𝑦 𝑀 = √𝑥𝑦
Vậy: 𝑀 = √𝑥+√𝑦 với x > 0, y > 0. √𝑥𝑦 b) Ta có: √𝑥 + √𝑦 1 1 𝑀 = = + √𝑥𝑦 √𝑥 √𝑦
Vì x > 0, y > 0 nên theo BĐT Cauchy, ta có: 𝑥 + 𝑦 ≥ 2√𝑥𝑦 4 ≥ 2√𝑥𝑦 2 ≥ √𝑥𝑦
Cũng theo BĐT Cauchy, ta có: 1 1 1 1 1 1 + ≥ 2√ . = 2√ ≥ 2. √ = √2 √𝑥 √𝑦 √𝑥 √𝑦 √𝑥𝑦 2 Dấu “=” xảy ra khi: 𝑥 + 𝑦 = 4 { 𝑥 = 𝑦 Hay: x = y = 2.
Vậy: Mmin = √2 khi và chỉ khi x = y = 2. T r a n g | 5
1.2: Cho các số dương a, b thoả mãn ab + a + b =1. a b ab + 1 Chứng minh: + = 2 a + 1 2 b + 1 ( 2 2 a + )( 1 2 b + ) 1 Hướng dẫn: Ta có:
𝑎2 + 1 = 𝑎2 + 𝑎𝑏 + 𝑎 + 1 = (𝑎 + 1)(𝑎 + 𝑏)
𝑏2 + 1 = 𝑏2 + 𝑎𝑏 + 𝑎 + 1 = (𝑏 + 1)(𝑎 + 𝑏) Khi đó: 𝑎 𝑏 𝑎 𝑏 + = + 𝑎2 + 1 𝑏2 + 1 (𝑎 + 1)(𝑎 + 𝑏) (𝑏 + 1)(𝑎 + 𝑏)
𝑎(𝑏 + 1) + 𝑏(𝑎 + 1) =
(𝑎 + 1)(𝑏 + 1)(𝑎 + 𝑏)
𝑎𝑏 + 𝑎𝑏 + 𝑎 + 𝑏 =
(𝑎 + 1)(𝑏 + 1)(𝑎 + 𝑏) 𝑎𝑏 + 1 = (1) 2(𝑎 + 𝑏) Lại có: 𝑎𝑏 + 1 𝑎𝑏 + 1 = √2(𝑎2 + 1)(𝑏2 + 1)
√2(𝑎 + 1)(𝑏 + 1)(𝑎 + 𝑏)2 𝑎𝑏 + 1 =
√2(𝑎𝑏 + 𝑎 + 𝑏 + 1)(𝑎 + 𝑏)2 𝑎𝑏 + 1 𝑎𝑏 + 1 = =
(𝑎 > 0, 𝑏 > 0) (2) √4(𝑎 + 𝑏)2 2(𝑎 + 𝑏) Từ (1) và (2) suy ra: 𝑎 𝑏 𝑎𝑏 + 1 + = 𝑎2 + 1 𝑏2 + 1 √2(𝑎2 + 1)(𝑏2 + 1)
Vậy: Đẳng thức được chứng minh.
Câu 2 (2,0 điểm): Cho tập hợp A = {0,1,2,3,4,5,6}. Gọi S là tập hợp các số có
3 chữ số khác nhau được lập thành từ các chữ số của tập hợp A. Chọn ngẫu nhiên
một số từ S, tính xác suất để số được chọn có chữ số cuối gấp đôi chữ số đầu. Hướng dẫn:
*Số các số có 3 chữ số thoả mãn đề bài là:
Hàng trăm có 6 cách chọn
Hàng chục có 6 cách chọn
Hàng đơn vị có 5 cách chọn
=> Không gian mẫu: n(Ω) = 6.6.5 = 180
*Gọi A là biến cố Số được chọn có chữ số cuối gấp đôi chữ số đầu. Ta có: T r a n g | 6
Gọi các số thoả mãn đề bài có dạng: 𝑎𝑏𝑐 ̅̅̅̅̅
(𝑎, 𝑏, 𝑐 ∈ 𝑁; 1 ≤ 𝑎 ≤ 6; 0 ≤ 𝑏, 𝑐 ≤ 6; 𝑎 ≠ 𝑏 ≠ 𝑐)
*Ta xét các trường hợp sau:
Trường hợp 1: a = 1 => c = 2
Số cách để chọn b là: 7 – 2 = 5 (cách)
Hay: Tồn tại 5 số thoả mãn đề bài trong trường hợp này.
Trường hợp 2: a = 2 => c = 4
Số cách để chọn b là: 7 – 2 = 5 (cách)
Hay: Tồn tại 5 số thoả mãn đề bài trong trường hợp này.
Trường hợp 1: a = 3 => c = 6
Số cách để chọn b là: 7 – 2 = 5 (cách)
Hay: Tồn tại 5 số thoả mãn đề bài trong trường hợp này.
Trường hợp 4: a > 3 => c > 6 (không thoả mãn)
Từ 4 trường hợp trên, suy ra: Tổng số các kết quả thuận lợi cho biến cố A là: n(A) = 5 + 5 + 5 = 15
Vậy: Xác suất của biến cố A là: 𝑛(𝐴) 15 1 𝑃(𝐴) = = = . 𝑛(Ω) 180 12
Câu 3 (2,0 điểm): Kết thúc năm học 2023-2024, Bình hỏi Tuấn: “Bạn có bao
nhiêu bài kiểm tra đạt điểm 8 và điểm 9 vậy?”. Tuấn trả lời: “Số bài kiểm tra đạt
điểm 8, điểm 9 của tớ nhiều hơn 21 và tổng số điểm của các bài kiểm tra đó là
183”. Em hãy tính giúp Bình xem Tuấn có bao nhiêu bài kiểm tra đạt điểm 8 và
bao nhiêu bài kiểm tra đạt điểm 9 nhé. Hướng dẫn:
*Gọi số bài kiểm tra đạt điểm 8 và điểm 9 mà Tuấn đạt được lần lượt là x và y (bài) (x,y ∈ N*) *Ta có:
- Vì số bài đạt điểm 8, điểm 9 của Tuấn nhiều hơn 21 nên: 𝑥 + 𝑦 > 21
- Vì tổng số điểm của các bài đó là 183 nên: 8𝑥 + 9𝑦 = 183 183 − 9𝑦 9𝑦 + 1 𝑥 = = 23 − (∗) 8 8
Nhận xét: Vì x là số tự nhiên và 23 cũng là số tự nhiên nên: 9𝑦 + 1 ∈ 𝑁 8 9𝑦 + 1 ⋮ 8 8𝑦 + 𝑦 + 1 ⋮ 8 𝑦 + 1 ⋮ 8 (1) T r a n g | 7 Mặt khác ta cũng có: 8𝑥 + 9𝑦 = 183 8(𝑥 + 𝑦) + 𝑦 = 183 183 > 8.21 + 𝑦 𝑦 < 15 𝑦 + 1 < 16 (2) Từ (1) và (2) suy ra: 𝑦 + 1 = 0 (loại) [ 𝑦 + 1 = 8 => y = 7 (thoả ĐKXĐ)
Thế vào (*) tìm được x = 15 (thoả ĐKXĐ)
Vậy: Bạn Tuấn có 15 bài kiểm tra đạt điểm 8 và 7 bài kiểm tra đạt điểm 9.
Câu 4 (2,0 điểm): Cho x, y là các số thực dương thay đổi và thoả mãn (2x + 9 y)3 4 2 x + 9 2 y = . 10 Chứng minh rằng: . 20 ( 4 2 2
x + y ) − 4x − 8y + 55 Hướng dẫn:
1. Đánh giá tử thức
Theo bất đẳng thức Cauchy, ta có (x,y > 0): 4𝑥2 + 1 ≥ 4𝑥 9𝑦2 + 9 ≥ 18𝑦 3 4𝑥2 + 9𝑦2 + 10 20 3 => (2𝑥 + 9𝑦)3 ≤ ( ) = ( ) = 1000 2 2 2. Đánh giá mẫu thức Ta đặt và có:
𝐴 = 4(𝑥2 + 𝑦2 ) − 4𝑥 − 8𝑦 + 55
𝐴 = (4𝑥2 − 4𝑥 + 1) + 4(𝑦2 − 2𝑦 + 1) + 50
𝐴 = (2𝑥 − 1)2 + 4(𝑦 − 1)2 + 50 ≥ 50
Từ 2 đánh giá trên, ta có: (2𝑥 + 9𝑦)3 1000 ≤ = 20
4(𝑥2 + 𝑦2) − 4𝑥 − 8𝑦 + 55 50
Vậy: Bất đẳng thức được chứng minh. Dấu “=” xảy ra khi: 1 𝑥 = ; 𝑦 = 1. 2 T r a n g | 8 Câu 5 (4,0 điểm):
a) Cho n là số nguyên dương và d là ước dương của 2
2n , chứng minh n2 + d
không phải là số chính phương.
b) Tìm nghiệm nguyên dương của phương trình: ( 5 2 2
x + xy + y ) = ( 7 x + 2 y). Hướng dẫn:
a) Vì 2n2 có ước dương là d nên:
2𝑛2 = 𝑑𝑘 (𝑘 ∈ 𝑁) 2𝑛2 𝑑 = 𝑘 Ta có: 2𝑛2 2 𝑛2 + 𝑑 = 𝑛2 + = 𝑛2 (1 + ) 𝑘 𝑘
Để n2 + d là số chính phương với n2 là số chính phương thì: 2 1 + là số chính phương 𝑘 Trường hợp 1: k = 1 2 1 + = 1 + 2 = 3 (loại) 𝑘 Trường hợp 2: k = 2 2 1 + = 1 + 1 = 2 (loại) 𝑘 Trường hợp 3: k > 2 2 1 < 1 + < 2 𝑘
Lúc này chắc chắn biểu thức trên không thể là số chính phương.
Vậy: Với các số n,d thoả mãn đề bài thì n2 + d không là số chính phương. b) Ta có:
5(𝑥2 + 𝑥𝑦 + 𝑦2) = 7(𝑥 + 2𝑦)
5𝑥2 + 𝑥(5𝑦 − 7) + 5𝑦2 − 14𝑦 = 0 (1)
Xét biệt thức của phương trình:
∆= (5𝑦 − 7)2 − 4.5. (5𝑦2 − 14𝑦)
∆= −75𝑦2 + 210𝑦 + 49
Để phương trình đã cho có nghiệm thì: ∆ ≥ 0
75𝑦2 − 210𝑦 − 49 ≤ 0 21 − 14√3 21 + 14√3 ≤ 𝑦 ≤ 15 15
Vì không có máy tính cầm tay, hãy đoán nghiệm: Lưu ý khi lấy xấp xỉ, (1) cần lấy khoảng cách 14√3 ≈ 14√4 = 28 gần, tránh sai lệch giá trị quá lớn. T r a n g | 9 Suy ra: 21 − 28 21 + 28 ≤ 𝑦 ≤ 15 15 −0,4(6) ≤ 𝑦 ≤ 3,2(6)
Mà y là số nguyên dương nên: 𝑦 ∈ {1; 2; 3}
Trường hợp 1: y = 1. Thế vào (1) ta được:
5𝑥2 + 𝑥(5𝑦 − 7) + 5𝑦2 − 14𝑦 = 0 5𝑥2 − 2𝑥 − 9 = 0 1 ± √46 𝑥 = (loại) 5
Trường hợp 2: y = 2. Thế vào (1) được:
5𝑥2 + 𝑥(5𝑦 − 7) + 5𝑦2 − 14𝑦 = 0 5𝑥2 + 3𝑥 − 8 = 0 𝑥 = 1 [ 8 𝑥 = − (loại) 5
Trường hợp 3: y = 3. Thế vào (1) được:
5𝑥2 + 𝑥(5𝑦 − 7) + 5𝑦2 − 14𝑦 = 0 5𝑥2 − 8𝑥 + 3 = 0 𝑥 = −1 [ 3 (loại) 𝑥 = − 5
Vậy: Phương trình đã cho có nghiệm nguyên dương duy nhất là: (𝑥; 𝑦) = (1; 2).
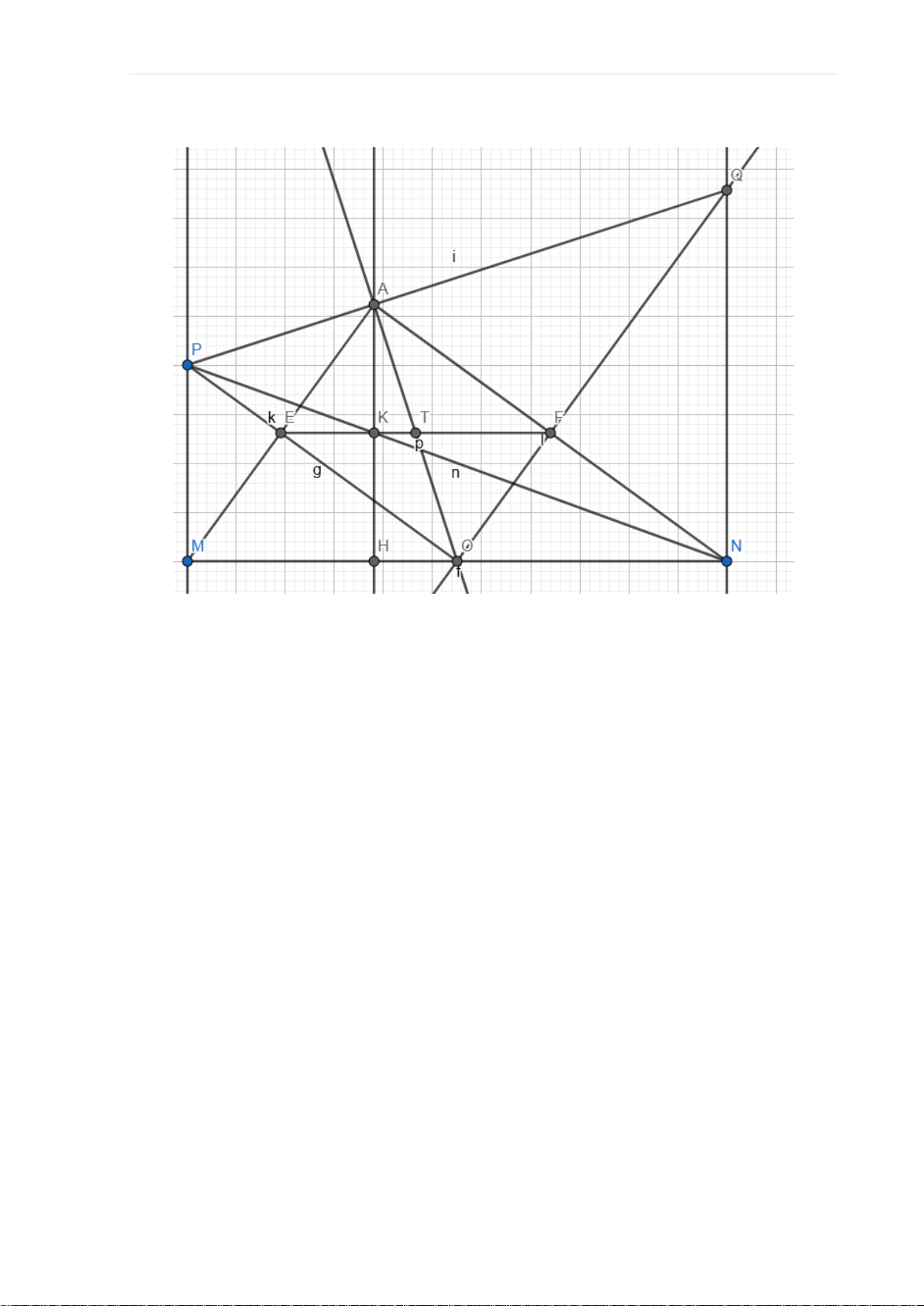
Câu 6 (6,0 điểm): Cho O là trung điểm của đoạn thẳng MN. Trên cùng một
nửa mặt phẳng có bờ là đường thẳng MN vẽ tia Mx, Ny cùng vuông góc với
MN. Trên tia Mx lấy điểm P (điểm P khác M), qua O kẻ đường vuông góc với
OP cắt Ny tại Q. Kẻ OA ⊥ PA tại A. Gọi E là giao điểm của AM và OP, F là giao điểm của AN và OQ. 2 MN
a) Chứng minh: MPO ~ NOQ và MP.NQ = 4
b) Chứng minh tứ giác EAFO là hình chữ nhật.
c) Từ A, kẻ AH ⊥ MN tại H. Gọi K là giao điểm của AH và NP. Chứng minh rằng: E,F,K thẳng hàng. Hướng dẫn: Ta có hình vẽ: T r a n g | 10
a) Nhận thấy hai tam giác PMO và QNO lần lượt vông tại M và N. Từ đó suy ra: 𝑀𝑃𝑂 ̂ + 𝑀𝑂𝑃 ̂ = 900 { 𝑁𝑂𝑄 ̂ + 𝑁𝑄𝑂 ̂ = 900 (1) Lại có: PO ⊥ OQ 𝑃𝑂𝑄 ̂ = 900 Ta có: 𝑀𝑂𝑁 ̂ = 1800 𝑀𝑂𝑃 ̂ + 𝑃𝑂𝑄 ̂ + 𝑄𝑂𝑁 ̂ = 1800 𝑀𝑂𝑃 ̂ + 𝑄𝑂𝑁 ̂ = 900 (2) Từ (1) và (2) suy ra: 𝑀𝑂𝑃 ̂ = 𝑁𝑄𝑂 ̂ Xét MPO và NOQ có: 𝑃𝑀𝑂 ̂ = 𝑂𝑁𝑄 ̂ = 900 (𝑐𝑚𝑡) 𝑀𝑂𝑃
̂ = 𝑁𝑄𝑂 (𝑐𝑚𝑡 ̂ ) => MPO ~ NOQ (g.g)
Ta chứng minh được các tứ giác OAPM, OAQN nội tiếp. Từ đó có: 𝑀𝐴𝑂 ̂ + 𝑂𝐴𝑁 ̂ = 𝑀𝑃𝑂 ̂ + 𝑂𝑄𝑁 ̂ T r a n g | 11 𝑀𝐴𝑁 ̂ = 𝑄𝑂𝑁 ̂ + 𝑂𝑄𝑁 ̂ = 900
=> Góc MAN là góc nội tiếp chắn nửa đường tròn (O ; 2R = MN) => A ∈ (O).
Theo tính chất của 2 tiếp tuyến cắt nhau, ta có: 𝑃𝐴 = 𝑃𝑀 { 𝑄𝐴 = 𝑄𝑁 => MP.NQ = AP.AQ (3)
Xét tam giác OPQ vuông tại O, ta chứng minh được:
𝑂𝐴2 = 𝐴𝑃. 𝐴𝑄 (4)
Ta có: O là trung điểm của MN (gt)
=> OA là đường trung tuyến của tam giác AMN vuông tại A
Theo tính chất đường trung tuyến, ta có: 𝑀𝑁
𝑂𝐴 = 𝑂𝑀 = 𝑂𝑁 = 2 𝑀𝑁2 𝑂𝐴2 = (5) 4
Từ (3) , (4) và (5) suy ra: 𝑀𝑁2 𝑀𝑃. 𝑁𝑄 = 4 b) Ta có: PM = PA
=> P thuộc trung trực của AM (6) => OP ⊥ AM = {E} => 𝐴𝐸𝑂 ̂ = 900 Ta có: 𝑀𝐴𝑁 ̂ = 900 { (𝑐𝑚𝑡) 𝑃𝑄𝑂 ̂ = 900 { 𝐸𝐴𝐹 ̂ = 900 𝐸𝑂𝐹 ̂ = 900 Xét tứ giác AEOF có: 𝐸𝐴𝐹 ̂ = 𝐴𝐸𝑂 ̂ = 𝐸𝑂𝐹 ̂ = 900
=> Tứ giác AEOF là hình chữ nhật (dhnb)
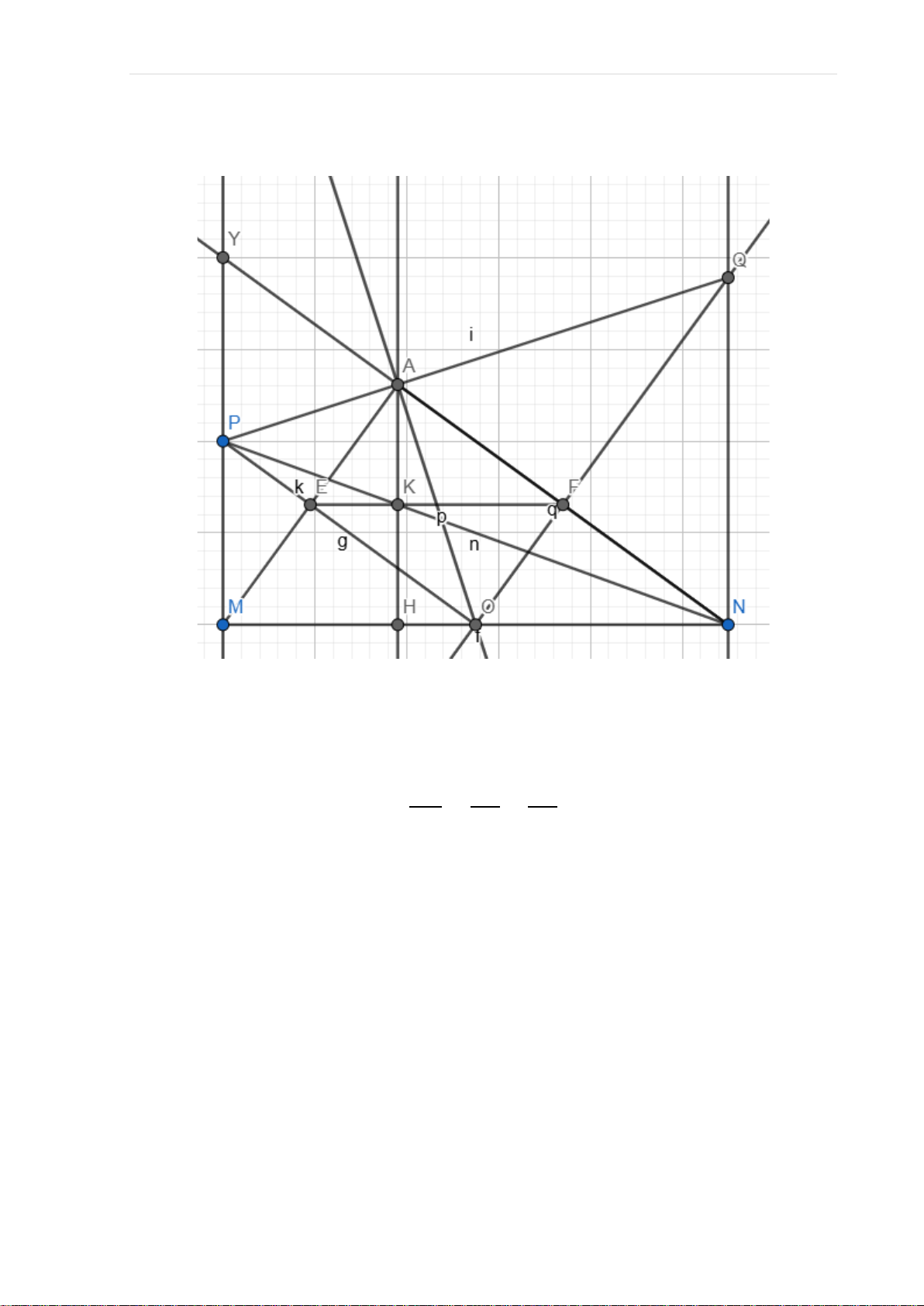
c) Gọi giao điểm của AH với EF là Z. Từ (6) ta cũng suy ra: E là trung điểm của AM
Tương tự, ta cũng có: F là trung điểm của AN
=> EF là đường trung bình của tam giác AMN => EF // MN (tính chất) => EZ // AH Xét tam giác AHM có: E là trung điểm AM T r a n g | 12 EZ // AH (cmt)
=> Z là trung điểm AH và EF đi qua Z
Lúc này, ta cần chứng minh K là trung điểm AH
Giả sử AN cắt PM tại Y.
Nhận xét: OP // MY (cùng vuông góc với AM) và O là trung điểm MN nên: P là trung điểm của MY.
Mà AH // MY (cùng vuông góc với MN) nên theo hệ quả của định lí Thalès, có 𝐾𝐻 𝐴𝐾 𝐴𝐾 = = 𝑃𝑀 𝐴𝑃 𝑌𝑃
=> MP đi qua trung điểm của AH
=> K là trung điểm của AH => K trùng với Z => E,K,F thẳng hàng. …HẾT… T r a n g | 13 UBND HUYỆN BÁT XÁT
KỲ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN LỚP 9 PHÒNG GD&ĐT
NĂM HỌC: 2024 - 2025 Môn thi: TOÁN HỌC ĐỀ
Thời gian làm bài: 150 phút (không kể thời gian giao đề) CHÍNH THỨC
(Đề thi gồm 01 trang, 07 câu) Câu 1 (4,0 điểm) x + 2 x 1 x − 1
1.1. Cho biểu thức: P = + + : (Với x ≥ 0, x ≠ 1)
x x −1 x + x +1 1− x 2
a) Rút gọn biểu thức P b) So sánh P2 và 2P x y z a b c 2 2 2 x y z 1.2. Cho
+ + = 1 và + + = 0 . Chứng minh rằng: + + = 1. a b c x y z 2 2 2 a b c
Câu 2 (2,0 điểm) Gieo một con xúc xắc cân đối và đồng chất 2 lần.
a) Mô tả không gian mẫu.
b) Tính xác suất của biến cố: “Lần đầu là số chính phương, lần sau là số lẻ”. Câu 3 (2,0 điểm)
Năm học 2023-2024, bạn An trúng tuyển lớp 10 trường THPT. Để chuẩn bị cho
năm học mới, lúc đầu An dự định mua 30 quyển vở và 10 cái bút cùng loại với tổng
số tiền phải trả là 340 nghìn đồng. Tuy nhiên, vì đạt danh hiệu “Học sinh giỏi” nên
An được nhận phiếu giảm giá 10% với vở và 5% với bút, do đó An quyết định mua
50 quyển vở và 20 cây bút với tổng số tiền phải trả sau khi giảm giá là 526 nghìn
đồng. Hỏi giá tiền mỗi quyển vở và mỗi cây bút khi chưa giảm giá là bao nhiêu?
Câu 4 (2,0 điểm) Cho 3 số thực a,b, c dương. Chứng minh rằng: 3 3 3 a + b + c 1 3
a + (b + c)3 3
b + (c + a)3 3
c + (a + b)3 Câu 5 (2,0 điểm)
5.1. Cho p là số nguyên tố lớn hơn 5. Chứng minh rằng 2024 p −1 chia hết cho 60.
5.2. Tìm x, y Z thoả mãn: 2y2 x + x + y +1 = x2 + 2y2 + xy Câu 6 (2,0 điểm) Cho phương trình: 2 x − 2 2
mx + m − m − 6 = 0 ( m là tham số). Với giá trị nào của m
thì phương trình đã cho có hai nghiệm x và x sao cho x + x = . 8 1 2 1 2
Câu 7 (6,0 điểm) Cho tam giác ABC nhọn (AB < AC), nội tiếp đường tròn (O).
Các đường cao AD, BE, CF của tam giác ABC đồng quy tại trực tâm H. Gọi K, Q
lần lượt là giao điểm của đường thẳng EF với hai đường thằng AH, AO. a) Chứng minh AQE ̂ = 900.
b) Gọi I là trung điểm của AH. Chứng minh IE2 = IK.ID.
c) Gọi R, J lần lượt là trung điểm của BE, CF. Chứng minh JR vuông góc với QD. -------HẾT------
HƯỚNG DẪN GIẢI ĐỀ HUYỆN BÁT XÁT Câu 1 (4,0 điểm) T r a n g | 14 x + 2 x 1 x − 1
1.1. Cho biểu thức: P = + + : (Với x ≥ 0, x ≠ 1)
x x −1 x + x +1 1− x 2
a) Rút gọn biểu thức P b) So sánh P2 và 2P x y z a b c 2 2 2 x y z 1.2. Cho +
+ = 1 và + + = 0 . Chứng minh rằng: + + = 1. a b c x y z 2 2 2 a b c Hướng dẫn: 1.1: a) Ta có: 𝑥 + 2 √𝑥 1 2 𝑃 = ( + − ) . 3 √𝑥 − 1 𝑥 + √𝑥 + 1 √𝑥 − 1 √𝑥 − 1 𝑥 + 2 √𝑥(√𝑥 − 1) 𝑥 + √𝑥 + 1 𝑃 = [ + − ]
(√𝑥 − 1)(𝑥 + √𝑥 + 1)
(√𝑥 − 1)(𝑥 + √𝑥 + 1)
(√𝑥 − 1)(𝑥 + √𝑥 + 1) 2 . √𝑥 − 1
𝑥 + 2 + 𝑥 − √𝑥 − 𝑥 − √𝑥 − 1 2 𝑃 = .
(√𝑥 − 1)(𝑥 + √𝑥 + 1) √𝑥 − 1 2 2(√𝑥 − 1) 𝑃 = 2
(√𝑥 − 1) (𝑥 + √𝑥 + 1) 2 𝑃 = 𝑥 + √𝑥 + 1 2 Vậy: 𝑃 = với x ≥ 0 , x ≠ 1. 𝑥+√𝑥+1 b) Ta có: 2 2 4 𝑃2 = ( ) = 𝑥 + √𝑥 + 1 2 (𝑥 + √𝑥 + 1) 4 2𝑃 = 𝑥 + √𝑥 + 1 Nhận xét: 𝑥 + √𝑥 + 1 ≥ 1 2
(𝑥 + √𝑥 + 1) ≥ 𝑥 + √𝑥 + 1 4 4 ≤ 2 (𝑥 + √𝑥 + 1) 𝑥 + √𝑥 + 1 𝑃2 ≤ 2𝑃 Dấu “=” xảy ra khi: 𝑥 + √𝑥 + 1 ≥ 1 𝑥 = 0 T r a n g | 15 Vậy: 𝑃2 ≤ 2𝑃 Cách tiếp cận khác: Ta có: 𝑥 + √𝑥 + 1 > 0 Mà: 2 > 0 nên P > 0 Lại có: 𝑥 + √𝑥 + 1 ≥ 1 2 2 ≤ = 2 𝑥 + √𝑥 + 1 1 𝑃 ≤ 2 𝑃2 ≤ 2𝑃 𝑃2 ≤ 2𝑃 Dấu “=” xảy ra khi: 𝑥 + √𝑥 + 1 ≥ 1 𝑥 = 0 Vậy: 𝑃2 ≤ 2𝑃 1.2: Ta có: 𝑎 𝑏 𝑐 + + = 0 𝑥 𝑦 𝑧
𝑎𝑦𝑧 + 𝑏𝑥𝑧 + 𝑐𝑥𝑦 = 0 𝑥𝑦𝑧
𝑎𝑦𝑧 + 𝑏𝑥𝑧 + 𝑐𝑥𝑦 = 0 Lại có; 𝑥 𝑦 𝑧 + + = 1 𝑎 𝑏 𝑐 𝑥 𝑦 𝑧 2 ( + + ) = 1 𝑎 𝑏 𝑐 𝑥2 𝑦2 𝑧2 𝑥𝑦 𝑦𝑧 𝑧𝑥 + + + 2 ( + + ) = 1 𝑎2 𝑏2 𝑐2 𝑎𝑏 𝑏𝑐 𝑐𝑎 𝑥2 𝑦2 𝑧2
𝑎𝑦𝑧 + 𝑏𝑥𝑧 + 𝑐𝑥𝑦 + + + 2. = 1 𝑎2 𝑏2 𝑐2 𝑎𝑏𝑐 𝑥2 𝑦2 𝑧2 + + + 2.0 = 1 𝑎2 𝑏2 𝑐2 𝑥2 𝑦2 𝑧2 + + = 1 𝑎2 𝑏2 𝑐2
Vậy: Ta có điều phải chứng minh.
Câu 2 (2,0 điểm) Gieo một con xúc xắc cân đối và đồng chất 2 lần.
a) Mô tả không gian mẫu. T r a n g | 16
b) Tính xác suất của biến cố: “Lần đầu là số chính phương, lần sau là số lẻ”. Hướng dẫn:
a) Gọi bộ số (i;j) là các bộ số thoả thuộc không gian mẫu.
Trong đó: 𝑖; 𝑗 ∈ 𝑁; 1 ≤ 𝑖; 𝑗 ≤ 6) và i là số chấm ở lần gieo thứ nhất, j là số chấm gieo ở lần thứ 2
Ta có các bộ số dạng (i;j) thoả mãn đề bài hay chính là không gian mẫu: (1;1) (1;2) (1;3) (1;4) (1;5) (1;6) (2;1) (2;2) (2;3) (2;4) (2;5) (2;6) (3;1) (3;2) (3;3) (3;4) (3;5) (3;6) (4;1) (4;2) (4;3) (4;4) (4;5) (4;6) (5;1) (5;2) (5;3) (5;4) (5;5) (5;6) (6;1) (6;2) (6;3) (6;4) (6;5) (6;6) => Có 36 bộ số (i;j)
Số phần tử của không gian mẫu là: n(Ω) = 36
b) Gọi L là biến cố: “Lần đầu là số chính phương, lần sau là số lẻ”.
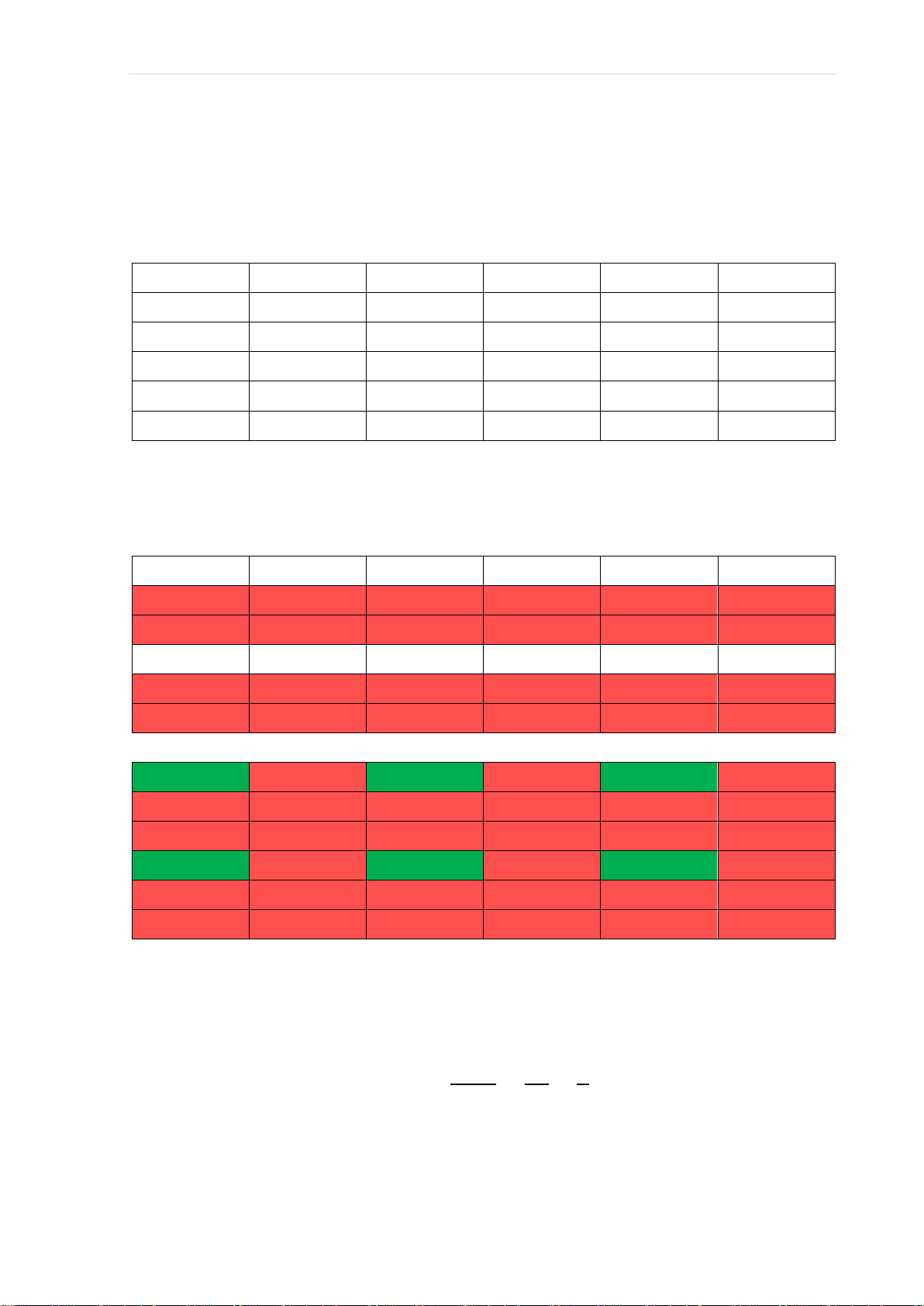
Xét số đầu tiên (số i) là số chính phương thì I chỉ có thể là 1 hoặc 4 (1;1) (1;2) (1;3) (1;4) (1;5) (1;6) (2;1) (2;2) (2;3) (2;4) (2;5) (2;6) (3;1) (3;2) (3;3) (3;4) (3;5) (3;6) (4;1) (4;2) (4;3) (4;4) (4;5) (4;6) (5;1) (5;2) (5;3) (5;4) (5;5) (5;6) (6;1) (6;2) (6;3) (6;4) (6;5) (6;6)
Xét số thứ hai (số j) là số lẻ nên j chỉ có thể là 1;3 hoặc 5 (1;1) (1;2) (1;3) (1;4) (1;5) (1;6) (2;1) (2;2) (2;3) (2;4) (2;5) (2;6) (3;1) (3;2) (3;3) (3;4) (3;5) (3;6) (4;1) (4;2) (4;3) (4;4) (4;5) (4;6) (5;1) (5;2) (5;3) (5;4) (5;5) (5;6) (6;1) (6;2) (6;3) (6;4) (6;5) (6;6)
(Ô tô màu đỏ là không thoả mãn)
=> Có 6 bộ số thoả mãn đề bài
=> Số các kết quả thuận lợi cho biến cố L là: n(L) = 6
Vậy: Xác suất của biến cố L là: 𝑛(𝐿) 6 1 𝑃(𝐿) = = = 𝑛(Ω) 36 6 Câu 3 (2,0 điểm) T r a n g | 17
Năm học 2023-2024, bạn An trúng tuyển lớp 10 trường THPT. Để chuẩn bị
cho năm học mới, lúc đầu An dự định mua 30 quyển vở và 10 cái bút cùng loại
với tổng số tiền phải trả là 340 nghìn đồng. Tuy nhiên, vì đạt danh hiệu “Học
sinh giỏi” nên An được nhận phiếu giảm giá 10% với vở và 5% với bút, do đó
An quyết định mua 50 quyển vở và 20 cây bút với tổng số tiền phải trả sau khi
giảm giá là 526 nghìn đồng. Hỏi giá tiền mỗi quyển vở và mỗi cây bút khi chưa giảm giá là bao nhiêu? Hướng dẫn:
Gọi giá tiền mỗi quyển cở và mỗi cây bút khi chưa giảm giá lần lượt là x,y
(nghìn đồng) (x,y ∈ 𝑁∗) Ta có:
- Số tiền phải trả khi mua 30 quyển vở và 10 cái bút khi chưa giảm giá là:
30𝑥 + 10𝑦 = 340 (nghìn đồng) 3𝑥 + 𝑦 = 34 (1)
- Giá tiền mỗi quyển vở khi giảm giá là: 9 (100% − 10%)𝑥 = 90%𝑥 = 𝑥 (nghìn đồng) 10
- Giá tiền mỗi cái bút khi giảm giá là: 19 (100% − 5%)𝑦 = 95%𝑦 = 𝑦 (nghìn đồng) 20
- Số tiền phải trả khi mua 50 quyển vở và 20 cái bút sau khi được giảm giá là: 9 19 50. 𝑥 + 20. 𝑦 = 526 (nghìn đồng) 10 20 45𝑥 + 19𝑦 = 526 (2)
Từ (1) và (2), ta có hệ phương trình: 3𝑥 + 𝑦 = 34 { 45𝑥 + 19𝑦 = 526
Giải ra ta được: x = 10 , y = 4 (thoả ĐKXĐ)
Vậy: Ban đầu khi chưa giảm giá, một quyển vở có giá 10 nghìn đồng và một cái
bút có giá 4 nghìn đồng.
Câu 4 (2,0 điểm) Cho 3 số thực a,b, c dương. Chứng minh rằng: 3 3 3 a + b + c 1 3
a + (b + c)3 3
b + (c + a)3 3
c + (a + b)3 Hướng dẫn: Ta có: 𝑎3 1 1 √ = = 𝑎3 + (𝑏 + 𝑐)3 √ 𝑏 + 𝑐 3 𝑏 + 𝑐 𝑏 + 𝑐 (𝑏 + 𝑐)2 1 + ( √ 𝑎 ) (1 + + 𝑎 ) [1 − 𝑎 𝑎2 ] T r a n g | 18
Theo bất đẳng thức Cauchy, ta có: 𝑏 + 𝑐 𝑏 + 𝑐 (𝑏 + 𝑐)2 1 (𝑏 + 𝑐)2 √(1 + ) [1 − + ] ≤ [2 + ] 𝑎 𝑎 𝑎2 2 𝑎2 1 1 => ≥ 𝑏 + 𝑐 𝑏 + 𝑐 (𝑏 + 𝑐)2 1 (𝑏 + 𝑐)2 √(1 + + 𝑎 ) [1 − 𝑎 𝑎2 ] 2 [2 + 𝑎2 ] 1 2𝑎2 ≥ 𝑏 + 𝑐 𝑏 + 𝑐 (𝑏 + 𝑐)2 2𝑎2 + (𝑏 + 𝑐)2 √(1 + + 𝑎 ) [1 − 𝑎 𝑎2 ]
Ta có bất đẳng thức phụ: 2(𝑥2 + 𝑦2) ≥ (𝑥 + 𝑦)2 Theo đó, ta có: 𝑎3 2𝑎2 √ ≥ 𝑎3 + (𝑏 + 𝑐)3 2𝑏2 + 2𝑏2 + 2𝑐2
Hoàn toàn tương tự, ta biến đổi và có: 2𝑎2 2𝑏2 2𝑐2 𝑉𝑇 ≥ + + = 1 2𝑏2 + 2𝑏2 + 2𝑐2 2𝑏2 + 2𝑏2 + 2𝑐2 2𝑏2 + 2𝑏2 + 2𝑐2
Vậy: Bất đẳng thức được chứng minh.
Dấu “=” xảy ra khi: a = b = c. Câu 5 (2,0 điểm)
5.1. Cho p là số nguyên tố lớn hơn 5. Chứng minh rằng 2024 p −1 chia hết cho 60.
5.2. Tìm x, y Z thoả mãn: 2y2 x + x + y +1 = x2 + 2y2 + xy Hướng dẫn:
5.1: Đặt: 𝐴 = 𝑝2024 − 1 a) Ta có:
Vì p là số nguyên tố lớn hơn 5 nên: p lẻ 𝑝1012 − 1 ⋮ 2 { 𝑝1012 + 1 ⋮ 2
=> (𝑝1012 − 1)(𝑝1012 + 1) ⋮ 4 𝑝2024 − 1 ⋮ 4 𝐴 ⋮ 4 (1) b) Ta có:
𝑝2 ≡ 0,1 (𝑚𝑜𝑑 3)
𝑝2024 ≡ 0,1 (𝑚𝑜𝑑 3)
Mà: p là số nguyên tố lớn hơn 5 nên p khôgn chia hết cho 3 hay:
𝑝2024 ≡ 1 (𝑚𝑜𝑑 3) 𝑝2024 − 1 ⋮ 3 T r a n g | 19 𝐴 ⋮ 3 (2)
c) Ta có: Vì p là số nguyên tố lớn hơn 5 nên p2 không chia hết cho 5 và:
𝑝2 ≡ 1, −1 (𝑚𝑜𝑑 5)
𝑝2024 ≡ 1 (𝑚𝑜𝑑 5) 𝑝2024 − 1 ⋮ 5 𝐴 ⋮ 5 (3)
d) Ta có: 3.4.5 = 60 và (3;4;5) = 1 (4)
Từ (1),(2),(3) và (4) suy ra: A chia hết cho 60 với p là số nguyên tố lẻ lướn hơn 5 (đpcm) 5.2: Ta có:
2𝑦2𝑥 + 𝑥 + 𝑦 + 1 = 𝑥2 + 2𝑦2 + 𝑥𝑦
2𝑦2𝑥 − 2𝑦2 + 𝑥 − 1 = 𝑥2 − 1 + 𝑥𝑦 − 𝑦 − 1
2𝑦2(𝑥 − 1) + (𝑥 − 1) = (𝑥 − 1)(𝑥 + 1) + 𝑦(𝑥 − 1) − 1
(𝑥 − 1)(2𝑦2 + 1) = (𝑥 − 1)(𝑥 + 𝑦 + 1) − 1
(𝑥 − 1)(𝑥 + 𝑦 + 1) − (𝑥 − 1)(2𝑦2 + 1) = 1
(𝑥 − 1)(𝑥 + 𝑦 − 2𝑦2) = 1
Vì (𝑥 − 1)(𝑥 + 𝑦 − 2𝑦2) = 1 nên 𝑥 − 1 và 𝑥 + 𝑦 − 2𝑦2 là các ước của 1 mà: Ư(1) = {1; −1} Trường hợp 1: 𝑥 − 1 = 1 {𝑥 + 𝑦 − 2𝑦2 = 1 => x = 2
=> 2𝑦2 − 𝑦 − 1 = 0 𝑦 = 1 => [ 1 𝑦 = − (loại) 2 Trường hợp 2: 𝑥 − 1 = −1
{𝑥 + 𝑦 − 2𝑦2 = −1 => x = 0
=> 2𝑦2 − 𝑦 − 1 = 0 𝑦 = 1 => [ 1 𝑦 = − (loại) 2
Vậy: Phương trình đã cho có nghiệm nguyên là:
(𝑥; 𝑦) = (2; 1); (0; 1). Câu 6 (2,0 điểm) Cho phương trình: 2 x − 2 2
mx + m − m − 6 = 0 ( m là tham số). Với giá trị nào của
m thì phương trình đã cho có hai nghiệm x và x sao cho x + x = . 8 1 2 1 2
Tài liệu liên quan:
-
Đề thi chọn HSG tỉnh năm học 2023-2024 môn Toán lớp 9
29 15 -
23 chuyên đề bồi dưỡng học sinh giỏi Toán lớp 9
36 18 -
Đề thi chọn học sinh giỏi tỉnh lớp 9 năm học 2025 – 2026 môn Toán
54 27 -
Bộ đề thi học sinh giỏi cấp tỉnh môn Toán lớp 9
48 24 -
Đề thi Học sinh giỏi toán lớp 9 năm 24-25 cấp thành phố Hồ Chí Minh
59 30