-
Thông tin
-
Hỏi đáp
Đề Thi HSG Vật Lí 12 Chuyên Sở Giáo Dục Quảng Nam 2022-2023 Có Đáp Án
Tài liệu đề thi học sinh giỏi Vật lí 12 trường chuyên Sở Giáo dục và đào tạo Quảng Nam năm 2022-2023 kèm đáp án chi tiết giúp bạn ôn luyện, học tốt môn học và đạt điểm cao.
Vật Lí 12 (302)
Đề Thi HSG Vật Lí 12 Chuyên Sở Giáo Dục Quảng Nam 2022-2023 Có Đáp Án
Tài liệu đề thi học sinh giỏi Vật lí 12 trường chuyên Sở Giáo dục và đào tạo Quảng Nam năm 2022-2023 kèm đáp án chi tiết giúp bạn ôn luyện, học tốt môn học và đạt điểm cao.
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI CẤP TỈNH THPT ĐỢT 1 TỈNH QUẢNG NAM
NĂM HỌC 2022 – 2023 ĐỀ CHÍNH THỨC Môn thi: VẬT LÍ
Thời gian: 180 phút (không kể thời gian giao đề)
(Đề thi có 03 trang)
Ngày thi: 07/10/2022
Câu 1. (3 điểm)
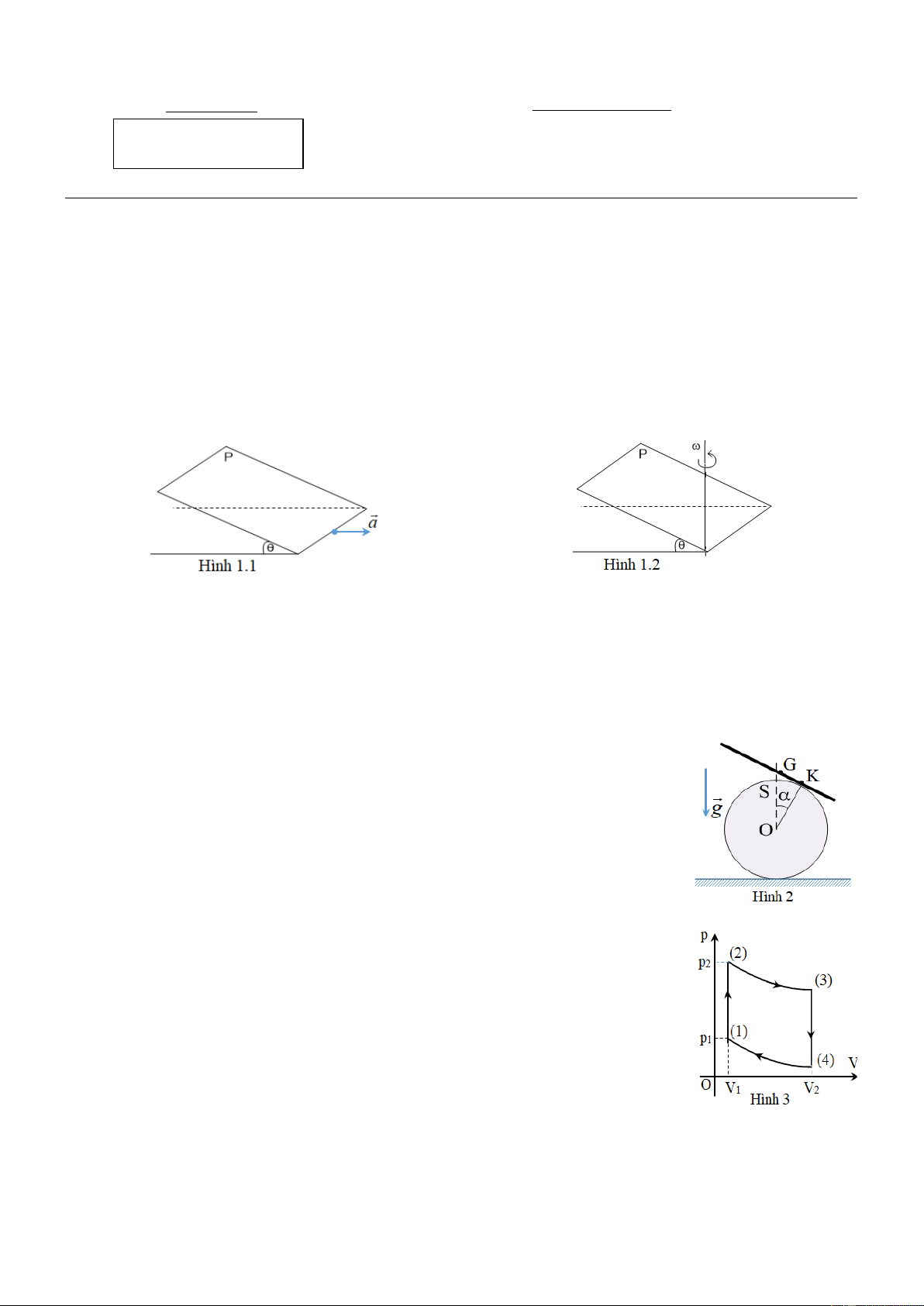
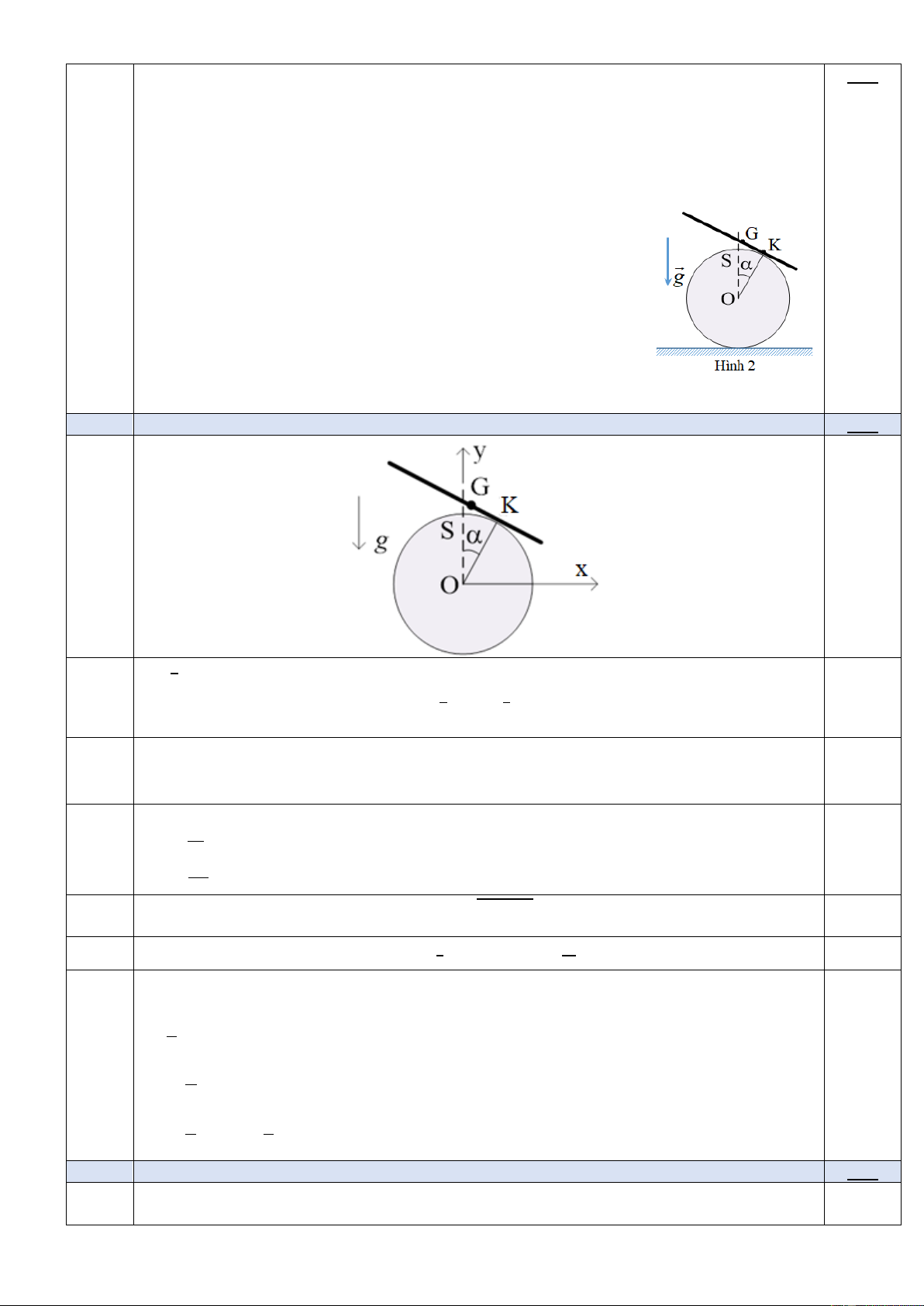
Một tấm ván phẳng P bám bụi đặt nghiêng một góc so với mặt phẳng ngang. Cho
rằng bụi bám trên tấm ván do ma sát khô với hệ số ma sát = tan, trong đó 0 /4.
Biết + = /2, gia tốc trọng trường là g.
1. Tấm ván chuyến động tịnh tiến với gia tốc 𝑎⃗ không đổi theo phương ngang, vuông góc
với giao tuyến của mặt phẳng ngang và mặt phẳng tấm ván theo chiều như hình vẽ (Hình 1.1).
Tìm điều kiện của gia tốc a để bụi vẫn còn bám trên tấm ván.
2. Tấm ván quay xung quanh trục thẳng đứng với tốc độ góc (Hình 1.2). Xác định vùng
trên tấm ván vẫn còn bám bụi với mọi giá trị của .
Câu 2. (3 điểm)
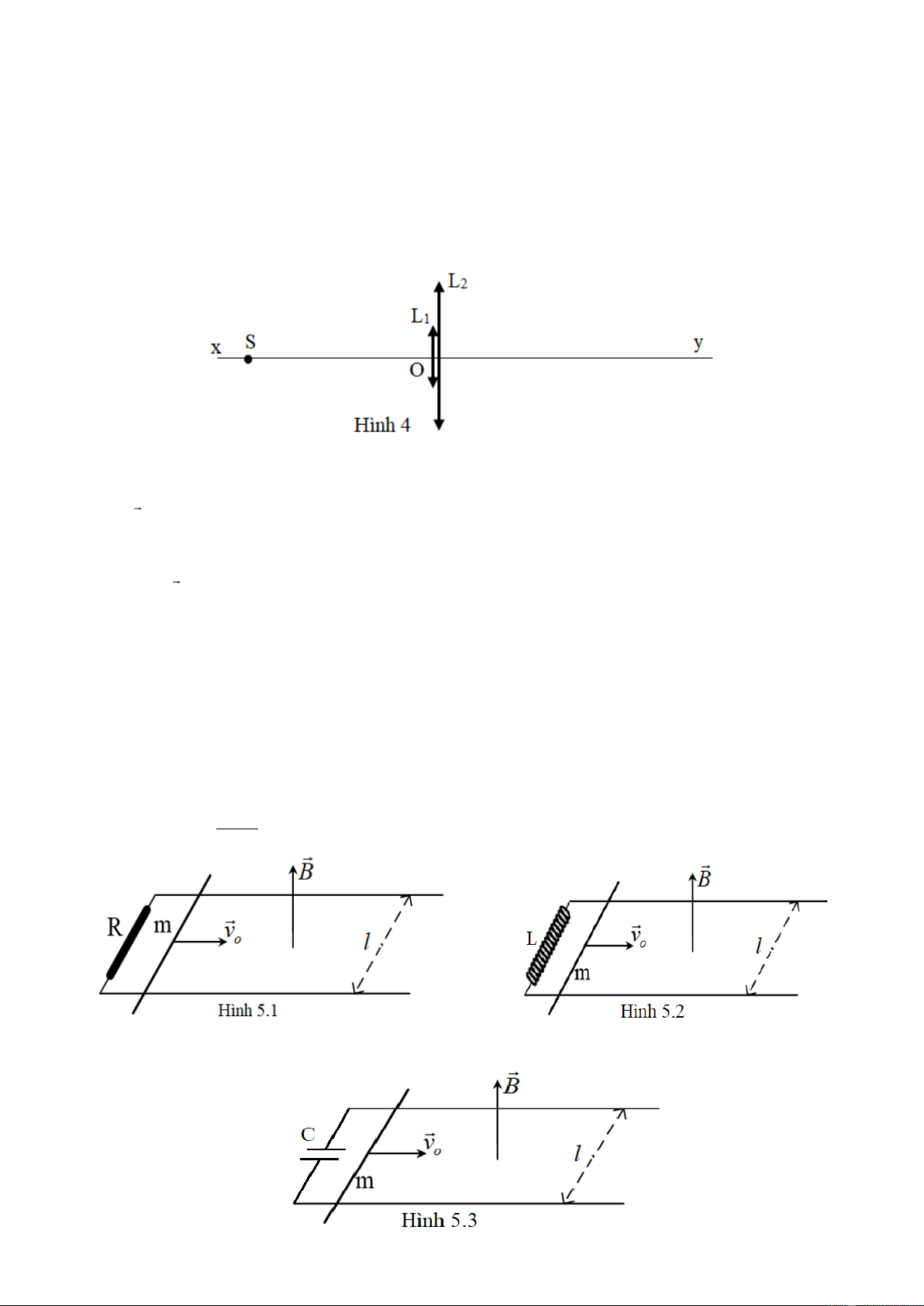
Một thanh cứng đồng chất, tiết diện không đáng kể, khối lượng m, dài 2a. Thanh được đặt
nằm ngang trên đỉnh S của khối trụ có bán kính tiết diện b được giữ đứng yên. Sau đó, thanh
được làm nghiêng một góc 0 và vẫn luôn tiếp xúc với khối trụ (Hình 2). Thả cho thanh chuyển
động không vận tốc đầu. Trong quá trình chuyển động, thanh luôn nằm trong mặt phẳng vuông
góc với trục của khối trụ.
1. Viết biểu thức động năng của thanh theo góc và tốc độ góc ’ ở
một thời điểm t bất kì.
2. Xét chuyển động với 0 < 0,1rad.
a. Xem 𝛼′ là đủ nhỏ và tích (𝑏𝛼) << a. Chứng tỏ thanh dao động
điều hòa và tìm chu kỳ dao động.
b. Tính giá trị nhỏ nhất của hệ số ma sát để thanh không trượt.
Câu 3. (4 điểm)
1. Một động cơ nhiệt thực hiện một chu trình (1) → (2) → (3) →
(4) → (1) như đồ thị (Hình 3). Xem tác nhân là khí lí tưởng đơn nguyên tử
và biết V4 = 6V1, p2 = 3p1. Các quá trình (2) → (3) và (4) → (1) là đoạn nhiệt.
a. Tính áp suất (theo p1) tại các đỉnh (3), (4) và tính nhiệt độ (theo
T1) tại các đỉnh (2), (3), (4) của đồ thị.
b. Tính nhiệt lượng tỏa ra hoặc thu vào (theo p1, V1) trong các quá
trình: (1) → (2), (2) → (3), (3) → (4), (4) → (1) và tính hiệu suất của chu trình.
2. Một mol khí thực có các hằng số Vander–Waals a và b. Khí đang ở trạng thái có nhiệt
độ T và thể tích V1 thì giãn nở đẳng nhiệt đến thể tích V2.
a. Tính công của chất khí này thực hiện (theo a, b, T, V1 và V2).
b. Áp dụng số cho ý 2a với a = 0,024 Nm4/mol2, b = 0,02 m3/mol2; V1 = 0,25 dm3,
V2 = 0,5 dm3 và T = 300K. Trang 1
Câu 4. (4 điểm)
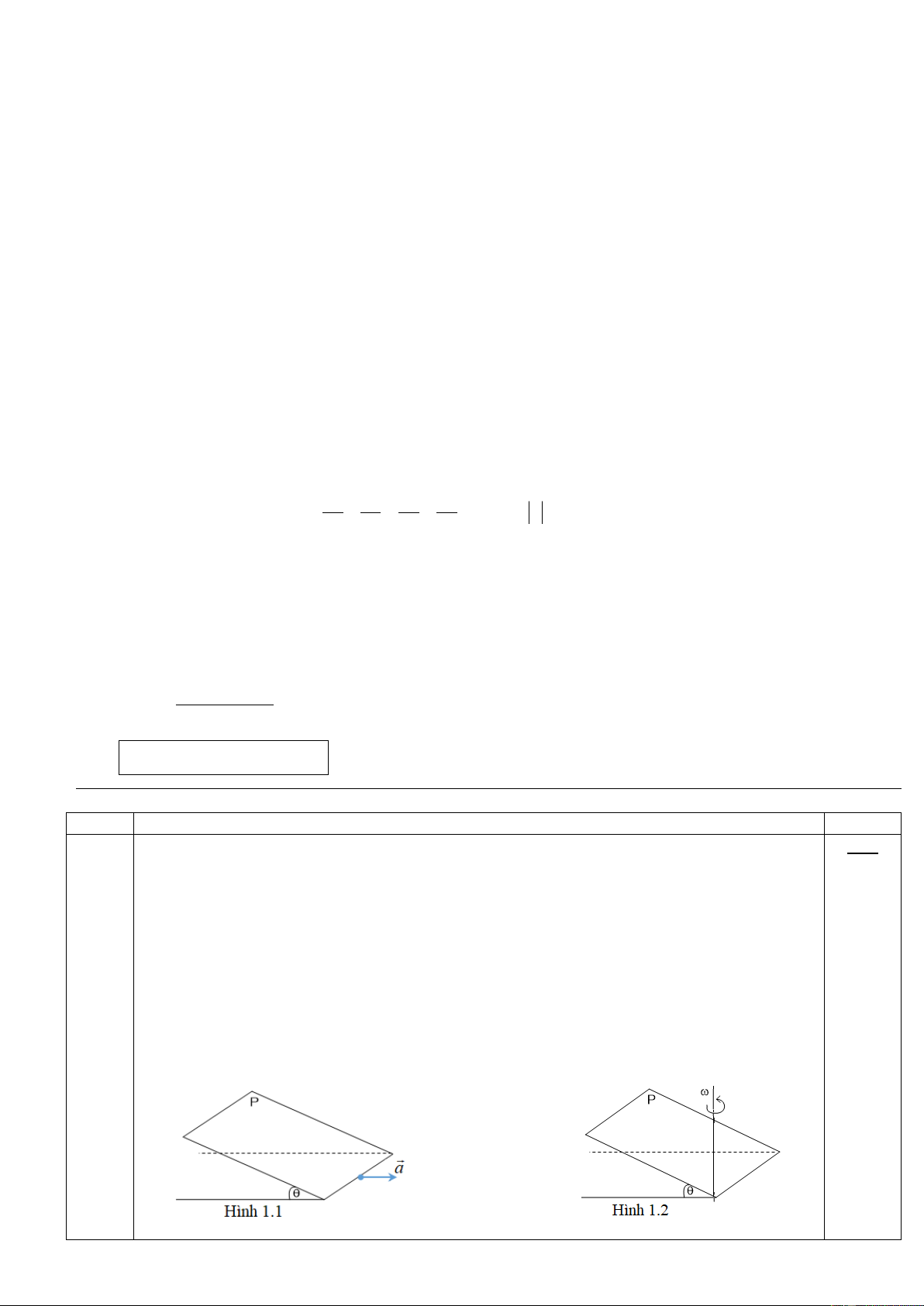
Thấu kính L1 có tiêu cự f1 = 20 cm và bán kính rìa R1 = 1 cm ; thấu kính L2 có tiêu cự
f2 = 20 cm và bán kính rìa R2 = 2 cm. Ghép sát hai thấu kính này thành hệ thấu kính đồng trục
chính xy như hình vẽ (Hình 4). Đặt trên trục chính xy của hệ thấu kính một điểm sáng S cách
quang tâm O của hệ 60 cm. Ở phía bên kia của hệ thấu kính, đặt một màn hứng ảnh (màn E)
vuông góc với trục chính sao cho trên màn thu được một vệt sáng tròn có diện tích nhỏ nhất
(Smin). Tính khoảng cách từ màn E đến O và tính Smin.
Câu 5. (4 điểm)
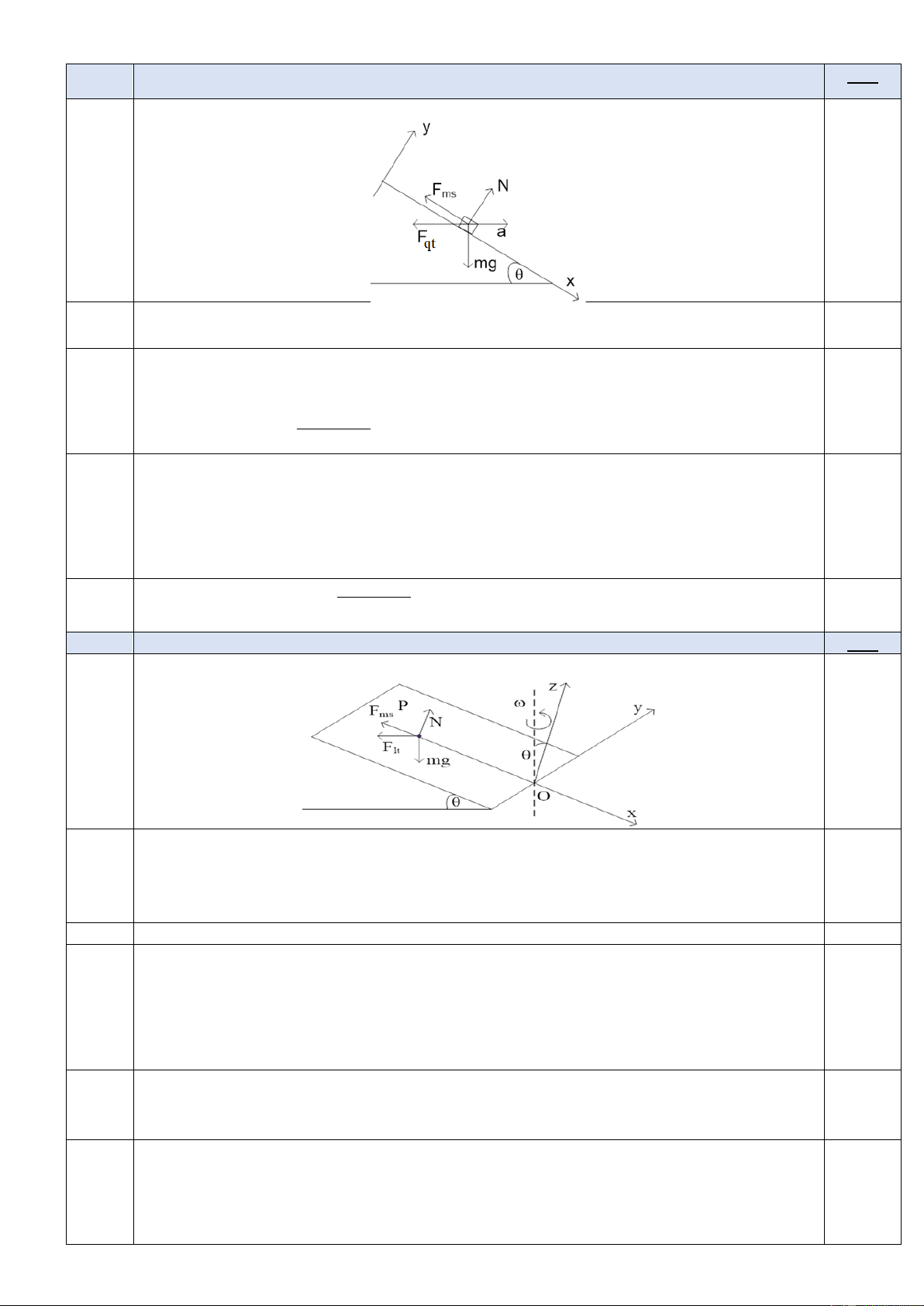
Hai thanh ray dẫn điện đặt nằm ngang, song song và cách nhau l trong từ trường có cảm
ứng từ B có phương thẳng đứng, hướng lên. Một thanh kim loại có khối lượng m đặt trên hai
thanh ray và vuông góc với hai thanh. Bỏ qua ma sát giữa thanh kim loại và hai thanh ray, xem
điện trở của thanh kim loại và hai thanh ray không đáng kể. Ban đầu, truyền cho thanh kim loại
một vận tốc v hướng dọc theo thanh ray. Viết phương trình chuyển động của thanh kim loại và o
tìm khoảng dịch chuyển lớn nhất của nó trong các trường hợp sau:
1. Cảm ứng từ B không đổi:
a. Đầu các thanh ray nối với điện trở R (Hình 5.1).
b. Đầu các thanh ray nối với cuộn dây thuần cảm có độ tự cảm L (Hình 5.2).
2. Cảm ứng từ B biến đổi theo thời gian theo biểu thức: B = t, trong đó là hằng số
dương, đầu các thanh ray nối với tụ điện có điện dung C (Hình 5.3). dx Cho biết: = arctan x + C 2 1+ x Trang 2
Câu 6. (2 điểm)
Xét chuyển động của một tấm nhựa phẳng trên một mặt bàn phẳng nằm ngang. Trong quá
trình chuyển động, tấm nhựa chịu tác dụng của lực ma sát trượt với hệ số ma sát trượt α và chịu
lực cản của môi trường. Biết lực cản của môi trường phụ thuộc vào vận tốc theo biểu thức: r r
f = −v (β là hệ số cản). Coi các va chạm trong quá trình làm thí nghiệm (nếu có) là hoàn toàn c đàn hồi. Cho các dụng cụ sau:
- Vật nhỏ có khối lượng m đã biết;
- Thước đo có vạch chia đến milimét;
- Các sợi dây mềm, mảnh, nhẹ, không giãn;
- Tấm nhựa phẳng hình chữ nhật;
- Bàn thí nghiệm, giá đỡ, giá treo cần thiết. Yêu cầu:
1. Trình bày cơ sở lí thuyết và xây dựng các công thức cần thiết để xác định hệ số ma sát
trượt α giữa tấm nhựa với mặt bàn và hệ số cản β của môi trường khi tấm nhựa chuyển động.
2. Trình bày cách bố trí thí nghiệm, thu thập và xử lí số liệu để xác định α và β. 2 3 4 5 Cho biết: x x x x
ln( 1 + x ) = x − + − +
− ... khi x 1. 2 3 4 5
--------------- HẾT ---------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI HỌC SINH GIỎI CẤP TỈNH THPT ĐỢT 1 TỈNH QUẢNG NAM NĂM HỌC 2022 - 2023 HƯỚNG DẪN CHẤM HDC CHÍNH THỨC MÔN: VẬT LÝ Câu/Ý Nội dung Điểm Câu 1
Câu 1. (3 điểm) 3,0đ
Một tấm ván phẳng P bám bụi đặt nghiêng một góc so với mặt phẳng
ngang. Cho rằng bụi bám trên tấm ván do ma sát khô với hệ số ma sát =
tan, trong đó 0 /4. Biết + = /2, gia tốc trọng trường là g.
1. Tấm ván chuyến động tịnh tiến với gia tốc 𝑎⃗ không đổi theo phương ngang,
vuông góc với giao tuyến của mặt phẳng ngang và mặt phẳng tấm ván theo chiều
như hình vẽ (Hình 1.1). Tìm điều kiện của gia tốc a để bụi vẫn còn bám trên tấm ván.
2. Tấm ván quay xung quanh trục thẳng đứng với tốc độ góc (Hình 1.2).
Xác định vùng trên tấm ván vẫn còn bám bụi với mọi giá trị của . Trang 3 Ý 1 1,0đ
Phân tích lực. Chọn hệ quy chiếu gắn với tấm ván 0,125
- Hạt bụi B cân bằng: 𝑚𝑔⃗ + 𝐹⃗ 0,125 𝑞𝑡 + 𝑁 ⃗⃗ + 𝐹⃗𝑚𝑠 = 0
- Trong đó; 𝑁 = 𝑚𝑔𝑐𝑜𝑠 + 𝑚𝑎𝑠𝑖𝑛 0,125
TH1: 𝑚𝑔𝑠𝑖𝑛 > 𝑚𝑎𝑐𝑜𝑠 (1): Lực ma sát nghỉ có chiều ngược chiều Ox:
𝑚𝑔𝑠𝑖𝑛 − 𝑚𝑎𝑐𝑜𝑠 − 𝐹𝑚𝑠 = 0
𝐹𝑚𝑠 = 𝑚𝑔𝑠𝑖𝑛 − 𝑚𝑎𝑐𝑜𝑠 ≤ 𝜇𝑁 = (𝑚𝑔𝑐𝑜𝑠 + 𝑚𝑎𝑠𝑖𝑛).cotag (2)
𝑠𝑖𝑛2−𝑐𝑜𝑠2 Từ (1) và (2) suy ra: 𝑔
≤ 𝑎 ≤ 𝑔𝑡𝑎𝑛 (*)
2𝑐𝑜𝑠𝑠𝑖𝑛 0,25
TH2: 𝑚𝑔𝑠𝑖𝑛 < 𝑚𝑎𝑐𝑜𝑠 (3): Lực ma sát nghỉ có chiều cùng chiều Ox:
𝑚𝑔𝑠𝑖𝑛 − 𝑚𝑎𝑐𝑜𝑠 + 𝐹𝑚𝑠 = 0
𝐹𝑚𝑠 = −𝑚𝑔𝑠𝑖𝑛 + 𝑚𝑎𝑐𝑜𝑠 ≤ 𝜇𝑁 = (𝑚𝑔𝑐𝑜𝑠 + 𝑚𝑎𝑠𝑖𝑛).cotag (4)
Từ (3) và (4) suy ra: 𝑎 ≥ 𝑔𝑡𝑎𝑛 (**) 0,25
𝑠𝑖𝑛2−𝑐𝑜𝑠2
Từ (*) và (**) suy ra: 𝑎 ≥ 𝑔 0,125
2𝑐𝑜𝑠𝑠𝑖𝑛 Ý 2 2,0đ
Chon hệ quy chiếu gắn với tấm ván. Vẽ các lực tác dụng lên 1 hat bụi 0,25
- Gọi 𝑛⃗ là vectơ pháp tuyến đơn vị hướng lên trên mặt phẳng. Khi đó, điều kiện cân bằng của
một hạt bụi có thể được viết dưới dạng: 𝑚𝑔⃗ + 𝐹⃗ 0,25 𝑙𝑡 + 𝑁 ⃗⃗ + 𝐹⃗𝑚𝑠 = 0
+ Đặt: 𝑓⃗ = 𝑚𝑔⃗ + 𝐹⃗𝑙𝑡 + Suy ra: 𝑓⃗ + 𝑁 ⃗⃗ + 𝐹⃗𝑚𝑠 = 0 (1)
- Để hạt bụi không trượt: 𝐹𝑚𝑠 ≤ 𝜇𝑁 ℎ𝑎𝑦 𝐹𝑚𝑠 − 𝜇𝑁 ≤ 0 (*) 0,125
- Để giải quyết bài toán tổng quát cho các hạt bụi trên tấm ván ở các vị trí khác nhau ta dùng các
phép toán véc tơ để chuyển các điều kiện các hạt bụi không trượt thành các biểu thức véc tơ
+ Nhân phần bên trái và bên phải của bất đẳng thức (*) với giá trị dương 𝐹𝑚𝑠 + 𝜇𝑁, ta được: 𝐹 2 𝑚𝑠 − 𝜇2𝑁2 ≤ 0
+ Chuyển thành phương trình véc tơ: (𝐹 ⃗⃗⃗⃗ ⃗⃗⃗⃗
𝑚𝑠, 𝐹𝑚𝑠) − 𝜇2(𝑁 ⃗⃗, 𝑁⃗⃗) ≤ 0 0,125
- Sau đây, dấu ngoặc đơn được sử dụng để biểu thị tích vô hướng. Có tính đến tính trực giao của các vectơ 𝐹 ⃗⃗⃗⃗ 𝑚𝑠 và 𝑁
⃗⃗, bất đẳng thức cuối cùng được viết là (𝐹 ⃗⃗⃗⃗ ⃗⃗⃗⃗ 0,125 𝑚𝑠 + 𝑁
⃗⃗, 𝐹𝑚𝑠 + 𝑁⃗⃗ ) − (1 + 𝜇2)(𝑁⃗⃗, 𝑁⃗⃗) ≤ 0 (2)
- Từ phép nhân vô hướng của phần bên trái và bên phải của đẳng thức (1) bởi 𝑛⃗ ta có
(𝑛⃗, 𝑓⃗) + (𝑛⃗, 𝑁
⃗⃗) = (𝑛⃗, 𝑓⃗) + 𝑁 = 0 suy ra: 𝑁 = −(𝑛⃗, 𝑓⃗)
- Từ đẳng thức (1) ta có: (𝐹 ⃗⃗⃗⃗ 𝑚𝑠 + 𝑁 ⃗⃗) = −𝑓⃗
- Thay 𝑁 = −(𝑛⃗, 𝑓⃗) và (𝐹 ⃗⃗⃗⃗ 𝑚𝑠 + 𝑁
⃗⃗) = −𝑓⃗ vào bất đẳng thức (2) ta được: Trang 4 2 (𝑓⃗,⃗𝑓
⃗⃗) − (1 + 𝜇2)(𝑛⃗, 𝑓⃗) ≤ 0 (3) 0,125
Bất đẳng thức (3) là điều kiện hạt bụi không trượt trên tấm ván
- Mặt khác để hạt bụi không rời tấm ván thì hợp lực 𝑓⃗ = 𝑚𝑔⃗ + 𝐹⃗
𝑙𝑡 phải hướng vào trong tấm
ván, góc làm bởi (𝑛⃗,⃗𝑓
⃗⃗) phải lớn hơn π/2 từ đó ta có : (𝑛⃗,⃗𝑓 ⃗⃗) < 0 (4) 0,125
Vậy các bất đẳng thức (3) và (4) là điều kiện để các hạt bụi vẫn bám trên tấm ván
- Gọi Oxyz là hệ quy chiếu gắn với tấm ván, O nằm tại giao điểm của mp P và trục quay, mp tọa
độ Oxy trùng với mặt phẳng P và trục Oz hướng theo pháp tuyến mặt phẳng P (xem hình); z = 0 là
phương trình của mặt phẳng P, 𝑛⃗ là pháp tuyến đơn vị của mặt phẳng này. - Ta có:
+ Véc tơ vận tốc góc của tấm ván là:
⃗⃗ = (−𝑠𝑖𝑛𝑖⃗ + 0𝑗⃗ + 𝑐𝑜𝑠𝑘⃗⃗)
+ Vectơ gia tốc trọng trường: 𝑔⃗ = 𝑔(𝑠𝑖𝑛𝑖⃗ + 0𝑗⃗ − 𝑐𝑜𝑠𝑘⃗⃗).
+ Hạt bụi B có vị trí được cho bởi vectơ bán kính vectơ (⃗𝑂𝐵
⃗⃗⃗⃗ )⃗⃗ = 𝑟⃗ = 𝑥𝑖⃗ + 𝑦𝑗⃗ + 𝑧𝑘⃗⃗
+ Lực quán tính li tâm được được cho bởi công thức: 𝐹 ⃗⃗⃗ 𝑙𝑡 = 𝑚𝑎 ⃗ 𝑙𝑡 ⃗⃗⃗ = 𝑚 ⃗⃗ (𝑟⃗
⃗⃗) = 𝑚2((cos 𝜃(𝑧 sin 𝜃 + 𝑥 cos 𝜃)𝑖⃗ + 𝑦𝑗⃗ + sin 𝜃(𝑧 sin 𝜃 +𝑥 cos 𝜃)𝑘⃗⃗ 0,125
Hạt bụi B thuộc về mặt phẳng P, tức là z = 0, biểu thức trên được viết là: 0,125 𝐹 ⃗⃗⃗ 𝑙𝑡 = 𝑚𝑎 ⃗ 𝑙𝑡
⃗⃗⃗ = 𝑚2(𝑥 cos2 𝜃 𝑖⃗ + 𝑦𝑗⃗ + 𝑥 sin 𝜃 cos 𝜃 𝑘⃗⃗) Kết quả là: 𝑓⃗ = 𝑚(𝑎 ⃗ 𝑙𝑡
⃗⃗⃗ + 𝑔⃗) == 𝑚[(2𝑥 cos2 𝜃 + 𝑔𝑠𝑖𝑛𝜃)𝑖⃗ + 2𝑦𝑗⃗ + (2𝑥 sin 𝜃 cos 𝜃 − 𝑔𝑐𝑜𝑠𝜃)𝑘⃗⃗]
(𝑓⃗, 𝑓⃗) = 𝑚2(𝑔2 + 𝜔4(𝑥2 𝑐𝑜𝑠2 𝜃 + 𝑦2))
(𝑓⃗, 𝑛⃗) = 𝑚(𝜔2𝑥 sin 𝜃 − 𝑔) cos 𝜃
- Khi đó, tính đến mối quan hệ giữa góc nghiêng của mặt phẳng và góc đã cho trong điều kiện,
bất đẳng thức (3) có thể được biểu diễn dưới dạng 2 sin2 𝛼 2cos2 𝛼−1 𝜔4𝑦2 + 2𝑔𝜔 𝑥 + 𝑔2 ≤ 0 cos 𝛼 cos2 𝛼 1 𝜔2 cos 𝛼 𝑔(2cos2𝛼 − 1) 𝑥 ≤ − ( 𝑦2 + ) 2 𝑔 sin2 𝛼 𝜔2 sin2 𝛼 cos 𝛼 0,125
Điều này có nghĩa là với 0 vùng của các giá trị cho phép là tập hợp các điểm có tọa độ x, y
trên mặt phẳng P thỏa mãn bất đẳng thức trên, miền các giá trị này được giới hạn bởi vùng bên
trong một parabol như hình vẽ: 0,125
Tọa độ đỉnh của parabol: 𝑆∗ = (𝑠∗, 0,0) 𝑔(1 − 2𝑐𝑜𝑠2𝛼) 0,125
𝑠∗ = 2𝜔2 𝑠𝑖𝑛2 𝛼 𝑐𝑜𝑠 𝜋
- Với 0 < 𝛼 < , đỉnh S nằm cao hơn dọc theo đường dốc so với điểm O 4 𝜋
- Với 𝛼 = đỉnh S trùng O 4
- Bất đẳng thức (4), suy ra: (𝜔2𝑥 𝑐𝑜𝑠 − 𝑔) 𝑠𝑖𝑛 𝛼 < 0 𝑔 0,125 𝑥 < 𝑥∗ = 𝜔2 𝑐𝑜𝑠 𝛼
Vậy nữa mặt phẳng giới hạn bởi 𝑥 < 𝑥∗ thỏa mãn điều kiện bất đẳng thức (4) và ta có 𝑆∗ < 𝑥∗
do đó các hạt bụi ở miền giới hạn bên trong Parabol thỏa mãn đồng thời hai điều kiện (3) và (4) 0,125 và luôn có bụi bám. Trang 5 Câu 2
Câu 2. (3 điểm) 3,0đ
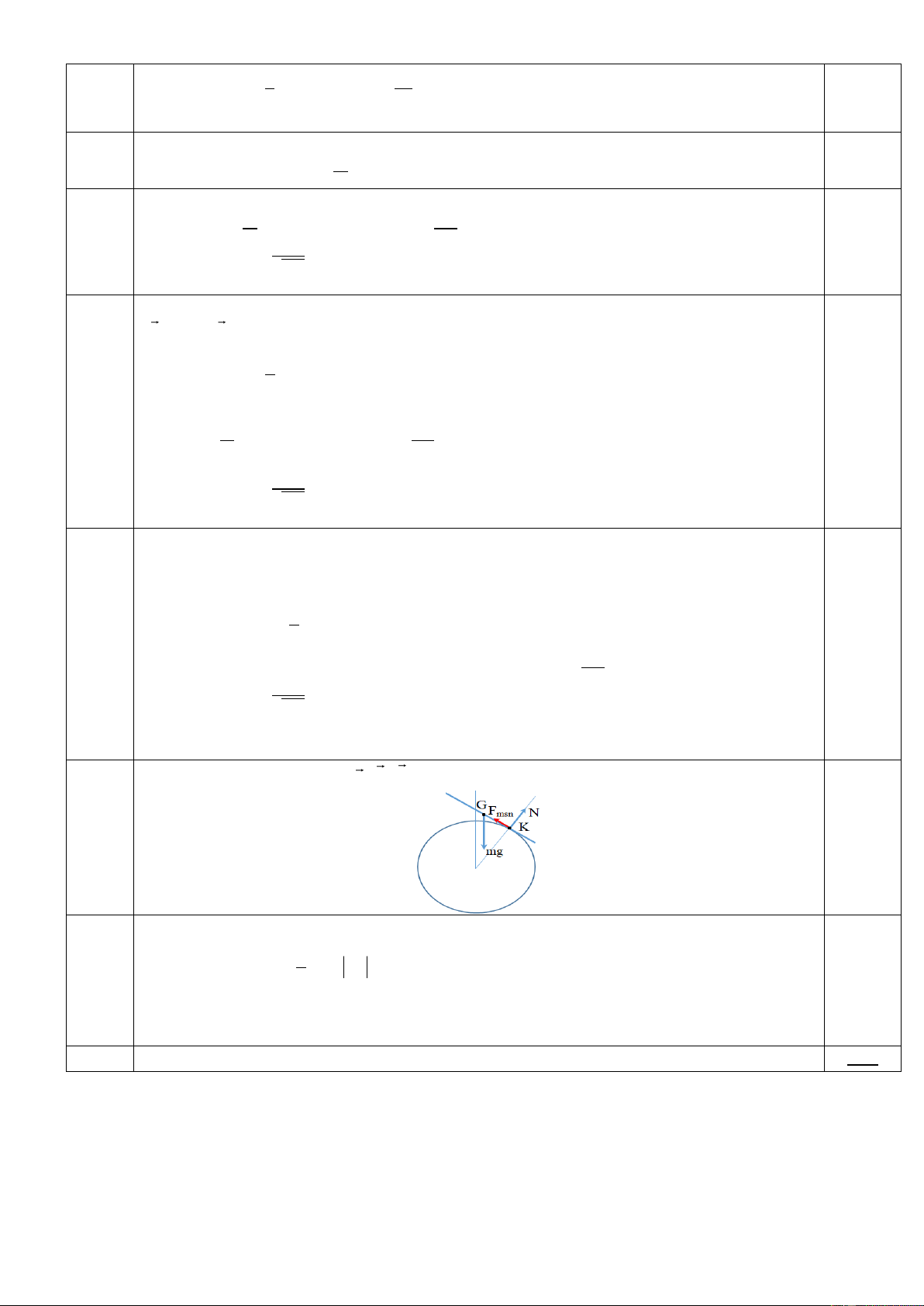
Một thanh cứng đồng chất, tiết diện không đáng kể, khối lượng m, dài 2a.
Thanh được đặt nằm ngang trên đỉnh S của khối trụ có bán kính tiết diện b được
giữ đứng yên. Sau đó, thanh được làm nghiêng một góc 0 và vẫn luôn tiếp xúc
với khối trụ (Hình 2). Thả cho thanh chuyển động không vận tốc đầu. Trong quá
trình chuyển động, thanh luôn nằm trong mặt phẳng vuông
góc với trục của khối trụ.
1. Viết biểu thức động năng của thanh theo góc và tốc độ
góc ’ ở một thời điểm t bất kì.
2. Xét chuyển động với 0 < 0,1rad.
a. Xem 𝛼′ là đủ nhỏ và tích (𝑏𝛼) << a. Chứng tỏ thanh
dao động điều hòa và tìm chu kỳ dao động.
b. Tính giá trị nhỏ nhất của hệ số ma sát để thanh không trượt. Ý 1 1,0đ 1
𝐼 = 𝑚𝑎2 là mô men quán tính của thanh đối với trục quay qua khối tâm G) 0,25 3 1 1
- Động năng của thanh ở thời điểm t: 𝑊 2 đ = 𝑚𝑣 + 𝐼(′)2 2 𝐺 2 0,25
(Trong đó vG là vận tốc khối tâm của thanh, ′ là vận tốc góc của thanh quanh khối tâm G)
- Ta có véc tơ xác định vị trí tâm G của thanh là: 𝑂𝐺 ⃗⃗⃗⃗ = 𝑂𝐾 ⃗⃗⃗⃗ + 𝐾𝐺 ⃗⃗⃗⃗ (1)
- Chuyển động lăn không trượt ta có IG bằng chiều dài cung KS, KG = b
- Chiếu (1) theo phương Ox, Oy ta được: 𝑥 = 𝑏𝑠𝑖𝑛 − 𝑏 𝑐𝑜𝑠, 𝑦 = 𝑏𝑐𝑜𝑠 + 𝑏 𝑠𝑖𝑛
Vận tốc của G theo các phương Ox, Oy là: 𝑑𝑥 𝑣 𝑥 =
= 𝑏′𝑐𝑜𝑠 − 𝑏(′𝑐𝑜𝑠 − ′𝑠𝑖𝑛) = 𝑏′𝑠𝑖𝑛 𝑑𝑡 𝑑𝑦 𝑣𝑦 =
= −𝑏′𝑠𝑖𝑛 + 𝑏(′𝑠𝑖𝑛 + ′𝑐𝑜𝑠) = 𝑏′𝑐𝑜𝑠 𝑑𝑡 0,25
Vận tốc chuyển động của khối tâm G là: 𝑣 2 2
𝐺 = √𝑣𝑥 + 𝑣𝑦 = 𝑏′ 1 𝑎2
Động năng của thanh ở thời điểm t: 𝑊đ = 𝑚′2 ((𝑏)2 + ) 0,25 2 3
Cách 2: Chọn trục quay tức thời qua điểm tiếp xúc K
Momen quán tính: IK = m.KG2 + IG 0,25 1 0,25 I + I = 2 2 ma ( m b ) 3 1 0,25 2 W = I ( ') d 2 I 1 1 2 2 2 W = m( ') a + (b ) 0,25 d 2 3 Ý 2 2,0đ Ý 2a
Chọn mốc thế năng trọng trường tại O, cơ năng của thanh: 0,25 Trang 6 1 𝑎2
𝑊 = 𝑊đ + 𝑊𝑡 = 𝑚′2 ((𝑏)2 +
) + 𝑚𝑔(𝑏𝑐𝑜𝑠 + 𝑏 𝑠𝑖𝑛) 2 3
- Đạo hàm biểu thức năng lượng theo thời gian, lưu ý cơ năng của thanh bảo toàn ta được 0,25 𝑎2
phương trình: " ((𝑏)2 +
) + 𝑏2′2 + 𝑔𝑏𝑐𝑜𝑠 = 0 (3) 3
- Khi ≪ 0,1𝑟𝑎𝑑, 𝑐𝑜𝑠 ≈ 1, các số hạng bậc 2 của và ′2 có thể bỏ qua khi đó phương trình 𝑎2 3𝑔𝑏 (3) trở thành:
" + 𝑔𝑏 = 0 ℎ𝑎𝑦 " + = 0 0,25 3 𝑎2 𝑎 - Chu kỳ: 𝑇 = 2𝜋 √3𝑔𝑏 0,25 Cách 2 (Ý 2a): '
M dt = dL → M = ' .I + ' I 0,25 K K K 1 2 2 2 2
−mgbcos =
ma + m(b ) '− 2mb ' 0,25 3
Khi ≪ 0,1𝑟𝑎𝑑, 𝑐𝑜𝑠 ≈ 1, các số hạng bậc 2 của và ” có thể bỏ qua khi đó phương trình (3) 0,25 𝑎2 3𝑔𝑏 trở thành:
" + 𝑔𝑏 = 0 ℎ𝑎𝑦 " + = 0 3 𝑎2 0,25 𝑎 - Chu kỳ: 𝑇 = 2𝜋 √3𝑔𝑏 Cách 3 (Ý 2a):
Chọn trục quay tức thời qua I và xem IK gần như không đổi khi thanh dao động nên: 0,25 M = −I '' K K 1 2 2
→ mgbcos = − ma + ( m b ) ' 0,25 3 3𝑔𝑏
Xem cosα = 1 và bỏ qua b.α so với a thì thu được kết quả: " + = 0 0,25 𝑎2 𝑎 - Chu kỳ: 𝑇 = 2𝜋 √3𝑔𝑏 0,25 Ý 2b
Lực tác dụng lên thanh gồm mg, N , f 0,25 msn
Tại vị trí biên, thanh không trượt: f
= mg sin mg 0,25 msn o 1 Tại vị trí biên: 2 Nb =
ma '' → N mg 0,25 3 f
= mg mg msn o 0,125 Suy ra: = 0,125 min o Câu 3
Câu 3. (4 điểm) 4,0đ Trang 7
1. Một động cơ nhiệt thực hiện một chu trình (1) →
(2) → (3) → (4) → (1) như đồ thị (Hình 3). Xem tác nhân là khí
lí tưởng đơn nguyên tử và biết V4 = 6V1, p2 = 3p1. Các quá
trình (2) → (3) và (4) → (1) là đoạn nhiệt.
a. Tính áp suất (theo p1) tại các đỉnh (3), (4) và tính
nhiệt độ (theo T1) tại các đỉnh (2), (3), (4) của đồ thị.
b. Tính nhiệt lượng tỏa ra hoặc thu vào (theo p1, V1)
trong các quá trình: (1) → (2), (2) → (3), (3) → (4), (4) → (1) và
tính hiệu suất của chu trình.
2. Một mol khí thực có các hằng số Vander–Waals a và b. Khí đang ở trạng
thái có nhiệt độ T và thể tích V1 thì giãn nở đẳng nhiệt đến thể tích V2.
a. Tính công của chất khí này thực hiện (theo a, b, T, V1 và V2).
b. Áp dụng số cho ý 2a với a = 0,024 Nm4/mol2, b = 0,02 m3/mol2; V1 =
0,25 dm3, V2 = 0,5 dm3 và T = 300K. Ý 1a 1,5đ p p p T (1) → (2): Đẳng tích: 1 2 2 1 = T = = 3T 2 1 T T p 0,5 1 2 1 p V V 1 (2) → (3): Đoạn nhiệt: 2 2 2
p V = p V p = = p = 3p 0,15p 0,25 3 3 2 2 3 2 1 1 V V 6 3 3 1 − 1 − − − V 1 Có: 1 1 2 T V = T V
T = T = 3T 0,9T 0,25 2 2 3 3 3 2 1 1 V 6 3 p V V 1 (4) → (1): Đoạn nhiệt: 1 1 1
p V = p V p = = p = p 0,05p 0,25 1 1 4 4 4 1 1 1 V V 6 4 4 1 − 1 − − − V 1 Có: 1 1 1 = = = TV T V T T T 0,3T 0,25 1 1 4 4 4 1 1 1 V 6 4 Ý 1b 1,0đ i i 0,25
(1) → (2): Thu: Q = C (T − T ) =
R(T − T ) =
( p V − p V ) = ip V = 3 p V 12 V 2 1 2 1 2 2 1 1 1 1 1 1 2 2 i i 0,25
(3) → (4): Tỏa: Q = C (T − T ) =
R(T − T ) =
( p V − p V ) 0 − ,9 pV 34 V 4 3 4 1 4 4 3 3 1 1 2 2
(2) → (3) và (4) → (1): Q23 = Q41 = 0 0,25 Q + Q
3 p V − 0,9 p V 0,25 Hiệu suất: 12 34 1 1 1 1 H = = = 0,7 Q 3 p V 12 1 Ý 2a 1,0đ a 0,25
Phương trình Van – der – Van cho 1 mol khí: p +
V − b = RT 2 ( ) V RT a 0,25 p = − 2 V − b V V dV dV − 0,5 V a V b a a A = pdV = RT − a = RT ln (V −b) 2 2 2 + = RT ln + − 2 V1 V − b V V V − b V V V 1 1 2 1 Ý 2b 0,5đ Thay số đúng: A = -79,8J 0,5 Câu 4
Câu 4. (4 điểm) 4,0đ Trang 8
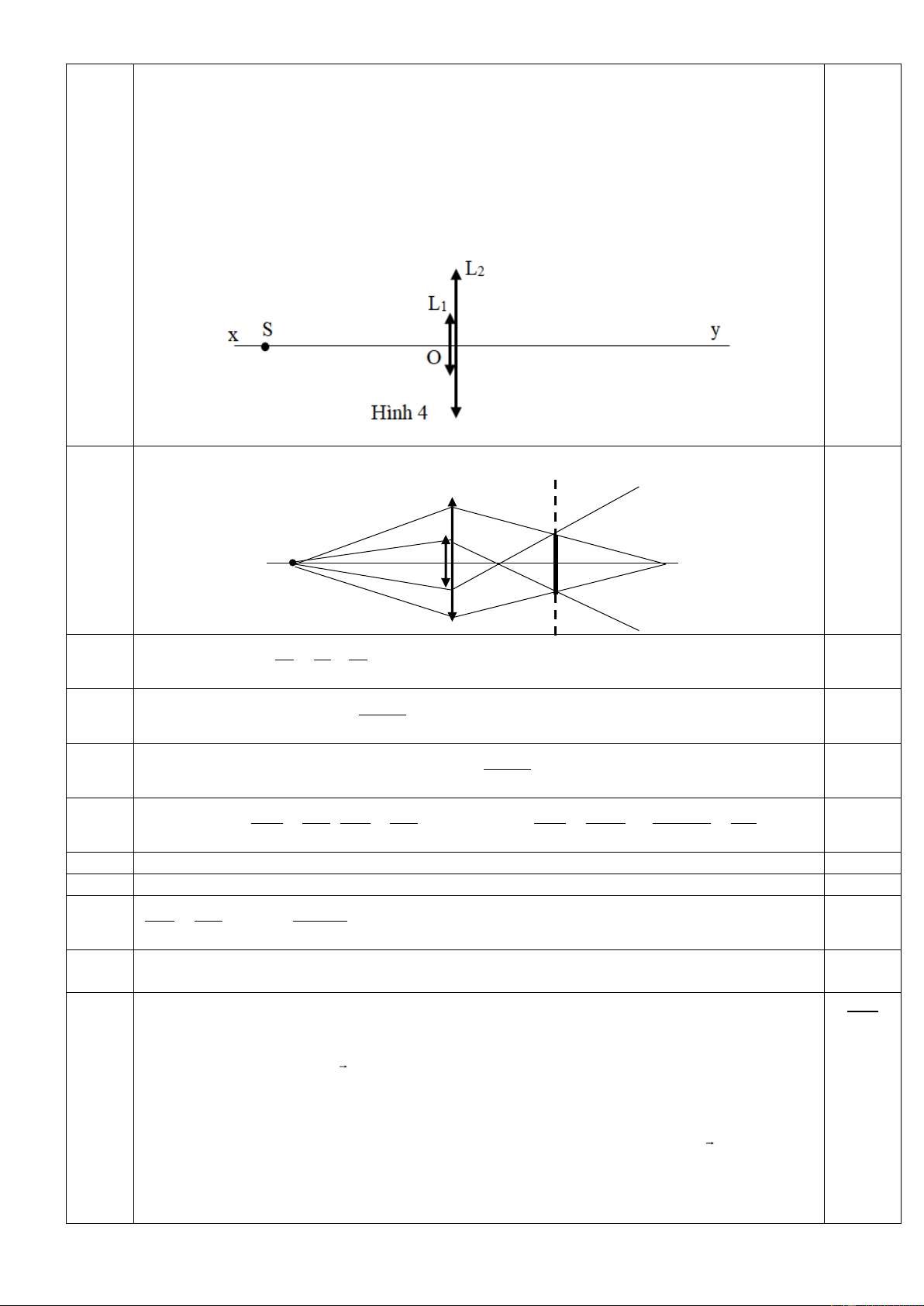
Thấu kính L1 có tiêu cự f1 = 20 cm và bán kính rìa R1 = 1 cm ; thấu kính L2
có tiêu cự f2 = 20 cm và bán kính rìa R2 = 2 cm. Ghép sát hai thấu kính này
thành hệ thấu kính đồng trục chính xy như hình vẽ (Hình 4). Đặt trên trục chính
xy của hệ thấu kính một điểm sáng S cách quang tâm O của hệ 60 cm. Ở phía
bên kia của hệ thấu kính, đặt một màn hứng ảnh (màn E) vuông góc với trục
chính sao cho trên màn thu được một vệt sáng tròn có diện tích nhỏ nhất
(Smin). Tính khoảng cách từ màn E đến O và tính Smin.
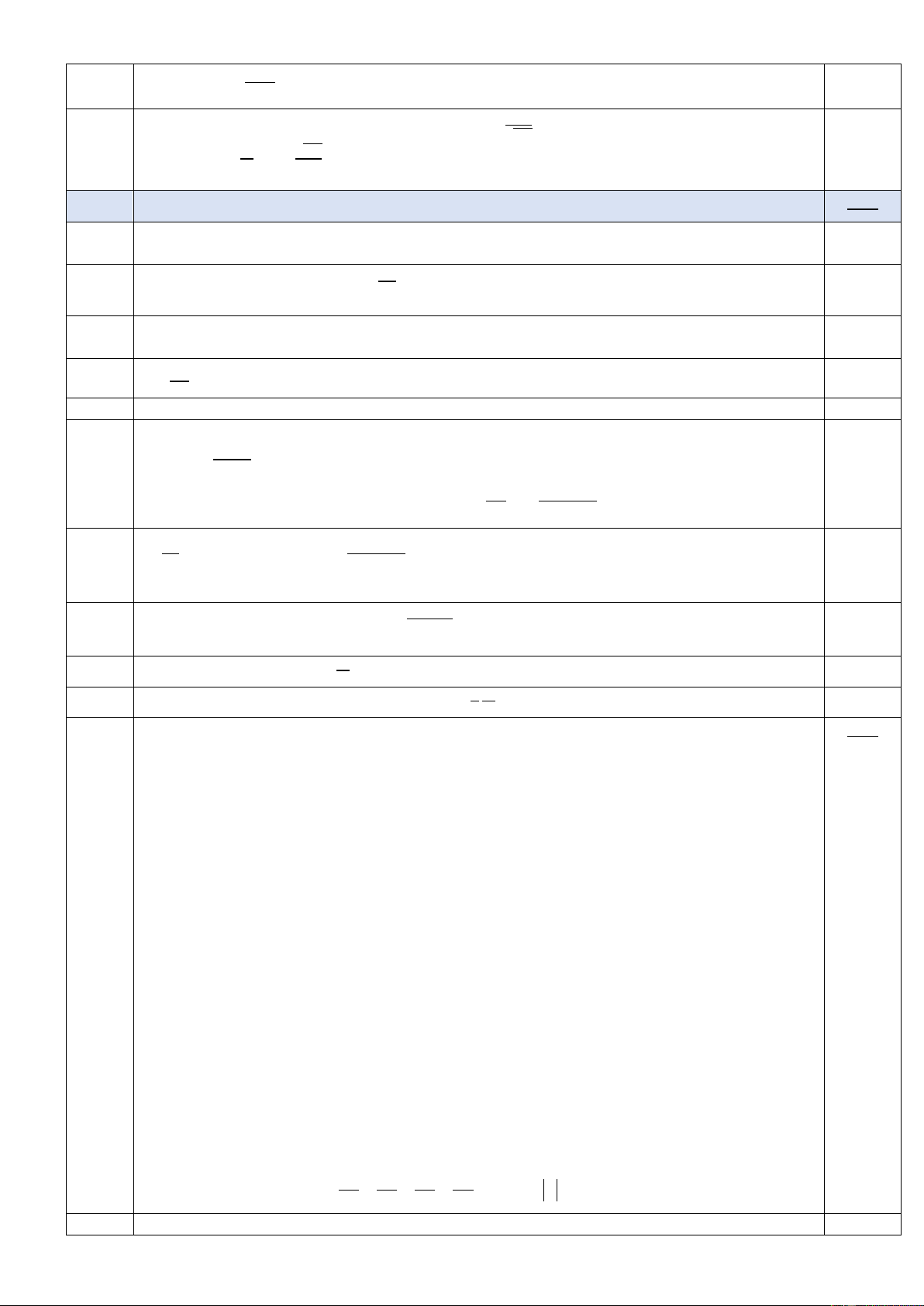
Vẽ đúng hình (có thể vẽ nửa trên hoặc nửa dưới) Màn E P M C 1,0 x S S1 S2 y I O D N Q 1 1 1 0,5 Tiêu cự của hệ TK: = + f =10cm h f f f h 1 2 df 0,25 Vị trí ảnh S h = = 1 của S qua hệ: ' d 12cm d − fh df 0,5 Vị trí ảnh S = =
2 của S qua phần riêng của TK L2: ' 2 d 30cm 2 d − f2 S I MI S I MI S I S I 18 − S I S I 0,25 Hình vẽ suy ra: 2 1 2 1 1 1 = ; = ; PO = 2CO = = S O PO S O CO S O 2S O 30 24 2 1 2 1 Suy ra được S1I = 8cm 0,25
Vị trí đặt màn E: OI = OS1 + S1I = 20 cm 0,5 S I MI C . O S I 0,5 1 1 = MI = = 2 / 3cm S O CO S O 1 1 Smin = π.MI2 ≈ 1,4 cm2 0,25 Câu 5 4,0đ
Câu 5. (4 điểm)
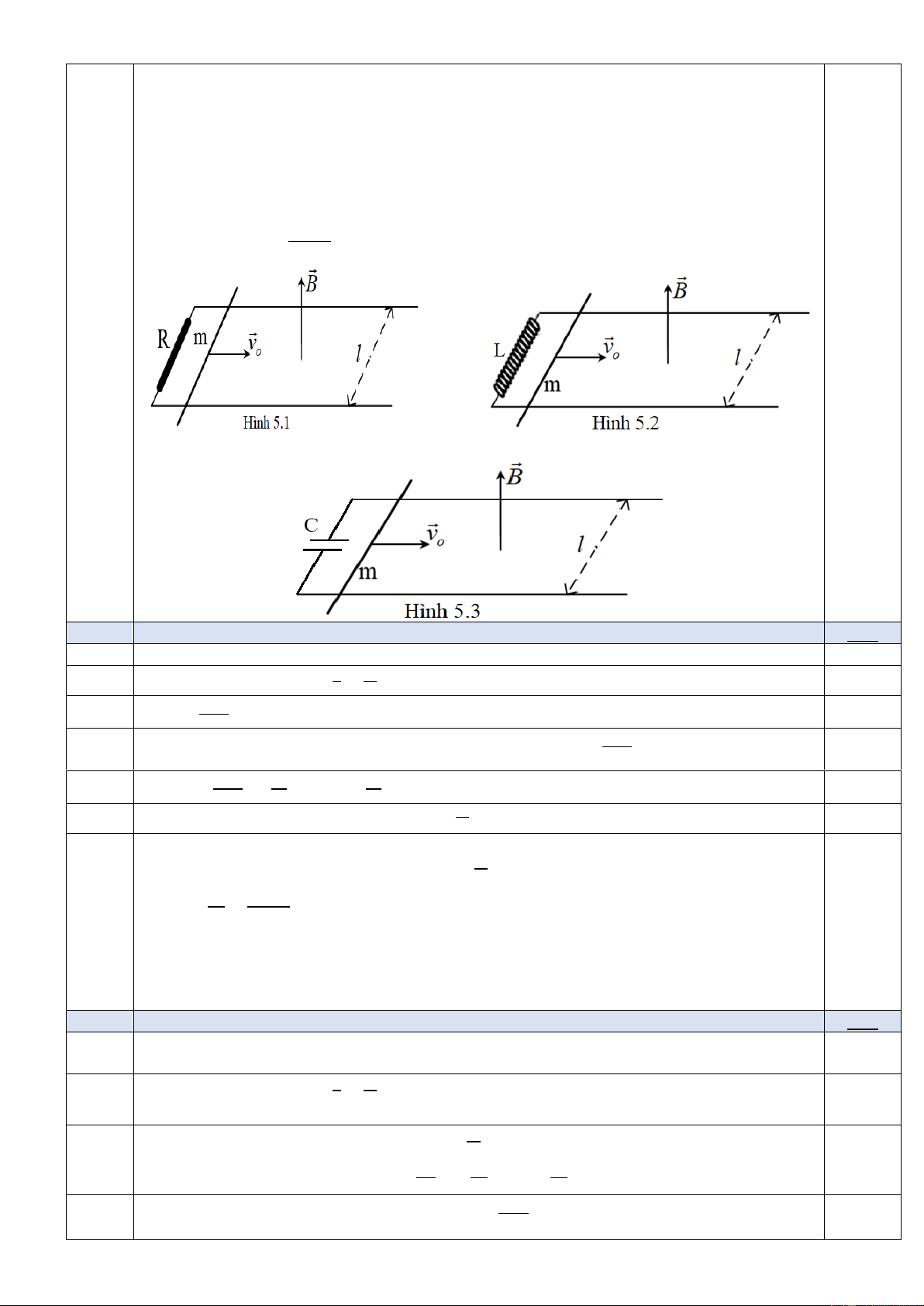
Hai thanh ray dẫn điện đặt nằm ngang, song song và cách nhau l trong từ
trường có cảm ứng từ B có phương thẳng đứng, hướng lên. Một thanh kim loại
có khối lượng m đặt trên hai thanh ray và vuông góc với hai thanh. Bỏ qua ma sát
giữa thanh kim loại và hai thanh ray, xem điện trở của thanh kim loại và hai thanh
ray không đáng kể. Ban đầu, truyền cho thanh kim loại một vận tốc v hướng dọc o
theo thanh ray. Viết phương trình chuyển động của thanh kim loại và tìm khoảng
dịch chuyển lớn nhất của nó trong các trường hợp sau: Trang 9
1. Cảm ứng từ B không đổi:
a. Đầu các thanh ray nối với điện trở R (Hình 5.1).
b. Đầu các thanh ray nối với cuộn dây thuần cảm có độ tự cảm L (Hình 5.2).
2. Cảm ứng từ B biến đổi theo thời gian theo biểu thức: B = t, trong đó
là hằng số dương, đầu các thanh ray nối với tụ điện có điện dung C (Hình 5.3). dx Cho biết: = arctan x + C 2 1+ x Ý 1a 1,0đ
Suất điện động trong mạch: 𝜀 = 𝑙𝐵𝑣 0,125 𝜀 𝑙𝐵
Dòng điện trong mạch: 𝑖 = = 𝑣 0,125 𝑅 𝑅 (𝑙𝐵)2 F = Bil =
𝑣 ngươc chiều vận tốc 0,125 𝑅 (𝑙𝐵)2
Phương trình động lực học cho thanh: 𝐹 = 𝑚𝑎 = −𝑖𝐵𝑙 𝑥" = − 𝑣 (1) 0,125 𝑚𝑅 (𝑙𝐵)2 𝑑𝑣 𝑑𝑣 Đặt = => = −𝛽𝑣⟹ = −𝛽𝑑𝑡 0,125 𝑚𝑅 𝑑𝑡 𝑣 𝑣
Tích phân 2 vế phương trình trên ta được: 𝑙𝑛
= −𝛽𝑡 => 𝑣 = 𝑣 𝑣 0ⅇ−𝛽𝑡 (2) 0,125 0
Tiếp tục tích phân 2 vế phương trình trên ta được quy luật chuyển động của thanh và tính được 𝑣
quãng đường mà thanh đi được đến dừng: 𝑥 = 0 (1 − ⅇ−𝛽𝑡) 0,125 𝛽 𝑣 𝑚𝑅𝑣 𝑥 0 0 𝑚𝑎𝑥 = = 0,125 𝛽 (𝑙𝐵)2 Ý 1b 1,0đ
Suất điện động trong mạch: 𝜀 = 𝑙𝐵𝑣 0,125 𝜀 𝑙𝐵
Dòng điện trong mạch: 𝑖 = = 𝑣 0,125 𝑅 𝑅 𝑑𝑖
Phương trình định luật Ôm có dạng: −𝑙𝐵𝑣 + 𝐿 = 0 0,125 𝑑𝑡 𝑑𝑥 𝑑𝑖 𝑙𝐵 → 𝑙𝐵 = 𝐿 → 𝑖 = 𝑥 0,125 𝑑𝑡 𝑑𝑡 𝐿 (𝑙𝐵)2
Phương trình động lực học: 𝐹 = 𝑚𝑥′′ = −𝑖𝐵𝑙 = − 𝑥 ; 0,125 𝐿 Trang 10 (𝑙𝐵)2 suy ra: 𝑥" = − 𝑥 0,125 𝑚𝐿 𝑙𝐵
Vậy thanh m dao động điều hòa với tần số góc: = 0,125 √𝑚𝐿 𝑣
Biên độ: 𝐴 = 0 = 𝑣 √𝑚𝐿 0 𝑙𝐵 0,125 Ý 2 2,0đ
Tại thời điểm t, diện tích giới hạn của mạch điện là S và tốc độ của thanh là v 𝑑𝜙
Suất điện động trên thanh: 𝜀 = −
= −(𝑙𝑣𝑡 + 𝑆) 0,25 𝑑𝑡
Có: 𝑞 = 𝐶(𝑙𝑣𝑡 + 𝑆) 0,25 𝑑𝑞 0,25 𝑖 =
= 𝐶(𝑙𝑡𝑎 + 2𝑙𝑣) 𝑑𝑡
F = 𝐵𝑖𝑙 = 𝑡𝑙𝐶(𝑙𝑡𝑎 + 2𝑙𝑣) 0,25
Phương trình động lực học: 𝑚𝑎 = −(𝑙)2𝐶𝑡(𝑡𝑎 + 2𝑣) 0,25 (𝑙)2𝐶 Đặt 2 = 𝑚 2 dv 2 tdt 2 2 2 2 2
a = − (at + 2vt) → a(1+ t ) = 2 − vt → = − 2 2 v 1+ t 0,25 v v 2 2 ln = −ln(1+ t ) o → v = (2) 2 2 v 1+ t 0,125 o 𝑡 𝑑𝑡
Tích phân phương trình (2): 𝑥 = 𝑣 0,125 0 ∫ 0 1+(𝑡)2 𝑣
Kết quả tích phân trên: 𝑥 = 0 𝑎𝑟𝑐𝑡𝑔𝑡 0,125 𝜋 𝑣
Quãng đường đi được lớn nhất của thanh: 𝑥 = 0 2 0,125 Câu 6 2,0đ
Câu 6. (2 điểm)
Xét chuyển động của một tấm nhựa phẳng trên một mặt bàn phẳng nằm ngang.
Trong quá trình chuyển động, tấm nhựa chịu tác dụng của lực ma sát trượt với hệ
số ma sát trượt α và chịu lực cản của môi trường. Biết lực cản của môi trường phụ r r
thuộc vào vận tốc theo biểu thức: f = −v (β là hệ số cản). Coi các va chạm trong c
quá trình làm thí nghiệm (nếu có) là hoàn toàn đàn hồi. Cho các dụng cụ sau:
- Vật nhỏ có khối lượng m đã biết;
- Thước đo có vạch chia đến milimét;
- Các sợi dây mềm, mảnh, nhẹ, không giãn;
- Tấm nhựa phẳng hình chữ nhật;
- Bàn thí nghiệm, giá đỡ, giá treo cần thiết. Yêu cầu:
1. Trình bày cơ sở lí thuyết và xây dựng các công thức cần thiết để xác định hệ số
ma sát trượt α giữa tấm nhựa với mặt bàn và hệ số cản β của môi trường khi tấm nhựa chuyển động.
2. Trình bày cách bố trí thí nghiệm, thu thập và xử lí số liệu để xác định α và β. x2 x3 x4 x5
Cho biết: ln( 1+ x ) = x − + − +
− ... khi x 1. 2 3 4 5 Ý 1
- Muốn xác định được các hệ số α và β liên quan đến quá trình chuyển động của tấm nhựa trên Trang 11
mặt bàn ta cần bố trí hệ thí nghiệm sao cho tạo
được vận tốc cho tấm và cần phải xác định được
khối lượng M của tấm nhựa. Có thể tạo vận tốc ban
đầu cho tấm nhựa bằng việc sử dụng va chạm của
vật m và tấm. Tạo vận tốc vật m trước khi va chạm m
vào M bằng việc cho vật m chuyển động dưới tác
dụng của trọng lực, thế năng chuyển hoá thành
động năng. Độ cao vật m ban đầu do với vị trí trước h
va chạm là h thì vận tốc vật m thu được là: 2 v 1 m = mgh v = 2gh (1). 1 0,25 2
- Vật m khi va chạm đàn hồi với M sẽ tạo vận tốc v2 cho M xác định từ hệ phương trình: ' mv = Mv + mv (*) 1 2 1 1 1 1 2 2 ' 2 mv = Mv + mv (**); 1 2 1 2 2 2 2m Suy ra v = v 0,25 2 1 M + (2) m
- Khi tấm với vận tốc ban đầu v2 chuyển động dưới lực cản của ma sát trượt và lực cản môi
trường, phương trình chuyển động cho tấm trên mặt bàn: dv Ma = − M g −v M = −Mg −v 0,25 dt u t du
- Đổi biến u = Mg + v , giải phương trình vi phân ta có: = − dt với u M u 0 0 − t Mg Mg
u = Mg + v ; ta được: M v = + v e − (3) 0 2 2 M v
- Thời gian mà tấm chuyển động (đến khi v = 0 ) là: 2 t = ln 1+ (4) 1 Mg t t 1 1 − t Mg M g
- Quãng đường mà tấm M trượt được là M s = vdt = + v e − d t 2 0 0 − t M Mg 1 Mg M Mg Mv Mg v M 2 2 s = − + v e − t + + v = 1 − ln 1+ (5) 2 1 2 v Mg 2 v 2 3 x x - Khai triển hàm 2 ln 1+
thành đa thức theo công thức: ln(1+ x) = x − + Mg 2 3 2 3 v v Ta được: 2 2 s = − (6) 0,25 2 2 2g 3 Mg
Như vậy, bằng việc đo khoảng cách dịch chuyển của tấm theo chiều cao vật m (hay theo vận tốc
ban đầu v2 của M) ta có thể xác định được α và β. Ý 2
* Xác định khối lượng vật M (sử dụng thước làm cân đòn và vật m đã biết để tính M) 0,25
* Bố trí thí nghiệm (như hình vẽ):
- Vật M để hơi nhô khỏi mép bàn một chút.
- Chiều dài dây buộc vật m phải phù hợp.
- Kéo lệch vật m lên độ cao h và thả để vật m đến va chạm vào M, đo quãng đường dịch chuyển của vật M. 0,25
- Ghi số liệu vào bảng: Lần 1 2 3 4 5 6 7 h s Trang 12 Xử lí số liệu: 2m
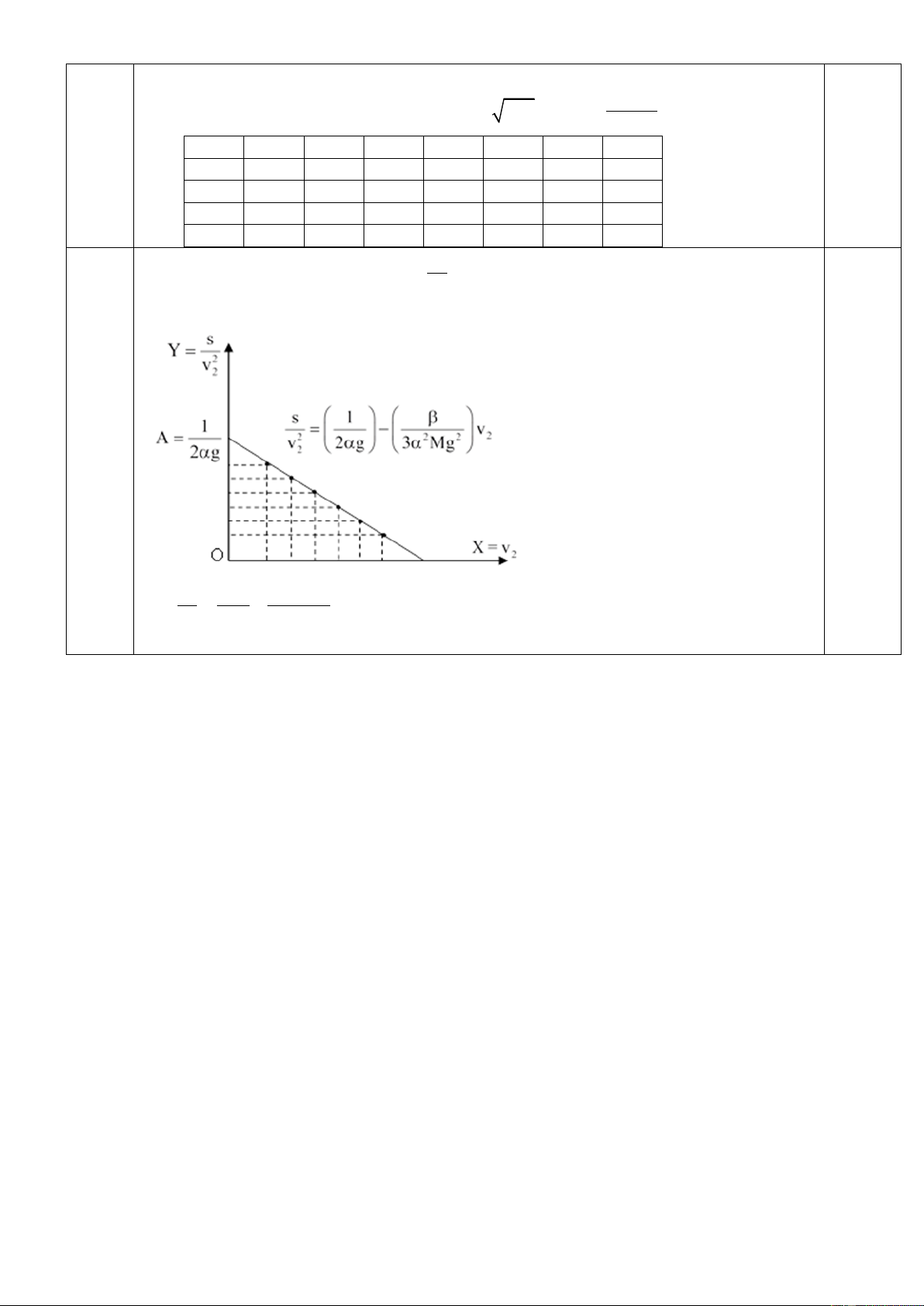
Tính các đại lượng liên quan theo công thức: v = 2gh và v = v . 1 2 1 M + m Lần 1 2 3 4 5 6 7 0,25 h v1 v2 s/v 2 2 s
Dựng đồ thị biểu diễn mối quan hệ: Y = theo X = v . 2 2 v2 Đồ thị có dạng: 0,25 s 1 v2 Y = = − = A − BX . 2 2 2 v 2 g 3 Mg 2
Xác định hệ số A, B từ đồ thị, từ đó tính được α và β. Ghi chú:
- Thí sinh giải bằng cách khác đúng vẫn đạt điểm tối đa.
- Không ghi đơn vị hoặc ghi sai thì trừ 0,25đ/1 lần và chi trừ tối đa 2 lần/toàn bài thi.
* Thí sinh không được sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm.
* Họ và tên thí sinh: ………………………………….. Số báo danh: ……........ Trang 13