Đề thi kết thúc học phần Nhập môn lý thuyết ma trận | Đại học Sư phạm Hà Nội
Đề thi kết thúc học phần | Đại học Sư phạm Hà Nội với những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.
Môn: Nhập môn lý thuyết ma trận 68 tài liệu
Trường: Đại học Sư Phạm Hà Nội 2.1 K tài liệu
Tác giả:
Preview text:
TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
ĐỀ THI KẾT THÚC HỌC PHẦN Khoa Toán - Tin
Môn thi: Nhập môn lý thuyết ma trận ————–
Thời gian làm bài: 60 phút
Câu 1. (3,5 điểm) Cho các ma trận 1 0 ! 1 A = −1 3 −1 −1 , B = , 0 2 2 1 m
trong đó m là tham số thực.
(a) Tính tổng tất cả các phần tử của ma trận BA.
(b) Tìm tất cả các số thực m để định thức của ma trận AB − I bằng 7,
trong đó I là ma trận đơn vị cấp 3.
Câu 2. (3,0 điểm) Cho ma trận 1 2 3 ! A = 2 5 7 . −2 −4 −6
(a) Tìm tất cả các giá trị riêng và các véctơ riêng của ma trận A.
(b) Tính định thức của ma trận A2021 + I, trong đó I là ma trận đơn vị cấp 3.
Câu 3. (2,0 điểm) Giải hệ phương trình tuyến tính x1 + x2 − x3 + 2x4 = 1 2x1 + x3 − x4 = −4 x1 − x2 + 3x3 − 5x4 = −8
−x1 + 3x2 − 6x3 + 10x4 = 14.
PHẦN TỰ CHỌN: Sinh viên chỉ cần làm một trong hai bài sau
Câu 4A. (1,5 điểm) Cho ma trận Y = (1 2 3 · · · 2021) và X là một ma
trận bất kì cỡ 2021 × 1. Chứng minh rằng ma trận XY không khả nghịch.
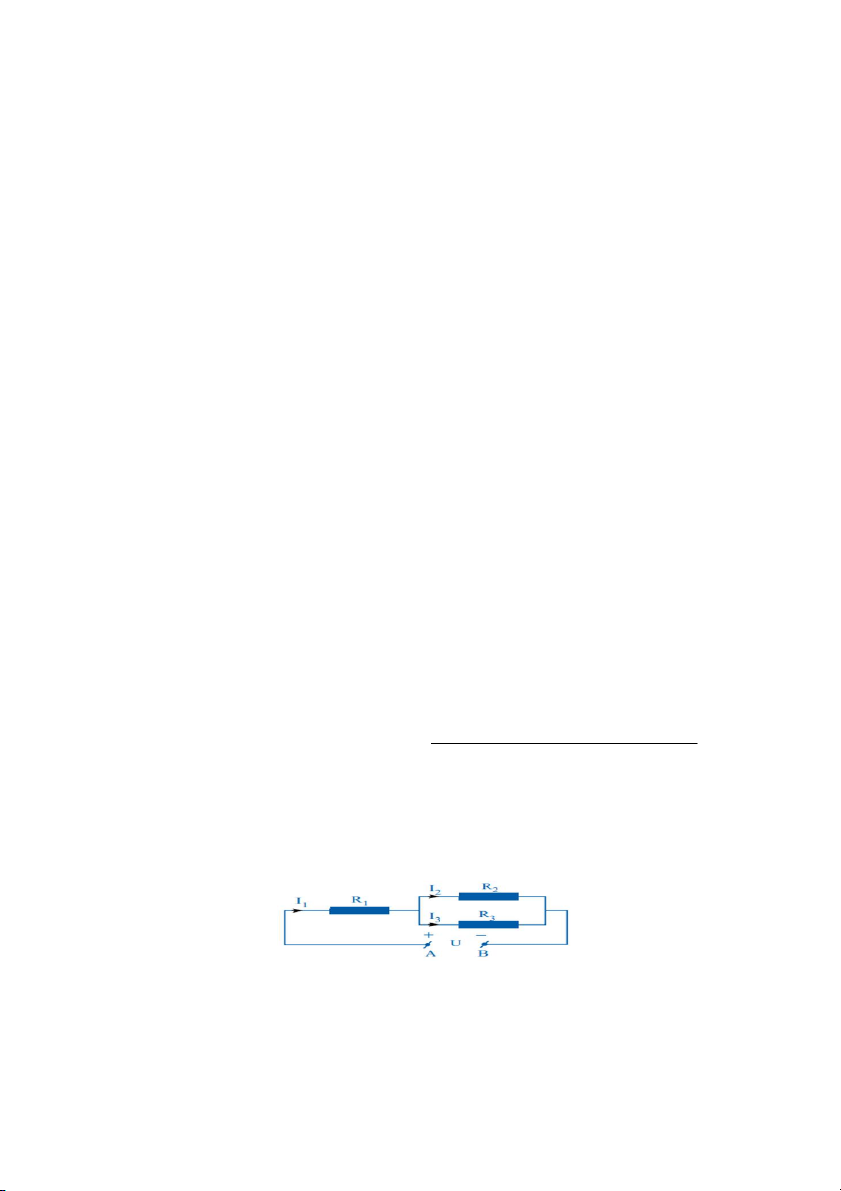
Câu 4B. (1,5 điểm) Cho một đoạn mạch điện như Hình A. Biết R1 = 36Ω, R
là cường độ dòng điện của 2
= 90Ω, R3 = 60Ω và U = 60V . Gọi I1 mạch chính, I và
là cường độ dòng điện của hai mạch rẽ. Tính I1, I2, I3. 2 I3 Hình A