Đề thi kết thúc học phần Toán kinh tế 2 | Học Viện Ngân hàng

ĐỀ THI SỐ 1
Thời gian làm bài: 90 phút
Câu I (2 điểm). Một công ti tài chính A chia khách hàng doanh nghiệp làm 3 nhóm: doanh nghiệp nhỏ; doanh
nghiệp vừa; doanh nghiệp lớn. Việc thống kê cho thấy tỉ lệ doanh nghiệp thua lỗ trong một năm tương ứng với các
loại trên là 30%; 15%; 5% và trong toàn bộ khách hàng của công ti A có 60% doanh nghiệp nhỏ; 30% doanh nghiệp
vừa; 10% doanh nghiệp lớn.
1) Tính tỉ lệ khách hàng doanh nghiệp của công ti A thua lỗ trong năm;
2) Nếu một doanh nghiệp là khách hàng của công ti A không thua lỗ trong năm, thì xác suất doanh nghiệp đó
thuộc nhóm doanh nghiệp nhỏ là bao nhiêu?
Câu II (1,5 điểm). Có hai loại cổ phiếu A và B được bán trên thị trường chứng khoán và lãi suất của chúng lần lượt
là các biến ngẫu nhiên X và Y (đơn vị: %). Giả s
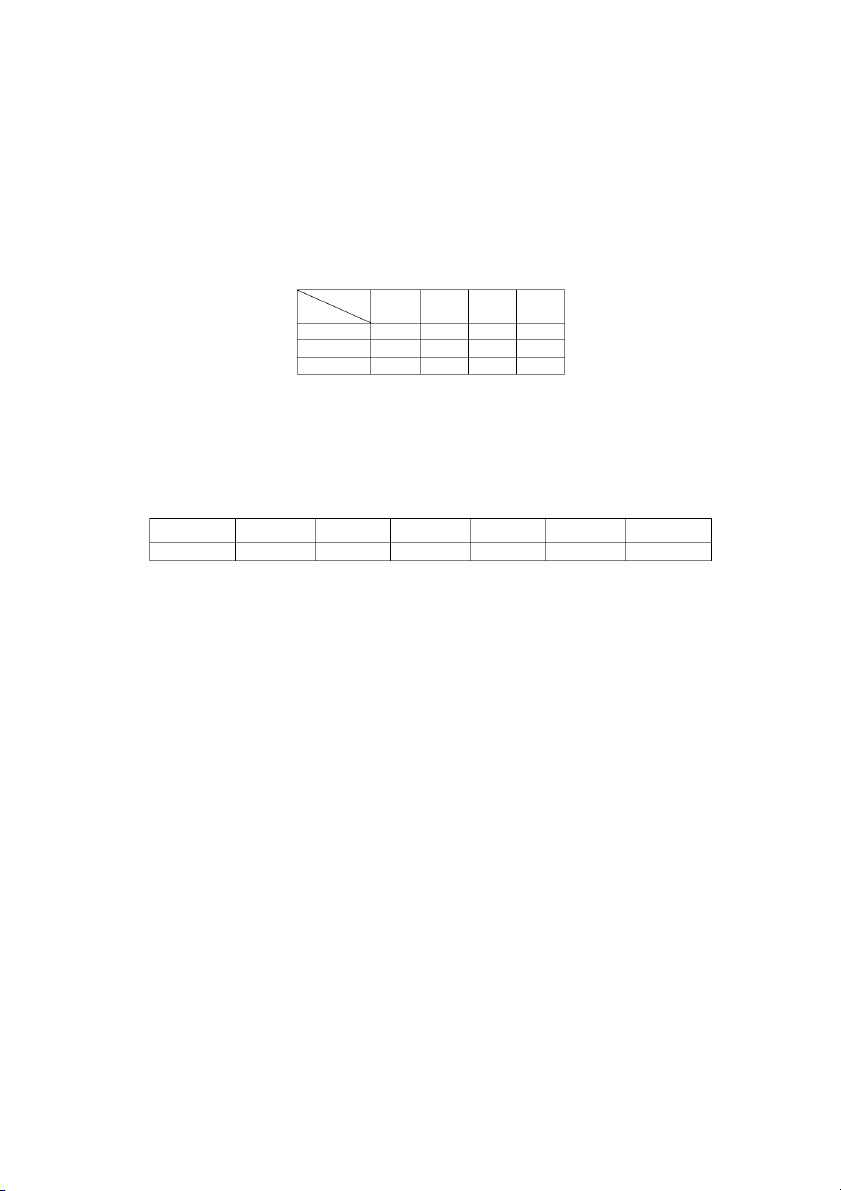
ử (𝑋; 𝑌) có bảng phân phối xác suất như sau: Y -2 0 5 10 X 0 0 0,05 0,05 0,1 4 0,05 0,1 0,25 0,15 6 0,1 0,05 0,1 0
Tính lãi suất kỳ vọng khi đầu tư vào loại cổ phiếu B, với điều kiện lãi suất của cổ phiếu A là 6%.
Câu III (1,5 điểm). Số tiền trung bình hàng năm mà các hộ gia đình Mỹ chi cho phương tiện đi lại hàng ngày là
$6312 (Theo Tạp chí Money, năm 2001). Giả sử rằng số tiền chi tiêu được phân phối chuẩn. Biết rằng 2,5% hộ gia
đình Mỹ chi tiêu ít hơn $1000 cho phương tiện đi lại hàng ngày. Độ lệch chuẩn của số tiền chi tiêu là bao nhiêu?
Câu IV (5 điểm). Đưa ra kết quả cho những câu hỏi dưới đây (các phép tính làm tròn đến 4 chữ số thập phân).
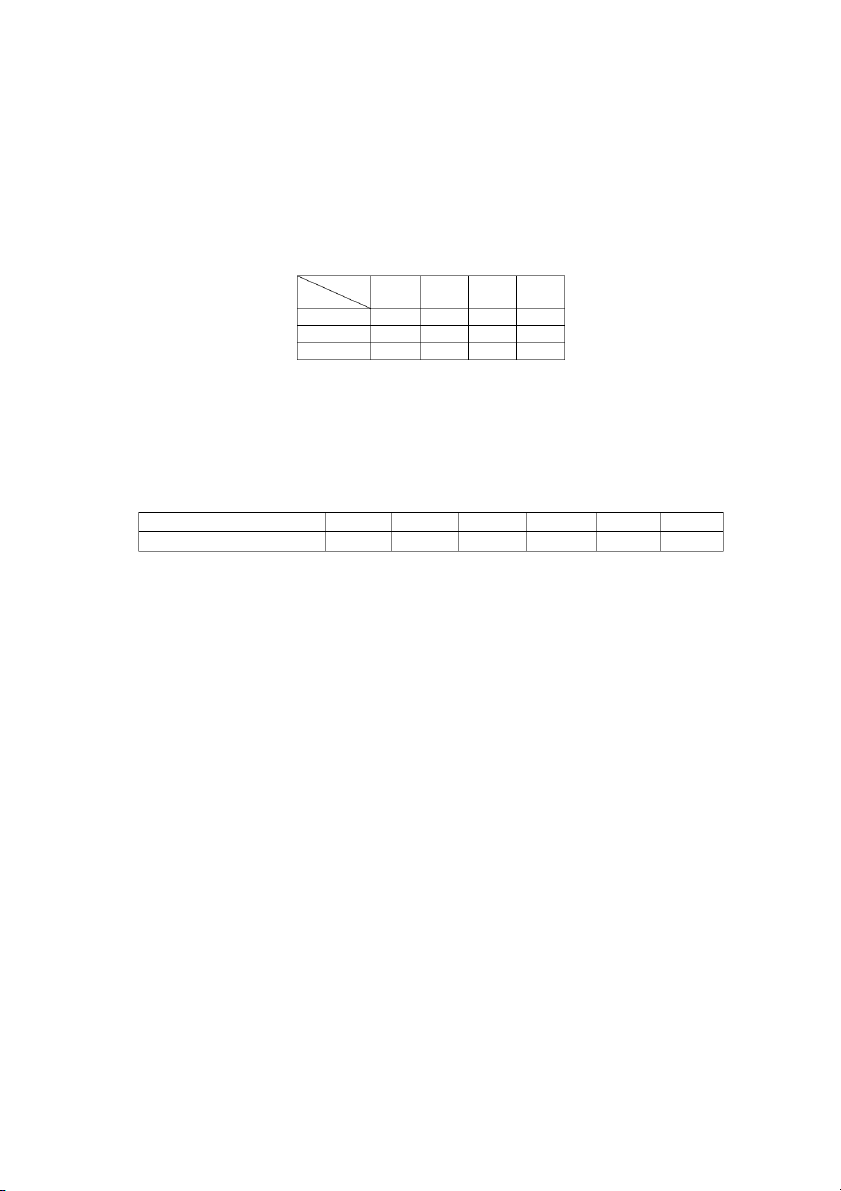
Năm 2022, khảo sát về thu nhập (triệu đồng/năm) của một số người làm việc ở một công ti, người ta thu được bảng số liệu: Thu nhập 200 260 – 270 330 – 340 400 – 410 470 – 480 540 – 550 650 – Số người 30 60 125 110 50 25
1) Những người có thu nhập từ 480 triệu đồng/năm trở lên là những người có thu nhập cao. Với độ tin cậy 95%,
tỉ lệ người có thu nhập cao của công ti không vượt quá bao nhiêu ?
2) Năm trước tỷ lệ nhân viên có thu nhập cao là 20%. Có ý kiến cho rằng năm nay do suy thoái kinh tế đã làm
giảm tỷ lệ nhân viên có thu nhập cao.
Với mức ý nghĩa 5%, hãy cho nhận xét về ý kiến trên?
3) Nếu muốn kiểm định xem “công ti báo cáo mức thu nhập bình quân của một người là 35 triệu đồng/tháng”
có đúng không thì giá trị quan sát của tiêu chuẩn kiểm định là bao nhiêu?
4) Khi ước lượng thu nhập trung bình của một người ở công ti này với độ chính xác 8 triệu đồng/năm thì độ tin cậy là bao nhiêu?
5) Với độ tin cậy 95%, độ lệch chuẩn về thu nhập của các nhân viên không vượt quá bao nhiêu? Giả sử thu nhập
của các nhân viên tuân theo quy luật phân phối (xấp xỉ) chuẩn.
6) Khi kiểm định giả thuyết “độ lệch chuẩn về thu nhập hàng tháng của các nhân viên cao hơn 9 triệu đồng” thì miền bác b
ỏ giả thuyết 𝐻0 với mức ý nghĩa 𝛼 thế nào?
7) Nếu muốn ước lượng tỷ lệ nhân viên có thu nhập cao với độ chính xác không vượt quá 0,035 và độ tin cậy
95% thì cần điều tra ít nhất bao nhiêu người? 8) Cho biết công th
ức để tìm khoảng tin cậy bên trái khi ước lượng trung bình của thu nhập với độ tin cậy 1 − 𝛼?
9) Có chấp nhận được báo cáo của công ti rằng, “trung bình của thu nhập của nhân viên cao hơn 3 triệ 3 u đồng/
tháng”, với mức ý nghĩa 5% không?
10) Nếu muốn ước lượng phương sai thu nhập c a
ủ nhân viên công ti với độ tin cậy 1 − 𝛼 thì có cần thêm giả
thiết gì về thu nhập của nhân viên công ti ? 2(399) 2(399)
Cho biết: 𝑢0.025 = 1.96; 𝜒0.95
= 353.6992; 𝜒0.05 = 446.5742; 𝑢0.05 = 1.6449
ĐỀ THI SỐ 2
Thời gian làm bài: 90 phút
Câu I (2 điểm). Với những khách mua hàng có xe đẩy hàng, 70% thanh toán bằng thẻ, 20% thanh toán bằng tiền
mặt, và 10% thanh toán bằng chuyển khoản. Với những khách hàng không dùng xe đẩy, 50% thanh toán bằng thẻ,
40% thanh toán bằng tiền mặt, và 10% thanh toán bằng chuyển khoản. Vào sáng thứ bảy, 80% người mua hàng
dùng xe đẩy và 20% không dùng xe đẩy.
a) Tính tỷ lệ khách hàng thanh toán bằng thẻ vào sáng thứ bảy.
b) Tính tỷ lệ khách hàng không thanh toán bằng tiền mặt vào sáng thứ bảy.
Câu II (1,5 điểm). Có hai loại cổ phiếu A và B được bán trên thị trường chứng khoán và lãi suất c a ủ chúng lần lượt
là các biến ngẫu nhiên X và Y (đơn vị: %). Giả sử (𝑋; 𝑌) có bảng phân phối xác suất như sau Y -2 0 5 10 X 0 0 0,05 0,05 0,1 4 0,05 0,1 0,25 0,15 6 0,1 0,05 0,1 0
Tính lãi suất kỳ vọng khi đầu tư vào loại cổ phiếu A, với điều kiện lãi suất của cổ phiếu B là −2%.
Câu III (1,5 điểm). Cục Thống kê Lao động Hoa Kỳ báo cáo rằng chi tiêu trung bình hàng năm cho thực phẩm và
đồ uống của tất cả các gia đình là $5700 (Theo Tạp chí Money, năm 2003). Giả sử rằng chi tiêu hàng năm cho thực
phẩm và đồ uống được phân phối chuẩn và độ lệch chuẩn là $1500. Tính tỷ lệ các gia đình chi hơn $7000 hàng năm
cho thực phẩm và đồ uống?
Câu IV (5 điểm). Đưa ra kết quả cho những câu hỏi dưới đây (các phép tính làm tròn đến 4 chữ số thập phân).
Điều tra doanh số bán hàng của một số hộ kinh doanh mặt hàng A năm 2022, được số liệu:
Doanh số (triệu đồng/tháng) 110 115 120 125 130 135 Số hộ gia đình 10 15 20 30 15 10
1) Ước lượng trung bình doanh số bán hàng một tháng của mỗi hộ ?
2) Với độ tin cậy 95% doanh số bán hàng trung bình của mỗi hộ trong một tháng không vượt quá bao nhiêu? ,
3) Những hộ có doanh số trên 125 triệu đồng /tháng là những hộ có doanh số cao. Với độ tin cậy 95%, tỉ lệ hộ
có doanh số cao không thấp hơn bao nhiêu?
4) Nếu muốn ước lượng tỉ lệ hộ có doanh số cao với độ chính xác 0,05 và độ tin cậy 95% thì phải điều tra thêm bao nhiêu hộ nữa?
5) Khoảng tin cậy đối xứng để ước lượng phương sai của doanh số bán hàng (giả thiết doanh số bán hàng của
các hộ kinh doanh mặt hàng A là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn) có dạng thế nào?
6) Có tài liệu cho rằng tỉ lệ hộ có doanh số cao năm 2022 là 30%. Khi kiểm định xem tỉ lệ trong tài liệu đó có chấp ận đượ nh
c không thì giá trị quan sát của tiêu chuẩn kiểm định là bao nhiêu?
7) Năm 2021 trung bình của doanh số bán hàng các hộ này là 1,44 tỷ đồng/năm. Kí hiệu 𝜇 là doanh số bán
hàng trung bình năm 2022. Khi kiểm định rằng doanh số bán hàng trung bình của các hộ năm 2022 có tăng lên hay không ?
thì cặp giả thuyết thế nào
8) Với mức ý nghĩa 5%, có thể chấp nhận báo cáo cho rằng độ biến động về doanh số bán hàng của các hộ
kinh doanh mặt hàng A là 50
(triệu đồng)2? Giả thiết doanh số bán hàng của các hộ kinh doanh mặt hàng A
là biến ngẫu nhiên có phân phối (xấp xỉ) chuẩn.
9) Biết rằng toàn vùng có 1000 hộ kinh doanh mặt hàng A. Với độ tin cậy 95%, số gia đình có mức doanh thu
trên 120 triệu đồng/ tháng ở vùng này không nhỏ hơn bao nhiêu?
10) Khi ước lượng trung bình của doanh số bán hàng các h
ộ kinh doanh mặt hàng A năm 2022 với độ chính xác 5 tri t
ệu đồng/ tháng thì độ in cậy là bao nhiêu? 2(99) 2(99)
Cho biết: u  2,3263;u  1,96; u  1,6449 ; 𝜒 = 128,422; 𝜒 = 73,3611 0,01 0,025 0,05 0,025 0,975
ĐỀ THI SỐ 3
Thời gian làm bài: 90 phút
Câu I (2 điểm). Hai người cùng đến xin việc tại một công ty. Khả năng được nhận vào làm việc của mỗi người
tương ứng là 40% và 50%, biết rằng việc công ty nhận ai vào làm là độc lập nhau.
1) Lập bảng phân phối xác suất của số người được nhận vào công ty.
2) Sau khi nghiên cứu hồ sơ, công ty thông báo chỉ có 1 người được nhận. Tính xác suất người được nhận vào
làm việc là người thứ nhất?
Câu II (1,5 điểm). Số người vào ngân hàng giao dịch trung bình trong một ngày làm việc hành chính là 120
người. Tính xác suất để trong một giờ có ít nhất 6 người vào giao dịch?
Câu III (1, 5 điểm). Công ty có 100 hóa đơn thanh toán, trong đó có 15 hóa đơn bị tính nhầm. Do đến hạn thanh
toán nên kế toán rút ngẫu nhiên ra 20 tờ hóa đơn gửi đi cho khách hàng thanh toán, mỗi hóa đơn sai bị trả lại gây
thiệt hại cho công ty 5 triệu đồng do bị kéo dài thời gian thanh toán. Tính trung bình số tiền thiệt hại của công ty?
Câu IV (5 điểm). Theo dõi giá bán hàng ngày của mặt hàng A cho kết quả sau Giá bán (triệu đồng) 34,2 34,3 34,4 34,5 34,6 34,7 34,8 34,9 35 Số ngày 5 8 12 17 21 15 12 7 3
Biết giá bán hàng ngày có luật phân phối xấp xỉ chuẩn. Hãy trả lời các câu hỏi sau (Các kết quả tính làm tròn đến
4 chữ số thập phân, nếu tính xấp xỉ.):
1/ Xác định trung bình mẫu và độ lệch chuẩn mẫu.
2/ Cho biết ước lượng tỷ lệ ngày có giá bán tối đa 34,8 triệu.
3/ Với độ tin cậy 95%, trung bình giá bán không quá bao nhiêu?
4/ Với độ tin cậy 95%, hãy tìm ước lượng khoảng của độ phân tán về giá bán.
5/ Với độ tin cậy 95%, tỷ lệ ngày mặt hàng A có giá bán dưới 34,5 triệu đồng không vượt quá bao nhiêu?
6/ Muốn ước tỷ lệ ngày có giá bán cao hơn 34,5 triệu đồng với độ chính xác không quá 6% thì cần điều tra tối thiểu bao nhiêu người?
7/ Tỷ lệ ngày có giá bán thấp hơn 34,4 triệu trước đây là 15%. Có ý kiến cho rằng tỷ lệ nà cao hơn hiện nay. y Cặp ?
giả thuyết để kiểm định ý kiến này thế nào
8/ Tính giá trị quan sát cho việc kiểm định ở ý 7.
9/ Có ý kiến cho rằng độ phân tán về giá bán mặt hàng A là 0,035 (triệu đồng)2. Hãy xác định cặp giả thuyết để
kiểm định ý kiến trên.
10/ Với mức ý nghĩa 5%, hãy nêu kết luận cho việc kiểm định ý 9/ 2(99)
Cho biết: 0(1) = 0,3413; u0,01 ≈ 2,3263 ; u0,025 ≈ 1,96; u0,05 ≈ 1,6449; 𝜒0,05 ≈ 123,2252; 𝜒2(99) 2(99) 2(99)
0,025 ≈ 128,422; 𝜒0,95 ≈ 77,0463; 𝜒0,975 ≈ 73,3611 HỌC VIỆN NGÂN HÀNG HƯỚNG DẪN LỜI GIẢI B MÔN TOÁN
ĐỀ THI KẾT THÚC HỌC PHẦN:
Toán kinh tế II – MAT11A 1 Đề thi số:
Áp dụng cho khoá/ hệ/ lớp: Đại học Thời gian làm bài: 90 phút.
Ca thi:…………… Ngày thi: ……………... Người duyệt đáp án:…………................ Đại di
ện Phòng TTKT: ………………………; Ngày nộp đáp: ..………………….......... Câu 1
𝐻1 ∶= “Một doanh nghiêp thuộc nhóm doanh nghiệp nhỏ”,
𝐻2 ∶= “Một doanh nghiêp thuộc nhóm doanh nghiệp vừa” ,
𝐻3 ∶= “Một doanh nghiêp thuộc nhóm doanh nghiệp lớn”,
𝐴 ∶= “Một doanh nghiêp thuộc thua lỗ trong năm”.
a) Theo Công thức xác suất đầy đủ:
𝑃(𝐴) = 𝑃(𝐻1)𝑃(𝐴|𝐻1) + 𝑃(𝐻2)𝑃(𝐴|𝐻2) + 𝑃(𝐻3)𝑃(𝐴|𝐻3)
= 0,6 ∙ 0,3 + 0,3 ∙ 0,15 + 0,1 ∙ 0,05 = 0,23.
 Tỉ lệ khách hàng doanh nghiệp của công ti A thua lỗ trong năm là 23%.
b) Xác suất phải tìm là 𝑃(𝐻 𝑃 𝐴|𝐻 0,6 ∙ (1 − 0,3) 6 𝑃(𝐻 1) ( 1) 1|𝐴) = 𝑃(𝐴) = 1 − 0,23 = 11. Câu 2
𝑃{𝑋 = 6} = 0.1 + 0,05 + 0.1 + 0 = 0.2 . 5 Bảng phân ph i
ố xác suất của Y, v u ki ới điề ện 𝑋 = 6, là Y -2 0 5 P 0.4 0.2 0.4
Lãi suất kỳ vọng khi đầu tư vào cổ phiếu B, với điều kiện lãi suất c a
ủ cổ phiếu A là 6%, là 𝐸(𝑌|𝑋 = 6) = 1.2 (%). Câu 3
Gọi X là số tiền hàng năm mà các hộ gia đình Mỹ chi cho phương tiện đi lại hàng ngày. (đơn vị: $)
Theo đề bài X có phân phối chuẩn 𝑁(𝜇, 𝜎2) trong đó: 𝜇 = 6312, 𝜎 là độ lệch chuẩn. Ta có: −5312
𝑃(𝑋 < 1000) = 0,025 ↔ Φ0 ( 𝜎 ) = −0,475 ↔ 𝜎 = 2710,2041 Câu 4 1) 21,96%
2) Chưa thể chấp nhận ý kiến. 3) 𝑡𝑞𝑠 = −4,331 3 4) 91,88% 5) 97,473 triệu đồng. 6) 𝑊 2
𝛼 = (𝜒𝛼 (𝑛 − 1); +∞) 7) 478
8) (−∞; 𝑥 + 𝑢 𝑠 𝛼 ) √𝑛
9) Chưa thể chấp nhận báo cáo.
10) Cần có thêm giả thiết “Thu nhập của nhân viên công ti là biến ngẫu nhiên phân phối (xấp xỉ) chuẩn”. HỌC VIỆN NGÂN HÀNG HƯỚNG DẪN LỜI GIẢI B MÔN TOÁN
ĐỀ THI KẾT THÚC HỌC PHẦN:
Toán kinh tế II – MAT11A Đề thi số: 3
Áp dụng cho khoá/ hệ/ lớp: Đại học Thời gian làm bài: 90 phút.
Ca thi:…………… Ngày thi: ……………... Người duyệt đáp án:…………................ Đại di
ện Phòng TTKT: ………………………; Ngày nộp đáp: ..………………….......... Câu 1
𝐻1 ∶= “Khách hàng mua hàng dùng xe đẩy”,
𝐻2 ∶= “Khách hàng mua hàng không dùng xe đẩy” ,
𝐴 ∶= “Khách hàng thanh toán bằng thẻ”,
𝐵 ∶= “Khách hàng không thanh toán bằng tiền mặt”
a) Theo công thức xác suất đầy đủ:
𝑃(𝐴) = 𝑃(𝐻1)𝑃(𝐴|𝐻1) + 𝑃(𝐻2)𝑃(𝐴|𝐻2) = 0,8 ∙ 0,7 + 0,2 ∙ 0,5 = 0,66.
b) 𝑃(𝐵) = 𝑃(𝐻1)𝑃(𝐵|𝐻1) + 𝑃(𝐻2)𝑃(𝐵|𝐻2) = 0,8 ∙ (1 − 0,2) + 0,2 ∙ (1 − 0,4) = 0,76 Câu 2
𝑃{𝑌 = −2} = 0 + 0,05 + 0.1 = 0,1 . 5
Bảng phân phối xác suất của X, với điều kiện 𝑌 = −2, là X 4 6 P 1 2 3 3 Lãi suất k
ỳ vọng khi đầu tư vào cổ phiếu A, với điều kiện lãi suất c a ủ cổ phiếu B là −2 , % là 𝐸(𝑋|𝑌 = −2) = 16 (%). 3 Câu 3 Gọi X là m
ức chi tiêu hàng năm cho đồ c
ăn thứ uống của các gia đình (đơn vị: $)
Theo đề bài X có phân phối chuẩn 𝑁(𝜇, 𝜎2) trong đó: 𝜇 = 5700, 𝜎 = 1500 Ta có 13
𝑃(𝑋 > 7000) = 0,5 − Φ0 (15) = 0,19306 Câu 4 1) (𝑥 − 𝑢 𝑠 𝑠 𝛼 ; 𝑥 + 𝑢𝛼 ) 2 √𝑛 2 √𝑛 2) 123,9328 triệu đồng. 3) 17,88% 4) 189 hộ
5) ((𝑛−1)𝑠2 ; (𝑛−1)𝑠2 )
𝜒𝛼2(𝑛−1) 𝜒2 (𝑛−1) 2 1−𝛼2 6) 𝑢𝑞𝑠 = −1,091 1
7) H0:  = 120, H1:  > 120.
8) Có thể chấp nhận báo cáo. 9) 469 hộ 10) 83,568% HỌC VIỆN NGÂN HÀNG
ĐÁP ÁN ĐỀ THI KẾT THÚC HỌC PHẦN B MÔN TOÁN TOÁN KINH TẾ II – MAT02H ĐỀ THI SỐ 3
Thời gian làm bài: 90 phút
Áp dụng cho khoá/ hệ/ lớp: Đại học
Ca thi:…………… Ngày thi: ……………... Ngày duyệt đề:………………................
Đại diện Phòng TTKT: ………………………; Người duyệt đề:………………….......... Câu 1:
a/ Gọi X là số người được nhận vào công ty.
Tập giá trị của X là {0; 1; 2}.
Gọi Ai = “Thí sinh thứ i được nhận vào công ty” (𝑖 = 1; 2)
Theo đề bài, ta có: 𝑃(𝐴1) = 0,4; 𝑃(𝐴2) = 0,5
A1 và A2 là hai biến cố độc lập, nên:
𝑃(𝑋 = 0) = 𝑃(A1 A2) = P(A1).P(A2) = 0,6.0,5 = 0,3
𝑃(𝑋 = 2) = 𝑃(A1A2) = 0,4.0,5 = 0,2
𝑃(𝑋 = 1) = 1 − 0,3 − 0,2 = 0,5
Bảng phân phối xác suất của X: X 0 1 2 P 0,3 0,5 0,2
b/ Công ty thông báo chỉ có 1 người được nhận, khi đó xác suất người thứ nhất được nhận vào làm là:
𝑃 ( A1 ) = P(A1{𝑋=1}) = P(A1A2) = 0,4.0,5 (0,5đ) { = 0,4 𝑋=1} P{𝑋=1} P{𝑋=1} 0,5 Câu 2:
Số người vào ngân hàng giao dịch trung bình trong một ngày làm việc hành chính là 120 người. Tính xác suất để trong
một giờ có ít nhất 6 người vào giao dịch?
Gọi X = Số người vào ngân hàng giao dịch trung bình trong một giờ E(X) = 120/8 = 15 Ta có X  P( = 15)
P(X ≥ 6) = 1 – P(X < 6) = 1 - ∑5 𝑒−1515𝑘 𝑖=0 ≈ 0,9944 𝑘! Câu 3:
Gọi X là số hóa đơn sai trong 20 tờ hóa đơn lấy ra, do việc lấy hóa đơn là phép lấy đồng thời nên X phân phối siêu bội H(100; 15; 20).
 E(X) = n.M/N = 20.15/100 = 3
Gọi Y là số tiền thiệt hại của công ty (triệu đồng)  Y = 5X  E(Y) = 5E(X) = 15 (triệu đồng) Câu 4:
1/ x = 34,587 và s ≈ 0,1983 2/ p ≈ 90/100 3/ 34,6199 4/ (0,0303; 0,0505) 5/ 0,3212 6/ 260 người
7/ Gọi p là tỷ lệ ngày có giá bán thấp hơn 34,4 triệu
H0: p = 0,15 và H1: p < 0,15 8/ Gqs = - 0,5601
9/ Gọi 2 là độ phân tán của giá bán
H0: 2 = 0,035 và H1: 2  0,035
10/ Với mức ý nghĩa 5%, cho rằng độ phân tán về giá bán mặt hàng A là 0,035 (triệu đồng2).