Đề thi kết thúc học phần - Xác suất thống kê (MI2020) | Trường Đại học Bách khoa Hà Nội

lOMoAR cPSD| 45254322
Trường ĐH Kinh tế - Kỹ thuật ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp
Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút
Tiết 4-5, ngày 25/06/2020 Đề số: 01
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 iểm): Cho hệ ầy ủ ba biến cố {A,B,C} với 2P(A)=P(B)=2P(C). Biết
biến cố F thỏa mãn: P(F/A)=0,25;
P(F/B)=0,28 và P(F/C)=0,35. Tính các xác suất sau:
1/. Tính xác suất P(F).
2/. Tính xác suất P{(A+ +B C F) / }=P(U/ F PUF PF PF PF) = ( . ) / ( ) = (
) / ( ) =1 Áp dụng CT: A.U = A; A.V = V Câu 2.(3 iểm):
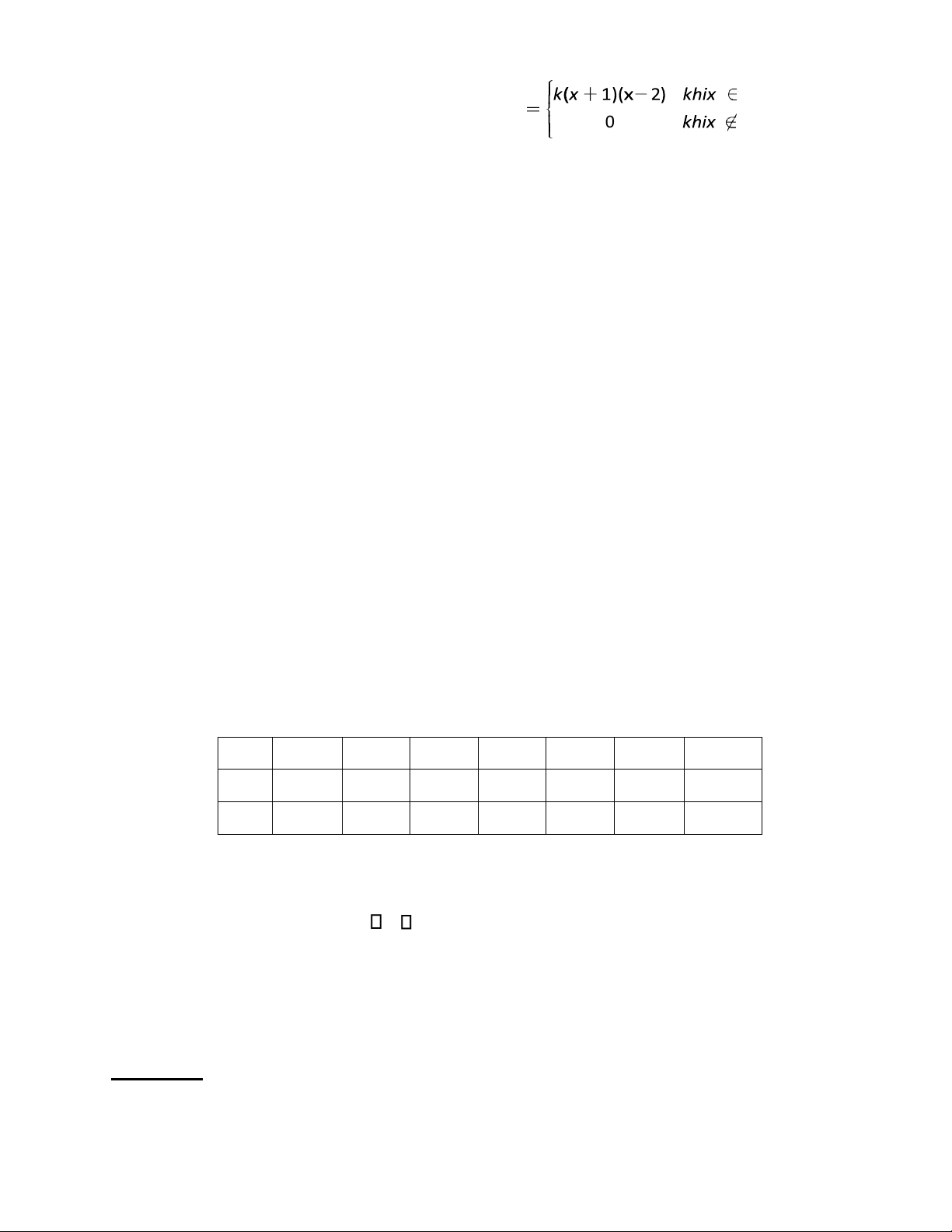
1/. Cho hàm mật ộ của biến ngẫu nhiên X: (2− x ) khi x [0,2] f x( ) = kx3 0 khi x [0,2]
a) Tìm k ể f(x) là hàm mật ộ. b) Tính xác suất P(X>ModX ).
2/. Cho X ~ N(5; 4,84); Y ~ B(10; 0,21) và ặt T = X – Y
a) Hãy tính giá trị của E(T). b) Tính xác suất P(X2 -2X > ModY).
Câu 3.( 3 iểm): Tốc ộ dowload mạng wifi của hãng VNPT tại tòa trung cư
A là biến ngẫu nhiên theo phân phối chuẩn, iều tra tốc ộ dowload của một
số hộ gia ình tại ây có số liệu như sau: cỡ mẫu=40 hộ; trung bình mẫu=30,2
(Mbps) và ộ lệch hiệu chỉnh=1,9 (Mbps); Trong ó có 11 hộ có tốc ộ
dowload thấp hơn so với gói cước ăng ký.
1/. Hãy ước lượng tốc ộ dowload trung bình của các hộ gia ình tại ây với ộ tin cậy 90%
2/. Hãy ước lượng tỷ lệ các hộ có tốc ộ dowload thấp hơn so với ăng ký với ộ tin cậy 95%
3/. Khi ước lượng tốc ộ dowload trung bình của các hộ tại ây với yêu cầu ộ
chính xác là 0,09 và ộ tin cậy là 90% thì cần khảo sát thêm bao nhiêu hộ gia ình nữa nữa? lOMoAR cPSD| 45254322
Câu 4.(2 iểm): Để khảo sát ộ cận thị (Diop) liên quan tới số giờ sử dụng
máy tính-iện thoại, của học sinh ở trường THCS Vĩnh Hưng , thu ược mẫu số liệu như sau:
xi(giờ) 3,5 3,7 3,7 3,8 3,8 3,9 4,0 4,2 yi( 1 1,25 1,5 1,5 1,5 1,75 1,75 2 Diop ) 4 2 6 6 4 6 2 5 ni (số họ sinh)
1/. Lập phương trình hồi quy tuyến tính mẫu, qua ó cho biết sự khác
biệt về ộ cận (Diop) ước lượng qua hàm hồi quy mẫu và số liệu quan sát
ược khi thời gian sử dụng ở mức 3,7 giờ.
Bấm máy tính ta ược các tham số:
A = -3,664; B = 1,364; r = 0,954
Vậy ta có phương trình hồi quy: y = A + Bx = -3,664 + 1,364x
Nếu x= 3,7 thì thay vào phương trình trên ta ược giá trị hồi quy của y là
1,383; giá trị thực tế của y là (1,25+1,5)/2 = 1,375 (lấy ở bảng trên). Giá
trị hồi quy khác với giá trị thực tế là 1,383 – 1,375 = 0,008.
2/. Có giả thiết cho rằng XY 0,97; hãy ưa ra kết luận với mức ý nghĩa 5%; n = ni = 35.
+ Chọn cặp giả thuyết: H0 : xy 0
1 xy 0 Với ρ0 = 0,97. H : 1
+ Tiêu chuẩn kiểm ịnh: U Z= −( ln1+ 0 − 0 ) n−3 U(0,1). 2 1− 0 2(n−1) lOMoAR cPSD| 45254322 Trong ó: 1 + r 1 + 0,954
Z = 12 ln 1 −r xy xy = 12 ln 1 −0,954 =1,874 + - Giá trị quan sát: 1 0 , 97 0,97
uqs = (1,874− 12ln 1 −0 , 97 − 2(35 1) − ) 35− =−3 1,3156.
+ Miền bác bỏ: Wα = (-∞; -uα) với α = 5% = 0,05 → uα = u0,05 = 1,64 (phụ lục 2) do ó Wα = (-∞; -1,64)
+ So sánh uqs với Wα ta thấy uqs Wα → chấp nhận H0.
+ Kết luận: Qua mẫu iều tra trên ta thấy giả thuyết cho rằng hệ số tương quan
giữa ộ cận và thời gian sử dụng iện thoại nhỏ hơn 0,97 là chưa úng. 3/. Hãy ước
lượng hệ số tương quan lý thuyết với ộ tin cậy 95%. Giải: Với Φ(zα) = γ/2 =
0,95/2 = 0,475 → zα = 1,96 (phụ lục 1), n = ni = 35, rxy = 0,954. Chọn thống kê:
Z = 12 ln11+−rrxyxy = 12 ln11+−0,9540,954 =1,874 1 1+ xy
Khoảng tin cậy của 2ln1− xy là:
(Z− rxy − z ; Z− rxy + z ) = 2(n−1) n−3 2(n−1) n−3 (1,874− 0,954 − 1,96 ;1,874− 0,954 + 1,96 ) = (1,513; 2,206) 2(35−1) 35−3 2(35−1) 35−3
Từ ó suy ra khoảng tin cậy của hệ số tương quan ρxy là: xy
(ee2 1,5132 1,513 +−11; ee2 2,2062 2,206 +−11) = (0,907; 0,976). lOMoAR cPSD| 45254322
---------------------------------------------------------- Hết----------------------------- -----------------------
Ghi chú: Sinh viên ược sử dụng bảng tra các giá trị tới hạn xác suất
Duyệt Hà nội, ngày
22 tháng 06 năm 2020
Trường ĐH Kinh tế - Kỹ
ĐỀ THI KẾT THÚC HỌC
PHẦN thuật Công nghiệp Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH Tiết 4-5, ngày
Thời gian làm bài: 90 phút 25/06/2020 Đề số 02
Họ tên SV:…………………………………………. Phòng
thi: ………………Số BD……………
Câu 1.(2 iểm): Cho hai biến cố A, B. Biết P(A+B) = 0,8; P(A) = 0,3; P(B) =0,6.
1/. Tìm xác suất P(AB).
2/. Đặt C A B AB= + = , tính xác suất: P(A|C) = P A AB(
/ ) =P A P AB( ). ( / A) P AB()
P AB() 1= −P AB() P ABA( ) P AB( )
P AB( / A) = −1 P AB A( / ) = −1 = −1 P A( ) P A( )
Câu 2.(3 iểm):
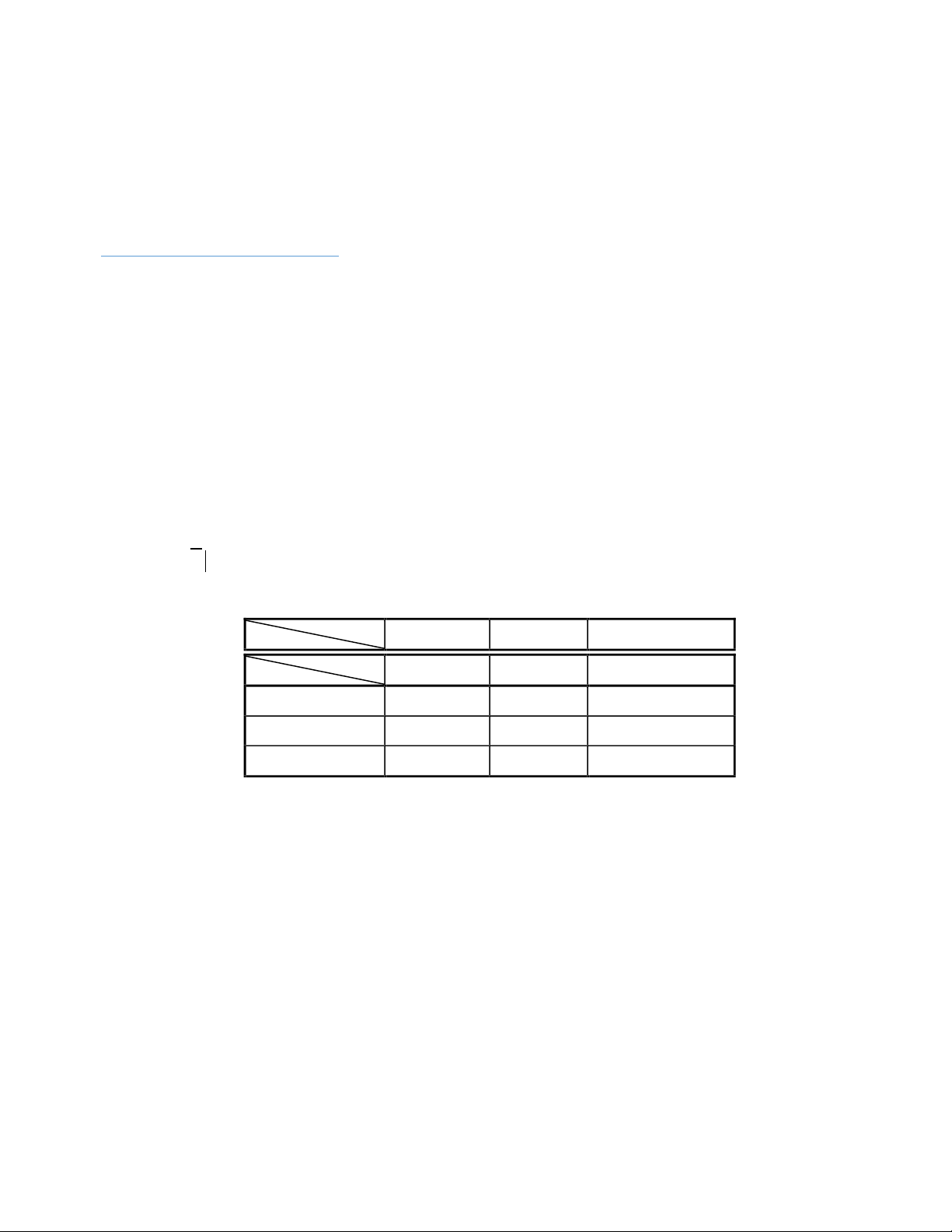
1/. Cho biến ngẫu nhiên X và Y có bảng phân phối ồng thời như sau : lOMoAR cPSD| 45254322 Y - 2020 0 2020 X - 2020 a 0,5a a 0 ,05 0 a ,5a 1 2020 ,15 0 a 2 a
a). Tìm hệ số a từ bảng phân phối. b). Tính MedZ với Z=X-Y.
2/. Hai biến ngẫu nhiên X; Y ộc lập thỏa mãn: X ~ N(5; 4); Y ~ P(3) và ặt T = X + Y
a) Hãy tính giá trị của D(T). b) Tính xác suất P(X2 -2X > modX).
Câu 3.(3 iểm): Số cuộc gọi ến/ngày ở trung tâm bảo hành máy tính của
hãng Dell (110 Thái Thịnh, Q. Đống Đa, Hà nội) là ại lượng tuân theo quy
luật chuẩn. Thống kê số cuộc gọi ến/ngày, ta có kết quả sau: cỡ mẫu n=36
ngày; trung bình mẫu=160,2 cuộc gọi và
ộ lệch hiệu chỉnh=2,3(cuộc
gọi). Trong ó có m=8 ngày trung tâm không áp ứng hết yêu cầu gọi bảo hành.
1/. Hãy ước lượng tỷ lệ của những ngày không áp ứng hết yêu cầu gọi ến với ộ tin cậy 95%.
2/. Hãy ước lượng số cuộc gọi trung bình ến trung tâm bảo hành với ộ tin cậy 90%
3/. Khi ước lượng số cuộc gọi trung bình ến trung tâm bảo hành với yêu cầu
ộ chính xác là 0,2(cuộc gọi) thì ộ tin cậy bằng bao nhiêu.
Câu 4.(2 iểm): Để khảo sát ộ cận thị (Diop) liên quan tới số giờ sử dụng máy
tính-iện thoại, của học sinh ở trường THCS Vĩnh Hưng , thu ược mẫu số liệu như sau:
xi(giờ) 3,5 3,7 3,7 3,8 3,8 3,9 4,0 4,2 yi( 1 1,25 1,5 1,5 1,5 1,75 1,75 2 Diop ) lOMoAR cPSD| 45254322 4 2 6 6 4 6 2 5 ni (số họ sinh)
1/. Lập phương trình hồi quy tuyến tính mẫu, qua ó cho biết sự khác
biệt về ộ cận (Diop) ước lượng qua hàm hồi quy mẫu và số liệu quan sát
ược khi thời gian sử dụng ở mức 3,8 giờ.
2/. Hãy ước lượng hệ số tương quan lý thuyết với ộ tin cậy 95%.
---------------------------------------------------------- Hết----------------------------- -----------------------
Ghi chú: Sinh viên ược sử dụng bảng tra các giá trị tới hạn xác suất
Duyệt Hà nội, ngày
22 tháng 06 năm 2020
Trường ĐH Kinh tế - Kỹ ĐỀ THI KẾT THÚC
HỌC PHẦN thuật Công nghiệp Môn : XÁC SUẤT
THỐNG KÊ – Hệ:
ĐH Tiết 8-9, ngày
Thời gian làm bài: 90 phút 25/06/2020
Đề số: 03
Họ tên SV:…………………………………………. Phòng
thi: ………………Số BD……………
Câu 1.(2 iểm): Cho hệ ầy ủ ba biến cố {A,B,C} với P(A)=P(B); P(C)=0,2.
Biết biến cố F thỏa mãn: P(F/A)=0,15; P(F/B)=0,25 và P(F/C)=0,35
1/. Tính xác suất P(F ) = 1 – P(F) 2/.
Tính xác suất: P( AF ) = 1 – P(A/F)
Câu 2.(3 iểm): lOMoAR cPSD| 45254322
1/. Cho hàm mật ộ của biến ngẫu nhiên X: [-1;2] 0 [-1;2] f x
a) Tìm k ể f(x) là hàm mật ộ. b) Tính P(X > m) biết m=EX
2/. Cho X ~ N(2, 9) ; Y~ B(20; 0,1). Đặt Z= X –ModY+ Y.DX
a) Hãy tính giá trị của E(5Z+1) b) Tính P(X2 +3X < 4)
Câu 3.( 3 iểm): Để khảo sát nhu cầu sử dụng thịt lợn của người dân trong
một tháng, người ta iều tra 100 người thấy: nhu cầu thịt lợn trung bình là
4,5 kg/tháng; ộ lệch hiệu chỉnh là 2,13kg.
1/. Hãy ước lượng nhu cầu sử dụng thịt lợn trung bình của người dân với ộ tin cậy 95%.
2/. Khi ước lượng nhu cầu sử dụng thịt lợn trung bình của người dân với ộ
chính xác là 0,1 thì ộ tin cậy bằng bao nhiêu.
3/.Nếu nhu cầu sử dụng thịt lợn trung bình của người dân là trên 5,5kg/tháng
thì cục quản lý thị trường sẽ can thiệp ể giảm giá thịt lợn. Với mức ý nghĩa
1% hãy cho biết người dân có ược giảm giá thịt hay không?
Câu 4.(2 iểm): Gọi Y (kg) là chỉ số cân nặng của trẻ em trong ộ tuổi 815 và
X là lượng sữa trẻ uống mỗi ngày (ml) (X;Y ều tuân theo quy luật chuẩn).
Điều tra ở một vùng ược kết quả như sau: X 130 150 180 200 230 240 300 Y 30 37 39 39 43 43 47 ni 10 13 14 10 11 8 10
1/. Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu muốn
cân nặng 40kg thì uống bao nhiêu sữa? Y = A + Bx
2/. Có giả thiết cho rằng XY 0,85 , hãy ưa ra kết luận với mức ý nghĩa 5%
---------------------------------------------------------- Hết----------------------------- -----------------------
Ghi chú: Sinh viên ược sử dụng bảng tra các giá trị tới hạn xác suất
Duyệt Hà nội, ngày lOMoAR cPSD| 45254322
22 tháng 06 năm 2020
Trường ĐH Kinh tế - Kỹ
ĐỀ THI KẾT THÚC HỌC
PHẦN thuật Công nghiệp Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH Tiết 8-9, ngày
Thời gian làm bài: 90 phút
25/06/2020 Đề số 04
Họ tên SV:…………………………………………. Phòng
thi: ………………Số BD……………
Câu 1.(2 iểm):
1/. Cho hai biến cố A và B ộc lập nhau. Biết: P(A) = 0,25 và P(B)=0,35. Tìm P(A+B)
2/. Cho hai biến cố A và B sao cho P(B)=0,4; P(AB)=0,15; P(A+B)=0,8.
Tính P(BA) = 1 – P(B/A) Câu 2.(3 iểm):
1/. Cho biến ngẫu nhiên X và Y có bảng phân phối ồng thời như sau : Y -2 -1 0 X 1 0 ,5a 0 ,5a a 2 0 ,1 a a 3 0,1 0 ,1 0,2
a). Tìm hệ số a từ bảng phân phối. b). Tính xác suất P(X2< DY).
2/. Một người bắn 10 lần ộc lập vào bia, xác suất bắn trúng ở mỗi lần ều là
0,4. Gọi X là số lần bắn trúng bia của người ó.
a). Hãy tính giá trị của E(X+ModX ) b). Tính P(X2 < 4).
Câu 3.( 3 iểm): Để khảo sát nhu cầu sử dụng thịt lợn của người dân trong
một tháng, người ta iều tra n=100 người thấy: nhu cầu thịt lợn trung bình
là 4,5 kg/tháng; ộ lệch mẫu hiệu chỉnh là 2,13 kg và có m=30 người có nhu
cầu thịt lợn cao.
1/. Hãy ước lượng tỷ lệ người có nhu cầu sử dụng thịt lợn cao với ộ tin cậy 95%. lOMoAR cPSD| 45254322
2/. Khi ước lượng nhu cầu sử dụng thịt lợn trung bình của người dân với ộ
chính xác là 0,35 và ộ tin cậy 99% thì cần khảo sát bao nhiêu người? 3/.Nếu
tỷ lệ người có nhu cầu sử dụng thịt lợn cao là trên 60% thì cục quản lý thị
trường sẽ can thiệp ể giảm giá thịt. Với mức ý nghĩa 1% hãy cho biết người
dân có ược giảm giá thịt hay không?
Câu 4.(2 iểm): Gọi Y (kg) là chỉ số cân nặng của trẻ em trong ộ tuổi 815 và
X là lượng sữa trẻ uống mỗi ngày (ml) (X;Y ều tuân theo quy luật chuẩn).
Điều tra ở một vùng ược kết quả như sau: X 130 150 180 200 230 240 300 Y 30 37 39 39 43 43 47 ni 10 13 14 10 11 8 10
1/. Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu muốn
cân nặng 49 kg thì cần uống bao nhiêu sữa?
2/. Hãy có thể nói hệ số tương quan giữa X và Y là 0,89 hay không với mức ý nghĩa 1%
---------------------------------------------------------- Hết--------------------------- -----------------------
Ghi chú: Sinh viên ược sử dụng bảng tra các giá trị tới hạn xác suất
Duyệt Hà nội, ngày
22 tháng 06 năm 2020
Trường ĐH Kinh tế - Kỹ
ĐỀ THI KẾT THÚC HỌC
PHẦN thuật Công nghiệp Môn : XÁC SUẤT THỐNG KÊ – Hệ: ĐH Tiết ……, ngày
Thời gian làm bài: 90 phút 25/06/2020 ĐỀ DỰ PHÒNG 01
Họ tên SV:…………………………………………. Phòng thi: ………………Số
BD…………… lOMoAR cPSD| 45254322
Câu 1.(2 iểm): Cho 2 biến cố A, B thỏa mãn: P(A)=0,6; P(B)=0,45 và P(AB)=0,25.
1/. Tính xác suất P(A+B).
2/. Tính xác suất P A B( /) =P A P B A( ). ( / ) ) P B( )
Câu 2.(3 iểm):
1/. Cho hàm mật ộ của biến ngẫu nhiên X:
f x( ) = k(x−1)(6− 2x ) khi x [1,3] 0 khi x [1,3]
a) Tìm k ể f(x) là hàm mật ộ. b) Đặt m0=E(X), tính
xác suất P(X>m0).
c) Tính D(X2 + 1) = D(X2) = E(X4) – [E(X2)]2
2/. Cho Cho X ~ N(3; 0,4) và Y là biến ngẫu nhiên số cuộc gọi ến trung tâm
cấp cứu 115 Hà Nội trong vòng 1 giờ, với E(Y)=(12 người). Giả sử và X, Y
là 2 biến ngẫu nhiên ộc lập; ặt Z =X-Y Y ~P(12) ; D(Y) = E(Y) = 12.
a) Hãy tính giá trị của D(Z) = D(X) + D(Y)
. b) Tính xác suất P(X2 -2X > modX). c)
Tính E(X + 1)2 = E(X2 + 2X + 1) = E(X2) + 2E(X) + 1 E(X) =
3; D(X) = 0,4 = E(X2) – [E(X)]2
→ E(X2) = [E(X)]2 + D(X) = 32 + 0,4 = 9,4.
Câu 3.( 3 iểm): Độ rượu (ơn vị: % vol) tuân theo luật chuẩn. Điều tra một
số sản phẩm rượu ngoại tại siêu thị A ta có số liệu sau: cỡ mẫu=36 chai;
trung bình mẫu=37,2 (% vol) và ộ lệch hiệu chỉnh=2,3(% vol).
Trong ó có 8 chai có ộ rượu lớn hơn 40 (% vol)- rượu mạnh.
1/. Hãy ước lượng tỉ lệ của những chai rượu mạnh với ộ tin cậy 90%. 2/.
Nếu dùng số liệu trên ể ước lượng ộ rượu trung bình với ộ chính xác 0,4 thì ộ tin cậy là bao nhiêu.
3/. Khi ước lượng tỷ lệ chai rượu mạnh với yêu cầu ộ chính xác là 0,02 thì ộ tin cậy là bao nhiêu?
Câu 4.(2 iểm): Theo dõi trọng lượng y(kg) và số năm tuổi x(năm) của một
số con bò trong một trang trại chăn nuôi ta có bảng số liệu sau: lOMoAR cPSD| 45254322 xi 1 3 5 7 9 11 13 15 yi 42 45 50 55 57 60 67 72 ni 3 4 2 6 6 4 6 2
Với biến ngẫu nhiên X ;Y ều tuân theo luật chuẩn.
1/. Lập phương trình hồi quy tuyến tính thực nghiệm, qua ó cho biết nếu số
tuổi là 10 năm thì trọng lượng là bao nhiêu?
2/. Hãy ước lượng hệ số tương quan ρxy với ộ tin cậy 99%.
---------------------------------------------------------- Hết----------------------------- -----------------------
Ghi chú: Sinh viên ược sử dụng bảng tra các giá trị tới hạn xác suất
Duyệt Hà nội, ngày
22 tháng 06 năm 2020
Trường ĐH Kinh tế - Kỹ
ĐỀ THI KẾT THÚC HỌC
PHẦN thuật Công nghiệp Môn : XÁC SUẤT THỐNG KÊ – Hệ:
ĐH Tiết ……, ngày
Thời gian làm bài: 90 phút 25/06/2020 ĐỀ DỰ PHÒNG 02
Họ tên SV:…………………………………………. Phòng thi: ………………Số
BD……………
Câu 1.(2 iểm):
1/. Cho hai biến cố A và B ộc lập nhau. Biết: P(A) = 0,15 và P(B)=0,55. Tìm P(A+B)
2/. Cho hai biến cố A và B sao cho P(B)=0,6; P(AB)=0,35; P(A+B)=0,85.
Tính PBA() = −1 PB A( /
) Câu 2.(3 iểm):
1/. Cho biến ngẫu nhiên X và Y có bảng phân phối ồng thời như sau : lOMoAR cPSD| 45254322 Y - 4 0 2 X 2 0,1 0 ,5a 0 ,2 3 0 ,5a a a 4 0 ,1 0 ,1 2 a
a). Tìm hệ số a từ bảng phân phối. b). Tính xác suất P(Y2< DX).
2/. X là biến ngẫu nhiên chỉ trọng lượng 1 loại trái cây biết trọng lượng
trung bình là 0,3kg, ộ lệch chuẩn 2,1. Giả thiết X tuân theo luật phân phối chuẩn, hãy:
a). Tính giá trị của E(3X+1) và D(2X-3). b). Tính P(X2 +3X< 4).
Câu 3.( 3 iểm): Để khảo sát nhu cầu sử dụng iện của người dân trong tháng
hè, người ta iều tra 100 hộ gia ình thấy: nhu cầu iện trung bình là
300kW/tháng; ộ lệch mẫu hiệu chỉnh là 6,02.
1/. Hãy ước lượng nhu cầu sử dụng iện trung bình với ộ tin cậy 95%. 2/.
Khi ước lượng nhu cầu sử dụng iện trung bình của người dân với ộ chính xác
là 1,15 và ộ tin cậy 99% thì cần khảo sát bao nhiêu hộ gia ình? 3/ Vào tháng
chính ông, nhu cầu sử dụng iện trung bình là 270 KW/tháng. Với mức ý nghĩa
1% có thể nói nhu cầu sử dụng iện của tháng hè và tháng chính ông là như nhau hay không?
Câu 4.(2 iểm): Để xác ịnh sự cân bằng giữa chiều cao (X cm) và cân nặng
(Y kg) của người dân trong vùng, người ta lấy một mẫu ược số liệu như sau:
X(cm 147, 147, 147, 152, 152, 152, 152, 16 16 167, 167, ) 5 5 5 5 5 5 5 0 0 5 5 Y(kg 44 48 60 48 54 60 64 60 64 54 64 ) Ni 1 2 1 1 3 2 1 4 1 1 3
1/. Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu cân
nặng 55 kg thì chiều cao là bao nhiêu
2/. Có thể nói hệ số tương quan giữa X và Y là trên 0,7 hay không với mức ý nghĩa 1%? lOMoAR cPSD| 45254322
---------------------------------------------------------- Hết----------------------------- -----------------------
Ghi chú: Sinh viên ược sử dụng bảng tra các giá trị tới hạn xác suất
Duyệt Hà nội, ngày
22 tháng 06 năm 2020