Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 năm học 2022 - 2023 - Đề số 5

Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2022 – 2023
Môn: Toán – Đề số 5 Thời gian: 90 phút
Câu 1: Cho biểu thức:  2x + 1 1   x + 4  P =  −  : 1−    2  x − 1 x − 1   x + x + 1  a. Rút gọn P
b. Tìm giá trị x dương để P nhận giá trị nguyên.
Câu 2: Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một mảnh vườn hình chữ nhật có diện tích 2
420m . Nếu tăng chiều dài lên 10m
và giảm chiều rộng đi 6m thì diện tích mảnh vườn không đổi. Tính chiều dài và
chiều rộng của mảnh vườn. Câu 3:  1 3 + = 5
 x − 2 y −1
1. Giải hệ phương trình:  2 7  + = 11
 x − 2 y −  1
2. Trong mặt phẳng tọa độ Oxy cho đường thẳng 2
d : 3x − y = 1− m và parabol (P): 2 y = 2x
a. Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi m .
b. Gọi x ,x lần lượt là hoành độ giao điểm của 2 giao điểm.Tìm m để 1 2
(x −1 x −1 = 4 1 )( 2 )
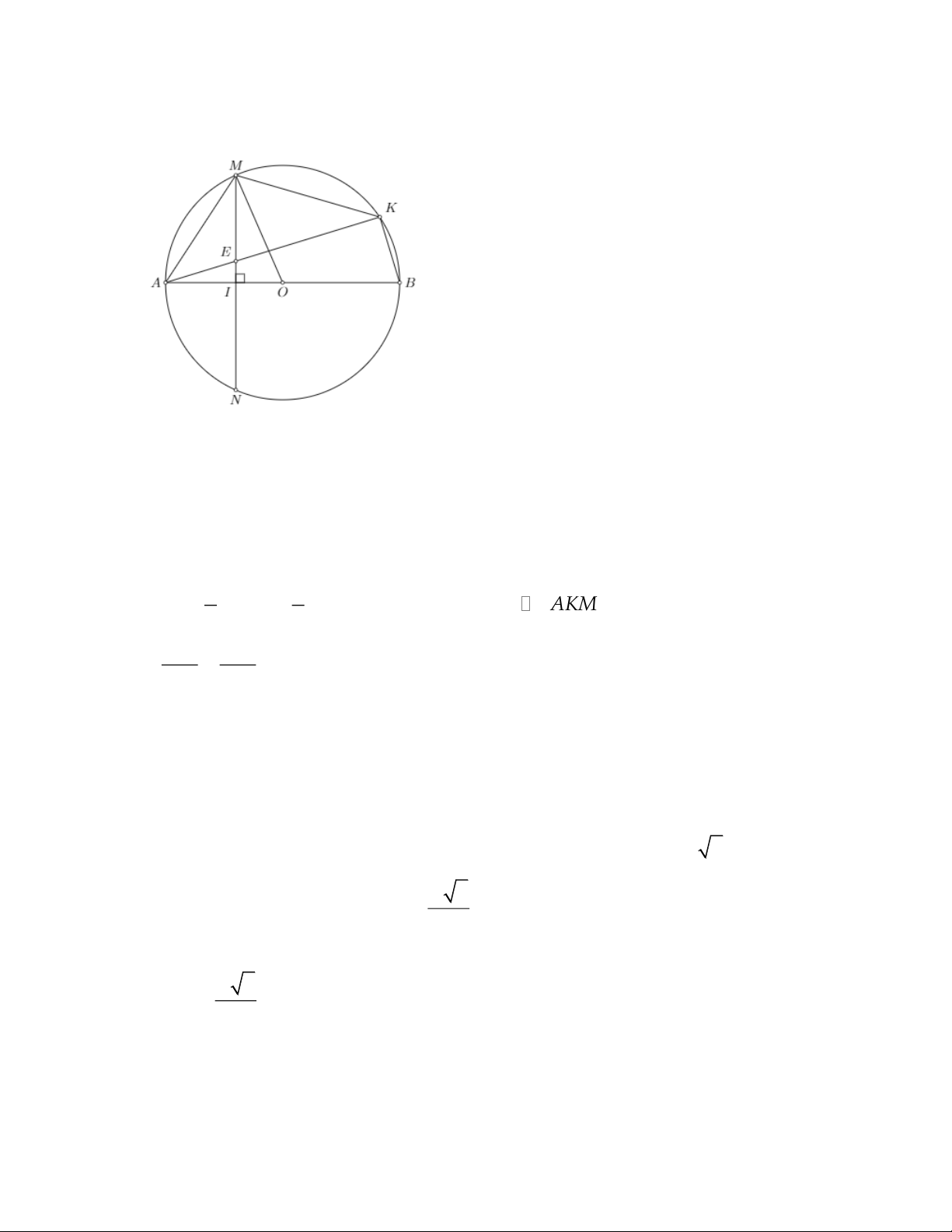
Câu 4: Cho đường tròn tâm O đường kính AB = 2R, dây MN vuông góc với đáy
AB tại I sao cho IA < IB. Trên đoạn MI lấy điểm E (E không trùng M và I). Tia EA
cắt đường tròn tại điểm thứ 2 là K.
a. Chứng minh: IEKB nội tiếp đường tròn b. Chứng minh: 2 AM = A . E AK c. Chứng minh: 2 A .
E AK + BI.BA = 4R
d. Xác định vị trí điểm I sao cho tam giác MIO đạt giá trị lớn nhất
Câu 5: Cho x, y, z là những số thực dương. Chứng minh: x y z + +  1 y + 2z z + 2x 2y + x
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2020 – 2021 Đề số 5
Câu 1: Điều kiện xác đinh: x  0, x  1  2x + 1 1   x + 4  a. P =  −  : 1−    3  x − 1 x − 1   x + x + 1     2x + 1 1 
 x + x + 1− x − 4  P =   ( −     
x − 1)(x + x + 1) : x − 1   x + x + 1   
2x + 1 − x − x − 1 x − 3 P = ( x − ) 1 (x + x + ) : 1 x + x + 1
x − 3 U (3) =  1  ,  3 x ( x −1) x + x + 1 P = (
x − 1)(x + x + 1) . x − 3 x 3 P = = 1+ x − 3 x − 3
b. Để P nhận giá trị nguyên thì x − 3 U (3) =  1  ,  3 x − 3 -1 1 -3 3 4 (TM) 16 (TM) 0 ( L) 81 (TM)
Kết luận : Vậy để P nhận giá trị nguyên thì x  {1,16,81} Câu 2:
Gọi chiều dài mảnh vườn là x (m), x > 0. Diện tích mảnh vườn là 420 2 m 420
Chiều rộng của mảnh vườn là (m) x
Khi tăng chiều dài thêm 10 m thì chiều dài thay đổi là: x + 10 (m) 420
Khi giảm chiều rộng đi 6 m thì chiều rộng thay đổi là: – 6 (m) x
Do diện tích mảnh vườn không đổi nên ta có phương trình: (   x + ) 420 10 − 6 =   420  x  x = 5 − + 5 29(TM) Dễ dàng tìm được   x = 5 − −  5 29(L)
Kết luận: Vậy chiều dài mảnh vườn là 5
− + 5 29 m, chiều rộng của mảnh vườn là 3 + 3 29 m Câu 3:
1. Điều kiện: x  2, y  1 1 1 Đặt a = ,b = x − 2 y − 1
Hệ phương trình trở thành:  a + 3b = 5 2a + 6b = 10 b = 1      2a + 7b = 11 2a + 7b = 11 a =    2  1 = 2   5 x − 2 x =     2 1  = 1  y =  1  y −1  
Vậy hệ phương trình có nghiệm (x y) 5 , =  ,1  2  2.
a. Phương trình hoành độ giao điểm: 2 2 2 2
2x = 3x − 1 + m  2x − 3x + 1 − m = 0 2  = − ( 2 − m ) 2 3 4.2. 1 = 1+ 8m  0 m 
Vậy (d) luôn cắt (P) tại 2 điểm phân biệt  −b 3 x + x = =  1 2 
b. Áp dụng hệ thức Viet ta có: a 2  c  2 x .x = = 1− m 1 2  a Từ hệ thức: ( − −
x − 1)(x − 1) = 4  x .x − (x + x ) 7 + 1 =  ( 2 1 − m ) 1 7 2 − =
 m = 4  m = 2 1 2 1 2 1 2 2 2 2 Vậy m = 2  …… Câu 4: Chứng minh
a. Ta có AB là đường kính, K thuộc đường tròn nên 0 AKB = 90 Ta có: 0
KEB = EIB = 90 nên tứ giác IEKB nội tiếp
b. Ta có: EAM = MAK ( cùng chắn cung nhỏ MK) 1 1 EMA = sdAN =
sdAM = MKA  AM  E AK  M 2 2 AE MA 2  =  . AE AK = MA MA KA
Tam giác MAB vuông tại M và MI là đường cao nên 2 I .
B BA = MB . Do đó: 2 2 2 A .
E AK + BI.BA = AM + MB = 4R
d. Chu vi tam giác OIM bằng MI + OI + MO
Mà MO = R không đổi nên chu vi tam giác IMO lớn nhất khi MI + MO lớn nhất 2
Ta có: (MI+MO)  2( 2 2 MI + IO ) 2 2
− 2OM = 2R  MI + MO  R 2 R 2
Dấu bằng xảy ra khi MI = MO = 2
Vậy chu vi tam giác OIM lớn nhất khi I nằm trên AB và cách O một khoảng R 2 bằng 2 Câu 5: Ta có: 2 2 x y z x y z
(x+ y + z)2 2 + + = + +  y + 2z z + 2x 2y + x xy + 2xz yz + 2xy xz + 2yz
3(xy + yz + zx)
(x+ y + z)2
Có nghĩa là ta sẽ chứng minh (  hay
xy + yz + zx) 1 3
(x + y + z)2  3(xy + yz + zx)
Đây là bất đẳng thức quen thuộc. Bạn đọc tự chứng minh