Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 năm học 2022 - 2023 - Đề số 2
Đề thi khảo sát chất lượng đầu năm môn Toán lớp 10 năm học 2022 - 2023 - Đề số 2 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Preview text:
Môn: Toán – Đề số 2 Thời gian: 90 phút
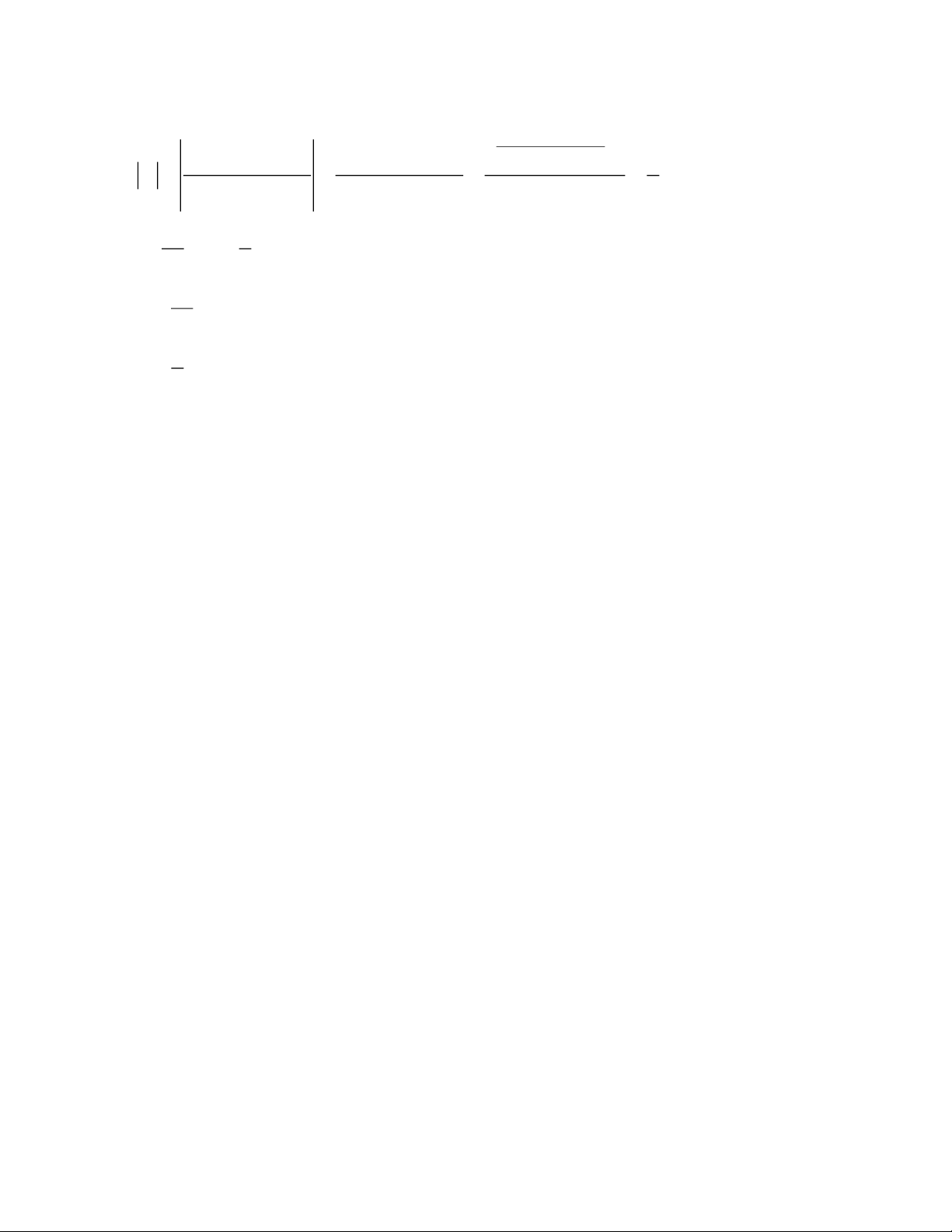
Câu 1: Cho biểu thức x x 2 2 − x A = + : −
,x 0,x 1 − −
x 1 x 1 x x x + x a. Rút gọn biểu thức
b. Biết P (x) = 4 . Tìm x
c. Tìm giá trị của x để P (x) 1
Câu 2: Cho phương trình 2
mx − x − 5m + 2 = 0
a. Giải phương trình khi m = 2
b. Tìm điều kiện của m để phương trình có 2 nghiệm phân biệt x ,x thỏa mãn 1 2 2 2
x + x − 2 x + x = 1 1 2 ( 1 2)
Câu 3: Cho parabol (P) 2
= x + 5x + 2 và đường thẳng (d) : y = mx
a. Vẽ (P) và d trên cùng hệ trục tọa độ
b. Tìm điều kiện của m để d cắt (P) tại 2 điểm phân biệt sao cho một điểm có hoành độ bằng 1
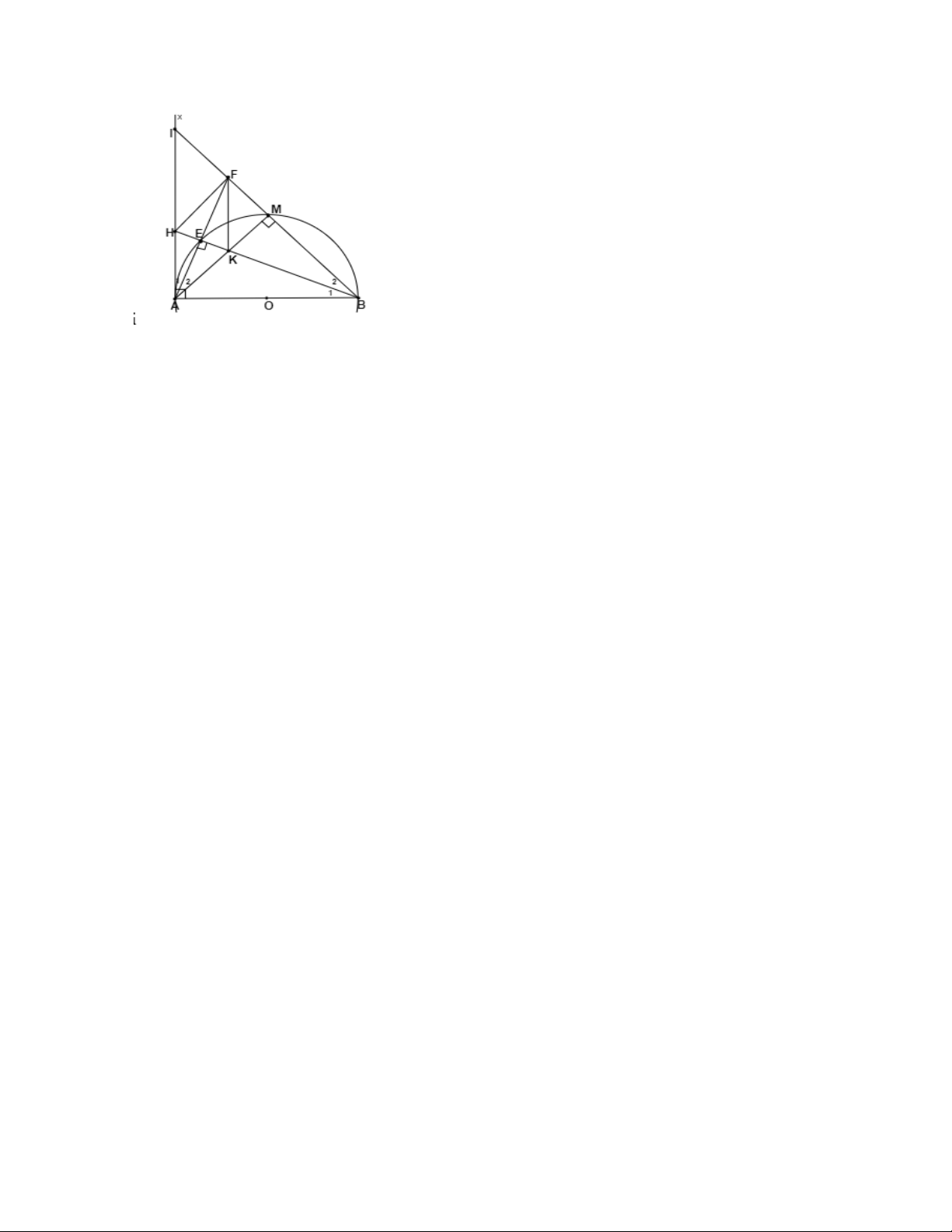
Câu 4: Cho nửa đường tròn tâm O đường kính AB điểm M bất kì nằm trên nửa
đường tròn. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ tiếp tuyến Ax.
Tia BM cắt Ax tại I, tia phân giác của MAI cắt nửa đường tròn tại E, cắt tia MN
tại F tia BE cắt Ax tại H, cắt AM tại K.
a. Chứng minh rằng: Tứ giác EFMK là tứ giác nội tiếp
b. Chứng minh tam giác BAF là tam giác cân c. AKFH là hình thoi
d. Xác định M để AKFI nội tiếp nửa đường tròn
Câu 5: Cho 2 số thực x, y không âm thay đổi. Tính giá trị lớn nhất, giá trị nhỏ
(1 − xy)(x − y)
nhất của biểu thức: A = ( 1 + x)2 (1+ y)2 Đề số 2 Câu 1: x x 2 2 − x A = + : − − −
x 1 x 1 x x x + x x ( x 1) + x 2 2 − x A = + : − x − 1 x − 1 x ( x x + 1) + 2 ( x 1) 2 + − + 2 x x x A = : x −1 x ( x +1)
x ( x + 2) x( x + 1) x A = . = x − 1 x ( x + 2) x − 1 x b. P (x) = 4 = x −
x + = ( x − )2 4 4 4 0 2 = 0 x = 2 x − 1
Vậy x = 2 thì P (x) = 4 2 1 3 x − + x x − x + 1 2 4
c. P (x) 1 1 0 0 x − 1 x − 1 x − 1 2 1 3 3 Do x − + x
x − 1 0 x 1 0 x 1 2 4 4 Vậy…… Câu 2:
a. Thay m = 2 vào phương trình ta có: 2 1 65
2x − x − 8 = 0 x = 4 1 65
Vậy với m = 2 phương trình có 2 nghiệm phân biệt x = 4
b. Để phương trình có 2 nghiệm phân biệt x ,x ta có: 0 1 2 2 = − ( − m) 2 1 4 2 5
m = 20m − 8m + 1 0 m 0 b 1 x + x = − = 1 2
Áp dụng hệ thức Viet ta có: a m c 2 − 5m x .x = = 1 2 a m Ta có biểu thức 2 −
x + x − (x + x ) = (x + x )2 2 2 1 2 5m 2 2
− 2x x − 2 x + x = − 2 − − 1 = 0 1 2 1 2 1 2 1 2
( 1 2) m m m 2 + 13 m = 2 − − = 9 9m 4m 1 0 (tm) 2 − 13 m = 9 Kết luận: …… Câu 3: a. Học sinh tự vẽ hình
b. Phương trình hoành độ giao điểm là: 2 2
x + 5x + 2 − mx = 0 x + (5 − m)x + 2 = 0
Để d cắt (P) tại 2 điểm phân biệt thì 0 = ( − m)2 2 5
− 4.2 = m − 10m + 17 0(*)
Áp dụng hệ thức Viet ta có: b
x + x = − = 5 − m 1 2 a c x .x = = 2 1 2 a
Do một giao điểm có hoành độ bằng 1 ta giả sử x = 1 x = 2 1 2
1+ 2 = 5 − m m = 2 thỏa mãn (*)
Vậy m = 1 thì d cắt (P) tại 2 điểm phân biệt sao cho có một điểm có hoành độ bằng 1 Câu 4: Chứng minh
a. Do M nằm trên nửa đường tròn nên 0 0
AMB = 90 AMF = 90
Do M nằm trên nửa đường tròn nên 0 0
AEB = 90 BEF = 90 0
AMF + BEF = 180 EFMK là tứ giác nội tiếp
b. Ta có AE là phân giác góc MAI IEM = MAE EA = ME EAB = MBE
Vậy BE là tia phân giác góc ABF (1)
Mặt khác BE ⊥ AF (2)
Từ (1) và (2) ta có tam giác BAF cân tại B
c. Theo chứng minh trên ta có tam giác BAF là tam giác cân tại B, BE là đường
cao nên BE cũng là trung tuyến EA = EF (3)
AF ⊥ HK (4), AE là phân giác của HAK Tam giác AHK là tam giác cân tại
A có AE là đường cao nên cũng là đường trung tuyến. Vậy EK = EH (5)
Từ (3), (4), (5) ta có AKHF là hình thoi
d. Ta có AKHF là hình thoi HA / /FK hay IA / /FK AKFI là hình thang
Để AKFI nột tiếp đường tròn thì AKFI là hình thang cân
AKFI là hình thang cân khi M là trung điểm của AB M là trung điểm của AB 0
ABM = IAM = 45
Tam giác ABI vuông tại A có 0 0
ABI = 45 AIB = 45 0
KAI = AIF = 45 AKFI là hình thang cân
Vậy khi M là trung điểm của cung AB thì tứ giác AKFI nội tiếp nửa đường tròn Câu 5: 2
x + y + xy + 1
(1 − xy)(x − y)
(1 − xy)(x − y) 2 1 A = = (
+ x)2 ( + y)2 ( + x)2 ( + y)2 (x + y + xy + )2 4 1 1 1 1 1 −1 1 P 4 4 1 − P = khi x = 0, y = 1 thì 4 1 P = khi x = 1, y = 0 4