

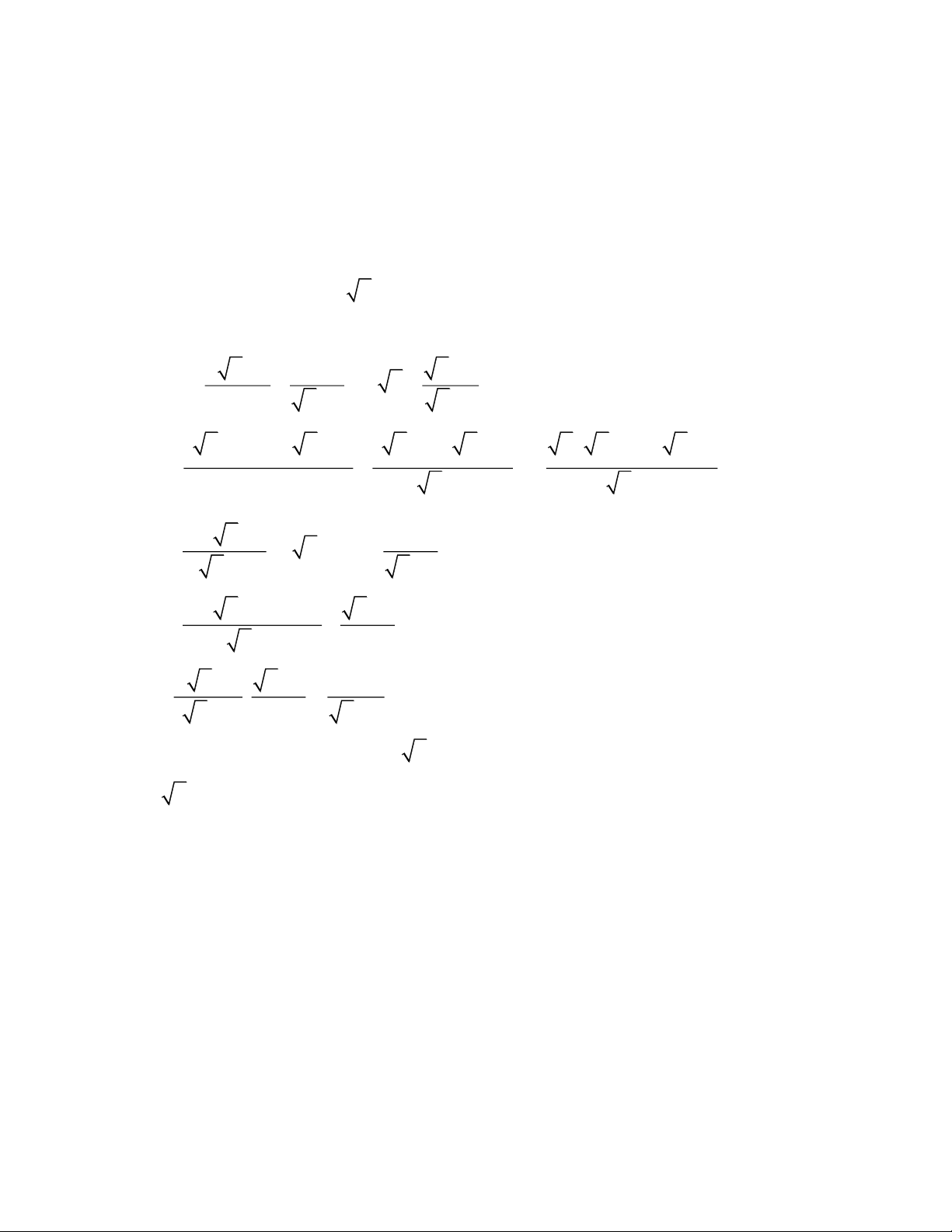

Preview text:
Đề thi khảo sát chất lượng đầu năm lớp 10 năm 2022 – 2023
Môn: Toán – Đề số 1 Thời gian: 90 phút
Câu 1: Cho biểu thức
x x +1 x −1 x − 4 A = − : x + x − 1 x − 1 x − 1
a. Tìm điều kiện xác định của biểu thức b. Rút gọn biểu thức
c. Tìm giá trị x nguyên để A nguyên
Câu 2: Cho phương trình 2 2
x − 2mx + m + m − 1 = 0
a. Giải phương trình khi m = 1
b. Xác định m để phương trình có hai nghiệm phân biệt x ,x thỏa mãn điều kiện 1 2 sau: 2 2
x + x + 2x − 3x x + 2x = 4 1 2 1 1 2 2 x
Câu 3: Cho parabol (P) 2 =
và đường thẳng (d) : y = 2x + 3 2
a. Vẽ (P) và d trên cùng hệ trục tọa độ
b. Tìm tọa độ giao điểm của (P) và d
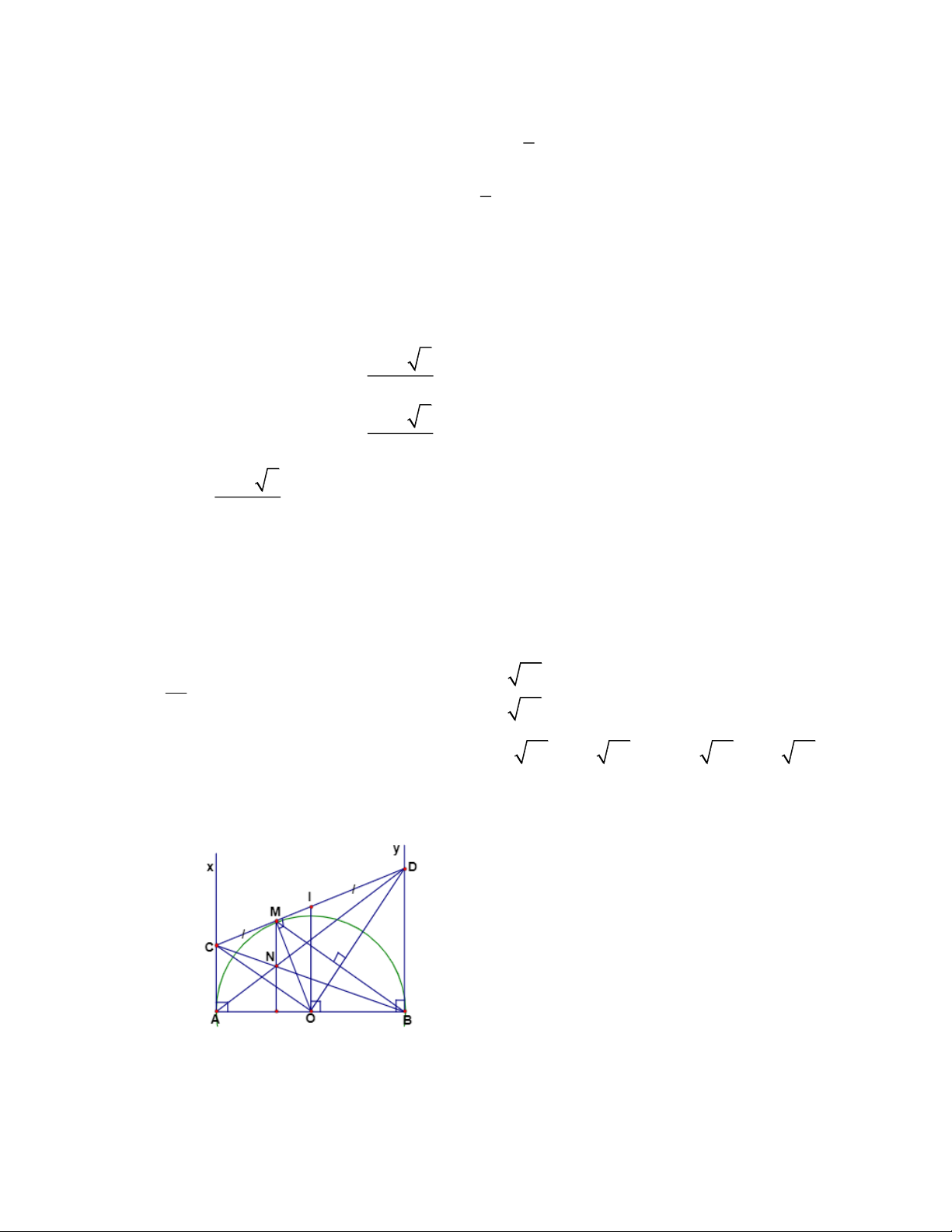
Câu 4: Cho nửa đường tròn đường kính AB = 2R . Từ A và B kẻ hai tiếp tuyến
Ax và By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ 3 cắt các tiếp
tuyến Ax, By lần lượt ở C, D. Các đường thẳng AD, BC cắt nhau tại N.
a. Chứng minh 4 điểm O, M, B, D cùng nằm trên một đường tròn, xác định tâm đường tròn đó b. Chứng minh: 0 COD = 90
c. Chứng minh AB là tiếp tuyến của đường tròn đường kính CD
d. Xác định vị trí của P để ACDB đạt giá trị nhỏ nhất
Câu 5: Cho 3 số thực dương thỏa mãn điều kiện xyz = 1. Chứng minh rằng: 1 1 1 + + 1 2 2 2 2 2 2 x + y + 1 y + z + 1 z + x + 1
Đáp án Đề thi khảo sát chất lượng đầu năm năm 2022 – 2023 Đề số 1 Câu 1: x − 1 0 x 1
a. Điều kiện xác định: x − 1 0 x 0 x 0
x x +1 x −1 x − 4 b. A = − : x + x − 1 x − 1 x − 1
( x 1)(x x 1) ( x 1)( x 1) x( x 1) x 4 + − + + − − + − A = − : x − 1 x − 1 x − 1 x − x +1 x − 4 A = −( x + 1) : x − 1 x −1
x − x +1− x +1 x −1 A = . x − 1 x − 4
− x + 2 x − 1 1 − A = . = x − 1 x − 4 x + 2 +
c. Để A đạt giá trị nguyên thì x + 2 U (1) = 1 x + 2 2 1
không có giá trị x nguyên nào để A đạt giá trị nguyên Câu 2:
a. Thay m = 1vào phương trình ta có:
x − x + = (x − )2 2 2 1 0 1 = 0 x = 1
Kết luận với m = 1 thì phương trình có nghiệm x = 1
b. Để phương trình có 2 nghiệm phân biệt x ,x thì: 1 2 ' 0 2 2
' = m − m − m + 1 = 1− m 0 m 1 b
x + x = − = 2m 1 2
Áp dụng hệ thức Vi – et ta có: a c 2 x .x = = m + m − 1 1 2 a 2 2
x + x + 2x − 3x x + 2x = 4 1 2 1 1 2 2
(x + x )2 − 5x x + 2 x + x = 4 1 2 1 2 ( 1 2) (2m)2 − 5( 2
m + m − 1) + 4m = 4 1 − + 5 m = 2 − − + = 2 m m 1 0 (Tm) 1 − − 5 m = 2 1 − 5 Vậy m =
thì phương trình có 2 nghiệm phân biệt thỏa 2 mãn: 2 2
x + x + 2x − 3x x + 2x = 4 1 2 1 1 2 2 Câu 3: a. Học sinh tự vẽ
b. Phương trình hoành độ giao điểm là: 2 x x = 2 + 10 2
= 2x + 3 x − 4x − 6 = 0 2 x = 2 − 10
Vậy tọa độ gia điểm của (P) và d là: A(2 + 10,7 + 2 10),B(2 − 10,7 − 2 10 ) Câu 4: Chứng minh a. Xét tứ giác OMBD có: 0
OMD + OBD = 180 Tứ giác OMBD nội tiếp đường OD
tròn tâm là trung điểm của OD và bán kính 2
b. Ta có : OC là phân giác góc AOM , OD là phân giác góc MOB Mặt khác 0
AOM + MOB = 180 0 COD = 90
c. Gọi I là trung điểm của CD
I là tâm đường tròn ngoại tiếp tam giác COD, IO là bán kính
Theo tính chất tiếp tuyến ta có: AC ⊥ AB, BD ⊥ AB BD / / AC . Vậy ACDB là hình thang
Ta lại có I là trung điểm của CD, O là trung điểm AB. Vậy OI là đường trung bình của hình thang ACDB
IO//AC, mà AC ⊥ AB IO ⊥ AB tại O. Vậy AB là tiếp tuyến tại O của
đường tròn đường kính CD
d. Ta có chu vi tứ giác ACDB = AB + AC + CD + BD mà AC + BD = CD nên chu
vi ACBD = AB + 2CD mà AB không đổi nên chu vi tứ giác ACDB nhỏ nhất
khi CD CD là khoảng cách giữa Ax và By tức là CD vuông góc với Ax và
By. Khi đó CD//AB. Vậy M là trung điểm của AB Câu 5: 2 2
x + y xy (x + y)( 2 2 2
x + y ) 2xy(x + y) 2 2 1 1
1 + x + y (x + y + z)xy 2 2 1 + x + y
(x + y + z)xy 1 z 1 x 1 y , , 2 2 2 2 2 2 1 + x + y
x + y + z 1 + y + z
x + y + z 1 + z + x x + y + z 1 1 1 z x y x + y + z + + + + = 1 = Vp 2 2 2 2 2 2 1 + x + y 1 + y + z 1 + z + x x + y + z x + y + z x + y + z x + y + z



