Đề thi KSCL đội tuyển HSG Toán 12 năm 2018 – 2019 trường Yên Lạc 2 – Vĩnh Phúc

SỞ GD&ĐT VĨNH PHÚC
KỲ THI KSCL ĐỘI TUYỂN HỌC SINH GIỎI KHỐI 12
TRƯỜNG THPT YÊN LẠC 2 ĐỀ THI MÔN: TOÁN NĂM HỌC 2018-2019
Thời gian làm bài: 180 phút, không kể thời gian giao đề Câu 1 (2.5 điểm). a) Cho hàm số 3 2 2
y  x  3mx  4m  2 có đồ thị là C . Tìm m để đồ thị hàm số C có m  m  hai điểm cực trị ,
A B sao cho diện tích tam giác ABC bằng 4 với điểm C 1;4. 2x  4
b) Cho hàm số y 
có đồ thị là C và hai điểm M  3;  0, N  1  ;  1 . Tìm trên đồ thị x 1
hàm số C hai điểm ,
A B sao cho chúng đối xứng nhau qua đường thẳng MN .
Câu 2 (2.0 điểm).
a) Giải phương trình: 2
4cos x1 sin x  2 3 cos xcos2x  1 2sin . x
b) Một hộp đựng 9 tấm thẻ được đánh số từ 1 đến 9. Hỏi phải rút ít nhất bao nhiêu thẻ để xác 5
suất có ít nhất một thẻ ghi số chia hết cho 4 phải lớn hơn . 6 2 2
3x  2x 5 2x x 1  2 y   2 1 y  2 y  2
Câu 3 (1.0 điểm).Giải hệ phương trình 
x, y 2 2
x  2y  2x  4y  3
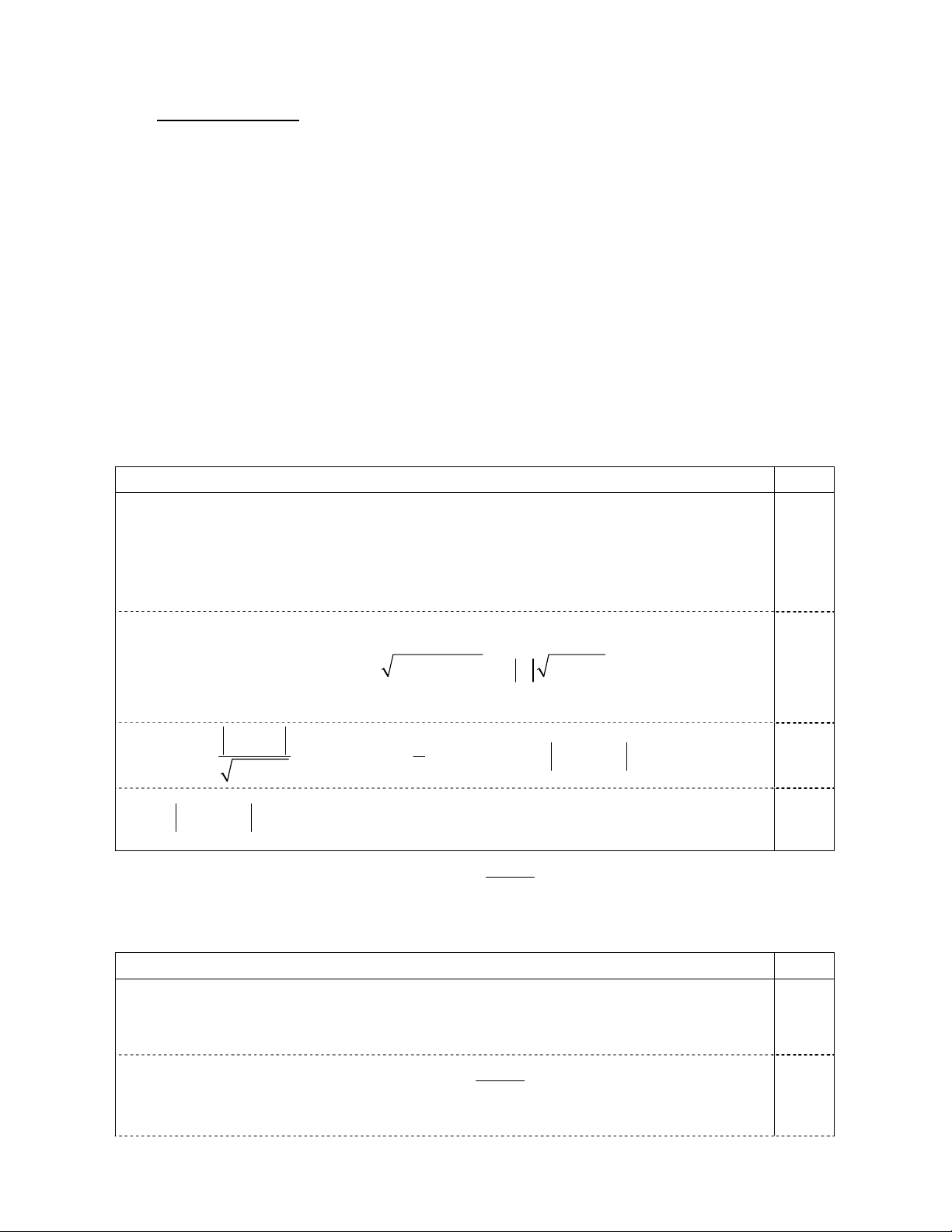
Câu 4 (1.5 điểm). Cho hình hộp đứng ABC .
D A B C D có các cạnh AB  AD  2, AA  3 1 1 1 1 1 và góc  0
BAD  60 . Gọi M , N lần lượt là trung điểm của các cạnh A D và A B . 1 1 1 1
a) Chứng minh rằng AC vuông góc với mặt phẳng BDMN  . 1
b) Tính thể tích khối chóp . A BDMN .
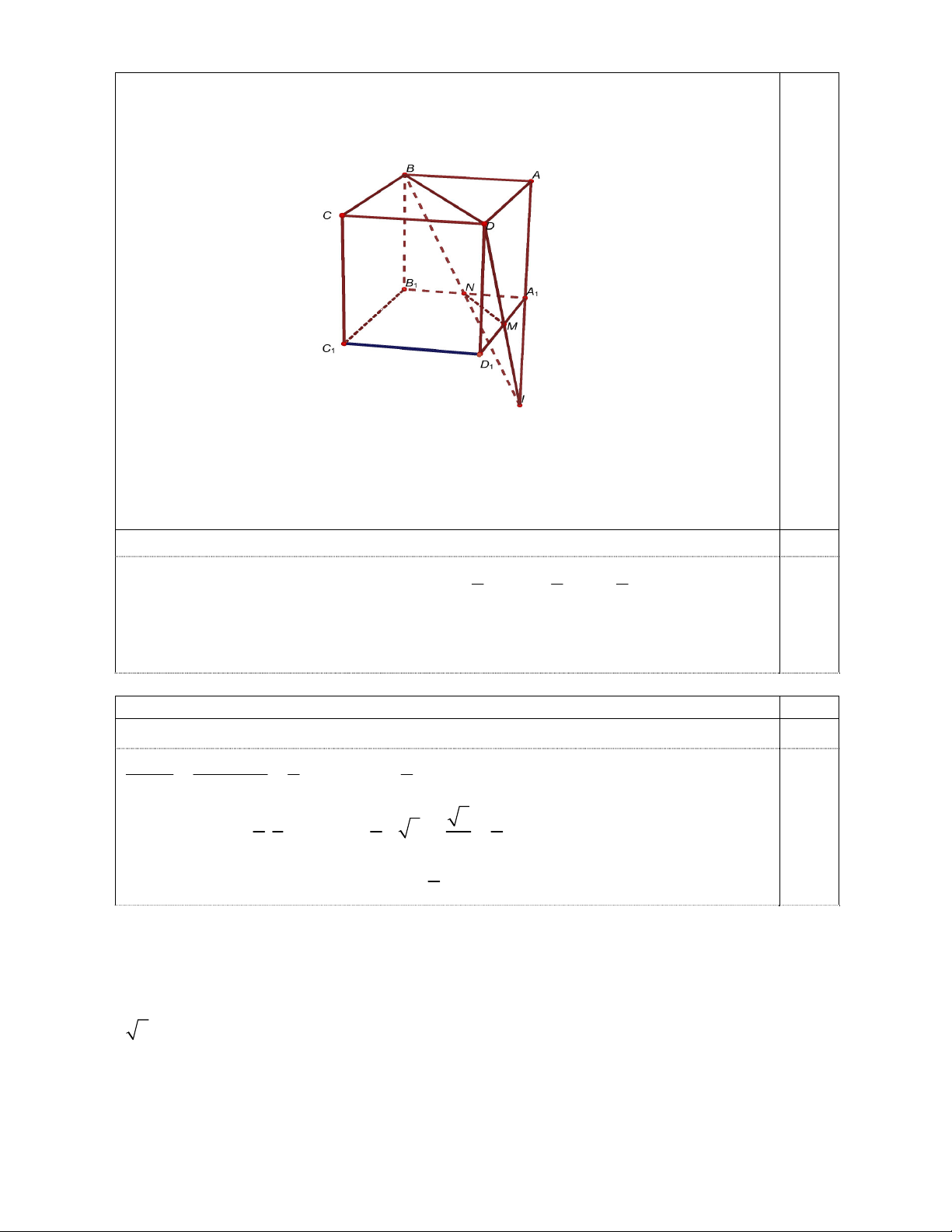
Câu 5 (1.0 điểm). Cho hình chóp S.ABCD , đáy ABCD là hình chữ nhật có AB  3, BC  6,
mặt phẳng SAB vuông góc với đáy, các mặt phẳng SBC và SCD cùng tạo với mặt
phẳng  ABCD các góc bằng nhau. Biết khoảng cách giữa hai đường thẳng SA và BD bằng
6. Tính thể tích khối chóp S.ABCD và cosin góc giữa hai đường thẳng SA và . BD
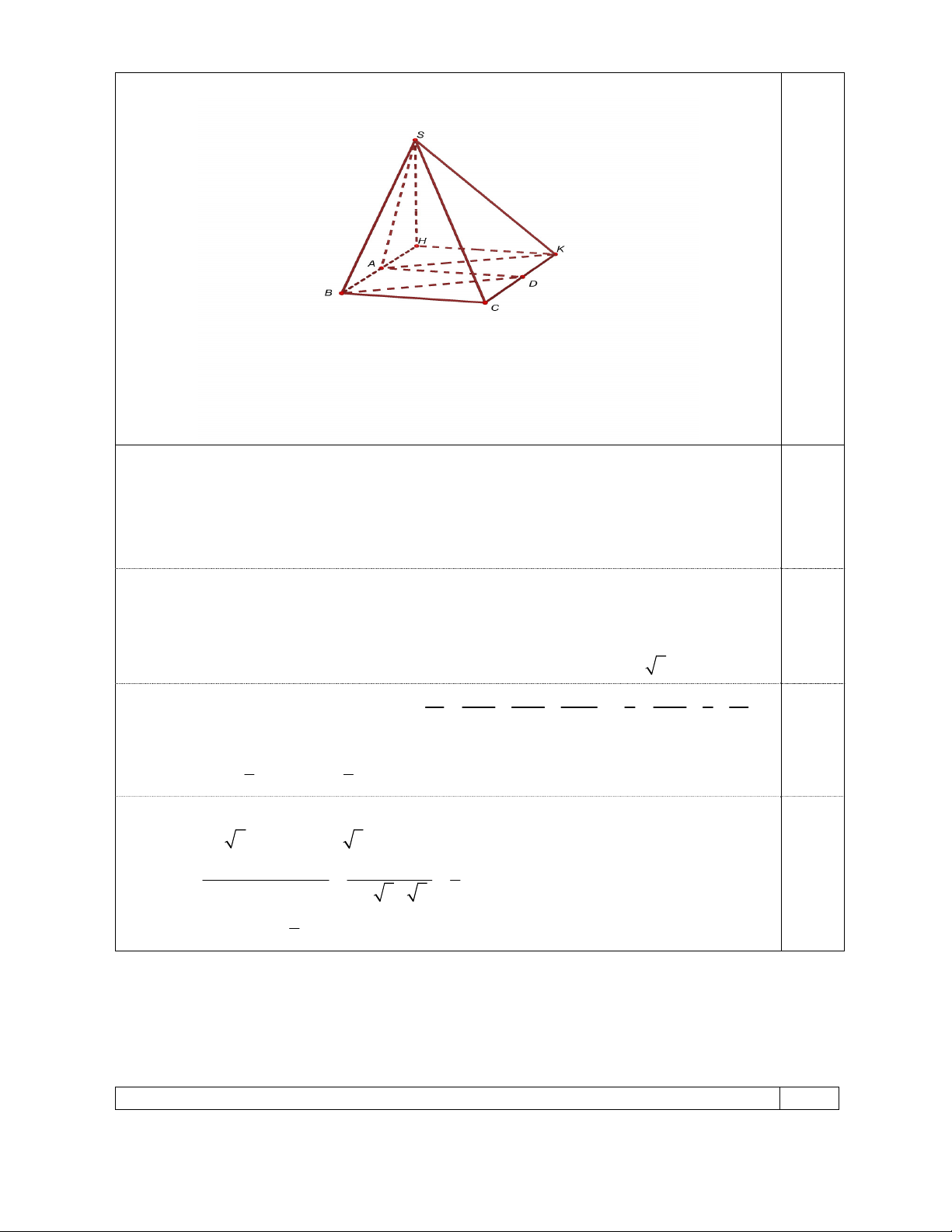
Câu 6 (1.0 điểm). Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC ngoại tiếp đường tròn tâm J 2; 
1 . Biết đường cao xuất phát từ đỉnh A của tam giác ABC có phương trình:
2x  y 10  0 và D2; 4
  là giao điểm thứ hai của AJ với đường tròn ngoại tiếp tam giác
ABC. Tìm tọa độ các đỉnh của tam giác ABC biết B có hoành độ âm và B thuộc đường
thẳng có phương trình x  y  7  0.
Câu 7 (1.0 điểm). Cho các số thực dương a, ,
b c thỏa mãn a  b  c  1.Tìm giá trị nhỏ nhất của biểu thức 7 121 A   . 2 2 2
a  b  c
14ab  bc  ca
------------------- Hết -------------------
- Thí sinh không sử dụng tài liệu và máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………………………….; Số báo danh:………………
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 12 THPT NĂM HỌC 2018-2019
HƯỚNG DẪN CHẤM MÔN: TOÁN
(Hướng dẫn chấm gồm 06 trang) I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải với những ý cơ bản phải có. Khi chấm bài thí
sinh làm theo cách khác nếu đúng và đủ ý thì vẫn cho điểm tối đa.
- Điểm toàn bài tính đến 0,25 và không làm tròn.
- Với bài hình học nếu thí sinh không vẽ hình phần nào thì không cho điểm tương ứng với phần đó. II. ĐÁP ÁN:
Câu 1.a (1.25 điểm) Cho hàm số 3 2 2
y  x  3mx  4m  2 có đồ thị là C . Tìm m để đồ thị m 
hàm số C có hai điểm cực trị ,
A B sao cho diện tích tam giác ABC bằng 4 với điểm m  C 1;4. Nội dung Điểm TXĐ: D  .  Đạo hàm: 2
y '  3x  6mx x  0 2
y '  0  3x  6mx  0  . 
Để đồ thị hàm số có hai điểm cực trị thì m  0. 0.25 x  2m
Tọa độ hai điểm cực trị là A 2 m   B 3 2 0;4 2 , 2 ;
m 4m  4m  2.  0.5 Ta có: AB   3 m  m  2 6 4 2 ; 4
 AB  4m 16m  2 m 1 4m . Phương trình đường 2 2
AB : 2m x  y  4m  2  0. 2   1 AB 6 2m d C;  , suy ra S
 d C AB AB  m  m . AB  C  ;  3 . 6 2 0.25 4 1 4m 2 m  1  Do đó 3
6m  2m  4  .  m  2  0.25 2x  4
Câu 1.b (1.25 điểm) Cho hàm số y 
có đồ thị là C và hai điểm x 1 M  3;  0, N  1  ; 
1 . Tìm trên đồ thị hàm số C hai điểm ,
A B sao cho chúng đối xứng
nhau qua đường thẳng MN . Nội dung Điểm
Phương trình đường MN : x  2y  3  0 .
Phương trình đường AB : y  2x  m . 0.25 2x  4 Khi đó hai điểm ,
A B có hoành độ thỏa mãn:
 2x  m . ĐK: x  1.  x 1 0.25 Pt 2
 2x  mx  m  4  0   1
Trang 1/6, HDC HSG12-Môn Toán
Để đường AB cắt C tại hai điểm phân biệt thì pt  
1 có hai nghiệm phân biệt   0 m  4  4 3 khác -1 2  
 m  8m  32  0   .
2  m  m  4  0 m  4  4 3  x  x 
Trung điểm I của đoạn AB có tọa độ 1
2 ; x  x  m 
với x , x là nghiệm 1 2   2  1 2 0.5 m  m m  của pt  
1 . Mà x  x   nên I  ; . 1 2   2  4 2  m m
Ta có: I  MN nên 
 2.  3  0  m  4  ( thỏa mãn). 4 2 0.25 Suy ra A0; 4
 , B2;0 hoặc A2;0, B0; 4  .
Câu 2.a (1.0 điểm) 2
4cos x1 sin x  2 3 cos xcos 2x  1 2sin . x Nội dung Điểm
Phương trình tương đương với: 2 2
2sin x(2cos x 1)  2 3 cos x cos 2x  4cos x 1  0. 0.25 2 2
 2sin xcos 2x  2 3 cos xcos 2x  3cos x  sin x  0 0.25
 2cos 2xsin x  3cos x   3cos x  sin x 3cos x sin x  0
  3cos x  sin x2cos2x  3cos x sin x  0 
+) 3 cos x  sin x  0  tan x   3  x    k. 3 0.25  5 x    k2 5    0.25 +) 6
2cos 2x  3 cos x  sin x  0  cos 2x  cos x      .  6  5 k2 x    18 3  5 5 k2
Vậy phương trình có nghiệm: x    k , x  
 2k , x   . 3 6 18 3
Câu 2.b (1.0 điểm) Một hộp đựng 9 tấm thẻ được đánh số từ 1 đến 9. Hỏi phải rút ít nhất bao 5
nhiêu thẻ để xác suất có ít nhất một thẻ ghi số chia hết cho 4 phải lớn hơn . 6 Nội dung Điểm
Trong 9 thẻ đã cho có hai thẻ ghi số chia hết cho 4 (các thẻ ghi số 4 và 8), 7 thẻ còn 0.25
lại ghi số không chia hết cho 4.
Giả sử rút x 1 x  9; x  , số cách chọn x từ 9 thẻ trong hộp là x C , số phần tử 9 của không gian mẫu là: x   C . 9
Gọi A là biến cố:” Trong số x thẻ rút ra, có ít nhất một thẻ ghi số chia hết cho 4”
Suy ra A là biến cố:” Lấy x tấm thẻ không có tấm thẻ nào chia hết cho 4”
Số cách chọn tương ứng với biến cố A là x A  C 7
Trang 2/6, HDC HSG12-Môn Toán x x C C 0.25
Ta có P  A 7   P A   x   7 1 x C C 9 9 x C 0.25
Do đó P  A 5 5 7 2   1
  x 17x  60  0  5  x 12  6  x  9 6 x C 6 9
Vậy giá trị nhỏ nhất của x là 6. Vậy số thẻ ít nhất phải rút là 6. 0.25 2 2
3x  2x 5 2x x 1  2 y   2 1 y  2y  2
Câu 3. (1.0 điểm) 
x, y 2 2
x  2y  2x  4y  3 Nội dung Điểm 2 2 3
 x  2x 5 2x x 1  2 y   2 1
y  2 y  2  0 (1)
Hệ đã cho trở thành:  2 2
x  2y  2x  4y  3  0 (2) 2 2
 3x  2x  5  2x x 1  2 y   2 2 2 1
y  2 y  2  x  2y  2x  4 y  3 0.25
 x  x x 1   y  2 1   y   1  y  2 2 2 1 1 (*) 2 Xét hàm số: 2 2 t
f (t)  t  t t 1 (t  ) có 2
f '(t)  2t  t 1 
 2t  2t  0 2 t 1
Suy ra f t là hàm số đồng biến trên  0.25
Do đó từ phương trình (*) ta có: x  y 1 thế vào phương trình (2) ta được:  2   y 2 y 2 1 2 y 2 y  2 1 4y 3 0 3y 4 y 4 0              3  0.25  y  2  +) Với y  2   x  1  2 5
+) Với y   x  3 3
Vậy hệ phương trình có nghiệm    ;
x y là:    5 3 1; 2 ; ; .    3 2  0.25
Câu 4.a (0.75 điểm) Cho hình hộp đứng ABC .
D A B C D có các cạnh 1 1 1 1
AB  AD  2, AA  3 và góc  0
BAD  60 . Gọi M , N lần lượt là trung điểm của các cạnh 1
A D và A B . Chứng minh rằng AC vuông góc với mặt phẳng BDMN  . 1 1 1 1 1
Trang 3/6, HDC HSG12-Môn Toán Nội dung Điểm
Ta có: BD  AC, BD  AA  BD  mp(ACC A )  AC  . BD 1 1 1 1 0.25  
     1  1 
1   
Mặtkhác: AC .BN   AB  BC  CC  2 2
BB  BA   AB  . BA BC  BB = 1 1  1  1  2  2 2    0.5
2 1 3  0. Suy ra AC  BN 2 . 1   Từ  
1 và 2  AC  (BCMN). 1
Câu 4.b (0.75 điểm) Tính thể tích khối chóp . A BDMN . Nội dung Điểm
Gọi AA  DM  BN  I  A , M , N lần lượt là trung điểm của AI, DI, BI. 1   1 0.25 V . IA IM .IN 1 3 I .AMN    V  V . A BDMN I . V I . A I . B ID 4 4 ABD I .ABD 3 1 1 3 3 Suy ra 2 V  . .I . A S  .2 3.2 .  dvtt 0.5 . A BCMN ABD    4 3 4 4 2 3
Vậy thể tích khối chóp . A BDMN bằng . 2
Câu 5 (1.0 điểm). Cho hình chóp S.ABCD , đáy ABCD là hình chữ nhật có AB  3, BC  6,
mặt phẳng SAB vuông góc với đáy, các mặt phẳng SBC và SCD cùng tạo với mặt
phẳng  ABCD các góc bằng nhau. Biết khoảng cách giữa hai đường thẳng SA và BD bằng
6. Tính thể tích khối chóp S.ABCD và cosin góc giữa hai đường thẳng SA và . BD
Trang 4/6, HDC HSG12-Môn Toán Nội dung Điểm
Hạ SH  AB H  AB  SH   ABCD
Kẻ HK  CD K CD  tứ giác HBCK là hình chữ nhật.
Ta có: BC  SAB  Góc giữa mặt phẳng SBC và  ABCD là:  SBH 0.25
CD  SHK   Góc giữa mặt phẳng SCD và  ABCD là:  SKH Theo giả thiết:  
SBH  SKH  SHB   S
 HK g  c  g  HK  HB  BC  6.
Do đó A là trung điểm của . HB Ta thấy 0.25
ABDK là hình bình hành  BD / / AK  BD / / SAK  mà SASAK 
Suy ra d BD, SA  d BD,SAK   d D,SAK   d H,SAK   h  6. 1 1 1 1 1 1 1 1
Do tam diện H.SAK vuông tại H nên:        2 2 2 2 2 h HS HA HK 6 HS 9 36  SH  6 0.25 1 1 Suy ra V  .SH.S  .6.3.6  36 (dvtt). S.ABCD 3 ABCD 3
Gọi  là góc giữa hai đường thẳng SA và BD    BD, SA   AK, SA
Ta có: SA  6 2, SA  AK  3 5. Trong tam giác SAK có: 2 2 2 
AS  AK  SK 45  45  72 1 cos SAK    . 0.25 2.AS.AK 2.3 5.3 5 5 Vậy  1
  SAK  arccos . 5
Câu 6. (1.0 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC ngoại tiếp đường tròn tâm J 2; 
1 . Biết đường cao xuất phát từ đỉnh A của tam giác ABC có phương trình:
2x  y 10  0 và D2; 4
  là giao điểm thứ hai của AJ với đường tròn ngoại tiếp tam giác
ABC. Tìm tọa độ các đỉnh của tam giác ABC biết B có hoành độ âm và B thuộc đường
thẳng có phương trình x  y  7  0. Nội dung Điểm
Trang 5/6, HDC HSG12-Môn Toán
AJ đi qua J 2;  1 và D 2; 4
  nên AJ có phương trình : x  2  0
Gọi H là chân đường cao xuất phát từ đỉnh A . Tọa độ điểm A thỏa mãn hệ : 0.25 x  2  0 x  2     A2;6.
2x  y 10  0 y  6
Gọi E là giao điểm thứ hai của BJ với đường tròn ngoại tiếp tam giác ABC. Ta có  
DB  DC  DB  DC và   EA  EC  1  
DBJ  sd EC  sd DC 1  
 sdEA sdDB   DJB  D  BJ cân tại . D 2 2
DB  DC  DJ hay D là tâm đường tròn ngoại tiếp tam giác JBC. 0.25
Suy ra B, C nằm trên đường tròn tâm D 2; 4   bán kính 2
JD  0  5  5 có phương
trình  x  2   y  2 2
4  25. Khi đó tọa độ B là hệ của nghiệm: 
 x  22   y  42  25 x  3  x  2 B 3;  4          0.25
x  y  7  0 y  4  y  9  B  2; 9  
Do B có hoành độ âm nên B  3;  4  .
BC đi qua B  3;  4
  và vuông góc AH nên có phương trình: x  2y 5  0. 
 x  2   y  2 2 4  25
Khi đó C là nghiệm của hệ:   C 5;0
x  2y  5  0 Vậy 0.25
A2;6, B 3  ; 4  , C 5;0.
Câu 7. (1.0 điểm) Cho các số thực dương a, ,
b c thỏa mãn a  b  c  1.Tìm giá trị nhỏ nhất của biểu thức 7 121 A   . 2 2 2
a  b  c
14ab  bc  ca Nội dung Điểm 1  2 2 2
a  b  c 2 2 2 2 
Ta có 1  a  b  c  a  b  c  2ab  bc  ca  ab  bc  ca  2 0.25 Do đó 7 121 A   2 2 2
a  b  c 7 1 2 2 2
a  b  c 
Trang 6/6, HDC HSG12-Môn Toán Đặt 2 2 2
t  a  b  c . Vì a, ,
b c  0 và a  b  c  1 nên 0  a  1, 0  b  1, 0  c  1 Suy ra 2 2 2
t  a  b  c  a  b  c  1 0.25
Mặt khác  a  b  c2 2 2 2
 a  b  c  ab  bc  ca   2 2 2 1 2
3 a  b  c  1 1 Suy ra 2 2 2 
t  a  b  c  . Vậy t  ;1 .   3 3  Xét hàm số   f t 7 121 1   ; t  ;1   t 7(1 t) 3  0.25 f t 7 121 '    2 t 71 t2 f t 7 '  0  t  18
Lập BBT của hàm số f t Dựa vào BBT suy ra   f t 324 1  ; t   ;1   . 7 3  0.25 324 1 1 1 Vậy min A 
đạt được khi a  ; b  ; c  . 7 2 3 6
------------------- Hết -------------------
Trang 7/6, HDC HSG12-Môn Toán