SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH
ĐỀ THI KHẢO SÁT CHẤT LƯỢNG LẦN 2
TRƯỜNG THPT LÝ THÁI TỔ NĂM HỌC 2018 - 2019
Môn thi: Toán – Lớp 10
Thời gian làm bài: 120 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
Ngày thi: 18 tháng 5 năm 2019
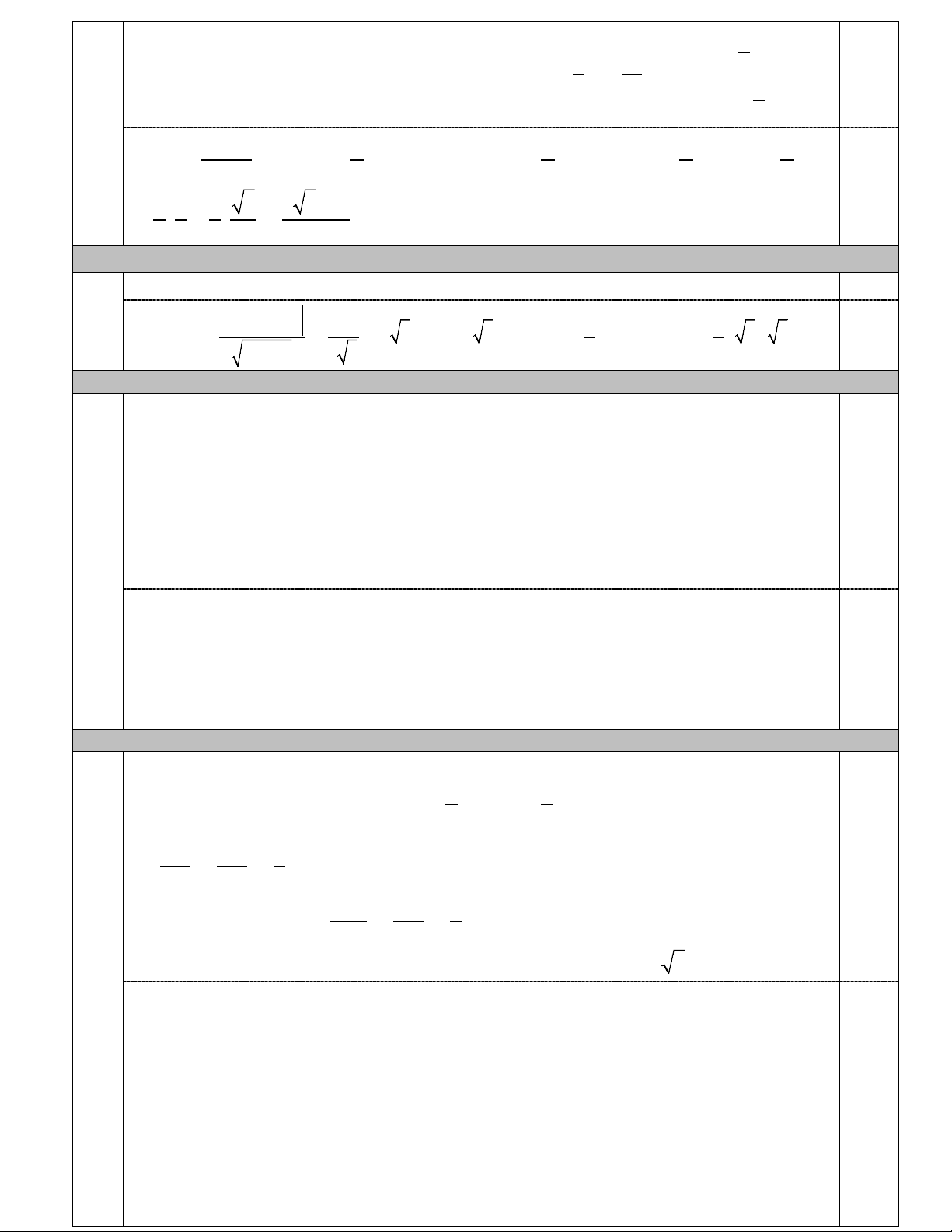
Câu I. (3,0 điểm) Giải các bất phương trình sau: 1) 1  1 x  2 2) 2
3x  7x  2  3x  1 3) 2 2
11x  41x  11  2 2x  1  x  3x  4 Câu II. (2,0 điểm)
1) Tìm tất cả các giá trị của tham số m để hàm số y x  2 3 m x  m  2 2 1 3 1 x 2m m 4         
có tập xác định là  .
2) Tìm m để đường thẳng y  x
  m cắt đồ thị hàm số 2
y  x m  
1 x  2m  2 tại hai điểm phân biệt ,
A B sao cho OA OB  4 (với O là gốc tọa độ).     Câu III. (1,0 điểm)   Cho 3
sin x    x  .Tính 2020 cos 2x, cos x     . 5 2   3 
Câu IV. (2,5 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A4;3,B 2;5,C 5;4.
1) Viết phương trình tổng quát của đường thẳng BC . Tính diện tích tam giác ABC.
2) Viết phương trình đường trònT  ngoại tiếp tam giác ABC.
3) Tìm điểm M thuộc đường trònT  sao cho ME  2MF đạt giá trị nhỏ nhất, vớiE 7;9,F 0;8.
Câu V. (1,0 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho elip E có tâm sai bằng 3 , chu vi hình chữ 2
nhật cơ sở bằng 12. Viết phương trình chính tắc của E. Biết M là điểm di động trên E, tính giá trị của biểu thức 2 2 2
P  MF  MF  5OM  3MF .MF . 1 2 1 2
Câu VI. (0,5 điểm) Cho tam giác nhọn ABC với H,E,K lần lượt là chân đường cao kẻ từ các đỉnh , A , B C .
Gọi diện tích các tam giác ABC và HEK lần lượt là S và S . Biết rằng S  4S , A  BC H  EK AB  C HE  K chứng minh A  BC đều.
--------------------------HẾT-----------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:........................................................... Số báo danh:.......................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH HƯỚNG DẪN CHẤM
TRƯỜNG THPT LÝ THÁI TỔ
THI KHẢO SÁT CHẤT LƯỢNG LẦN 2 NĂM HỌC 2018 - 2019
Môn: Toán – Lớp 10 Câu
Lời giải sơ lược Điểm i.1. (1,0 điểm) 1 3  x  1   0 0,5 x  2 x  2  2  x  3
Vậy tập nghiệm của bất phương trình là 0,5 S 2;3   I.2. (1,0 điểm)  x  2  2 3
 x  7x  2  0  Bất phương trình   1     x  0,5 2 3
 x  7x  2  3x 1    3   2 3
 x  10x  3  0   x  2    1  1  x x       3  3  2     x  3 1  0,5   x  3  3  
Vậy tập nghiệm của bất phương trình là 1 S  2  ;3         3   I.3. (1,0 điểm)  2 11
 x  41x 11  0  Điều kiện: 2  x 1  0  x  4(*)  0,25  2 x   3x  4  0 
Khi đó, bất phương trình tương đương với 2 2
11x  41x  11  2 2x  1  x  3x  4 2 2 2
 11x  41x  11  8x  4  x  3x  4  4 (2x  1)(x  3x  4) 2 2
 10x  46x  19  4 (2x  1)(x  3x  4) 0,25 2 2
 5(2x  9x  4)  (x  1)  4 (x  1)(2x  9x  4) 2 2 2x  9x  4 2x  9x  4  5  1  4 x  1 x  1 2 Đặt 2x  9x  4 t 
t  0 , bất phương trình trở thành  x 1 0,25 2 2 1 t 0 5t 1 4t 5t 4t 1 0 t 1     
        0  t  1 5 2 2x  9x  4 2 2  0 
 1  2x  9x  4  x  1  2x  10x  5  0 x  1 0,5 5  15 5  15   x  2 2  
Kết hợp với điều kiện (*) suy ra tập nghiệm của bất phương trình là 5  15  S 4;     2     II(1,0 điểm) Hàm số y x  2 3 m x  m  2 2 1 3 1 x 2m m 4        
 có tập xác định là  . x  2 3 m x  m  2 2 1 3 1 x 2m m 4        0 x     0,25 *, Nếu 2 3
g x  m x   m   2 2 ( ) 3
1 x  2m  m  4 không có nghiệm x  1 thì f x x  2 3 m x  m  2 2 ( ) 1 3 1 x 2m m 4        
 đổi dấu khi qua x  1
Khi đó ycbt không được thỏa mãn 0,5
* Do đó x  2 3 m x  m  2 2 1 3 1 x 2m m 4        0 x   
 điều kiện cần là g(1)  0 m   1 2 2 2 m  3m 1 2m m 4 0 m 2m 3 0              m   3  Thử lại
* Với m   f x  x   x  x   x  2 3 2 2 1 ( ) 1 ( 4 3)
1 (x  3x  3)  m  1 ( không : thỏa mãn) 0,25
* Với m    f x  x   x  x   x  2 3 2 2 3 ( ) 1 (9 8 17)
1 (9x  x  17)  0x  R
suy ra m  3 thỏa mãn.
Vậy giá trị cần tìm là m  3 II(1,0 điểm)
Xét phương trình hoành độ giao điểm của 2 đồ thị : 2
x m   2
1 x  2m  2  x
  m  x  mx  m  2  0 (1) 0,25
Đường thẳng y  x
  m cắt đồ thị hàm số 2
y  x m  
1 x  2m  2 tại hai điểm phân biệt ,
A B  (1) có hai nghiệm phân biệt 2
   0  m  4m  8  0 (luôn đúng) 0,25 Gọi ( A x ; x
  m),B(x ; x
  m) ở đó x ,x là nghiệm của (1) 1 1 2 2 1 2 Có 2 2 2 2 2
OA  x  ( x
  m)  2x  2mx  m  m  2m  4 0,25 1 1 1 1 2 2 2 2 2
OB  x  ( x
  m)  2x  2mx  m  m  2m  4 2 2 2 2 m   0 Theo giả thiết 2 2 OA OB 4 m 2m 4 2 m 2m 0            m   2  0,25 
Vậy giá trị cần tìm là m  0;m  2 III(1,0 điểm) 2   Có 2 3   7
cos 2x  1  2 sin x  1  2    0,25 5 25 
Có  x    cos x  0 0,25 2  4 2    cos x  (l) Mặt khác 2 2 2 2 3   16  5
sin x  cos x  1  cos x  1 sin x  1       5 25  4
cos x   (t / m)  5  2020               cos x    cos x  
   673  cos x                 
cos x cos  sin x sin  3 3   3    3 3 0,5 4 1 3 3 3 3  4  .  .  5 2 5 2 10 IV.1 (1 điểm)
Viết phương trình đường thẳng BC : x  7y  33  0 0,5 4 21 33 50 1 1 d( , A BC)  
 5 2,BC  5 2  S  d( ,
A BC).BC  5 2.5 2  25 0,5 2 2 A  BC 1  7 5 2 2 2 IV.2 (1 điểm)
Gọi phương trình đường tròn T  ngoại tiếp tam giác ABC. là 2 2
x  y  2ax  2by  c  0 Do ,
A B,C  (T ) nên ta có 0,5 16
  9  8a  6b c  0
4254a10bc  0 25
 1610a  8b c  0  a   1 b    1  c   23 0,5 
Phương trình đường tròn ngoại tiếp tam giác ABC là T  2 2
x  y  2x  2y  23  0 IV.3 (0,5 điểm)
Ta thấy IE  10  2IM  
Gọi K là điểm trên tia IE sao cho 1 5
IK  IE  K  ;3 4 2  Có IM IK 1   ,  MIK chung 0,25 IE IM 2 MK IK 1  I  KM  I  ME  
  ME  2MK ME IM 2
Khi đó, ME  2MF  2MK  2MF  2(MK  MF)  2KF  5 5
Dấu “= ” xảy ra M là giao điểm của đoạn FK và T 
Phương trình FK : 2x  y  8  0  x   1  
 M(1;6)(t / m) 0,25 2
 x  y  8  0  y   6  
Tọa độ điểm M thỏa mãn   2 2  x
  y  2x  2y  23  0  x   5   
 M(5;2)(loai) y    2 
Vậy M(1;6) là điểm cần tìm. V (1,0 điểm) 2 2 x y
Gọi phương trình chính tắc của (E) : 
 1(a  b  0) a b 0,25 2 2 Vì  3 a b 3
E  có tâm sai bằng    a  2b , 2 a 2
Mặt khác chu vi hình chữ nhật cơ sở bằng 12 nên 4(a b)  12  a b  3
Từ đó suy ra a  2;b  1 2 2 x y 0,25
Vậy phương trình chính tắc của (E) :   1 4 1 2 2 x y
Với mọi M(x ;y )  (E) : 
 1(a  b  0), ta biến đổi được kết quả 0 0 a b 0,25 2 2 2
MO  MF .MF  a b 1 2
Khi đóP  MF  MF  5OM  3MF .MF  MF  MF 2 2 2 2 2
 5(MO  MF .MF ) 0,25 1 2 1 2 1 2 1 2 2 2 2 2 2
 4a  5(a b )  a   5b  9 VI(0,5 điểm)
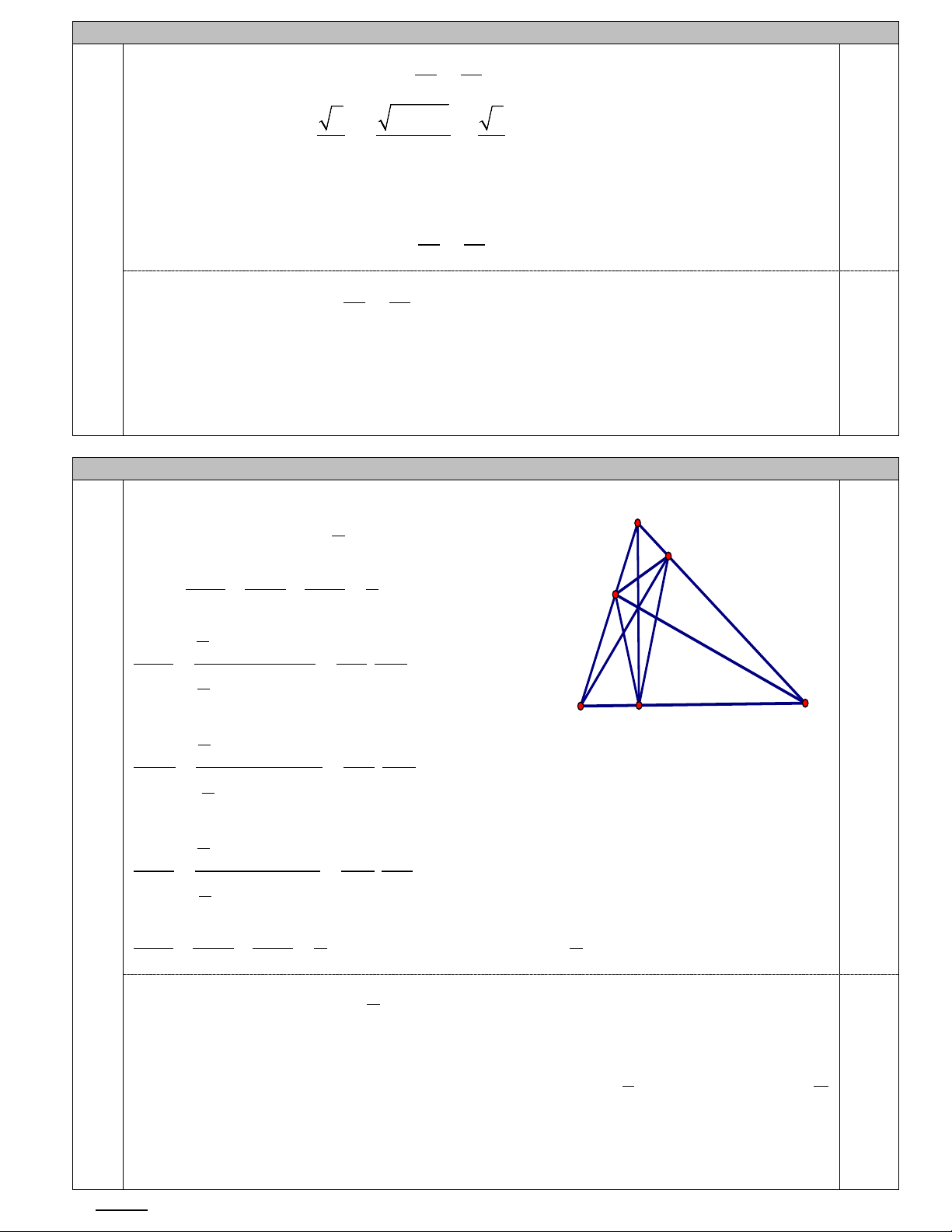
Đặt S = SABC thì từ giả thiết suy ra 3 A S + S + S = S EAK KBH HCE E 4 S S S EAK KBH HCE 3 ⇒ + + = K S S S 4
1 AE.AKsin A S AE AK EAK 2 2 = = . = cos . A cos A = cos 1 A S . sin AB AC AB AC A 2 B C 1 H 0,25
BK.BH.sin B S BK BH KBH 2 2 = = . = cos . B cos B = cos 1 B S . sin BC AB AB BC B 2
1 CH.CE.sinC S CH CE HCE 2 2 = = .
= cosC.cosC = cos 1 C S . sin AC BC AC BC C 2 S S S EAK KBH HCE 3 2 2 2 3 + +
= ⇔ cos A + cos B + cos C = S S S 4 4 2 2 2 3 2
cos A  cos B  cos C 
 2  2 cos 2A  2  2 cos 2B  4 cos C  3 4 2 2 2
 4 cos C  4 cosC.cos(A  B)  cos (A  B)  1 cos (A  B)  0  0,25 1   2   2 c  
 osC  cos(A  B) C  
 2 cosC  cos(A  B)  sin (A  B)  0     2   3  si
 n(AB)  0 A     B    A  BC đều (đpcm)
▪ Chú ý: Các cách giải đúng khác với đáp án đều được điểm tối đa
Document Outline

• Đề KSCL Toán 10
• Đáp án Toán 10_KSL2-18-19