Đề Thi Olimpic Toán 11 Sở GD&ĐT Quảng Nam 2019 (Có đáp án)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLYMPIC QUẢNG NAM NĂM 2019 QUẢNG NAM
Môn thi: TOÁN – Lớp 11
Thời gian: 150 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC Ngày thi : 21/3/2019
Câu 1 (3,0 điểm). Giải các phương trình sau: a) 3 3 2
1+ cos x - sin x = 2sin x b) 2
3 sin 3x - (4sin x +1)cos x = 0 Câu 2 (4,0 điểm).
a) Chứng minh mệnh đề sau bằng phương pháp quy nạp: “ Tổng các góc trong của đa
giác lồi có n cạnh bằng 0 (n - 2).180 ”. 2n + 3
b) Cho dãy số (u ), biết: u = 2, u = 3u +
với n ³ 1. Tìm số hạng tổng quát n 1 n 1 + n 2 n + n của dãy số (u ). n Câu 3 (6,0 điểm).
a) Cho số nguyên dương n thỏa mãn: 2 C , 45 và 2 (C
-1) theo thứ tự lập thành cấp số n 1 - n 1 + æ 2 n ö
cộng. Tìm số hạng không chứa x trong khai triển của x x - với x > 0. ç ÷ è x ø
b) Gọi X là tập hợp tất cả các số tự nhiên có 5 chữ số khác nhau được lập từ các chữ số
0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên từ X ra một số. Tính xác suất để chọn được số
không có hai chữ số chẵn đứng liền kề. 3 3 ì x - 2. x +1 ï khi x > 1
c) Cho hàm số f (x) = í - . x 1 ïî2mx + 4 khi x £1
Tìm giá trị của tham số m để hàm số f (x) liên tục tại x = . 1 Câu 4 (3,0 điểm).
a) Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng (d) : x - y + 2 = 0,
(d ') : x - y + 3 = 0. Biết phép vị tự tâm A(0;1), tỉ số k biến đường thẳng (d) thành đường
thẳng (d ') . Viết phương trình ảnh của đường tròn 2 2
(C) : (x - 2) + ( y +1) = 9 qua phép vị tự
tâm A, tỉ số k.
b) Trong mặt phẳng, cho hai điểm A, B cố định, điểm M di động trên nửa mặt phẳng bờ
AB sao cho tam giác ABM vuông tại M. Trên nửa mặt phẳng bờ AB không chứa điểm M vẽ tia
Bx vuông góc với BM. Trên tia Bx lấy điểm C sao cho BM = BC. Qua điểm C dựng đường
thẳng d vuông góc với AB cắt tia BM ở N. Hãy xác định phép quay biến AM thành BN. Khi M
di động thì điểm N di động trên đường nào? Câu 5 (4,0 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy,
AB = a, AD = a 3, SA = 2 . a
a) Tính khoảng cách giữa hai đường thẳng AC và SB theo a .
b) Gọi G là trọng tâm của tam giác SCD, M là trung điểm của SC, j là góc giữa hai
đường thẳng AG và BM. Tính cosj .
–––––––––––– Hết ––––––––––––
Họ và tên thí sinh: …..…………………………………….; Số báo danh:……………………........... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLYMPIC QUẢNG NAM NĂM 2019 QUẢNG NAM
Môn thi: TOÁN – Lớp 11
ĐÁP ÁN – THANG ĐIỂM Môn thi: TOÁN
(Đáp án – Thang điểm gồm 07 trang) Câu 1 (3,0 điểm) a 3 3 2
1+ cos x - sin x = 2sin x 1,5 Û ( x - x)( 2 2 x + x x + x) 2 2 pt cos sin cos sin .cos sin
+cos x -sin x = 0 0.25
Û (cos x -sinx)(1+sin .xcos x)+(cos x -sinx)(cos x +sinx) = 0 0.25
Û (cos x -sinx)(1+sin .xcos x +cos x +sinx) = 0 0.25
Û (cos x -sinx)(1+sin ) x (1+cos x) = 0 é p = - + p ésinx = 1 - x k2 ê 2 ê ê Û cos x = 1 -
(0.25) Û x = p + k2p (0.5) 0.75 ê ê
êcos x - sinx = 0 ë ê p êx = + kp ë 4 b 2
3 sin 3x - (4sin x +1)cos x = 0 1,5 2
3 sin3x - (4sin x +1)cos x = 0 Û 3 sin3x - 2.sin 2 .
x sin x - cos x = 0 0.25
Û 3sin3x + (cos3x - cos x) - cos x = 0 0.25
Û 3sin 3x + cos3x = 2cos x 0.25 p
Û cos(3x - ) = cos x 0.25 3 é p x = + kp ê 6 Û ê ( k Î ! ). 0.5 p p ê x = + k. êë 12 2 p p p
Vậy phương trình có nghiệm là: x = + kp , x = + k. 6 12 2 Câu 2 (4,0 điểm)
Chứng minh mệnh đề sau bằng phương pháp quy nạp : “ Tổng các góc trong của a
đa giác lồi có n cạnh bằng 0 (n - 2)180 . ”. 2,0
- Xét n = 3: Mệnh đề trở thành “ tổng các góc trong của một tam giác bằng 1800 ” là 0.25 mệnh đề đúng.
- Giả sử mệnh đề trên đúng với một số tự nhiên k tùy ý ( k ³ 3) tức là: 0 0.25
“ Tổng các góc trong của đa giác lồi có k cạnh bằng (k - 2)180 . ”
- Ta đi chứng minh mệnh đề trên đúng với n = k +1, tức là đi chứng minh 0 0.25
“ Tổng các góc trong của đa giác lồi có k +1 cạnh bằng (k -1)180 . ”
+ Xét đa giác lồi có k + 1 cạnh A1A2….Ak+1.
Nối A1 và Ak ; khi đó tổng các góc trong của đa giác lồi có k + 1 cạnh A1A2….Ak+1 bằng 0.5
tổng các góc trong của tam giác A1AkAk+1 cộng với tổng các góc trong của đa giác lồi k cạnh A1A2….Ak.
Do đó tổng các góc là: 1800 + (k – 2).1800 = (k – 1).1800 0.5 Trang 2
Suy ra mệnh đề đúng với n = k +1. 0.25
Vậy mệnh đề đã cho đúng với mọi số thự nhiên n thỏa n ³ 3. 2n + 3
Cho dãy số (u ), biết: u = 2, u = 3u +
với n ³ 1. Tìm số hạng tổng n 1 n 1 + n 2 n + n b 2,0
quát của dãy số (u ). n 3(n + 1) - n æ 3 1 ö u = 3u + = 3u + - n 1 + n n ç ÷ 0.5 n(n + 1) è n n +1ø 1 æ 1 ö Û u + = 3 u + (*) n 1 + ç n ÷ 0.5 n +1 è n ø 1 1 0.25
Đặt v = u + Þ v = u +
, khi đó (*) trở thành: v = 3v . n n n 1 + n 1 + n 1 + n n n +1 1 - 0.25
Suy ra (v ) là cấp số nhân có công bội q=3. Do đó v = v .3n . n n 1 1
Mà v = u + = 2 +1 = 3. Suy ra n 1 v 3.3 - = = 3n . 1 1 n 0.25 1 1 n n 1
u + = 3 Û u = 3 - 0.25 n n n n Câu 3 (6,0 điểm)
Cho số nguyên dương n thỏa mãn: 2 2 C , 45 à v (C
-1) theo thứ tự lập thành cấp n 1 - n 1 + a æ 2 n 2,0 ö
số cộng. Tìm số hạng không chứa x trong khai triển của x x - với x > 0. ç ÷ è x ø
Theo tính chất của cấp số cộng ta có: 2 2 C
+ C -1 = 2.45 (điều kiện * nΕ ,n ³ 3) 0.25 n 1 - n 1 + (n - )
1 (n - 2) n(n + ) 1 Û + = 91 0.25 2 2 2
Û n - n - 90 = 0 0.25 én = 10 Û . Vậy n = 10 . ê 0.25 ën = 9 - (l) n 10 Ta có æ 2 ö æ 3 2 ö x x - = x - . ç ÷ ç ÷ è x ø è x ø
Số hạng tổng quát trong khai triển nhị thức trên là: 10- æ - k 2 k k ö k - k 1 k 3 30 3 T = C x = C x . 2 -
(với k £ • ,k £10). k 1 + 10 ( ) ç ÷ 10 ( ) 2k 0.25 è x ø x k 30 5k ( 2)k C x - Û - 0.25 10
Số hạng không chứa x khi 30 - 5k = 0 hay k = 6. 0.25
Vậy số hạng không chứa x trong khai trên trên là: C 2 - =13440. 10 ( )6 6 0.25
Gọi X là tập hợp tất cả các số tự nhiên có 5 chữ số khác nhau được lập từ các chữ b
số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Chọn ngẫu nhiên từ X ra một số. Tính xác suất để 2,0
chọn được số không có hai chữ số chẵn đứng liền kề.
- Số phần tử của không gian mẫu là 5 4
n(W) = A - A = 27216 10 9 0.25
Gọi A là biến cố: “ chọn được số không có hai chữ số chẵn đứng liền kề ”. Trang 3
- Xét số chọn từ X có dạng abcde , vị trí các chữ số tương ứng các ô ngang dưới đây:
Khi đó A xảy ra các trường hợp sau: 0.25
* Trường hợp 1: Số có 5 chữ số lẻ. Trường hợp này có 5! số
* Trường hợp 2: Số có đúng 1 chữ số chẵn.
+ Khả năng 1: a là chữ số chẵn. Khả năng này có 1 C .( 4 C .4! 4 5 ) số. 0.25
+ Khả năng 2: a là chữ số lẻ. Khả năng này có 1 C .( 1 3 C .C .4! 5 5 4 ) số.
* Trường hợp 3: Số có đúng 2 chữ số chẵn.
+ Khả năng 1: a là chữ số chẵn, khi đó b là số lẻ. Khả năng này có 1 1 C .C ( 1 2 C .C .3! 4 5 4 4 ) số. 0.25
+ Khả năng 2: a là chữ số lẻ, khi đó có 3 cách chọn ra 2 ô cho hai số chẵn
không kề nhau (ô2-ô4, ô2-ô5, ô3-ô5). Khả năng này có 1 C .( 2 3.C . ) 2! ( 2 C .2! 5 5 4 ) số. 0.25
* Trường hợp 4: Số có đúng 3 chữ số chẵn. c c c
Trường hợp này có: 4.4.3.5.4 = 960 số 0.25 1 ( n ) A = 5!+ C .( 4 C . ) 1 4! +C .( 1 3 C .C . ) 1 1 4! + C .C ( 1 2 C .C .3 ) 1 ! + C .( 2 3.C . ) 2! ( 2 C .2! +960 =10440 4 5 5 5 4 4 5 4 4 5 5 4 ) 0.25 n(A) 10440 145
Vậy xác suất của biến cố A là P(A)= = = 0.25 n(Ω) 27216 378 3 3 ì x - 2. x +1 ï khi x > 1
c Cho hàm số f (x) = í x -1 2,0 ïî2mx + 4 khi x £1
Tìm giá trị của tham số m để hàm số f (x) liên tục tại x = . 1 f (1) = 2m + 4 0,25
lim f (x) = 2m + 4 0,25 x 1- ® 3 3 3 3
é(x -1) - 2( x -1)ù éæ x -1ö æ x -1öù
lim f (x) = lim ê ú = lim êç ÷ - 2ç ÷ú 0,25 ç ÷ x 1+ x 1+ - x 1 x 1 + ® ® ® ë û êëè x -1 ø x -1 è øúû 3 x -1 + Tính được: lim = 3 + 0,5 x 1 ® x -1 3 x -1 1 + Tính được: lim = + 0,25 x 1 ® x -1 3 2 7
Suy ra lim f (x) = 3 - = x 1+ ® 3 3 Để f ( )
x liên tục tại x = 1 thì lim f ( ) x = lim f ( ) x = f (1) 0,25 x 1+ x 1- ® ® 5 0,25
Suy ra: m = - là giá trị cần tìm. 6 Trang 4 Câu 4 (3,0 điểm)
Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng (d) : x - y + 2 = 0,
(d ') : x - y + 3 = 0. Biết phép vị tự tâm A(0;1), tỉ số k biến đường thẳng (d)
thành đường thẳng (d ') . Viết phương trình ảnh của đường tròn 1,5 2 2
(C) : (x - 2) + ( y +1) = 9 qua phép vị tự tâm A, tỉ số k.
+ Chọn M (0;2) Îd , phép vị tự V
biến M thành M '(0;k +1) 0.25 (A,k) a
+ M '(0;k +1) thuộc d ' nên 0 - (k +1) + 3 = 0 . Suy ra k = 2. 0.25
+ Đường tròn (C) có tâm I (2; 1 - ), bán kính R = 3. 0.25
+ Gọi đường tròn (C ') có tâm I ', bán kính R ' là ảnh của đường tròn (C) qua phép vị tự V . (A,k)
+ R' = k .R = 2 .3 = 6 0.25 !!!" !!"
+ AI ' = 2.AI Þ I '(4;- 3). 0.25
Phương trình đường tròn (C ') là (x - )2 +( y + )2 4 3 = 36 0.25
Trong mặt phẳng, cho hai điểm A, B cố định, điểm M di động trên nửa mặt phẳng
bờ AB sao cho tam giác ABM vuông tại M. Trên nửa mặt phẳng không chứa điểm b
M vẽ tia Bx vuông góc với BM. Trên tia Bx lấy điểm C sao cho BM = BC. Qua 1,5
điểm C dựng đường thẳng d vuông góc với AB cắt tia BM ở N. Hãy xác định
phép quay biến AM thành BN. Khi M di động thì điểm N di động trên đường nào? M B’ N A K O’ B O M HV 0.25 N A B O C x C x Ta có ∑ ∑
ABM = BCN ( góc có cạnh tương ứng vuông góc), nên ABM D = N D CB (g. .
c g). Suy ra AM = BN 0.25
Ta thấy M di động trên nửa đường tròn đường kính AB, tâm O (trung điểm AB)
Trung trực AB cắt nửa đường tròn trên tại K (điểm chính giữa cung AB) Trang 5
- Xét hai tam giác AMK và BNK có: AM = BN, KA = KB, ∑ ∑ MAK = NBK 0.25 Suy ra AM D K = BN D K ( .
c g.c) nên KM = KN 0.25 + Hơn nữa ∑ ∑ 0
KMN = KAB = 45 nên tam giác KMN vuông cân tại K.
Xét phép quay tâm K góc quay 900. Ï A Ô a B Ta có Q : Ô Ì fi Q AM = BN 0 0 ( ) 0.25 (K,90 ) M Ô a N (K,90 ) Ô Ó
(Trường hợp M trùng K thỏa yêu cầu)
M di động trên nửa đường tròn tâm O đường kính AB, nên N di động trên ảnh của
nửa đường tròn (O) qua phép quay Q
0 là nửa đường tròn (O’) đường kính BB’ 0.25 ( K ,90 )
qua K (xem hình vẽ). Câu 6 (4,0 điểm)
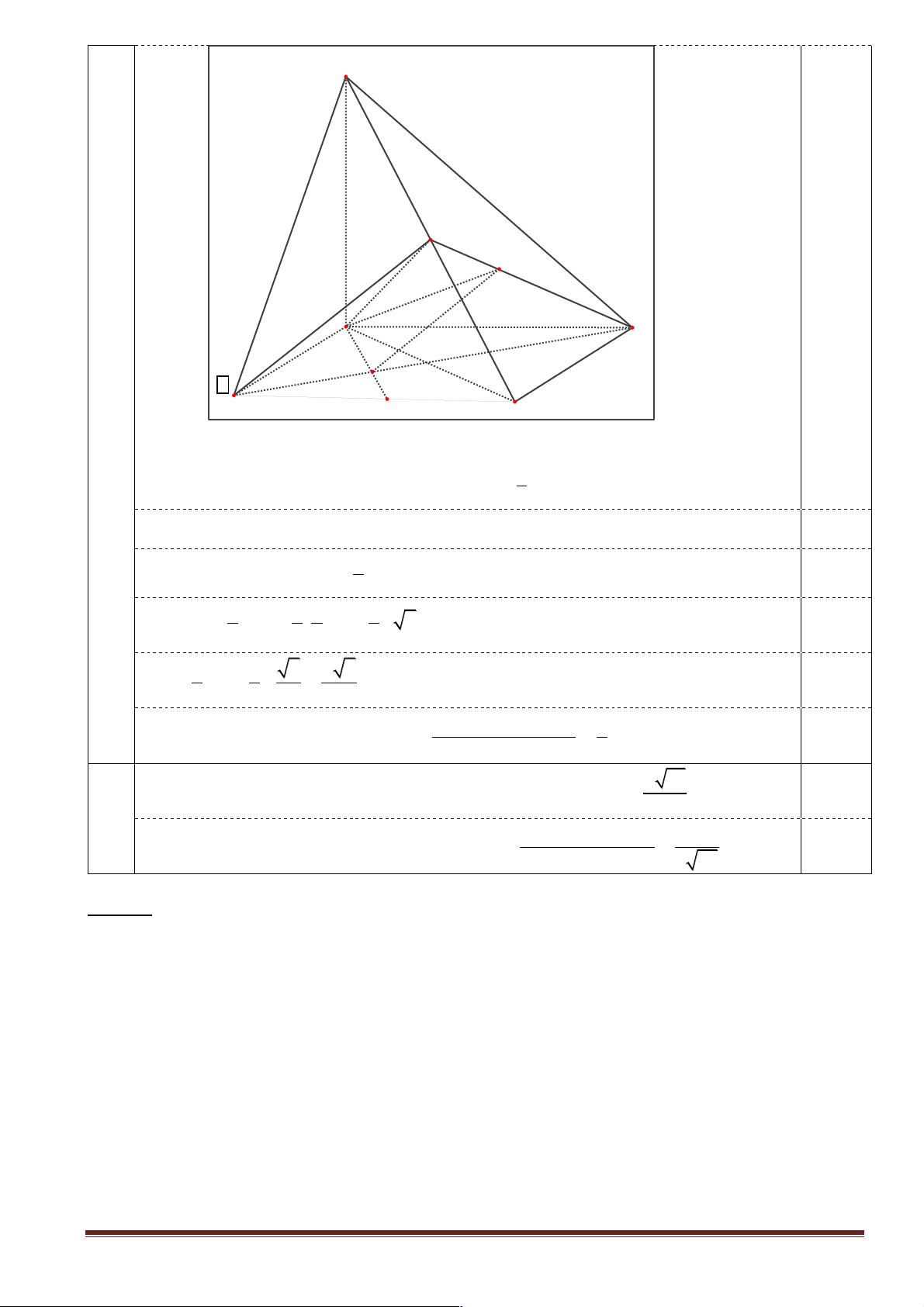
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt đáy,
AB = a, AD = a 3 , SA = 2 . a
a) Tính khoảng cách giữa hai đường thẳng AC và SB theo a .
b) Gọi G là trọng tâm của tam giác SCD, M là trung điểm của SC, j góc giữa hai đường
thẳng AG và BM. Tính cosj . S 2a M K G A a 3 D a H B C
(Hình vẽ phục vụ câu a - 0,5 điểm) a
Tính khoảng cách giữa hai đường thẳng AC và SB theo a . 1,5
+ Qua B, dựng đường thẳng d song song với AC, hạ AH vuông góc với d tại H.
Suy ra d(AC,SB)=d(AC,(SHB))=d(A,(SHB)) 0,5
+ Lập luận suy ra được d(A,(SHB))=AK 0,25 Trang 6 1 1 1 = + , AS = 2a 2 2 2 AK AS AH a 3
+ AH = d(B, AC) = 0,5 2 1 1 1 1 4 19 2a 3 Suy ra = + = + = Þ AK = 2 2 2 2 2 2 AK (2a) æ ö 4a 3a 12a 19 a 3 0,25 ç ÷ 2 è ø b
Gọi G là trọng tâm của tam giác SCD, M là trung điểm của SC, j góc giữa hai 2,0
đường thẳng AG và BM. Tính cosj . !!!" !!!!" !!!" !!!!" AG BM j = (AG BM) . cos cos , = !!!" !!!!" AG . BM 0,25 !!!" 1 !!!" !!!" !!!" 1 !!!" 1 !!!" !!!" 1 !!!"
AG = ( AS + AC + AD) = AS + ( AB + AD) + AD 0,25 3 3 3 3 !!!" 1 !!!" 1 !!!" 2 !!!"
Þ AG = AS + AB + AD 3 3 3
!!!!" !!!!" !!!" 1 !!!" !!!" !!!" 1 !!!" 1 !!!" !!!" !!!"
BM = AM - AB = ( AS + AC) - AB = AS + ( AB + AD) - AB 0,25 2 2 2 !!!!" 1 !!!" 1 !!!" 1 !!!"
Þ BM = AS - AB + AD 2 2 2 2 2 2 2
!!!" !!!!" 1 !!!"2 1 !!!"2 1 !!!"2 4a a 3a 3a .
AG BM = AS - AB + AD = - + = 0,5 6 6 3 6 6 3 2 2
!!!"2 æ 1 !!!" 1 !!!" 2 !!!"ö 1 1 4 2 2 2 2 AG = AG =
AS + AB + AD
= AS + AB + AD 0,25 ç ÷ è 3 3 3 ø 9 9 9 2 2 2 2 2 4a a 4a 17a a 17 Þ AG = + + = Þ AG = 9 9 3 9 3 2 !!!!" !!!" !!!" !!!" 2 æ 1 1 1 ö 1 1 1 2 2 2 2 BM = BM =
AS - AB + AD
= AS + AB + AD ç ÷ 0,25 è 2 2 2 ø 4 4 4 2 2 2 2 4a a 3a 2 Þ BM = + +
= 2a Þ BM = a 2 4 4 4 9 Suy ra cosj = . 0,25 2 34 b Cách khác: Trang 7 S 0.25 M G D A E B F C 1
Gọi E là điểm trên đường chéo BD sao cho BE = BD, suy ra GE // BM 3
Do đó (BM AG) = (GE AG) ∑ ; ; = AGE = j 0.25 1 0.25
Ta có BM = AM = DM = SC ( trung tuyến = nửa cạnh huyền) 2 2 2 1 2 0.25
Nên GE = BM = . SC = a 2 (1) 3 3 2 3 0.25 2 2 7 a 7 AE = AF = a =
(2) ( với F trung điểm BC ) 3 3 2 3 2 2 2 0.25
MA + MD - AD 1
Tam giác AMD cân ở M nên cos M = = 2 . MA MD 4 0.25 a Trongtam giác AMG có 2 2 2 17
AG = AM + MG - 2AM .MG.cos M = (3) 3 2 2 2 0.25 GA GE AE 9
Từ (1); (2) và (3) Trong tam giác AGE có os c j + - = = 2 . AG GE 2 34
Ghi chú: Nếu học sinh có cách giải khác đúng thì Ban Giám khảo thảo luận và thống nhất thang điểm
cho phù hợp với Hướng dẫn chấm. Trang 8