Đề Thi Olimpic Toán 11 Tỉnh Quảng Nam 2017-2018 (có đáp án)

SỞ GIÁO DỤC VÀ ĐÀO TẠO QUẢNG NAM
KỲ THI OLIMPIC QUẢNG NAM NĂM 2018
Môn thi : TOÁN - Lớp: 11 ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi có 01 trang) Câu 1 (3,0 điểm). é p - ù
a. Tính tổng các nghiệm của phương trình: 2
sin x + 5 = 6cos x trên đoạn ;p . ê 2 ú ë û b. Giải phương trình: 3
3cosx -1 = 4cos x - 3 sin3 . x Câu 2 (4,0 điểm).
a. Xét tính tăng giảm và bị chặn của dãy (un ) biết: 1 1 1 u = + + ! + (n Î N*) . n n +1 n + 2 2n b. Cho dãy (u u = 2 u = 3u + 4n n Î N * n ) biết và với 1 n 1 + n u
Tìm số hạng tổng quát của dãy (u lim n n ) . Tính . un 1+ Câu 3 (4,0 điểm).
a. Gọi X là tập hợp các số tự nhiên có 3 chữ số ( không nhất thiết đôi một khác nhau )
được thành lập từ các chữ số 2,0,1,8. Chọn ngẫu nhiên một phần tử từ tập X . Tính xác suất
để phần tử được chọn là số chia hết cho 3 .
b. Trên 2 đường thẳng song song D và d , ta lần lượt gắn vào đó m điểm và n điểm
sao cho m + n = 17 ( ,
m n Î N *). Tìm m , n để số các tam giác có 3 đỉnh là 3 điểm trong 17
điểm phân biệt ở trên là lớn nhất. 2 ì6 - x - x ï khi x ¹ 2
Câu 4 (2,0 điểm). Cho hàm số f ( x) = í | x - 2 | ïî 5 khi x = 2
Xét tính liên tục của hàm số f ( x) tại điểm x = 2 . Câu 5 (3,0 điểm).
Trong mặt phẳng Oxy, cho đường tròn (C) 2 2
: x + y - 2x + 4y - 4 = 0 và điểm ( A 3, - 1 ) .
Gọi I là tâm của đường tròn (C) . M là điểm thay đổi trên (C) sao cho ba điểm , A M , I
không thẳng hàng. Tia phân giác góc ∑
AIM cắt đường thẳng AM tại N . Gọi (K ) là tập hợp
các điểm N khi M thay đổi trên (C). Viết phương trình đường (K ). Câu 6 (4,0 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , BD = a . Cạnh bên SA
vuông góc với mặt phẳng ( ABCD) và SA = a .
a. Tính cosin góc giữa 2 đường thẳng SB và AD . Page 1
b. Gọi (a ) là mặt phẳng qua A song song với BD và cắt cạnh SC tại M sao cho
khoảng cách từ C đến mặt phẳng (a ) bằng 3 lần khoảng cách từ S đến mặt phẳng (a ) .
Tính diện tích thiết diện tạo bởi mặt phẳng (a ) và hình chóp S.ABCD .
––––––––––– Hết ––––––––––––
Họ và tên thí sinh: …..…………………………………….; Số báo danh: ……………………...
Thí sinh không được sử dụng máy tính cầm tay
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLIMPIC QUẢNG NAM NĂM 2018 QUẢNG NAM
Môn thi: TOÁN Lớp : 11
ĐÁP ÁN – THANG ĐIỂM
Đáp án gồm 05 trang () Câu Nội dung Điểm 1 é p - ù 1,5
a. Tính tổng các nghiệm của phương trình: 2
sin x + 5 = 6cos x trên đoạn ;p . ê 2 ú ë û 2 2
sin x + 5 = 6cos x Þ 6s in x + sin x -1 = 0 0.25 1 1 Þ sinx = - ; sinx = 0.25 2 3 • 1 p - p sinx = - ( xÎ[ ,p ] ) Þ x =- 0.25 2 2 6 • 1 p - 1 1 sinx = ( xÎ[
,p ] ) Þ x = arcsin , x = p - arcsin 3 2 3 3 0.25 p - p 1 1 5p
Tổng các nghiệm phương trình trên [
,p ] là - + arcsin +p - arcsin = 2 6 3 3 6 0.5
b/ Giải phương trình: 3cosx -1 = 4cos3x - 3 sin3x. 1,5
3cosx -1 = 4cos3x - 3 sin3x Û -1 = 4cos3x -3cosx - 3 sin3x 0.25
Û -1 = cos3x - 3 sin3x Û 3 sin3x - cos3x =1 0.25 p p p Û 1
sin ( 3x - ) = Û sin ( 3x - ) = sin 0.25 6 2 6 6 Û p p p 5p 3x - = + k2p hoặc 3x - = + k2p ( k Î ! ) 0.25 6 6 6 6 +0,5 2 1 1 1
a. Xét tính tăng giảm và bị chặn của dãy (un) biết u = + +!!+ . n n +1 n + 2 2n 1.5 1 1 1 1 n Ta có: 0 < un = + + + ...+ < < 1, " n ÎN*
n +1 n + 2 n + 3 2n n +1 0,25 + 0,25 Þ (u n) bị chặn. 0.25 02.5 Page 2 1 1 1 1 1 1 1 1 1 u - u = + + ...+ + + - ( + + + ...+ ) n 1 + n n + 2 n + 3
2n 2n +1 2n + 2
n +1 n + 2 n + 3 2n 0.25 1 1 1 1 1 = + - = - > 0 0.25
2n +1 2(n +1) n +1 2n +1 2(n +1) Þ (un) là dãy tăng.
b. Cho dãy (un) biết u1 = 2 và u
= 3u + 4n với nÎN*. n 1 + n u
Tìm số hạng tổng quát của dãy (u n) . Tính lim n . 2,5 un 1+
. + Tìm số hạng tổng quát của dãy (un) Ta có: u = 3u + 4n (1) n 1 + n • Tìm số α : n 1 u
+a.4 + = 3.(u +a.4n) (2) 0.5 n 1 + n 0.25 n n 1 (1),(2) (3.4 4 + Þ - ) = 4n a Þ a = 1 - • (2) viết lại: n 1 u
- 4 + = 3.(u - 4n) + 0.25 n 1 n Xét dãy (v 0.5
n) với v1=-2, vn+1= 3vn ( n ³ 1) - ở đây vn =un-4n. Khi đó v 0.5
n = -2. 3n-1 Þ un-4n = -2. 3n-1 Þ un = 4n -2. 3n-1 u
+ Tính lim n . u n 1 + n n 1 - n u 4 - 2.3 4 1 lim n = lim = lim = 0.5 n 1 + n n 1 u 4 - 2.3 4 + 4 n 1 + 3
a. Gọi X là tập hợp các số tự nhiên có 3 chữ số ( không nhất thiết đôi một khác 2,0
nhau ) được thành lập từ các chữ số 2,0,1,8. Chọn ngẫu nhiên một phần tử từ tập X . Tính
xác suất để phần tử được chọn là số chia hết cho 3 .
Gọi số được chọn là a a a (a ¹ 0) 1 2 3 1 0.5
Tính số phần tử của không gian mẫu: n(W) = 3.4.4 = 48
Gọi A là biến cố: ‘‘ số được chọn là số chia hết cho 3 ’’
a a a chia hết cho 3 khi: (a + a + a 1 2 3 ) chia hết cho 3. 0.5 1 2 3
Liệt kê các số gồm: 111,222,888, và hoán vị của các bộ số (2;2;8); (8;8;2); (1;2;0)
;(1;8;0) . (Lưu y, chữ số a ¹ 0 ) . 1 0.5
Do đó số kết quả thuận lợi để có A là n( A) =17 n
Vậy xác suất cần tìm: P ( A) (A) 17 = = 0.5 n(W) 48
b. Trên 2 đường thẳng song song D và d , ta lần lượt gắn vào đó m điểm và n 2.0
điểm sao cho m + n = 17 ( ,
m n Î N *). Tìm m , n để số các tam giác có 3 đỉnh là 3 điểm
trong 17 điểm phân biệt đã cho là lớn nhất.
Mỗi tam giác cần xác lập có 1 đỉnh nằm trên một đường thẳng và 2 đỉnh nằm trên
đường thẳng còn lại.
Trường hợp 1: Một trong hai số m hoặc n là bằng 1 - chẳng hạn m =1, khi đó n =16 và
số các tam giác có được từ 17 điểm này là 2 1.C = 120 0.5 16 Page 3
Trường hợp 2: m, n đều lớn hơn 1.
Số các tam giác có được từ 17 điểm này là (n -1)n (m -1)m 2 2 . m C + nC = . m + . n n m 2 2 0.5 mn 15 = .(m + n - 2) = mn 2 2 15 15 2 2 = .4mn =
.[(m + n) - (m - n) ] 8 8 0,25 15 2 2 = - - .[17 (m n) ] 8 15 15 2 2 £ (17 -1 ) = .288 = 540. 8 8 0.25
Dấu bằng xảy ra khi |m-n| =1, m,n Î N* 0.25
Þ m=9 , n=8 hoặc ngược lại.
Kết luận : Số tam giác là lớn nhất khi m=9, n=8 hoặc ngược lại. 0.25 4 2 ì6 - x - x 2,0 ï khi x ¹ 2
Cho hàm số f ( x) = í | x - 2 | ï î 5 khi x = 2
Xét tính liên tục của hàm số f ( x) tại điểm x = 2 . 2 2 6 - x - x 6 - x - x 0.25 lim f (x) = lim = lim x®2+ x®2+ - x®2 | x 2 | + x - 2 (x - 2)(-x - 3) = lim 0.25 x®2+ (x - 2) 0.25 = lim (-x - 3) = 5 - x®2+ 2 2 6 - x - x 6 - x - x 0.25 lim f (x) = lim = lim x®2- x®2- - x®2 | x 2 | - 2 - x (x - 2)(-x - 3) = lim 0.25 x®2- 2 - x 0.25 = lim (x + 3) = 5 x®2-
Vì lim f (x) ¹ lim f (x) nên hàm số không có giới hạn tại x=2 nên không thể liên tục tại 0.5 x 2+ x 2- ® ® x=2. 5
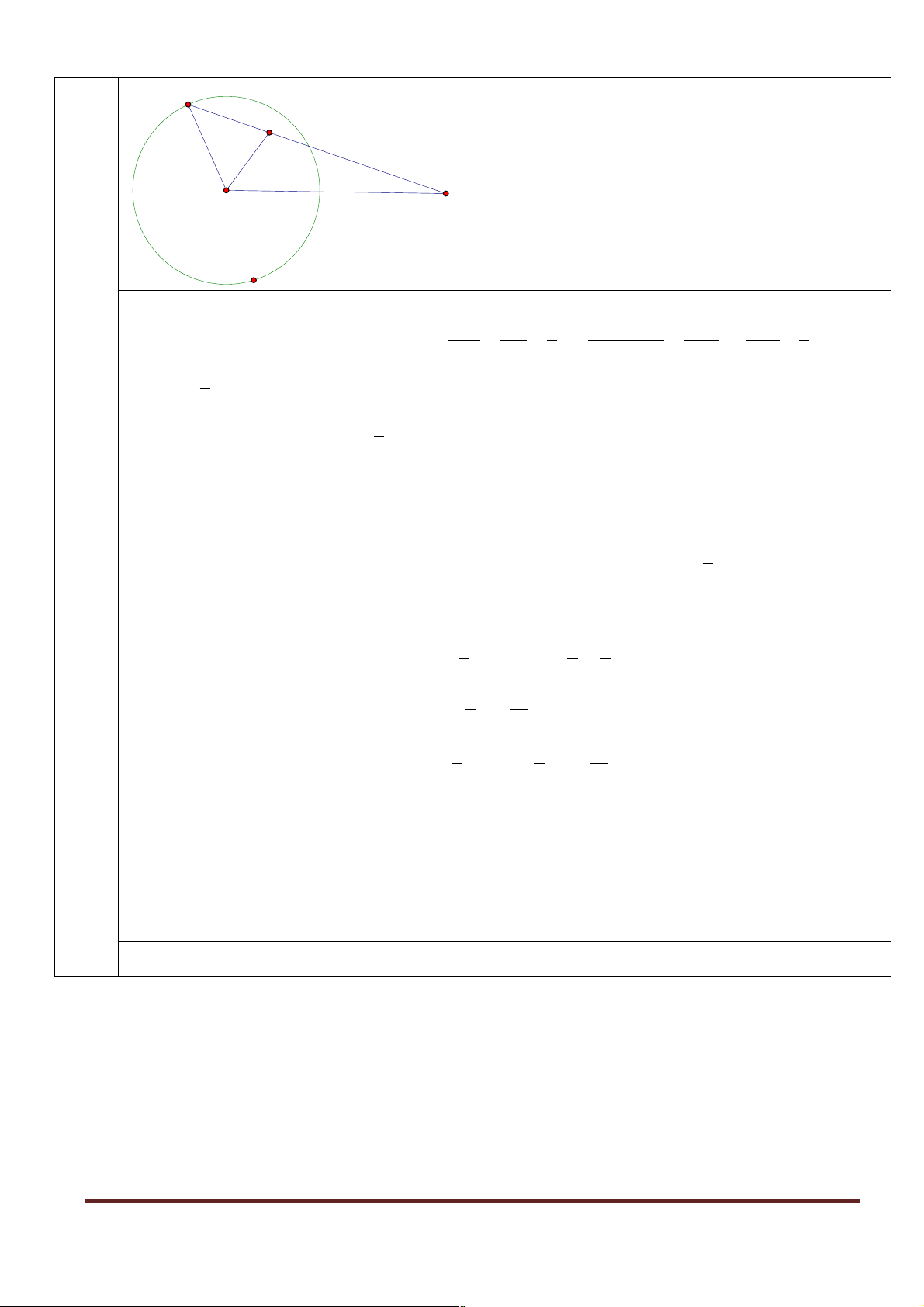
Trong mặt phẳng Oxy, cho đường tròn (C) 2 2
: x + y - 2x + 4y - 4 = 0 và điểm ( A 3, - 1 ) . 3,0
Gọi I là tâm của đường tròn (C). M là điểm thay đổi trên (C) sao cho 3 điểm , A M , I
không thẳng hàng. Tia phân giác góc ∑
AIM cắt đường thẳng AM tại N . Gọi (K ) là tập
hợp các điểm N khi M thay đổi trên (C). Viết phương trình đường (K ) . Hình vẽ: Page 4 M N I A
(C) có tâm I(1,-2) và bán kính R =3 . Tính được IA = 5. 0.5 MN IM 3 MN + AN + AM
Vì IN là tia phân giác của góc ∑ AIM nên = = 3 5 8 Þ = Þ = AN IA 5 AN 5 AN 5 !!!" !!!!" Þ 5
AN = AM (*) (do N nằm giữa A và M ) 8 0.5 5
Vậy phép vị tự tâm A, tỉ số k = biến điểm M thành điểm N. 0.25 8 0.25
Gọi P,Q là 2 giao điểm của đường thẳng IA và (C).
Do đó khi M chạy khắp đường tròn (C) ( M ¹ P, M ¹ Q) thì N chạy khắp (K) với (K) 5
đường tròn (C’) là ảnh của đường tròn (C) qua phép vị tự tâm A tỉ số k = ( trừ 2 điểm 0.5 8
là ảnh của P,Q qua phép vị tự trên).
Viết phương trình đường tròn (C’). !!!" !!" 0.5 5 æ 1 7 ö
Gọi I’ là tâm đường tròn (C’), ta có: AI ' = AI Þ I ' - ;- ç ÷ 8 è 2 8 ø 5 15
R’ là bán kính đường tròn (C’), ta có: R’ = R = . 0.25 8 8 2 2 2 0.25 æ 1 ö æ 7 ö æ15 ö
Vậy phương trình đường tròn (C’) : x + + y + = ç ÷ ç ÷ ç ÷ è 2 ø è 8 ø è 8 ø 6
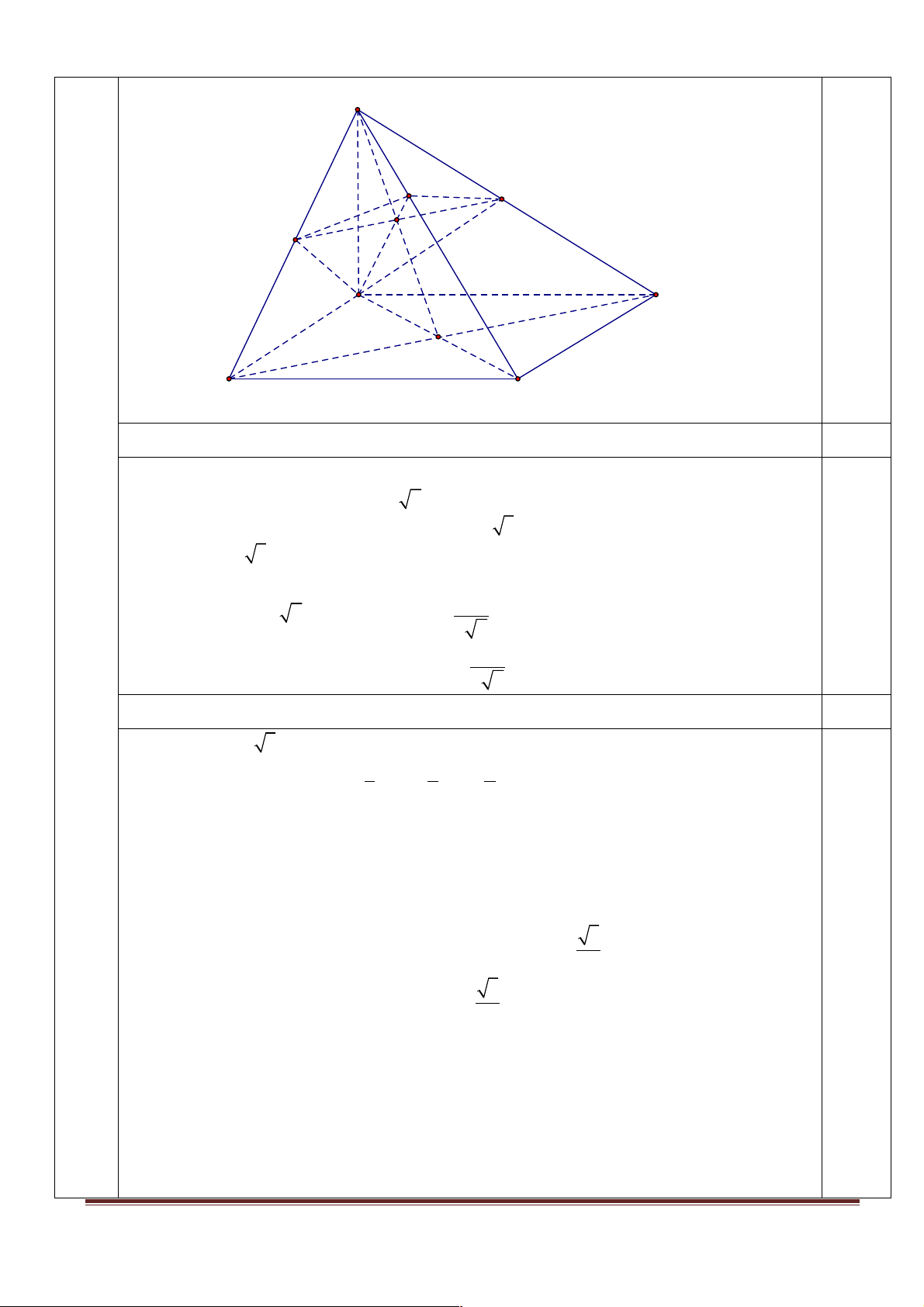
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , biết BD = a ; cạnh bên 4.0
SA vuông góc với mặt phẳng ( ABCD) và SA = a .
a. Tính cosin góc giữa 2 đường thẳng SB và AD .
b. Gọi (a ) là mặt phẳng qua A song song với BD và cắt cạnh SC tại M sao
cho khoảng cách từ C đến mặt phẳng (a ) bằng 3 lần khoảng cách từ S đến mặt phẳng
(a ) . Tính diện tích thiết diện tạo bởi mặt phẳng (a ) và hình chóp S.ABCD .
Hình vẽ: ( Phục vụ câu a :0.25 điểm và câu b 0.25 điểm) 0.5 Page 5 S a M E F I a A B a a O D C
a. Tính cosin góc giữa 2 đường thẳng SB và AD . 1.5 Tính góc ∑ SBC . 0.25
D SAB vuông cân tại A Þ SB = a 2 . 0.25
Gọi O là tâm hình thoi ABCD. AC = 2 AO = a 3 0.25 SA =a, AC = a 3 Þ SC = 2a
Ta có: SC2 = SB2+BC2-2SB.BC . cos B 1
4a2 = 2a2+ a2 - 2.a2 2 cos BÞ cosB = - 2 2 0.5 1
Gọi q là góc giữa SB và BC , ta có: cosq = 0.25 2 2
b. Tính diện tích thiết diện tạo bởi mặt phẳng (a ) và hình chóp S.ABCD . 2.0
Ta có: AC = a 3 và SA =a Þ SC =2a. • 1 1 a
d(C, α) = 3 d(S, α) Þ SM = CM = SC = 0.25 3 4 2
• Gọi I là giao điểm của SO và AM.
Trong mp (SBD) kẻ đường thẳng song song BD cắt SB, SD tại E và F. 0.5
Thiết diện tạo bởi (α) và hình chóp S.ABCD là tứ giác AEMF. 0.25
Ta có BD ^ (SAC) Þ EF ^ (SAC) Þ EF ^ AM (Þ SAEMF = ½ AM. EF.) • Tính AM, EF 3
Xét D SAM , tính AM theo hệ thức cosin ta được AM = a 0.25 2 3
(có thể kiểm chứng AM ^ SC Þ … AM = a ) 2
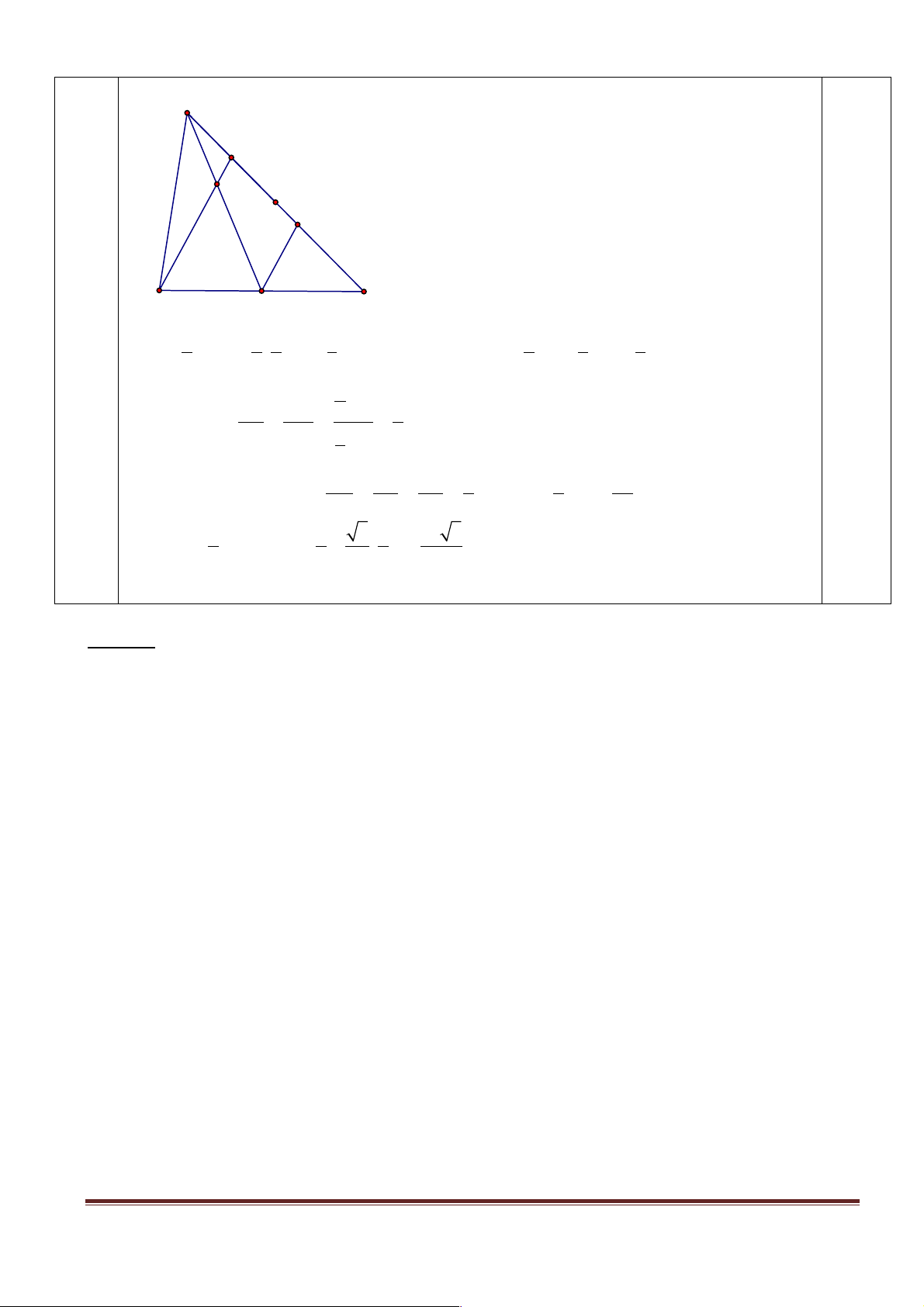
Xét D SAC – Kẻ ON // AM. O là trung điểm AC Þ N là trung điểm CM. Page 6 S M I N 0.25 / / 0.25 A C O 1 1 3 3 MN = CM = . SC = 1 3
SC Þ SN = SI+MN = SC + 5 SC = SC 0.25 2 2 4 8 4 8 8 1 SC SI SM 2 ON // AM Þ 4 = = = SO SN 5 5 SC 8 EF SE SI 2 a Xét D SBD, EF // BD Þ = = = 2 2 Þ EF = BD = BD SC SO 5 5 5 2 • 1 1 3 2 a 3 SAEMF = AM. EF= .a . a = . 2 2 2 5 10
Ghi chú: Nếu học sinh có cách giải khác đúng thì Ban Giám khảo thảo luận và thống nhất thang
điểm cho phù hợp với Hướng dẫn chấm. Page 7