Đề thi Olympic 30 tháng 04 năm 2025 Toán 10 trường chuyên Lê Hồng Phong – TP HCM
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi Olympic truyền thống 30 tháng 04 năm 2025 lần thứ XXIX môn Toán 10 trường THPT chuyên Lê Hồng Phong, thành phố Hồ Chí Minh. Kỳ thi được diễn ra vào ngày 05 tháng 04 năm 2025. Đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm.
Chủ đề: Đề HSG Toán 10 130 tài liệu
Môn: Toán 10 3 K tài liệu
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLYMPIC TRUYỀN THỐNG 30 THÁNG 4 THÀNH PHỐ HỒ CHÍ MINH
LẦN THỨ XXIX - NĂM 2025 TRƯỜNG THPT CHUYÊN LÊ HỒNG PHONG Môn: TOÁN Khối: 10
Ngày thi: 05/04/2025
ĐÁP ÁN CHÍNH THỨC Câu Nội dung Điểm
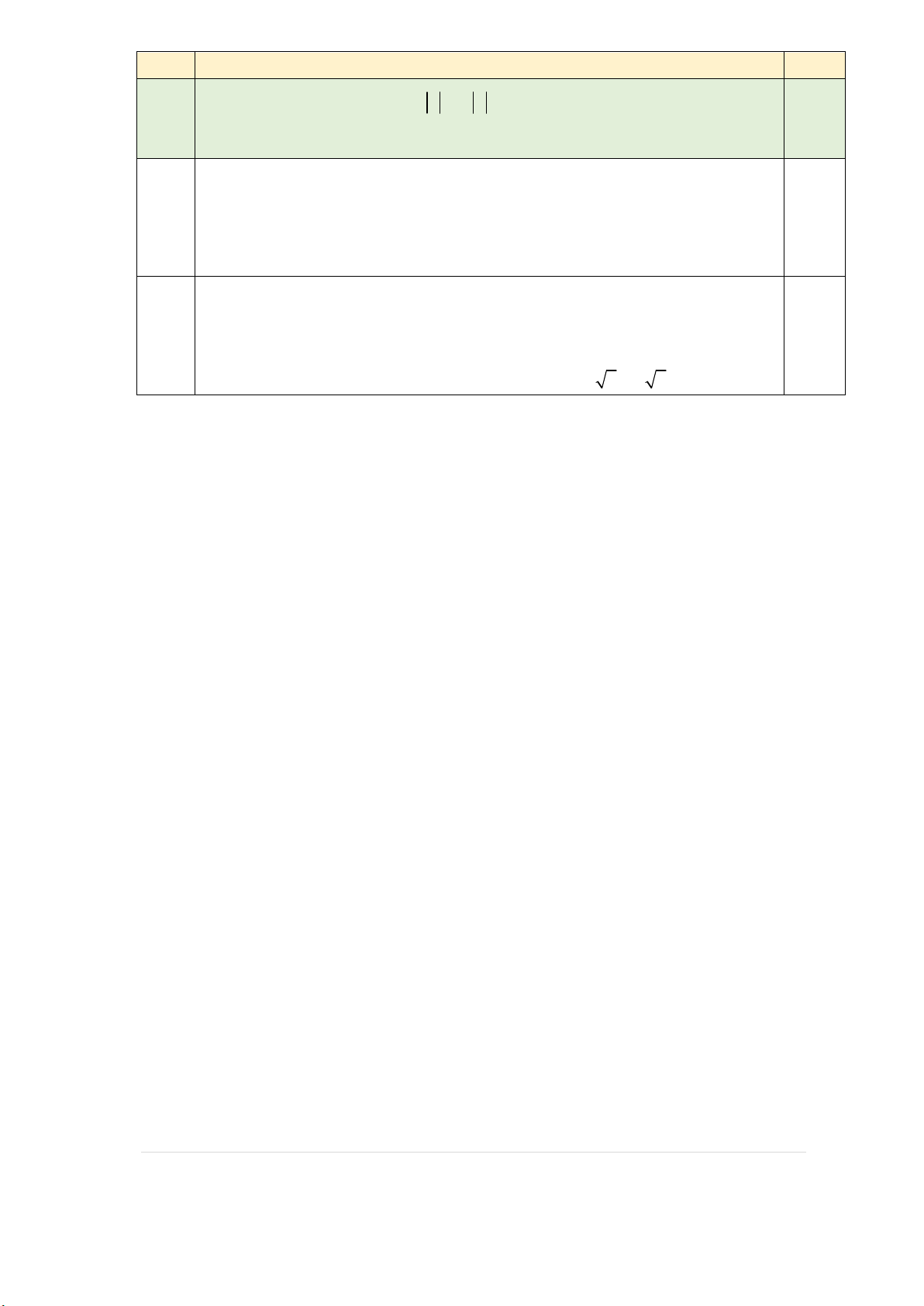
Cho các số thực a , a ,..., a ,b ,b ,..., b thỏa mãn a 0 với mọi i 1,..., 30 . 1 2 30 1 2 30 i Hỏi phương trình 1 3
max a x b , a x b ,..., a x b 4 1 1 2 2 30 30
có nhiều nhất bao nhiêu nghiệm?
Giả sử phương trình đã cho có 3 nghiệm x x x . Suy ra tồn tại chỉ số 1 2 3 1 i 30 để 1.5
a x b max{a x b , a x b ,, a x b } 4; i 2 i 1 1 2 2 30 30
ngoài ra ta có a x b 4, a x b 4 . i 1 i i 3 i
Nói cách khác, hàm tuyến tính a x b 4 nhận giá trị 0 tại x và không dương i i 2
tại x , x . Điều này chỉ xảy ra khi nó là hàm hằng bằng 0 ; nghĩa là a 0, b 4 , 1 1 3 i i
mâu thuẫn. Như vậy, phương trình đã cho có không quá 2 nghiệm.
Đảo lại, với a a 1, a 1
,b b 0 ta dễ thấy phương trình 1 29 30 1 30 0.5 max{x, }
x 4 có 2 nghiệm là x 4 .
K ỳ t h i O l y m p i c t r u y ề n t h ố n g 3 0 / 4 l ầ n t h ứ X X I X n ă m 2 0 2 5 1 Câu Nội dung Điểm
Cho các số thực x, y thỏa mãn x 3, y 3 . Chứng minh rằng: 2 4 2 x 2 0 1 y 1 4 x 1 y 1 164
Một mặt, do | x |,| y | 3 , ta có 2 2 2 2
(x 1)( y 1) 4(x 1)( y 1) (x 1)( y 1) 4(| x | 1 )(| y | 1 ) 2 2 2
(3 1)(3 1) 4(3 1)(3 1) 164
Dấu "=" đạt được khi x y 3 Mặt khác, 2 2 2 2 2 2
(x 1)( y 1) 4(x 1)( y 1) x y x y 1 4xy 4x 4 y 4 2 2 2
(xy 1) (x y 2) 0
Dấu "=" đạt được khi xy 1, x y 2 hay (x, y) (1 2,1 2) .
K ỳ t h i O l y m p i c t r u y ề n t h ố n g 3 0 / 4 l ầ n t h ứ X X I X n ă m 2 0 2 5 2 Câu Nội dung Điểm
Các số thực dương a , a ,, a
được viết trên một vòng tròn theo thứ tự đó. 1 2 100
Biết rằng mỗi số lớn hơn tích của hai số liền trước nó: với mọi 1 i 100 thì 3 4 a a a (ta quy ước a a , a
a ). Hỏi có nhiều nhất bao nhiêu số i i 1 i2 101 1 102 2
nguyên dương trong các số a , a ,, a 1 2 100
Chúng ta sẽ chỉ ra rằng hai số hạng liên tiếp không thể đồng thời là số nguyên
dương được. Thật vậy, giả sử ngược lại, a , a là hai số nguyên dương liên tiếp. i i 1 Suy ra, vì a a a nên a a 1 . Tương tự, a a a nên a a . i 2 i i 1 i2 i 1 i3 i2 i 1 i3 i2 2
Cứ lập luận như vậy, ta suy ra a
a 1 với mọi k . Nói riêng, điều này có k 1 k
nghĩa là a a a
a , mâu thuẫn. Như vậy, trong 100 số hạng 1 2 100 1 a ,, a
có nhiều nhất 50 số nguyên dương. 1 100
Hơn nữa, nếu có 50 số nguyên dương thì chúng là các số hạng chỉ số chẵn hoặc
là các số hạng chỉ số lẻ. Giả sử a , a ,, a là các số nguyên dương (trường hợp 1 3 99 a ,, a
là các số nguyên dương lập luận tương tự). Khi này bằng cách nhân 2 100 1
các bất đẳng thức a a a , a a a , , a
a a lại, ta được 2 100 1 4 3 2 100 99 2 a a a a a a
, kéo theo 1 a a a , vô lý. 2 4 100 1 2 100 1 3 99
Như vậy, trong các số a ,, a
, có nhiều nhất 49 số nguyên dương. Ví dụ sau 1 100
đây cho thấy giá trị này đạt được: 1 1 1 1 1
a a a 1, a , a ,, a , a . 2 4 98 1 3 99 100 100 99 51 50
K ỳ t h i O l y m p i c t r u y ề n t h ố n g 3 0 / 4 l ầ n t h ứ X X I X n ă m 2 0 2 5 3 Câu Nội dung Điểm
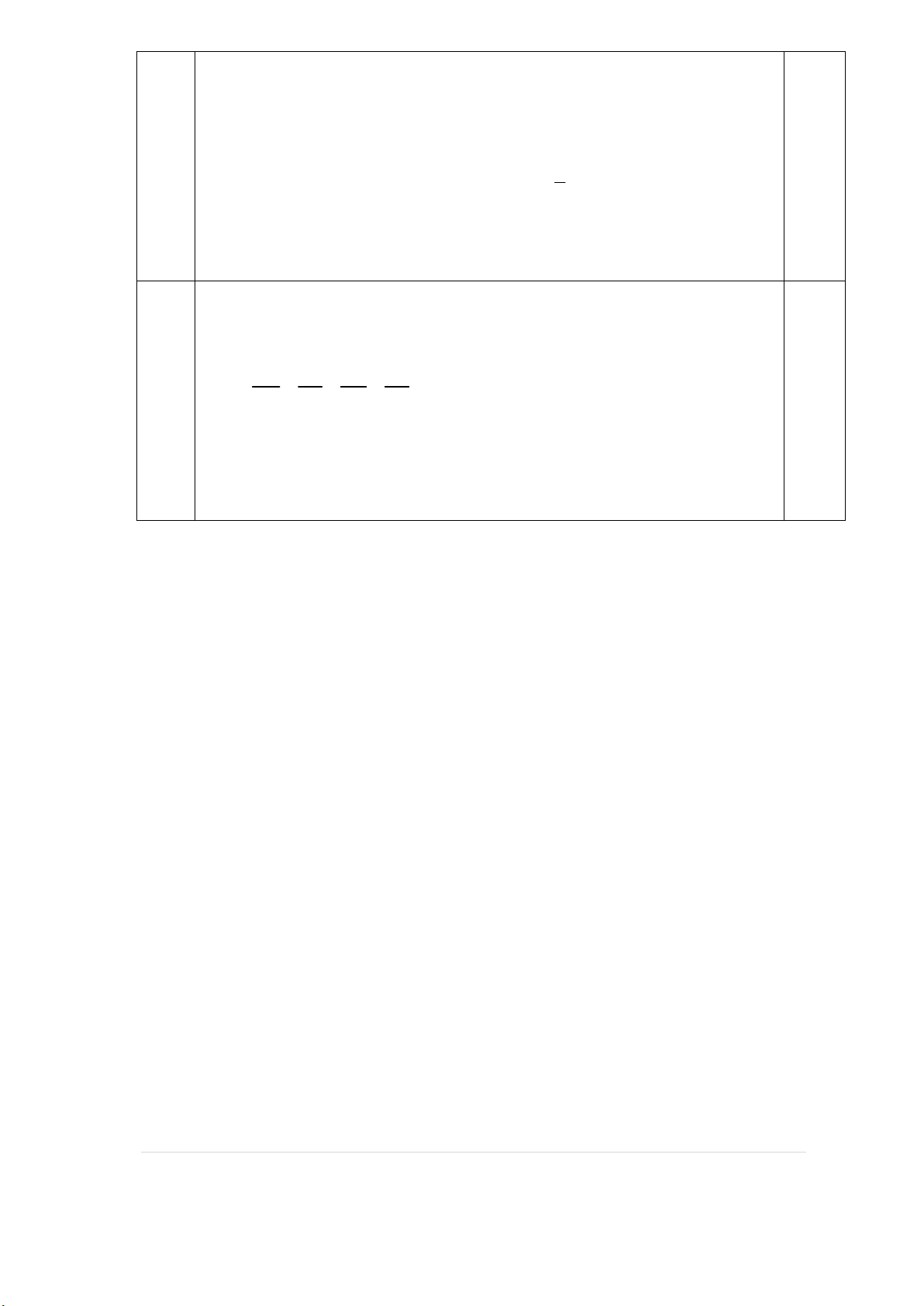
Cho các số nguyên dương a, b với a b . Biết rằng 3 3
a b là một ước của 4 4 2 2
ab(a b ) . Chứng minh rằng 3
(a b) 3ab
Đặt a dm, b dn , với d gcd(a, b) , như vậy gcd(m, n) 1. Điều kiện của bài toán chứng tỏ 3 3 3 4 2 2
d (m n )∣d mn(m n ) , kéo theo 3 3 2 2
(m n ) dm ∣
n(m n ) , hay 2 2 2
(m n)(m mn n )∣dmn(m n)(m n) , nghĩa là 2 2
(m mn n ) d
∣ mn(m n) . Để ý rằng hiển nhiên 2 2 2 2
gcd(m mn n , m) gcd(m mn n , n) 1. Ngoài ra, ta cũng có 2 2
gcd(m mn n , m n) 1. Thật vậy, nếu 2 2 k m ∣
mn n và
k∣m n thì 2 k (
∣ m n)n n chứng tỏ 2 k n ∣ ; tương tự 2 k m ∣ , do đó 1 k g
∣ cd(m, n) 1, hay k 1. Từ đó 2 2
m mn n ∣d , kéo theo 2 2 2
d m mn n (m n) 3mn 3mn . Suy ra 1 3 3 3 3 2 2
(a b) d (m n) d d d d 3mn 3ab
K ỳ t h i O l y m p i c t r u y ề n t h ố n g 3 0 / 4 l ầ n t h ứ X X I X n ă m 2 0 2 5 4 Câu Nội dung Điểm
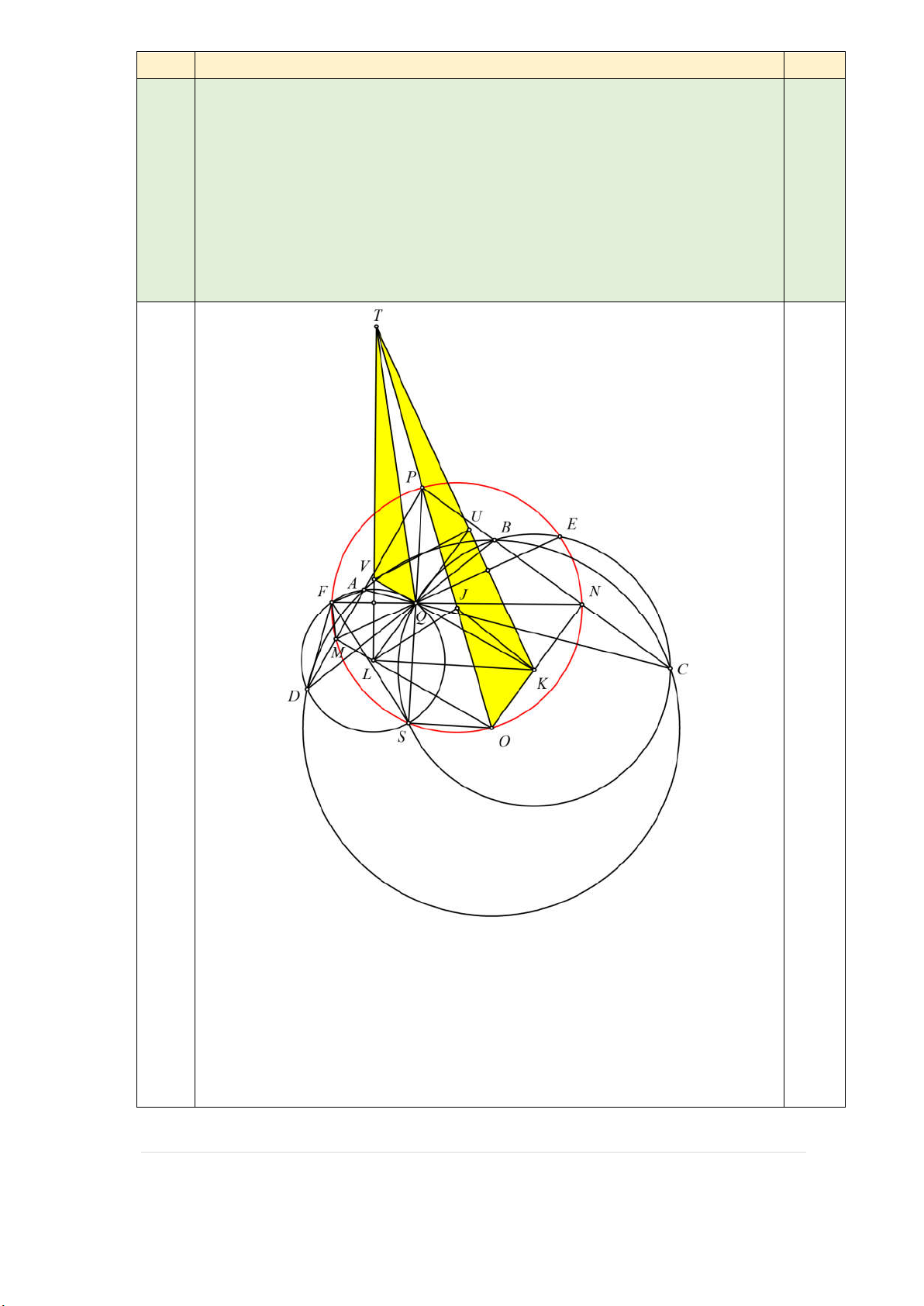
Cho tứ giác ABCD nội tiếp đường tròn (O) . Các đường thẳng AD và BC cắt
nhau tại P , các đường thẳng AC và BD cắt nhau tại Q . Gọi M và N tương
ứng là trung điểm của AD và BC . Ký hiệu (L) và (K ) tương ứng là đường tròn
ngoại tiếp tam giác QAD và tam giác QBC . Đường thẳng MQ cắt lại (K ) tại 5
điểm E (khác Q ), đường thẳng NQ cắt lại (L) tại điểm F (khác Q ). 5
a) Chứng minh rằng các điểm P, O, E, F , M , N cùng thuộc một đường tròn.
b) Đường thẳng đi qua L và vuông góc với QF cắt đường thẳng đi qua K và
vuông góc với QE tại điểm T. Chứng minh rằng các điểm T , P và O thẳng hàng. 5.a 2
Do QAD ~ QBC nên MQD NQC , suy ra NQ là đường đối trung của
tam giác AQD . Ta thu được tứ giác AFDQ điều hòa. Suy ra
QFM QFD MFD QAD QFA QBC QDA MPN.
Suy ra M , F , P, N đồng viên. Tương tự M , E, P, N đồng viên. Lại có PMO PNO 90
nên PO là đường kính của (PMN ) . Vậy
P, O, E, F , M , N đều nằm trên đường tròn đường kính O . P
K ỳ t h i O l y m p i c t r u y ề n t h ố n g 3 0 / 4 l ầ n t h ứ X X I X n ă m 2 0 2 5 5
Gọi J là trung điểm của OP . LQ cắt TK tạiU , KQ cắt TL tại V . (L) giao
(K ) tại S khác . Q
Hiển nhiên P thuộc trục đẳng phương của (L) và (K ) nên P, Q, S thẳng hàng. Đồng thời ta cũng có PSO 90 . 5.b 1 1.5
Ta có JL FS , LK QS nên J LK FS Q FLQ QLT . 2
Tương tự JKL QKT , suy ra Q, J liên hợp đẳng giác trong tam giácTLK .
Do đó TQ,TJ đẳng giác trong L TK . (1)
Mặt khác, ta cũng có QLT QSF QNP QMP QSE QKT , suy
ra tứ giác LKUV nội tiếp.
Lại có LQ BC nên LQ KO , tương tự suy ra LQKO là hình bình hành. VQ VQ VU TV Từ đó . OK QL LK TK 1.5
Mà TKO TUQ TVQ nên TVQ ~ TKO( . c g.c).
Vậy TQ,TO đẳng giác trong LT K . (2)
Từ (1) và (2) suy ra T , P, J , O thẳng hàng.
K ỳ t h i O l y m p i c t r u y ề n t h ố n g 3 0 / 4 l ầ n t h ứ X X I X n ă m 2 0 2 5 6
Document Outline
- 01. Toan 10
- 01. OLP2025. TOAN 10. DAP AN