Đề thi Olympic Toán 10 năm 2024 – 2025 liên cụm trường THPT – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
LIÊN CỤM TRƯỜNG THPT
LỚP 10, LỚP 11 NĂM HỌC 2024 – 2025 Môn thi: TOÁN 10 ĐỀ CHÍNH THỨC
t 15 tháng 3 năm 2025 T 150
(Đề thi gồm 02 trang)
PHẦN I. TRẢ LỜI NGẮN (10,0 điểm)
Thí sinh trả lời từ câu 1 đến câu 10. Với mỗi câu hỏi, thí sinh viết kết quả vào giấy thi. x  2m  2
Câu 1.(1,0 điểm) Tập hợp tất cả các giá trị thực của tham số m để hàm số y  x  xác định trên m  1
 ;0 có dạng T   ;  a ; b  . K đó .
a b có giá trị bằng bao nhiêu?
Câu 2.(1,0 điểm) Đ ểm kiểm tra môn Toán của một nhóm gồm 10 học s ư s u 3 4 4,5 5 6 6,5 8 8,5 9 10
K đó tru vị của mẫu số liệu trên bằng bao nhiêu?
Câu 3.(1,0 điểm) Cho parabol P 2
: y  ax  bx  4 đ qu đ ểm A1;7 và có trục đối xứng x  1  . Tích
ab nhận giá trị bằng bao nhiêu?
Câu 4.(1,0 điểm) Cho Parabol 2
y  x  2mx  m . Khi m t đổ
i, tập hợp đỉnh của Parabol là một đư ng
cong cắt đư ng thằng y  x 1 tạ đ ểm A ,
a b . Tổng a  b bằng bao nhiêu?
Câu 5.(1,0 điểm) Tro ăm 2025, một cửa hàng kinh doanh xe máy dự định kinh doanh hai loại xe máy
Lead và xe máy Vision, với tổng số vố đầu k ô vượt quá 36 tỉ đồng. Giá nhập về 1 chiếc xe máy
Lead là 40 triệu đồng, lợi nhuận dự kiến là 5 triệu đồng một chiếc. Giá nhập về 1 chiếc xe máy Vision là
30 triệu đồng, lợi nhuận dự kiến là 3, 2 triệu đồng một chiếc. Cử ước tính rằng tổng nhu cầu thị
trư k ô vượt quá 1100 chiếc xe cả hai loại và nhu cầu xe Le d k ô vượt quá 1,5 lần nhu cầu xe
Vision. Hỏi lợi nhuận có thể t u được lớn nhất của cửa hàng là bao nhiêu tiền? (Viết câu trả l t eo đơ vị triệu đồng).
Câu 6.(1,0 điểm) Có bao nhiêu giá trị nguyên của tham số m để p ươ trì 2
x  4x  m  0 có hai nghiệ dươ p â ệt ?
Câu 7. (1,0 điểm) Cho tam giác ABC , trọng tâm G . Trên cạnh AB kéo dài lấ đ ểm I sao cho B là tru đ ể 2
m AI. Trên cạnh AC lấ đ ểm J sao cho AJ 
AC . Biết IG  kIJ, hỏi k bằng bao nhiêu? 5
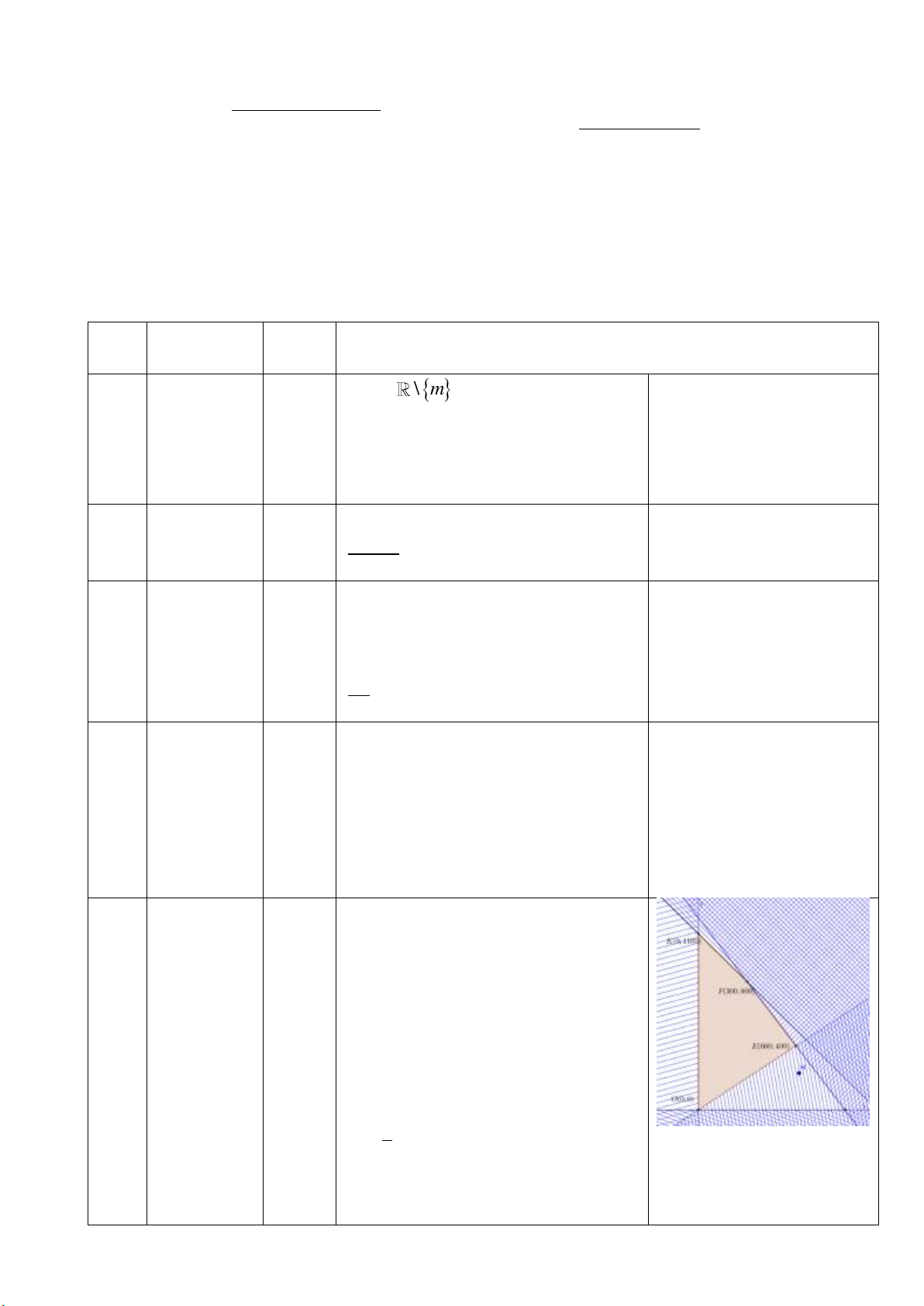
Câu 8.(1,0 điểm) Để đo c ều cao CD của cây cổ thụ, bạn An chọn trên mặt đất đ ểm , A B có
khoảng cách AB  12m cùng thẳng hàng với chân C của gốc câ để đặt giác kế. Chân của giác kế có
chiều cao h  1,3m . Gọ đ ểm quan sát A ; B cùng thẳng hàng với C thuộc chiều cao CD 1 1 1 của cây cổ
thụ. Bạ Bì đo được góc 0 DAC  49 và góc 0
DB C  35 . Bạ A đo c ều cao của cây cổ thụ đó 1 1 1 1
bằng bao nhiêu (kết quả trò đến hàng phần chục). 1
Câu 9.(1,0 điểm) Ký hiệu a, ,
b c lầ ượt độ dài các cạ đố đ ện vớ các đỉnh ,
A B, C của tam giác
ABC . Biết tam giác ABC có các cạnh thoả hệ thức a b  ca b c  3ab . K đó số đo của góc C bằng bao nhiêu ?
Câu 10.(1,0 điểm) Cho ABC đều có cạnh bằng 2a . Gọi d đư ng thẳng qua A và song song với
đư ng thẳng BC và đ ểm M d động trên đư ng thẳng d . Tìm giá trị nhỏ nhất của MA 2MB  MC .
PHẦN II. TỰ LUẬN (10,0 điểm)
Thí sinh trả lời từ câu 11 đến câu 13. Với mỗi câu hỏi, thí sinh trình bày lời giải vào giấy thi.
Câu 11.(4,0 điểm) Trong hệ toạ độ Oxy , cho parabol P 2 2
: y  x  3mx  2m  m 1 v đư ng thẳng
D: y  x 2. Tìm tất cả các giá trị của tham số m để D cắt P tạ đ ểm phân biệt , A B sao cho
diện tích tam giác OAB đạt giá trị nhỏ nhất.
Câu 12.(4,0 điểm) Trong mặt phẳng với hệ tọ độ Oxy , cho tam giác ABC vuông cân tại B . Các đ ểm
M , N lầ ượt tru đ ểm của A ,
B AC và I 7; 
3 là trọng tâm tam giác ABN . Đ ểm E thuộc cạnh
AC sao cho IE  IA ( E k ác A) v đư ng thẳng IE : x  2y 13  0 . Biết điểm M thuộc đư ng thẳng
d : x3y 12  0, B thuộc đư ng thẳng d : x y 2  0 và A có o độ lớ ơ 5. Tìm tọ độ 2  1  các đ ểm , A , B C .
Câu 13.(2,0 điểm) Có bao nhiêu số tự nhiên có 3 chữ số dạng abc thỏa mãn a , b , c độ dài 3 cạnh
của một tam giác cân ( kể cả t ác đều )?
--------- HẾT ---------
Cán bộ coi thi không giải thích gì thêm
Họ v tê t í s ……………………………… Số áo d ………………………
Họ tên, chữ kí cán bộ coi thi thứ nhất: Họ tên, chữ kí cán bộ coi thi thứ hai: 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
LIÊN CỤM TRƯỜNG THPT LỚP 10, LỚP 11
NĂM HỌC 2024 – 2025 Môn thi: TOÁN 10 Ngày thi: 15/3/2025 HƯỚNG DẪN CHẤM
(Hướng dẫn chấm gồm 4 trang)
PHẦN I - Trả lời ngắn (10,0 điểm). CÂU ĐÁP SỐ ĐIỂM GHI CHÚ +) D  \   m .
+)Hàm số xác định trên  1  ;0 khi và 1 0 1,0 T   ;    1 0; m  chỉ khi m   0 1;0   . m  1 
Số trung vị của mẫu số liệu trên là 2 6,25 1,0 6  6,5  6,25 6, 25 . 2
+) Parabol đi qua điểm A1;7 nên ta có 2 7  . a 1  .
b 1 4  a  b  3 . a 1 3 2 1,0    
+)Trục đối xứng x  1  nên ab 1.2 2 b   2 b   1
  b  2a . 2a
+) Tọa độ đỉnh I của Parabol là x  m  x  m  I  I +)Phương trình hoành độ   2 2
y  m  2m  m  2 y  m   m I  I giao điểm: 2
x  x  x 1 4 1  1,0 2
 y  x  x .  x  1  . Suy ra y  0. I I I
+)Suy ra tập hợp đỉnh của Parabol là 2
y  x  x +) Gọi ,
x y lần lượt là số xe máy Lead
và số xe máy Vision nhập về để lợi nhuận thu được là lớn nhất
x 0;y 0. Ta có hệ BPT  x  0 y 0 5 4280 1,0  
40x  30y  36000 I 
x  y 1100   3 x  y   2 Lợi nhuận: F  ,
x y  5x 3,2y F 0;0  0 1 F 600;40  0  4280 F 300;80  0  4060 F 0;110  0  3520 . +) Phương trình 2
x  4x  m  0 có hai Vậy có 3 giá trị nguyên của 6 3 1,0 m  4
nghiệm dương phân biệt   m thỏa mãn. m  0 2
+)Ta có: IJ  AJ  AI  AC  2AB . 5 A
+)Gọi M là trung điểm của BC . Khi J G đó 1
AM   AB  AC. B 5 C 2 M 7 1,0 6 2 1 1 +) AG  AM  AB  AC . I 3 3 3 5 1 5
5IJ  6IG hay IG  IJ . Ta có IG  AC  AB . 6 3 3 +)Ta có 0
C D  B Dsin 35 1 1 +) 0 B D 12 12sin131 1   B D  . 0 0 1 0 sin131 sin14 sin14 CD  22,8m . 8 22,8 1,0 Khi đó 0
CD 1,3  C D 1,3  B Dsin 35 1 1 0 0 12sin 35 sin131 . 1,3  22,772 0 sin14
a bca bc  3ab Ta có: +) 2 2 2
 c  a  b  ab 9 0 120 1,0 2 2 2
c  a  b  2ab cos C . 0 C 120 Vậy 0 C 120 .
Xét điểm I sao cho: IA 2IB  IC  0
 IA 2IA ABIC  0 BA  BC  IA 
 BK (với K là 2
trung điểm AC ),  I là điểm thứ 4 M A
của hình bình hành AIBK .
MA 2MB  MC  I K 10 a 3 1,0 Ta có: 2MI
M d  GTNN đạt được khi IM  d B C . Khi đó: 0 0
MAI  MAB  IAB  60  ABK  30 . 0 0
2IM  2IAsin 30  2BK sin 30 1 2 2
 2 4a  a .  a 3. 2 TỔNG 10,0 điểm 2
PHẦN II - Tự luận (10,0 điểm). Câu Hướng dẫn chấm Điểm Câu 11
Trong hệ toạ độ Oxy , cho parabol P 2 2
: y  x  3mx  2m  m 1… 4,0
(4,0 điểm) Phương trình hoành độ giao điểm của D và P: 2 2
x  3mx  2m  m 1  x  2 2
 x  m  2 3
1 x  2m  m 1  0   * . 1,5
D cắt P tại hai điểm phân biệt , A B  PT  
* có hai nghiệm phân biệt x , x ; 2
  0  m 2m5  0, m   . 1 2
x  x  3m1 1 2
Theo hệ thức Vi-et ta có:  . 2
x x  2m  m 1  1 2 1,5 A
 x ; x  2 1 1  2 Giả sử 
 AB  2x  x   2 2 m  2m  5 2 1  B
 x ; x  2 2 2 
Mặt khác: d O D 2 ;   2 . 2 1,0 Khi đó: 1 S  d O D AB  m  m   m    . OAB    2 . ; . 2 2 5  2 2 1 4 2 2 2 Vậy m  1.  Câu 12
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC vuông cân tại B … 4,0 (4,0 điểm) B d 1:x+3y-12=0
d2:x+y+2=0 M 0,5 I(7;3) IE:x+2y-13=0 A J K N E C
Gọi a  BA  BC . Khi đó ta tính được 2 2 a 2 a a
 a   a  a 10 BN  ; MN  ; MI  ; BI        ; 2 2 6  2   6  6 1,0 Ta tính đượ 1 a 2 1 1 1 a 2 a 2 c IK  BN  ; JK  JN  . .  ; 3 6 3 3 2 2 12 a 2 a 2 a 2  a 10 AK    . Suy ra 2 2
IE  AI  IK  AK  . 12 4 3 6 a 2 a 2 a 2
Ta có NE  KE  KN    . 3 6 6 1,0 5a 5 Suy ra 2 2 2 2 2 2
BE  BN  NE 
 BE  a  BI  IE . 3 9 3
Suy ra tam giác BIE vuông tại I .
Suy ra BI : 2x  y 11 B  BI d  3; 5  . 2   a 10 0,5 Suy ra BI  4 5   a 12 2 . 6
Gọi M d  M 12  3t;t  A  21 6t;2t  5 . 1     0,5 a 10 t   3 A  3;11 2 2  
Ta có AI  14  6t   2t  2   4 5     6 t  1 A   15;7
Do hoành độ A lớn hơn 5 . Ta chọn A15;7, suy ra N  3;7  C   9  ;7 . 0,5 Câu 13 2,0
Có bao nhiêu số tự nhiên có 3 chữ số dạng abc thỏa … (2,0 điểm) 0   y  2x 
Gọi độ dài cạnh bên và cạnh đáy của tam giác cân là x , y  0   y  9 0  x  9  0,5 0   y  9 Th1: 
suy ra có 9.5  45 cặp số. 5  x  9 x  i Th2: 
với 1  x  4 . Với mỗi giá trị của i , có 2i 1 số. 1
  y  2i 1 0,5
Do đó, trường hợp này có: 2.1  1  2.2   1  2.3   1  2.4   1  16 cặp số Suy ra có 61 cặp số  ;
x y . Với mỗi cặp  ;
x y ta viết số có 3 chữ số trong đó
có 2 chữ số x , một chữ số y . Trong 61 cặp có:
+ 9 cặp x  y , viết được 9 số. 1,0
+ 52 cặp x  y , mỗi cặp viết được 3 số nên có 3.52  156 số.
Vậy tất cả có 165 số.
Chú ý: Học sinh làm theo cách khác nhưng đúng vẫn cho điểm tối đa. 4
Document Outline

• 8.Đề Toán 10 2024-2025
• 8.HDC Toán 10 2024-2025