Đề thi Olympic Toán 8 năm 2024 – 2025 phòng GD&ĐT Thạch Thất – Hà Nội

UBND HUYỆN THẠCH THẤT
KỲ THI OLYMPIC CÁC MÔN VĂN HOÁ LỚP 8THCS
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HUYỆN THẠCH THẤT NĂM HỌC 2024-2025 ================ Đề thi môn: TOÁN.
Thời gian làm bài: 120 phút (không kể thời gian giao đề) (Đề thi gồm 02 trang) 2 2 2 2 Bài 1 (5 điểm  + −   + +  ). Cho biểu thức: x y x y x y 2 = +   : 1 x y A + . 2 2 1− xy 1+ xy   1− x y 
a) Tìm điều kiện xác định rồi rút gọn biểu thức A.
b) Tìm giá trị của biểu thức A khi x ≥ 0 và là nghiệm của phương trình 2x +1 =1.
Bài 2 (4 điểm). Trong túi đựng 48 viên bi có cùng kích thước và khối lượng với hai màu
đỏ và xanh. Lấy ngẫu nhiên một viên bi từ túi. Biết rằng xác suất lấy được viên bi màu đỏ
bằng 92% xác suất lấy được viên bi màu xanh. Tính số viên bi màu đỏ và số viên bi màu xanh có trong túi.
Bài 3 (2 điểm). Cách đây hai năm chị An có gửi 250.000.000 đồng vào ngân hàng A
theo kỳ hạn 1 năm, lãi suất kép (tiền lãi được nhập vào vốn ban đầu để tính lãi tiếp).
Năm nay chị An nhận được số tiền là 289.444 .000 đồng. Hỏi lãi suất ngân hàng là bao
nhiêu phần trăm, biết lãi suất không thay đổi?
Bài 4 (2 điểm) Tính giá trị biểu thức:
𝑃𝑃 = 𝑥𝑥+2𝑥𝑥𝑥𝑥+1 + 𝑥𝑥+2𝑥𝑥𝑥𝑥+1 + 𝑥𝑥+2𝑥𝑥𝑥𝑥+1 biết 𝑥𝑥𝑥𝑥𝑥𝑥 = 1
𝑥𝑥+𝑥𝑥𝑥𝑥+𝑥𝑥𝑥𝑥+1
𝑥𝑥+𝑥𝑥𝑥𝑥+𝑥𝑥𝑥𝑥+1
𝑥𝑥+𝑥𝑥𝑥𝑥+𝑥𝑥𝑥𝑥+1
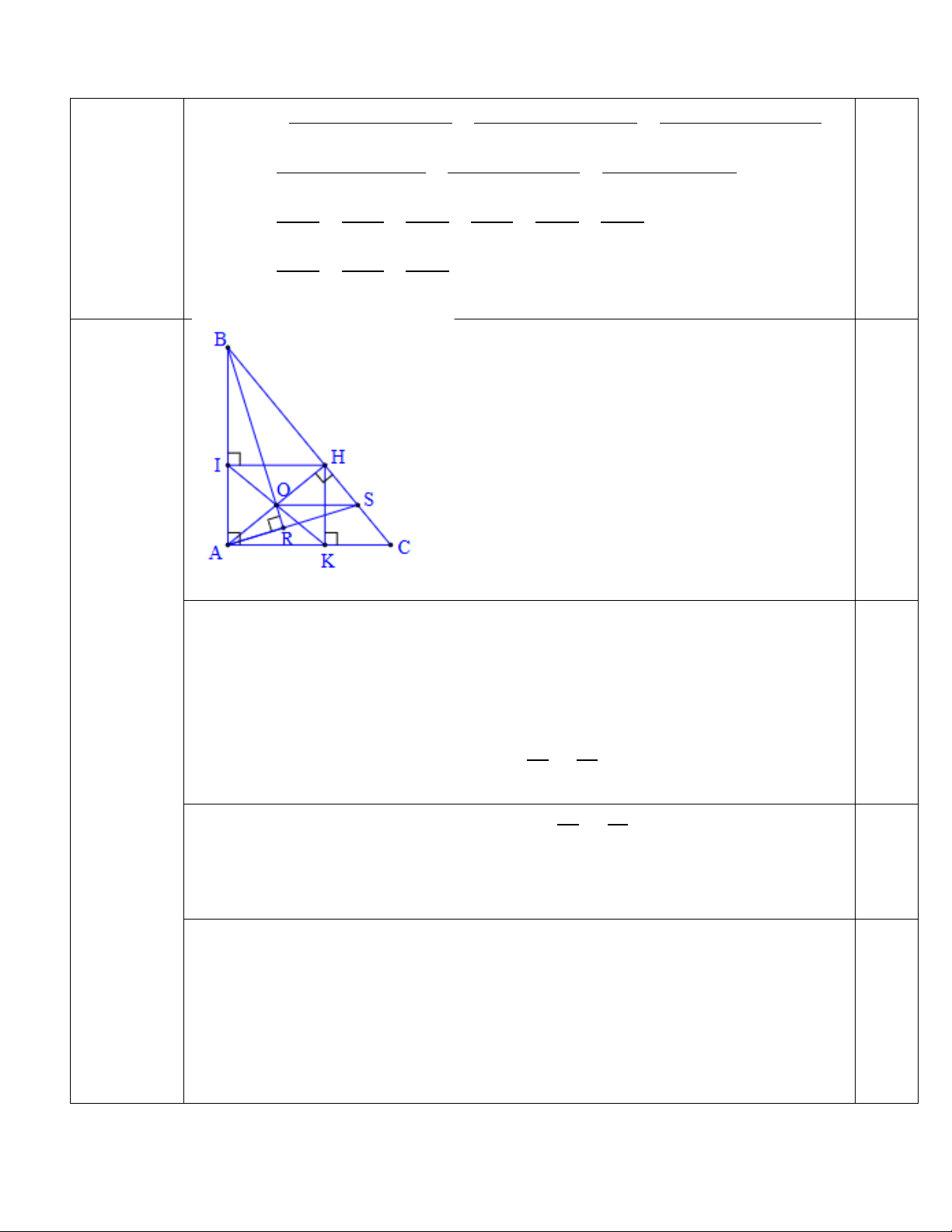
Bài 5 (5 điểm) Cho tam giác ABC vuông tai A, đường cao AH, từ H kẻ HI vuông góc
với AB tại I, HK vuông góc với AC tại K.
a) Chứng minh tam giác AKI đồng dạng với tam giác ABC suy ra AI. AB = AK. AC.
b) Chứng minh góc ABK = góc ACI.
c) Gọi O là trung điểm của đoạn IK. Từ A vẽ đường thẳng vuông góc với đường thẳng
BO tại R. Đường thẳng AR cắt cạnh BC tại S. Chứng minh S là trung điềm của đoạn thẳng HC.
Bài 6 (2 điểm) Một robot chuyển động từ A đến B theo cách sau: Sau khi đi được 4m
dừng lại 1 giây, rồi đi tiếp 8m dừng lại 2 giây, đi tiếp 12 m dừng lại 3 giây, … Cứ như vậy,
thời gian robot đi từ A đến B kể cả dừng là 155 giây. Tính khoảng cách từ A đến B. Biết
rằng khi đi robot luôn có tốc độ là 2m/s.
----------------------------------------Hết--------------------------------------------
(Cán bộ coi thi không giải thích gì thêm).
Họ và tên thí sinh ....................................................................Số báo danh............... 1 UBND HUYỆN THẠCH THẤT
HƯỚNG DẪN CHẤM THI OLYMPIC CÁC MÔN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
VĂN HOÁ LỚP 8THCS NĂM HỌC 2024-2025 ================ MÔN TOÁN
(Hướng dẫn chấm gồm 03 trang) Câu Đáp án Điểm
Điều kiện xác định của biểu thức A là: xy ≠ 1; xy ≠ 1 − (*) 0,5 Bài 1 (5đ) 2 2 2 2  x + y x − y  
x + y + 2x y  A = +   : 1 + 2 2 1− xy 1+ xy   1− x y   2 2
(x + y).(1+ xy) + (x − y).(1− xy) 1 = . − x y 2 2 2 2 2 1− (xy)
1+ x + y + x y 2,5 2 2x(1+ y ) 2x = = 2 2 2
(1+ x ).(1+ y ) 1+ x
b) x ≥ 0 nên 2x +1 > 0 suy ra 2x +1 = 2x +1. 2
Do đó 2x +1 =1 có dạng 2x + 1 = 1 hay x = 0 (thỏa mãn điều kiện).
Với x = 0 thì giá trị của biểu thức A là 0. Bài 2 (4đ)
Gọi số bi đỏ trong túi là x viên (48> x > 0), suy ra số bi xanh trong túi là (48 – x) viên. 0,5
Xác suất lấy được viên bi màu đỏ và viên bi màu xanh lần lượt là: x 48 − x ; . 1 48 48 Ta có − x 48 = 0,92. x 1 48 48 (1). Giải (1) có x = 23. 1
Vậy số viên bi màu đỏ và viên bi màu xanh có trong túi lần lượt là 23 viên và 25 viên 0,5
Bài 3 (2,0đ) Đặt 𝑥𝑥 là lãi suất ngân hàng A cho kỳ hạn 1 năm. (𝑥𝑥 > 0) 0,5
Số tiền nhận được sau năm đầu tiên: 250(1 + 𝑥𝑥) triệu đồng.
Sau khi kết thúc năm thứ 2, số tiền chị An nhận được là:
250(1 + 𝑥𝑥)(1 + 𝑥𝑥) = 250(1 + 𝑥𝑥)2. 0,5
Ta có: 250(1 + 𝑥𝑥)2 = 289,444 (𝑥𝑥 + 1)2 = 1,57776 0,5 𝑥𝑥 + 1 = 1,076 𝑥𝑥 = 0,076 0,25
Vậy lãi suất ngân hàng là 7,6%/năm. 0,25 2
𝑦𝑦𝑦𝑦(𝑥𝑥 + 2𝑥𝑥𝑦𝑦 + 1)
𝑥𝑥𝑦𝑦(𝑦𝑦 + 2𝑦𝑦𝑦𝑦 + 1)
𝑥𝑥𝑦𝑦(𝑦𝑦 + 2𝑦𝑦𝑥𝑥 + 1) Bài 4 (2đ)
𝑃𝑃 = 𝑦𝑦𝑦𝑦(𝑥𝑥 + 𝑥𝑥𝑦𝑦 + 𝑥𝑥𝑦𝑦 + 1) + 𝑥𝑥𝑦𝑦(𝑦𝑦 + 𝑦𝑦𝑦𝑦 + 𝑥𝑥𝑦𝑦 + 1) + 𝑥𝑥𝑦𝑦(𝑦𝑦 + 𝑦𝑦𝑥𝑥 + 𝑦𝑦𝑦𝑦 + 1)
(1 + 𝑦𝑦) + 𝑦𝑦(1 + 𝑦𝑦) 1 + 𝑦𝑦 + 𝑦𝑦(1 + 𝑥𝑥) 1 + 𝑥𝑥 + 𝑥𝑥(1 + 𝑦𝑦) 1,0
= (1 + 𝑦𝑦)(1 + 𝑦𝑦) + (1 + 𝑦𝑦)(1 + 𝑥𝑥) + (1 + 𝑥𝑥)(1 + 𝑦𝑦) 𝑦𝑦 1 1 𝑦𝑦 1 𝑥𝑥 =
1 + 𝑦𝑦 + 1 + 𝑦𝑦 + 1 + 𝑥𝑥 + 1 + 𝑦𝑦 + 1 + 𝑦𝑦 + 1 + 𝑥𝑥
𝑦𝑦 + 1 1 + 𝑦𝑦 1 + 𝑥𝑥 1,0
= 𝑦𝑦 + 1 + 1 + 𝑦𝑦 + 𝑥𝑥 + 1 = 3 Bài 5 (5đ) 1,25
a) Tứ giác AKHI có A� = K� = Î = 90∘ nên AKHI là hình chữ nhật, ta có: AKI � = AH �I. 1,5 Lại có AH �I = ABC � (cùng phụ với góc BH �I ). Suy ra AKI � = ABC �
Hai tam giác AKI và ABC có A� chung, AKI � = ABC � nên 0,25
△ AKI đồng dạng △ ABC (gg) ⇒ AK = AI ⇒ AI. AB = AK. AC. AB AC
b) Theo trên, △ AKI đồng dạng ΔABC ⇒ AK = AI. AB AC
Và hai tam giác AKB và AIC có A� chung 1,0
nên △ AKB đồng dạng △ AIC (cgc). Từ đó ta có ABK � = ACI � .
c) Xét tam giác 𝐴𝐴𝐴𝐴𝐴𝐴 có 𝐴𝐴𝐴𝐴 và 𝐴𝐴𝐵𝐵 là đường cao nên 𝑂𝑂 là trực tâm tam
giác 𝐴𝐴𝐴𝐴𝐴𝐴, do đó 𝐴𝐴𝑂𝑂 ⊥ AB, suy ra SO//AC.
Mặt khác, theo trên thì tứ giác AKHI là hình chữ nhật nên O là trung điểm 1,0
AH. Như vậy trong tam giác AHC, SO là đường trung bình. Từ đó ta có S là trung điểm của HC. 3 Bài 6 (2đ)
Gọi số lần đi là x (lần) (x ∈*), Số lần dừng là x-1 (lần) x Thời gian đi là: 4 8 12 4 + + +...+
= 2 + 4 + 6 +...+ 2x = x(x +1) (giây) 2 2 2 2 1,0 Thời gian dừng là x(x −1)
1+ 2 + 3+...+ (x −1) = (giây) 2 Theo bài ra ta có x(x −1) x(x +1) + =155 2
2x2 +2x + x2- x = 310
3x2 + x - 310 =0.
(x- 10)(3x+11) = 0 1,0 x=10 (thỏa mãn)
Thời gian đi là 10.(10+1) = 110 giây
Khoảng cách từ A đến B là 110.2= 220 (m). Hết
( Học sinh có cách giải khác đúng cho điểm tương đương; điểm toàn bài làm tròn đến 0,25điểm)
Xem thêm: ĐỀ THI HSG TOÁN 8
https://thcs.toanmath.com/de-thi-hsg-toan-8
Document Outline

• Đề thi Olympic Toán 8(2024-2025)
• Hướng dẫn chấm Toán Olimpic Toán 8
• HSG 8