Đề Thi Thử HSG Toán 8 THCS Nga Yên 2025-2026 Có Đáp Án
Để biểu diễn sự thay đổi của một đại lượng theo thời gian, ta dùngloại biểu đồ nào trong các loại biểu đồ sau. Bạn Bình hỏi: Nhà bạn đang dùng bao nhiêu chiếc xe đạp? Bình đã hỏi 4 bạn và ghi lại câu trả lời: 1; 100; 2; 3. Số liệu không hợp lí trong dãy số liệu trên. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Chủ đề: Đề thi Toán 8 460 tài liệu
Môn: Toán 8 1.9 K tài liệu
Tác giả:
Preview text:
ĐỀ 1
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2025-2026 MÔN: TOÁN 8
I. TRẮC NGHIỆM. (2,0 điểm)
Chọn chữ cái in hoa đứng trước câu trả lời em cho là đúng trong mỗi câu sau:
Câu 1: Kết quả phép chia đa thức 2 2
3x y + 3xy cho đơn thức 3xy có kết quả là: A. x + y
B. 3x + 3y C. 3x + y
D. x + 3y 1
Câu 2: Giá trị của biểu thức 2
−9x − 6x + 5 tại x = − là: 3 A. 1 B. 1 − C. 6 D. – 6 3 3
Câu 3: Trong các điểm sau, điểm nào thuộc đồ thị hàm số: y = 2x +3 ? A. (– 2; 0) B. ( 4 ; 6 ) C. (1; – 5) D. (1; 5)
Câu 4: Hình bình hành có một đường chéo là phân giác của một góc là:
A. Hình thang cân B. Hình thoi C. Hình vuông D. Hình chữ nhật
II. TỰ LUẬN. (8,0 điểm)
Bài 1: (1,5 điểm)
1) Phân tích các đa thức sau thành nhân tử: a) x2 – xy + 5x – 5y b) 2 2
x − 2xy − 25 + y
2) Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biến x:
A = (x – 5)(x + 5) – x(x + 1) + x + 12 x 2 1 3
Bài 2: (2,0 điểm) Cho biểu thức: A = − + : với x 2 2
x − 4 x − 2 x + 2 x − 2
a) Rút gọn biểu thức A b) Tính giá trị của A khi x thoả mãn: 2 x − 2x = 0
c) Tìm x nguyên lớn nhất để biểu thức A nhận giá trị nguyên.
Bài 3: (1,5 điểm) Cho hàm số: y = (m – 1)x − 1 có đồ thị là đường thẳng d.
1) Tìm điều kiện của m để hàm số trên là hàm số bậc nhất.
2) Khi m = 3, hãy vẽ đồ thị hàm số rồi tính khoảng cách từ gốc toạ độ O(0; 0) đến đường thẳng d.
Bài 4: (2,5 điểm)
1) Cho ABC vuông tại A có đường cao AH. Từ H kẻ HN ⊥ AC , HM ⊥ AB .
a) Chứng minh tứ giác AMHN là hình chữ nhật.
b) Lấy D sao cho M là trung điểm của DH, lấy E sao cho N là trung điểm của EH.
Chứng minh tứ giác AMNE là hình bình hành. c) Chứng minh: 2 2 2 BC = BD + CE + 2BH.HC .
2) Một khối Rubik có dạng hình chóp tam giác đều. Biết
chiều cao bằng 5,2 cm, thể tích của khối Rubic là 45,24 cm3.
Tính diện tích đáy của khối Rubik.
Bài 5: (0,5 điểm) Cho 3 số a, b, c thỏa mãn đồng thời: a + b + c = 6 và 2 2 2 a + b + c = 12 .
Tính giá trị của biểu thức: = ( − )2023 + ( − )2023 + ( − )2023 P a 3 b 3 c 3 .
Họ và tên học sinh:...................................................Số báo danh:.......... Trang 1 HƯỚNG DẪN CHẤM
HỌC KỲ I NĂM HỌC 2025 – 2026 MÔN TOÁN 8
I/ TRẮC NGHIỆM. (2,0 điểm) Mỗi câu đúng được 0,5 điểm Câu 1 2 3 4 Đáp án A C D B
II/ TỰ LUẬN. (8,0 điểm)
Bài 1: (1,5 điểm)
1. Phân tích các đa thức sau thành nhân tử. a) x2 – xy + 5x – 5y b) 2 2 x − 2xy − 25 + y
2. Chứng minh giá trị biểu thức sau không phụ thuộc vào giá trị của biến x.
A = ( x – 5)( x + 5) – x( x+ 1) + x + 12 Bài Nội dung Điểm
1.a) x2 – xy + 5x – 5y
= (x2 – xy) + (5x – 5y) = x(x – y) + 5(x - y) 0,25 = (x – y)(x + 5) 0,25 1.b) 2 2
x − 2xy − 25 + y 2 2 2 2
= (x − 2xy + y ) − 25 = (x − y) − 5 0,25
= (x − y − 5)(x − y + 5) 0,25 Bài 1
2. Ta có: A = (x + 5 )(x – 5) – x(x + 1) + x + 12 (1,5 đ) 2 2 2 2
= x − 25 − x − x + x +12 = (x − x ) + (x − x) + ( 2 − 5 +12) 0,25 = 0 + 0 + ( 1 − 3) = 1 − 3
Vậy giá trị của biểu thức A không phụ thuộc vào giá trị của biến x. 0,25 x 2 1 3
Bài 2: (2,0 điểm) Cho biểu thức: A = − + : với x 2 2
x − 4 x − 2 x + 2 x − 2
b) Rút gọn biểu thức A b) Tính giá trị của A khi x thoả mãn: 2 x − 2x = 0
c) Tìm x nguyên lớn nhất để biểu thức A nhận giá trị nguyên. Bài Đáp án Điểm x 2 1 3 A = − + : ĐKXĐ: x 2 2 x − 4 x − 2 x + 2 x − 2 Bài 2: x 2 1 3 (2,0 đ) A = − + : 0,25đ − + − + − (x 2)(x 2) x 2 x 2 x 2 x 2(x + 2) 1(x − 2) x − 2 A = − + .
(x 2)(x 2) (x 2)(x 2) (x 2)(x 2) − + − + − + 3
x − 2x − 4 + x − 2 x − 2 A = . 0,25đ (x − 2)(x + 2) 3 6 − x − 2 A = . (x − 2)(x + 2) 3 0,25đ Trang 2 2 − A = x + 2 . 0,25đ 2 − Vậy A = x + với x 2 2
b) Tính giá trị của A khi x thoản mãn: 2 x − 2x = 0 Ta có: 2 x − 2x = 0
x(x − 2) = 0 x =
x = Tm x 0 0 ( 2) x 2 0 − =
x = 2 (Ktm x 2 ) 0,25 2 −
Với x = 0 thay vào biểu thức A ta được: A = = 1 − 0 + 2
Vậy A = - 1 khi x thỏa mãn: 2 x − 2x = 0 0,25
( Không đối chiếu với ĐKX Đ trừ 0,25 điểm )
c) Tìm x nguyên lớn nhất để biểu thức A nhận giá trị nguyên. 2 − Ta có: A = x x + với 2 2
Do x nguyên nên x + 2 nguyên.
Khi đó biểu thức A nhận giá trị nguyên khi 2 − nhận giá trị nguyên x + 2 0,25
2 (x + 2) x + 2 là ước của 2 x + 2 1 ; 2
Vì x là số nguyên lớn nhất nên x + 2 nhận ước nguyên lớn nhất
x + 2 = 2 x = 2 − 2 = 0 (T / m)
Vậy x = 0 là giá trị cần tìm. 0,25
(Không đối chiếu với ĐKX Đ trừ 0,25 điểm )
Bài 3: (1,5 điểm) Cho hàm số: y = (m – 1)x − 1 có đồ thị là đường thẳng d.
1) Tìm điều kiện của m để hàm số trên là hàm số bậc nhất.
2) Khi m = 3, hãy vẽ đồ thị hàm số rồi tính khoảng cách từ gốc toạ độ O(0; 0) đến đường thẳng d. Bài Nội dung Điểm
1/a) Để hàm số y = (m – 1)x − 1 là hàm số bậc nhất thì m −1 0 m 1 0,25
Vậy với m 1 thì hàm số trên là hàm số bậc nhất.
c) Vẽ đồ thị hàm số:
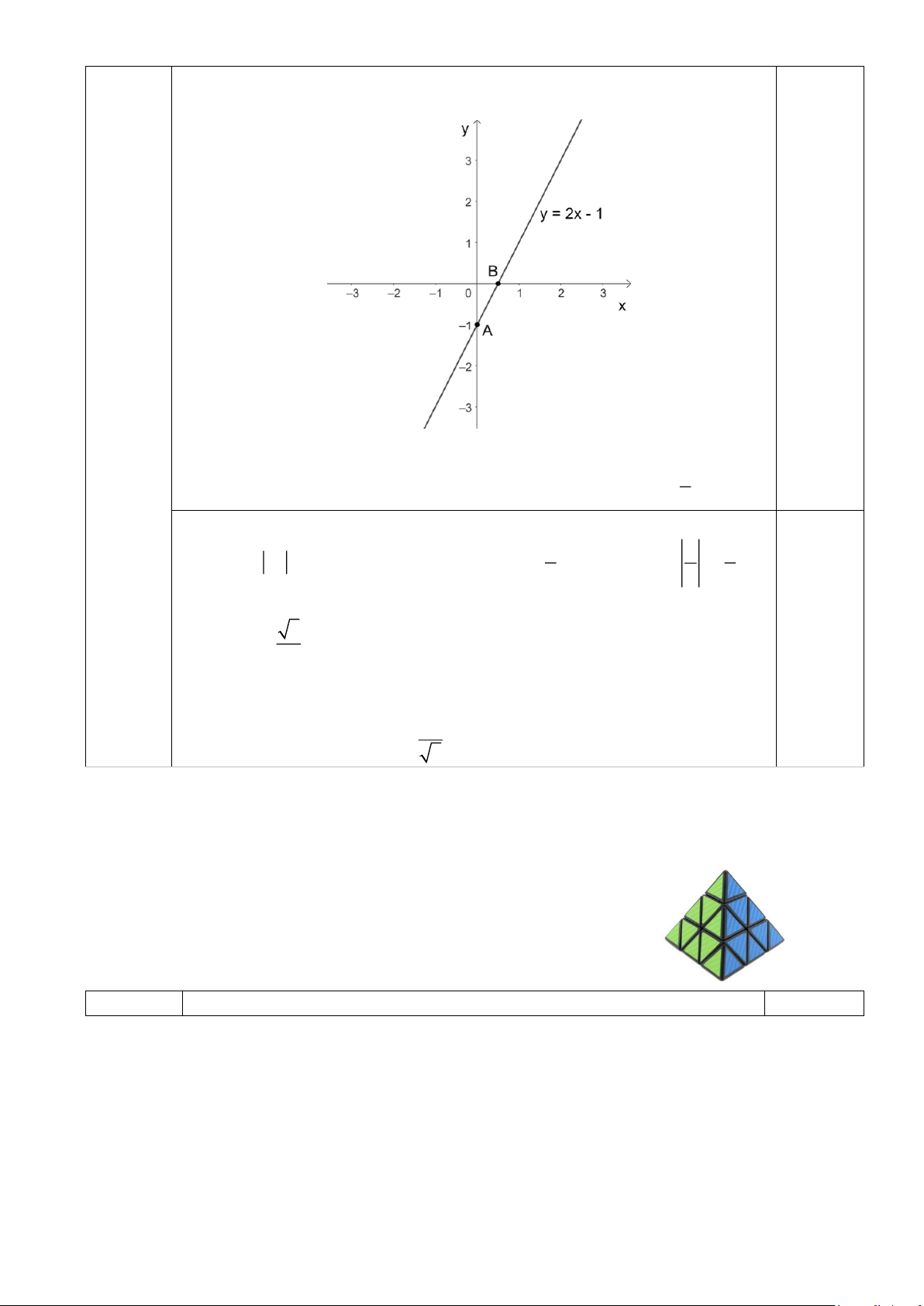
+Với m = 3 hàm số trở thành: y = 2x − 1 Bài 3 0,25
(1,5 đ) + Cho x = 0 = y = 1 − = A(0;− ) 1 Oy 1 1 0,25 Cho y = 0 = x = B ;0 Ox 2 2 Trang 3 +Vẽ đồ thị hàm số. 0,25 Vậy với m = 3:
Đồ thị hs là đường thẳng đi qua 2 điểm A (0; −1) và B( 1 ; 0) 2
b) Khi m = 3, đồ thị hàm số y = 2x − 1 cắt trục Oy tại điểm A(0; -1) => OA = 1
− = 1 và cắt trục Ox tại điểm B( 1 ; 0) => OB 1 = = 1 2 2 2
+ Do tam giác OAB vuông tại O nên áp dụng định lý pytago tính được AB = 5 0,25 2
+Vẽ OH ⊥ (d) (H thuộc d) => khoảng cách từ O(0;0) đến d bằng OH,
Ta có: OA. OB = OH.AB (= 2SOAB) (1)
Từ đó tính được OH = 1 5 0,25
Bài 4: (2,5 điểm)
1) Cho ABC vuông tại A có đường cao AH. Từ H kẻ HN ⊥ AC , HM ⊥ AB .
a) Chứng minh tứ giác AMHN là hình chữ nhật.
b) Lấy D sao cho M là trung điểm của DH, lấy E sao cho N là trung điểm của EH.
Chứng minh tứ giác AMNE là hình bình hành. c) Chứng minh: 2 2 2 BC = BD + CE + 2BH.HC .
2) Một khối Rubik có dạng hình chóp tam giác đều. Biết
chiều cao bằng 5,2 cm, thể tích của khối Rubic là 45,24 cm3.
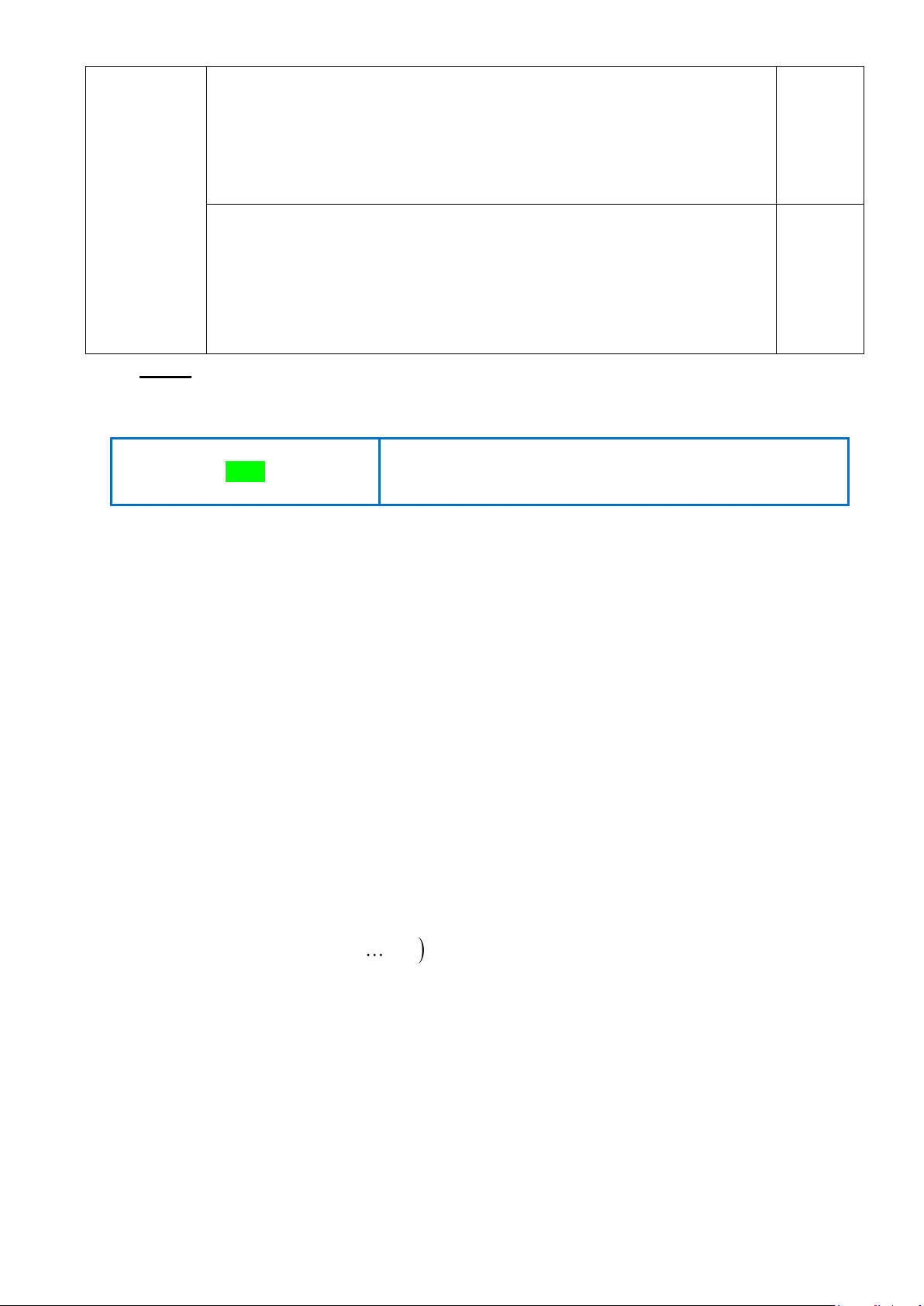
Tính diện tích đáy của khối Rubik. Bài 4 Nội dung Điểm Trang 4 1) (2,0 đ) Xét tứ giác AMNH có:
MAN = 90 ( ABC vuông tại A )
AMH = 90 (HM ⊥ AB) 0,5
ANH = 90 (HN ⊥ AC)
Vậy tứ giác AMHN là hình chữ nhật (vì có 3 góc vuông) 0,5
b) Tứ giác: AMNE có:
AM = HN (cạnh đối hình chữ nhật AMHN)
EN = HN (N là trung điểm của EH) AM = NE 0,25
Lại có AM //NE ( AM // HN và H, N, E thẳng hàng)
Vậy tứ giác AMNE là hình bình hành (Tứ giác có 2 cạnh đối
song song và bằng nhau là hình bình hành) 0,25
c) Ta có AB ⊥ DH tại M (gt)
M là trung điểm của DH (gt)
AB là đường trung trực của DH
BD = BH ( 1 )
Tương tự có CE = HC ( 2 ) 0,25
+ Do BC = BH + HC 2 2 2
BC = BH + HC + 2 BH. HC ( 3 ) Từ (1), (2) và (3) 2 2 2
BC = BD + EC + 2 BH. HC (đpcm) 0,25
2) 0,5đ 2) Diện tích đáy của khối Rubik đó là : Ta có: 1 2
V = S.h S = 3V : h = 3.45, 24 : 5, 2 = 26,1cm 0,25 3
Vậy diện tích đáy của khối Rubik là 2 26,1cm 0,25
Bài 5: (0,5 điểm) Cho a, b, c thỏa mãn đồng thời a + b + c = 6 và 2 2 2 a + b + c = 12 .
Tính giá trị của biểu thức : = ( − )2023 + ( − )2023 + ( − )2023 P a 3 b 3 c 3 . Bài Nội dung Điểm Ta có : 2 2 2 2 2 2
a + b + c = 12 a + b + c −12 = 0 2 2 2 2 2 2
a + b + c − 24 +12 = 0 a + b + c − 4(a + b + c) +12 = 0 2 2 2 − + + − + + − + = a 4a 4 b 4b 4 c 4c 4 0 Bài 5 Trang 5 (0,5 đ)
(a − )2 + (b − )2 + (c − )2 2 2 2 = 0 0,25 a − 2 = 0
b − 2 = 0 a = b = c = 2 c − 2 = 0
Thay a = b = c = 2 vào P, ta được
P = (2 − 3)2023 + (2 − 3)2023 + (2 − 3)2023 = (− )2023 1 + (− )2023 1 + (− )2023 1 = −3 0,25
Vậy P = - 3 khi a, b, c thỏa mãn đề bài.
Chú ý: Học sinh làm cách khác đúng vẫn được điểm tối đa.
Điểm bài khảo sát là tổng điểm các bài thành phần, làm tròn đến 0,5.
ĐỀ ÔN TẬP CUỐI HỌC KỲ I ĐỀ 2 NĂM HỌC 2025-2026 MÔN: TOÁN 8
Phần 1. Trắc nghiệm khách quan (3,0 điểm).
Mỗi câu hỏi sau đây đều có bốn lựa chọn, trong đó chỉ có một câu trả lời đúng. Hãy
khoanh tròn vào chữ cái trước câu trả lời đúng.
Câu 1. Kết quả của phép nhân 2x(3x −1) bằng: A. 2 6x −1 B. 6x −1 C. 2 6x − 2x D. 2 3x − 2x
Câu 2. Kết quả của phép chia 2
(20x y −10xy) : 5xy là : A. 4xy −10xy B. 4x − 2 C. 4x − 2y D. 4xy − 2
Câu 3. Đẳng thức nào sau đây là hằng đẳng thức ?
A. a + 2b = 2a + b B. 3a −1 = 2a + 3
C. 2(a − 2) = 4a D. a(a − ) 2
2 = a − 2a
Câu 4. Khai triển (x y)2 − ta được: A. (x − y)2 2 2
= x − 2xy + y B. (x − y)2 2 2
= x + 2xy + y C. (x − y)2 2 2
= x − 2xy − y D. (x − y)2 2 2
= x − 4xy + 4y Câu 5. Cho 3 x − = (x − )( 2 125 5 x +
+ 25) . Biểu thức thích hợp điền vào chỗ trống là: A. −5x B. 5x C. 10x D. −10x
Câu 6. Phân tích đa thức 4x − 8y thành nhân tử ta được : A. 4(x + 2y) B. 4(x − 4y) C. 4(x − 2y) D. 4(x −8y)
Câu 7. Biết x(x − 2) = 0 , thì x có giá trị là : A. x = 2 B. x = 0; x = 2
C. x = 0; x = −2 D. x = 0
Câu 8. Để biểu diễn sự thay đổi của một đại lượng theo thời gian, ta dùngloại biểu đồ nào
trong các loại biểu đồ sau :
A.Biểu đồ đoạn thẳng B. Biểu đồ tranh C. Biểu đồ cột
D. Biểu đồ hình quạt tròn Trang 6
Câu 9. Bạn Bình hỏi: Nhà bạn đang dùng bao nhiêu chiếc xe đạp? Bình đã hỏi 4 bạn và ghi lại câu trả
lời: 1; 100; 2; 3. Số liệu không hợp lí trong dãy số liệu trên là: A. 1 B. 3 C. 2 D. 100
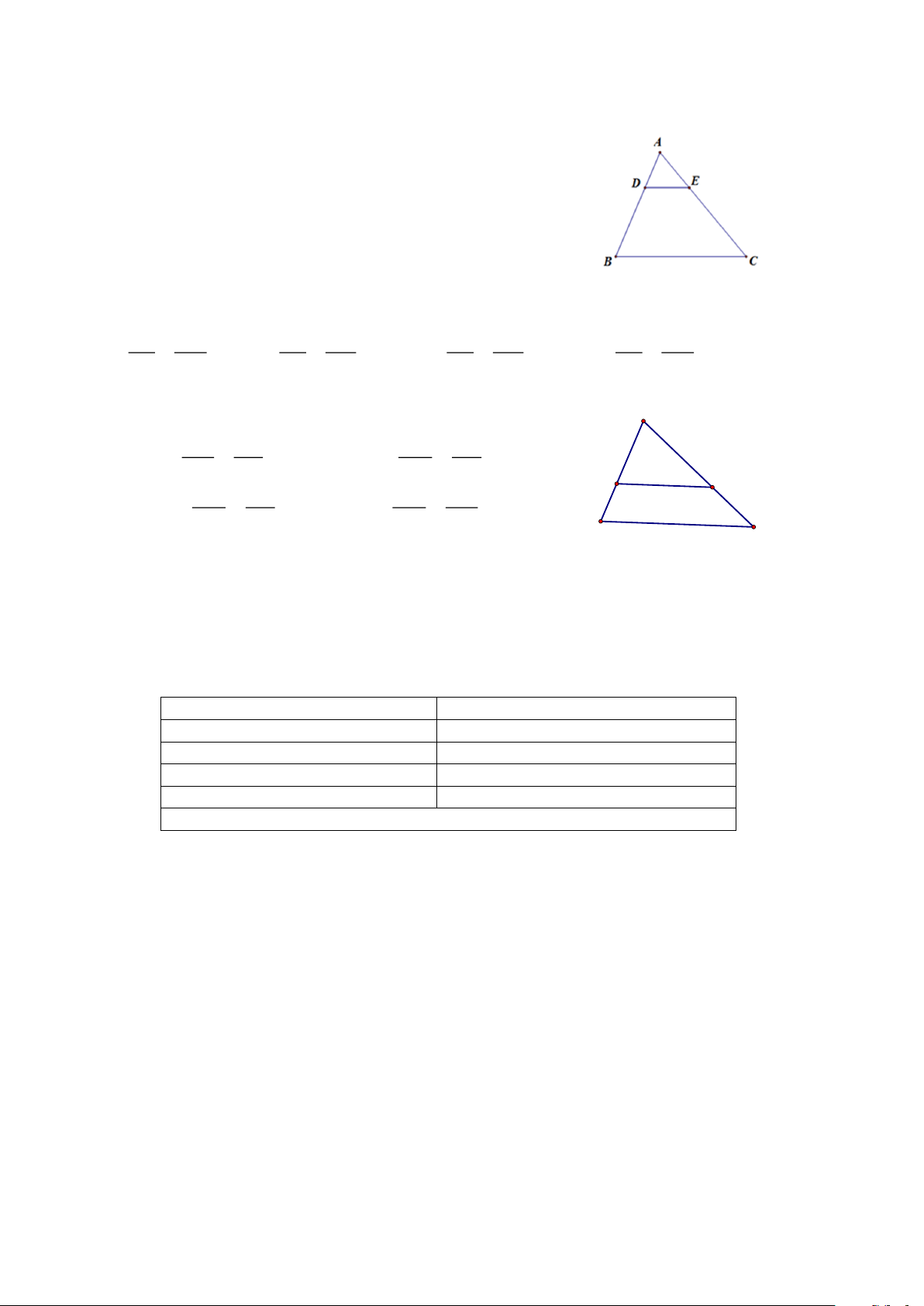
Câu 10. Cho hình vẽ, trong đó DE // BC, AD = 3
DB = 6, AE = 4. Độ dài EC bằng: A. 4 B. 1 C. 6 D. 8
Câu 11. Nếu tam giác ABC có BM là tia phân giác của
ABC ( M AC) thì: A. AB = AM B. AB = MC C. AB = MC D. AB = AM BC MC BC MB BC AC BC AC
Câu 12. Cho ABC , M AB , N AC (hình vẽ ). Từ điều kiện nào sau đây có thể suy ra MN // BC . A BM AN AM AN A. = B. = AB AC MB AC AM AN AM AN M N C. = D. = AB AC MN MN
Phần 2. Tự luận ( 7,0 điểm) B C
Câu 13. (1,0 điểm). Cho biểu thức P = ( x + )( 2 x − x + )−( 3 4 4 16
64 − x ) + 2021. Thu gọn và tính giá trị
biểu thức P khi x = 1 .
Câu 14. (1,0 điểm). Phân tích các đa thức sau thành nhân tử.
a) x ( x − y) + (9x − 9y) b) 2 2
x − 6x − y + 9
Câu 15. (1,5 điểm). Biểu đồ sau biểu diễn số lượng các bạn học sinh lớp 8A yêu thích một số môn học. Môn học Số lượng Toán @ @ @ @ @ Ngữ văn @ @ Tiếng Anh @ @@ Giáo dục thể chất @ @
Mỗi @ ứng với 3 học sinh
Lập bảng thống kê và vẽ biểu đồ cột biểu diễn dữ liệu trên ?
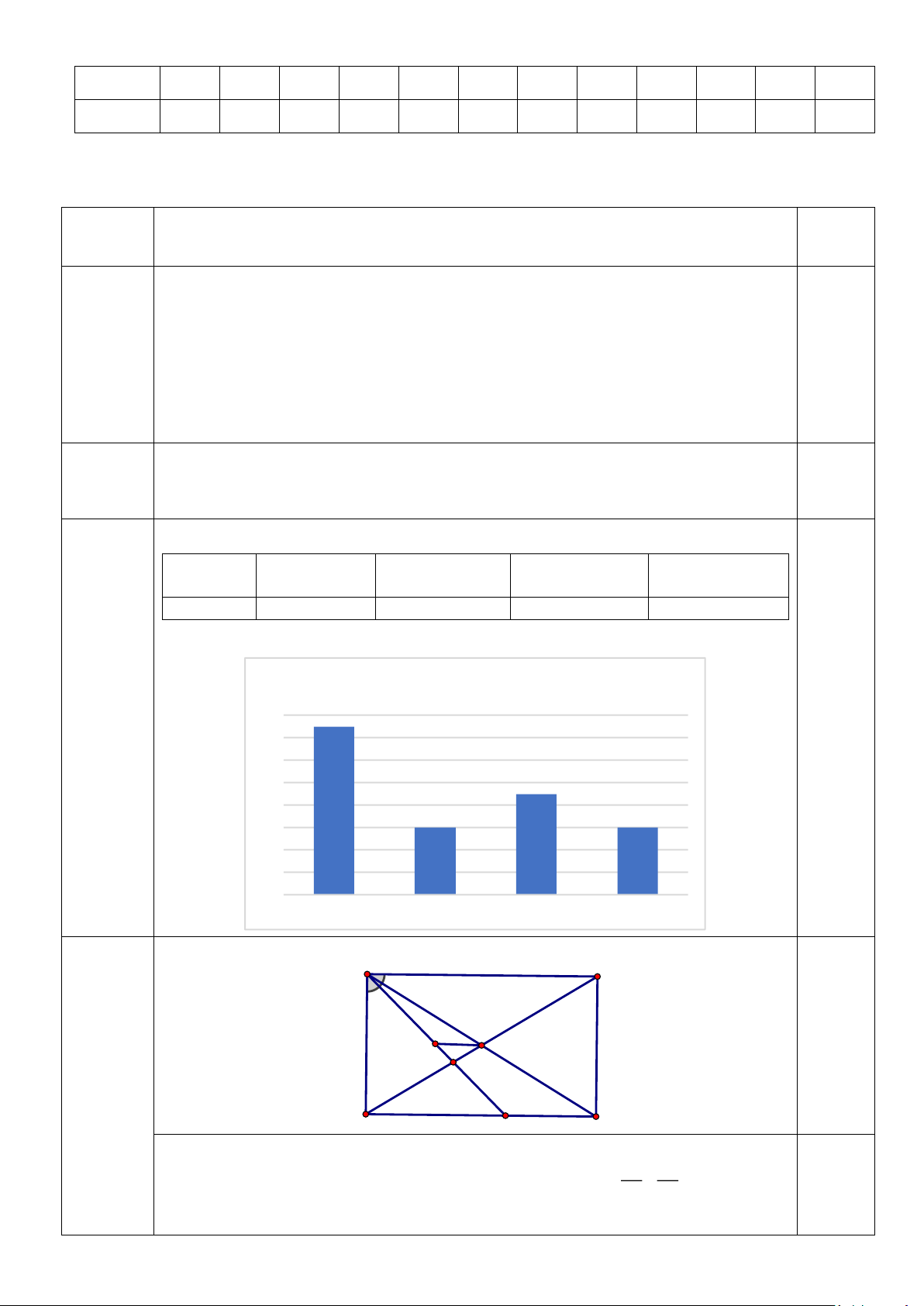
Câu 16. (2,5 điểm). Cho hình chữ nhật ABCD, biết AD = 6cm, AB = 8cm, BD = 10 cm. Tia phân gác của D
BA cắt BD, CD lần lượt tại P, Q. Gọi O là giao điểm của AC và BD, F là trung điểm của AQ.
a) Tính độ dài các đoạn thẳng DP, BP.
b) Chứng minh OF vuông góc với AD. c) Chứng minh O . B PQ = P . D FA
Câu 17. (1,0 điểm). Tìm x , biết ( x )3 + ( x)3 + ( x)3 2 - 5 2- 3- = 0
HƯỚNG DẪN CHẤM KIỂM TRA CHẤT LƯỢNG HỌC KỲ I NĂM HỌC: 2024-2025 MÔN: TOÁN 8.
Phần 1. Trắc nghiệm khách quan (3,0 điểm). Mỗi ý đúng cho 0,25 điểm. Trang 7 Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C B D A B C B A D D A C
Phần 2. Tự luận (7,0 điểm). Câu Hướng dẫn chấm Điểm Ta có: P = ( x + 4)( 2
x − 4x +16) − ( 3 64 − x ) + 2021 Câu 13 (1,0 đ) = ( x + 4) 2 2
x − 4x + 4 − ( 3 64 − x ) 0,25 + 2021 0,25 3 3 3
= x + 4 − 64 + x + 2021 0,25 3 = 2x + 2021 0,25
Khi x = 1 , bểu thức P có giá trị là: 3 P = 2.1 + 2021= 2023 Câu 14
a) x ( x − y) + (9x − 9y) = x ( x − y) + 9( x − y) = ( x − y)( x + 9) 0,5 (1,0 đ) 2 0,5 b) 2 2 2 2
x − x − y + = x − x + − y = (x − ) 2 6 9 ( 6 9)
3 − y = (x −3+ y)(x −3− y) Bảng thống kê. Môn học Toán Ngữ văn Tiếng Anh Giáo dục 0,5 thể chất Số lượng 15 6 9 6
Biểu đồ. Vẽ đúng, đẹp. Câu 15
Môn học yêu thích của học sinh lớp 8A (1,5đ) 16 14 12 1 10 8 6 4 2 0 Toán Ngữ Văn Tiếng Anh GD TC Vẽ hình đúng A B Câu 16 0,25 F O (2,5 đ) P C D
a) Gọi độ dài đoạn DP = x, thì BP =10 – x. Q DP D A
Trong tam giác ABD có AP là phân giác của D BA nên ta có: = 0,25 BP AB 0,25 Trang 8 x 6 3 = = 4x = 3(10− ) x 10− x 8 4 30 30 40 7x = 30 x = 10− x = 10− = 0,25 7 7 7 30 40 Vậy DP = ; BP = 7 7
b) Chứng minh OF vuông góc với AD.
Có : O là giao điểm hai đường chéo AC và BD của hình chữ nhật ABCD nên O là trung điểm của AC
F là trung điểm của AQ (gt)
Do đó OF là đường trung bình của tam giác ACQ, suy ra OF//CQ , hay OF//CD (1) 0,25
ABCD là hình chữ nhật nên CD ⊥ D A (2). 0,25
Từ (1) và (2) suy ra OF ⊥ AD 0,25
c) Vì OF song song với CD nên OF song song với DQ và AB
Tam giác APB có OF song song AB nên OP FP OP OB =
( Định lí Ta - lét), suy ra = (1) OB A F FP A F OP PD OF song song DQ nên = (2) ( Định lí Ta - lét) 0,25 FP PQ 0,25 OB PD
Từ (1) và (2) suy ra = O . B PQ = P . D FA FA PQ 0,25
Đặt a = 2x − 5;b = 2 − ;
x c = 3− x . Nhận thấy a + b + c = 0 0,25
Với a + b + c = a+ b = −c (a+ b)3 3 0 = −c 3 3 3
a + b + c = 3
− ab(a+ b) = −3ab(−c) = 3abc (1) 0,25
Áp dụng đẳng thức (1) ta có: Câu 17
( x )3 + ( x)3 + ( x)3 2 - 5 2- 3- = 0 3(2x- )
5 (2- x)(3- x) = 0 0,25 (1,0 đ) 3(2x- )
5 (2- x)(3- x) = 0 (2x- ) 5 = 0 hoÆ c (2- x) = 0 ho ( Æ c 3- x) = 0 5 x = hoÆ c x = 2 hoÆ c x = 3. 2 5 0,25
Vậy x = ; x = 2 ; x = 3. 2
Chú ý : Đối với phần tự luận.
- Học sinh làm cách khác đúng ở mỗi bài vẫn cho điểm tối đa.
- Bài hình không vẽ hình, hoặc vẽ hình sai cơ bản thì không chấm điểm ĐỀ 3
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2024-2025 MÔN: TOÁN 8
PHẦN I. TRẮC NGHIỆM (5,0 ĐIỂM)
Câu 1: Phân tích đa thức 2
4x −1 thành nhân tử ta được kết quả là
A. (2x −1)(2x +1) B. 2 (4x −1) C. 2 (2x −1)
D. (4x −1)(4x +1)
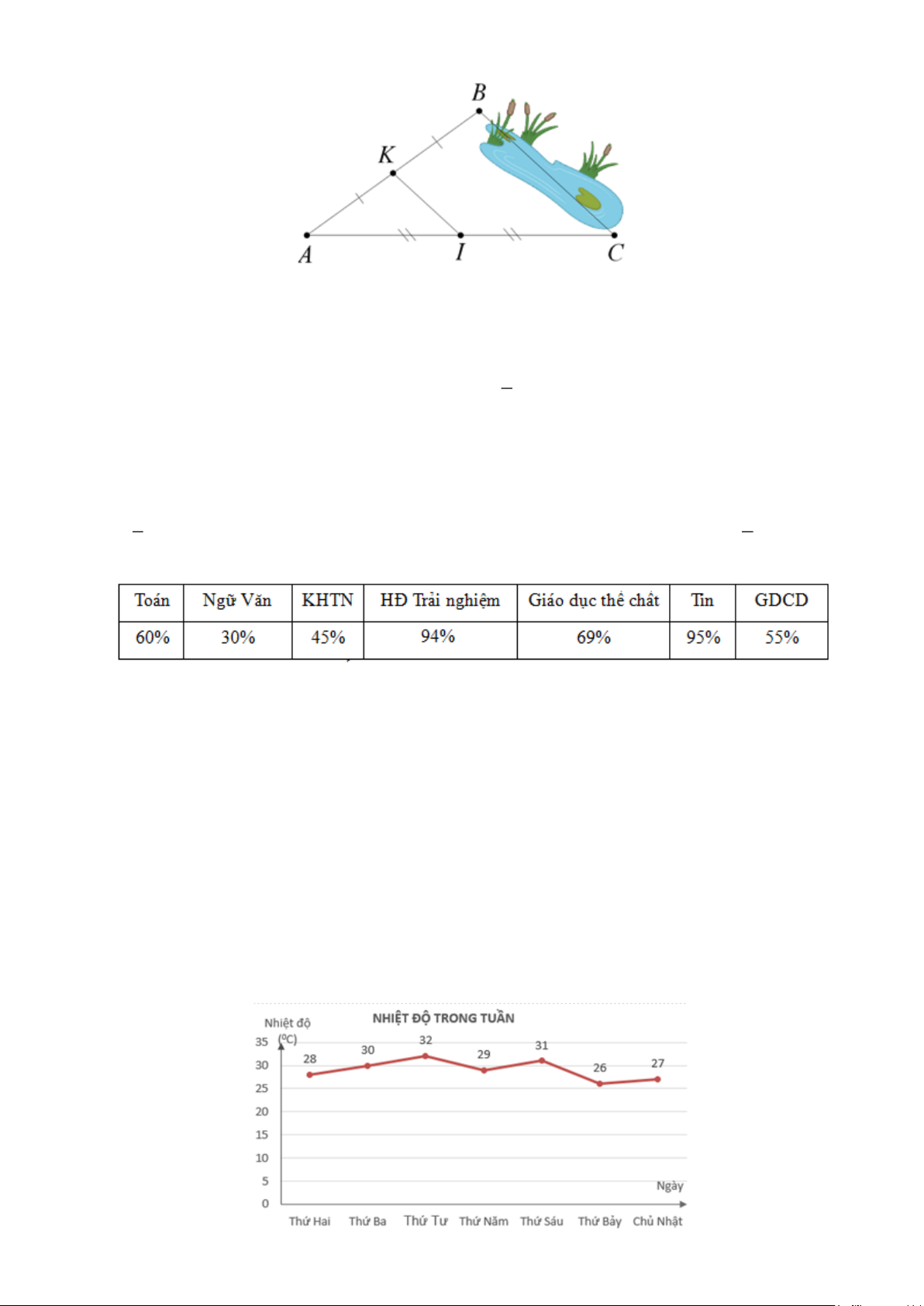
Câu 2: Giữa hai điểm B và C bị ngăn cách bởi hồ nước (như hình bên). Hãy xác định độ dài BC mà không cần
phải bơi qua hồ. Biết rằng đoạn thẳng KI dài 25m và K là trung điểm của AB , I là trung điểm của AC Trang 9 . A. 25m B. 20m C. 12,5m D. 50m
Câu 3: Phân tích đa thức mx + my + m thành nhân tử ta được kết quả là
A. m(x + y + m)
B. m(x + y + ) 1
C. m(x + y ) –1
D. m( x + y) 1
Câu 4: Kết quả sau khi thu gọn của đơn thức: ( 2 −4x y) 3 2 . x y là 2 A. 6 2 2x y . B. 5 3 2x y . C. 5 2 −2x y . D. 5 3 2 − x y .
Câu 5: Có bao nhiêu đơn thức trong các biểu thức: 2 ;
x 3; x + 5y; x − . y ? A. 3. B. 5. C. 2 D. 4.
Câu 6: Tỉ số của đoạn thẳng AB = 10dm và đoạn thẳng CD = 5m là: 1 1 A. . B. 2. C. 5. D. . 5 2
Câu 7: Thu thập số liệu về yêu thích một số môn học được kết quả như sau
Học sinh yêu thích môn học nào nhất? A. Toán.
B. Hoạt động trải nghiệm. C. Tin.
D. Giáo dục thể chất.
Câu 8: Đơn thức đồng dạng với đơn thức 2 3y là A. 2 − y B. y6. C. -3y. D. 2y3.
Câu 9: Cho hình thang cân ABCD có AB // CD và A =125 . Khi đó B bằng A. 65 . B. 90 . C. 125 . D. 55 .
Câu 10: Phân tích đa thức 3x(x − y) −5x + 5y thành nhân tử ta được kết quả là
A. (x − y)(3x + 5)
B. (3x −5)(x − y)
C. (x + y)(3x −5)
D. ( x + y)(3x + 5)
Câu 11: Lập phương một tổng của 2x và 3y là:
A. ( x − y)3 2 3 B. 3 3 2x + 3y
C. ( x + y)3 2 3
D. ( x + y)2 2 3
Câu 12: Biểu đồ sau thể hiện sự biến đổi nhiệt độ trong một tuần của một thành phố. Trang 10
Ngày nào trong tuần đó có nhiệt độ cao nhất? A. Thứ Tư. B. Thứ Ba. C. Thứ Năm. D. Thứ Sáu.
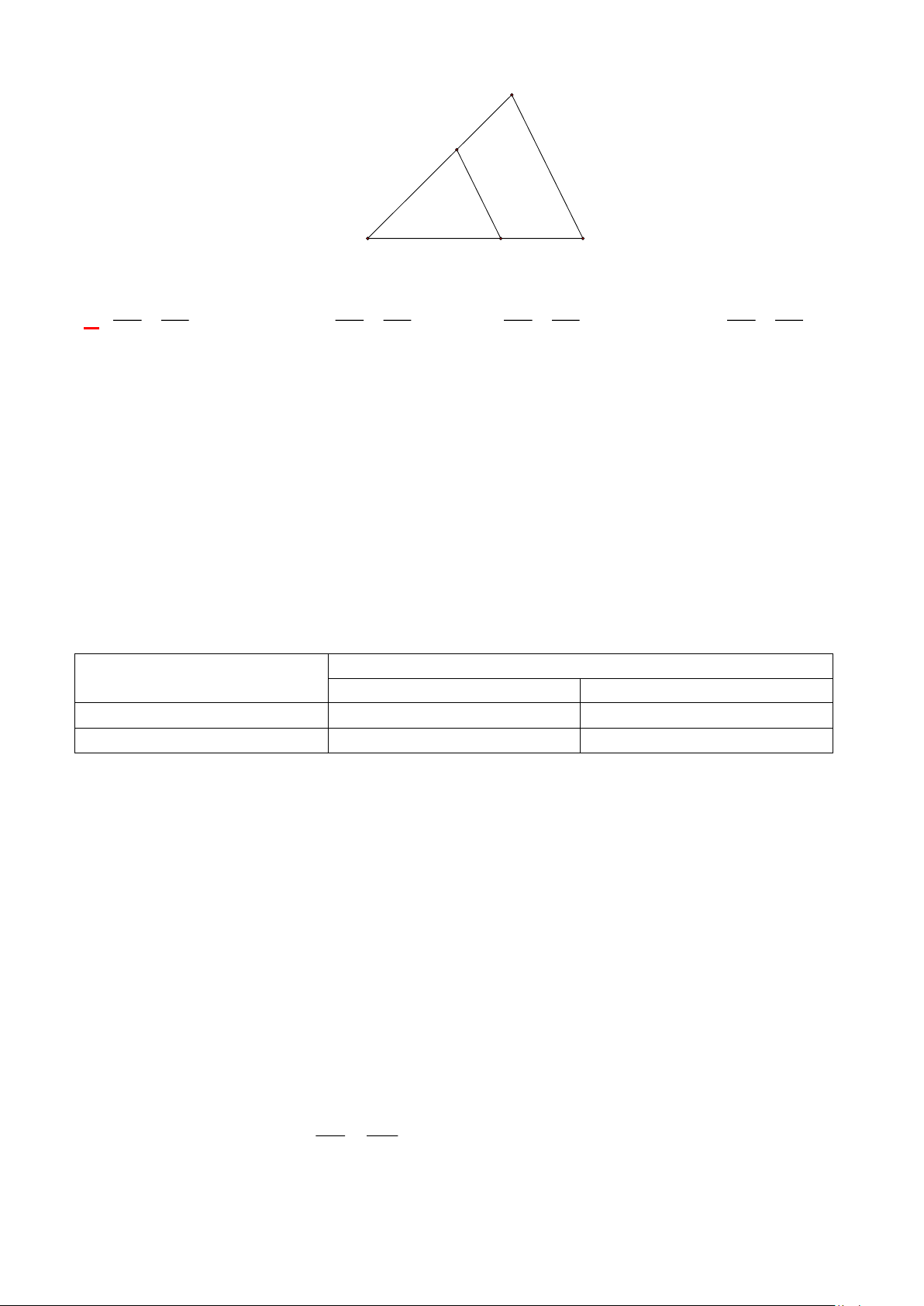
Câu 13: Cho ABC Một đường thẳng song song với BC cắt AB tại D, cắt AC tại E. Qua E kẻ đường
thẳng song song với CD cắt AB tại F, Biết AB = 25cm, AF = 9cm. Khi đó độ dài AD bằng A. 8cm B. 15cm C. 18cm D. 14cm
Câu 14: Bác Hưng muốn gửi tiết kiệm 300 triệu đồng kì hạn 12 tháng tại ngân hang An Bình với lãi
suất 8,1% / năm. Số tiền lãi bác Hưng nhận được sau 1 năm là
A. 124,58 triệu đồng
B. 24,3 triệu đồng
C. 12,15 triệu đồng.
D. 324,3 triệu đồng.
Câu 15: Cho ∆ ABC. Các đường phân giác AD, BE, CF. Khẳng định nào dưới đây đúng ?. BD AE FA BD CE FA BD AE FB A. . . = 1. B. . . = 1. C. . . = 1. D. CD CE FB CD AE FB CD CE FA BD CE FB . . = 1. CD AE FA MN
Câu 16: Cho ∆ ABC, M thuộc cạnh AB, N thuộc cạnh AC, biết MN // BC và AM = 2MB. Tỉ số BC bằng: 2 3 A. 3 B. 2 C. . D. . 3 2
Câu 17: Tập hợp các giá trị của x thoả mãn 3 x = 4x là A. 2 − ; 2 . B. 0; 2 . C. 0; 2 − D. 0; 2 − ; 2 .
Câu 18: Kết quả rút gọn biểu thức A = (a + b)3 + (a −b)3 2 − 6ab bằng A. 3 2b . B. 3 2a . C. 3 −2b . D. 3 −2a .
Câu 19: Hình thang cân là hình thang có
A. hai góc kề bằng nhau.
B. hai góc đối phụ nhau.
C. hai góc đối bằng nhau.
D. hai góc kề một đáy bằng nhau.
Câu 20: Kết quả của phép chia ( 6 4 3 x y : x y) là A. 3 3 x y B. 4 2 x y C. 2 4 x y D. 3 4 x y
Câu 21: Tính giá trị biểu thức 6 4 3 2
B = x − 2x + x + x − x khi 3 x − x = 7 A. 49 . B. 343 . C. 56 D. 70 .
Câu 22: Cho ∆ ABC cân tại A, đường cao AM. Gọi D là điểm đối xứng với A qua M. Tứ giác ABDC là hình gì?
A. Hình chữ nhật. B. Hình thang cân. C. Hình thoi. D. Hình bình hành.
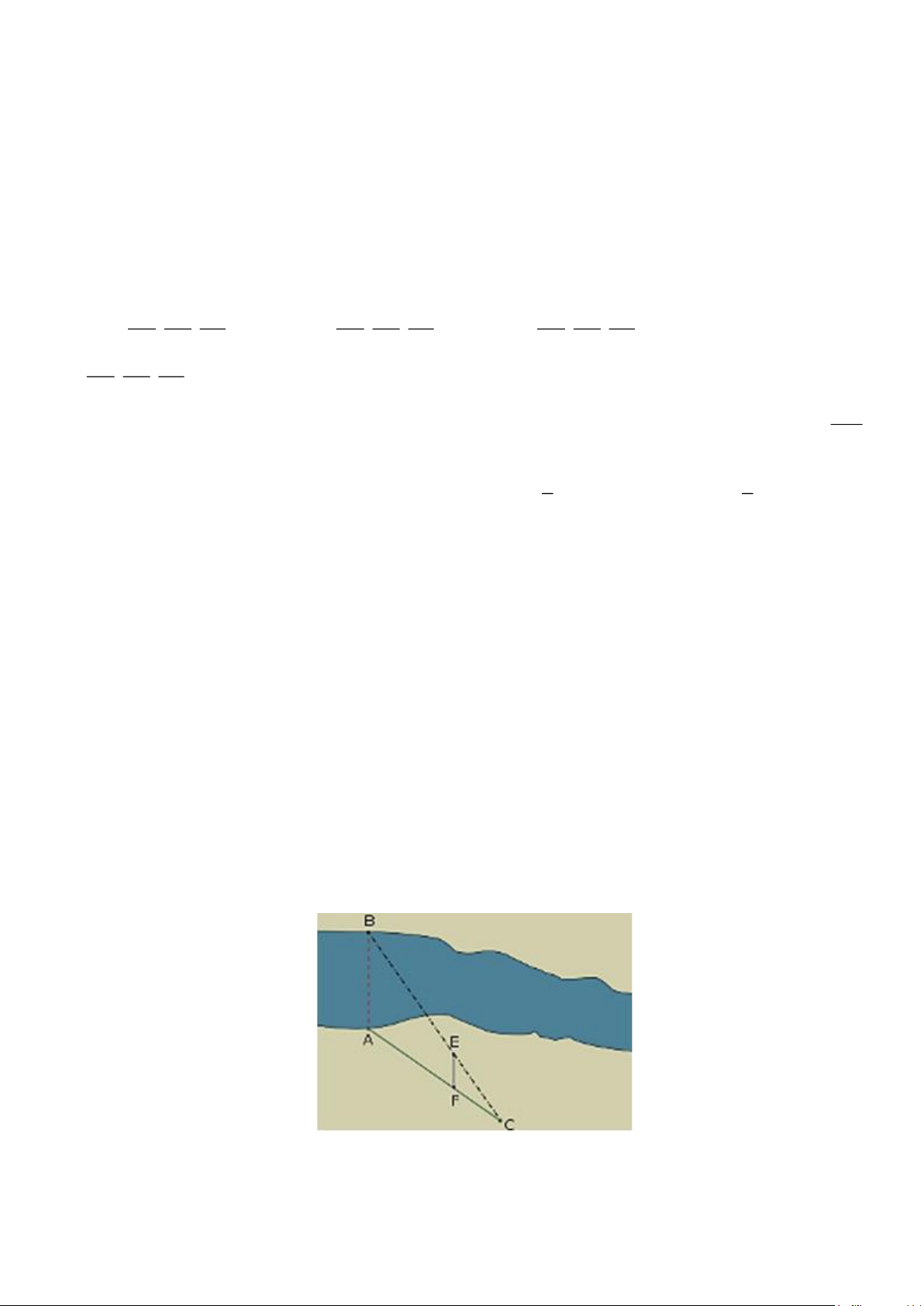
Câu 23: Để xác định độ rộng AB của một đoạn mương, người ta tiến hành đo đạc như hình vẽ dưới
đây. Hãy tính chiều rộng AB của đoạn mương biết: AB // FE; AC = 28 m; FE = 5 m; FC = 7 m . A. 20 m. B. 18 m . C. 21 m . D. 25 m .
Câu 24: Cho ∆ ABC, phân giác AD ( D BC) , biết: AB = 10cm, AC = 19cm, BD = 5cm. Độ dài đoạn thẳng CD bằng: Trang 11 50 A. 20cm B. 38cm C. 9,5cm D. cm. 19
Câu 25: Cho 2x − y = 9 . Tính 3 2 2 3 2 2
A = 8x −12x y + 6xy − y +12x −12xy + 3y + 6x − 3y +11 . A. A =1000 B. A =1010 C. A = 990 D. A =1001
PHẦN II. TỰ LUẬN (5,0 ĐIỂM)
Bài 1: (1,5 điểm).
a) Tính nhanh giá trị của biểu thức 2 2
A = m – 2mn + n tại m = 168 và n = 68 .
b) Phân tích đa thức sau thành nhân tử B = ( 2
x −16) + xy + 4y . c) Tìm x , biết: 2 x − 6x = 0 .
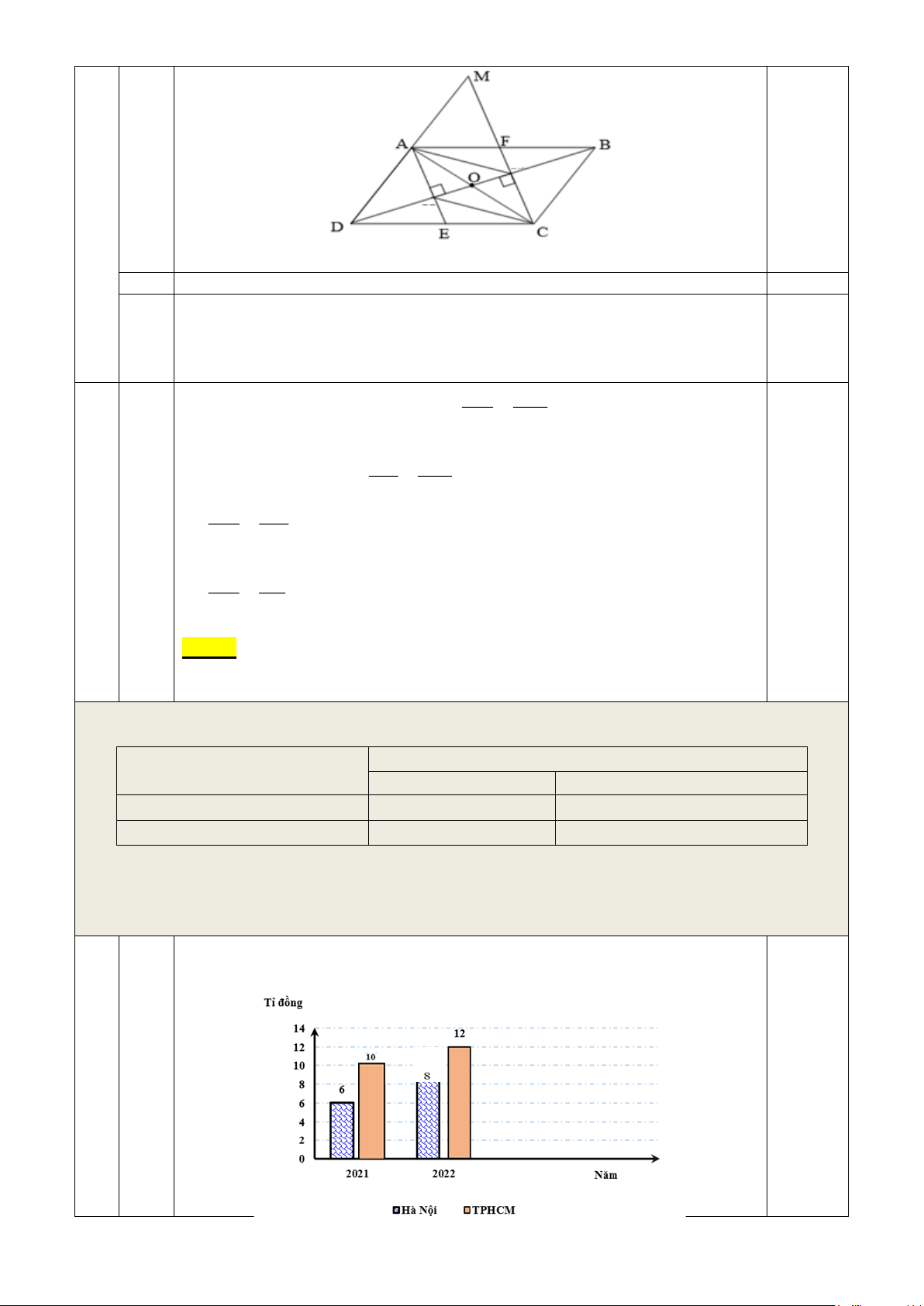
Bài 2: (2,0 điểm). Cho hình bình hành ABCD có AB BC và A tù. Gọi O là giao điểm của hai
đường chéo AC và BD. Qua A vẽ đường thẳng vuông góc với BD và cắt DC tại E, Qua C vẽ đường thẳng
vuông góc với BD và cắt AB tại F.
a) Chứng minh tứ giác AECF là hình bình hành.
b) Gọi M là giao điểm của hai đường thẳng AD và CF. Chứng minh MC.CE = MF.AB .
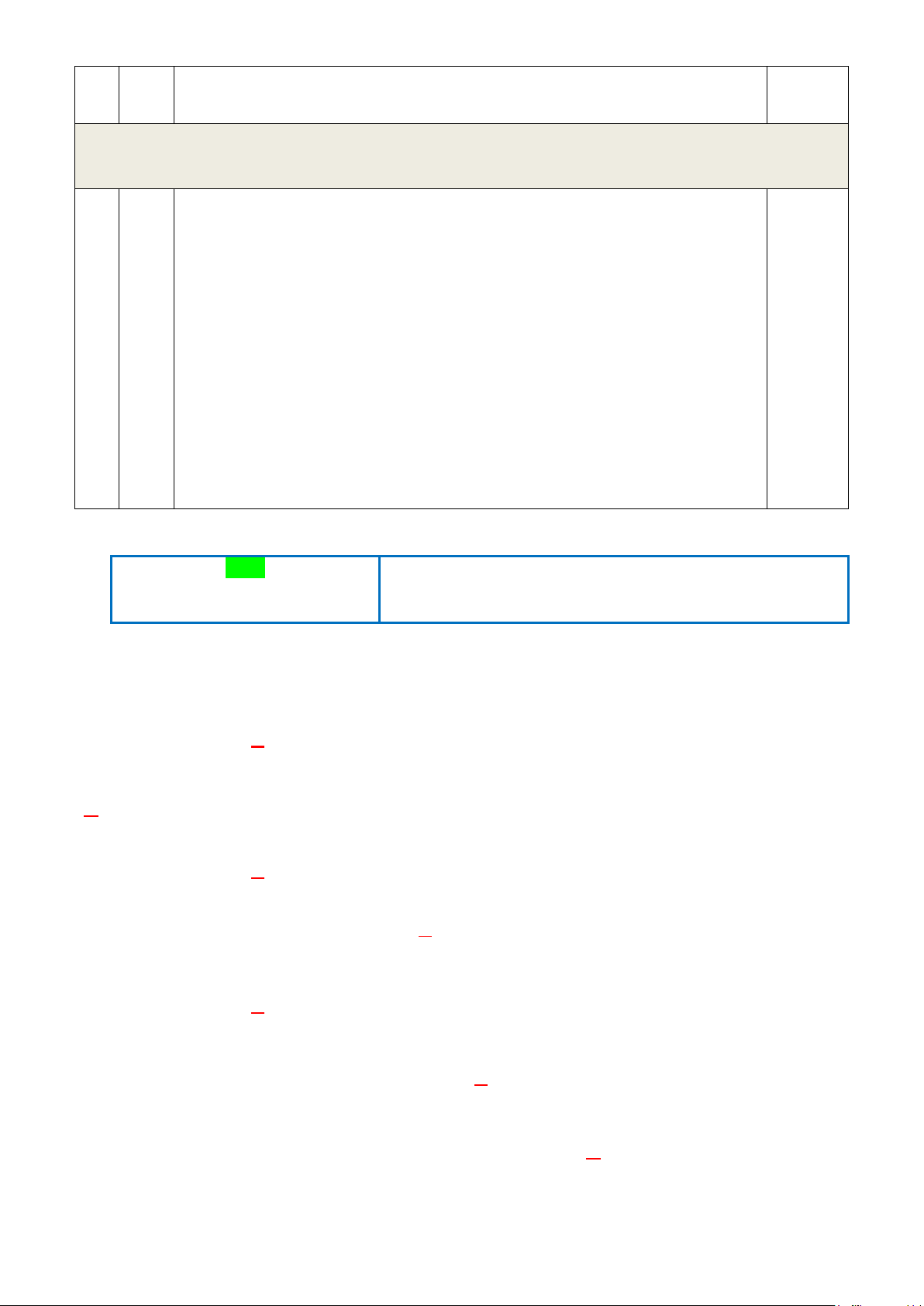
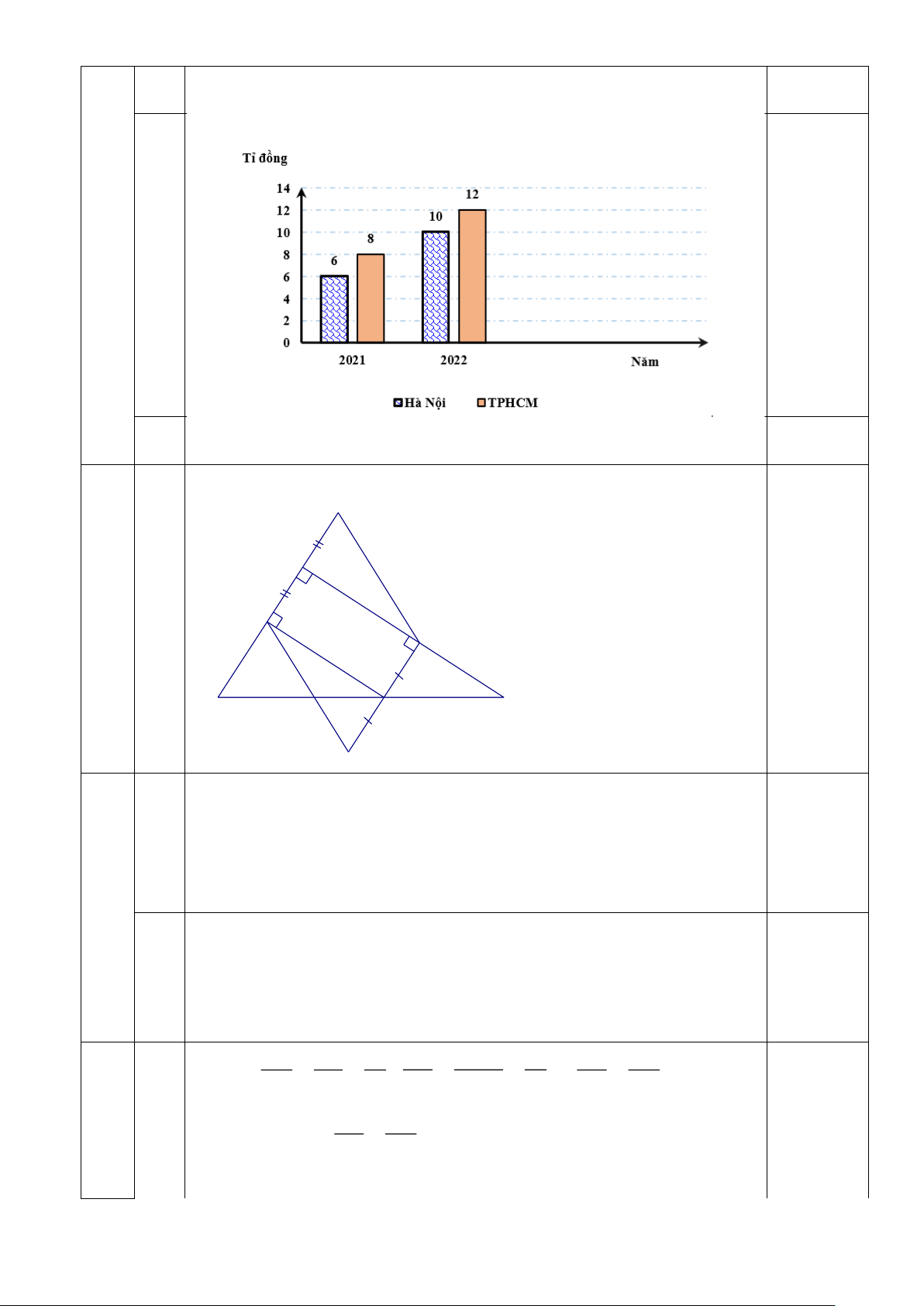
Bài 3: (1,0 điểm).Doanh thu (đơn vị: tỉ đồng) của hai chi nhánh một công ty trong năm 2021 và 2022
được cho trong bảng sau: Chi nhánh Năm 2021 2022 Hà Nội 6 8 Thành phố Hồ Chí Minh 10 12
a) Em hãy lựa chọn dạng biểu đồ thích hợp rồi vẽ biểu đồ đã chọn để so sánh doanh thu của
hai chi nhánh này trong hai năm 2021 và 2022 ?
b) Trong giai đoạn 2021− 2022 doanh thu của hai chi nhánh là bao nhiêu?
Bài 4: (0,5 điểm).Cho các số thực x, y, z thỏa mãn x + y + z = 9 và 2 2 2
x + y + z = 27 . Tính giá trị biểu
thức P = ( x − )22 + ( y − )23 + ( z − )24 2 3 4 . ------- HẾT ------- ĐÁP ÁN
Phần I. Đáp án câu trắc nghiệm: 163 264 362 461 565 660 1 A D B A D D 2 D C C B D D 3 B C D D A C 4 D C B B B B 5 C B A C D B 6 A B A A D C 7 C C A A C D 8 A C B D B B Trang 12 9 C C A C B D 10 B D C B B A 11 C C A C D A 12 A B A C C D 13 B C A D A D 14 B C A D B C 15 B D A D A A 16 C D C C D C 17 D B B D D D 18 B B C D C D 19 D D D C A B 20 A C D A A B 21 C C A D C A 22 C B C D A B 23 A C C B C B 24 C B A D B C 25 B C A C A A
II. TỰ LUẬN (5,0 điểm) BÀI NỘI DUNG ĐIỂM Bài 1(1,5 điểm)
a) Tính nhanh giá trị của biểu thức 2 2
A = m – 2mn + n tại m = 168 và n = 68 .
b) Phân tích đa thức sau thành nhân tử B = ( 2
x −16) + xy + 4y . c) Tìm x , biết: 2 x − 6x = 0 . a 2
A = m – 2mn + n = (m − n)2 2 0,25 1
Tại m = 168 và n = 68 thay vào biểu thức A ta được; A = ( − )2 2 168 68 = 100 = 10000 0,25 b B = ( 2
x −16) + xy + 4y 0,25
= (x − 4)(x + 4) + y(x + 4)
= (x + 4)(x − 4 + y) 0,25 c 2 x − 6x = 0 .
x ( x − 6) = 0 0,25 x = 0 x = 0 0,25 . Vậy x 0; 6 x 6 0 − = x = 6
Bài 2 (2,0đ): Cho hình bình hành ABCD có AB BC và A tù. Gọi O là giao điểm của hai
đường chéo AC và BD. Qua A vẽ đường thẳng vuông góc với BD và cắt DC tại E, Qua C vẽ đường
thẳng vuông góc với BD và cắt AB tại F.
a) Chứng minh tứ giác AECF là hình bình hành.
b) Gọi M là giao điểm của hai đường thẳng AD và CF. Chứng minh MC.CE = MF.AB . Trang 13 2 Vẽ hình, ghi GT,KL đúng 0,25 a Xét tứ giác AECF có
AF // CE (AB // CD - hai cạnh đối hình bình hành) 0,25
AE // CF (AE và CF cùng vuông góc với BD) 0,25
Tứ giác AECF là hình bình hành. 0,25 b MC DM
MCD: AF // CD (do AB // CD) = (Định lí Thalès) MF AM 0,5 DC DM Có: AE // CM = (Định lí Thalès) CE AM 0,5 MC DC = (Định lí Thalès) MF CE
Mà AB = CD; AF = EC (hai cạnh đối hình bình hành) MC AB = MC . CE = MF . AB. MF CE
Lưu ý: Học sinh dùng hệ quả ta lét hoặc các chứng minh mà đúng thì vẫn chấm đủ điểm.
Bài 3 (1,0 điểm): Doanh thu (đơn vị: tỉ đồng) của hai chi nhánh một công ty trong năm 2021 và
2022 được cho trong bảng sau: Chi nhánh Năm 2021 2022 Hà Nội 6 8 Thành phố Hồ Chí Minh 10 12
a) Em hãy lựa chọn dạng biểu đồ thích hợp rồi vẽ biểu đồ đã chọn để so sánh doanh thu của hai chi
nhánh này trong hai năm 2021 và 2022 ?
b) Trong giai đoạn 2021− 2022 doanh thu của hai chi nhánh là bao nhiêu? 3 a
Để biễu diễn doanh thu của hai chi nhánh một công ty trong bảng thống kê
đã cho ta có thể chọn dạng biểu đồ cột kép. 0,25 0,5 Trang 14 b
Trong giai đoạn 2021− 2022 doanh thu của hai chi nhánh là: 0,25
6 +10 + 8 +12 = 36 (tỉ đồng)
Bài 4. (0,5 điểm) Cho các số thực x, y, z thỏa mãn x + y + z = 9 và 2 2 2
x + y + z = 27 . Tính giá trị
biểu thức P = ( x − )22 + ( y − )23 + ( z − )24 2 3 4 .
Ta có: ( x + y + z)2 = ( 2 2 2
3 x + y + z ) 0,1 2 2 2 2 2 2
x + y + z + 2xy + 2yz + 2xz = 3x + 3y + 3z 2 2 2
2x + 2y + 2z − 2xy − 2yz − 2xz = 0 0,1 0,1
(x − y)2 + ( y − z)2 + (x − z)2 = 0 ( ) 1 0.1
(x − y)2 0
(x − y)2 = 0 x = y 0.1
Do ( y − z)2 0 nên từ (1) ta có: ( y − z)2 = 0 y = z x = y = z
( x − z)2 0 2 z = x − = (x z) 0
Mà x + y + z = 9 x = y = z = 3
Thay x; y; z vào biểu thức P ta được:
P = ( − )22 + ( − )23 + ( − )24 3 2 3 3 3 4 = 1+ 0 +1 = 2 ĐỀ 4
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2024-2025 MÔN: TOÁN 8
A. Trắc nghiệm (3 điểm)
Câu 1 ( NB). Trong các biểu thức đại số sau, biểu thức đại số nào không phải đơn thức ? A. 2. B. 5x + 9. C. x3y . D. x.
Câu 2 (NB). Khai triển hằng đẳng thức ( x + )2 1 ta được : A. 2 x + 2x +1. B. 2 x − 2x +1. C. 2 x + x +1. D. 2 x + 2x + 2 .
Câu 3 (NB). Tính ( x − 2)( x + 2) ta được: A. 2 x + 4x + 4 . B. 2 x − 4 . C. 2 x + 4 . D. x −16 .
Câu 4 (NB). Biểu thức 3 2 2 3
x − 3x y + 3xy − y viết được dưới dạng nào sau đây? A. ( + )2 x y . B. ( − )2 x y . C. ( − )3 x y . D. ( + )3 x y .
Câu 5 (NB). Kết quả của phép tính ( x − )( 2 2
5 x + 5x + 5 ) là A. x − ( )3 3 2 5 . B. 3 x −125 . C. ( x − )3 5 . D. 3 3 x + 5 .
Câu 6 (NB). Khai triển biểu thức ( x + )3
1 ta được kết quả là A. 3 2
x − 3x + 3x −1. B. 3 2
x + 3x + 3x +1. C. 3 2
x + 9x + 3x +1. D. 3 2
x − 9x + 3x −1.
Câu 7 (NB). Tứ giác ABCD là hình bình hành nếu A. AB // CD .
B. AB = CD .
C. AD // BC .
D. AB // CD; AD // BC .
Câu 8 (NB). Khi muốn biểu diễn tuổi thọ trung bình của người Việt Nam qua 30 năm. Ta nên
lựa chọn biểu đồ nào: A. Biểu đồ tranh.
B. Biểu đồ cột kép. Trang 15
C. Biểu đồ đoạn thẳng.
D. Biểu đồ hình quạt tròn.
Câu 9 (NB). Một xí nghiệp bình xét thi đua cho mỗi thành viên cuối năm theo 4 mức: Tốt,
Khá, Trung bình, Chưa đạt. Sau khi bình xét, tỉ lệ xếp loại thi đua theo 4 mức: Tốt, Khá, Trung
bình, Chưa đạt lần lượt là: 30%; 40%; 25%; 5% . Hãy lựa chọn biểu đồ thích hợp để biểu diễn dữ liệu trên: A. Biểu đồ tranh.
B. Biểu đồ cột kép.
C. Biểu đồ đoạn thẳng.
D. Biểu đồ hình quạt tròn.
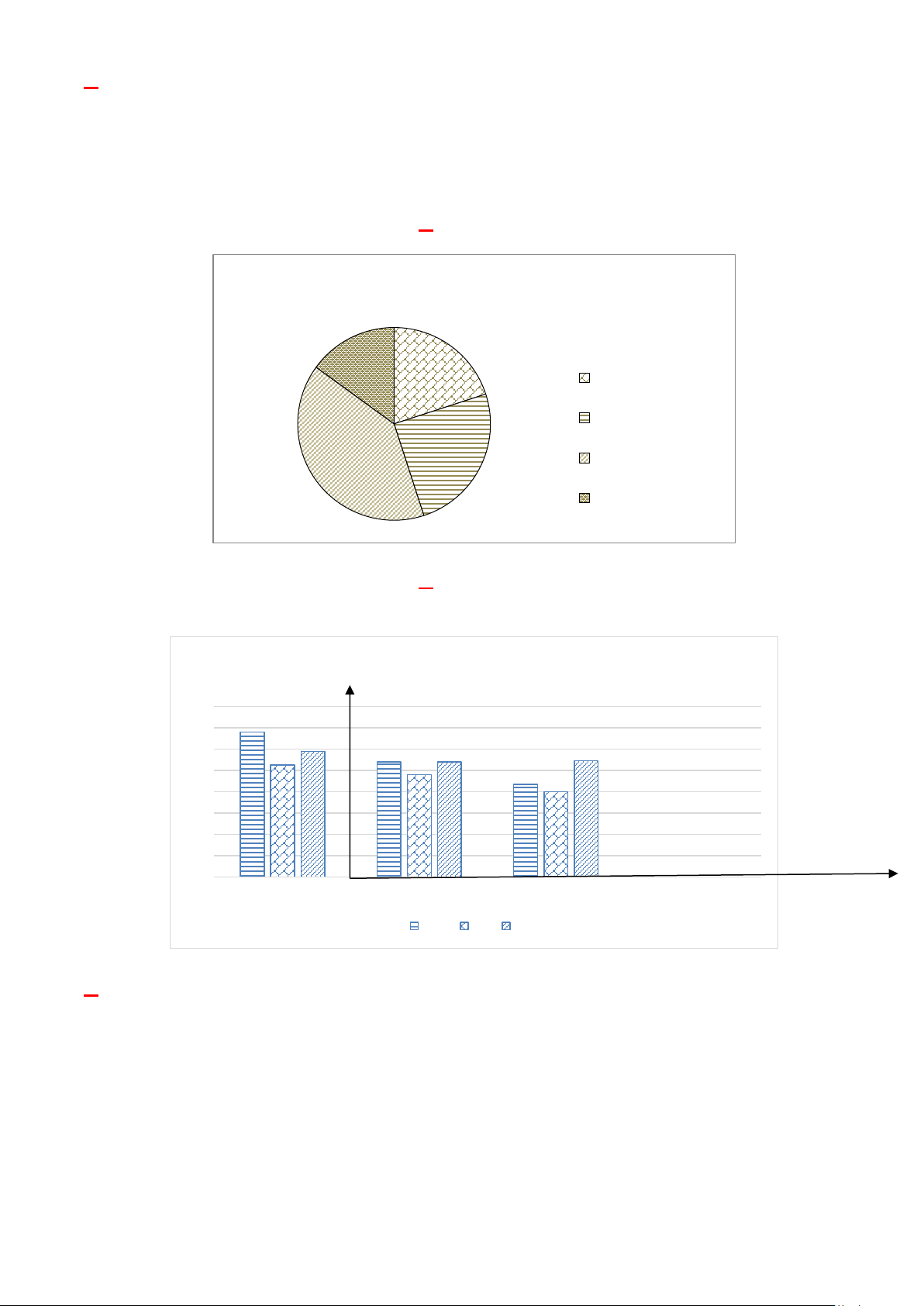
Câu 10 (NB). Quan sát biểu đồ dưới đây:
TỈ LỆ CÁC MẶT HÀNG BÁN ĐƯỢC TRONG
MỘT NGÀY Ở MỘT CỬA HÀNG 15% Áo quần Dày dép 25% 40% Túi xách Mặt hàng khác
Hãy cho biết mặt hàng quần áo và túi xách bán được trong ngày chiếm bao nhiêu phần trăm? A. 20% . B. 30% . C. 60% . D. 40% .
Câu 11 (NB). Dựa vào bảng xếp hạng huy chương SEA Games 32 tổ chức tại Campuchia
tháng 5 / 2023 của nhóm ba nước dẫn đầu.
Xếp hạng huy chương SEA Games 32 tại Campuchia Ngày 17/5/2023 160 136 140 118 120 108 105 108 109 96 100 87 80 80 60 40 20 0 Việt Nam Thái Lan Indonesia Vàng Bạc Đồng
Em hãy cho biết nhận xét nào sau không đúng:
A. Đoàn thể thao Thái Lan đứng đầu bảng tổng sắp huy chương SEA Games 32
B. Số huy chương vàng của đoàn thể thao Việt Nam tại SEA Games 32 là nhiều nhất.
C. Tại SEA Games 32 , Đoàn thể thao Việt Nam có tổng số huy chương nhiều nhất.
D. Đoàn thể thao Indonesia có tổng số huy chương ít nhất
Câu 12 (TH). Cho hình vẽ. Trang 16 A D C E B
Biết AB // DE , áp dụng định lí Thales ta có hệ thức đúng là A. AC BC = . B. AC BC = . C. AC CE = . D. AC CE = . CD CE AE CD CD BC BC CD B. Tự luận (7đ) Câu 13 (VD). Thu gọn đa thức sau: 2 x y ( 2 x − y) 2 − x ( 2 2 3 . 2
4 . x y − y ) (0,5đ) Câu 14. 14.1 (NB). Tính : ( − )2 x y (0,25đ)
14.2 (TH). Tìm x, biết : ( x − )2 5
1 − (5x − 4)(5x + 4) = 7 (0,5đ)
14.3 (VD). Tính giá trị biểu thức: C = ( x + y − )2 − ( x + y − )( y − ) + ( y − )2 7 2 7 6 6 tại x = 101 (0,75đ) Câu 15
Doanh thu (đơn vị: tỉ đồng) của hai chi nhánh một công ty trong năm 2021 và 2022 được cho trong bảng sau: Chi nhánh Năm 2021 2022 Hà Nội 6 8 Thành phố Hồ Chí Minh 10 12
15.1 (TH) Em hãy lựa chọn dạng biểu đồ thích hợp để so sánh doanh thu của hai chi
nhánh này trong hai năm 2021 và 2022 ? (0,25đ)
15.2. (VD) Hãy vẽ biểu đồ đã chọn để so sánh doanh thu của hai chi nhánh này trong hai năm 2021 và 2022 ? (0,5đ)
15.3. (VD) Trong giai đoạn 2021− 2022 doanh thu của hai chi nhánh là bao nhiêu? (0,25đ)
Câu 16 (1,5 đ) Cho tam giác ABC vuông tại A . Gọi M là một điểm bất kì trên cạnh huyền
BC . Gọi D và E lần lượt là chân đường vuông góc kẻ từ M xuống AB và AC .
a) Tứ giác ADME là hình gì? Vì sao?
b) Lấy điểm I sao cho A là trung điểm của ID ; điểm K sao cho M là trung điểm của
EK . Chứng minh EI = DK và EI //DK .
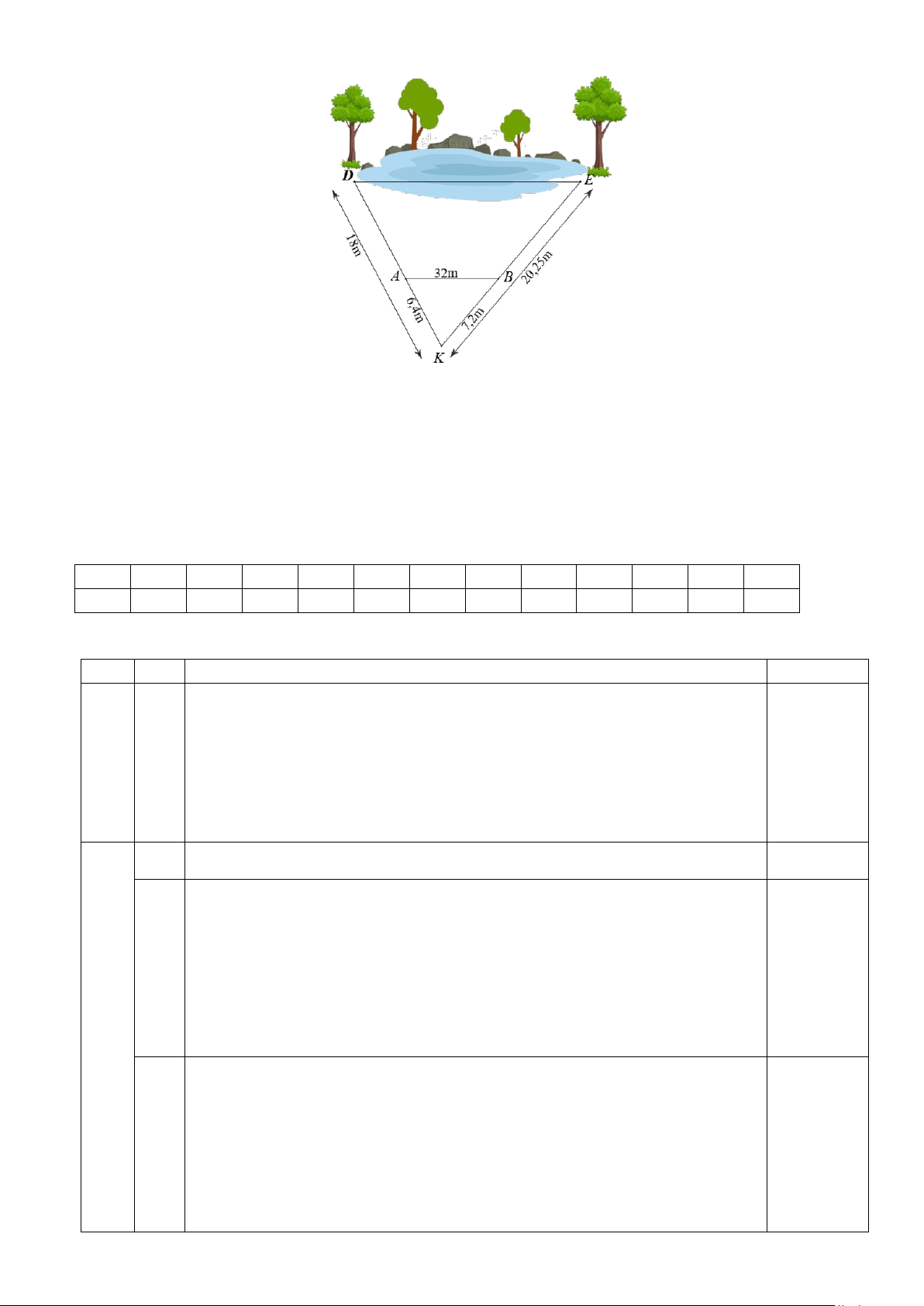
Câu 17 (1,5đ) Bạn Hiển đo được khoảng cách từ vị trí mình đứng (điểm K ) đến cây D và cây
E ở hai bên hồ nước lần lượt là KD = 18m và KE = 20,25m . Để tính độ dài DE , Hiển xác
định điểm A nằm giữa K , D và điểm B nằm giữa K , E sao cho KA = 6,4m , KB = 7, 2m , và
đo khoảng cách giữa A và B là AB = 32m . KB AK a) (NB) Chứng minh = KE AD
b) (TH) Chứng minh AB //DE
c) (VD) Tính khoảng cách giữa D và E . Trang 17 Câu 18.
18.1 Tìm cặp số tự nhiên ( ; x y) sao cho 2 2 x + 55 = 4 y
18.2 Tính giá trị biểu thức sau một cách hợp lý 13 12 11 10 2
F = x − 9x + 9x − 9x + ...− 9x + 9x − 2 với x = 8 HƯỚNG DẪN CHẤM
A. Trắc nghiệm (3 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 ĐA B A B C B B D C D C A A B. Tự luận (7 điểm) Câu Ý Đáp án Biểu điểm 13 Thu gọn đa thức sau: 2 x y ( 2 x − y) 2 − x ( 2 2 3 . 2
4 . x y − y ) 4 2 2 4 2 2
= 3x y − 3x y − 4x y + 4x y 0,25 = ( 2 2 2 2
x y − x y ) − ( 4 4 4 3 4x y − 3x y) 2 2 4 = x y − x y 0,25 14 14.1 Ta có ( − )2 x y 2 2
= x − 2xy + y 0,25 14.2 Ta có ( x − )2 5
1 − (5x − 4)(5x + 4) = 7 2 x − x + − ( 2 25 10 1 25x −16) = 7 2 2
25x −10x +1− 25x +16 = 7 −10x = −10 0,25 x = 1 Vậy x = 1. 0,25
14.3 Ta có C = (x + y − )2 − (x + y − )( y − ) + ( y − )2 7 2 7 6 6
C = ( x + y − ) − ( y − ) 2 7 6 0,25 C = ( x − )2 1
Thay x = 101 vào C , ta có: C = ( − )2 2 101 1 = 100 = 10000 0,25
Vậy với x = 101 thì C = 10000 0,25 Trang 18 15
15.1 Để biễu diễn doanh thu của hai chi nhánh một công ty trong bảng 0,25
thống kê đã cho ta có thể chọn dạng biểu đồ cột kép. 15.2 0,5
15.3 Trong giai đoạn 2021− 2022 doanh thu của hai chi nhánh là: 0,25
6 +10 + 8 +10 = 34 (tỉ đồng) 16 Vẽ hình, viết GT, KL 0,5đ I A D E B C M K
a) Xét tứ giác ADME có: ·
DAE = 90 ( ABC vuông tại A ) ·
ADM = 90 ( MD ⊥ AB ) ·
AEM = 90 ( ME ⊥ AC )
Suy ra ADME là hình chữ nhật 0,5đ
b) AD = ME; AD//ME (Tính chất hình chữ nhật)
Mà A là trung điểm của DI ; M là trung điểm của KE nên suy ra
DI = KE; DI //KE
Suy ra DIEK là hình bình hành 0,25
Suy ra DK //EI và DK = EI 0,25 17 AK 6,4 16 KB 7,2 16 0,5 a) Ta có = = ; = = KB AK = AD 18 45 KE 20,25 45 KE AD KB AK b) Xét KDE = có
Suy ra AB// DE ( định lí Talet đảo) 0,5 KE AD
c) Vì AB //DE (cm câu a) Trang 19 KA AB =
( hệ quả định lí Talet) KD DE 6,4 32 0,25 hay = DE = 90(m) 18 DE
Vậy khoảng cách giữa D và E là 90m . 0,25 18 18.1 Ta có: 2 2 x + 55 = 4 y 2 2 4 y − x = 55
(2y − x)(2y + x) = 55 0,25
Nhận xét: x + 2y 2y − x 0 nên ta có: 2y + x = 55 x = 27 TH1: 2y − x = 1 y =14 2y + x =11 y = 4 TH2: 2y − x = 5 x = 3 Vậy ( ;
x y) có thể là (27;14) và (3;4) 0,25
18.2 Với x = 8 thì x +1 = 9 ta có: 13
F = x − ( x + ) 12 x + (x + ) 11 x − (x + ) 10 x + − (x + ) 2 1 1 1 ... 1 x + (x + ) 1 x − 2 F = x − 2 0,25 F = 8 − 2 = 6
Vậy với x = 8 thì F = 6 0,25 ĐỀ 5
ĐỀ ÔN TẬP CUỐI HỌC KỲ I NĂM HỌC 2024-2025 MÔN: TOÁN 8
PHẦN I. Trắc nghiệm (3 điểm) Chọn phương án trả lời đúng nhất của mỗi câu hỏi sau rồi ghi vào giấy làm bài.
Câu 1: Đơn thức 2 3 2
3 2x y z có bậc là A. 5 . B. 7 . C. 8. D. 6 . 1 − Câu 2: Đơn thức 2 2
x y9z có phần hệ số là 3 1 A. − . B. 3 . C. −3 . D. −27 . 3
Câu 3: Trong các đa thức sau, đa thức nhiều biến là A. 3
7xy − 2y . B. 3
6 y + 2 y . C. 2 5z −1 . D. 2
4x − 3x .
Câu 4: Với a, b là hai số bất kì, đẳng thức nào sau đây không phải là hằng đẳng thức? A. 2 2 2
a − 2ab + b = (a − b) . B. 2 a −1 = 3a . C. 2
a(2a + b) = 2a + ab . D. 2
b(a − b) = ab − b .
Câu 5: Hằng đẳng thức lập phương của một tổng là A. 3 3 2 2 3
(A + B) = A − 3A B + 3AB − B . B. 3 3 2 2
A + B = (A + B)(A − AB + B ) . C. 3 3 2 2 3
(A + B) = A + 3A B + 3AB + B . D. 3 3 2 2 3
(A + B) = A + 2A B + 2AB + B . Trang 20