lOMoAR cPSD| 47167580
SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁI NGUYÊN ĐỀ KIỂM
TRA ĐÁNH GIÁ CUỐI HỌC KÌ II NĂM HỌC 2023- 2024
TRƯỜNG THPT NGÔ QUYỀN MÔN: TOÁN 11 Thời gian
làm bài: 90 phút (không kể thời MÃ ĐỀ gian giao ề) 101
Đề kiểm tra gồm: 05 trang
A. PHẦN TRẮC NGHIỆM (7 iểm )
Câu 1: Bảng số liệu ghép nhóm sau cho biết chiều
cao (cm) của 50 học sinh lớp 11A. Khoảng chiều cao (cm) 145;150 150;155 155;160 160;165 165;170 Số học sinh 7 14 10 10 9
Khi ó số học sinh có chiều cao dưới 160 cm là A. 7. B. 14. C. 10. D. 31.
Câu 2: Bảng số liệu ghép nhóm sau cho biết chiều
cao (cm) của 50 học sinh lớp 11A. Khoảng chiều cao (cm) 145;150 150;155 155;160 160;165 165;170 Số học sinh 7 14 10 10 9
Tính chiều cao trung bình (cm) của 50 học sinh lớp 11A. A. 157,5(cm). B. 155,5(cm). C. 150(cm). D. 160(cm).
Câu 3: Cho A , B là hai biến cố ộc lập. Đẳng thức nào sau ây úng? A. P AB
P A P B . B. P AB P A P B . . C. P AB
P A P B . D. P AB
P A P B .
Câu 4: Cho số thực dương a và số nguyên dương
n tùy ý. Mệnh ề nào dưới ây úng? 2n n n
A. a a2 n .
B. a a2n .
C. an an . D. an a2 .
Câu 5: Cho a là số thực dương. Viết biểu thức P a
a 2. dưới dạng lũy thừa mũ hữu tỉ cơ
số a ta ược kết quả là lOMoAR cPSD| 47167580
A. P a .
B. P a . C. P a .
D. P a5 .
Câu 6: Cho a là số thực dương. Viết biểu thức P 3 7 1 a a .
dưới dạng lũy thừa mũ hữu tỉ cơ số a ta ược kết quả là
A. P a .
B. P a . C. P a .
D. P a .
Câu 7: Viết biểu thức P x x x 2
3.3 với x 0 dưới dạng lũy thừa với số mũ hữu tỷ. A. P x .
B. P x . C. P x . D. P x .
Câu 8: Biết log 7a 2. Tính log 49a a. A. 3. B. 5. C. 4. D. 3.
Câu 9: Với a là số thực dương tùy ý, log2 8a bằng A. log2 a .
B. 3log2 a . C. log2 a 2 . D. 3 log2 a . A. y
5 2 x . B. y 3 x .
C. y 0,7 x . D. y 2e x.
Câu 11: Hình bên là ồ thị của ba hàm số y ax , y bx
, y cx 0 a b c, , 1 ược vẽ trên cùng
một hệ trục tọa ộ. Khẳng ịnh nào sau ây là khẳng ịnh úng? lOMoAR cPSD| 47167580
A. a c b . B. a b c y
D. c b a . y = b x
Câu 12: Tìm tập xác ịnh của hàm số y y = c x log y = a x A. D 3;4 . O x C. D 0;3 3;4 . . C. bac . D. 2 D ;0 4; . 4xx 3 . 2 ln x x e
Câu 13: Trong các hàm số sau, hàm số nào B. D ; . ồng biến trên ? 0 4 3
D. y 2024x . A. y log x 2 x . B. y 0, .
C. y 2 x .
Câu 14: Tập nghiệm S của bất phương trình log2 2x 3 0 là A. S ; 1 . B. S
1; . C. S D. S ;0 ; 1 . .
Câu 15: Tập nghiệm của bất phương trình (1)𝑥2−4𝑥−12 > 1 là: 3
A. (-∞;-6) ∪ (2; +∞) B. (-2;6)
C. (-∞;-2) ∪ (6; +∞) D. (-6;2)
Câu 16: Cho hàm số y f x xác ịnh trên khoảng
a b; và iểm x0
a b; . Khẳng ịnh nào sau ây úng? A. f x 0 xlim0 x f
xx xf0 x0 . B. f x0 x xlim 0 f xx0
x0f x . C. f x 0 x xlim 0 f
xx xf0 x0 . D. f x 0 x xlim 0 f
xx xf0 x0 .
Câu 17: Hệ số góc của tiếp tuyến của ồ thị hàm số 𝑦
= 𝑓(𝑥) tại iểm 𝑀0(𝑥0; 𝑓(𝑥0)) là: A. 𝑓′ (𝑥0) B. 𝑓(𝑥0) C. 𝑥0
D. − 𝑓′ (𝑥0) lOMoAR cPSD| 47167580
Câu 18: Một chất iểm chuyển ộng có phương trình s
3t2 7t (t tính bằng giây, s tính bằng mét). Vận tốc
của chất iểm tại thời iểm t0 3 (giây) bằng. A. 22 m s/ . B. 25 m s/ . C. 48 m s/ . D. 11 m s/ .
Câu 19: Đạo hàm y của hàm số y sin x cosx là
A. y 2cosx. B. y 2sin x .
C. y sin x cos x . D. y cosx sin x .
Trang2 | 4 m ª 1 0 1
Câu 21: Đạo hàm cấp hai của hàm số y sin 2x là
A. y ' 4cos2 .x B. y ' 4sin 2 .x
C. y ' 2cos2 .x D. y ' 4cos2 .x
Câu 22: Đạo hàm của hàm số y cos x2 x 2 là
A. y ' 2x 1 sin x2 x 2 . B. y ' sin x2 x 2. 2 x2 x 2 2 C. y '
x 1 sin x2 x 2 . D. y '
sin x2 x 2 . 2 x2 x 2 2 x2 x 2 1
Câu 23: Đạo hàm cấp hai của hàm số y là x D. y A. C. y 3 y
1 . B. y 12 . x 2 3 . x 3 . x x
Câu 24: Mệnh ề nào sau ây là úng?
A. Hai mặt phẳng vuông góc với nhau thì mọi
ường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia. lOMoAR cPSD| 47167580
B. Hai mặt phẳng phân biệt cùng vuông góc với
một mặt phẳng thì vuông góc với nhau.
C. Hai mặt phẳng phân biệt cùng vuông góc với
một mặt phẳng thì song song với nhau.
D. Hai mặt phẳng vuông góc với nhau thì mọi
ường thẳng nằm trong mặt phẳng này và vuông
góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.
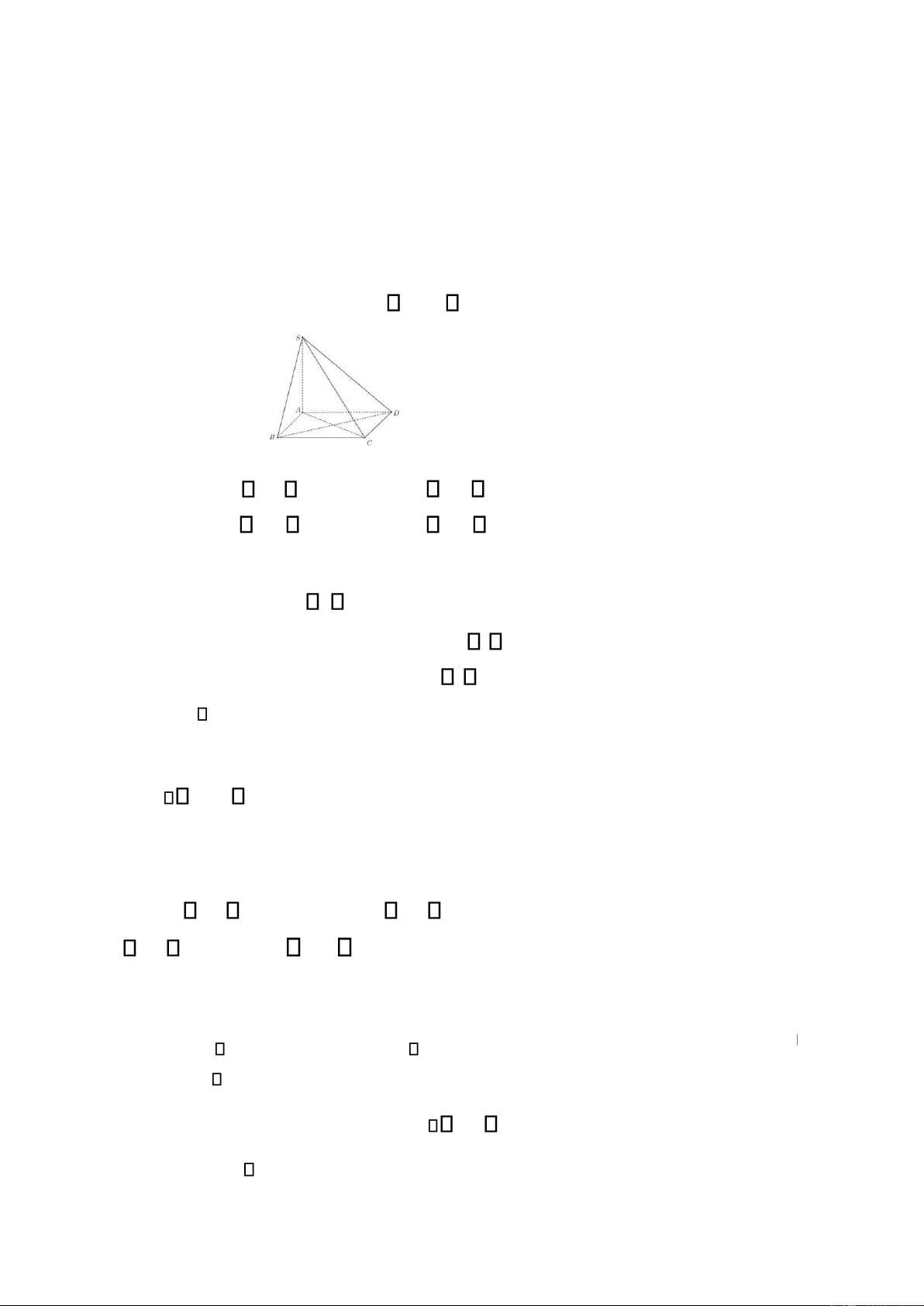
Câu 25: Cho hình chóp S ABCD. có áy là hình
vuông, SA vuông góc với áy. Mặt phẳng nào sau ây
không vuông góc với ABCD A. SAB . B. SAC . C. SBD . D. SAD .
Câu 26: Nếu d vuông góc với mọi ường thẳng
nằm trong mặt phẳng P thì
A. d / /( )P B. d nằm trong măt phẳng P
. C. d cắt và không vuông góc với P .
D. d (P)
Câu 27: Cho hình chóp SABCD. có SA
ABCD và ABCD là hình chữ nhật. Hỏi
ường thẳng BC vuông góc với măt phẳng nào sau ây
A. SAB . B. SAC .
C. SBC . D. ABC .
Câu 28: Cho hình chóp SABCD. có áy ABCD là hình
vuông tâm O. Cạnh bên SA vuông góc với áy.
Khẳng ịnh nào sau ây là úng?
A. SA SD
B. BC AD .
C. SA BD
D. AD SC.
Câu 29: Cho hình chóp S ABC. có SA ABC và
AB BC. Gọi I là trung iểm của BC . Góc lOMoAR cPSD| 47167580 phẳng nhị diện , A BC S, là góc nào sau ây? A. SBA. B. SCA. C. SCB. D. SIA
Câu 30: Cho các ường thẳng a b, và các mặt phẳng ,
. Chọn mệnh ề úng trong các mệnh ề sau a b A. ba a b . B. ba . C. aa . D. aa b b// .
Trang3 | 4 m ª 1 0 1
Câu 31: Cho hình chóp S ABCD. có áy ABCD là
hình bình hành và SA vuông góc với mặt phẳng
ABCD . Mặt phẳng nào sau ây vuông góc với mặt phẳng ABCD ? A. SBD . B. SAD . C. SCD . D. SBC .
Câu 32: Cho hình lập phương ABCDA BCD. '
có cạnh bằng a ( tham khảo hình vẽ bên dưới). A' D' C' B' D A B C K h o ả n g c á c h g lOMoAR cPSD| 47167580 i ữ a A B v à B C / b ằ n g a 5 a 2 A. . B. . C. a 2 . D. a . 2 2
Câu 33: Cho hình chóp S ABC.
có ba cạnh SA, SB, SC ôi một
vuông góc với nhau. Biết
SA = SB = SC = a. Khoảng cách
từ S ến mặt phẳng ABC bằng a 6 a 5 a a 3 A. . B. . C. . D. . 2 2 3 3
Câu 34: Cho hình chóp S ABC. có áy ABC là tam giác
vuông tại A. SB vuông góc ABC . Góc
giữa SC với SAB là góc giữa
A. SC và AB .
B. SC và AC .
C. SC và AS .
D. SC và CB. lOMoAR cPSD| 47167580
Câu 35: Cho hình hộp chữ nhật ABCDABCD. ’ ’ ’ ’có
AB a AD a ; 3 , góc giữa AC và DD/ bằng 300
Khoảng cách giữa hai mặt phẳng áy ABCD và
ABCD’ ’ ’ ’ của hình hộp chữ nhật bằng. A. a 6 . B. 2 3a . C. 2 3a. D. a 3 . 6 3
B. PHẦN TỰ LUẬN (3 iểm )
Câu 36 (0,5 iểm): Trường THPT Ngô Quyền Có
13 học sinh được bình chọn " Học sinh ưu tú ",
trong đó khối 12 có 8 học sinh nam và 3 học sinh
nữ, khối 11 có 2 học sinh nam. Chọn ngẫu nhiên 3
học sinh bất kỳ để trao thưởng, tính xác suất để 3
học sinh được chọn có cả nam và nữ đồng thời có
cả khối 11 và khối 12. Câu 37 (0,5 iểm): Một vật
chuyển động có phương trình S 2t4 3t3 4t2
5t 6 m , t là thời gian tính bằng giây. Tính gia
tốc của vật tại thời iểm t 2s.
Câu 38 (0,5 iểm): Tính ạo hàm của hàm số y sin x cosx sin x cosx
Câu 39 (0,5 iểm): Cho hình chóp S.ABC áy là tam
giác vuông tại B, SA vuông góc với áy . Chứng
minh mp (SBA) vuông góc với mp (SBC).
Câu 40 (0,5 iểm): Cho hình chóp S ABCD. có áy
ABCD là hình chữ nhật AB 2a và AD a , cạnh bên
SA vuông góc với áy. Tính khoảng cách từ iểm C ến
mặt phẳng (SBD), biết số o góc [S,BD,A] bằng 600.
Bài 6 (0,5 iểm): Cho hình chóp S ABCD. có áy
ABCD là hình thang vuông tại A và D ; AB AD 2a
DC a . Điểm I là trung iểm oạn AD , mặt phẳng SIB và
SIC cùng vuông góc với mặt phẳng
ABCD . biết số o góc [S,BD,A] bằng 600. Tính
khoảng cách từ D ến SBC theo a . HẾT
Trang4 | 4 m ª 1 0 1 lOMoAR cPSD| 47167580
SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁI NGUYÊN ĐỀ
KIỂM TRA ĐÁNH GIÁ CUỐI HỌC KÌ II
TRƯỜNG THPT NGÔ QUYỀN NĂM HỌC 2023-2024 MÔN: TOÁN 11 Thời gian
làm bài: 90 phút (không kể thời MÃ ĐỀ gian giao ề) 102
Đề kiểm tra gồm: 04 trang
A. PHẦN TRẮC NGHIỆM (7 iểm )
Câu 1: Cho mẫu số liệu ghép nhóm về số tiền mà
sinh viên chi cho thanh toán cước iện thoại trong tháng Số tiền (nghìn [0;50) [50;100) [100;150) [150;200) [200;250) ồng) Số sinh viên 5 12 23 17 3
Có bao nhiêu sinh viên chi từ 100 ến dưới 150 nghìn
ồng cho việc thanh toán cước iện thoại trong tháng A. 5 B. 23 C. 12 D. 17
Câu 2: Cho mẫu số liệu ghép nhóm về tuổi thọ (
ơn vị tính là năm) của một loại bóng èn mới như sau. Tuổi thọ [2;3,5) [3,5;5) [5;6,5) [6,5;8) Số bóng èn 8 22 35 15
Số trung bình cộng của mẫu số liệu ghép nhóm trên
là( kết quả làm tròn ến hàng phần nghìn) A. 5,0. B. 5,32. C. 5,75. D. 6,5.
Câu 3: Cho A , B là hai biến cố xung khắc; Đẳng thức nào sau ây úng? A. A B. B. B A. C. A B . D. A B . n
Câu 4: Cho a là số thực dương, và n là số tự nhiên,
n 2 . Khi ó a bằng: 1 n 11 A. an . B. an . C. a . D. a n .
Câu 5: Cho a là số thực dương. Giá trị của biểu thức P a a bằng A. a . B. a5 . C. a . D. a . lOMoAR cPSD| 47167580
Câu 6: Rút gọn P a 2. 1 2 1 ,a 0. a A. a . B. a C. a . D. a .
Câu 7: Cho hai số dương a b a, 1 . Mệnh ề nào dưới ây sai? log ab
A. loga a 2a . B. logaa .
C. log 1a 0. D. a b .
Câu 8: Cho hai số dương a b; với a 1, khi ó loga4 ab bằng 2 . 22 1 2 A. loga b B. 1 1loga b C. 4loga b D. 4 4loga b 4 4
Câu 9: Tính giá trị của biểu thức: P loga2 a b10 2 log a a log3b b 2 b A. 3 . B. 1 . C. 2 . D. 2 .
Câu 10: Trong các hàm số sau, hàm số nào là hàm số mũ? A. y x B. y x C. y D. y 3x
Câu 11: Đường cong ở hình bên là ồ thị của hàm số nào dưới ây? 3 2 3x lOMoAR cPSD| 47167580 A. y log2 x 1. B. y log x 1. y log . 1 C. 1 x 3 2 D. y log3 x.
Câu 12: Tìm tập xác ịnh của hàm số y log2024 3x x 2 . A. D B. D 0; C. D ; 0 3; D. D 0; 3
Câu 13: Trong các hàm số sau hàm số nào nghịch biến trên ? A. log3 x2
B. y log x3 C. y
4e x D. y 52 x
Câu 14: Tìm tập nghiệm S của bất phương trình log3 2x 3 log3 1 x A. 23; B. 23; 32 C. 32;1 D. ; 32 3
Câu 15: Gọi x x1, 2 là hai nghiệm của phương trình 2 x x 5 2 2 3
2 3x . Giá trị A x x 1 2 bằng? A. A 2 . B. A 1. C. A 2 . D. A 1.
Câu 16: Cho hàm số y f x xác ịnh trên thỏa mãn f x lim
f 3 2. Khẳng ịnh nào sau ây lOMoAR cPSD| 47167580 x 3 x 3 úng? A. f 2 3. B. f x 2 . C. f x 3. D. f 3 2 .
Câu 17: Hệ số góc của tiếp tuyến với ồ thị hàm số f x
x3 tại iểm M( 2 ;8)là A. 192. B. 12. C. 12. D. 192.
Câu 18: Một vật giao ộng iều hòa có phương trình
quãng ường phụ thuộc thời gian s Asin t .
Trong ó A , , là hằng
số, t là thời gian. Khi ó
biểu thức vận tốc của
vật là? A. v Acos t B. v A cos t
C. v A cos t D. v Acos t
Câu 19: Đạo hàm của hàm số f x( ) 2 3x2 bằng biểu thức nào sau ây? 1 6x2 3x
3x 2 2 3x2 2 2 3x2 2 3x2 2 3x2 A. . B. . C. . D. .
Câu 20: Cho hàm số y ln ex m2 . Tìm m ể y 1 . A. m
e; e . B. m e. 1 C. m . D. m e . e Câu 21: Tính ạo hàm của lOMoAR cPSD| 47167580 hàm số f x sin 22 x cos3x .
Trang 2 | 4 m ª 1 0 2 A. f
x 2sin4x 3sin3x . B. f
x 2sin4x 3sin3x . C. f
x sin4x 3sin3x . D. f
x 2sin2x 3sin3x
Câu 22: Cho hàm số f x 2x3 x , giá trị của f 1 bằng A. 6 . B. 5. C. 12. D. 12.
Câu 23: Đạo hàm cấp hai của hàm số y sin2 x là A. y '' cos x2 .
B. y '' 2sin 2x. C. y 2cos2x.
D. y '' 2cos x .
Câu 24: Cho hình lập phương ABCD ABCD. . A' C' A C
Đường thẳng BD vuông góc với ường thẳng nào sau ây? A. AA'. B. CD.
C. AD . D. BD . D ' B' D B
Câu 25: Qua iểm O cho trước, có bao nhiêu mặt
phẳng vuông góc với ường thẳng cho trước? A. Vô số. B. 2 . C. 3 . D. 1.
Câu 26: Cho mặt phẳng ( )P và ường thẳng c
không nằm trên ( )P . Khi ó, ( )P c nếu: lOMoAR cPSD| 47167580
A. Mặt phẳng ( )P chứa hai ường thẳng ab,
thỏa mãn ab, cùng vuông góc với ường thẳng c .
B. Mặt phẳng ( )P chứa một ường thẳng
vuông góc với ường thẳng c .
C. Mặt phẳng ( )P chứa ít nhất hai ường thẳng
vuông góc với ường thẳng c .
D. Mặt phẳng ( )P chứa hai ường thẳng cắt
nhau ab, thỏa mãn ab, cùng vuông góc với ường thẳng c .
Câu 27: Cho hình chóp S ABCD. có áy ABCD
là hình vuông và SA vuông góc với mặt
phẳng áy. Chọn áp án úng:
A. BA (SAC)
B. BA (SBC)
C. BA (SAD)
D. BA (SCD)
Câu 28: Cho hình chóp S ABCD. có áy là hình
vuông, cạnh bên SA vuông góc với áy (ABCD) .
Khẳng ịnh nào sau ây sai?
A. CD (SBC). B. SA ABC ( ).
C. BC (SAB) .
D. BD (SAC).
Câu 29: Cho hình chóp SABC. có áy ABC là
tam giác vuông cân tại A và AB a 2. Biết SA
ABC và SA a . Tính số o góc nhị diện S BC A, , . A. 30 . B. 45 . C. 60 . D. 90 .
Câu 30: Cho hình chóp S ABC. có SA ABC ;
tam giác ABC ều cạnh a và SA a . Tìm góc giữa ường
thẳng SC và mặt phẳng ABC . A. 60o . B. 45o . C. 135o . D. 90o .