lOMoAR cPSD| 47167580
Bước 1: Tính detA = m – 13 và detB = m – 7.
Bước 2: Suy ra det(AB) = (m – 13)(m – 7).
Bước 3: Kết luận AB khả nghịch khi và chỉ khi m 7 hoặc m 13.
Sinh viên ó giải như thế là úng hay sai? Nếu sai thì sai từ bước nào? A. Lời
giải úng; B. Lời giải sai từ bước 1;
C. Lời giải sai từ bước 2;
D. Lời giải sai ở bước 3. x x2 x3 x 2 x2010 x2011 0
Câu 1B Số nghiệm thực của phương trình (ẩn x) : 0 x2 x2008 x = 0 là 1 x 0 2009 1 0 0 1
A. 1; B. 2; C. 3; D. 4.
Câu 1C Xét bài toán: Cho hệ phương trình tuyến tính phụ thuộc tham số thực m
x yz 2t u 2;
2x y z 5t u 6;
3x 2y z 4t u 5;
4x 3y 2z 6t 2u m.
Tìm m ể hệ có nghiệm. Với m tìm ược, hệ có duy nhất nghiệm hay vô số nghiệm? Một
sinh viên giải bài toán theo các bước dưới ây.
Bước 1: Lập ma trận hệ A số và ma trận mở rộng [A|B] của hệ. Biến ổi sơ cấp ta tính ược rank(A) =
3 với mọi m, còn rank([A|B]) = 3 khi và chỉ khi m = 7.
Bước 2: Từ ó suy ra hệ có nghiệm khi và chỉ khi m = 7.
Bước 3: Khi m = 7, vì hệ có 4 phương trình, mà rank(A) = ran([A|B]) = 3 nên hệ có vô số nghiệm. Lời
giải ó hoàn toàn úng hay có sai lầm? Nếu có sai lầm thì ở bước nào?
A. Lời giải hoàn toàn úng; B. Lời giải phạm sai lầm ở bước 1; C. Lời
giải phạm sai lầm ở bước 2; D. Lời giải phạm sai lầm ở bước 3.
Câu 2 Xét một thị trường gồm ba loại hàng hóa. Hàm cung, hàm cầu và giá của chúng thỏa mãn các iều kiện sau
Qs1 2 4p1 p2 p3; Qs2 1 p1 4p2 p3; Qs3 2 p1 p2 4p3;
Qd1 10 2 p1 p2 p3; Qd2 1 p1 2p2 p3; Qd3 3 p1 2p2 2p3 .
Điểm cân bằng thị trường ( p p p
)của từng loại hàng hóa là: 1, 2, 3
A. (2, 3, 1); B. (3, 1, 2); C. (1, 2, 3); D. Một bộ ba khác.
Câu 3 Xét mô hình IS-LM như sau I = 30 – 15r; C = 60 + 0,1Y; L = 3Y – 10r; M0 = 1140 và G0 = 360.
Ở ây r là lãi suất, C là tiêu dùng dân cư, L lượng cầu tiền mặt, M0 là lượng cung tiền mặt, Y là tổng thu lOMoAR cPSD| 47167580
nhập quốc dân, I là ầu tư chính phủ, G0 là chi tiêu chính phủ. Tìm thu nhập và lãi suất cân bằng Y , r . A. (Y =
400, r = 6); B. (Y = , r =
); C. (Y = 40, r = 0,6); D. Một cặp giá trị khác. 0,2 0,3 0,2
Câu 4 Giả sử một quốc gia có ba ngành sản xuất với ma trận hệ số ầu vào A = 0,4 0,1 0,2 và nhu 0,1 0,3 0,2
cầu cuối cùng của các ngành lần lượt là 10, 5, 6. Tìm ầu ra cho mỗi ngành.
A. x1= 24,84; x2 = 20,68; x3 = 18,36; B. x1= 18,36; x2 = 24,84; x3 = 20,68;
C. x1= 20,68; x2 = 18,36; x3 = 24,84; D. Một áp án khác.
Câu 5 (Khó - Bí mật không bật mí!)
Câu 6 KGVT, ĐLTT, Cơ sở, Tọa ộ
Câu 6A Xác ịnh giá trị thực của m ể hệ ba vector dòng dưới ây ộc lập tuyến tính trong R4. u 2,1,1,m v , 2,1, 1,m w , 10,5, 1,5m
A. m 0 ; B. 0 m 1 C. m tùy ý
D. Không có giá trị m nào.
Câu 6B Xác ịnh iều kiện của tham số thực của m ể hệ ba vector dòng dưới ây là cơ sở của R3. u 1,3,1 , v 2,7,5 , w 5,16,m
A. Không có giá trị m nào; B. m = 8; C. m tùy ý; D. m 8.
Câu 6C Xét không gian các vectơ dòng R3với cơ sở (u1 = (1, 0, 0), u2 = (1, 1, 0), u3 = (0, – 1, 1)). Tọa ộ
(x, y, z) của vectơ dòng v = (m, 0, 1) trong R3ối với cơ sở này là
A. (x, y, z) = (m – 1, 1, 1); B. (x, y, z) = (m, 0, 0);
C. (x, y, z) = (m – 2, 2, 2); D. (x, y, z) = (m, 0, 1).
Câu 7, 8 Dạng toàn phương
Câu 7 Cho dạng toàn phương 3 biến x, y, z phụ thuộc tham số thực m q =
q(x, y, z) = mx2 – 4mxy + 2mxz + (5m + 1)y2 – 2(3m + 1)yz + 3(m + 1)z2. Chọn
khảng ịnh sai trong các khẳng ịnh dưới ây. A.
(q không âm) (cả m, m + 1, m + 2 ều không âm) m ≥ 0. B.
(q xác ịnh dương) (cả m, m + 1, m + 2 ều dương) m > 0. C.
(q không dương) (cả m, m + 1, m + 2 ều âm) m < – 2. lOMoAR cPSD| 47167580 D.
(q ổi dấu) (trong m, m + 1, m + 2 có ít nhất một cặp trái dấu) – 2 < m < 0.
Câu 8 (Khó – Bí mật không bật mí!) Câu 9, 10 QHTT
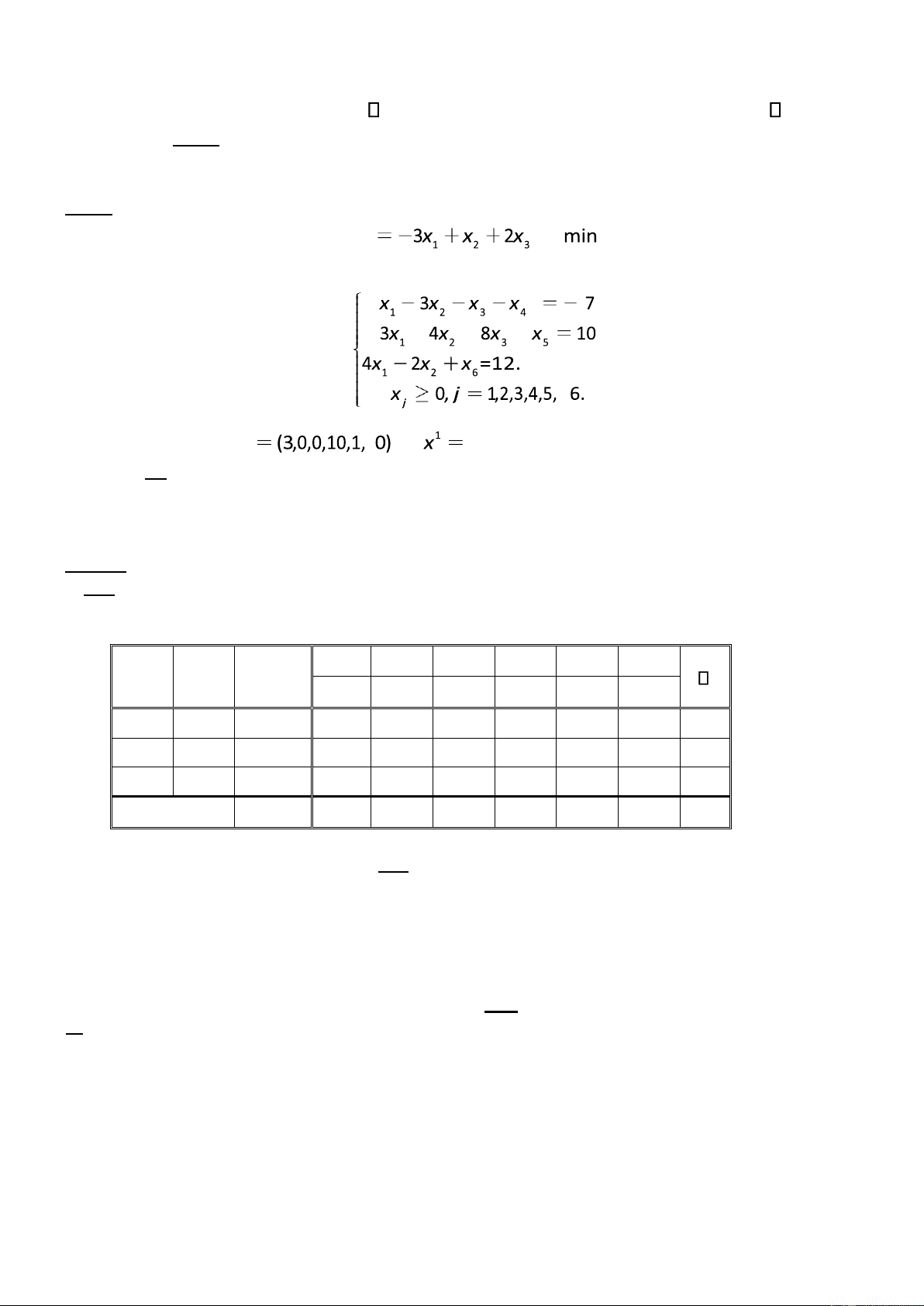
Câu 9 Cho bài toán QHTT sau: f
với các iều kiện ràng buộc
Xét các vectơ sau: x0 và (5,4,0,0,11,0). Tìm khẳng ịnh sai.
A. x0, x1 ều là phương án; B. x0 là phương án cực biên;
C. Chỉ có x1 là phương án cực biên ; D. x1 là phương án cực biên.
Câu 10 Xét một bài toán QHTT dạng chính tắc chuẩn (N) có 6 biến xj, j = 1, 2, 3, 4, 5, 6 với hàm mục tiêu
ạt min. Giả sử với P.A.C.B x* = (x1, x2, x3, 0, 0, 0) mà ba biến ầu là các biến cơ sở ta lập ược bảng ơn hình tương ứng như sau: Biến Hệ số x1 x2 x3 x4 x5 x6 cơ sở cơ sở PACB i c1 c2 c3 c4 c5 c6 x1 c1 2 1 0 0 1 1 1 2 x2 c2 12 0 1 0 1 0 – 1 12 x3 c3 9 0 0 1 2 4 – 3 9/2 Bảng 1 … 0 0 0 – 2 0 – 3
Khẳng ịnh nào trong các khẳng ịnh sau là úng?
A. PACB ang xét chưa tối ưu nhưng có thể cải tiến ể ược PATU ;
B. PACB ang xét là PATU duy nhất của bài toán ã cho;
C. PACB ang xét là PATU của bài toán ã cho nhưng không phải là PATU duy nhất.
D. Bài toán vô nghiệm.
Câu 11, 12, 13 Phép tính vi phân 1 biến và ứng dụng Câu U
11 Xét các khẳng ịnh dưới ây. U
11.1. Xét hàm doanh thu R= R(Q) theo biến sản lượng Q. Doanh thu cận biên tại mức sản lượng
Q = Q0 là MR(Q0) = R ’(Q0).
11.2. Doanh thu cận biên tại mức sản lượng Q0 chính là xấp xỉ lượng thay ổi của doanh thu khi sản
lượng tăng lên 1 ơn vị từ mức Q0 lên mức Q0 + 1. lOMoAR cPSD| 47167580
11.3. Giả sử Q = S(P) là hàm cầu trong kinh tế biểu thị sự phụ thuộc của lượng cung Q =Qs theo sự
biến ổi của giá P (trong giả thiết các yếu tố khác không ổi). Hệ số co giãn của cung theo giá tại mức
giá P = P0 là (P0) = S P'( 0)
P0 . S P( 0)
11.4. Hệ số co giãn (P0) của cầu theo giá tại mức giá P0 chính là xấp xỉ lượng tăng của lượng cầu khi
giá tăng lên 1 % từ mức P0 lên mức P0 + (1%)P0.
Số khẳng ịnh úng trong các khẳng ịnh trên là A. 1; B. 2; C. 3; D. 4.
Câu 12 Một công ty ộc quyền sản xuất và tiêu thụ một loại sản phẩm ó trên thị trường. Giả sử hàm cầu (theo U U
giá P) của sản phẩm ó là Q = 1500 – 5P. Doanh thu R và doanh thu cận biên MR (theo sản lượng Q) tại mức
sản lượng Q = 650 ( ơn vị sản phẩm) là:
A. R = 300Q – 0,2Q2; MR(650) = 40; B. R = 300 – 0,2Q; MR(650) = – 0,2;
C. R = 1500P – 5P2; MR(650) = -200; D. Một phương án khác. U
Câu 13 (Khó – Bí mật không bật mí!)
Câu 14, 15, 16, 17 Phép tính vi phân hàm hai biến và ứng dụng
Câu 14 Cho hàm sản xuất Cobb-Douglas QK L aK L( , ) 2 ở ó a, , là các hằng số dương ã cho, K là U
lượng vốn ầu tư vào sản xuất, L là lượng lao ộng dùng trong quá trình sản xuất. Xét các khẳng ịnh dưới ây.
14.1. Q là hàm thuần nhất bậc + tức là Q(tK, tL) = t + Q(K,L) với mọi t > 0.
14.2. Hiệu quả sản xuất giảm theo quy mô khi và chỉ khi 2 + < 1.
14.3. Hiệu quả sản xuất không tăng theo quy mô khi và chỉ khi 2 + ≤ 1.
Trong các khẳng ịnh trên, có bao nhiêu khẳng ịnh sai? A. 0; B. 1; C. 2; D. 3. U
Câu 15 Một doanh nghiệp có hàm sản xuất QK L( , ) 2K L0,3 0,5 ở đó K là lượng vốn đầu tư vào sản xuất, L là
lượng lao động dùng trong quá trình sản xuất. Giả sử doanh nghiệp đó tiến hành sản xuất trong quỹ ngân sách
cố định 4800$. Hỏi doanh nghiệp đó cần sử dụng bao nhiêu đơn vị vốn và bao nhiêu đơn vị lao động để có
sản lượng tối đa biết rằng giá thuê một đơn vị tư bản là 6$, còn giá thuê một đơn vị lao động là 2$?
A. K= 300, L = 1500; B. K= 400, L = 1200; C. K= 500, L = 900; D. Một cặp giá trị khác.
Câu 16 Một công ty sản xuất hai loại hàng hoá có hàm cầu lần lượt là 4 2 2 4 lOMoAR cPSD| 47167580
Q1 280 3P1 3P2; Q2 420 3P1 3P2 (P1, P2 lần lượt là giá của hai loại hàng hóa ó).
Giả sử tổng chi phí ược xác ịnh bởi công thức TC Q( ) 6Q 2 2 1 6Q2 Q1 QQ1 2 Q2 .
Tìm mức sản lượng Q1, Q2 ể công ty thu ược lợi nhuận tối a.
A. Q1 = 106, Q2 = 71; B. Q1 = 71, Q2 = 106; C. Q1 = 105, Q2 = 70; D. Q1 = 70, Q2 = 105.
Câu 17 (Khó – Bí mật không bật mí)
Câu 18, 19 Tích phân hàm 1 biến và ứng dụng
Câu 18 Cho biết hàm cầu và hàm cung ối với một loại hàng hóa nào ó là
Qd = 113 p ; Qs = p 1 (p là giá của loại hàng hóa ó).
Hãy tính thặng dư của nhà sản xuất (PS) và thặng dư của người tiêu dùng (CS) ối với loại hàng hóa ó. 833 686 686 511 A. PS , CS ; B.) PS 3 , CS 3 ; 3 3 510 688 C. PS , CS
; D. Một kết quả khác. 3 3
Câu 19 Giả sử một doanh nghiệp có lượng ầu tư ( ơn vị tính: triệu ồng) theo thời gian t cho bởi I(t) = 350t0,75; t ≥ 0.
Hãy xác ịnh quỹ vốn tại thời iểm t = 1 doanh nghiệp ó biết rằng quỹ vốn ban ầu là K0 = 100.
A. 300; B. 250; C. 200; D. 150. Câu 20 PTVP cấp 1
Câu 20 Nghiệm tổng quát của phương trình vi phân xy y x' (x > 0) là x x .
A. y = x(C + lnx); B. y = x(C – lnx); C. y
C ln x ; D. y C ln x