


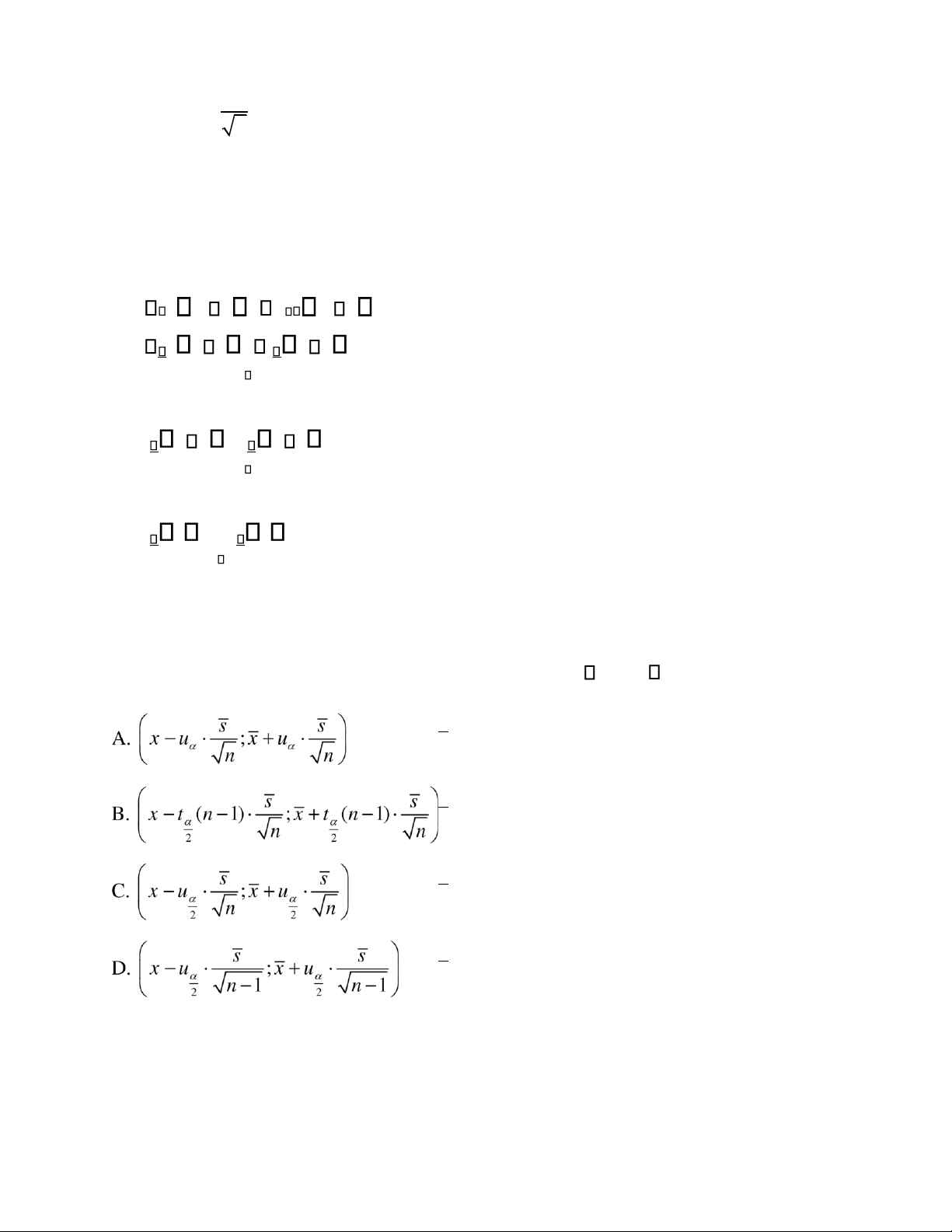







Preview text:
lOMoAR cPSD| 45764710
ĐỀ THI TRẮC NGHIỆM
MÔN: LÝ THUYẾT XÁC SUẤT VÀ THỐNG KÊ TOÁN Câu 1
Một công ty ấu thầu ba dự án 1 2 3, , . Gọi Ai là biến cố “Công ty trúng thầu dự án thứ i”,
i 1 3, . Nội dung của biến cố A1 A2A3 là:
A. Công ty trúng thầu ít nhất 1 dự án
B. Công ty trúng thầu cả 3 dự án
C. Công ty trúng thầu 1 dự án
D. Công ty trúng thầu ít nhất 2 dự án Câu 2
Một kho hàng chứa sản phẩm của 3 nhà máy 1 2 3, , . Chọn ngẫu nhiên một sản phẩm của
kho hàng. Gọi Ai là biến cố “Chọn ược sản phẩm của nhà máy i”, i 1 3, . Khẳng ịnh nào
dưới ây là khẳng ịnh úng?
A. Các biến cố A ,A ,A1 2 3 ộc lập với nhau
B. Các biến cố A ,A ,A1 2
3 ộc lập với nhau và lập thành một hệ ầy ủ các biến cố
C. Các biến cố A ,A ,A1 2
3 lập thành một hệ ầy ủ các biến cố
D. Các biến cố A ,A ,A1 2 3 không ộc lập với nhau, không lập thành một hệ ầy ủ các biến cố Câu 3
Cho A,B,C là 3 biến cố bất kì. Biến cố ABC tương ương với biến cố nào sau ây? A. A.B.C B. A B C lOMoAR cPSD| 45764710 C. A B C D. A B C Câu 4
Có ba người, mỗi người bắn một viên ạn vào bia. Gọi Ai là biến cố "Người thứ i bắn
trúng bia", i 1;3. Khi ó, biến cố "Cả ba người không bắn trúng bia" là: A. AAA1 2 3 B. A A A1 2 3
C. A1 A2 A 3 D. A A A1 2 3 Câu 5 Cho P A 0,4;P B 0,3;P AB
0,2. Khi ó, P A B bằng: A. 0,7 B. 0,9 C. 0,3 D. 0,5 Câu 6
Kiểm tra 3 sản phẩm của một cửa hàng. Gọi Ai là biến cố “Sản phẩm thứ i bị lỗi”i 1,3 và
A là biến cố “Có úng một sản phẩm bị lỗi”. Khẳng ịnh nào dưới ây úng?
A. A A1 A A 2 3 B. A A A 2. 3 A A1. 3 A A1. 2 lOMoAR cPSD| 45764710 C. AAA1 2 3 A D. A A A A 1. 2. 3
A A A1. 2. 3 A A A1. 2. 3 Câu 7
Một người bắn 3 viên ạn vào bia. Gọi Ai là biến cố “Viên ạn thứ i trúng bia” i 1,3 và A là
biến cố “bia bị trúng ạn”. Khẳng ịnh nào dưới ây úng?
A. A A A A1 2 3 B. A A A A 1. 2. 3
A A A1. 2. 3 A A A1. 2. 3
C. A A1 A2 A3 D. A A1 A2 A3 Câu 8
A, B là 2 biến cố, biểu thức AB V biểu thị mối quan hệ giữa A và B là: B. Đối lập C. Độc lập D. Không có quan hệ A. Xung khắc Câu 9
Có 3 người cùng bắn vào một mục tiêu, mỗi người bắn 1 phát. Gọi Ai là biến cố “Người
thứ i bắn trúng mục tiêu” (i 1,3). Biến cố “Chỉ có người thứ 2 bắn trúng mục tiêu” ược
biểu diễn qua các biến cố A A1, 2 , A3 là: A. A A A1. 2. 3 B. A A A1. 2. 3 C. A A A1 2 3
D. A A A A A A A A A1. 2. 3 1. 2. 3 1. 2. 3 lOMoAR cPSD| 45764710 Câu 10
Một xạ thủ bắn vào mục tiêu 10 lần, khả năng bắn trúng mục tiêu ở mỗi lần là 90%. Gọi
X là số lần xạ thủ ó bắn trúng mục tiêu trong 10 lần bắn. Khẳng ịnh nào dưới ây là khẳng ịnh úng?
A. X ~ B( ; ,9 0 9487)
B. X ~ N(10 0 9; , )
C. X ~ B(10 0 9; , )
D. X ~ N(10 0 9; , 2 ) Câu 11
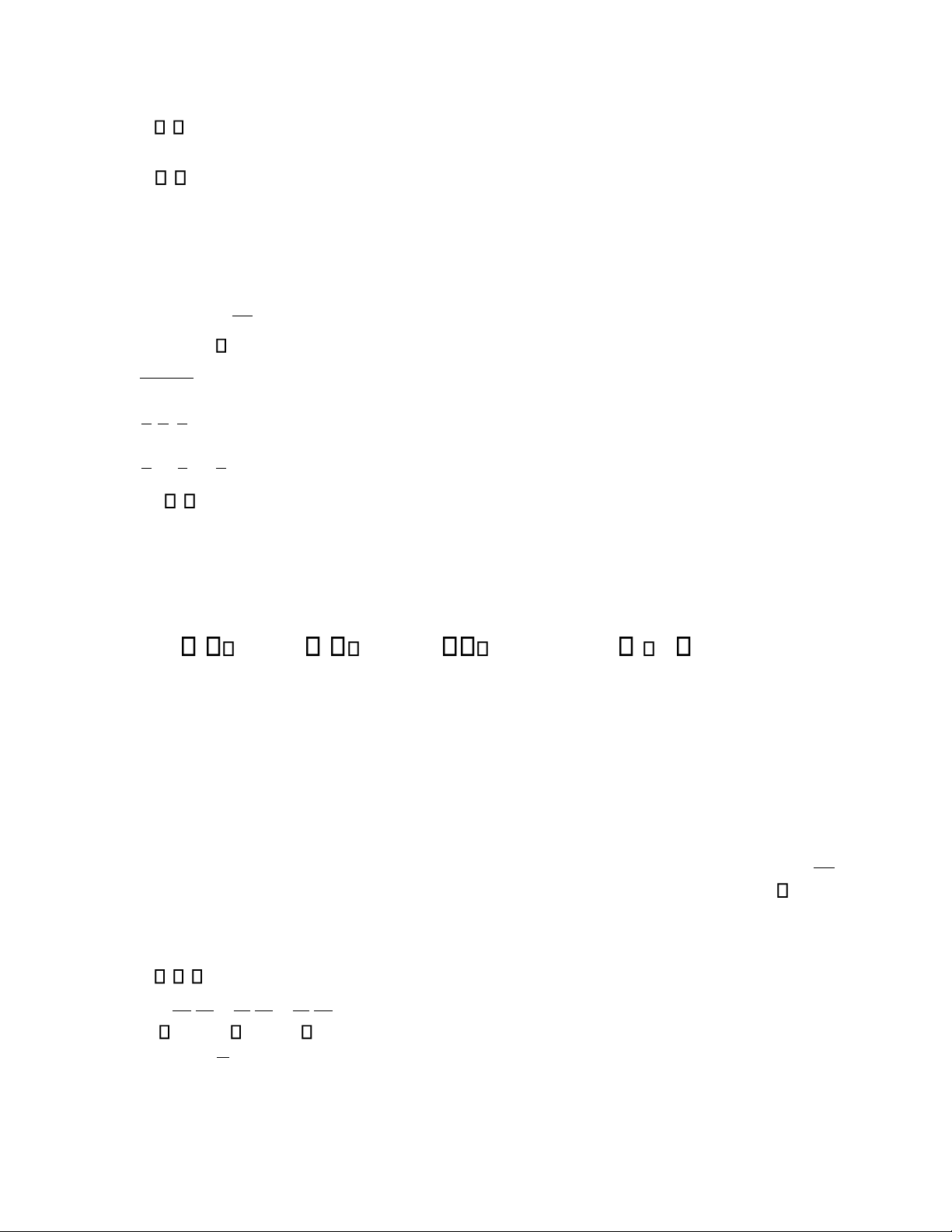
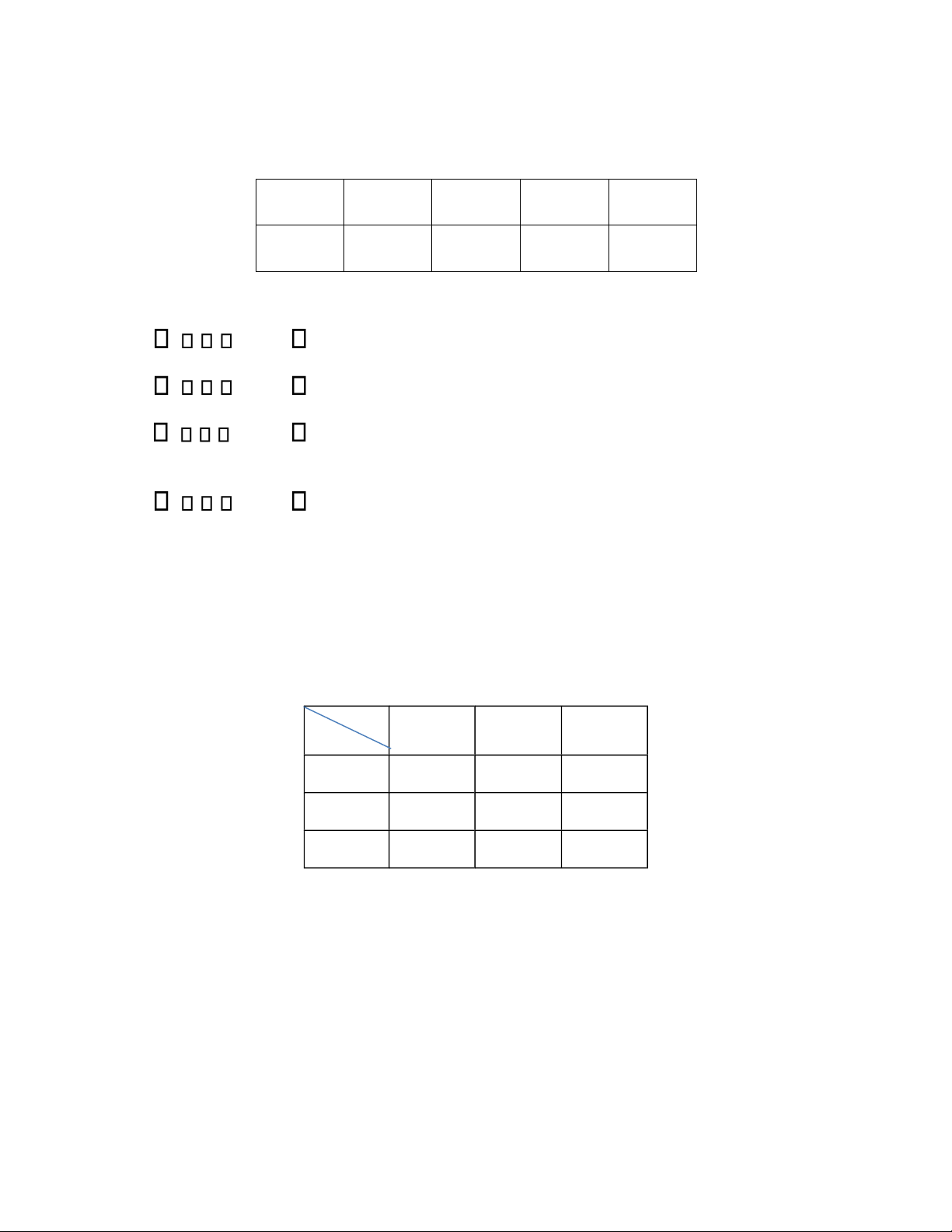
Cho ại lượng ngẫu nhiên hai chiều ( X ,Y ) có bảng phân phối xác suất: X 10 12 15 Y 25 01, 02, 02, 30 01, 01, 01, 35 008 , 007 , 005 ,
Khẳng ịnh nào dưới ây là khẳng ịnh sai?
A. P( X 10,Y 25) 0 1,
B. P( X 10 / Y 25) 0 1,
C. P ( X 10).(Y 25) 0 1, D. P ( X,Y ) (10 25, ) 0 1, Câu 12
Cho X và Y là hai ại lượng ngẫu nhiên có vọng toán lần lượt là 12 5, và 16 8, . Vọng toán
của ại lượng ngẫu nhiên 2X Y là: A. 418, lOMoAR cPSD| 45764710 B. 66 8, C. 33 2, D. 8 2, Câu 13.
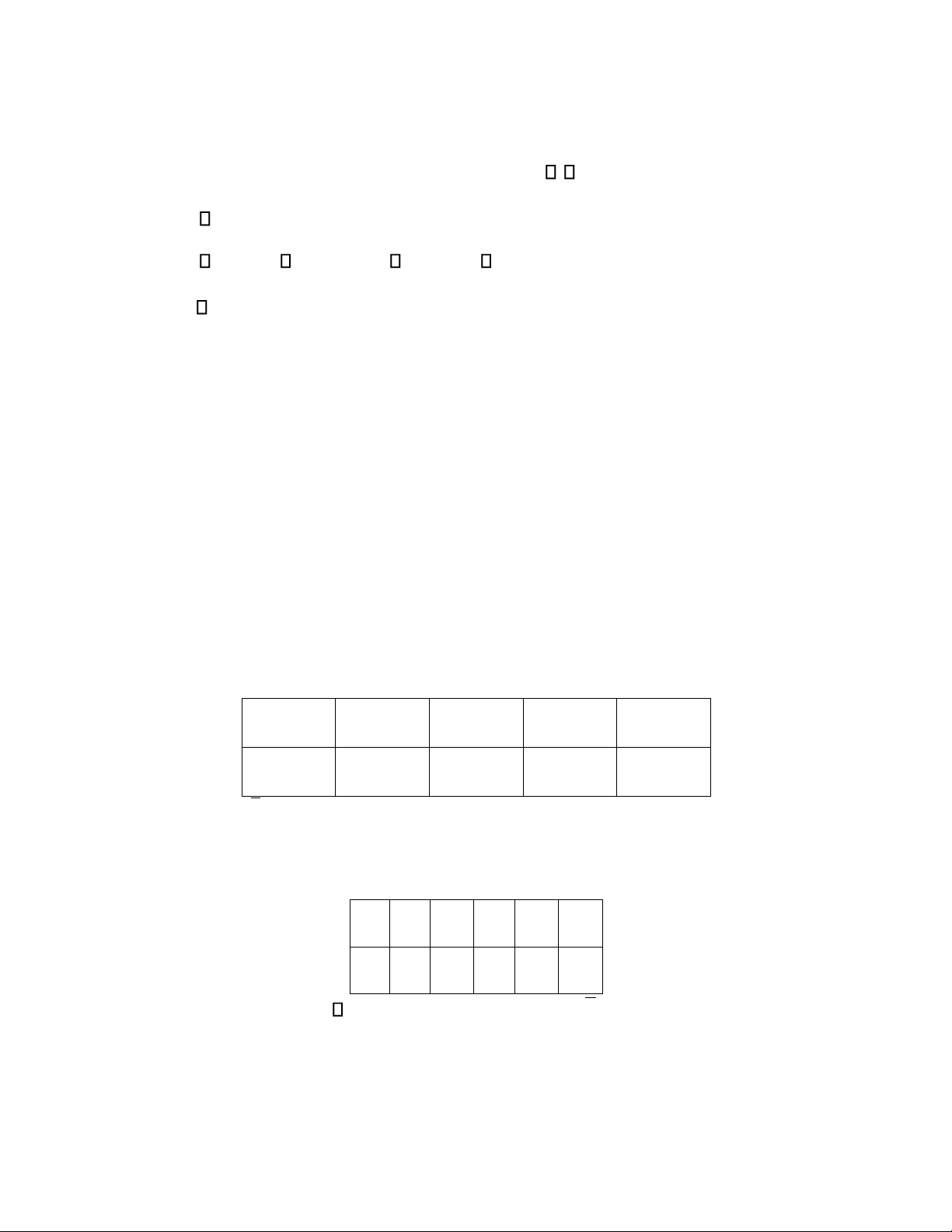
Cho ại lượng ngẫu nhiên rời rạc X có bảng phân phối xác suất X 1 2 3 4 5
P 0,15 0,2 0,25 0,3 p Khi ó p bằng: A. 0,35 B. 0,1 C. 0,05 D. 0,1 Câu 14
Cho ại lượng ngẫu nhiên rời rạc X có bảng phân phối xác suất X 1 2 3 4 5
P 0,1 0,2 0,3 0,25 0,15 Cho biết E X
3,15. Khi ó D X ược tính theo biểu thức nào trong các biểu thức bên dưới? A. D X 1 .0,12 2 .0,22 3 .0,32 4 .0,252 5 .0,152 B. D X 1 .0,12 2 .0,22 3 .0,32 4 .0,252 5 .0,152 3,152 C. D X 1 .0,12 2 .0,22 3 .0,32 4 .0,252 5 .0,152 3,15 D. D X
1.0,12 2.0,22 3.0,32 4.0,252 5.0,152 3,152 lOMoAR cPSD| 45764710 Câu 15
Cho ại lượng ngẫu nhiên X có bảng phân phối xác suất như sau 1 2 3 4 X P 0,1 0,3 0,25 0,35
Chọn một áp án úng trong các áp án sau: A. P 1 X 3 0,4 B. P 1 X 3 0,4 C. P 1 X 3 0,4 D. P 1 X 3 0,4 Câu 16
Thu nhập trong một năm của các cặp vợ chồng ở một ịa phương là ại lượng ngẫu nhiên hai
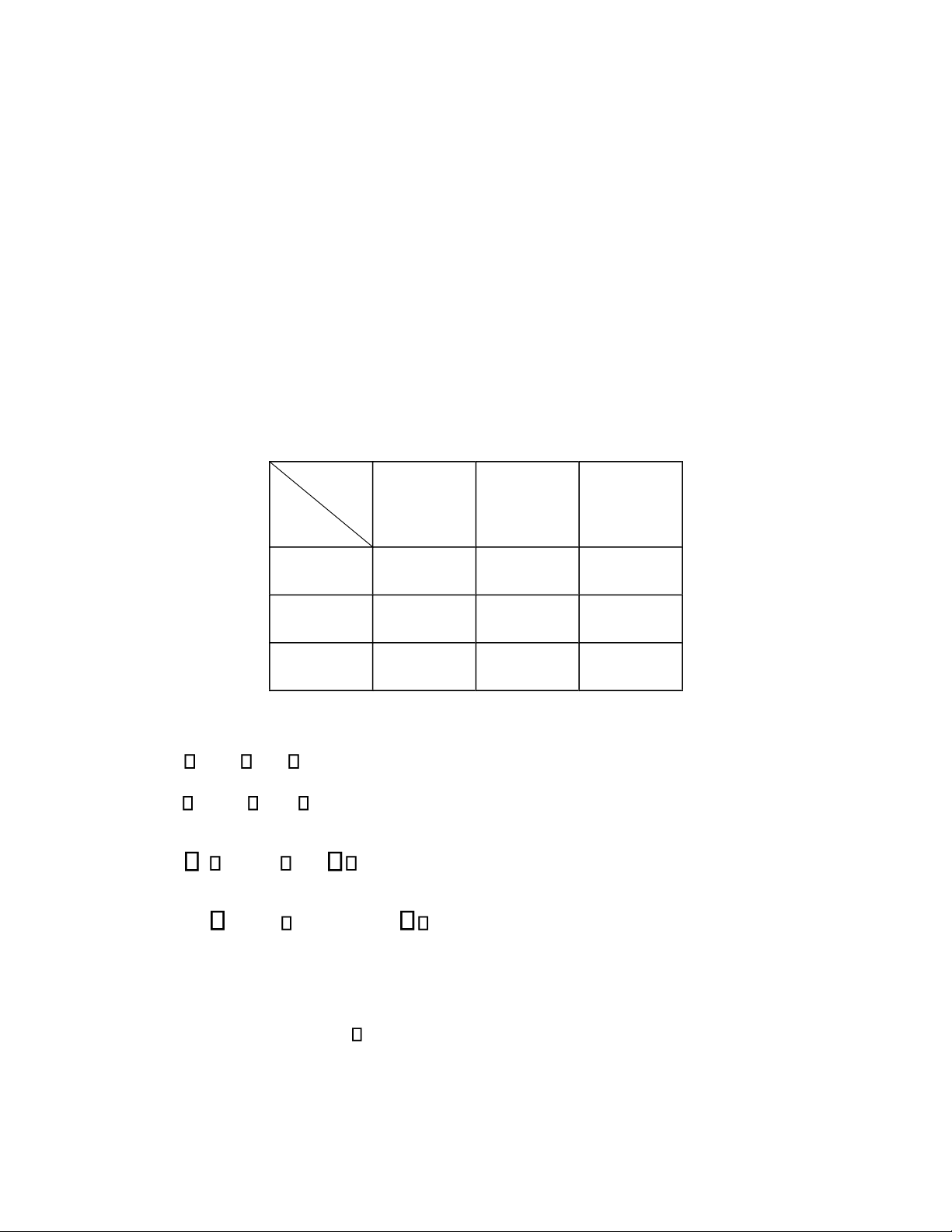
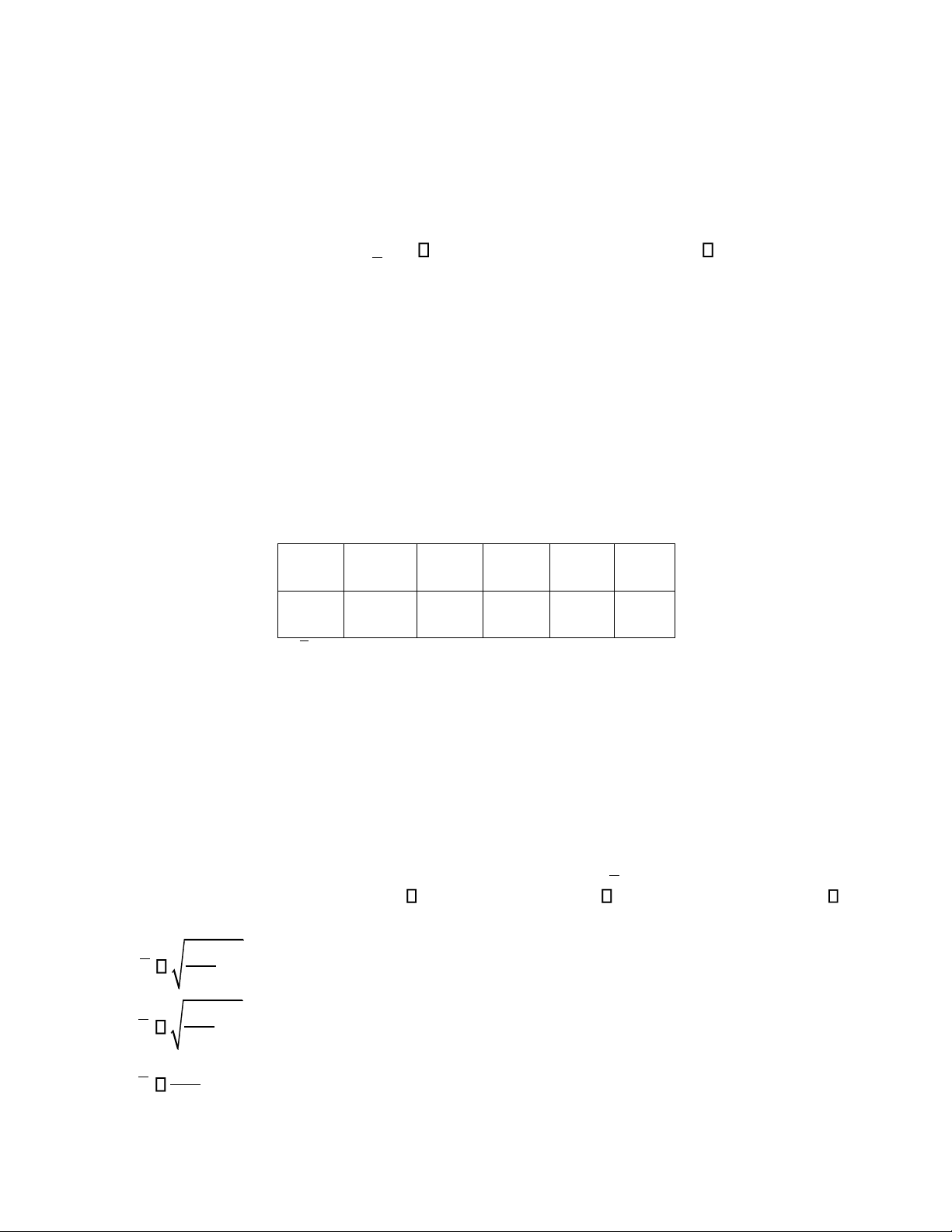
chiều có bảng phân phối xác suất ồng thời như sau: Y 50 70 100 X 0, 1 0 , 15 0 , 05 40 0 , 05 0, 25 , 0 15 60 0 , 05 , 0 15 0 , 05 80
Trong ó, X (triệu ồng) là thu nhập của vợ, Y (triệu ồng) là thu nhập của chồng. Xác suất
cặp vợ chồng ó có tổng thu nhập dưới 110 triệu ồng một năm là: A. 0,15 B. 0,05 C. 0,1 D. 0,25 lOMoAR cPSD| 45764710 Câu 17
Cho X , Y là các ại lượng ngẫu nhiên, biểu thức E(2X 5Y 3) bằng:
A. 2 (E X) 5 ( )E Y
B. 2 (E X) 5 ( )E Y 3 C. 4 (E X) 25 ( )E Y 9
D. 4 (E X) 25 ( )E Y Câu 18
Một công nhân sản xuất 10 sản phẩm, xác suất mỗi sản phẩm ạt tiêu chuẩn bằng 0,8. Gọi
X là số sản phẩm ạt tiêu chuẩn trong 10 sản phẩm công nhân sản xuất ra. Quy luật phân
phối xác suất của X là: A. N(10;0,8) B. N(10;0,8 )2 C. B(10;0,8 )2 D. B(10;0,8) Câu 19 Cho dãy thống kê: X 250 315 389 455 m 18 30 42 10
Trung bình mẫu x là… Câu 20 Cho dãy thống kê: X 12 14 16 18 20 m 15 20 35 20 10
Cho biết kích thước mẫu n 100. Khi ó trung bình mẫu x là: A. 15,8 B. 16 lOMoAR cPSD| 45764710 C. 1580 D. 20 Câu 21
Cho một mẫu có kích thước mẫu là n 20 và ộ lệch tiêu chuẩn mẫu là s 5. Khi ó ộ lệch
tiêu chuẩn mẫu iều chỉnh s là: A. 5,26316 B. 5,12989 C. 4,87340 D. 2,29416 Câu 22 Cho dãy thống kê X 28 30 32 34 36 m 2 10 15 13 10
Ta có trung bình mẫu x bằng: A. 32 B. 32,76 C. 10 D. 32,67 Câu 23
Cho một mẫu có kích thước mẫu n 101 trung bình mẫu x 125 và phương sai mẫu s2 25. Biểu thức úng là: 100 A. s .25 101 101 B. s .25 100 101 C. s .25 100 lOMoAR cPSD| 45764710 D. s .25 Câu 24
Mối quan hệ giữa phương sai mẫu iều chỉnh và phương sai mẫu là:
A. S2(X) 1 S2(X) n B. S2(X) 1 S2(X) n 1 C. S2(X) n S2(X) n 1
D. S2(X) n 1S2(X) n Câu 25
Cân 100 quả xoài chín tại một nhà vườn thuộc tỉnh Vĩnh Long, ược bảng thống kê sau:
Khối lượng (kg) [0,4;0,56) [0,56;0,63) [0,63;0,71) [0,71;0,9) Số quả 17 28 32 23
Tần suất quả xoài chín có khối lượng từ 0,63 kg trở lên ở trong mẫu là: A. 0,55 B. 0,23 C. 0,32 D. 0,45 Câu 26
Để ước lượng chiều cao trung bình của học sinh ở một trường tiểu học, người ta chọn ngẫu
nhiên một mẫu gồm 200 học sinh, o chiều cao và thống kê số liệu. Muốn tìm giá trị tới hạn
ể thay số vào khoảng tin cậy khi ước lượng chiều cao trung bình học sinh trường ó, cần
phải sử dụng bảng số nào sau ây? lOMoAR cPSD| 45764710
A. Bảng giá trị tới hạn Student
B. Bảng giá trị tới hạn Khi bình phương
C. Bảng giá trị tới hạn Fisher
D. Bảng giá trị tới hạn chuẩn Câu 27
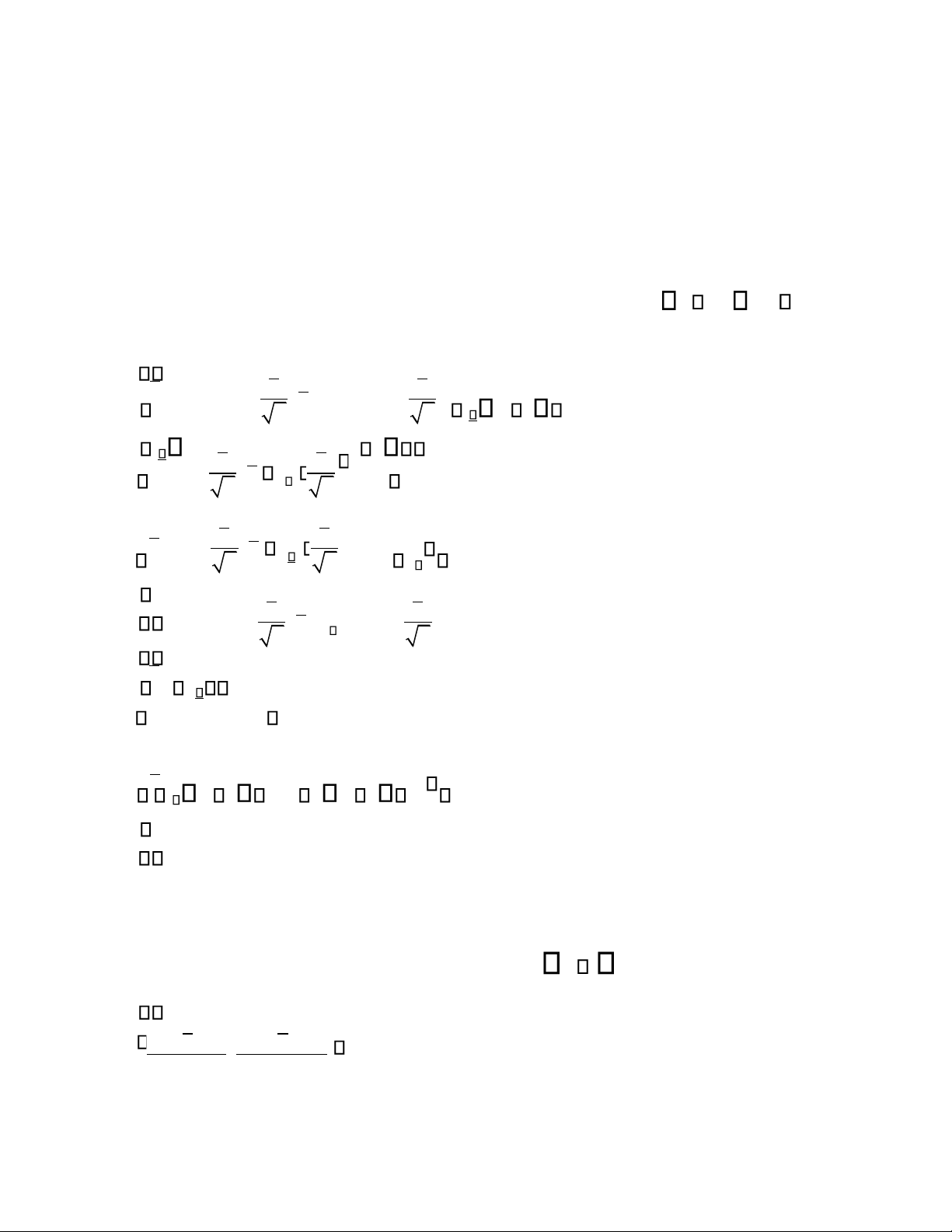
Công thức khoảng tin cậy cho vọng toán trong trường hợp mẫu lớn n 30 và chưa biết là: s s A. x t n 1 ;x n n t n 1 s s ; 2 x u 2 n n s s ; x u u n 2 n B. x s n n C. x u 2 t n 1 ;x t n 1 s D. x Câu 28
Công thức khoảng tin cậy cho phương sai khi X N a~ ; 2 với a chưa biết là: 2 ns ns 2 lOMoAR cPSD| 45764710 A. 22 n 1 ; 12 2 n 1 2 2 n 1 s n 1 s B. 22 n 1 ; 12 2 n 1 ns2 ns2 C. 2 n 1 ; 12 n 1 ns2 ns2 D. 22 n 1 ; 12 2 n 1 Câu 29
Công thức khoảng tin cậy cho vọng toán trong trường hợp mẫu nhỏ (n 30), X có phân
phối chuẩn và chưa biết là x
; x . Khi ó ược xác ịnh theo công thức: s 1 n A. t n 2 s n B. u s n 2 C. u 2 D. t n 1 s lOMoAR cPSD| 45764710 n 2 Câu 30
Để xác ịnh khoảng tin cậy của phương sai trong bài toán ước lượng phương sai của ại lượng
ngẫu nhiên có phân phối chuẩn với vọng toán chưa biết, cần xác ịnh các giá trị tới hạn nào? A. 2 n 1 ; 12 n 1 B. 2 n 1 ; 2 n 1 1 2 2 C. f n 1 ; f n 1 1 2 2 D. f
n ; f n 1 2 2 Câu 31
Trong bài toán ước lượng cho vọng toán a (trường hợp n 30và chưa biết), khoảng tin cậy của a là: lOMoAR cPSD| 45764710 Câu 32
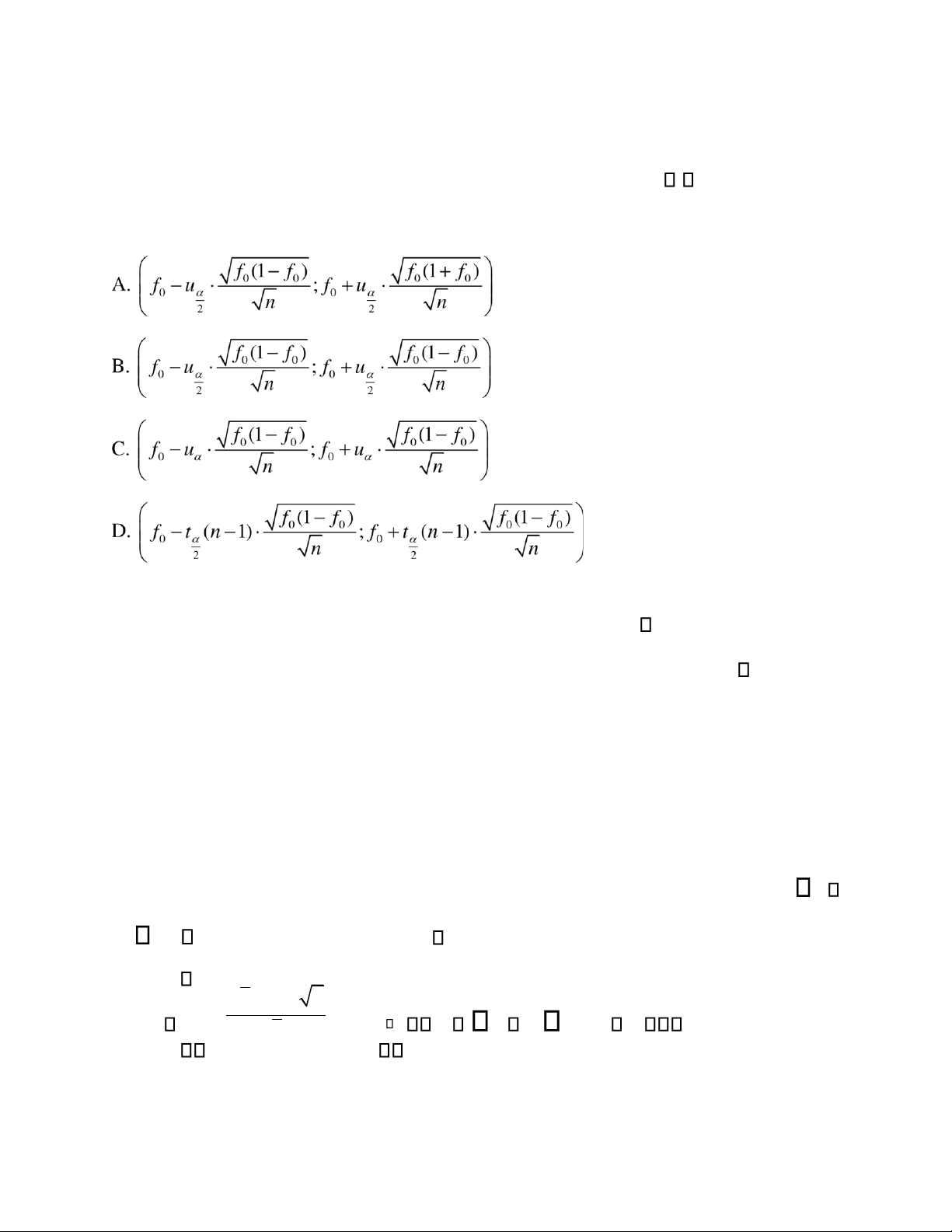
Trong bài toán ước lượng cho xác suất p (số liệu mẫu thỏa mãn nf0(1 f0) 20), khoảng tin cậy của p là: Câu 33
Khi kiểm ịnh phương sai của ại lượng ngẫu nhiên có nhận giá trị 2 0 hay không, ể tính
giá trị quan sát của ại lượng thống kê, số liệu nào sau ây không cần dùng? A. 02 B. a0 C. Kích thước mẫu D. Phương sai mẫu Câu 34
Miền bác bỏ giả thuyết H0 trong bài toán kiểm ịnh vọng toán trường hợp mẫu lớn n
30 và chưa biết với ối thuyết H1 :a a0 là: A. W G X a 0 n :G u S lOMoAR cPSD| 45764710 X a n B. W G 0 :G u S 2 C. W G X a 0 n :G u S S D. W
G X a n :G u Câu 35
Miền bác bỏ giả thuyết H 2
0 trong bài toán so sánh phương sai trường hợp X N a1 ~ 1; 1 , X 2 2 2 2 ~ N a
2; 2 và a a1, 2 chưa biết với ối thuyết H1 : 1 2 là: A. W
F S122 : F f
n1 1;n2 1 hoÆc F f n1 1;n2 1 S2 1 2 2
B. W F S122 : F f
n1 1;n2 1 hoÆc F f n1 1;n2 1 S2 1 2 2 C. W
F S122 : F f
n1 1;n2 1 hoÆc F f n1 1;n2 1 S2 1 2 2 S12 1 2 1 2 D. W F
2 : F f n 1;n 1 hoÆc F f n 1;n 1 lOMoAR cPSD| 45764710 S2 1 2 2 Câu 36
Cho bài toán kiểm ịnh: "Doanh số bán hàng trung bình của nhân viên ở cửa hàng A ược
nhận ịnh là 780 nghìn ồng/ngày. Trong một chương trình khuyến mại, iều tra ngẫu nhiên
doanh số bán hàng của 80 nhân viên thì thấy doanh số bán hàng trung bình là 920 nghìn
ồng/ngày với ộ lệch tiêu chuẩn mẫu là 120 nghìn ồng/ngày. Với mức ý nghĩa 5% có thể
cho rằng chương trình khuyến mại ó ã làm tăng doanh số bán hàng trung bình của các nhân
viên bán hàng ở cửa hàng A hay không?".
Cặp giả thuyết H0 và ối thuyết H1 của bài toán kiểm ịnh ã cho là: H a0 : 920 A. 1 920 H a: H a0 : 920 B. H a1 : 920 H a0 : 780 C. H a1 : 780
D. H a10 : 780780 H a: Câu 37 Cho hai ĐLNN X X 2 2
1, 2 có phân phối chuẩn X N a1 ~
1; 1 ; X2 ~ N a 2; 2 . Miền bác bỏ H a a 0 : 1 2
giả thuyết H0 trong bài toán kiểm ịnh H a a1 : 1 2 là: lOMoAR cPSD| 45764710 XX A. 1 2 W G : G u 2 2 S 1 S2 n n 1 2 B. W
G X X12 22 :G u Sn11 Sn22 X X1 2 C. W G 2 2 :G u S1 S 2 n1 n 2 D. W
G X X12 22 : G u Sn11 Sn22 Câu 38
Trong bài toán kiểm ịnh cho vọng toán a (trường hợp n 30 và chưa biết), ại lượng thống
kê ược chọn, với giả thuyết H0 úng là: lOMoAR cPSD| 45764710
A. G (X a n 0) S B. G (X a n )
C. G (X a n 0) 1 S
D. G (X a n 0) S Câu 39
Trong bài toán kiểm ịnh giả thuyết H0 :a a0 , ối thuyết H a1 : a0 với iều kiệnn 30 và
chưa biết, miền bác bỏ giả thuyết H0 là: ) n A. W T (X a0
:T t (n 1) S n
B. W T (X a0) :T t ( )n S C.W
T (X a0) n :T t (n 1) S D. W
T (X a0) n :T t (n 1) S 2 Câu 40
Một máy gồm ba bộ phận hoạt ộng ộc lập nhau, xác suất bộ phận thứ nhất, thứ hai, thứ ba
bị hỏng tương ứng là 008007 01, ; , ; , . Xác suất ể chỉ có bộ phận thứ hai không bị hỏng là: lOMoAR cPSD| 45764710 A. 000744, B. 093, C. 005796, D. 0008, Câu 41
Một người i mua hàng hai lần với xác suất lần ầu mua phải hàng xấu là 015, ; xác suất lần
hai mua phải hàng xấu là 01, . Xác suất người ó có ít nhất một lần mua phải hàng xấu là: A. 025, B. 0235, C. 022, D. 0015, Câu 42
Có hai máy, mỗi máy sản xuất một sản phẩm. Xác suất ể sản phẩm do máy thứ nhất, thứ
hai sản xuất không ạt yêu cầu lần lượt là 0,1 và 0,05. Xác suất ể có ít nhất một sản phẩm không ạt yêu cầu là: A. 0,145 B. 0,155 C. 0,15 D. 0,955 Câu 43
Một công ty ấu thầu hai dự án. Xác suất ể công ty trúng thầu dự án thứ nhất là 0,3. Xác
suất ể công ty trúng thầu dự án thứ hai là 0,35. Xác suất ể công ty trúng thầu cả hai dự án
là 0,1. Xác suất ể công ty trúng thầu úng một dự án là: A. 0,44 B. 0,65 C. 0,45 lOMoAR cPSD| 45764710 D. 0,55 Câu 44
Một ngân hàng phát hành hai loại thẻ thanh toán M và N. Tỉ lệ khách của ngân hàng sử
dụng thẻ loại M, N tương ứng là 40%, 55% và cả hai loại là 30%. Chọn ngẫu nhiên một
khách của ngân hàng ó. Xác suất người ó chỉ sử dụng 1 loại thẻ của ngân hàng là: A. 0,95 B. 0,35 C. 0,51 D. 0,65 Câu 45
Một người ầu tư vào ba loại cổ phiếu ABC, , . Xác suất trong khoảng thời gian T các cổ
phiếu này tăng giá lần lượt là là 0,6; 0,7; 0,8. Biết rằng các cổ phiếu A B C, , hoạt ộng ộc
lập nhau, xác suất trong thời gian T có úng một cổ phiếu tăng giá là: A. 2,1 B. 0,976 C. 0,188 D. 0,26 Câu 46
Một người ầu tư vào 2 dự án một cách ộc lập, khả năng có lãi của từng dự án tương ứng là
0,4; 0,5. Xác suất ể có ít nhất một dự án có lãi là: A. 0,9 B. 0,7 C. 0,2 D. 0,5 lOMoAR cPSD| 45764710 Câu 47
Trong một khoa iều trị, 60% bệnh nhân mắc bệnh X, 40% bệnh nhân bị bệnh Y. Loại bệnh
X có khả năng biến chứng là 9%, loại bệnh Y có khả năng biến chứng là 7%. Chọn ngẫu
nhiên một bệnh nhân ở khoa ó. Xác suất bệnh nhân này bị biến chứng là: A. 0,082 B. 0,08 C. 0,82 D. 0,078 Câu 48
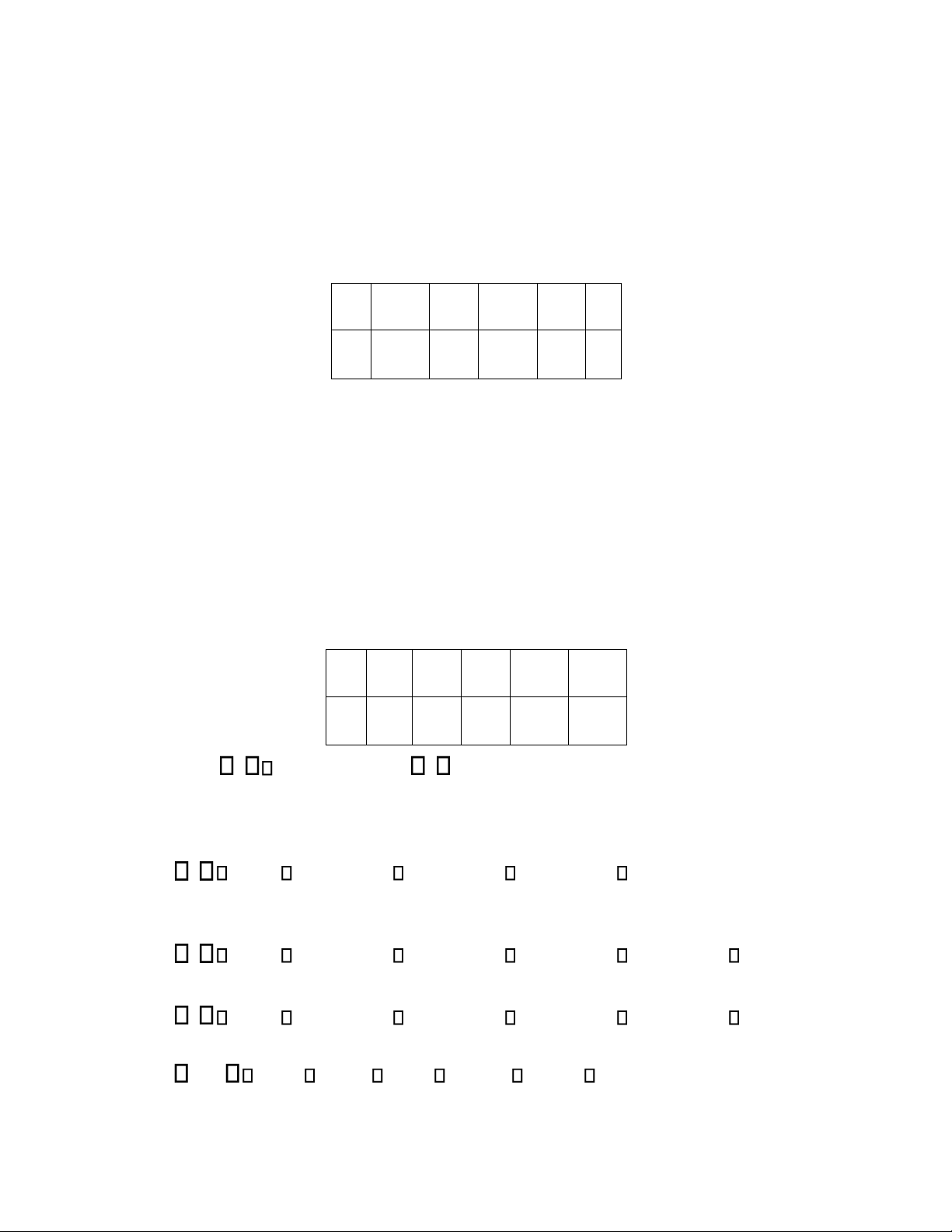
Cho X là thu nhập ( ơn vị: triệu ồng/tháng), Y là số lần i du lịch trong năm của nhân viên ở
một công ty có bảng phân phối xác suất ồng thời như sau: X 15 20 25 Y 2 01, 022 , 02, 3 018 , 015 , 015 ,
Thu nhập trung bình của những nhân viên có 2 lần i du lịch trong năm ở công ty ó là: A. 20 35, triệu ồng/tháng
B. 19 6875, triệu ồng/tháng C. 20 9615, triệu ồng/tháng
D. 20 triệu ồng/tháng Câu 49
Người ta vận chuyển một lô hàng gồm 10 sản phẩm với xác suất mỗi sản phẩm bị hỏng
trong quá trình vận chuyển là 0 2, . Khả năng trong 10 sản phẩm ó có nhiều hơn 8 sản
phẩm bị hỏng trong quá trình vận chuyển là: A. 0 0000737, B. 0 0000042, C. 0 0000779,