BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI TUYỂN SINH ĐẠI HỌC NĂM 2011 Môn: TOÁN; Khối: D ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút, không kể thời gian phát đề
PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm) 2x +1
Câu I (2,0 điểm) Cho hàm số y = ⋅ x +1
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2. Tìm k để đường thẳng y = kx + 2k + 1 cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho khoảng
cách từ A và B đến trục hoành bằng nhau.
Câu II (2,0 điểm)
sin 2x + 2cos x − sin x − 1 1. Giải phương trình = 0. tan x + 3
2. Giải phương trình log ( 2 8 − x + log
1+ x + 1− x − 2 = 0 (x ∈ \). 2 ) 1 ( ) 2 4 4x − 1
Câu III (1,0 điểm) Tính tích phân I = d . x ∫ 2x + 1 + 2 0
Câu IV (1,0 điểm) Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, BA = 3a, BC = 4a;
mặt phẳng (SBC) vuông góc với mặt phẳng (ABC). Biết SB = 2a 3 và n
SBC = 30 .D Tính thể tích
khối chóp S.ABC và khoảng cách từ điểm B đến mặt phẳng (SAC) theo a. 3 2
⎧⎪2x − (y + 2)x + xy = m
Câu V (1,0 điểm) Tìm m để hệ phương trình sau có nghiệm: ⎨
(x, y ∈\). 2
⎪⎩x + x − y =1− 2m
PHẦN RIÊNG (3,0 điểm): Thí sinh chỉ được làm một trong hai phần (phần A hoặc B)
A. Theo chương trình Chuẩn
Câu VI.a (2,0 điểm)
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có đỉnh B(– 4; 1), trọng tâm G(1; 1) và đường
thẳng chứa phân giác trong của góc A có phương trình x – y – 1 = 0. Tìm tọa độ các đỉnh A và C. x +1 y z − 3
2. Trong không gian với hệ toạ độ Oxyz, cho điểm A(1; 2; 3) và đường thẳng d: = = ⋅ 2 1 2 −
Viết phương trình đường thẳng ∆ đi qua điểm A, vuông góc với đường thẳng d và cắt trục Ox.
Câu VII.a (1,0 điểm) Tìm số phức z, biết: z – (2 + 3i) z = 1 – 9i.
B. Theo chương trình Nâng cao
Câu VI.b (2,0 điểm)
1. Trong mặt phẳng toạ độ Oxy, cho điểm A(1; 0) và đường tròn (C): x2 + y2 – 2x + 4y – 5 = 0. Viết
phương trình đường thẳng ∆ cắt (C) tại hai điểm M và N sao cho tam giác AMN vuông cân tại A.
x −1 y − 3 z
2. Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ : = = và mặt phẳng 2 4 1
(P) : 2x − y + 2z = 0. Viết phương trình mặt cầu có tâm thuộc đường thẳng ∆, bán kính bằng 1 và
tiếp xúc với mặt phẳng (P). 2 2x + 3x + 3
Câu VII.b (1,0 điểm) Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = trên x + 1 đoạn [0; 2].
----------- Hết ----------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:.............................................; Số báo danh:................................
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN – THANG ĐIỂM
⎯⎯⎯⎯⎯⎯⎯⎯
ĐỀ THI TUYỂN SINH ĐẠI HỌC NĂM 2011 ĐỀ CHÍNH THỨC Môn: TOÁN; Khối D
(Đáp án - thang điểm gồm 04 trang)
ĐÁP ÁN − THANG ĐIỂM Câu Đáp án Điểm I
1. (1,0 điểm)
(2,0 điểm) • Tập xác định: D = \ \{−1}. • Sự biến thiên: 1 0,25
– Chiều biến thiên: y ' =
> 0, ∀ x ∈ D. 2 (x + 1)
Hàm số đồng biến trên các khoảng (– ∞; – 1) và (– 1; + ∞).
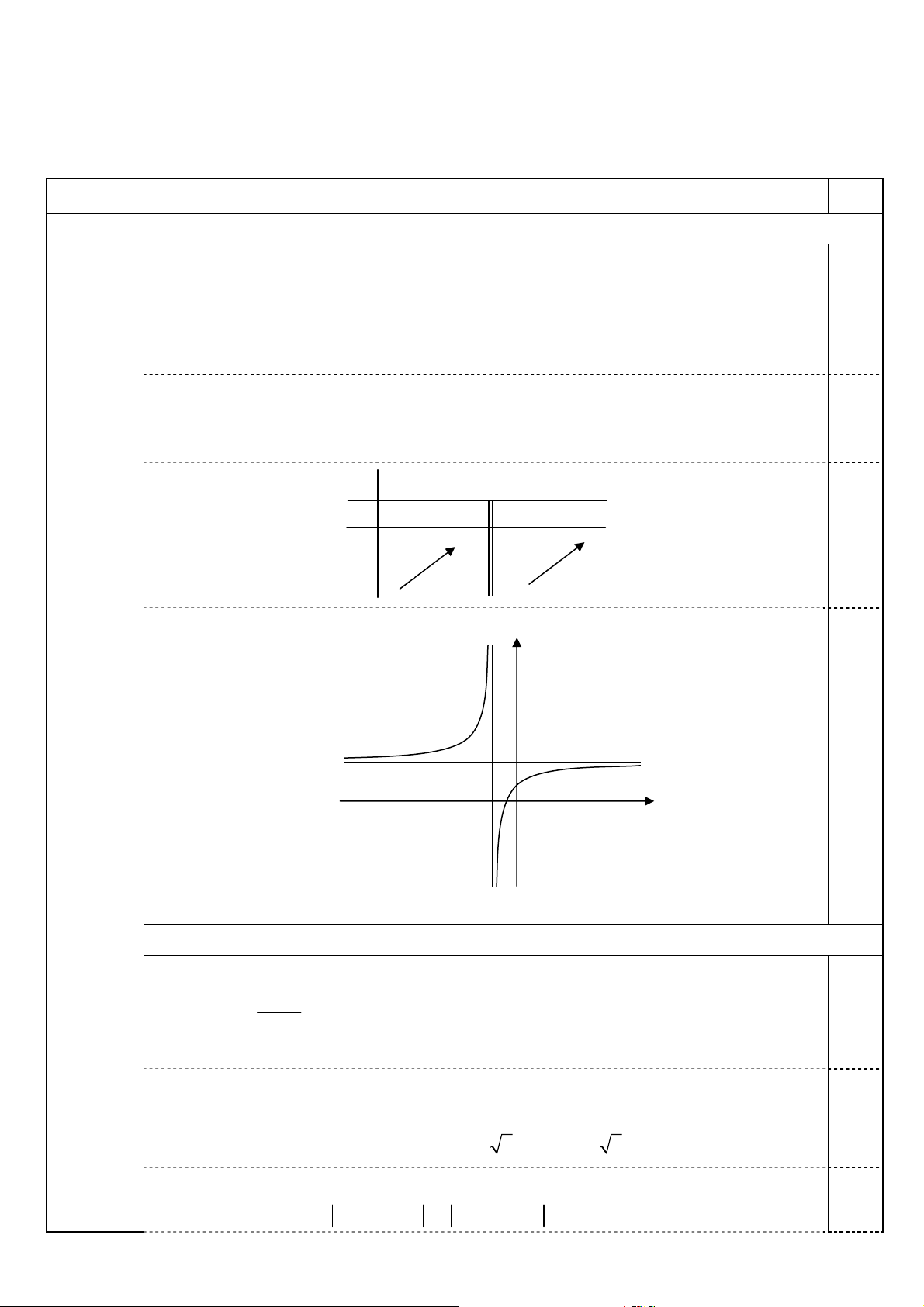
– Giới hạn và tiệm cận: lim y = lim y = 2; tiệm cận ngang: y = 2. x → −∞ x → +∞ 0,25
lim y = + ∞, lim y = – ∞; tiệm cận đứng: x = – 1. x ( )1− → − x ( )1+ → −
– Bảng biến thiên: x − ∞ –1 + ∞ y’ + + + ∞ 0,25 2 y 2 − ∞ • Đồ thị: y 2 0,25 1 – 1 O x
2. (1,0 điểm)
Gọi d: y = kx + 2k + 1, suy ra hoành độ giao điểm của d và (C) là nghiệm phương trình: 2x +1 kx + 2k + 1 =
⇔ 2x + 1 = (x + 1)(kx + 2k + 1) (do x = – 1 không là nghiệm) 0,25 x +1
⇔ kx2 + (3k – 1)x + 2k = 0 (1).
d cắt (C) tại hai điểm phân biệt A và B, khi và chỉ khi (1) có hai nghiệm phân biệt ⎧k ≠ 0 ⎧k ≠ 0 ⎧k ⎪ ≠ 0 ⇔ 0,25 ⎨ ⇔ ⎨ ⇔ ⎨ (*). ⎩Δ > 0 2
⎩k − 6k +1 > 0
⎪⎩k < 3− 2 2 ∨ k > 3+ 2 2.
Khi đó: A(x1; kx1 + 2k + 1) và B(x2; kx2 + 2k + 1), x1 và x2 là nghiệm của (1). 0,25
d(A, Ox) = d(B, Ox) ⇔ kx + 2k +1 = kx + 2k +1 1 2 Trang 1/4 Câu Đáp án Điểm
⇔ k(x1 + x2) + 4k + 2 = 0 (do x1 ≠ x2).
Áp dụng định lý Viét đối với (1), suy ra: (1 – 3k) + 4k + 2 = 0 ⇔ k = – 3, thỏa mãn (*). 0,25
Vậy, giá trị cần tìm là: k = – 3. II
1. (1,0 điểm)
(2,0 điểm) Điều kiện: cosx ≠ 0, tanx ≠ − 3 (*). 0,25
Phương trình đã cho tương đương với: sin2x + 2cosx – sinx – 1 = 0
⇔ 2cosx(sinx + 1) – (sinx + 1) = 0 ⇔ (sinx + 1)(2cosx – 1) = 0. 0,25 π 1 π
⇔ sinx = – 1 ⇔ x = – + k2π hoặc cosx = ⇔ x = ± + k2π. 0,25 2 2 3 π
Đối chiếu điều kiện (*), suy ra nghiệm: x = + k2π (k ∈ Z). 0,25 3 2. (1,0 điểm)
Điều kiện: – 1 ≤ x ≤ 1 (*).
Khi đó, phương trình đã cho tương đương với: log ( 2 8 x log ⎡4 1 x 1 ⎤ − = + +
− x 0,25 2 ) 2 ⎣ ( )⎦
⇔ 8 – x2 = 4( 1+ x + 1− x) ⇔ (8 – x2)2 = 16( 2 2 + 2 1− x ) (1). 0,25 Đặt t = 2
1− x , (1) trở thành: (7 + t2)2 = 32(1 + t) ⇔ t4 + 14t2 – 32t + 17 = 0 0,25
⇔ (t – 1)2(t2 + 2t + 17) = 0 ⇔ t = 1. Do đó, (1) ⇔ 2
1− x =1 ⇔ x = 0, thỏa mãn (*). 0,25
Vậy, phương trình có nghiệm: x = 0. III
Đặt t = 2x +1 ⇒ 4x = 2(t2 – 1), dx = tdt. 0,25
(1,0 điểm) Đổi cận: x = 0 ⇒ t = 1; x = 4 ⇒ t = 3. 3 3 2t − 3t 3 ⎛ 10 ⎞ I = dt ∫ = 2 2t ∫⎜ − 4t + 5 − ⎟dt 0,25 t + 2 ⎝ t + 2 1 1 ⎠ 3 3 ⎛ 2t ⎞ = 2 ⎜
− 2t + 5t − 10ln t + 2 ⎟ 0,25 ⎝ 3 ⎠ 1 34 3 = +10ln . 0,25 3 5 IV
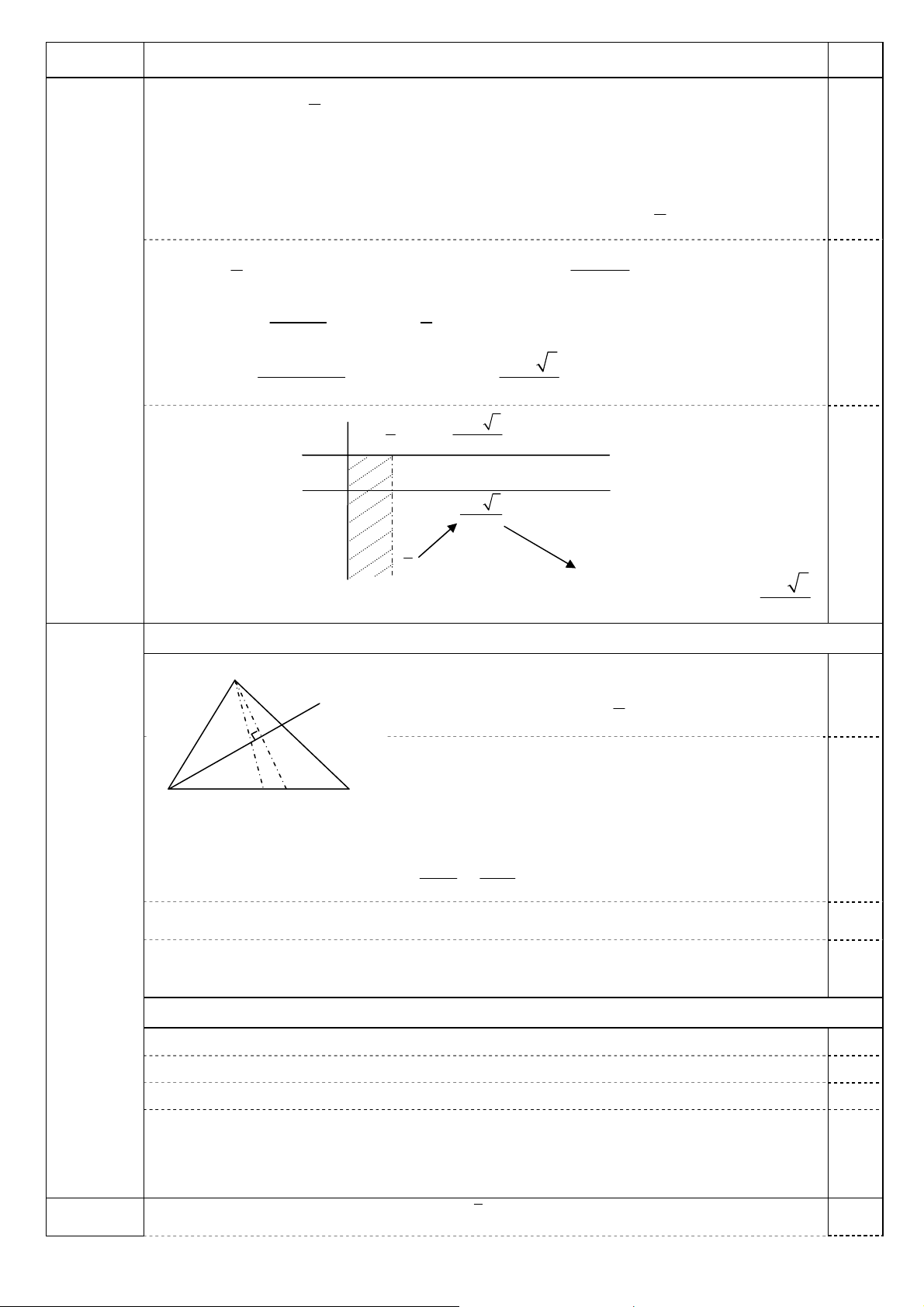
Hạ SH ⊥ BC (H ∈ BC); (SBC) ⊥ (ABC) ⇒ SH ⊥ (ABC); SH = SB.sin n SBC = a 3. 0,25
(1,0 điểm) 1 S
Diện tích: SABC = BA.BC = 6a2. 2 0,25 1 Thể tích: VS.ABC = S a . 3 ABC.SH = 3 2 3 B H K C
Hạ HD ⊥ AC (D ∈ AC), HK ⊥ SD (K ∈ SD) D
⇒ HK ⊥ (SAC) ⇒ HK = d(H, (SAC)). 0,25 BH = SB.cos n
SBC = 3a ⇒ BC = 4HC A
⇒ d(B, (SAC)) = 4.d(H, (SAC)). HC 3a Ta có AC = 2 2
BA + BC = 5a; HC = BC – BH = a ⇒ HD = BA. = . AC 5 0,25 SH.HD 3a 7 6a 7 HK = =
. Vậy, d(B, (SAC)) = 4.HK = . 2 2 SH + HD 14 7 V 2
⎧⎪(x − x)(2x − y) = m
(1,0 điểm) Hệ đã cho tương đương với: ⎨ 0,25 2
⎪⎩(x − x) + (2x − y) =1− 2 . m Trang 2/4 Câu Đáp án Điểm 1
Đặt u = x2 – x, u ≥ – ; v = 2x – y. 4 uv ⎧ = m 2 u
⎧ + (2m −1)u + m = 0 (1)
Hệ đã cho trở thành: ⎨ ⇔ ⎨ 0,25 u
⎩ + v = 1− 2m
⎩v =1− 2m − . u 1
Hệ đã cho có nghiệm, khi và chỉ khi (1) có nghiệm thỏa mãn u ≥ – . 4 1 2 −u + u
Với u ≥ – , ta có: (1) ⇔ m(2u + 1) = – u2 + u ⇔ m = . 4 2u +1 2 u − + u 1
Xét hàm f(u) =
, với u ≥ – ; ta có: 0,25 2u +1 4 2 2u + 2u −1 −1+ 3 f '(u) = –
; f '(u) = 0 ⇔ u = . 2 (2u +1) 2
Bảng biến thiên: u 1 − 1 − + 3 + ∞ 4 2 f '(u) + 0 – 2 − 3 0,25 2 f(u) 5 − 8 – ∞ 2 − 3
Suy ra giá trị cần tìm là: m ≤ . 2 VI.a 1. (1,0 điểm) JJJG JJJG
(2,0 điểm) B
Gọi D(x; y) là trung điểm AC, ta có: BD = 3GD
⎧x + 4 = 3(x −1) ⎛ 7 ⎞ 0,25 ⇔ ⎨ ⇒ D ; 1 . ⎜ ⎟
⎩y −1 = 3(y −1) ⎝ 2 ⎠
Gọi E(x; y) là điểm đối xứng của B qua phân giác trong G •
d: x – y – 1 = 0 của góc A.
Ta có EB vuông góc với d và trung điểm I của EB A D E C
thuộc d nên tọa độ E là nghiệm của hệ: 0,25 1(
⎧ x + 4) +1(y −1) = 0 ⎪ ⎧x + y + 3 = 0 ⎨ x − 4 y +1 ⇔ ⎨ ⇒ E(2; – 5). ⎪ − − 1 = 0
⎩x − y − 7 = 0 ⎩ 2 2
Đường thẳng AC đi qua D và E, có phương trình: 4x – y – 13 = 0. 0,25
⎧x − y −1 = 0
Tọa độ A(x; y) thỏa mãn hệ: ⎨
⇒ A(4; 3). Suy ra: C(3; – 1). 0,25
⎩4x − y −13 = 0
2. (1,0 điểm)
Mặt phẳng (P) đi qua A, vuông góc với d, có phương trình: 2x + y – 2z + 2 = 0. 0,25
Gọi B là giao điểm của trục Ox với (P), suy ra ∆ là đường thẳng đi qua các điểm A, B. 0,25
B ∈ Ox, có tọa độ B(b; 0; 0) thỏa mãn phương trình 2b + 2 = 0 ⇒ B(– 1; 0; 0). 0,25 ⎧x =1+ 2t ⎪
Phương trình ∆: ⎨y = 2 + 2t 0,25 ⎪z ⎩ = 3 + 3t. VII.a
Gọi z = a + bi (a, b ∈ R), ta có: z – (2 + 3i) z = 1 – 9i ⇔ a + bi – (2 + 3i)(a – bi) = 1 – 9i 0,25 Trang 3/4 Câu Đáp án Điểm
(1,0 điểm) ⇔ – a – 3b – (3a – 3b)i = 1 – 9i 0,25
⎧− a − 3b =1 ⇔ ⎨ 0,25 3 ⎩ a − 3b = 9 ⎧a = 2 ⇔ ⎨
Vậy z = 2 – i. 0,25 b ⎩ = 1. − VI.b 1. (1,0 điểm)
(2,0 điểm) y
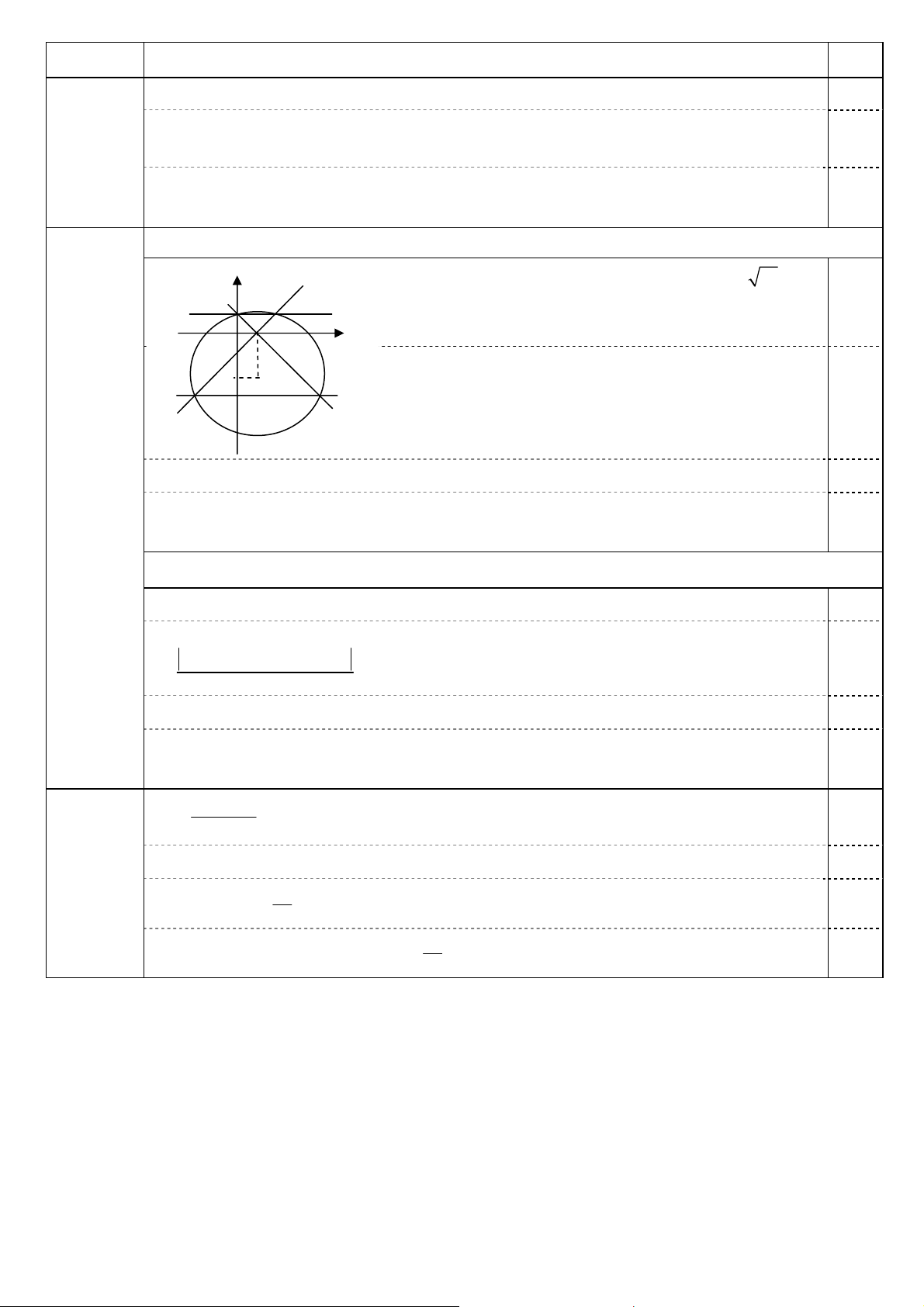
Đường tròn (C) có tâm I(1; – 2), bán kính bằng 10. 1
Ta có: IM = IN và AM = AN ⇒ AI ⊥ MN; suy ra phương 0,25 A
trình ∆ có dạng: y = m. O x
Hoành độ M, N là nghiệm phương trình: – 2 I
x2 – 2x + m2 + 4m – 5 = 0 (1). – 3 0,25 M N
(1) có hai nghiệm phân biệt x1 và x2, khi và chỉ khi:
m2 + 4m – 6 < 0 (*); khi đó ta có: M(x1; m) và N(x2; m). JJJJG JJJG
AM ⊥ AN ⇔ AM.AN = 0 ⇔ (x1 – 1)(x2 – 1) + m2 = 0 ⇔ x1x2 – (x1 + x2) + m2 + 1 = 0. 0,25
Áp dụng định lý Viét đối với (1), suy ra: 2m2 + 4m – 6 = 0 0,25
⇔ m = 1 hoặc m = – 3, thỏa mãn (*). Vậy, phương trình ∆: y = 1 hoặc y = – 3. 2. (1,0 điểm)
Gọi I là tâm của mặt cầu. I ∈ ∆, suy ra tọa độ I có dạng: I(1 + 2t; 3 + 4t; t). 0,25
Mặt cầu tiếp xúc với (P), khi và chỉ khi: d(I, (P)) = 1
2(1+ 2t) − (3 + 4t) + 2t 0,25 ⇔ = 1 3
⇔ t = 2 hoặc t = – 1. Suy ra: I(5; 11; 2) hoặc I(– 1; – 1; – 1). 0,25 Phương trình mặt cầu: 0,25
(x – 5)2 + (y – 11)2 + (z – 2)2 = 1 hoặc (x + 1)2 + (y + 1)2 + (z + 1)2 = 1. 2 VII.b 2x + 4x y ' = ; 0,25 2
(1,0 điểm) (x + 1)
y' = 0 ⇔ x = – 2 hoặc x = 0. 0,25 17
y(0) = 3, y(2) = . 0,25 3 17
Vậy: min y = 3, tại x = 0; max y = , tại x = 2. 0,25 [0; 2] [0; 2] 3
------------- Hết ------------- Trang 4/4