Đề thi và đáp án môn Toán khối D năm 2013

BOÄ GIAÙO DUÏC VAØ ÑAØO TAÏO
ÑEÀ THI TUYEÅN SINH ÑAÏI HOÏC NAÊM 2013 −−−−−−−−−− Moân: TOAÙN; Khoái D ÑEÀ CHÍNH THÖÙC
Thôøi gian laøm baøi: 180 phuùt, khoâng keå thôøi gian phaùt ñeà
−−−−−−−−−−−−−−−−−−−
I. PHAÀN CHUNG CHO TAÁT CAÛ THÍ SINH (7,0 ñieåm)
Caâu 1 (2,0 ñieåm). Cho haøm soá y = 2x3 − 3mx2 + (m − 1)x + 1 (1), vôùi m laø tham soá thöïc.
a) Khaûo saùt söï bieán thieân vaø veõ ñoà thò cuûa haøm soá (1) khi m = 1.
b) Tìm m ñeå ñöôøng thaúng y = −x + 1 caét ñoà thò haøm soá (1) taïi ba ñieåm phaân bieät.
Caâu 2 (1,0 ñieåm). Giaûi phöông trình sin 3x + cos 2x − sin x = 0. Caâu 3 (1,0 1
ñieåm). Giaûi phöông trình √ √ 2 log x + log 1 x = log√ x x + 2. 2 1 − 2 − 2 2 2 1 Z Caâu 4 (1,0 (x + 1)2
ñieåm). Tính tích phaân I = dx. x2 + 1 0
Caâu 5 (1,0 ñieåm). Cho hình choùp S.ABCD coù ñaùy laø hình thoi caïnh a, caïnh beân SA vuoâng goùc vôùi ñaùy, \
BAD = 120◦, M laø trung ñieåm cuûa caïnh BC vaø \
SM A = 45◦. Tính theo a theå tích cuûa
khoái choùp S.ABCD vaø khoaûng caùch töø ñieåm D ñeán maët phaúng (SBC).
Caâu 6 (1,0 ñieåm). Cho x, y laø caùc soá thöïc döông thoûa maõn ñieàu kieän xy ≤ y − 1. Tìm giaù trò lôùn nhaát cuûa bieåu thöùc x + y x − 2y P = − . px2 − xy + 3y2 6(x + y)
II. PHAÀN RIEÂNG (3,0 ñieåm): Thí sinh chæ ñöôïc laøm moät trong hai phaàn (phaàn A hoaëc phaàn B)
A. Theo chöông trình Chuaån Caâu 7.a (1,0 9 3
ñieåm). Trong maët phaúng vôùi heä toïa ñoä Oxy, cho tam giaùc ABC coù ñieåm M − ; 2 2
laø trung ñieåm cuûa caïnh AB, ñieåm H(−2; 4) vaø ñieåm I(−1; 1) laàn löôït laø chaân ñöôøng cao keû töø B
vaø taâm ñöôøng troøn ngoaïi tieáp tam giaùc ABC. Tìm toïa ñoä ñieåm C.
Caâu 8.a (1,0 ñieåm). Trong khoâng gian vôùi heä toïa ñoä Oxyz, cho caùc ñieåm A(−1; −1; −2), B(0; 1; 1)
vaø maët phaúng (P ) : x+y+z−1 = 0. Tìm toïa ñoä hình chieáu vuoâng goùc cuûa A treân (P). Vieát phöông
trình maët phaúng ñi qua A, B vaø vuoâng goùc vôùi (P ).
Caâu 9.a (1,0 ñieåm). Cho soá phöùc z thoûa maõn ñieàu kieän (1 + i)(z − i) + 2z = 2i. Tính moâñun cuûa soá phöùc z − 2z + 1 w = . z2
B. Theo chöông trình Naâng cao
Caâu 7.b (1,0 ñieåm). Trong maët phaúng vôùi heä toïa ñoä Oxy, cho ñöôøng troøn (C) : (x−1)2+(y−1)2 = 4
vaø ñöôøng thaúng ∆ : y − 3 = 0. Tam giaùc MNP coù tröïc taâm truøng vôùi taâm cuûa (C), caùc ñænh N
vaø P thuoäc ∆, ñænh M vaø trung ñieåm cuûa caïnh MN thuoäc (C). Tìm toïa ñoä ñieåm P .
Caâu 8.b (1,0 ñieåm). Trong khoâng gian vôùi heä toïa ñoä Oxyz, cho ñieåm A(−1; 3; −2) vaø maët phaúng
(P ) : x − 2y − 2z + 5 = 0. Tính khoaûng caùch töø A ñeán (P ). Vieát phöông trình maët phaúng ñi qua A vaø song song vôùi (P ). Caâu 9.b (1,0 2x2
ñieåm). Tìm giaù trò lôùn nhaát vaø giaù trò nhoû nhaát cuûa haøm soá − 3x + 3 f (x) = x + 1 treân ñoaïn [0; 2].
−−−−−−Heát−−−−−−
Thí sinh khoâng ñöôïc söû duïng taøi lieäu. Caùn boä coi thi khoâng giaûi thích gì theâm.
Hoï vaø teân thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ; Soá baùo danh: . . . . . . . . . . . . . . . . . . . .
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN – THANG ĐIỂM
⎯⎯⎯⎯⎯⎯⎯⎯
ĐỀ THI TUYỂN SINH ĐẠI HỌC NĂM 2013 ĐỀ CHÍNH THỨC Môn: TOÁN; Khối D
(Đáp án - thang điểm gồm 04 trang) Câu Đáp án Điểm 1
a. (1,0 điểm)
(2,0 điểm) Khi m = 1 ta có 3 2
y = 2x − 3x + 1.
• Tập xác định: D = . \ 0,25 • Sự biến thiên: - Chiều biến thiên: 2 y ' = 6x − 6 ;
x y ' = 0 ⇔ x = 0 hoặc x =1. Các khoảng đồng biến: ( ;
−∞ 0) và (1; + ∞); khoảng nghịch biến: (0; 1).
- Cực trị: Hàm số đạt cực tiểu tại x = 1, yCT = 0; đạt cực đại tại x = 0, yCĐ = 1. 0,25
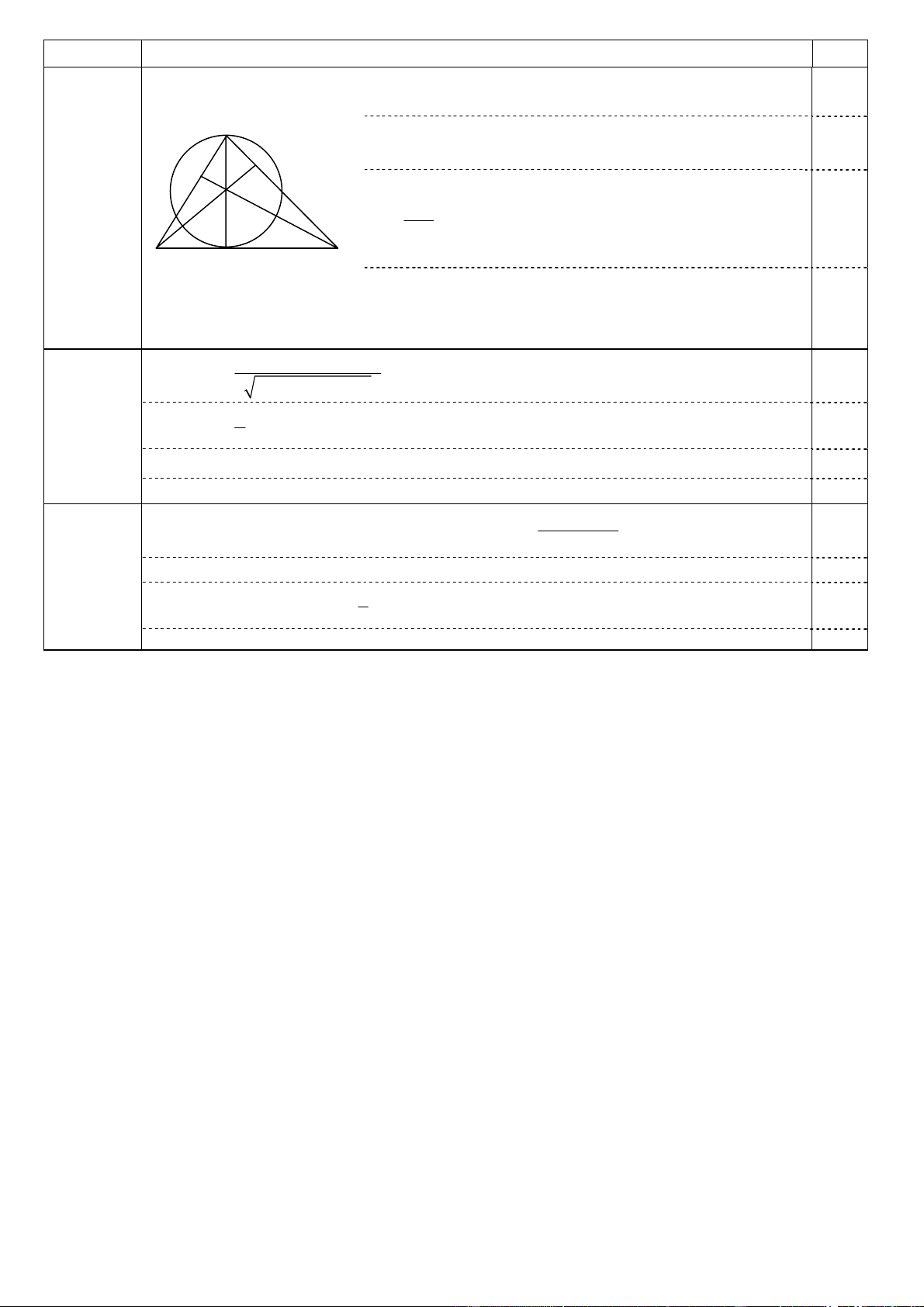
- Giới hạn: lim y = − ; ∞ lim y = + . ∞ x→−∞ x→+∞ - Bảng biến thiên: x − ∞ 0 1 + ∞ y ' 0 0 + + − 1 + ∞ 0,25 y − ∞ 0 • Đồ thị: y 1 0,25 O 1 x
b. (1,0 điểm)
Phương trình hoành độ giao điểm của đồ thị hàm số (1) với đường thẳng y = −x +1 là 0,25 3 2
2x −3mx + (m−1)x +1= −x +1 ⎡x = 0 ⇔ ⎢ 2
⎣2x −3mx + m = 0 (*). 0,25
Yêu cầu của bài toán ⇔ phương trình (*) có hai nghiệm phân biệt khác 0 2 9 ⎧ m −8m > ⇔ 0 ⎨ 0,25 ⎩m ≠ 0 ⇔ 8
m < 0 hoặc m > . 0,25 9 Trang 1/4 Câu Đáp án Điểm 2
Phương trình đã cho tương đương với 2cos 2xsin x + cos 2x = 0 0,25
(1,0 điểm)
⇔ cos 2x(2sin x +1) = 0. 0,25 π π
• cos2x = 0 ⇔ x = + k (k ∈]). 0,25 4 2 ⎡ π x = − + k2π ⎢ 6
• 2sin x +1 = 0 ⇔ ⎢ (k ∈]). 7π ⎢x = + k2π ⎢ 0,25 ⎣ 6 π π π 7π
Vậy nghiệm của phương trình đã cho là x =
+ k , x = − + k2π, x =
+ k2π (k ∈]). 4 2 6 6 3 2
(1,0 điểm) Điều kiện: 0 < x
x < 1. Phương trình đã cho tương đương với = x − 2 x + 2 0,25 1− x 2 x x 2 ⎛ x ⎜ 1⎞⎛ x ⎟⎜ 2⎞ ⇔ = + ⇔ + − ⎟ = 0 0,25 2 (1− x ) 1− x ⎝ 1− x ⎠⎝1− x ⎠ x ⇔ − 2 = 0 (do x > 0 ) 0,25 1− x 1− x ⇔ x = 4−2 3. 0,25
Đối chiếu với điều kiện ta được nghiệm của phương trình đã cho là x = 4− 2 3. 4 1 1 1 ⎛ 2x ⎞ 2
(1,0 điểm) Ta có = ⎜1+ ⎟d = d x I x x + ∫ ∫ ∫ d . x 0,25 2 2 ⎝ x +1 ⎠ x +1 0 0 0 1 1 • dx = x =1 ∫ . 0,25 0 0 1 2x 1 2 •
dx = ln(x +1) = ln 2 ∫ . 0,25 2 0 x +1 0 Do đó I =1+ ln 2. 0,25 5 n o n o
BAD =120 ⇒ ABC = 60 ⇒ AB Δ C đều
(1,0 điểm) a 3 2 0,25 ⇒ a 3 AM = ⇒ S = . S 2 ABCD 2 SA
Δ M vuông tại A có n o
SMA = 45 ⇒ ΔSAM a 3
vuông cân tại A ⇒ SA = AM = . 2 0,25 3 H 1 A Do đó a = A S = S V . S . . ABCD D 3 ABCD 4
Do AD||BC nên d (D,(SBC)) = d ( , A (SBC)).
Gọi H là hình chiếu vuông góc của A trên SM. 0,25
Ta có AM ⊥ BC và SA ⊥ BC ⇒ BC ⊥ (SAM ) B M C
⇒ BC ⊥ AH ⇒ AH ⊥ (SBC) ⇒ d( ,
A (SBC)) = AH . AM 2 a 6 Ta có AH = = , 2 4 0,25 a 6
suy ra d(D,(SBC)) = . 4 Trang 2/4 Câu Đáp án Điểm 6 2 x y −1 1 1 1 ⎛ 1 1 ⎞ 1
(1,0 điểm) Do x > 0, y > 0, xy ≤ y −1 nên 0< ≤ = − = − − ≤ . 0,25 2 2 ⎜ ⎟ y y y y 4 ⎝ y 2 ⎠ 4 t +1 t − 2 Đặt x t = 1
, suy ra 0 < t ≤ . Khi đó P = − . y 4 2 6(t +1) t −t + 3 t +1 t − 2 1 7 −3t 1 Xét f (t) = −
, với 0 < t ≤ . Ta có f '(t) = − . 2 6(t +1) 2 t − t + 3 4 2 3 2 (t −t +3) 2(t +1) 0,25 1
Với 0 < t ≤ ta có 2
t − t + 3 = t(t −1) + 3< 3; 7 −3t > 6 và t +1>1. 4 7 −3t 7 −3t 1 1 1 1 1 Do đó > > và −
> − . Suy ra f '(t) > − > 0. 2 3 2 ( 2 t − t + 3) 6 3 3 2(t +1) 2 3 2 ⎛ 1 ⎞ 5 7
Do đó P = f (t) ≤ f ⎜ ⎟ = + . 0,25 ⎝ 4 ⎠ 3 30 1 5 7 Khi x = và y = 5 7 2, ta có P = +
. Vậy giá trị lớn nhất của P là + . 0,25 2 3 30 3 30 7.a JJJG ⎛ 7 1 ⎞
(1,0 điểm) IM = ⎜ − ;
⎟. Ta có M ∈ AB và AB ⊥ IM nên đường ⎝ 2 2 ⎠ 0,25 B
thẳng AB có phương trình 7x − y +33 = 0. A∈ AB ⇒ ( A ;
a 7a + 33). Do M là trung điểm của AB nên JJJG JJJG M
B(−a − 9; −7a − 30). Ta có HA ⊥ HB ⇒ HA.HB = 0 0,25 I 2
⇒ a +9a + 20 = 0⇒ a = 4 − hoặc a = −5. • Với a = 4 − ⇒ (
A −4;5), B(−5; −2). Ta có BH ⊥ AC nên A H C
đường thẳng AC có phương trình x + 2 y −6 = 0. Do đó 0,25 2 2 C(6 − 2 ;
c c). Từ IC = IA suy ra (7 − 2c) + (c −1) = 25. Do
đó c =1 hoặc c = 5. Do C khác A, suy ra C(4;1). • Với a = 5 − ⇒ ( A 5 − ; 2 − ), B( 4
− ;5). Ta có BH ⊥ AC nên
đường thẳng AC có phương trình 2x − y +8 = 0. Do đó 0,25 2 2
C(t; 2t + 8). Từ IC = IA suy ra (t +1) + (2t + 7) = 25. Do đó
t = −1 hoặc t = −5. Do C khác A, suy ra C( 1 − ;6). 8.a
Gọi H là hình chiếu vuông góc của A trên (P). Suy ra H ( 1
− +t;−1+t;−2+t). 0,25
(1,0 điểm) 5 ⎛ 2 2 1 ⎞ H ∈(P) ⇔ ( 1 − +t)+( 1 − +t)+ ( 2
− +t)−1= 0 ⇔ t = . Do đó H ⎜ ; ;− ⎟. 0,25 3 ⎝ 3 3 3 ⎠ JJJG
Gọi (Q) là mặt phẳng cần viết phương trình. Ta có AB = (1;2;3) và vectơ pháp tuyến của (P) là JG JG 0,25
n = (1;1;1). Do đó (Q) có vectơ pháp tuyến là n ' = ( 1 − ;2; 1 − ).
Phương trình của mặt phẳng (Q) là: x − 2y + z +1= 0. 0,25 9.a
Điều kiện của bài toán tương đương với (3+i)z = −1+3i 0,25
(1,0 điểm) ⇔ z = .i 0,25
Suy ra w = −1+ 3 .i 0,25
Do đó môđun của w là 10. 0,25 Trang 3/4 Câu Đáp án Điểm 7.b
Ta có tâm của (C) là I (1;1). Đường thẳng IM vuông góc với Δ 0,25
(1,0 điểm)
nên có phương trình x =1. Do đó M (1;a). M Do 2
M ∈(C) nên (a 1 − ) = .
4 Suy ra a = −1 hoặc a = 3. 0,25
Mà M ∉Δ nên ta được M (1; 1 − ).
N ∈Δ ⇒ N ( ;
b 3). Trung điểm của MN thuộc (C) I 2 ⎛ b +1 ⎜ 1⎞ ⇒ − ⎟ +(1− )2
1 = 4 ⇒ b = 5 hoặc b = −3. 0,25 ⎝ 2 ⎠
Do đó N (5;3) hoặc N ( 3 − ;3). P N P∈Δ ⇒ P( ; c 3). JJJG JJG
- Khi N(5;3), từ MP ⊥ IN suy ra c = 1. − Do đó P( 1 − ;3). 0,25 JJJG JJG - Khi N ( 3
− ;3), từ MP ⊥ IN suy ra c = 3. Do đó P(3;3). 8.b |( 1 − )− 2.3− 2( 2 − )+5| d ( , A (P)) =
(1,0 điểm) 0,25 2 2 2 1 + ( 2 − ) + (−2) 2 = . 0,25 3 JG
Vectơ pháp tuyến của (P) là n = (1; 2 − ; 2 − ). 0,25
Phương trình mặt phẳng cần tìm là x − 2 y − 2z + 3= 0. 0,25 2 9.b 2x + 4x −6
Ta có f (x) xác định và liên tục trên đoạn [0;2] ; f '(x) = .
(1,0 điểm) 0,25 2 (x +1) Với x [0
∈ ; 2] ta có f '(x) = 0 ⇔ x =1. 0,25 5
Ta có f (0) = 3; f (1) =1; f (2) = . 0,25 3
Giá trị nhỏ nhất của f(x) trên đoạn [0; 2] là 1; giá trị lớn nhất của f(x) trên đoạn [0; 2] là 3. 0,25
------------- Hết ------------- Trang 4/4