Đề thi xác suất thống kê | Đại học Kinh tế kỹ thuật công nghiệp

lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 13
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 điểm): Cho hai biến cố A và B. Biết rằng P(A + B) = 0,88; P(A) = 0,6; P(B) = 0,7.
a) Tính P(AB) và chứng tỏ A và B độc lập với nhau.
b) Tính xác suất để chỉ có biến cố A xảy ra? Câu 2.(3 điểm):
1. Cho bảng phân phối đồng thời: Y -2 0 1 4 X -2 0,5a a 0,5a 1,5a 1 0,4 0,5a 1,5a 0,5a
a)Xác định giá trị của a? b)Tính E(X + 2Y – 1) và E(Y|X = 1)?
2.Một lớp học có 50 sinh viên trong đó có 30 nam. Lấy ngẫu nhiên ra 10 sinh viên để tham gia hội
sinh viên tình nguyện, gọi X là số sinh viên nữ có trong 10 sinh viên. Biết Y N(5; 4). a)Hãy tính
E(2X + DY – 1)? b)Tính P(Y2 – 4Y – 2 < 3)?
Câu 3.( 3 điểm): Để khảo sát tác dụng của một loại thức ăn mới đến trọng lượng trứng gà, người ta khảo
sát 100 quả thấy trọng lượng trung bình là 37,05(g); độ lệch mẫu hiệu chỉnh 5,82. Trong đó có 20 quả đạt chất lượng tốt.
a). Hãy ước lượng trọng lượng trứng trung bình với độ tin cậy 95%.
b). Khi ước lượng tỷ lệ quả trứng đạt chất lượng tốt với độ chính xác là 0,08 thì độ tin cậy là bao nhiêu?
c). Trọng lượng trung bình của trứng gà ban đầu là 35,58 (g). Với mức ý nghĩa 1% có thể nói loại thức ăn
mới làm tăng trọng lượng trứng gà hay không?
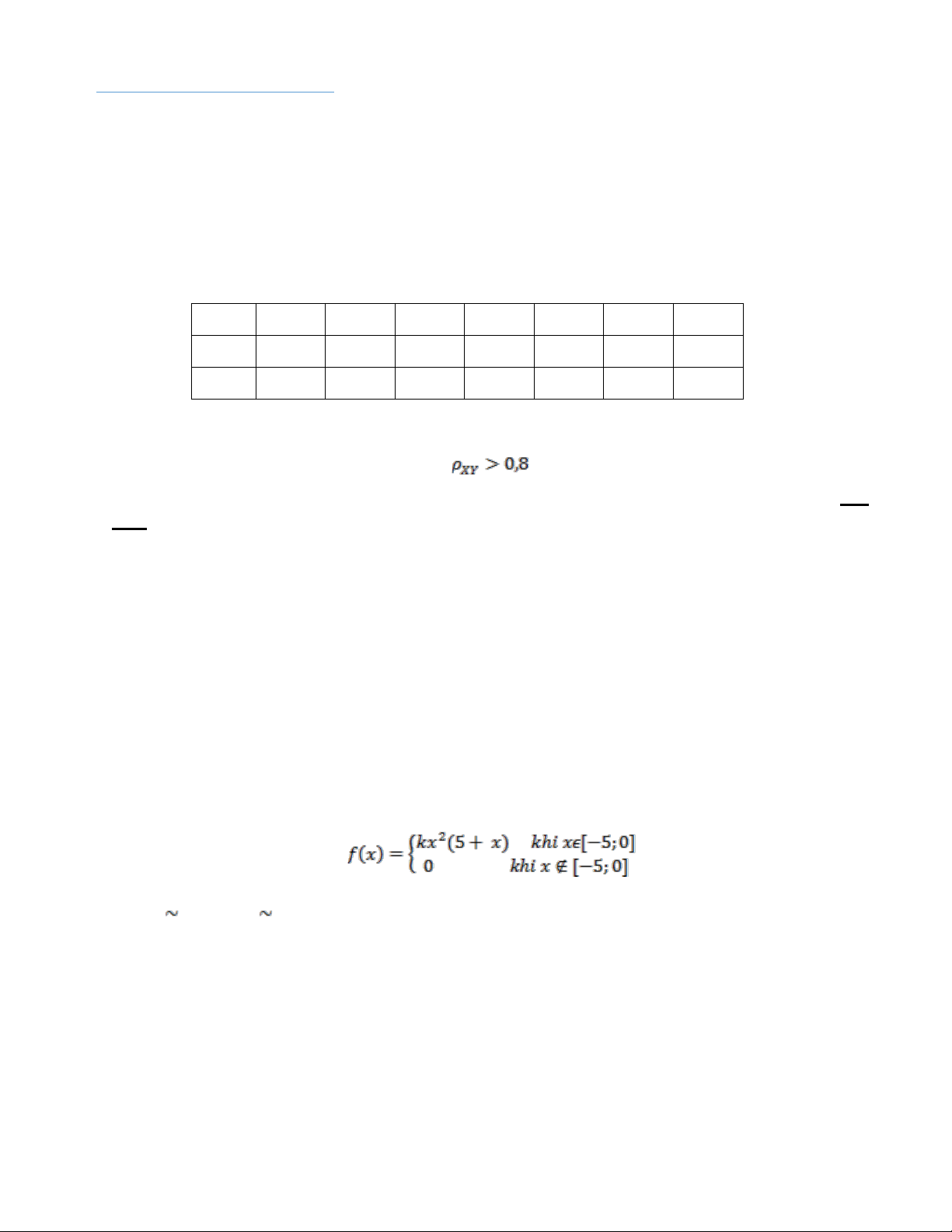
Câu 4.(2 điểm): Theo dõi độ dày của một loại giấy và thời gian phân hủy ta được bảng số liệu sau:
(biết độ dày X(mm) và thời gian phân hủy Y(tháng)) X 1,3 3,3 10,3 16,3 26,3 36,3 Y 10 13 15 19 20 25 Ni 3 4 5 5 3 6
a). Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu độ dày của giấy là 30 mm
thì thời gian phân hủy là bao nhiêu?
b).Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 14
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho hai biến cố A và B. Biết rằng P(A + B) = 0,9; P(A) = 0,7; P(B) = 0,8.
a) Tính P(AB) và chứng tỏ A và B phụ thuộc nhau?
b) Tính xác suất để chỉ có một trong hai biến cố A, B xảy ra?
Câu 2.(3 điểm):
1.Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ. b)Tính DX và P(X2 – 0,5 < 0)?
2.Cho X N(4;1); Y B(5; 0,2) và đặt T = 2X + 3Y – modX.modY.
a)Hãy tính giá trị của E(T)? b)Tính xác suất P(Y = 3)?
Câu 3.( 3 điểm): Thời gian (giờ) để một loại sơn khô khi sơn tường là một chỉ số quan trọng khi sản xuất
của công ty sơn EXPO. Để đánh giá một mẫu sơn mới sản xuất, hãng tiến hành lấy mẫu với số liệu: cỡ
mẫu=36; trung bình mẫu là 1,428 giờ; độ lệch hiệu chỉnh là 0,179.
a). Kỹ sư phụ trách nghiên cứu mẫu sơn mới này cho rằng thời gian khô là dưới 1,5 (giờ). Hãy kết luận
với mức ý nghĩa 5%.
b). Khi ước lượng thời gian khô trung bình với yêu cầu độ chính xác là 0,07 thì độ tin cậy bằng bao nhiêu?
c). Nếu yêu cầu ước lượng thời gian khô trung bình với độ chính xác 0,065 và độ tin cậy 99% thì cần
khảo sát thêm bao nhiêu mẫu nữa?
Câu 4.(2 điểm): Để điều tra về chiều cao (X cm) và cân nặng (Y kg) của học sinh lớp 1 ở địa phương A ta có số liệu như sau: xi(cm) 75,6 80,6 85,6 90,6 95,6 100,6 105,6 yi(kg) 16 20 23 25 28 32 34 ni(hs) 2 3 5 7 4 2 1
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu chiều cao là 110 cm thì
trọng lượng của học sinh lớp 1 của địa phương A ước tính qua hàm hồi quy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 15
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho hai biến cố A, B thỏa mãn: P(A) = 0,2; P(B) = 0,25 và P(AB) = 0,01.
a) Tính xác suất PA( .B) .
b) Đặt T = A + B. Hãy so sánh hai giá trị xác suất : P(A/T) và P(B/T).
Câu 2.(3 điểm):
1.Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ? b)Tính D(3 + 2X2)?
2.Trong một lô 100 sản phẩm có 75 sản phẩm loại I. Lấy ngẫu nhiên 45 sản phẩm để kiểm tra, gọi X
là số sản phẩm loại I gặp được khi kiểm tra. Biết Y N(3;4). a)Tính giá trị của E(X + 5Y)? b)Tính E(X2)?
Câu 3.( 3 điểm): Đo độ bền (kg/cm2) của một số con sợi ta có số liệu sau: cỡ mẫu 80 con sợi, độ bền trung
bình = 2,34 kg/cm2, độ lệch mẫu hiệu chỉnh = 0,321 kg/cm2, trong đó có 30 con sợi có độ bền trên 2,5
kg/cm2 được coi là loại A.
a). Hãy ước lượng độ bền trung bình của các con sợi với độ tin cậy 95%.
b). Hãy ước lượng tỷ lệ con sợi loại A với độ tin cậy 94%.
c). Để ước lượng độ bền trung bình của các con sợi với độ chính xác 0,098 thì độ tin cậy sẽ là bao nhiêu?
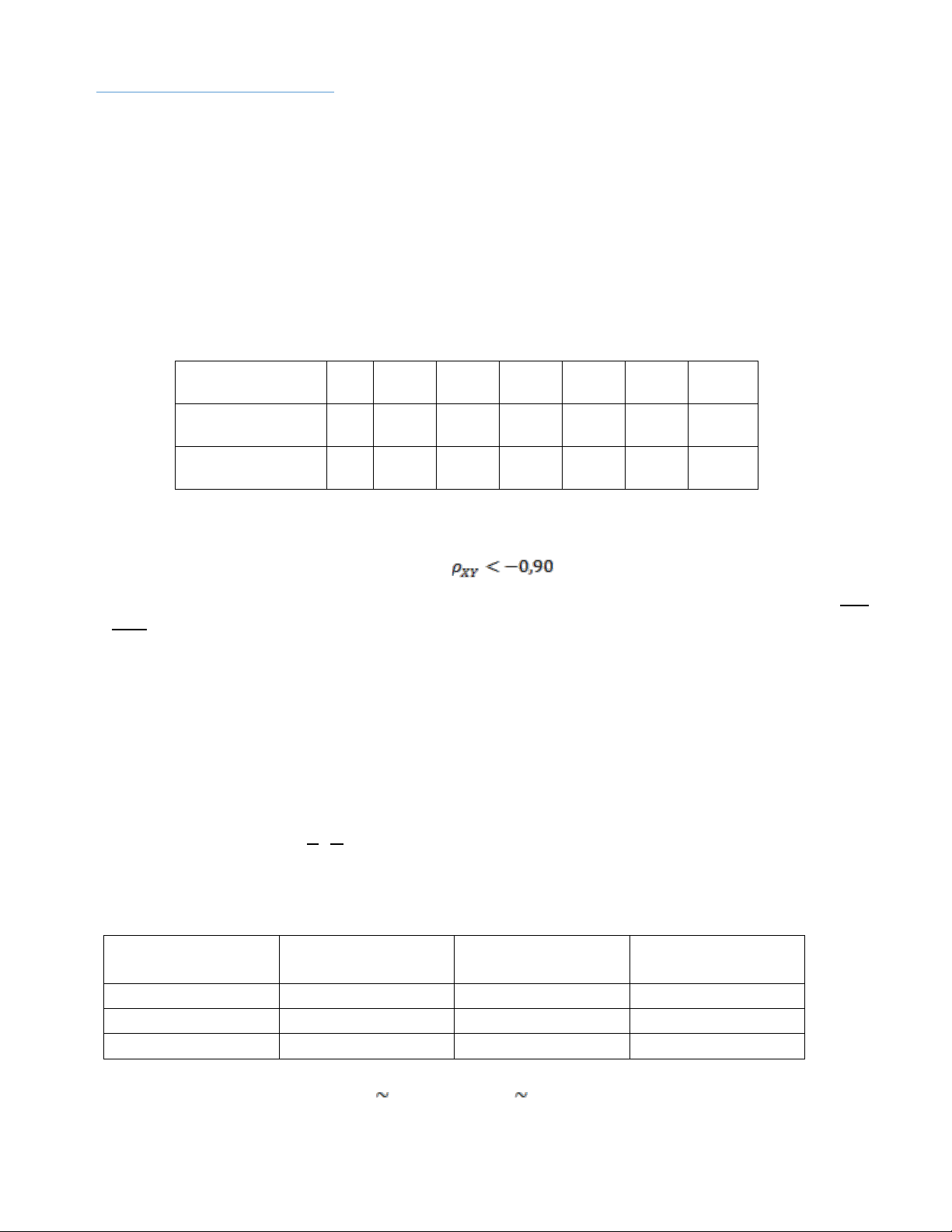
Câu 4.(2 điểm): Để điều tra về mức thu nhập X (triệu/tháng) và nhu cầu về một loại hàng hóa Y (kg/tháng)
của người dân thủ đô ta có số liệu như sau: xi (triệu/tháng) 4,3 5,3 6,3 7,3 8,3 9,3 10,3 yi (kg/tháng) 1,6 1,8 2,3 2,5 2,8 3,2 3,4 ni (người) 3 5 5 8 7 4 2 lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 16
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết với mức thu nhập là 11
triệu/tháng thì nhu cầu về một loại hàng hóa Y của người dân thủ đô ước tính qua hàm hồi quy là bao nhiêu?
b) Hãy ước lượng hệ số tương quan ρxy với độ tin cậy 96%.
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho hệ đầy đủ 3 biến cố {A, B , C } với P(A) = 0,3; P(B) = 2P(A). Biết biến cố F thỏa
mãn: P(F/A) = 0,02; P(F/B) = 0,35; P(F/C) = 0,5. a)Tính xác suất P(F)? b)
Tính giá trị P A F P A F( / ) + ( / ) Câu 2.(3 điểm):
1.Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ. b)Tính E(3X3 – 2)?
2.Một sinh viên đi thi chỉ thuộc 30 câu trong 50 câu ở đề cương. Mỗi đề thi có 10 câu hỏi thuộc đề cương,
gọi Y là số câu hỏi sinh viên đó không thuộc trong đề thi. Biết X N(4; 0,09); đặt Z = X + 3Y - modX
a)Tính giá trị của EZ? b)Tính P(Y = 3)?
Câu 3.( 3 điểm): Năng suất Hồ tiêu tại vùng X là các biến ngẫu nhiên có phân phối chuẩn. Có kết quả điều
tra: cỡ mẫu=100 ha; trung bình mẫu=16,2 (tạ) và độ lệch hiệu chỉnh=2,3. Trong đó có 18 ha có năng suất cao.
a). Với độ tin cậy 90% hãy ước lượng tỷ lệ số ha có năng suất cao.
b). Khi ước lượng năng suất hồ tiêu trung bình tại vùng X với độ tin cậy 93% và độ chính xác 0,4 thì cần
điều tra thêm bao nhiêu điểm thu hoạch nữa?
c). Nếu lấy số liệu trên để ước lượng tỷ lệ số ha có năng suất cao với yêu cầu độ chính xác là 0,065 thì độ
tin cậy tương ứng là bao nhiêu? lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 17
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 4.(2 điểm): Để điều tra về chiều cao (X cm) và cân nặng (Y kg) của học sinh lớp 1 ở địa phương A ta có số liệu như sau: xi(cm) 75,4 80,4 85,4 90,4 95,4 100,4 105,4 yi(kg) 16 20 23 25 28 32 34 ni(hs) 2 3 5 7 4 2 1
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu chiều cao là 110 cm thì
trọng lượng của học sinh lớp 1 của địa phương A ước tính qua hàm hồi quy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho 3 biến cố A, B, C có quan hệ độc lập. Biết P(A) = 0,8; P(B) = 0,9 và P(C) = 0,75. Đặt T = A + B + C. a) Tính xác suất P(T)? b) Tính P[(B + C)/T]?
Câu 2.(3 điểm):
1.Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ? b)Tính D( X2 + 4)? 2.
Cho X N(5;4); Y H(25;10;15/25) và đặt T = 2X + 5Y – 7.medX.
a)Hãy tính giá trị của E(T)? b)Tính E(X2)? Câu 3.( 3 điểm): Số đơn hàng online ở
một cửa hàng quần áo là đại lượng tuân theo quy luật chuẩn. Theo dõi số đơn hàng online/ ngày ở cửa hàng
ta có kết quả sau: cỡ mẫu 60 ngày, trung bình mẫu là 150,2 và độ lệch hiệu chỉnh là 3,6 trong đó có 5 ngày
cửa hàng bị quá tải trong việc vận hành đơn. a). Hãy ước lượng số đơn hàng online trung bình của cửa
hàng với độ tin cậy 96%.
b). Khi ước lượng tỷ lệ những ngày cửa hàng bị quá tải đơn với độ chính xác 0,06 và độ tin cậy 95% thì
cần điều tra thêm bao nhiêu ngày nữa? lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 18
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
c). Chủ cửa hàng khẳng định tỷ lệ những ngày cửa hàng bị quá tải không vượt quá 7%. Hãy cho kết luận với mức ý nghĩa 2% ?
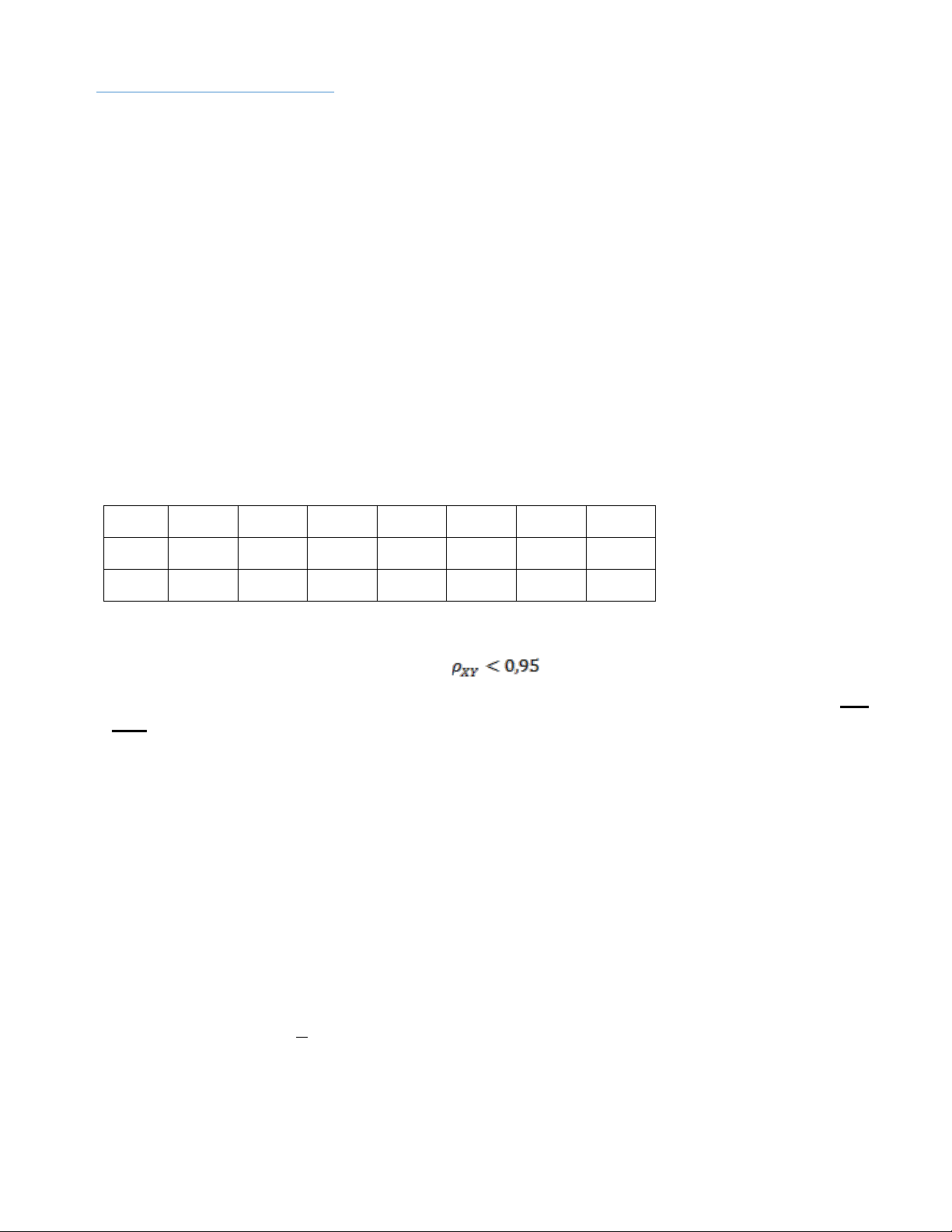
Câu 4.(2 điểm): Để điều tra về mức thu nhập X (triệu/tháng) và nhu cầu về một loại hàng hóa Y (kg/tháng)
của người dân thủ đô ta có số liệu như sau: xi (triệu/tháng) 4,3 5,3 6,3 7,3 8,3 9,3 10,3 yi (kg/tháng) 1,6 1,8 2,3 2,5 2,8 3,2 3,4 ni (người) 3 5 5 8 7 4 2
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết với nhu cầu về một loại hàng
hóa 3 kg/tháng thì mức thu nhập của người dân thủ đô ước tính qua hàm hồi quy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho hệ đầy đủ 3 biến cố {A, B , C } với P(A) = 0,15; P(B) = 3P(A). Biết biến cố F thỏa
mãn: P(F/A) = 0,02; P(F/B) = 0,45; P(F/C) = 0,25. a) Tính xác suất P(F)?
b) Tính giá trị PC F( | ) ?
Câu 2.(3 điểm):
1.Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau: Y -3 3 6 X -2 a 0,5a a 2 0,05 a 1,5a 3 0,15 0,1 0,2
a)Tìm hệ số a từ bảng phân phối. b)Tính P(|X – Y| < 2)?
2.Cho 2 biến ngẫu nhiên độc lập: X N(8; 1,44) và Y B(10; 0,6); đặt Z = 5X – 2Y + 100.
a)Hãy tính D(Z)? b)Tính P(X < 9, Y = E(Y))? lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 19
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 3.( 3 điểm): Trọng lượng (gam) của một loại sản phẩm của một dây chuyền sản xuất là BNN có phân
bố chuẩn. Điều tra trên một mẫu 100 sản phẩm, ta thu được trọng lượng trung bình mẫu là 1805g và độ
lệch mẫu hiệu chỉnh là 55g.
a). Hãy ước lượng trọng lượng trung bình của sản phẩm của dây chuyền với độ tin cậy 98%.
b). Khi ước lượng trọng lượng trung bình của sản phẩm của dây chuyền với độ chính xác là 10g thì độ tin cậy bằng bao nhiêu?
c). Quản đốc dây chuyền khẳng định rằng trọng lượng trung bình của sản phẩm là 1850g, hãy cho kết luận
với mức ý nghĩa 5%.
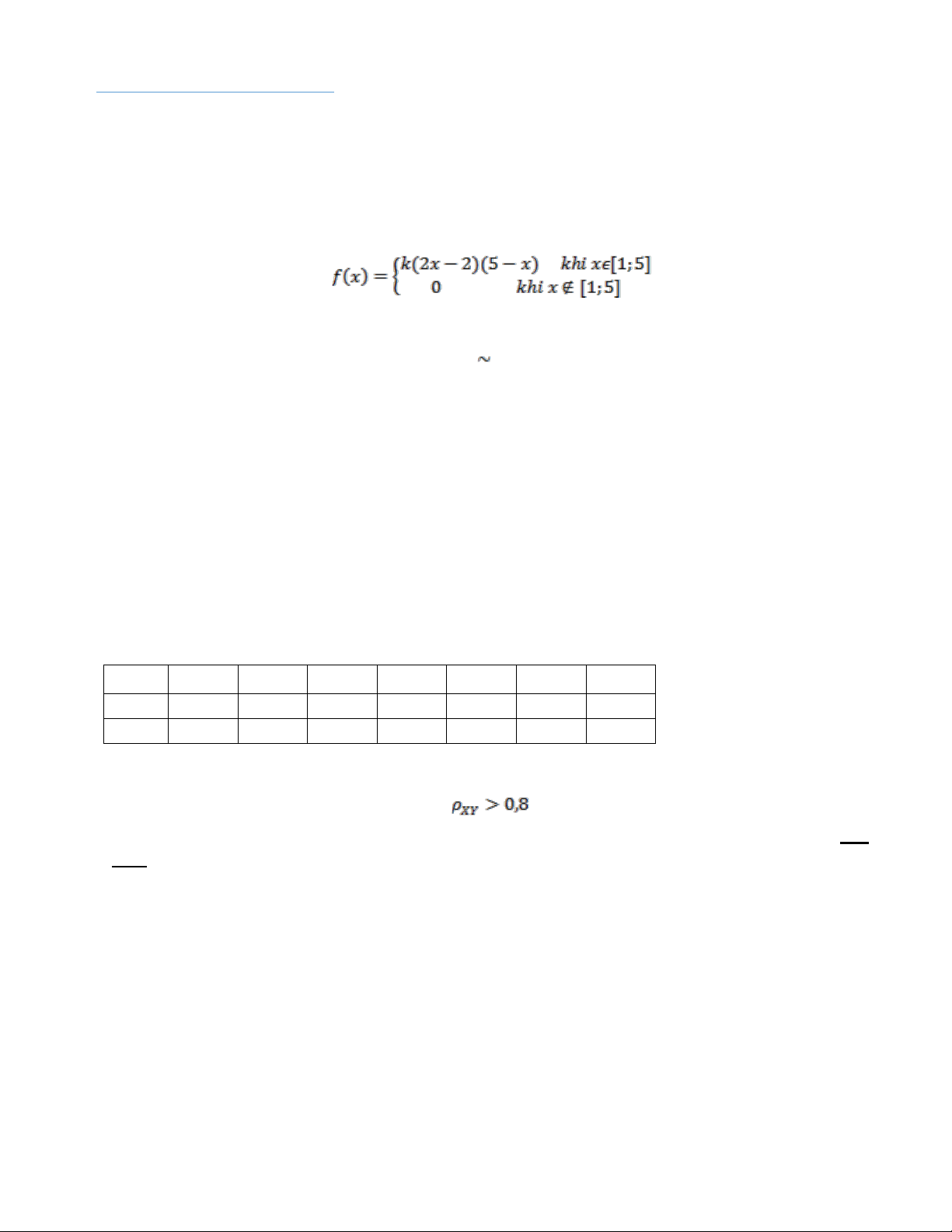
Câu 4.(2 điểm): Để điều tra về chiều cao (X cm) và cân nặng (Y kg) của học sinh lớp 1 ở địa phương A ta có số liệu như sau: xi(cm) 75,8 80,8 85,8 90,8 95,8 100,8 105,8 yi(kg) 16 20 23 25 28 32 34 ni(hs) 2 3 5 7 4 2 1
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu chiều cao là 110 cm thì
trọng lượng của học sinh lớp 1 của địa phương A ước tính qua hàm hồi quy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho hai biến cố A và B. Biết rằng P(A + B) = 0,7; P(A) = 0,5; P(B) = 0,6.
a) Tính P(AB) và kiểm tra xem A, B độc lập hay phụ thuộc?
b) Tính xác suất để chỉ có một trong 2 biến cố A, B xảy ra?
Câu 2.(3 điểm):
1.Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ? b)Tính E(5X3 + 6)?
2. Cho X N(5;9); Y B(10; 0,2) và đặt T = 2X + 5Y – 7.ModX.ModY.
a)Hãy tính giá trị của E(T)? b)Tính E(X2)? lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 20
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 3.( 3 điểm): Điểm số của môn xác suất thống kê là đại lượng tuân theo quy luật chuẩn. Theo dõi số
sinh viên thi đạt môn xác suất năm học 2021-2022 có kết quả sau: cỡ mẫu = 100, TB mẫu = 6,7 và độ lệch
hiệu chỉnh = 0,51 trong đó có 15 sinh viên đạt điểm giỏi (≥ 9).
a). Hãy ước lượng điểm trung bình môn xác suất của sinh viên với độ tin cậy 96%.
b). Khi ước lượng tỷ lệ những sinh viên đạt điểm giỏi với yêu cầu độ chính xác là 0,08 thì độ tin cậy là bao nhiêu?
c). Phòng khảo thí cho rằng tỷ lệ sinh viên đạt điểm giỏi không quá 10%. Hãy cho kết luận với mức ý nghĩa 2% ?
Câu 4.(2 điểm): Để điều tra về chiều cao (X cm) và cân nặng (Y kg) của học sinh lớp 1 ở địa phương A ta có số liệu như sau: xi(cm) 75,2 80,2 85,2 90,2 95,2 100,2 105,2 yi(kg) 16 20 23 25 28 32 34 ni(hs) 2 3 5 7 4 2 1
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu chiều cao là 110 cm thì
trọng lượng của học sinh lớp 1 của địa phương A ước tính qua hàm hồi quy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho hai biến cố A và B. Biết rằng P(A + B) = 0,78; P(A) = 0,65; P(B) = 0,77.
a) Tính P(AB) và kiểm tra xem A, B độc lập hay phụ thuộc?
b) Tính xác suất PA B( + )?
Câu 2.(3 điểm):
1.Cho hàm mật độ của biến ngẫu nhiên X: lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 21
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
a)Tìm k để f(x) là hàm mật độ? b)Tính P(-3 < X < 4)?
2.Trong một lô 100 sản phẩm có 75 sản phẩm loại I. Lấy ngẫu nhiên 45 sản phẩm để kiểm tra, gọi X là
số sản phẩm loại I gặp được khi kiểm tra. Biết Y N(3;4).
a)Tính giá trị của E(4X + 3Y)? b)Tính P(X < 2)?
Câu 3.( 3 điểm): Theo dõi mức tiêu hao nhiên liệu của một loại xe bus X chạy trên quãng đường 100 km,
được số liệu sau: số chuyến xe: 35, mức tiêu hao trung bình 18,5 lít, độ lệch hiệu chỉnh là 2,15. Trong đó
có 7 chuyến xe có mức tiêu hao trên 20 lít. Biết rằng lượng tiêu hao nhiên liệu là BNN tuân theo luật chuẩn.
a). Hãy ước lượng mức tiêu hao trung bình cho loại xe bus X với độ tin cậy 95%.
b). Nếu muốn ước lượng mức tiêu hao trung bình cho loại xe bus X với độ chính xác là 0,68 thì độ tin cây là bao nhiêu?
c). Xe có mức tiêu hao nhiên liệu trên 20 lít là xe cần kiểm tra kỹ thuật. Hãy ước lượng tỷ lệ các xe cần
kiểm tra kỹ thuật với độ tin cậy 99%.
Câu 4.(2 điểm): Để điều tra về chiều cao (X cm) và cân nặng (Y kg) của học sinh lớp 1 ở địa phương A ta có số liệu như sau: xi(cm) 75,4 80,4 85,4 90,4 95,4 100,4 105,4 yi(kg) 16 20 23 25 28 32 34 ni(hs) 2 3 5 7 4 2 1
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu chiều cao là 110 cm thì
trọng lượng của học sinh lớp 1 của địa phương A ước tính qua hàm hồi quy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYỆT KHOA KHOA HỌC ỨNG DỤNG
Câu 1.(2 điểm): Cho hệ biến cố đầy đủ A, B, C . Biết P(A) =0,25, P(B) = 2 P(C). Cho biến cố F thỏa mãn
P(F|A)=0,65; P(F|B)=0,2; P(F|C) = 0,32.
a). Tính xác suất P(F). lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 22
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
b). Tính xác suất P( A+C + AB + BC)? Câu 2.(3 điểm):
1.Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau: Y -3 -2 2 3 X -3 a 2a 4a 4a 3 4a a 3a a
a)Tìm hệ số a từ bảng phân phối. b)2 biến ngẫu nhiên X và Y có độc lập không? Vì sao?
2.Một sinh viên đi thi chỉ thuộc 35 câu trong 50 câu ở đề cương. Mỗi đề thi có 10 câu hỏi thuộc đề
cương, gọi Y là số câu hỏi sinh viên đó thuộc. Biết X N(4;9); đặt Z = EX2 + Y - modX a)Tính
giá trị của EZ? b)Tính P(Y > 1)?
Câu 3.( 3 điểm): Điều tra về thu nhập cá nhân (TNCN) sau khi giảm trừ gia cảnh của 100 người làm việc
ở tập đoàn A thu được kết quả: trung bình mỗi người có thu nhập 15,45 triệu/tháng; độ lệch hiệu chỉnh là
2,69 triệu/tháng và có 75 người phải nộp thuế TNCN.
a). Hãy ước lượng tỉ lệ những người phải nộp thuế TNCN ở tập đoàn A với độ tin cậy 90%.
b). Hãy ước lượng thu nhập trung bình của những người làm việc tại tập đoàn A với độ tin cậy 99%.
c). Khi ước lượng thu nhập trung bình của những người làm việc tại tập đoàn A với sai số 0,6 triệu/tháng
thì độ tin cậy là bao nhiêu?
Câu 4.(2 điểm): Để điều tra về mức thu nhập X (triệu/tháng) và nhu cầu về một loại hàng hóa Y (kg/tháng)
của người dân thủ đô ta có số liệu như sau: xi (triệu/tháng) 4,2 5,2 6,2 7,2 8,2 9,2 10,2 yi (kg/tháng) 1,6 1,8 2,3 2,5 2,8 3,2 3,4 ni (người) 3 5 5 8 7 4 2
a) Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết với mức thu nhập là 11
triệu/tháng thì nhu cầu về một loại hàng hóa Y của người dân thủ đô ước tính qua hàm hồi quy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất
DUYỆT KHOA KHOA HỌC ỨNG DỤNG lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 23
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
Câu 1.(2 điểm): Cho cố A và B độc lập nhau. Biết rằng P(A + B) = 0,9; P(A) = 0,5 và P(B) = a. a) Tìm giá trị của a?
b) Cho biến cố D = A + B + C có P(D) = 0,96 và giả sử A, B, C độc lập hãy tính xác suất P(B + C )?
Câu 2.(3 điểm):
1.Cho hàm mật độ của biến ngẫu nhiên X:
a)Tìm k để f(x) là hàm mật độ? b)Tính P( X > ModX)?
2. Cho X N(5;4); Y H(25;10;15/25) và đặt T = 2X + Y – 3.medX.
a)Hãy tính giá trị của E(T)? b)Tính P(X2 + 3X – 4 < 0)?
Câu 3.( 3 điểm): Để khảo sát nhiệt độ trong mùa hè này, người ta điều tra 35 ngày thì thấy: nhiệt độ trung
bình là 26,90C; độ lệch mẫu hiệu chỉnh là 1,250C và thấy có 10 ngày nóng. a). Hãy ước lượng nhiệt độ
trung bình của mùa hè này với độ tin cậy 92%.
b). Để ước lượng nhiệt độ trung bình của mùa hè với độ chính xác là 0,30C và độ tin cậy 94% thì cần khảo sát bao nhiêu ngày?
c). Hãy ước lượng tỷ lệ ngày nóng của mùa hè này với độ tin cậy 95%.
Câu 4.(2 điểm): Theo dõi độ dày của một loại giấy và thời gian phân hủy ta được bảng số liệu sau:
(biết độ dày X(mm) và thời gian phân hủy Y(tháng)) X 1,4 3,4 10,4 16,4 26,4 36,4 Y 10 13 15 19 20 25 Ni 3 4 5 5 3 6
a) Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu độ dày của giấy là 30 mm thì
thời gian phân hủy là bao nhiêu?
b) Với mức ý nghĩa 5%, có thể cho rằng không?
---------------------------------------------------------- Hết----------------------------------------------------- Ghi
chú: Sinh viên được sử dụng bảng tra các giá trị tới hạn xác suất lOMoAR cPSD| 45470709
Trường ĐH Kinh tế - Kỹ thuật
ĐỀ THI KẾT THÚC HỌC PHẦN Công nghiệp Môn : XÁC
SUẤT THỐNG KÊ – Hệ: ĐH
Thời gian làm bài: 90 phút Đề số: 24
(Lần 1, kỳ 1 năm 2022-2023)
Họ tên SV:…………………………………………. Phòng thi: ………………Số BD……………
DUYỆT KHOA KHOA HỌC ỨNG DỤNG