
























Preview text:
Trang chủ (/) Danh mục khoá học (/tat-ca-khoa-hoc) NEU TOÁN GIẢI
TÍCH (NEU Toán cho các nhà kinh tế) (/khoa-hoc-4820189300391936) Đề
cuối kỳ số 1 (/bai-hoc/de-cuoi-k-so-1-4804884117323776) QUAY VỀ Câu 1 Tìm hàm hợp với
Giải thích: Thay thành trong biểu thức Câu 2
Công ty của Vicky có thể sản xuất đầu ghi âm kĩ thuật số với
chi phí cho mỗi sản phẩm là 40$. Ước tính rằng nếu giá bán
mỗi sản phẩm là p đô-la thì người tiêu dung sẽ mua 120 – p
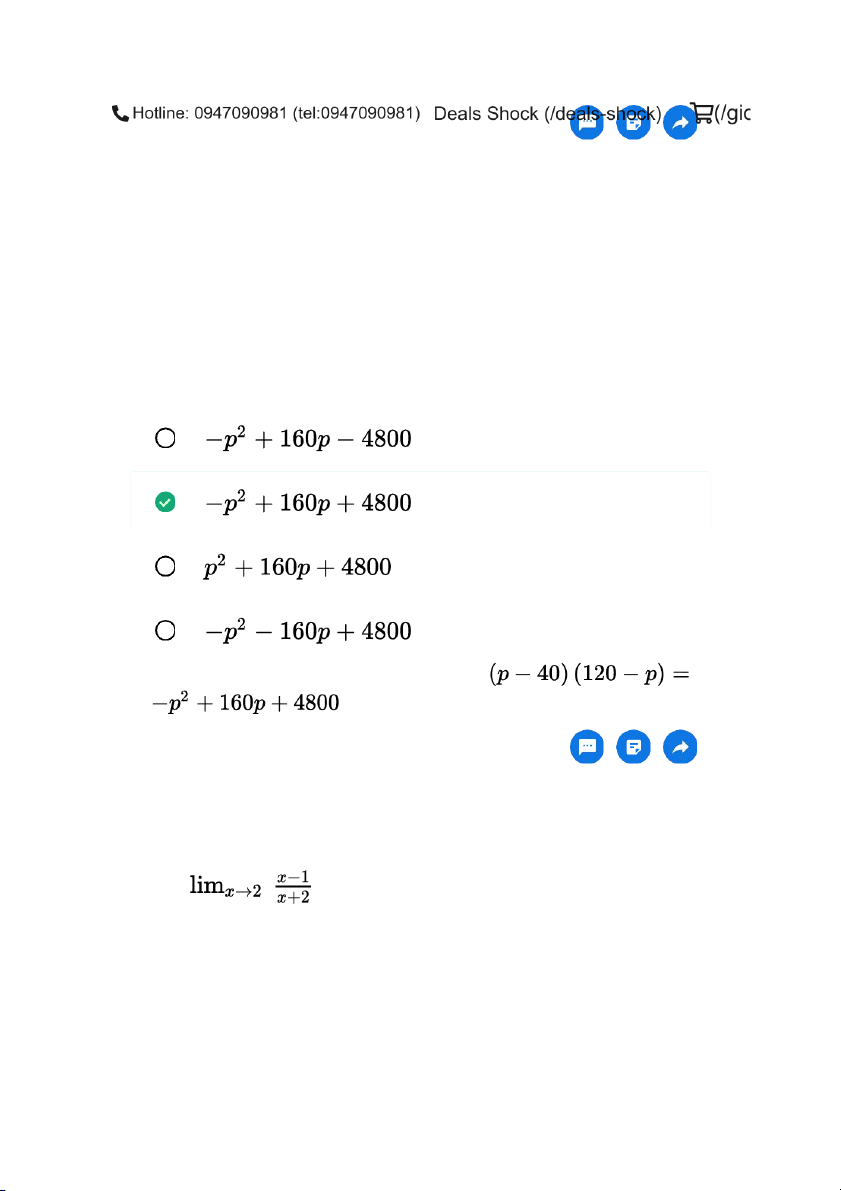
sản phẩm một tháng. Biểu diễn lợi nhuận hang tháng dưới dạng hàm của giá cả
Giải thích: Lợi nhuận hang tháng : Câu 3 Tính 0 3 không tồn tại 1 Giải thích:
. Vì giới hạn của tử là
và khác 0 nên ta có thể kết luận rằng giới
hạn của phân thức không tồn tại Câu 4
James, quản lí của một nhà máy xác định rằng khi x% công suất
của nhà máy được sử dụng , tổng chi phí để vận hành là C tram đô-la với
Công ty có chính sách bảo trì
luân phiên để cố gắng đảm bảo sử dụng 80% công suất nhà máy.
Vậy chi phí mà James phải trả bằng bao nhiêu khi nhà máy vận
hành với công suất lí tưởng này ? 8 5 7 70 Giải thích: Câu 5
Tìm giá trị của x sao cho bị gián đoạn :
Hàm số gián đoạn với mọi x
Hàm số liên tục với mọi x Giải thích: . vậy
hàm số không liên tục hay gián đoạn tại Câu 6
Độ dốc của tiếp tuyến đồ thị hàm số tại -27 25 -25 27 Giải thích: Câu 7
Tốc độ thay đổi trung bình của theo x khi x thay đổi từ đến -14 -15 14 15 Giải thích: Câu 8
Tìm tất cả các điểm trên đồ thị hàm số có tiếp tuyến tại đó là đư ngang : ( ; ( ; ( ; ( ; Giải . Thay vào
ta được các giá trị -2 và 0.; do đó tại các
tiếp tuyến với đồ thị là đường thẳng nằm ngang Câu 9
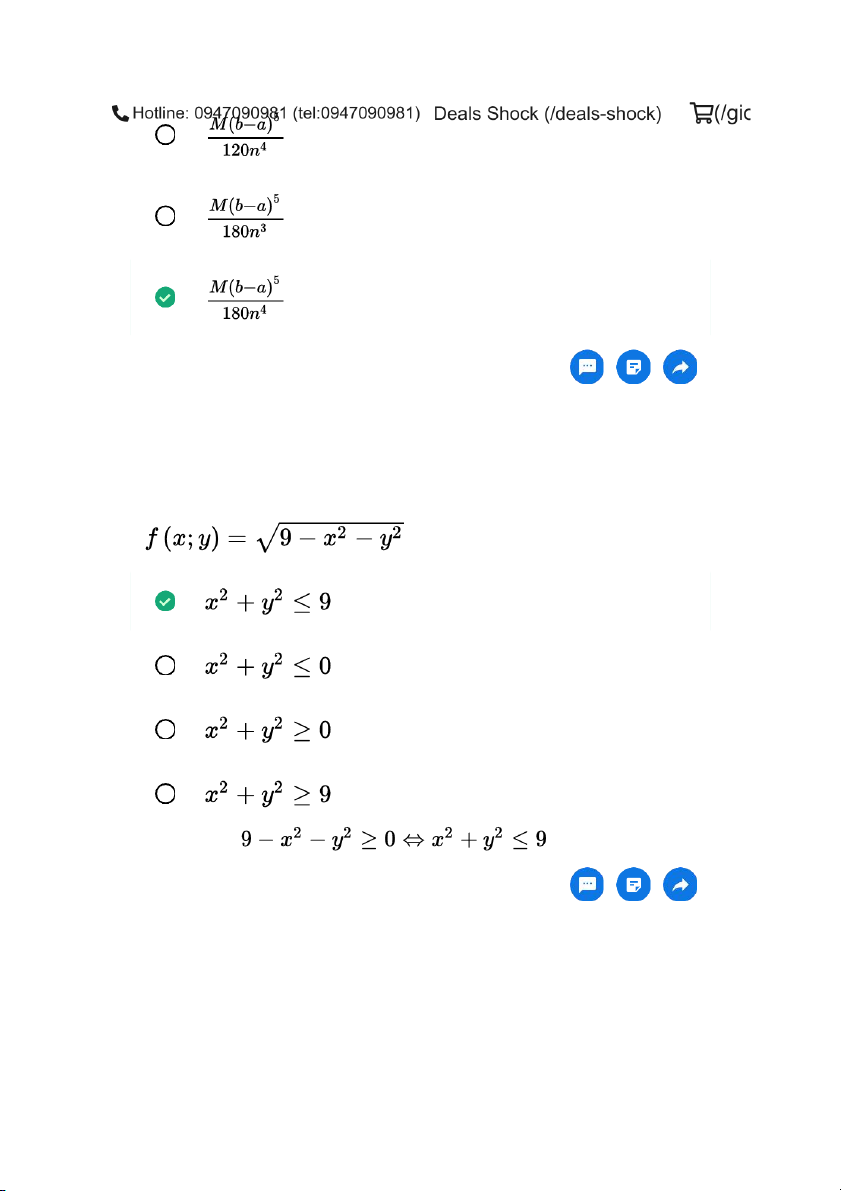
Tính đạo hàm của hàm số : Giải Câu 10 Tìm chi phí cận biên : Giải thích: Tính Câu 11
Tổng chi phí sản xuất x đơn vị của một loại hang hoá C(x) nghìn đô-la, với . Với
mức sản xuất x nào thì chi phí bình quân đạt tối thiểu 11 8 9 10 Giải thích: Chi phí bình quân A(x) tăng khi
A(x) giảm khi x > 11. Vậy chi phí bình quân đạt tối thiểu Khi x = 11 Câu 12
Xác định điểm uốn của hàm số (-1;2) (1;2) (1;-2) (-1;-2) Giải thích: điểm uốn
của đồ thị hàm số là (-1;2) Câu 13
Một nghiên cứu về hiệu quả của ca sáng ở một nhà máy ( 7 giờ sán
trưa ) cho thấy, trung bình một công nhân đên slamf việc lúc 7 giờ
xuất được Q đơn vị sản phẩm trong t giờ sau, với
.Tại thời điểm nào trong ca làm việc sáng thì công nhân làm việc k nhất ? 12 giờ 12 giờ 30 phút 8 giờ 30 phút 9 giờ 30 phút Giải thích: .Hàm hiệu suất là hàm .
tại t=5 hay tại 12 giờ thì công nhân làm việc kém hiệu quả nhất Câu 14
Tìm các hằng số A,B và C sao cho hàm số A +
có cực trị tương đối tại (2;11) và một điểm uốn tại (1;5) Giải thích:
có cực trị tương đối tại (2;11) ; có 1 điểm uốn (1;5) Câu 15
Xác định cầu co giãn, không co giãn hay co giãn đơn vị : cầu không co giãn cầu co giãn đơn vị cầu co giãn Giải thích: . Vậy cầu co giãn Câu 16
Giải phương tình vi phân phân li biến số với giá trị ban đầu tương ứng : khi Giải thích: khi Câu 17 Tính tích phân : Giải thích: . Đặt Câu 18
Ở một nhà máy, chi phí cận biên là đô-la mỗi đơn
vị khi mức sản lượng là q đơn vị. Tính chi phí để sản xuất 14
đơn vị nếu chi phí cố định là b. 1400 1200 1500 1000 Giải thích: Câu 19
Sau t tháng làm việc, một nhân viên bưu điện có thể sắp xếp
lá thư mỗi giờ. Tốc độ sắp xếp
trung bình của nhân viên bưu điện là bao nhiêu trong 3 tháng làm việc đầu tiên ? 1000 400 492.83 500 Giải thích: Câu 20
Ở một nhà máy, chi phí cận biên là đô-la mỗi đơn
vị khi mức sản xuất là q đơn vị. Tổng chi phí sản xuất sẽ
tăng bao nhiêu nếu mức sản xuất tăng từ 10 lên 13 đơn vị ? 750 700 885 774 Câu 21
Một khoản đầu tư sẽ sinh ra một dòng thu nhập liên tục với tốc đ
đô-la mỗi năm trong 5 năm. Nếu tài khoản được trả lãi với lãi suấ
liên tục thì tài khoản có bao nhiêu tiền vào cuối giai đoạn đầu tư 5 n 0 114.17 200 117.14 Giải , Câu 22 Tính Giải thích: Câu 23 -1 2 0 1 Giải thích: = Câu 24 Cho hàm số
liên tục trên [2;8]. Khi đó, tích phân = Giải thích: = + = Câu 25
Theo một thí nghiêm tâm lí, tỷ lệ người tham gia cần nhiều
hơn t phút để hoàn thành một nhiệm vụ được xác định bởi 0.705 0.375 0.295 0.625 Giải thích: =0.705 Câu 26 $$ Câu 27
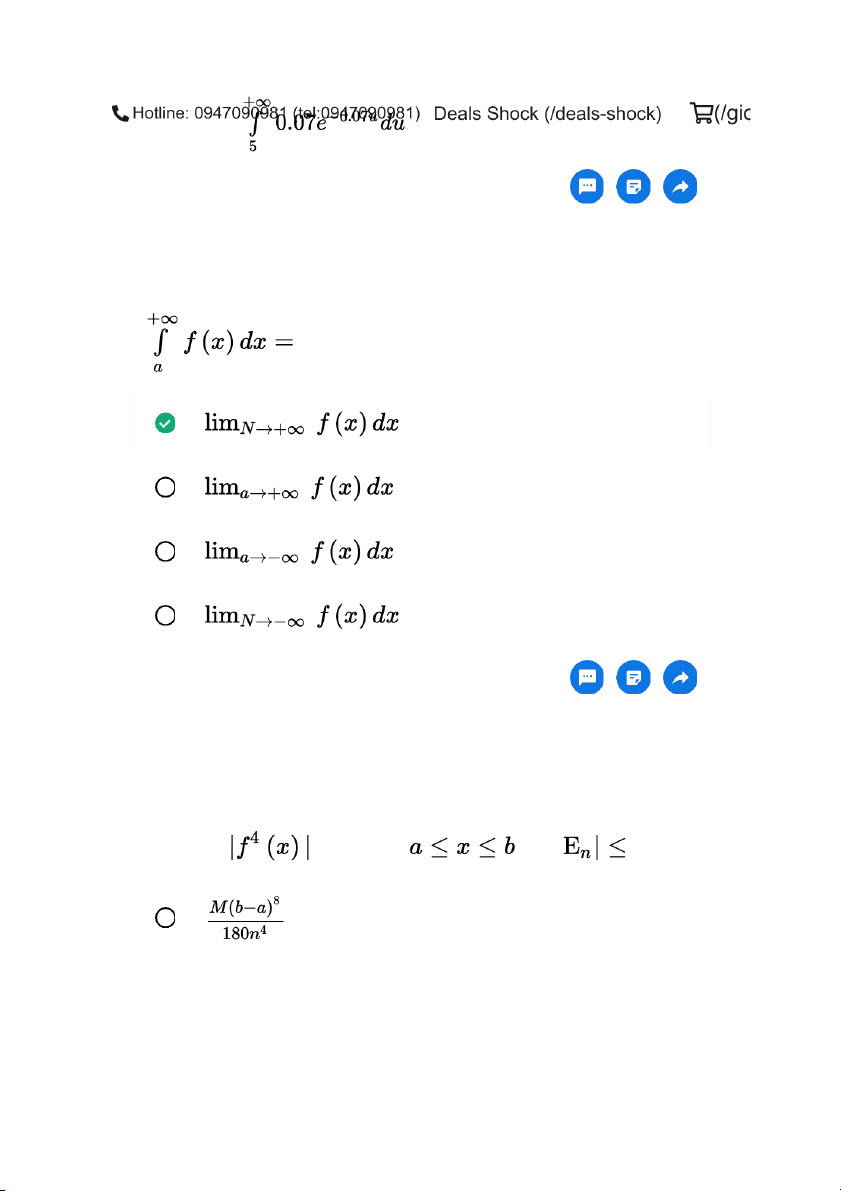
Ước lượng sai số theo quy tắc Simpson: Nếu M là giá trị lớn nhất của trên đoạn thì : | Câu 28 Mô tả tập xác định của hàm số : Giải thích: Câu 29 Tính của $$ Câu 30 Tính của hàm số Giải thích: Câu 31
Tìm tất cả các điểm tới hạn của hàm số điểm tới hạn :
Hàm số đạt cực đại tương đối tại điểm (-2;0) và có một điểm
Hàm số đạt cực tiểu tương đối tại điểm (2;0) và có một điểm
Hàm số đạt cực đại tương đối tại điểm (2;0) và có một điểm
Hàm số đạt cực đại tương đối tại điểm (-2;0) và có một điểm Giải thích: số có 2 điểm tới hạn là ,
đại tương đối tại điểm (2;0) và có một điểm yên ngựa (-2;0) Câu 32
Công thức độ dốc của đường mức : $$ Câu 33 Cho hàm số . Độ dốc của
đường mức của hàm số tại điểm là Giải thích: Câu 34
“Một doanh nghiệp sản xuất một loại sản phẩm có hàm sản xuất
. Doanh nghiệp này nhận được hợp
đồng cung cấp 900 sản phẩm. Tìm K, L để doanh nghiệp sản
xuất theo hợp đồng tốn ít chi phí nhất khi giá thuê tư bản và lao động lần lượt là
à12”. Khi giải bài toán này bằng
phương pháp nhân tử Lagrange, ta lập hàm Larange
Giải thích: lí thuyết về phương pháp lập hàm Larange Câu 35
Anna quản lí 150 căn hộ tại Mỹ. Tất cả các căn hộ đều có t hể dược
1,200 đô-la mỗi tháng mỗi căn, nhưng với mỗi lần tăng giá thuê
thêm 100 đô-la thì sẽ có thêm 5 căn hộ không được thuê. Biể
doanh thu hang tháng R thu được từ việc cho thuê căn hộ dưới dạ
giá cho thuê mỗi căn hộ hang tháng p $$ ;
Giải thích: Gọi t là số lần tăng giá thì doanh thu hang tháng sẽ là : Câu 36
Một phòng trưng bày nghệ thuật cung cấp 50 bức ảnh in của
một nghệ sĩ nổi tiếng. Nếu mỗi bức ảnh in được định giá p đô-
la thì số bức ảnh in sẽ bán được là . Tìm mức
giá p tại đó cầu co giãn đơn vị Giải thích: Câu 37 $$ Câu 38
Một thị trường hoà vốn khi nào : Câu 39
Một thị trường cân bằng khi nào : Câu 40
Công thức tính khoảng cách giữa 2 điểm $$




