Đề Toán tuyển sinh lớp 10 THPT năm 2019 – 2020 sở GD&ĐT Bắc Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ðỀ THI TUYỂN SINH LỚP 10 TH PHỔ THÔNG BẮC GIANG NĂM HỌC 2019 - 2020 ----------------- MÔN THI: TOÁN ĐỀ THI CHÍNH THỨC Ngày thi: 02/6/2019
(Đề thi gồm 02 trang)
Thời gian làm bài 120 phút, không kể thời gian giao ñề) Mã ñề 101
PHẦN I. TRẮC NGHIỆM (3,0 ñiểm)
Câu 1: Giá trị của tham số m ñể ñường thẳng y = mx +1 song song với ñường thẳng y = 2x − 3 là A. m = 3 − . B. m = 1 − . C. m = 1. D. m = 2.
Câu 2: Tổng hai nghiệm của phương trình 2
x − 4x + 3 = 0 bằng A. −4. B. 4. C. 3. D. −3.
Câu 3: Giá trị nào của x dưới ñây là nghiệm của phương trình 2
x + x − 2 = 0 ? A. x = 4. B. x = 3. C. x = 2. D. x = 1.
Câu 4: ðường thẳng y = 4x − 5 có hệ số góc bằng A. 5 − . B. 4. C. 4 − . D. 5.
Câu 5: Cho biết x = 1 là một nghiệm của phương trình 2
x + bx + c = 0 . Khi ñó ta có
A. b + c = 1.
B. b + c = 2.
C. b + c = 1 − .
D. b + c = 0.
Câu 6: Tất cả các giá trị của x ñể biểu thức x − 3 có nghĩa là A. x ≥ 3. B. x ≤ 3. C. x < 3. D. x > 3.
Câu 7: Cho tam giác ABC có AB = 3cm, AC = 4 cm, BC = 5cm . Phát biểu nào dưới ñây ñúng?
A. Tam giác ABC vuông.
B. Tam giác ABC ñều.
C. Tam giác ABC vuông cân.
D. Tam giác ABC cân.
Câu 8: Giá trị của tham số m ñể ñường thẳng y = (2m + )
1 x + 3 ñi qua ñiểm A( 1 − ;0) là A. m = 2 − . B. m = 1. C. m = 1 − . D. m = 2.
Câu 9: Căn bậc hai số học của 144 là A. 13. B. 1 − 2. C. 12 và 1 − 2. D. 12.
Câu 10: Với x < 2 thì biểu thức 2
(2 − x) + x − 3 có giá trị bằng A. 1 − . B. 2x − 5. C. 5 − 2 . x D. 1. 3 + 3
Câu 11: Giá trị của biểu thức bằng 3 +1 1 1 A. 3. B. ⋅ C. ⋅ D. 3. 3 3 x − y = 1
Câu 12: Hệ phương trình 
có nghiệm là ( x ; y . Giá trị của biểu thức x + y bằng 0 0 ) x + 2 y = 7  0 0 A. 1. B. 2 − . C. 5. D. 4. Câu 13:
Cho tam giác ABC vuông tại A , có BC = 4 cm, AC = 2 cm . Tính sin ABC. 3 1 1 3 A. ⋅ B. ⋅ C. ⋅ D. ⋅ 2 2 3 3 Câu 14:
Tam giác ABC cân tại B có =120o ABC
, AB =12 cm và nội tiếp ñường tròn (O). Bán kính của ñường tròn (O) bằng A. 10 c . m B. 9 c . m C. 8 c . m D. 12 c . m
Câu 15: Biết rằng ñường thẳng y = 2x + 3 cắt parabol 2
y = x tại hai ñiểm. Tọa ñộ của các giao ñiểm là A. (1; ) 1 và (−3;9). B. (1; ) 1 và (3;9). C. ( 1 − ; ) 1 và (3;9). D. ( 1 − ; ) 1 và (−3;9).
Câu 16: Cho hàm số y = f ( x) = ( 4
1+ m ) x +1 , với m là tham số. Khẳng ñịnh nào sau ñây ñúng? A. f ( ) 1 > f (2).
B. f (4) < f (2).
C. f (2) < f (3). D. f (− ) 1 > f (0). x + y = 3
Câu 17: Hệ phương trình 
có nghiệm ( x ; y thỏa mãn x = 2 y . Khi ñó giá trị của m là 0 0 ) mx − y = 3  0 0 A. m = 3. B. m = 2. C. m = 5. D. m = 4.
Câu 18: Tìm tham số m ñể phương trình 2
x + x + m +1 = 0 có hai nghiệm x , x thỏa mãn 2 2 x + x = 5. 1 2 1 2 A. m = 3 − . B. m = 1. C. m = 2. D. m = 0.
Câu 19: Cho tam giác ABC vuông tại A , có AC = 20c .
m ðường tròn ñường kính AB cắt BC tại M ( M không
trùng với B ), tiếp tuyến tại M của ñường tròn ñường kính AB cắt AC tại I. ðộ dài ñoạn AI bằng A. 6 c . m B. 9cm C. 10 c . m D. 12c . m Câu 20: Cho ñường tròn ( ;
O R) và dây cung AB thỏa mãn 90 . o AOB =
ðộ dài cung nhỏ AB bằng π R π R 3π R A. ⋅ B. π . R C. ⋅ D. ⋅ 2 4 2
PHẦN II. TỰ LUẬN (7,0 ñiểm)
Câu 1 (2,0 ñiểm). x − y = 2
a) Giải hệ phương trình  ⋅ 3x + 2 y = 11   2(x 2 x )1  − + 2 x −1 x
b) Rút gọn biểu thức A =  −  :
với x > 0; x ≠ 4 .  x − 4 x + 2  x − 2  
Câu 2 (1,0 ñiểm). Cho phương trình 2 x − (m + )
1 x + m − 4 = 0 ( ) 1 , m là tham số.
a) Giải phương trình (1) khi m = 1.
b) Tìm giá trị của m ñể phương trình (1) có hai nghiệm x , x 1 2 thỏa mãn
( 2x −mx +m)( 2x −mx +m = 2. 1 1 2 2 )
Câu 3 (1,5 ñiểm). ðầu năm học, Hội khuyến học của một tỉnh tặng cho trường A tổng số 245 quyển sách gồm 1 2
sách Toán và sách Ngữ văn. Nhà trường ñã dùng số sách Toán và
số sách Ngữ văn ñó ñể phát cho các bạn 2 3
học sinh có hoàn cảnh khó khăn. Biết rằng mỗi bạn nhận ñược một quyển sách Toán và một quyển sách Ngữ văn.
Hỏi Hội khuyến học tỉnh ñã tặng cho trường A mỗi loại sách bao nhiêu quyển?
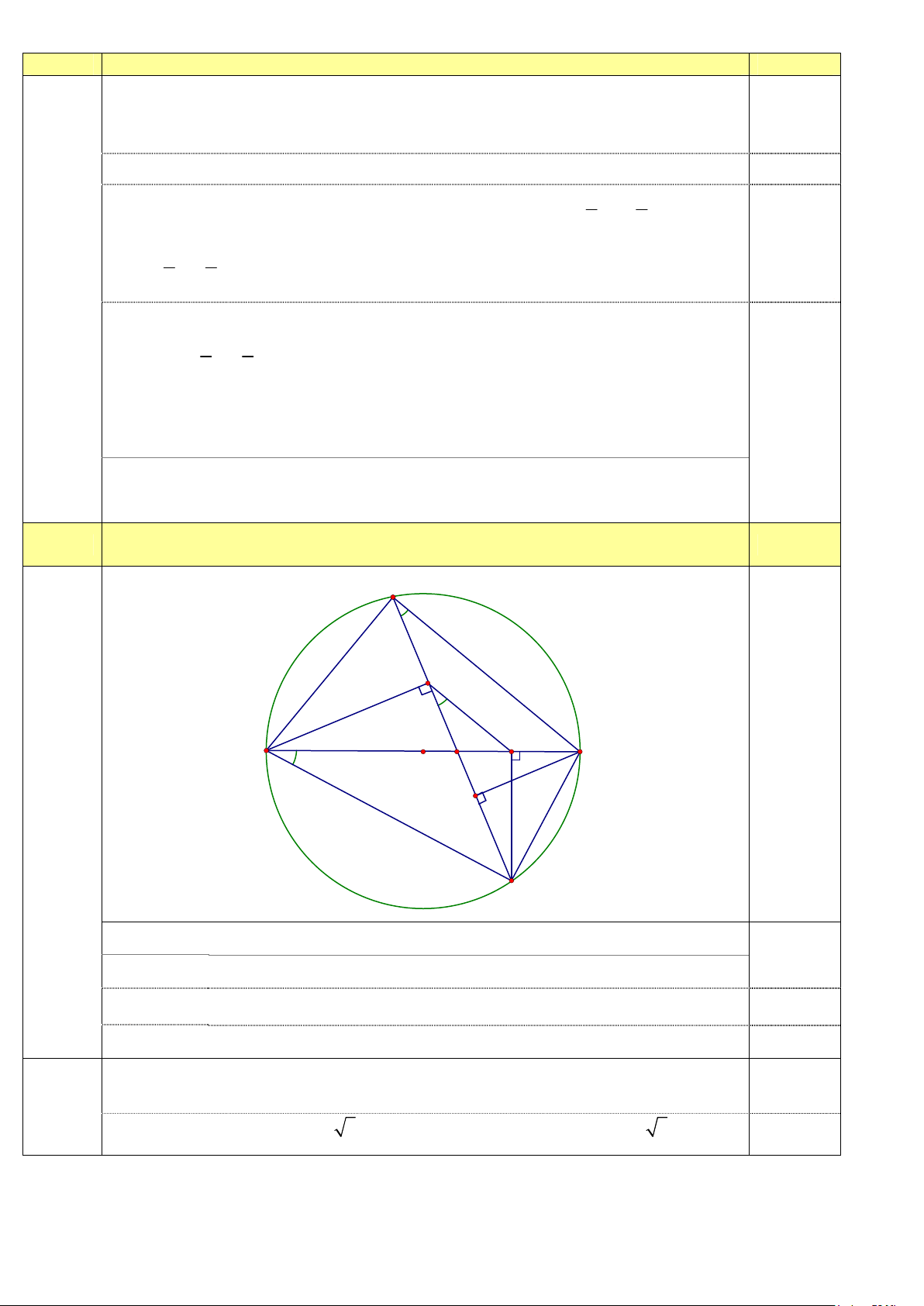
Câu 4 (2,0 ñiểm). Cho tam giác ABC nội tiếp ñường tròn (O) ñường kính AC ( BA < BC) . Trên ñoạn thẳng
OC lấy ñiểm I bất kỳ ( I ≠ C). ðường thẳng BI cắt ñường tròn (O) tại ñiểm thứ hai là .
D Kẻ CH vuông
góc với BD ( H ∈ BD), DK vuông góc với AC ( K ∈ AC).
a) Chứng minh rằng tứ giác DHKC là tứ giác nội tiếp.
b) Cho ñộ dài ñoạn thẳng AC là 4 cm và 60o ABD =
. Tính diện tích tam giác AC . D
c) ðường thẳng ñi qua K song song với BC cắt ñường thẳng BD tại E. Chứng minh rằng khi I thay ñổi
trên ñoạn thẳng OC ( I ≠ C ) thì ñiểm E luôn thuộc một ñường tròn cố ñịnh.
Câu 5 (0,5 ñiểm). Cho x, y là các số thực thỏa mãn ñiều kiện 2 2
x + y = 1. Tìm giá trị nhỏ nhất của biểu thức
P = (3 − x)(3 − y).
-------------------------------Hết--------------------------------
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ............................................. Số báo danh:...........................................................
Cán bộ coi thi 1 (Họ tên và ký): .........................................................................................................
Cán bộ coi thi 2 (Họ tên và ký): .........................................................................................................
SỞ GIÁO DỤC VÀ ðÀO TẠO
HƯỚNG DẪN CHẤM BÀI THI TUYỂN SINH LỚP 10 BẮC GIANG
TRUNG HỌC PHỔ THÔNG NGÀY THI: 02/06/2019
MÔN THI:TOÁN- PHẦN TỰ LUẬN
HDC ðỀ CHÍNH THỨC
Bản hướng dẫn chấm có 04trang Câu
Hướng dẫn, tóm tắt lời giải ðiểm Câu 1 (2,0ñiểm) x − y = 2 x = 2 + y  Ta có  ⇔  0,5 3x + 2 y = 11 3 
 (2 + y) + 2y = 11  = a) 5y 5 ⇔  0,25 (1,0 x = 2 + y  ñiểm) x = 3 ⇔  . y =1  0,25
Vậy hệ phương trình có nghiệm (x; y) = (3;1) .
Với x > 0; x ≠ 4 , ta có   x − x +
(2 x − )1( x −2 2 4 2 ) x 0,25 A =  −  
( x + 2)( x − 2)
( x +2)( x −2) : x −2    b) 2x − 4 x + 2 2x − 5 x + 2 x =  −  : 0,25 (1,0 
( x + 2)( x − 2) ( x + 2)( x − 2)  x − 2 ñiểm)  x x = ( x +2)( x − 0,25 2): x − 2 1 = 1 . Kết luận A = ⋅ 0,25 x + 2 x + 2 Câu 2 (1,0ñiểm) a)
Với m = 1, phương trình (1) trở thành 2
x − 2x − 3 = 0. 0,25 (0,5 ñiểm)
Giải ra ñược x = 1 − , x = 3. 0,25 ∆ = (m + )2
1 − (m − ) = m − m + = (m − )2 2 4 4 2 17 1 +16 > 0, m ∀ ∈ . ℝ 0,25
Kết luận phương trình luôn có hai nghiệm x , x với mọi m. 1 2 2 x − (m + ) 2
1 x + m − 4 = 0 ⇔ x − mx + m = x + 4. 1 1 1 1 1 b) Tương tự 2
x − mx + m = x + 4. 2 2 2 (0,5
( 2x −mx +m)( 2x −mx +m = 2 1 1 2 2 ) ñiểm) 0,25
⇔ ( x + 4 x + 4 = 2 ⇔ x x + 4 x + x +16 = 2 * . 1 )( 2 ) 1 2 ( 1 2 ) ( )
Áp dụng ñịnh lí Viet, ta có: ( ) ( −
⇔ m − ) + (m + ) 14 * 4 4
1 +16 = 2 ⇔ 5m +14 = 0 ⇔ m = ⋅ Kết luận. 5 Câu 3 (1,5ñiểm)
Gọi số sách Toán và sách Ngữ văn Hội khuyến học trao cho trường A lần lượt là 0,25 , x y (quyển), ( * , x y ∈ ℕ ) .
Vì tổng số sách nhận ñược là 245 nên x + y = 245 ( ) 1 0,5 1 2
Số sách Toán và Ngữ văn ñã dùng ñể phát cho học sinh lần lượt là x và y (quyển) 2 3 0,25 1 2 Ta có: x = y (2) (1,5 2 3 ñiểm) x + y = 245  ðưa ra hệ 1 2 . x = y 2 3 0,25 x = 140
Giải hệ ñược nghiệm  ⋅ y = 105 
Kết luận: Hội khuyến học trao cho trường 140 quyển sách Toán và 105 quyển sách 0,25 Ngữ văn Câu 4 (2,0ñiểm) B E K A C O I H a) D (1,0 ñiểm) + Chỉ ra ñược 0 DHC = 90 ; 0,25 + Chỉ ra ñược 0 AKC = 90 0,25
Nên H và K cùng thuộc ñường tròn ñường kính CD 0,25
+ Vậy tứ giác DHKC nội tiếp ñược trong một ñường tròn. 0,25 b) Chỉ ra ñược 0 ACD = 60 ; 0 ADC = 90 0,25 (0,5 ñiểm)
Tính ñược CD = 2 c ;
m AD = 2 3 cm và diện tích tam giác ACD bằng 2 2 3 cm . 0,25
Vì EK / / BC nên DEK = DBC. c)
Vì ABCD nội tiếp nên
DBC = DAC. Suy ra DEK = DAK. 0,25 (0,5
Từ ñó tứ giác AEKD nội tiếp và thu ñược o = = 90 ⇒ = 90o AED AKD AEB . ñiểm)
Kết luận khi I thay ñổi trên ñoạn OC thì ñiểm E luôn thuộc ñường tròn ñường kính 0,25 A . B cố ñịnh. Câu 5 (0,5ñiểm) ( − + + =
− x)( − y) = − ( x + y) 18 6 ( x y) 2xy P 3 3 9 3 + xy = 2 17 + ( 2 2
x + y ) − 6( x + y) + 2xy 8 + ( x + y)2 − 6( x + y) + 9 = = 0,25 2 2 (x + y −3)2 = + 4. 2 Từ 2 2
x + y = 1chỉ ra ñược ( x + y)2 ≤ 2 ⇒ − 2 ≤ x + y ≤ 2; (0,5 ñiểm)
Suy ra − 2 − 3 ≤ x + y − 3 ≤ 2 − 3 < 0. (x y ) ( − + − )2 2 2 3 3 19 − 6 2 P = + 4 ≥ + 4 = ⋅ 2 2 2 0,25 19 − 6 2 2
Vậy giá trị nhỏ nhất của P là khi x = y = ⋅ 2 2
(Chú ý: Nếu học sinh dò ñúng ñáp án nhưng không lập luận ñúng thì không cho ñiểm). Tổng 7,0 ñiểm
Lưu ý khi chấm bài:
- Trên ñây chỉ là sơ lược các bước giải, lời giải của học sinh cần lập luận chặt chẽ, hợp logic. Nếu
học sinh trình bày cách làm ñúng khác thì cho ñiểm các phần theo thang ñiểm tương ứng.
- Với Câu1 ý a nếu học sinh dùng MTCT bấm và cho ñược kết quả ñúng thì cho 0,75 ñiểm
- Với Câu4, nếu học sinh không vẽ hình thì không chấm.
- ðiểm toàn bài không ñược làm tròn.
----------------*^*^*----------------