Đề Xác suất thống kê | Đại học Kinh tế kỹ thuật công nghiệp

lOMoAR cPSD| 45315597 – SỐ 01
Câu 1.(2 điểm): Cho hai biến cố A, B. Biết P(A+B) = 0,7; P(A) = 0,3; P(B) =0,6.
1. Tìm xác suất P(AB).
2. Đặt C A B , tính xác suất: P(A|C)
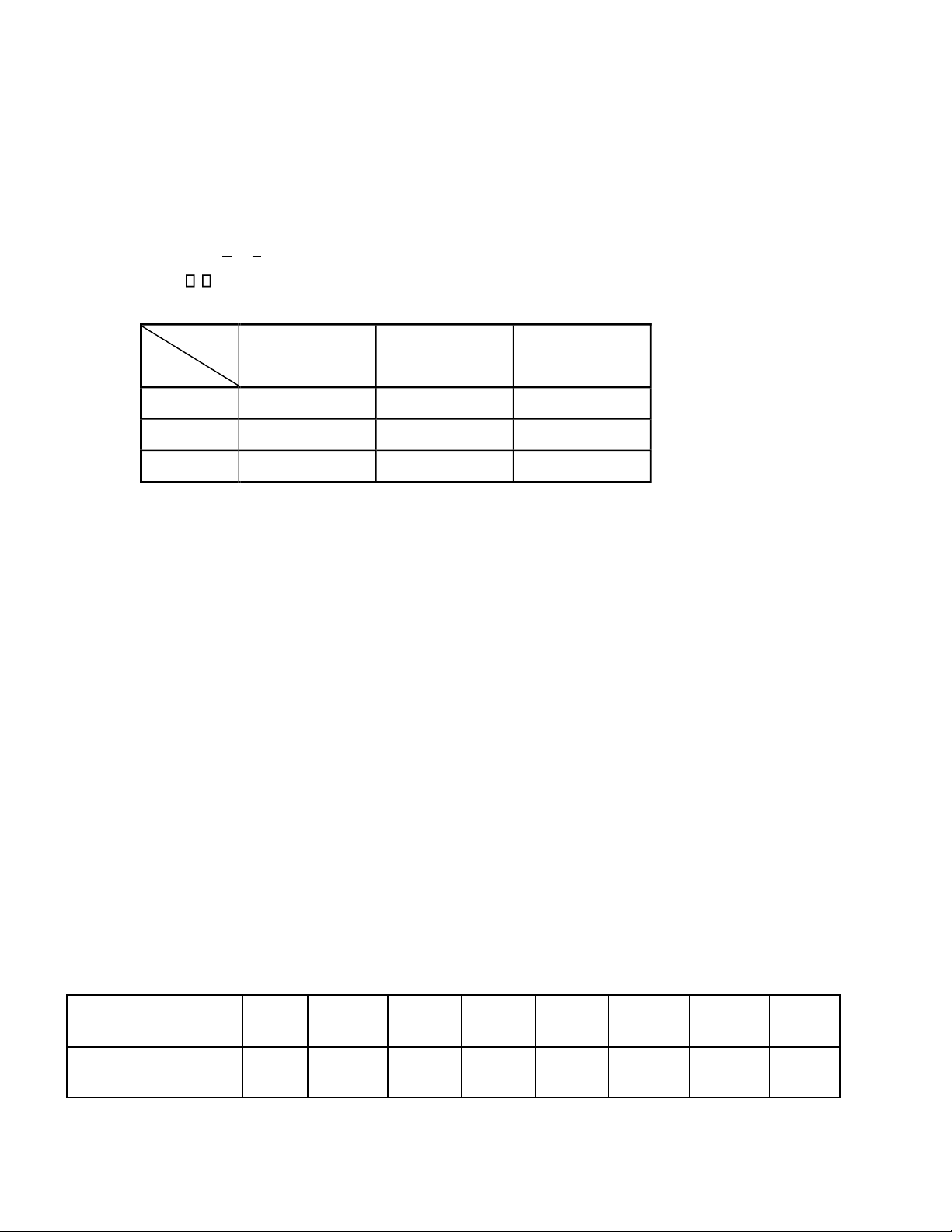
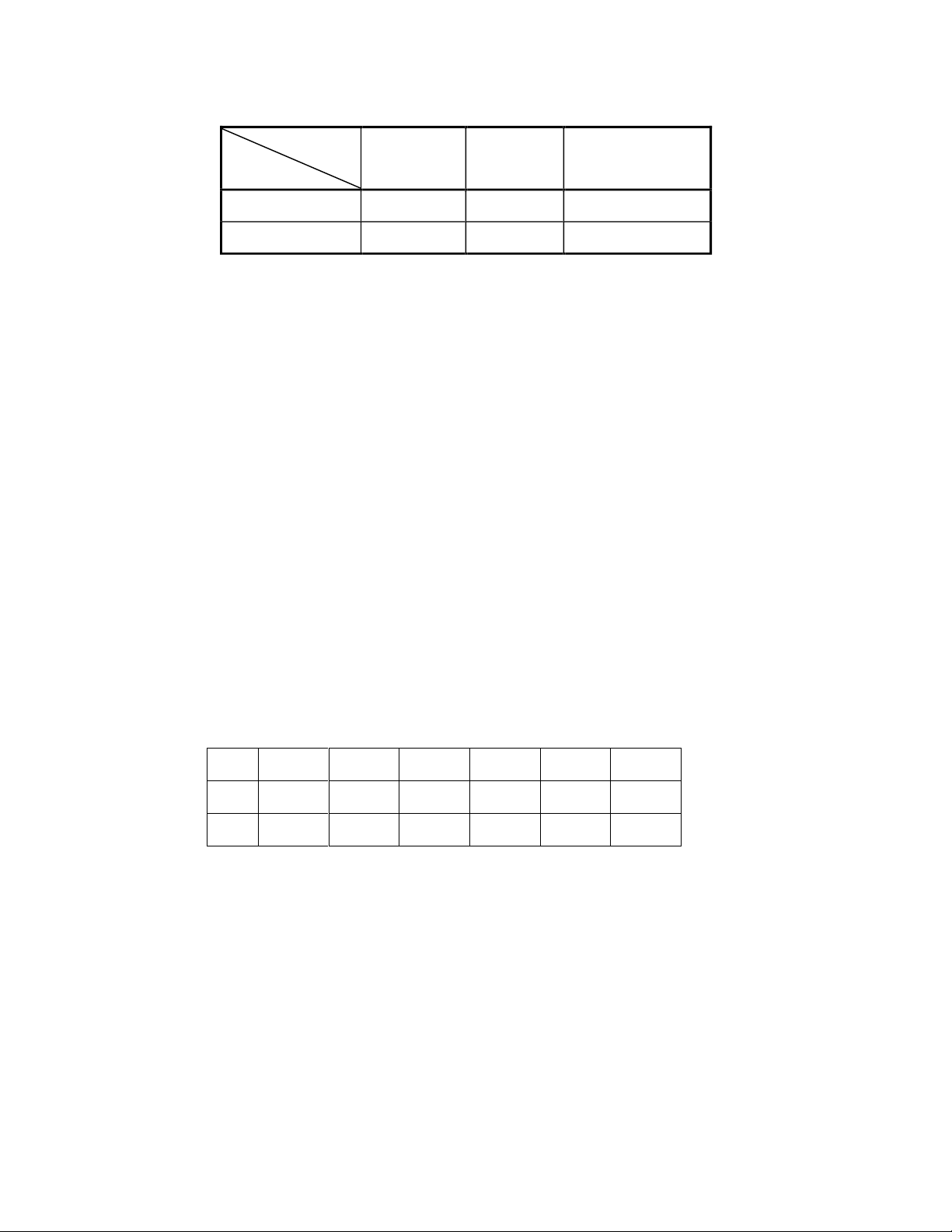
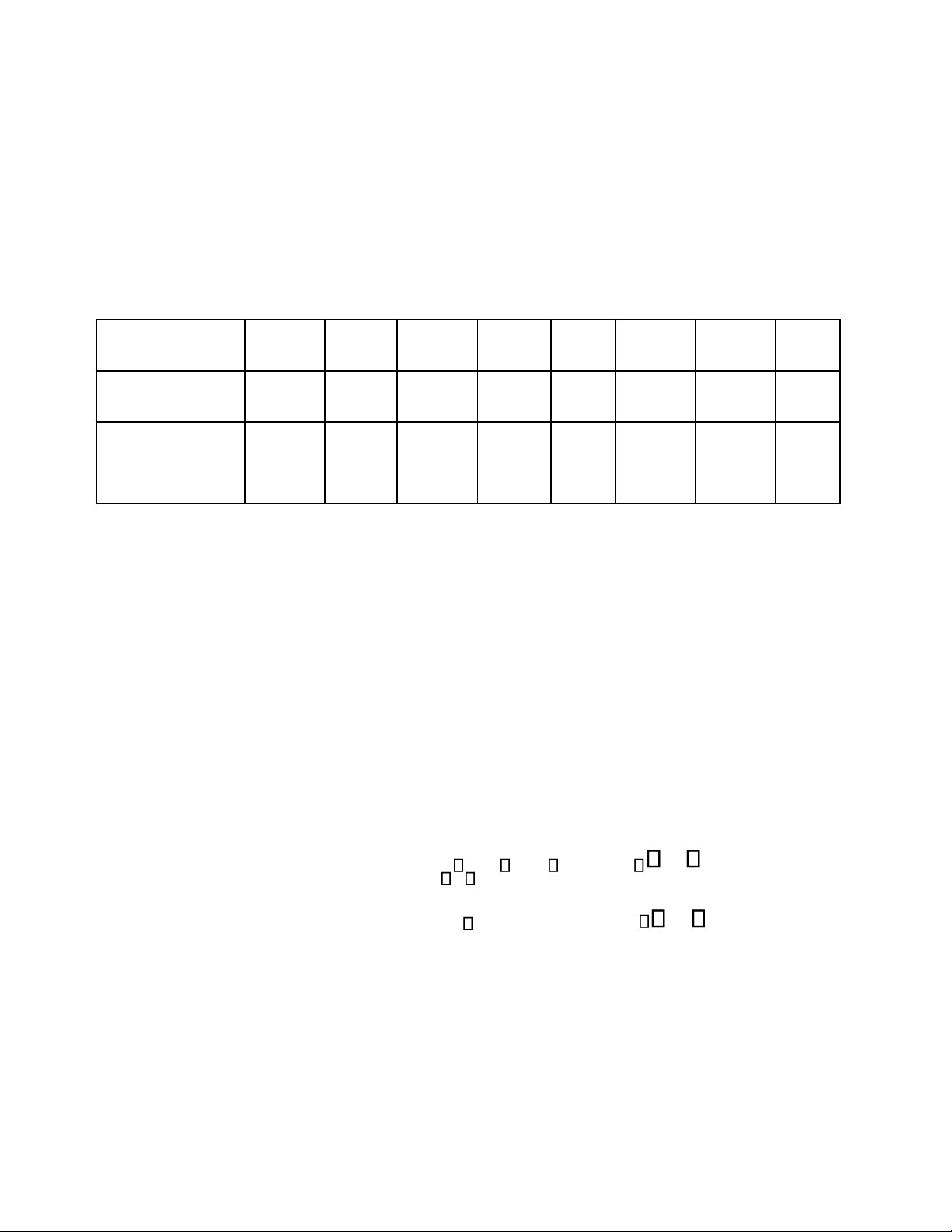
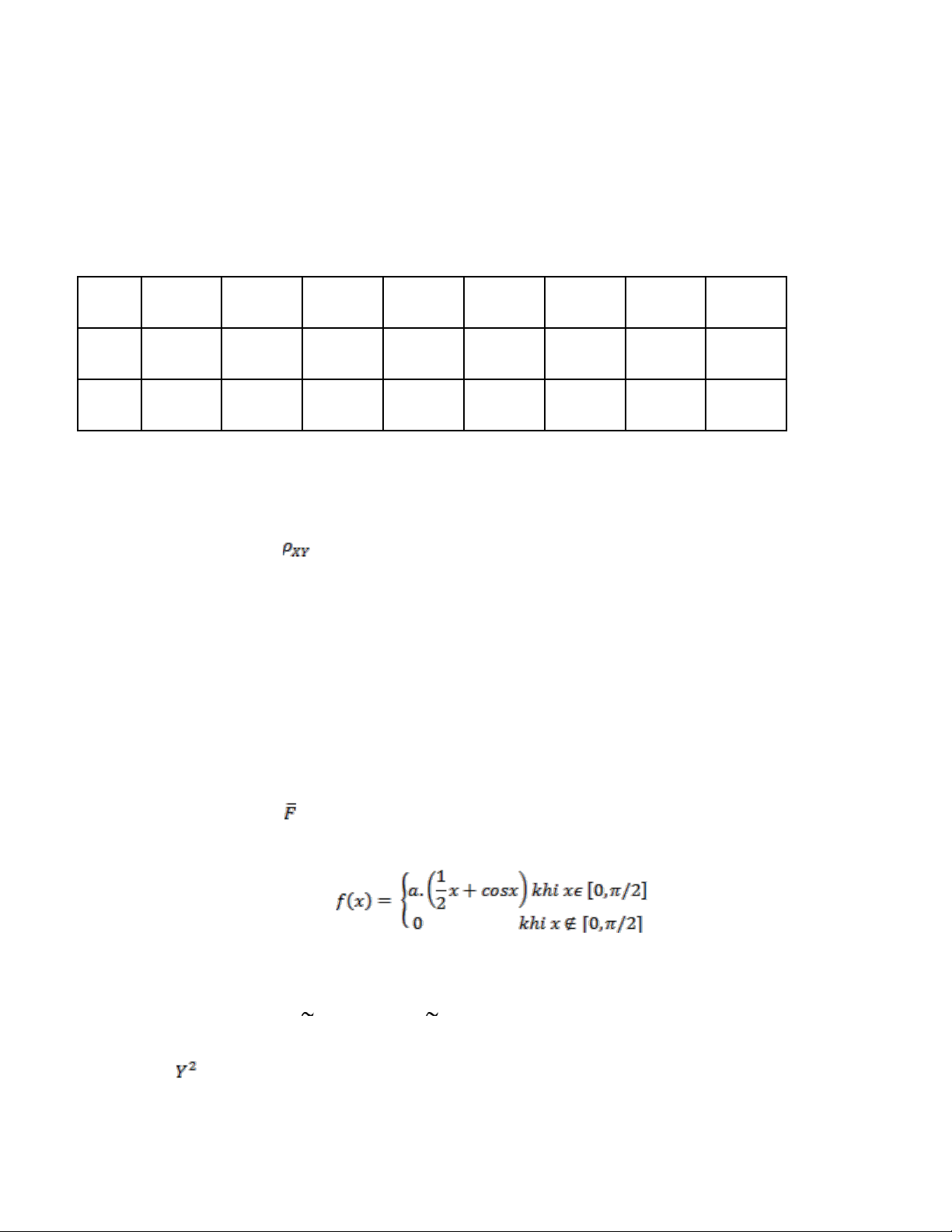
Câu 2.(1,5 điểm): Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y
- 2 02 1 0 2 02 1 X - 202 1 0 5 , a a a 0 0 ,05
1 , 5 a ,5a 1 202 1 0 , 15 1 5 , a a
1. Tìm hệ số a từ bảng phân phối .
2. Tính MedZ với Z=X+Y.
Câu 3 (1,5 điểm): Cho biến ngẫu nhiên X ~ N(5; 4), xét biến ngẫu nhiên Y= X2 -2X, hãy:
1. Tính giá trị kỳ vọng E(Y).
2. Tính xác suất P(Y > modX).
Câu 4.(3 điểm): Số cuộc gọi đến đặt lịch giao dịch/ngày ở cửa hàng Toyota Long Biên (7&9 Đường
Nguyễn Văn Linh, Q. Đống Đa, Hà nội) là đại lượng tuân theo quy luật chuẩn. Thống kê số cuộc gọi
đến/ngày, ta có kết quả sau: cỡ mẫu=36 ngày; trung bình mẫu=160,2 cuộc gọi và độ lệch hiệu
chỉnh=2,3(cuộc gọi). Trong đó có 8 ngày cửa hàng phải hủy lịch đặt giao dịch.
1. Hãy ước lượng tỷ lệ của những ngày phải hủy lịch với độ tin cậy 95%.
2. Hãy ước lượng số cuộc gọi trung bình đến đặt lịch giao dịch với độ tin cậy 90%
3. Khi ước lượng số cuộc gọi trung bình đến cửa hàng với yêu cầu độ chính xác là 0,2(cuộc gọi) thì độ tin cậy bằng bao nhiêu.
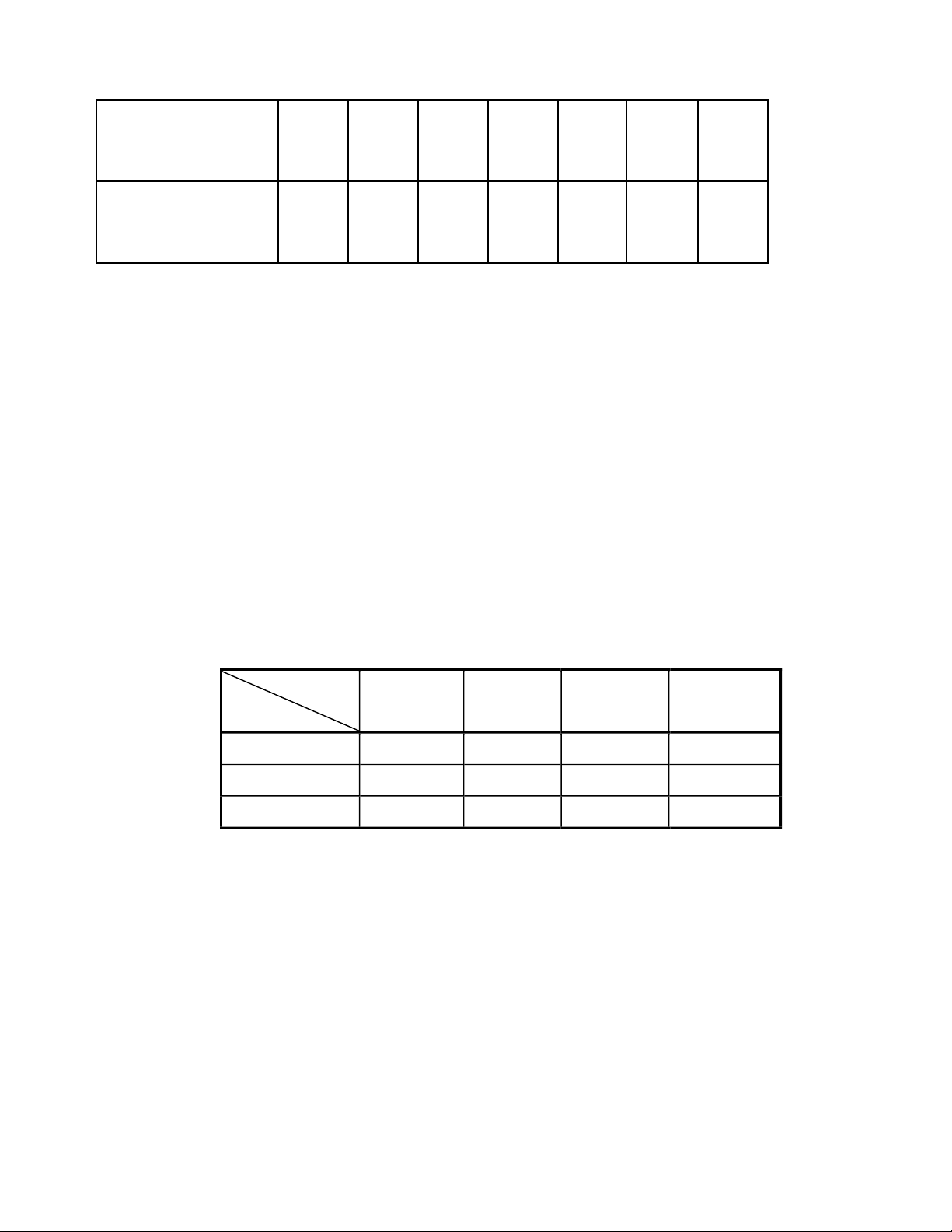
Câu 5.(2 điểm): Để khảo sát ảnh hưởng của chi phí quảng cáo (triệu đồng) đến doanh số tăng thêm
(%), của sản phẩm iphone 12 dịp cuối năm 2020 tại chuỗi cửa hàng Thế giới di động, người ta khảo
sát một mẫu với số liệu như sau:
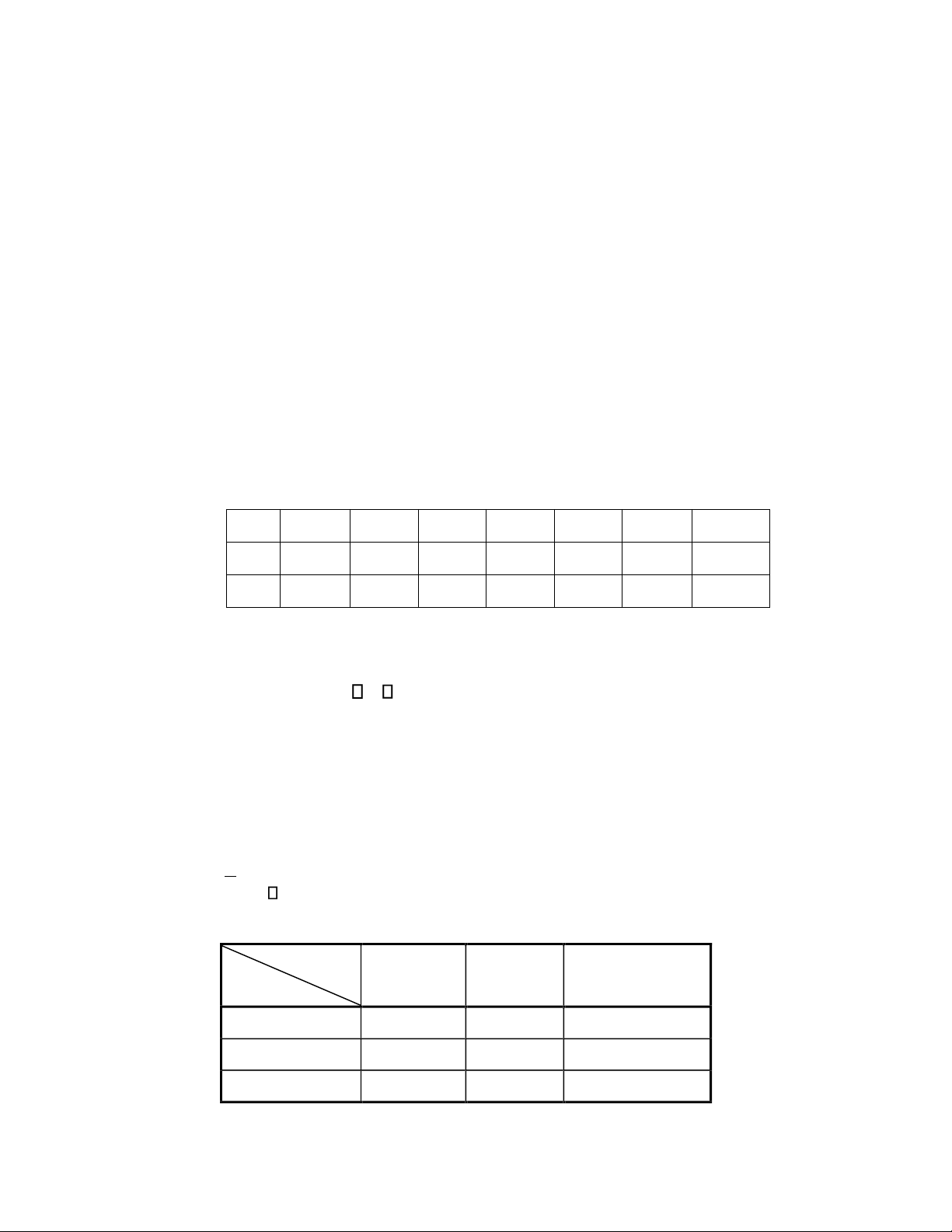
xi(triệu đồng) 35 37 37 38 38 39 40 42 yi(%) 1 1,25 1,5 1,5 1,5 1,75 1,75 2 lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ –
ni (số cửa 4 2 6 6 4 6 2 5 hàng) 1.
Lập phương trình hồi quy tuyến tính mẫu (với biến độc lập là chi phí quảng cáo), qua đó cho
biết sự khác biệt về doanh số tăng thêm khi ước lượng qua hàm hồi quy mẫu và số liệu quan sát
được khi quảng cáo với chi phí ở mức 38 triệu. 2.
Hãy ước lượng hệ số tương quan xy giữa chi phí quảng cáo và doanh số tăng thêm của sản
phảm iphone 12, với độ tin cậy 95% SỐ 02
Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=0,2; P(B)=3P(C). Biết biến cố F
thỏa mãn: P(F/A)=m; P(F/B)=0,015 và P(F/C)=0,25. 1. Tìm m biết P(F)=0,179. 2.
Tính xác suất để có ít nhất hai trong ba biến cố A; B; C xảy ra. Câu 2.(1,5 điểm):
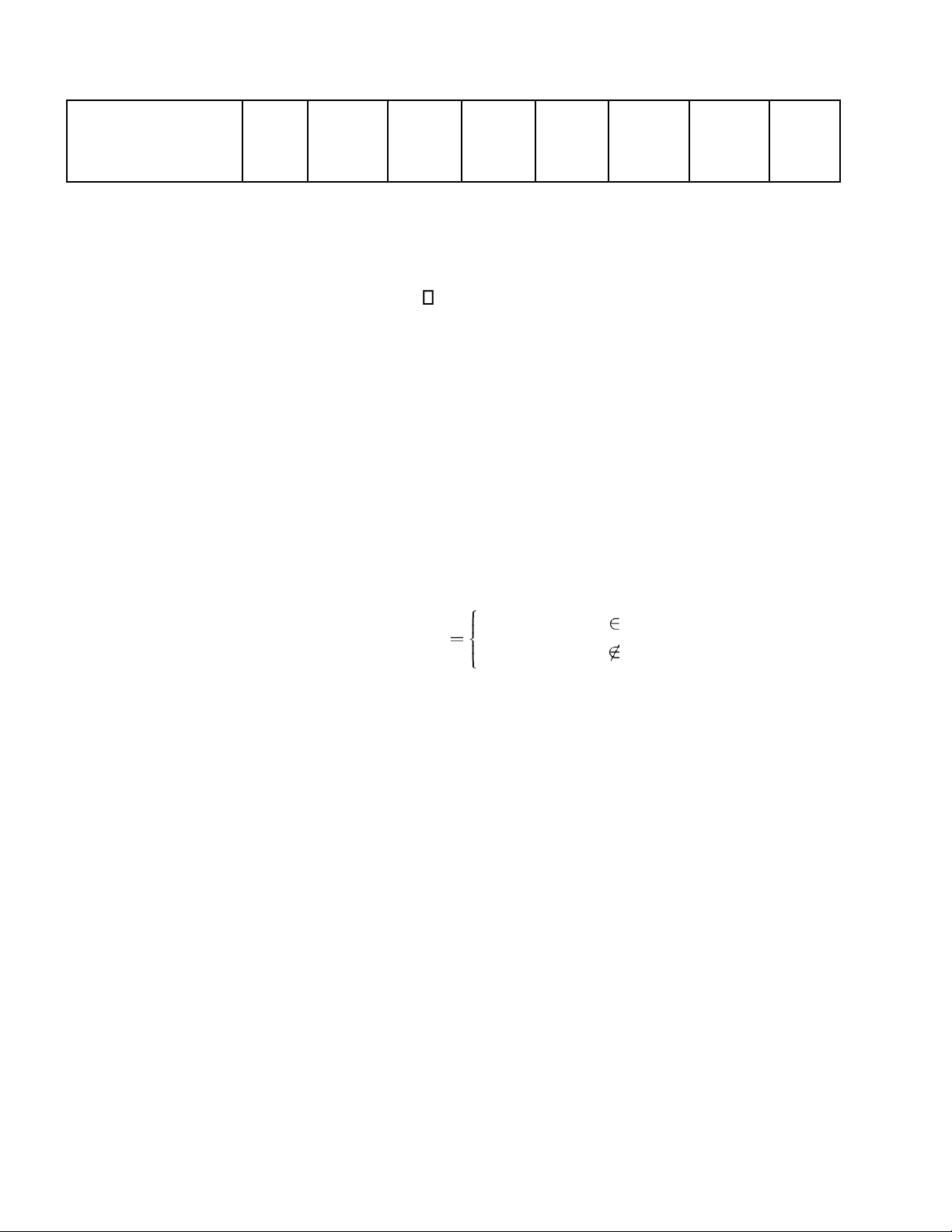
Cho hàm mật độ của biến ngẫu nhiên X: f x
k x. (x0 2) khixkhix[0[0;;2]2]
1. Tìm k để f(x) là hàm mật độ.
2. Tính P(X > m) biết m=ModX
Câu 3.(1,5 điểm):. Có 10 loại vắc-xin với xác suất sẽ được đưa vào sử dụng trong tháng đều là 0,8. Gọi
X là số vắc-xin sẽ được đưa vào sử dụng.
1. Tính trung bình có bao nhiêu vắc-xin sẽ được sử dụng? 2. Tính P(X > 2)
Câu 4.( 3 điểm): Để điều tra nhu cầu mua sắm online của người dân, người ta khảo sát 100 người
thấy nhu cầu mua sắm online trung bình là 5,5 lần/tháng, độ lệch mẫu hiệu chỉnh là 4,33 trong đó có
30 người rất thích mua sắm online.
1. Hãy ước lượng nhu cầu mua sắm online trung bình của người dân với độ tin cậy 95%.
2. Khi ước lượng tỷ lệ người rất thích mua sắm online với độ chính xác là 0,1 thì độ tin cậy bằng bao nhiêu.
3. Với mức ý nghĩa 1% hãy cho biết tỷ lệ người rất thích mua sắm online có trên 40% hay không? lOMoAR cPSD| 45315597 –
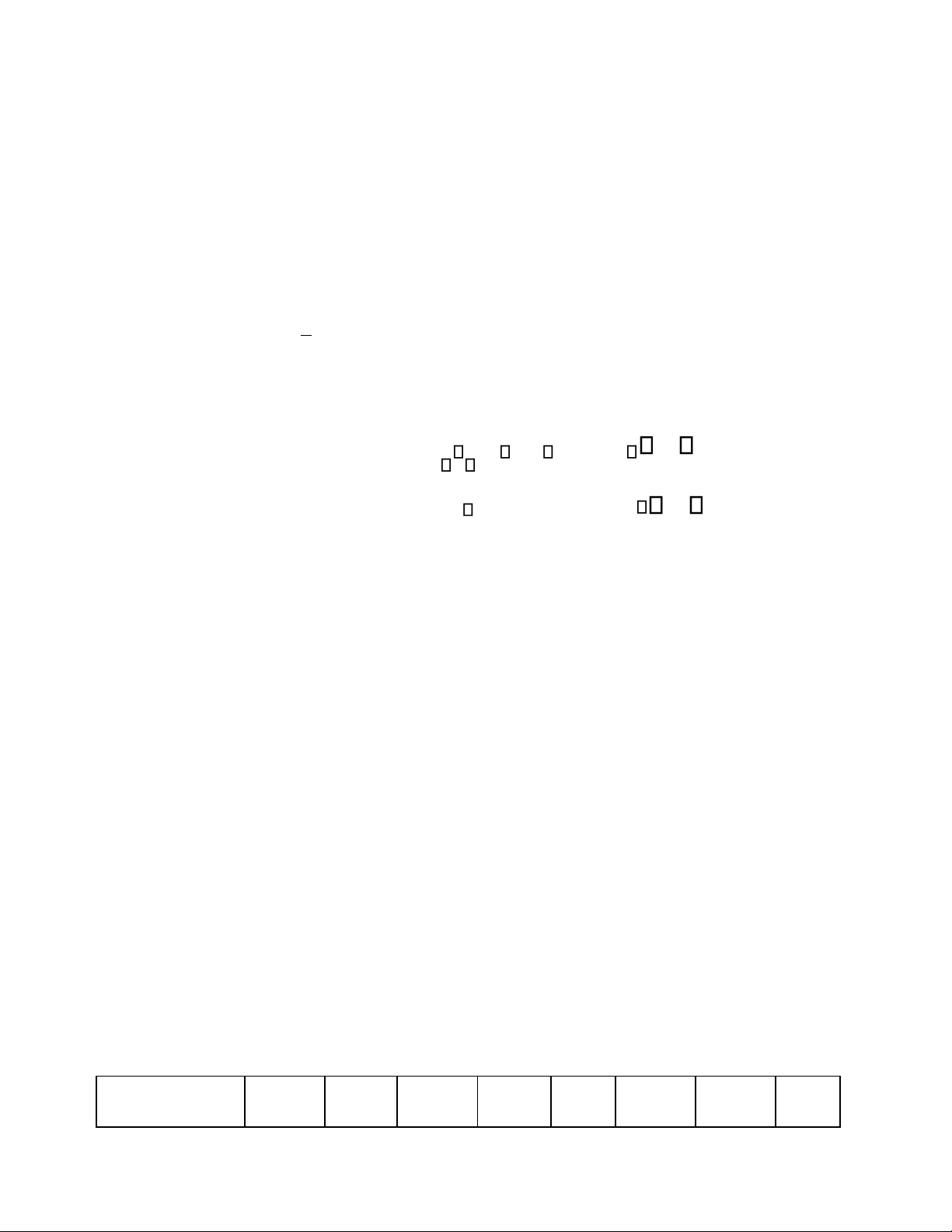
Câu 5.(2 điểm): Khảo sát quan hệ giữa kết quả học tập môn ĐSTT (X) và kết quả môn QHTT (Y) của
sinh viên trường UNETI được kết quả sau: (X;Y đều tuân theo quy luật chuẩn). X 3,5 3,5 5,5 5,5 7 7 8 8 9 9 Y 3,5 5 4 6 4 8 5 8 6 9 ni 8 6 10 9 2 10 3 15 4 14
1. Lập phương trình hồi quy tuyến tính thực nghiệm? So sánh sự chênh lệch điểm môn
QHTT giữa số liệu thực tế với số liệu qua phương trình hồi quy tại x = 5,5
2. Có thông tin cho rằng XY 0,8 , hãy đưa ra kết luận với mức ý nghĩa 5% SỐ 03
Cho hai biến cố A và B biết: P( B) = 0,4; P(A) = a; P(A/B) = 0,25; P(B / A) 0,5
1. Tìm giá trị của a=?
2. Cho biến cố C độc lập với biến cố A.B và P(A.B.C)=0,05. Tính P(C+AB).
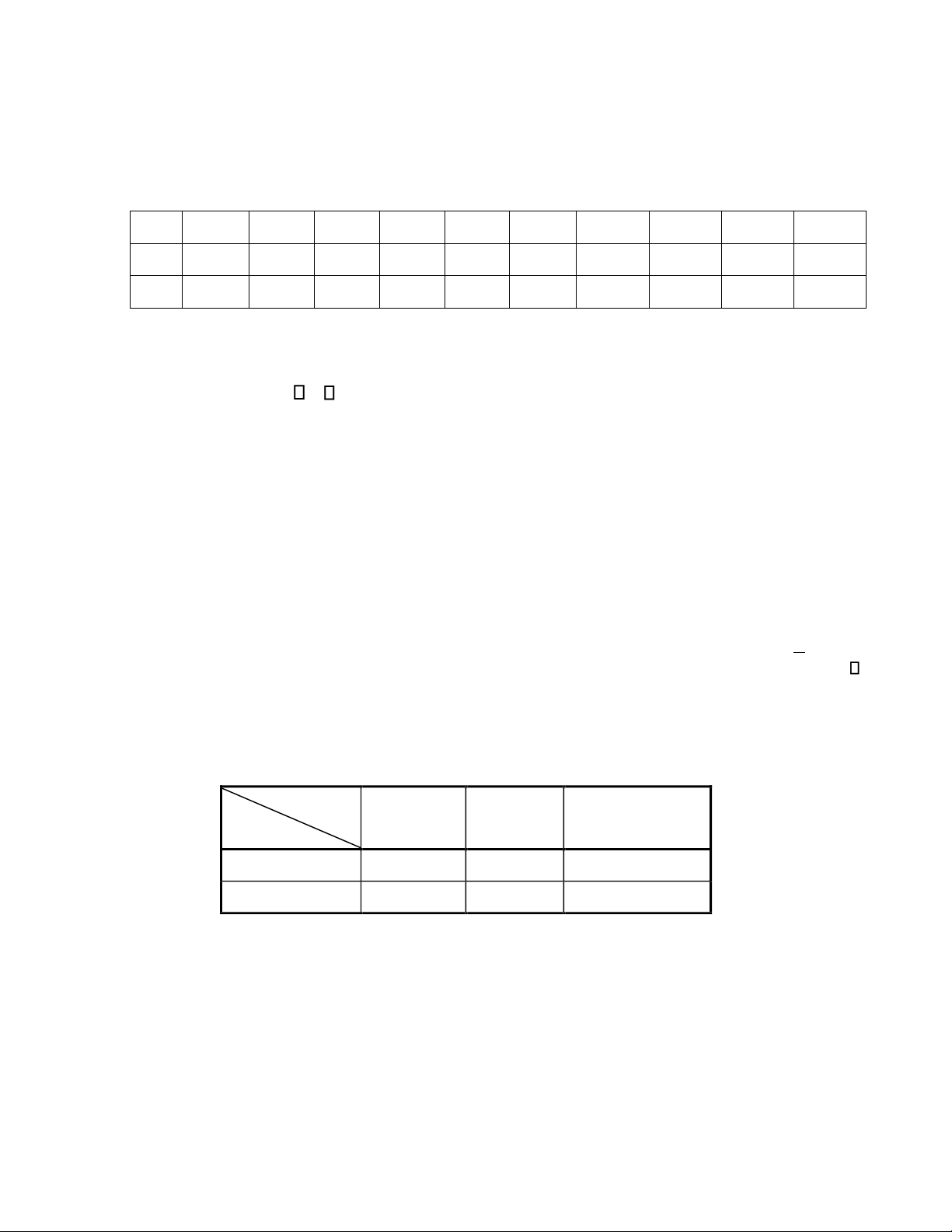
Câu 2.(1,5 điểm): Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y - 1 0 1 X - 1 0 ,5a 0 ,5a a 2 0 ,2 a a
1). Tìm hệ số a từ bảng phân phối. 2).
Tính xác suất P(X2< 40EY).
Câu 3.(1,5 điểm): Gọi X là biến ngẫu nhiên chỉ chiều cao của trẻ sơ sinh tuân theo quy luật chuẩn với
chiều cao trung bình là 50 cm, độ lệch chuẩn là 2 1). Hãy tính giá trị của E(2X+DX )
2). Tính P(X2 < 3025). lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ –
Câu 4.( 3 điểm): Để điều tra nhu cầu mua sắm online của người dân, người ta khảo sát 100 người
thấy nhu cầu mua sắm online trung bình là 5 lần/tháng, độ lệch mẫu hiệu chỉnh là 4,33 trong đó có
30 người rất thích mua sắm online.
1) Hãy ước lượng tỷ lệ người rất thích mua sắm online với độ tin cậy 95%.
2) Khi ước lượng nhu cầu mua sắm online trung bình của người dân với độ chính xác là 0,65 và độ tin
cậy 99% thì cần khảo sát bao nhiêu người?
3) Với mức ý nghĩa 1% hãy cho biết nhu cầu mua sắm online trung bình của người dân có là 5,5 hay không?
Câu 5.(2 điểm): Khảo sát quan hệ giữa kết quả học tập môn ĐSTT (X) và kết quả môn QHTT (Y) của
sinh viên trường UNETI được kết quả sau: (X;Y đều tuân theo quy luật chuẩn). X 3,5 3,5 5,5 5,5 7 7 8 8 9 9 Y 3,5 5 4 6 4 8 5 8 6 9 ni 8 6 10 9 2 10 3 15 4 14
1. Lập phương trình hồi quy tuyến tính thực nghiệm? So sánh sự chênh lệch điểm môn QHTT giữa số
liệu thực tế với số liệu qua phương trình hồi quy tại x = 7
2. Có thể nói XY 0,7 hay không? với mức ý nghĩa 1% SỐ 04
Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=P(B)=2P(C). Biết biến cố F thỏa mãn:
P(F/A)=0,25; P(F/B)=0,35 và P(F/C)=0,15.
1). Tính xác suất P(F)
2). Cho D là biến cố độc lập với A+B thỏa mãn P(D.(A+B)) =0,4. Tính P(D+A+B) Câu
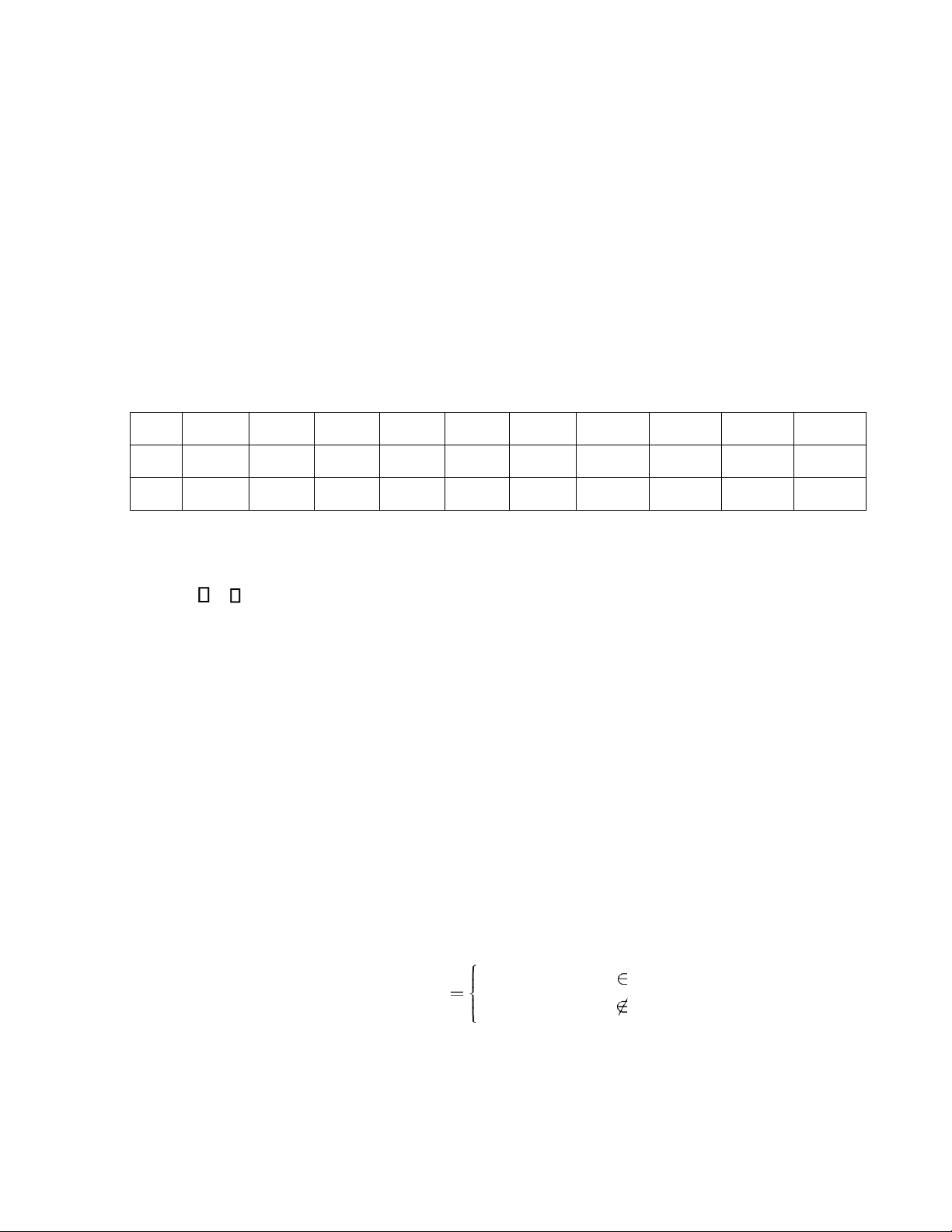
2.(1,5 điểm): Cho hàm mật độ của biến ngẫu nhiên X: f x
k.x(x0 6) khixkhix[0[0;;6]6]
1) Tìm k để f(x) là hàm mật độ.
2) Tính P(X < m) biết m = ModX. lOMoAR cPSD| 45315597 –
Câu 3.(1,5 điểm): X là biến ngẫu nhiên tuân theo quy luật chuẩn chỉ độ dày của một loại sách, biết
độ dày trung bình là 5cm; độ lệch chuẩn 2,1cm. 1). Hãy tính D(Z) biết Z = X.EX - modX
2). Tính P(X2 +3X < 0).
Câu 4.( 3 điểm): Để khảo sát tác dụng của một loại thức ăn mới đến trọng lượng trứng gà, người ta
khảo sát 100 quả thấy trọng lượng trung bình là 37,05(g); độ lệch mẫu hiệu chỉnh 5,82. Trong đó có
20 quả đạt chất lượng tốt.
1). Hãy ước lượng trọng lượng trứng trung bình với độ tin cậy 95%.
2). Khi ước lượng tỷ lệ quả trứng đạt chất lượng tốt với độ chính xác là 0,08 thì độ tin cậy là bao nhiêu?
3). Trọng lượng trung bình của trứng gà ban đầu là 35,58 (g). Với mức ý nghĩa 1% có thể nói loại thức
ăn mới làm tăng trọng lượng trứng gà hay không?
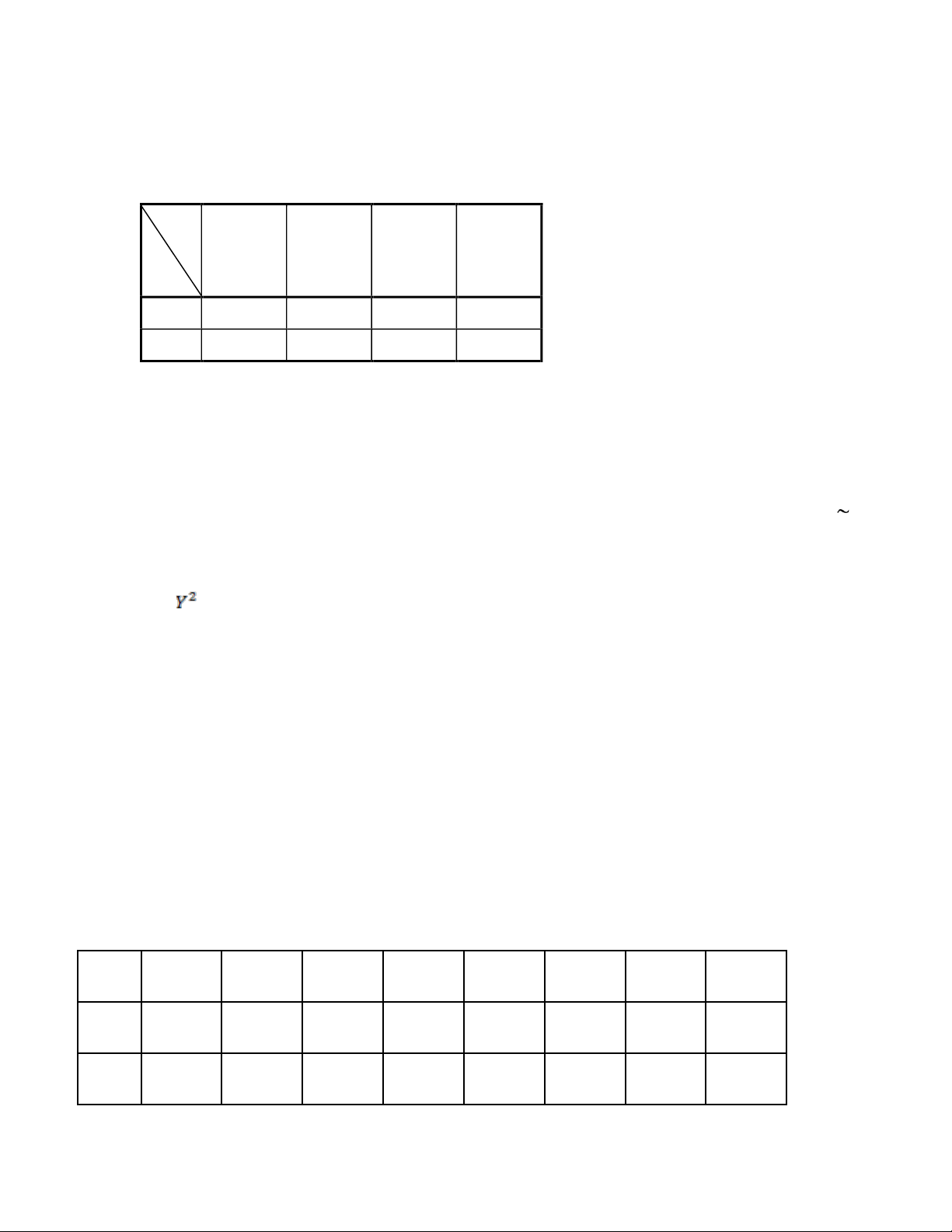
Câu 5.(2 điểm): Theo dõi độ dày của một loại giấy và thời gian phân hủy ta được bảng số liệu sau:
(biết độ dày X(mm) và thời gian phân hủy Y(tháng)) X 1 3 10 16 26 36 Y 10 13 15 19 20 25 Ni 3 4 5 5 3 6
1). Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu độ dày của giấy là 30 mm thì
thời gian phân hủy là bao nhiêu?
2). Có thể nói hệ số tương quan giữa X và Y là trên 0,7 hay không? với mức ý nghĩa 1%? SỐ 05
Cho 2 biến cố A, B thỏa mãn: P(A)=0,15; P(B)=0,35 và P(B|A)=0,4.
1). Tính xác suất P( AB. ) .
2). Tính xác suất để chỉ có một trong hai biến cố A, B xảy ra. lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ –
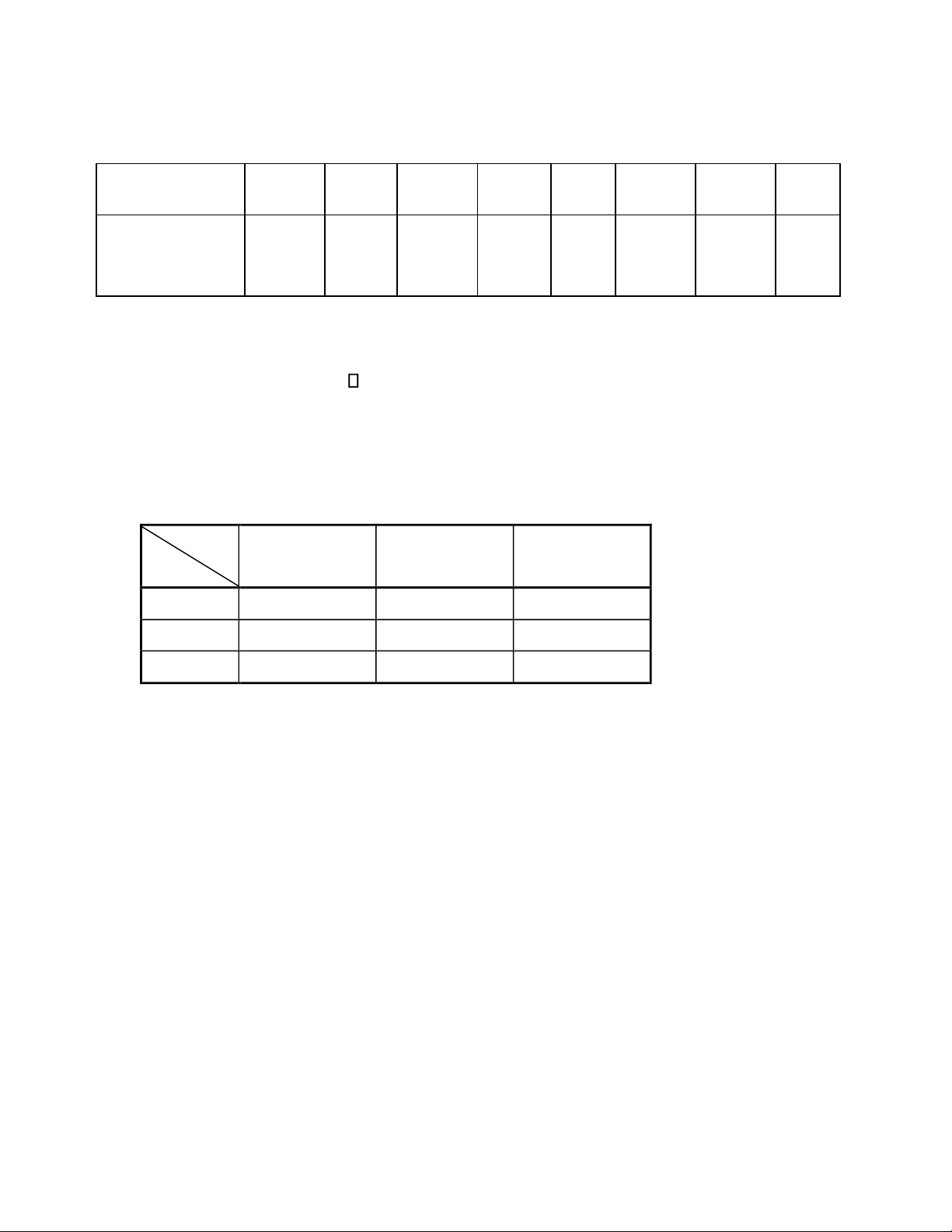
Câu 2.(1,5 điểm): Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y - 4 - 3 - 2 X 0 0 15 , a a 1 0 ,05 a a
1). Tìm hệ số a từ bảng phân phối. Tính P(Y = -2|X = 1)
2). Tính Med Z với Z = X + Y
Câu 3.(1,5 điểm): Cho X~ B(50; 0,4)
1). Hãy tính giá trị của E(2X+DX )
2). Tính P(X2 < 4).
Câu 4.( 3 điểm): Để khảo sát tác dụng của một loại thức ăn mới đến chất lượng của trứng gà, người
ta khảo sát 100 quả thấy trọng lượng trung bình là 37,05(g); độ lệch mẫu hiệu chỉnh 5,82, trong đó
có 20 quả đạt chất lượng tốt.
1). Hãy ước lượng tỷ lệ quả trứng đạt chất lượng tốt với độ tin cậy 95%.
2). Khi ước lượng trọng lượng trung bình của trứng gà với độ chính xác là 0,89 và độ tin cậy 99% thì
cần khảo sát bao nhiêu quả trứng?
3). Tỷ lệ quả đạt chất lượng tốt ban đầu là 15%. Với mức ý nghĩa 1% có thể nói loại thức ăn mới làm
tăng tỷ lệ quả đạt chất lượng tốt hay không?
Câu 5.(2 điểm): Theo dõi độ dày của một loại giấy và thời gian phân hủy ta được bảng số liệu sau:
(biết độ dày X(mm) và thời gian phân hủy Y(tháng)) X 1 3 10 16 26 36 Y 10 13 15 19 20 25 Ni 3 4 5 5 3 6
1). Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết thời gian phân hủy là bao nhiêu
tháng, nếu độ dày của giấy là 20mm?
2). Hãy ước lượng hệ số tương quan giữa X và Y với độ tin cậy 95%? SỐ 06 lOMoAR cPSD| 45315597 –
Cho 2 biến cố A, B độc lập nhau. Biết P(A)=0,8 và P(A+B)=0,93.
1). Tính xác suất P(B).
2). Đặt C = A+B. Tính xác suất P(B/C).
Câu 2.(1,5 điểm): Cho hàm mật độ của biến ngẫu nhiên X:
k(4 x ) khi x [ 2;2] f x( ) 2 0 khi x [ 2;2]
1) Tìm k để f(x) là hàm mật độ.
2) Tính D(100 – 2X).
Câu 3.(1,5 điểm): Cho 2 biến ngẫu nhiên độc lập: X ~ N(5; 0,81) và Y ~ B(6; 0,4); đặt Z =3X-2Y 1) Hãy tính D(Z).
2) Tính xác suất P(11X-X2 > 28).
Câu 4.(3 điểm): Điều tra về năng suất lúa của địa phương A ta có số liệu sau: cỡ mẫu=40 thửa ruộng;
năng suất trung bình mẫu=18,2 (tạ/ha) và độ lệch hiệu chỉnh=1,5(tạ/ha). Trong đó có 10 thửa có năng
suất vượt trội.
1). Hãy ước lượng tỉ lệ thửa ruộng vượt trội với độ tin cậy 97%.
2). Nếu dùng số liệu trên để ước lượng năng suất lúa trung bình với độ chính xác 0,5 (tạ/ha) thì độ tin cậy là bao nhiêu?
3). Người ta cho rằng năng suất lúa của địa phương A thấp hơn mức trung bình của cả nước là
19 (tạ/ha). Hãy cho kết luận với mức ý nghĩa 5%.
Câu 5.(2 điểm): Theo dõi trọng lượng y(kg) và số tháng tuổi x(tháng) của một giống lợn trong một trang
trại chăn nuôi ta có bảng số liệu sau: xi 2 3 4 5 6 7 8 yi 32 40 50 62 73 86 97 ni 2 4 5 6 7 5 1
1). Hãy ước lượng hệ số tương quan giữa trọng lượng và tuổi của lợn với độ tin cậy 93%. 2). Lập
phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu số tháng tuổi là 10
tháng thì trọng lượng của lợn ước tính qua hàm hồi quy là bao nhiêu? lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ – SỐ 07
Câu 1.(2 điểm): Cho hai biến cố A và B. Biết: P(A) = 0,5; P(B)=0,6 và P(A+B)=0,7.
1). Chứng tỏ rằng hai biến cố A và B phụ thuộc nhau.
2). Tính P( BA)
2). Tính xác suất D(X+Y).
Câu 3.(1,5 điểm): Cho 2 biến ngẫu nhiên độc lập: X ~ N(4; 0,64) và Y ~ B(5; 0,3); đặt Z =2XY+100 1) Hãy tính D(Z). 2) Tính P(MedX-ModY
Câu 4.( 3 điểm): Để khảo sát nhu cầu sử dụng điện của người dân trong tháng hè, người ta điều tra
60 hộ gia đình thấy: nhu cầu điện trung bình là 300kW/tháng; độ lệch mẫu hiệu chỉnh là 4,5kW.
1). Hãy ước lượng nhu cầu sử dụng điện trung bình trong tháng hè với độ tin cậy 96%.
2). Khi ước lượng nhu cầu sử dụng điện trung bình của người dân với độ chính xác là 1 kW và độ tin
cậy 93% thì cần khảo sát bao nhiêu hộ gia đình?
3). Vào tháng mùa đông nhu cầu sử dụng điện trung bình là 290 KW/tháng. Với mức ý nghĩa 5% liệu
có thể cho rằng nhu cầu sử dụng điện của tháng hè cao hơn tháng đông hay không?
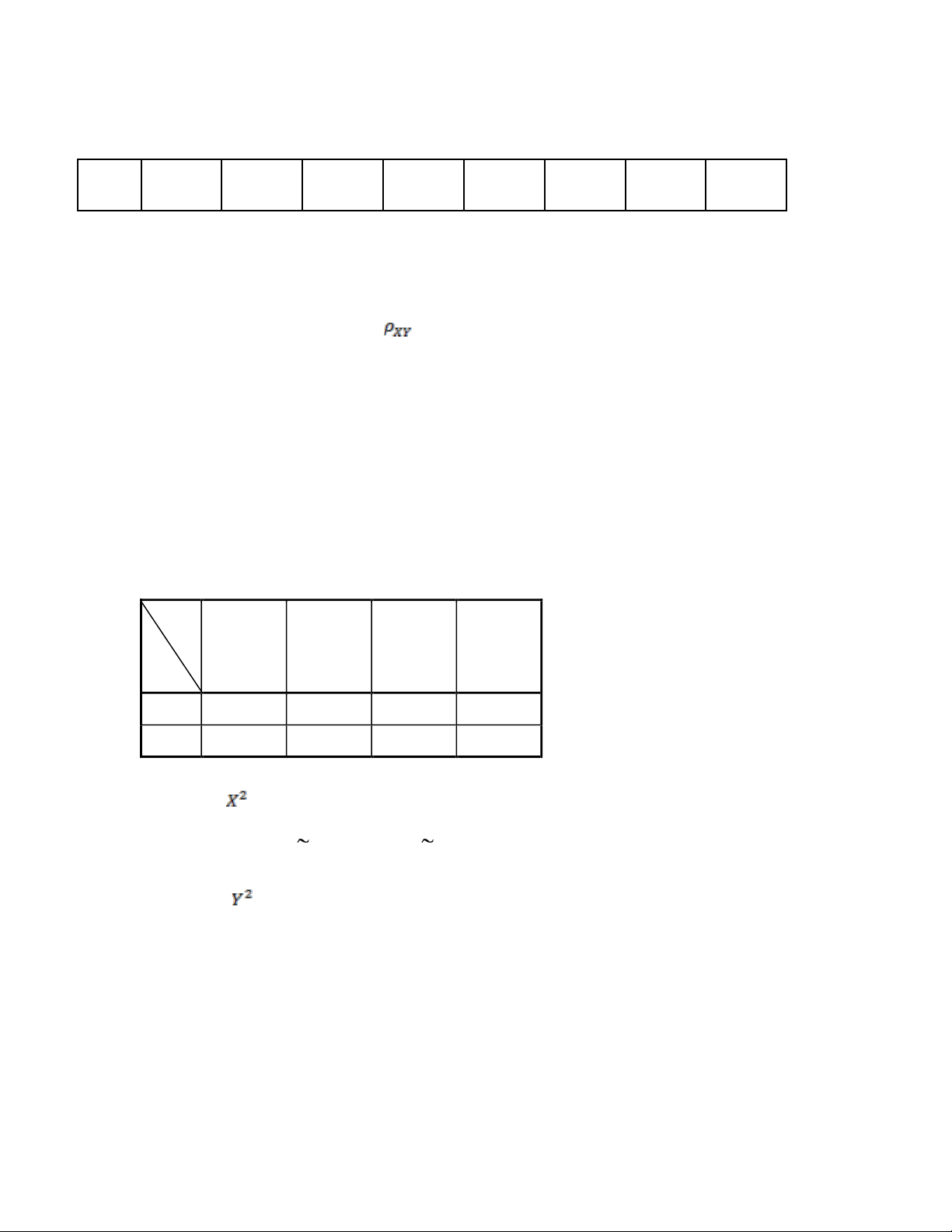
Câu 5.(2 điểm): Để điều tra về chiều cao (X cm) và cân nặng (Y kg) của học sinh lớp 1 ở địa phương A ta có số liệu như sau: xi(cm) 75 80 85 90 95 100 105 yi(kg) 16 20 23 25 28 32 34 ni(hs) 2 3 5 7 4 2 1
1). Hãy kiểm định giả thuyết cho hệ số tương quan giữa trọng lượng và chiều cao của học sinh
lớp 1 của địa phương A là 0,9 với mức ý nghĩa 5%. lOMoAR cPSD| 45315597 –
2). Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu chiều cao là 110 cm thì
trọng lượng của học sinh lớp 1 của địa phương A ước tính qua hàm hồi quy là bao nhiêu?
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ SỐ 08
Câu 1.(2 điểm): Cho hệ biến cố đầy đủ {A, B, C} và biến cố F. Biết P(A)=0,4; P(B)=2P(C);
P(F/A)=0,3; P(F/B)=0,6 và P(F/C)=0,5.
1). Tính xác suất P(F). 2).
Tính P A F( / ).
Câu 2.(1,5 điểm): Cho hàm mật độ của biến ngẫu nhiên liên tục X: f x( )
k (4x x) khi x [0;4] 0 khi x [0;4]
1) Tìm k để f(x) là hàm mật độ. 2) Tính P(X
Câu 2.(1,5 điểm): Cho 2 biến ngẫu nhiên độc lập: X ~ N(6; 0,49) và Y ~ B(5; 0,4); đặt Z =X.E(Y) – Y.MedX + 2.
a) Hãy tính E(Z). b) Tính xác suất P(X>5, Y=ModY).
Câu 3.(3 điểm): Kiểm tra ngẫu nhiên trọng lượng của 50 sản phẩm của một lô hàng thì thấy trọng
lượng trung bình là 59,5gam, độ lệch chuẩn hiệu chỉnh là 2,5gam và thấy 5 sản phẩm không đạt yêu cầu về trọng lượng.
1. Nếu muốn sai số của ước lượng tỷ lệ sản phẩm không đạt yêu cầu là 4% và độ tin cậy 94% thì phải
kiểm tra bao nhiêu sản phẩm.
2. Hãy ước lượng trọng lượng trung bình của sản phẩm với độ tin cậy 90%
3. Nếu lô hàng có trọng lượng trung bình của sản phẩm là 60 gam thì được xuất xưởng, hỏi với mức ý
nghĩa 5% thì lô hàng trên có được xuất xưởng hay không?
Câu 4.(2 điểm): Để nghiên cứu về mối liên hệ giữa tuổi nghề X và năng suất lao động Y ở một phân
xưởng ta có mẫu số liệu như sau:
xi (năm) 1 2 3 4 5 6 7 lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ –
yi (kg/giờ) 5 6, 7, 9, 11 13 14 5 5 5 n 2 4 6 8 7 5 3 i (số công nhân) 1.
Hãy ước lượng hệ số tương quan giữa tuổi nghề và năng suất lao động của phân xưởng với độ tin cậy 98%. 2.
Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết nếu tuổi nghề là 8 năm thì
năng suất lao động ước tính qua hàm hồi quy là bao nhiêu? SỐ 09
Câu 1.(2 điểm): Cho ba biến cố A, B và C độc lập nhau. Biết: P(A)=0,6; P(B)=0,5 và P(A+B+C)=0,94.
1). Tính P(C).
2). Tính P{(A+B)/(A+B+C)}.
Câu 2.(1,5 điểm): Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y 0 1 2 P(X) X 0 a 0 15 , a 2 2 a 3 a 0 15 , P(Y) 1
1). Xác định giá trị của a.
2). Tính Med(X + 2Y).
Câu 3.(1,5 điểm): Cho 2 biến ngẫu nhiên độc lập: X ~ N(8; 1,44) và Y ~ B(10; 0,6); đặt Z =X – 2Y+1000. 1) Hãy tính D(Z).
2) Tính P(X<10, Y=E(Y)).
Câu 4.( 3 điểm): Để khảo sát nhiệt độ trong mùa hè này, người ta điều tra 35 ngày thì thấy: nhiệt độ
trung bình là 26,90C; độ lệch mẫu hiệu chỉnh là 1,250C và thấy có 10 ngày nóng.
1). Hãy ước lượng nhiệt độ trung bình của mùa hè này với độ tin cậy 92%. lOMoAR cPSD| 45315597 –
2). Để ước lượng nhiệt độ trung bình của mùa hè với độ chính xác là 0,30C và độ tin cậy 94% thì cần khảo sát bao nhiêu ngày?
3). Hãy ước lượng tỷ lệ ngày nóng của mùa hè này với độ tin cậy 95%.
Câu 5.(2 điểm): Để điều tra về mức thu nhập X (triệu/tháng) và nhu cầu về một loại hàng hóa Y
(kg/tháng) của người dân thủ đô ta có số liệu như sau: xi 4 5 6 7 8 9 10 (triệu/tháng) yi (kg/tháng) 1,6 1,8 2,3 2,5 2,8 3,2 3,4 ni (người) 3 5 5 8 7 4 2
1). Hãy kiểm định giả thuyết cho rằng hệ số tương quan giữa nhu cầu về một loại hàng hóa Y và mức
thu nhập X là trên 0,9 với mức ý nghĩa 5%.
2). Lập phương trình hồi quy tuyến tính thực nghiệm, qua đó cho biết với mức thu nhập là 11
triệu/tháng thì nhu cầu về một loại hàng hóa Y của người dân thủ đô ước tính qua hàm hồi quy là bao nhiêu? lOMoAR cPSD| 45315597 –
Câu 1.(2 điểm):
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ SỐ 10
Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=P(B)=2P(C). Biết biến cố F thỏa
mãn: P(F|A)=0,25; P(F|B)=0,35 và P(F|C)=0,45. Tính các xác suất sau:
1). Tính xác suất P(F).
2). Tính xác suất P(B | F)
Câu 2.(1,5 điểm): Cho hàm mật độ của biến ngẫu nhiên X: f (x)
k(x 1)(3 x) khix 1,3 0 khix 1,3
1) Tìm k để f(x) là hàm mật độ. 2) Tính ModX
Câu 3.(1,5 điểm): Một đề thi trắc nghiệm gồm 100 câu hỏi, mỗi câu có 5 đáp án trong đó có 1 đáp
án đúng. Một thí sinh đi thi không học bài, thí sinh chọn ngẫu nhiên một phương án cho mỗi câu và
làm hết 100 câu. Gọi X là số câu thí sinh đó trả lời đúng.
1) Hãy tính giá trị của E(X),DX
2) Tính xác suất sinh viên trả lời đúng từ 10 đến 30 câu
Câu 4.( 3 điểm): Số lượng khách hàng đến thăm quan và mua sắm ở cửa hàng quần áo Elise, chi
nhánh Phố Huế, Hà Nội là biến ngẫu nhiên theo phân phối chuẩn. Điều tra số lượng khách hàng tại
đây trong 70 ngày thu được kết quả trung bình mỗi ngày có 126 khách và độ lệch hiệu chỉnh là
14,9782 khách, trong đó có 19 ngày đông khách (tức là số khách đến trong ngày đó lớn hơn 135)
1). Hãy ước lượng tỉ lệ những ngày đông khách với độ tin cậy 90%?
2). Khi ước lượng số lượng khách hàng trung bình mỗi ngày, yêu cầu độ chính xác 0,5 thì độ tin cậy là bao nhiêu?
3). Người quản lý cửa hàng báo cáo rằng tỉ lệ ngày đông khách là 25%; với mức ý nghĩa 5% hãy nhận xét về báo cáo đó?
Câu 5.(2 điểm): Để khảo sát mối liên hệ giữa thời gian đọc sách X và thời gian sử dụng Internet Y của
sinh viên trường ĐH Kinh tế-Kỹ thuật Công nghiệp , thu được mẫu số liệu như sau:
xi(giờ) 1,25 1,5 1,5 2 2 2,25 2,5 3 lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ – SỐ 11
Câu 1.(2 điểm):
yi( giờ ) 3 3 2,25 2,5 2 1,75 1,75 1 4 2 6 6 4 6 2 5 ni(sốsinh viên)
1). Lập phương trình hồi quy tuyến tính mẫu, qua đó tính thời gian đọc sách ước lượng qua hàm hồi
quy mẫu khi thời gian sử dụng Internet ở mức 2,5 giờ.
2). Có giả thuyết cho rằng < -0,97 , hãy đưa ra kết luận với mức ý nghĩa 5%
Cho hai biến cố A, B. Biết P(A+B) = 0,8; P(A) = 0,7; P(B) =0,4.
1). Tìm xác suất P(AB) và chứng tỏ A và B phụ thuộc nhau.
2). Tính xác suất để chỉ có biến cố A xảy ra.
Câu 2.(1,5 điểm): Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y - 2020 0 2020 X - 2020 0,5a ,5a 0 a 0 0 ,15 0 ,5a 1 ,5a 2020 0 , 15 a 2a
1 ) . Tì m hệ số a từ bảng phân phối .
2). Tính MedZ với Z=X+Y.
Câu 3.(1,5 điểm): Một đề thi trắc nghiệm gồm 100 câu hỏi, mỗi câu có 5 đáp án trong đó có 1 đáp
án đúng. Một thí sinh đi thi không học bài, thí sinh chọn ngẫu nhiên một phương án cho mỗi câu và
làm hết 100 câu. Gọi X là số câu thí sinh đó trả lời đúng.
1)Tính xs thí sinh trả lời đúng được từ 10 câu
2) Hãy tìm số câu trả lời đúng có khả năng nhất
Câu 4.(3 điểm): Số lượng khách hàng đến thăm quan và mua sắm ở cửa hàng quần áo Elise, chi
nhánh Phố Huế, Hà Nội là biến ngẫu nhiên theo phân phối chuẩn. Điều tra số lượng khách hàng tại
đây trong 70 ngày thu được kết quả trung bình mỗi ngày có 126 khách và độ lệch hiệu chỉnh là
14,9782 khách, trong đó có 19 ngày đông khách (tức là số khách đến trong ngày đó lớn hơn 135)
1) Hãy ước lượng số lượng khách trung bình đến cửa hàng với độ tin cậy 90%? lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ –
Câu 1.(2 điểm):
2) Khi ước lượng tỉ lệ ngày đông khách, yêu cầu độ chính xác 0,05 thì độ tin cậy là bao nhiêu? 3)
Người quản lý cửa hàng báo cáo rằng trung bình mỗi ngày có khoảng 130 khách hàng đến thăm quan
và mua sắm; với mức ý nghĩa 5% hãy nhận xét về báo cáo đó?
Câu 5.(2 điểm): Để khảo sát mối liên hệ giữa thời gian đọc sách X và thời gian sử dụng Internet Y của
sinh viên trường ĐH Kinh tế-Kỹ thuật Công nghiệp , thu được mẫu số liệu như sau:
xi(giờ) 1,25 1,5 1,5 2 2 2,25 2,5 3
yi( giờ ) 3 3 2,25 2,5 2 1,75 1,75 1 4 2 6 6 4 6 2 5 ni(sốsinh viên)
1). Lập phương trình hồi quy tuyến tính mẫu, qua đó tính thời gian đọc sách ước lượng qua hàm
hồi quy mẫu khi thời gian sử dụng Internet ở mức 2,75 giờ.
2). Hãy ước lượng hệ số tương quan lý thuyết với độ tin cậy 95%. SỐ 12
Cho hệ đầy đủ ba biến cố {A,B,C} với P(A)=2P(B); P(C)=0,1. Biết biến cố F
thỏa mãn: P(F/A)=0,25; P(F/B)=0,35 và P(F/C)=0,45
1). Tính xác suất P(F).
2). Tính xác suất: P(A+B+AB+ABC)
Câu 2.(1,5 điểm): Cho hàm mật độ của biến ngẫu nhiên X: f (x)
k(x 2)(4 x) khix 2,4 0 khix 2,4
1) Tìm k để f(x) là hàm mật độ.
2) Tính xác suất P(X >3)
Câu 3.(1,5 điểm): Cho X ~ N(5, 9) ; Y~ B(30; 0,1). Đặt Z= X.EY –3ModX + Y.DX
1) Hãy tính giá trị của E(2Z+1)
2) Tính P(X2 +3X < 4) lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ – SỐ 13
Câu 1.(2 điểm):
Câu 4.( 3 điểm): Biết rằng thu nhập là ĐLNN tuân theo luật chuẩn và nếu có thu nhập sau khi trừ
hết các yếu tố giảm trừ gia cảnh mà lớn hơn 10 triệu/tháng thì phải nộp thuế thu nhập cá nhân. Điều
tra thu nhập sau khi giảm trừ gia cảnh của 100 người làm việc ở tập đoàn A thu được kết quả: trung
bình mỗi người có thu nhập 15,45 triệu/tháng; độ lệch hiệu chỉnh là 7,6901 triệu/tháng và có 75
người phải nộp thuế thu nhập cá nhân.
1). Hãy ước lượng tỉ lệ những người phải nộp thuế thu nhập cá nhân ở tập đoàn A với độ tin cậy 90%?
2). Hãy ước lượng thu nhập trung bình của những người làm việc tại tập đoàn A với độ tin cậy 99%?
3). Bộ phận Công đoàn của tập đoàn báo cáo rằng thu nhập trung bình mỗi người ở đây là 14,5
triệu/tháng, với độ tin cậy 95% hãy nhận xét về báo cáo trên?
Câu 5.(2 điểm): Gọi Y (kg) là chỉ số cân nặng của trẻ em trong độ tuổi 8-15 và X là lượng sữa trẻ uống
mỗi ngày (ml) (X;Y đều tuân theo quy luật chuẩn). Điều tra ở một vùng được kết quả như sau: X 150 180 210 230 250 240 300 Y 32 39 41 43 45 47 49 ni 10 13 14 10 11 8 10
1 ). Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu muốn cân nặng 40kg thì uống bao nhiêu sữa?
2). Có giả thuyết cho rằng XY 0,85 , hãy đưa ra kết luận với mức ý nghĩa 5%
Cho hai biến cố A và B độc lập nhau. Biết: P(A) = 0,25 và P(B)=0,35. 1).Tìm P(A+B)
2). Tính P(A| B) P(B | A)
Câu 2.(1,5 điểm): Cho biến ngẫu nhiên X và Y có bảng phân phối đồng thời như sau : Y - 2 - 1 0 X - 2 ,5a 1 0 ,5a a - 1 0 ,1 a a 0 0 1 , 0 1 , 0 , 2 lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ –
Câu 1.(2 điểm):
1). Tìm hệ số a từ bảng phân phối.
2). Tính xác suất P(X2< 3)+P(Y = 0).
Câu 34.(1,5 điểm): Cho X ~ N(5, 9) ; Y~ B(30; 0,1). Đặt Z= X.EY –3ModX + Y.DX
1) Hãy tính giá trị của E(2Z - 1) 2) Tính P(Y5 < 4)
Câu 4.( 3 điểm): Biết rằng thu nhập là ĐLNN tuân theo luật chuẩn và nếu có thu nhập sau khi trừ
hết các yếu tố giảm trừ gia cảnh mà lớn hơn 10 triệu/tháng thì phải nộp thuế thu nhập cá nhân. Điều
tra thu nhập sau khi giảm trừ gia cảnh của 100 người làm việc ở tập đoàn A thu được kết quả: trung
bình mỗi người có thu nhập 15,45 triệu/tháng; độ lệch hiệu chỉnh là 7,6901 triệu/tháng và có 75
người phải nộp thuế thu nhập cá nhân.
1 ). Hãy ước lượng tỉ lệ những người phải nộp thuế thu nhập cá nhân ở tập đoàn A với độ tin cậy 99%?
2 ). Hãy ước lượng thu nhập trung bình của những người làm việc tại tập đoàn A với độ tin cậy 90%?
3 ). Bộ phận Công đoàn của tập đoàn báo cáo rằng tỉ lệ những người phải nộp thuế thu nhập cá nhân
trong tập đoàn là 60%, với độ tin cậy 95% hãy nhận xét về báo cáo trên?
Câu 5.(2 điểm): Gọi Y (kg) là chỉ số cân nặng của trẻ em trong độ tuổi 8-15 và X là lượng sữa trẻ
uống mỗi ngày (ml) (X;Y đều tuân theo quy luật chuẩn). Điều tra ở một vùng được kết quả như sau: X 150 180 210 230 250 240 300 Y 32 39 41 43 45 47 49 ni 10 13 14 10 11 8 10
4 ). Lập phương trình hồi quy tuyến tính thực nghiệm? và cho biết nếu muốn cân nặng 42 kg thì cần uống bao nhiêu sữa?
5 ). Hãy ước lượng hệ số tương quan lý thuyết với độ tin cậy 95% lOMoAR cPSD| 45315597
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ – SỐ 14
Câu 1.(2 điểm): Cho 3 biến cố A, B, C có quan hệ độc lập. Đặt T = A + B + C. Biết P(A) = 0,25 , P(AB) = 0,05 , P(T) = 0,46. 1. Tính P(C).
2. Tín h P( { A + C } |T ).
Câu 2.( ,
1 5 điểm): Cho bảng phân phối đồng thời - 2 0 1 4 0 ,5a a ,5a 0 1,5a 1 0 4 , 0,5a ,5a 1 0 ,5a X -2
1). Tìm hệ số a .
2). Tính E ( X + 2Y – 1) và E ( Y | X = 1) ?
Câu 3.(1,5 điểm): . Một lớp học có 50 sinh viên trong đó có 30 nam. Lấy ngẫu nhiên ra 10 sinh viên
để tham gia hội sinh viên tình nguyện, gọi X là số sinh viên nữ có trong 10 sinh viên. Biết Y N ( 5; 4).
1) Hãy tính giá trị E ( 2X + DY – 1).
2) Tính P( - 4Y – 2 < 3) ?
Câu 4.( 3 điểm): Đơn hàng online ở một cửa hàng quần áo là đại lượng tuân theo quy luật chuẩn.
Theo dõi số đơn hàng online/ ngày ở cửa hàng ta có kết quả sau: cỡ mẫu 60 ngày, trung bình mẫu là
150,2 và độ lệch hiệu chỉnh là 3,6, trong đó có 5 ngày cửa hàng bị quá tải trong việc vận hành đơn.
1. Hãy ước lượng số đơn hàng online trung bình của cửa hàng với độ tin cậy 96% ?
2. Khi ước lượng tỷ lệ những ngày cửa hàng bị quá tải đơn với độ chính xác 0,23 và độ tin cậy 95% thì
cần điều tra thêm bao nhiêu ngày nữa?
3. Chủ cửa hàng khẳng định tỷ lệ những ngày cửa hàng bị quá tải không vượt quá 7%. Hãy cho kết luận với mức ý nghĩa 2% ?
Câu 5.(2 điểm): Để tìm hiểu mối liên hệ giữa thu nhập của hộ gia đình với giá trị của các gói bảo hiểm
người ta thống kê trên 50 hợp đồng bảo hiểm thu được bảng số liệu sau: xi 22 25 27 28 29 30 31 33 yi 11 12,5 13 14 14,5 16 16,5 17 ni 3 2 2 10 5 8 15 5
Với biến BNN X về tổng thu nhập của hộ gia đình (triệu) và Y chỉ giá trị gói bảo hiểm (triệu/năm). lOMoAR cPSD| 45315597
1. Lập phương trình hồi quy tuyến tính thực nghiệm và cho biết sai số về giá trị gói hợp đồng bảo hiểm
ứng với mức thu nhập 28 triệu đồng giữa số liệu thực tế và qua hàm hồi quy?
2. Có thông tin cho rằng
> 0,67, hãy đưa ra kết luận với mức ý nghĩa 2%?
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ
Câu 1.(2 điểm): Cho hệ đầy đủ {A, B, C} có P(F|A) = 0,15, P(F|B) = 0,32, P(F|C) = 0,48, P(C ) = 0,2, P( F ) = 0,335.
1. Tính P(A), P(B).
2. Tính P( A + B + BC| ).
Câu 2.(1,5 điểm): Cho hàm mật độ của đại lượng ngẫu nhiên liên tục X:
1) Tìm hệ số a .
2) Tính P( X < ModX) ?
Câu 3.(1,5 điểm): Một lớp học có 60 sinh viên trong đó có 45 nam. Lấy ngẫu nhiên ra 10 sinh viên
để tham gia hội sinh viên tình nguyện, gọi X là số sinh viên nam có trong 10 sinh viên. Biết Y N ( 5; 4).
1) Hãy tính giá trị E ( 2X + D(3Y )– 1).
2) Tính P( - 4Y +4 < 3) ?
Câu 4.( 3 điểm): Đơn hàng online ở một cửa hàng quần áo là đại lượng tuân theo quy luật chuẩn.
Theo dõi số đơn hàng online/ ngày ở cửa hàng ta có kết quả sau: cỡ mẫu 60 ngày, trung bình mẫu là
150,2 và độ lệch hiệu chỉnh là 3,6, trong đó có 5 ngày cửa hàng bị quá tải trong việc vận hành đơn.
1. Hãy ước lượng tỷ lệ những ngày bị quá tải đơn của cửa hàng với độ tin cậy 96% ?
2. Khi ước lượng số đơn hàng trung bình của cửa hàng với độ chính xác 0,23 thì độ tin cậy bằng bao nhiêu?
3. Chủ cửa hàng khẳng định số đơn hàng trung bình là 160. Hãy cho kết luận với mức ý nghĩa 2% ?
Câu 5.(2 điểm): Để tìm hiểu mối liên hệ giữa thu nhập của hộ gia đình với giá trị của các gói bảo
hiểm người ta thống kê trên 50 hợp đồng bảo hiểm thu được bảng số liệu sau: xi 22 25 27 28 29 30 31 33 yi 11 12,5 13 14 14,5 16 16,5 17 lOMoAR cPSD| 45315597 – SỐ 17 ni 3 2 2 10 5 8 15 5
Với biến BNN X về tổng thu nhập của hộ gia đình (triệu đồng) và Y chỉ giá trị gói bảo hiểm (triệu/năm).
1. Lập phương trình hồi quy tuyến tính thực nghiệm và cho biết giá trị gói bảo hiểm ứng với mức thu
nhập 26( triệu đồng) của hộ gia đình?
2. Hãy ước lượng hệ số tương quan với mức ý nghĩa 2%?
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ – SỐ 16
Câu 1.(2 điểm): Cho 2 biến cố A, B. Biết rằng P(AB) = 0,25, P(A) = 0,5; P(B) = 0,4.
1. Tính P(A+B), P( A|B)?
2. Cho D là biến cố xung khắc với A, P(DB) = 0,3. Tính P( D| A + B).
Câu 2.(1,5 điểm): Cho bảng phân phối đồng thời -1 0 1 3 X -2 0,5a 2a 0,5a 1,5a 1 0,2 0,5a 1,5a 1,5a 1) Tìm hệ số a .
2) Tính E ( + 2Y – 1) và P ( Y= 0 | X = 1) ?
Câu 3.(1,5 điểm): Cho X B(3; 0,2); Y N ( 6; 0,9).
1) Hãy tính giá trị E (X. DX+ Y.DY – 1).
2) Tính P( - 4Y + 3 < ModX)?
Câu 4.(3 điểm): Số sinh viên đạt môn xác suất thống kê là đại lượng tuân theo quy luật chuẩn. Theo
dõi số sinh viên thi đạt môn xác suất năm học 2019-2020 có kết quả sau: cỡ mẫu = 100, TB mẫu =
6,7 và độ lệch hiệu chỉnh = 0,51 trong đó có 15 sinh viên đạt điểm giỏi (≥ 9).
1. Hãy ước lượng điểm trung bình môn xác suất của sinh viên với độ tin cậy 96% ?
2. Khi ước lượng tỷ lệ những sinh viên đạt điểm giỏi với yêu cầu độ chính xác là 0,01 thì độ tin cậy là bao nhiêu? lOMoAR cPSD| 45315597
3. Phòng khảo thí cho rằng tỷ lệ sinh viên đạt điểm giỏi không quá 10%. Hãy cho kết luận với mức ý nghĩa 2% ?
Câu 5.(2 điểm): Nghiên cứu về mối liên hệ giữa giá vàng và giá cổ phiếu của một công ty bất động sản ta có số liệu sau: xi 35 35,5 36 37 40 41 42 45 yi 1,5 1,5 2 2,5 2,5 3 3,5 4 ni 1 1 1 1 1 1 1 1
Với biến BNN X về giá vàng (triệu đồng/ lượng) và Y chỉ giá cổ phiếu (nghìn/ 1cổ phiếu).
1. Lập phương trình hồi quy tuyến tính thực nghiệm và cho biết sai số về giá cổ phiếu ứng với mức giá
vàng 37 triệu đồng/lượng giữa số liệu thực tế và qua hàm hồi quy?
2. Có giả thiết cho rằng
< 0,91, hãy đưa ra kết luận với mức ý nghĩa 2%?
ĐỀ THI HỌC PHẦN XÁC SUẤT THỐNG KÊ
Câu 1.(2 điểm): Cho hệ biến cố đầy đủ { A, B, C}. Biết rằng P(F|A) = 0,35, P(F|B) = 0,24; P(F|C) =
0,45, P(AF) = 0,7, P(B) = 7P(C). 1. Tính P(F)?
2. Tính P( A + B + BC| )?
Câu 2.(1,5 điểm): Cho hàm mật độ của đại lượng ngẫu nhiên liên tục X:
1) Tìm hệ số a .
2) Tính P ( X < ModX) ?
Câu 3.(1,5 điểm): Cho X B(5; 0,3); Y N (5; 0,4).
1) Hãy tính giá trị E (2 DX + DY – 1).
2) Tính P( - 4Y < ModX. ModY)?