Điều kiện cần và đủ là gì? Ví dụ về điều kiện cần và đủ
Trước khi định nghĩa "Điều kiện cần và đủ là gì?" ta cần hiểu thuật ngữ liên quan là "mệnh đề".
1. Mệnh đề là gì?
Một mệnh đề (mệnh đề logic) là một câu khẳng định có tính đúng hay một câu khẳng định có tính
sai. Một mệnh đề không thể vừa đúng lại vừa sai.  Lưu ý:
- Các câu hỏi, câu cảm thán, câu mệnh lệnh không phải là mệnh đề.
- Câu mà chưa thể nói đúng hay sai nhưng chắc chắn nó chỉ đúng hoặc sai, không thể vừa đúng
vừa sai cũng là mệnh đề. Ví dụ: 'Có sự sống ngoài Trái Đất' là mệnh đề.
- Câu không phải là câu khẳng định nhưng không có tính đúng sai thì không phải là mệnh đề.
Để hiểu rõ hơn, ta theo dõi ví dụ dưới đây: Câu Mệnh đề đúng Mệnh đề sai Không là mệnh đề 1 + 6 = 7 X 1 + 6 = 8 X 141 chia hết cho 9 X
0,1 có thuộc tập số tự nhiên N không? X Cấm đi lối này! X
2. Điều kiện cần và đủ là gì? Ví dụ điều kiện cần và đủ
Theo Từ điển Tiếng Việt, "điều kiện" được hiểu là điều nêu ra như một đòi hỏi trước khi thực hiện
một việc nào đó. Trên cơ sở đó, điều kiện cần là yếu tố không thể thiếu để đạt được mục tiêu nào
đó. Điều kiện đủ là tổng hợp tất cả các yếu tố, khi có hay thỏa mãn điều kiện này thì có được tất
cả. Điều kiện cần và điều kiện đủ thường luôn được đặt tương phản với nhau. Điều kiện cần và đủ
được phát biểu như sau:
Khi mệnh đề "A ⇒ B" (đọc là: A kéo theo B hoặc A suy ra B), thì B là điều kiện cần để có A.
 Ví dụ: Nếu trong mặt phẳng, hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì hai
đường thẳng đó song song với nhau.
 Trong mặt phẳng, hai đường thẳng song song với nhau là điều kiện cần để hai đường thẳng
cùng vuông góc với đường thẳng thứ ba.
Khi mệnh đề đảo "B ⇒ A" cũng đúng thì A là điều kiện đủ để có B.
 Vẫn ví dụ trên: Trong mặt phẳng, hai đường thẳng cùng vuông góc với đường thẳng thứ ba là
điều kiện đủ để hai đường thẳng đó song song với nhau
Kết luận, A và B vừa là điều kiện cần, vừa là điều kiện đủ của nhau. Trường hợp này ta nói rằng: A
là điều kiện cần và đủ của B.
Ngoài cách gọi là "điều kiện cần và đủ" thì còn có thể nói là "nếu và chỉ nếu", "khi và chỉ khi", hoặc "tương đương"
Ví dụ 1: Cho mệnh đề "Tam giác cân khi và chỉ khi có đường trung tuyến bằng nhau".
Điều kiện cần và đủ được phát biểu như sau: Điều kiện cần và đủ để tam giác cân là hai đường
trung tuyến của nó bằng nhau.
Ví dụ 2: Cho mệnh đề "Một số chia hết cho 2 khi và chỉ khi nó có chữ số tận cùng là số chẵn"
 Một số chia hết cho 2 là điều kiện cần và đủ để nó có chữ số tận cùng là số chẵn
Ví dụ 3: Cho mệnh đề "Một tứ giác nội tiếp được trong một đường tròn khi tổng hai góc đối diện của nó bằng 180°"
 Điều kiện cần để tứ giác có tổng số đo hai góc đối diện bằng 180° là tứ giác đó nội tiếp trong một đường tròn
 Điều kiện đủ để tứ giác nội tiếp được trong một đường tròn là tứ giác có tổng số đo hai góc đối diện bằng 180°
Như vậy, điều kiện cần và đủ để tứ giác nội tiếp được trong một đường tròn là tổng hai góc đối diện của nó bằng 180°
Ví dụ 4: Cho mệnh đề "Nếu hai tam giác bằng nhau (A) thì chúng có diện tích bằng nhau (B)"
 Hai tam giác bằng nhau là điều kiện đủ để chúng có diện tích bằng nhau (A ⇒ B)
 Hai tam giác có diện tích bằng nhau là điều kiện cần để chúng bằng nhau (B ⇒ A)
 Tuy nhiên, điều kiện cần và đủ để thỏa mãn mệnh đề trên lại không có, bởi lẽ, A ⇒ B đúng nhưng B ⇒ A chưa chắc đúng.
 Vì, hai tam giác có diện tích bằng nhau ta chưa thể kết luận được ngay rằng hai tam giác đó bằng nhau. Chứng minh:     
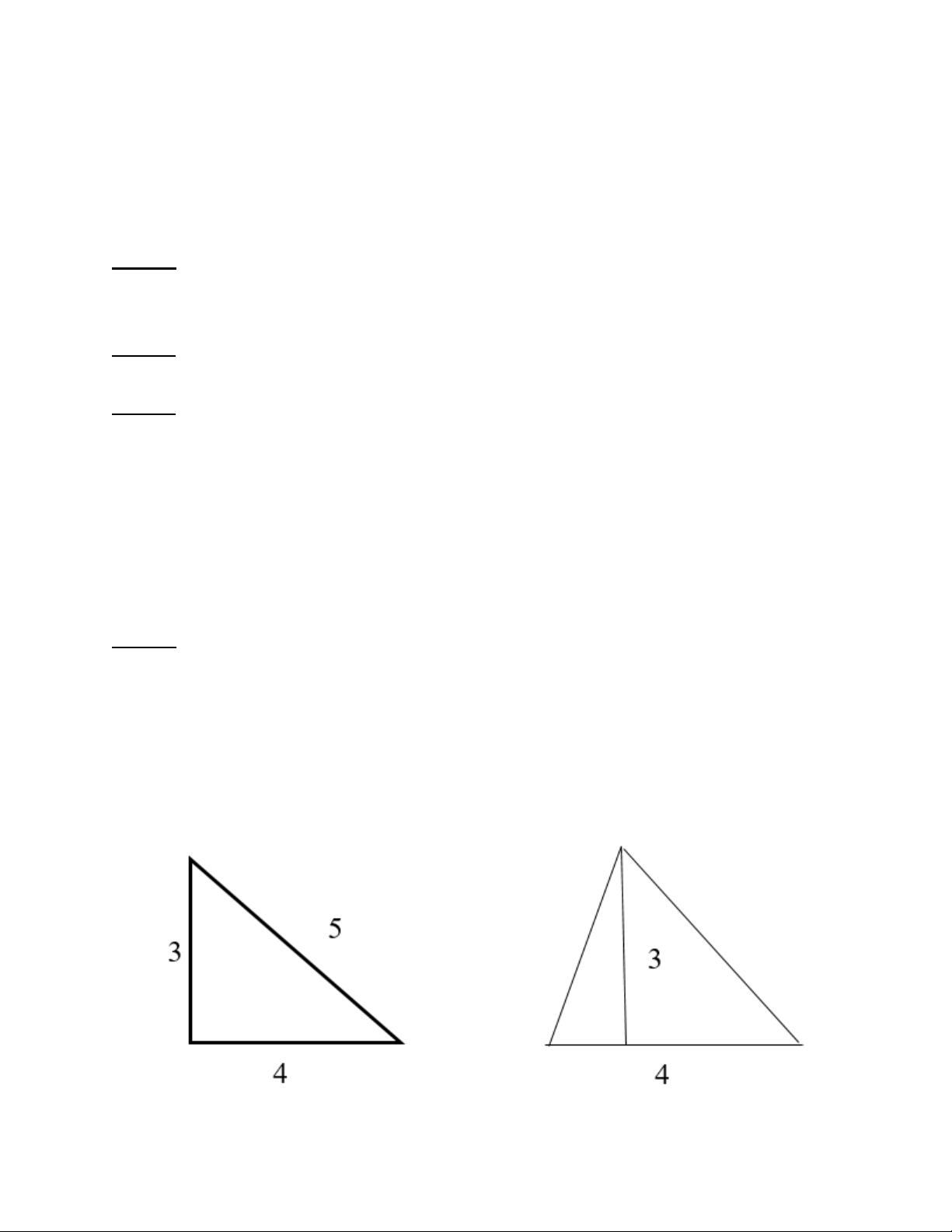
- Xét hai hình tam giác trên, Tam giác vuông có S = 1/2 * (3*4) = 6
Tam giác nhọn có S = 1/2 * (3*4) = 6
Mặc dù S của hai tam giác bằng nhau nhưng hai tam giác này không thể bằng nhau được, giữa
chúng không có mối liên hệ nào với nhau vì một bên là tam giác vuông, bên còn lại là tam giác nhọn.
Kết luận: Không có điều kiện cần và đủ của mệnh đề "Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau"
3. Bài tập "Điều kiện cần và đủ"
Bài 1. Các câu dưới đây, câu nào là mệnh đề đúng, câu nào mệnh đề sai, câu nào không là mệnh đề.
a. Số pi có lớn hơn 3,1 không?
b. Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau
c. Một tứ giác là hình thoi tương đương hai đường chéo vuông góc với nhau
d. Phương trình x2 + 2015x - 2016 = 0 vô nghiệm
e. P: "Nếu tam giác ABC có AB2 + AC2 = BC2 thì đó là tam giác ABC là tam giác vuông"
f. Bây giờ là mấy giờ?
g. 7 không phải là số nguyên tố LỜI GIẢI
Câu không phải mệnh đề là a, f
Câu là mệnh đề sai g, b, c, d
Câu là mệnh đề đúng e
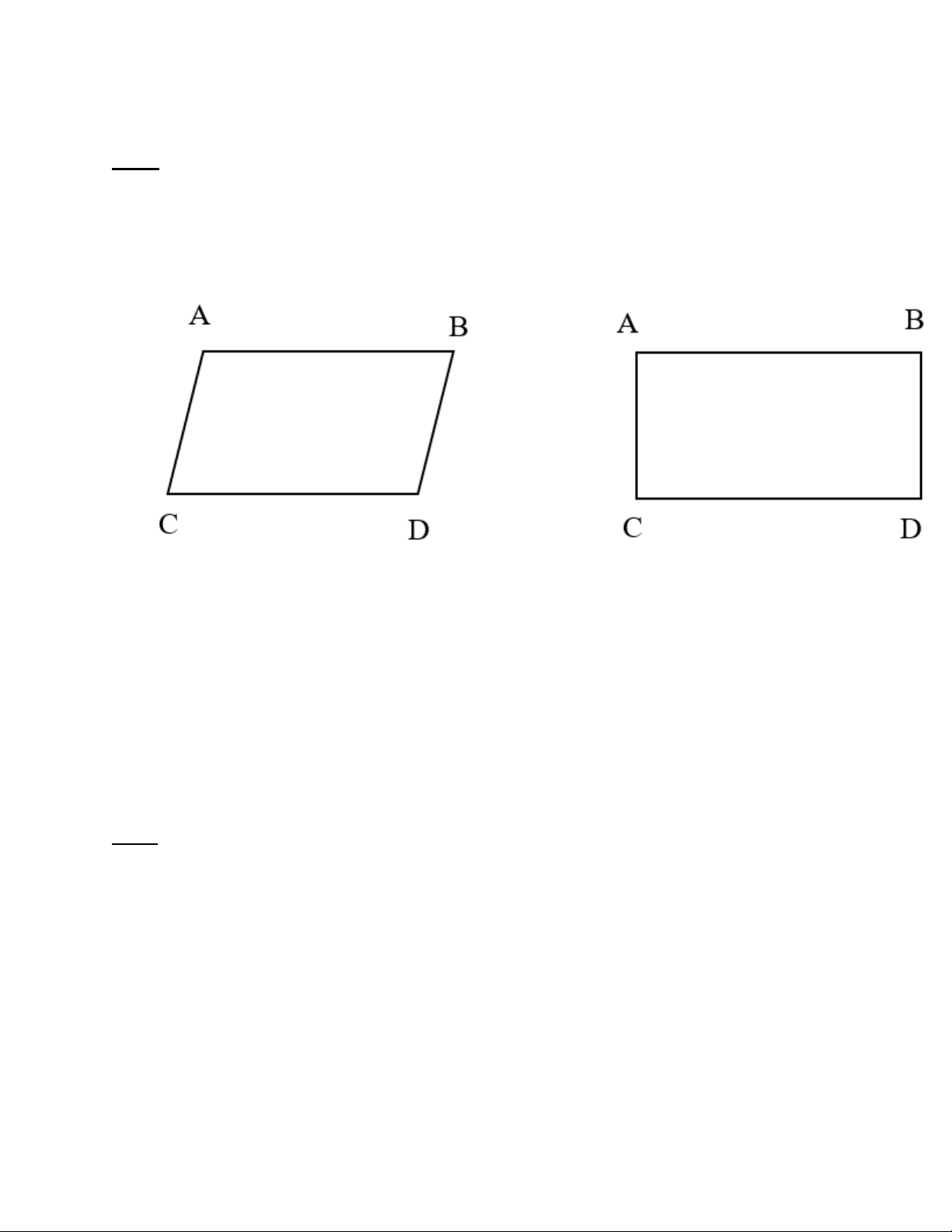
Bài 2: Cho tứ giác ABCD, phát biểu điều kiện cần và đủ để a. ABCD là hình bình hành
b. ABCD là hình chữ nhật LỜI GIẢI
a. Điều kiện cần và đủ để tứ giác ABCD là hình bình hành ⇔ AC // BD và AC = BD
Hoặc, điều kiện cần và đủ để tứ giác ABCD là hình bình hành ⇔ AD giao với BC tại một điểm
(gọi là O) và AO = OD = 1/2 AD
b. Điều kiện cần và đủ để tứ giác ABCD là hình chữ nhật ⇔ góc CAB = góc ACD = góc CDB = 90°
Hoặc, điều kiện cần và đủ để tứ giác ABCD là hình chữ nhật ⇔ ABCD là hình bình hành và có một góc vuông
Bài 3. Dùng thuật ngữ "điều kiện cần", "điều kiện đủ" để phát biểu các định lý sau dây:
a. Nếu số nguyên dương có chữ số tận cùng bằng 5 thì chia hết cho 5
b. Nếu tứ giác là hình thoi thì hai đường chéo vuông góc với nhau
c. Nếu hai tam giác bằng nhau thì chúng có các góc tương ứng bằng nhau
d. Nếu số nguyên dương b chia hết cho 24 thì chia hết cho 4 và 6 LỜI GIẢI
a. Số nguyên dương có chữ số tận cùng bằng 5 là điều kiện đủ để chia hết cho 5
Số nguyên dương chia hết cho 5 là điều kiện cần để nó nó chữ số tận cùng bằng 5
b. Tứ giác là hình thoi là điều kiện đủ để nó có hai đường chéo vuông góc với nhau
Tứ giác có hai đường chéo vuông góc với nhau là điều kiện cần để tứ giác đó là hình thoi
c. Hai tam giác bằng nhau là điều kiện đủ để các góc của chúng tương ứng bằng nhau
Hai tam giác có các góc tương ứng bằng nhau là điều kiện cần để chúng bằng nhau.
d. Số nguyên dương b chia hết cho 24 là điều kiện đủ để nó chia hết cho 4 và 6
Số nguyên dương b chia hết cho 4 và 6 là điều kiện cần để nó chia hết cho 24
Bài 4. Cho tam giác ABC. Xét các mệnh đề sau:
A: "Tam giác ABC là tam giác vuông"
B: "Tam giác ABC có một góc bằng tổng hai góc còn lại"
Phát biểu mệnh đề A ⇔ B bằng 4 cách? LỜI GIẢI
 Tam giác ABC là tam giác vuông là điều kiện cần và đủ để tam giác ABC có một góc bằng tổng hai góc còn lại
 Tam giác ABC là tam giác vuông tương đương tam giac ABC có một góc bẳng tổng hai góc còn lại
 Tam giác ABC là tam giác vuông khi và chỉ khi tam giác ABC có một góc bằng tổng hai góc còn lại
 Tam giác ABC là tam giác vuông nếu và chỉ nếu tam giác ABC có một góc bằng tổng hai góc còn lại