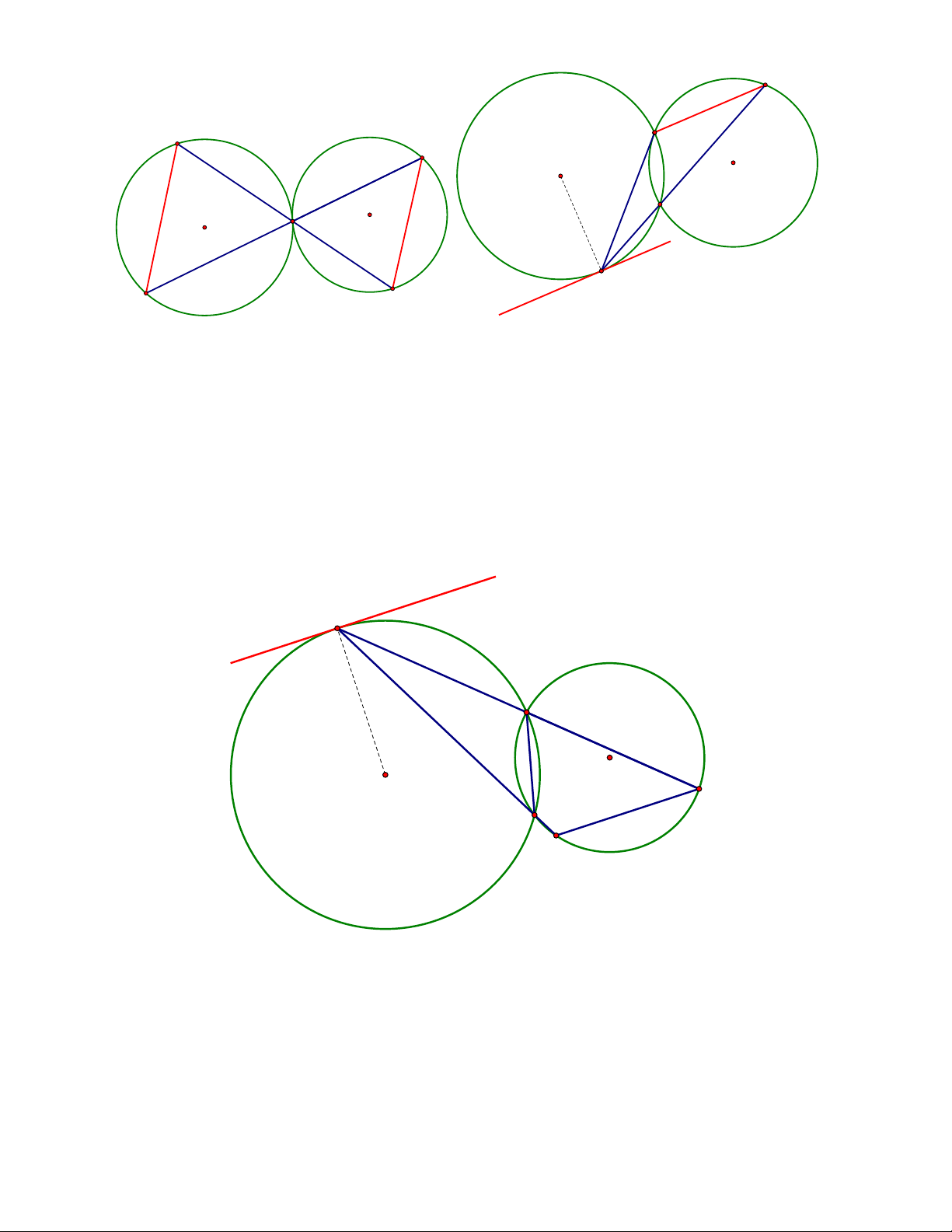



Preview text:
ĐỊNH LÍ REIM VÀ ỨNG DỤNG
(Theo tạp chí Epsilon, số 14, 12/2018) I. ĐỊNH LÍ
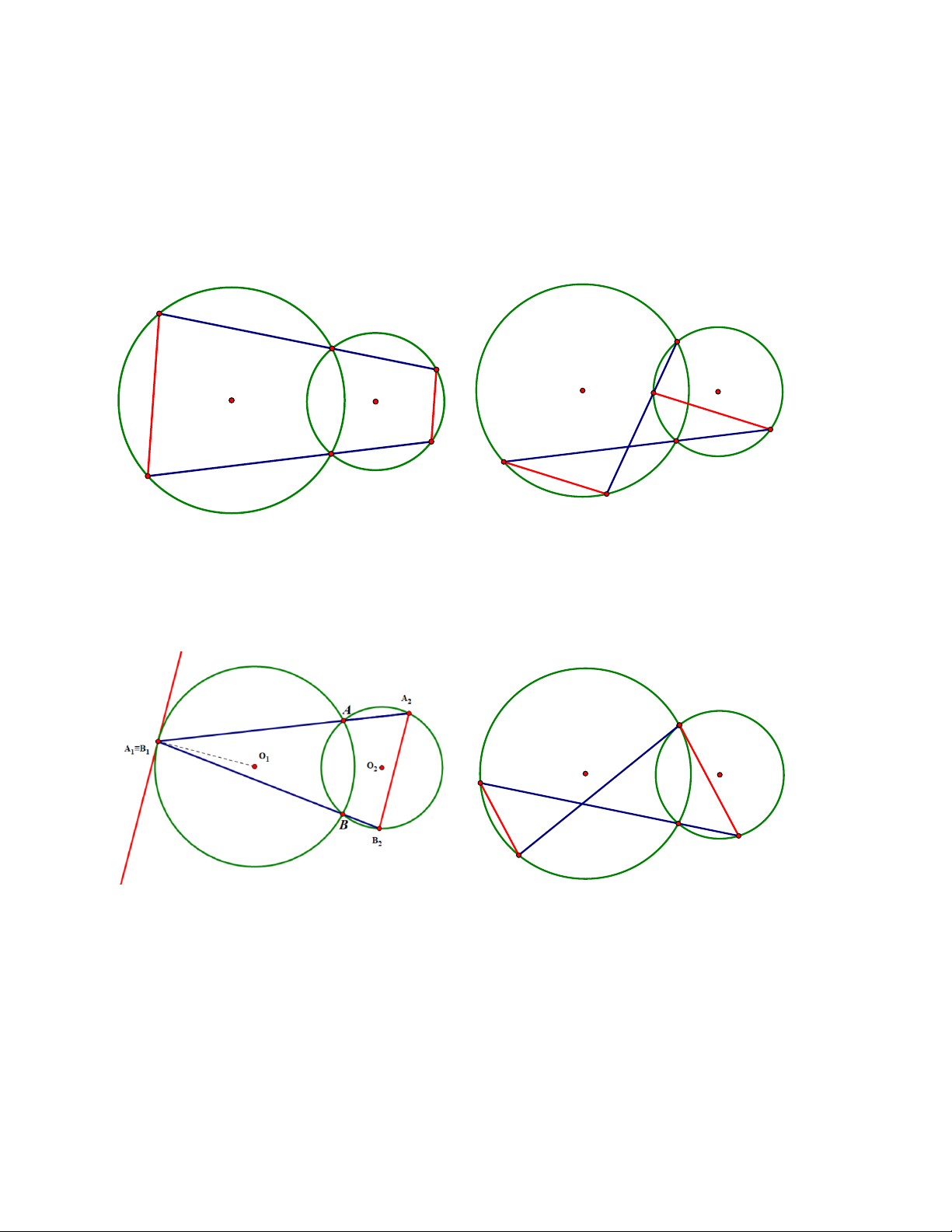
Định lí Reim: Cho hai đường tròn (O ) và (O ) cắt nhau tại A và B . Một đường thẳng 1 2
đi qua A cắt (O ) và (O ) thứ tự tại A và A ; và một đường thẳng đi qua B cắt (O ) và 1 2 1 2 1
(O ) thứ tự tại B và B . Khi đó A A / /B B . 2 1 2 1 2 1 2 A1 A A A2 O1 A2 O2 O1 O2 B2 B2 B B B1 B1 A1
Ngoài ra định lí vẫn đúng trong các trường hợp suy biến khi các điểm trùng nhau và khi đó
ta xem cạnh do một cặp điểm trùng nhau là tiếp tuyến tại cặp điểm trùng nhau đó hoặc hai
đường tròn (O ) và (O ) tiếp xúc với nhau. Các trường hợp được minh họa bằng các hình 1 2 vẽ: A≡A2 O1 B O2 1 B B2 A1 B2 A≡A2 B1 A2 O2 O1 A≡B O O2 1 A1≡B1 A B 1 2
Định lí Reim đảo: Cho bốn điểm ,
A A , B, B cùng nằm trên đường tròn (O ) . Trên các 1 1 1
đường thẳng AA , BB lấy các điểm A và B khác tương ứng sao cho A A / /B B thì khi 1 1 2 2 1 2 1 2
đó tồn tại đường tròn (O ) đi qua bốn điểm ,
A B, A , B . 2 2 2
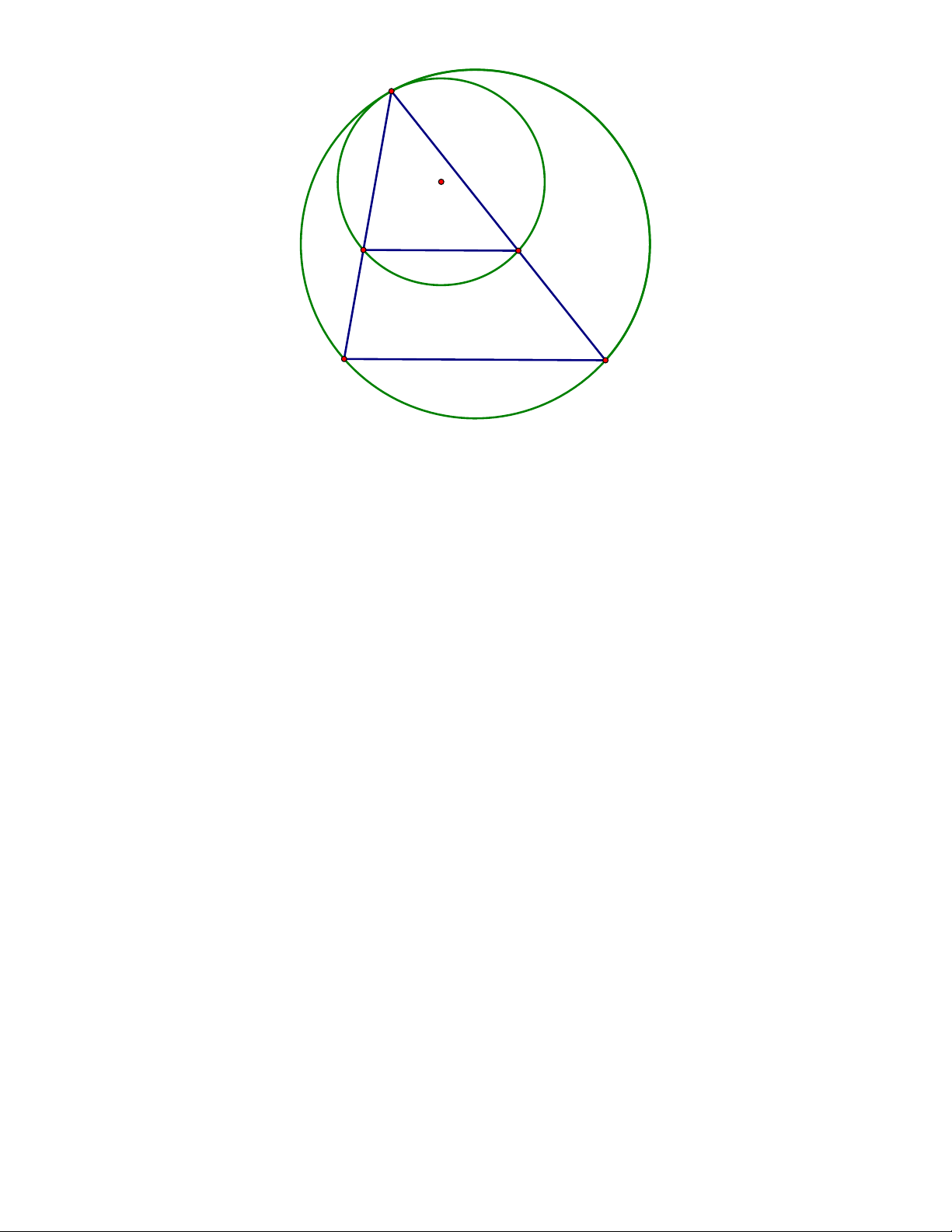
Hệ quả 1. Cho tam giác ABC nội tiếp đường tròn ( )
O . Một đường tròn (O ') đi qua các
đỉnh B và C lần lượt cắt các đường thẳng AB và AC tại B' và C ' khác A. Đường thẳng
t đi qua đỉnh A. Khi đó t tiếp xúc với ( )
O khi và chỉ khi t / /B'C '. A B O' O B' C C'
Hệ quả 2. Cho tam giác ABC . Các điểm B' và C ' lần lượt nằm trên các đường thẳng
AB và AC và khác với các đỉnh của tam giác. Khi đó hai đường tròn ngoại tiếp của các
tam giác ABC và AB'C ' tiếp xúc với nhau (tại A) khi và chỉ khi BC / /B'C ' . A B C B' C'
II. BÀI TẬP ÁP DỤNG
Ví dụ 1 (Netherlands IMO TST1- 2019 p4): Cho tam giác không cân ABC . Lấy hai điểm ,
D E trên cạnh AC sao cho , A E, ,
D C thẳng hàng theo thứ tự. Đường thẳng đi qua E và
song song với BC cắt đường tròn ngoại tiếp tam giác ABD tại F sao cho E, F nằm cùng
một phía với bờ là đường thẳng .
AB Đường thẳng đi qua E và song song với AB cắt
đường tròn ngoại tiếp tam giác BDC tại G sao cho E,G nằm cùng một phía với bờ là đường thẳng .
BC Chứng minh rằng ,
D F, E,G đồng viên.
Ví dụ 2 (China MO 2012p1). Cho tam giác ABC có A có số đo lớn nhất. Trên đường tròn
ngoại tiếp tam giác ABC lấy điểm D là trung điểm cung ABC và E là trung điểm cung
ACB . Đường tròn c đi qua ,
A B và tiếp xúc với AC tại A đường tròn c đi qua , A E và 1 2
tiếp xúc với AD tại A. đường tròn c và c cắt nhau tại ,
A P . Chứng minh rằng AP là 1 2
phân giác của BAC .
Ví dụ 3 (Netherlands IMO TST3- 2019 p1): Cho tứ giác ABCD nội tiếp đường tròn ( ) O
. Gọi AC BD = E . Một đường thẳng l bất kì đi qua E cắt AB tại P và cắt BC tại Q .
Một đường tròn tiếp xúc với l tại E và đi qua D . Gọi R (R D) là giao điểm của và ( )
O . RP cắt đường tròn ( )
O tại điểm thứ hai là Y . Chứng minh rằng YC / /PE và , B , Q , R P đồng viên.
Ví dụ 4. (USA TST 2019 P2) Cho tam giác nhọn ABC nội tiếp đường tròn ( ) O và có trực tâm H . Gọi ,
D E lần lượt là các điểm trên cạnh AB và AC sao cho AD = AE . Các đường
thẳng lần lượt đi qua B và C cùng song song với DE cắt ( )
O tại P và Q theo thứ tự. Gọi
là đường tròn ngoại tiếp tam giác ADE .
a) Chứng minh hai đường thẳng PE,QD cắt nhau tại một điểm trên .
b) Chứng minh rằng nếu đi qua H thì hai đường thẳng PD và QE cắt nhau tại một điểm trên .
Ví dụ 5 (IMO 2019 p2) Cho tam giác ABC , điểm A nằm trên cạnh BC và điểm B nằm 1 1 trên cạnh . AC Lấy hai điểm ,
P Q lần lượt nằm trên đoạn AA và BB sao cho PQ / / AB . 1 1
Lấy điểm P nằm trên đường thẳng PB sao cho B nằm giữa P và P sao cho PPC = BAC 1 1 1 1 1
. Tương tự điểm Q nằm trên đường thẳng QA sao cho A nằm giữa Q và Q sao cho 1 1 1 1
QQ C = CBA . Chứng minh rằng các điểm P ,Q , P và Q đồng viên. 1 1 1
Ví dụ 6 (APMO 2019 p3): Cho tam giác không cân ABC nội tiếp đường tròn ( ) O . Lấy
M là trung điểm BC . Trên đường thẳng AM lấy điểm P ( ,
A M) . Đường tròn ngoại
tiếp các tam giác BPM và CPM cắt ( )
O lần lượt tại D( B) và E( C) . Đường thẳng
DP và EP cắt đường tròn ngoại tiếp CPM và BPM tại X ,Y( )
P tương ứng. Chứng
minh rằng khi P thay đổi thì đường tròn ngoại tiếp tam giác AXY luôn đi qua điểm T cố định khác A.
Ví dụ 7 (Ibero American MO 2019 p3). Cho tam giác ABC nội tiếp đường tròn ( ) O .
Đường thẳng đi qua B và song song với AC cắt đường tròn ( ) O tại ( D D ) B và đường
thẳng đi qua C và song song với AB cắt đường tròn ( )
O tại E(E )
B . Các đường thẳng A ,
B CD cắt nhau tại P và các đường thẳng AC, BE cắt nhau tại Q . Gọi M là trung điểm
của DE . Đường thẳng AM cắt ( )
O tại Y(Y )
A và cắt đường thẳng PQ tại J . Đường
thẳng PQ cắt đường tròn ngoại tiếp tam giác BCJ tại Z(Z J) . Nếu các đường thẳng B ,
Q PC cắt nhau tại X , chứng minh rằng X nằm trên đường thẳng YZ.
Ví dụ 8: Cho tam giác ABC nhọn không cân nội tiếp đường tròn ( )
O . Giả sử AB AC .
Gọi H là trực tâm và I là tâm đường tròn nội tiếp tam giác ABC . Gọi F là trung điểm
của cung BC (chứa điểm H ) của đường tròn ngoại tiếp tam giác BHC . Gọi X là điểm
trên cung AB của đường tròn ( )
O không chứa điểm C sao cho AXH = AFH . Gọi K là
tâm đường tròn ngoại tiếp tam giác XIA . Chứng minh rằng các đường thẳng AO và KI
cắt nhau tại một điểm trên ( ) O .
Ví dụ 9 (USA TST 2019 P5) Cho tam giác ABC nhọn không cân có trực tâm H và nội tiếp đường tròn ( )
O . Đường thẳng đi qua H cắt các cạnh A ,
B AC lần lượt tại E và F .
Gọi K là tâm đường tròn ngoại tiếp tam giác AEF , đường thẳng AK cắt đường tròn ( ) O
tại điểm thứ hai là D . Chứng minh rằng đường thẳng HK và đường thẳng đi qua D vuông
góc với BC cắt nhau tại một điểm trên ( ) O .
Ví dụ 10 (VMO 2020 D2 P6) Cho tam giác ABC nhọn không cân có trực tâm H và ,
D E, F là chân các đường cao kẻ từ , A ,
B C theo thứ tự. DE, DF lần lượt cắt đường tròn
đường kính AD tại điểm thứ hai là M và N . Lấy các điểm P A ,
B Q AC sao cho NP ⊥ A , B MQ ⊥ AC
a) Chứng minh rằng EF là tiếp tuyến của đường tròn ngoại tiếp tam giác APQ .
b) Lấy T là tiếp điểm của EF và đường tròn ngoại tiếp tam giác APQ . Gọi
DT MN = K và L là điểm đối xứng của A qua đường thẳng MN . Chứng minh
rằng MN, EF cắt nhau tại một điểm trên đường tròn ngoại tiếp tam giác DLK .
Ví dụ 11 (Iranian TST 2019) Cho tam giác ABC có A
= 60. Dựng ra phía ngoài tam
giác ABC hai tam giác đều ABK, ACL . Đường thẳng CK và AB cắt nhau tại S , đường
thẳng AC và BL cắt nhau tại R , đường thẳng BL và CK cắt nhau tại T . Chứng minh
rằng tâm đẳng phương của ba đường tròn (BSK),(CL )
R và (BTC) nằm trên đường trung
tuyến đỉnh A của tam giác ABC .
Ví dụ 12 (IGO 2020 Intermediate P3) Cho tam giác nhọn ABC có AC AB , trực tâm
H và M là trung điểm đoạn BC . Đường trung tuyến AM cắt đường tron ngoại tiếp tam
giác ABC tại điểm thứ hai là X . Đường thẳng CH cắt đường trung trực của BC tại E và
cắt đường tròn ngoại tiếp tam giác ABC tại điểm thứ hai là F . Gọi là đường tròn ngoại
tiếp tam giác X , E, F . Lấy điểm J trên sao cho CB / /HJ và J nằm khác phía H với
bờ là AB . Chứng minh rằng JB và EM cắt nhau tại một điểm trên .
BÀI TẬP TỰ LUYỆN
Bài 1 (Ibero American MO p4). Cho hình thang ABCD có AB / /CD và nội tiếp trong đường tròn ( ) O . Gọi ,
P Q là hai điểm trên cạnh AB ( ,
A B ) sao cho AP = Q .
B Gọi E, F
là giao điểm thứ hai của các đường thẳng C , P CQ với ( )
O tương ứng. Các đường thẳng A ,
B EF cắt nhau tại G . Chứng minh rằng DG là tiếp tuyến với ( ) O .
Bài 2 (International Olympiad Tuymaada (Russia) 2019 P8) Cho tam giác ABC có góc
B tù và AB BC nội tiếp đường tròn ( )
O . Gọi N là trung điểm của ABC . Đường tròn
ngoại tiếp tam giác B
ON cắt AC tại X và Y . Đường thẳng BX cắt đường tròn ( ) O tại
điểm thứ hai là P và đường thẳng BY cắt đường tròn ( )
O tại điểm thứ hai là Q . Chứng minh rằng ,
P Q và điểm đối xứng của N qua AC thẳng hàng.
Bài 3 (IMOC 2021 G10) Cho tam giác ABC nhọn không nội tiếp đường tròn ( ) O và
ngoại tiếp đường tròn (I) . Đường tròn (I) tiếp xúc với cạnh BC tại điểm D . Gọi H là
trực tâm tam giác IBC , N là trung điểm của BAC và X là giao điểm của OI và NH.
Lấy P là điểm đối xứng của A qua OI . Chứng minh rằng các đường tròn ngoại tiếp tam
giác IDP và IHX tiếp xúc nhau.
Bài 4 (IMO 2018 Shortlist G1) Cho tam giác nhọn ABC nội tiếp đường tròn . Các điểm ,
D E lần lượt nằm trên các đoạn AB và AC sao cho AD = AE . Đường trung trực của
đoạn BD và CE cắt các cung nhỏ AB, AC của đường tròn theo thứ tự tại F và G .
Chứng minh rằng các đường thẳng DE và FG hoặc song song hoặc cùng nằm trên một đường thẳng.
Bài 5: (Albanians Cup in Mathematics 2021, P2 day 1) Cho tam giác không cân ABC
có đường phân giác AD, đường cao BE và CF . Gọi X = AD BE,Y = AD BF và H
là trực tâm tam giác ABC . Lấy điểm P trên AB và điểm Q trên AC sao cho trung điểm
của đoạn PQ là trực tâm của tam giác HXY . Chứng minh rằng , B C, , P Q cùng nằm trên một đường tròn.




