

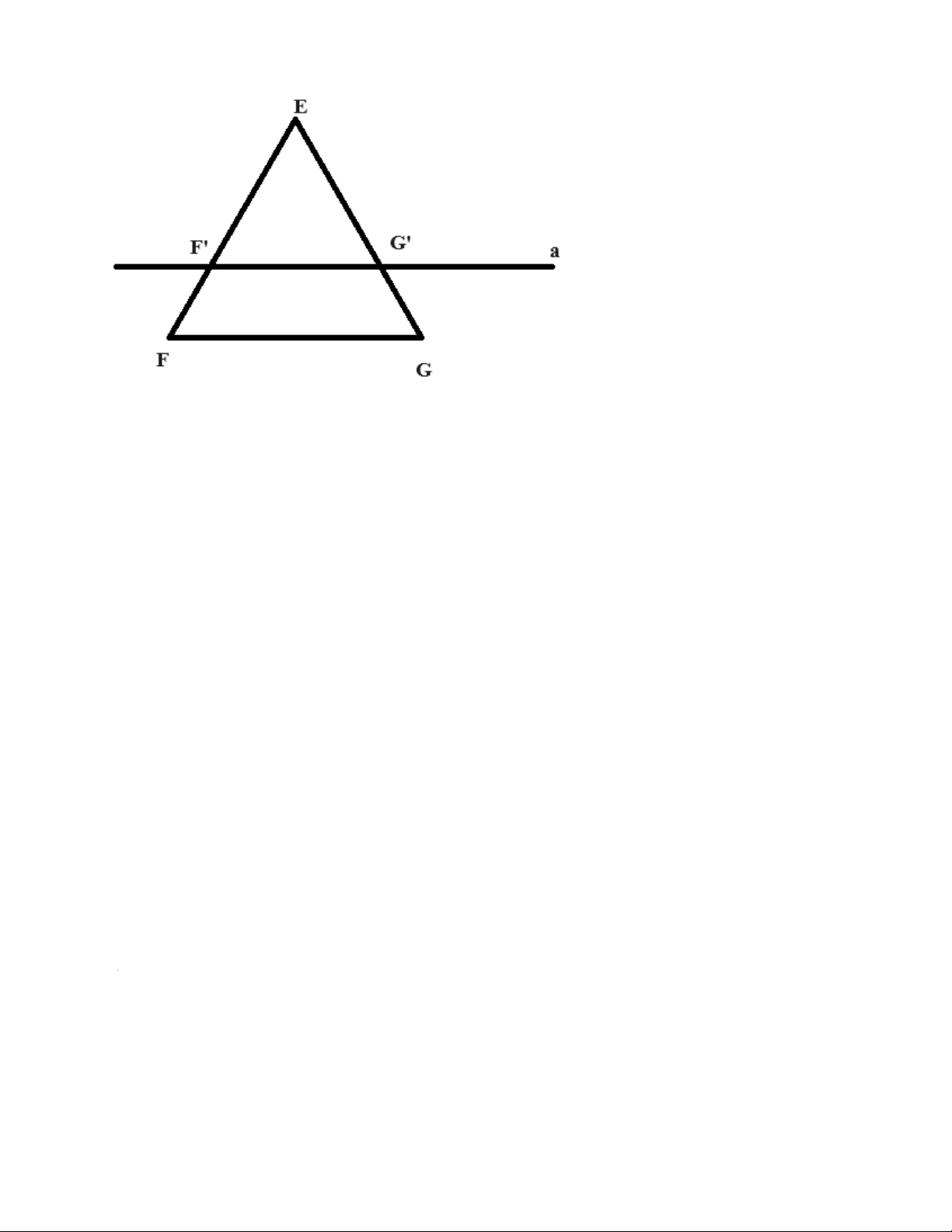

Preview text:
Định lý Talet trong tam giác và trong hình thang
1. Định lý Talet trong tam giác
1.1. Lý thuyết về tỷ số của hai đoạn thẳng
Lý thuyết về tỷ số của hai đoạn thẳng là một khái niệm quan trọng trong hình học và toán học. Nó giúp
chúng ta so sánh độ dài của hai đoạn thẳng và xác định mối quan hệ tỷ lệ giữa chúng. Dưới đây là một số
thông tin chi tiết về lý thuyết này:
Khái niệm về tỷ số của hai đoạn thẳng
Tỷ số của hai đoạn thẳng là một phép tính dựa trên độ dài của chúng. Để tính tỷ số, chúng ta cần đo độ dài
của cả hai đoạn thẳng bằng cùng một đơn vị đo, ví dụ như centimet (cm) hoặc inch (in). Tỷ số của hai đoạn
thẳng AB và CD thường được kí hiệu là
Đoạn thẳng tỷ lệ:
Hai đoạn thẳng AB và CD được gọi là tỷ lệ với hai đoạn thẳng A'B' và C'D' nếu tồn tại một tỷ lệ thức tương
đương giữa chúng. Điều này có nghĩa là tỷ số của đoạn AB và đoạn A'B' bằng tỷ số của đoạn CD và đoạn C'D'. Cụ thể, nếu
thì ta nói AB và CD tỷ lệ với A'B' và C'D'.
Tính chất quan trọng:
Tính chất quan trọng của đoạn thẳng tỷ lệ là nó cho phép ta thể hiện sự tương quan tỷ lệ giữa các đoạn
thẳng trong hình học. Nếu hai đoạn thẳng tỷ lệ với nhau, thì nếu chúng được mở rộng hoặc thu hẹp cùng
một lượng, tỷ số của chúng vẫn không đổi.
Ứng dụng trong hình học và toán học:
Lý thuyết tỷ số của hai đoạn thẳng rất hữu ích trong hình học và toán học. Nó được sử dụng để giải quyết
các bài toán liên quan đến tỷ lệ, tương tự và đối xứng trong hình học. Nó cũng thường xuất hiện trong các
bài toán liên quan đến biến đổi đồ thị và giải tích.
Trong tổng quan, lý thuyết tỷ số của hai đoạn thẳng là một khái niệm quan trọng giúp chúng ta hiểu và xác
định mối quan hệ tỷ lệ giữa các đoạn thẳng trong không gian hình học và toán học.
1.2. Định lý Talet trong hình tam giác
Hình tam giác (triangle) là một đa giác có ba đỉnh, ba cạnh và ba góc. Tam giác là một trong những hình học
cơ bản và quan trọng nhất trong toán học và hình học. Dưới đây là một số đặc điểm cơ bản về hình tam giác:
Hình tam giác có ba điểm gọi là đỉnh. Các đỉnh này được ký hiệu bằng chữ cái hoa thường A, B, và C hoặc
bất kỳ cách ký hiệu nào khác. Hình tam giác có ba đoạn thẳng gọi là cạnh. Các cạnh được ký hiệu bằng các
chữ cái tương ứng với các đỉnh, ví dụ AB, BC, và CA. Hình tam giác có ba góc. Góc được hình thành bởi
hai đoạn thẳng kết nối các đỉnh gọi là góc của tam giác. Tổng số độ của ba góc bên trong hình tam giác luôn
bằng 180 độ. Điều này được gọi là tính chất "tổng độ của tam giác."
Loại tam giác dựa trên góc và cạnh:
- Tam giác vuông: Có một góc vuông, tức là một góc bằng 90 độ.
- Tam giác tù: Có ít nhất một góc lớn hơn 90 độ.
- Tam giác nhọn: Tất cả các góc trong đều nhỏ hơn 90 độ.
Loại tam giác dựa trên độ dài các cạnh:
- Tam giác đều: Các cạnh và góc của tam giác đều bằng nhau. Tất cả các góc là góc bằng 60 độ.
- Tam giác cân: Có ít nhất hai cạnh bằng nhau.
- Tam giác vuông cân: Là tam giác vuông và cân đồng thời.
Hình tam giác là một phần quan trọng của hình học và toán học và được sử dụng rộng rãi để giải quyết các
bài toán và phân tích các tương tác trong không gian hai chiều.
Định lý Talet thuận trong tam giác là một khái niệm quan trọng trong hình học tam giác, và nó liên quan đến
sự tỷ lệ giữa các đoạn thẳng trong tam giác và đường thẳng cắt chúng. Dưới đây là chi tiết về định lý Talet
thuận và định lý Talet đảo:
Định lý Talet thuận trong tam giác:
Giả sử chúng ta có một tam giác EFG và một đường thẳng F'G' song song với cạnh FG và cắt hai cạnh EF
và EG tại các điểm F' và G' tương ứng.
Khi đó, ta có các tỷ số sau:
Điều này có nghĩa rằng đoạn EF' và đoạn EG' có tỷ số độ dài bằng tỷ số độ dài của cạnh EF và cạnh EG.
Tương tự, đoạn FF' và GG' cũng có tỷ số độ dài tương ứng với cạnh EF và cạnh EG.
Định lý Talet đảo:
Ngược lại, định lý Talet đảo khẳng định rằng nếu một đường thẳng cắt hai cạnh của tam giác và đoạn thẳng
được định ra trên hai cạnh này có tỷ số độ dài tương ứng, thì đường thẳng đó sẽ song song với cạnh còn lại của tam giác.
Điều này được thể hiện bằng các tỷ số sau:
Khi điều kiện trên được thỏa mãn, ta có F'G' song song với FG
Hệ quả của định lý Talet:
Hệ quả quan trọng của định lý Talet là nếu một đường thẳng cắt hai cạnh hoặc phần kéo dài của hai cạnh
của tam giác và song song với cạnh còn lại, thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỷ lệ
với ba cạnh của tam giác ban đầu. Cụ thể:
Điều này đồng nghĩa với việc đường thẳng cắt tạo ra một tam giác tương tự (tam giác có các góc tương tự
và các cạnh tỷ lệ với tam giác ban đầu).
2. Định lý Talet trong hình thang
Định lý Talet trong hình thang là một định lý quan trọng trong hình học giúp xác định tỷ lệ giữa các đoạn
thẳng trong một hình thang khi một đường thẳng song song với hai đáy của hình thang cắt hai cạnh bên.
Dưới đây là chi tiết về định lý Talet trong hình thang và cách áp dụng nó trong một bài toán cụ thể:
Định lý Talet trong hình thang:
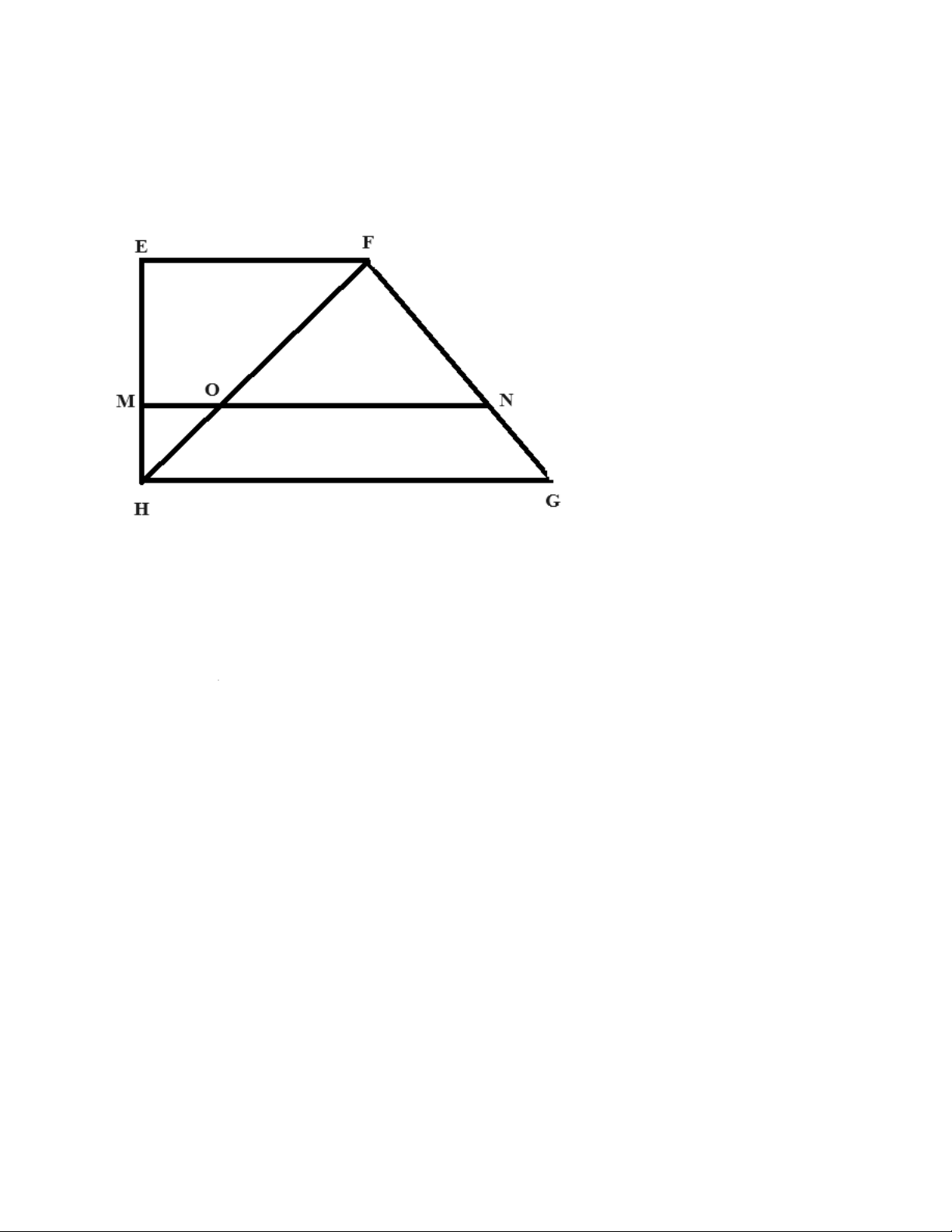
Giả sử chúng ta có một hình thang EFGH với hai đáy EF và GH, và điểm N thuộc đoạn FG và điểm M
thuộc đoạn EH. Nếu đường thẳng MN song song với hai đáy EF và HG và cắt hai cạnh bên FG và EH lần
lượt tại các điểm M và N, thì tỷ số giữa các đoạn thẳng tương ứng trên các đáy là bằng nhau:
Ngược lại, nếu tỷ số , thì đường thẳng MN sẽ song song với đáy EF và HG của hình thang.
Áp dụng định lý Talet trong bài toán:
Giả sử chúng ta có một hình thang EFGH với đáy EF song song với đáy GH (EF < HG), và đường thẳng
MN song song với đáy EF và GH. Đường thẳng MN cắt hai cạnh FG và EH lần lượt tại các điểm M và N.
Biết rằng FG = 6 cm, FN = 4 cm và EH = 9cm chúng ta cần tìm độ dài của EM. Lời giải:
Theo định lý Talet, chúng ta có:
Thay các giá trị đã biết vào phương trình:
Bây giờ, để tìm độ dài BN, ta có thể giải phương trình: 4 x 9 = EM x 6 36 = EM x 6 EM = 6
Vậy độ dài của đoạn thẳng EM là 6 cm.
3. Bài tập tự luyện
Bài 1. Viết tỷ số của các cặp đoạn thẳng có độ dài như sau: a) AB = 8 cm; CD = 9 cm. Ta có: b) EF = 6 dm, GH = 3 dm Ta có: c) MN = 18 cm; PQ = 6dm Ta có:
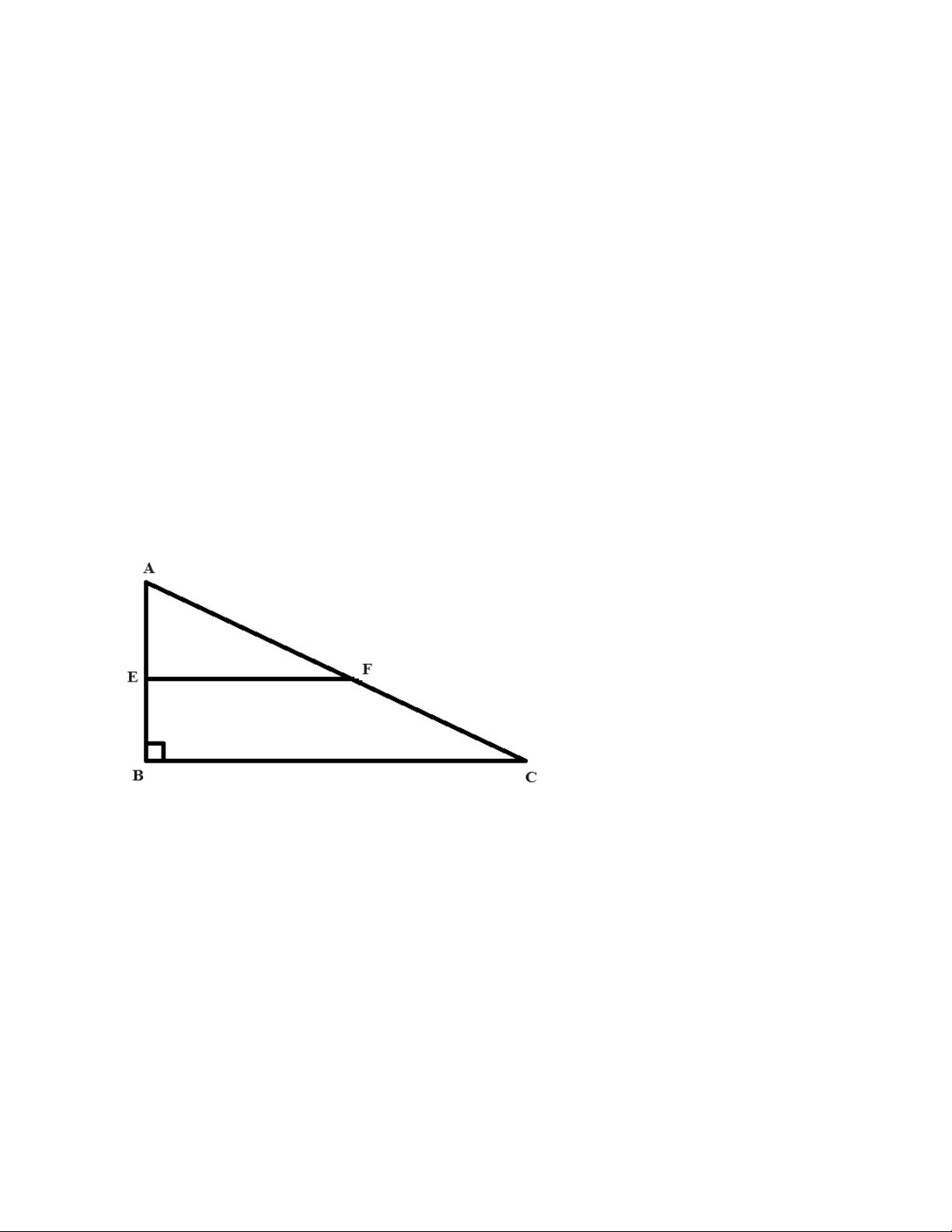
Bài 2: Tìm giá trị của đoạn EB trên hình vẽ sau, biết Tam giác ABC là tam giác vuông tại B, có: AC = 10 dm,
AE = 3 dm, AF = 4 dm và EF song song với BC Lời giải: Thấy: AF + FC = AC thì 4 + FC = 10 FC = 10 - 4 = 6 (dm)
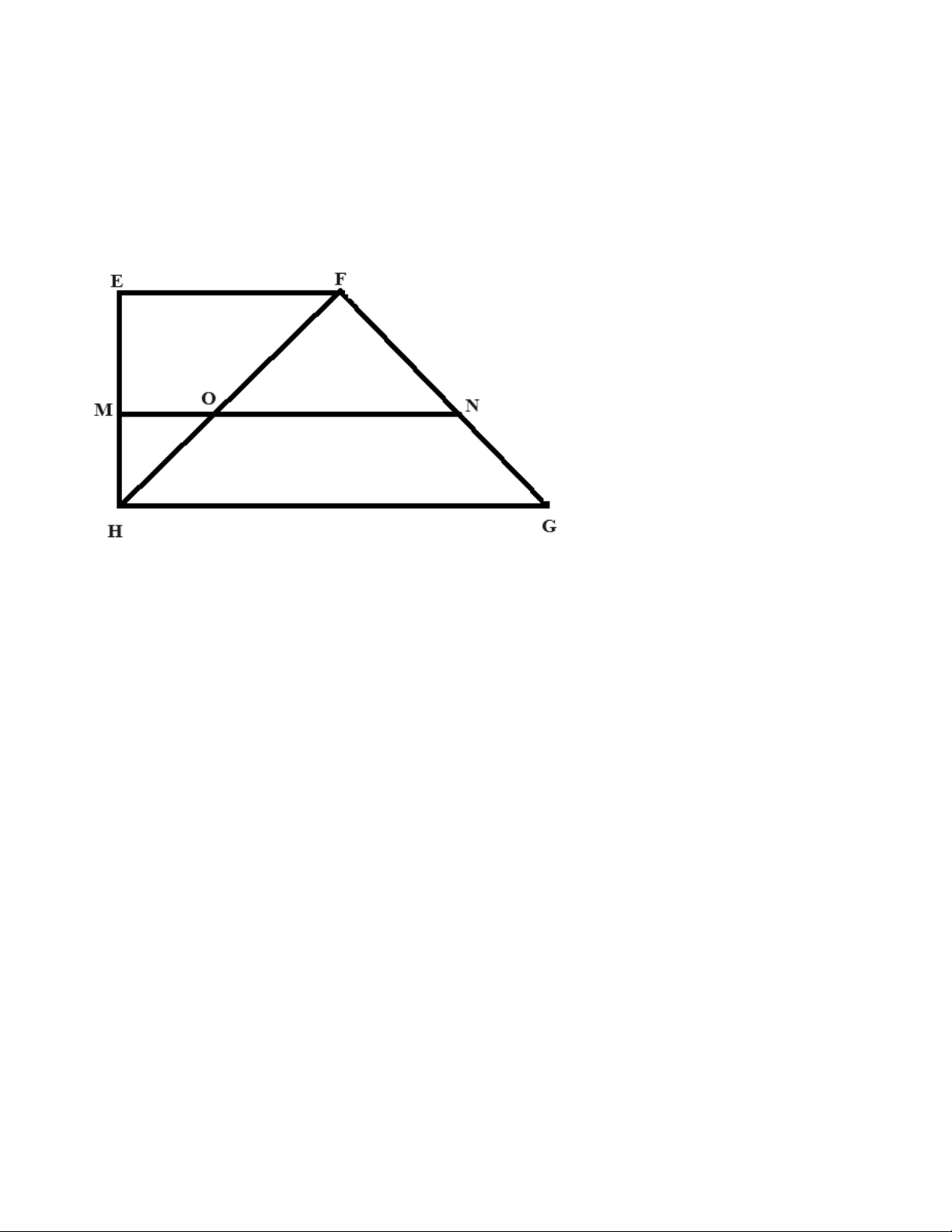
Ta có EF song song với BC thì có các tỷ số như sau: 4 x BE = 3 x 6 4 x BE = 18 BE = 4,5 (dm) Đáp số: 4,5 dm Bài 3: Cho hình vẽ sau:
trong đó MN song song HG, FN = 12 cm, HM = 18 cm, FG= 36 cm. Độ dài EH bằng bao nhiêu? Lời giải:
Ta có: MN song song với HG thì các tỷ số như sau: Thay các số liệu vào: 2 x EH = 18 x 3 2 x EH = 54 EH = 27 (cm) Đáp số: 27 cm
4. Lưu ý khi làm bài tập vè định lý Talet trong hình tam giác, hình thang
Khi học về định lý Talet trong tam giác và hình thang, bạn cần biết rõ về hình thang là gì. Hình thang là một
loại tứ giác có hai đoạn đối diện song song gọi là đáy, và các cạnh còn lại được gọi là cạnh bên. Dưới đây là
một số đặc điểm chính của hình thang:
Đáy: Hình thang có hai đoạn đối diện gọi là đáy. Đáy này có thể là hai đoạn thẳng hoàn toàn song song
hoặc có thể là hai đoạn thẳng không hoàn toàn song song.
Cạnh bên: Các cạnh của hình thang là các đoạn thẳng khác không nằm giữa đáy. Trong hình thang, các
cạnh bên không bằng nhau đối diện nhau và có thể có chiều dài khác nhau.
Đỉnh: Các đỉnh của hình thang là các điểm nối các đoạn thẳng với nhau. Hình thang có hai đỉnh trên đáy và hai đỉnh dưới đáy.
Góc trong: Hình thang có bốn góc, và các góc này nằm trong hình thang. Các góc trong của hình thang
không nhất thiết phải bằng nhau.
Góc ngoài: Hình thang cũng có bốn góc ngoài, là các góc được hình thành bên ngoài hình thang khi kéo các đoạn thẳng bên ra.
Định lý Talet trong tam giác và hình thang liên quan đến việc xác định tỉ lệ giữa các đoạn thẳng khi một
đường thẳng cắt chúng một cách đặc biệt. Hình thang là một ví dụ thường được sử dụng để áp dụng định lý Talet trong hình học.




