Đồ thị hàm hợp chứa mũ – lôgarit

Tài liệu gồm 17 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Đồ thị hàm hợp chứa mũ – lôgarit; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

17 trang 7 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
ĐỒ THỊ HÀM HỢP CHỨA MŨ – LÔGARIT
Câu 1. Cho hàm số
y f x liên tục trên
và có đồ thị hàm số
y f x
được mô tả như hình vẽ bên. Phương trình
2
2 1 2 ln 1f x x x
có bao
nhiêu nghiệm phân biệt biết rằng
0 1f và
y f x là hàm đa thức?
A. 2 B. 4 C. 0 D. 3
Lời giải
Chọn D
Ta xét
2
2 2ln 1y f x x x
2
2
2 2 2
1
y x f x x
x
1
2 2
1
y x f t
t
.
Trong đó
2
2t x x
và ta có
1
0
1
y f t
t
. Ta chú ý với 1x thì
2
1 1 1t x
.
Do vậy
2
1
2
2
0
0 2
0 1 2 2 1
2 2
3 1
x
x
t x x
y t x x x
t x x
x

. Ta có BBT:
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 2 TÀI LIỆU ÔN THU THPT QUỐC GIA
Chú ý rằng
0 1
f
còn
2
0
2 0 0 2 1
f f f x dx f S f S
với
S
là diện tích
phần tô đậm. Dễ thấy
0,75 1
S
còn
2ln 3 1,099 2 2ln 3 0,099 1
f S
.
Vì vậy đường thẳng
1
y
cắt đồ thị hàm số
2
2 2ln 1
y f x x x
tại 3 điểm phân biệt.
Câu 2. Cho hàm số
y f x
như hình vẽ. Hỏi hàm số
2
1
2
f x
y f e f x f x
có tất cả bao nhiêu điểm cực trị ?
A.
5
. B.
6
. C.
3
. D.
9
.
Lời giải
Chọn B
2
1
' ' . ' . 1
2
f x f x
y f e f x f x f x e f x
2
' 0
' 0 1 0 1
1
' 0 2
2
f x
f x
f x
y e f x
f e f x f x
.Cho
1
' 0
1
x
f x
x
.
Đặt
t f x
. Giải
1 : 1 0.
t
e t
Xét
1 ' 1
t t
h t e t h t e
.
' 0 0
h t t
.
BBT:
Do đó
0
h t t
h t
tiếp xúc với trục
Ox
. Pt
1
có nghiệm kép, nghiệm này không là cực
trị.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Giải
2
:
2
2
1
1 3
2
1
1 4
2
t
t
e t t
e t t
.
Giải
3 :
2
1
1 0.
2
t
e t t
Xét
2
1
1 ' 1 0
2
t t
k t e t t k t e t t
.
' 0 0
k t t
BBT:
Pt
3
có nghiệm
0 0
t f x
. Pt
3
có 3 nghiệm phân biệt
1 2 3
1, 0;1 , 1
x x x
.
Giải
4 :
2
1
1 0.
2
t
e t t
Xét
2
1
1 ' 1 0
2
t t
l t e t t l t e t t
.
' 0 0
l t t
.
BBT:
Nhận xét:
2
1
1
2
t
l t e t t
có
2 . 3 0
l l
0
l t
có 1 nghiệm
1
3; 2
t t
1
f x t
có 1 nghiệm Pt
4
có 1 nghiệm.
Vậy
' 0
g x
có 6 nghiệm phân biệt tức hàm số có 6 điểm cực trị.
Câu 3. Cho hàm số bậc bốn
f x
có đồ thị như hình vẽ sau. Có bao nhiêu
giá trị nguyên của
m
[ 2021;2021]
để phương trình sau có hai nghiệm dương phân biệt
3
2
( )
log [ ( ) ] ( )
f x
x f x mx mx f x
mx
A.
2019
. B.
2021
. C.
2020
. D.
2022
.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 4 TÀI LIỆU ÔN THU THPT QUỐC GIA
Lời giải
Chọn A
Từ đồ thị hàm số suy ra
f x
có ba điểm cực trị là
1;0;1
. Do đó
2 4 2
( ) 1 ( )
4 2
a a
f x ax x f x x x b
.
Mặt khác, vì đồ thị hàm số
( )
f x
đi qua hai điểm
(0;4), (1;3)
nên
4 2
( ) 2 4 3,
f x x x x
.
Điều kiện
2
( )
0 suy ra 0
f x
m
mx
.
3
2
( )
log [ ( ) ] ( )
f x
x f x mx mx f x
mx
2 2 2
log ( ) ( ) ( ) log
f x f x xf x mx mx x mx
.
2 2
log ( 1) ( ) 1 . ( ) log ( 1) 1 .
x f x x f x x mx x mx
(*)
(Do
1 0
x
).
Xét hàm số ( ) log
g t t t
với
0
t
. Ta có
1
( ) 1 0
.ln10
g t
t
với
0
t
.
Từ (*) ta có
2
4 2
2
2 2
( ) 2 4 2
( 1) ( ) ( 1) 6
f x x x
x f x x mx m x
x x x
.
Đặt
2
2 2,
u x
x
khi đó
2
6, 2 2.
m u u
Ứng với mỗi giá trị của
2 2
u
cho ta hai giá trị dương của
x
nên yêu cầu bài toán đưa về
điều kiện là tìm
m
để phương trình
2
6
m u
có đúng một nghiệm
2 2.
u
Đặt
2
( ) 6
h u u
với
2 2.
u
Bảng biến thiên của hàm số
( )
h u
.
Từ bảng biến thiên suy ra
2
m
thỏa yêu cầu bài toán.
Do
m
và
[ 2021;2021]
m
nên
3; 4; ; 2021
m
.
Vậy có 2019 giá trị của
m
thỏa mãn đề bài.
Câu 4. Cho hàm số
y f x
có đạo hàm trên
và có bảng biến thiên sau:
Có bao nhiêu giá trị nguyên của
m
để phương trình sau có đúng 2 nghiệm phân biệt:
4
2
2
2 log 4 5
f x
f x
f f x m
x
A.
2019
. B.
2021
. C.
2020
. D.
2022
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
Chọn A
Xét hàm số
4
2
2
2 log 4 5
f x
f x
y g x f f xx
TXĐ:
4
2
2
2 4
4
2 ln 2.
4 5 ln 2
.
f x
f x
f x f x
f x
g
f x
f x
x f x
f x
4
2
2
5
.
2
2
2 . . 2 ln 2.
4 ln 2
f x
f x
f
x
x
f x f x
f x
f xf
, 1;2
2
0 , 2;3
0
1, 2, 3
x
f x
g x x
f x
x x x
Bảng biến thiên
Đồ thị minh họa :
Từ bảng biến thiên, hình vẽ và
m
ta có :
16
34
m
m
Câu 5. Cho hàm số
y f x
có bảng biến thiên như hình dưới.
Có bao nhiêu số nguyên dương
m
để phương trình
6 4
log 2 log
f x m f x
có 4 nghiệm
phân biệt.
12
0
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 6 TÀI LIỆU ÔN THU THPT QUỐC GIA
A.
1.
B.
3.
C.
16.
D.
15.
Lời giải
Chọn A
Đặt
6 4
4
log 2 log 2.4 6 6 2.4 . *
2 6
t
t t t t
t
f x
t f x m f x m m
f x m
Xét hàm số
6 2.4
t t
g t có
0 3
2
3 ln16 ln16
' 0 6 ln 6 4 ln16 ln .
2 ln6 ln 6
t
t t
g t t
Có
1 3
2
0 log 2.
g t t Hàm số
g t
có bảng biến thiên như hình vẽ.
Nếu phương trình
*
có 1 nghiệm
t
thì phương trình đã cho không thể có 4 nghiệm
Nếu phương trình
*
có 2 nghiệm
3 4
t t
thì khi đó dựa vào bảng bt của
g t
có
3 4 0 1
;
t t t t
Do đó phương trình
4
4
t
f x
có 3 nghiệm thực phân biệt.
Vậy
3
4
t
ycbt pt f x
phải có nghiệm duy nhất .Hay
3
;1
t

.
Mà
1 2
g
. Khi đó
2 0
m
thì
*
có 2 nghiệm
3 4
,
t t
thỏa
3
;1
t

.
Vậy
1
m
là giá trị nguyên duy nhất thỏa mãn.
Câu 6. Cho hàm số
y f x
có đồ thị như hình vẽ
Biết
3 10
f
. Có bao nhiêu giá trị nguyên của
m
để phương trình
2
x
f f f e m
có bốn nghiệm .
A.
6
. B.
7
. C.
5
. D.
10
.
Lời giải
Chọn A
Đặt 0
x x x
e t t e x e
làm hàm số luôn đồng biến .
Hàm số
y f x
có hai cực trị tại
1 2
1; 1
x x
tương ứng tại đó
1 2
1; 3
y y
.
Từ đó ta có bảng sau.
0
0
-2,014
-2
+
0
t
1
t
0
1
-∞
-∞
g(t)
g'(t)
t
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
Vậy phương trình
2
x
f f f e m
có bốn nghiệm 10 3m .
Vậy có
6
giá trị nguyên của
m
thỏa mãn .
Câu 7. Cho hàm số
f x liên tục trên
có đồ thị
y f x như hình vẽ
dưới đây.
Khi đó, số nghiệm thực của phương trình
2 1
x
f f f
là
A. 8 . B. 5. C. 3 . D. 4 .
Lời giải
Chọn A
Theo đồ thị, ta có:
2 2
2 1
2 1
x
x
x
f f
f f f
f f
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 8 TÀI LIỆU ÔN THU THPT QUỐC GIA
*
2
2 1;2
2 1;0 ( )
2 2
log
2 1 2 2; 1 ( )
0
2 1
2 1
2 2 ( )
x
x
x
x x
x
x
x
a
b ptvn
f
x a
f f c ptvn
x
f
ptvn
*
2
2
2
2 2 ( )
2 2; 1 ( )
2
2 0;1 2 0;1
log
2 2 2 2 1;2 2 1;2 log
log
2 1;2 2 1;2
2
2 1;0 ( )
2 2; 1 ( )
x
x
x
x x
x x x x
x x
x
x
x
d ptvn
e ptvn
f a
f f
x f
f f f b g g x g
x h
h h
f c
k ptvn
m ptvn
Từ đồ thị, ta thấy
a f g h
. Do đó, phương trình có
5
nghiệm phân biệt.
Câu 8. Cho hàm số
( )
y f x
có đồ thị biểu diễn như hình vẽ và đồ thị đạo hàm không tiếp xúc với
trục hoành. Khi ấy, hãy tính số nghiệm của phương trình dưới đây
( ) ( )
( ).2 2 ( ).3 ( ) 2 ( )
f x f x
f x f x f x f x
A.
6
. B.
7
. C.
8
. D.
5
.
Lời giải
Chọn B
Từ đồ thị hàm số suy ra
( ) 0
f x
có các nghiệm
1 2 3 4
x x x x
và
( ) 0
f x
có các nghiệm
là
1 2 3 4
a a a a
và phương trình
f x
cũng chỉ có 4 nghiệm này ( vì đồ thị đạo hàm
không tiếp xúc với trục hoành). Từ đồ thị ta có
4 4
a x
.
( ) ( )
( ).2 2 ( ).3 ( ) 2 ( )
f x f x
f x f x f x f x
( ) ( )
( ) 2 1 2 ( ) 3 1 0
f x f x
f x f x
(1).
a
3
a
2
a
1
a
4
x
4
x
3
x
2
x
1
y
x
O
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
Dễ nhận thấy
1 2 3 4 1 2 3
, , , , , ,
x x x x a a a
là các nghiệm của phương trình (1).
Ta chứng minh rằng phương trình (1) chỉ có 7 nghiệm phân biệt
1 2 3 4 1 2 3
, , , , , ,
x x x x a a a
.
Thật vậy:
Trường hợp 1: Nếu
1
x x
thì
( ) ( )
( ) ( )
( ) 0 3 1 3 1 0
(1) 0
( ) 0
2 1 2 1 0
f x f x
f x f x
f x
VT
f x
Trường hợp 2: Nếu
1 1
x x a
thì
( ) ( )
( ) ( )
( ) 0 3 1 3 1 0
(1) 0
( ) 0
2 1 2 1 0
f x f x
f x f x
f x
VT
f x
.
Thực hiện tương tự đối với các khoảng còn lại ta thấy VT(1) luôn âm hoặc luôn dương trên các
khoảng đó. Vậy phương trình đã cho có 7 nghiệm.
Câu 9. Cho hàm số
( )
y f x
có đạo hàm liên tục trên
. Hàm số
y f x
có đồ thị như hình sau đây
Hàm số
2
1
2ln
2
g x f x x
đồng biến trên khoảng
A.
4
;1
5
. B.
6
;2
5
. C.
1
0;
2
. D.
3 7
;
5 10
.
Lời giải
Chọn C
Với
0,
x
có
2 2 2
1 1 1
2 . 2. 0 . 1 *
2 2
g x x f x x f x
x
Đặt
2 2
1 1
.
2 2
t x x t
Khi đó
*
trở thành
1 2
1
2 2 1
t f t f t
t
.
Vẽ
2
( ) :
2 1
C y
t
trên cùng hệ trục.
Dễ thấy trên
1
0;
2
thì đồ thị
f t
nằm bên trên đồ thị
2
2 1
t
nên suy ra
2
2 1
f t
t
trên
x
y
1,5
0,5
0,5 2
3
-1
2
1
-2
-1
O
1
x
y
1,5
0,5
0,5 2
3
-1
2
1
-2
-2 -1
O
1
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 10 TÀI LIỆU ÔN THU THPT QUỐC GIA
1
0;
2
tức
2
0
2 1
f t
t
trên
1
0;
2
.
Suy ra
1
'( ) 0, 0;
2
g x x
tức
( )
g x
đồng biến trên khoảng
1
0;
2
.
Câu 10. Cho hàm số
( )
f x
liên tục trên
R
và có đồ thị
( ) : '( )
C y f x
như hình vẽ bên. Hàm số
2
2 2 9
( ) 9 1 9
x
y g x f x x e
đồng biến trên từng khoảng
; , ;
a b c d
và
; ;a b c d
. Gọi
max max( )
m b a d c
. Khẳng định đúng là:
A.
6
m
. B.
3
m
. C.
2 5
m . D.
2 3 5
m
.
Lời giải
Chọn B
Ta có:
2
2 2 9
( ) 9 1 9
x
y g x f x x e
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
2 2
2
2
2 9 9 2
2 2 2
2 9 2
2 2
2 9
2
'( ) ' 9 . . 1 9
9 9 9
'( ) ' 9 . 9
9 9
'( ) ' 9 .
9
x x
x
x
x x x
y g x f x e e x
x x x
x x
g x f x e x
x x
x
g x f x x e
x
Cho
2
2 9
2
'( ) 0 ' 9 . 0
9
x
x
g x f x x e
x
2
2
2 9
2 2 9
2
0
0
1
' 9 0
' 9 9 . ,(*)
9
x
x
x
x
f x e
f x x e
x
Ở phương trình (*), ta đặt:
2
9
t x
thì phương trình thành:
'( )
t
f t te
(*)
Phương trình (*) cũng chính là phương trình hoành độ giao điểm của hai đồ thị hàm số
'( )
y f t
và
t
y te
. Từ đó, dựa vào hình vẽ ta suy ra được các nghiệm đó là:
2 2
2 2
9 ; 3 9 ; 3
; 3
; 3;3
2
9 2 9 2
x a x a
t a
x
t
x x
 

Đến đây ta nhận thấy với
; 3
a

thì phương trình
2
9
x a
vô nghiệm nên suy ra:
2
9 2 5
x x
Từ đó ta có bàng xét dấu đạo hàm của hàm số
( )
y g x
như sau:
Dựa vào BBT trên, ta kết luận hàm số
( )
y g x
đồng biến trên từng khoảng
3; 5 , 0; 5
Suy ra
max max( ) max 5 3 max 5 0 3
m b a d c
.
Câu 11. Cho hàm số
f x
xác định, liên tục trên
và
'
f x
có bảng xét
dấu như sau
Số điểm cực trị của hàm số
2
2
x x
f e
là
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn D
Đặt
2
2
x x
g x f e
Vì
f x
xác định trên
suy ra
g x
xác định trên
.
Hơn nữa
2
2
2 2
,
x x x x
g x f e f e g x x
.
Suy ra
g x
là hàm số chẵn, đồ thị hàm số
g x
đối xứng qua trục
Oy
.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 12 TÀI LIỆU ÔN THU THPT QUỐC GIA
Xét
0
x
2
2
x x
g x f e
2 2
2 2
2 1 . .
x x x x
g x x e f e
2 2 2
2 2 2
2 1 0 2 1 0
0
0 1 0,
x x x x x x
x x
g x
f e e vì e x
2
1
2 1 0
2
2 0
2 0
x
x
x x
x vì x
.
Nếu
2
x
thì
2
2 0
x x
thì
2
2
1
x x
e
suy ra
2
2
0
x x
f e
.
Nếu
0 2
x
thì
2
2 0
x x
thì
2
2
0 1
x x
e
suy ra
2
2
0
x x
f e
.
Từ đó ta có bảng xét dấu
g x
trên
0;

.
Suy ra
g x
có hai điểm cực trị dương.
Do
g x
là hàm số chẵn, liên tục trên
suy ra
g x
có 5 điểm cực trị trên
.
Câu 12. Cho hàm số
y f x
là hàm số chẵn trên tập số thực
và có đồ thị như hình vẽ. Biết rằng
tồn tại các giá trị của tham số
m
để phương trình
2 2
2
3.3 4 3 3 3 3 0
f x f x
m f x m
có đúng 7 nghiệm thực phân biệt. Tổng lập phương các giá trị đó của
m
là
A.
8
. B. 1. C.
7
. D. 7.
Lời giải
Chọn B
Từ đồ thị hàm số
y f x
ta suy ra đồ thị hàm số
f x
như sau:
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
Xét phương trình
2 2
2
3.3 4 3 3 3 3 0
f x f x
m f x m
(1)
Đặt
, 0
t f x t
, phương trình (1) trở thành
2 2
2
3.3 4 3 3 3 3 0
t t
m t m
(2)
Vì
f x
là hàm số chẵn nên
,f x f x x
. Do đó, nếu
0
x
là một nghiệm của
phương trình
2 2
2
3.3 4 3 3 3 3 0
f x f x
m f x m
(1) thì
0
x
cùng là nghiệm của (1).
Nếu phương trình (1) có đúng 7 nghiệm thì (1) có nghiệm
0
0
x
mà
0 0
f
nên phương
trình (1) trở thành
0 0 2
1
3.3 4.0 3 3 3 3 0 3 3 6 0
2.
m
m m m m
m
Đảo lại:
* Với
1
m
: Phương trình (1) trở thành
2 2
2
3.3 4 6 3 3 0
t t
t
2
2
2
2
2
2
2 2
2 3 2 3
3
3.3 2 3 2 3 (3)
3
2 3 2 3 3.3 2 3 2 3 (4)
3
3
t
t
t
t
t t t
t t t
t t t t t t
Xét (3):
2
2
(3) 3. 3 1 2 3 0
t
t t t
mà
2
0
3 3 1
t
và
2 2
3
t t t t
với mọi
0
t
nên
(3) 0
t
.
Xét (4):
2
2
2
2
2
2 2
2 3 4 3
9 3
(4) 3.3 2 3 2 3
3
2 3 2 3 2 3 2 3
t
t
t t t
t t t
t t t t t t
(5)
Từ (3) và (5) ta suy ra
2
2
3
3.3 4 6
3
t
t
t
hay
2
2
3
3.3 4 6 0
3
t
t
t
.
Xét hàm số
2
2
3
3.3 4 6
3
t
t
h x t
, ta thấy
2 2
6ln 3. . 3 3 4
t t
h x t
;
2 2 2 2
2
6ln3. 3 3 2 .ln3. 3 3 0, 0
t t t t
h x t t

nên
h t
đồng biến mà
0 . 1 0
h h
nên phương trình
0
h t
có duy nhất một nghiệm
0
0;1
t t
. Từ đó suy ra phương trình
0
h t
có nhiều nhất hai nghiệm mà
0 1 0
h h
nên
h t
có đúng hai nghiệm là
0; 1
t t
.
Dựa vào đồ thị ta thấy: với
0
t
thì phương trình (1) có 3 nghiệm
x
, với
1
t
thì phương trình
(1) có 4 nghiệm
x
. Tổng cộng 7 nghiệm, do đó
1
m
thoả mãn.
* Với
2
m
: Phương trình (1) trở thành
2
2 2 2 2
2
2
3 1 0
3.3 2 4 3 3 3 0 3 3 1 8 .3 0 0
0
t
t t t t
t t t
t
.
Trường hợp này phương trình đã cho có 3 nghiệm, giá trị
2
m
loại.
Vậy
1
m
là giá trị cần tìm.
Câu 13.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 14 TÀI LIỆU ÔN THU THPT QUỐC GIA
Cho hàm số
y f x
có đạo hàm trên
R
và đồ thị của hàm số dưới đây là của
y f x
Biết rằng
2
A B
x x
. Tìm số điểm cực trị của hàm
g x
h x e
với
2019 2018 ... ... 2019 2020g x f x f x f x f x f x
A.
1
. B.
2020
. C.
2
. D.
0
.
Lời giải
Chọn D
Gọi
,a b
lần lượt là các nghiệm của phương trình
' 0f x
với
2b a
Khi ấy ta có:
2f x k x a x b k x a x a
.
Ta có:
g x
h x e
. Số điểm cực trị của hàm
g x
h x e
bằng chính số nghiệm của phương
trình
0 . 0 0
g x
h x g x e g x
2019 2018 ... ... 2019 2020 0f x f x f x f x f x
. 2019 2021 ... . 2 .. . 2020 2018 0k x a x a k x a x a k x a x a
. 2020 1 2020 1 ... . 1 1 1 1k x a x a k x a x a
... . 2019 1 2019 1 0k x a x a
2 2 2
. 2020 1 ... . 1 1 ... . 2019 1 0k x a k x a k x a
2 2 2
4040
. 2020 ... 1 ... 2019 ( ... ) 0
k
k x a k x a k x a k k
2 2 2
. 2020 ... 1 ... 2019 4040 0k x a k x a k x a k
2 2
2
. 2.2020 2020 ... . 2. 1k x a x a k x a x a
2
2
... . 2.2019 2019 4040 0k x a x a k
2
4040 2. 2020 2019 ... 1 0 ... 2019x a x a
2
2 2 2 2
2020 40401 02019 ... 0 1 ... 2019
2019
2
1
2 2
4040 2. 2020 4040 2020 0 (*)
2.
k
x x a xa
2
2019
2
1
2
*
4040 4.4040 2020 4040 02.
k
x
nên suy ra (*) vô nghiệm
Từ đó suy ra hàm số
g x
h x e
không có điểm cực trị.
Câu 14. Cho hàm số
y f x
có đạo hàm trên
và hàm
y f x
có đồ
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
thị như hình vẽ.
Trên đoạn
3;4
hàm số
2
1 ln 8 16
2
x
g x f x x
có bao nhiêu điểm cực trị?
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn C
Ta có:
2
1 ln 8 16
2
x
g x f x x
2
1 2 8 1 2
1 1
2 2 8 16 2 2 4
x x x
g x f f
x x x
.
1 2
0 1 0
2 2 4
x
g x f
x
.(1)
Đặt
1
1 ;3 , 3;4
2 2
x
t x
, (1) thành:
1 2 2
2 2 2 4 1
f t f t
t t
.
Ta thấy hàm
2
1
u t
t
nghịch biến trên
1
;3
2
, như vậy đồ thị hàm số
f t
và đồ thị hàm
số
2
1
u t
t
trên
1
;3
2
trên cùng một hệ trục như sau:
Do đó trên
1
;3
2
phương trình
0 2
2
1 0
1
1;3 2 1 0;4
t x
f t t x
t
t a x a
.
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Trang 16 TÀI LIỆU ÔN THU THPT QUỐC GIA
Như vậy
0
g x
có các nghiệm đơn
2
0
2 1
x
x
x a
trên đoạn
3;4
, do đó hàm số
g x
có
3
điểm cực trị trên đoạn
3;4
.
Câu 15. Cho hàm số
y f x
với đạo hàm
f x
có đồ thị như hình vẽ.
Trên đoạn
0;3
. Hàm số
2
2 1
1 2020
x
g x f x e
có mấy điểm cực trị
A.
7
. B.
4
. C.
8
. D.
5
.
Lời giải
Chọn B
Xét hàm số
2
2 1
1 2020
x
g x f x e
có
2
2 1
2 1 2
x
g x xf x xe
2
2 1
2 1
x
g x x f x e
2
2
2 1
2 1
0
0
1 0 *
* 1
x
x
x
g x
f x e
f x e
1
Đặt
2
1
x t
với
0;3 1;8
x t
Ta có :
2
1
x t
Phương trình
1
t
f t e
2
Xét hàm số
t
y e
có đồ thị trên cùng hệ tọa độ với đồ thị hàm số
f t
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
Từ đồ thị ta thấy phương trình
2
có ba nghiệm
1;0
0;1
1;2
t a
t b
t c
+) Với
2 2
1 1
t a x a x a
có một nghiệm
0;3
+) Với
2 2
1 1
t b x b x b
có một nghiệm
0;3
+) Với
2 2
1 1
t c x c x c
có một nghiệm
0;3
Vậy phương trình
0
g x
có tất cả bốn nghiệm đơn phân biệt
0;3
nên hàm số
g x
có
bốn điểm cực trị.
_______________ TOANMATH.com _______________
| 1/17
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
ĐỒ THỊ HÀM HỢP CHỨA MŨ – LÔGARIT Câu 1.
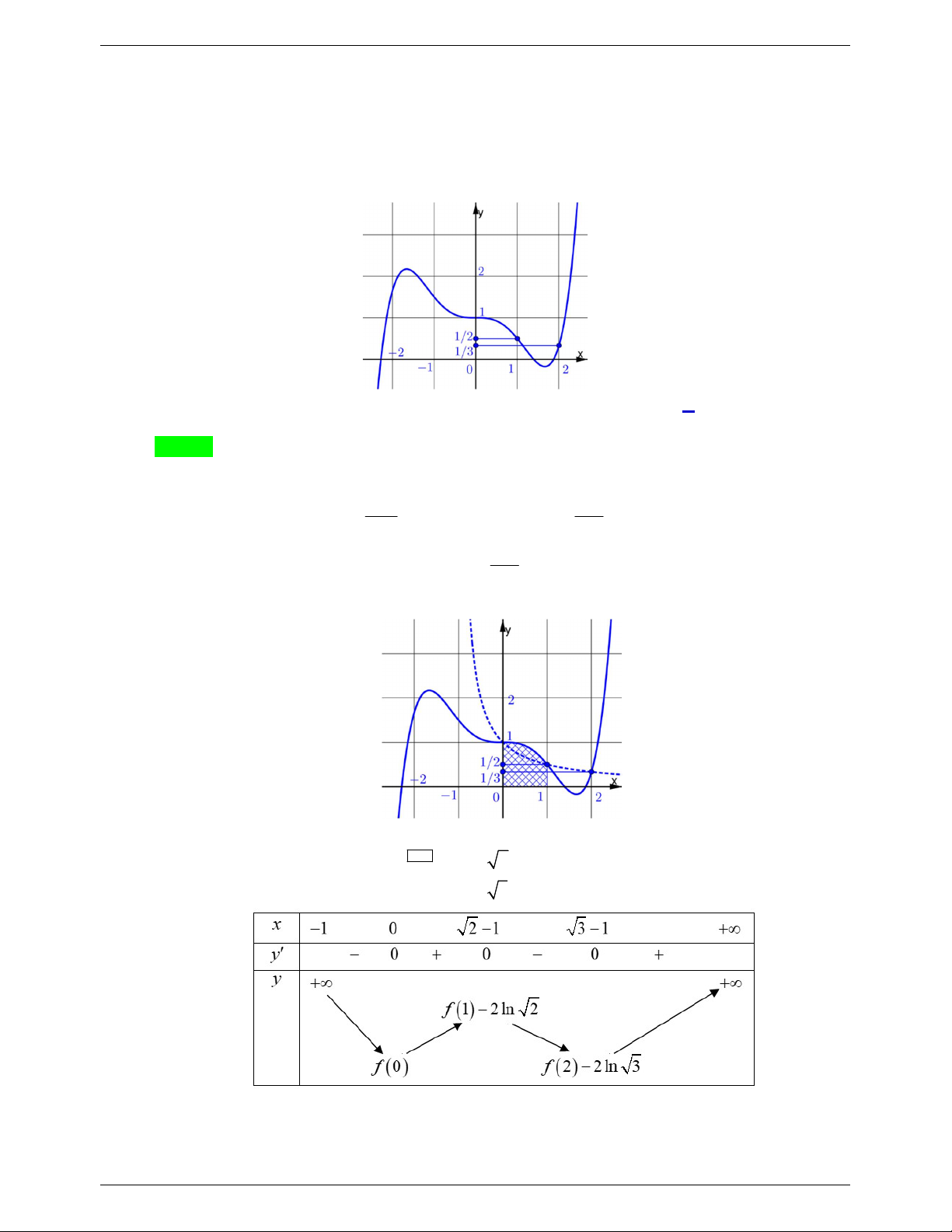
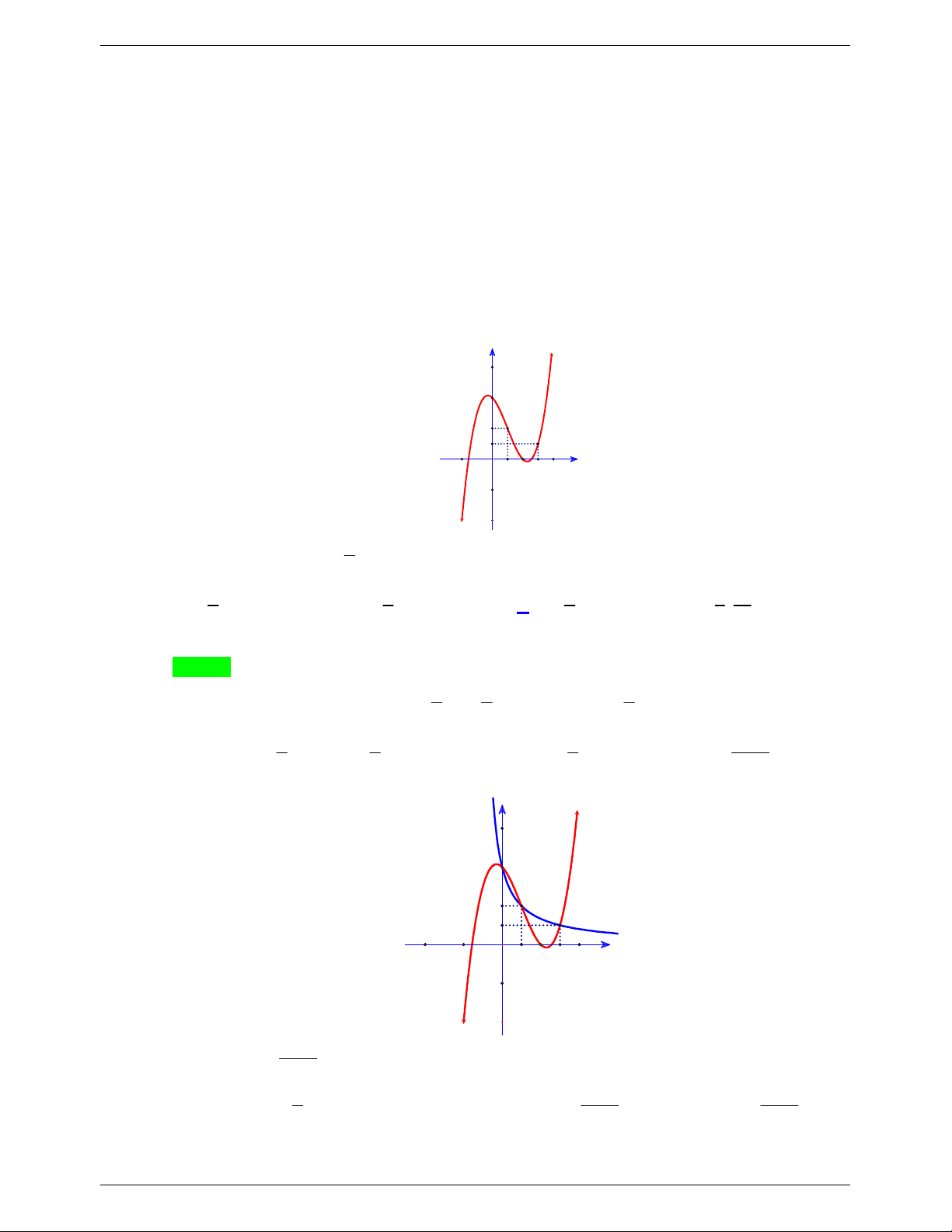
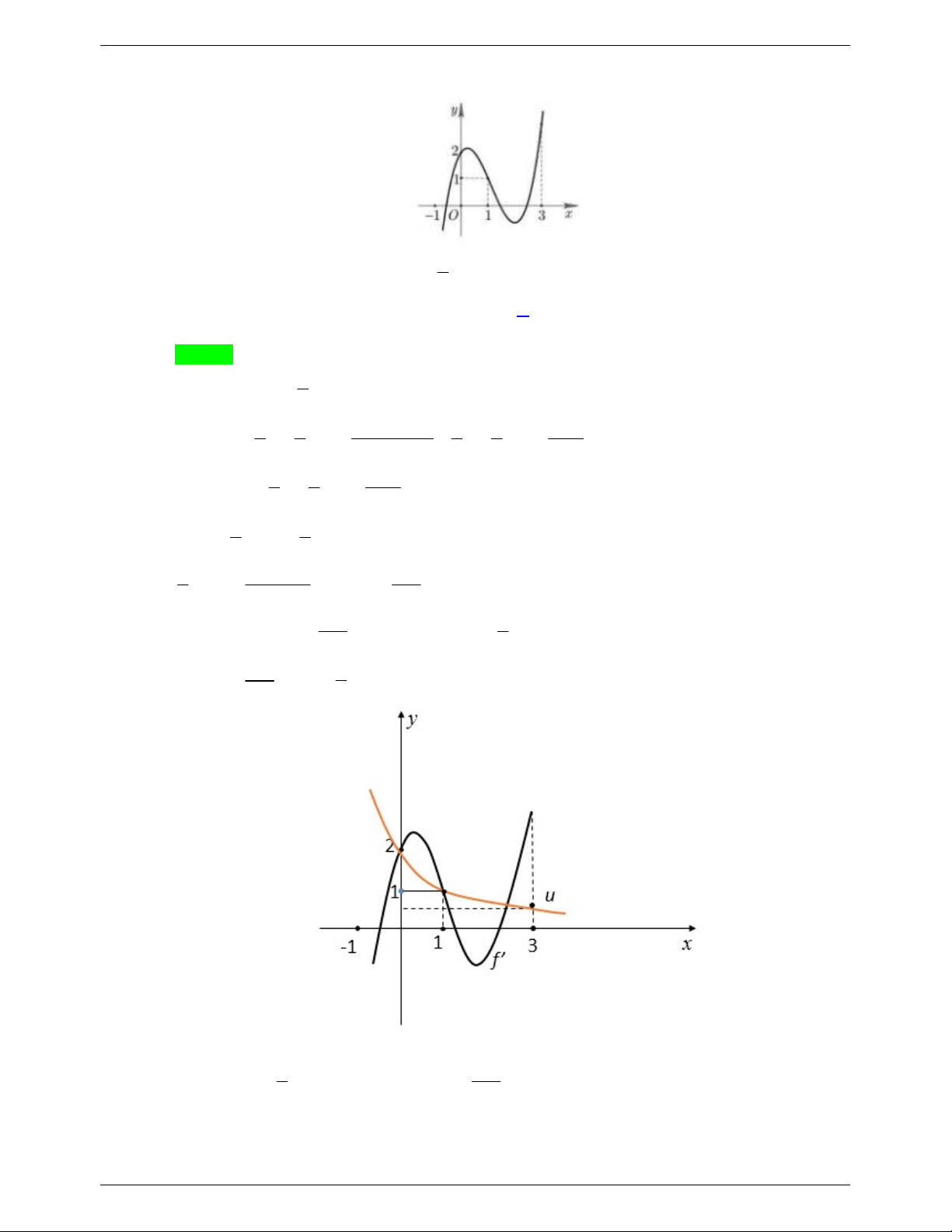
Cho hàm số y  f  x liên tục trên  và có đồ thị hàm số
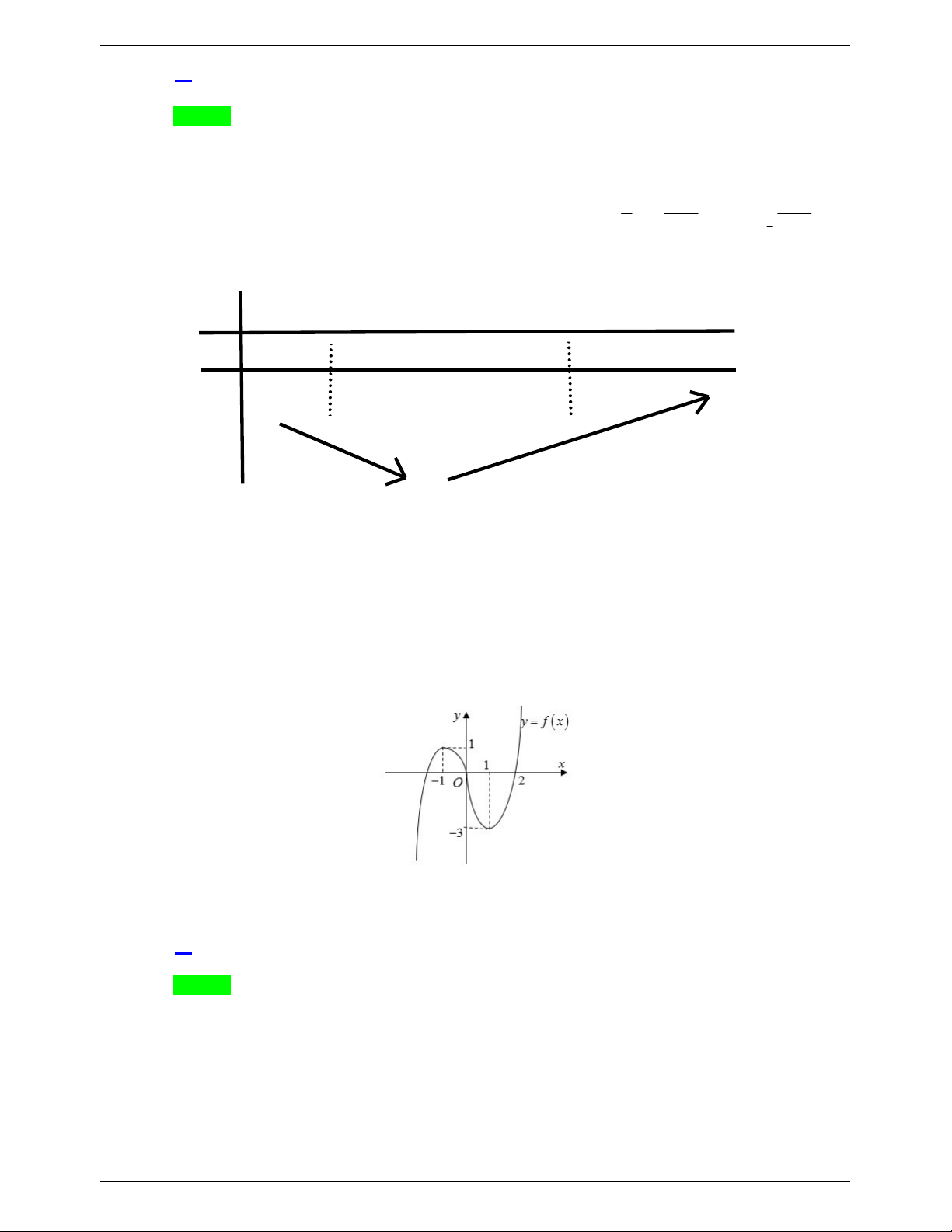
y  f  x được mô tả như hình vẽ bên. Phương trình f  2
x  2x  1 2ln x   1 có bao
nhiêu nghiệm phân biệt biết rằng f 0  1 và y  f  x là hàm đa thức? A. 2 B. 4 C. 0 D. 3 Lời giải Chọn D Ta xét y  f  2
x  2x  2ln  x   1   
y  2x  2 f  2 2 x  2x 
 y   x   f t 1 2 2    . x 1  t 1 Trong đó 2
t  x  2x và ta có y   f t 1 0 
. Ta chú ý với x  1 thì t 1 t   x  2 1 1  1  . 2 t  0  x  2x x  0   Do vậy 2 x 1
y  0  t  1  x  2x   x  2 1   . Ta có BBT:  2 t 2 x 2x     x  3 1  
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC 2
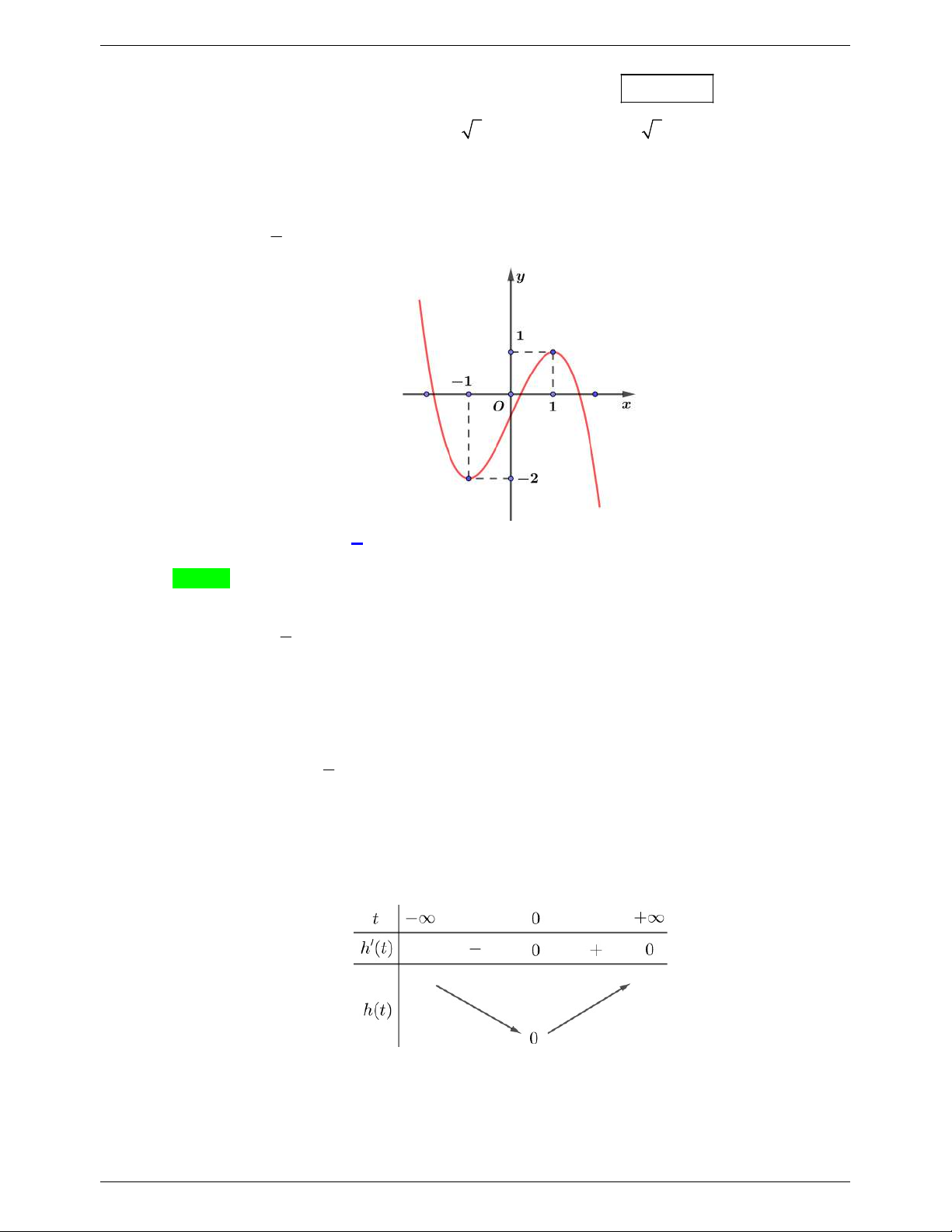
Chú ý rằng f 0  1 còn f 2  f 0  f 
 xdx  f 0 S  f 2  S 1 với S là diện tích 0
phần tô đậm. Dễ thấy 0,75  S  1 còn 2ln 3  1,099  f 2  2ln 3  S  0,099 1.
Vì vậy đường thẳng y 1 cắt đồ thị hàm số y  f  2
x  2x  2ln x  
1 tại 3 điểm phân biệt. Câu 2.
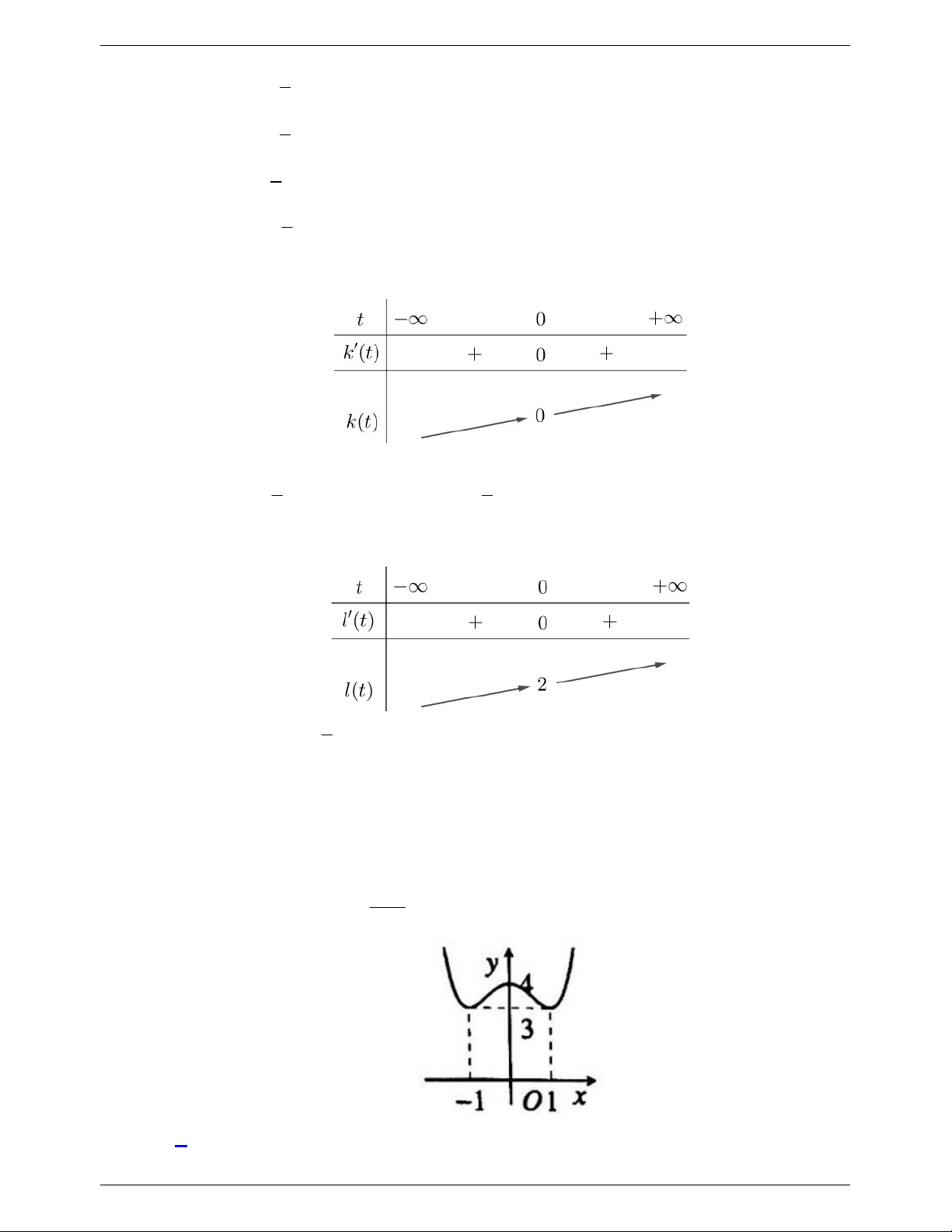
Cho hàm số y  f x như hình vẽ. Hỏi hàm số  f x 1    y  f e  
 f x2  f x có tất cả bao nhiêu điểm cực trị ? 2    A. 5 . B. 6 . C. 3 . D. 9 . Lời giải Chọn B  f x 1  y '  f ' e  
 f x2  f x .f 'x fx .e  f x 1 2        f 'x  0  x  f  x y '  0  e
 f  x 1 0   1 .Cho f x 1 '  0  .   x  1   f x 1  f ' e   
 f x2  f x  0 2   2 
Đặt t  f  x . Giải   1 : t e  t 1  0. Xét   t   1 '  t h t e t h t  e 1 .
h 't  0  t  0 . BBT: Do đó ht  0 t
  ht tiếp xúc với trục Ox . Pt  
1 có nghiệm kép, nghiệm này không là cực trị. Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC  t 1 2 e  t  t  1 3  Giải 2 : 2  .  t 1 2 e  t  t  1 4  2 t 1 Giải 3 : 2 e  t  t 1  0. 2 t 1 Xét   2    1 '  t k t e t t k t  e  t 1  0 t  . 2
 k 't  0  t  0 BBT:
Pt 3 có nghiệm t  0  f  x  0 . Pt 3 có 3 nghiệm phân biệt x  1  , x  0;1 , x  1. 1 2   3 t 1 t 1 Giải 4 : 2
e  t  t 1  0. Xét   2    1 '  t l t e t t l t  e  t 1  0 t  . 2 2
 l 't  0  t  0 . BBT: t 1 Nhận xét: l t 2
 e  t  t 1có l  2
 .l 3  0  l t  0 có 1 nghiệm 2 t  t  3
 ;2  f x  t có 1 nghiệm Pt 4 có 1 nghiệm. 1   1
Vậy g 'x  0 có 6 nghiệm phân biệt tức hàm số có 6 điểm cực trị.
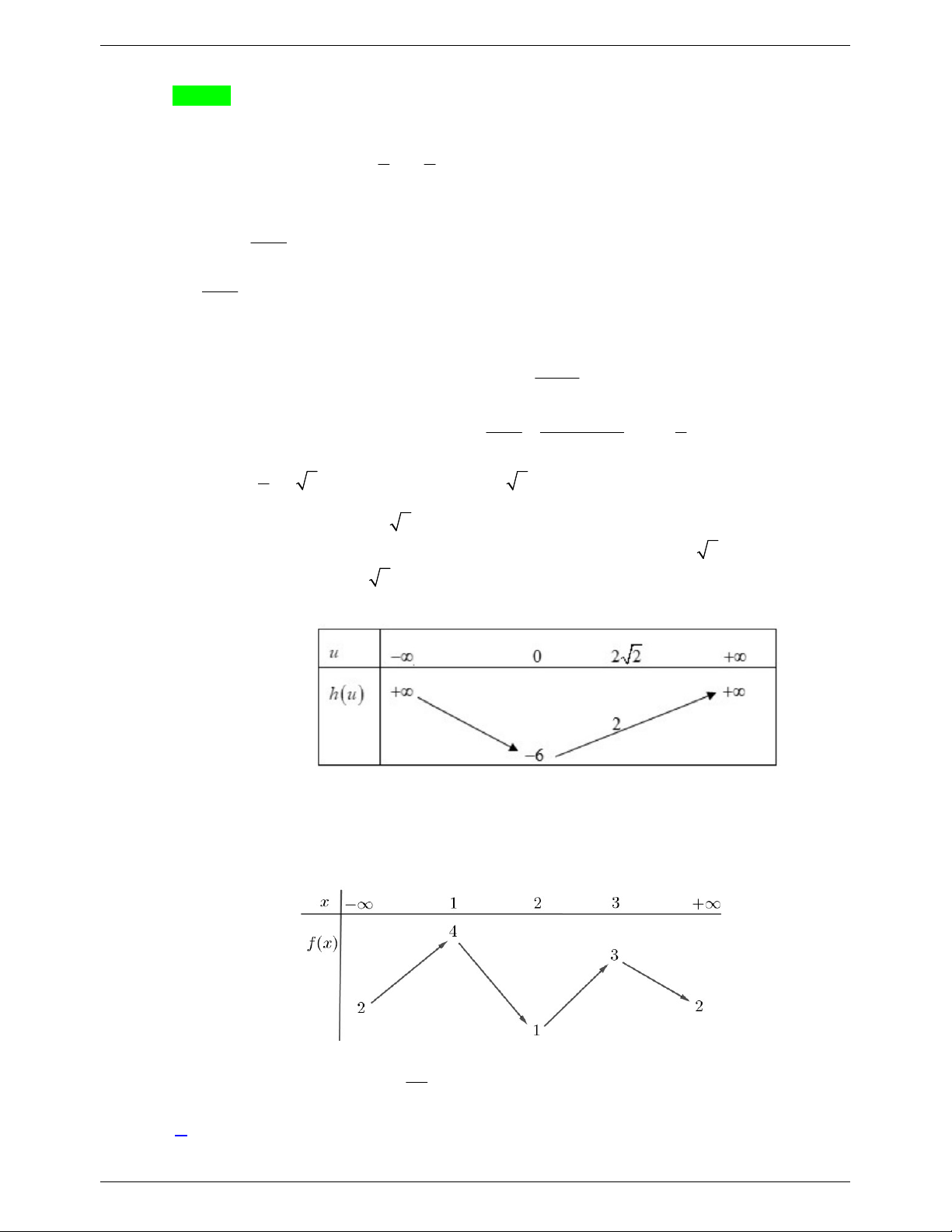
Câu 3. Cho hàm số bậc bốn f  x có đồ thị như hình vẽ sau. Có bao nhiêu
giá trị nguyên của m [ 2
 021;2021] để phương trình sau có hai nghiệm dương phân biệt f (x) 3 log  [
x f (x)  mx]  mx  f (x) 2 mx A. 2019 . B. 2021. C. 2020 . D. 2022 .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Lời giải Chọn A
Từ đồ thị hàm số suy ra f  x có ba điểm cực trị là 1;0;1. Do đó f  x  ax  a a 2 x   4 2 ( )
1  f (x)  x  x  b . 4 2
Mặt khác, vì đồ thị hàm số f (x) đi qua hai điểm (0; 4), (1;3) nên 4 2
f (x)  x  2x  4  3, x  . f (x) Điều kiện  0 suy ra m  0 . 2 mx f (x) 3 log  [
x f (x)  mx]  mx  f (x)  f x  f x  xf x   2 mx  2  mx  x  2 log ( ) ( ) ( ) log mx . 2 mx 
 x  f x  x   f x   2
x  mx    x   2 log ( 1) ( ) 1 . ( ) log ( 1) 1 .mx  (*) (Do x 1  0 ). 1
Xét hàm số g(t)  log t  t với t  0 . Ta có g (  t)  1  0 với t  0 . t.ln10 2 4 2 f (x) x  2x  4  2  Từ (*) ta có 2
(x 1) f (x)  (x 1)mx  m    x   6 . 2 2   x x  x  2
Đặt u  x   2 2, khi đó 2 m  u  6, u   2 2. x
Ứng với mỗi giá trị của u  2 2 cho ta hai giá trị dương của x nên yêu cầu bài toán đưa về
điều kiện là tìm m để phương trình 2
m  u  6 có đúng một nghiệm u  2 2. Đặt 2
h(u)  u  6 với u  2 2.
Bảng biến thiên của hàm số h(u) .
Từ bảng biến thiên suy ra m  2 thỏa yêu cầu bài toán. Do m   và m[ 2
 021;2021] nên m 3; 4;; 202  1 .
Vậy có 2019 giá trị của m thỏa mãn đề bài.
Câu 4. Cho hàm số y  f  x có đạo hàm trên  và có bảng biến thiên sau:
Có bao nhiêu giá trị nguyên của m để phương trình sau có đúng 2 nghiệm phân biệt: f  x 4  f x 2 2
 log  f x  4 f x  5  m 2       A. 2019 . B. 2021. C. 2020 . D. 2022 . Lời giải Trang 4
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Chọn A 4 f x 
Xét hàm số y  g  x   f x 2  2
 log  f x  4 f x  5 2       TXĐ:  4 f x   f  x  f x  f  x f x 4 2 4 g x          2 .ln 2. f  x      2 f  x 2  f 
x 4 f x  5ln 2   4       f   x   f   x fx f x f  x   2 2 2 . .2 .ln 2.   2  f  x 2
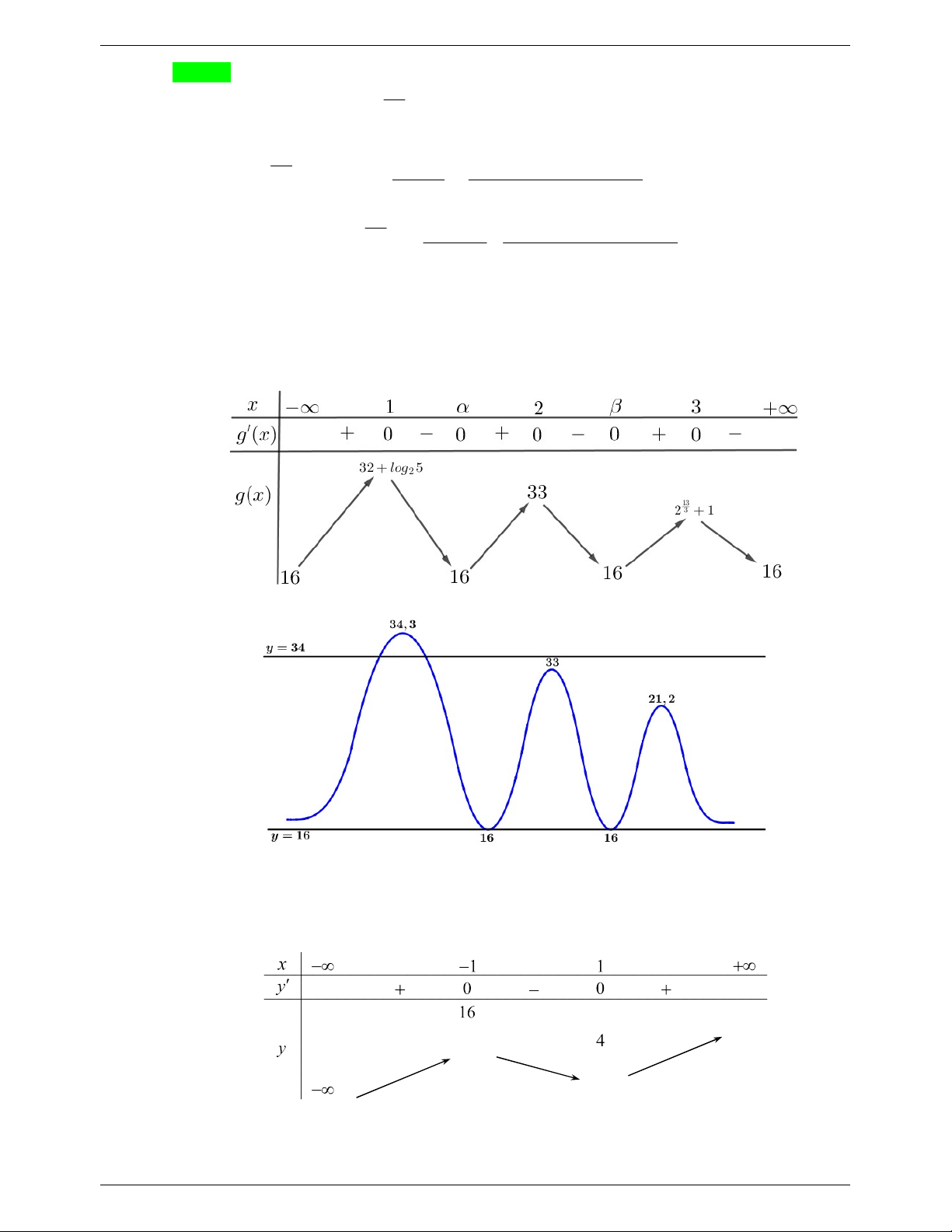
 f x  4 f x  5 ln 2     x  , 1;2  f  x   g x 2  0  
 x  ,  2;3  f    x  0 x 1, x  2, x  3  Bảng biến thiên Đồ thị minh họa :
Từ bảng biến thiên, hình vẽ và m   ta có : m 16  m  34
Câu 5. Cho hàm số y  f x có bảng biến thiên như hình dưới. 12 0
Có bao nhiêu số nguyên dương m để phương trình log 2 f x  m  log f x có 4 nghiệm 6     4    phân biệt.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC A. 1. B. 3. C. 16. D. 15. Lời giải Chọn A  f x  4t
Đặt t  log 2 f x  m  log f x  
 2.4t  m  6t  m  6t  2.4t. * 6     4      2 f  x t    m  6  3 t t t  ln16 ln16 Xét hàm số   6t 2.4t g t  
có g 't   0  6 ln 6  4 ln16    t  ln .   0 3  2  ln 6 ln 6 2
Có g t  0  t  log 2. Hàm số g t có bảng biến thiên như hình vẽ. 1 3 2 t -∞ 1 t -∞ 0 t1 g'(t) 0 + 0 g(t) -2 0 -2,014 Nếu phương trình  
* có 1 nghiệm t thì phương trình đã cho không thể có 4 nghiệm Nếu phương trình  
* có 2 nghiệm t  t thì khi đó dựa vào bảng bt của g t có t  t  t ;t 3 4  0 1 3 4
Do đó phương trình   4 4t f x 
có 3 nghiệm thực phân biệt. Vậy    3  4t ycbt pt f x
phải có nghiệm duy nhất .Hay t   ;  1 . 3   Mà g  
1  2 . Khi đó 2  m  0 thì  
* có 2 nghiệm t ,t thỏa t   ;  1 . 3   3 4
Vậy m  1là giá trị nguyên duy nhất thỏa mãn.
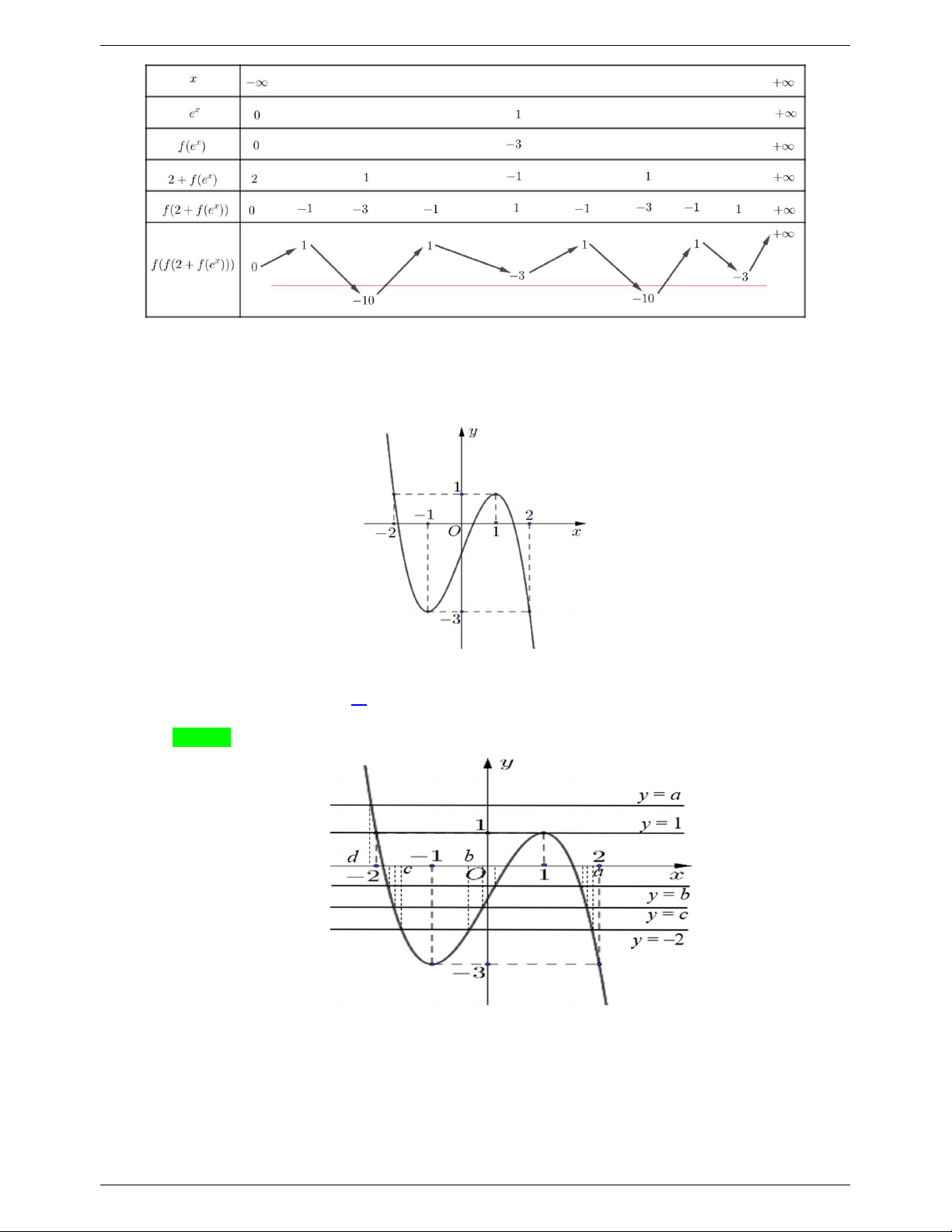
Câu 6. Cho hàm số y  f x có đồ thị như hình vẽ Biết f  3    1
 0 . Có bao nhiêu giá trị nguyên của m để phương trình  2   x f f f e    m có bốn nghiệm . A. 6 . B. 7 . C. 5. D. 10. Lời giải Chọn A Đặt x x      0 x e t t e x
  e làm hàm số luôn đồng biến .
Hàm số y  f x có hai cực trị tại x  1; x 1 tương ứng tại đó y 1; y  3  . 1 2 1 2 Từ đó ta có bảng sau. Trang 6
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Vậy phương trình  2   x f f
f e    m có bốn nghiệm  10  m  3.
Vậy có 6 giá trị nguyên của m thỏa mãn .
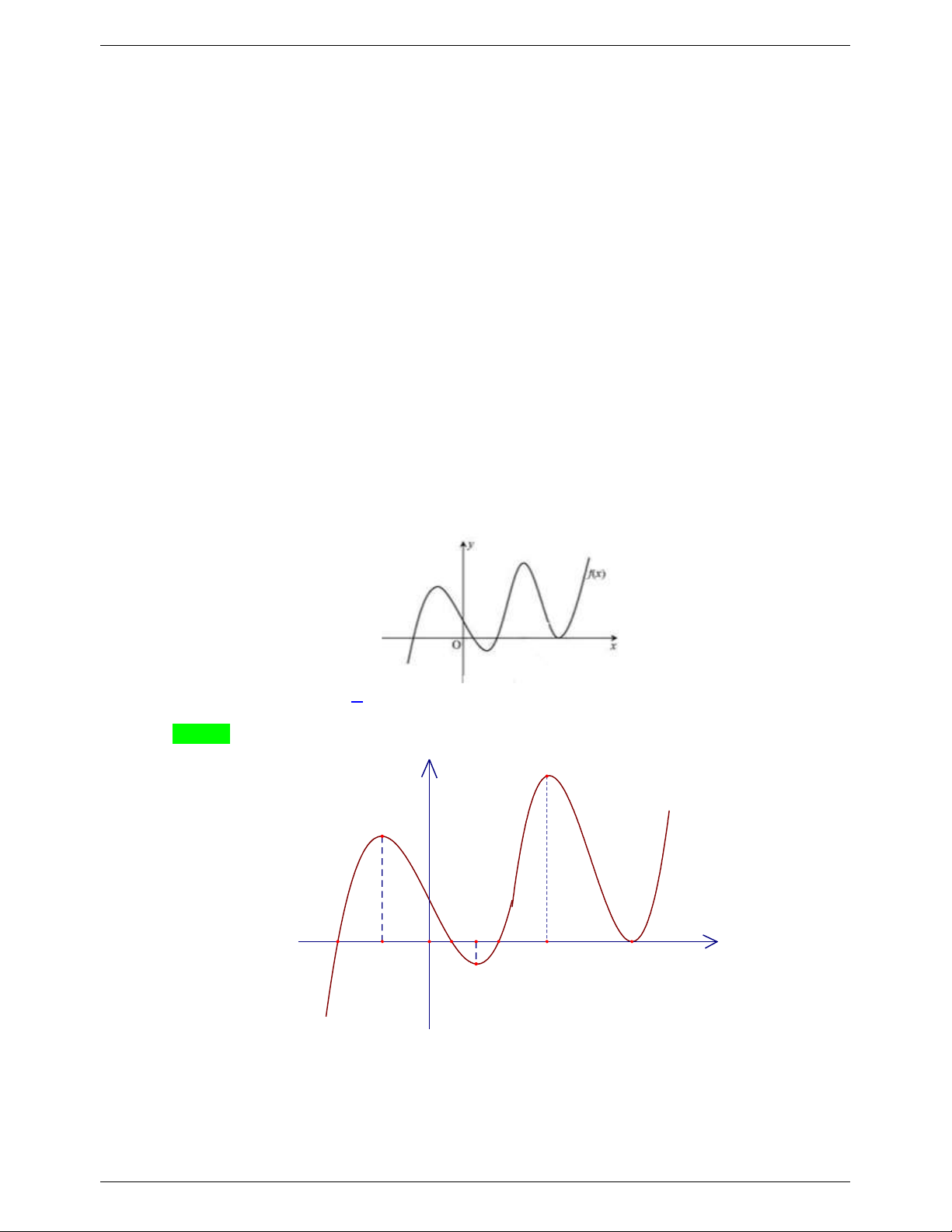
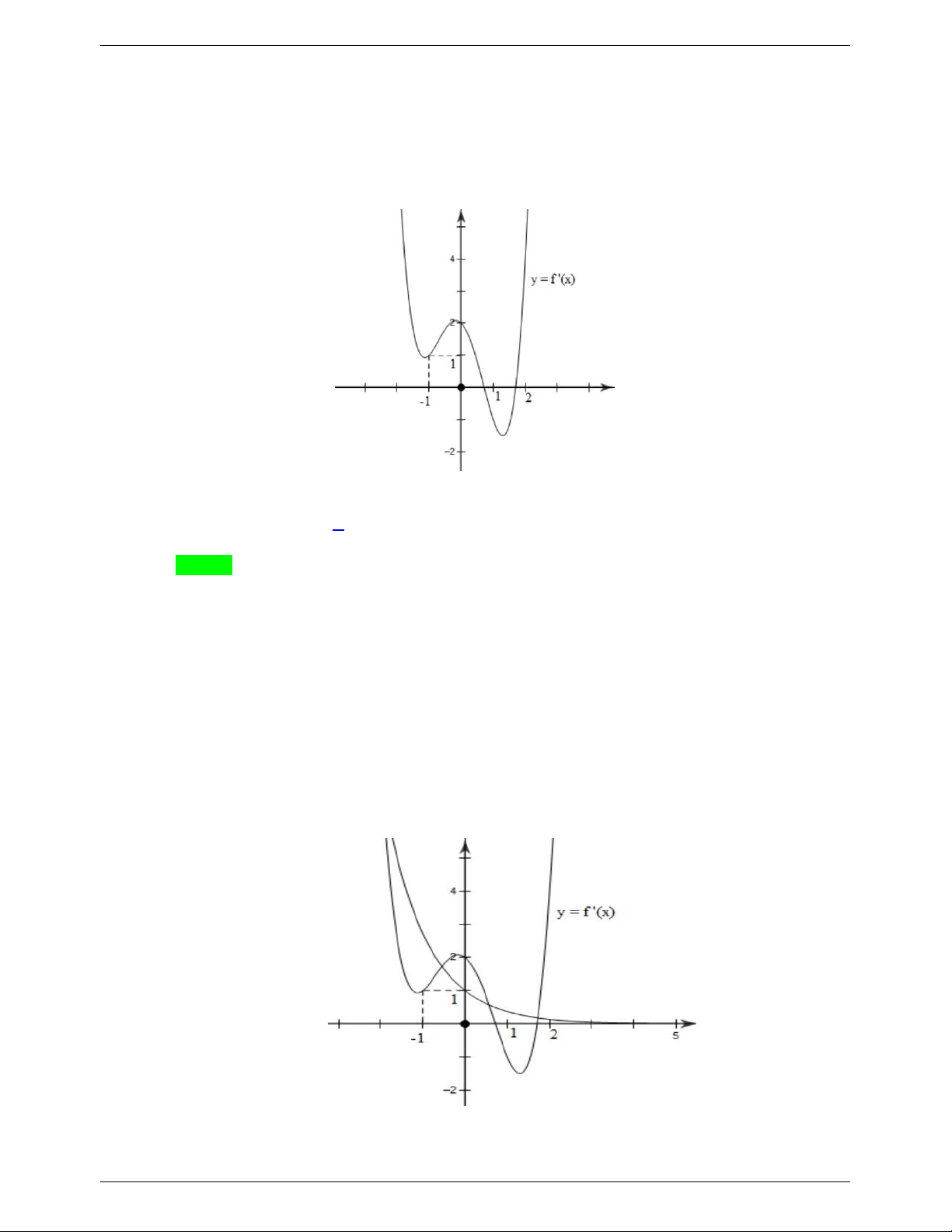
Câu 7. Cho hàm số f  x liên tục trên  có đồ thị y  f x như hình vẽ dưới đây.
Khi đó, số nghiệm thực của phương trình   2x f f f  1 là A. 8 . B. 5 . C. 3 . D. 4 . Lời giải Chọn A  f  f 2x   2 
Theo đồ thị, ta có: f  f  f 2x     1 
   f f 2x 1
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC 2x  a 1;2  2x  b   ptvn x  1;0 ( )  f 2  2  x  log a * f  f 2x     1 x            f   c ptvn 2x  2  2;  2 1 ( )  1 x  0 2x 1  2x  2  ( ptvn)  2x  d  2 ( ptvn)  2x  e 2  ;  1 ( ptvn) f 2x  a    2x  f   0;  1 2x  f 0;  1 x  log f 2  
* f  f 2x   2  f 2x   b    2x  g 1;2  2x  g 1;2   x  log g 2        f  2   c 2x  h 1;2 2x x  h  1;2 x  log h  2  2x  k  1  ;0 ( ptvn)  2x  m    2  ;  1 ( ptvn)
Từ đồ thị, ta thấy a  f  g  h . Do đó, phương trình có 5 nghiệm phân biệt.
Câu 8. Cho hàm số y  f (x) có đồ thị biểu diễn như hình vẽ và đồ thị đạo hàm không tiếp xúc với
trục hoành. Khi ấy, hãy tính số nghiệm của phương trình dưới đây f (x) f ( x) f (x).2  2 f (x).3  f (x)  2 f (x) A. 6 . B. 7 . C. 8 . D. 5 . Lời giải Chọn B y a a 2 4 x1 a O x2 x3 a 1 3 x4 x
Từ đồ thị hàm số suy ra f (x)  0 có các nghiệm x  x  x  x và f (
 x)  0 có các nghiệm 1 2 3 4
là a  a  a  a và phương trình f (
 x)  0 cũng chỉ có 4 nghiệm này ( vì đồ thị đạo hàm 1 2 3 4
không tiếp xúc với trục hoành). Từ đồ thị ta có a  x . 4 4 f ( x) f ( x) f (x).2  2 f (x).3
 f (x)  2 f (x)  f x  f(x)    f  x  f (x) ( ) 2 1 2 ( ) 3   1  0 (1). Trang 8
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
Dễ nhận thấy x , x , x , x , a , a , a là các nghiệm của phương trình (1). 1 2 3 4 1 2 3
Ta chứng minh rằng phương trình (1) chỉ có 7 nghiệm phân biệt x , x , x , x , a , a , a . 1 2 3 4 1 2 3 Thật vậy: f (x) f ( x)  f (x)  0 3   1 3  1  0
Trường hợp 1: Nếu x  x thì       VT(1)  0 1 f ( x) f (x)  f (x)  0 2 1 2 1  0 f (x) f ( x)  f (x)  0 3   1 3  1  0
Trường hợp 2: Nếu x  x  a thì       VT(1)  0 . 1 1 f ( x) f (x)  f (x)  0 2 1 2 1  0
Thực hiện tương tự đối với các khoảng còn lại ta thấy VT(1) luôn âm hoặc luôn dương trên các
khoảng đó. Vậy phương trình đã cho có 7 nghiệm. Câu 9.
Cho hàm số y  f (x) có đạo hàm liên tục trên  . Hàm số
y  f  x có đồ thị như hình sau đây y 3 2 1 0,5 -1 O 0,5 1 1,5 2 x -1 -2  1  Hàm số g  x 2  f x   2ln x  
đồng biến trên khoảng  2   4   6   1   3 7  A. ;1   . B. ; 2   . C. 0;  . D. ;   .  5   5   2   5 10  Lời giải Chọn C  1  1  1 
 Với x  0, có g x 2 2 2  2 . x f  x 
 2.  0  x . f  x  1       *  2  x  2  1 1  1  2  Đặt 2 2
t  x   x  t  .Khi đó   * trở thành t 
f t 1  f t    . 2 2  2  2t 1 y 3 2 1 0,5 -2 -1 O 0,5 1 1,5 2 x -1 -2 2  Vẽ (C) : y  trên cùng hệ trục. 2t 1  1  2 Dễ thấy trên 0; 
 thì đồ thị f t nằm bên trên đồ thị nên suy ra f t 2  trên  2  2t 1 2t 1
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC  1   1  0;   tức f t  2   0 trên 0;   .  2  2t 1  2   1   1  Suy ra g '(x)  0, x   0; 
 tức g(x) đồng biến trên khoảng 0;  .  2   2  Câu 10.
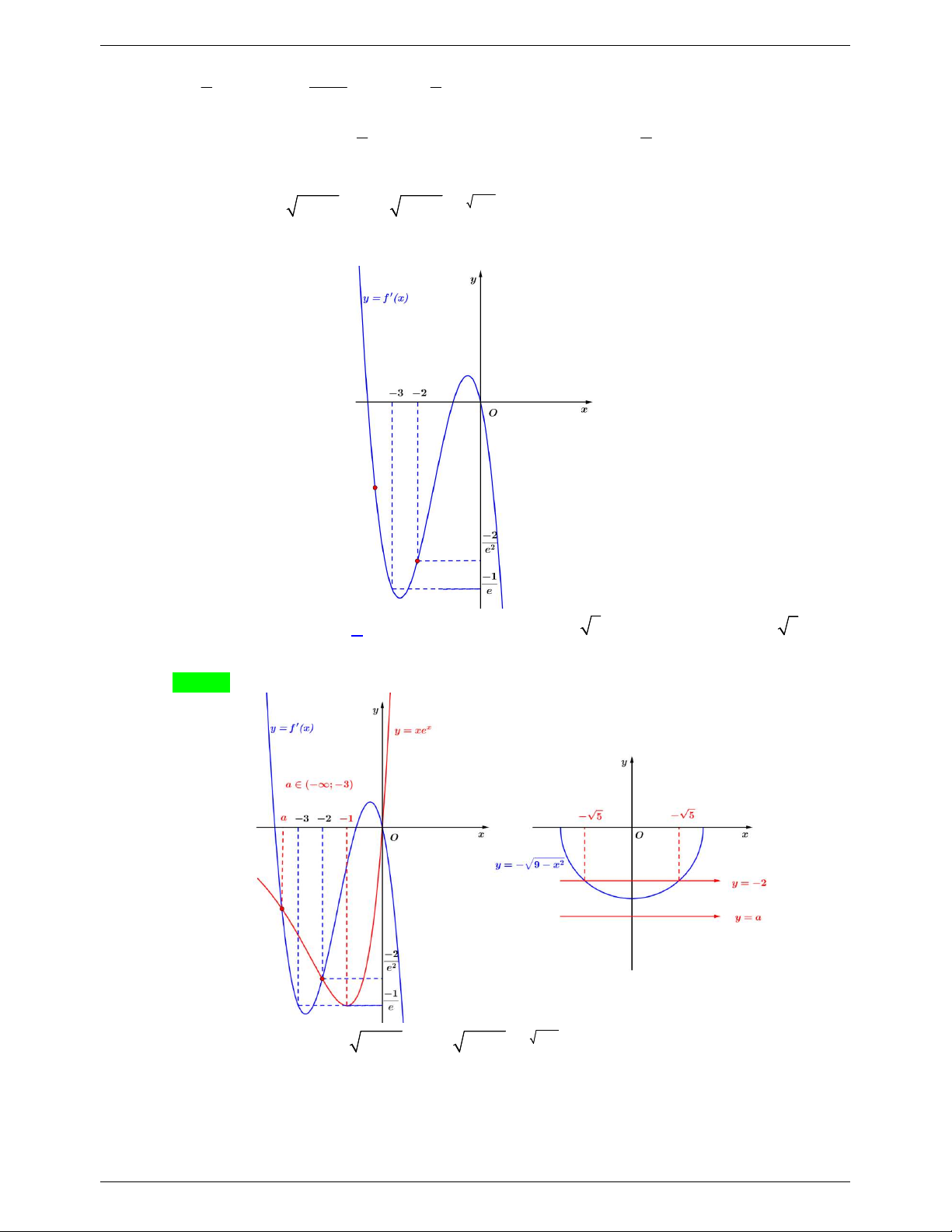
Cho hàm số f (x) liên tục trên R và có đồ thị (C) : y  f '(x) như hình vẽ bên. Hàm số     2 2 2 9 ( ) 9 1 9 x y g x f x x e        
đồng biến trên từng khoảng a;b, ; c d  và
 ;ab ;cd   . Gọi m  maxb  a  max(d c) . Khẳng định đúng là: A. m  6 . B. m  3 . C. m  2 5 . D. m  23 5 . Lời giải Chọn B  Ta có:     2 2 2 9 ( ) 9 1 9 x y g x f x x e         Trang 10
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC x x   x  y  g '(x)  f ' 2  9  x  2 2 9 x  9  .e  . x e  2 1 9  x 2 2 2  9  x 9  x 9  x x x  g '(x)  f ' 2  9  x  2  9  . x e  2  9  x 2 2  9  x 9  x x  g '(x)  f ' 2  9  x  2  9  . x x e 2 9  x x Cho g '(x)  0  f ' 9 x  2 2  9  . x x e  0 2 9  x x  0 x  0   1    f ' 9 x  2  x  e  0  f '     9  x  2 2 9 2 2  9   9  x . x e , (*) 2 9 x
Ở phương trình (*), ta đặt: 2
t   9  x thì phương trình thành: '( ) t f t  te (*)
Phương trình (*) cũng chính là phương trình hoành độ giao điểm của hai đồ thị hàm số y  f '(t) và t
y  te . Từ đó, dựa vào hình vẽ ta suy ra được các nghiệm đó là: t  a  ;  3   2  9 x a  ; 3 2         9  x  a  ;  3       ; x   3  ;  3     2  2 t 2  9  x  2   9  x  2
Đến đây ta nhận thấy với a  ;
 3 thì phương trình 2
 9  x  a vô nghiệm nên suy ra: 2
 9  x  2  x   5
Từ đó ta có bàng xét dấu đạo hàm của hàm số y  g(x) như sau:
Dựa vào BBT trên, ta kết luận hàm số y  g(x) đồng biến trên từng khoảng 3; 5,0; 5
Suy ra m  max b  a  max(d  c)  max  5  3  max  5  0  3 .
Câu 11. Cho hàm số f  x xác định, liên tục trên  và f ' x có bảng xét dấu như sau
Số điểm cực trị của hàm số f  2x x 2 e    là A. 2 . B. 3 . C. 4 . D. 5 . Lời giải Chọn D Đặt g  x f  2x x 2 e    
Vì f  x xác định trên  suy ra g  x xác định trên  . 2 2 Hơn nữa g x x  f    x 2 e  f  x x2 e  gx,x.
Suy ra g  x là hàm số chẵn, đồ thị hàm số g  x đối xứng qua trục Oy .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Xét x  0 g  x f  2x x 2 e   
  gx  x  2xx e  f  2 2 x x2 2 1 . . e  2x 1  0 2x 1  0 g x  0      f    2xx e   2  0 x x e  1   2 2 2 x  x2 vì e  0, x    1 2x 1  0 x     2  . 2 x x 2 0     x  2  vì x  0 Nếu x  2 thì 2
x  x  2  0 thì 2x x 2
e    1suy ra f  2x x 2 e    0. Nếu 0  x  2 thì 2 x  x  2  0 thì 2 x x 2 0 e     1suy ra f  2x x 2 e     0.
Từ đó ta có bảng xét dấu g x trên 0;  .
Suy ra g  x có hai điểm cực trị dương.
Do g  x là hàm số chẵn, liên tục trên  suy ra g  x có 5 điểm cực trị trên  .
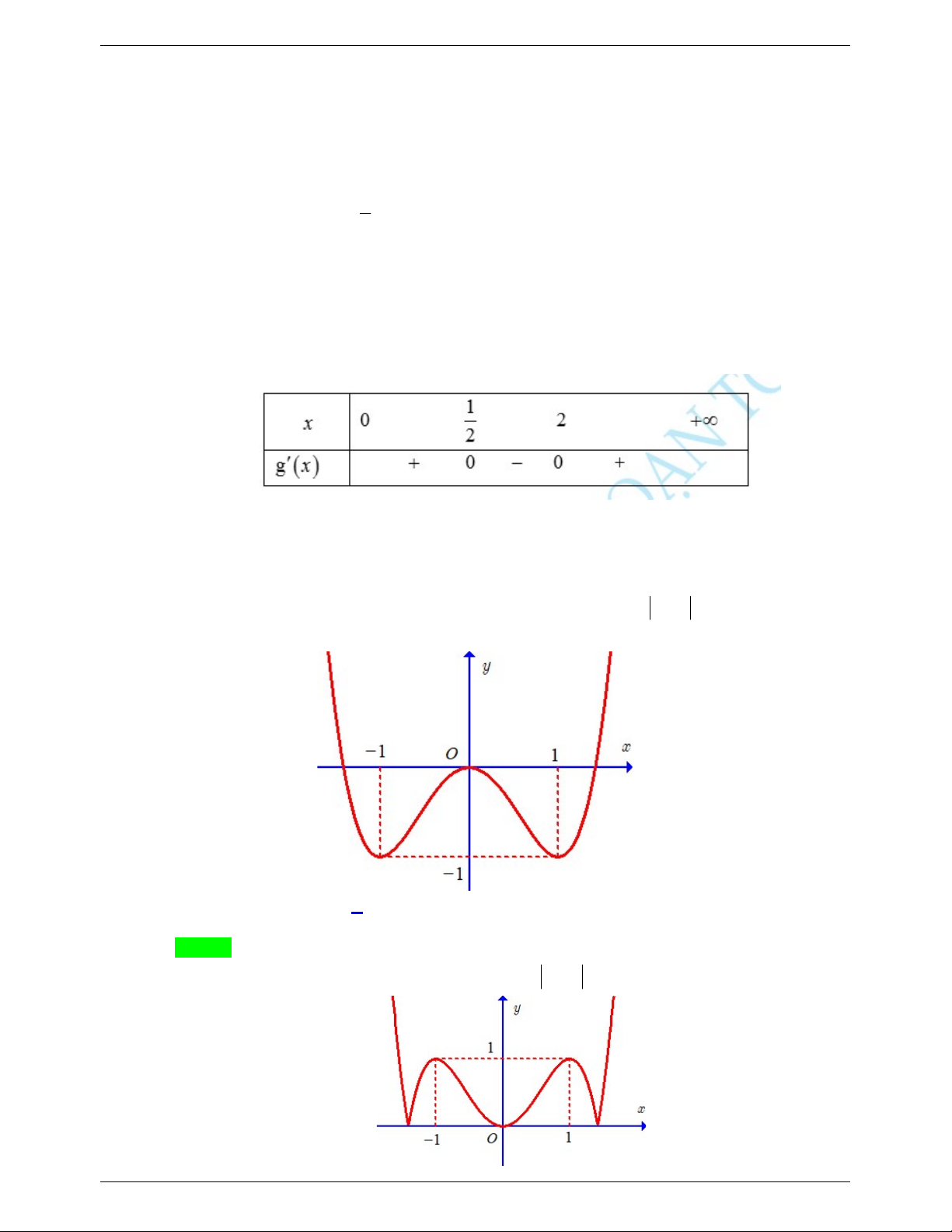
Câu 12. Cho hàm số y  f  x là hàm số chẵn trên tập số thực  và có đồ thị như hình vẽ. Biết rằng
tồn tại các giá trị của tham số 2 2 m để phương trình 2 f  x 3.3
 m 4 f x  3m  3 f x 3  3  0
có đúng 7 nghiệm thực phân biệt. Tổng lập phương các giá trị đó của m là A. 8 . B. 1. C. 7 . D. 7. Lời giải Chọn B
Từ đồ thị hàm số y  f  x ta suy ra đồ thị hàm số f  x như sau: Trang 12
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC Xét phương trình 2 f  x 3.3
 m 4 f x  3m  3 2 2 f  x 3  3  0 (1)
Đặt t  f  x ,t  0 , phương trình (1) trở thành 2 t      2 2 3.3 4 3 3 3t m t m  3  0 (2)
Vì f  x là hàm số chẵn nên f x  f  x, x
 . Do đó, nếu x là một nghiệm của 0 phương trình 2 f  x 3.3
 m 4 f x  3m  3 2 2 f x 3
 3  0 (1) thì x cùng là nghiệm của (1). 0
Nếu phương trình (1) có đúng 7 nghiệm thì (1) có nghiệm x  0 mà f 0  0 nên phương 0 trình (1) trở thành m  1 0
3.3  m 4.0  3m  3 0 2
3  3  0  3m  3m  6  0   m  2. Đảo lại: * Với 2 2
m  1: Phương trình (1) trở thành 2 3.3 t  4  63t t  3  0 2  2 t   t  t t 2 3 2 3 2 3  t 2
3.3  2t  3 2 t  3t (3)  3    2  2 t 2     2 t t t   t   t  t t 2 3 2 3 3.3 2 3 2 3 (4) 3   3 2 Xét (3): t 2 (3)  3. 3
 1  2 t 3t t  0 t     mà 2 0 3  3  1 và 2 2
t  3t  t  t với mọi
t  0 nên (3)  t  0 . 2 2 2t  3  4 t  3t 2   t   9 3 Xét (4): 2 (4)  3.3   
 2t  3  2 t  3t (5) 2 2 2 2t  3  2 t  3t 2t  3  2 t  3t 3t t 3 t 3 Từ (3) và (5) ta suy ra 2 3.3   4t  6 hay 2 3.3   4t  6  0 . 2 3t 2 3t t 3 Xét hàm số h  x 2  3.3 
 4t  6 , ta thấy    2 2 6 ln 3. . 3t 3 t h x t     4; 2 3t    2 2 t t     2 2 2 6ln 3. 3 3 2 .ln 3. 3t 3t h x t        0, t   0 
nên ht đồng biến mà h0.h 
1  0 nên phương trình ht  0 có duy nhất một nghiệm
t  t  0;1 . Từ đó suy ra phương trình ht  0 có nhiều nhất hai nghiệm mà 0   h0  h 
1  0 nên ht có đúng hai nghiệm là t  0;t 1.
Dựa vào đồ thị ta thấy: với t  0 thì phương trình (1) có 3 nghiệm x , với t  1 thì phương trình
(1) có 4 nghiệm x . Tổng cộng 7 nghiệm, do đó m  1 thoả mãn.
* Với m  2 : Phương trình (1) trở thành t   
2t   t   t     t   2 2 2 2 2 2 t 3 1 0 3.3 2 4 3 3 3 0 3 3 1  8t.3  0    t  0 . t  0
Trường hợp này phương trình đã cho có 3 nghiệm, giá trị m  2 loại.
Vậy m  1 là giá trị cần tìm. Câu 13.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC
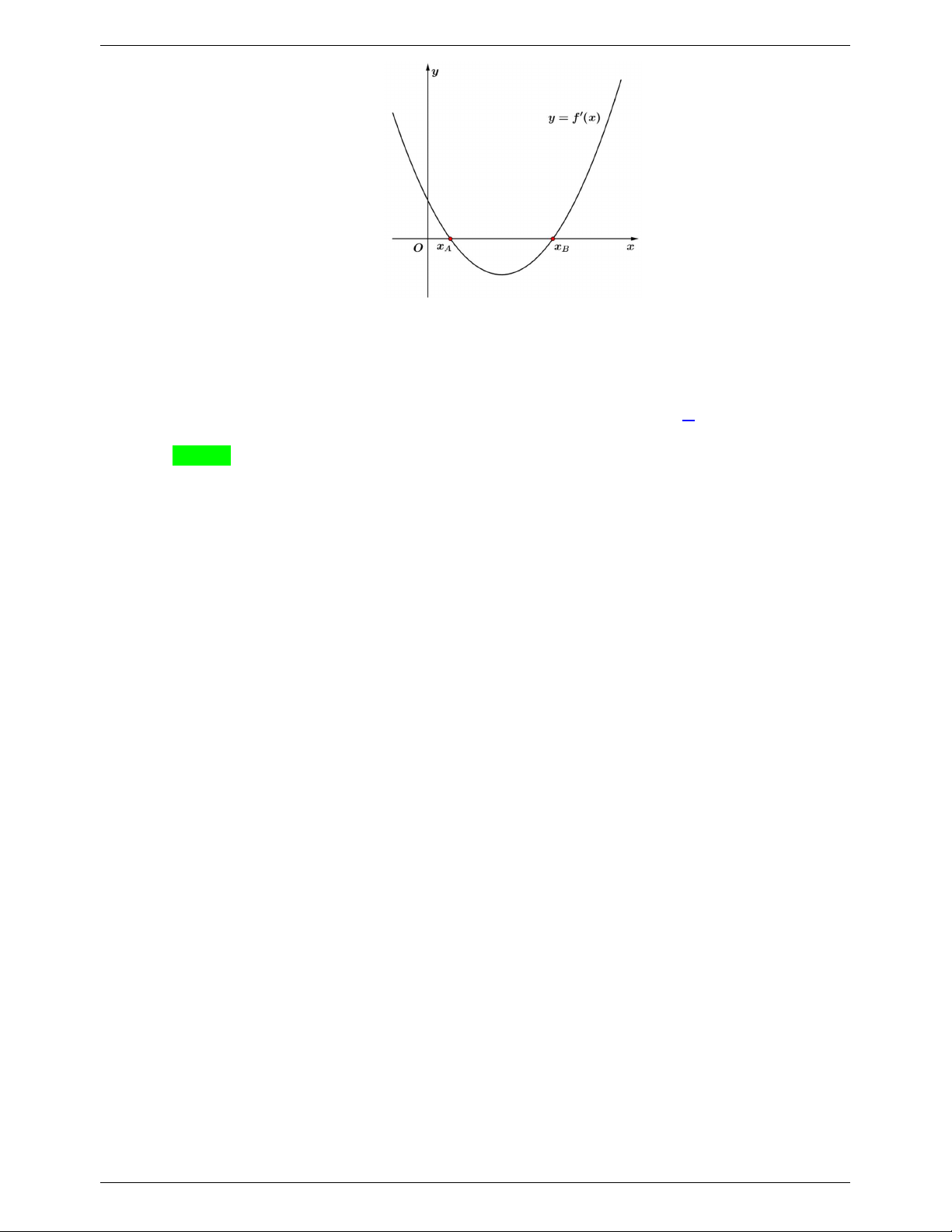
Cho hàm số y  f x có đạo hàm trên R và đồ thị của hàm số dưới đây là của y  f  x
Biết rằng x  x  2 . Tìm số điểm cực trị của hàm h x gx  e với A B
g x  f x  2019  f  x  2018 ... f  x ... f  x  2019  f x  2020 A. 1 . B. 2020 . C. 2 . D. 0 . Lời giải Chọn D
Gọi a,b lần lượt là các nghiệm của phương trình f ' x  0 với b  a  2
Khi ấy ta có: f  x  k  x  a x b  k  x  a x  a  2 . Ta có: h x gx  e
. Số điểm cực trị của hàm h x gx  e
bằng chính số nghiệm của phương trình
h x  0  g x gx .e  0  gx  0
 f  x  2019  f x  2018 ... f x ... f x  2019  f x  2020  0
 k.x  a  2019x  a  202 
1 ... k. x  ax  a  2 .. k. x  a  2020x  a  2018  0
 k.x  a  2020  1  x  a  2020  
1 ... k. x  a 1  1  x  a 1  1 .
 .. k.x  a  2019   1 x  a  2019   1  0  k x  a 
2     k x  a  2     k x  a  2 . 2020 1 ... . 1 1 ... . 2019 1  0      
 k. x  a  20202 ... k x  a  2
1  ...  k x  a  20192  (k ... k)  0  4  040k  k  x  a 
2   k x  a  2   k x  a  2 . 2020 ... 1 ... 2019  4040k  0  k x  a2  x  a
   k x  a2 2 . 2.2020 2020 ... .  2.x  a 1    
  k x  a2  x  a 2 ... . 2.2019  2019   4040k  0    x  a2 4040
 2. x  a2020  2019 ...1 0 ... 2019  2   2  0192 ...  2 2
1  0 1  ... 20192 2020   4040  0  
 4040x  a2  2. 2
 020x  a  4040   2  020 2019 2 2  2. x  0 (*) k 1  2019   2 2 2
   4040  4.4040 2020 4040  2. x  0 nên suy ra (*) vô nghiệm *    k 1  
Từ đó suy ra hàm số h x gx  e
không có điểm cực trị.
Câu 14. Cho hàm số y  f  x có đạo hàm trên  và hàm y  f  x có đồ Trang 14
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC thị như hình vẽ.  x  Trên đoạn  3
 ;4 hàm số g x  f      2 1
ln x  8x 16 có bao nhiêu điểm cực trị?  2  A. 2 . B. 1. C. 3. D. 0 . Lời giải Chọn C  x  Ta có: g  x  f      2 1 ln x  8x 16  2        gx 1 x 2x 8 1 x 2  f  1   f  1    . 2   2  2  x  8x 16 2  2  x  4   g x 1 x 2  0  f  1   0   .(1) 2  2  x  4 x  1 
Đặt t  1  ;3 , x
 3;4, (1) thành: 2  2    1 f t 2   f t  2  . 2 2t  2  4 t 1  1  Ta thấy hàm u t 2 
nghịch biến trên  ;3 , như vậy đồ thị hàm số f t và đồ thị hàm t 1  2     1  số u t 2 
trên  ;3 trên cùng một hệ trục như sau: t 1  2    t  0 x  2  1  2   Do đó trên  ;3 
phương trình f t   t  1  x  0 . 2    t 1    t a 1;3    x  2a   1    0;4
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC x  2 
Như vậy g x  0 có các nghiệm đơn x  0  trên đoạn  3
 ;4, do đó hàm số g x có x  2a    1
3 điểm cực trị trên đoạn  3  ;4 .
Câu 15. Cho hàm số y  f  x với đạo hàm f  x có đồ thị như hình vẽ. Trên đoạn 0;  3 . Hàm số     2 2 1 1 x g x f x e    
 2020có mấy điểm cực trị A. 7 . B. 4 . C.8 . D. 5. Lời giải Chọn B Xét hàm số     2 2 1 1 x g x f x e      2020 có       2 2 1 2 1  2 x g x xf x xe           2 2 1 2 1 x g x x f x  e      x  0
g x  0   f    2 x   2 1 1 x  e  0*   1
*  f  2x   2 1 1 x  e Đặt 2
x 1  t với x 0;  3  t  1  ;  8 Ta có : 2
x  t 1 Phương trình   1   t f t e   2 Xét hàm số t y e 
có đồ thị trên cùng hệ tọa độ với đồ thị hàm số f t Trang 16
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ – LOGARIT - VD_VDC t  a  1  ;0 
Từ đồ thị ta thấy phương trình 2 có ba nghiệm t   b0;  1 t  c    1;2 +) Với 2 2
t  a  x 1  a  x  a 1 có một nghiệm 0;  3 +) Với 2 2
t  b  x 1  b  x  b 1 có một nghiệm 0;  3 +) Với 2 2
t  c  x 1  c  x  c 1 có một nghiệm 0;  3
Vậy phương trình g x  0 có tất cả bốn nghiệm đơn phân biệt 0; 
3 nên hàm số g x có bốn điểm cực trị.
_______________ TOANMATH.com _______________
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17