Học viện Hàng Không Việt Nam – Khoa Không lưu
Dòng chuyển động không
nhớt và không nén được
qua biên dạng cánh – Lý thuyết cánh 2D 1
GVHD: Nguyễn Ngọc Hoàng Quân
Học viện Hàng Không Việt Nam – Khoa Không lưu Phần 1 Phần 2 Phần 3
QUỸ ĐẠO & LƯU TUYẾN LƯU SỐ ĐỊNH LÝ JOUKOWSKI Phần 4
LÝ THUYẾT CÁNH MỎNG
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)
Unsteady Motion: If at various points of the flow field quantities
(velocity, density, pressure) associated with the fluid flow change with
time, the motion is said to be unsteady.  
u (u= x y, z ),t , ,  (= x y, z,)t , p, ( p x = y z , t,)
Steady Motion: If at various points of the flow field quantities
(velocity, density, pressure) associated with the fluid flow remain
unchanged with time, the motion is said to be steady.  
u (u= x y, )z, ,  (= x y, )z, p, ( p x = y, ) z , 3
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)
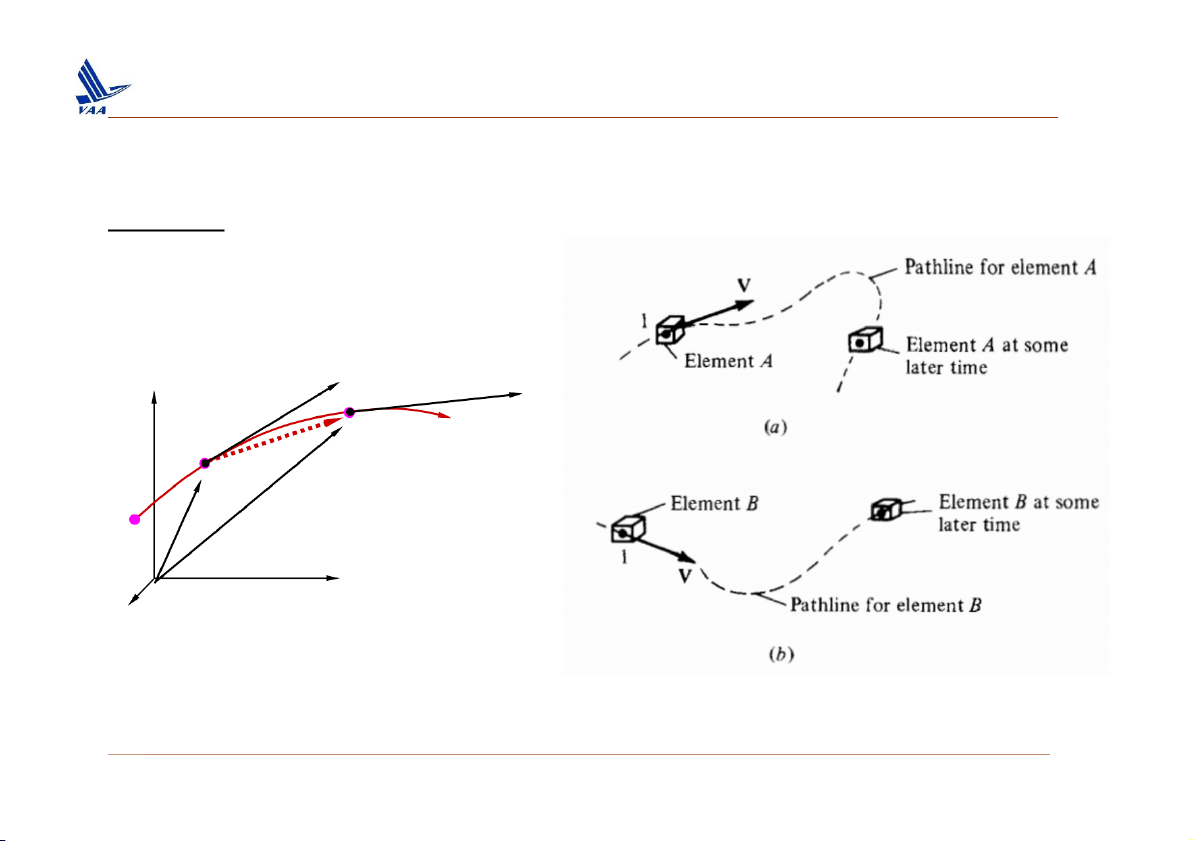
Pathline: The curve described in space by a moving fluid element i
known as its trajectory or pathline.  V (t) y A  V ( t d)t   A +  x x = ( t d)t x d A + x = x (t) A x z
Pathlines for two different fluid elements passing
through the same point in space: unsteady flow 4
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)
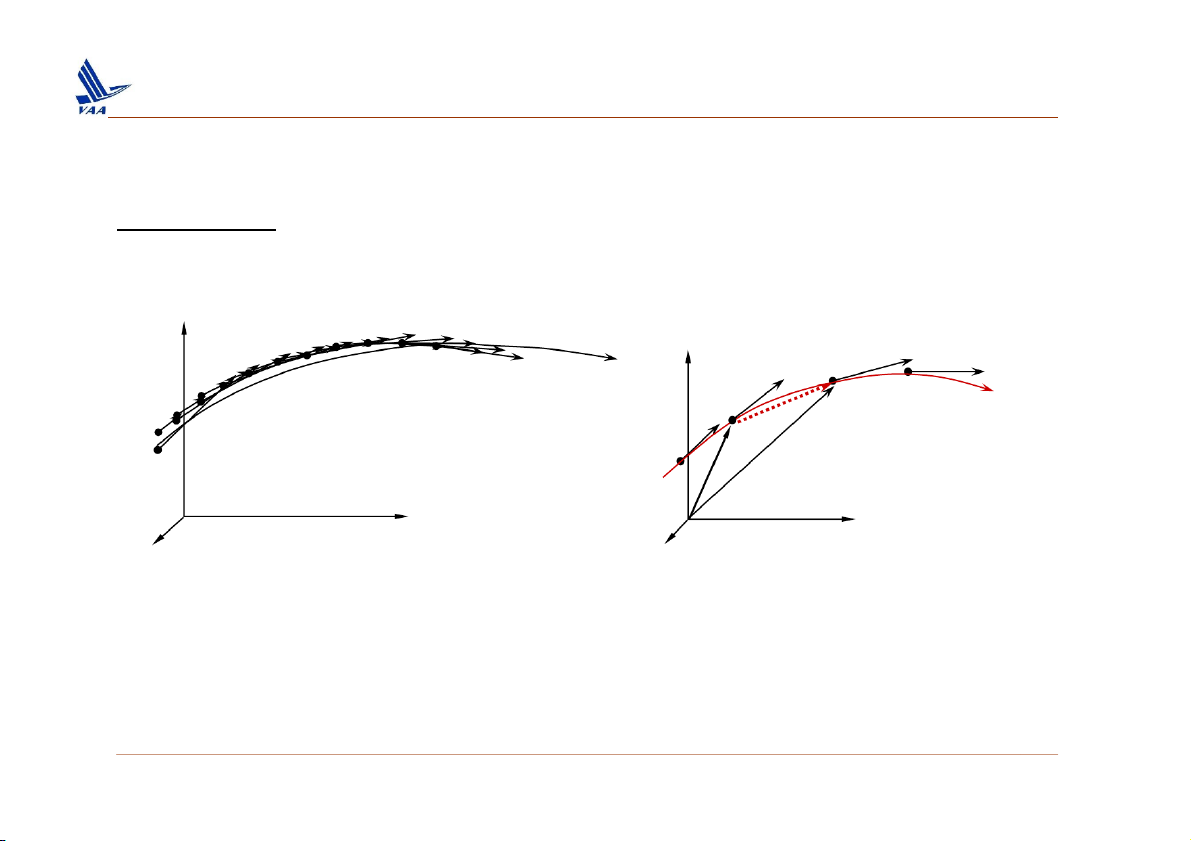
Streamline: is a curve whose tangent at any point is in the direction of
the velocity vector at that point. y    ( V x+ ,x d )t s (streamline y    ( V ,x )t  coordinate) x d   s x d C x + x d  B x d (streamline A coordinate) x x z x z Note that here x d
is the displacement along the streamline.
For steady flow, streamlines and pathlines are the same. 5
Học viện Hàng Không Việt Nam – Khoa Không lưu
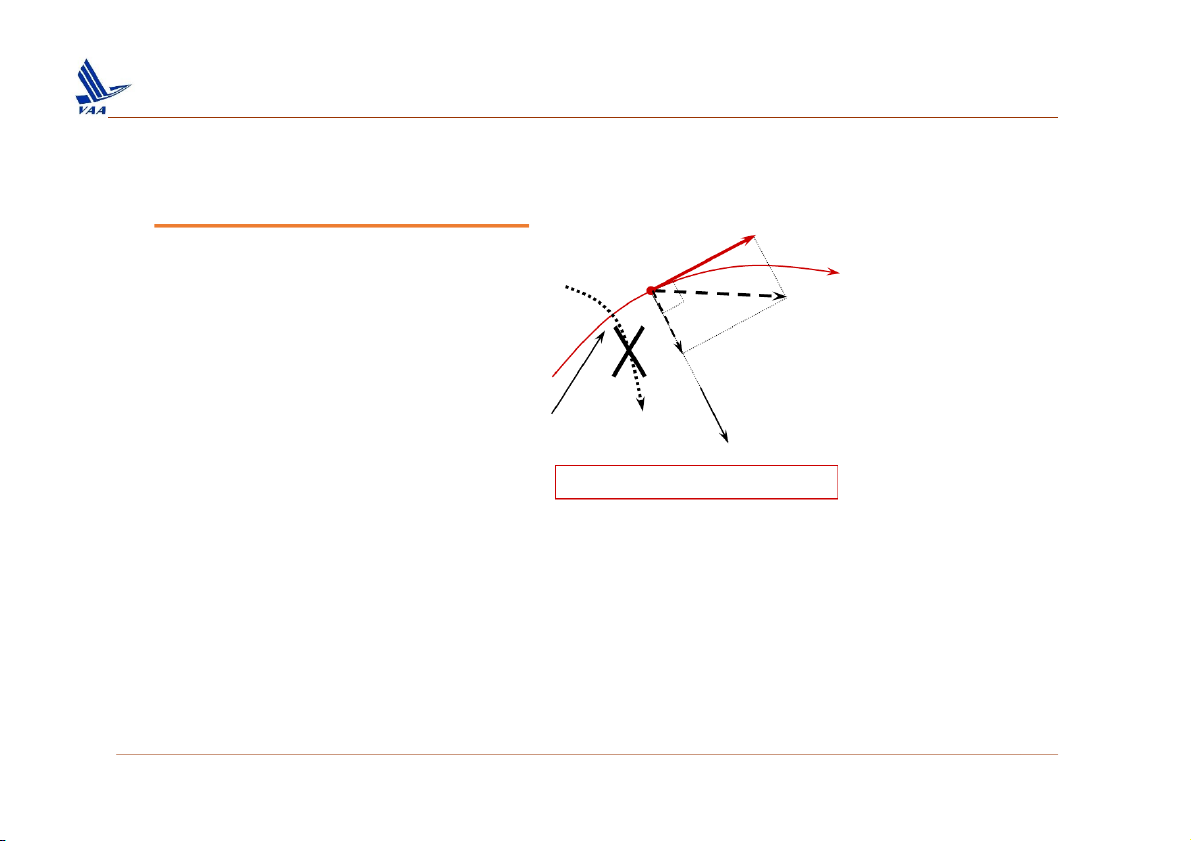
1. Quỹ đạo (pathline) và lưu tuyến (streamline)   ❑ Properties of Streamline V= tV = tV teˆ s (streamline coordinate)     V= tV + n V = tV   V = V ˆe = 0 n n n Not al owed ˆe ( unitnorma)l n No flow across streamline   •
By its definition, it fol ows tha Vtn = 0 .
• Hence, there can be no flow across a streamline. •
Note that only the normal component of velocity can transport fluid
from one side of the curve to the other. 6
Học viện Hàng Không Việt Nam – Khoa Không lưu
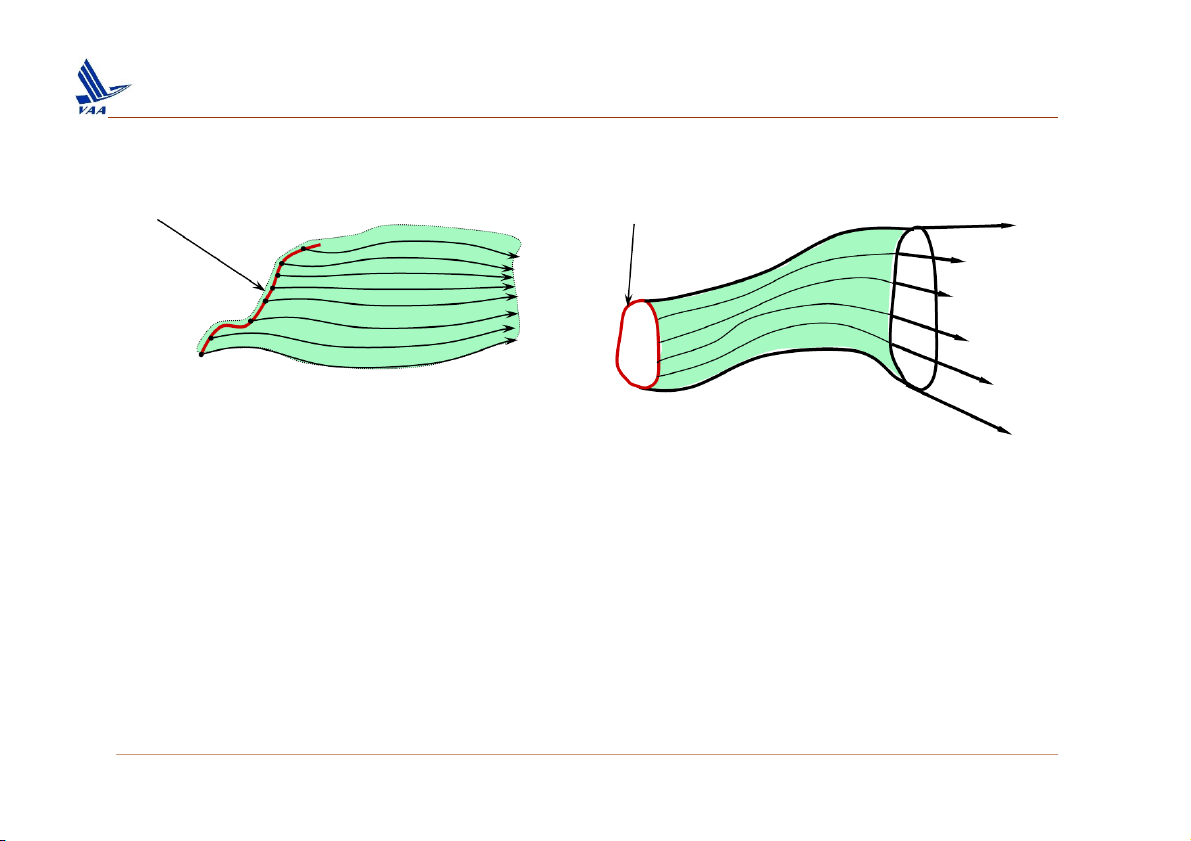
1. Quỹ đạo (pathline) và lưu tuyến (streamline) Arbitrary open curve C Arbitrary closed curve C Stream Surface Stream Tube Stream Surface
• Starting from an arbitrary open curve C.
• If we trace out streamlines that start from points on this curve, we have a stream surface that contains C. Stream Tube
On the other hand, if we choose a closed curve, we have a stream tube. ▪
From the definition of streamline, no flow can cross a stream tube. ▪
Therefore, a stream tube acts like an imaginary pipe/channel. ▪
Due to this property, stream tube is a useful tool for analysis. 7
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)
Flow past an airfoil, visualized by dye in water tunnel.
(From Van Dyke, M., 1982, An Album of Fluid Motion, Parabolic Press). 8
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)  = 10o  = 25o  = 30o+  = 30o- 9
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)
Flow past a damper, visualized by smoke-wire. 10
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)
Flow past a block showing horseshoe vortex (top-right and bottom), visualized by smoke-wire. 11
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline)
Consider r the coordinate of a point P andr the direction of the
streamline passing through this point. If u is the velocity vector of the
flow passing through P at a time t, by definition of a streaml u ine,
parallel todr . Hence, from the definition of the vector cross product: u d r  d r  u = 0 t r i j k Cartesian dx dy dz= 0  ( wdy− v ) dz i + ( udz − ) wdx+ (j vd − x )udy= 0k u v w Stream function – Hàm dòng d x d y d z In 2D dy v = = (*) = u v w dx u 12
Học viện Hàng Không Việt Nam – Khoa Không lưu
1. Quỹ đạo (pathline) và lưu tuyến (streamline) ▪ Exercises 1:
Consider the velocity field given by u = y/(x2 + y2) and v = -x/(x2
Calculate the equation of the streamline passing through the point (0,5) 13
Học viện Hàng Không Việt Nam – Khoa Không lưu
2. Lưu số (circulation)
Fundamental to the calculation of aerodynamic lift.
Consider a closed curve C in a flow field. Let V and ds be the velo
and directed line segment, respectively, at a point on C. The circulatio
denoted by Г is defined as  = − Vds C 14
Học viện Hàng Không Việt Nam – Khoa Không lưu
2. Lưu số (circulation) ▪ Exercises 2:
For the velocity field given in Exercise 1, calculate the circulation arou
circular path of radius 5 m. Assume that u and v given in Exercise units of meters per second. 15
Học viện Hàng Không Việt Nam – Khoa Không lưu
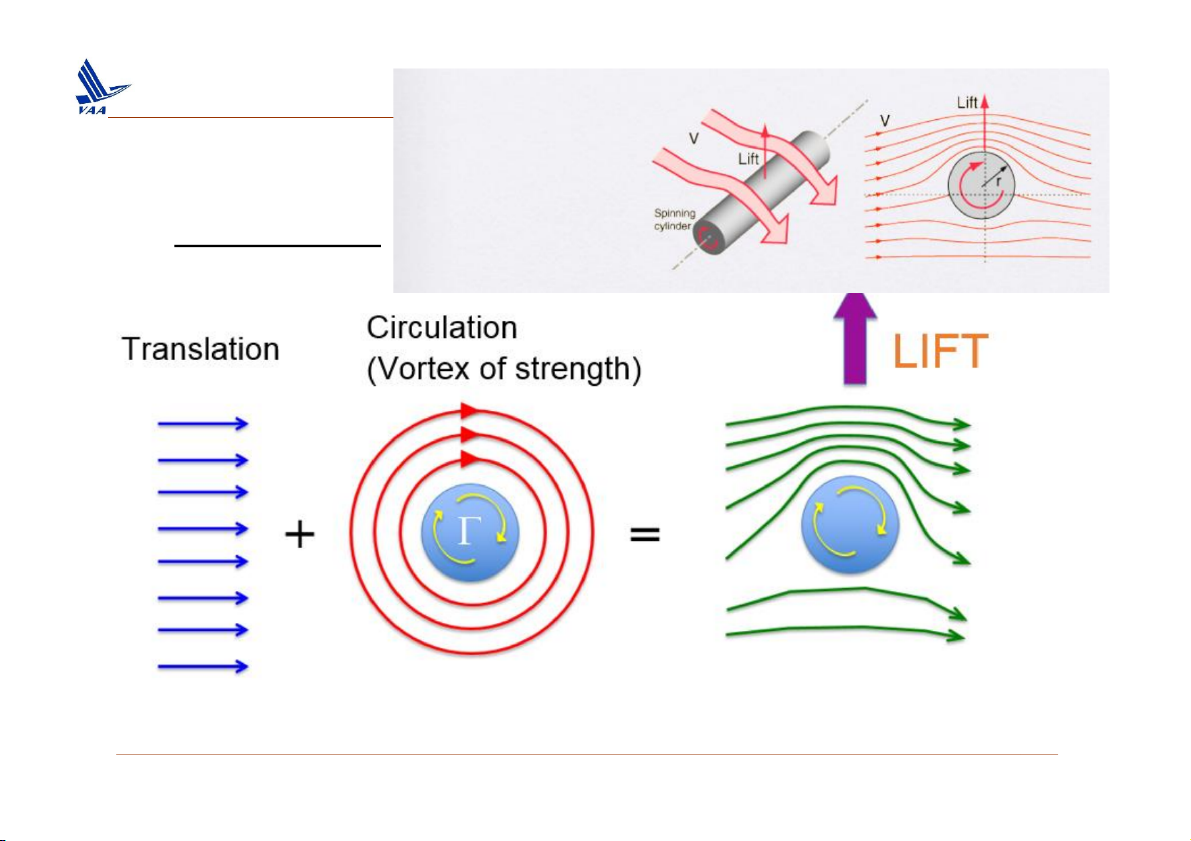
2. Lưu số (circulation) ❑ Magnus Effect
Lift generated by rate of rotation of the cylinder 16
Học viện Hàng Không Việt Nam – Khoa Không lưu
2. Lưu số (circulation) ❑ Magnus Effect 17
Học viện Hàng Không Việt Nam – Khoa Không lưu
2. Lưu số (circulation) ❑ Magnus Effect
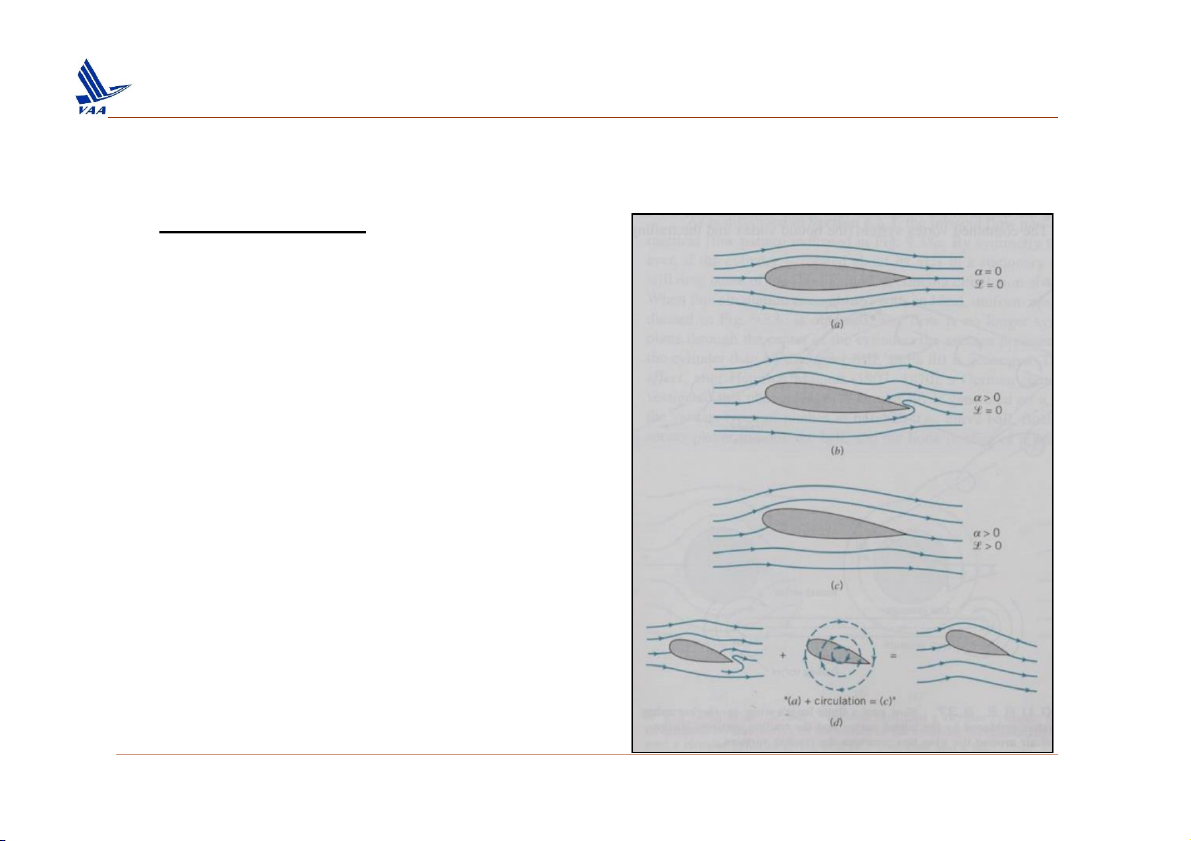
“In order for lift to be generated there
must be a net circulation around the profile.” PG 448 OUR BOOK 18
Học viện Hàng Không Việt Nam – Khoa Không lưu
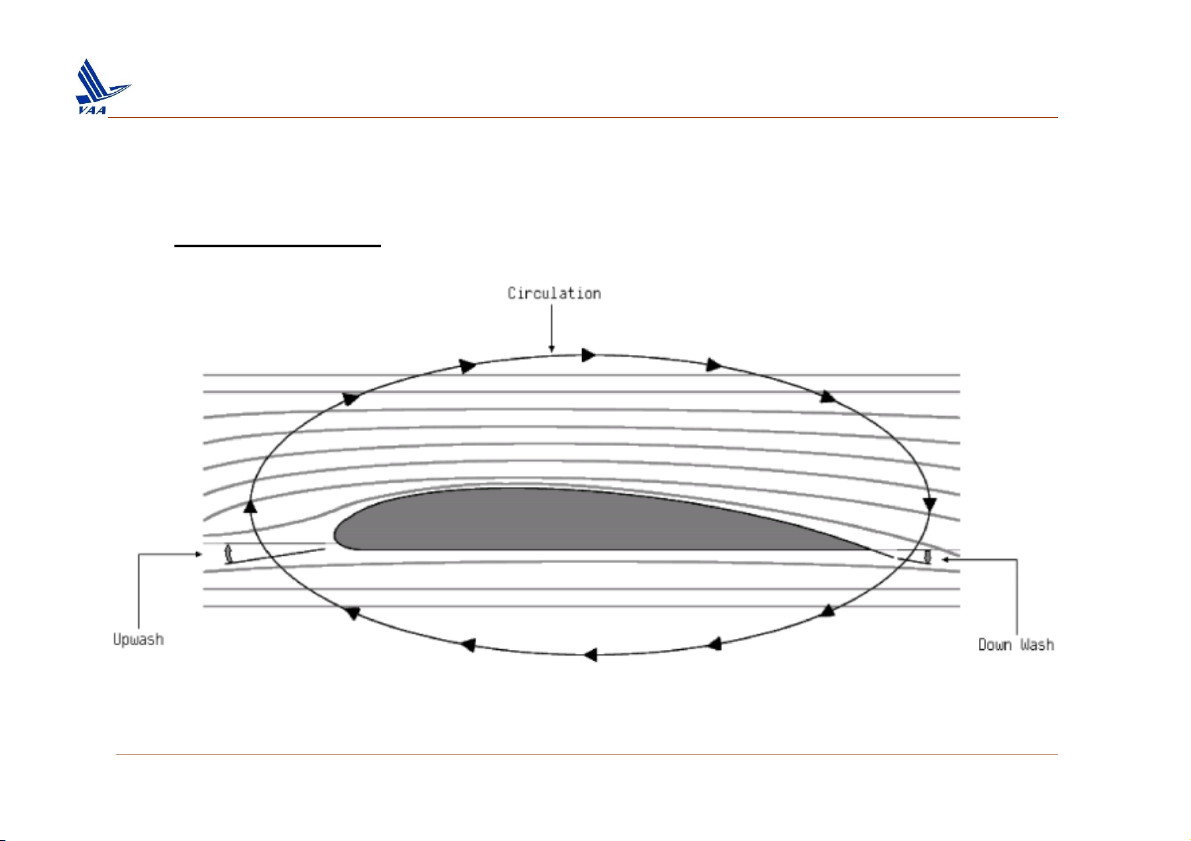
2. Lưu số (circulation) ❑ Magnus Effect Inviscid flow,  = 0 NO LIFT Inviscid flow,  > 0 NO LIFT Inviscid flow,  > 0 + circulation = LIFT 19
Học viện Hàng Không Việt Nam – Khoa Không lưu
3. Định lý Joukowski
For a closed two-dimensional body of arbitrary shape, the lift per unit span is L V =    
This result underscores the importance of the concept of circulation.
The Kutta-Joukowski theorem states that lift per unit span on a two
dimensional body is directly proportional to the circulation around the body. 20