Đường trung tuyến là gì? Tính chất, công thức tính đường trung tuyến và bài tập
Đường trung tuyến là gì? Tính chất và công thức tính và bài tập áp dụng là gì? Cùng theo doi bài viết
dưới đây của Luật Minh Khuê để hiểu hơn về đường trung tuyến nhé!
1. Định nghĩa về đường trung tuyến
Đương trung tuyến trong một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tớitrung điểm của
cạnh đối diện. Mỗi tam giác đều có ba đường trung tuyến.
Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai
cạnh kề có chiều dài bằng nhau.
2. Tính chất về đường trung tuyến
- Ba đường trung tuyến của một tam giác cùng đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.
Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
- Tam giác vuông là một tam giác đặc biệt với một góc lớn 90 °C, hai cạnh tạo nên góc vuông này luôn
vuông góc với nhau, do vậy mà đường trung tuyến của tam giác vuông sẽ mang những tính chát của
đường trung tuyến tam giác.
Trong một tam giác bất kì, đường trung tuyến ứng với cạnh huyền của tam giác sẽ có độ dài bằng 1/2 cạnh huyền.
- Mỗi trung tuyến chia diện tích tam giác thành hai phần bằng nhau. Ba trung truyến chia tam giác
thành sau tam giác nhỏ với diện tích bằng nhau.
- Đường trung tuyến trong tam giác cân
Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Và chia tam giác thành hai tam giác bằng nhau.
- Đường trung tuyến trong tam giác đều
Ba đường trung truyến của tam giác đều sẽ chia tam giác đó thành sáu tam giác có diện tích bằng nhau.
Trong tam giác đều đường thẳng đi qua một đỉnh bất kì và đi qua trọng tâm của tam giác sẽ chia tam
giác đó thành hai tam giác có diện tích bằng nhau.
3. Định lí của đường trung tuyến trong tam giác
Định lí 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm, điểm gặp nhau của ba đường
trung tuyến được gọi là trọng tâm của tam giác đó.
Định lí 2: Đường trung tuyến của tam giác chia tam giác thành hai tam giác có diện tích bằng nhau. Va
đường trung tuyến chia tam giác thành sáu tam giác nhỏ với diện tích bằng nhau.
Định lí 3: Về vị trí trọng tâm: trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài
đường trung tuyến đi qua đỉnh ấy.
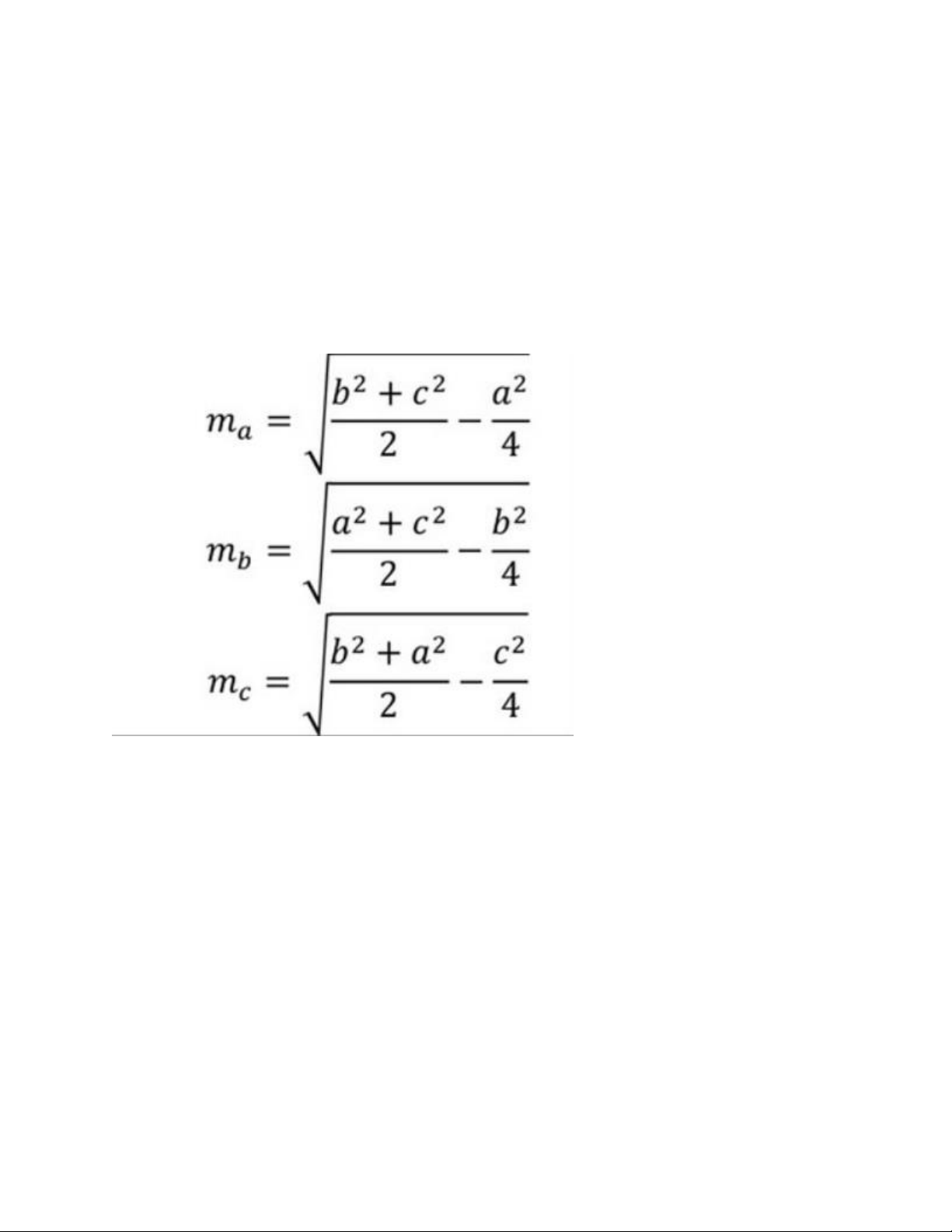
4. Công thức tính độ dài của đường trung tuyến
Độ dài đường trung tuyến của một tam giác được tính thông qua độ dài các cạnh của tam giác và
được tính bằng định lý apollonnius. Trong đó:
• a, b, c là các cạnh của tam giác
• ma, mb, mc là các đường trung tuyến của tam giác
5. Bài tập vận dụng
Câu1: Cho tam giác ABC cân biết AB = AC = 10 cm, BC = 12 cm. M là trung điểm BC. Độ dài trung tuyến AM là : A. 22 cm B. 2 cm C. 6 cm D. 8 cm
Câu 2: Tam giác ABC có trung tuyến AM = 9 cm và trọng tâm G. Độ dài đoạn AG là: A. 4,5 cm B. 3 cm C. 6 cm D. 4 cm
Câu 3: Cho tam giác ABC có hai đường trung tuyến BM và CN. Nếu BM = CN thì tam giác ABC là tam giác gì? A. tam giác cân B. tam giác vuông C. tam giác đều
D. tam giác vuông cân
Câu 4: Cho hai đường thẳng xx' và yy' gặp nhau ở O. Trên tia Ox lấy hai điểm A và B sao cho A nằm
giưac O và B, AB = 2 OA. Trên yy' lấy hai điểm L và M sao cho O là trung điểm của đoạn thẳng Lm. Nối
B với L, B và M và gọi P là trung điể của đoạn thẳng MB, Q là trung điểm của đoạn thẳng LB. Chứng
minh các đoạn thẳng LP và MQ đi qua A.
Câu 5: Cho tam giác ABC có BM và Cn là hai đường trung tuyến cắt nhau tại G. Kéo dài BM lấy đoạn
ME = MG. Kéo dài CN lấy đoạn NF = NG. Chứng minh a, EF = BC
b, đường thẳng AG đi qua trung điểm BC.
Câu 6: Cho một tam giác ABC cân có AB = AC = 17 cm, BC = 16 cm. Hãy kẻ đường trung tuyến AM a, Tính độ dài AM
b, Chứng minh AM vuông góc với BC
Câu 7: Cho điểm G là trọng tâm của tam giác đều ABC, hãy chứng minh rằng các cạnh GA, GB, GC bằng nhau.
Câu 8: Cho tam giác ABC, trên cạnh đối của cạnh AB, hãy lấy điểm D sao cho đoạn thẳng AD = AB, trên
cạnh AC lấy điểm E sao cho đoạn thẳng AE = 1/3 AC, đoạn thẳng BE cắt CD tại điểm M . Hãy chứng minh: a, AM = 1/2 BC
b, M là trung điểm của CD
Câu 9: Cho tam giác DÈ cân tại D có đường trung tuyến DI
a, Chứng minh tam giác DEI = tam giác DFI
b, Các góc DIE và góc DIF là góc gì?
c, DE = DF = 13 cm, EF = 10 cm. Tính DI
Câu 10: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA a, Tính số góc ABD
b, Chứng minh góc ABC = góc BAD
c, So sánh độ dài AM và BC
Câu 11: Cho tam giác ABC nhọn ( AB < AC ), đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA.
a, Chứng minh tam giác AMB = tam giác DMC và AB // CD
b, Gọi F là trung điểm CD, tia FM cắt AB tại K. Chứng minh M là trung điểm KF
c, Gọi E là trung điểm của AC, BE cắt AM tại điểm G, I là trung điểm của AF. Chứng minh ba điểm K, G và I thẳng hàng
Câu 12: Giả sử hai đường trung tuyến BD và CE của tam giác ABC có độ dài bằng nhau và cắt nhau tại G.
a, Tam giác BGC là tam giác gì?
b, So sánh tam giác BCD và tam giác CBE
c, Tam giác ABC là tam giác gì?
Câu 13: Trên đường trung tuyến AD của tam giác ABC, lấy hai điểm I và G sao cho AI = IG = GD. Gọi E là trung điểm của AC.
a, Chứng minh B, G, E thẳng hàng và so sánh BE và GE
b, CI cắt GE tạo O, điểm O là gì của tam giác ABC. Chứng minh BE = 9 OE
Câu 14: Cho tam giác ABC vuông tại A có AB = 8 cm, BC = 10 cm lấy điểm M trên cạnh AB sao cho BM =
4 cm. lấy điểm D sao cho A là trung điểm của DC. a, Tính AD
b, Điểm M là gì của tam giác BCD
c, Gọi E là trung điểm của BC, chứng minh D, M, E thẳng hàng
Câu 15: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA
a, Tính số đo của ABD
b, Chứng minh góc ABC = góc BAD
c, So sánh độ dài AM = BC
Câu 16: Cho tam giác ABC nhọn ( AB < AC ), đường trung tuyến AM. Trên tia đối của MA lấy điểm D sao cho MD = MA
a, Chứng minh tam giác AMB = tam giác DMC và AB // CD
b, Gọi F là trung điểm CD, tia FM cắt AB tại K. Chứng minh M là trung điểm KF.
c, Gọi E là trung điểm của AC, BE cắt AM tại G, I là trung điểm của AF. Chứng minh K, G và I thẳng hàng
Câu 17: Trên đường trung tuyến AD của tam giác ABC, lấy hai điểm I và G sao cho AI = IG = GD. Gọi E là trung điểm của AC.
a, Chứng minh B, G, E thẳng hàng và so sánh BE và GE
b, CI cắt GE tại O, điểm O là gì của tam giác ABC. Chứng minh BE = 9 OE
Câu 18: Cho tam giác ABC vuông tại A có AB = 8 cm, BC = 10 cm, lấy điểm M trên cạnh AB sao cho BM =
4 cm, lấy điểm D sao cho A là trung điểm của DC. a, Tính AD
b, Điểm M là gì của tam giác BCD
c, Gọi E là trung điểm của BC. Chứng minh D, M, E thẳng hàng
Trên đây là bài viết của Luật Minh Khuê về nội dung đường trung tuyến là gì? Tính chất, công thức tính
đường trung tuyến . Hy vọng bài viết hữu ích đối với bạn đọc. Trân trọng cảm ơn!