Ebook Vật lý đại cương 1 | Đại học Bách Khoa Hà Nội

Ebook Vật lý đại cương 1 | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn:

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

117 trang 7 tháng trước

Tác giả:

Profile Thùy Dương
EBOOK VẬ ẠT LÝ Đ I CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 3
LỜI NÓI ĐẦU
Vậ ạt lý đ i cương 1 là một trong nh ạ ầững môn đ i cương mà h u hết các sinh viên trư ng Đờ ại
họ ộ ọ ộ ộ ọc Bách Khoa Hà N i (RHUST) đều ph i hả c qua ít nhất m t lần trong đời. Đây là m t h c
phầ ản tuy không kquas khó nhưng đòi h i sinh viên phỏ i có s đào sâu lý thuyự chăm chỉ ết
và d a vào ậự đó để làm các bài t p.
Môn này có khá nhiều tài liệu tham khảo khác nhau từ bài giả ậng, bài t p, tài liệ ếu lý thuy t,
vv được chia sẻ trên chính website tailieuhust.com của chúng mình nhưng nó l i không ạ
đư ạợc liền m ch thành một khiến cho nhiều bạn không biế dụ ết ph ửải h c và sọ ng như th
nào? Bên c nh đó cũng có khá nhi u photo, viạ ều là tài liệ ết tay nên ch t lưấ ợ ợng không đư c
tốt lắm.
Để giúp các bạn sinh viên có thể có đư t lý đ t lược một tài liệu Vậ ạ ấi cương 1 ch ợng, dùng
cho các kỳ ỳ thi giữa kỳ và cu i kố chỉ trong 1 cu n mà không phố ải cầ dụ ền sử ng quá nhi u
file khác nhau nên mình và team Tài Li u HUST đã cùng nhau biên so n ra b u này. ệ ạ ộ tài liệ
Đây cũng là l n đ u tiên b t lý đ i cương 2 này đư c biên soầ ầ ộ tài liệu Vậ ạ ợ ạn nên cũng không
thể tránh đư ẫ ạợc những sai sót, v n mong được các b n góp ý để hoàn thiện hơn trong
tương lai. Team biên so n tài li u xin gạ ệ ửi lời cảm ơn chân thành tới các bạn.
Ngoài ra khi s u này, b ng h ng h n thi trử dụ ệng tài li ạn còn được sử dụ ệ thố ọc online, luyệ ắc
nghiệm tại:
Các bạn cũng có th p nhanh bể truy cậ ằ ặng cách quét mã QR bìa sách hoở c ở dưới đây:
Tài liệu tham khảo:
Bộ câu hỏi trắc nghiệm th y Tr n Thiên Đầ ầ ức b i ản mớ
Công th ắức tr c nghiệ ếm Vậ ạt lý đ i cương c a Vũ Tiủ n Lâm
Câu h i và đáp án tỏ ự luận đề thi VLĐC1 (quán photo)
Mọi ý kiến đóng góp và thắ ắc m c mọi người có thể liên hệ qua:
Website: tailieuhust.com
Email: tailieuhustgroup@gmail.com
Fanpage: Tài liệu HUST (tailieuhust.com)
Group học tập: Bachkhoa Universe – Góc học tập và thảo luận
TAILIEUHUST.COM
4 Group: Bachkhoa Universe – Góc học tập và thảo luận
NỘI DUNG TÀI LIỆU
PHẦN I. CÔNG THỨC VÀ BÀI TẬP TR C NGHIẮ ỆM ........................................................................... 5
Chương 1. Độ ọ ểng h c chất đi m ............................................................................................................ 5
A. Công thức ............................................................................................................................................... 5
B. Bài tậ ắp tr c nghiệm ........................................................................................................................... 7
Chương 2-3. Độ ọ ể ệ ể độ ọ ắnng lực h c chất đi m – h chất đi m – ng lực h c vật r ............ 14
A. Công thức ............................................................................................................................................ 14
B. Bài tậ ắp tr c nghiệm ........................................................................................................................ 17
Chương 4. Năng lượng ........................................................................................................................... 29
A. Công thức ............................................................................................................................................ 29
B. Bài tậ ắp tr c nghiệm ........................................................................................................................ 30
Chương 5: Trườ ấng h p dẫn .................................................................................................................. 40
A. Công thức ............................................................................................................................................ 40
B. Bài tậ ắp tr c nghiệm ........................................................................................................................ 41
Chương 6. Dao động – sóng ................................................................................................................ 46
A. Công thức ............................................................................................................................................ 46
B. Bài tậ ắp tr c nghiệm ........................................................................................................................ 47
Chương 7. Nguyên lý thứ nhấ ựt của nhiệ ột đ ng l c họ ế ộc và thuy t đ ng học phân tử
............................................................................................................................................................................ 51
A. Công thức ............................................................................................................................................ 51
B. Bài tậ ắp tr c nghiệm ........................................................................................................................ 54
Chương 8. Nguyên lý th ủứ hai c a nhiệ ộ ọt đ ng lực h c ............................................................ 62
A. Công thức ............................................................................................................................................ 62
B. Bài tậ ắp tr c nghiệm ........................................................................................................................ 63
PHẦN II. CÂU H BÀI TỎI VÀ ẬP TỰ LUẬN .......................................................................................... 69
PHẦN III. MỘT S THI GIỐ ĐỀ ỮA KỲ .................................................................................................... 110
1. Đề 1 thi giữ ỳa k ................................................................................................................................... 110
2. Đề 2 thi giữ ỳa k ................................................................................................................................... 113
3. Đề thi giữ ỳa k 3 ................................................................................................................................... 115
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 5
PHẦ ỨN I. CÔNG TH C VÀ P TR C NGHIBÀI TẬ Ắ ỆM
Chương 1. Độ ọ ểng h c chất đi m
A. Công thức
1. Chuyể ộ ẳ ền đ ng th ng đ u và những đạ ặi lượng đ c trưng
- Vận t c, gia tố ốc và phương trình chuyển động:
const
0 .
.
v
a x v t
s v t
=
= → =
=
2. Chuyể ộ ẳ ổ ềun đ ng th ng thay đ i đ
- Vận tốc và gia tốc:
0
const
v v at
a
= +
=
.
- Phương trình chuy ộển đ ng:
2 2
0 0 0
1 1
2 2
s v t at x x v t at= + → = + +
.
- Hệ thức liên hệ:
2 2
0
2v v as− =
.
3. Chuyể ộn đ ng tròn
- Gia t c hưố ớng tâm và gia tốc tiế ếp tuy n:
2
2
n
t
v
a r
r
a r
ω
β
= =
=
. với
β
=
const là gia tốc góc.
- c Gia tố toàn phần:
2 2 4 2
n t
a a a r
ω β
= + = +
.
- M ột số công thức liên hệ:
.
- Phương trình chuy ộển đ ng:
.
- Trường h n đ ng tròn đợp chuyể ộ ều:
0 0
const
t
t
ω
ϕ ϕ ω
=
= +
.
4. Chuyể ộn đ ng rơi tự do
- Vận tốc và quãng đường chuyển động:
0
2 2
0
2
0
2
1
2
v v gt
v v gs
s v t gt
= +
→ − =
= +
.
TAILIEUHUST.COM
6 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
- Thời gian rơi từ độ cao
h
đến khi ch m đạ ất:
2h
t
g
=
.
5. Chuyể ộn động parabol (chuyển đ ng ném xiên)
- Quỹ đạo là nhánh parabol có bề lõm quay xuống:
2
2 2
0
tan
2 cos
g
y x x
v
α
α
= − +
.
- Tầm ném xa:
2 2
0 0
max
sin 2
.
v v
L L
g g
α
= ⇒ =
khi
45
α
°
=
.
- Độ cao c c đự ại:
2 2
0
max
sin 2
2
v
h
g
α
=
.
- Bán kính cong:
2 2
n
n
v v
a R
R a
= → =
.
- Tại gốc:
2
0
0
cos
cos
n
v v
v
R
a g
g
α
α
=
→ =
= ⋅
- Tạ ỉi đ nh:
2 2
0
0
cos
cos
x
n
v v v
v
R
a g
g
α
α
= =
→ =
=
.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 7
B. Bài tập trắc nghiệm
Câu 1.
Một chất điểm chuy ng có phương trình: ển độ �
𝑥 𝑥 = 𝑎𝑎sin 𝜔𝜔𝜔𝜔
𝑦 𝑦
= 𝑏𝑏cos 𝜔𝜔𝜔𝜔
. Cho 𝑎 𝑎 = =𝑏 𝑏 30 cm và
𝜔 𝜔 = 10𝜋 𝜋 rad/s. Gia t ng c a ch m có giá trốc chuyển độ ủ ất điể ị bằng:
A.
296 301 281 331,1 m/s
2
. B. ,1 m/s
2
. C. ,1 m/s
2
. D. ,1 m/s
2
.
Lời giải:
Ta có phương trình chuyển động:
�
𝑥 𝑥 = 𝑎 𝑎 sin 𝜔𝜔𝜔𝜔
𝑦 𝑦
= 𝑏 𝑏 cos 𝜔𝜔 𝜔𝜔
⇒ �
𝑥𝑥
𝑎 𝑎
= sin 𝜔𝜔𝜔𝜔
𝑦𝑦
𝑏 𝑏
= cos 𝜔𝜔𝜔𝜔
→
sin
2
𝜔𝜔𝜔𝜔 𝜔𝜔𝜔𝜔+ cos
2
= 1 ⇒ �
𝑥𝑥
𝑎𝑎
�
2
+ �
𝑦𝑦
𝑏𝑏
�
2
= 1 ⇒ 𝑥𝑥
2
+ 𝑦𝑦
2
= 𝑅𝑅
2
𝑣𝑣ớ𝑖𝑖 𝑅 𝑅 = 𝑎 𝑎 = 𝑏𝑏
Suy ra v n đật chuyể ộng theo qu đạỹ o tròn.
Ta có:
�
𝑣𝑣
𝑥 𝑥
= =𝑥𝑥
′
𝑅𝑅𝜔𝜔 cos 𝜔𝜔𝜔𝜔
𝑣𝑣
𝑦 𝑦
= 𝑦𝑦
′
= −𝑅𝑅𝜔𝜔 sin 𝜔𝜔𝜔𝜔
𝑣 𝑣
=
�
𝑣𝑣
𝑥𝑥
2
+ 𝑣𝑣
𝑦𝑦
2
=
�
𝑅𝑅
2 2
𝜔𝜔
2
cos
2
𝜔𝜔𝜔𝜔 + 𝑅𝑅 𝜔𝜔
2
sin
2
𝜔𝜔𝜔𝜔 = 𝑅𝑅𝜔𝜔
Gia t n đ ng c a chốc chuyể ộ ủ ất điểm:
𝑎𝑎
ℎ𝑡𝑡
=
𝑣𝑣
2
𝑅 𝑅
= 𝜔𝜔
2
𝑅 𝑅 =
(
10𝜋𝜋
)
2
. 0,3 ≈ 296,1 /
(
𝑚𝑚 𝑠𝑠
2
)
Câu 2. Thả t rơi tự do m t nhột vậ ỏ ừ độ cao ℎ = 17,6 m. Quãng đư ng mà v t rơi đườ ậ ợc
trong a th0,1 s cuố ủi cùng c ời gian rơi là:
A. 1, 1, 2, 2,608 m. B. 808 m. C. 208 m. D. 408 m.
Lời giải:
Ta có phương trình li độ ủ c a vật là: 𝑥𝑥
(
𝜔𝜔
)
=
1
2
𝑔𝑔𝜔𝜔
2
Tổng th ạời gian rơi cho tới khi ch m đất là: 𝜔𝜔
𝑟 𝑟
=
�
2ℎ
𝑔 𝑔
=
�
2.17,6
𝑔 𝑔
(𝑠𝑠)
Quãng đư ậ c trong a thờng v t rơi đượ 0,1 𝑠𝑠 cuối cùng củ ời gian rơi là:
𝑥𝑥
(
𝜔𝜔 − 𝑥𝑥 𝜔𝜔
𝑟𝑟
) (
𝑟 𝑟
− 0.1
)
=
1
2
𝑔𝑔
[
𝜔𝜔
𝑟𝑟
2
−
(
𝜔𝜔
𝑟 𝑟
− 0,1
)
2 2
]
= 1,808
(
𝑚𝑚
)
với 𝑔 𝑔 = 9,8 /𝑚𝑚 𝑠𝑠
Câu 3. Thả rơi t do m t nh . Th i gian c t đi hự ột vậ ỏ từ độ cao ℎ = 17,6 m ờ ần thiết để vậ ết
1 m/s m cuối củ ộa đ cao ℎ là: (cho 𝑔 𝑔 = 9,8
2
)
A. 5, 5, s263 10.
−2
s. B. 463 10.
−2
. C. 5, s 4, s863 ⋅ 10
−2
. D. 863 ⋅ 10
−2
.
TAILIEUHUST.COM
8 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Lời giải:
Thời gian v t rơi đưậ ợc quãng đường h là: t1=
2h
g
Thời gian vật rơi quãng đường (h – 1) là: t2=
2( 1)h
g
−
Thời gian v t rơi h i khi th cao h là:ậ ết 1 m cuố ả từ độ
∆
-t= t1 t2 =
2h
g
-
2( 1)h
g
−
Thay s
ố h=17,6(m); g=9,8(m/s
2
) =>
∆
t
≈
2
5,463.10
−
(s)
Câu 4. Một ô tô b u ch y vào đo n đưắt đầ ạ ạ ờng vòng bán kính và dài 𝑅 𝑅 = 1,3 km 600 m với
vận tốc 𝑣𝑣
0
= 54 km/h. Ô tô ch y hạ ế ờt quãng đư ng trong thời gian 𝜔 𝜔 = 17 s. Coi chuy n ể
động là nhanh d ốần đ u, gia tề c toàn ph n c a ô tô cu i đo n đưầ ủ ố ạ ờng vòng bằng:
A.
2, m/s 4, m/s 3, m/s869
2
B. 119
2
. C. 369
2
D. 3,119 . m/s
2
Lời giải:
Đổi v= 54 (km/h) = 15(m/s); R= 1,3 km =1300m
Vì đoàn tàu di chuyển nhanh dần đ u ta có công thề ức: S=
0
v
t +
2
1
2
tt
a t
=>
tt
a
=
0
2
2( )s v t
t
−
Vận tốc c i cuủa đoàn tàu tạ ối đư ng bờ ằng: v=
0
v
+
tt
a
t =
0
2S
v
t
−
Gia t c hư i đưố ớng tâm c a đoàn tàu tủ ại cuố ờng là:
2
2
0
2
( )
ht
S
v
v
t
a
R R
−
= =
Gia t c toàn ph n c i đưố ầ ủ ốa đoàn tàu tại cu ờng là:
2
2
2
0
2 2
0
2
2
( )
2( )
tp
tt ht
S
v
s v t
t
a a a
t R
−
−
= + = +
Thay số S= 600m;
0
v
=15 m/s; t=17s; R= 1300m =>
tp
a
≈
3,369
m/s
2
Câu 5. Một ôtô chuyể ế ề ển động bi n đ i đổ u lần lượt đi qua hai đi m A và B cách nhau 𝑆 𝑆 =
25 m trong kho ng thả ời gian 𝜔 𝜔 = 1,6 s , v n tậ ốc ô tô n tở B là 12 m/s. Vậ ố ủc c a ôtô ở A
nhận giá trị nào sau đây:
A. 18 25, . . . . m/s B. 18 75, m/s C. 19 25, m/s D. 20 75, m/s
Lời giải:
Ô tô chuy n đ ng bi n đ i đ u nên ta có: ) / t ể ộ ế ổ ề V
B
= V + at => a = (V
A
B
- V
A
(1)
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 9
S = V
A
t + (at
2
)/2 (2)
Thay (1) vào (2) => S = V
A
t +
(VB VA − )t
2
(3)
Từ dữ ệ ề ki n đ bài cho thay vào (3) ta được: V
A
= 19,25 m/s
Câu 6. Một bánh xe có bán kính ụ ủ𝑅 𝑅 = 12 cm lúc đầu đ ng yên sau đó quay quanh trứ c c a
nó v ố nh ố ủ ộới gia t c góc 𝛽 𝛽 = 3,14rad/s
2
. Sau giây thứ ất gia t c toàn ph n cầ a m t điểm trên
vành bánh là:
A.
120 17, . . . . cm/s
2
B. 126 17, cm/s
2
C. 130 17, cm/s
2
D. 124 17, cm/s
2
Lời giải:
Phương trình vận tốc góc w= 𝑤𝑤
0
+ βt= 0 + βt= βt (do ban đ u đ ng yên ầ ứ 𝑤𝑤
0
= 0)
⟹ Gia t c pháp tuyố ến a
n
= 𝑤𝑤
2
R =( βt)
2
R
Gia t p tuyốc tiế ến: a
t
= βR
Gia t c toàn phố ần: a = �a
t
2
+ a
n
2
= � �β
(
βt
)
4
R
2
+ β
2
R
2
= βR
2
t
4
+ 1
Sau giây thứ nhất ⟹ t = 1
⟹
a = βR
�
β
2
t
4
+ 1 = 3,14 ∗ 0,12
�
3,14
2
+ 1 = 1,2417 �
m
s
2
� = 124,17 �
cm
s
2
�
Câu 7. Kỷ l ục đ y tẩ ạ ở Hà Nội là 14 07, m. Nếu tổ chức đ y tẩ ạ ở Xanh Pêtecbua trong điều
kiệ ậ ỉ ẽn tương tự (cùng v n t c ban đố ầu và góc nghiêng) thì k lục s là: (cho gia tốc trọng
trư
ờng ở Hà Nội là 𝑔𝑔
1
= 9,727 m/s
2
, ở Xanh Pêtecbua là 𝑔𝑔
2
= 9,810 m/s
2
, bỏ qua chiều
cao c i đủa ngườ ẩy)
A. 16 951, . . . . m B. 12 951, m C. 15 951, m D. 13 951, m
Lời giải:
Chọn hệ quy chiếu như hình v ọẽ. Gốc t a độ nằ ị ềm tại v trí b u ném, chiắt đầ u dương của
trục Oy hướng lên ngược chiề ểu v i gia t c g, g c th i điớ ố ố ời gian cũng là thờ m bắt đầu ném
vật.
Áp d i v i v t ném t
ụng công th m xa đôức tầ ớ ậ ại mặt đất: L=
v
2
sin 2θ
g
(1)
Trong cùng đi n ném (cùng v u và cùng góc nghiêng) nên ta có:ề ệu ki ậ ần t c ban đố
v
2
sin 2θ= const (2)
Từ (1), (2) => L1.g1= L2.g2
V
ậy kỷ l ục đ y tẩ ạ ở Xanh Petecbua là: L2=
L1.g1
g2
=
14 07 727, ∗9,
9
,81
≈ 13 951, m
TAILIEUHUST.COM
10 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Câu 8. Một ngườ ời đ ng cách con đưứ ng th ảng ẳng một kho ℎ = 50 m để chờ ô tô. Khi th y ấ
đầu ô tô còn cách mình mộ n t đoạ 𝑎 𝑎 = 200 m thì người ấy b u ch y (th ng, đắt đầ ạ ẳ ều, theo
một hư ng đớng nào đó) ra đườ ể đón gặp ô tô. Biế ểt vận t c ô tô là . Đố 𝑣 𝑣 = 36 km /h có thể
gặ ả ạ ậ ấp đư c ô tô, ngượ ời ấy ph i ch y v i vớ n t c nhố ỏ nh t 𝑣𝑣
min
bằng bao nhiêu?
A. 2,5 m/s m/s 3 m/s m/s. B. 3,25 . C. . D. 2,75 .
Lời giải:
Chọn hệ trụ ọ ộc t a đ Oxy như hình vẽ ọ, gốc t a
độ vị tại A- trí ban đ a oto, g c thầu củ ố ời gian là
lúc người đó bắt đầu chuyển động
Gọi
1
v
(m/s) là v n t y c i đó.ậ ốc chạ ủa ngườ
α là góc t i 2 vecto v n tạo bở ậ ốc
+ Chi c Ox ta có:ếu theo trụ
Tọ ểa độ ô tô đi t i thạ ời đi m t (s) là:
1
x
= vt
Tọ ểa độ của ngư ạời ch y t i th i điạ ờ m t(s) là:
2
x
=
1
v
tcosα + AH
Tạ ểi th i điờ m 2 vậ ặt g p nhau:
1
x
=
2
x
=> (
v
–
1
v
tcosα)t = AH (1)
+ Chi c Oy ta có:ếu theo trụ
Tọ ểa độ người chạy t i th i điạ ờ m t(s):
2
y
=
1
v
tsinα - h
2 vật gặp nhau:
2
y
= 0 =>
1
v
tsinα = h (2)
Từ (1) và (2)
1 min
2 2
V V 2,5( m / s)
sin cos
hv hv h h
v
AH h a a
AH h
α α
= ≥ = ⇒ = =
+
+
Câu 9. Một hòn đá được ném theo phương ngang t ủ ốừ độ cao đ lớn v i v n tớ ậ c 𝑣𝑣
0
=
12 m/s. Gia t c pháp tuy n c a hòn đá sau giây th ng (lố ế ủ ứ 2 có giá trị bằ ấy 𝑔 𝑔 = 9,8 m/s
2
)
A.
4, 5, 5, 4,617 m/s
2
. B. 117 m/s
2
. C. 867 m/s
2
. D. 867 m/s
2
.
Lời giải:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 11
- Chọn hệ trục tọa độ Oxy như hình v , g c thẽ ố ời
gian lúc vậ ắt b t đầu chuyển động.
- Theo trục
Ox
: Vận tốc của vật là:
0x
v v=
- Theo tr c Oy:ụ
Vận tốc của vậ ạt t i th i điờ ểm
t(s)
là:
vy gt=
Vậy độ lớn v n tậ ốc chuyển đ ng cộ ủa v ạật t i t là:
2 2 2 2
0
v ( )
x y
v v v gt= + = +
Gia t p tuy n cốc tiế ế ủa vậ ạt t i
t
lcó độ ớn là:
2
at
dv g t
dt v
= =
Gia t c pháp tuy n cố ế ủa vật tại
t
có giá trị là:
2 2
0
n
a g
t
v
g a
v
= − =
⇒
Gia t c pháp tuy n cố ế ủa v ạật t i giây thứ 2 là:
( )
2
n
a (2) 5,117 m / s=
Câu 10. Một bánh xe bắt đầu quay quanh m ụ ốột tr c c định đi qua tâm vành bánh và
vuông góc v nh bới mặt ph ng bánh xe, có góc quay xác đẳ ị ẳng biểu thức: 𝜑 𝜑 = 𝑎𝑎𝜔𝜔
2
; trong
đó là th𝑎 𝑎 = 0,125rad/s
2
; 𝜔𝜔 ời gian. Đi m A trên vành bánh xe sau có v n tể 2 s ậ ốc dài 𝑣 𝑣 =
2 m/s. Gia t c toàn ph n c m A khi đó có giá trố ầ ủa điể ị b ằng:
A.
2
√
2 m/s 5 m/s 5 m/s 2 m/s
2
. B. 2
√
2
. C. √
2
. D.
√
2
.
Lời giải:
Tốc đ góc cộ ủa bánh xe là:
w 2
d
at
dt
φ
= =
Bán kính của bánh xe là:
2 t
r
v v
w a
= =
Gia t c góc c a bánh xe là: ố ủ
2a
dw
dt
β
= =
Gia t p tuy n cốc tiế ế ủa điểm A là:
at r
2
v v
at t
β β
= = =
Gia t c pháp tuy n cố ế ủa điềm A là:
2
n
a w r 2atv= =
Gia t c toàn ph n cố ầ ủa điềm
A
là:
2
2
(2atv) 2( / )
tp
v
a m s
t
= + =
TAILIEUHUST.COM
12 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Câu 11. Chất đi ắểm b t đầu chuyển động trên đường tròn bán kính
R 2( m)=
. Vận tốc của
chất đi c vào quãng đư ng đi đưểm phụ thuộ ờ ợc S theo công thức
v a s=
với
2
2( / )a m s=
.
Góc giữa vector vận tốc
v
và gia t ầốc toàn ph n
γ
sau
3 s
i đượ ởc xác định b
A.
tg 8,6
α
=
B.
tg 9
α
=
C.
tg 9, 2
α
=
C.
tg 9, 6
α
=
Lời giải:
- Ta có:
2 (1)
ds ds
v a s a s adt at s
dt
s
= ⇒ = ⇔ = ⇔ =
∫ ∫
Thay
2
3( ) 9( )
2
at
t s s m
= ⇒ = =
- Gia t c hưố ớng tâm:
2 9 6
m
v a s
s
= = =
⇒
2 2
2
6
18
2
n
v m
a
R s
= = =
Từ (1)
2 2 2 2 2
2
2 2 2.2
, 2
4 4 4 4
a t ds a t dv a m
s v a
dt dt s
⇒ = ⇒ = = ⇒ = = =
- Ta có góc giữa
v
và
γ
là góc giữa
a
và
γ
18
tan 9
2
n
a
a
α
⇒ = = =
Câu 12. Từ đỉnh đồi cao, một quả pháo được bắn ch ch lên phía trên mế ột góc
30a
°
=
so
với phương n m ngang v i v n t c đằ ớ ậ ố ầu nòng là
0
400( m / s)v =
. Sau khi b n mắ ột khoảng
thời gian
t
5( )s=
, góc
ϕ
giữa hư ng c n tớ ủa vậ ốc quả pháo và hư a gia t c toàn ớng củ ố
ph ứần thỏa măn giá tr nào dư qua sị ới đây ( bỏ c cản không khí. Gia tố ọc tr ng trường bẳng
( )
2
9,8 m / sg =
A.
tg 1,894
β
= −
B.
tg 2,894
β
= −
C.
tg 2,094
β
= −
D.
2, 294tg
β
= −
Lời giải:
Ta có phương trình v n tậ ốc của vật là
0
0
cos 400cos30 200 3
sin 200 9,8
x
y
m
v v
s
v v gt t
α
α
°
= = =
= − = −
Tại t = 5 ta có
151( / ) 0
y
mv s= >
Gọ ối gia t c toàn phần là
g
→
Góc hợp bởi
( ; )v g
là
γ
như hình vẽ:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 13
Có
151
tan
200 3
y
x
v
v
ϕ
= =
Mà
1 200 3
90 tan cotg 2, 29
tan 151
γ ϕ γ ϕ
ϕ
°
−
= + ⇒ = − = = − = −
.
TAILIEUHUST.COM
14 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Chương 2-3. Độ ọ ể ệ ể độ ọ ắnng lực h c chất đi m – h chất đi m – ng lực h c vật r
A. Công thức
Chương 2:
1. Các định luật Newton
- Đị ậ ứnh lu t Newton th nhất: Nếu một vật không ch u tác d ng c a lị ụ ủ ực nào hoặc chịu tác
dụng c a các l c có hủ ự ợp lực bằng không thì nó giữ nguyên trang thái đứng yên hoặc
chuy ộển đ ng thẳ ềng đ u.
0 0.F a= ⇒ =
∑
- Đị ậ ứnh lu t Newton th hai: Gia tốc củ ộa m t vật cùng hướ ớng v i lực tác dụ ộng lên v t. Đậ
lớn củ ốa gia t c tỉ l lệ thu ộận v i đớ ớn c a l c và tủ ự ỉ l ệ nghịch v i kh ng cớ ối lượ ủa vật.
.
F
F m a a
m
= ⋅ ⇒ =
∑
∑
- Đị ậ ứnh lu t Newton th ba: Trong m i trư p, khi v t A tác d ng lên vọ ờng hợ ậ ụ ật B m t lộ ực, thì
vậ ịt B cũng tác d ng l c. Hai l c này có cùng giá trụ ại A một lự ự , cùng độ lớn nhưng ngược
chiều nhau.
.
AB BA
F F= −
2. Một số loại lực cơ học
- Lực ma sát:
.
ms
F N
µ
=
với
µ
s là hệ ố ma sát,
N
là áp lực
- Lực hướng tâm:
2
ht
mv
F
r
=
.
- Lực quán tính li tâm trong chuy ộng tròn đển đ ều:
2
lt ht
mv
F F
r
= =
.
- Lực căng (xét vật
1
m
với
2
m
):
2 1 2
( )T m g m a m g a= − = −
.
3. Độ ợng lư ng và xung lượng
- Độ biến thiên động lượng:
2
1
2 1
t
t
k k k Fdt∆ = − =
∫
.
với
2
1
t
t
Fdt
∫
là xung lượng c a lủ ực
F
trong khoảng thời gian từ
1 2
t t→
.
- Xung lực:
.p F t∆ = ∆
.
4. Các loạ ại va ch m
Động năng
& Đ ng lưộ ợng
Va ch m đàn hạ ồi
2 2 2 2
1 1 2 2 1 1 2 2
2 2 2 2
m v m v m v m v
+ = +
1 2 1 2
p p p p
′ ′
+ = +
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 15
2 2 2 2
1 1 2 2 1 1 2 2
m v m v m v m v→ + = +
1 1 2 2 1 1 2 2
i
m v m v m v m v→ + = +
Va chạm không đàn hồi
Không bảo toàn
( )
1 1 2 2 1 2
m v m v m m v+ = +
1 1 2 2
1 2
m v m v
v
m m
+
→ =
+
5. Moment độ ợng lư ng
- Liên hệ giữa moment động lượng và đ ng: ộng lượ
L r p= ×
.
- lĐộ ớn moment động lượng:
.sinL rmv mr v
θ
⊥
= =
. hay
.L I
ω
=
.
Chương 3:
1. Đị ộ ợnh luậ ảt b o toàn đ ng lư ng
- Động lượng:
p mv=
. - Bảo toàn động lượng:
p p
′
=
∑ ∑
.
2. B o toàn moment đả ộ ợng lư ng
- Phương trình cơ b n cả ủa chuyển động quay:
.M I
β
=
.
- Bảo toàn moment động lượng:
1 2 1 2 1 1 2 2 1 1 2 2
L L L L I I I I
ω ω ω ω
′ ′ ′ ′
+ = + → + = +
.
- Đị ềnh lý v moment động lượng:
i
dL
M
dt
=
∑
.
- Các phương trình động l c hự ọc:
0
2
0
2 2
0
1
.
2
2
t
t t
ω ω β
ϕ ϕ ω β
ω ω βϕ
= +
= + +
− =
3. Moment quán tính của các loại vật rắn
- Moment quán tính của v ắ ấật r n b t k i v c quay:ỳ đố ới trụ
2
1
.
i
object
i
I m r r dm= ∆ =
∑
∫
- Moment quán tính củ ốa ch m có khất điể i lượng
m
đối với trục quay:
2
. I mr=
- Moment quán tính của thanh dài chi c vuông góc và đi qua tâm c a ều dài l, đ i vố ới trụ ủ
thanh:
2
1
.
12
I ml=
TAILIEUHUST.COM
16 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
- Moment quán tính của đĩa tròn ho đặặc trụ c đ ng ch t có kh ng m, bán kính R: ồ ấ ối lượ
2
1
.
2
I mR=
- Moment quán tính của vành hoặc trụ ố rỗng đồng ch t khấ i lượng m, bán kính R:
2
.I mR=
- Moment quán tính c ồủa kh u đ c đối cầ ặ ng chất:
2
2
.
5
I mR=
- Moment quán tính của thanh dài l, tr ầục quay đi qua 1 đ u thanh:
2
1
.
3
I ml=
4. Độ ọng lực h c vậ ắt r n quay
- Công thức liên hệ vận tốc và gia tốc:
2
2
;
t n
v
v r a r a r
r
ω β ω
= → = = =
5. Chuyể ộ ắnn đ ng lăn của vật r
- Trường h p lăn không trượ ợt:
v r a r
ω β
= → =
- -Định lý Steiner Huygens: Mômen quán tính củ ộ ố ộ c nào đó a m t vật rắn đ i với m t trụ
bằng mômen quán tính của vật rắn đ i v c song song đi qua kh i tâm c ng vố ới trụ ố ộ ới tích số
của kh i lương vố ật rắn và bình phương khoảng cách giña hai trục.
𝐼𝐼
𝑂 𝑂
= 𝐼𝐼
𝐺 𝐺
+ 𝑚𝑚𝑟𝑟
2
.
Trong đó:
Io _ mô men quán tính củ ố ụa vật đ i với tr c quay đi điểm O
𝐼𝐼
𝐺 𝐺
− mô men quán tính của vật đối với trục quay đi qua kh i tâm ố G
𝑚𝑚
−
khố ủi lượng c a vật.
- Động năng của chuyển động lăn:
• Trường hợp lăn: 𝑊 𝑊 = 𝑊𝑊
𝑡𝑡𝑡𝑡
+ 𝑊𝑊
𝑞 𝑞
=
𝑚𝑚𝑣𝑣
2
2
+
𝐼𝐼
𝐺𝐺
𝜔𝜔
2
2
.
• Trường h p quay: ợ 𝑊 𝑊 = 𝑊𝑊
𝑞 𝑞
=
𝐼𝐼
𝑂𝑂
𝜔𝜔
2
2
=
�
𝐼𝐼
𝐺𝐺
+𝑚𝑚𝑟𝑟
2
�
𝜔𝜔
2
2
=
𝐼𝐼
𝐺𝐺
𝜔𝜔
2
2
+
𝑚𝑚𝑟𝑟
2
𝜔𝜔
2
2
.
6. Công thức Huygens-Steiner
𝐼𝐼
𝑂 𝑂
= 𝐼𝐼
𝐺 𝐺
+ 𝑚𝑚𝑟𝑟 𝐼𝐼
2
hay
𝑧 𝑧
= 𝐼𝐼
𝐶𝐶𝐶𝐶
+ 𝑀𝑀𝐷𝐷
2
.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 17
B. Bài tậ ắp tr c nghiệm
Câu 1. Ở thời đi m ban để ầu mộ ốt ch m có khất điể i lượng 𝑚 𝑚 = 1 kg có v n tậ ốc 𝑣𝑣
0
=
20 m/s. Ch m chất điể ịu lực cản 𝐹𝐹
𝑐 𝑐
= −𝑟𝑟𝑣𝑣 (biết 𝑟 𝑟 = ln 2,𝑣𝑣 là v n tậ ốc chất điểm). Sau 2,2 s
vậ ển t a chốc củ ất đi m là:
A. 4, m/s353 . . . . B. 3,953 m/s C. 5,553 m/s D. 3,553 m/s
Lời giải:
Áp d ng đụ ịnh luật II Newton ta có:
c
F ma= ⇒
𝐹𝐹
𝑐 𝑐
= =−𝑟𝑟𝑣𝑣 𝑚𝑚𝑎𝑎 = 𝑚 𝑚
𝑑𝑑𝑣𝑣
𝑑𝑑𝑡𝑡
⇒ −
𝑟𝑟
𝑚 𝑚
𝑑𝑑𝜔𝜔 =
𝑑𝑑𝑣𝑣
𝑣 𝑣
⇒ � −
𝑟𝑟
𝑚 𝑚
𝑑𝑑𝜔𝜔 =
𝑡𝑡
0
�
𝑑𝑑𝑣𝑣
𝑣𝑣
𝑣𝑣
𝑣𝑣
0
⇒ −
𝑟𝑟𝜔𝜔
𝑚 𝑚
= ln 𝑣 𝑣
|
𝑣𝑣
0
𝑣 𝑣
= ln
𝑣𝑣
𝑣𝑣
0
⇒
𝑣 𝑣 = 𝑣𝑣
0
× 𝑒𝑒
−
𝑟𝑟
𝑚𝑚
𝑡 𝑡
= 20 × 𝑒𝑒
− ln2 2× ,2
≈ 4,353
Câu 2. M ột viên bi nhỏ 𝑚 𝑚 = 14 g rơi theo phương th ng đẳ ứng không vậ ần t c ban đố u
trong không khí, l ủa không khí ực cản c 𝐹𝐹
𝑐𝑐
�
�
�
= −𝑟𝑟𝑣𝑣 l(tỷ ệ ngược chi c), ề ốu v i v n tớ ậ 𝑟𝑟 s là hệ ố
cản. V n tậ ốc c c bực đ i mà viên bi đạ ạt đượ ằng 𝑣𝑣
max
= =60 m/s. Cho 𝑔 𝑔 10 m/s
2
. Hệ số cản
có giá trị:
A.
2, /m333 10.
−3
Ns . B. 2, 363 10.
−3
Ns/m.
C.
2, /m353 10.
−3
Ns . D. 2, /m343. 10
−3
Ns .
Lời giải:
Khi th do c n t i v n t khi v n t n thả vật rơi tự ó lực cả ỉ lệ vớ ậ ốc thì ật đạt vậ ố đủc lớn, đế ời điểm
lực cản có l l p lđộ ớn bằng độ ớn của trọ ựng l c tác dụng l n vê ật thì khi đó hợ ực tác dụng lên
vật bằng 0 và vật rơi v i v n tớ ậ ốc không đổi 𝑣𝑣
𝑚𝑚𝑚𝑚𝑥𝑥
Do đó, ta có: �𝐹𝐹
𝑐𝑐
max
� = 𝑟𝑟𝑣𝑣
max
= 𝑃 𝑃 = 𝑚𝑚𝑔𝑔
⇒ 𝑟𝑟
=
𝑚𝑚𝑔𝑔
𝑣𝑣
max
=
0,014.10
60
= 2,333.10
−3
(
𝑁𝑁𝑠𝑠/𝑚𝑚
)
Câu 3. Một tàu điện sau khi su ng n i gia tất phát chuy ng trên đưển độ ờ ằm ngang vớ ốc 𝑎 𝑎 =
0,7 m/s
2
. 11 giây sau khi bắt đầu chuyể ển đ i ta tộng ngườ ắt động cơ và tàu chuy n động
cho đ ố . Cho ế ện khi d ng hừ ẳn. H s ma sát trên quãng đư ng ờ 𝑘 𝑘 = 0,01 𝑔 𝑔 = 10 m/s
2
. Thời
gian chuyển đ ng cộ ủa toàn bộ tàu là
A. 92,8 s. B. 84 88,8 s . C. s. D. 86,4 s .
Lời giải:
Giai đoạn 1, sau 11s v n tật đạt vậ ốc tối đa là:
𝑣𝑣
max
= 𝑎𝑎𝜔𝜔 = 0,7.11 = 7,7 (𝑚𝑚/𝑠𝑠)
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 19
Tại điểm rơi, 𝑁𝑁
𝑠 𝑠
= 0, do đó: 𝑚𝑚𝑔𝑔
𝑅𝑅−Δℎ
𝑅 𝑅
= 𝑚 𝑚
𝑣𝑣
2
𝑅 𝑅
⇒ 𝑣𝑣
2
= 𝑔𝑔(𝑅𝑅 − Δℎ)
Lại có, áp dụng định luậ ảt b o toàn cơ năng ta được:
𝑚𝑚𝑔𝑔𝑅𝑅 = 𝑚𝑚𝑔𝑔
(
𝑅𝑅 − Δℎ
)
+
1
2
𝑚𝑚𝑣𝑣
2
⇒ 𝑣𝑣
2
= 2𝑔𝑔Δℎ ⇒ 𝑔𝑔 𝑅𝑅 − Δℎ 𝑔𝑔Δℎ
( )
= 2
⇒ Δℎ
=
𝑅𝑅
3
=
2
3
= 0,667
(
𝑚𝑚
)
Câu 6. Mộ ốt đoàn tàu kh i lượng 30 tấn chuyể ờn động trên đư ng ray n i vằm ngang vớ ận
tố ổc không đ i bằng 12 km 200/h. Công su u máy là ấ ầt đ kW. Gia tốc trọng trư ng ờ 𝑔 𝑔 =
9,8 m/s
2
. H ma sát bệ số ằng:
A.
23, 4.10
−2
. . . . B. 20 41 10, .
−2
C. 22 10, 4.
−2
D. 21 41 10, .
−2
Lời giải:
Đổi
10
12( km / h) ( m / s)
3
v = =
Ta có:
3
200.10
. 600( )
10
3
P
P F v F N
v
= ⇒ = = =
Mà
2
3
6000
6000( ) 20, 41.10
30 10 9,8
ms
ms
F
F F mg N
mg
µ µ
−
= = = ⇒ = = =
⋅ ⋅
Câu 7. Một chất điểm bắt đầu trượt từ đỉnh mặt phẳng
nghiêng góc m ngang (xem hình v𝛼𝛼 so v i phương nớ ằ ẽ ệ). H
số ma sát gi t phữa vật và mặ ẳng nghiêng là 𝑘𝑘; khối lượng
của vật là 𝑚𝑚 (lấy 𝑔 𝑔 = 9,81 m/s
2
). Cho 𝑚 𝑚 = 2,5 kg, 𝑘 𝑘 =
0,2, m,ℎ = 8 𝛼 𝛼 = 30
∘
. Mômen t ng h c tác dổ ợp các lự ụng lên
chất điểm đ i vố ới O là:
A. 62,107Nm. B . C . . . 45 652Nm, . 52 234Nm, D. 55 527Nm,
Lời giải:
Chọn hệ trụ ộc tọa đ Oxy như hình v , chiẽ ều dương
cùng chiều chuyể ịn đ ng c t chộ ủa vật Vậ u tác d ng cụ ủa
các l c: trự ọng lực
P
, ph n lả ực
N
và l c ma sát ự
ms
f
Áp d ng đụ ịnh luật II Newton, ta có:
(1)
ms
P N f ma+ + =
Chiếu (1) lên trục
: 0 cos cos
n
Ox N P N P mg
α α
− = ⇔ = =
TAILIEUHUST.COM
20 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Chiếu (1) lên trục
sin
: sin
mx
t ms ms
P f
Oy P f ma P f ma a
m
α
α
−
− = ⇔ − = ⇒ =
Mà
cos (sin cos )
ms
f kN kmg F mg k
α α α
= = ⇒ = −
Mômen tổng h p các v c d ng lên ch m đ i vợ ật tá ụ ất điể ố ới
O
chính là công của lực
F
tác
dụ ểng lên đi m
O
. .cos (sin cos ). .cos 30 55,525( )
F
A F h mg k h N
α α α
°
= = − =
Câu 8. Một ô tô khối lượng 𝑚 𝑚 = 550 kg chuyể ền đ ng động thẳ u xuố ộng d c trên mố t mặt
phẳng nghiêng, góc nghiêng 𝛼𝛼 so với mặt đất n m ngang có ằ sin =𝛼 𝛼 = 0,0872; cos 𝛼 𝛼
0,9962. L c kéo ô tô bự ằng 𝐹𝐹
𝑘 𝑘
= 550 10 N, cho 𝑔 𝑔 = m/s
2
. Hệ số ma sát gi a ô tô và mữ ặt
đường là:
A. 0,158 B. 0,188 C. 0,208 D. 0,198
Lời giải:
Chọ ụn tr c Oxy như hình v . Chiẽ ều dương cùng
chiề ểu chuy n đ ng v i ô tôộ ớ
Ô tô ch u tác d ng c a các l c kéo ị ụ ủ ực: lự
F
của
động cơ ô tô, tr ng lọ ực
P
, ph n l p tuyả ực tiế ến
N
của m c ma sát c a mặt đư ng và lờ ự ủ ặt đư ng ờ
ms
f
Áp d ng đụ ịnh luật II Newton, ta có
0
ms
F P N f+ + + =
(vì ô tô chuyề ền đ ng động thẳ u)
Chiếu phương trình này nên phương chuy ủển đ ng cộ a ô tô, ta được:
sin 0
k ms
F f P
α
− + =
sin
sin sin cos sin 0,188
cos
k
k ms
F mg
F f P kN P kmg mg k
mg
α
α α α α
α
+
⇒ = − = − = − ⇒ = =
Câu 9. Một quả c ầu có khối lượng 𝑚 𝑚 = 100 g đư ầợc g n vào đắ u sợi dây có khối lượng
không đáng k ầể. Một đ u dây gắn vào điể địm O cố nh. Sợi dây có chiều dài 𝑙 𝑙 = 50 cm. Cho
vật chuyển động tròn quanh n O trong m ạặt ph ng đ ng. Tẳ ứ i vị trí cao nhất B quả ầ ậ c u có v
tốc 𝑣𝑣
𝑛 𝑛
= 3,2 = 9, m/s. L y ấ 𝑔 𝑔 81 m/s
2
. S c căng c a s i dây t i v p nh t A có giá trứ ủ ợ ạ ị trí thấ ấ ị:
A. 9, 7, N 6, 5, N953 N. B. 953 . C. 953 N. D. 953 .
Lời giải:
Chọ ốn m c thế năng tại vị trí A
Áp d ng đ ng t i hai vụ ị ợnh luậ ảt b o toàn Năng lư ạ ị trí A và B ta có:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 21
2 2 2 2
1 1
0 2
2 2
A B A B B A B B
W W mv mv mgh v v gh= ⇔ + = + ⇔ = +
2
29,86
A
v⇒ =
Áp d ng đ t II Niu Tơn t i đi m A theo ng đ ng ta có:ụ ịnh luậ - ạ ể phương thẳ ứ
2
6,953
A
ht ht
v
T P F mg ma mg m
l
= + = + = + =
(N)
Câu 10. Một hòn bi khối lượng 𝑚𝑚
1
đến va ch i và xuyên tâm vạm hoàn toàn đàn hồ ới hòn
bi 𝑚𝑚
2
ban đ u đ ng yên. Sau va chầ ứ ạm chúng chuy ộ u nhau vển đ ng ngược chiề ới cùng độ
l
ớn v n t c. Tậ ố ỉ s ố kh ợối lư ng của chúng
𝑚𝑚
1
𝑚𝑚
2
là:
A. 1/6. B. 1. C. 1/2. . D. 1/3
Lời giải:
Ch ầọn chi u đi chuyề ều dương là chi ển ban đ u của
1
m
Sau va chạm vật
1
m
chuy ộển đ ng ngư u dương và vậợc chiề t
2
m
chuyển động theo chiều
dương với cùng v n t c vậ ố
Bảo toàn động lượng ta có:
1 1 2 1 1 1 2
( )m v m v m v m v v m v= − ⇒ + =
(1)
Bảo toàn động năng ta có
2 2 2 2 2 2
1 1 1 2 1 1 2
1 1 1
( )
2 2 2
m v m v m v m v v m v= + ⇔ − =
(2)
Lấ /y (2) (1) ta có :
1 1
2v v v v v− = ⇔ =
(3)
Thay (3) vào (1) ta có:
1
1 2
2
1
.3 .
3
m
m v m v
m
= ⇒ =
Câu 11. Một phi công thực hiện vòng tròn nhào l ố ủộn trong m t ph ng. V n tặ ẳng đứ ậ c c a
máy bay không đ ng áp l a phi công lên ghổi 𝑣 𝑣 = 900 km/h. Giả sử rằ ực lớn nh ủất c ế bằng
5 lần tr ng lọ ực của ngư ấời. L y 𝑔 𝑔 = 10 m/s
2
. Bán kính quỹ đạo vòng nhào lộn có giá trị
bằng
A. . 1562 1584 1594 1573,5 m. B. ,1 m . C. ,4 m. D. ,3 m
Lời giải:
Các lực tác d ng lênụ máy bay và phi công: Tr ng l c P , ph n l c Qọ ự ả ự
Áp d ng đ t II Niuụ ịnh luậ -tơn ta có:
ht ht
P Q ma Q ma P+ = ⇒ = −
Áp lực lên gh t khi P và ế lớn nhấ
ht
a
ngược hướng
⇒
Áp lực max t i đi p nhạ ểm thấ ất:
ht ht
P Q ma Q ma P+ = ⇒ = −
TAILIEUHUST.COM
22 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
2 2
5
4
ht
v v
Q ma P mg m mg R
R g
⇒ = + ⇔ = + ⇒ =
Thay số:
2
900 / 250 / ; 10 / 1562,5v km h m s g m s R m= = = ⇒ =
Câu 12. Một thanh chi u dài ề 𝑙 𝑙 = 0,9 m, khối lượng 𝑀 𝑀 = 6 kg có th quay tể ự do xung quanh
một trục nằm ngang đi qua một đầu của thanh. Một viên đ n khạ ối lượng 𝑚 𝑚 = 0,01 kg bay
theo hương nằm ngang v ậ a thanh và mới v n t i xuyên vào d u kia cốc 𝑣 𝑣 = 300 tm/s ớ ầ ủ ắc
vào thanh. ậVận t c góc c a thanh ngay sau khi viên đ n đố ủ ạ p vào đầu thanh là:
A. 2, /s 1, /s 1, /s 1, /s429rad . B. 915rad . C. 144rad . D. 658rad .
Lời giải:
Mô-men đ ng lư c khi va chộ ợng trướ ạm là:
.
t
L v p pl mvl= = =
Sau va ch n và thanh sạm viên đạ ẽ chuyển đ ng vộ ới cùng gia
tốc góc
ω
Mo-men đ ng lư ng sau va chộ ợ ạm là:
2
2
( )
3
s th d
Ml
L I I ml
ω ω
= + = +
Áp d ng đụ ịnh luật bảo toàn Động lượng:
2
2
2
2
3
3
t s
Ml mvl
L L mvl ml
Ml
ml
ω ω
ω
= ⇔ = + ⇒ =
+
Thay số ta được
1, 658
ω
≈
(rad/s)
Câu 13. Mộ ỏt vật nh có khối lượng 𝑚𝑚 buộc vào đầu sợi dây mảnh chiều dài 𝑙 𝑙 = 1,5 m, dầu
kia giữ cố định. Cho vật quay trong m m ngang vặ ẳ ằt ph ng n ới v n tậ ốc góc không đổi sao
cho s . Cho ỏợ ới dây h p vợ i phương th ng đ ng mẳ ứ ột góc 𝛼 𝛼 = 30
∘
𝑔 𝑔 = 10 m/s
2
, b qua lực
cản không khí. Tốc độ góc có giá trị:
A. 2, /s 2, /s 3, /s 2, /s575rad . B. 775rad . C. 075rad . D. 675rad .
Lời giải:
Chọ ốn m c thế năng tại vị ề trí căn bằng, chi u dương hướng xuống
Trong quá trình dao đ ậộng, v t ch u tác d a các l ng lị ụng củ ực: trọ ực
( )P
, lực căng dây
( )T
và l ng tâm ực hướ
ht
F
Áp d ng đ t II Newton, ta có: ụ ịnh luậ
0
ht
P T F+ + =
Chiế ều (1) lên chi u dương Ox
sin 30 0 sin 30
ht ht
F T F T
° °
− = ⇒ =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 23
Chiếu (1) lên trục
Oy : cos 0 cos cos30
cos 30
mg
P T P T mg T T
α α
°
°
− = ⇒ = ⇔ = ⇔ =
3
sin 30 tan 30
3
ht
F T mg mg
° °
⇒ = = =
. Mà
2 2
.sin 30
ht ht
F ma m R m l
ω ω
°
= = =
2 2
1 2
.sin 30 2,775(rad / s)
2
3 3 3
.
mg g g
m l l
l
ω ω ω
°
= ⇔ = ⇒ = =
Câu 14. Một ô tô có khối lượng 𝑚 𝑚 = 2,1 tấn chuy n để ộng trên đo m ngang vạn đường nằ ới
vậ ấn t c không đố ổi 𝑣𝑣
0
= 54 km/h. Công su t của ô tô bằng 9,8 kW. Lấy 𝑔 𝑔 = 9,8 m/s
2
. Hệ số
ma sát gi t đư ng có giá trữa bánh xe và mặ ờ ị bằng
A.
0, 0,305 10.
−1
. B. 0, 281 10.
−1
. C. 0, 317 10.
−1
. D. 341 10.
−1
.
Lời giải:
- Ch ọn hệ quy chiếu Oxy chiều dương của Ox cùng chiều
với chiều của vận tốc ô tô; trụ ớc Oy hư ng lên
- G s ọi K là hệ ố ma sát của mặt đường ta có 𝐹𝐹
𝑘𝑘
. 𝑉 𝑉 =
𝑃𝑃
𝑘 𝑘
= 9800
Do 𝐹𝐹
𝑘𝑘
là ên lực kéo củ ầa đ u máy n 𝐹𝐹
𝑘 𝑘
=
9800
15
=
1960
3
(N)
Theo đị ậnh lu t 2 Newton: 𝐹𝐹
𝑘𝑘
�
�
�
�
+ 𝐹𝐹
𝑚𝑚𝑠𝑠
�
�
�
�
�
�
+ 𝑃𝑃
�
+ 𝑁𝑁
�
�
= 𝑚𝑚𝑎𝑎
Mặt khác ô tô chuyển động với vận tốc không đổi nên 𝑎𝑎 = 0
�
.
Chiếu theo chiều dương của Oy ta được: 𝐹𝐹
𝑘 𝑘
− 𝐹𝐹
𝑚𝑚𝑠𝑠
= 0
𝐹𝐹
𝑚𝑚𝑠𝑠
= 𝐹𝐹
𝑘 𝑘
⟺ 𝐾𝐾𝑚𝑚𝑔𝑔 = 𝐹𝐹
𝑘 𝑘
⟹ 𝐾𝐾 =
𝐹𝐹
𝑘𝑘
𝑚𝑚𝑔𝑔
=
1960
3
2100
∗ 9,8
≈ 0,317 ∗ 10
−1
Câu 15. Mộ ốt tàu đi t phát chuy ng trên đưện khi xuấ ể ộn đ ờng n m ngang v i gia tằ ớ c 𝑎 𝑎 =
0,9 m/s
2
, 13 s sau khi bắt đầu chuyển đ i ta t t đ n động ngườ ắ ộng cơ và tàu chuyể ộng cho
đế ện khi d ng l i h n. Hừ ạ ẳ số ma sát trên đường 𝑘 𝑘 = 0,01. Cho 𝑔 𝑔 = 10 m/s
2
. Thời gian
chuyển động toàn b ủộ c a tàu là:
A. 130 . . . . s B. 126,8 s C. 125,2 s D. 128,4 s
Lờ ảii gi
- Chọn hệ quy chiếu như hình v ộẽ, gốc tọa đ trùng v ậới v t, g c th i gian t i th i đi m vố ờ ạ ờ ể ật
bắt đầu xuất phát t
o
= 0, v
o
=0
- Con tàu chuy ộển đ ng trong hai giai đoạn:
TAILIEUHUST.COM
24 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
+ Giai đoạn 1: tàu chuy ộng nhanh dển đ ần đ u về ới
gia t c a trong thố ời gian t
1
+ Giai đoạn 2: tàu chuy ộ n ển đ ng ch m d n đ u đậ ầ ề ế
khi d ng h n v i gia t gây ra b
ừ ẳ ớ ốc a
′
ởi lực ma sát
cùng phương và ngư ậợ ềc chi u v n tốc
Phương trình v ố ủận t c c a tàu giai đoạn 1 là: v =
v
0
+ a(𝜔𝜔
1
− t
o
)
V
ận t a tàu khi h n 1 làố ủc c ết giai đoạ : v = v
0
+ at = 0 + 0,9.
1
13 11= ,7 m/s
Sau khi tắt động cơ, định luật II Newton cho tàu: P
�
�
+ N
�
�
+ F
ms
�
�
�
�
�
�
�
= ma
�
Chiếu theo chiều Oy: N − P = 0 ⇔ N = P = mg
Chiếu theo chiều Ox: − −F
ms
= ma
′
⇔ −Kmg = ma
′
=> a
′
= −Kg = 0,01.10 = 0,1 (m/s
2
)
Sau khi tắt động cơ, phương trình vận tốc của tàu giai đoạn 2 là:
v
′
= v − a
′
∗ t
2
⇔ 0 = 11,7 +
(
−0,1
)
t
2
⇔ t
2
= 117(s)
Thời gian chuyển động toàn bộ tàu:
t = t
1
+ t
2
= 117 + 13 = 130
(
s
)
Câu 16. Mộ ột ngư ằời kéo xe b ng m t hợp lực với phương ngang một góc 𝛼 𝛼 = 30
∘
. Xe có
khối lượng và chuy a bánh xe 𝑚 𝑚 = 240 kg ể ện động v i v n t i. Hớ ậ ố ổc không đ số ma sát giữ
và mặt đư ng ằờ 𝑘 𝑘 = 0,26. L y ấ 𝑔 𝑔 = 10 m/s
2
. L c kéo có giá trự ị b ng:
A. 622 59, . . . . N B. 626 49, N C. 614 79, N D. 618 69, N
Lời giải:
Chọn hệ quy chiếu Oxy như hình vẽ. Oy hướng lên Ox cùng
hướng với hướng chuyển động.
Vì vật chịu hợp lực nhưng lại chuyển động đều nên 𝑎𝑎 = 0
�
Áp dụng ậ
định lu t II Newton: 𝐹𝐹
+ N
�
�
+P
�
�
+ F
ms
�
�
�
�
�
�
�
= 0
�
Chiếu theo chiều Oy ta có:
N – P + F sin α = 0 ⇔ N = mg – F sin α
Chiếu theo chiều Ox ta có: F cos α α – F
ms
= 0 ⇔ F cos – KN = 0
⇔ ⇔ F cos α – K(mg – F sin α
) = 0 F(cos α + K sin α) = Kmg
⇒ F =
Kmg
K sin α+cos α
= 626,49(N)
Câu 17. Mộ ốt đĩa tròn kh i lượng 𝑀 𝑀 = 155 kg mđỡ ột ngư ng ờ ợi có khối lư 𝑚 𝑚 = 51 kg. Lúc
đầu người đứng ở mép và đĩa quay v ậới v n tốc góc 𝜔𝜔
1
= 10 vòng/phút quanh trục đi qua
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 25
tâm đĩa. V a đĩa khi ngư i đi vào đúng tâm c a đĩa là (coi ngưận t c góc cố ủ ờ ủ ời như 1 chất
điểm)
A. 2, /s 2, /s 1, /s 0, /s006rad . B. 276rad . C. 736rad . D. 926rad .
Lời giải:
Coi ngư t điời như m t chộ ấ ểm, đ t bán kính đĩa là r ta có ặ 𝑤𝑤
1
= 10
𝑣𝑣
𝑃 𝑃
=
20𝜋𝜋
60
=
𝜋𝜋
3
(rad/s)
Vì là hệ kín nên momen đ o toàn. ộ ủng lư ng l c trư c và lúc sau cợ ứ ớ a hệ được bả
Khi người đứng mép đĩa:ở 𝐿𝐿
1
= 𝐼𝐼
1
𝑤𝑤
1
= �𝐼𝐼
𝑛𝑛𝑔𝑔ườ𝑖𝑖
+ 𝐼𝐼
đĩ𝑚𝑚
� = �𝑚𝑚𝑅𝑅
2
+
1
2
𝑚𝑚𝑅𝑅
2
� 𝑤𝑤
1
Giai đoạn sau: đ ý là khi ngư i đi vào tâm đĩa thì coi như kho ng cách tể ờ ả ừ người tới tâm
đĩa là 0. Điều này kéo theo mômen quán tính của ngư ng 0.ời v i tâm đĩa coi như bớ ằ
𝐿𝐿 𝐼𝐼
2
=
2
𝑤𝑤
2
= 𝐼𝐼
đĩ𝑚𝑚
𝑤𝑤
2
=
1
2
𝑀𝑀𝑅𝑅 𝑤𝑤
2
2
Áp d ng đụ ị ộnh luật bảo toàn đ ng lượng ta có:
𝐿𝐿
1 2
= 𝐿𝐿 ⟹ �𝑚𝑚 +
1
2
𝑀𝑀� 𝑤𝑤
1
=
1
2
𝑀𝑀𝑤𝑤
2
⟺ 𝑤𝑤
2
=
(
2𝑚𝑚+𝐶𝐶
)
𝐶 𝐶
𝑤𝑤
1
= 1,736 /𝑟𝑟𝑎𝑎𝑑𝑑 𝑠𝑠
Câu 18. Mộ ột người đ y xe mẩ t lực hướng xuống theo phương h i phương ngang mợp vớ ột
góc i lư𝛼 𝛼 = 30
∘
. Xe có khố ợng và chuy𝑚 𝑚 = 230 kg ể ện đ ng v i v n t c không đ i. Hộ ớ ậ ố ổ số
ma sát gi ặt đư ng ấ a ngưữa bánh xe và m ờ 𝑘 𝑘 = 0,23. L y . L c đ y c𝑔 𝑔 = 9,81 m/s
2
ự ẩ ủ ời có giá
trị bằng:
A. 693 28 690 98 686 38 697 88, N. B. , N. C. , N. D. , N.
Lời giải:
- Chọn chi u dương cùng chiề ề ểu chuy n động
-Khi xe chuy ủể ịn đ ng, chộ u tác d ng cụ a các lực:
trọng lực
P
, ph n lả ực
N
′
, l c đ y ự ẩ
F
′
và lực ma
sát
f
′
- Vì xe chuy n đ ng v i v n tể ộ ớ ậ ốc không đ i nên ổ
0a =
Áp d ng đụ ịnh luật II Newton, ta có:
0
ms
P N f F
′ ′
+ + + =
(1)
Chiếu (1) lên trục
0.Oy : sinN F P
α
′ ′
− − =
Chiếu (1) lên trục
Ox : c o. os c s.0
ms ms
F f F f
α α
′ ′ ′ ′
− = ⇒ =
Mà lực ma sát tác dụng lên xe:
( )
.sin
ms
f kN k P F
α
′ ′ ′
= = +
TAILIEUHUST.COM
26 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Hay
( )
cos . sin 690,98( )
n
.
cos si
kP
F k P F F N
k
α α
α α
′ ′ ′
= + ⇒ = =
−
Câu 19. Mộ ốt ô tô kh i lượng 𝑚 𝑚 = 1,5 tấn đang đi trên đường ph m ngang v c đẳ ằng n ới tố ộ
21 m/s bỗng nhiên phanh l ộ n trung bình cại. Ô tô d ng l i sau khi trưừ ạ ợt thêm 25 m. Đ lớ ủa
lực ma sát là:
A. 13, 53 10 13 23 10 12.
3
N. B. , .
3
N. C. ,63 ⋅ 10 14 13 10
3
N. D. , .
3
N.
Lời giải:
Gia tốc:
( )
2 2
2 2
2
0
0 21
8,82 m / s
2 2.25
v v
a
s
−
−
= = = −
Độ lớn trung bình của lực ma sát là:
8,82 1,5 1000 13230( )
ms
F ma N= = − ⋅ ⋅ = −
Câu 20. Mộ ốt v m có khật coi là chất điể i lượng 𝑚𝑚 b ắ ầt đ u trượt từ đỉnh mặt phẳng
nghiêng góc m ngang (xem hình v ố𝛼𝛼 so v i phương nớ ằ ẽ ệ). H s ma sát giữa vật và mặt
phẳng nghiêng là ộ ủ ố𝑘𝑘. Mômen đ ng lư ng cợ a ch m đất điể i v i đi i th i điớ ểm O tạ ờ ểm 𝜔𝜔 có
giá trị là:
A. 𝑚𝑚𝑔𝑔ℎ𝜔𝜔 𝛼𝛼 − 𝑘𝑘sin 𝛼𝛼(sin cos 𝛼𝛼).
B. 𝑚𝑚𝑔𝑔ℎ𝜔𝜔cos cos 𝛼𝛼(sin 𝛼𝛼 − 𝑘𝑘 𝛼𝛼).
C. 𝑚𝑚𝑔𝑔ℎ𝜔𝜔cos cos 𝛼𝛼( 𝛼𝛼 − 𝑘𝑘sin 𝛼𝛼).
D. mght (sin 𝛼𝛼 − 𝑘𝑘cos 𝛼𝛼).
Lời giải:
- Chọn hệ quy chiếu như hình v ốẽ, g c th i gian là lúc vờ ậ ắt b t
đầu chuyển động.
- Các lực tác dụng lên vật:
P
- trọng lực của vật;
N
- áp lực;
ms
f
lực ma sát giữa vậ ẳt và mặt ph ng
- Áp d ng đụ ịnh luật 2 Niuton ta được:
( )
ms x y ms
F P N f P P N f= + + = + + +
(*)
Chiếu lên tr c Ox ta có: ụ
x ms x
F P f P kN= − = −
(1)
Chiếu lên tr c Oy ta có: ụ
y y
N P 0 N P− = ⇒ =
Mô men t ng h c tác d ng lên v i vổ ợp các lự ụ ật đố ới O là
Mo Fd( , O) mgh cos (sin k cos )F
α α α
= = −
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 27
Vậy momen đ ng lư ng c y đôí vộ ợ ủa vậ ới
O
là:
0
L M t mght cos (sin k cos )
α α α
= = −
Câu 21. Một hạt chuyển đ t phộng trong mặ ẳng 𝑂𝑂𝑥𝑥𝚤𝚤 → t ừ điểm 1 có bán kính vector 𝑟𝑟
1
�
�
�
�
=
(𝑖𝑖
+ 2𝑗𝑗
)m đế ển đi m 2 có bán kính vector 𝑟𝑟
2
�
�
�
�
= (2𝑖𝑖
− 3𝑗𝑗
)𝑚𝑚, 𝑖𝑖
và 𝑗𝑗
là các vector đơn v trong ị
tọa độ -Đề các. Hạt chuy ộ ụ ủển đ ng dưới tác d ng c a l c có bi u thự ể ức 𝐹𝐹
�
�
= (3𝑖𝑖
− 4𝑗𝑗
) N. Công
thực hi n b c đó là:ệ ởi lự
A. 5 J. B. −17 23 J. C. J. . D. 17 J
Lời giải:
Độ dờ i của hạt đó là:
2 1
(1; 5)s r r= − = −
Công thự ực hi n bệ ởi l c
F
là:
A . 23( N)F S= =
Câu 22. Một phi công đang lái máy bay thực hiện vòng tròn nhào lộn trong một mặt
ph ựẳ ảng đ ng v i v n tứ ớ ậ ốc 700 km /h. Gi thiế ể ịt phi công có th ch u đ ng sự tăng tr ng ọ
lượng lên 3 lần. Bán kính nhỏ nh ủ ất c a vòng tròn nhào l đạt đưộn mà máy bay có thể ợc là
(cho 𝑔 𝑔 = 9,8 m/s
2
�
A. . 1979 1929 m. B. m. C 2029 1779 m. D. m.
Lời giải:
Các lực tác dụng lên phi cônglà: P, F , N
ht
Do v n đ , nên ta có: ật chuyể ộng tròn 𝐹𝐹
ℎ𝑡𝑡
�
�
�
�
�
= 𝑃𝑃
�
+ 𝑁𝑁
�
�
=> 𝑁𝑁
�
�
�
�
= 𝐹𝐹
ℎ𝑡𝑡
�
�
�
�
− 𝑃𝑃
�
�
�
=>�𝑁𝑁
�
�
�
�
�= �𝐹𝐹
ℎ𝑡𝑡
�
�
�
�
�
− 𝑃𝑃
�
�
�
� ≤ F
ht
+ P
=> Áp lực tác dụng lên phi công l n nhớ ấ ạt t i vị trí thấ ất và bp nh ằng:
N
max
= F
ht
+ P
Mà N
max
≤ F 3P =>
ht
≤ 2P => a
ht
≤ 2g
=>
𝑣𝑣
2
𝑟 𝑟
≤ 2g => r ≥
𝑣𝑣
2
2𝑔𝑔
= 1929 (m)
Câu 23. Mộ ỏt viên bi nh
10( g)m =
rơi theo phương thăng đ ng không vứ ậ ần t c ban đố u
trong không khí, l ủa không khí ực cản c
c
F rv= −
l(tỷ ệ ngược chi c), ề ốu v i v n tớ ậ
r
s là hệ ố
cả ận. V n tốc c c bực đ i mà viên bi đạ ạt đượ ằng
max
50( m / s)v =
. Cho gia tốc trọng trư ng ờ
g =
( )
2
10 m / s
. H n có giá trệ số cả ị:
A.
3
2,02.10 Ns / m
−
B.
3
1,99 10 Ns / m
−
⋅
C.
3
2.10 Ns / m
−
D.
3
2,03.10 Ns / m
−
TAILIEUHUST.COM
28 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Lời giải:
Chọn chi u hưề ều dương là chi ớng xu ấ i vecto g)ống mặt đ t (cùng chiều vớ
Các lực tác d ng lên viên bi là tr ng lụ ọ ực
P
và lực cản
C
F
Áp d ng dụ ịnh luật II Newton ta có:
C
P F ma+ =
Chiếu lên chiều dương ta được:
dv dv
mg rv ma mg rv m dt
rv
dt
g
m
− = ⇔ − = ⇔ =
−
Đặt
r
g v u
m
− = ⇒
vi phân 2 vế:
r m
dv du dv du
m r
− = ⇒ = −
m du r du
dt dt
r u m u
⇒ = − ⋅ ⇒ − =
∫ ∫
0
ln ln ln
v
r
g v
r r r
m
t u g v t
m m m g
−
⇔ − = = − ⇔ − =
3
max
max
1 2.10
r r
t t
m m
r m mg mg Ns
g v ge v g e v r
m r r v m
− −
−
⇒
− = ⇔ = − ⇒ = =
⇒ =
Câu 24. Một thanh đ ấồng ch t có độ dài
, khối lượng
m
. Đ i v c quay nào dư i đây ố ới trụ ớ
momen quán tính củ ỏa thanh là nh nhất
A. Song song và cách thanh một khoảng bằng 1
B. Đi qua khối tâm và vuông góc với thanh
C. Vuông góc và đi qua một đầu thanh
D. Đi qua khối tâm và làm với thanh một góc
2
π
α
<
Lời giải:
Song song và cách thanh 1 khoảng
2
: I m=
Đi qua khối tâm và vuông góc thanh:
2
12
m
I
=
Vuông góc và đi qua 1 đầu thanh:
2
3
m
I
=
Đi qua kh o vối tâm và tạ ới thanh 1 góc
2
: sin
2 12
m
I
π
α α
< =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 29
Chương 4. Năng lượng
A. Công thức
1. Động năng và thế năng
- Động năng:
2
1
W
2
d
mv=
. - Thế năng:
2
1
W
2
t
k x= ⋅∆
.
2. Công
2 1
.A F s
A E E
=
= −
.
3. Bài toán tìm điề ệnu ki
- Khoảng cách
h∆
(tính từ đỉnh mặ ắt cầ ậu) v t b t đầu rơi khỏi mặt cầu:
3
R
h∆ =
.
- V sận t c bé nhố ất để ợi dây treo v t n t ph ng đậ ặng quay tròn trong mặ ẳ ẳng th ứng:
5v gl=
.
- V ận t c dài c a c t đ ng chố ủ ộ ồ ất bị đổ khi chạm đất:
3v gh=
.
4. Bài toán va chạm
- Va ch m đàn h i xuyên tâm: B ng lưạ ồ ảo toàn động năng và độ ợng
( )
( )
1 2 1 2 2
2 2 2 2
1
1 1 2 2 1 1 2 2
1 2
2 1 2 1 1
1 1 2 2 1 1 2 2
2
1 2
2
2 2 2 2
2
m m v m v
v
m v m v m v m v
m m
m m v m v
m v m v m v m v
v
m m
′
′ ′
′ ′
′
− +
=
+
+ = +
⇒
− +
+ = +
=
+
– Va chạm mềm:
( )
1 1 2 2
1 1 2 2 1 2
1 2
m v m v
m v m v m m v v
m m
+
+ = + ⇒ =
+
5. Bảo toàn cơ năng:
- tĐị ếnh lu ổật: T ng động năng và th năng của hệ ại th i điờ ểm 1 bằng t ng đổ ộng năng và
thế năng c ạủa hệ t i th i đi m 2ờ ể :
truoc sau
.E E=
TAILIEUHUST.COM
30 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
B. Bài tậ ắp tr c nghiệm
Câu 1. Mộ ốt ch m khất điể i lượng 𝑚 𝑚 = 0,2 kg được ném lên từ O với v n tậ ốc 𝑣𝑣
0
= 7 m/s
theo phương h ỏ ủợ ớp v t ph ng nới mặ ẳ ằm ngang v i một góc 𝛼 𝛼 = 30
∘
, b qua s ảức c n c a
không khí, cho 𝑔 𝑔 = 9,8 m/s
2
. Mômen đ ng lư ng c a ch m đ i v i vộ ợ ủ ất điể ố ới O tạ ị trí cao
nh ủất c a chuyể ển động chất đi m là:
A.
0, /s 0, /s 0, /s 0, /s052kgm
2
. B. 218kgm
2
. C. 758kgm
2
. D. 488kgm
2
.
Lời giải:
Chọn hệ trục
Oxy
như hình v ốẽ. G c tọa độ tại v trí bị ắt
đầu ném, chi u dương hư ống, cùng chiề ớng xu ều với gia
tốc
g
Gia tốc:
0
x
y
a
a g
=
= −
Vận tốc:
0 0
0 0
cos
sin
x x x
y y y
v v a t v
v v a t v t gt
α
= + =
= + = −
Phương trình chuyể ển đ ng c a chộ ủ ất đi m:
2
00
2
2
0
0
1
: cos
:
2
1
1
: sin
:
2
2
x x
y y
Ox x v tOx x v t a t
Oy y v t gt
Oy y v t a t
α
α
=
= +
⇒
= −
= +
Tạ ị ể ểi v trí cao nhất của chuy n đ ng chộ ất đi m:
0
0
sin
0 sin
y
v t
v v t gt t
g
= = − ⇒ =
Và
2 2 2 2
2
0 0 0
0 0
sin sin sin1 1 1
sin sin
2 2 2
v v v
y h v t gt v
g g g
α α α
α α
= = ⋅ + = ⋅ − =
⇒
Ta có: ℎ
max
=
1
2
𝑣𝑣
0
2
sin
2
α
𝑔 𝑔
=
1
2
7
2
.sin
2
30
∘
9
,8
= 0,625(𝑚𝑚)
Động lượng
p
tại th i điở ểm t bất kì:
( )
x y x y
p t p i p j mv i mv j= + = +
Xét tích có hư ng cớ ủa hai vector:
1 2 3
u u i u j u k= + +
và
1 2 3
v v i v j v k= + +
2 3 1 3 1 2
1 2 3
2 3 1 3 1 2
1 2 3
i j k
u u u u u u
uv u u u i j k
v v v v v v
v v v
= = − +
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 31
Áp d a chúng ta và chú ý các thành phụ ủng vào bài toán c ần liên quan tới trục
z
coi như
bằng 0:
( )
0 0
0
0 0
0
y x x y
x y x y
i j k
v v v v
r v v v i j k v y v x k
y x x y
x y
⋅ = = − + = −
Mômen động lư a ch m đ i vợng củ ất điể ố ới
O
t ại vị trí cao nh n đ ng chất của chuyể ộ ất điểm
là:
( )
2
0 0 0 0
1
cos . . . sin cos sin
2
x y
L v y v x v t m v gt mv v t gt
α α α α
= − = − − −
( )
2 2 3 2
2 2
0 0
0 0
2
sin sin1 1
cos cos cos 0,758 kgm / s
2 2 2
v v
mgv t mgv m
g g
α α
α α α
= = = =
Câu 2. Một cột đ ấồng ch t có chiều cao ℎ = 8 m, đang ở vị trí thẳng đứng (chân cột tì lên
mặt đất) thì bị đổ xuống. Gia tốc trọng trường 𝑔 𝑔 = 9,8 m/s
2
. Vận t c dài cố ủa đỉnh cột khi
nó chạ ằm đất b ng giá tr nào dư i đâyị ớ
A. 16 836, . . . . m/s B. 14 836, m/s C. 15 336, m/s D. 14 336, m/s
Lời giải:
Chọn m c th ng tố ế nă ạ ặi m t đất
Ở vị ậ trí thẳng đứng, v t có thế năng: 𝑊𝑊
𝑡 𝑡
=
1
2
𝑚𝑚𝑔𝑔ℎ = 𝑊𝑊
Khi đỉnh cột ch ng n ng lạm đất, vật có độ ă à 𝑊𝑊
đ
= =𝑊 𝑊
1
2
𝐼𝐼𝜔𝜔
2
Lại có: quán tính của c i v c quay t n cộ đốt ới trụ ại châ ột là 𝐼 𝐼 =
1
3
𝑚𝑚ℎ
2
Áp d ng đụ ịnh luậ ảt b o toàn cơ năng ta có:
2 2
1 1 1
2 2 3
mgh mh
ω
⇒ = ⋅
Vậy v n t c dài cậ ố ủa đỉnh c t khi nó ch m độ ạ ất là:
3 3.9,8.8 15,336( m / s)v h gh
ω
⇒ = = = ≈
Câu 3. Một ống thủy tinh nhỏ khối lượng 𝑀 𝑀 = 120 g bên trong có vài gi t ête đưọ ợc đ y ậ
bằng 1 nút cố định có khố ủ ội lượng g. ng th𝑚 𝑚 = 10 Ố y tinh đư c treo ợ ở đầu m t sợi dây
không giãn, kh ng không đáng k u dài ối lượ ể ề, chi 𝑙 𝑙 = 60 cm (hình v ). Khi hơ nóng ốẽ ng
thủy tinh ở vị trí th ấ ậ quay đư ả vòng ấp nh t, ête b c hơi và nút bố t ra. Đ ng có thể ố ể ợc c
xung quanh đi ố Cho ểm treo O, v n tậ c bậ ất bé nh t của nút là: ( 𝑔 𝑔 = 10 m/s
2
)
.
A. 69 127, . . . . m/s B. 64 027, m/s C. 70 827, m/s D. 65 727, m/s
H
TAILIEUHUST.COM
32 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Lời giải
Gọi H là điểm cao nhất của quỹ đạo, mốc thế năng tại A.
Để ố ng có thể quay được cả vòng xung quanh điểm treo O
thì tại H d y khâ ông được trùng, hay 𝑇𝑇
𝐻 𝐻
≥ 0 (𝑇𝑇
𝐻𝐻
l là ực căng
dây tại H).
Tại H ta có:
2
H
H H H H H
v
F P T ma mg T T m mg
l
= + ⇔ = + ⇔ = −
Do đó 𝑇𝑇
𝐻 𝐻 𝐻 𝐻
≥ 0 ⇔ 𝑣𝑣 ≥
�
𝑔𝑔𝑙𝑙 hay: 𝑣𝑣
𝐻𝐻
𝑚𝑚𝑚𝑚𝑚𝑚
=
�
𝑔𝑔𝑙𝑙
Á úp dụng định luậ ảt b o toàn độ ượ ống l ng cho ng và n t tại A:
𝑚𝑚𝑣𝑣
𝑚 𝑚
= 𝑀𝑀𝑣𝑣
𝐶 𝐶
⇒ 𝑣𝑣
𝑚 𝑚
=
𝑀𝑀
𝑚 𝑚
𝑣𝑣
𝐶𝐶
Á ô ú óp dụng định luậ ảt b o toàn cơ năng cho vật M (ống kh ng tính n t) t i A vạ à H, ta c :
𝑊𝑊
𝐴 𝐴
=
1
2
𝑀𝑀. 𝑣𝑣
𝐶𝐶
2
= 𝑊𝑊
𝐻 𝐻
=
1
2
𝑀𝑀. 𝑣𝑣
𝐻𝐻
2
+ 𝑀𝑀𝑔𝑔ℎ
2 2
4 4 5 5
M H M
v v gl gl gl gl v gl⇒ = + ≥ + = ⇒ ≥
120
5 5.10.0, 6 65,727
10
m M
M M
v v gl
m m
⇒ = ≥ = ≈
Câu 4. Ở đầu sợi dây OA chiều dài 𝑙𝑙 có treo m t n . Đột vậ ặng 𝑚𝑚 ể vậ t quay tròn trong mặt
ph ứẳng thẳng đ ng thì t i đi m th p nh t ph i truyạ ể ấ ấ ả ền cho v ộật m t vận tốc theo phương
nằm ngang có độ lớ ờn là (cho gia tố ọc tr ng trư ng bằng 𝑔𝑔 )
A.
�
5𝑔𝑔𝑙𝑙. B.
�
𝑔𝑔𝑙𝑙. C.
�
5𝑙𝑙
𝑔 𝑔
. . D. 2𝑔𝑔𝑙𝑙
Lời giải:
Chọn chiều dương và gốc tọa độ như hình vẽ:
Sức căng
T
cực tiể ế ể ểu khi vật lên đ n đi m cao nh t PT Newton II t i điấ ạ m cao
nhất B:
2
min
B
v
mg T m
l
+ =
Áp d ng ĐLBT cơ năng: ụ
2 2
1 1
2
2 2
A B
mv mv mgl= +
2
min
1 1
2
2 2
A
mv mgl lT mgl⇒ = + +
Để vậ ứ ể ấ t quay tròn trong m t ph ng đặ ẳng thẳ ng thì t i điạ m th p nhấ t thì
min
0T ≥
2
min
1 5
5 5
2 2
A
mv mgl v gl v gl⇒ ≥ ⇒ ≥ ⇒ =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 33
Câu 5. Một viên bi có kh , v n tối lượng 𝑚𝑚 ậ ốc 𝑣𝑣 bắ ẳn th ng góc vào m ng. ột bức tư ng phờ ẳ
Sau khi va ch m viên bi bay ngư i v n t i đạ ợc trở lạ ới vậ ốc bằng 4 /5𝑣𝑣 . Gọ ộng năng ban đầu
của viên bi là 𝐸𝐸, độ biến thiên động năng và đ và ta có:ộng lư ng c a viên bi là ợ ủ Δ𝑊𝑊 Δ𝑝𝑝
A. Δ𝑊𝑊 = 0 và Δ𝑝𝑝 Δ𝑊𝑊= 2(2𝑚𝑚𝐸𝐸)
1/2
. C. = −
5𝐸𝐸
9
và Δ𝑝𝑝 =
5 2( 𝑚𝑚𝐸𝐸)
1 2/
3
.
B. Δ𝑊𝑊 = −
3𝐸𝐸
4
và Δ𝑝𝑝 =
3 2( 𝑚𝑚𝐸𝐸)
1/2
2
. D. Δ𝑊𝑊 = −
9𝐸𝐸
25
và Δ𝑝𝑝 =
9 2( 𝑚𝑚𝐸𝐸)
1/2
5
.
Lời giải:
Δ𝑊𝑊 𝑊𝑊=
𝑠 𝑠
− 𝑊𝑊
𝑡 𝑡
=
1
2
𝑚𝑚𝑣𝑣
𝑠𝑠
2
−
1
2
𝑚𝑚𝑣𝑣
𝑡𝑡
2
=
1
2
𝑚𝑚 ��
4
5
𝑣𝑣�
2
− 𝑣𝑣
2
�
= −
9
25
×
1
2
𝑚𝑚𝑣𝑣
2
= −
9𝐸𝐸
25
Câu 6. Một vật cố b kh ợối lư ng 𝑚 𝑚 = 10 kg ắt đầu trượt từ đỉnh dốc một mặ ẳt ph ng
nghiêng cao ố . Cho ℎ = 20 m. Khi t i chân dớ c có v n tậ ốc 𝑣 𝑣 = 15 m/s 𝑔 𝑔 = 10 m/s
2
. Công
của l c ma sát có đự ộ l ớn là:
A. 867 853 875,7 J. B. ,1 J . C. . . J D. 860,4 J
Lời giải:
Chọ ốn m t làm gặ ất đ c tính thế năng
( )
0
t
W =
, chi n đ ng c t trên mề ểu chuy ộ ủa vậ ặt dốc là
chiề ịu dương. Do ch u tác d ng c a l c ma sát (ngoụ ủ ự ại lực không phải là lực th ), nên cơ ế
năng c t có giá ủa v a vật không b o toàn. Trong trư p này, đ n cơ năng cả ờng, hợ ộ biến thiê ủ ậ
trị bằng công của l c ma sát:ự
22
0
2 1 0
2 2
mvmv
A W W mgh mgh
= − = + − +
Thay số:
0 0
0, 0, 2( m), 15( m / s), 0v h v h= = = =
2
0
1
875( )
2
A mv mgh J⇒ = − =
Câu 7. Một con l c đơn có ắ 𝑚 𝑚 = 120 g được kéo l ch v i phương th ng đệ ớ ẳ ứng một góc 𝛼 𝛼 =
90 10
∘
, sau đó thả rơi cho 𝑔 𝑔 = m/s
2
. L c căng c c đ a dây treo làự ự ại củ
A. 4, 3, N 3,6 4, N791 N. B. 997 . C. N. D. 394 .
Lời giải:
Chuy ộ ủển đ ng c a vật
m
là chuyể ền động tròn đ u trên quỹ đạo có bán kính 1
Áp d ng đụ ịnh luật bảo toàn cơ năng:
2
max
0
1
2 1 cos 1 cos
d t t
mgl mgl
W W W W mv
α α
= + = ⇒ + =
− −
( )
0
2 cos cosv gl
α α
⇒ = −
TAILIEUHUST.COM
34 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Chọn chi u dương hưề ớng xu ng và g năng tạố ốc thế i vị trí cân
bằng. Vật chịu tác d a các l c: Lụ ủng c ự ực căng dây
( )T
, trọng
lực
P
Áp d ng đụ ịnh luật II Newton:
P T ma+ =
Chiế ề ẽu (1) lên chi u dương hình v :
2
cos
n
v
T P ma T mg m
l
α
− = ⇒ − = ⋅
(trọng lực đóng vai trò lực
hướng tâm)
( ) ( )
0 0
cos 2 cos cos 3cos 2cosT mg mg mg
α α α α α
⇒ = + − = −
max 0 max
0 3 cos 3.0,12.10.cos90 3, 6( N)T T mg
α α
°
⇔ = ⇒ = = =
Câu 8. Một đĩa tròn đ ấồng ch t bán kính 𝑅 𝑅 = 0,15 m, có thể quay xung quanh một trục
nằm ngang vuông góc v i dĩa và cách tâm đĩa m t đoạớ ộ n 𝑅𝑅/2. Đĩa b u quay tắ ầt đ ừ vị trí cao
nh ủất c a tâm đĩa với v n t c đ ng 0. V p nhậ ố ầu bằ ận tốc khi tâm đĩa trí thở vị ấ ất là
A. 13 199rad 49 915rad 12 226rad 50 888rad, /s. B. , /s. C. , /s. D. , /s.
Lời giải:
Chọ ốn m c thế năng tạ trí thấ ấi vị p nh t
Thế năng tại vị trí cao nhất:
W
t
mgR=
Độ ịng năng tại v tí thấp nhất:
2
d
1
W
2
I
ω
=
Mô-men quán tính củ ố ụa đĩa đ i với tr c quay:
2
2
2
1 3
2 2 4
R mR
I mR m
= + =
Áp d ng đụ ịnh luật bảo toàn năng lượng:
2 2 2
1 3 8
13,199
2 8 3
g
mgR I mgR mR
R
ω ω ω
= ⇔ = ⇒ = ≈
(rad/s)
Câu 9. Một thanh đồng chất chiều dài quay quanh m m ngang đi qua 𝑙𝑙 có thể ột trục nằ
mộ ủt đầu c a thanh và vuông góc với thanh. Vận t c góc c u ph i truyố ực tiể ả ền cho thanh ở
vị ể ế ị trí cân b ng đằ nó đ n đư c vợ trí nằm ngang là:
A. �
3𝑔𝑔
𝑙 𝑙
. B. �
6𝑔𝑔
𝑙 𝑙
. C. �
2𝑔𝑔
𝑙 𝑙
. D. �
9𝑔𝑔
𝑙 𝑙
.
Lời giải:
Chọ ố nn m c thế ăng tạ trí thấ ấi vị p nh t.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 35
Thế năng tại v trí nị ằm ngang là:
W
t
mgl=
Độ ịng năng tại v trí thấp nhất:
2
d
1
W
2
mv=
Áp d ng đụ ịnh luật bảo toàn năng lượng ta có
2
1
2
2
mgl mv v gl= ⇒ =
Vận t c góc t i thiố ố ể ểu đ thanh đế ịn được v trí nằm ngang là
2v g
l l
ω
= =
Câu 10. Giả s l l cự ực cản củ ụa nư c tác dớ ng lên xà lan tỉ ệ với tố ộc đ ủa xà lan đối v i nướ ớc.
Một tàu kéo cung c p công suấ ất 𝑃𝑃
1
= =250 mã lực (1 mã lực 746 W) cho xà lan khi
chuy ốển đ ng vộ ới t c độ 𝑣𝑣
1
= 0,25 m/s. Công suấ ầ t đt c n thiế ể kéo xà lan v c đới tố ộ 𝑣𝑣
2
=
0, m/s75 là:
A. 2240 mã l B. 2220 mã l C. 2250 mã l D. 2270 mã lực. ực. ực. ực.
Lời giải:
Giả s s l ử hệ ố ực cản c a nư c là: K ủ ớ
Vì l n c a nư c đực cả ủ ớc tỉ ệ vớ l i tố ộ ủ c a xà lan nên F
C
= KV (1)
Ta th y xà ng v i v n t i nên l c kéo và l t tiêu lấ lan chuy n độể ớ ậ ốc không đổ ự ực cản đã triệ ẫn
nhau
=> F
K
�
�
�
�
+ F
C
�
�
�
�
= 0
�
Mặt khác hai lực này cùng phương ngược chiều nên => F = 0 = F
K
– F
C
⇔ F
K
C
(2)
Công thức tính công su (3) ất kéo là P = F
K
V
Từ (1), (2) và (3) => P = KV
2
=> �
P
1
= KV
1
2
P
2
= KV
2
2
=>
P
2
P
1
=
V
2
2
V
1
2
=> P
2
=
V
2
2
V
1
2
P
2
=
V
2
2
V
1
2
P
1
= �
0,75
0
,25
�
2
P
1
= 9P
1
Thay số vào ta được P
2
= 2250 (mã lực)
Câu 11. Một khẩu pháo có khố n theo phương làm vi lượng 𝑀 𝑀 = 480 kg bắ ạn m t viên độ ới
mặt ngang m t góc ạộ 𝛼 𝛼 = 60
∘
. Kh ng c a viên đối lượ ủ n 𝑚 𝑚 = 5 kg, v n t c đậ ố ầu nòng 𝑣 𝑣 =
400 54 m/s. Khi b n b t lùi v phía sau mắ ệ pháo giậ ề ột đoạn 𝑠 𝑠 = cm. Lực cản trung bình tác
dụ ịng lên quả pháo có giá tr :
A. −2129 N. B. −1929 . N
C. −2229 N. D. −2029 N.
Lời giải:
Chọn chi u dương cùng chiề ề ều với chi u của v
o
TAILIEUHUST.COM
36 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Bảo toàn động lượng theo phương ngang cho hệ ngay trước và sau khi b n ta cóắ :
M𝑣𝑣
0
− 𝑚𝑚𝑣𝑣𝑚𝑚𝑚𝑚𝑠𝑠(a)= 0 ⟺ 𝑣𝑣
0
=
𝑚𝑚
𝐶 𝐶
𝑣𝑣𝑚𝑚𝑚𝑚𝑠𝑠(a) =
5
480
∗ 400 ∗ cos
(
60
0
)
=
25
12
𝑚𝑚/𝑠𝑠
Sau đó, do toàn bộ pháo b động năng cả ị ệ ế lực cản tri t tiêu đ n lúc dừng:
𝑊𝑊
đ
= 𝐴𝐴
𝑐𝑐ả𝑛𝑛
⟺
1
2
𝑀𝑀𝑣𝑣
0
2
= |𝐹𝐹
𝑐𝑐
|S ⟺|𝐹𝐹
𝑐𝑐
|=
1
2
𝐶𝐶𝑣𝑣
0
2
𝑆 𝑆
=
480∗�
25
12
�
2
2∗0,54
= 1929(N)
=> 𝐹𝐹
𝑐 𝑐
= −1929 (N) (vì vector F cản ngược chiều dương nên giá trị của nó mang dấu –)
Câu 12. Một thanh mảnh đ ộồng ch t có đấ dài 𝑙𝑙 có th c đi qua để quay quanh một trụ ầu
thanh và vuông góc với thanh. Lúc đ u thanh ầ ở vị trí n nh rơi xu ng. Vằm ngang, cho tha ố ận
tốc dài ở đầu dưới của thanh khi thanh rơi tới vị trí thẳ ng là:ng đứ
A.
�
2𝑔𝑔𝑙𝑙. . . B.
�
𝑔𝑔𝑙𝑙 C.
�
3𝑔𝑔𝑙𝑙 D. 0
Lời giải:
Chọ ốn m c thế năng tạ trí thấ ấ a thanhi vị p nh t củ
Tạ ịi v trí thấp nhất
( )
2
max dmax
1
2
v v W W mv= ⇒ = =
Tạ ịi v trí cao nhất
tmax
( 0)v W W mgl= ⇒ = =
Áp d ng đụ ịnh luật bảo toàn năng lượng:
2
1
2
2
mv mgl v gl= ⇒ =
Câu 13. Hai quả c ầu 𝐴𝐴 và 𝐵𝐵 đư đầợ ởc treo u hai s nh không dãn dài b ng nhau. ợi dây mả ằ
Hai đ u kia c i dây đư c vào mầ ủa các sợ ợc buộ ột cái giá sao cho các quả cầu tiếp xúc với
nhau và tâm của chúng cùng n ủằm trên một đườ ợng n m ngang. Khằ ối lư ng c a các quả cầu
𝑚𝑚
A
= 165 g và 𝑚𝑚
B
= 750 g. Kéo quả cầu A lệ ị ếch kh i vỏ trí cân b ng đằ n độ cao ℎ = 6 cm
và thả ra. Sau va chạ ả ầ m, qu c u B được nâng kên độ cao là (coi va chạm hoàn toàn đàn
hồi, cho 𝑔 𝑔 = 9,8 m/s
2
)
A. 1, 7, 7, 1,764 mm. B. 991 mm. C. 804 mm. D. 951 mm.
Lời giải:
Chọn mốc thế năng tại vị trí thấp nhất, ta thấy hệ hai vật là hệ kín vì vậy có thể áp dụng
mọi định luật bảo toàn cơ năng và động năng
Đặt 𝑣𝑣 𝑣𝑣
0
;
1
; 𝑣𝑣
2
lần lượt là vận tốc cực đại của vật A trước khi va chạm; vận tốc của vật A sau
khi va chạm; vận tốc của vật B sau khi va chạm
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 37
Đặt
h’
là chiều cao cực đại của vật B
Áp dụng định luật bảo toàn cơ năng cho vật A để
tính vận tốc trước khi va chạm ta có
𝑚𝑚
𝐴𝐴
𝑔𝑔ℎ =
1
2
𝑚𝑚
𝐴𝐴
𝑣𝑣
0
2
⟹ 𝑣𝑣
0
2
= 2𝑔𝑔ℎ (1)
Vì là va chạm đàn hồi ta áp dụng định luật bảo toàn
động lượng cho hai vật
𝑚𝑚
𝐴𝐴
𝑣𝑣
0
�
�
�
�
= 𝑚𝑚
𝐴𝐴
𝑣𝑣
1
�
��
�
+ 𝑚𝑚
𝐵𝐵
𝑣𝑣
2
�
�
�
�
→ 𝑚𝑚
𝐴𝐴
(
𝑣𝑣
0
− 𝑣𝑣
1
)
= 𝑚 𝑚
𝐵𝐵
𝑣𝑣
2
(2)
Áp dụng định luật bảo toàn cơ năng cho hai vật ngay sau khi va chạm
1
2
𝑚𝑚
𝐴𝐴
𝑣𝑣
0
2
=
1
2
𝑚𝑚
𝐴𝐴
𝑣𝑣
1
2
+
1
2
𝑚𝑚
𝐵𝐵
𝑣𝑣
2
2
⟺ 𝑚𝑚
𝐴𝐴
(
𝑣𝑣
0
2
− 𝑣𝑣
1
2
)
= 𝑚𝑚
𝐵𝐵
𝑣𝑣
2
2
(3)
Từ (1), (2) suy ra 𝑣𝑣
1
= 𝑣𝑣
2
− 𝑣𝑣
0
tiếp tục thay vào (2) để triệt tiêu 𝑣𝑣
1
ta được
𝑣𝑣
2
=
2𝑚𝑚
𝐴𝐴
𝑣𝑣
0
𝑚𝑚 +𝑚𝑚
𝐴𝐴 𝐵𝐵
(4)
Tiếp tục áp dụng định luật bảo toàn cơ năng để tìm h cực đại của vật B ta có
1
2
𝑚𝑚
𝐵𝐵
𝑣𝑣
2
2
= 𝑚𝑚
𝐵𝐵
𝑔𝑔h’ ⟹ h’ =
𝑣𝑣
2
2
2𝑔𝑔
Thay (1) và (4) để tìm giá trị của ta được h’
h’ = (
2𝑚𝑚
𝐴𝐴
𝑚𝑚
𝐴 𝐴
+ 𝑚𝑚
𝐵𝐵
)
2
ℎ = 0,7804
(
𝑚𝑚𝑚𝑚
)
= 7,804(𝑚𝑚𝑚𝑚)
Câu 14. Hai hòn bi có khối lượng 𝑚𝑚
1 1
và 𝑚𝑚
2
= 𝑚𝑚 /2 được treo b ng 2 s i dây có cùng ằ ợ
chiều dài 𝑙𝑙 = 6 m vào m t điộ ểm. Kéo lệch hòn bi cho đ𝑚𝑚
1
ến khi dây treo nằm ngang rồi
th ạả ra đ nó va chể m vào bi . Sau va ch𝑚𝑚
2
ạm hai hòn bi dính vào nhau và lên tới độ cao
cực đại là: (cho 𝑔 𝑔 = 9,8 m/s
2
)
A. 2, 2, 2, 2,827 m. B. 907 m. C. 667 m. D. 747 m.
Lời giải:
Áp d ng đụ ịnh luật bảo toàn cơ năng (cho hệ gồm hòn bi 1
và Trái Đ t; ch n m c tính th i v trí cân b ng cấ ọ ố ế năng tạ ị ằ ủa
hòn bi 1 trư c va ch c v n tớ ạm) ta tính đượ ậ ốc
v
của hòn bi 1
trước va chạm:
1 1
1
0 0 2
2
m v
m gl v gl+ = + ⇒ =
(1)
Ngay sau va chạm cả hai hòn bi có cùng vận tốc
v
′
. Áp
dụ ị ảng đ nh luật b o toàn động lượng ta có:
TAILIEUHUST.COM
38 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
( )
1 1
1 1 2
1
1 2
1
2 2
2
3 3
2
m v m v
m v m m v v v gl
m
m m
m
′ ′
= + ⇒ = = = =
+
+
(2)
Độ ệng năng của h hai hòn bi sau va chạm là:
2 2
2 2
1 2
1 1
3 1 2
2 2 4 3 3
d
m v m v
W m v m v mgl
′ ′
′ ′
= + = = =
Sau va chạm hai hòn bi dính vào nhau và tiếp n n đ a hòn bi 1. ối chuyể ộng tròn ban đầu củ
Động năng
d
W
′
c ủa hệ hai hòn bi chuyển động thành th năng ế
( )
1 2 1
3
2
t
W m m gh m gh
′
= + =
của hai hòn bi ở độ cao tối đa
h
(chọ ốn m c tính thế năng như trên)
Câu 15. Có ba v t, cùng kh u đật đ ấồng ch ối lượng: cầ ặc, trụ ụ đặc và tr rỗng cùng được thả
lăn không trư ặ ng ợt từ đỉnh một m t phẳ nghiêng. V ng nghiêng lật nào t i chân m t phớ ặ ẳ ớn
nhất:
A. Cả 3 vật. r c B. Trụ đặc. C. Trụ ỗng. D. Quả ầu đặc.
Lời giải:
Gọi
h
là độ cao từ đỉ ếnh m ng nghiêng đặt phẳ n v trí cị ủa vật
sau
( s)t
x
là quãng đư t đi đường vậ ợc sau
t(s)
Vật tham gia 2 chuyển động: chuyển động quay và chuyển
độ ị ế ểng t nh ti n v c đới tố ộ di chuy n chính là tôc đ ủộ dài tại 1 điể ềm ở b mặt c a vật
Áp d ng đụ ịnh luật bảo toàn cơ năng ta được:
2 2
mv Iw 2mgh 2mgx sin
α
+ = =
(1)
Lấ ếy vi phân 2 v của (1) với
/ r wv =
ta có:
( ) ( )
2 2 2 2
dv dx
mvr Iv dv mgr sin dx mvr Iv mgr sin
dt dt
α α
+ = = + =
( )
2
2 2
2
sin
mr I a mgr sin a
mgr
mr I
α
α
⇒ + = ⇒ =
+
+ TH1: V u đậ ầt là c ặc:
2
I 2mr / 5=
1
5
g sin
7
a
α
⇒ =
+ TH2: Vậ đặt là trụ c:
2
I mr / 2=
2
2
a g sin
3
α
⇒ =
+ TH3: Vật là trụ ỗ r ng:
2
I mr=
3
1
g sin
2
a
α
⇒ =
1 1
2 3 4
2,667( m)
3 2 9
d t
W W m gl m gh h l
′ ′
= ⇔ = ⇒ = =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 39
Từ ể ể 3TH trên cho th y c u đấ ầ ặc chuy n đ ng v i gia t t nên th i gian độ ớ ốc lớn nhấ ờ đi cùng 1
quãng đường là nhỏ nhất.
Câu 16. Hai quả c ầu A và B đượ ởc treo hai đầu sợi dây mảnh không dãn dài b ng nhau. ằ
Hai đ u kia c i dây đư c vào m t cái giá sa p xúc vầ ủa các sợ ợc buộ ộ o cho các quả cầu tiế ới
nhau và tâm của chúng cùng n ộ ốằm trên m t đường n m ngang. Khằ i lượng của các quả ầ c u
𝑚𝑚
𝐴 𝐴
= =165 g và 𝑚𝑚
𝐵 𝐵
750 g. Kéo quả c ầu A lệ ịch kh i vỏ trí cân b ng đ n đằ ế ộ cao ℎ = 6 cm và
thả đư ra. Sau va ch ầạ ảm, qu c u B ợc nâng lên độ cao là: (coi va chạm là hoàn toàn không
đổ )i, cho 𝑔 𝑔 = 9,8 m/s
2
A. 7, 1, 2, 7,617 mm. B. 951 mm. C. 958 mm. D. 804 mm.
Lời giải:
Áp d ng ĐL bụ ảo toàn và chuy n hóa năng lưể ợng:
V
ận tốc của vậ ạt A t i th i điờ ểm va chạm là:
𝑚𝑚
𝐴𝐴
𝑣𝑣
2
2
= m
A
gh
=> v
A
=
�
2𝑔𝑔ℎ
Vận tốc c m là:ủa vậ ạt B ngay sau khi va ch v
B
’ =
(
𝑚𝑚
𝐵𝐵
−𝑚𝑚
𝐴𝐴
)
𝑣𝑣
𝐵𝐵
+2𝑚𝑚 𝑣𝑣
𝐴𝐴 𝐴𝐴
𝑚𝑚 +𝑚𝑚
𝐴𝐴 𝐵 𝐵
=
2𝑚𝑚
𝐴𝐴
𝑣𝑣
𝐴𝐴
𝑚𝑚 +𝑚𝑚
𝐴𝐴 𝐵𝐵
Độ cao c c lên sau khi va chủa vật B nâng đượ ạm là:
Áp d ng ĐLBTVCH năng lư
ụ ợng: gh m
B B
=
𝑚𝑚 𝑣𝑣
𝐵𝐵
𝐵𝐵
′
2
2
=>
h
B
=
𝑣𝑣
𝐵𝐵
′
2
2𝑔𝑔
= (
2𝑚𝑚
𝐴𝐴
𝑚𝑚 +𝑚𝑚
𝐴𝐴 𝐵𝐵
)
2
. ℎ = 7,804 mm
Câu 17. Mộ ốt vật có kh i lượng 𝑚𝑚
1
= 2 kg chuyển đ ng v c độ ới tố ộ t𝑣𝑣
1
= 6 m/s ới va chạm
xuyên tâm vào vậ ng t có khối lượ 𝑚𝑚
2
= 3 kg đứng yên. Va chạm là hoàn toàn mề ệm. Nhi t
lượng tỏa ra trong quá trình va chạm là:
A. 21,3 J. B. 21 22 22,6 J. C. ,2 J. D. ,5 J.
Lời giải:
Vận tốc của hệ vật m
1
và m
2
sau khi va chạm là:
Áp dụng công thức: 𝑣 𝑣 =
𝑚𝑚
1
𝑚𝑚 +𝑚𝑚
1 2
𝑣𝑣
1
Nhiệt lư ng tợ ỏa ra trong quá trình va chạm là:
Q =
-A = W
d1
– W
d2
=
1
2
𝑚𝑚
1
𝑣𝑣
1
2
−
1
2
(
𝑚𝑚
1
+ 𝑚𝑚
2
)
(
𝑚𝑚
1
𝑚𝑚 +𝑚𝑚
1 2
𝑣𝑣
1
)
2
=
1
2
𝑚𝑚
1
𝑚𝑚
2
𝑚𝑚 +𝑚𝑚
1 2
𝑣𝑣
1
2
= 21,6 (J)
TAILIEUHUST.COM
40 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Chương 5: Trườ ấng h p dẫn
A. Công thức
1. Định luật Newton
- Lự ểc hút c a hai chủ ất đi m
m
và
m
' cách nhau đo n ạ
r
:
2
11
2 2
Nm
. 6,67 10 .
.
kg
m
F F G
m
G
r
′
′ −
= = = ⋅
Lưu ý:
• Công thức này chỉ áp dụng cho chất điểm.
• Đổi v i v n thì phớ ật lớ ải dùng phương pháp tích phân.
• Hai quả cầu đ ng ch t thì có thồ ấ ể dùng được trong đó r là khoảng cách gi a 2 tâm ữ
cầu.
2. Gia tố ọ ờc tr ng trư ng
- Gia tốc tr i mọng trư ạờng t ặt đất:
0
2
GM
g
R
=
.
- Gia tốc trọng trư ng ờ ở độ cao
2
:
( )
h
GM
h g
R h
=
+
.
- Liên hệ giữa gia tốc tr i mọng trư ạờng t ặt đất và tại độ cao
h
:
2
0
2
2
0
1
( )
1
h
h
g
R
g g
g R h
h
R
= → =
+
+
Khi
h R
ta có thể áp d c gụng công thứ ần đúng:
1 (1 ) 1
n
x x nx→ + ≈ +
.
2
0
2
1
1 1 2 . Thay vào ta có: 1 2 .
1
h h
h h h
g g g
R R R
h
R
−
= + ≈ − = −
+
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 41
B. Bài tậ ắp tr c nghiệm
Câu 1. Một quả cầu đ ng ch t khồ ấ ối lượng 𝑚𝑚
1
đặt cách đ ng chầu một thanh đồ ất một
đoạ ằn b ng 𝑎𝑎 trên phương kéo dài của thanh. Thanh có chiều dài ng 𝑙𝑙, khối lượ 𝑚𝑚
2
. Lực hút
của thanh lên quả c ầu là:
A. 𝐺 𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑚𝑚
(𝑚𝑚+𝑙𝑙)
. B. 𝐺 𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑚𝑚
(𝑚𝑚−𝑙𝑙)
. C. 𝐺 𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑚𝑚
2
. D. 𝐺 𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑚𝑚𝑙𝑙
.
Lời giải:
Vi phân thanh các đo ng dm và cách đầạn dx có khối lượ u thanh gầ ản với qu cầu khoảng x
Do thanh đ
ồng ch t , ta có:ấ
𝑑𝑑𝑚𝑚
𝑚𝑚
2
=
𝑑𝑑𝑥𝑥
𝑙 𝑙
=> dm =
𝑚𝑚
2
𝑙 𝑙
dx
Lự
c hút c n dx lên quủa đoạ ả cầu là: dF = G
𝑚𝑚
1
𝑑𝑑𝑚𝑚
(
𝑚𝑚+ 𝑥𝑥)
2
= G
𝑚𝑚 𝑚𝑚
1 2
𝑙𝑙
(𝑚𝑚+ 𝑥𝑥)
2
𝑑𝑑𝑥𝑥
Lực hút của tha ảnh lên qu c ầu là:
F =
∫
G
𝑚𝑚 𝑚𝑚
1 2
𝑙𝑙
(𝑚𝑚+ 𝑥𝑥)
2
𝑑𝑑𝑥𝑥
𝑙𝑙
0
= −𝐺𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑙𝑙
(𝑚𝑚+𝑥𝑥)
�
0
𝑙 𝑙
= −𝐺𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑙𝑙
(
𝑚𝑚+𝑙𝑙
)
+ 𝐺 𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑙𝑙𝑚𝑚
= 𝐺 𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑙 𝑙
�
1
𝑚 𝑚
−
1
𝑚𝑚+𝑙𝑙
� = 𝐺 𝐺
𝑚𝑚
1
𝑚𝑚
2
𝑚𝑚(𝑚𝑚+𝑙𝑙)
Câu 2. Một vệ tinh có khố o tròn bán kính i lượng 𝑚 𝑚 = 150 kg chuyể ỹn động trên qu đạ 𝑟 𝑟 =
7, 4. = 5,10
6
m quanh Trái Đ t. Cho khấ ối lượng trái đất 𝑀 𝑀 98.10
24
kg. Cho bi t h ng sế ằ ố hấp
dẫ đạn 𝐺 𝐺 = 6, 67 10.
−11
N ⋅ m /
2
kg
2
. T c đố ộ vệ tinh trên quỹ o đó là:
A. 7, /s 6, 7, 6,042 km . B. 742 /skm . C. 342 /skm . D. 442 /skm .
Lời giải:
Lự ệ
c hư ng lên vớng tâm tác dụ tinh là: F
ht
= F
hd
= G
𝐶𝐶𝑚𝑚
𝑟 𝑟
2
=>
ma
ht
= G
𝐶𝐶𝑚𝑚
𝑟 𝑟
2
=>
a
ht
= G
𝐶𝐶
𝑟 𝑟
2
mà a
ht
=
𝑣𝑣
2
𝑟 𝑟
=> v =
�
𝑎𝑎
ℎ𝑡𝑡
𝑟𝑟 = �
𝐺 𝐺
𝐶𝐶
𝑟 𝑟
= 7342 (m/s) = 7,342 (km/s)
Câu 3. Gọi
M
và
R
lần lư t là kh ng và bán kính c a Trái Đợ ối lượ ủ ất.
G
là h ng sằ ố hấp dẫn
vĩ trụ,
g
và
0
g
l ần lư t là gia tợ ốc trọng trư ng ờ ở độ cao
h
và m t. Công thặt đấ ức nào dưới
đây đúng với h b t kấ ỳ:
a
x
dx
TAILIEUHUST.COM
42 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
A.
2
( )
GM
g
R h
=
+
B.
2
GM
g
R
=
C.
0
2
1
h
g g
R
= −
D.
2
2
1
h
GM
R
g
R
−
=
Lời giải:
+ T i đạ ộ cao
h
bất kì, l c h p d n gi a Trái Đự ấ ẫ ữ ất và vật:
2
( )
hd
GMm
F
R h
=
+
2 2
Mà
( ) ( )
hd
GMm GM
F P mg mg g
R h R h
+ = = ⇔ = ⇔ =
+ +
Câu 4. Hai kh u giối cầ ống nhau đư t sao cho tâm cách nhau khoợc đặ ảng
r
thì l c h p dự ấ ẫn
giữa chúng là
F
. N u thay m u trên b ng m t kh u đ ng chế ộ ốt trong hai kh i cầ ằ ộ ối cầ ồ ất khác
nhưng có bán kính l nguyên khoớn gấ ẫp hai, v n giữ ảng cách gi a hai tâm (hai kh ầữ ối c u
không ch m nhau) thì lạ ự ữc h p d n giấ ẫ a chúng lúc này là:
A.
2 F
. B.
16 F
. C.
8 F
. D.
4 F
.
Lời giải:
Khi bán kính khối cầu tăng gấp hai
( )
2 2
2r r
′
=
thì kh ng c a khối lượ ủ ối c u là:ầ
3 3
2 2
(2 ) 8m DV D r D r m
π π
′ ′ ′
= = = =
Khi giữ nguyên khoảng cách gi a 2 tâm (do hai kh ầữ ối c u không chạm nhau) thì lực hấp
dẫn giữa 2 quả cầu này là:
1 2 1 2
2 2
8
.8
hd
m m m m
F G G F
r r
′
= = =
Câu 5. Ở mặt đ t vậất, mộ t có tr ng lưọ ợng
10 N
. N n v t này cao cách Trái Đế ểu chuy ậ ở độ ất
một khoảng
R
(
R
là bán kính Trái Đ ng lư ng cất) thì trọ ợ ủa vật bằng
A.
1 N
. B.
2,5 N
. C.
5 N
. D.
10 N
.
Lời giải:
Tại mặt đất ta có
2
10
hd
Mm
F P N G
R
= = =
Tại độ cao cách Trái Đất một khoảng
R
(với
R
là bán kính Trái Đ ng lư ng cất) thì trọ ợ ủa
vật bằng:
2 2
2,5 N
( ) (2 ) 4
hd
Mm Mm P
P F G G
R h R
′ ′
= = = = =
+
Câu 6. Biết gia tốc rơi tự do ở đỉnh và chân một ng n núi l n lưọ ầ ợt là 9,809
2
/m s
và 9.810
2
/m s
. Coi Trái Đ t là đ ng ch t và chân núi cách tâm Trái Đ u cao cấ ồ ấ ất 6370km. Chiề ủa
ngọn núi này là?
A. 324.7 m B. 640 m C. 649.4 m D. 325 m
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 43
Lời giải:
Ta có gia t c rơi t do t i đố ự ạ ỉnh có độ cao h có công thức tính là:
2
( )
h
M
g G
R h
=
+
Gia t c rơi t do tố ự ại chân núi
0
2
( 0) :
M
h g G
R
= =
2
h
g R h
g R
+
⇒ =
9,810
1 6370 1 0,3246 km
9,809
h
g
h R
g
⇒ = − = − ≈
Câu 7. Coi khoảng cách trung bình gi ất và tâm M t Trăng gữa tâm Trái Đ ặ ấp 60 lần bán
kinh Trái Đ ng M t Trăng nh ng Trái Đ n. Xét vất; khối lượ ặ ỏ hơn khối lượ ấ ầt 81 l ật
M
nằm
trề ẳn đường th ng n i tâm Trái Đố ất và tâm M t Trăng mà ặ ở đó có l c h p d n c a Trái Đự ấ ẫ ủ ất
và của M t Trăng cân b i bán kính Trái Đ ng cách tậ ằng nhau. So vớ ất, khoả ừ
M
đến tâm
Trát Đấ ất g p
A. 56,5 lần. B. 54 lần. C. 48 lần. D. 32 lần.
Lời giải:
Gọi
x
là kho ng cách tả ừ tâm Trái Đ t (TĐ) đấ ến vật
m
đặ ạt t i đi m ta xét nên khoể ảng cách
từ tâm c ặủa M t Trăng (MT) đ n vế ật là
60R x−
.
Ta có:
TD m MT m
F F
− −
=
2 2
.
( )
.
TD MT
M m M m
G G
x R x
⇒ =
−
2 2
81.
9 54
(60 ) 60
MT MT
M M x
x R
x R x R x
⇒ = ⇒ = ⇒ =
− −
Chọn đáp án (B).
Câu 8. Cho tam giác vuông cân
ABC
vuông tại
C
, có cạnh huy n ề
AB R=
. T i ba đạ ỉnh
A, B
và C c a tam giác, ngư ặ ất điủ ời ta đ t 3 ch ểm có kh ng l n lưối lượ ầ ợt là
m, 2 m
và
3 m
.
Tìm l c h p d n tác d ng lên chự ấ ẫ ụ ất đi ạểm t i
C
.
A.
2
2
3 5
m
G
R
B.
2
2
6 5
m
G
R
C.
2
2
12
m
G
R
D.
2
2
6
m
G
R
Lời giải:
Do tam giác
ABC
cân tại
C
nên ta có:
2
R
AB BC= =
TAILIEUHUST.COM
44 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
- Lự ểc h p d n tác d ng lên chấ ẫ ụ ất đi m tại C là:
C AC BC
F F F= +
Mà
2
2 2
2
2 2
6
12
A C
AC
B C
BC
M M m
F G G
r R
M M m
F G G
r R
= =
= =
2
2 2
2
6 5
C AC BC
m
F F F G
R
⇒ = + =
Câu 9. Kim tinh (còn gọ ọi là sao Thái B ch, sao Hôm ho c sao Mai) đư c gạ ặ ợ i là "hành tinh
sinh đôi" v i Trái Đ t do kh , kích thư c g n gi ng v i Trái Đ t Trái Đớ ấ ối lượng ớ ầ ố ớ ất. Biế ất và Kim
Tinh có đườ ợng kính lần lư t là
12740 km
và
12090 km
. Kh ng c a Kim Tinh bối lượ ủ ằng
81,5%
khố ủ ủi lượng c a Trái Đ t. Tính gia t c rơi t do trên bấ ố ự ề mặt c a Kim Tinh bi c rơi tết gia tố ự
do trên b a Trái Đề mặt củ ất có giá trị
2
9,81 m / s
T
g =
.
A.
2
13, 37 m / s
B.
2
8,88 m / s
. C.
2
7, 20 m / s
. D.
2
1,67 m / s
.
Lời giải:
Gia tốc trên b mề ặt Kim Tinh:
2
K
K
K
M
g G
R
=
Gia t c trên b t Trái Đố ề mặ ất:
2
T
T
T
M
g G
R
=
Mà
2
2
2 2
0,815
9,81, 8,88 m / s
6045
K K T T
K K
T T K
g M R M
g g
g M R
= → = → =
Câu 10. Trong một quả cầu bằng chì bán kính
R
, ngư i ta khoét mờ ộ ỗt l hình c u bán kính ầ
R / 2
. Tìm l c do qu u tác d ng lên v t nhự ả ầ c ụ ậ ỏ
m
trên đường n i tâm hai hình cố ầu, cách
tâm hình c ộ n ầu lớn m t đoạ
d
, biết rằng khi chưa khoét quả cầu có khối lượng
M
.
A.
2 2
2
2
7 8 2
8
2
d dR R
F GMm
R
d d
− +
= ⋅
−
B.
2 2
2
2
7 8 2
8
2
d dR R
F GMm
R
d d
+ +
= ⋅
−
C.
2 2
2
2
7 8 2
2
d dR R
F GMm
R
d d
− +
= ⋅
−
D.
2 2
2
2
7 8 2
4
2
d dR R
F GMm
R
d d
− +
= ⋅
−
Lời giải:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 45
- Phầ ẽn khoét đi s hút
m
lực h p dấ ẫn:
1
2
2
k
M m
F G
R
d
=
−
Lực h p d n do cấ ẫ ả cquả ầu đặt tác dụng lên
2
2
:
Mm
m F G
d
=
2 1
2
2
(*)
2
k
MM
F F F Gm
d
R
d
⇒ = − = −
−
- cQuả ầ ấu đ ng chồ t nên:
3
3
( / 2) 1
8 8
kK
k
VM R M
M
M V R
= = = → =
Thay vào (*) ta được:
2 2
2
2
7 8 2
.
8
2
d dR R
F GMm
R
d d
− +
=
−
TAILIEUHUST.COM
46 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Chương 6. Dao động – sóng
A. Công thức
1. Dao động cơ điều hòa
- . Phương trình dao đ ng: ộ 𝑥 𝑥 = 𝐴𝐴cos
(
𝜔𝜔
0
𝜔 𝜔 + 𝜑𝜑
)
- Biên độ dao đ ng: ộ 𝐴 𝐴 = 𝑥𝑥
max
.
-
Tần số góc riêng: 𝜔𝜔
0
=
�
𝑘𝑘
𝑚𝑚
.
- Pha củ ộa dao đ ng:
(
𝜔𝜔
0
𝜔 𝜔 + 𝜑𝜑 𝜑𝜑
)
, là pha ban đầu củ ộa dao đ ng.
- Vận tốc củ ộa dao đ ng: 𝑣 𝑣 =
𝑑𝑑𝑥𝑥
𝑑𝑑𝑡𝑡
= −𝐴𝐴𝜔𝜔
0
sin
(
𝜔𝜔
0
𝜔 𝜔 + 𝜑𝜑
)
.
2. Con lắ ậc v t lý
- Tần số góc: 𝜔 𝜔 = �
𝑚𝑚𝑔𝑔𝑚𝑚
𝐼 𝐼
.
Trong đó: L là khoảng cách t i tâm đ n tr c quay, ừ khố ế ụ 𝐼𝐼
−
moment quán tính của v t đậ ối với
trục quay.
3. Dao động cơ tắt dần
-
Phương trình dao đ ắộng t t dần: 𝑥 𝑥 = 𝐴𝐴 𝜔𝜔
0
𝑒𝑒
−𝛽𝛽𝑡𝑡
cos (𝜔𝜔𝜔𝜔 + 𝜑𝜑). với 𝜔 𝜔 = �
0
2
− 𝛽𝛽
2
.
- Giảm lượng loga: 𝛿 𝛿 = ln
𝐴𝐴( )𝑡𝑡
𝐴𝐴
(𝑡𝑡+𝑇𝑇)
= 𝛽𝛽𝑇𝑇.
- . Biên độ dao đ ắộng t t dần: 𝐴𝐴 ⇒ −𝐴𝐴 ≤ 𝑥𝑥 ≤ 𝐴𝐴
0
𝑒𝑒
−𝛽𝛽𝑡𝑡
0
𝑒𝑒
−𝛽𝛽𝑡𝑡
0
𝑒𝑒
−𝛽𝛽𝑡𝑡
Nhận xét: H c hi n dao đ ng tệ ỉ ch thự ệ ộ ắt dần khi 𝜔𝜔
0
> 𝛽𝛽.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 47
B. Bài tậ ắp tr c nghiệm
Câu 1. Mộ ột ch m dao đất điể ng điều hòa với chu kì 𝑇𝑇
0
= 2 s, pha ban đầu 𝜑 𝜑 =
𝜋𝜋
3
. Năng
lượng toàn phầ và l t đi ấn 𝑊 𝑊 = 2,6. 10
−5
J ực tác d ng lên chụ ấ ểm lúc lớn nh t 𝐹𝐹
0
= 2.10
−3
N.
Phương trình dao độ ểng nào sau đây là đúng chất đi m trên:
A. 2, 29sin � 𝜋𝜋𝜔𝜔 +
𝜋𝜋
3
� cm. B. 2,7sin �𝜋𝜋𝜔𝜔 +
2𝜋𝜋
3
� cm.
C. 2,6cos �𝜋𝜋𝜔𝜔 +
𝜋𝜋
3
� cm. D. 2, 28cos � 𝜋𝜋𝜔𝜔 +
𝜋𝜋
3
� cm.
Lời giải:
Năng l n ph n W l ng c a con l c, l c d ng l n chượng toà ầ à c ơ nă ủ ắ ực tá ụ ê ấ ểt đi m lúc lớn nhất
𝐹𝐹
0
= 𝑘𝑘𝐴𝐴
Ta có: 𝑊 𝑊 = 2,6.10
−5
=
1
2
𝑘𝑘𝐴𝐴
2
=
1
2
𝐹𝐹𝐴𝐴 ⇒ 𝐴𝐴 =
2𝑊𝑊
𝐹 𝐹
=
2 2 6. , .10
−5
2
.10
−3
= 2,6(𝑚𝑚𝑚𝑚)
Chu kì 𝑇𝑇
0
= 2 =
2𝜋𝜋
𝜔 𝜔
⇒ 𝜔𝜔 = 𝜋𝜋
Do đó, phương trình dao độ ủng c a chất điểm là 2,6 cos �𝜋𝜋𝜔𝜔 +
𝜋𝜋
3
�
Câu 2. Một con l c lò xo ắ 𝑚 𝑚 = 10 g, dao động điều hòa với độ dời 𝑥 𝑥 = 8cos �5𝜋𝜋𝜔𝜔 +
𝜋𝜋
2
� cm.
Kí hiệu 𝐹𝐹
0
là l c cự ực đ i tác dạ ụng lên con lắc và là năng lư𝑊𝑊 ợng c a con l c. Kủ ắ ết luận nào
dưới đây đúng:
A. 𝐹𝐹
0
= 0,3 . N, = 0, 9.𝑊 𝑊 10
−2
J C. 𝐹𝐹
0
= 0,3 . N, = 0, 8.𝑊 𝑊 10
−2
J
B. 𝐹𝐹
0
= 0,2 . N, 𝑊 𝑊 = 0, 8.10
−2
J D. 𝐹𝐹
0
= 0,2 . N, 𝑊 𝑊 = 0, 9.10
−2
J
Lời giải:
Ta có:
𝜔 𝜔 =
�
𝑘𝑘
𝑚 𝑚
⇒ 𝑘𝑘 = 𝜔𝜔
2
𝑚 𝑚 =
(
5𝜋𝜋
)
2
. 0,01 ⇒ 𝐹𝐹
0
= 𝑘𝑘𝐴𝐴 = 0,08.0, 501.
(
𝜋𝜋
)
2
≈ 0,2(𝑁𝑁)
𝑊 𝑊 =
1
2
𝑘𝑘𝐴𝐴
2
=
1
2
(
5𝜋𝜋
)
2
. 0,01.0,08 10
2
≈ 0,8.
−2
(
𝐽𝐽
)
Câu 3. Một con l c toán có sắ ợi dây 𝑙 𝑙 = 1 m, c sau ứ Δ𝜔𝜔 = 0,8 phút thì biên độ dao đ ng ộ
giả ầm 2 l n. Giảm lượng lôga c ng giá trủa con l c đó bắ ằ ị nào sau đây (cho 𝑔 𝑔 = 9,8 m/s
2
)
A.
3, 2, 3,489 10.
−2
. B. 898 10.
−2
. C. 2, 701 10.
−2
. D. 292 10.
−2
.
Lời giải:
Ta có:
0
g
l
ω
=
Tại t bất kì ta có:
0
( )
0
.
( ) ln 2
2 2 2
( ) .
t
t
t t
A e
A t
e
A t t A e t
β
β
β
β
−
∆
− +∆
= ⇔ = ⇒ = ⇒ =
+ ∆ ∆
TAILIEUHUST.COM
48 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Giảm lư a con lợng loga củ ắc là:
2
2 2 2
0
2 ln 2 2 ln 2 2
. 2,898.10
ln 2
T
t t
g
l t
π π π
σ β β
ω
ω β
−
= = = × = × ≈
∆ ∆
−
−
∆
Câu 4. Một con l c toán có sắ ợi dây 𝑙 𝑙 = 65 cm. Biết rằng sau thời gian 𝜏 𝜏 = 6 phút, nó mất
99% năng lư ng lôga c ắ n giá trợng. Giảm lượ ủa con l c nhậ ị nào dư i đâyớ ?
A.
0, 1,975 10.
−2
. B. 1, 125 10.
−2
. C. 1, 035 10.
−2
. D. 065 10.
−2
.
Lời giải:
Tại t bất kì ta có:
2
0
( )
0
.W( ) ( ) ln10
100 100 10 10
W( ) ( ) .
t
t
A et A t
e
t A t A e
β
βτ
β τ
β
τ τ τ
−
− +
= ⇒ = ⇔ = ⇒ = ⇒ =
+ +
Lượng giả ắm loga c a con lủ c:
2
2 2 2
0
2 ln10 2 ln10 2
. 1, 035.10
ln10
T
g
l
π π π
σ β β
ω τ τ
ω β
τ
−
= = = × = × ≈
−
−
Câu 5. Một ch m dao đ i chu kì và biên đ n tất điể ộng điều hòa vớ 1,4 s ộ 8 cm. Vậ ốc chất
đi ạ ằ
ểm trên t i v trí mà li đị ộ b ng
1
2
b biên độ ằng giá trị nào dưới đây:
A. 0, m/s311 . . . . B. 0,321 m/s C. 0,331 m/s D. 0,341 m/s
Lời giải:
Áp dụng phương trình v ố ủề m i liên hệ c a A, x, v:
2 2
2 2 2 2 2 2 2
2 2
0,08 0,04 0,311( m / s)
2 1, 4
v A
A x v A x A
T
π π
ω
ω
= + ⇒ = − = − = − =
Câu 6. Một con l c toán có sắ ợi dây dài là , và c𝑙𝑙 ứ sau Δ𝜔 𝜔 = 5 phút thì biên độ dao đ ng ộ
giảm 2 l m lưầ ản. Gi ợng lôga c ắ ng trư ng ủa con l c đó là . Cho gia t𝛿 𝛿 = 0,023 ố ọc tr ờ 𝑔 𝑔 =
9,8 m/s
2
. H i đây:ỏi 𝑙𝑙 bằng giá tr nào dưị ớ
A. 2, 2, 1, 2,554 m. B. 044 m. C. 704 m. D. 214 m.
Lời giải:
Thiết lập phương trình dao độ ủng t n cắt dầ a con l c lò xo. Trong trư ng h p này, hắ ờ ợ ợp lực
tác d ảụng lên qu cầu:
C
F F kx rv+ = − −
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 49
Phương trình cơ b ủa chuy ộản c ển đ ng trong trườ ợng h p này là
ma kx rv= − −
Hay:
2 2
2 2
0
d x dx d x r dx k
m r kx x
dt dt dt m dt m
= − − ⇔ + + =
(1)
Đặt
2
r
m
β
=
s t (hệ ố ắt dần)
Phương trình (1) tr thành ở
2
2
0
2
2 0
d x dx
x x
dt dt
β ω
+ + =
(2)
(2) gọi là phương trình vi phân củ ộ n. Theo toán họa dao đ ng tắ ầt d c giải tích, khi
0
ω β
>
,
nghiệm phương trình này có dạng:
Đây là bi u th c đ ng t ng sể ứ ộ ủ ộ dời c a dao đ ắt dầ ằn. H ố
ω
cgọi là tần số ủ ộa dao đ ng tắt
dần:
2 2
0
ω ω β
= −
Theo bài ra, ta có:
. .300 3
0
1 1
7,7.10
2 2
t
x
e e
A
β β
β
− ∆ − −
= = ⇒ = ⇒ ≈
Giảm lượng loga của con lắc:
0,023 2,987( s)T T
δ
δ β
β
= = ⇒ = =
Chu kỳ
T
củ ộa dao đ ng t n là: ắt dầ
2 2
2
0
2 2 2
2,987( s) 2,214( m)T l
g
l
π π π
ω
ω β
β
= = = = ⇒ =
−
−
Câu 7. Một con l c v t lý đưắ ậ ợc cấu t o bạ ằng một thanh đ t diồng chất tiế ệ ền đ u có độ dài
bằng 𝑙𝑙 và trục quay O c mủa nó cách trọng tâm G ột kho ng bả ằng 𝑥𝑥. Biết rằng chu kỳ dao
độ ấ ịng 𝑇𝑇 của con l c này là nhắ ỏ nh t, 𝑥𝑥 nhận giá tr nào dưới đây:
A.
1
√
3
. B. 1/2. C.
1
4
√
3
. D.
1
2 3
√
.
Lời giải:
Chu k ộỳ dao đ ng
T
của con lắc:
2
I
T
mgd
π
=
Với
1 2
I I I= +
với
1
I
là moment quán tính c a thánh và ủ
2
I
là moment quán tính của chất
điểm đ i vố ới trục quay
2 2
2 2
2
2
1 2
12 12
( ) 2 2
12
l l
m x x
ml
I I I mx d x T
mgx gx
π π
+ +
= + = + = ⇒ = =
TAILIEUHUST.COM
50 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
2
2 2
max
0 2 0
12
12 2 3
x
l l l
T T x x x
′
⇔ = ⇒ − + = ⇒ = =
Câu 8. Một xe lửa gồm nhiề ệu toa đư ặợc đ t trên các lò xo c a hủ thố ỗng bánh xe. M i lò xo
của toa xe chịu một trọng lượng 𝑃 𝑃 = 5.10
4
N nén lên nó. Xe l rung độ nh nhửa bị ng mạ ất
khi nó ch ố ộ nố ủ ộ ỗạy với t c đ 𝑣 𝑣 = 26 m/s qua các chỗ i c a đường ray. Đ dài m i thanh ray
bằng 𝑙 𝑙 = 12,5 m. Hệ s ố đàn hồi của các lò xo nhận giá trị nào dưới đây (cho 𝑔 𝑔 = 9,8 m/s
2
)
A.
82, 64 10.
4
N/m. B. 88 64 10, .
4
N/m.
C.
87 14 10, .
4
N/m. D. 84 14 10, .
4
N/m.
Lời giải:
Con l ộ nh nh ng hư ng (chu k ủ ùng ắc dao đ ng mạ ấ ảt khi x y ra cộ ở ỳ ộ dao đ ng riêng c a vật tr
chu k ỗ nố ủỳ qua các ch i c a đường ray):
12,5
0,48( )
26
S
T s
v
= = =
Mặt khác:
4
4
5.10
5.10 ( ) 5102, 04( kg)
9,8
P
P N mg m
g
= = ⇒ = = =
Mà
2 2
4
2 2
)
. .4 4 5102,04
2 0, 48( ) 87, 4.10 ( N / m
0,48
m m
T s k
k T
π π
π
= = ⇒ = = =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 51
Chương 7. Nguyên lý thứ nhất của nhiệ ộ ọ ế ột đ ng lực h c và thuy t đ ng học phân tử
A. Công thức
1. Phương trình trạng thái của khí lý tưởng
𝑃𝑃𝑉𝑉
=
𝑚𝑚
𝜇 𝜇
𝑅𝑅𝑇𝑇 = 𝑛𝑛𝑅𝑅𝑇𝑇.
- c Giá trị ủa R
• Hệ SI: R = 8.314 J/ P( mmol. K → Pa), V
(
3
)
• R = 0.082 L. /atm mol. K → P(atm), V (lít)
2. Nhiệt
- Nhiệt dung riêng: là lư ầợng nhiệt c n thiế ể ệt đ tăng nhi t độ của 1kg ch t tăng thêm 1 đấ ộ.
𝑑𝑑𝑄𝑄
𝑃 𝑃
= 𝑚𝑚. 𝑚𝑚
𝑃𝑃
𝑑𝑑𝑇𝑇 𝑑𝑑𝑄𝑄 c hoặ
𝑣 𝑣
= 𝑚𝑚. 𝑚𝑚
𝑣𝑣
𝑑𝑑𝑇𝑇 : (đơn vị J. kg
−1 −1
K ).
- Nhiệt dung riêng mol (nhiệt dung riêng phân t n thiử): là lương nhiệt cầ ế ểt đ tăng 1 mol
chất tăng thêm 1 độ.
𝑑𝑑𝑄𝑄 𝐶𝐶
𝑃 𝑃
= 𝑛𝑛.
𝑃𝑃
𝑑𝑑𝑇𝑇 𝑑𝑑𝑄𝑄 c hoặ
𝑣 𝑣
= 𝑛𝑛. 𝐶𝐶
𝑣𝑣
𝑑𝑑𝑇𝑇 (đơn vị: J.mol
−1
K
−1
).
- Liên hệ giữa 𝑚𝑚 và 𝐶𝐶: 𝑚𝑚𝑚𝑚 → 𝐶𝐶= 𝑛𝑛𝐶𝐶 =
𝑚𝑚
𝑛 𝑛
𝑚 𝑚 = 𝜇𝜇𝑚𝑚. với 𝜇𝜇
−
khối lượng m t mol chộ ất.
3. Hệ ố s Poisson
𝛾 𝛾
=
𝐶𝐶
𝑝𝑝
𝐶𝐶
𝑣 𝑣
=
𝑚𝑚
𝑝𝑝
𝑚𝑚
𝑣 𝑣
=
𝑖 𝑖 + 2
𝑖 𝑖
. với
�
𝐶𝐶
𝑝 𝑝
=
𝑖 𝑖 + 2
𝑖 𝑖
𝑅𝑅
𝐶𝐶
𝑣 𝑣
=
𝑖𝑖
2
𝑅 𝑅
.
Trong đó: 𝑖𝑖
−
bậc tự do. Đơn nguyên tử ử: 𝑖 𝑖 = 3, Hai nguyên t : 𝑖 𝑖 = 5, Ba nguyên tử: 𝑖 𝑖 = 6 …
4. Công và ba tr ng thái cơ bạ ản
- Công: 𝐴 𝐴 = ∫
𝑣𝑣
1
𝑣𝑣
2
𝑝𝑝𝑑𝑑𝑉𝑉.
- Đẳng tích: 𝑉 𝑉 = const →
𝑃𝑃
1
𝑇𝑇
1
=
𝑃𝑃
2
𝑇𝑇
2
.
- Đẳng áp: 𝑃 𝑃 = const →
𝑉𝑉
1
𝑇𝑇
1
=
𝑉𝑉
2
𝑇𝑇
2
.
- Đẳ ệng nhi t: 𝑇 𝑇 = const → 𝑃𝑃
1
𝑉𝑉
1
= 𝑃𝑃
2
𝑉𝑉
2
.
5. Phương trình cơ b n cả ủa thuyế ột đ ng học phân tử
TAILIEUHUST.COM
52 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
- Áp suất lên thành bình: 𝑝 𝑝 =
1
3
𝑛𝑛
0
𝑚𝑚
0
𝑣𝑣
2
�
�
�
=
2
3
𝑛𝑛
0
𝑚𝑚
0
𝑣𝑣
2
�
�
�
�
2
=
2
3
𝑛𝑛
0
W
�
.
- Độ ị ếng năng t nh ti n trung bình: W
�
=
3
2
𝑅𝑅𝑇𝑇
𝑁 𝑁
=
3
2
𝑘𝑘𝑇𝑇.
- Vận tốc căn quân phương: 𝑣𝑣
𝑐 𝑐
=
�
3𝑘𝑘𝑇𝑇
𝑚𝑚
0
=
�
3𝑅𝑅𝑇𝑇
𝜇 𝜇
.
- M ật độ phân tử: 𝑛𝑛
0
=
𝑝𝑝
𝑘𝑘𝑇𝑇
.
- Vận tốc trung bình: 𝑣𝑣‾ =
�
8𝑅𝑅𝑇𝑇
𝜋𝜋𝑛𝑛
0
𝑚𝑚
0
=
�
8𝑅𝑅𝑇𝑇
𝜋𝜋𝜇𝜇
.
- Vận tốc xác suất lớn nhất: 𝑣𝑣
𝑥𝑥𝑠𝑠
=
�
2𝑘𝑘𝑇𝑇
𝑚𝑚
0
.
6. Công thức khí áp
- Công thức khí áp:
0
0
0
0
.
m gh
kT
m gh
kT
p p e
n n e
−
−
=
=
- Nhận xét:
• Khí quyển có ranh giới rõ rệt.
• Mật độ hạt gi ầảm d n theo chi u cao.ề
• Công thức khí áp mang tính gần đúng (trong ph không lạm vi ℎ ớn, độ vài km).
7. Nộ ị ậi dung đ nh lu t I
- Độ biên thiên nội năng c a h ng tủ ệ bằ ổng công và nhi nhệ ệt lư ng mà hợ ận được: Δ𝑈𝑈 =
𝐴 𝐴 + 𝑄𝑄.
. Hay 𝑄 𝑄 = Δ𝑈𝑈 𝐴𝐴+
- Các trường h p đợ ặc biệt:
• Đoạn nhiệ ệt: H không trao đổi nhiệt với bên ngoài nên: 𝑄 𝑄 = Δ𝑈𝑈 + 𝐴 𝐴 = 0.
• Đẳng áp: 𝑄 𝑄 = Δ𝑈𝑈 Δ𝑈𝑈 𝑝𝑝𝑑𝑑𝑉𝑉+ 𝐴 𝐴 = + .
• Đẳng tích: 𝑄 𝑄 = Δ𝑈𝑈.
• Đẳn ệg nhi t: 𝑄 𝑄 = 𝐴𝐴.
8. Hiệ ợ ện tư ng đoạn nhi t
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 53
- Công thức đoạn nhiệt: 𝑝𝑝
1
𝑉𝑉
1
𝛾 𝛾
= 𝑝𝑝
2
𝑉𝑉
2
𝛾𝛾
hoặc 𝑇𝑇
1
𝑉𝑉
1
𝛾𝛾−1
= 𝑇𝑇
2
𝑉𝑉
2
𝛾𝛾−1
.
- Công thức tổng quát công sinh b i hở ệ: 𝐴 𝐴 = ∫
𝑉𝑉
1
𝑉𝑉
2
𝑝𝑝𝑑𝑑𝑉𝑉.
- Công trong các trường hợp:
• Đẳng áp: 𝑝 𝑝 = const, 𝐴 𝐴 = 𝑝𝑝
(
𝑉𝑉
2
− 𝑉𝑉
1
)
= 𝑝𝑝Δ𝑉𝑉.
• Đẳng tích: 𝑉 𝑉 = const, 𝐴 𝐴 = 0.
• Đẳ ệng nhi t: 𝑇 𝑇 = const, 𝐴 𝐴 = ∫
𝑉𝑉
1
𝑉𝑉
2
𝑛𝑛𝑅𝑅𝑇𝑇
𝑉 𝑉
𝑑𝑑𝑉𝑉 �= 𝑛𝑛𝑅𝑅𝑇𝑇ln
𝑉𝑉
2
𝑉𝑉
1
�.
• Đoạn nhiệt: 𝑝𝑝𝑉𝑉
𝛾 𝛾
= const = 𝐾𝐾 → 𝑝𝑝 =
𝐾𝐾
𝑉𝑉
𝛾 𝛾
= 𝐾𝐾𝑉𝑉
−𝛾𝛾
,
𝐴 𝐴 = 𝐾𝐾 �
𝑉𝑉
2
𝑉𝑉
1
𝑉𝑉
−𝛾𝛾
𝑑𝑑𝑉𝑉 = 𝐾 𝐾
𝑉𝑉
−𝛾𝛾+1
−𝛾𝛾
+ 1
�
𝑉𝑉
1
𝑉𝑉
2
=
𝐾𝐾𝑉𝑉
2
−𝛾𝛾+1
− 𝐾𝐾𝑉𝑉
1
−𝛾𝛾+1
−𝛾𝛾 + 1
.
TAILIEUHUST.COM
54 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
B. Bài tậ ắp tr c nghiệm
Câu 1. Một khối khí Hiđđô bị nén đế ển th tích bằng 1/2 lúc đầu khi nhiệt độ không đổi.
Nếu v n t c trung bình c a phân tậ ố ủ ử hidro lúc đầu là 𝑉𝑉 thì v n t c trung bình sau khi nén làậ ố
A. 2 V. . B. 4 V C. 1 V. D. V/2.
Lời giải:
Nén đẳng nhiệt
C
ông thức tính v nậ tốc trung b a ch t khình củ ấ í là 𝑣 𝑣 =
�
8𝑘𝑘𝑇𝑇
𝑚𝑚𝜋𝜋
chỉ phụ thuộc nhiệ đột nên vận
tốc trung bình không đổi
Câu
2. 1 g khí hiđtrô
(
H
2
)
đự ểng trong một bình có th tích 5 l. Mật độ phân tử của ch t khí ấ
đó là: (cho h ng sằ ố khí 𝑅 𝑅 = 8, 31 10.
3
J/kmol.K; hằng số Boltzmann
(
𝑘 𝑘 = 1, 38 10.
23
J/K
)
A.
6, 022 10.
25
phân tử /m
3
. C. 5, 522 10.
25
phân tư /m
3
.
B.
4, 522 10.
25
phân tử /m
3
. D. 7, 022 10.
25
. phân tử /m
3
Lời giải:
Số phân tử khí là: 𝑁 𝑁 = 𝑛𝑛. 𝑁𝑁
𝐴 𝐴
=
𝑚𝑚
𝜇 𝜇
𝑁𝑁
𝐴𝐴
Hằng số Boltzmann 𝑘 𝑘 =
𝑅𝑅𝑇𝑇
𝑉 𝑉
=
𝑅𝑅
𝑁𝑁
𝐴 𝐴
= 1,28.10
−23
(
𝐽𝐽𝐾𝐾⁄ )
⇒ 𝑁𝑁
𝐴 𝐴
=
𝑅𝑅
𝑘 𝑘
⇒ 𝑁𝑁 =
𝑚𝑚
𝜇 𝜇
.
𝑅𝑅
𝑘𝑘
M
ật độ phân tử của ch t khấ í là
𝑁𝑁
𝑉 𝑉
=
𝑚𝑚𝑅𝑅
𝜇𝜇𝑘𝑘𝑉𝑉
= 6,022.10
25
Câu 3. Khố ủi lượng c a 1kmol s -chất khí là 𝜇 𝜇 = 30 kg kmol/ và hệ ố Poat xông của ch t khí là ấ
𝛾 𝛾 = 1,4. Nhi ng áp c a khí bệt dung riêng đẳ ủ ằng? Hằng số khí 𝑅 𝑅 = 8, 31 10.
3
Jkmol
−1
K
−1
A. 995 kg 982 kg 930 kg 969,5 J/( . K). B. ,5 J/( . K). C. ,5 J/( . K). D. ,5 J/( kg ⋅ K).
Lời giải:
Hệ số Poisson 𝛾 𝛾 =
𝐶𝐶
𝑝𝑝
𝐶𝐶
𝑣 𝑣
= 1,4
Lại có: 𝐶𝐶
𝑝 𝑝
− 𝐶𝐶
𝑣 𝑣
= 𝑅𝑅
Do đó: 𝛾 𝛾 =
𝐶𝐶
𝑝𝑝
𝐶𝐶
𝑣 𝑣
=
𝐶𝐶
𝑝𝑝
𝐶𝐶
𝑝𝑝
−𝑅𝑅
⇒ 𝐶𝐶
𝑝 𝑝
=
𝛾𝛾𝑅𝑅
𝛾𝛾−1
Nhiệt dung ri ng ng ê đẳ áp của khí:
𝑚𝑚
𝑝 𝑝
=
𝐶𝐶
𝑝𝑝
𝜇 𝜇
=
𝛾𝛾𝑅𝑅
𝜇𝜇
(
𝛾𝛾 − 1
)
=
1,4.8,31.10
3
30
(
1,4 − 1
)
≈ 969,5
(
𝐽 𝐽 𝑘𝑘𝑔𝑔
⁄
. 𝐾𝐾
)
Câu
4. Một khối khí ôxy
(
O
2
)
b ị nung nóng từ nhiệt dộ 240 K đến 267
∘
C. N u v n tế ậ ốc
trung bình của phân t ôxy lúc đử ầu là 𝑣𝑣 thì lúc sau là:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 55
A. 1, 1, 1,5 1,635𝑣𝑣. B. 55𝑣𝑣. C. 𝑣𝑣. D. 𝑣𝑣.
Lời giải:
Công thức tính v n tậ ốc trung bình của phân tử khí:
8kT
v
m
π
=
1
1
2 2
1 1
2
2
8
267 273
Hay 1,5
240
8
kT
v
v T
m
v T
kT
v
m
π
π
=
+
= = =
=
Câu
5. Hai khối khí O
2
và H
2
có cùng mật đ t dộ số hạt. Nhiệ ộ của khối khí O
2
là 120
∘
C,
nhiệt độ c t ủa khối khí H
2
là 60
∘
C. Áp suất của O
2
và H
2
theo thứ ự là 𝑃𝑃
1
và 𝑃𝑃
2
. Ta có:
A. 𝑃𝑃
1
= 0,98𝑃𝑃
2
. B. 𝑃𝑃
1
= 1,18𝑃𝑃
2
.
C. 𝑃𝑃
1
= 0,88𝑃𝑃
2
. D. 𝑃𝑃
1
= 1,28𝑃𝑃
2
.
Lời giải:
Mật độ phân tử chất khí:
0
A
NN m
n
V V
µ
= = ×
Theo phương trình Clapeyron -Mendeleev:
0
1
A
m m p p p
pV RT n N
V RT RT T k
µ µ
= × ⇒ = ⇒ = × = ×
(k là hằng số Boltzmann)
Vì hai khối khí
2
O
và
2
H
có cùng mật độ số hạt và nhiệt độ không đổi
⇒
Áp suất không
đổi
Quá trình đẳng tích:
1 1
1 2
2 2
120 273
1,18 1,18
60 273
p T
p p
p T
+
= = ≈ ⇒ ≈
+
Câu 6. 𝑀 𝑀 = 18 g khí đang chiế ểm th tích 𝑉 𝑉 = 4 lít ở nhiệt độ 𝜔 𝜔 = 22
∘
C. Sau khi hơ nóng
đẳ ằng áp, khối lượng riêng c a nó bủ ng 𝜌 𝜌 = 6.10
−4
g/cm
3
. Nhiệt độ của kh i khí sau khi hơ ố
nóng là:
A. 2213 . . . . K B. 2113 K C. 2013 K D. 1913 K
Lời giải:
Trước khi hơ nóng:
1 1
m
pV RT
µ
=
Sau khi hơ nóng:
2
2 2 2
2
RTm m
pV RT p RT
V
ρ
µ µ µ
= ⇒ = =
TAILIEUHUST.COM
56 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Lấy
1 1
1 2
2 1
(1)
2213( )
(2)
mT mT
V T K
T V
ρ ρ
⇒ = ⇒ = =
Câu
7. Mộ ốt kh i ôxy
(
O
2
)
ở nhiệt độ 20
∘
C. Đ n t c căn quân phương c a phân tể nâng vậ ố ủ ử
lên gấp đôi, nhiệt độ của khí là:
A.
899
∘
C. . . . B. 919
∘
C C. 929
∘
C D. 889
∘
C
Lời giải:
Công th ầức tính v n t c căn quậ ố n phương:
3
C
kT
v
m
=
(với
k
là h ng sằ ố Boltzmann)
Ta có:
1
2 2
1
1 1 2 1
2 1
2 2 1 1
2
2
3
2
(20 273) 1172( )
3
kT
v
T v v v
m
T T K
T v v v
kT
v
m
=
⇒ = ⇒ = = + =
=
Câu 8. Nhiệt độ của m t kh i plasma khí coi là khí lí tư ng trên mộ ố ở ặt trời là 2,6 ⋅ 10
6
K. Vận
tốc căn quân phương của các đi do trong khện tử tự ối khí đó là:
(
𝑚𝑚
e
= 9, 1.10
−31
kg, 𝑘 𝑘 =
1,
38.10
−23
J/K
)
A.
11, 876 10.
6
m/s. B. 10 876 10, .
6
. m/s
C. 13 10,876 ⋅
6
m/s. D. 12 876 10, .
6
. m/s
Lời giải:
Công thức vận tốc căn quân phương 𝑣𝑣
𝑐 𝑐
=
�
3𝐾𝐾𝑇𝑇
𝑚𝑚
0
⟹ 𝑣𝑣
𝑐 𝑐
=
�
3 ∗ ∗2,6 10
6
∗ 1,38 ∗ 10
−23
9,1
∗ 10
−31
≈ 10,876 ∗ 10
6
�
𝑚𝑚
𝑠 𝑠
�
Câu 9. Hai bình khí cùng th i năng. Bình 1 ch , bình 2 chể tích, cùng nộ ứa khí Heli (He) ứa
Nitơ
(
N
2
)
. Coi các khí lí tư ng. Gở ọi 𝑝𝑝
1
và 𝑝𝑝
2
là áp suất tương ứng c a bình 1 và 2. Ta có:ủ
A. 𝑝𝑝
1
= 𝑝𝑝
2
. B. 𝑝𝑝
1
=
3𝑝𝑝
2
5
. C. 𝑝𝑝
1
=
2𝑝𝑝
2
5
. D. 𝑝𝑝
1
=
5𝑝𝑝
2
3
.
Lời giải:
Vì hai bình khí có cùng thể tích
⇒
quá trình đẳng tích
Biến thiên nội năng trong qua trình đẳng tích:
2 2 2
m i i i
U RT nRT PV
µ
∆ = ⋅ ⋅ = =
Khí Heli
3i→ =
và khí Nito
5i→ =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 57
Ta có:
1 1
1 1 1 1
2 2 1 1 1 2
2 2 2 2 1 2
2 2 2 1
1 2 1 2
. . .
2 2
5 5
. . . 1
2 2 3 3
;
i i
U n RT PV
i i i P P i
U n RT PV P P
i P P i
V V V U U U
∆ = =
∆ = = ⇒ = ⋅ ⇒ = = ⇒ =
= = ∆ = ∆ = ∆
Câu 10. Khố ủ ội lượng riêng c a m t ch t khí ; v n tấ 𝜌 𝜌 = 5.10
−2
kg/m
3
ậ ốc căn quân phương
của các phân tử khí này là 𝑣 𝑣 = 450 m/s. Áp suất củ ố ụa kh i khí tác d ng lên thành bình là:
A.
3575 3675 3475 3375 N/m
2
. B. N/m
2
. C. N/m
2
. D. N/m
2
.
Lời giải:
Áp d c tính v n t c căn quân phương c a phân tụng công thứ ậ ố ủ ử khí:
v =
�
3𝑅𝑅𝑇𝑇
𝜇 𝜇
=> RT = v
2
𝜇𝜇/3
Phương trình trạng thái khí lý tưởng:
pV =
𝑚𝑚
𝜇 𝜇
𝑅𝑅𝑇𝑇 => p =
𝜌𝜌
𝜇 𝜇
𝑅𝑅𝑇𝑇 =
𝜌𝜌
𝜇𝜇
v
2
𝜇𝜇/3 = 𝜌𝜌𝑣𝑣
2
/3 = 3375 (N/m2)
Câu 11. Mộ ốt kh i khí nitơ
(
N
2
)
biến đổi trạng thái sao cho áp suất của nó tăng 2 lầ ận và v n
t
ốc căn quân phương củ n. Trong quá trình đó, kha các phân tử tăng
√
2 lầ ối lượng riêng
của kh i khí nitơ thay đ i như thố ổ ế nào?
A. Gi
ảm
√
2 l l lần. B. Tăng
√
2 ần. C. Tăng 2
√
2 ần. D. Không đổi.
Lời giải:
Áp d ng thái khí lý tưụng phương trình trạ ởng ta được:
pV =
𝑚𝑚
𝜇 𝜇
𝑅𝑅𝑇𝑇 => p =
𝜌𝜌
𝜇 𝜇
𝑅𝑅𝑇𝑇 => 𝜌 𝜌 =
3𝑝𝑝
𝑣𝑣
2
Ta có:
𝜌𝜌
2
𝜌𝜌
1
=
𝑝𝑝
2
𝑣𝑣
1
2
𝑝𝑝 𝑣𝑣
1
2
2
= 1
Vậy kh ng riêng c a kh i khí không đối lượ ủ ố ổi.
Câu 12. Mộ ốt kh i khí oxy
(
O
2
)
biến đổi trạ ảng thái sao cho kh ng riêng c a nó giối lượ ủ m
1,5 lần và t c đố ộ trung bình của các phân t m 1,5 l n. Trong quá trình đó, áp suử giả ầ ất mà
khí ôxy tác dụng lên thành bình thay đổi như thế nào?
A. Giảm 3,375 lần. B. Giảm 1,225 lần. C. Gi 5 lảm 2,2 ần. D. Giả ầm 1,837 l n.
Lời giải:
Theo bài ra, ta có:
pV
n
RT
= =
const
TAILIEUHUST.COM
58 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Ỏ trạng thái
1 1
1
1:
p V
n
RT
=
và ở trạng thái
2 2 2 1 2
2 1 2 1
2 :
p V p V T
n
RT p V T
= ⇒ = ⋅
Công thức tính v n tậ ốc trung bình của phân tử khí:
8kT
v
m
π
=
Hay
1
2
1
2 2
1 1
2
2
8
8
kT
v
v T
m
v T
kT
v
m
π
π
=
⇒ =
=
và
1 1
1 2
2 2
2 1
m V
V
m V
V
ρ
ρ
ρ
ρ
=
⇒ =
=
2
2 1 2 2 2
1 2 1 1 1
8
27
p V T v
p V T v
ρ
ρ
⇒ = ⋅ = ⋅ =
Câu 13. Một xi lanh có pit - tông có thể di đ c. Trong xi ng m t khộng đượ -lanh đự ộ ối khí lí
tưởng. Vỏ xi lanh không d t. Nẫn nhiệ ếu áp suất không khí trong xi lanh tăng 2 lần thì nội
năng củ ổa khí thay đ i như thế thế nào? (gọi
γ
là hệ s ố Poatxông)
A Tăng
1
2
γ
−
l ần B.tăng
1
2
γ
γ
−
l ần C.Tăng
1
2
γ
γ
−
l ần D.Tăng
1
2
γ
γ
+
l ần
Lời giải:
Do vỏ xi lanh không d n nhiẫ ệt
→
quá trình diễ ện ra bên trong xi lanh là đoạn nhi t.
+ Ta có phương trình:
1
1 1
2 1
1 1 2 2
1 2
P T
T P T P
P T
γ
γ γ
γ
γ γ
−
− −
= ⇔ =
+ Mà
1 1
1 1
2 1 2 11
2
2 2 2
2
T T
P P T T
T
γ γ
γ γ
γ
γ
− −
−
= ⇒ = ⇔ = = ⋅
(1)
Nội năng:
R
2
i U
U n T
T
= ⇒ =
const
2
i
nR=
1 2 2
2 1
1 2 1
(2)
U U T
U U
T T T
⇒ = ⇔ =
Từ (1) và (2) ta có:
1
2 1
2U U
γ
γ
−
=
Câu 14. Mộ ốt kh i khí ôxy
( )
2
O
có kh ng riêng là ối lượ
( )
3
0,59 kg / m
ρ
=
. sổ Avôgađrô
26
N 6,023 10 ( J / kmol)= ⋅
. T t khí và đỷ số áp suấ ộng năng tị ếnh ti n trung bình của phân tử
khí là:
A
24
6,873.10 ( Pa / J)
B.
24
8,993 10 ( Pa / J)⋅
C.
24
8,463 10 ( Pa / J)⋅
D.
24
7, 403 10 ( Pa / J)⋅
Lời giải:
Áp d c tính áp su t khí theo đụng công thứ ấ ộng năng tịnh tiến trung bình:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 59
0 0
2 2
W
3 3W
p
p n n= ⇒ =
2
3
p N
W v
⇔ = ⋅
với
N
là số phân tử;
A
N
là số Avôgađro
23
24
2 2 2 2 2 6,023.10
.0,59 7, 403.10
W 3 3 3 W 3 3 0,032
A A A
A
nN N Np m m p
N
v v v
ρ
µ µ µ
⇔ = ⋅ = ⋅ = ⋅ ⋅ ⇔ = ⋅ = ⋅ =
Câu 15. Tổng động năng t nh tiị ến trung bình c a các phân tủ ử khí Nito
( )
2
N
chứa trong
một khí cầu bằng
3
5.10 ( J)w
−
=
và vận t c căn quân phương c a phân tố ủ ử khí đó là
e
v =
3
2.10 ( m / s)
. Kh g khí nitơ trong khí cối lượn ầu là:
A.
5
2,84.10 ( kg)
−
B.
9
2,5.10 ( kg)
−
C.
3
3, 01.10 (Kg)
−
D.
3
2,33.10 ( kg)
−
Lời giải:
Ta có:
3 3 3 3
W W W
2 2 2 2
A
A A
R m R m
N N KT N T N T RT
N N
µ µ
= ⋅ = ⋅ = ⋅ ⋅ ⇔ = ⋅ ⋅ ⋅ = ⋅ ⋅
(1)
Vận tốc căn quân phương:
2
3 3
c c
RT RT
v v
µ µ
= ⇒ =
(2)
Từ
(2)
và
2 9
2
2
(1) W 2,5.10 ( kg)
2
c
c
m W
v m
v
−
⇒ = ⇒ = =
Câu 16. Một kh ng có thối khí lí tườ ể tích
( )
3
6 mV =
dãn nở đẳng nhiệt từ áp suất
2(at)
đến
1( )at
. Lư p cho quá trình này là:ợng nhiệt đã cung cấ
A.
5
9,16.10 ( )J
B.
5
10,16.10 ( )J
C.
5
8,16.10 ( )J
D.
5
5,16.10 ( )J
Lời giải:
Quá trình là đẳng nhiệt
2 1
1 1 2 2
1 2
2
2
1
V P at
PV PV
V P at
⇒ = ⇔ = = =
Do quá trình là đẳng nhiệt
0 0T U⇒ ∆ = ⇒ ∆ =
Theo Nguyên lí 1 Nhi t đ ng l c hệ ộ ự ọc:
,Q U A A A
′ ′ ′
= ∆ + =
là công khi th c hiự ện
Ta có:
2 2 2 2
1 1 1 1
1 1
R
PdV R
V V V V
V V V V
n T dV dV
A dV n T PV
V V V
′
= = = =
∫ ∫ ∫ ∫
4 5
2
1 1
1
ln 2.9,81.10 6.ln 2 8,16.10 ( ). .
V
A PV J
V
′
⇒ = = =
5
8,16.10 ( )Q A J
′
⇒ = =
Câu 17. Nén đ t 3 lít không khí t 1 at. Tìm nhi a ra biẳng nhiệ ở áp suấ ệt tỏ ế ểt rằng th tích
cuối cùng bằng
1/10
thể tích ban đầu.
A.
676 J−
B.
872 J−
C.
512 J−
D.
911 J−
Lời giải
TAILIEUHUST.COM
60 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Theo Nguyên lí thứ nh ủất c a nhiệt độ ọng l c hự c, nhiệt lư ng mà kh i khí nh n đượ ố ậ ợc là
Q A U∆ = + ∆
Do là quá trình đẳng nhi t nên ệ
0
V
U nC T∆ = ∆ =
Nhiệt lư ng mà kh n đượ ối khí nhậ ợc
2 2
1 1
2
1 1
1
d ln
V V
V V
VdV
Q A p V pV p V
V V
∆ = = = =
∫ ∫
4 3
1
9,81.10 3.10 ln 676 J.
10
Q
−
⇒ ∆ = ≈ −
(tỏa nhiệt)
Câu 18. Một bình kín thể tích 2 lít, đựng
12 g
khí nitơ ở nhiệt độ
10 C
°
. Sau khi hơ nóng, áp
suất trung bình lên tới
4
10 mmHg
. Tìm nhi t lư ng mà kh i khí đã nh n đư c, biệ ợ ố ậ ợ ết bình
giãn nỏe
A.
4,1 kJ
B.
5,1 kJ
C.6,1 kJ D.
8,1 kJ
Lời giải:
Do bình giãn nở kém nên thể tích của bình coi như không đổi, quá trình là đẳng tích
Ta có nguyên lí I nhi ng l c hệt độ ự ọc
( )
2 1
iR
2
m
Q A U U T T
µ
∆ = + ∆ = ∆ = ⋅ −
2 1 2 1
2 2
i m m i m
Q RT RT p V RT
µ µ µ
∆ = − = −
(
2
N
là khí lưỡng nguyên tử
5,C 5
2
V
R
i
= =
Thay số
4 6 3 3
2 1
10 mmHg 1,33.10 Pa, V 2.10 m , T 283 Kp
−
= = = =
4,1 kJQ∆ =
Câu 19. 7 gam khí cacbonic được hơ nóng cho tới khi nhiệt độ tăng thêm
10 C
°
trong điều
kiệ ến giãn nở tự do. Công củ ộa khí sinh ra và đ bi n thiên nộ ủ ối năng c a kh i khí l n lưầ ợt là?
A.
14,2 J
và
32,1 J
B.
13, 2 J
và
39,7 J
C.
19,1 J
và
39,7 J
D.
12,2 J
và
32,1 J
Lời giải
Quá trình giãn n do ta có th n đúng là đở tự ể coi gầ ẳng áp (giãn nở trong khí quyền, áp
suất bằng áp su t khí quyấ ển)
Công do khí sinh ra khi giãn nở:
( ) ( )
2 1 2 1 2 1
m m m
A p V V RT RT R T T
µ µ µ
= − = − = −
7
.8,31.10 13, 2
44
A J⇒ = ≈
Độ ế bi n thiên nộ ủ ối năng c a kh i khí:
R 7 6.8,31
10 39,7 J
2 44 2
m i
U T
µ
∆ = ⋅ ∆ = ⋅ ⋅ ≈
(
2
CO
b là khí đa nguyên tử nên số ậc tự do c a phân tủ ử là 6).
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 61
Câu 20. Một ch t khí đ ng đấ ựng trong m t xilanh đ t thẳộ ặ ứng có pittông khối lượng không
đáng k ng đư ầ ả ằể di độ ợc. Hỏi c n ph i th c hi n m t công bự ệ ộ ng bao nhiêu để nâng pittông
lên cao thêm m t khoộ ảng
1
10 cmh =
nế ều chi u cao ban đ a c t không khí làầu củ ộ
0
15 cmh =
, áp su t khí quy n là ấ ể
0
p =
lat di ặt pittông ện tích m
2
10 cmS =
. Nhiệt độ ủ c a khí coi là
không đổi trong suốt quá trình.
A.
3,2 J
B.
2,6 J
C.
2,3 J
D.
10,2 J
Lời giải
Công do khí
sinh
ra là
0 11
0 0 0 0 0
0 0
ln ln
h h
V
A p V p V
V h
+
= =
Nên khi bi n đ i khí nh n vào mế ổ ậ ột công:
0
0 0 0
0 1
ln
h
A p V
h h
− =
+
Công c ấủa áp su t khí quyển:
0 1k
A p Sh=
Ta có th y công c n th c hi n bao gể thấ ầ ự ệ ồm công truyền cho khí và công thẳng l c do áp ự
suất khí quy n gây ra:ể
1
0 1 10
0
ln 1
k
h
A A A p S h h
h
′
= − = − +
= 2,3J
Câu 21.
3
2m
khí giãn nở đẳng nhiệt từ áp suất
5p =
at đ ng ế ện áp su t 4 at. Tính nhiấ t lượ
cung c p cho khí trong quá trình giãn nấ ở.
A.
5
5,2.10 J
B.
5
2, 2.10 J
C.
5
1,4 10 J⋅
D.
5
2,9.10 J
Lời giải:
Theo nguyên lí I, nhiệt nhận vào của khí:
Q A U= + ∆
Trong quá trình đ t, nẳng nhiệ ội năng
0U∆ =
và công là:
2
1
2 1
1 1 1 1 1 2
1 2
d ln ln
V
V
V p
A p V p V p V p V
V p
= = = =
∫
4 5
5
2.5.9,81.10 ln 2, 2. 0
4
. 1Q A J= = =
TAILIEUHUST.COM
62 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Chương 8. Nguyên lý thứ hai của nhiệ ộ ọt đ ng lực h c
A. Công thức
1. Máy nhiệt
- Công: 𝐴 𝐴 =
|
𝑄𝑄
ℎ
|
−
|
𝑄𝑄
𝑐𝑐
|
.
Nếu ch t sinh công là khí thì: ấ 𝐴 𝐴 = 𝐴𝐴
𝑑 𝑑
+ 𝐴𝐴
𝑣 𝑣
= ∫
𝑉𝑉
1
𝑉𝑉
2
𝑝𝑝
1
𝑑𝑑𝑉𝑉 + ∫
𝑉𝑉
2
𝑉𝑉
1
𝑝𝑝
2
𝑑𝑑𝑉𝑉 = ∫
𝑉𝑉
1
𝑉𝑉
2
(
𝑝𝑝
1
− 𝑝𝑝
2
)
𝑑𝑑𝑉𝑉.
- Hiệu suất của máy nhiệt: 𝜂 𝜂 =
𝐴𝐴
|
𝑄𝑄
ℎ
|
=
|
𝑄𝑄
ℎ
|
−
|
𝑄𝑄
𝑐𝑐
|
|
𝑄𝑄
ℎ
|
= 1 −
|
𝑄𝑄
𝑐𝑐
|
|
𝑄𝑄
ℎ
|
.
2. Máy lạnh
- s Hệ ố làm lạnh: 𝜀 𝜀 =
|
𝑄𝑄
𝑐𝑐
|
𝐴 𝐴
=
|
𝑄𝑄
𝑐𝑐
|
|
𝑄𝑄
ℎ
|
−
|
𝑄𝑄
𝑐𝑐
|
=
𝑇𝑇
𝑐𝑐
𝑇𝑇
ℎ
−𝑇𝑇
𝑐𝑐
.
3. Chu trình Carnot
- M
ối liên hệ giữa nhi n nóng và nhiệt nh n đưậ ợc từ nguồ ệ ồt nhả cho ngu n lạnh:
|
𝑄𝑄
𝑐𝑐
|
|
𝑄𝑄
ℎ
|
=
𝑇𝑇
𝑐𝑐
𝑇𝑇
ℎ
.
- Hiệu suất của chu trình Carnot: 𝜂 𝜂 = 1 −
𝑇𝑇
𝑐𝑐
𝑇𝑇
ℎ
.
4. Entropy
- Công thức Entropy: Δ𝑆𝑆 𝑆𝑆=
2
− 𝑆𝑆
1
= ∫
𝑆𝑆
1
𝑆𝑆
2
𝑑𝑑𝑄𝑄
𝑇 𝑇
.
- . Quá trì ệ ịnh đo n nhiạ t thuận ngh ch: Δ𝑆𝑆 = 0
- . Nguyên lý tăng Entropy: Δ𝑆𝑆 ≥ 0
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 63
B. Bài tậ ắp tr c nghiệm
Câu 1. Một đ ạt động cơ nhi t hoệ ộng theo chu trình Carnot thuận nghịch giữa 2 nguồn
điện có nhiệ ế ậ ệt độ 400 K và 100 K. N u nó nh n 1 lượng nhi t 6 kJ củ ồa ngu n nóng trong
mỗi chu trình thì công mà nó sinh ra trong mỗi chu trình là:
A. 4,5 2,5 1,5 6,5 kJ. B. kJ. C. kJ. D. kJ.
Lời giải:
Hiệ ấu su t chu trình Carnot: 𝜂 𝜂 = 1 −
𝑇𝑇
2
𝑇𝑇
1
𝑇𝑇
1
, 𝑇𝑇
2
l ần lượt là nhiệt độ nguồn nóng và nhiệt độ ồ ngu n lạnh
Lại có: 𝜂 𝜂 =
𝐴𝐴
′
𝑄 𝑄
𝐴𝐴
′
, 𝑄𝑄 lần lượt là c ông sinh ra trong mỗi chu trình và nhiệt lượng nhận được trong mỗi chu
trình
Do đó: 𝜂 𝜂 = 1 −
𝑇𝑇
2
𝑇𝑇
1
=
𝐴𝐴
′
𝑄 𝑄
⇒ 𝐴𝐴
′
= 𝑄𝑄 �1 −
𝑇𝑇
2
𝑇𝑇
1
� = 6. �1 −
100
400
� = 4,5
(
𝑘𝑘𝐽𝐽
)
Câu 2. Một mol khí hidro nguyên tử được nung nóng đẳng áp, thể tích gấ ầp 8 l n. Entropy
c (Của nó biến thiên một lư ng bợ ằng? ho h ng sằ ố khí 𝑅 𝑅 = 8,31 J/ mol.K)
A. . 43 43 44 44,2 J/K . B. ,7 J/K . C. ,2 J/K . D. ,7 J/K
Lời giải:
Độ biến thi n Entropy: ê 𝑑𝑑𝑆𝑆 =
𝑑𝑑𝑄𝑄
𝑇 𝑇
Quá ì tr nh đẳng áp: 𝛿𝛿𝑄𝑄 = 𝑛𝑛𝐶𝐶
𝑝𝑝
𝑑𝑑𝑇𝑇 = 𝑛 𝑛
𝑖𝑖+2
𝑖 𝑖
𝑅𝑅𝑑𝑑𝑇𝑇
⇒ Δ𝑆𝑆 � 𝑛𝑛
=
𝑖 𝑖 + 2
2
𝑅 𝑅
𝑑𝑑𝑇𝑇
𝑇𝑇
𝑇𝑇
2
𝑇𝑇
1
= 𝑛 𝑛
𝑖 𝑖 + 2
2
𝑅 𝑅 ln 𝑇 𝑇
|
𝑇𝑇
1
𝑇𝑇
2
= 𝑛 𝑛
𝑖 𝑖 + 2
2
𝑅 𝑅 ln
𝑇𝑇
2
𝑇𝑇
1
Nung n
óng đẳng áp, do đó:
𝑇𝑇
2
𝑇𝑇
1
=
𝑉𝑉
2
𝑉𝑉
1
⇒ Δ𝑆𝑆
= 𝑛 𝑛
𝑖 𝑖 + 2
2
𝑟 𝑟 ln
𝑉𝑉
2
𝑉𝑉
1
= 43,2
(
𝐽𝐽𝐾𝐾
⁄ )
Câu 3. Một động cơ nhiệt làm việc theo chu trình Carnot có công su ộất 50 kW. Nhiệt đ
c
ủa nguồn nóng là , nhi127
∘
C ệt độ của nguồn lạnh là ng tác nhân nh31
∘
C. Nhi t lưệ ợ ận của
nguồn nóng trong một phút có giá trị:
A. 12200 kJ. B. 12600 kJ. C. 12500 kJ. D. 12300 kJ.
Lời giải:
TAILIEUHUST.COM
64 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Hiệu suất chu trình Carnot:
2
2
1
1
50 625
1 ( )
127 273
3
1
1
31 273
n
n
TA A
Q kJ
T
Q T
T
η
= = − ⇒ = = =
+
−−
+
Nhiệ ồt lượng tác nhân c a nguủ n nóng trong 1 phút là:
625
' . 60 12500( )
3
n
Q Q t kJ= = × =
Câu 4. Một động cơ nhiệt làm việc theo chu trình Carnot v i nhi ộớ ệt đ nguồn nóng là
100
∘
C. Trong mỗi một chu trình tác nhân nh ủ n nóng một nhiận c a nguồ ệt lượng 10 kcal và
th ạực hi . Nhi n lện công 15 kJ ệt độ ủ c a nguồ nh là: (cho 1 cal = 4,18 J )
A. . 212 15, . . . K B. 231 15, K C. 239 15, K D. 245 15, K
Lời giải:
Với
1 2
;T T
l ần lư t là nhi t đợ ệ ộ nguồn nóng và nhiệt độ nguồn lạnh
Mặt khác:
1
A
Q
η
′
=
Với
A
′
là công sinh ra trong mỗi chu trình và
1
Q
là nhi ng nhệt lượ ận đư c trong mợ ỗi chu
trình
Hiệu suất theo chu trình Carnot:
2 2
2 1
1 1 1 1 1
15
1 1 1 363 1 232,92( )
10.4,186
T T
A A A
T T K
T Q T Q Q
η
′ ′ ′
= − = ⇒ = − ⇒ = − = ⋅ − ≈
Câu 5. Một máy nhi t lí tưệ ởng làm việc theo chu trình Carnot, sau mỗi chu trình thu được
600 calo t
ừ nguồn nóng có nhiệt độ ộ 127
∘
C. Nhi t đệ nguồn lạnh là 27
∘
C. Công do máy
sinh ra sau một chu trình là cho bi( ết 1 cal ≈ 4, J)184
A. 627 647 637 657,6 J. B. ,6 J . C. ,6 J. D. ,6 J.
Lời giải:
Hiệu suất theo chu trình Carnot:
2
1
1
T
T
η
= −
với
1 2
;T T
l ần lượt là nhiệt độ nguồn nóng và
nhi ộệt đ ngu nhồn lạ
Mặt khác:
1
A
Q
η
′
=
với
A
′
là công sinh ra trong mỗi chu trình và
1
Q
là nhiệt lượng nh n ậ
được trong mỗi chu trình
Hay
2 2
1
1 1 1
300
1 1 600.4,186. 1 627, 6( )
400
T TA
A Q J
T Q T
η
′
′
= − = ⇒ = − = − =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 65
Câu 6. Cho một chu trình Carnot thuận nghịch, độ biến thiên entropy trong quá trình đẳng
nhi ố ố nhiệ ệt có h s là Δ𝑆𝑆 = 1kcal/K; hiệu s ệt độ giữa 2 đường đẳng nhiệt là Δ𝑇𝑇 = 300 K; 1
cal = 4,18 J. Nhi t lưệ ợng đã chuyển hóa thành công trong chu trình đang xét là
A.
12, 54 10.
5
J. . . . B. 12 04 10, .
5
J C. 13 54 10, .
5
J D. 11 04 10, .
5
J
Lời giải:
Nhiệt lượng chuyển hóa thành công trong chu trình đang xét là
⇔ 𝐴𝐴 ∆𝑆𝑆∆𝑇𝑇= = 4180 12 54 10.300 = , .
5
(
𝐽𝐽
)
Câu 7. Một động cơ nhiệt làm việc theo chu trình Carnot b ng không khí lằ ấy ở áp suất ban
đầ ầu 𝑃𝑃
1
= 7,0 at. Thể tích ban đ u của không khí ng nhi𝑉 𝑉
1
= 2dm
3
. Sau l n giãn đầ ẳ ệt lần
th ấứ nh t nó chi m thế ể tích 𝑉𝑉
2
= 5dm
3
và sau khi giãn đoạ t thn nhiệ ể tích của khí là 𝑉𝑉
3
=
8,1dm
3
. Áp suấ ạt khí sau khi giãn đo n nhiệt có giá tr ằị 𝑃𝑃
3
b ng:
A.
12, 98 10 10 98 10 13 98 10 15 98 10.
4
Pa. B. , .
4
Pa. C. , .
4
Pa D. , .
4
Pa.
Lời giải:
Từ ệ => (1) → (2) : Đẳng nhi t P
2
=
𝑃𝑃
1
𝑉𝑉
1
𝑉𝑉
2
Từ (2) → (3) : Đoạn nhiệt => P
3
=
𝑃𝑃
2
𝑉𝑉
2
𝛾𝛾
𝑉𝑉
3
𝛾 𝛾
=
𝑃𝑃
1
𝑉𝑉
1
𝑉𝑉
2
𝛾𝛾−1
𝑉𝑉
3
𝛾 𝛾
= 1.452 at = 13, 98.10
4
Pa
Câu 8. Một động cơ nhi t có hiệ ệu suất 10% và nhả nhiệ ồt cho một ngu n có nhiệt độ 450
K. Nó nhận nhi n có nhiệ ồt từ một ngu ệt độ ít nhất là:
A. 479 514 507 500 K. B. K. C. K. D. K.
Lời giải:
Hiệu suất theo chu trình Carnot:
2
1
1
T
T
η
= −
Với
1 2
;T T
l ần lư t là nhi t đợ ệ ộ nguồn nóng và nhiệt độ nguồn lạnh
2 2
1
1
450
1 0,1 500( )
1 1 0,1
T T
T K
T
η
η
⇒ = − = ⇒ = = =
− −
Câu 9. Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 10kW. Nhiệt đôk
của nguồn nóng là
100 c
°
, nhiệt độ của nguồn lạnh là
0 C
°
. Nhi t lưệ ợng tác nhân nh cho ả
nguồn lạnh, trong m là bao nhiột phút có giá trị êu?
A
3
1,438.10 ( )kJ
B.
3
1,638.10 ( kJ)
C.
3
1.738.10 ( )kJ
D.
3
1,338.10 ( kJ)
Lời giải:
TAILIEUHUST.COM
66 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Ta có
1 1 2
1 2 1
1 2 1 2 1 2
1
T T T
Q A Q Q A A A
T T T T T T
′
= ⇒ = − = − =
− − −
3 5
).10.10 60 6.10 (A Pt J+ = = =
5 3
2
273
6.10 1, 638.10 ( )
10
.
0
Q kJ
′
⇒ = =
Câu 10. Hơ nóng
1 mol
khí lí tư ng lưở ỡng nguyên tử từ nhiệt độ
1
T
đên
2
T
bằng hai quá
trình đẳng áp và đẳng tích. Gọi biến thiên entropi trong mỗi quá trình đ ng áp, đẳ ẳng tích
lần lượt là
P
S∆
và
V
S∆
Khi đó:
A.
1,8
P V
S S∆ = ∆
B.
1, 4
P V
S S∆ = ∆
C.
1,6
P V
S S∆ = ∆
D.
2,0
P V
S S∆ = ∆
Lời giải
Lưỡng nguyên tử:
5i =
Xét quá trình đ ng áp: ẳ
p
dQ nC dT=
:
2 1 2
1 1 1
T T T
p
p p
T T T
nC dT
dQ dT
S nC
T T T
∆ = = =
∫ ∫ ∫
2 2 2
1 1 1
2 7
ln .ln ln
2 2
p p
T T T
i
S nC n R R
T T T
+
⇔ ∆ = = =
Xét quá trình đẳng tích:
2 2 2
1 1 1
T T T
V
c V
T T T
nC dTdQ dT
S nC
T T T
∆ = = =
∫ ∫ ∫
2 2 2
1 1 1
5
ln ln ln
2 2
c V
T T Ti
S nC n R R
T T T
⇒ ∆ = = =
7 7
1, 4
5 5
p
p c c
S
S S S
S
∆
⇒ = ⇒ ∆ = ∆ = ∆
∆
Câu 11. Một máy hơi nư c có công suớ ất 14,7kW, tiêu th 8,1kg than trong m t giụ ộ ờ. Năng
suất t t cỏa nhiệ ủa than là
7800kcal / kg
. Nhiệt độ của nguồn nóng
200 C
°
, nhiệt độ ủ c a
ngu ủồ ệ ến l nh là 58. Tìm hiạ u suất thực t c a máy. So sánh hi t đó v i hiệu suấ ớ ệu suất lý
tưởng c a máy nhiủ ệt làm việc theo chu trình Cácnô v ồn nhiới những ngu ệt kể trên.
Lời giải
Hiệu suất lý tưởng
14,7.3600
100% 100% 20%
8,1.7800.4,18
ich
toanphan
Q
h
Q
= = =
Hiệu suất lý tưởng
lt
h
theo chu trình Cácnô:
200 58
100% 100% 30%
200 273
n l
lt
n
T T
h
T
−
−
= = =
+
2
3
lt
h h⇒ =
. Vậy hiệu suất thực tế nhỏ hơn 1,5 lần hiệu suất lý tưởng.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 67
Câu 12. Một máy làm lạnh lý tư ng, chở ạy theo chu trình
Cacno ngược lấy nhiệt tứ nguồn lạnh
0 C
°
nhả cho bình
nước sôi ở
100 C
°
. Tính lượ ởng nư n ớc cầ làm đông nguồn
lạnh để có thể biến
1 kg
nước thành hơi bình sôi. Cho biở ết
nhiệt nóng ch ủảy riêng c a nư c đớ á là
5
3, 35.10 J / kg
λ
=
và
nhi ủệt hóa hơi riêng c a nước là
2, 26.10 J / kgL
°
=
.
Lời giải:
Sơ đ máy lồ ạ dạnh có ng tương tự như hình vẽ.
Nhi ừệt nh n tậ nguồn lạnh
Q
, nhả ra nguồn nóng là
1
Q
, h nh khi máy ch y theo ệ số làm lạ ạ
chu trình Carnot ngược:
2 2 2
2 1
1 2 1 2 1
Q T T
Q Q
Q Q T T T
= → =
− −
(1)
Nhiệt lư ng c n làm bay hơi nượ ầ ớc:
1
Q Lm=
(2)
Khối lượng nư n làm nóng chớc cầ ảy là
2
:m Q m
λ
′ ′
=
(3)
Từ (1), (2) và (3) ta có:
6
2
5
1
2, 26.10 273
, .1 4, 93 kg.
3, 35.10 373
TL
m m
T
λ
′
= ⋅ = ≈
Câu 13. Một kmol khí lý tư c hi n mởng thự ệ ột chu trình gồm 2 quá trình đẳng tích và hai
quá trình đẳng áp. Khi đó thể tích của khí thay đổi từ
3
1
25 mV =
đến
3
2
50 mV =
và áp suất
từ
1
1p =
at đến
2
2p at=
. H i công th c hi n b i chu trình này nhỏ ự ệ ở ỏ hơn bao nhiêu l n công ầ
thực hi n b ng đệ ởi chu có các đưtrình Cacno ờ ẳng nhiệt ứng với nhiệt độ lớn nh ỏất và nh
nh ủất c a chu trình nói trên, n ng nhiếu khi giãn đẳ ệt th tích tăng lên gể ấp đôi?
Lời giải:
Công th ảực hi n trong cệ chu trình:
( )( )
2 1 2 1
A p p V V= − −
(1)
Trong chu trình Cacno, nhiệt độ nguồn nóng
2
T
ứng với
điểm
( )
2 2
,V p
, nhiệt độ nguồn lạnh
1
T
ứng v i điớ ểm
( ) (
1 1 1 1 1
, / RV p T p V n⋅ =
và
)
2 2 2
/ RT p V n=
.
Trong một chu trình tác nhân nh n nhiậ ệt
2
2 2
1
ln
V
p V
V
′
′
(2)
Với hiệu suất:
2 1 2 2 1 1
2 2 2
T T p V p V
T p V
η
− −
= =
(3)
Từ (2) và (3), suy ra công khí sinh ra trong một chu trình:
( )
2
1 2 2 1 1
1
ln
V
A Q p V p V
V
η
′
′
′
= = −
(4)
TAILIEUHUST.COM
68 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Giãn đ ng nhiẳ ệ ểt th tích tăng lên gấp đôi nên
2
1
2
V
V
′
′
=
. K t hế ợp (4) và (1) ta có:
( )
( )( )
2
2 2 1 1
1
1 2 2 1
ln
(2.50 1.25) ln 2
2,1
(2 1)(50 25)
V
p V p V
V
A
A p p V V
′
′′
−
−
→ = = ≈
− − − −
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 69
PHẦN II. CÂU HỎI VÀ BÀI TẬP TỰ LUẬN
Câu 1.
1. Định nghĩa vecto gia t m và ý nghĩa c a các vecto gia tốc. Nêu đ c điặ ể ủ ốc tiế ếp tuy n,
gia tốc pháp tuyến
2. Bài toán: Từ đỉ nh tháp có độ cao h, người ta ném m i đột hòn đá xu ng dưố ớ ất với
vận t c ban đố ầu
0
v
theo phương h ộợp v i phương th ng đ ng mớ ẳ ứ t góc
α
(hình vẽ)
a. Viết phương trình chuyể ện đ ng cộ ủa hòn đá trong h tọa
độ vuông góc, v ố ọ ộ u ném (hình ới g c t a đ tạ ắi điểm b t đầ
vẽ)
b. Cho
2
0
30 ; 20 / 2; 60 ; 9,8 / sh m v m g m
α
°
= = = =
. Tìm thời
gian bay và tố ộ ủc đ c a hòn đá khi chạm đất.
c. Tìm gia t c pháp tuy n t i đi m ch m đố ế ạ ể ạ ất. Bỏ qua lực
cản của không khí
Lời giải
1. Lý thuyết
Đị ốnh nghĩa vecto gia t c:
Vecto gia t ng vectơ bi c trưng ốc là đ i lưạ ợ ể ịu th cho gia t c. Gia t c là đ ng v t lý đố ố ại lượ ậ ặ
cho sư biến thiên nhanh hay ch ủậm c a vận tốc.
Gia tốc tiế ếp tuy n:
Đặc điểm:
- Điểm đặt tại M
- Có phương trùng với tiế ế ỹp tuy n của qu đạo tại
M
.
- u Có chiề là chiề ểu chuy n động khi v tăng và ngược lại khi v giảm.
- lCó độ ớn b ng đằ ạo hàm vận t c theo thố ời gian
t
dv
a
dt
=
.
Ý nghĩa: Vecto gia tốc tiế ếp tuy n đ c trưng cho sặ ự biến thiên của vecto vận t c vố ề độ ớn l .
Gia tốc pháp tuyến:
Đặc điểm:
- Điểm đặt tại M
- Có phương vuông góc với tiế ế ỹp tuy n qu đạo tại
M
.
- Có chiều hướng vào tâm . (hướng vào phía lõm của quỹ đạo)
TAILIEUHUST.COM
70 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
- lĐộ ớn bằng:
2
n
v
a
R
=
.
Ý nghĩa: Vecto gia t c pháp tuyố ến đặc trưng cho sự biến thiên v phương c n ề ủa vecto vậ
tốc.
2. Bài toán:
a. Chọn h ọệ t a độ như hình vẽ:
2
0 0
2
0 0
1
2
1
2
x x
y y
x x v t a t
y y v t a t
= + +
= + +
Với
0
0
0
0 0
2
0 0
0
sin
0
0
sin .
1
cos
cos .
2
0
x
y
x
y
x
y
x v t
v v
v v
y v t gt
a
a g
α
α
α
α
=
=
=
=
⇒
=
= +
=
=
b. Th i gian bay: ờ
2
4,9 10 30 0y h t t= ⇒ + − =
1,66t s⇒ =
Tốc độ khi chạ ấm đ t
2 20
0
sin 10 3 /
31,47 /
cos 26, 27 /
x
x y
y
v v m s
v v v m s
v v gt m s
α
α
= =
⇒ = + =
= + =
c. Ta có:
2
10 3
sin 9,8 5,39 m / s
31,47
x
n
v
a g g
v
β
= = = =
Câu 2:
1. Trình bày các v n đấ ề sau:
a. H quy chi nguyên lí tương đệ ếu quán tính và ối Galileo.
b. H quy chiệ ếu không quán tính và lực quán tính ly tâm.
2. Bài toán: Người ta chèo một con thuyền qua sông theo hướng vuông góc với bờ
sông v i v n tớ ậ ốc 7,2
km / h
. Nư y đã mang con thuy n vớc chả ề ề phía xuôi dòng một
khoảng
150 m
. Tìm:
a. V n t c đ i vậ ố ủc c a dòng nướ ố ới bờ sông.
b. Th n đ c sông. Cho bi t chi ng c a sông bời gian cầ ể ề thuy n qua đượ ế ều rộ ủ ằng
0,5 km
.
Lời giải
1. Lý thuyết
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 71
a. Hệ quy chiếu quán tính là h nh luệ ế ệ ế ị quy chi u mà trên h quy chi u đó, các đ ật quán tính
của Newton được nghiệm đúng.
- Nguyên lý tương đ i hối Galileo: Mọ ệ quy chiếu chuyể ề ện động thẳng đ u đ i v i hố ớ quy
chiếu quán tính cũng là h u quán tính hay cá nh lu c nghiệ ế quy chi c đị ật Niuton đượ ệm
đúng trong h ng thệ ế ể quy chi u chuy n độ ẳng đề ệ ểu đ i v i hố ớ quy chi u quán tính.
Điề ệ ếu đó có nghĩa là: các phương trình đ ng l c h c trong các hộ ự ọ quy chi u quán tính có
dạ ấng như nhau, các phương trình cơ học b t biến đ i v i phépố ớ biến đổi Galileo.
b. Trong 1 h quy chi n đ ng có gia t c so v i 1 hệ ếu chuyể ộ ố ớ ệ quy chiếu quán tính, các định
luật Niuton không đư c nghiợ ệ ệ ếm đúng n a là hữ quy chi u không quán tính.
Lự ệ ệ ếc quán tính ly tâm và l t hiực quán tính xuấ n trên 1 v t n m yên trong hậ ằ quy chi u
quay so v i 1 hớ ệ ế quy chi u quán t ốí ệnh. Nó là h cquả ủa trư ng gia tờ c, xu t hi n trong hấ ệ ệ
quy chiếu phi quán tính. Cũng có thể hi ủểu lự ực ly tâm là ph n lả c c a l ng tâm tác ực hướ
động vào v t đang chuyậ ển động theo một đường cong, để giữ cho vậ ằ ằt n m cân b ng
trong hệ ế quy chi u.
hr
F m a= − ⋅
Lực quán tính ly tâm có cùng độ lớn nhưng ngượ ớc chiều v i lực hướng tâm.
2. Bài toán:
0
v
c là v n t n so v i nưậ ốc thuyề ớ ớ
u
là v n tậ ốc dòng nước
v
là v n t n so vậ ốc thuyề ới bờ
a. Ta có:
0
7.2 / 2 /v km h m s= =
0 0
tan
BC ut u
AB v t v
α
= = =
0
0
150
Mà 0,3 0, 3 0,3. 0.6( m / s)
500
BC u
u v
AB v
= = ⇒ = ⇒ = =
b. Thời gian c n đầ ể qua sông:
0
500
250( )
2
AB
t s
v
= = =
Câu 3:
1. Lý thuyết
a. Nêu định nghĩa độ ế ị ề độ ểng lượng, thi t lập các đ nh lí v ng lư ng c a chợ ủ ất đi m, ý nghĩa
của động lượng và xung lượng c a lủ ực.
b. Trình bày đ ng lư ng c a h m cô l p và đị ộnh lu o toàn đật bả ợ ủ ệ ể chất đi ậ ịnh lu o toàn ật bả
động lượng theo mộ ủt phương c a hệ ể chất đi m.
TAILIEUHUST.COM
72 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
2. Bài toán:
Hai hòn bi có khối lượng
1
m
và
1
2
m
2
m
=
đư ằợc treo b ng 2 s i dây có cùng chiợ ều dài
6(m)l =
vào m t điộ ể ệm. Kéo l ch hòn bi
1
m
cho đ ồến khi dây treo nằm ngang r i th ra đả ể
nó va chạm vào bi
2
m
. Sau va chạm hai hòn bi dính vào nhau và lên tới đ cao c c độ ự ại là?
Biết
( )
2
9,8 m / sg =
Lời giải
1. Lý thuyết
a. Đị ợnh nghĩa đ ng lưộ ng: Độ ể ịng lư ng c a m t chợ ủ ộ ất đi m là đ i lư ng v t lý đư c xác đạ ợ ậ ợ nh
bằng tích số giữa khối lượng và vận tốc của ch m đó.ất điể
Vectơ đ ng lưộ ợng:
K mv=
- Định lý 1: Theo định lu t II Newton, ta có: ậ
F ma=
.
Vậy: Đ o hàm đ ng lư ng c a 1 chạ ộ ợ ủ ất điể ịm đ i v i th i gian có giá trố ớ ờ bằng l c (hay tự ổng
hợ ể ểp lực) tác dụng lên chất đi m đó. Bi u thức
dK
F
dt
=
- Định lý 2: Theo đ nh lý I:ị
1
2 2
1
1
2
2 1
t
K
K
t
t
t
dK
F dK Fdt dK Fdt
dt
K K K Fdt
= ⇔ = ⇔ =
⇔ ∆ = − =
∫ ∫
∫
(
.F t= ∆
nếu
F
không đổi)
1
2
t
t
Fdt
∫
gọi là xung lư ng cợ ủaa lực
F
trong khoảng thời gian
1 2
t t→
.
Vậy: Độ biến thiên đ ủộng lượng c a 1 ch m trong m t khoất điể ộ ảng thời gian nào đó có giá
trị bằng xung lượng củ ổa l c (hay tự ng hợp lực) tác dụng lên chất điểm trong khoảng thời
gian đó. Biểu thức
2
1
t
t
K Fdt∆ =
∫
- Ý nghĩa c ng lưủa độ ợng:
+ Đ ng lư ng độ ợ ặc trưng cho chuyền độ ề ng v mặ ậ ặt độ ọng l c hự c và v n t c cũng đố c trưng
cho chuyể ền đ ng vộ mặt động học.
+ Đ ng lư ng đ c trưng cho khộ ợ ặ ả năng truyền chuyền động.
- Ý nghĩa của xung lượng:
. .K F t∆ = ∆
+ Xung lư ng c a mợ ủ ột lực trong khoảng thời gian
t∆
đặc trưng cho tác d ng c a lụ ủ ực
trong khoảng th i gian đó.ờ
( )dv d mv dK
m F F F
dt dt dt
⇔ = ⇔ = ⇔ =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 73
b. Định lu o toàn củật bả a hệ chuyển đ ng cô lộ ập và theo phương.
- C ủa hế chất điểm (chuyển động)
Theo đ nh lý 2 v ng lưị ề độ ợng ta có
( )
1 1 2 2 n n
d
m v m v m F
dt
v+ +…+ =
với
F
. là t i lổng h p các ngoợ ạ ực tác d ng lên hụ ệ
1. Xét h cô l p thì: ệ ậ
0
F =
, tức là
1 1 2 2 n n
m v m v m v+ +…+ =
const.
⇒
t ổ ộ ủng đ ng lư ng cợ a 1 hệ cô l p là đậ ại lư i (đượng không đổ ợc bảo toàn)
2. Theo 1 phương c a hủ ệ ể chất đi m
1 1 2 2 n n
m v m v m v+ +…+ =
const
Khi đó: Hình chiế ộ ệu củ ổa t ng đ ng lư ng c t hợ ủa mộ lên phương
x
đó là một đại lượng
được bảo toàn.
2. Bài toán:
Đặ ế ịt mốc th năng tại v trí cân b ng c a hòn bi 1 trư c va chằ ủ ớ ạm.
Áp d ng đụ ịnh luật bảo toàn cơ năng ta có:
1 1
1
0 0 2
2
m v
m gl v gl+ = + ⇒ =
(1)
Ngay sau va chạm cả hai hòn bi có cùng v ốạn t c
'v
. Áp d ng đụ ị ộnh lu o toàn đật bả ng
lượng ta có:
( )
1 1
1 1 2
1
1 2
1
2
'
3
2
'
2
2
3
m v m v
m v m m v v v gl
m
m m
m
= + ⇒ = = = =
+
+
(2)
Độ ệng năng của h hai hòn bi sau va chạm là:
2 2
'2 2
1 2
1 1
3 1 2
2 2 4 3 3
d
m v m v
W m v m v mgl
′ ′
′
= + = = =
Sau khi va ạch m thì hai hòn bi dính vào nhau và ti ụếp t c chuyể ịn đ a bộng tròn củ 1. Động
năng của hệ ị hai hòn b chuyể ến thành th năng
( )
1 1 2 1
3
2
W m m gh m gh
′
= + =
Của hai hòn bi ố ố năng như trên) ở độ cao t i đa h (m c thế
1 1
2 3 4
2,667( )
3 2 9
d
W W m gl m gh h l m
′ ′
= ⇔ = ⇒ = =
Câu 4:
1. Trình bày các vấn đề sau:
a. H quy chi u quán tính và nguyên lý tương đệ ế ối Galileo
b. H quy chiệ ếu không quán tính và lực quán tính ly tâm.
TAILIEUHUST.COM
74 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
2. Bài toán:
Từ ỉ một đ nh tháp
A
cao
h 25 m=
người ta ném một hòn đá lên phía trên theo phương
hợp v i phương nớ ằm ngang m t, góc ộ
30
α
°
=
với tốc độ
0
15 m / sv =
(hình vẽ ị). Xác đ nh:
a. Qu a hòn đá, ch n gỹ đạo củ ọ ố ọc t a độ ở chân tháp.
b. T c đ a h n đá sau 2 giây kố ộ củ ỏ ể từ khi ném.
c. Th i gian đ ng đ m ném xa tính t y ờ ể hòn đá rơi xuố ất và tầ ừ chân tháp. Lấ
2
9,8 m / sg =
Lời giải:
1. Lý thuyết: tương tự câu 2
2. Bài toán: Chọn gốc như hình vẽ
Ta có phương trình v n tậ ốc:
0
0
cos
sin
x
y
V V
V V gt
α
α
=
= −
Phương trình chuyể độn ng:
0
2
0
cos
1
sin
2
x v t
y v t gt h
α
α
=
= − +
0
cos
x
t
V
α
⇒ =
a. Thay
0
cos
x
t
V
α
=
vào y ta có:
2 2
2 2
0
1
tan 25 0, 029
2 cos
3
y
y h x x y x x
V
α
α
= + − ⋅ ⇔ = + −
Suy ra quỹ đạo là 1 nhánh parabol
b. Ta có
7,5 3
7,5 9,8
x
y
v
v t
=
= −
. Sau t = 2s thì
7,5 3 m / s
121.1 m / s
x
y
v
v
=
= −
2 2
17,75 m / s
x y
v v v⇒ = + =
c. Tìm thời gian chạm đất t ta giải phương trình y=0
2
4,9 7,5 25 0 3,15t t t s⇔ − + + = ⇔ =
Tầm xa:
(3,15) 7,5. 3.3,15 40,92L x m= = =
Câu 5:
Lý thuyết
a. Thi p các đ ng lư ng c a ch m. Ý nghĩa c ng c a lết lậ ị ề độnh Iý v ợ ủ ấ ểt đi ủa xung lượ ủ ực.
b. Trình bày định lu o toàn đ nh lu o toàn ật bả ộ ể ịng lư ng cua hợ ộ chất đi m cô lập và đ ật bả
độ ượng l ng theo mộ ủt phương c a hệ ể chất đi m.
Bài toán:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 75
Một bì cát có khối lượng
M
đư ằ ảợc treo b ng mợt sợi dây m nh không giãn. B ộắn m t viên
đạn có khối lượng
m
theo phương ngang và có t c đố ộ v vào b c vào ì ị cát. Viên đ n bạ mắ
đó và b cát đư ầì ợc nâng lên đ n đ cao h so v i v ban đế ộ ớ ị í tr u. Tính t c đ y theo các đố ộ ại
lượng m,
M, h, g
.
Lời giải:
1. Lý thuyết: tương tự câu 3
2. Bài toán
- t - Chọ ốn m c thế năng ại vị trí A, g i v’ là v n tọ ậ ốc của hệ bì đạn ngay sau khi đ n xuyên vàoạ
- - m Coi hệ bì cát là hệ cô l p có: ậ độ ệng lư ng hợ trước khi va chạ là
1
K mv=
và ng động lượ
hệ sau khi va chạm là
2
K ( ) 'm M v= +
Áp d ng đụ ị ộnh luật bảo toàn đ ng lượng ta có:
21
( )K K mv m M v
′
= ⇒ = +
(1)
Cơ năng tại A (sau khi đ n xuyên vào bì):ạ
' 2
1
( ).
2
( )
A
W m M v= ⋅ +
Cơ năng tại B:
W =(m+M)gh
B
Theo định lu o toàn cơ năng ta có:ậ ảt b
2
1
( ) ( )
2
A B
W m M ghW m M v
′
= ⇔ + = +
2v gh
′
⇔ =
(2)
Từ (1):
.m v
v
m M
′
=
+
thay vào (2) ta được:
.
2 2
M v m M
gh V gh
mm M
+
= ⇔ = ⋅
+
Câu 6:
1. Nêu quan ni ọệ ềm v không gian và thời gian trong cơ h c Newton. Phép bi n đế ổi
Galileo. Phát bi i Galileoểu nguyên lý tương đố
2. Bài toán: M ột vật A có khối lượng
A
m
đặ ặ ẳt trên m t ph ng nghiêng một góc
α
nối
với v t B có khậ ối lượng
B
m
bằng một sợi dây mảnh không giãn vắt qua ròng rọc có
kh ợối lư ng không đáng kể (hình vẽ ệ). H số ma sát giữa vậ ặt A và m t phẳng nguyên
là k. B a ròng rỏ ủ qua ma sát c ọc.
a. Tìm đi u ki n cề ệ ủ ốa tỉ s
A
B
m
m
để vật B đi lên
b. Tìm gia t c căng cố ủc c a các vật và lự ủa dây khi đó.
Lời giải:
1. Lý thuyết:
Quan niệ ềm v không gian và th i gian:ờ
- Thời gian có tính chất tuyệt đối không ụph thuộc vào h quy chiệ ếu
TAILIEUHUST.COM
76 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
- V ị trí không gian có tính chất tương đối ph c vào h quy chiụ ộ thu ệ ếu
- Khoảng không gian có tính ch ối không phụất tuyệt đ c thu c vào h quy chiộ ệ ếu
Chứng minh: Xét 2 hệ trụ ọc t a
Oxyz
quy ư c đ ng yên, hớ ứ ệ
O x
′
'y'z' chuyển đ ng tộ ị ếnh ti n
đố ệi v i hớ
Oxyz
. Ta giả định
O x'
′
luôn trượt dọc theo
Ox
,
O y
′ ′
và
O z
′
' song song và cùng
chiều với
Oy,Oz
. Với mỗ ội hệ tọa đ ta gắn vào một đồng hồ để chỉ thời gian. Xét một
điểm
M
có tọ ộa đ không gian và th i gian trong hờ ệ tọa độ Oxyz là
t, x, y
, z; trong hệ tọa
độ ể O'x'y'z' là t', x', y', z'. Theo các quan đi m của Newton:
- Thời gian có tính tuy ối không phụệt đ thuộ ệ ếc vào h quy chi u:
t t
′
=
(1)
- V ị trí của điểm
M
được xác định tùy theo hệ ế quy chi u:
x x=
' +OO';
; (2)y y z z
′ ′
= =
Như vậy: vị trí trong không gian có tính tương đ u. Do đó: ố ụi ph thuộc vào h quy chiệ ế
chuyển động có tính tương đối tùy thu c vào h quy chiộ ệ ếu.
- Khoả ểng cách gi a hai điữ m bất kì trong không gian là một đại lượng không phụ ộ thu c
vào h ng cách 2 điệ ế ả quy chi u. Kho ểm
A, B
l trong 2 hệ ần lượt là:
o B A
B A
l x x
l x x
′ ′
= −
= −
ta lại có
A A
B A B A o
B B
x O O x
x x x x l l
x O O x
′ ′
′ ′
′ ′
= +
⇔ − = − ⇔ =
= +
hay ta có thể nói không
gian có tính tuyệ ệ ết đố ụi, không ph thường vào h quy chi u.
Phép bi n đế ổi Galileo:
Chúng ta xét m t trưộ ờng hợp riêng: chuyển ủđộng c a h O' là chuy n đệ ể ộng th ng và đẳ ều.
Nếu tại
t 0, O
′
=
trùng với
O
thì:
O O Vt
′
=
V là v n t n đ ng c a hậ ốc chuyể ộ ủ ệ
O
′
. Theo
(1)
và
(2)
ta có:
x x=
'
Vt+
';
; ; (3)y y z z t t
′
′
= = =
Và ngư ạợc l i:
; ; ;x x Vt y y z z t t
′ ′ ′ ′ ′
= − = = =
(4)
Các công thức (3) và (4) gọ ổi là phép bi n đế i Galileo: chúng cho ta cách chuy ọển các t a độ
không gian, thời gian t quy chi u O' sang h quy chiừ hệ ế ệ ếu
O
và ngược lại.
Nguyên lý tương đối Galileo:
+ Phát bi i h quy chi n đ ng đ u đ i v t h quy chiểu 1: Mọ ệ ế ểu chuy ộng thẳ ề ố ới mộ ệ ếu quán
tính cũng là hệ quy chiếu quán tính.
+ Phát biểu 2: Các đ nh luị ật Newton được nghiệ ệm đúng trong h quy chi n đế ểu chuy ộng
thẳng đ u đ i v i h quy chiề ố ớ ệ ếu quán tính.
+ Phát bi u 3: Các phương trình đ ng l c h c trong các h quy chiể ộ ự ọ ệ ếu quán tính có dạng
như nhau.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 77
2. Bài toán:
Chọn chi ủ như hình vều dương c a hệ ẽ.
Phương trình của định lu t II Newton vậ ới các vật A B là:
(
: sin cos )
:
A A
B B
A m g k T m a
B T m g m a
α α
− = =
− =
( )
(sin cos )
A B A B
m g k m g m m a
α α
⇒ − − = +
a. Đi u ki n đ B đi lên làề ệ ể :
( )
0 (sin cos ) 0. .
A A BB
m m a m g k m g
α α
⇔ + > ⇔ − − >
(sin cos )
A B
m k m
α α
⇔ − >
hay
sin cos
B
A
m
k
m
α α
< −
b. Khi đó ta có:
(sin cos )
(sin cos 1)
( )
.
.
A B
A B
A B
B
A B
m k m
a g
m m
m m k
T m g a g
m m
α α
α α
− −
= ⋅
+
− +
= + = ⋅
+
Câu 7:
1. Nêu quan ni ọệ ềm v không gian và thời gian trong cơ h c Newton. Phép bi n đế ổi
Galileo. Phát bi i Galileoểu nguyên lý tương đố
2. Bài toán: Một ngư ạời đang ch y với tốc độ
2 m / sv =
thì ném t i trướ ớc một hòn đá
với tốc độ so v i ngướ ời là
0
5 m / sv =
. Bỏ qua m a ngưọ ủi ma sát và chi u cao cề ời.
a) Tìm góc nghiêng
α
c ủa vận t c hòn đá so v i ngư i đố ớ ờ ể hòn đá có tầ ạm bay xa c c đự i.
b) Tính t c đố ộ
v
′
của hòn đá so với mặt đất trong trường h p câu ợ
a
Lời giải
1. Lý thuyết: như câu 6
2. Bài tập:
a. Ta có
0
v v v
′
= +
(1)
Để hòn đá có t nhầm bay xa ất thì
v
′
phải h p vợ ới phương ngang góc
45
°
nên
'
x y
v v
′
=
.
Chiếu (1) lên 2 phương Ox và
0 0
: cos sinOy v v v
α α
+ =
2 2 2 2 2
0 0 0 0 0
cos 1 cos 2 cos 2 cos 0v v v v vv v v
α α α α
⇒ + = − ⇒ + + − =
2
0 0
1
cos 2
2
v v
v v
α
⇒ = − + −
(2)
TAILIEUHUST.COM
78 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Thay số ta được
cos 0,478 (61, 45)
α α
°
= ⇒ =
.
b) Ta có
2 2 2
0 0
2 cosv v v vv
α
′
= + +
Thay (2) vào bi u thể ức trên, ta tìm được:
2 2 2 2
0 0
2v v v v v
′
= + −
c Thay số đượ
6,2 m / sv
′
=
Câu 8:
1. Trình bày đ nh lý vị ề mômen độ ủ ộ ủ ộng lư ng cợ a m t ch m và cất điể a m t hệ chất
đi ậ ảể ịm đ i v i g a đ . Đố ớ ốc tọ ộ nh lu t b o toàn mômen động lư ng c a chợ ủ ất đi m và ể
hệ ể chất đi m.
2. Bài toán:
Từ ỉ một đ nh tháp có độ cao h ngư ốời ta ném m t h n đá có khộ ò i lượng m lên phía trên với
vận tốc
0
v
theo phương hơp với phương ngang một góc
α
. Tìm mô men ngo c và mô ại lự
men đ ng lư ng c a hòn đá đ i v i gộ ợ ủ ố ớ ốc
O
ở thời điếm
t
(gốc
O
chọn t i vạ ị trí chân của
tháp).
Lời giải:
1. Lý thuyết:
+ Đ nh lý v ng lư ng c a m t ch m đ i v i g : Đị ề momen độ ợ ủ ộ ất điể ố ớ ốc tọ ộa đ ạo hàm theo thời
gian củ ộa momen đ ng lượng đ i vố ới
O
của m t chộ ất điểm chuyển đ ng b ng tộ ằ ổng
momen đối với
O
của các l c tác đ ng lên ch u thự ụ ất điểm. Biể ức:
/ ( )
dL
o F
dt
=
M
.
+ Đ nh lý v ng lư ng c a m t hị ề momen độ ợ ủ ộ ệ ể chất đi m đ i v i g : Đố ớ ố ọ ộc t a đ ạo hàm theo
thời gian c a m ng lư ng c a m t h ng tủ omen độ ợ ủ ộ ệ bằ ổng momen các ngo ụại lực tác d ng
lên h u thệ ể. Bi ức:
/ ( )
i
dL
o F
dt
= =
∑
M M
+ Định luậ ảt b o toàn:
- Đố ể ờ ể ểi với chất đi m: Trong trư ng h p chợ ất đi m chuy n động luôn luôn ch ụ ủịu tác d ng c a
một lực xuyên tâm
F
luôn đi qua tâm
O
c ố định. Thì momen độ ủng lượng c a chất điểm là
một đại lượng bảo toàn. Biểu thức:
/ ( ) 0 const o F L= ⇔ =

M
- Đố ệi v i hớ chất điể ệm: H chấ ặt đi ậểm cô l p ho c chịu tác d ng cụ ủa các ngoại lực sao cho
tổng momen các ngo ố ốạ ấi lực y đ i v i đi m gớ ể c
O
bằng 0, thì t ng momen đ ng lưổ ộ ợng
của hệ là một đ ảại lượng b o toàn.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 79
2. Bài toán:
- c Ngoại lực tác dụng vào hòn đá chỉ có trọng lự
Phương trình v ủận tốc c a hòn đá:
0
0
cos
sin
x
y
v
v
tv
v
g
α
α
=
= −
Phương trình chuyển đ ng cộ ủa hòn đá:
0
2
0
cos
1
sin
2
x v
y h v t gt
α
α
=
= + −
Momen của ngoại lực:
( / )
| | .| | .sin( , ) r.mg. sin(OMA) . .
M
P O
x
M r P r p r p r mg
r
= ∧ = = =
0
( / )
cos
P O
M mgv t
α
⇔ =
Momen động lượng:
0
( / )
.cos .
P O
dL
M L mgv t dt C
dt
α
= ⇒ = +
∫
2
0
1
cos
2
mgv t C
α
= ⋅ +
Tại
0 0
0; . n cos. sit L mv h mv h
β α
= = =
2
0 0
1
cos cos
2
L mgv t mv h
α α
⇒ = +
Câu 9:
1. Tính công củ ộa l c h p d n khi mự ấ ẫ t vật có khối lượng
m
chuyển động trong trư ng ờ
hấp d n gây b t có khẫ ởi một vậ ối lượng
M
t ừ vị trí
1
r
đế ịn v trí
2
r
(Xem các vật như
chất điể ẽ ểm, có v hình). Từ đó suy ra bi u thức tính thế ể năng c t điủa chấ m trong
trường h p dấ ẫn.
2. Bài toán:
Tính th p d a m t m cách Trái đ t (có khế năng hấ ẫn củ ột vậ ấ ối lượng
M
) một khoảng
I
tính
từ tâm trái đất. Từ đó tính th ủế năng c a vật có khối lượng
m
khi vật
m
mcách bề ặt trái
đất một khoảng
h R<<
, l y m c thấ ố ế năng tại mặt đất bằng không.
Lời giải:
1. Lý thuyế :t
Công của lực
F
trong chuyển d i vi phân ờ
ds PQ
=
mà
. . .cosdA F PQ F PQ
α
= =
Nế ẽu ta v
QH OP⊥
thì ta có
.cosPQ PH
α
= −
.
Nhưng vì
PQ
là một chuyển d i vi phân nên ta đờ ặt
OP r OH OQ r dr= → ≈ = +
mà
PH OH OP r dr r dr= − = + − =
Thay tất cả vào ta có
.dA F dr= −
.
TAILIEUHUST.COM
80 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Công của lực
F
trong chuy ủển dời c a
(m)
t ừ vị trí
1
r
đế ịn v trí
2
r
trong trường hấ ẫp d n
M
là:
2
1
2
2
2
2 1
1 1
. .
r
r
r
r
Mm
A Fdr G dr G M
r r r
= − = − = −
∫ ∫
.
Dự ứa vào công th c bên ta th y công c a l p dấ ủ ực hấ ẫn
F
không phụ thuộc đư ng đi mà chờ ỉ
phụ ố thuộc vào v m đị trí điể ầu và điểm cu i.
+ Ta có
( ) ( )
1 2
2 1 1 2
1 1
A W W
t t
Mm Mm
GMm r r G C G C
r r r r
= − = − = − ⋅ + − − ⋅ +
- Tổ ếng quát: Th năng c a ủ
(m)
t ại vị trí cách
O
một khoảng
r
là:
W ( )
t
Mm
r G C
r
= − ⋅ +
với
C
là h ng sằ ố tùy ch n. Đọ ặc biệt
W ( )
t
C∞ =
.
2. Bài toán:
+ Th a m cách Trái đế năng củ ột vật m ất
(M)
một khoảng
r
tính từ tâm trái đất:
W( )
GMm
r C
r
= − +
+ Lấy m c th t, bi u th c tính th a ch ng hố ế năng là mặt đấ ể ứ ế năng củ ất đi m trong trưể ờ ấp
dẫn của trái đất là
( )
W
R
GMm r R
r
−
=
+ Khi
( )r R h h R= +
, ta có:
r R h− =
và
2
0
2
R W
GMm
r R h mg h
R
≈ ⇒ = =
với
2
0
2
9,8 m / s
GM
g
R
= ≈
là gia tốc trọng trư ặờng trên m t đất.
Câu 10:
1. Xét chuy ộ ủ ủển đ ng c a viên đ ng h p d n cạn trong trườ ấ ẫ a trái đất. Tính v n t c vũ trậ ố ụ
cấp I và cấp II
2. Bài toán: M t ộ ỏt vật nh rư ừợt không ma sát t đỉnh một bán cầu xuống dư t. Cho ới đấ
bán kính
2
3 m, g 10 m / sR = =
. Bỏ qua lực cản của không khí.
a. T cao nào so vừ độ ới mặt đất vậ ắt đ ầt b ầu rời kh i bán cỏ u.
b. Tìm t c đ t khi b i kh i bán c u và tố ộ ủ c a vậ ắt đầu rờ ỏ ầ ại mặ đất t.
Lời giải:
1. Lý thuyết:
Chuyển động trong trường h p d n cấ ẫ ủa trái đất
- c c Sự phụ thuộ ủa G theo độ cao:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 81
Ta có:
22 2 2
2
. . . .
( )
hd
Mm M M M
F P G mg g G G G
r r R h
R h
R
R
= ⇒ = ⇒ = = =
+
+
2 2
0 0 0
2
1
R h h h
g g g g g r
R R R
− −
+
⇒ = = + ⇒ = −
- : Các vận t c vũ trố ụ
Từ ể 1 đi m A g n m t đ i ra b n 1 v t m vầ ặ ất, ngườ ắ ậ ới
0
v
có th y ra các trư ng h p sau:ể xả ờ ợ
+
0
v
t nhỏ thì viện đ i rơi xu ng đạ ố ấ
+ Nếu
0
v
đủ ệ ể lớn thì vi n đ n có thạ không rơi xuống m n đặt đất và chuyể ộng tròn xung
quanh trái đ đạất ho c theo quặ ỹ o elip.
+ Nếu
0
v
l t ớn hơn nữa thì v t có thậ ể chuyển động ra xa trái đấ
Chú ý:
+ Giá trị ể ệ vận t c nhố ỏ nhất đ vi n đ n vạ ắt đầu chuyển động tròn xung quanh trái đ t đưấ ợc
gọi là v n t c vũ trậ ố ụ cấp 1
+ Giá tr t bị vận t c đố ể vậ ắt đầu chuyển đ c g n t c vũ trộng ra xa trái đất đượ ọi là vậ ố ụ cấp 2
Tính v n t c vũ trậ ố ụ cấp 1:
2
0 0
y
n y
v
a g v g R
R
= = ⇒ ≈
Tính v n t c vũ trậ ố ụ cấp 2:
matdat
W W
∞
=
2 2
2 2
mv mvMm Mm
G G
R
∞ ∞
⇒ + − = + −
∞
Điề ệ ể vậu ki n đ t ra xa vô cùng:
0v
∞
≥
2
0
2
2 .
0 2 2
2
II
II I
mv Mm G MR
G v g R v
R R
⇒ + − ≥ ⇒ ≥ = =
2. Bài toán:
a. Ch năng tạ ặọn m c thố ế i m t đ ạất. Xét t i v trí Bị
Áp d ng đ nh lý II Newton ta có:ụ ị
F P N= +
,
chiếu lên phương hướng tâm, chi u dương ề
hướng vào tâm ta có:
2
cos
B
ht ht
F P N ma m
R
v
α
= − = = ⋅
TAILIEUHUST.COM
82 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Vật rời kh i bán cỏ ầu khi N = 0
2 2
cos
B B
h
mg m g
R R R
v v
α
⇒ = ⋅ ⇔ ⋅ =
2
B
V gh⇔ =
Áp d ng đụ ịnh luật bảo toàn cơ năng tại A và B
2
1 3 2
2
2 2 3
B
mgR mgh mv mgR mgh h R m= + ↔ = ⇔ = =
Vậ ạy t i độ cao 2m so với mặt đất vậ t đ ầt bắ ầu rời bán c u.
b. Vận t c khi r i bán cố ờ ầu:
10.2 4, 47 m / s
B
v gh= = =
- Tốc độ khi chạm đ t: Áp d ng đấ ụ ịnh luậ ảt b o toàn cơ năng ta có
2
1
2 2 10.3 7, 75 m / s
2
A d d d
W W MgR mv V gR= ⇔ = ⇔ = = ⋅ =
Câu 11:
1. Tìm bi u th c đ a ch m. Tr h bày đ nh lý vể ứ ộng năng củ ất điể ìn ị ề động năng của chất
điểm.
2. Bài toán:
Một vệ tinh có khối lượng
150 kgm =
chuyển động trên qu đạỹ o tròn có bán kính
7300 kmR =
i đối vớ tâm Trái Đ t. Tính đấ ộng năng, cơ năng và t tinh trên quốc độ của vệ ỹ
đạo. Cho biết
11
6,67.10G
−
=
2 2
Nm / kg
. Kh ng Trái Đối lượ ất
24
5,98.10 kgM =
. Bỏ qua lực
cản của không khí.
Lời giải:
1. Lý thuyết:
- Định nghĩa: Đ ộ ủộng năng là ph ng v n đần cơ năng tương ứ ới chuyể ng c a các v t. Là đậ ại
lượng thể ệ ậ hi n m i phố ụ thuộc vào v n tốc chuy ộ ủển đ ng c a vật thể do công của ngoại lực
tác dụng.
- Biểu thức: Có
.dA F ds=
⇒
(2)
(1)
A Fds
=
∫
Mà
dv
F ma m
dt
= =
2
(2) (2) (2) 2
(1) (1) (1) 1
d
2
dv ds v
A m ds m dv mvdv m
dt dt
⇒ = = = =
∫ ∫ ∫ ∫
( )
( )
2
1
2 22 2
(2)
2 1
(1)
2 2 2 2
v
v
mv mvmv mv
A d d
−
⇔ = = = −
∫ ∫
2
/ 2
d
W mv⇒ =
- Định lý: đ n thiên đ a 1 chộ biế ộ ủng năng c ất đi m trong 1 quãng đưể ờng nào đó bằng
công của ngo t đi quãng đư ng đóại lực tác d ng lên chụ ấ ểm sinh ra từ ờ . Biểu thức:
2 1d d
A W W= −
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 83
2. Bài tập:
Thế ệ năng của v tinh trong trư ẫ a trái đấờng h p dấ n củ t là:
( )
t
R
Mm
W r G= − ⋅
(mốc thế năng tại vô cực)
Thế ệ năng của v tính:
0 0
2
..
t t
d
d td
t
Mm
W G m g R mg R
R
R
R
= − ⋅ + = −
5 9
0
6400
1 150.9,8.6400.10 1 1,16.10 J.
730
t
td
d
R
mg R
R
= ⋅ − = − =
- V ệ tinh chuy ộng tròn, l ủển đ ực h p d n cấ ẫ a trái đ c hưất đóng vai trò là lự ớng tâm
2
2
F F
hd ht
Mm V
G m
R R
= ⇒ ⋅ = ⋅
2
1 1
2 2 2
d d
Mm mv
W G W U
R
−
⇒ = ⋅ = ⇒ =
với U =
Mm
G
R
− ⋅
Thay s ta có: U =ố
Mm
G
R
− ⋅
=
9
8,2.10 J−
9
4,1.10
d
W J⇒ =
- Cơ năng của vệ tinh:
9
1
4,1.10
2
d
W W U U J= + = = −
- c Tốc độ ủa vệ tinh:
9
2
2.4,12.10
7412 m / s
m 150
d
W
v = = =
Câu 12:
1. Nêu các đặc điểm đ ng hộ ọc của chuy ộ nh ti n và chuyển đ ng tị ế ển động quay quanh
một trục cố định của vật rắn.
2. Bài toán: Một c t cộ ồt đ ng chấ ó chiều cao
5 mh =
b đang d g thựn ẳ ìng đứng th ị đổ
quay quanh chân của nó xu ng m t ph ng nố ặ ẳ ằm ngang. Xác định:
a. V n t c d t khi ch m đậ ố ài của đỉnh cộ ạ ất.
b. Vị ể trí của đi m
M
trên cột sao cho khi
M
chạ ậm đất thì v n tốc của nó đúng b n ằng vậ
tốc chạm đ t cùa mấ ột vật thả t ự do từ vị trí
M
. (cho
2
9.8 m / sg =
)
Lời giải:
1. Lý thuyết:
Đặ ể ủ ểc đi m đ ng hộ ọc c a chuy n đ ng tộ ị ếnnh ti
- Khi v n đ ng t n, m i điậ ắt r n chuyể ộ ị ếnh ti ọ ểm của vật rắn có quỹ đạo giống nhau.
- Tại mỗi th i đi m, m i điờ ể ọ ểm của vậ ắt r n đều có cùng v ốận t c và gia tốc
- Gọi
a
là gia tốc chung cho các điểm của vậ ắt r n
1 2
, , ,
n
m m m…
chịu sự tác d a ụng củ
1 2
, , ,
n
F F F…
song song và cùng chiều. Khi đó ta có:
1 1 22
; ;....;
n n
m a F m a F m a F= = =
TAILIEUHUST.COM
84 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
⇒
Khi nghiên u chuy nh ti ủ n nghiên ccứ ể ịn đ ng tộ ến c a 1 vậ ắt r n, ta chỉ cầ ứu chất điểm
bất kì là đ c vàượ người ta thường ch n khọ ối tâm.
Chuyển động quay quanh một trụ ốc c định của vật rắn
- Do khoảng cách gi ất điữa các ch ểm của vật rắn không thay đ i nên mổ ọi chất điểm đều
chuy ộển đ ng tròn và có tâm quay trên cùng 1 trở ục quay.
- Trong cùng 1 khoảng thời gian, m i đi m trên v n cùng quay đư c 1 góc.ọ ể ật rắ ợ
- Tạ ể ểi cùng th i điờ m, mọi chất đi m có cùng
,
ϖ β
ivớ
2
2
;
d d d
dt dt dt
θ ω θ
ω β
= = =
- Tạ ểi th i điờ m t, vectơ vận tốc dài
v
và
t
a
củ ụa ch m cách trất điể c quay 1 khoảng
r
, được
xác định bởi công thức:
;v r
a r
ω
β
= ∧
= ∧
2. Bài toán:
- M ốc thế năng tại mặt đất, thế năng củ ộ ộa c t tính t i kh i tâm c a cạ ố ủ t:
mgh
1
2
t
W =
Khi rơi xu ng, c t có đố ộ ộng năng quay
2 2 2
1
2 6
1
d
W Iw mh w= =
Áp d ng đ nh lý bụ ị ảo toàn cơ năng
2 2
1 1 3
W
2 6
t d
w
W
g
mgh mh
ω ω
= ⇔ = ⇔ =
Vận t c đố ỉnh cột khi ch m đạ ất:
3 12,12 m / sv wh gh= = =
Vật thả rơi tự do tại M thì v n t m đậ ốc chạ ất là:
2
M M
v gx
′
=
Khi c t ch m độ ạ ất:
3
M M M
g
v x x
h
ω
′
= =
Vì
3 2
2 3,33 m
3
M M M M M
g
v v gx x x h
h
′
= ⇔ = ⇔ = ≈
Câu 13:
1. Thiết lập phương trình cơ bản của vật rắn quay xung quanh mộ ụ ốt tr c c định. Nêu ý
nghĩa c ng trong ph ng trủa c c đá ại lượ ươ ình đó. ủa momen quán Nêu đ c điặ ểm c
tính.
2. Bài toán: Một vật
m 1 kg=
u đượcc n i vố ới một đầ dây cu n vào mố ột trụ đặc và
đư ảợc th rơi xuống như hình v ụ ó bán kính ẽ. Tr c
10 cmR =
và có khối lượng
M 6 kg=
. Bỏ lqua ực ma sát và khôi lư a dâợng củ y.
a. Tìm đ n gia t c dài cộ lớ ố ủa vật
m
và l a dây. Cho ực căng củ
2
g 10 m / s=
.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 85
b. T m công th c hi c căng c y khi tr quay đì ự ện bởi lự ủa dâ ụ ượcc một góc
4
π
t (kể ừ lúc bắt
đầu thả vật)
Lời giải:
1. Lý thuyết:
Phương trình cơ bả ủn c a v quay xung quanh mậ ắt r n ột trục cố đị nh:
M I
β
=
Gọi
i
M
clà một chất điểm bất kỳ ủ ụa vật rắn, cách tr c một khoảng
i
r
ứng v i bán kớ ính vecto
i i
OM r=
có khối lượng
i
m
và ch a ịu tác d ng cụ ủ
ngoại lực tiế ếp tuy n
ti
F
. Chất điểm
i
M
s ẽ chuyển đ ng vộ ới vecto gia
tốc tiế ếp tuy n
ti
a
cho bởi:
.
i ti ti
m a F=
Nhân có hướ ế vớng hai v i vecto bán kính
i
r
ta được:
.
i ti i ti i
m a r F r∧ = ∧
mà
( )
i ti i i i ti i
m a r do F r∧ = = ∧

M M
Lại có
( )
( )
(
2
, . . . 0 . 0.
ti i i i i i i i i
a r r r r r r r r
β β β β β
∧ = − = − ⊥ → =
2
. .
i
i i
m r
β
⇒ =
M
. Tính v i hớ ệ vậ t rắn ta có
2
. .
i i i
i i
m r M
β
=
∑ ∑
2
(1)
i i
i
i
i
I m r
I
β
= ⋅
⇒ ⋅ =
=
∑
∑

M
M M
. Phương trình (1) đư c g i là phư ng trình cơ b n cợ ọ ờ ả ủa chuy n ệ
động quay của vật rắn xung quanh một trục.
Với: I là momen quán trính c ụủa v ắật r n đ i vố ới tr c
∆
.
M
là t i lổng h p momen cợ ủa các ngoạ ực tác d ng lên vụ ật rắn.
β
là gia tốc góc.
Đặc điểm của momen quán tính
- Là đ ng v t lý đại lượ ậ ặc trưng cho tính bảo toàn trạng thái của hệ trong chuyển độ ng
quay
- Momen quán tính phụ n trong h thu ủộc vào khối lượng c a các thành phầ ệ và kho ng ả
cách giữa các thành phần trong h ụệ đế n tr c quay.
2. Bài toán:
a. Phương trình đ nh luị ật II Newton cho vật: P – T = ma
Phương trình momen lực:
.
T
M T R I I
R
a
β
= = =
TAILIEUHUST.COM
86 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Từ ệ đó ta có h :
2
1
2
m
a
g T ma
TR MR
R
− =
= ⋅
2
9,8 7,35
3 2, 45 m / s
T a T N
T a a
+ = =
⇔ ⇒
= =
b. Khi tr c 1 gócụ quay đượ
4
π
0,025 (rad)S R
ϕ π
⇒ = ⋅ =
Công c c căng dâyủa lự
. 0,58 JA T S= =
Câu 14:
1. Thiế ểt lập bi u th c tính công cứ ủa ngoại lực trong chuyển độ ủng quay c a vật rắn
xung quanh mộ ụ ốt tr c c đị ị ề độ ắnh. Suy ra đ nh lý v ng năng của vật r n trong chuyển
động quay.
2. Bài toán: Một vô lăng d ng đĩa trơn đ ng ạ ồng tính có khối lượ
m 40 kg=
, bán kính
R 0, 5 m=
đang quay xung quanh tr c đi qua tâm và vuông góc v t đĩa vụ ới mặ ới tốc
độ góc n
240n =
lvòng/ phút. Tác dụ ộng lên vô lăng m t lực hãm. Tìm độ ớn của
mômen hãm trung bình trong các trường hợp:
a. Vô lăng d ng lừ ại trong
40 s
.
b. Vô lăng d ng l i sau khi quay đư c 5 vòng k khi tác d ng lừ ạ ợ ể từ ụ ực hãm.
Lời giải:
1. Lý thuyết:
Thiết lậ ứp biểu th c:
- Trong trư ng hờ ợp một v ắật r n quay xung quanh một trục
∆
các
lực tác d ng đụ ều là lực tiế ếp tuy n. Công vi phân của một lực tiếp
tuyến
t
F
cho bởi:
.
t
dA F ds=
. Xong lại có
.ds r d
α
=
với
d
α
là góc
quay ứng v n dới chuyể ời
ds
, v y ậ
..
t
dA r F d
α
=
.
Theo định nghĩa ta có
.
t
r F = M
là momen c a lủ ực
t
F
đối với trục
quay
∆
, do đó
.dA d
α
= M
Tích phân hai v t kho i gian h n, trong đó vế trong mộ ảng thờ ữu hạ ận tốc góc
ω
biến thiên
từ
1
ω
đến
2
ω
ta được công toàn phần c c tác d ng lên v n quay tủa ngoại lự ụ ậ ắt r ừ vị trí 1
(ứng với
1
ω
) đ n vế ị trị 2 ( ứng với
)
2
ω
là:
2 2
2 1
. .
2 2
I I
A
ω ω
= −
.
+ Suy ra đ n quay có biộ ủng năng c a vậ ắt r ểu thức là:
2
.
W
2
d
I
ω
=
Định lý đ trong chuyộng năng của vậ ắt r n ển đ ng quay:ộ
Độ ắng năng của vật r n quay b ng n a tích cằ ử ủa momen quán tính của vật rắn và bình
phương vận t c góc cố ủa vật rắn xung quanh mộ ốt trục c định.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 87
2. Bài tập:
a. Áp d ng đ nh lý v ng lưụ ị ề momen độ ợng:
L M t∆ = ∆
2
2 1
0 . . ( / )
2 60
mR n
M N m
t
π
π
⇒ = − = −
∆
b. Áp d ng đ nh lý đ n quay ta có:ụ ị ộng năng của 1 vật rắ
2
0 .
2
d
I
A W M
ϖ
θ
= ∆ = − = ∆
2
2 2
1
1 1 2 1
. . . . 16 ( )
2 2 2 2 60 2 .5
I mR n
M Nm
n
ϖ π
π
π π
⇒ = = − = −
Câu 15:
1. Thiết lập phương trình dao độ ủ ụ n ng t n cắt dầ a con l c lò xo dư i tác dắ ớ ng c a lủ ực cả
có đ n t . T m công th c tính gi m lư ng l ng tộ lớ ỷ vớ lệ i tố ộc đ ì ứ ả ợ oga c a dao đủ ộ ắt
dần.
2. Bài toán: Một con l ng tắc 10 xo dao độ ắt dần v i biên đớ ộ ban đầu
0
12 cmA =
. Sau
2,4 phút biên đ a nó gi n 6cm.ộ củ ảm cò
a. T m hì ệ số tắt dần.
b. Sau bao lâu biên độ chỉ còn
2 cm
.
Lời giải:
1. Lý thuyết
Các lực tác d ng lên vụ ật:
c
kv
F kx
F rv
= −
= −
Áp d ng đ t II Newton ta cóụ ịnh luậ :
kv c
F F ma+ =
, chi u lên chiế ều dương:
kx rv ma− − =
hay
2
2
d x dx
m kx r
dt dt
= − −
.
2
2
0
d x r dx k
x
dt m dt m
⇔ + ⋅ + =
.
Đặt
2
0
k
m
ω
=
hay
2
r
m
β
=
2
2
0
x
2 0.
d x d
x
dt dt
β ω
⇒ + + =
Nghiệm của phương trình trên có dạng:
đó là phương trình dao đ ng ộ
tắt dần với
2 2
0
ω ω β
= −
.
Giảm lượng loga: loga tự nhiên củ ố ộ ộ p cách nhau 1 chu ka s 2 biên đ dao đ ng liên tiế ỳ
T
.
Đặt
10
t
A A e
β
−
= ⋅
⇒
Giảm lượng loga:
0
( )
( )
ln ln ln
( )
.
.
t
T
t T
A eA t
e T
A t T A e
β
β
β
δ δ β
−
− +
= = = ⇒ =
+
.
TAILIEUHUST.COM
88 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
2. Bài tập
a. Biên đ ng t n cộ ộ dao đ ắt dầ ó
10
t
A A e
β
−
= ⋅
Sau t = 144s, biên độ giảm từ 12cm xu ng còn 6cm, thay vào công thố ức trên ta có:
144 3 1
6 12. 4,8.10 se
β
β
− ⋅ − −
= =⇒
b. Biên độ giảm còn 2cm. Thay vào công th c trênứ ta có:
3
2
4,8 10
2
2 12. 373( s)
t
e t
−
− ⋅
= ⇒ =
Câu 16:
1. Trình bày:
a. Khái niệ ệ ệm h nhi t đ ng và khí lý ộ tư ng.ở
b. Thiết lập phương tr ạình tr ng thái khí lý tư ng cho 1 mol khí và m t kh i khí có khở ộ ố ối
lượng b t kấ ỳ (có hình v minh họẽ a).
2. Bài toán:
Trong một ngày tr ạời l nh ở nhiệt độ
15 C
°
, th tích và áp su a khí bên trong m p xe ể ất củ ột lố
ô tô đo đư ầợc l n lượt là
3
15dm
và 1,70 at. Sau đó, khi xe ch ng cao tạy tr n đưệ ờ ốc, nhiệt độ
khí bên trong lốp đo được là
45 C
°
và thể tích cũng tăng lên thành
3
15,9dm
. Coi khí bên
trong l ấốp xe là khí lý tư ng, tính áp suở t lốp xe khi đó.
Lời giải:
1. Lý thuyết:
a. Hệ ệ nhi t đ ấ ạộng là m t hộ ệ c u t o bởi 1 số lớn các h t (phân t , nguyên t t này ạ ử ừ, …) các hạ
luôn chuyển động h n đỗ ộn không ngừng và không ng ng trao đ i nhau khi tương tác.ừ ổi vớ
- Khí lý tưởng là khí tuân theo hoàn toàn chính xác 2 đ nh lu c nghiị ật thự ệm là Boyle-
Mariotte và Gay Lusac, …
+ H khí b a các phân tệ ỏ qua tư ng tác giở ữ ử
+ H khí b a các phân tệ ỏ qua kích thước củ ử (các phân t c coi là chử đượ ất điểm)
b. Thiết lập phương trình tr ủạng thái c a khí lý tưởng
- Xét quá trình biế ịn đôi m t kh i khí xác độ ố nh từ trạng thái
( )
1 1 1
p , V , T
sang tr ng thái ạ
( )
2 2 2
p , V , T
Giả s ử có 1 mol khí
- Xét quá trình đẳng nhiệt
1 1
M M
′
có
1
1 1 1 2 1 1
2
V V (1)
V
p p p p
V
′ ′
= ⇔ =
- Xét quá trình đẳng tích
2 1
M M
′
có
1 2 2
1 1
1 2 2
T (2)
p p p
p
T T T
′
′
= ⇔ =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 89
Từ (1) và (2) ta có:
1 2 1 1 2 2
1 1
2 2 1 2
T
V p p V p V
p
V T T T
= ⇔ =
pV
T
⇒ =
const là phương trình trạng thái khí lý tưởng
- Như vậy đ i v i 1 mol khí lý tưố ớ ởng
R
pV
T
=
(
R
là h ng sằ ố không đổi)
pV RT⇔ =
Đố ỳi v t kh i khí b t kới mộ ố ấ có kh ng m:ối lượ
v
m
µ
=
(V là thể tích 1 mol khí)
Khi đó phương trình trạng thái khí trở thành:
pV
m
RT
µ
=
2. Bài tập:
Áp dụng phương trình trạng tháu của khí lý tưởng ta có:
1 1 2 2 1 1 2
2
1 2 1 2
p V PV PV T
p
T T T V
= ⇔ = ⋅
2
1, 7.15 318
1,77 at
288 15,9
p⇒ = ⋅ =
Câu 17:
1. Trình bày
a ả. Nội dung cơ b n của thuyết độ ọng h c phân từ kh ởí lý tư ng.
b. Viế ì ết phương tr nh cơ b n cả ủa thuy t đ âộng học ph n tử và phương trình tr ng thái c a ạ ủ
kh ởí lý tư ng.
2. Bài toán:
Một bình dung tích
5V l=
áở p suất
8p =
atm chứa 2 mol khí Oxy (
2
O
) ế. Bi t kh i lưố ợng
phân t ủừ c a
2
O
là
32 g / mol
µ
=
, tính:
a. Động năng chuy ộ nh ti n trung bình cến đ ng tị ế ủ ộa m t phân tử khí
2
O
.
b. Trung b a bình ph n tình củ ương vậ ốc một phân tử khí
2
O
.
Cho biết
5 23 1
A
1 atm 1, 013.10 P, N 6,023.10 mol
−
= =
Lời giải:
1. Lý thuyết:
a. N i dung cơ b n c ng h c phân t khí lý tưộ ả ủ ếa thuy t độ ọ ử ởng
- rCác chất khí có cấu tạo gián đoạn và gồm một số ất lớn phân tử
TAILIEUHUST.COM
90 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
- Các phân tử chuy ộển đ ng h n loỗ ạn không ng ng. Khi chuy ộừ ển đ ng chúng va ch m vào ạ
nhau và va chạm vào thành bình
- Cường độ chuy ủể ộn đ ng c a phân tử biể ệu hi n e nhiỏ ệt đ t độ của kh i khí. Nhiố ệ ộ càng
cao thì các phân t n đử chuyể ộng càng mạnh
- r Kích thước phân tử ất nhỏ so v i khoớ ảng cách giữa chúng
- Các phân tử không tương tác với nhau trừ lúc va chạm
b. Phương trình:
- : Phương trình cơ b n c ng h c phân tả ủ ộa thuyết đ ọ ử
0
2
3
d
P n W=
- Phương trình trạng thái c a khí lý tưủ ởng:
m
pV nRT RT
µ
= =
2. Bài tập:
a. ng năng Độ tị ếnh ti n trung bình của 1 phân tử Oxi là:
5 2
21
23
3 8,1,03.10 .5.10
5,05.10
2 2 2 2.6,023.10
d
A A
i R i PV
W T
N nN
−
= ⋅ ⋅ = ⋅ = ⋅ =
b. Ta có:
2 2
2. .
2
.1 1
. .
d A
d
A
W n N
W mv v
n N n
µ
= ⋅ ⇔ =
21 23
2 5
3
2
2.5,05 10 6,023.10
1,9.10 m / s
32.
.
10
.
d A
W N
v
µ
−
−
⋅
= = ⇔ =
Câu 18:
1. Trình bày
a. Từ phương trình thuyết đ ấ ẫộ ọng h c phân tử ch t khí hãy d n ra bi u th c đề ứ ộng năng
chuyển động nhiệ ít và suy ra công thức t nh vận tốc căn quân phương của các phân tử khí.
b. u c Nê khái niệm bậ tư do, n i dung đ t phân bộ ịnh luậ ố đều theo các bậc tự do, từ đó suy
ra biểu thức nội năng cho mộ ốt kh i khí có kh ng b t kố ượi l ấ ỳ
2. n: Bài toá Mộ ốt kh i khí
( )
2
Oxy O
được đựng trong m t bình chộ ứa hình lập phương
có kích thước mỗi cạ ằnh b ng
0,10 m
, ở áp suất là
5
1,013.10 Pa
bvà nhiệt độ ằng
27 C
°
, tính:
a ă. Động n ng chuyển đ ng tộ ịnh tiến trung bình của m t phân tộ ử khí
2
O
;
b. Số các phân tử khí
2
O
có trong bình khí nói trên.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 91
(Cho biết,
23
1,38.10 / , 32 g / molk J K
µ
−
= =
).
Lời giải:
1. Lý thuyết:
a. Từ phương trình thuy ộ ọết đ ng h c phân t t khí ử chấ
0
2
3
d
P n W=
0
3
(*)
2
d
P
W
n
⇒ =
Xét m t mol khí lý tưộ ởng: PV=RT suy ra P = RT/V. Thay vào (*) ta có:
0
3
2
d
RT
W
Vn
=
Mà
0
.
A
V n N=
3
2
d
A
RT
W
N
⇒ =
.
- Định nghĩa v ốc căn quân phương: ận t
2
c
v v=
Đặt
23
1,38.10 ( / )
A
R
k J k
N
= =
: h ng sằ ố Boltsman
2
3 1 3
2 2
d c c
kT
W kT mv v
m
⇒ = = ⇒ =
3 3 3
c
A
kT RT kT
v
m mN
µ
⇒ = = =
b. B p cậc t c lự t do c a 1 hủ ệ là số ọa độ độ ậ ần thiết đ ảể mô t trạng thái của hệ trong không
gian. Đố ệi v i hớ khí có phân tử đơn nguyên t i vử: i = 3. Đố ớ ỡi lư ng nguyên tử: i = 5. Đối với
đa nguyên tử: i = 6
- Định lu ốật phân b đều động năng theo các bậc tự do: Đ a m t phân tộng năng củ ộ ử khí
đư ậ doợc phân b u trên các bố đề c tự
- : Biể ỳu th c n i năng c a kh i khí b t kứ ộ ủ ố ấ
Có động năng trung bình của 1 phân tử là:
2
d
KT
W i=
Nộ ỳi năng củ ộ ốa m t kh i khí có khố i lượng b t kấ là:
.
. . . . .
2 2 2
d d A
A
i KT i RT m i
U W N W N N U RT
N
µ
= = = = ⇒ =
2. Bài tập:
a. Động năng:
21
23
3 8,31
.300 6, 21.10 ( )
2 2 6,023.10
3
A
d
N
W
R
T J
′ −
= ⋅ ⋅ = ⋅ =
b. Số phân tử trong bình là:
22
0
. 2, 45.10
P
N n V V
RT
= = =
Câu 19:
1. Thiết lập
TAILIEUHUST.COM
92 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
a. Công thức khí áp cho một cột khí lý tưởng ở độ cao h so vớ mặ ất đ t (có hình v minh ẽ
họa).
b. Biểu thức của định luật phân bố phân tử theo thế năng
2. Bài toán: Ở ề ệ ệ đi u ki n áp suất bằng at và nh1 i t độ
20 C
°
, m i trong tột ngườ rạng
thái t ằng 0,5 lĩ hổ ểnh, hít vào p i một lư ng khí có thợ tích b . Biết rằng trong không
khí s Oxy chiố phân tử ế ệm tỷ l 21% (coi không khí là khí lý tưởng), tính số phân t ử
Oxy trong mỗi lần hít vào, khi người đó ở:
a. Trên mặt đất
b. Trên ngọn núi có độ cao h=2000m và nhiệt độ vẫn là
20 C
°
. Biết không khí có
29 g / mol
µ
=
và
8.31 J / mol.KR =
Lời giải
1. Lý thuyết:
a. Công th ng ức khí áp cho một cột khí lý tưở ở độ cao
h
t so với mặ ất đ
- Chọn phương
Oz
hướng lên các điểm như hình vẽ, ta có
dp gdz
ρ
= −
, trong đó
p
RT
µ
ρ
=
dp gdz dz
p dp g
RT p RT
µ µ
⇒ = − ⇔ = −
Tích phân hai vế từ
O
đến
h
( )
( ) 0
p h h
p O
dp g gh
dz
p RT RT
µ µ
= − = −
∫ ∫
p(h) p(o) p(o)=
mgh
gh
kTRT
e e
µ
−−
⇔ =
b. Đ t phân bịnh luậ ố theo thế năng:
(o)
o
n
và
( )
o
n h
là m i các áp suật độ các phân tử khí tạ ất
p(o)
và
p(h)
Ta có
( ) ( )
p(h) p(o)
o o
n h n o
=
t ừ
đó suy ra
( ) ( )
gh
RT
o o
n h n o e
µ
−
=
Mà
mN m
R R k
µ
= =
nên
( ) ( )
mgh
kT
o o
n h n o e
−
=
, Đặt
t
W mgh=
⇒
Mật độ phân tử chất khí đ c thặt trong t trưmộ ờng lự ế phụ thuộc vào th năng trong ế
trư ựờng l c thế đó.
2. Bài tập:
a. T a khí lý tưừ phương trình tr ng thái cạ ủ ởng ta có:
4 3
9,81.10 .0,5.10
0,02 mol
8,31.293
PV
n
RT
−
= = =
Số phân tử Oxy hít vào là:
24
0, 21. . 2,53 10 ( )
A
N n N pt= = ⋅
b. Áp suất không khí t i đạ ộ cao h = 2000m
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 93
3
29 10 9,8.2000
4 4
8,31.293
.
9,8.10 7,8 10 Pa( ) .
mgh
kT
o
P eP h e
−
−
⋅
−
= ≈ ⋅= ⋅
Số phân tử Oxy hít vào là:
4
2 21
4
0 0
1
)
7,8.10
2,53.10 2,01 .10
9,81.1
. (
0
mgh
kT
h
n n e pt
−
= = ⋅ =
Câu 20:
1. Trình bày
a. Khái niệm công và nhiệt trong m t quá trình cân bằộ ng.
b. Nội dung, biể ,u thức ý nghĩa và ảhệ qu củ ọa nguyên lý 1 nhi ng l c hệt độ ự c.
2. Bài toán: Một khối khí đự ứng trong một bình ch a có áp suất không đổi là 2,3.10
Pa
đư th ằợc nén từ ể tích b ng
3
1,7 m
xuống còn
3
1,2 m
. Khi đó, n i năng kh i khí giộ ố ảm
đi m t lư ng bộ ợ ằng
5
1,4 10 J⋅
. Tính:
a. Công khối khí nhận đư c khi bợ ị nén.
b. Nhiệt lư ng khợ ối khí sinh ra trong quá trình nén.
Lời giải:
1. Lý thuyết:
a. Công là đ trao đ ng thông qua chuy ng ại lượng đ c trưng cho m c đặ ứ ộ ổi năng lượ ển độ
có hư ủớng c a hệ
Nhi ứệt là đ ng đại lượ ặc trưng cho m c độ trao đ ng thông qua mổi năng lượ ức độ chuyển
độ hỗ ệng n lo n c a các phân tạ ủ ử trong h .
b.
Nội dung: Trong m t quá trình bi n đ i, độ ế ổ ộ biến thiên năng lượng c a hủ ệ trong quá
trình biến đổi bằng tổng công và nhiệ ệt h nhận được trong quá trình đó.
Biểu thức:
U A Q∆ = +
W A Q∆ = +
. - Hệ đứng yên
W U=
U A Q⇒ ∆ = +
Đố ếi v i quá trình biớ n đổi vô cùng nhỏ
dU dA dQ= +
.
Ý nghĩa:
- Nếu
2 1
0, 0 0A Q U U U> > ⇒ ∆ = − >
→
Nộ ệi năng tăng, h nhận công và nhiệt.
- Nếu
0, 0 0A Q U< < → ∆ < →
Nội năng giảm.
→
Hệ sinh công
A
′
, t a ra nhiỏ ệt
Q
′
.
Hệ quả:
- Đố ệi v i hớ cô lập:
TAILIEUHUST.COM
94 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
+ Hệ không trao đổi ra môi trường bên ngoài: A = 0 = Q thì
U∆
=0 nên nội năng
được bảo toàn
+ Hệ cô l p g m 2 hậ ồ ệ con: Q = 0
1 2 1 2
0Q Q Q Q⇒ + = ⇒ = −
⇒
Kế ệ hệ ệ ệt luận: Trong m t hộ cô l p g m 2ậ ồ con nhi t lư ng do v t này t a ra bợ ậ ỏ ằng nhi t
lượ ợng do vật kia thu vào và ngư c lại
- Đố ệi v i hớ biến đổi theo chu kỳ:
U∆
= 0
0A Q A Q⇒ + = ⇒ = −
⇒
c b b Kết luận: Trong m t chu trình công mà hộ ệ nhận đượ ằng nhiệ ệt lư ng cho 1 hợ ỏ ra
và ngư ạợc l i
⇒
Không tồn t i đ ng cơ vĩnh cạ ộ ữu lo i Iạ
2. Bài toán:
a. Công không khí nhận đư c (quá trình đợ ẳng áp):
( )
5
2
5
1
2,3.10 (1,2 1, 7) 1,15.10 ( J)A P V V= − − = − ⋅ − =
b. Áp d ng nguyên lý I nhi ng l c h c ta có n t kh i khí sinh ra làụ ệt độ ự ọ hiệ ố :
5 5 5
1,4.10 1,15.10 2,25.10Q Q U A
′
= − = −∆ + = + =
Câu 21:
1. Xét m t kh i k ng bi n đ i theo quộ ố hí ưở lý t ế ổ á trình cân b ng đằ ẳng áp:
a. Viết phương trình và vẽ đồ thị của quá trình trong hệ OpV.
b. Thiết lập biểu thức tính công và nhiệt trong quá trì ế đónh bi n đổi .
2. Bài toán: Hơ nóng 10g khí Oxy ở nhiệt độ 10 đ i thộ C tớ ể tích 4 lít trong khi vẫn
gi ấữa nguyên áp su t ở 3at. Tính:
a. Công do khối khí th c hiự ện
b. Nhiệt lư ng mợ à khố íi kh nhận được.
Lời giải:
1. Lý thuyết:
a. Quá trình đẳng áp là quá trình ạng thái, trong đó áp biến đổi tr
suất của kh i khí không đố ổi
P const=
Phương trình
1 2
1 2
const hay
n
n
VV VV
T T T T
= = = =
- : Đồ thị OPV
b.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 95
- Công:
( )
2
1
1 2
A p V V
V
V
pdV= − = −
∫
. Quy ư c: A>0 là nh n công; A<0 là sinh côngớ ậ
- Nhiệt:
( )
2
1
2 1
Q T
T
p p p
T
m m m
Q C dT C T T C
δ
µ µ µ
= = = − = ∆
∫ ∫
Trong đó
p
2
C
2
i
R
+
=
là nhiệt dung mol đẳng áp
2. Bài toán:
a. Công do không khí sinh ra:
( )
2 1
A A P V V
′
= − = −
Thể tích khí trước khi hơ:
3
1 1 1 1
9
1 10 1
8,31.283 2, 5.10 (l)
32 3.9,81.10
m m
PV T V R T
P
µ µ
−
= ⋅ ⇔ = ⋅ ⋅ ⋅ = ⋅ =
4 3
3.9,81.10 (4 2,5) 10 441 JA
′ −
⇒ = − ⋅ =
b. Nhiệt độ khối khí sau khi hơ nóng là:
2
2 1
1
453
V
T T
V
= ⋅ =
Nhiệt lư ng kh i khí nh n đượ ố ậ ợc là:
2 10 7
. . . . .8,31.(453 283) 1545 J
2 32 2
m i
Q R T
µ
+
= ∆ = − =
Câu 22:
1. Xét m t kh i khi lý tư ng bi n độ ố ở ế ổi theo quá trình cân b n nhiằng đoạ ệt:
a. Định nghĩa và thi ậết l p phương trình liên h ủệ giữa áp suất và thể tích c a kh i khí trong ố
quá trình biến đ i đó.ổ
b. V cẽ dạng đồ thị ủ ụa quá trình trên tr c tọa độ OpV. Vì sao trên đồ thị. OpV đường đoạn
nhiệ ờt dốc hơn đư ng đẳng nhiệt?
2. Bài toán: Một kh i khí: đơn nguyên t , ban đ u có áp suố ử ầ ất bằng
5
1,5.10 Pa
và thể
tích bằng
3
0,08 m
, đư c n n thợ én đoạn nhiệt đế ể í t ch
3
0,04 m
. Tính
a. Áp suât kh i kố hí cuối quá trình nén.
b. Công kh c trong quá trình.ối khí nh n đưậ ợ
Lời giải:
1. Lý thuyết:
Quá trình đoạn nhiệt là quá trình trong đó h không trao đệ ổi nhiệt v i mô trướ ờng
Q const hay Q 0
δ
= =
a. Ta có:
TAILIEUHUST.COM
96 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
Ta có:
.R
2
v
m i m
U T C T
µ µ
= ⋅ =
và
dA p V
δ
= −
d
V
m m RT
C dT p V dV
V
µ µ
⇒ = − = −
Hay
0
V
V
dV dT R dV
C dT RT
V T C V
= − ⇔ + ⋅ =
ln ln const
V
R
T V
C
⇒ + =
Do
( )
1
1 ln ( 1) ln ln
P V
V V
C CR
T V T V
C C
γ
γ γ
−
−
= = − ⇒ + − = ⋅ =
const
1
1
const
. const
const
PV
T V
TP
γ
γ
γ
γ
−
−
=
⇒ = →
=
b. Giải thích: Đường đoạ t do:n nhiệt d ẳốc hơn đ ng nhiệ
+ Trong quá trình nén đoạn nhiệt (1-2):
A 0
δ
>
nên
dU 0>
, do đó
dT 0>
nghĩa là nhiệt độ khối khí tăng
lên, đường đoạ ện nhi t đi lên nhanh hơn đường đẳng nhiệt.
+ Trong quá trình giãn đoạn nhiệt (1-2):
A 0
δ
<
nên
dU 0<
, do đó
dT 0<
nghĩa là nhiệt độ khối khí giảm
và đư ng đoờ ạ ện nhi t đi xuống nhanh hơn đẳ ệng nhi t
Như vậy trên đồ thị
(p, V)
đường đoạ ện nhi t dốc hơn đư ng đờ ẳng nhiệt
2. Bài toán:
2 5
1, 67
3
i
i
γ
+
= = =
a. Áp su t kh i khí cấ ố ủa quá trình nén:
5
1
1 1 2 2 2 1
2
4,77.10 pa
V
p V p V p p
V
γ
γ γ
= ⇔ = ⋅ =
b. Công mà khối nhận được là:
( ) ( )
2 1 2 1 2 2 1 1
1
. . . . . .
2
2 2
m i m m i
A U R T T RT RT PV p V
µ µ µ
= ∆ = − = − = −
( )
5 5
3
. 4,77.10 0, 04 1, 5.10 0,08 10620( J)
2
. .A⇒ = − =
Câu 23:
1. Lý thuyết:
a. Phát biểu nguyên lý 2 nhi ộ ọ ủệt đ ng l c hự c dư i d ng c n cớ ạ ổ điể a Clausius và Thomson và
nêu ý nghĩa c a nguyên lýủ .
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 97
b. Thiết Iập biể ịu thức đ nh lư ủợng c a nguyên lý 2.
2. Bài toán: Trong m i chu tr ng cơ c a m t xe ô tô t n mỗ ì ộnh hoạt động, đ ủ ộ ải cầ ột
nhiệt lư ng bợ ằng
4
10 J
để sinh công. bằng
3
2.10 J
. Tính:
a. Hiệu suất của động cơ.
b. Nhiệt lượng nhả cho ngụồ nh trong m i chu trình.n lạ ỗ
Lời giải:
1. Lý thuyết:
a. Phát bi t không th ng truyể ệu của Clausius: Nhi ể độ tự ề vận từ t lạ ậnh sang v t nóng hơn
- Phát biểu của Thomson: Không th ạ ng tuể ế ch t o đư t máy hoợc mộ ạt độ ần hoàn biến đổi
liên tục nhi t thành công mà không nh nh mệ ờ làm lạ ột vật và xung quanh không chịu một
sự thay đ i đổ ồng thời nào. Những động cơ như v y là đ ng cơ vĩnh cậ ộ ửu loại II.
- Ý nghĩa:
+ Khắc ph c đư c nh n ch a nguyên lý Iụ ợ ữ hạng ế củ
+ Không thể t chế ạo đư c đ ng cơ vĩnh cợ ộ ửu loại hai
b. Thiết lập biể ịu th c đứ nh lượng:
Từ ể bi u thức tính hiệu suất chu trình Các-nô
2 2
1 1
T Q
T Q
′
⇒ =
kế ịt h p v i đợ ớ nh nghĩa hiệu suất ta được
1 2 1 2 2 2 1 2
1 1 1 1 1 2
0
Q Q T T T Q Q Q
Q T T Q T T
′ ′
− −
≤ ⇔ ≤ ⇔ + ≤
Giả thiế ệ ết h bi n đ i theo m m vô sổ ột chu trình gồ ố quá trình đẳng nhiệt và đoạn nhiệ ết k
tiếp nhau, tương i nhiứng vớ ệt độ và nhi a các nguệt lư ng cợ ủ ồn nhiệt bên ngoài là
1 2 i
T , T , , T ,… …
và
1 2 i
Q ,Q , Q ,… …
khi đó ta có
0
i
i
i
Q
T
≤
∑
Nế ệ ế ệu coi h ti p xúc v i vô sớ ố nguồn nhi t có nhiệt độ
T
vô cùng g n nhau và bi n thiên ầ ế
liên tục; mỗi quá trình nh n nhiậ ệt
Q
δ
t ừ nguồn nhi nh lư ủệ ểt, ta có bi u th c đứ ị ợng c a
nguyên lý II là
0
T
δ
≤
∫
Q
- Dấu “=" ứng với chu trình thu n nghậ ịch
- Dấu "<" ng vứ ới chu trình không thu n nghậ ịch
2. Bài toán:
TAILIEUHUST.COM
98 Group: Bachkhoa Universe – Góc học tậ ảp và th o luận
a. Hiệu suất động cơ:
3
4
1
2.10
20%
'
10
A
Q
η
= = =
b. Nhiệ ồt nhả cho ngu n lạnh là:
3 3
2 1
4
10 2.10 8.10 JQ Q A
′ ′ −
= − = − =
Câu 24:
1. Xét chu trình Carnot thuận nghịch
a. Vẽ đồ thị chu trình trên trụ ọ ộ ọi tên các quá trình trong chu trình, chc t a đ OpV và g ỉ rõ
quá trình nào hệ nhiệt động nh n nhiậ ệt từ nguồn nóng và quá trình nào h ảệ nh nhiệt cho
ngu nh.ồn lạ
b. Thi u th c tính và nêu k n v t hoế ểt lập bi ứ ết luậ ề ệ hi u suấ ạt động cơ nhi ng theo ệ ột hoạt đ
chu trình.
2. Bài toán: Mộ ột đ ng cơ nhiệt làm việc theo chu trình carnot, trong mỗi chu trình
nhận được 2000 J nhiệt lư ng tợ ừ nguồn nóng. Nhiệt độ củ ồa ngu n nóng là
227 C
°
,
nhiệt độ của ngu ạồn l nh là
27 C
°
. Tính:
a ấ. Hiệu su t của động cơ.
b. Công mà động cơ th c hiự ện trong mỗi chu trình.
Lời giải:
1. Lý thuyết:
a. Chu trình cano thu n ngh ồ ng nhiậ ịch g m 2 quá trình đẳ ệt
thuận nghịch và đoạn nhiệ ịt thuận ngh ch
Đồ ị th :
- -Chu trình Các nô thuận
+ Quá trình 1 2: Giãn đ- ẳng nhiệt ở
1
T
, tác nhân thu nhiệt
1
Q
từ nguồn nóng
+ Quá trình 2 , t gi-3: Giãn đoạn nhiệt ảm:
1 1
1 2 1 2 2 3
. .:T T T V T V
γ γ
− −
→ =
+ Quá trình 3 4: Nén đ- ẳng nhiệt ở
2
T
, tác nhân tỏa nhiệt
2
Q
cho nguồn lạnh
+ Quá trình 4 1: Nén đo- ạn nhiệ ệt, nhi t độ tăng từ
2
T
lên
1
T
:
1
1 2
1
1 4
. .T V T V
γ γ
− −
=
- Chu trình các nô ngh ch ngư i chu trình thu- ị ợc loại vớ ận.
b. Thi u thế ểt lập bi ức tính hiệu suất
32
1 1 2 2 2
1 4
Q ln ; Q ln
V
Vm m
RT Q RT
V V
µ µ
′
= = − =
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tậ ảp và th o luận 99
Trong các quá trình đoạn nhiệt
2 3−
à v
4 1−
, ta có:
1 1 1 1
1 2 2 3 1 1 2 4
&TV T V TV T V
γ γ γ γ
− − − −
= =
$
Suy ra:
1 1
3 32 2
1 4 1 4
V VV V
V V V V
γ γ
− −
= ⇔ =
⇒
-Công thức tính hiêu suất chu trình Các nô:
3
2
2 4 2
2
1 1
1
1
ln
1 1 hay 1
ln
Vm
RT
Q V T
Vm
Q T
RT
V
µ
η η
µ
′
= − = − = −
Kế ệ ật luận: hi u suất của chu trình Các-nô thu n nghị ỉch đ i v i khí lý tư ng chố ớ ở phụ thuộc
vào nhiệt độ của nguồn nóng và lạnh.
Mở rộng thêm:
- Phát bi ật Cacno: Hi ảể ịu đ nh lu ệu suất của tất c các đ ng cơ thuộ ận ngh y theo chu ịch chạ
trình Cacno v ồn nóng và nguồ nh đ ng nhau, không phới cùng ngu n lạ ều bằ ụ thuộc vào tác
nhân cũng như cách chế ệ ị tạo máy. Hi u suất của động cơ không thuận ngh ch thì nh hơn ỏ
hiệ ịu suất củ ộa đ ng cơ thuận ngh ch.
- Phương hướng th tăng hiực tế để ệu suất của động cơ nhiệt: tăng
1
T
giảm
2
T
và chế tạo
gần đúng động cơ thuận nghịch.
2. Bài toán:
a. Hi ng cơ:ệu suất độ
1
2
27 273
1 1 40%
227 273
T
T
η
+
= − = − =
+
b. Công mà đ ng cơ th c hiộ ự ện trong mỗi chu trình:
1
1
. 0, 4.2000 800( J)
A
A Q
Q
η η
′
′
= ⇔ = = =
Câu 25:
1. Trình bày
a. Khái niệ ệ ệm và các tính ch t hàm entropi c t hấ ủa mộ nhi t động.
b. ý Biể ị êu th c đứ nh lượng của nguy n l 2 vi i dế ướt d ạng hàm entropi
c. Nội dung nguyên lý tăng entropi.
2. Bài toán:
Tính độ biến thiên entropy khi cho dãn đ ng nhiẳ ệt
6 g
khí Hydro từ áp suất
1.00kPa
đến áp
suất
50kPa
.
Lời giải:
1. Lý thuyết:
TAILIEUHUST.COM
100 Group: Bachkhoa Universe – Góc học tập và th o luả ận
a.
Khái niệm hàm entropy:
Xét quá trình thu ạng ạ c vào tr ng thái ậ ịn ngh ch từ tr thái (1) đến tr ng thái (2) chỉ phụ thuộ ạ
đầu và tr ng thái cuạ ối. Hàm entropy
S
là hàm đư c đợ ịnh nghĩa bởi biểu thức:
d
Q
S
T
δ
=
Tính chất:
- S có giá trị xác định và không phụ thuộc vào quá trình của hệ từ trạng thái này sang
trạng tháu khác.
- S là một đại lượng có tính cộng được.
- cS đư c xác đ nh sai kém m t h ng sợ ị ộ ằ ố ộng
0 0
Q
S S , S
T
δ
= +
∫
là giá trị entropy t i gạ ốc tính
toán, quy ước
0
S 0=
tại
T 0 K=
.
b. Biể ị ếu th c đứ nh lượng nguyên lý II vi t dư ạới d ng hàm entropy:
(2)
(1)
Q
S
T
δ
∆ ≥
∫
+ Dấu “=” ứng với quá trình thuậ ịn ngh ch
+ Dấu “>” ng vứ ới quá trình không thu n nghậ ị ệch v i hớ số cô lập
c. Nội dung nguyên lý tăng entropy: Với quá trình nhiệ ế ệt động thực t xảy ra trong m t hộ
cô l p, entropy c a hậ ủ ệ luôn luôn tăng.
2. Bài toán:
Đối v i khí lý tướ ởng:
2 2
1 1
ln ln
V
T VM m
S C R
T V
µ µ
∆ = ⋅ + ⋅ ⋅
Vì quá trình là nén đẳng nhi t nên ệ
2 1
1 2
V P
V P
=
1
2
6 100
. .ln .8,31.ln 17, 28 J / K
2 50
PM
S R
P
µ
⇒ ∆ = = =
Câu 26:
1. Trình bày
a. Những sự khác biệt trong mô hình khí lý tưởng và khí thực.
b. Khái niệ ế ì ạm cộng tích, nội áp và thi t lập phương tr nh tr ng thái cho kh c trên cơ sí thự ở
phương trình trạng thái khí lý tường.
2. Bài toán:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 101
Tính nhiệt độ của
3,5 g
khí Oxy chiếm thể tích
3
90 cm
ở áp suất
2,8MPa
nếu được coi là
khí lý tư c. Rút ra nh n xét v n đư c. Cho biởng và khí thự ậ ề ế các k t quả nhậ ợ ết
5 3 2
a 1,37.10 Jm / kmol ; b 0,03= =
3
m / kmol
.
Lời giải:
1. Lý thuyết:
a.
Mô hình khí lý tưởng:
- Có kích thư ỏớc nh và không đáng kể
- Phân tử không tương tác trừ lúc va chạm
- Thể tích kh i khí chính là thố ể tích dành cho chuyển đ do c a các ph n tộng nhiệt tự ủ ầ ử khí
Mô hình khí thực:
- Khi nén ho n nhau nên không ặc hạ nhi ộệt đ , th i khí gi m; lúc đó các phân tể tích khố ả ử gầ
thể bỏ qua tương tác giữa chúng
- Thể tích riêng c a các phân tủ ử cũng chi ộếm m t phần đáng k không th qua nóể ể bỏ
- Các phân tử khí có tương tác v i nhau nên áp suớ ất thực của kh i khí giố ảm đi do tương
tác tĩnh đi àm gi m tác dện l ả ụng lên thành bình.
b. Khái niệm
Cộng tích: Là hi ốệu s hiệu chính về ể ệ th tích, ký hi u b
Nội áp: Là số hiệu chính về ệ áp suất, ký hi u
i
2
p
t
a
v
=
1. Thiết lậ ạ ựp phương trình tr ng thái khí th c:
Giả s ử có
1 mol
c khí thự
- Thể tích:
t
V
là thể tích
1 mol
khí th c, thự ể tích dành cho chuyển động nhiệt.
t
V V b= −
- Áp suất: p là áp suất lúc các phân tử khí không hút nhau,
t
p
là áp suất khí thực.
t i
p p p= +
⇒
Thay vào phương trình tr ng thái khí lý tưạ ởng:
( )
t t2
p V b RT
t
a
pV RT
V
= ⇔ + − =
Vậy phương trình trạ vớng thái i 1 mol khí thực là
2
p + ( )
a
V b RT
V
− =
Phương trình ố trạng thái v i 1 khớ i khí th t kực bấ ỳ:
2
2 2
p + ( )
m a m m
V b RT
V
µ µ µ
− =
TAILIEUHUST.COM
102 Group: Bachkhoa Universe – Góc học tập và th o luả ận
2. Bài toán:
- : Mô hình khí lý tưởng
Từ phương trình tr ng tháiạ ta có:
277
PV
T K
mR
µ
= =
- Mô hình khí thực:
Từ phương trình tr ng thái ta có: ạ
2
2 2
p + ( ) 286
m a m
T V b K
mR V
µ
µ µ
= − =
- Nhận xét: Ở áp suất nhỏ nhi ộệt đ khối khí tính đư c dợ ựa trên hai phương trình khác nhau
xấp xỉ nhau nên v ụẫn có th áp dể ng mô hình khí lý tư ng cho khí Oxiở
Câu 27:
1. Thiết lập các đ nh lý vị ề mômen động lư ng (2 đ nh lý) cợ ị ủa vật rắn quay quanh trục
cố định.
2. Bài toán: Một thanh chiều dài
0,9( m)l =
, khối lượng
6(kg)M =
có thể quay tự do
xung quanh m ụột tr c nằm ngang đi qua m a thanh. Một đầu củ ột viên đ n khạ ối
lượng
0,01( kg)m =
bay theo hư i v n tớng nằm ngang vớ ậ ốc
300( m / s)=
tới xuyên
vào đầ a thanh và mắc vào thanh. Vậ a thanh nu kia củ n tố ốc g c củ gay sau khi viên
đạ ận đ p vào đầu thanh là bao nhiêu?
Lời giải:
1. Lý thuyết:
Vật rắn:
( )
i i i i i i i
i i i
L L r mv m r r
ω
= = ∧ = ∧ ∧
∑ ∑ ∑
( )
( )
2
. .
i i i i i i i
L m r r m r L I
ω ω ω
⇒ = Σ = Σ ⇒ =
- Định lý 1:
( )
dL d d
I I I
dt dt dt
ω
ω β µ
= = = =
Vậ ạy: Đ o hàm mômen động lượng
L
theo th ằời gian b ng tổng mômen l ụng lên ực tác d
vật rắn theo trục đó.
.
dL
dt
µ
=
- Định lý 2: Ta có
.dL dt
µ
=
Xét
µ
tác d ng trong khoảng thụ ời gian
2 1
t t t∆ = −
2
1
2 1
t
t
L L L dt
µ
⇒ ∆ = − =
∫
là xung lư ng mômen.ợ
Vậy: Độ biến thiên mômen độ ụng lư ng c a vợ ủ ậ ắt r n quay quanh 1 tr c có giá trị bằng xung
lượ ờng c a mômen l c tác d ng lên vủ ự ụ ật rắn trong th i gian
t∆
. Nếu
µ
=
const
L t
µ
⇒ ∆ = ∆
.
2. Bài tập:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 103
Xét h c va ch ng đ ng lưệ trướ ạm: Tổ ộ ợng cả hệ:
p mv=
(vì mỗi viên đạn có vận tốc
v
) mô
men đ ng lư c khi va chộ ợng trướ ạm là:
. .sin 1.L r p p mvl
α
= = =
Vậy momen quán tí ệnh của h vật sau va chạm:
sau 1 2
L I I
ω ω
= +
-
1
I
là momen ch n) đ i vất điểm (viên đạ ố ới trục quay
2
1
I ml=
-
2
I
là moment quán tính của thanh mảnh
2
2 2
2
'
2
12 12 3
l
M
Ml Ml
I
= = =
( )
2
2
1 2
3
s
Ml
L I I ml
ω ω
⇒ = + = +
Áp d ng đụ ịnh luật bảo toàn momen động lượng
2
2
2
2
1, 658(rad / s)
3
1
3
3
t s
Ml mvl v
L L mvl ml
M
Ml
l
ml
m
ω
= ⇔ = + ⇒ = =
+
+
Câu 28: Một quả cầu khối lượng
2 kg
, chuyền đ ng v i v n tộ ớ ậ ốc
3 m / s
, va ch m xuyên tâm ạ
với một quả cầu thứ hai khối lượng
3 kg
đang chuyển động cùng chiều v u thới quả cầ ứ
nh ốất v ậới v n t c
1 m / s
. Tìm v n t u sau va ch m nậ ố ủc c a các quả ầ c ạ ếu:
a. Va chạm là hoàn toàn đàn hồi.
b. Va ch m là không đàn hạ ồi (mềm).
Lời giải:
a. Va chạm hoàn toàn đàn hồi
+ Áp d ng đụ ịnh lu o toàn đật bả ộng lượng ta có:
2
' '
1 1 2 1 1 2 2
m v m v m v m v+ = +
( ) ( )
1 1 1 2 2 2
m v v m v v
′ ′
⇒ − = −
(1)
+ Áp d ng bụ ảo toàn cơ năng ta có:
2 2 2 2
1 1 2 2 1 1 2 2
2 2 2 2
m v m v m v m v
′ ′
+ = +
( ) ( )
2 2 2 2
1 1 1 2 2 2
m v v m v v
′ ′
⇒ − = −
(2)
1 1 2 2
(2)
(1)
v v v v
′ ′
⇒ + = +
2 1
2v v
′ ′
⇒ − =
( ) ( )
1 1 1 2 1 2
2m v v m v v
′ ′
⇒ − = + −
1 1
6 2 6 3 3v v
′ ′
⇔ − = + −
1
3
( m / s)
5
v
′
⇒ =
2
13
( m / s)
5
v
′
⇒ =
.
b) Va chạm mềm
TAILIEUHUST.COM
104 Group: Bachkhoa Universe – Góc học tập và th o luả ận
+)
( )
1 1 2 2
1 1 2 2 1 2
1 2
9
( m / s)
5
m v m v
m v m v m m V V
m m
+
+ = + ⇒ = =
+
.
Câu 29: Một quả cầ ặu đ c có khối lượng
1, 4(Kg)m =
, lăn không trượt với v n tậ ốc
1
V 10( m / s)=
thành tường rồi bậ ật ra v i vớ n tốc
2
V 8( m / s)=
. Nhi t lư ng tệ ợ ỏa ra trong va
chạm đó là?
Lời giải:
Sau va ch ng năng cạm độ ủa vật giảm. Độ giảm đ ng năng này tộ ỏa ra dưới dạng nhiệt. Khi
chuy ộ ộển động, quả cầu v a có đừ ng năng tị ếnh ti n, v a có đừ ng năng quay Đ ng năng cộ ủa
qu t:ả cầu đ c, đ ng chặ ồ ất, lăn không trượ
2 2 2 2 2 2
1 1 2 1 1
W
2 2 5 5 2
dp
I mR mR mv
ω ω ω
= = ⋅ = =
Moment quán ủ ồtính c a quả ầ ặ c u đ c đ ng chất:
2
2
5
I mR=
Độ ị ếng năng t nh ti n của quả cầu đặc:
2
( )
W
2
d tt
mv
=
2 2 2
( ) ( )
1 1 7
W W W
5 2 10
d d q d u
mv mv mv⇒ = + = + =
Nhiệt lư ng tợ ỏa ra do va chạm là:
( ) ( )
2 2 2 2
2 1
7 7
W 1, 4 10 8 35, 25( )
10 10
d
Q m v v J= − = − − = − ⋅ ⋅ − = −
Câu 30:
1. Trình bày đ t phân bịnh luậ ố tphân tử heo vận t đó suy ra công thốc Maxwell. Từ ức
tính v ố n nh ốc trung bình củ khí (không phận t c có xác suất lớ ất và vận t a phân tử ải
tích phân). Cho biết ý nghĩa c i v n t c này.ủa các loạ ậ ố
2. Bài toán: Khố ủ ội lượng riêng c a m t ch t khí ấ
( )
2 3
5.10 kg / m
ρ
−
=
; v n t c căn quậ ố ân
phương c ửủa các phân t khí này là
450( m / s)v =
. Áp suất của kh i khí tác dố ụng lên
thành bình là:
Lời giải:
1. Lý thuyết:
1. Đị ậ ốnh lu t phân b phân tử theo vận tốc của Maxwell
+ Thực nghiệm chứng t ng các phân t khí có v n tỏ rằ ử ậ ốc rất lớn
0 v< < ∞
. Giả s ử khí có
n
phân t ố phân tử, dn là s ử có v n t c trong khoậ ố ảng
v dv+
(%)
dn
n
⇒
là số phần trăm ph n tầ ử có v n t c n m trong kho ng này hay ậ ố ằ ả
dn
n
là xác suất
tìm th ằ ảấ ầy ph n t có v n t c nử ậ ố m trong kho ng
v dv+
.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 105
+
( )F v
là một hàm phụ thuộc vào
v
, g i là hàm phân bọ ố.
+
( )F v dv
là xác suất phân tử có v n tậ ốc trong khoảng
( , ) ( )
dn
v v dv F v dv
n
+ ⇒ =
0 0 0
( ) ( )
dn
F v dv n n F v dv
n
∞ ∞ ∞
⇒ = ⇒ =
∫ ∫ ∫
0
( ) 1F v dv
∞
⇒ =
∫
là đi ẩề ệu ki n chu n hóa củ ốa hàm phân b .
Từ đó Maxwell tìm được:
2
0
3
2
2
0
2
4
( )
2
m v
kT
m
F v v e
kT
π
−
= ⋅
+ Xét
( )
0 ( )
dF v
F v
dv
= ⇒
đạt max tại
xs
0
2 2kT RT
v v
m
µ
= = =
(xác suấ ầt ph n tử có v là cao
nhất).
→
Vận tốc trung bình:
0
0
8 8
( )
kT kT
v F v vdv
m
π πµ
∞
= = =
∫
Vận tốc căn quân phương:
2 2
00
2
0
3 3 3
( )
c c
kT kT RT
v v F v v dv v
m m
µ
∞
−
= = = ⇒ = =
∫
+
xs c
v v v< <
.
2. Bài toán:
Áp d ng thái khí lí tưụng phương trình ạ tr ởng:
PV n PV RT PV P P
n
m
RT RT m
V
µ µ ρ
= ⇒ = ⇒ = = =
Vận t c căn quố ân phương của các phân tử khí:
2
3
3
c
c
vRT RT
v
µ µ
= ⇒ =
( )
2 2
2
3375 /
3 3
c c
v vP
P N m
ρ
ρ
⇒ = ⇒ = ⋅ =
Câu 31: Tổng động năng tt trung bình của các phân tử khí
2
N
chứa trong 1 khí cầu
3
0,02 mV =
là
3
5.10 J
và vận tốc căn quân phương của 1 phân tử là
3
2.10 m / s
.
a. Tìm khối lượng
2
N
chứa trong khí cầu.
b. Áp suất khí tác dụng lên thành khí cầu.
Lời giải:
a.
2
3RT
V
µ
=
TAILIEUHUST.COM
106 Group: Bachkhoa Universe – Góc học tập và th o luả ận
2
2
3 3 2 1
W ( kg) 2,5( g)
2 2 400
i m m
U RT V m
i i V
ω
µ
= = ⋅ ⋅ = ⇒ = = =
b.
3 3 2
W R 1666,67( )
2 2 3
n T V p Pa
V
ω
ρ
= = ⇒ = =
Câu 3 2:
1. Định nghĩa trạ ằng thái cân b ng, quá trình cân bằ t quá trình ting. Mộ ến hành như
thế nào có thể xem như là cân b ng? Vì sao?ằ
2. Bài toán: Có hai bình c ố i nhau b ng có khóa, đ ng cùng ầu đư c nợ i vớ ằng một ố ự
một ch t khí. Áp suấ ất ở bình th nhứ ất là
5 2
2.10 N / m
, ở bình thứ hai là
6 2
10 N / m
.
Mở khóa nh nhàng đẹ ể hai bình thông với nhau sao cho nhi ộệt đ khí vẫn không
đổi. Khi đã cân b ng, áp suằ ất ở hai bình là
5 2
4 10 N / m⋅
. Tìm th a bình cể tích củ ầu
thứ hai, nế ếu bi t thể ấ tích của bình c u thầ ứ nh t là
3
15 dm
.
Lời giải:
1. Lý thuyế :t
- c Trạng thái cân bằng là trạng thái trong đó thông số ủa hệ được hoàn toàn xác định và
sẽ tồn t i mãi mãi nạ ếu không có tác đ bên ngoài.ộng từ
- l Quá trình cân bằng à quá trình biến đ i gổ ồm mộ ỗt chu i liên tiếp các trạng thái cân bằng.
- M ột quá trình đư ấợc thực hi n rệ t ch m, ho c nói m t chậ ặ ột cách chặ ẽ vô cùng chậm, để có
đủ ế thời gian thi t lậ ạp l i sự cân b ng m a hằ ới củ ệ thì quá trình đó được coi là quá trình cân
bằng.
Giả ại thích: Trong m t quá trình bi n đ i, hộ ế ổ ệ chuyển từ tr ng thái cân b ng ằ ạng này sang tr
thái cân b ng ti ạng thái cân b ng trưằ ếp theo thì tr ằ ớc đã b phá h y, nó thay đ i theo thị ủ ổ ời
gian.
2. Bài toán
Khi mở khóa cho hai bình thông nhau ta có phương trình trạng thái
( )
1 2
1 2
M M
p V V RT
µ
+
+ =
(1)
Từ phương trình trạng thái của khí ở bình 1:
1 1 1
1 1 1
, ta có: ,
M p V
p V RT M
RT
µ
µ
= =
Từ phương trình tr ng thái c 2: ạ ủa khí ở bình
2
2 2
M
p V RT
µ
=
, ta có:
2 2
2
p V
M
RT
µ
=
.
Thay
1
M
và
2
M
vào (1) ta có:
( )
( )
1 1
3 3
2
5.10 m
p p V
V
p p
α
−
−
= =
−
.
Câu 33:
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 107
1. Hãy thi p công th c tính áp su a khí quy n phết lậ ứ ất củ ể ụ thuộc vào độ cao. Từ đó suy
ra định lu ốật phân b Boltzman.
2. Bài toán: 6,5g hydro ở nhiệt độ
27 C
°
, nh n đư t nên thậ ợc nhiệ ể tích giãn nở gấp
đôi, trong đi ấề ệu ki n áp su t không đổi. Tính:
a. Công mà khí sinh ra
b. Độ biến thiên nộ ủ ối năng c a kh i khí
c. Nhi t lư p cho khệ ợng đã cung cấ ối khí.
Lời giải:
1. Lý thuyết
Xét cột không khí cao dh, diện tích đáy
2
1m
, ở độ cao
h
. Áp suất đáy dưới
p
.
⇒
Áp suất đáy trên:
(
0p dp dp+ <
, do lên cao áp su m) và ất giả
dp dP= −
(do
)
2
1S m=
(trọng lư ng cợ ột không khí).
⇒
Số phân tử nằm trong cột
0 0
dh : d
n
d n S h n dh= =
.
⇒
Trọng lư ng cợ ột dh:
0
.dP dn mg mgn dh= =
hay
0
dp mgn dh= −
d .
mg dp mg
dp p h dh
kT p kT
⇒ = − ⇔ = −
maidat 0
0
dh ln
h h
dp mg p mg
h
p kT p kT
⇒ = − ⇒ = −
∫ ∫
0
.
mgh
kT
p p e⇒ = ⇒
Áp suất giảm khi độ cao tăng.
- cĐịnh lu ốật phân b ủa Boltzman:
0 0, mat dat 0, mat dat
.
mg wt
kT kT
h
n n e n e
− −
= =
.
2. Bài toán:
Do quá trình giãn nở là đẳng áp nên ta có:
3
1
. 8,1.10
M
A p V RT J
µ
′
= ∆ = =
và
( )
2 1
.
2
M i
U R T T
µ
∆ = ⋅ −
Từ phương trình đẳng áp ta có:
2
2 1 1
1
2 .
V
T T T
V
= =
Do đó:
3
20, 2 10
2
M i
U RT J
µ
∆ = ⋅ = ⋅
.
Theo nguyên lý thứ nh ủất c a nhiệt động học.
3
28,3.10Q U A U A J
′
= ∆ − = ∆ + =
Câu 34: Nén
10 g
khí oxy từ đi ẩề ệu ki n tiêu chu n đ n thế ể tích 4 lít. Tìm:
a. Áp su a kh i khí sau mấ t đt và nhiệ ộ ủ c ố ỗi quá trình nén đẳng nhiệ ệt và đoạn nhi t.
TAILIEUHUST.COM
108 Group: Bachkhoa Universe – Góc học tập và th o luả ận
b. Công cầ t đn thiế ể nén khí trong mỗ đó, suy ra nên nén theo cách nào là i trư p. Tờng hợ ừ
lợi nhất.
Lời giải:
a. Nén đẳng nhiệt:
2 1
273 KT T= =
và
5 2
1
2 1
2
5.10 N / m .
V
p p
V
= =
Nén đoạn nhiệt:
1
1
2
2
520 K
V
T T
V
γ
−
Γ
= =
và
5 2
1
2 1
2
9,5.10 N / m
V
p p
V
γ
= ⋅ =
b. Công nén khí trong quá trình đ ng nhiẳ ệt là:
2
1
ln 1115
pM
A RT J
p
µ
= ⋅ =
Công nén khí trong quá trình đoạn nhiệt là
2 2 1 1
1500
1
p V p V
A J
γ
−
= =
−
Như vậy nén đẳng nhiệt sẽ có lợi hơn.
Câu 35: Tác nhân c a mủ ộ ột đ ng cơ nhiệt là một mol khí lí tưởng đơn nguyên t n ử ự, th c hiệ
một chu trình gồm hai quá trình đằng tích và hai quá trình đẳng áp như hình vẽ ể. Các đi m
chính giữa c i và đư ng đủa quá trình đ ng áp phía dưẳ ớ ờ ẳng tích bên trái có cùng nhi ộệt đ
1
T
, trong khi các đi m chính gi a c ng để ữ ủa quá trình đ ng áp phía trên và đưẳ ờ ẳng tích bên
phải có cùng nhiệt độ
2
T
. Tìm hiệu suất của chu trình đó.
Lời giải:
Từ phương trình trạng thái ta có:
2 2 2
1 1 1
P V T
P V T
= =
(1)
Khi chỉ ệ nhận nhi t lư ng tích 1ợng trong quá trình đẳ -2 và
quá trình đẳng áp 2-3:
12 23v p
Q C T C T= ∆ + ∆
.
( ) ( )
2 1 1 1 2 2 2 1
3 5
2 2
Q p V p V p V p V= − + −
Thay vào (1) ta có:
2 2
1 1
1 1
51
1 3
2
T T
Q p V
T T
= − +
Công khí th c trong quá trình:ực hi n đưệ ợ
( )( )
2 1 2 1
A p p V V= − −
Thay (1) vào A ta có:
2
2
1 1
1
1
T
A p V
T
= −
⇒
Hiệu suất của chu trình trên là:
( )
2 1
2 1
2
5 3
T T
A
H
Q T T
−
= =
+
.
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 109
Câu 36: Mộ ột đ ng cơ nhiệ ệt làm vi c theo chu trình Cacno, sau m i chu trình sinh mộỗ t công
4
7,35 10 JA = ⋅
. Nhiệt độ của nguồn nóng là
100 C
°
, nhiệt độ của nguồn lạnh là
0 C
°
. Tìm:
a. Hiệu suất của động cơ
b. Nhiệ ật lượng nh n được của nguồn nóng sau một chu trình
c. Nhiệt lượng nhả cho nguồ t chu trình.n l nh sau mạ ộ
Lời giải:
a. Ta có:
2
1
273
1 1 26,81(%)
373
T
H
T
= − = − =
b. Ta có:
4
1
1
7,35.10
0, 2681
A A
H Q
Q H
= ⇒ = =
1
274151( )Q J⇒ =
c.
1 2 2 1
200651( )A Q Q Q Q A J
′ ′
= − ⇒ = − =
.
Câu 37: Tính độ biến thiên entropy khi biến đổi 1g nướ ởc
0 C
°
thành hơi ở
100 C
°
.
Lời giải:
+ Ta có:
1 2
S S S∆ = ∆ + ∆
+ Có
2
1
31 2
1
1
d 373
ln 10 4200.ln 1, 31( J / K).
273
T
T
Q Tmc T dT
S mc mc
T T T T
δ
−
∆ = = = = = =
∫ ∫ ∫
(1)
+ Có
6 3
2
2 2 2
2 2 2
1 1 1 2, 26.10 10
6,06( J / K)
7
.
3 3
Q
S Q Q
T T T T Lm
δ
δ
−
∆ = = = = = =
∫ ∫
(2)
Từ (1) và (2)
7,37( J / K)S⇒ ∆ =
TAILIEUHUST.COM
110 Group: Bachkhoa Universe – Góc học tập và th o luả ận
PHẦN III. MỘT S THI GIỐ ĐỀ ỮA KỲ
Đề thi giữa kỳ sẽ do giáo viên d ắạy l p ra vớ ới hình thức tr c nghiệm. Một đề có từ – 10 20
câu h i v i thỏ ớ ời gian thích hợp (tùy giáo viên). Các câu hỏ ệi thư ng trích tờ ừ bộ trắc nghi m
ở trên và sách bài tập. Chính vì v mình nêu dưậy nh ng đữ ề ới đây (đề thi thật) là giúp các
bạn hình dung ra đề ỳ ệ ẽ thi giữa k và luy n t p nên mình sậ không có l n ời giả ại ở đây. Các b
xem cách làm ở trên nhé.
1. Đề 1 thi giữ ỳa k
Câu 1: Một con l c toán có sắ ợi dây dài 90 cm và cứ sau khoảng thời gian dt = 0.5 phút thì
biên đ m lư a con l c đó bộ gi ầảm 4.5 l n. Giả ợng loga củ ắ ằng bao nhiêu? (cho g = 9.81 m/s2)
A.
9,84.10
-2
B.
12,2.10
-2
C.
2,76.10
-2
D.
5,25.10
-2
Câu 2: Từ một dộ cao đủ lờn người ta ném một hòn đá theo phương nằm ngang so với mặt
đấ ầ ết v ậới v n tố n đc bạ u 20m/s. Tính gia t c pháp tuyố n của hoàn đá sau lúc ném 0.5 giây
(cho g = 9.81 m/s2)
A.
3.5 m/s
2
B.
9.5 m/s
2
C.
12.3 m/s
2
D.
7.5 m/s
2
Câu 3: Một ô tô chuy n đ n đổể ộng biế i đều lần lượt đi qua 2 đi m A và B cách nhau 36m ể
trong kho ủ ỏ ốảng th ậời gian t = 1.5s. V n tốc c a ô tô B là 30m/s. Hở i v n tậ c tại A?
A. 16 m/s
B. 18 m/s
C. 20 m/s
D. 22 m/s
Câu 4: Một ô tô bắt đầ ạy vào đo n đư ng tròn có bán kính 1km và dài 620 m vu ch ạ ờ ới vận
tốc bạn đầu 54km/h trong th i gian 15s. Tính gia tờ ốc toàn ph n cầ ủa ô tô ở cuối đo n đưạ ờng,
coi chuyể ền đ n động là nhanh dầ u.
E.
9.12 m/s
2
F.
7.55 m/s
2
G.
3.55 m/s
2
H.
5.77 m/s
2
Câu 5: Một sợi dây mảnh OA dài l = 22cm đầu O cố đị ầnh, đ u A buộc vào vật nhỏ có thể
quay tròn trong mặ ẳ trí thất ph ng đ ng xung quanh O. T i vứ ạ ị p nh n ph i truyấp cầ ả ền cho vật
vận t c bé nhố ất bằng bao nhiêu để vậ ể t có th đi qua điểm cao nh t, lấ ấy g = 9.81 m/s2
A. 3.28 m/s
B. 4.23 m/s
C. 2.38 m/s
D. 5.43 m/s
Câu 6: Mộ ột vậ t đầu trư ng trên mt bắ ợt xuố t mặt ph ng p vơi phương ngang ẳ nghiêng hợ
góc 45 đ t đư c quãng đư ma sát ộ. Khi trượ ợ ờng s = 40 cm, v c v = 1.5 m/s. Hật có vận tố ệ số
giữa vật và mặt phẳng nghiêng bằng bao nhiêu? Cho g = 9.81 m/s2
A. 0.3
B. 0.4
C. 0.6
D. 0.5
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 111
Câu 7: Một phi công ngồi trên ghế máy bay nhào l n theoộ một đường tròn bán kinh R =
1000 m trong m t ph ng th ng đặ ẳ ẳ ứng. Vận tố ủ ổc c a máy bay không đ i v = 540 km/h. Lấy g
= 9.81 m/s2. Tại vị trí thấp nhất của vòng tròn nhào l c nén c a phi công lên ghộn, lự ủ ế ngồi
bằng bao nhiêu biết kh ng c a phi công là 80kối lượ ủ g?
A. 2585 N
B. 4236 N
C. 3872 N
D. 5324 N
Câu 8: Chất điểm khối lượng m = 30 gam được ném lên từ một điểm O trên mặt đ t vấ ới vận
tốc ban đầu v0 = 15 m/s theo hướng nghiêng góc a = 45 độ với mặt phẳng nằm ngang. Giá
trị ể mô men đ ng lư ng c a chộ ợ ủ ất đi m đ i vố ới điểm O tại th i đi m mà ch m ch m đờ ể ất điể ạ ất
là: (b c cỏ qua sứ ản không khí, g = 9.81 m/s2)
A.
3.5 kgm
2
/s
B.
5.6 kgm
2
/s
C.
7.3 kgm
2
/s
D.
8.2 kgm
2
/s
Câu 9: Một đĩa tròn khối lượng m = 2.5kg, bán kính R = 0.4m đang quay với vận tốc góc
900 vòng/phút. Tác dụng lên đĩa một momen hãm; đĩa quay ch n và sau th i gian dt ậ ầm d ờ
= 15 giây thì dừng l i. Tính l c hãm ti p tuyạ ự ế ến?
A. -5.51 N
B. -4.13N
C. -1.34N
D. -3.14N
Câu 10: Hai v t có khậ ối lượng m1 = 2.1kg, m2 = 3.3kg được n i vố ới
nhau b ộằng m t sợi dây không dãn và đặt trên mặt bàn n ngang. ằm
Dùng một sợi dây khác vắt qua ròng rọc (có kh i lưố ợng không đáng
kể) một đầu dây bu c vào v t m2, độ ậ ầu kia buộc vào vật thứ 3 có khối
lượng m3 = 5.6kg. Hệ được bố trí như hình v . Tính lẽ ực căng sợi dây
do vật m3 gây ra. (SBT)
A. 23 N
B. 17 N
C. 27 N
D. 12 N
Câu 11: Một khẩu pháo có khố n mi lượng M = 800kg bắ ột viên đạn theo phương hợ ớp v i
phương ngang m t góc 60 đ ng c a viên đạộ ộ. Khối lượ ủ n m = 7kg, vậ ần tốc đ u nòng v =
380m/s. Khi b pháo gi t đo ản trung bình tác dắn bệ ật lùi v sau mề ộ ạn s = 45 cm. Lực c ụn lên
khẩu pháo có giá trị là?
A. 4257 N
B. 2457 N
C. 2547 N
D. 5247 N
Câu 12: Người ta chèo một con thuy n qua sông theo hư n tốề ớng vuông góc với vậ c 3.6
km/h. Nước đã mang con thuy phía xuôi dòng m ảng 120m. Về ền v ột kho ận t ủốc c a dòng
nướ ớc đ i vố i bờ sông nh ng bao nhiêu? Cho bi ộ ủận giá trị bằ ế ềt chi u r ng c a sông là S =
0.6km.
A. 0.4 m/s
B. 0.2 m/s
C. 0.6 m/s
D. 0.8 m/s
TAILIEUHUST.COM
112 Group: Bachkhoa Universe – Góc học tập và th o luả ận
Câu 13: Một ô tô có khối lượng m = 1228kg chạy lên d c v i v n tố ớ ậ ốc không đổi v = 72km/h.
Mặt đư ng dờ ốc hợp với mặt phẳng ngang một góc a sao cho sina = 0.05; cosa = 1. Hệ s ố
ma sát giữa mặt đường và bánh xe là k = 0.05. Lấy g = 9.81 m/s2. Khi đó công suất của động
cơ ô tô bằng bao nhiêu?
A. 26kW
B. 32 kW
C. 24 kW
D. 30 kW
Câu 14: Một quả cầu có khối lượng m = 0.3 kg được đ t cách đặ ầu một thanh đồng chất một
khoảng a = 0.4 cm sao cho tâm quả cầu n a thanh. Thanh có chiằm trên phương củ ều dài l
= 7cm và kh ng M = 1kg. Lối lượ ực hút của thanh lên quả cầu bằng bao nhiêu? Cho hằng số
hấ )
p d n vũ trẫ ụ G = 6.67.10
-11
N.m
2
/(kg
2
A.
7,67.10
-8
N
B.
6,76.10
-8
N
C.
6,76.10
-8
N
D.
7,67.10
-8
N
Câu 15: Cho h ố trí như hình vệ vậ t được b ẽ. Sợi dây không giãn.
Khố ể ệi lượng c a ròng r c và c a s i dây không đáng kủ ọ ủ ợ . H số ma
sát của vật 1 đôi với mặt ph ng nẳ ằm ngang k = 0.25. Tính lực căng
của sợi dây khi m1 = 90g, m2 = 120g?
A. 0.82 N
B. 1.24 N
C. 0.63 N
D. 0.23 N
Câu 16: Từ đỉ nh tháp cao 30m người ta ném một hòn đá lên phía
trên vớ ới vận tốc v0 = 20m/s theo phương hợp v i phương ngang một góc 45 độ. Thời gian
rơi của hòn đá nhận giá tr nào dưị ới đây?
A. 6.3 s
B. 4.3 s
C. 3.4 s
D. 2.1 s
Câu 17: Một vật có khối lư i va ch hai có khợ ớng m1 = 6kg chuyển động t ạm vào vật thứ ối
lượng m = 1kg đang đứng yên. Coi va chạm là xuyên tâm và hoàn toàn đàn h t thồi. H i vỏ ậ ứ
nhất truyền cho v hai bao nhiêu ph ộật thứ ần trăm đ ng năng của mình sau va chạm?
A. 51 %
B. 34%
C. 66 %
D. 49%
Câu 18: Xác đ i lưịnh mô men quán tính c a thanh có khốủ ợng m = 15kg dài L = 90cm đối
với trụ quay đi qua tr ng tâm c a thanh và họ ủ ợp với thanh một góc 60 độ.
A.
1,20 kg.m
2
B.
0,76 kg.m
2
C.
0,34 kg.m
2
D.
1,43 kg.m
2
Câu 19: Một vật rơi tự do t cao 25m t đất) và m t viên đ n đưừ điể độm A ở (đối với mặ ộ ạ ợc
bắn đồng thời từ mặt đất lên cao với vận tốc ban đầu 14m/s theo phương th ng đ ng đi ẳ ứ
qua đi qua lểm a. Bỏ ực cản không khí. Lấ ảy g = 9.81 m/s2. Kho ng cách giữa viên đ n và vạ ật
rơi sau thời gian 0.8 giây bằng?
A. 5.0 m
B. 8.0 m
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 113
C. 13.8 m
D. 10.3 m
Câu 20: Tác d ng m p tuyụ ột lực tiế ến Ft = 100N lên một bánh xe đang đứng yên có bán kình
R = 0.3M và có mô men quán tính I = 18kg.m2. Hỏi v n t c dài tậ ố ại một đi m trên vành bánh ể
xe sau khi tác d ng lụ ực 10 giây?
A. 5 m/s
B. 12 m/s
C. 8 m/s
D. 3 m/s
2. Đề thi giữa kỳ 2
Câu 1: Một trụ đặc có khối lượng M = 105 kg, bán kính R = 0.5m đang quay xung quanh
trục củ ụa nó. Tác d ng lên trụ một l t trực hãm F = 257.3 N, tiếp tuy n vế ới mặ ụ và vuông góc
vớ dừi trục quay. Sau thời gian ∆𝜔𝜔 = 2.6s trụ ng l n t c góc cạ ậi. V ố ủa trụ lúc bắt đầu tác dụng
lực hãm là:
A. 21.8 rad/s
B. 25.5 rad/s
C. 22.1 rad/s
D. 21.2 rad/s
Câu 2: Một vật có kh n đ ng v c đ i va chối lượng m1 = 2kg chuyể ộ ới tố ộ v1 = 5m/s tớ ạm
xuyên tâm vào vật có kh ng yên. Va ch m là hoàn toàn m m. Nhiối lượng m2 = 3kg đứ ạ ề ệt
lượng toả ra trong quá tr ạ ình va ch m là:
A. 34.8 J
B. 14.2 J
C. 15.0 J
D.
Câu 3: Thả t rơi tự do m t nhột vậ ỏ ừ độ cao h = 17.6m. Quãng đường mà v t rơi đưậ ợc
trong 0.1s cu a thố ủi cùng c ời gian rơi là:
A. 2.2 m
B. 1.8 m
C. 2.4 m
D. 1.6m
Câu 4: Một phi công th c hiự ện vòng tròn nhào lộn trong m t ph ng. V n tặ ẳng đứ ậ ốc của
máy bay không đ ng áp l a phi công lên ghổi v = 800 km/h. Giả ằ sử r ực lớn nhất củ ế bằng 5
lần tr ng lọ ực của ngườ ỹi. Lấy g = 9.8 m/s2. Bán kính qu đạo vòng nhào lộn có giá trị bằng:
A. 1473.3 m
B. 1562.5 m
C. 1394.4 m
D. 1259.8 m
Câu 5: Một vật nhro có kh i lương m bu c vào mố ộ ột sợi dây mảnh chiều dài l = 1.5m; đầu
kia giữ cố định. Cho vật quay trong m ẳ ằm ngang vặt ph ng n ới tốc độ góc không đổi sao
cho dây h p v i phương th ng đợ ớ ẳ ứng 1 góc 𝛼𝛼 = 30 . Cho g = 9.8 m/s2, b độ ỏ qua l ảực c n
không khí. Vận t c góc có giá trố ị:
A. 2.54 rad/s
B. 2.63 rad/s
C. 2.75 rad/s
D. 2.84 rad/s
Câu 6: Ở đầu một sợi dây dài l = 50 cm có treo mộ ỏt vậ ặt n ng. H i tạ ấ ải đi m th p nhể ấ t ph i
truyền cho vật một vận tốc bé nhất bằng bao nhiêu để vậ ể t có th quay tròn trong mặt
phẳng đ ng. Lứ ấy g = 9.8 m/s2
A. 4.9 m/s
B. 4.4 m/s
TAILIEUHUST.COM
114 Group: Bachkhoa Universe – Góc học tập và th o luả ận
C. 4.0 m/s
D.
Câu 7: Một thanh dài l = 1m, kh ng M = 6kg có thối lượ ể quay tự do xung quanh mộ ụt tr c
nằm ngang đi qua m a thanh. M ng ộ ủt đầu c ộ ốt viên đ n khạ i lượng m = 10g bay theo hướ
nằm ngang v ậ ầ a thanh và m c vào thanh. Với v n t i xuyên vào đốc v = 500 m/s tớ u kia củ ắ ận
tố ủc góc c a thanh ngay sau khi viên đ n đạ ập vào thanh là:
A. 2.5 rad/s
B. 2.9 rad/s
C. 2.8 rad/s
D. 2.1 rad/s
Câu 8: Từ ỉ một đ nh tháp cao h = 20m, người ta ném một hòn đá khối lượng 50g theo
phương nghiêng với mặ ẳ ằ ật ph ng n m ngang, v i vớ n t c ban đố ầu v0 = 18 m/s. Khi rơi tới
mặt đấ ật hòn đá có v n t a lốc v = 24 m/s. Tính công củ ực cản của không khí lên hòn đá.
A. -2.7 J
B. -1.8 J
C. -4.2 J
D. -3.5 J
Câu 9: Một con l c đơn có m c kéo lắ = 140g đượ ệch ra v i phương th ng đớ ẳ ứng một góc 𝛼𝛼
= 90 đ rơi, cho g = 10 m/s2. Lộ, sau đó thả ực căng cực đại của dây treo là:
A. 4.04 N
B. 4.20 N
C. 3.27 N
D. 3.96 N
Câu 10: Một đĩa tròn đồng chất bán kính R = 20 cm, khối lượng m = 2.2 kg có thể quay
quanh một trục nằm ngang vuông góc v i đĩa và cách tâm đĩa m t đoớ ộ ạ ần R/2. Đĩa bắt đ u
quay t ng v i v i v n t c ban đừ ứ vị trí tương ớ ị trí cao nhất của tâm đĩa vớ ậ ố ầ ằu b ng 0. Xác
định mômen độ ủ ố ụng lư ng cợ a đĩa đ i với tr c quay khi đĩa đi qua vị trí th p nhấ ất.
A.
0.662 kgm
2
s
-1
B.
0.686 kgm
2
s
-1
C.
0.754 kgm
2
s
-1
D.
0.368 kgm
2
s
-1
Câu 11: Trên m i ta đ t có khột đĩa nằm ngang đang quay, ngườ ặ t vt mộ ậ ối lượng m = 1 kg
cách tr i có ục quay r = 50 cm. H ng k = 0.25. Lệ số ma sát gi a vữ ật và đĩa bằ ực ma sát phả
độ ể vậ lớn b ng bao nhiêu đằ t được giữ trên đĩa quay v i v n tớ ậ ốc n = 12 vòng/ phút.
A. 0.897 N
B. 0.612 N
C. 0.789 N
D. 0.564 N
Câu 12: Một con l c v t lý đưắ ậ ợc cấu t o bạ ằng m t thanh đ t diộ ồng chất, tiế ệ ền đ u có độ
dài bằ ả ng x. ng ng l = 50cm và trục quay O c a nó cách tr ng tâm G mủ ọ ột kho ng bằ Biết rằ
chu k ộ ủ ỏ nhỳ dao đ ng T c a con l c này là nhắ ấ ịt, x nhận giá tr nào dưới đây:
A. 13.7 cm
B. 45.6 cm
C. 12.1 cm
D. 14.4 cm
Câu 13: Trên một trụ rỗ ống kh i lượng m = 1.2kg, người ta cu n mộ ột
sợi dây không giãn có khối lượng và đường kính nhỏ không đáng kể.
Đầ địu tự do c c g n trên mủa dây đượ ắ ộ ốt giá c nh (hình v ụẽ ể). Đ tr rơi
dưới tác d ng cụ ủa tr ng ọng lự ức. Tìm s c căng c a dây treo. Cho biủ ết rằ
gia t ng trư ng có giá trố ọc tr ờ ị g = 10m/s
A. 6 N
B. 7 N
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 115
C. 4 N
D. 5 N
Câu 14: Một người ng i trên ghồ ế Giucopxki và cầm trong tay hai quả tạ ả, mỗi qu có khối
lượng 10 kg. Khoảng cách từ mỗi quả tới trụ ốc quay là 0.75m. Ghế quay v i v n tớ ậ c góc 2
vòng/s. H i v n t i đó co tay l i đ ng cách t n trỏ ậ ốc củ ế nếa gh u ngườ ạ ể khoả ừ mỗi quả tạ đế ục
quay ch còn là 20cm, cho biỉ ết mômen quán tính của ngư i và gh c quay là 2.5 ờ ế đố i với trụ
kg.m2
A. 53.7 rad/s
B. 52.36 rad/s
C. 55.8 rad/s
D. 62.4 rad/s
3. Đề thi giữ ỳa k 3
Câu 1: Một vật khối lượng m trư t không ma sát tợ ừ đỉnh một mặt cầu xuống dưới. Hỏi từ
khoảng cách nào tính từ chân m hỏặ ầt c u vật bắt đầu rơi k i mặ ầt c u.
Cho bán kình mặt cầu là R = 90cm.
A. 0.3 m
B. 0.5 m
C. 0.6 m
D. 0.4 m
Câu 2: Phả ậi ném một v t theo phương thẳng đứ ừng t độ cao h = 30 m
với vân t c v0 bố ằng bao nhiêu đ ốể nó rơi xu ng mặt đất trước 1s so v i trư ng h p vớ ờ ợ ật tự
rơi tự do? G = 10m/s2.
A. 13.45 m/s
B. 12.25 m/s
C. 9.75 m/s
D. 8.79 m/s
Câu 3: Một xe l a bử ắt đầu chuy ộng nhanh dển đ ầ ẳn đ u trên mề ột đư ng thờ ng ngang qua
trư ứ ứớ ờc mặt một ngư i quan sát đ ng ngang toa tàu th ấ ng toa xe thứ nh t. Biết rằ nhất đi
qua trư t ngư t th i gian t i toa th 8 s đi qua trư t ngước mặ ời quan sát hế ờ = 8s. Hỏ ứ ẽ ớc mặ ời
quan sát trong bao lâu?
A. 1.20s
B. 1.46s
C. 3.21s
D. 2.16s
Câu 4: Một hòn đá được ném theo phương nằm ngang với vân tốc v0 = 15m/s. Tính gia
tố ủc pháp tuyến c a hòn đá sau lúc ném 2 giây. (g = 10 m/s2)
A. 2
𝑚𝑚
𝑠𝑠
2
B. 4
𝑚𝑚
𝑠𝑠
2
C. 6
𝑚𝑚
𝑠𝑠
2
D. 8
𝑚𝑚
𝑠𝑠
2
Câu 5: Mộ ột xe chuy n để ng từ đỉnh một dốc phẳng có độ cao h = 80 cm nằm nghiêng
góc 𝛼𝛼 = 30 độ so với mặt n n l i sau khi đã đi đư c đoằm ngang và d ẳừng h ạ ợ ạ ằn n m ngang
CB. H ma sát gi Xác đệ số ữa xe và mặt đư ng trên các đoạờ n DC và CB là k = 0.2. ịnh độ dài
quãng đư ng CB.ờ
A. 1.74 m
B. 2.61 m
C. 2.28 m
D. 2.69 m
TAILIEUHUST.COM
116 Group: Bachkhoa Universe – Góc học tập và th o luả ận
Câu 6: Từ độ cao h = 30m, một hòn đá được ném lên phía trên v i v n tớ ậ ốc v0 = 15m/s
theo phương h ộ ộ nh v ủợp v t ph ng nới mặ ẳ ằm ngang m t góc bằng 45 đ . Xác đị ận tốc c a
hòn đá lúc chạ ấm đ t. Lấ y g = 10m/s2
A. 34.21 m/s
B. 28.72 m/s
C. 26.71 m/s
D. 33.18 m/s
Câu 7: Mộ ốt ch m khất điể i lượng m = 0.3 kg được ném lên từ một đi m O v i v n tể ớ ậ ốc v0 =
9m/s theo phương h p v t ph ng nợ ới mặ ẳ ằm ngang m t góc ộ 𝛼𝛼 = 30 độ - b ỏ qua sức cản
củ ộa không khí, cho g = 9.8 m/s2. Mômen đ ng lư ng c a chợ ủ ất điể ếm đối v i O khi lên đớ n
độ cao c c đự ại là:
A.
3.226 kgm
2
/s
B.
2.416 kgm
2
/s
C.
1.865 kgm
2
/s
D.
2.054 kgm
2
/s
Câu 8: Mộ ột người kéo xe b ng mằ t lực hợp phương ngang m t góc ộ 𝛼𝛼 = 30 độ. Xe có khối
lượ ớng m = 250kg và chuyển đ ng vộ i v n t c không đ i. Hậ ố ổ ệ số ma sát gi a bánh xe và ữ
mặt đường k = 0.2. Lấy g = 10m/s2. Lực kéo có giá trị b ằng:
A. 517.58 N
B. 561.15 N
C. 550.71 N
D. 543.21 N
Câu 9: Trên một đĩa nằm ngang đang quay, ngư ặời ta đ t một vật có khối lượng m = 500g
cách trục quay r = 60 cm. H ng k = 0.1. Vệ số ma sát gi a vữ ặt và đĩa bằ ới v n tậ ốc góc nào
thì i đĩa?vật bắt đầu trư t khợ ỏ
A. 1.7 rad/s
B. 1.3 rad/s
C. 2.2 rad/s
D. 2.8 rad/s
Câu 10: Mộ ố ố ốt ô tô kh i lượng m = 550kg chuyển động thẳng đều xu ng d c trên một mặt
phẳng nghiêng, góc nghiêng 𝛼𝛼 so v m ngang có sinới mặt đất nằ 𝛼𝛼 = 0.0872; cos 𝛼𝛼 =
0.9962. L ma sát gi t đư ng là: ực kéo ô tô b ng Fằ
k
= 550N. Hệ số ữa ô tô và mặ ờ
A. 0.158
B. 0.188
C. 0.208
D. 0.198
Câu 11: Xác đị ỳnh chu k của m t con lộ ắc toán chiề ếu dài l = 50cm, bi t nó sau khoảng thời
gian t = 6 phút nó mất 99% năng lượng.
A. 1.42s
B. 1.82s
C. 1.66s
D. 1.74s
Câu 12: Từ đỉnh một mặ ẳt ph ng nghiêng cao h = 80cm, người ta cho m ng chộ ồt v t đậ ất
có hình vành tròn lăn không trượt trên m t phặ ẳng nghiêng đó. Tìm v ủận t c dài cố a các vật
ở cuối mặ ẳt ph ng nghiêng.
A. 2.8 m/s
B. 2.2 m/s
C. 3.3 m/s
D. 3.6 m/s
Câu 13: Một quả cầ ặu đ c đ ng ch ó kh i v n tồ ất c ối lượng m = 2kg, lăn không trượt vớ ậ ốc v1
= 10 m/s đ c v2 = 8m/s. Tính nhiến đ ng r i v n tập vào thành tườ ồi bật ra vớ ậ ố ệt lượng toả
ra trong va chạm đó.
A. 54.6 J
B. 50.4 J
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 117
C. 48.6 J
D. 58.6 J
Câu 14: Tính công c n thiầ ế ểt đ làm cho vô lăng hình vành tròn bán kính 1m, khối lượng
500 kg đang đ ậ c góc 60 vòng/ phút.ứng yên quay v i vớ n tố
A. 9869.6 J
B. 8956.2 J
C. 9163.5 J
D. 9673.7 J
Câu 15: Một hệ gồm trụ đặc đ ng ch t khồ ấ ối lượng M = 1.54kg và một vậ ặt n g khối lượng
m = 800g được n i v ng mố ới nhau bằ ột sợi dây và vắt qua ròng rọc như hình vẽ. Bỏ qua
kh ớố ọi lượng c a dây, c a ròng rủ ủ c và c n vủa khung gắ i trụ. Tính gia t t n ng. L y g ố ủc c a vậ ặ ấ
= 9.8 m/s2
A. 1.16
𝑚𝑚
𝑠𝑠
2
B. 2.52
𝑚𝑚
𝑠𝑠
2
C. 1.78
𝑚𝑚
𝑠𝑠
2
D. 2.15
𝑚𝑚
𝑠𝑠
2
| 1/117
| | Tải xuống

Preview text:

EBOOK VẬT LÝ ĐẠI CƯƠNG 1 LỜI NÓI ĐẦU Vật lý ạ
đ i cương 1 là một trong những môn ạ đ i cương mà ầ
h u hết các sinh viên trường Đại
học Bách Khoa Hà Nội (RHUST) đều phải học qua ít nhất một lần trong đời. Đây là ộ m t học
phần tuy không kquas khó nhưng đòi hỏi sinh viên p ả
h i có sự chăm chỉ đào sâu lý thuyết
và dựa vào đó để làm các bài ậ t p.
Môn này có khá nhiều tài liệu tham khảo khác nhau từ bài giảng, bài ậ
t p, tài liệu lý thuyết,
vv được chia sẻ trên chính website tailieuhust.com của chúng mình nhưng nó lại không được liền ạ
m ch thành một khiến cho nhiều bạn không biết phải học và ử s dụng như thế
nào? Bên cạnh đó cũng có khá nhiều là tài liệu photo, viết tay nên chất lượng không được tốt lắm.
Để giúp các bạn sinh viên có thể có được một tài liệu Vật lý đại cương 1 c ấ h t lượng, dùng
cho các kỳ thi giữa kỳ và cuối ỳ
k chỉ trong 1 cuốn mà không phải cần sử dụng quá nhiều
file khác nhau nên mình và team Tài Liệu HUST đã cùng nhau biên soạn ra bộ tài liệu này.
Đây cũng là lần đầu tiên bộ tài liệu Vật lý đại cương 2 này được biên soạn nên cũng không
thể tránh được những sai sót, ẫ v n mong được các ạ
b n góp ý để hoàn thiện hơn trong
tương lai. Team biên soạn tài liệu xin gửi lời cảm ơn chân thành tới các bạn.
Ngoài ra khi sử dụng tài liệu này, bạn còn được sử dụng hệ thống học online, luyện thi trắc nghiệm tại:
Các bạn cũng có thể truy cập nhanh bằng cách quét mã QR ở bìa sách h ặ o c ở dưới đây:
Tài liệu tham khảo:
 Bộ câu hỏi trắc nghiệm thầy Trần Thiên Đức bản mới  Công thức t ắ r c nghiệm Vật lý ạ đ i cương của Vũ T ế i n Lâm
 Câu hỏi và đáp án tự luận đề thi VLĐC1 (quán photo)
Mọi ý kiến đóng góp và thắc mắc mọi người có thể liên hệ qua: Website: tailieuhust.com
Email: tailieuhustgroup@gmail.com
Fanpage: Tài liệu HUST (tailieuhust.com)
Group học tập: Bachkhoa Universe – Góc học tập và thảo luận
Group: Bachkhoa Universe – Góc học tập và thảo luận 3 TAILIEUHUST.COM NỘI DUNG TÀI LIỆU
PHẦN I. CÔNG THỨC VÀ BÀI TẬP TRẮC NGHIỆM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Chương 1. Động học chất đ ể
i m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
A. Công thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
B. Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Chương 2-3. Động lực học chất đ ể
i m – hệ chất đ ể
i m – động lực học vật rắn . . . . . . 14
A. Công thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
B. Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Chương 4. Năng lượng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
A. Công thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
B. Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Chương 5: Trường hấp dẫn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
A. Công thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
B. Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Chương 6. Dao động – sóng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
A. Công thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
B. Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Chương 7. Nguyên lý thứ nhất của nhiệt động lực học và thu ế y t ộ đ ng học phân tử
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
A. Công thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
B. Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Chương 8. Nguyên lý thứ hai ủ
c a nhiệt động lực học . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
A. Công thức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
B. Bài tập trắc nghiệm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
PHẦN II. CÂU HỎI VÀ BÀI TẬP TỰ LUẬN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
PHẦN III. MỘT SỐ ĐỀ THI GIỮA KỲ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 1. Đề thi giữa ỳ
k 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 2. Đề thi giữa ỳ
k 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113 3. Đề thi giữa ỳ
k 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
4 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
PHẦN I. CÔNG THỨC VÀ BÀI TẬP TRẮC NGHIỆM
Chương 1. Động học chất đ ể i m A. Công thức 1. Chuyển ộ đ ng thẳng ề
đ u và những đại lượng đặc trưng v = const 
- Vận tốc, gia tốc và phương trình chuyển động: a =0 → x = .vt s = .vt2. Chuyển ộ
đ ng thẳng thay đổi ều đ
v = v + at - Vận tốc và gia tốc: 0  . a  = const - Phương trình chuyển ộ đ ng: 1 2 1 2 s = v t +
at → x = x + v t + at . 0 0 0 2 2 - Hệ thức liên hệ: 2 2
v − v = 2as . 0 3. Chuyển ộ đ ng tròn 2  v 2 a = = ω r
- Gia tốc hướng tâm và gia tốc tiếp tu ế y n: nr
. với β = const là gia tốc góc . a = βrt - Gia tốc toàn phần: 2 2 4 2 a =
a + a = r ω + β . n t 2π 2π r
- Một số công thức liên hệ: v = ω ; r T = = . ω v ω = ω + βt t 0  - Phương trình chuyển ộ đ ng:  1 2 ϕ = ϕ + ω t + t β . t 0 0 2  β = const  ω = const
- Trường hợp chuyển động tròn đều:  . ϕ = ϕ +  ω t t 0 0 4. Chuyển ộ đ ng rơi tự do
v = v + gt 0 
- Vận tốc và quãng đường chuyển động: 2 2  1
→ v − v = 2gs . 0 2 s = v t + gt  0  2
Group: Bachkhoa Universe – Góc học tập và thảo luận 5 TAILIEUHUST.COM - Thời gian rơi từ
độ cao h đến khi chạm đất: 2h t = . g
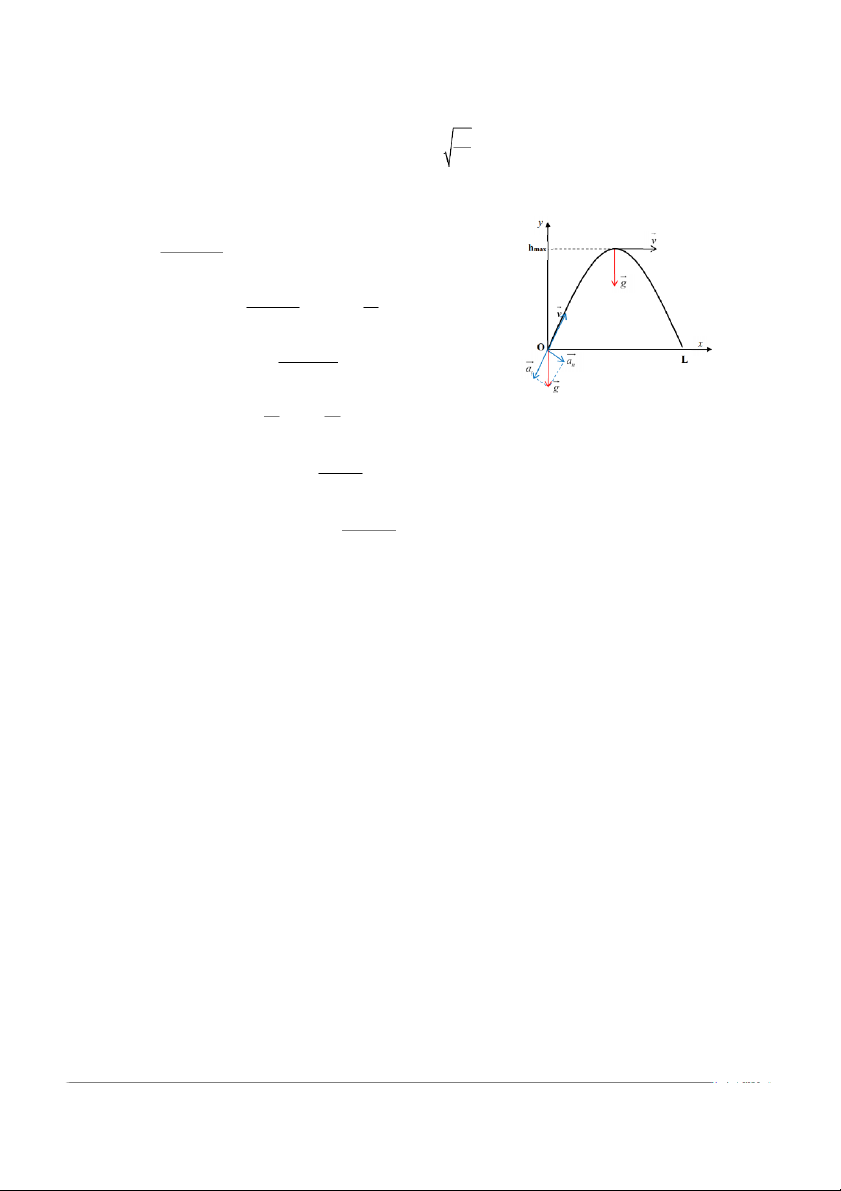
5. Chuyển động parabol (chuyển động ném xiên)
- Quỹ đạo là nhánh parabol có bề lõm quay xuống: g 2 y = − x + x tan α . 2 2 2v cos α 0 2 2 v sin 2α v - Tầm ném xa: 0 0 L = . ⇒ L = khi α 45° = . max g g 2 2 v sin 2α - Độ cao cực đại: 0 h = . max 2g 2 2 - Bán kính cong: v v a = → R = . n R an 2  = - Tại gốc: v v0 v0 → R =  a = g ⋅ α α  n cos g cos 2 2  = = α α - Tại ỉ đ nh: v v v x cos 0 v cos 0 → R =  . a = g gn
6 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
B. Bài tập trắc nghiệm
Câu 1. Một chất điểm chuyển động có phương trình: �𝑥 𝑥 = 𝑎𝑎sin 𝜔𝜔𝜔𝜔. Cho 𝑎 𝑎 = 𝑏 𝑏 = 30 cm và
𝑦 𝑦 = 𝑏𝑏cos 𝜔𝜔𝜔𝜔
𝜔 𝜔 = 10𝜋𝜋 rad/s. Gia tốc chuyển động của chất điểm có giá trị bằng: A. 296,1 m/s2. B. 301,1 m/s2. C. 281,1 m/s2. D. 331,1 m/s2. Lời giải:
Ta có phương trình chuyển động: 𝑥𝑥 = sin 𝜔𝜔𝜔𝜔
�𝑥 𝑥 = 𝑎 𝑎 sin 𝜔𝜔𝜔𝜔 𝑎 ⇒ 𝑎 �
𝑦 𝑦 = 𝑏 𝑏 cos 𝜔𝜔𝜔𝜔
𝑦𝑦 = cos 𝜔𝜔𝜔𝜔 𝑏 𝑏 2 𝑥𝑥𝑦𝑦2
→ sin2 𝜔𝜔𝜔𝜔 + cos2 𝜔𝜔𝜔𝜔 = 1 ⇒ � �
+ �� = 1 ⇒ 𝑥𝑥2 + 𝑦𝑦2 = 𝑅𝑅2 𝑣𝑣ớ𝑖𝑖 𝑅 𝑅 = 𝑎 𝑎 = 𝑏𝑏 𝑎𝑎 𝑏𝑏
Suy ra vật chuyển động theo quỹ đạo tròn. 𝑣𝑣 𝑥𝑥′
𝑅𝑅𝜔𝜔 cos 𝜔𝜔𝜔𝜔 Ta có: � 𝑥 𝑥 = =
𝑣𝑣𝑦 𝑦 = 𝑦𝑦′ = −𝑅𝑅𝜔𝜔 sin 𝜔𝜔𝜔𝜔 𝑣 𝑣 = �𝑣𝑣 2 + 2 = � 𝑥𝑥 𝑣𝑣𝑦𝑦 𝑅𝑅2 2
𝜔𝜔2 cos2 𝜔𝜔𝜔𝜔 + 𝑅𝑅 𝜔𝜔2 sin2 𝜔𝜔𝜔𝜔 = 𝑅𝑅𝜔𝜔
Gia tốc chuyển động của chất điểm: 𝑣𝑣2 𝑎𝑎ℎ = ( 𝑡𝑡 =
𝜔𝜔2𝑅 𝑅 = (10𝜋𝜋)2. 0,3 ≈ 296,1 𝑚𝑚/𝑠𝑠2) 𝑅 𝑅
Câu 2. Thả rơi tự do một vật nhỏ từ độ cao ℎ = 17
,6 m. Quãng đường mà vật rơi được trong 0,1 s cuối cùng ủ c a thời gian rơi là: A. 1,608 m. B. 1,808 m. C. 2,208 m. D. 2,408 m. Lời giải:
Ta có phương trình li độ của vật là: 𝑥𝑥(𝜔𝜔) = 1 𝑔𝑔𝜔𝜔2 2
Tổng thời gian rơi cho tới khi c ạ
h m đất là: 𝜔𝜔𝑟 𝑟 = �2ℎ= �2.17,6 (𝑠𝑠) 𝑔 𝑔 𝑔 𝑔 Quãng đường ậ
v t rơi được trong 0,1 𝑠𝑠 cuối cùng của thời gian rơi là:
𝑥𝑥(𝜔𝜔 ) − 𝑥𝑥(𝜔𝜔 2 𝑟𝑟 𝑟 𝑟 − 0.1 𝑔 ) 𝑔[ = 1 𝜔𝜔 − (𝜔𝜔 𝑚𝑚 𝑠𝑠 2 𝑟𝑟 𝑟 𝑟 − 0,1)2 2
] = 1,808 (𝑚𝑚) với 𝑔 𝑔 = 9,8 /
Câu 3. Thả rơi tự do một vật nhỏ từ
độ cao ℎ = 17,6 m. Thời gian cần thiết để vật đi hết
1 m cuối của độ cao ℎ là: (cho 𝑔 𝑔 = 9,8 m/s2 ) A. 5, 263.10−2 s. B. 5, 463.10−2 s. C. 5,863 ⋅ 10−2 s. D. 4,863 ⋅ 10−2 s.
Group: Bachkhoa Universe – Góc học tập và thảo luận 7 TAILIEUHUST.COM Lời giải:
Thời gian vật rơi được quãng đường h là: t1= 2h g
Thời gian vật rơi quãng đường (h – 1) là: t2= 2(h−1) g
Thời gian vật rơi hết 1 m cuối khi thả từ độ cao h là: ∆ t= t1-t2 = 2h - 2(h−1) g g
Thay số h=17,6(m); g=9,8(m/s2) => ∆t ≈ 2 5, 463.10− (s)
Câu 4. Một ô tô bắt đầu chạy vào đoạn đường vòng bán kính 𝑅 𝑅 = 1,3 km và dài 600 m với
vận tốc 𝑣𝑣0 = 54 km/h. Ô tô chạy hết quãng đường trong thời gian 𝜔 𝜔 = 17 s. Coi chuyển
động là nhanh dần đều, gia ố t c toàn ph n
ầ của ô tô cuối đoạn đường vòng bằng: A. 2,869 m/s2 B. 4,119 m/s2. C. 3,369 m/s2 D. 3,119 m/s2. Lời giải:
Đổi v= 54 (km/h) = 15(m/s); R= 1,3 km =1300m −
Vì đoàn tàu di chuyển nhanh dần đều ta có công thức: S= 2(s v t) v t + 1 2 a = 0 0 a t => tt 2 2 tt t 2S
Vận tốc của đoàn tàu tại cuối đường bằng: v= v + a t = −v 0 tt 0 t 2S 2 − 2 ( v ) 0
Gia tốc hướng tâm của đoàn tàu tại cuối đường là: v t a = = ht R R
Gia tốc toàn phần của đoàn tàu tại c ố u i đường là: 2  2S  2 2 ( − v )  −  0 2( s v ) t   2 2 0 t a = a + a = +     tp tt ht 2  tR    
Thay số S= 600m; v =15 m/s; t=17s; R= 1300m => a ≈3,369 m/s2 0 tp
Câu 5. Một ôtô chuyển động b ế i n đổi ề
đ u lần lượt đi qua hai điểm A và B cách nhau 𝑆 𝑆 =
25 m trong khoảng thời gian 𝜔 𝜔 = 1,6 s, vận tốc ô tô ở B là 12 m/s. Vận tốc ủ c a ôtô ở A
nhận giá trị nào sau đây: A. 18,25 m/s. B. 18,7 5 m/s. C. 19,2 5 m/s. D. 20,7 5 m . /s Lời giải:
Ô tô chuyển động biến đổi đều nên ta có: VB = VA + at => a = (VB - VA ) / t (1)
8 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 S = VA t + (at2)/2 (2 ) Thay (1) vào (2) => S = V − )t A t + (VB VA (3) 2 Từ dữ kiện ề
đ bài cho thay vào (3) ta được: VA = 19,25 m/s
Câu 6. Một bánh xe có bán kính 𝑅 𝑅 = 12 cm lúc đầu đứng yên sau đó quay quanh t ụ r c ủ c a nó với gia ố
t c góc 𝛽 𝛽 = 3,14rad/s2. Sau giây thứ nhất gia tốc toàn phần ủ c a ộ m t điểm trên vành bánh là: A. 120,17 cm/s2. B. 126,1 7 cm/s2. C. 130,1 7 cm/s2. D. 124,1 7 cm/s2. Lời giải:
Phương trình vận tốc góc w= 𝑤𝑤0+ βt= 0 + βt= βt (do ban đầu đứng yên 𝑤𝑤0 = 0)
⟹ Gia tốc pháp tuyến an = 𝑤𝑤2R =( βt)2R
Gia tốc tiếp tuyến: at = βR
Gia tốc toàn phần: a = �a 2 2 2
t + an = �(βt)4R2 + β2R2 = βR�β t4 + 1
Sau giây thứ nhất ⟹ t = 1 m cm
⟹ a = βR�β2t4 + 1 = 3,14 ∗ 0,12�3,142 + 1 = 1,2417 � � = 124,17 � � s2 s2
Câu 7. Kỷ lục đẩy tạ ở Hà Nội là 14,0
7 m. Nếu tổ chức đẩy tạ ở Xanh Pêtecbua trong điều kiện tương tự (cùng ậ
v n tốc ban đầu và góc nghiêng) thì kỉ lục ẽ s là: (cho gia tốc trọng
trường ở Hà Nội là 𝑔𝑔1 = 9,727 m/s2, ở Xanh Pêtecbua là 𝑔𝑔2 = 9,810 m/s2, bỏ qua chiều cao của người đẩy) A. 16,951 m. B. 12,95 1 m. C. 15,95 1 m. D. 13,95 1 m. Lời giải:
Chọn hệ quy chiếu như hình vẽ. Gốc ọ t a độ nằm tại ị
v trí bắt đầu ném, ch ề i u dương của
trục Oy hướng lên ngược chiều với gia tốc g, gốc thời gian cũng là thời đ ể i m bắt đầu ném vật. Áp dụng công thức t m
ầ xa đôi với vật ném tại mặt đất: L= v2 sin 2θ (1 ) g Trong cùng điều k ệ
i n ném (cùng vận tốc ban ầ
đ u và cùng góc nghiêng) nên ta có: v2 sin 2θ= const (2)
Từ (1), (2) => L1.g1= L2.g2
Vậy kỷ lục đẩy tạ ở Xanh Petecbua là: L2= L1.g1 = 14,07∗9,727 ≈ 13,951 m g2 9,81
Group: Bachkhoa Universe – Góc học tập và thảo luận 9 TAILIEUHUST.COM
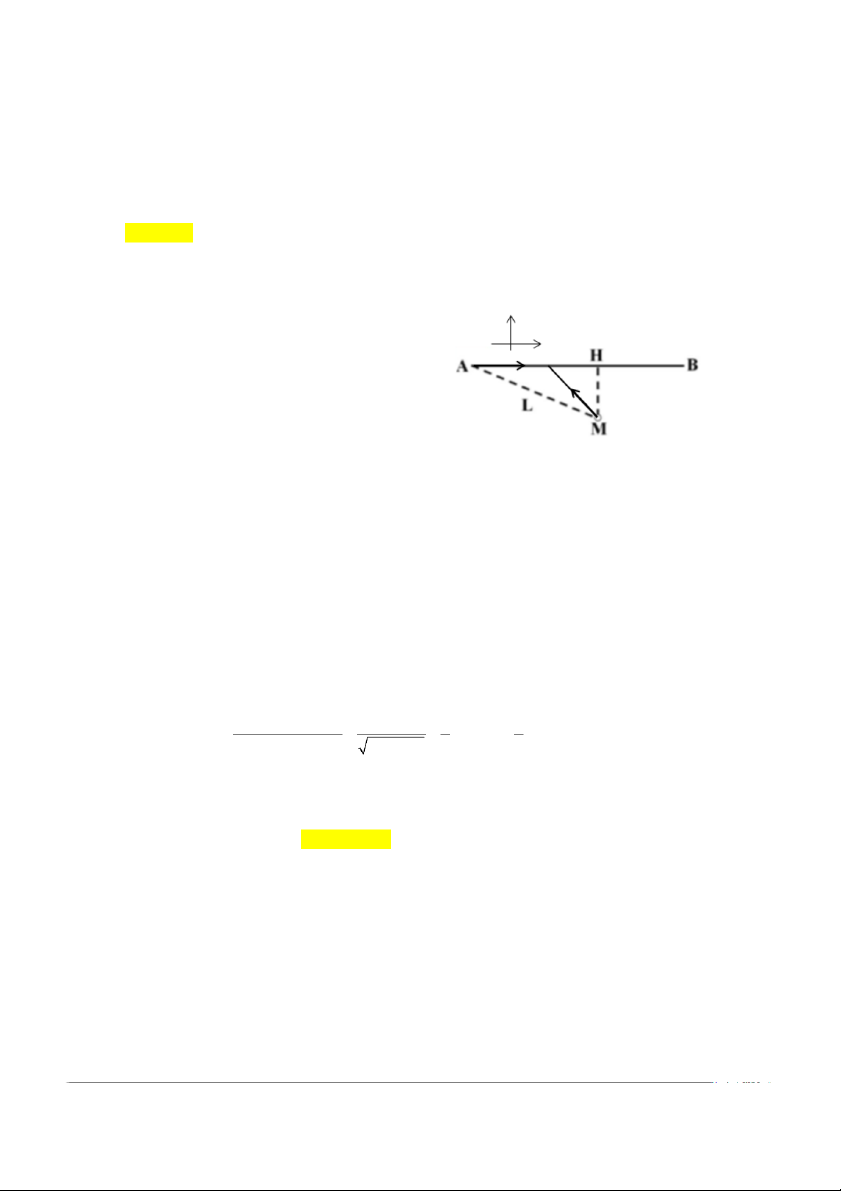
Câu 8. Một người đứng cách con đường thẳng một kh ả
o ng ℎ = 50 m để chờ ô tô. Khi thấy
đầu ô tô còn cách mình một đoạn 𝑎 𝑎 = 200 m thì người ấy bắt đầu chạy (thẳng, đều, theo
một hướng nào đó) ra đường để đón gặp ô tô. Biết vận tốc ô tô là 𝑣 𝑣 = 36 k m/h. ể Đ có thể
gặp được ô tô, người ấy p ả h i c ạ h y với ậ
v n tốc nhỏ nhất 𝑣𝑣min bằng bao nhiêu? A. 2,5 m/s. B. 3,2 m/s 5 . C. 3 m/s. D. 2,7 m/s 5 . Lời giải: Chọn hệ trục ọ t a ộ
đ Oxy như hình vẽ, gốc ọ t a
độ tại A-vị trí ban đầu của oto, gốc thời gian là
lúc người đó bắt đầu chuyển động
Gọi v (m/s) là vận tốc chạy của người đó . 1
α là góc tạo bởi 2 vecto vận tốc
+ Chiếu theo trục Ox ta có:
Tọa độ ô tô đi tại thời đ ể i m t (s) là: x = vt 1
Tọa độ của người c ạ h y tại thời đ ể
i m t(s) là: x = v tcosα + AH 2 1 Tại thời đ ể
i m 2 vật gặp nhau: x = x => ( v – v tcosα)t = AH (1) 1 2 1
+ Chiếu theo trục Oy ta có:
Tọa độ người chạy tại thời đ ể
i m t(s): y = v tsinα - h 2 1
2 vật gặp nhau: y = 0 => v tsinα = h (2) 2 1 Từ (1) và (2) hv hv h h v = ≥ = ⇒ V = V = 2,5( m / s) 1 min 2 2
AH sinα + h cosα a a AH + h
Câu 9. Một hòn đá được ném theo phương ngang từ độ cao ủ đ lớn với vận ố t c 𝑣𝑣0 =
12 m/s. Gia tốc pháp tuyến của hòn đá sau giây thứ 2 có giá trị bằng (lấy 𝑔 𝑔 = 9,8 m/s2 ) A. 4,617 m/s2. B. 5,117 m/s2. C. 5,867 m/s2. D. 4,867 m/s2. Lời giải:
10 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
- Chọn hệ trục tọa độ Oxy như hình vẽ, gốc thời
gian lúc vật bắt đầu chuyển động.
- Theo trục Ox : Vận tốc của vật là: v = v x 0 - Theo trục Oy :
Vận tốc của vật tại thời điểm t(s) là: vy = gt
Vậy độ lớn vận tốc chuyển động của vật tại t là: 2 2 2 2
v = v + v = v + (gt) x y 0 2
Gia tốc tiếp tuyến của vật tại dv g t t có độ lớn là: at = = dt v v
Gia tốc pháp tuyến của vật tại t có giá tr ịlà: 2 2 0 a = g − a = g n t v
⇒ Gia tốc pháp tuyến của vật tại giây thứ 2 là: a (2) = 5,117 ( 2 m / s n )
Câu 10. Một bánh xe bắt đầu quay quanh một trục ố
c định đi qua tâm vành bánh và
vuông góc với mặt phẳng bánh xe, có góc quay xác đ n
ị h bẳng biểu thức: 𝜑 𝜑 = 𝑎𝑎𝜔𝜔2; trong
đó 𝑎 𝑎 = 0,125rad/s2; 𝜔𝜔 là thời gian. Điểm A trên vành bánh xe sau 2 s có vận tốc dài 𝑣 𝑣 =
2 m/s. Gia tốc toàn phần của điểm A khi đó có giá trị bằng: A. 2√2 m/s2. B. 2√5 m/s2. C. √5 m/s2. D. √2 m/s2. Lời giải: φ
Tốc độ góc của bánh xe là: d w = = 2at dt
Bán kính của bánh xe là: v v r = = w 2 t a dw
Gia tốc góc của bánh xe là: β = = 2a dt
Gia tốc tiếp tuyến của điểm A là: v v at = βr = β = 2at t
Gia tốc pháp tuyến của điềm A là: 2 a = w r = 2atv n 2
Gia tốc toàn phần của điềm  v  A là: 2 a =
+ (2atv) = 2(m / s) tp    t
Group: Bachkhoa Universe – Góc học tập và thảo luận 11 TAILIEUHUST.COM
Câu 11. Chất điểm ắ
b t đầu chuyển động trên đường tròn bán kính R = 2( m) . Vận tốc của
chất điểm phụ thuộc vào quãng đường đi được S theo công thức v = a s với 2
a = 2(m / s) .
Góc giữa vector vận tốc v và gia tốc toàn p ầ
h n γ sau 3 s được xác định bởi A. tg α = 8,6 B. tg α = 9 C. tg α = 9, 2 C. tg α = 9,6 Lời giải: - Ta có: ds ds v = a s ⇒ = a s ⇔ adt = ⇔ at = 2 s(1) ∫ ∫ dt s 2 Thay  at t = 3( ) s ⇒ s = = 9( ) m    2    - Gia tốc hướng tâm: m
v = a s = 2 9 = 6   ⇒  s  2 2 v 6  m a = = =18 n  2  R 2  s  2 2 2 2 2 Từ (1) a t ds 2a t dv 2a 2.2  m  ⇒ s = ⇒ v = = ⇒ a, = = = 2  2 4 dt 4 dt 4 4  s  - Ta có góc giữa a
v và γ là góc giữa a và γ 18 ⇒ tan n α = = = 9 a 2
Câu 12. Từ đỉnh đồi cao, một quả pháo được bắn chếch lên phía trên một góc a 30° = so
với phương nằm ngang với vận tốc đầu nòng là v = 400( m / s). Sau khi bắn một khoảng 0
thời gian t = 5(s) , góc ϕ giữa hướng của vận tốc quả pháo và hướng của gia tốc toàn
phần thỏa măn giá trị nào dưới đây ( bỏ qua sức cản không khí. Gia tốc t ọ r ng trường bẳng g = ( 2 9,8 m / s ) A. tg β = −1,894 B. tg β = −2,894 C. tg β = −2,094 D. tgβ = −2, 294 Lời giải: Ta có phương trình v n ậ tốc của vật là  °  mv = v cos  α = 400cos30 = 200 3 x 0     s
v = v sin α − gt = 200 −9,8t y 0 
Tại t = 5 ta có v = 151(m / s) > 0 y Gọi gia ố
t c toàn phần là g → Góc hợp bởi (v ; g ) là γ như hình vẽ:
12 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 v Có y 151 tan ϕ = = v 200 3 x − ° 1 200 3
Mà γ = ϕ + 90 ⇒ tan γ = − cotg ϕ = = − = −2, 29. tan ϕ 151
Group: Bachkhoa Universe – Góc học tập và thảo luận 13 TAILIEUHUST.COM
Chương 2-3. Động lực học chất đ ể i m ệ – h chất đ ể
i m – động lực học vật rắn A. Công thức Chương 2:
1. Các định luật Newton - Định l ậ u t Newton t ứ
h nhất: Nếu một vật không ch u
ị tác dụng của lực nào hoặc chịu tác
dụng của các lực có hợp lực bằng không thì nó giữ nguyên trang thái đứng yên hoặc chuyển ộ đ ng thẳng ề đ u. F = 0 ⇒ a = 0. ∑ - Định l ậ u t Newton t ứ
h hai: Gia tốc của ộ m t vật cùng hướng ớ
v i lực tác dụng lên vật. ộ Đ
lớn của gia tốc tỉ lệ thuận với ộ
đ lớn của lực và tỉ lệ nghịch với khối lượng của vật. ∑ F
∑F = m ⋅a ⇒a = . m - Định l ậ u t Newton t ứ
h ba: Trong mọi trường hợp, khi vật A tác dụng lên vật B một lực, thì
vật B cũng tác dụng lại A một lực. Hai lực này có cùng giá t ịr, cùng độ lớn nhưng ngược chiều nhau. F = −F . AB BA
2. Một số loại lực cơ học
- Lực ma sát: F = µ N.với µ là hệ số ma sát, N là áp lực ms 2 - mv
Lực hướng tâm: F = . ht r 2 - mv
Lực quán tính li tâm trong chuyển ộ
đ ng tròn đều: F = F = . lt ht r
- Lực căng (xét vật m với m ): T = m g − m a = m (g − a) . 1 2 2 1 2
3. Động lượng và xung lượng -
Độ biến thiên động lượng: t 2 k ∆ = k − k = Fdt ∫ . 2 1 t1 với t2 Fdt ∫
là xung lượng của lực F trong khoảng thời gian từ t → t . 1 2 t1 - Xung lực: p ∆ = F. t ∆ .
4. Các loại va chạm Động năng & Động lượng Va chạm đàn hồi 2 2 2 2 m v m v m v m v ′ ′ + = + 1 1 2 2 1 1 2 2 + = + p p p p 1 2 1 2 2 2 2 2
14 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 2 2 2 2
→ m v + m v = m v + m v i 1 1 2 2 1 1 2 2
→ m v + m v = m v + m v 1 1 2 2 1 1 2 2 Va chạm không đàn hồi Không bảo toàn
m v + m v = m + m v 1 1 2 2 ( 1 2 ) m v + m v 1 1 2 2 → v = m + m 1 2 5. Moment động l ợ ư ng
- Liên hệ giữa moment động lượng và động lượng: L = r × p . - l
Độ ớn moment động lượng: L = rm .
v sinθ = mr v. hay = ω . ⊥ L I. Chương 3:
1. Định luật bảo toàn ộ đ ng l ợ ư ng
- Động lượng: p = mv .
- Bảo toàn động lượng: p p′ = ∑ ∑ .
2. Bảo toàn moment động l ợ ư ng
- Phương trình cơ bản của chuyển động quay: M = I.β .
- Bảo toàn moment động lượng: L L L′ L′ I ω I ω I ω′ I ω′ + = + → + = + . 1 2 1 2 1 1 2 2 1 1 2 2 - Định lý ề v moment động lượng: dL M = ∑ . i dt ω = ω + βt 0 
- Các phương trình động lực học:  1 2 ϕ
 =ϕ +ωt + β t . 0 2  2 2 ω − ω = 2 βϕ  0
3. Moment quán tính của các loại vật rắn
- Moment quán tính của vật rắn ấ b t kỳ i đố với trục quay: 2 I = ∑ m ∆ r = r d . m ∫ 1 i object i
- Moment quán tính của chất điểm có k ố
h i lượng m đối với trục quay : 2 I = mr .
- Moment quán tính của thanh dài chiều dài l, đối với trục vuông góc và đi qua tâm của 1 thanh: 2 I = ml . 12
Group: Bachkhoa Universe – Góc học tập và thảo luận 15 TAILIEUHUST.COM
- Moment quán tính của đĩa tròn hoặc trụ đặc đồng chất có khối lượng m, bán kính R: 1 2 I = mR . 2
- Moment quán tính của vành hoặc trụ rỗng đồng chất k ố h i lượng m, bán kính R: 2 I = mR .
- Moment quán tính của khối cầu đặc ồ đ ng chất: 2 2 I = mR . 5 1
- Moment quán tính của thanh dài l, trục quay đi qua 1 ầ đ u thanh: 2 I = ml . 3
4. Động lực học vật ắ r n quay 2
- Công thức liên hệ vận tốc và gia tốc : v 2
v = ωr → a = β r; a = = ω r t n r 5. Chuyển ộ
đ ng lăn của vật ắn r
- Trường hợp lăn không trượt: v = ωr → a = βr - Định lý Steine -
r Huygens: Mômen quán tính của ộ m t vật rắn ố đ i với ộ m t trục nào đó
bằng mômen quán tính của vật rắn đối với trục song song đi qua khối tâm cộng với tích số
của khối lương vật rắn và bình phương khoảng cách giña hai trục.
𝐼𝐼𝑂 𝑂 = 𝐼𝐼𝐺 𝐺 + 𝑚𝑚𝑟𝑟2. Trong đó:
Io _ mô men quán tính của vật đối với t ụ r c quay đi điểm O 𝐼𝐼 ố
𝐺 𝐺 − mô men quán tính của vật đối với trục quay đi qua kh i tâm G 𝑚𝑚−khối lượng ủ c a vật.
- Động năng của chuyển động lăn:
• Trường hợp lăn: 𝑊 𝑊 = 𝑊𝑊 + 𝐼𝐼𝐺𝐺𝜔𝜔2 .
𝑡𝑡𝑡𝑡 + 𝑊𝑊𝑞 𝑞 = 𝑚𝑚𝑣𝑣2 2 2
• Trường hợp quay: 𝑊 𝑊 = 𝑊𝑊
= 𝐼𝐼𝐺𝐺𝜔𝜔2+ 𝑚𝑚𝑟𝑟2𝜔𝜔2 .
𝑞 𝑞 = 𝐼𝐼𝑂𝑂𝜔𝜔2
= �𝐼𝐼𝐺𝐺+𝑚𝑚𝑟𝑟2�𝜔𝜔2 2 2 2 2
6. Công thức Huygens-Steiner 𝐼𝐼 2 hay
𝑂 𝑂 = 𝐼𝐼𝐺 𝐺 + 𝑚𝑚𝑟𝑟
𝐼𝐼𝑧 𝑧 = 𝐼𝐼𝐶𝐶𝐶𝐶 + 𝑀𝑀𝐷𝐷2.
16 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
B. Bài tập trắc nghiệm
Câu 1. Ở thời điểm ban đầu một chất điểm có k ố h i lượng 𝑚 𝑚 = 1 k g có vận tốc 𝑣𝑣0 =
20 m/s. Chất điểm chịu lực cản 𝐹𝐹
là vận tốc chất điểm). Sau
𝑐 𝑐 = −𝑟𝑟𝑣𝑣 (biết 𝑟 𝑟 = ln 2, 𝑣𝑣 2,2 s
vận tốc của chất điểm là: A. 4,353 m/s. B. 3,95 3 m/s. C. 5,55 3 m/s. D. 3,55 3 m/s. Lời giải:
Áp dụng định luật II Newton ta có: 𝑑𝑑𝑣𝑣
F = ma ⇒ 𝐹𝐹 −𝑟𝑟𝑣𝑣 𝑚𝑚𝑎𝑎 = 𝑚 𝑚 c 𝑐 𝑐 = = 𝑑𝑑𝑡𝑡 𝑟𝑟 𝑑𝑑𝑣𝑣 𝑡𝑡 𝑟𝑟 𝑣 𝑑𝑑 𝑣 𝑣𝑣 𝑟𝑟𝜔𝜔 𝑣𝑣 ⇒ − 𝑑𝑑𝜔𝜔 = ⇒ � − 𝑑𝑑𝜔𝜔 � = ⇒ − = ln 𝑣𝑣 𝑣 |𝑣 = ln 𝑚 𝑚 𝑣 𝑣 𝑚 𝑚 𝑣𝑣0 0 𝑣𝑣 𝑚 𝑚 𝑣𝑣 𝑣𝑣0 0 ⇒ 𝑣 𝑣 = 𝑣𝑣 × ,2 0 × 𝑒𝑒− 𝑟𝑟
𝑚𝑚𝑡 𝑡 = 20 × 𝑒𝑒− ln 2 2 ≈ 4,353
Câu 2. Một viên bi nh ỏ 𝑚 𝑚 = 1
4 g rơi theo phương thẳng đứng không vận tốc ban ầ đ u
trong không khí, lực cản ủ c a không khí 𝐹𝐹 � �
(tỷ ệ ngược chiều với vận t c ố ), là hệ ố 𝑐𝑐 = −𝑟𝑟𝑣𝑣 l 𝑟𝑟 s
cản. Vận tốc cực đại mà viên bi đạt được bằng 𝑣𝑣max = 60 m/s. Cho 𝑔 𝑔 = 10 m/s2. Hệ số cản có giá trị: A. 2,333. 10−3N /m s . B. 2, 363.10−3Ns/m. C. 2,353. 10−3N /m s . D. 2,343. 10−3N /m s . Lời giải:
Khi thả vật rơi tự do có lực cản tỉ lệ với vận tốc thì khi vật đạt vận tốc đủ lớn, đến thời điểm lực cản có l
độ ớn bằng độ lớn của trọng ự
l c tác dụng lên vật thì khi đó hợp lực tác dụng lên
vật bằng 0 và vật rơi với vận tốc không đổi 𝑣𝑣 𝑚𝑚𝑚𝑚𝑥𝑥 Do đó, ta có: �𝐹𝐹 � 𝑐𝑐 = 𝑟𝑟𝑣𝑣 max
max = 𝑃 𝑃 = 𝑚𝑚𝑔𝑔 𝑚𝑚𝑔𝑔0,014.10 ⇒ 𝑟𝑟 = =
= 2,333.10−3 (𝑁𝑁𝑠𝑠/𝑚𝑚) 𝑣𝑣max 60
Câu 3. Một tàu điện sau khi suất phát chuyển động trên đường nằm ngang với gia tốc 𝑎 𝑎 =
0,7 m/s2. 11 giây sau khi bắt đầu chuyển động người ta tắt động cơ và tàu chuyển động
cho đến khi dừng hẳn. ệ
H số ma sát trên quãng đường 𝑘 𝑘 = 0,0 .
1 Cho 𝑔 𝑔 = 10 m/s2. Thời
gian chuyển động của toàn bộ tàu là A. 92,8 s. B. 84,8 s. C. 88 s. D. 86,4 s. Lời giải:
Giai đoạn 1, sau 11s vật đạt vận tốc tối đa là:
𝑣𝑣max = 𝑎𝑎𝜔𝜔 = 0,7.11 = 7,7 (𝑚𝑚/𝑠𝑠)
Group: Bachkhoa Universe – Góc học tập và thảo luận 17
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 Tại điểm rơi, 𝑅𝑅−Δℎ 𝑣𝑣2
𝑁𝑁𝑠 𝑠 = 0, do đó: 𝑚𝑚𝑔𝑔
= 𝑚 𝑚⇒ 𝑣𝑣2 = 𝑔𝑔(𝑅𝑅 − Δℎ) 𝑅 𝑅 𝑅 𝑅
Lại có, áp dụng định luật bảo toàn cơ năng ta được:
𝑚𝑚𝑔𝑔𝑅𝑅 = 𝑚𝑚𝑔𝑔(𝑅𝑅 − Δℎ) 𝑚𝑚 + 1
𝑣𝑣2 ⇒ 𝑣𝑣2 = 2𝑔𝑔Δℎ ⇒ 𝑔𝑔(𝑅𝑅 − Δℎ) = 𝑔𝑔 2 Δℎ 2 𝑅𝑅 2 ⇒ Δℎ = = = 0,667(𝑚𝑚) 3 3
Câu 6. Một đoàn tàu khối lượng 30 tấn chuyển động trên đường ray nằm ngang với vận tốc không ổ
đ i bằng 12 km/h. Công suất đầu máy là 200 kW. Gia tốc trọng trường 𝑔 𝑔 =
9,8 m/s2. Hệ số ma sát bằng: A. 23, 4.10−2. B. 20, 41.10−2. C. 22, 1 4. 0−2. D. 21, 41.10−2. Lời giải: 10 Đổi v =12( km / h) = ( m / s) 3 3 Ta có: P 200.10
P = F.v ⇒ F = = = 600(N) v 10 3 Mà Fms 6000 − 2
F = F = µmg = 6000(N ) ⇒ µ = = = 20, 41.10 ms 3 mg 30⋅10 ⋅ 9,8
Câu 7. Một chất điểm bắt đầu trượt từ đỉnh mặt phẳng
nghiêng góc 𝛼𝛼 so với phương nằm ngang (xem hình vẽ). ệ H
số ma sát giữa vật và mặt phẳng nghiêng là 𝑘𝑘; khối lượng
của vật là 𝑚𝑚 (lấy 𝑔 𝑔 = 9,8 1 m/s2 ). Cho 𝑚 𝑚 = 2,5 kg, 𝑘 𝑘 =
0,2, ℎ = 8 m, 𝛼 𝛼 = 30∘. Mômen tổng hợp các lực tác dụng lên
chất điểm đối với O là: A. 62,107Nm. B. 45,652N . m C. 52,234Nm. D. 55,527N . m Lời giải: Chọn hệ trục tọa ộ
đ Oxy như hình vẽ, chiều dương
cùng chiều chuyển động của vật Vật c ị h u tác dụng của
các lực: trọng lực P , phản lực N và lực ma sát f ms
Áp dụng định luật II Newton, ta có: P + N + f = ma (1) ms
Chiếu (1) lên trục Ox: N− P = 0 ⇔ N = Pcos α = mg cos α n
Group: Bachkhoa Universe – Góc học tập và thảo luận 19 TAILIEUHUST.COM P sin α − f
Chiếu (1) lên trục Oy: P − f = ma⇔ Psin mx
α − f = ma⇒ a= t ms ms m
Mà f = kN = kmgcosα ⇒ F = m (
g sin α − kcos α) ms
Mômen tổng hợp các vật tác dụng lên chất điểm đối với O chính là công của lực F tác dụng lên đ ể i m O A F .h.cosα mg (sinα
k cosα ).h.cos 30° = = − = 55,525(N ) F
Câu 8. Một ô tô khối lượng 𝑚 𝑚 = 550 kg chuyển động thẳng ề đ u xuống dốc trên ộ m t mặt
phẳng nghiêng, góc nghiêng 𝛼𝛼 so với mặt đất nằm ngang có sin 𝛼 𝛼 = 0,0872; cos 𝛼 𝛼 =
0,9962. Lực kéo ô tô bằng 𝐹𝐹 ữ ặt
𝑘 𝑘 = 550 N, cho 𝑔 𝑔 = 10 m/s2. Hệ số ma sát gi a ô tô và m đường là: A. 0,158 B. 0,188 C. 0,208 D. 0,198 Lời giải: Chọn t ụ
r c Oxy như hình vẽ. Chiều dương cùng
chiều chuyển động với ô tô
Ô tô chịu tác dụng của các lực: lực kéo F của
động cơ ô tô, trọng lực P , phản lực tiếp tuyến N
của mặt đường và lực ma sát của mặt đường f ms
Áp dụng định luật II Newton, ta có
F + P + N + f
= 0 (vì ô tô chuyền động thẳng ề đ u) ms
Chiếu phương trình này nên phương chuyển động ủ
c a ô tô, ta được: F − f +P sinα = 0 k ms F + mg sinα
⇒ F = f − Psinα = kN − Psinα = kmg cosα − mg sin k α ⇒ k = = 0,188 k ms mg cosα
Câu 9. Một quả cầu có khối lượng 𝑚 𝑚 = 10 0 g được gắn vào ầ
đ u sợi dây có khối lượng không đáng kể. Một ầ
đ u dây gắn vào điểm O cố định. Sợi dây có chiều dài 𝑙 𝑙 = 50 cm. Cho
vật chuyển động tròn quanh O trong mặt phẳng đứng. ạ
T i vị trí cao nhất B quả cầu có ậ v n tốc 𝑣𝑣 ấ ứ ủ ợ ạ ị trí thấ ấ ị:
𝑛 𝑛 = 3,2 m/s. L y 𝑔 𝑔 = 9,81 m/s2. S c căng c a s i dây t i v p nh t A có giá tr A. 9,953 N. B. 7,953 N. C. 6,953 N. D. 5,953 N. Lời giải: Chọn ố
m c thế năng tại vị trí A
Áp dụng định luật bảo toàn Năng lượng tại hai vị trí A và B ta có:
20 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 1 1 2 2 2 2 W = W ⇔ mv + 0 =
mv + mgh ⇔ v = v + 2gh 2 ⇒ v = 29,86 A B 2 A 2 B B A B B A
Áp dụng định luật II Niu-Tơn tại điểm A theo phương thẳng đ n ứ g ta có: 2 v A
T = P + F = mg + ma = mg + m = 6,953(N) ht ht l
Câu 10. Một hòn bi khối lượng 𝑚𝑚1 đến va chạm hoàn toàn đàn hồi và xuyên tâm với hòn
bi 𝑚𝑚2 ban đầu đứng yên. Sau va chạm chúng chuyển ộ
đ ng ngược chiều nhau với cùng độ
lớn vận tốc. Tỉ số khối l ợ
ư ng của chúng 𝑚𝑚1 là : 𝑚𝑚2 A. 1/6. B. 1. C. 1/2. D. 1/3. Lời giải:
Chọn chiều dương là ch ề i u đi chuyển ban ầ đ u của m 1
Sau va chạm vật m chuyển ộ
đ ng ngược chiều dương và vật m chuyển động theo chiều 1 2 dương với cùng vận t c ố v
Bảo toàn động lượng ta có: m v = m v − m v ⇒ m (v + v) = m v (1 ) 1 1 2 1 1 1 2
Bảo toàn động năng ta có 1 1 1 2 2 2 2 2 2 m v = m v +
m v ⇔ m (v − v ) = m v (2) 1 1 1 2 1 1 2 2 2 2 Lấy (2 /
) (1) ta có : v − v = v ⇔ v = 2v (3) 1 1 Thay (3) vào (1) ta có: m 1 1
m .3v = m .v ⇒ = 1 2 2 m 3
Câu 11. Một phi công thực hiện vòng tròn nhào lộn trong mặt phẳng đứng. Vận ố t c ủ c a
máy bay không đổi 𝑣 𝑣 = 900 km/h. Giả sử rằng áp lực lớn nhất của phi công lên ghế bằng
5 lần trọng lực của người. ấ
L y 𝑔 𝑔 = 10 m/s2. Bán kính quỹ đạo vòng nhào lộn có giá trị bằng A. 1562,5 m. B. 1584,1 m. C. 1594,4 m. D. 1573,3 m. Lời giải:
Các lực tác dụng lên máy bay và phi công: Tr n ọ g lực P , phản lực Q
Áp dụng định luật II Niu-tơn ta có: P + Q = ma ⇒ Q = ma − P ht ht
Áp lực lên ghế lớn nhất khi P và a ngược hướng ⇒ Áp lực max tại điểm thấp nhất : ht
P + Q = ma ⇒ Q = ma − P ht ht
Group: Bachkhoa Universe – Góc học tập và thảo luận 21 TAILIEUHUST.COM 2 2 v v
⇒ Q = ma + P ⇔ 5mg = m + mg ⇒ R = ht R 4g Thay số: 2
v = 900km / h = 250m / s; g = 10m / s ⇒ R = 1562,5m
Câu 12. Một thanh chiều dài 𝑙 𝑙 = 0,9 m, khối lượng 𝑀 𝑀 = 6 k
g có thể quay tự do xung quanh
một trục nằm ngang đi qua một đầu của thanh. Một viên đạn khối lượng 𝑚 𝑚 = 0,01 kg bay
theo hương nằm ngang với ậ
v n tốc 𝑣 𝑣 = 300 m/s tới xuyên vào dầu kia của thanh và mắc
vào thanh. Vận tốc góc của thanh ngay sau khi viên đạn ậ đ p vào đầu thanh là: A. 2,429ra /s d . B. 1,915ra /s d . C. 1,144rad/s. D. 1,658rad/s. Lời giải:
Mô-men động lượng trước khi va chạm là: L = v p = pl = mvl t .
Sau va chạm viên đạn và thanh sẽ chuyển động với cùng gia tốc góc ω
Mo-men động lượng sau va chạm là: 2 Ml 2 L ( ω I I ) ω  = + =  +ml s th d 3  
Áp dụng định luật bảo toàn Động lượng: 2  Mlmvl 2
L = L ⇔ mvl = ω + ml ⇒ ω = t s   2 3  Ml    2 ω  + ml  3  
Thay số ta được ω ≈ 1, 658 (rad/s)
Câu 13. Một vật n ỏ
h có khối lượng 𝑚𝑚 buộc vào đầu sợi dây mảnh chiều dài 𝑙 𝑙 = 1,5 m, dầu
kia giữ cố định. Cho vật quay trong mặt p ẳ
h ng nằm ngang với vận tốc góc không đổi sao cho sợi dây hợp ớ v i phương th n
ẳ g đứng một góc 𝛼 𝛼 = 30∘. Cho 𝑔 𝑔 = 10 m/s2, ỏ b qua lực
cản không khí. Tốc độ góc có giá trị: A. 2,575ra /s d . B. 2,775ra /s d . C. 3,075rad/s. D. 2,675rad/s. Lời giải: Chọn ố
m c thế năng tại vị trí căn bằng, chiều dương hướng xuống
Trong quá trình dao động, ậ v t ch u
ị tác dụng của các lực: trọng lực (P), lực căng dây (T)
và lực hướng tâm F Áp dụng định luật II Newton, ta có: P + T + F = 0 ht ht Chiếu (1) lên ch ề i u dương Ox F T sin 30° 0 F T sin 30° − = ⇒ = ht ht
22 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 ° mg
Chiếu (1) lên trục Oy : P − T cosα = 0 ⇒ P = T cosα ⇔ mg = T cos30 ⇔ T = cos 30° ° ° 3
⇒ F = T sin 30 = mg tan 30 = mg . Mà 2 2 F ma mω R mω . l sin 30 ° = = = ht 3 ht ht ° mg 1 g 2g 2 2 mω . l sin 30 = ⇔ ω .l = ⇒ ω = = 2,775(rad / s) 3 2 3 3l
Câu 14. Một ô tô có khối lượng 𝑚 𝑚 = 2,1 tấn chuyển động trên đoạn đường nằm ngang với
vận tốc không đổi 𝑣𝑣0 = 54 km/h. Công s ấ
u t của ô tô bằng 9,8 kW. Lấy 𝑔 𝑔 = 9,8 m/s2. Hệ số
ma sát giữa bánh xe và mặt đường có giá trị bằng A. 0, 305.10−1. B. 0, 281.10−1. C. 0, 317.10−1. D. 0, 341.10−1. Lời giải:
- Chọn hệ quy chiếu Oxy chiều dương của Ox cùng chiều
với chiều của vận tốc ô tô; trục Oy h ớ ư ng lên
- Gọi K là hệ số ma sát của mặt đường ta có 𝐹𝐹𝑘𝑘. 𝑉 𝑉 = 𝑃𝑃𝑘 𝑘 = 9800 1960
Do 𝐹𝐹𝑘𝑘 là lực kéo của ầ
đ u máy nên 𝐹𝐹𝑘 𝑘 = 98 0 = (N) 15 3 Theo định l ậ u t 2 Newton: 𝐹𝐹 � � � � � 𝑘𝑘
+ 𝐹𝐹𝑚𝑚𝑠+𝑠𝑃𝑃 �+ 𝑁𝑁 �= 𝑚𝑚𝑎𝑎
Mặt khác ô tô chuyển động với vận tốc không đổi nên 𝑎𝑎 = 0 � .
Chiếu theo chiều dương của Oy ta được: 𝐹𝐹𝑘 𝑘 − 𝐹𝐹𝑚𝑚𝑠𝑠 = 0 1960 𝐹𝐹 𝐹𝐹 3 𝑘𝑘 ≈ 0,317
𝑚𝑚𝑠𝑠 = 𝐹𝐹𝑘 𝑘 ⟺ 𝐾𝐾𝑚𝑚𝑔𝑔 = 𝐹𝐹𝑘 𝑘 ⟹ 𝐾𝐾 = = ∗ 10−1 𝑚𝑚𝑔𝑔2100 ∗ 9,8
Câu 15. Một tàu điện khi xuất phát chuyển ộ
đ ng trên đường nằm ngang với gia ố t c 𝑎 𝑎 =
0,9 m/s2, 13 s sau khi bắt đầu chuyển động người ta tắt động cơ và tàu chuyển động cho
đến khi dừng lại hẳn. ệ
H số ma sát trên đường 𝑘 𝑘 = 0,01. Cho 𝑔 𝑔 = 10 m/s2. Thời gian
chuyển động toàn bộ của tàu là: A. 130 s. B. 126 ,8 s. C. 125 ,2 s. D. 128 ,4 s. Lời g ải i
- Chọn hệ quy chiếu như hình vẽ, gốc tọa độ trùng với ậ
v t, gốc thời gian tại thời điểm vật
bắt đầu xuất phát to= 0, vo=0 - Con tàu chuyển ộ đ ng trong hai giai đoạn:
Group: Bachkhoa Universe – Góc học tập và thảo luận 23 TAILIEUHUST.COM
+ Giai đoạn 1: tàu chuyển ộ
đ ng nhanh dần đều với
gia tốc a trong thời gian t1
+ Giai đoạn 2: tàu chuyển ộ
đ ng chậm dần đều đến
khi dừng hẳn với gia tốc a′ g ây ra bởi lực ma sát
cùng phương và ngược ch ề i u ậ v n tốc Phương trình vận ố t c ủ
c a tàu giai đoạn 1 là: v = v0 + a(𝜔𝜔1 − to) Vận tốc ủ
c a tàu khi hết giai đoạn 1 là: v = v0 + at1 = 0 + 0,9.13 = 11,7 m/ s
Sau khi tắt động cơ, định luật II Newton cho tàu: P�+ N�+ F� � �� ms = ma�
Chiếu theo chiều Oy: N − P = 0 ⇔ N = P = mg
Chiếu theo chiều Ox: −Fms = ma′ ⇔ −Kmg = ma′ => a′ = −Kg = 0,01.10 = −0,1 (m/s2)
Sau khi tắt động cơ, phương trình vận tốc của tàu giai đoạn 2 là:
v′ = v − a′ ∗ t2 ⇔ 0 = 11,7 + (−0,1)t2 ⇔ t2 = 117(s)
Thời gian chuyển động toàn bộ tàu: t = t1 + t2 = 117 + 13 = 130(s)
Câu 16. Một người kéo xe ằ b ng ộ
m t hợp lực với phương ngang một góc 𝛼 𝛼 = 30∘. Xe có
khối lượng 𝑚 𝑚 = 240 kg và chuyển động với vận tốc không ổ đ i. ệ
H số ma sát giữa bánh xe
và mặt đường 𝑘 𝑘 = 0,26. Lấy 𝑔 𝑔 = 10 m/s2. Lực kéo có giá trị bằng: A. 622,59 N. B. 626,4 9 N. C. 614,7 9 N. D. 618,6 9 N. Lời giải:
Chọn hệ quy chiếu Oxy như hình vẽ. Oy hướng lên Ox cùng
hướng với hướng chuyển động.
Vì vật chịu hợp lực nhưng lại chuyển động đều nên 𝑎𝑎 = � 0
Áp dụng định luật II Newton: 𝐹𝐹 + � N � +P� + F���� ms = 0 �
Chiếu theo chiều Oy ta có:
N – P + F sin α = 0 ⇔ N = mg – F sin α
Chiếu theo chiều Ox ta có: F cos α – Fms = 0 ⇔ F cos α – KN = 0
⇔ F cos α – K(mg – F sin α ) = 0 ⇔ F(cos α + K sin α) = Kmg Kmg ⇒ F = = 626,49(N) K sin α+cos α
Câu 17. Một đĩa tròn khối lượng 𝑀 𝑀 = 155 kg đỡ một người có khối l ợ ư ng 𝑚 𝑚 = 51 kg. Lúc
đầu người đứng ở mép và đĩa quay với ậ
v n tốc góc 𝜔𝜔1 = 10 vòng/phút quanh trục đi qua
24 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
tâm đĩa. Vận tốc góc của đĩa khi người đi vào đúng tâm của đĩa là (coi người như 1 chất điểm) A. 2,006ra /s d . B. 2,276ra /s d . C. 1,736rad/s. D. 0,926rad/s. Lời giải:
Coi người như một chất điểm, đặt bán kính đĩa là r ta có 𝑤𝑤1 = 10 𝑣𝑣 = 20𝜋𝜋 = 𝜋𝜋 (rad/s) 𝑃 𝑃 60 3
Vì là hệ kín nên momen động lượng lức trước và lúc sau ủ
c a hệ được bảo toàn.
Khi người đứng ở mép đĩa: 𝐿𝐿1 = 𝐼𝐼1𝑤𝑤1 = �𝐼𝐼 �
𝑛𝑛𝑔𝑔ườ𝑖𝑖 + 𝐼𝐼đĩ𝑚𝑚 = �𝑚𝑚 𝑚𝑚 𝑅𝑅2 𝑅𝑅2� + 1 𝑤𝑤 2 1
Giai đoạn sau: để ý là khi người đi vào tâm đĩa thì coi như khoảng cách từ người tới tâm
đĩa là 0. Điều này kéo theo mômen quán tính của người với tâm đĩa coi như bằng 0. 1 𝐿𝐿 2
2 = 𝐼𝐼2𝑤𝑤2 = 𝐼𝐼đĩ𝑚𝑚𝑤𝑤2 = 𝑀𝑀𝑅𝑅 𝑤𝑤 2 2
Áp dụng định luật bảo toàn động lượng ta có:
𝐿𝐿1 = 𝐿𝐿2 ⟹ �𝑚𝑚 + 1
𝑀𝑀� 𝑤𝑤 𝑀𝑀𝑤𝑤 𝑤𝑤
𝑟𝑟𝑎𝑎𝑑𝑑 𝑠𝑠 2 1 = 1 2
2 ⟺ 𝑤𝑤2= (2𝑚𝑚+𝐶𝐶) 𝐶 𝐶 1 = 1,736 /
Câu 18. Một người đẩy xe ộ
m t lực hướng xuống theo phương hợp với phương ngang một
góc 𝛼 𝛼 = 30∘. Xe có khối lượng 𝑚 𝑚 = 230 k
g và chuyển động với vận tốc không đổi. ệ H số
ma sát giữa bánh xe và ặ
m t đường 𝑘 𝑘 = 0,23. ấ
L y 𝑔 𝑔 = 9,81 m/s2. Lực đẩy của người có giá trị bằng: A. 693,28 N. B. 690,98 N. C. 686,38 N. D. 697,88 N. Lời giải:
- Chọn chiều dương cùng chiều chuyển động
-Khi xe chuyển động, c ị h u tác dụng ủ c a các lực:
trọng lực P , phản lực N′ , lực đẩy F ′ và lực ma sát f ′
- Vì xe chuyển động với vận tốc không đổi nên a = 0
Áp dụng định luật II Newton, ta có: P N ′ f F ′ + + + = (1) ms 0
Chiếu (1) lên trục Oy : N′ F′ − .sinα − P = 0
Chiếu (1) lên trục Ox : F′ .cosα f ′ 0 F′ . o c sα f ′ − = ⇒ = ms ms
Mà lực ma sát tác dụng lên xe: f ′ kN ′ k( P F′ = = + .sinα ms )
Group: Bachkhoa Universe – Góc học tập và thảo luận 25 TAILIEUHUST.COM ′ ′ ′ kP
Hay F .cosα = k.(P + F sinα) ⇒ F = = 690,98(N ) cosα − ksin α
Câu 19. Một ô tô k ố
h i lượng 𝑚 𝑚 = 1,5 tấn đang đi trên đường phẳng ằ n m ngang với tốc độ
21 m/s bỗng nhiên phanh lại. Ô tô dừng lại sau khi trượt thêm 25 m. ộ Đ lớn trung bình của lực ma sát là: A. 13, 53.103 N. B. 13, 23.103 N. C. 12,63 ⋅ 103 N. D. 14, 13.103 N. Lời giải: 2 2 2 2 − Gia tố − c: v v 0 21 0 a = = = 8 − ,82( 2 m / s ) 2s 2.25
Độ lớn trung bình của lực ma sát là: F = ma = 8 − ,82 1 ⋅ ,5⋅1000 = 1 − 3230(N) ms
Câu 20. Một vật coi là chất điểm có k ố
h i lượng 𝑚𝑚 bắt đầu trượt từ đỉnh mặt phẳng
nghiêng góc 𝛼𝛼 so với phương nằm ngang (xem hình vẽ). ệ
H số ma sát giữa vật và mặt
phẳng nghiêng là 𝑘𝑘. Mômen ộ đ ng lượng ủ c a chất điểm ố
đ i với điểm O tại thời điểm 𝜔𝜔 có giá trị là :
A. 𝑚𝑚𝑔𝑔ℎ𝜔𝜔sin 𝛼𝛼(sin 𝛼𝛼 − 𝑘𝑘cos 𝛼𝛼).
B. 𝑚𝑚𝑔𝑔ℎ𝜔𝜔cos 𝛼𝛼(sin 𝛼𝛼 − 𝑘𝑘cos 𝛼𝛼).
C. 𝑚𝑚𝑔𝑔ℎ𝜔𝜔cos 𝛼𝛼(cos 𝛼𝛼 − 𝑘𝑘sin 𝛼𝛼).
D. mght (sin 𝛼𝛼 − 𝑘𝑘cos 𝛼𝛼). Lời giải:
- Chọn hệ quy chiếu như hình vẽ, ố
g c thời gian là lúc vật bắt đầu chuyển động.
- Các lực tác dụng lên vật: P - trọng lực của vật; N - áp lực; f
lực ma sát giữa vật và mặt p ẳ h ng ms
- Áp dụng định luật 2 Niuton ta được:
F = P + N + f
= P + P + N + f (*) ms ( x y ) ms
Chiếu lên trục Ox ta có: F = P − f = P − kN (1) x ms x
Chiếu lên trục Oy ta có: N − P = 0 ⇒ N = P y y
Mô men tổng hợp các lực tác dụng lên vật đối với O là
Mo = Fd(F, O) = mgh cosα (sinα − k cosα )
26 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Vậy momen động lượng của vậy đôí với O là: L = M t = mght cosα (sinα −k cosα ) 0
Câu 21. Một hạt chuyển động trong mặt phẳng 𝑂𝑂𝑥𝑥𝚤𝚤 → từ điểm 1 có bán kính vecto � � r = 𝑟𝑟1
(𝑖𝑖 + 2𝑗𝑗 )m đến đ ể i m 2 có bán kính vector �𝑟 � 𝑟
= 2(2𝑖𝑖 − 3𝑗𝑗 )𝑚𝑚, 𝑖𝑖 và 𝑗𝑗 là các vector đơn vị trong
tọa độ Đề-các. Hạt chuyển ộ đ ng dưới tác ụ d ng ủ
c a lực có biểu thức 𝐹𝐹
�= (3𝑖𝑖 − 4𝑗𝑗 ) N. Công
thực hiện bởi lực đó là: A. 5 J. B. −17 J. C. 23 J. D. 17 J. Lời giải:
Độ dời của hạt đó là:
s = r − r = (1; −5) 2 1 Công thực hiện bởi ự l c F là :
A = F.S = 23( N)
Câu 22. Một phi công đang lái máy bay thực hiện vòng tròn nhào lộn trong một mặt phẳng đ n ứ g với vận tốc 700 k
m/h. Giả thiết phi công có t ể h c ị h u đựng ự s tăng trọng
lượng lên 3 lần. Bán kính nhỏ nhất của vòng tròn nhào lộn mà máy bay có thể đạt được là (cho 𝑔 𝑔 = 9,8 m/s2� A. 1979 m. B. 1929 m. . C 2029 m. D. 1779 m. Lời giải:
Các lực tác dụng lên phi cônglà: P, Fht, N
Do vật chuyển động tròn, nên ta có: 𝐹𝐹 ��ℎ𝑡𝑡= 𝑃𝑃 �+ 𝑁𝑁 � => 𝑁𝑁 � � = 𝐹𝐹 � � � � � � � � �� � � ℎ => � �= � � + P 𝑡𝑡− 𝑃𝑃 𝑁𝑁 𝐹𝐹 − ℎ𝑡𝑡 𝑃𝑃 ≤ Fht
=> Áp lực tác dụng lên phi công lớn nhất tại vị trí thấp n ấ h t và bằng: Nmax = Fht + P Mà Nmax ≤ 3P F
=> ht ≤ 2P => aht ≤ 2g => 𝑣𝑣2 ≤ 2g =
> r ≥ 𝑣𝑣2 = 1929 (m) 𝑟 𝑟 2𝑔𝑔
Câu 23. Một viên bi n ỏ
h m =10( g) rơi theo phương thăng đứng không vận t c ố ban ầ đ u
trong không khí, lực cản ủ
c a không khí F = −rv (tỷ lệ ngược chiều với vận t c
ố ), r là hệ số c cản. ậ
V n tốc cực đại mà viên bi đạt được bằng v
= 50( m / s) . Cho gia tốc trọng trường max g = ( 2
10 m / s ) . Hệ số cản có giá trị: A. −3 2, 02.10 Ns / m B. −3 1, 99⋅10 Ns / m C. 3 − 2.10− Ns / m D. 3 2, 03.10 Ns / m
Group: Bachkhoa Universe – Góc học tập và thảo luận 27 TAILIEUHUST.COM Lời giải:
Chọn chiều dương là ch ề
i u hướng xuống mặt đất (cùng chiều với vecto g)
Các lực tác dụng lên viên bi là trọng lực P và lực cản F C
Áp dụng dịnh luật II Newton ta có: P + F = ma C
Chiếu lên chiều dương ta được: dv dv
mg − rv = ma ⇔ mg − rv = m ⇔ dt = dt rv g − m Đặt r g −
v = u ⇒ vi phân 2 vế: r m
− dv = du ⇒ dv = − du m m r m du r du ⇒ dt = − ⋅ ⇒ − dt = ∫ ∫ r u m u r v g − v rrr ⇔ − = ln = ln − ⇔ − = ln m t u g v t   mm m g 0 r r − t  − t r mmg mg −  Ns m m 3 ⇒ g − v = ge ⇔ v = g 1 − e ⇒ v = ⇒ r = = 2.10   max   m r r v   m   max
Câu 24. Một thanh đồng c ấ
h t có độ dài , khối lượng m. Đối với trục quay nào dưới đây
momen quán tính của thanh là nhỏ nhất
A. Song song và cách thanh một khoảng bằng 1
B. Đi qua khối tâm và vuông góc với thanh
C. Vuông góc và đi qua một đầu thanh π
D. Đi qua khối tâm và làm với thanh một góc α < 2 Lời giải:
Song song và cách thanh 1 khoảng 2 : I = m 2
Đi qua khối tâm và vuông góc thanh: m I = 12 2
Vuông góc và đi qua 1 đầu thanh: m I = 3 2 π
Đi qua khối tâm và tạo với thanh 1 góc m α < :I = sinα 2 12
28 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Chương 4. Năng lượng A. Công thức
1. Động năng và thế năng 1 1 - Động năng: 2 W = mv . - Thế năng: 2 W = k ⋅ x ∆ . d t 2 2  =
2. Công A F.s  .
A = E − E  2 1
3. Bài toán tìm điều k ện i - Khoảng cách R h
∆ (tính từ đỉnh mặt cầu) ậ
v t bắt đầu rơi khỏi mặt cầu: ∆h = . 3
- Vận tốc bé nhất để sợi dây treo vật nặng quay tròn trong mặt phẳng thẳng đứng: v = 5gl .
- Vận tốc dài của cột đồng chất b ịđổ khi chạm đất: v = 3gh .
4. Bài toán va chạm
- Va chạm đàn hồi xuyên tâm: Bảo toàn động năng và động lượng  − + ′ ( m m v 2m v 1 2 ) 1 2 2 2 2 ′2 ′2 v m v m v m v m v =   1 1 1 2 2 1 1 2 2  + = +  m + m 1 2  2 2 2 2 ⇒  ′ ′ − +   ′ (m m v 2m v 2 1 ) 2 1 1
m v + m v = m v + m v  1 1 2 2 1 1 2 2 v = 2  m + m  1 2 +
– Va chạm mềm: m v + m v = (m + m ) m v m v 1 1 2 2 v ⇒ v = 1 1 2 2 1 2 m + m 1 2 5. Bảo toàn cơ năng: - Định luật: ổ
T ng động năng và thế năng của hệ tại thời điểm 1 bằng tổng động năng và
thế năng của hệ tại thời điểm 2: E = E . truoc sau
Group: Bachkhoa Universe – Góc học tập và thảo luận 29 TAILIEUHUST.COM
B. Bài tập trắc nghiệm
Câu 1. Một chất điểm k ố
h i lượng 𝑚 𝑚 = 0,2 k
g được ném lên từ O với vận tốc 𝑣𝑣0 = 7 m/s
theo phương hợp với mặt phẳng nằm ngang ớ
v i một góc 𝛼 𝛼 = 30∘, ỏ b qua sức ả c n ủ c a
không khí, cho 𝑔 𝑔 = 9,8 m/s2. Mômen động lượng của chất điểm đối với O tại vị trí cao
nhất của chuyển động chất điểm là: A. 0,052kgm2/s. B. 0,218kgm2/s. C. 0,758kgm2/s. D. 0,488kgm2/s. Lời giải:
Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí bắt
đầu ném, chiều dương hướng x ố u ng, cùng chiều với gia tốc g a = x 0 Gia tốc:  a = −g y
v = v + a t = v cos α Vận tốc: x 0x x 0 
v = v + a t = v sin t − gt y 0 y y 0   1 2
Ox : x = v t + a t
Ox: x = v cosα t 0x x 0  
Phương trình chuyển động của chất điểm: 2  ⇒  1 2 1 Oy y = v αt − gt 2 : sin   0
Oy : y = v t + a t 0y y  2  2 Tại ị
v trí cao nhất của chuyển động chất điểm: v sint 0
v = 0 = v sint − gt ⇒ t = y 0 g 2 2 2 2 α α α Và 1 v sin 1 v sin 1 v sin 2 0 0 0
y = h = v sinα ⋅ t + gt = v sinα ⋅ − = 0 0 2 g 2 g 2 g ⇒ 2 Ta có: 𝑣𝑣 sin2 α 72.sin2 30∘ ℎ 0 max = 1 = 1 = 0,625(𝑚𝑚) 2 𝑔 𝑔 2 9,8
Động lượng p tại thởi điểm t bất kì: (
p t) = p i + p j = mv i + mv j x y x y
Xét tích có hướng của hai vector: u = u i + u j + u k và v = v i + v j + v k 1 2 3 1 2 3 i j k u u u u u u 2 3 1 3 1 2 uv = u u u = i − j + k 1 2 3 v v v v v v 2 3 1 3 1 2 v v v 1 2 3
30 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới trục z coi như i j k v v v v bằng 0: y 0 x 0
r ⋅ v = v v 0 x y = i − j +
k = v y − v x k x y ( x y ) y 0 x 0 x y x y 0
Mômen động lượng của chất điểm đối với O tại v ịtrí cao nhất của chuyển động chất điểm là:  
L = v y − v x = v cos α.t.m. v α− gt − mv α v t α − gt x y ( sin ) 1 2 cos sin 0 0 0  0   2  2 2 3 2 1 α α 2 1 v sin v sin 0 0
= mgv t cosα = mgv cosα = m cosα = 0, 758 kgm / s 0 0 2 ( 2 ) 2 2 g 2g
Câu 2. Một cột đồng c ấ
h t có chiều cao ℎ = 8 m, đang ở vị trí thẳng đứng (chân cột tì lên
mặt đất) thì bị đổ xuống. Gia tốc trọng trường 𝑔 𝑔 =
9,8 m/s2. Vận tốc dài của đỉnh cột khi
nó chạm đất bằng giá trị nào dưới đây A. 16,836 m/s. B. 14,83 6 m/s. C. 15,33 6 m/s. D. 14,33 6 m/s. Lời giải:
Chọn mốc thế năng tại ặ m t đất
Ở vị trí thẳng đứng, ậ
v t có thế năng: 𝑊𝑊𝑡 𝑡 = 1
𝑚𝑚𝑔𝑔ℎ = 𝑊𝑊 2
Khi đỉnh cột chạm đất, vật có động năng là 1 𝑊𝑊đ = 𝑊 𝑊 = 𝐼𝐼𝜔𝜔2 2
Lại có: quán tính của cột i đố với tr c
ụ quay tại chân cột là 𝐼 𝐼 = 1𝑚𝑚ℎ2 3 1 1 1
Áp dụng định luật bảo toàn cơ năng ta có: 2 2
⇒ mgh = ⋅ mh ω 2 2 3
Vậy vận tốc dài của đỉnh cột khi nó chạm đất là: ⇒ v =ω h = 3gh = 3.9,8.8 ≈15,336( m / s)
Câu 3. Một ống thủy tinh nhỏ khối lượng 𝑀 𝑀 = 12
0 g bên trong có vài giọt ête được đậy
bằng 1 nút cố định có khối lượng 𝑚 𝑚 = 10 g. n
Ố g thủy tinh được treo ở đầu một sợi dây
không giãn, khối lượng không đáng kể, ch ề
i u dài 𝑙 𝑙 = 60 cm (hình vẽ). Khi hơ nóng ống
thủy tinh ở vị trí thấp n ấ
h t, ête bốc hơi và nút ậ
b t ra. Để ống có thể quay được ả c vòng
xung quanh điểm treo O, vận ố t c bật bé n ấ h t của nút là: C ( ho 𝑔 𝑔 = 10 m/s2). H A. 69,127 m/s. B. 64,02 7 m/s. C. 70,82 7 m/s. D. 65,72 7 m/s.
Group: Bachkhoa Universe – Góc học tập và thảo luận 31 TAILIEUHUST.COM Lời giải
Gọi H là điểm cao nhất của quỹ đạo, mốc thế năng tại A.
Để ống có thể quay được cả vòng xung quanh điểm treo O
thì tại H dây không được trùng, hay 𝑇𝑇 là l
𝐻 𝐻 ≥ 0 (𝑇𝑇𝐻𝐻 ực căng dây tại H). Tại H ta có: 2 vH
F = P + T ⇔ ma = mg + T ⇔ T = m − mg H H H H H l Do đó 𝑇𝑇 hay:
𝐻 𝐻 ≥ 0 ⇔ 𝑣𝑣𝐻 𝐻 ≥ �𝑔𝑔𝑙𝑙 𝑣𝑣𝐻𝐻 = �𝑔𝑔𝑙𝑙 𝑚𝑚𝑚𝑚𝑚𝑚
Áp dụng định luật bảo toàn động ượ
l ng cho ống và nút tại A: 𝑀𝑀
𝑚𝑚𝑣𝑣𝑚 𝑚 = 𝑀𝑀𝑣𝑣𝐶 𝐶 ⇒ 𝑣𝑣𝑚 𝑣𝑣 𝑚 = 𝑚 𝑚 𝐶𝐶
Áp dụng định luật bảo toàn cơ năng cho vật M (ống k ô
h ng tính nút) tại A và H, ta ó c : 𝑊𝑊 2 2 ⇒ = + ≥ + = ⇒ ≥ 𝐴 𝐴 = 1 𝑀𝑀. 𝑣𝑣 = 𝑊𝑊 𝑀𝑀. 𝑣𝑣 + 𝑀𝑀𝑔𝑔ℎ 2 2 v v gl gl gl gl v gl M H 4 4 5 M 5 2 𝐶𝐶 𝐻 𝐻 = 1 2 𝐻𝐻 M M 120 ⇒ v = v ≥ 5 gl = 5.10.0, 6 ≈ 65,727 m M m m 10
Câu 4. Ở đầu sợi dây OA chiều dài 𝑙𝑙 có treo một vật nặng 𝑚𝑚. Để vật quay tròn trong mặt phẳng thẳng ứ
đ ng thì tại điểm thấp nhất phải truyền cho vật một vận tốc theo phương
nằm ngang có độ lớn là (cho gia tốc t ọ
r ng trường bằng 𝑔𝑔 ) A. �5𝑔𝑔𝑙𝑙. B. �𝑔𝑔𝑙𝑙. C. �5𝑙𝑙 . D. 2𝑔𝑔𝑙𝑙. 𝑔 𝑔 Lời giải:
Chọn chiều dương và gốc tọa độ như hình vẽ:
Sức căng T cực tiểu khi vật lên ế đ n đ ể
i m cao nhất PT Newton II tại điểm cao 2 nhất B: vB mg + T = m min l Áp dụng ĐLBT cơ năng: 1 2 1 2 1 1 mv = mv + 2mgl 2
⇒ mv = mgl + lT + 2mgl 2 A 2 B A min 2 2
Để vật quay tròn trong mặt phẳng thẳng đứng thì tại đ ể
i m thấp nhất thì T ≥ 0 min 1 5 2
⇒ mv ≥ mgl ⇒ v ≥ 5gl ⇒ v = 5gl A min 2 2
32 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Câu 5. Một viên bi có khối lượng 𝑚𝑚, vận tốc 𝑣𝑣 bắn thẳng góc vào một bức tường ph n ẳ g.
Sau khi va chạm viên bi bay ngược trở lại với vận tốc bằng 4𝑣𝑣/5. Gọi động năng ban đầu
của viên bi là 𝐸𝐸, độ biến thiên động năng và động lượng của viên bi là Δ𝑊𝑊 và Δ𝑝𝑝 ta có: / A. Δ ( 𝑚𝑚𝐸𝐸)1 2
𝑊𝑊 = 0 và Δ𝑝𝑝 = 2(2𝑚𝑚𝐸𝐸)1/2. C. Δ𝑊𝑊 = và− 5𝐸𝐸 Δ𝑝𝑝 = 5 2 . 9 3 B. Δ ( 𝑚𝑚𝐸𝐸)1/2 ( 𝑚𝑚𝐸𝐸)1/2 𝑊𝑊 = − 3𝐸𝐸 và Δ𝑝𝑝 = 3 2 . D. Δ𝑊𝑊 = − 9𝐸𝐸 và Δ𝑝𝑝 = 9 2 . 4 2 25 5 Lời giải: 1 1 1 4 2 91 9𝐸𝐸 Δ𝑊𝑊 = 𝑊𝑊 2 2 =
𝑠 𝑠 − 𝑊𝑊𝑡 𝑡 = 𝑚𝑚𝑣𝑣 − 𝑚𝑚𝑣𝑣 𝑚𝑚 ��
𝑣𝑣� − 𝑣𝑣2� = −× 𝑚𝑚𝑣𝑣2 = − 2 𝑠𝑠 2 𝑡𝑡 2 5 25 2 25
Câu 6. Một vật cố khối l ợ ư ng 𝑚 𝑚 = 1
0 kg bắt đầu trượt từ đỉnh dốc một mặt p ẳ h ng
nghiêng cao ℎ = 20 m. Khi tới chân ố
d c có vận tốc 𝑣 𝑣 = 15 m/s. Cho 𝑔 𝑔 = 10 m/s2. Công
của lực ma sát có độ lớn là: A. 867,7 J. B. 853,1 J. C. 875 J. D. 860 ,4 J. Lời giải: Chọn mặt đất làm ố
g c tính thế năng (W = 0 , chiều chuyển động của vật trên mặt dốc là t ) chiều dương. Do c ị
h u tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ
năng của vật không bảo toàn. Trong trường, hợp này, độ biến thiên cơ năng của vật có giá
trị bằng công của lực ma sát: 2 2  mv   mv  0
A = W −W =  + mgh  −  + mgh  2 1 0 2 2     Thay số: 1
v = 0, h = 0, 2( m), v = 15( m / s), h = 0 2 ⇒ A =
mv − mgh = 875(J ) 0 0 0 2
Câu 7. Một con lắc đơn có 𝑚 𝑚 = 120 g được kéo lệch với phương th n
ẳ g đứng một góc 𝛼 𝛼 =
90∘, sau đó thả rơi cho 𝑔 𝑔 = 10 m/s2. Lực căng cực đại của dây treo là A. 4,791 N. B. 3,997 N. C. 3,6 N. D. 4,394 N. Lời giải: Chuyển ộ đ ng ủ
c a vật m là chuyển động tròn đều trên quỹ đạo có bán kính 1
Áp dụng định luật bảo toàn cơ năng: 1 2 mgl mgl
W = W + W = W ⇒ mv + = d t tmax 2 1− cos α 1− cos α0
⇒v = 2gl (cos α −cos α 0 )
Group: Bachkhoa Universe – Góc học tập và thảo luận 33 TAILIEUHUST.COM
Chọn chiều dương hướng xuống và gốc thế năng tại vị trí cân
bằng. Vật chịu tác dụng ủ
c a các lực: Lực căng dây (T) , trọng
lực P Áp dụng định luật II Newton: P + T = ma Chiếu (1) lên ch ề i u dương hình vẽ: 2 v
T − P = ma ⇒ T − mg cos α = m⋅
(trọng lực đóng vai trò lực n l hướng tâm)
⇒T = mg cos α + 2mg (cos α −cos α = mg 3cos α − 2cos α 0 ) ( 0 ) T α 0 T 3mg cos α 3.0,12.10.cos 90° ⇔ = ⇒ = = =3,6( N) max 0 max
Câu 8. Một đĩa tròn đồng c ấ
h t bán kính 𝑅 𝑅 = 0,15 m, có thể quay xung quanh một trục
nằm ngang vuông góc với dĩa và cách tâm đĩa một đoạn 𝑅𝑅/2. Đĩa bắt đầu quay từ vị trí cao
nhất của tâm đĩa với vận tốc đầu bằng 0. Vận tốc khi tâm đĩa ở vị trí thấp nhất là A. 13,199rad/s. B. 49,915rad/s. C. 12,226rad/s. D. 50,888rad/s. Lời giải: Chọn ố
m c thế năng tại vị trí thấp n ấ h t
Thế năng tại vị trí cao nhất: W = mgR t 1 Động năng tại ị v tí thấp nhất: 2 W = Iω d 2
Mô-men quán tính của đĩa đối với t ụ r c quay: 2 2 1  R  3mR 2 I = mR + m =   2  2  4
Áp dụng định luật bảo toàn năng lượng: 1 3 8g 2 2 2 mgR = Iω ⇔ mgR = mR ω ⇒ ω = ≈13,199 (rad/s) 2 8 3R
Câu 9. Một thanh đồng chất chiều dài 𝑙𝑙 có thể quay quanh một trục nằm ngang đi qua
một đầu của thanh và vuông góc với thanh. Vận tốc góc cực tiểu phải truyền cho thanh ở vị trí cân bằng ể đ nó đến được ị v trí nằm ngang là: A. �3𝑔𝑔. B. �6𝑔𝑔. C. �2𝑔𝑔. D. �9𝑔𝑔. 𝑙 𝑙 𝑙 𝑙 𝑙 𝑙 𝑙 𝑙 Lời giải: Chọn ố
m c thế năng tại vị trí thấp n ấ h t.
34 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Thế năng tại vị trí nằm ngang là: W = mgl t 1 Động năng tại ị v trí thấp nhất: 2 W = mv d 2
Áp dụng định luật bảo toàn năng lượng ta có 1 2 mgl =
mv ⇒ v = 2gl 2
Vận tốc góc tối thiểu ể đ thanh đến được ị v trí nằm ngang là v 2g ω = = l l
Câu 10. Giả sự lực cản của nước tác ụ d ng lên xà lan t l ỉ ệ với tốc ộ
đ của xà lan đối với nước.
Một tàu kéo cung cấp công suất 𝑃𝑃1 = 250 mã lực (1 mã lực = 746 W) cho xà lan khi chuyển động với ố
t c độ 𝑣𝑣1 = 0,25 m/s. Công suất cần thiết để kéo xà lan với tốc độ 𝑣𝑣2 = 0,75 m/s là : A. 2240 mã lực. B. 2220 mã lực. C. 2250 mã lực. D. 2270 mã lực. Lời giải: Giả sử
hệ số lực cản của nước là: K
Vì lực cản của nước tỉ lệ với tốc độ của xà lan nên FC = KV (1)
Ta thấy xà lan chuyển động với vận tốc không đổi nên lực kéo và lực cản đã triệt tiêu lẫn nhau => F � � � � � K + FC = 0 �
Mặt khác hai lực này cùng phương ngược chiều nên => FK – FC = 0 ⇔ FK = FC (2)
Công thức tính công suất kéo là P = FKV (3) 2 2
Từ (1), (2) và (3) => P = KV2 => �P 1 = KV1 => P2 = V2 P 2 2 2 = KV2 P1 V1 2 2 2
=> P2 = V2 P2 = V2 P1 = �0,75� P1 = 9P1 V2 2 1 V1 0,25
Thay số vào ta được P2= 2250 (mã lực)
Câu 11. Một khẩu pháo có khối lượng 𝑀 𝑀 = 480 kg bắn một viên ạ đ n theo phương làm với
mặt ngang một góc 𝛼 𝛼 = 60∘. Khối lượng của viên ạ
đ n 𝑚 𝑚 = 5 kg, vận tốc đầu nòng 𝑣 𝑣 =
400 m/s. Khi bắn bệ pháo giật lùi về phía sau một đoạn 𝑠 𝑠 = 54 cm. Lực cản trung bình tác
dụng lên quả pháo có giá trị: A. −2129 N. B. −1929 N. C. −2229 N. D. −2029 N. Lời giải:
Chọn chiều dương cùng chiều với ch ề i u của vo
Group: Bachkhoa Universe – Góc học tập và thảo luận 35 TAILIEUHUST.COM
Bảo toàn động lượng theo phương ngang cho hệ ngay trước và sau khi bắn ta có:
M𝑣𝑣0 − 𝑚𝑚𝑣𝑣𝑚𝑚𝑚𝑚𝑠𝑠(a)= 0 ⟺𝑣 𝑣𝑣 𝑣𝑚0 = 𝑚𝑚 𝑚𝑚𝑚𝑠𝑠(a ∗ ) 4 = 5
00 ∗ cos(600) = 25 𝑚𝑚/𝑠𝑠 𝐶 𝐶 480 12
Sau đó, do toàn bộ động năng cả pháo bị lực cản tr ệ i t tiêu ế đ n lúc dừng: 1 2 2 1 𝐶𝐶𝑣𝑣0 480∗�25 � 𝑊𝑊 2= | |S 2 |= 12 đ = 𝐴𝐴 = = 1929(N) 𝑐𝑐ả𝑛𝑛 ⟺ 𝑀𝑀𝑣𝑣 𝐹𝐹 ⟺|𝐹𝐹 2 0 𝑐 𝑐 𝑐 𝑐 𝑆 𝑆 2∗0,54
=> 𝐹𝐹𝑐 𝑐 = −1929 (N) (vì vector F cản ngược chiều dương nên giá trị của nó mang dấu –)
Câu 12. Một thanh mảnh đồng chất có ộ
đ dài 𝑙𝑙 có thể quay quanh một trục đi qua đầu
thanh và vuông góc với thanh. Lúc đầu thanh ở vị trí nằm ngang, cho thanh rơi xuống. Vận
tốc dài ở đầu dưới của thanh khi thanh rơi tới vị trí thẳng đứng là: A. �2𝑔𝑔𝑙𝑙. B. �𝑔𝑔𝑙𝑙. C. �3𝑔𝑔𝑙𝑙. D. 0 Lời giải: Chọn ố
m c thế năng tại vị trí thấp n ấ h t của thanh Tại ị
v trí thấp nhất (v = v ) 1 2 ⇒ W = W = mv max dmax 2 Tại ị
v trí cao nhất (v = 0) ⇒ W = W = mgl tmax 1
Áp dụng định luật bảo toàn năng lượng: 2
mv = mgl ⇒ v = 2 gl 2
Câu 13. Hai quả cầu 𝐴𝐴 và 𝐵𝐵 được treo ở đầu hai sợi dây mảnh không dãn dài bằng nhau.
Hai đầu kia của các sợi dây được buộc vào một cái giá sao cho các quả cầu tiếp xúc với
nhau và tâm của chúng cùng nằm trên một đường nằm ngang. Khối lượng ủ c a các quả cầu
𝑚𝑚A = 165 g và 𝑚𝑚B = 750 g. Kéo quả cầu A lệch khỏi ị v trí cân bằng ế đ n độ cao ℎ = 6 cm
và thả ra. Sau va chạm, q ả
u cầu B được nâng kên độ cao là (coi va chạm hoàn toàn đàn
hồi, cho 𝑔 𝑔 = 9,8 m/s2 ) A. 1,764 mm. B. 7,991 mm. C. 7,804 mm. D. 1,951 mm. Lời giải:
Chọn mốc thế năng tại vị trí thấp nhất, ta thấy hệ hai vật là hệ kín vì vậy có thể áp dụng
mọi định luật bảo toàn cơ năng và động năng
Đặt 𝑣𝑣0; 𝑣𝑣1; 𝑣𝑣2 lần lượt là vận tốc cực đại của vật A trước khi va chạm; vận tốc của vật A sau
khi va chạm; vận tốc của vật B sau khi va chạm
36 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Đặt h’ là chiều cao cực đại của vật B
Áp dụng định luật bảo toàn cơ năng cho vật A để
tính vận tốc trước khi va chạm ta có 𝑚𝑚 2 2 𝐴𝐴𝑔𝑔ℎ = 1 𝑚𝑚 ⟹ 𝑣𝑣 = 2𝑔𝑔ℎ (1 ) 2 𝐴𝐴𝑣𝑣0 0
Vì là va chạm đàn hồi ta áp dụng định luật bảo toàn
động lượng cho hai vật 𝑚𝑚� � �� � � ( (2) 𝐴𝐴𝑣𝑣 = 0𝑚𝑚𝐴𝐴𝑣𝑣 + 1𝑚𝑚𝐵𝐵𝑣𝑣
→2𝑚𝑚𝐴𝐴 𝑣𝑣0 − 𝑣𝑣1) = 𝑚𝑚𝐵𝐵𝑣𝑣2
Áp dụng định luật bảo toàn cơ năng cho hai vật ngay sau khi va chạm 1 𝑚𝑚 2 = 1 𝑚𝑚 2 + 1 𝑚𝑚
2 ⟺ 𝑚𝑚 (𝑣𝑣2 − 𝑣𝑣2) = 𝑚𝑚 2 (3 ) 2 𝐴𝐴𝑣𝑣0 2 𝐴𝐴𝑣𝑣12 𝐵𝐵𝑣𝑣2 𝐴𝐴 0 1 𝐵𝐵𝑣𝑣2
Từ (1), (2) suy ra 𝑣𝑣1 = 𝑣𝑣2 − 𝑣𝑣0 tiếp tục thay vào (2) để triệt tiêu 𝑣𝑣1 ta được 𝑣𝑣 (4)
2 = 2𝑚𝑚𝐴𝐴𝑣𝑣0 𝑚𝑚 +𝑚𝑚 𝐴𝐴 𝐵𝐵
Tiếp tục áp dụng định luật bảo toàn cơ năng để tìm h cực đại của vật B ta có 2 1 𝑚𝑚 2 = 𝑚𝑚 2 𝐵𝐵𝑣𝑣2
𝐵𝐵𝑔𝑔h’ ⟹ h’ = 𝑣𝑣2 2𝑔𝑔
Thay (1) và (4) để tìm giá trị của h’ ta được 2𝑚𝑚 h’ = ( 𝐴𝐴
)2ℎ = 0,7804(𝑚𝑚𝑚𝑚) = 7,804(𝑚𝑚𝑚𝑚)
𝑚𝑚𝐴 𝐴 + 𝑚𝑚𝐵𝐵
Câu 14. Hai hòn bi có khối lượng 𝑚𝑚1 và 𝑚𝑚2 = 1
𝑚𝑚 /2 được treo bằng 2 sợi dây có cùng chiều dài 𝑙𝑙 =
6 m vào một điểm. Kéo lệch hòn bi 𝑚𝑚1 cho đến khi dây treo nằm ngang rồi thả ra để nó va c ạ
h m vào bi 𝑚𝑚2. Sau va chạm hai hòn bi dính vào nhau và lên tới độ cao
cực đại là: (cho 𝑔 𝑔 = 9,8 m/s2 ) A. 2,827 m. B. 2,907 m. C. 2,667 m. D. 2,747 m. Lời giải:
Áp dụng định luật bảo toàn cơ năng (cho hệ gồm hòn bi 1
và Trái Đất; chọn mốc tính thế năng tại vị trí cân bằng của
hòn bi 1 trước va chạm) ta tính được vận tốc v của hòn bi 1 m v trước va chạm: 1 1 0 + m gl =
+ 0 ⇒ v = 2gl (1) 1 2
Ngay sau va chạm cả hai hòn bi có cùng vận tốc v′ . Áp dụng ị
đ nh luật bảo toàn động lượng ta có:
Group: Bachkhoa Universe – Góc học tập và thảo luận 37 TAILIEUHUST.COM
m v = (m + m ) ′ ′ m v m v 2 2 1 1 v ⇒ v = = = v = 2gl (2 ) 1 1 2 m + m m1 3 3 1 2 m + 1 2 2 ′ 2 ′ Động năng của ệ
h hai hòn bi sau va chạm là: ′ m v m v 3 ′ 1 2 1 2 2 2 W = +
= m v = m v = mgl d 1 1 2 2 4 3 3
Sau va chạm hai hòn bi dính vào nhau và tiếp nối chuyển động tròn ban đầu của hòn bi 1. Động năng ′ 3
W ′ của hệ hai hòn bi chuyển động thành thế năng W = m +m gh = m gh t ( 1 2 ) d 1 2 của hai hòn bi ở
độ cao tối đa h (chọn ố
m c tính thế năng như trên) ′ ′ 2 3 4 W = W ⇔ m gl = m gh ⇒ h = l = 2, 667( m) d t 1 1 3 2 9
Câu 15. Có ba vật đồng c ấ
h t, cùng khối lượng: cầu đặc, trụ đặc và trụ rỗng cùng được thả
lăn không trượt từ đỉnh một mặt phẳng nghiêng. Vật nào tới chân mặt phẳng nghiêng lớn nhất: A. Cả 3 vật. B. Trụ đặc . C. Trụ rỗng. D. Quả cầu đặc . Lời giải:
Gọi h là độ cao từ đỉnh mặt phẳng nghiêng đến vị trí của vật sau t( s)
x là quãng đường vật đi được sau t(s)
Vật tham gia 2 chuyển động: chuyển động quay và chuyển
động ịtnh tiến với tốc độ di chu ể
y n chính là tôc độ dài tại 1 điểm ở bề mặt của vật
Áp dụng định luật bảo toàn cơ năng ta được: 2 2
mv + Iw = 2mgh = 2mgx sin α (1) Lấy vi phân 2 ế
v của (1) với v / r = w ta có: ( 2 + ) 2 = α = ( 2 + ) dv 2 dx mvr Iv dv mgr sin dx mvr Iv = mgr sinα dt dt ⇒ ( mgr α mr + I ) 2 sin 2 2 a = mgr sin α ⇒ a = 2 mr + I 5
+ TH1: Vật là cầu đặc: 2
I = 2mr / 5 ⇒ a = g sin α 1 7
+ TH2: Vật là trụ đặc: 2 2 I = mr / 2 ⇒ a = g sinα 2 3 + TH3: Vật là trụ ỗ r ng: 1 2 I = mr ⇒ a = g sinα 3 2
38 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Từ 3TH trên cho thấy cầu đặc chu ể
y n động với gia tốc lớn nhất nên thời gian ể đ đi cùng 1
quãng đường là nhỏ nhất.
Câu 16. Hai quả cầu A và B được treo ở hai đầu sợi dây mảnh không dãn dài bằng nhau.
Hai đầu kia của các sợi dây được buộc vào một cái giá sao cho các quả cầu tiếp xúc với
nhau và tâm của chúng cùng nằm trên ộ
m t đường nằm ngang. Khối lượng của các quả cầu 𝑚𝑚 ầu A lệch khỏi ị
v trí cân bằng đến độ cao 𝐴 𝐴 = 165 g và 𝑚𝑚 = 𝐵 𝐵 750 g. Kéo quả c ℎ = 6 cm và thả ra. Sau va chạm, q ả
u cầu B được nâng lên độ cao là: (coi va chạm là hoàn toàn không
đổi, cho 𝑔 𝑔 = 9,8 m/s2 ) A. 7,617 mm. B. 1,951 mm. C. 2,958 mm. D. 7,804 mm. Lời giải:
Áp dụng ĐL bảo toàn và chuyển hóa năng lượng:
Vận tốc của vật A tại thời điểm va chạm là: 𝑚𝑚𝐴𝐴𝑣𝑣2 = mAgh 2 => vA = �2𝑔𝑔ℎ
Vận tốc của vật B ngay sau khi va chạm là: vB’ =
(𝑚𝑚𝐵𝐵−𝑚𝑚𝐴𝐴)𝑣𝑣𝐵𝐵+2𝑚𝑚 𝑣𝑣 𝐴𝐴
𝐴𝐴 = 2𝑚𝑚𝐴𝐴𝑣𝑣𝐴𝐴 𝑚𝑚𝐴𝐴+𝑚𝑚𝐵 𝐵 𝑚𝑚 +𝑚𝑚 𝐴𝐴 𝐵𝐵
Độ cao của vật B nâng được lên sau khi va chạm là: ′ 2
Áp dụng ĐLBTVCH năng lượng: mBghB = 𝑚𝑚 𝑣𝑣 𝐵𝐵 𝐵𝐵 2 ′ 2
=> hB = 𝑣𝑣𝐵𝐵 = ( 2𝑚𝑚𝐴𝐴 )2. ℎ = 7,804 mm 2𝑔𝑔 𝑚𝑚 +𝑚𝑚 𝐴𝐴 𝐵𝐵
Câu 17. Một vật có k ố
h i lượng 𝑚𝑚1 = 2 kg chuyển động với tốc độ 𝑣𝑣1 = 6 m/s tới va chạm
xuyên tâm vào vật có khối lượng 𝑚𝑚2 = 3 kg đứng yên. Va chạm là hoàn toàn mềm. Nh ệ i t
lượng tỏa ra trong quá trình va chạm là: A. 21,3 J. B. 21,6 J. C. 22,2 J. D. 22,5 J. Lời giải:
Vận tốc của hệ vật m1 và m2 sau khi va chạm là:
Áp dụng công thức: 𝑣 𝑣 = 𝑚𝑚1 𝑣𝑣 𝑚𝑚 1 1+𝑚𝑚2
Nhiệt lượng tỏa ra trong quá trình va chạm là: Q = -A = W 2 𝑚𝑚1𝑚𝑚2 2 d1 – Wd2 = 1𝑚𝑚 − 1 (𝑚𝑚 𝑣𝑣 𝑣𝑣 = 21,6 (J ) 2 1𝑣𝑣1 2 1 + 𝑚𝑚2) ( 𝑚𝑚1 𝑚𝑚 1)2 = 1 1 1+𝑚𝑚2 2 𝑚𝑚1+𝑚𝑚2
Group: Bachkhoa Universe – Góc học tập và thảo luận 39 TAILIEUHUST.COM
Chương 5: Trường hấp dẫn A. Công thức
1. Định luật Newton
- Lực hút của hai chất điểm m và m ' cách nhau đoạn r : ′ 2 ′ m.m 1 − 1 Nm F = F = G . G = 6, 67⋅10 . 2 2 r kg Lưu ý:
• Công thức này chỉ áp dụng cho chất điểm.
• Đổi với vật lớn thì phải dùng phương pháp tích phân.
• Hai quả cầu đồng chất thì có thể dùng được trong đó r là khoảng cách giữa 2 tâm cầu.
2. Gia tốc trọng tr ờ ư ng GM
- Gia tốc trọng trường ạ t i mặt đất: g = . 0 2 R
- Gia tốc trọng trường ở độ cao GM h: g = . h 2 ( R + ) h
- Liên hệ giữa gia tốc trọng trường ạ
t i mặt đất và tại độ cao h : 2 g R 1 h = → g = g 2 h 0 2 g (R + h)   0 h 1 +    R Khi h
R ta có thể áp dụng công thức gần đúng: 1 → (1+ )n x x ≈1+ nx . −2 1  h hh  = 1+
≈ 1− 2 . Thay vào g ta có: g = g 1− 2 .     2 h h 0  h   R RR  1+    R
40 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
B. Bài tập trắc nghiệm
Câu 1. Một quả cầu đ n
ồ g chất khối lượng 𝑚𝑚1 đặt cách đầu một thanh đồng chất một đoạn ằ
b ng 𝑎𝑎 trên phương kéo dài của thanh. Thanh có chiều dài 𝑙𝑙, khối lượng 𝑚𝑚2. Lực hút
của thanh lên quả cầu là : A. 𝑚𝑚 𝑚𝑚 𝑚𝑚 𝑚𝑚 𝐺 𝐺 1𝑚𝑚2 . B. 𝐺 𝐺 1𝑚𝑚2 . C. 𝐺 𝐺 1𝑚𝑚2 . D. 𝐺 𝐺 1𝑚𝑚2 . 𝑚𝑚(𝑚𝑚+𝑙𝑙) 𝑚𝑚(𝑚𝑚−𝑙𝑙) 𝑚𝑚2 𝑚𝑚𝑙𝑙 Lời giải: dx a x
Vi phân thanh các đoạn dx có khối lượng dm và cách đầu thanh gần với q ả u cầu khoảng x
Do thanh đồng chất , ta có: 𝑑𝑑𝑚𝑚= 𝑑𝑑𝑥𝑥 => dm = 𝑚𝑚2dx 𝑚𝑚2 𝑙 𝑙 𝑙 𝑙
Lực hút của đoạn dx lên quả cầu là: dF = G 𝑚𝑚1𝑑𝑑𝑚𝑚 = G 𝑚𝑚1𝑚𝑚2𝑑𝑑𝑥𝑥 (𝑚𝑚+ 𝑥𝑥)2 𝑙𝑙(𝑚𝑚+ 𝑥𝑥)2
Lực hút của thanh lên quả cầu là : 𝑙 𝑙 F = ∫ G 𝑙𝑙 𝑚𝑚1𝑚𝑚2 𝑚𝑚 𝑚𝑚 𝑚𝑚 𝑚𝑚 𝑚𝑚 𝑑𝑑𝑥𝑥 = −𝐺𝐺 1𝑚𝑚2�= −𝐺𝐺 1𝑚𝑚2 + 𝐺 𝐺 1𝑚𝑚2 = 𝐺 𝐺 1𝑚𝑚2 �1− 1 � = 𝐺 𝐺 1𝑚𝑚2 0 𝑙𝑙(𝑚𝑚+ 𝑥𝑥)2 𝑙𝑙(𝑚𝑚+𝑥𝑥) 0 𝑙𝑙(𝑚𝑚+𝑙𝑙) 𝑙𝑙𝑚𝑚 𝑙
𝑙 𝑚 𝑚 𝑚𝑚+𝑙𝑙 𝑚𝑚(𝑚𝑚+𝑙𝑙)
Câu 2. Một vệ tinh có khối lượng 𝑚 𝑚 = 150 k
g chuyển động trên quỹ đạo tròn bán kính 𝑟 𝑟 =
7, 4.106 m quanh Trái Đất. Cho khối lượng trái đất 𝑀 𝑀 = 5, 98.1024 kg. Cho biết hằng số hấp
dẫn 𝐺 𝐺 = 6, 67.10−11 N ⋅ m2/kg2. Tốc độ vệ tinh trên quỹ đạo đó là: A. 7,042 k /s m . B. 6,742 km/s. C. 7,342 km/s. D. 6,442 km/s. Lời giải:
Lực hướng tâm tác dụng lên ệ
v tinh là: Fht = Fhd = G𝐶𝐶𝑚𝑚 𝑟𝑟2
=> maht = G𝐶𝐶𝑚𝑚 𝑟𝑟2
=> aht = G𝐶𝐶 mà aht = 𝑣𝑣2 𝑟𝑟2 𝑟 𝑟 => v = �𝑎𝑎 𝐶𝐶 ℎ = � 𝑡𝑡 𝑟𝑟 𝐺 𝐺 = 7342 (m/s) = 7,342 (km/s) 𝑟 𝑟
Câu 3. Gọi M và R lần lượt là khối lượng và bán kính của Trái Đất. G là hằng số hấp dẫn
vĩ trụ, g và g lần lượt là gia tốc trọng trường ở
độ cao h và mặt đất. Công thức nào dưới 0
đây đúng với h bất kỳ:
Group: Bachkhoa Universe – Góc học tập và thảo luận 41 TAILIEUHUST.COM  2h GM 1−   A. GM GM  2h   R g = B. g = C. g = g 1 − D. g = 2 0   (R +h) 2 RR  2 R Lời giải: + Tại độ cao GMm
h bất kì, lực hấp dẫn giữa Trái Đất và vật: F = hd 2 (R + ) h GMm GM
+ Mà F = P= mg ⇔ = mg ⇔ g = hd 2 2 (R + h) (R + h)
Câu 4. Hai khối cầu giống nhau được đặt sao cho tâm cách nhau khoảng r thì lực hấp dẫn
giữa chúng là F . Nếu thay một trong hai khối cầu trên bằng một khối cầu đồng chất khác
nhưng có bán kính lớn gấp hai, ẫ
v n giữ nguyên khoảng cách giữa hai tâm (hai khối ầ c u
không chạm nhau) thì lực hấp dẫn g ữ i a chúng lúc này là: A. 2 F . B. 16 F . C. 8 F . D. 4 F . Lời giải:
Khi bán kính khối cầu tăng gấp hai (r′ = 2r thì khối lượng của khối cầu là : 2 2 ) ′ ′ 3 ′ 3
m = DV = Dπ r = Dπ (2r) = 8m 2 2
Khi giữ nguyên khoảng cách giữa 2 tâm (do hai khối ầ
c u không chạm nhau) thì lực hấp
dẫn giữa 2 quả cầu này là: m m′ m .8m 1 2 1 2 F = G = G = 8F hd 2 2 r r
Câu 5. Ở mặt đất, một vật có trọng lượng 10 N . Nếu chuyển vật này ở độ cao cách Trái Đất
một khoảng R ( R là bán kính Trái Đất) thì trọng lượng của vật bằng A. 1 N . B. 2,5 N . C. 5 N. D. 10 N . Lời giải: Tại mặt đất ta có Mm
F = P = 10 N = G hd 2 R
Tại độ cao cách Trái Đất một khoảng R (với R là bán kính Trái Đất) thì trọng lượng của vật bằng: ′ ′ Mm Mm P P = F = G = G = =2,5 N hd 2 2 (R + h) (2R) 4
Câu 6. Biết gia tốc rơi tự do ở đỉnh và chân một ngọn núi lần lượt là 9,809 2
m / s và 9.810 2
m / s . Coi Trái Đất là đồng chất và chân núi cách tâm Trái Đất 6370km. Chiều cao của ngọn núi này là? A. 324.7 m B. 640 m C. 649.4 m D. 325 m
42 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 Lời giải:
Ta có gia tốc rơi tự do tại đỉnh có độ cao h có công thức tính là: M g = G h 2 ( R + ) h
Gia tốc rơi tự do tại chân núi M
(h = 0) : g = G 0 2 R 2 gR + h ⇒ =  gR hg   9,810  ⇒ h = R −1 = 6370  −1 ≈ 0,3246 km  g   9,809   h   
Câu 7. Coi khoảng cách trung bình giữa tâm Trái ấ
Đ t và tâm Mặt Trăng gấp 60 lần bán
kinh Trái Đất; khối lượng Mặt Trăng nhỏ hơn khối lượng Trái Đất 81 lần. Xét vật M nằm
trền đường thẳng nối tâm Trái Đất và tâm Mặt Trăng mà ở đó có lực hấp dẫn của Trái Đất
và của Mật Trăng cân bằng nhau. So với bán kính Trái Đất, khoảng cách từ M đến tâm Trát Đất gấp A. 56,5 lần. B. 54 lần. C. 48 lần. D. 32 lần. Lời giải:
Gọi x là khoảng cách từ tâm Trái Đất (TĐ) đến vật m đặt tại điểm ta xét nên khoảng cách từ tâm của ặ
M t Trăng (MT) đến vật là 60R − x . Ta có: M .m M .m F = F TD MT ⇒ G = G TD− m MT − m 2 2 x (R − x) 81.M M x MT MT ⇒ = ⇒
= 9 ⇒ x = 54 R Chọn đáp án (B) . 2 2 x (60 R − ) x 60 R − x
Câu 8. Cho tam giác vuông cân ABC vuông tại C, có cạnh huyền AB = R . Tại ba đỉnh
A, B và C của tam giác, người ta ặ đ t 3 c ấ
h t điểm có khối lượng lần lượt là m, 2 m và 3 m.
Tìm lực hấp dẫn tác dụng lên chất điểm ạ t i C . 2 2 2 2 A. m m m m 3 5G B. 6 5G C. 12G D. 6G 2 R 2 R 2 R 2 R Lời giải: Do tam giác R
ABC cân tại C nên ta có: AB = BC = 2
Group: Bachkhoa Universe – Góc học tập và thảo luận 43 TAILIEUHUST.COM
- Lực hấp dẫn tác dụng lên chất điểm tại C là: F = F + F C AC BC 2  M M m A C 6 F = G = GAC 2 2 Mà  r R  2 M M 12mB C F = G = G BC 2 2  r R 2 m 2 2
⇒ F = F + F = 6 5G C AC BC 2 R
Câu 9. Kim tinh (còn gọi là sao Thái Bạch, sao Hôm hoặc sao Mai) được ọ g i là "hành tinh
sinh đôi" với Trái Đất do khối lượng, kích thước gần giống với Trái Đất. Biết Trái Đất và Kim
Tinh có đường kính lần l ợ
ư t là 12740 km và 12090 km. Khối lượng của Kim Tinh bằng 81,5% khối lượng ủ
c a Trái Đất. Tính gia tốc rơi tự do trên bề mặt của Kim Tinh biết gia tốc rơi tự
do trên bề mặt của Trái Đất có giá trị 2 g = 9,81 m / s . T A. 2 13, 37 m / s B. 2 8,88 m / s . C. 2 7, 20 m / s . D. 2 1, 67 m / s . Lời giải: M
Gia tốc trên bề mặt Kim Tinh: K g = G K 2 RK
Gia tốc trên bề mặt Trái Đất: MT g = G T 2 RT 2 g M R 0,815M Mà K K T T 2 = → g = 9,81, → g = 8,88 m / s 2 K 2 K g M R 6045 T T K
Câu 10. Trong một quả cầu bằng chì bán kính R , người ta khoét một lỗ hình cầu bán kính
R / 2 . Tìm lực do quả cầu tác dụng lên vật nhỏ m trên đường nối tâm hai hình cầu, cách tâm hình cầu lớn ộ
m t đoạn d , biết rằng khi chưa khoét quả cầu có khối lượng M . 2 2 − + 2 2 + + A. 7d 8dR 2R 7d 8dR 2R F = GMm ⋅ B. F = GMm⋅ 2  2 R   R  2 8d d −   2 8d d −    2   2  2 2 − + 2 2 − + C. 7d 8dR 2R 7d 8dR 2R F = GMm ⋅ D. F = GMm⋅ 2  2 R   R  2 d d −   2 4d d −    2   2  Lời giải:
44 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 - Phần khoét đi ẽ s hút M m m lực hấp dẫn: k F = G 1 2  R d −    2 
Lực hấp dẫn do cả quả cầu đặt tác dụng lên Mm m : F = G 2 2 d     M Mk F F F Gm  ⇒ = − = − (*) 2 1 2 2  d R     d −      2   3
- Quả cầu đồng chất nên: M V ( R / 2) 1 M K k = = = → M = 3 M V R 8 k 8 2 2 Thay vào (*) ta đượ − + c: 7d 8dR 2R F = GM . m 2   2 R 8d d −    2 
Group: Bachkhoa Universe – Góc học tập và thảo luận 45 TAILIEUHUST.COM
Chương 6. Dao động – sóng A. Công thức
1. Dao động cơ điều hòa - Phương trình dao đ n
ộ g: 𝑥 𝑥 = 𝐴𝐴cos (𝜔𝜔0𝜔 𝜔 + 𝜑𝜑).
- Biên độ dao động: 𝐴 𝐴 = 𝑥𝑥max.
- Tần số góc riêng: 𝜔𝜔0 = �𝑘𝑘. 𝑚𝑚
- Pha của dao động: (𝜔𝜔0𝜔 𝜔 + 𝜑𝜑), 𝜑𝜑 là pha ban đầu của dao động.
- Vận tốc của dao động: 𝑣 𝑣 = 𝑑𝑑𝑥𝑥= −𝐴𝐴𝜔𝜔 𝑑𝑑𝑡𝑡
0sin (𝜔𝜔0𝜔 𝜔 + 𝜑𝜑). 2. Con lắc vật lý
- Tần số góc: 𝜔 𝜔 = �𝑚𝑚𝑔𝑔𝑚𝑚 . 𝐼 𝐼 Trong đó: L l
à khoảng cách từ khối tâm đến trục quay, 𝐼𝐼−moment quán tính của vật đối với trục quay.
3. Dao động cơ tắt dần
- Phương trình dao động ắ
t t dần: 𝑥 𝑥 = 𝐴𝐴 2
0𝑒𝑒−𝛽𝛽𝑡𝑡cos (𝜔𝜔𝜔𝜔 + 𝜑𝜑). với 𝜔 𝜔 = �𝜔𝜔0 − 𝛽𝛽2. - Giảm lượng loga: 𝑡𝑡
𝛿 𝛿 = ln 𝐴𝐴( ) = 𝛽𝛽𝑇𝑇. 𝐴𝐴(𝑡𝑡+𝑇𝑇) - Biên độ dao động ắ
t t dần: 𝐴𝐴0𝑒𝑒−𝛽𝛽𝑡𝑡 ⇒ −𝐴𝐴0𝑒𝑒−𝛽𝛽𝑡𝑡 ≤ 𝑥𝑥 ≤ 𝐴𝐴0𝑒𝑒−𝛽𝛽𝑡𝑡. Nhận xét: Hệ c ỉ
h thực hiện dao động tắt dần khi 𝜔𝜔0 > 𝛽𝛽.
46 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
B. Bài tập trắc nghiệm
Câu 1. Một chất điểm dao ộ
đ ng điều hòa với chu kì 𝑇𝑇0 = 2 s, pha ban đầu 𝜑 𝜑 = 𝜋𝜋 . Năng 3
lượng toàn phần 𝑊 𝑊 = 2,6. 10−5 J và lực tác dụng lên chất điểm lúc lớn nhất 𝐹𝐹0 = 2.10−3 N.
Phương trình dao động nào sau đây là đúng chất điểm trên:
A. 2,9sin �2𝜋𝜋𝜔𝜔 + 𝜋𝜋 � cm.
B. 2,7sin �𝜋𝜋𝜔𝜔 + 2𝜋𝜋 � cm. 3 3
C. 2,6cos �𝜋𝜋𝜔𝜔 + 𝜋𝜋 � cm.
D. 2,8cos �2𝜋𝜋𝜔𝜔 + 𝜋𝜋 � cm. 3 3 Lời giải:
Năng lượng toàn phần W là cơ năng c a ủ con lắc, lực tác d n ụ g lên chất đ ể i m lúc lớn nhất 𝐹𝐹0 = 𝑘𝑘𝐴𝐴 Ta có: . , .10−5 𝑊 𝑊 = 2,6.10−5 = 1 𝑘𝑘𝐴𝐴2 = 1
𝐹𝐹𝐴𝐴 ⇒ 𝐴𝐴 = 2𝑊𝑊
= 2 2 6 = 2,6(𝑚𝑚𝑚𝑚) 2 2 𝐹 𝐹 2.10−3
Chu kì 𝑇𝑇0 = 2 = 2𝜋𝜋 ⇒ 𝜔𝜔 = 𝜋𝜋 𝜔 𝜔
Do đó, phương trình dao động ủ
c a chất điểm là 2,6 cos �𝜋𝜋𝜔𝜔 + 𝜋𝜋 � 3
Câu 2. Một con lắc lò xo 𝑚 𝑚 = 10 g, dao động điều hòa với độ dời 𝑥 𝑥 = 8cos �5𝜋𝜋𝜔 � 𝜔 c + 𝜋𝜋 m. 2
Kí hiệu 𝐹𝐹0 là lực cực đại tác dụng lên con lắc và 𝑊𝑊 là năng lượng của con lắc. Kết luận nào dưới đây đúng:
A. 𝐹𝐹0 = 0,3 N, 𝑊 𝑊 = 0, 9.10−2 J.
C. 𝐹𝐹0 = 0,3 N, 𝑊 𝑊 = 0, 8.10−2 J.
B. 𝐹𝐹0 = 0,2 N, 𝑊 𝑊 = 0, 8.10−2 J.
D. 𝐹𝐹0 = 0,2 N, 𝑊 𝑊 = 0, 9.10−2 J. Lời giải:
Ta có: 𝜔 𝜔 = �𝑘𝑘⇒ 𝑘𝑘 = 𝜔𝜔2𝑚 𝑚 = (5𝜋𝜋)2. 0,01 ⇒ 𝐹𝐹
01. ( 𝜋𝜋)2 ≈ 0,2(𝑁𝑁) 𝑚 𝑚 0 = 𝑘𝑘𝐴𝐴 = 0,08.0, 5 1 1
𝑊 𝑊 =𝑘𝑘𝐴𝐴2 = (5𝜋𝜋)2. 0,01.0,082 ≈ 1 0,8. 0−2(𝐽𝐽) 2 2
Câu 3. Một con lắc toán có sợi dây 𝑙 𝑙 = 1 m, cứ sau Δ𝜔𝜔 = 0,8 phút thì biên độ dao động giảm 2 ầ
l n. Giảm lượng lôga của con lắc đó bằng giá trị nào sau đây (cho 𝑔 𝑔 = 9,8 m/s2) A. 3, 489.10−2. B. 2, 898.10−2. C. 2, 701.10−2. D. 3, 292.10−2. Lời giải: Ta có: g ω = 0 l −β t Tạ A(t ) A .e i t bất kì ta có: β∆t ln 2 0 = 2 ⇔ = 2 ⇒ e = 2 ⇒ β = − β( t+∆ ) A(t + t ∆ ) A . t e ∆t 0
Group: Bachkhoa Universe – Góc học tập và thảo luận 47 TAILIEUHUST.COM
Giảm lượng loga của con lắc là: 2π ln 2 2π ln 2 2π − 2 σ = β .T = β = × = × ≈ 2,898.10 2 2 2 ω t ∆ ω − β t ∆ g  ln 2 0 −   l  ∆t
Câu 4. Một con lắc toán có sợi dây 𝑙 𝑙 = 65 cm. Biết rằng sau thời gian 𝜏 𝜏 = 6 phút, nó mất
99% năng lượng. Giảm lượng lôga của con ắ
l c nhận giá trị nào dưới đây? A. 0, 975.10−2. B. 1, 125.10−2. C. 1, 035.10−2. D. 1, 065.10−2. Lời giải: Tại t bất kì ta có: 2 W(t)  ( A t)  A . −β t e βτ ln 10 0 = 100⇒ = 100 ⇔ = 10⇒ e = 10⇒ β =   − β (t+τ ) W(t + τ ) A(t +  τ) A .e  τ 0
Lượng giảm loga của con ắ l c: 2π ln10 2π ln10 2π −2 σ = β.T = β = × = × ≈1, 035.10 2 2 2 ω τ ω −β τ 0 g  ln10  −   l  τ 
Câu 5. Một chất điểm dao động điều hòa với chu kì 1,4 s và biên độ 8 cm. Vận tốc chất điểm trên ạ
t i vị trí mà li độ bằng 1 biên độ bằng giá tr ịnào dưới đây : 2 A. 0,311 m/s. B. 0,32 1 m/s. C. 0,33 1 m/s. D. 0,34 1 m/s. Lời giải:
Áp dụng phương trình về mối liên hệ của A, x, v: 2 2  v  2π  A  2π 2 2 2 2 2 2 2 A = x +
⇒ v = ω A −x = A − =
0, 08 − 0, 04 = 0,311( m / s)  ω      T  2  1, 4
Câu 6. Một con lắc toán có sợi dây dài là 𝑙𝑙, và cứ sau Δ𝜔 𝜔 = 5 phút thì biên độ dao động
giảm 2 lần. Giảm lượng lôga của con ắ
l c đó là 𝛿 𝛿 = 0,02 . 3 Cho gia tốc t ọ r ng trường 𝑔 𝑔 =
9,8 m/s2. Hỏi 𝑙𝑙 bằng giá trị nào dưới đây: A. 2,554 m. B. 2,044 m. C. 1,704 m. D. 2,214 m. Lời giải:
Thiết lập phương trình dao động tắt dần ủ
c a con lắc lò xo. Trong trường hợp này, hợp lực
tác dụng lên quả cầu: F + F = −kx − rv C
48 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 Phương trình cơ bản ủ c a chuyển ộ đ ng trong trường ợ
h p này là ma = −kx − rv 2 2 Hay: d x dx d x r dx k m = −r − kx ⇔ + + x = 0 (1 ) 2 2 dt dt dt m dt m Đặt r β = (hệ số tắt dần) 2m 2
Phương trình (1) trở thành d x dx 2 x + 2β +ω x = 0 (2 ) 2 0 dt dt
(2) gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi ω > β , 0
nghiệm phương trình này có dạng: −βt x = A e cos( t ω +ϕ) 0
Đây là biểu thức độ dời ủ
c a dao động tắt dần. ằ
H ng số ω gọi là tần số của dao động tắt dần: 2 2 ω = ω − β 0 Theo bài ra, ta có: x β − . t ∆ 1 β − .300 1 3 − = e = ⇒ e = ⇒ β ≈ 7,7.10 A 2 2 0 δ
Giảm lượng loga của con lắc: δ = T β = 0,023 ⇒ T = = 2,987( s) β π π π Chu kỳ 2 2 2
T của dao động tắt dần là: T = = =
= 2,987( s) ⇒ l = 2, 214( m) 2 2 ω ω − β g 2 0 − β l
Câu 7. Một con lắc vật lý được cấu tạo bằng một thanh đồng chất tiết diện ề đ u có độ dài
bằng 𝑙𝑙 và trục quay O của nó cách trọng tâm G một khoảng bằng 𝑥𝑥. Biết rằng chu kỳ dao
động 𝑇𝑇 của con lắc này là nhỏ nhất, 𝑥𝑥 nhận giá t ịr nào dưới đây: A. 1. B. 1/2. C. 1 . D. 1 . √3 4√3 2√3 Lời giải: Chu kỳ dao động I
T của con lắc: T =2π mgd
Với I = I + I với I là moment quán tính của thánh và I là moment quán tính của chất 1 2 1 2
điểm đối với trục quay 2 2     2 l 2 l m x + x +     2 ml 12 12 2    
I = I + I =
+ mx (d = x) ⇒T = 2π = 2π 1 2 12 mgx gx
Group: Bachkhoa Universe – Góc học tập và thảo luận 49 TAILIEUHUST.COM 2   ′ l l l 2 2 T
⇔ T = ⇒ x − x + = ⇒  x = = x 0 2 0 max 12   12 2 3
Câu 8. Một xe lửa gồm nhiều toa được ặ
đ t trên các lò xo của ệ h thống bánh xe. ỗ M i lò xo
của toa xe chịu một trọng lượng 𝑃 𝑃 = 5.104 N nén lên nó. Xe lửa bị rung động mạnh nhất khi nó chạy với ố t c ộ
đ 𝑣 𝑣 = 26 m/s qua các chỗ nối ủ c a đường ray. ộ Đ dài mỗi thanh ray
bằng 𝑙 𝑙 = 12,5 m. Hệ số đàn hồi của các lò xo nhận giá trị nào dưới đây (cho 𝑔 𝑔 = 9,8 m/s2 ) A. 82, 64.104 N/m. B. 88, 64.104 N/m. C. 87, 14.104 N/m. D. 84, 14.104 N/m. Lời giải: Con lắc dao ộ
đ ng mạnh nhất khi xảy ra cộng hưởng (chu kỳ dao động riêng ủ c a vật trùng chu kỳ qua các c ỗ h nối ủ c a đường ray): S 12, 5 T = = =0, 48( ) s v 26 4 Mặt khác: 4 P 5.10
P = 5.10 (N ) = mg ⇒ m = = = 5102,04( kg) g 9,8 2 2 m 4π .m 4π .5102,04 Mà 4 T = 2π
= 0, 48(s) ⇒ k = = = 87, 4.10 ( N / ) m 2 2 k T 0, 48
50 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Chương 7. Nguyên lý thứ nhất của nhiệt động lực học và thu ế y t ộ
đ ng học phân tử A. Công thức
1. Phương trình trạng thái của khí lý tưởng 𝑚𝑚 𝑃𝑃𝑉𝑉 =
𝑅𝑅𝑇𝑇 = 𝑛𝑛𝑅𝑅𝑇𝑇. 𝜇 𝜇 - Giá tr c ị ủa R
• Hệ SI: R = 8.314 J/mol. K → P(Pa), V(m3)
• R = 0.082 L. atm/mol. K → P(atm), V (lít) 2. Nhiệt
- Nhiệt dung riêng: là lượng nhiệt cần thiết để tăng nhiệt độ của 1kg chất tăng thêm 1 độ. 𝑑𝑑𝑄𝑄 hoặc (đơn vị ).
𝑃 𝑃 = 𝑚𝑚. 𝑚𝑚𝑃𝑃𝑑𝑑𝑇𝑇
𝑑𝑑𝑄𝑄𝑣 𝑣 = 𝑚𝑚. 𝑚𝑚𝑣𝑣𝑑𝑑𝑇𝑇 : J. kg−1 −1 K
- Nhiệt dung riêng mol (nhiệt dung riêng phân tử): là lương nhiệt cần thiết để tăng 1 mol chất tăng thêm 1 độ. 𝑑𝑑𝑄𝑄 𝐶𝐶 hoặc (đơn vị: J.mol ). 𝑃 𝑃 = 𝑛𝑛. 𝑃𝑃𝑑𝑑𝑇𝑇
𝑑𝑑𝑄𝑄𝑣 𝑣 = 𝑛𝑛. 𝐶𝐶𝑣𝑣𝑑𝑑𝑇𝑇 −1 K−1
- Liên hệ giữa 𝑚𝑚 và 𝐶𝐶: 𝑚𝑚𝑚𝑚 = 𝑛𝑛𝐶𝐶 → 𝑚 𝐶𝐶 𝑚 = = 𝑚𝑚
𝜇𝜇𝑚𝑚. với 𝜇𝜇 ộ ất. 𝑛 𝑛 −khối lượng m t mol ch 3. Hệ ố s Poisson 𝑖 𝑖 + 2 𝐶𝐶 𝐶𝐶 𝑅𝑅 𝑝𝑝 𝑚𝑚𝑝𝑝 𝑖 𝑖 + 2 𝑝 𝑝 = 𝛾 𝛾 = = = . với � 𝑖 𝑖 . 𝐶𝐶 𝑖𝑖
𝑣 𝑣𝑚𝑚𝑣 𝑣 𝑖 𝑖 𝐶𝐶𝑣 𝑣 = 𝑅 𝑅 2
Trong đó: 𝑖𝑖−bậc tự do. Đơn nguyên tử: 𝑖 𝑖 = 3, Hai nguyên ử
t : 𝑖 𝑖 = 5, Ba nguyên tử: 𝑖 𝑖 = 6 …
4. Công và ba trạng thái cơ bản - Công: 𝑣𝑣
𝐴 𝐴 = ∫ 2 𝑝𝑝𝑑𝑑𝑉𝑉. 𝑣𝑣1
- Đẳng tích: 𝑉 𝑉 = const → 𝑃𝑃1 = 𝑃𝑃2. 𝑇𝑇1 𝑇𝑇2
- Đẳng áp: 𝑃 𝑃 = const → 𝑉𝑉1 = 𝑉𝑉2. 𝑇𝑇1 𝑇𝑇2
- Đẳng nhiệt: 𝑇 𝑇 = const → 𝑃𝑃1𝑉𝑉1 = 𝑃𝑃2𝑉𝑉2.
5. Phương trình cơ bản của thuyết động học phân tử
Group: Bachkhoa Universe – Góc học tập và thảo luận 51 TAILIEUHUST.COM � ��
- Áp suất lên thành bình: 𝑚𝑚 𝑝 𝑝 = 1 𝑛𝑛 � � �= 2 𝑛𝑛 0𝑣𝑣2 = 2 𝑛𝑛 3 0𝑚𝑚0𝑣𝑣2 3 0 2 3 0W � .
- Động năng tịnh tiến trung bình: W � = 3𝑅𝑅𝑇𝑇 = 3 𝑘𝑘𝑇𝑇. 2 𝑁 𝑁 2
- Vận tốc căn quân phương: 𝑣𝑣𝑐 𝑐 = �3𝑘𝑘𝑇𝑇 = �3𝑅𝑅𝑇𝑇. 𝑚𝑚0 𝜇 𝜇
- Mật độ phân tử: 𝑛𝑛0 = 𝑝𝑝 . 𝑘𝑘𝑇𝑇
- Vận tốc trung bình: 𝑣𝑣‾ = � 8𝑅𝑅𝑇𝑇 = �8𝑅𝑅𝑇𝑇 . 𝜋𝜋𝑛𝑛0𝑚𝑚0 𝜋𝜋𝜇𝜇
- Vận tốc xác suất lớn nhất: 𝑣𝑣𝑥𝑥𝑠𝑠 = �2𝑘𝑘𝑇𝑇 . 𝑚𝑚0
6. Công thức khí áp − 0 m ghkTp = p e - Công thức khí áp: 0  . − 0 m ghkT n  = n e 0 - Nhận xét:
• Khí quyển có ranh giới rõ rệt.
• Mật độ hạt giảm ầ d n theo chiều cao.
• Công thức khí áp mang tính gần đúng (trong phạm vi ℎ không lớn, độ vài km).
7. Nội dung định luật I -
Độ biên thiên nội năng của hệ bằng tổng công và nhiệt lượng mà ệ
h nhận được: Δ𝑈𝑈 = 𝐴 𝐴 + 𝑄𝑄. Hay 𝑄 𝑄 = Δ𝑈𝑈 + . 𝐴𝐴
- Các trường hợp đặc biệt: • Đoạn nhiệt: ệ
H không trao đổi nhiệt với bên ngoài nên: 𝑄 𝑄 = Δ𝑈𝑈 + 𝐴 𝐴 = 0.
• Đẳng áp: 𝑄 𝑄 = Δ𝑈𝑈 + 𝐴 𝐴 = Δ𝑈𝑈 + 𝑝𝑝𝑑𝑑𝑉𝑉.
• Đẳng tích: 𝑄 𝑄 = Δ𝑈𝑈.
• Đẳng nhiệt: 𝑄 𝑄 = 𝐴𝐴. 8. Hiện t ợ ư ng đoạn nh ệ i t
52 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
- Công thức đoạn nhiệt: 𝑝𝑝 𝛾 𝛾 𝛾𝛾 𝛾𝛾−1 𝛾𝛾−1 1𝑉𝑉1 = 𝑝𝑝2𝑉𝑉 hoặc 2 𝑇𝑇1𝑉𝑉1 = 𝑇𝑇2𝑉𝑉 . 2
- Công thức tổng quát công sinh bởi hệ: 𝑉𝑉
𝐴 𝐴 = ∫ 2 𝑝𝑝𝑑𝑑𝑉𝑉. 𝑉𝑉1
- Công trong các trường hợp:
• Đẳng áp: 𝑝 𝑝 = const, 𝐴 𝐴 = 𝑝𝑝(𝑉𝑉2 − 𝑉𝑉1) = 𝑝𝑝Δ𝑉𝑉.
• Đẳng tích: 𝑉 𝑉 = const, 𝐴 𝐴 = 0. • 𝑉𝑉2 𝑉𝑉2
Đẳng nhiệt: 𝑇 𝑇 = const, 𝐴 𝐴 = ∫ 𝑛𝑛𝑅𝑅𝑇𝑇𝑑𝑑𝑉𝑉 = 𝑛𝑛𝑅𝑅𝑇𝑇 �l.n � 𝑉𝑉1 𝑉 𝑉 𝑉𝑉1
• Đoạn nhiệt: 𝑝𝑝𝑉𝑉𝛾 𝛾 = const = 𝐾𝐾 → 𝑝𝑝 = 𝐾𝐾
= 𝐾𝐾𝑉𝑉−𝛾𝛾, 𝑉𝑉𝛾 𝛾 𝑉𝑉 𝑉𝑉 2 𝑉𝑉 2 −𝛾𝛾+1
𝐾𝐾𝑉𝑉−𝛾𝛾+1 − 𝐾𝐾𝑉𝑉−𝛾𝛾+1
𝐴 𝐴 = 𝐾𝐾 � 𝑉𝑉−𝛾𝛾𝑑𝑑𝑉𝑉 = 𝐾 𝐾� = 2 1 . − − 𝑉𝑉 𝛾𝛾 + 1 𝛾𝛾 + 1 1 𝑉𝑉1
Group: Bachkhoa Universe – Góc học tập và thảo luận 53 TAILIEUHUST.COM
B. Bài tập trắc nghiệm
Câu 1. Một khối khí Hiđđô bị nén đến t ể
h tích bằng 1/2 lúc đầu khi nhiệt độ không đổi.
Nếu vận tốc trung bình của phân tử hidro lúc đầu là 𝑉𝑉 thì vận tốc trung bình sau khi nén là A. 2 V. B. 4 V. C. 1 V. D. V/2. Lời giải: Nén đẳng nhiệt
Công thức tính vận tốc trung bình c a
ủ chất khí là 𝑣 𝑣 = �8𝑘𝑘𝑇𝑇 chỉ ph
ụ thuộc nhiệt độ nên vận 𝑚𝑚𝜋𝜋
tốc trung bình không đổi
Câu 2. 1 g khí hiđtrô (H2) đựng trong một bình có t ể
h tích 5 l. Mật độ phân tử của chất khí
đó là: (cho hằng số khí 𝑅 𝑅 = 8, 31.103 J/kmol.K; hằng số Boltzmann (𝑘 𝑘 = 1, 38.1023 J/K)
A. 6, 022.1025 phân tử /m3. C. 5, 522.1025 phân tư /m3.
B. 4, 522.1025 phân tử /m3.
D. 7, 022.1025 phân tử /m3. Lời giải:
Số phân tử khí là: 𝑁 𝑁 = 𝑛𝑛. 𝑁𝑁 𝐴 𝐴 = 𝑚𝑚 𝑁𝑁 𝜇 𝜇 𝐴𝐴
Hằng số Boltzmann 𝑘 𝑘 = 𝑅𝑅𝑇𝑇= 𝑅𝑅 = 1,28.10−23(⁄𝐽𝐽𝐾𝐾 ) ⇒ 𝑁𝑁 ⇒ 𝑁𝑁 = 𝑚𝑚 . 𝑅𝑅 𝑉 𝑉 𝑁𝑁 𝐴 𝐴 = 𝑅𝑅 𝐴 𝐴 𝑘 𝑘 𝜇 𝜇 𝑘𝑘
Mật độ phân tử của chất khí là 𝑁𝑁 = 𝑚𝑚𝑅𝑅= 6,022.1025
𝑉 𝑉 𝜇𝜇𝑘𝑘𝑉𝑉
Câu 3. Khối lượng ủ
c a 1kmol chất khí là 𝜇 𝜇 = 3
0 kg/kmol và hệ số Poat-xông của chất khí là
𝛾 𝛾 = 1,4. Nhiệt dung riêng đẳng áp của khí bằng? Hằng số khí 𝑅 𝑅 = 8, 31.103Jkmol−1 K−1 A. 995,5 k J/( g. K). B. 982,5 k J/( g. K). C. 930,5 k
J/( g. K). D. 969,5 J/(kg ⋅ K). Lời giải:
Hệ số Poisson 𝛾 𝛾 = 𝐶𝐶𝑝𝑝= 1,4 𝐶𝐶𝑣 𝑣
Lại có: 𝐶𝐶𝑝 𝑝 − 𝐶𝐶𝑣 𝑣 = 𝑅𝑅
Do đó: 𝛾 𝛾 = 𝐶𝐶𝑝𝑝= 𝐶𝐶𝑝𝑝 ⇒ 𝐶𝐶 𝐶𝐶 𝑝 𝑝 = 𝛾𝛾𝑅𝑅
𝑣 𝑣 𝐶𝐶𝑝𝑝−𝑅𝑅 𝛾𝛾−1
Nhiệt dung riêng đẳng áp của khí: 𝐶𝐶 1,4.8,31.103 𝑝𝑝 𝛾𝛾𝑅𝑅 𝑚𝑚 = = ⁄ . 𝑝 𝑝 =
≈ 969,5(𝐽 𝐽 𝑘𝑘𝑔𝑔 𝐾𝐾)
𝜇 𝜇 𝜇𝜇(𝛾𝛾 − 1) 30(1,4 − 1)
Câu 4. Một khối khí ôxy (O2) b ịnung nóng từ nhiệt dộ 240 K đến 267∘C. Nếu vận tốc
trung bình của phân tử ôxy lúc đầu là 𝑣𝑣 thì lúc sau là:
54 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 A. 1,35𝑣𝑣. B. 1,55𝑣𝑣. C. 1,5𝑣𝑣. D. 1,6𝑣𝑣. Lời giải: Công thức tính v n
ậ tốc trung bình của phân tử khí: 8kT v = mπ  8kT1 v  = 1  mπ v T 267 + 273 2 2 Hay  = = =1,5  8kT v T 240 1 1 2 v = 2  mπ
Câu 5. Hai khối khí O2 và H2 có cùng mật độ số hạt. Nhiệt dộ của khối khí O2 là 120∘C,
nhiệt độ của khối khí H2 là 60∘C. Áp suất của O2 và H2 theo thứ tự là 𝑃𝑃1 và 𝑃𝑃2. Ta có: A. 𝑃𝑃1 = 0,98𝑃𝑃2. B. 𝑃𝑃1 = 1,18𝑃𝑃2. C. 𝑃𝑃1 = 0,88𝑃𝑃2. D. 𝑃𝑃1 = 1,28𝑃𝑃2. Lời giải:
Mật độ phân tử chất khí: N m N A n = = × 0 V µ V
Theo phương trình Clapeyron -Mendeleev: m m p p p 1 pV = × RT ⇒ = ⇒ n =
× N = × (k là hằng số Boltzmann) 0 A µ V µ RT RT T k
Vì hai khối khí O và H có cùng mật độ số hạt và nhiệt độ không đổi ⇒Áp suất không 2 2 đổi Quá trình đẳng tích: + p T 120 273 1 1 = =
≈ 1,18 ⇒ p ≈ 1,18p 1 2 p T 60 + 273 2 2
Câu 6. 𝑀 𝑀 = 18 g khí đang chiếm t ể
h tích 𝑉 𝑉 = 4 lít ở nhiệt độ 𝜔 𝜔 = 22∘C. Sau khi hơ nóng
đẳng áp, khối lượng riêng của nó ằ
b ng 𝜌 𝜌 = 6.10−4 g/cm3. Nhiệt độ của khối khí sau khi hơ nóng là: A. 2213 K. B. 211 3 K. C. 2013 K. D. 1913 K. Lời giải: Trước khi hơ nóng: m pV = RT 1 1 µ ρ Sau khi hơ nóng: m m RT2 pV = RT ⇒ p = RT = 2 2 2 µ V µ µ 2
Group: Bachkhoa Universe – Góc học tập và thảo luận 55 TAILIEUHUST.COM Lấy (1) mT mT 1 1 ⇒V = ⇒ T = = K 1 2 2213( ) (2) ρT ρV 2 1 Câu 7. Một k ố
h i ôxy (O2) ở nhiệt độ 20∘C. Để nâng vận tốc căn quân phương của phân tử
lên gấp đôi, nhiệt độ của khí là: A. 899∘C. B. 919∘C. C. 929∘ . C D. 889∘ . C Lời giải: Công thức tính v n ậ tốc căn q ầ u n phương: 3kT v =
(với k là hằng số Boltzmann) C m  3kT1 v = 2 2 1        Ta có: m T v v 2v 1 1 2 1  ⇒ = ⇒   T = T = (20 +273) =1172(     K) 2 1  3kT T v v v 2  2   1   1  2 v = 2  m
Câu 8. Nhiệt độ của một khối plasma khí coi là khí lí tưởng trên mặt trời là 2,6 ⋅ 106 K. Vận
tốc căn quân phương của các điện tử tự do trong khối khí đó là: (𝑚𝑚e = 9, 1.10−31 kg, 𝑘 𝑘 = 1, 38.10−23 J/K) A. 11, 876.106 m/s. B. 10, 876.106 m/s. C. 13,876 ⋅ 106 m/s. D. 12, 876.106 m/s. Lời giải:
Công thức vận tốc căn quân phương 𝑣𝑣𝑐 𝑐 = �3𝐾𝐾𝑇𝑇 𝑚𝑚0
3 ∗ 2,6 ∗ 106 ∗ 1,38 ∗ 10−23 𝑚𝑚 ⟹ 𝑣𝑣𝑐 𝑐 = � ≈ 10,876 ∗ 106 � � 9,1 ∗ 10−31 𝑠 𝑠
Câu 9. Hai bình khí cùng thể tích, cùng nội năng. Bình 1 chứa khí Heli (He ,) bình 2 chứa
Nitơ (N2). Coi các khí lí tưởng. Gọi 𝑝𝑝1 và 𝑝𝑝2 là áp suất tương ứng của bình 1 và 2. Ta có: A. 𝑝𝑝1 = 𝑝𝑝2. B. 𝑝𝑝1 = 3𝑝𝑝2 . C. 𝑝𝑝 . D. 𝑝𝑝 . 5 1 = 2𝑝𝑝2 5 1 = 5𝑝𝑝2 3 Lời giải:
Vì hai bình khí có cùng thể tích ⇒ quá trình đẳng tíc h
Biến thiên nội năng trong qua trình đẳng tích: m i i i U ∆ =
⋅ ⋅ RT = nRT = PV µ 2 2 2
Khí Heli → i = 3 và khí Nito → i = 5
56 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1  i i 1 1 ∆U = .
n . RT = . PV 1 1 1 1  2 2   Ta có: i i i P P i 5 5 2 2 1 1 1 2 ∆U = . n .RT = .PV ⇒1 = ⋅ ⇒ = = ⇒ P = P 2 2 2 2 1 2 2 2 i P P i 3 3  2 2 2 1 V
 =V =V ; U ∆ = U ∆ = U ∆ 1 2 1 2 
Câu 10. Khối lượng riêng ủ c a ộ
m t chất khí 𝜌 𝜌 = 5.10−2 kg/m3; vận tốc căn quân phương
của các phân tử khí này là 𝑣 𝑣 = 450 m/s. Áp suất của k ố h i khí tác ụ d ng lên thành bình là: A. 3575 N/m2. B. 3675 N/m2. C. 3475 N/m2. D. 3375 N/m2. Lời giải:
Áp dụng công thức tính vận tốc căn quân phương của phân tử khí:
v = �3𝑅𝑅𝑇𝑇 => RT = v2𝜇𝜇/3 𝜇 𝜇
Phương trình trạng thái khí lý tưởng:
pV = 𝑚𝑚 𝑅𝑅𝑇𝑇 => p = 𝜌𝜌 𝑅𝑅𝑇𝑇 = v 𝜌𝜌
2𝜇𝜇/3 = 𝜌𝜌𝑣𝑣2/3 = 3375 (N/m2) 𝜇 𝜇 𝜇 𝜇 𝜇𝜇 Câu 11. Một k ố
h i khí nitơ (N2) biến đổi trạng thái sao cho áp suất của nó tăng 2 lần và ậ v n
tốc căn quân phương của các phân tử tăng √2 lần. Trong quá trình đó, khối lượng riêng
của khối khí nitơ thay đổi như thế nào? A. Giảm √2 lần. B. Tăng √2 lần. C. Tăng 2√ l 2 ần. D. Không đổi. Lời giải:
Áp dụng phương trình trạng thái khí lý tưởng ta được:
pV = 𝑚𝑚 𝑅𝑅𝑇𝑇 => p = 𝜌𝜌
𝑅𝑅𝑇𝑇 => 𝜌 𝜌 = 3𝑝𝑝 𝜇 𝜇 𝜇 𝜇 𝑣𝑣2 2
Ta có: 𝜌𝜌2 = 𝑝𝑝2𝑣𝑣1 = 1 𝜌𝜌 2 1 𝑝𝑝1𝑣𝑣2
Vậy khối lượng riêng của khối khí không đổi. Câu 12. Một k ố
h i khí oxy (O2) biến đổi trạng thái sao cho khối lượng riêng của nó g ả i m
1,5 lần và tốc độ trung bình của các phân tử giảm 1,5 lần. Trong quá trình đó, áp suất mà
khí ôxy tác dụng lên thành bình thay đổi như thế nào?
A. Giảm 3,375 lần. B. Giảm 1,225 lần. C. Giảm 2, 5 2 lần. D. Giảm 1,837 lần. Lời giải: Theo bài ra, ta có: pV n = = const RT
Group: Bachkhoa Universe – Góc học tập và thảo luận 57 TAILIEUHUST.COM Ỏ trạng thái p V p V p V T 1 1 1: n = và ở trạng thái 2 2 2 1 2 2 :n = ⇒ = ⋅ RT RT p V T 1 2 1 2 1 Công thức tính v n
ậ tốc trung bình của phân tử khí: 8kT v = mπ  8kT1 v = 2 1  π   m = ρ V ρ Hay m v T V 2 2  ⇒ =   và 1 1 1 2  ⇒ =  8kT v Tm =  ρ V V ρ 1  1 2 2 2 2 1 v = 2  mπ 2 p V T ρ  v  8 2 1 2 2 2 ⇒ = ⋅ = ⋅ =   p V T ρ v 27 1 2 1 1  1 
Câu 13. Một xi lanh có pit -tông có thể di động được. Trong xi-lanh đựng một khối khí lí
tưởng. Vỏ xi lanh không dẫn nhiệt. Nếu áp suất không khí trong xi lanh tăng 2 lần thì nội năng của khí thay ổ
đ i như thế thế nào? (gọi γ là hệ số Poatxông) γ 1 − γ γ A Tăng 1 2γ − lần B.tăng 2 γ lần C.Tăng γ 1 2 − lần D.Tăng γ 1 2 + lần Lời giải: Do vỏ xi lanh không d n
ẫ nhiệt → quá trình diễn ra bên trong xi lanh là đoạn nhiệt. 1 γ − 1 −γ 1 −γ γ   + Ta có phương trình: P T γ γ 2 1 T P = T P ⇔   = 1 1 2 2 P T  1  2 1−γ γ 1 − + Mà T T 1 γ 1 P = 2P ⇒ = 2 ⇔ T = = T ⋅ 2 γ (1) 2 1 2 1−γ 1 T2 2 γ Nội năng: i U i U U T U = nRT ⇒ = const = nR 1 2 2 ⇒ = ⇔ U = U (2) 2 T 2 2 1 T T T 1 2 1 γ 1 −
Từ (1) và (2) ta có: U = 2 γ U 2 1 Câu 14. Một k ố
h i khí ôxy (O có khối lượng riêng là ρ = ( 3
0,59 kg / m ) . sổ Avôgađrô 2 ) 26
N = 6,023 ⋅10 ( J / kmol) . Tỷ số áp suất khí và động năng tịnh tiến trung bình của phân tử khí là: A 24 6,873.10 ( Pa / J) B. 24 8,993⋅10 ( Pa / J) C. 24 8, 463⋅10 ( Pa / J) D. 24 7, 403 1 ⋅ 0 ( Pa / J) Lời giải:
Áp dụng công thức tính áp suất khí theo động năng tịnh tiến trung bình:
58 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 2 p 2 p N p = n W ⇒ = 2 n ⇔ = ⋅
với N là số phân tử; N là số Avôgađro 0 0 A 3 W 3 W 3 v 23 p 2 nN 2 m 2 N m p 2 N 2 6, 023.10 A A A 24 ⇔ = ⋅ = N ⋅ = ⋅ ⋅ ⇔ = ⋅ ρ = ⋅ .0,59 = 7, 403.10 W 3 v 3 A µv 3 µ v W 3 µ 3 0, 032
Câu 15. Tổng động năng t n
ị h tiến trung bình của các phân tử khí Nito (N chứa trong 2 ) một khí cầu bằng −3
w = 5.10 ( J) và vận tốc căn quân phương của phân tử khí đó là v = e 3
2.10 ( m / s) . Khối lượng khí nitơ trong khí cầu là: A. −5 2,84.10 ( kg) B. 9 2,5.10− ( kg) C. −3 3, 01.10 (Kg) D. −3 2,33.10 ( kg) Lời giải: Ta có: 3 3 R m 3 R 3 m
W = N ⋅ W = N ⋅ KT = N ⋅ ⋅ T ⇔ W = ⋅N ⋅ ⋅ T = ⋅ ⋅RT (1) A 2 2 N µ 2 N 2 µ A A
Vận tốc căn quân phương: 3RT 3RT 2 v = ⇒ v = (2) c c µ µ Từ m 2W (2) và 2 9 (1) W v m 2,5.10− ⇒ = ⇒ = = ( kg) 2 2 c vc
Câu 16. Một khối khí lí tường có thể tích V = ( 3
6 m ) dãn nở đẳng nhiệt từ áp suất 2(at)
đến 1(at) . Lượng nhiệt đã cung cấp cho quá trình này là: A. 5 9,16.10 (J ) B. 5 10,16.10 (J ) C. 5 8,16.10 (J ) D. 5 5,16.10 (J ) Lời giải: Quá trình là đẳng nhiệ V P 2at t 2 1 ⇒ PV = PV ⇔ = = = 2 1 1 2 2 V P 1at 1 2
Do quá trình là đẳng nhiệt ⇒ T ∆ = 0 ⇒ U ∆ = 0
Theo Nguyên lí 1 Nhiệt động lực học: Q U A′ A′ , A′ = ∆ + = là công khi thực hi ện Ta có: V V ′ R V V n T dV dV 2 2 2 2 A = PdV = dV = n RT = PV 1 1 ∫ ∫ ∫ ∫ 1 V 1 V 1 V 1 V V V V ′ V2 4 5 ⇒ A = PV .ln
= 2.9,81.10 .6.ln 2 = 8,16.10 (J ) ′ 5
⇒ Q = A = 8,16.10 (J ) 1 1 V1
Câu 17. Nén đẳng nhiệt 3 lít không khí ở áp suất 1 at. Tìm nhiệt tỏa ra biết rằng thể tích
cuối cùng bằng 1/10 thể tích ban đầu. A. −676 J B. −872 J C. −512 J D. −911 J Lời giải
Group: Bachkhoa Universe – Góc học tập và thảo luận 59 TAILIEUHUST.COM
Theo Nguyên lí thứ nhất của nhiệt động lực ọ h c, nhiệt lượng mà kh i ố khí nhận được là Q ∆ = A + U ∆
Do là quá trình đẳng nhiệt nên ∆U = nC T ∆ = 0 V Nhiệt lượng mà khố V V dV V i khí nhận được 2 2 2 Q ∆ = A = p dV = pV = p V ln ∫ ∫ 1 1 1 V 1 V V V1 − 1 4 3 ⇒ ∆Q = 9,81.10 3 . .10 ln ≈ 6 − 76 J (tỏa nhiệt) 10
Câu 18. Một bình kín thể tích 2 lít, đựng 12 g khí nitơ ở nhiệt độ 10°C . Sau khi hơ nóng, áp
suất trung bình lên tới 4
10 mmHg . Tìm nhiệt lượng mà khối khí đã nhận được, biết bình giãn nỏe A. 4,1 kJ B. 5,1 kJ C.6,1 kJ D. 8,1 kJ Lời giải:
Do bình giãn nở kém nên thể tích của bình coi như không đổi, quá trình là đẳng tích
Ta có nguyên lí I nhiệt động lực học m iR Q ∆ = A + U ∆ = U ∆ = ⋅ (T −T 2 1 ) µ 2 i m mi m  ∆ R Q = RT − RT = p V − RT
(N là khí lưỡng nguyên tử i =5,C = 5 2 1   2 1   2 µ µ 2   µ  2 V 2  Thay số 4 6 3 − 3
p = 10 mmHg = 1, 33.10 Pa, V = 2.10 m , T = 283 K Q ∆ = 4,1 kJ 2 1
Câu 19. 7 gam khí cacbonic được hơ nóng cho tới khi nhiệt độ tăng thêm 10°C trong điều
kiện giãn nở tự do. Công của khí sinh ra và ộ
đ biến thiên nội năng ủ c a k ố h i khí lần lượt là? A. 14, 2 J và 32,1 J B. 13, 2 J và 39,7 J C. 19,1 J và 39,7 J D. 12, 2 J và 32,1 J Lời giải
Quá trình giãn nở tự do ta có thể coi gần đúng là đẳng áp (giãn nở trong khí quyền, áp
suất bằng áp suất khí quyển)
Công do khí sinh ra khi giãn nở: = ( m m m A p V V − = RT − RT = R T −T 2 1 ) 2 1 ( 2 1) µ µ µ 7 ⇒ A = .8,31.10 ≈ 13, 2J 44
Độ biến thiên nội năng ủ c a khối khí: m R i 7 6.8,31 U ∆ = ⋅ T ∆ = ⋅ 10 ⋅ ≈39,7 J µ 2 44 2
(CO là khí đa nguyên tử nên số bậc tự do của phân tử là 6) . 2
60 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Câu 20. Một chất khí đựng trong một xilanh đặt thẳng đứng có pittông khối lượng không
đáng kể di động được. Hỏi ầ
c n phải thực hiện một công ằ
b ng bao nhiêu để nâng pittông
lên cao thêm một khoảng h = 10 cm nếu chiều cao ban đầu của cột không khí là h =15 cm 1 0
, áp suất khí quyển là p = lat diện tích ặ m t pittông 2
S = 10 cm . Nhiệt độ của khí coi là 0
không đổi trong suốt quá trình. A. 3,2 J B. 2,6 J C. 2,3 J D. 10, 2 J Lời giải + Công do khí V h h sinh ra là 1 0 1 A = p V ln = p V ln 0 0 0 0 0 V h 0 0  
Nên khi biến đổi khí nhận vào một công: h0
−A = p V ln   0 0 0 h +h  0 1  Công của áp s ấ
u t khí quyển: A = p Sh k 0 1
Ta có thể thấy công cần thực hiện bao gồm công truyền cho khí và công thẳng lực do áp suất khí quyển gây ra:     ′ h1
A = A − A = p S h −h ln 1 +    = 2,3J k 0 1 10  h    0   Câu 21. 3
2m khí giãn nở đẳng nhiệt từ áp suất p = 5 at đến áp suất 4 at. Tính nh ệ i t lượng
cung cấp cho khí trong quá trình giãn nở. A. 5 5, 2.10 J B. 5 2, 2.10 J C. 5 1, 4 ⋅10 J D. 5 2,9.10 J Lời giải:
Theo nguyên lí I, nhiệt nhận vào của khí: Q = A + ∆U
Trong quá trình đẳng nhiệt, nội năng ∆U = 0 và công là: V 2 V p 2 1 A =
p dV = p V ln = p V = p V ln ∫ 1 1 1 1 1 2 1 V V p 1 2 5 4 5
Q = A = 2.5.9,81.10 .ln = 2, 2.10 J 4
Group: Bachkhoa Universe – Góc học tập và thảo luận 61 TAILIEUHUST.COM
Chương 8. Nguyên lý thứ hai của nhiệt động lực học A. Công thức 1. Máy nhiệt
- Công: 𝐴 𝐴 = |𝑄𝑄ℎ| − |𝑄𝑄 | 𝑐𝑐 .
Nếu chất sinh công là khí thì: 𝑉𝑉 𝑉𝑉 𝑉𝑉 𝐴 𝐴 = 𝐴𝐴 2 1 2
𝑑 𝑑 + 𝐴𝐴𝑣 𝑣 = ∫ 𝑝𝑝 𝑝𝑝 (𝑝𝑝 𝑉 1𝑑𝑑𝑉𝑉 + ∫ 𝑉1
𝑉𝑉2𝑑𝑑𝑉𝑉 = ∫
1 − 𝑝𝑝2)𝑑𝑑𝑉𝑉. 2 𝑉𝑉1
- Hiệu suất của máy nhiệt: 𝜂 𝜂 = 𝐴𝐴= |𝑄𝑄ℎ|−|𝑄𝑄𝑐𝑐|= 1 − |𝑄𝑄𝑐𝑐|. |𝑄𝑄ℎ| |𝑄𝑄ℎ| |𝑄𝑄ℎ| 2. Máy lạnh
- Hệ số làm lạnh: 𝜀 𝜀 = |𝑄𝑄𝑐𝑐| =
|𝑄𝑄𝑐𝑐| = 𝑇𝑇𝑐𝑐 .
𝐴 𝐴 |𝑄𝑄ℎ|−|𝑄𝑄𝑐𝑐| 𝑇𝑇ℎ−𝑇𝑇𝑐𝑐 3. Chu trình Carnot
- Mối liên hệ giữa nhiệt nhận được từ nguồn nóng và nhiệt nhả cho nguồn lạnh: |𝑄𝑄𝑐𝑐|= 𝑇𝑇𝑐𝑐. |𝑄𝑄ℎ| 𝑇𝑇ℎ
- Hiệu suất của chu trình Carnot: 𝜂 𝜂 = 1 − 𝑇𝑇𝑐𝑐 . 𝑇𝑇ℎ 4. Entropy - Công thức Entropy: Δ 𝑆𝑆 𝑆𝑆 = 𝑆𝑆 2
2 − 𝑆𝑆1 = ∫ 𝑑𝑑𝑄𝑄 . 𝑆𝑆1𝑇 𝑇
- Quá trình đoạn nhiệt thuận ng ị h ch: Δ𝑆𝑆 = . 0
- Nguyên lý tăng Entropy: Δ𝑆𝑆 ≥ . 0
62 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
B. Bài tập trắc nghiệm
Câu 1. Một động cơ nhiệt hoạt động theo chu trình Carnot thuận nghịch giữa 2 nguồn điện có nhiệt độ 40 0 K và 100 K. ế
N u nó nhận 1 lượng nhiệt 6 kJ của nguồn nóng trong
mỗi chu trình thì công mà nó sinh ra trong mỗi chu trình là: A. 4,5 kJ. B. 2,5 kJ. C. 1,5 kJ. D. 6,5 kJ. Lời giải: Hiệu s ấ
u t chu trình Carnot: 𝜂 𝜂 = 1 − 𝑇𝑇2 𝑇𝑇1
𝑇𝑇1, 𝑇𝑇2 lần lượt là nhiệt độ nguồn nóng và nhiệt độ ng ồ u n lạnh
Lại có: 𝜂 𝜂 = 𝐴𝐴′ 𝑄 𝑄
𝐴𝐴′, 𝑄𝑄 lần lượt là công sinh ra trong mỗi chu trình và nhiệt lượng nhận được trong mỗi chu trình
Do đó: 𝜂 𝜂 = 1 − 𝑇𝑇2= 𝐴𝐴′ ⇒ 𝐴𝐴′ = 𝑄𝑄 �1 − 𝑇𝑇2 � = 6. �1 − 100 � = 4,5(𝑘𝑘𝐽𝐽) 𝑇𝑇1 𝑄 𝑄 𝑇𝑇1 400
Câu 2. Một mol khí hidro nguyên tử được nung nóng đẳng áp, thể tích gấp 8 ầ l n. Entropy
của nó biến thiên một lượng bằng? (Cho hằng số khí 𝑅 𝑅 = 8,3 1 J/ mol.K ) A. 43,2 J/K. B. 43,7 J/K. C. 44,2 J/K. D. 44,7 J/K. Lời giải:
Độ biến thiên Entropy: 𝑑𝑑𝑆𝑆 = 𝑑𝑑𝑄𝑄 𝑇 𝑇 Quá trình đẳng áp: 𝑖𝑖+2
𝛿𝛿𝑄𝑄 = 𝑛𝑛𝐶𝐶𝑝𝑝𝑑𝑑𝑇𝑇 = 𝑛 𝑛 𝑅𝑅𝑑𝑑𝑇𝑇 𝑖 𝑖 𝑇𝑇2
𝑖 𝑖 + 2 𝑑𝑑𝑇𝑇 𝑖 𝑖 + 2 𝑖 𝑖 + 2 𝑇𝑇2 ⇒ Δ𝑆𝑆 = � 𝑛𝑛 𝑅 𝑅 = 𝑛 𝑛 𝑅 𝑅 ln 𝑇𝑇𝑇 𝑇2 |= 𝑛 𝑛 𝑅 𝑅 ln 2 𝑇𝑇 2 𝑇𝑇1 2 𝑇𝑇1 𝑇𝑇1
Nung nóng đẳng áp, do đó: 𝑇𝑇2 = 𝑉𝑉2 𝑇𝑇1 𝑉𝑉1 𝑖 𝑖 + 2 𝑉𝑉2 ⇒ Δ𝑆𝑆 = 𝑛 𝑛 𝑟 𝑟 ln = 43,2 (𝐽𝐽 ⁄ 𝐾𝐾 ) 2 𝑉𝑉1
Câu 3. Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 50 kW. Nhiệt độ
của nguồn nóng là 127∘ ,
C nhiệt độ của nguồn lạnh là 31∘C. Nhiệt lượng tác nhân nhận của
nguồn nóng trong một phút có giá trị: A. 12200 kJ. B. 1260 0 kJ. C. 12500 kJ. D. 1230 0 kJ. Lời giải:
Group: Bachkhoa Universe – Góc học tập và thảo luận 63 TAILIEUHUST.COM
Hiệu suất chu trình Carnot: A T A 50 625 2 η = = 1− ⇒ Q = = = (kJ ) n Q T T 127 + 273 2 3 n 1 1− 1 − T 31+ 273 1
Nhiệt lượng tác nhân của nguồn nóng trong 1 phút là: 625
Q' = Q .t = ×60 =12500( kJ) n 3
Câu 4. Một động cơ nhiệt làm việc theo chu trình Carnot với nhiệt độ nguồn nóng là
100∘C. Trong mỗi một chu trình tác nhân nhận ủ c a ngu n
ồ nóng một nhiệt lượng 10 kcal và thực hiện công 15 k .
J Nhiệt độ của nguồn ạ
l nh là: (cho 1 cal = 4,18 J ) A. 212,15 K. B. 231,1 5 K. C. 239,1 5 K. D. 245,1 5 K. Lời giải:
Với T ;T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 1 2 ′ Mặt khác: A η = Q1
Với A′ là công sinh ra trong mỗi chu trình và Q là nhiệt lượng nhận được trong mỗi chu 1 trình
Hiệu suất theo chu trình Carnot: T A′ T A′ A′    15  2 2 η =1− = ⇒ = 1− ⇒ T = T 1− = 363⋅ 1− ≈ 232,92(K) 2 1     T Q T Q Q    10.4,186  1 1 1 1 1
Câu 5. Một máy nhiệt lí tưởng làm việc theo chu trình Carnot, sau mỗi chu trình thu được
600 calo từ nguồn nóng có nhiệt độ 127∘C. Nhiệt ộ
đ nguồn lạnh là 27∘C. Công do máy
sinh ra sau một chu trình là ( cho biết 1 cal ≈ 4,184 J) A. 627,6 J. B. 647,6 J. C. 637,6 J. D. 657,6 J. Lời giải: Hiệ T
u suất theo chu trình Carnot: 2 η =1−
với T ;T lần lượt là nhiệt độ nguồn nóng và T 1 2 1 nhiệt độ nguồn lạnh A′ Mặt khác: η =
với A′ là công sinh ra trong mỗi chu trình và Q là nhiệt lượng nhận Q 1 1
được trong mỗi chu trình ′   Hay T A ′ T  300  2 2 η =1− =
⇒ A = Q 1−  = 600.4,186. 1− = 627,6(J ) 1   T Q T    400  1 1 1
64 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Câu 6. Cho một chu trình Carnot thuận nghịch, độ biến thiên entropy trong quá trình đẳng nhiệt có ệ
h số là Δ𝑆𝑆 = 1kcal/K; hiệu số nhiệt độ giữa 2 đường đẳng nhiệt là Δ𝑇𝑇 = 300 K; 1
cal = 4,18 J. Nhiệt lượng đã chuyển hóa thành công trong chu trình đang xét là A. 12, 54.105 J. B. 12, 04.105 J. C. 13, 54.105 J. D. 11, 04.105 J. Lời giải:
Nhiệt lượng chuyển hóa thành công trong chu trình đang xét là
⇔ 𝐴𝐴 = ∆𝑆𝑆∆𝑇𝑇 = 4180.300 = 12,54. 105(𝐽𝐽)
Câu 7. Một động cơ nhiệt làm việc theo chu trình Carnot bằng không khí lấy ở áp suất ban
đầu 𝑃𝑃1 = 7,0 at. Thể tích ban ầ
đ u của không khí 𝑉𝑉1 = 2dm3. Sau lần giãn đẳng nhiệt lần
thứ nhất nó chiếm thể tích 𝑉𝑉2 = 5dm3 và sau khi giãn đoạn nhiệt thể tích của khí là 𝑉𝑉3 =
8,1dm3. Áp suất khí sau khi giãn đ ạ
o n nhiệt có giá trị 𝑃𝑃3 bằng: A. 12, 98.104 Pa. B. 10, 98.104 Pa. C. 13, 98.104 Pa D. 15, 98.104 Pa. Lời giải:
Từ (1) → (2) : Đẳng nhiệt => P2 = 𝑃𝑃1𝑉𝑉1 𝑉𝑉2 𝛾𝛾 𝛾𝛾−1
Từ (2) → (3) : Đoạn nhiệt => P3 = 𝑃𝑃2𝑉𝑉2 = 𝑃𝑃1𝑉𝑉1𝑉𝑉2 𝛾 𝛾 = 1.452 at = 13, 98.104 Pa 𝑉𝑉 𝛾 𝛾 3 𝑉𝑉3
Câu 8. Một động cơ nhiệt có hiệu suất 10% và nhả nhiệt cho một nguồn có nhiệt độ 450
K. Nó nhận nhiệt từ một nguồn có nhiệt độ ít nhất là: A. 479 K. B. 514 K. C. 507 K. D. 500 K. Lời giải: Hiệ T
u suất theo chu trình Carnot: 2 η =1− T1
Với T ;T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 1 2 T T 450 2 2 ⇒η = 1− = 0,1 ⇒T = = = 500(K ) 1 T 1 −η 1 −0,1 1
Câu 9. Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 10kW. Nhiệt đôk
của nguồn nóng là 100°c , nhiệt độ của nguồn lạnh là 0°C . Nhiệt lượng tác nhân nhả cho
nguồn lạnh, trong một phút có giá trị là bao nhiêu? A 3 1, 438.10 (kJ ) B. 3 1, 638.10 ( kJ) C. 3 1.738.10 (kJ ) D. 3 1, 338.10 ( kJ) Lời giải:
Group: Bachkhoa Universe – Góc học tập và thảo luận 65 TAILIEUHUST.COM   Ta có T ′ T T 1 1 2 Q = A
⇒ Q = Q − A = A −1 =   A 1 2 1 T − T T − T T − T 1 2  1 2  1 2 3 5 + ′ 273
A = Pt = 10.10 .60 = 6.10 (J ) 5 3 ⇒ Q =6.10 . =1,638.10 ( k ) J 2 100
Câu 10. Hơ nóng 1 mol khí lí tưởng lưỡng nguyên tử từ nhiệt độ T đên T bằng hai quá 1 2
trình đẳng áp và đẳng tích. Gọi biến thiên entropi trong mỗi quá trình đẳng áp, đẳng tích lần lượt là S ∆ và S ∆ Khi đó: P V A. S ∆ = 1,8∆S B. S ∆ = 1, 4 S ∆ C. S ∆ = 1,6 S ∆ D. S ∆ = 2,0 S ∆ P V P V P V P V Lời giải
Lưỡng nguyên tử: i = 5 dQ nC dT Xét quá trình đẳng áp: T T T dT dQ = nC dT : 2 1 2 p S ∆ = = = nC ∫ ∫ ∫ p p p T T T 1 T 1 T 1 T T i + 2 T 7 T 2 2 2 ⇔ ∆S = nC ln = n R.ln = R ln p p T 2 T 2 T 1 1 1
Xét quá trình đẳng tích: T dQ nC dT dT 2 T2 T2 V S ∆ = = = nC ∫ ∫ ∫ c V T T T 1 T 1 T 1 T T i T 5 T S ∆ 2 2 2 ⇒ ∆S = nC ln = n Rln = Rln p 7 7 ⇒ = ⇒ S ∆ = S ∆ =1, 4 S ∆ c V T 2 T 2 T S ∆ 5 p 5 c c 1 1 1
Câu 11. Một máy hơi nước có công suất 14,7kW, tiêu thụ 8,1kg than trong một giờ. Năng
suất tỏa nhiệt của than là 7800kcal / kg . Nhiệt độ của nguồn nóng 200°C , nhiệt độ của
nguồn lạnh là 58. Tìm h ệ i u suất thực ế
t của máy. So sánh hiệu suất đó với hiệu suất lý
tưởng của máy nhiệt làm việc theo chu trình Cácnô với những nguồn nhiệt kể trên. Lời giải Hiệu suất lý tưởng Q 14, 7.3600 ich h = 100% = 100% = 20% Q 8,1.7800.4,18 toanphan − − Hiệ T T
u suất lý tưởng h theo chu trình Cácnô: 200 58 n l h = 100% = 100% = 30% lt lt T 200 + 273 n 2
⇒ h = h . Vậy hiệu suất thực tế nhỏ hơn 1,5 lần hiệu suất lý tưởng. 3 lt
66 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Câu 12. Một máy làm lạnh lý tưởng, chạy theo chu trình
Cacno ngược lấy nhiệt tứ nguồn lạnh 0°C nhả cho bình
nước sôi ở 100°C . Tính lượng nước cần làm đông ở nguồn
lạnh để có thể biến 1 kg nước thành hơi ở bình sôi. Cho biết
nhiệt nóng chảy riêng ủ c a nước đá là 5 λ = 3,35.10 J / kg và nhiệt hóa hơi riêng ủ
c a nước là L 2, 26.10° = J / kg . Lời giải:
Sơ đồ máy lạnh có dạng tương tự như hình vẽ.
Nhiệt nhận từ nguồn lạnh Q , nhả ra nguồn nóng là Q , hệ số làm lạnh khi máy chạy theo 1 chu trình Carnot ngược: Q T T 2 2 2 = → Q = Q (1) 2 1 Q −Q T T − T 1 2 1 2 1
Nhiệt lượng cần làm bay hơi nước: Q = Lm(2) 1
Khối lượng nước cần làm nóng chảy là m′ : Q λ m′ = (3 ) 2 6 Từ ′ L T 2, 26.10 273 (1), (2) và (3) ta có: 2 m = ⋅ m = , .1≈ 4, 93 kg. 5 λ T 3, 35.10 373 1
Câu 13. Một kmol khí lý tưởng thực hiện một chu trình gồm 2 quá trình đẳng tích và hai
quá trình đẳng áp. Khi đó thể tích của khí thay đổi từ 3 V = 25 m đến 3
V = 50 m và áp suất 1 2
từ p = 1 at đến p = 2at . Hỏi công thực hiện bởi chu trình này nhỏ hơn bao nhiêu lần công 1 2
thực hiện bởi chu trình Cacno có các đường đẳng nhiệt ứng với nhiệt độ lớn nhất và nhỏ
nhất của chu trình nói trên, nếu khi giãn đẳng nhiệt thể tích tăng lên gấp đôi? Lời giải: Công thực hiện trong ả
c chu trình: A = (p − p V −V (1) 2 1 ) ( 2 1 )
Trong chu trình Cacno, nhiệt độ nguồn nóng T ứng với 2
điểm (V , p , nhiệt độ nguồn lạnh T ứng với điểm 2 2 ) 1
(V , p ⋅ T = pV / nR và T = p V / nR . 2 2 2 ) 1 1 ) ( 1 1 1 ′
Trong một chu trình tác nhân nhận nhiệ V t 2 p V ln (2) 2 2 V ′1 T T p V p V Với hiệu suất: 2 1 2 2 1 1 η − − = = (3) T p V 2 2 2 ′ Từ ′ V
(2) và (3), suy ra công khí sinh ra trong một chu trình:A = Q η =( p V −pV ) 2 ln (4) 1 2 2 1 1 V ′ 1
Group: Bachkhoa Universe – Góc học tập và thảo luận 67 TAILIEUHUST.COM ′ Giãn đẳng nhiệt thể V
tích tăng lên gấp đôi nên 2 = 2 . Kết hợp (4) và (1) ta có: V ′1 ′
( p V − pV ) V2 ln ′ 2 2 1 1 A V′ (2.50− 1.25) ln 2 1 → = = ≈ A ( 2,1 p − p V −V (2 1 − )(50 −25) 1 2 ) ( 2 1 )
68 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
PHẦN II. CÂU HỎI VÀ BÀI TẬP TỰ LUẬN Câu 1.
1. Định nghĩa vecto gia tốc. Nêu đặc điểm và ý nghĩa của các vecto gia tốc tiếp tu ế y n, gia tốc pháp tuyến
2. Bài toán: Từ đỉnh tháp có độ cao h, người ta ném một hòn đá xuống dưới đất với
vận tốc ban đầu v theo phương hợp với phương thẳng đ n ứ g ộ m t góc α (hình vẽ) 0
a. Viết phương trình chuyển động của hòn đá trong hệ tọa độ vuông góc, với ố g c ọ t a độ tại điểm ắ b t đầu ném (hình vẽ) b. Cho ° 2 h = 30 ;
m v = 20m / 2;α = 60 ; g = 9,8m / s . Tìm thời 0 gian bay và tốc ộ
đ của hòn đá khi chạm đất.
c. Tìm gia tốc pháp tuyến tại điểm chạm đất. Bỏ qua lực cản của không khí Lời giải 1. Lý thuyết
Định nghĩa vecto gia ố t c:
Vecto gia tốc là đại lượng vectơ biểu t ị
h cho gia tốc. Gia tốc là đại lượng vật lý đặc trưng
cho sư biến thiên nhanh hay chậm ủ c a vận tốc.
Gia tốc tiếp tu ế y n: Đặc điểm: - Điểm đặt tại M
- Có phương trùng với tiếp tu ế
y n của quỹ đạo tại M .
- Có chiều là chiều chuyển động khi v tăng và ngược lại khi v giảm.
- Có độ lớn bằng đạo hàm vận tốc theo thời gian dv a = . t dt
Ý nghĩa: Vecto gia tốc tiếp tu ế
y n đặc trưng cho sự biến thiên của vecto vận tốc về độ lớn.
Gia tốc pháp tuyến: Đặc điểm:
- Điểm đặt tại M
- Có phương vuông góc với tiếp tu ế y n q ỹ u đạo tại M .
- Có chiều hướng vào tâm (hướng vào phía lõm của quỹ đạo).
Group: Bachkhoa Universe – Góc học tập và thảo luận 69 TAILIEUHUST.COM 2 - l Độ ớn bằng: v a = . n R
Ý nghĩa: Vecto gia tốc pháp tuyến đặc trưng cho sự biến thiên về phương của vecto vận tốc. 2. Bài toán:  1 2
x = x + v t + a t 0 0x x 
a. Chọn hệ tọa độ như hình vẽ: 2  1 2
y = y +v t + a t 0 0 y y  2 x = 0 0 y = 0 0  x  = v sinα .t 0 v = v sinα Với  0x 0   ⇒  1 2 v = v cos α = α + 0y 0 y v cos .t gt   0  2 a =0 xa  = g y  b. Thời gian bay: 2
y = h ⇒ 4,9t + 10t − 30 = 0 ⇒ t = 1, 66s
v = v sin α =10 3 m / s Tốc độ khi chạm ấ đ t x 0 2 2 
⇒ v = v + v = 31, 47 m / s x y
v = v cosα + gt = 26, 27 m / sy 0 c. Ta có: v 10 3 x 2
a = g sin β = g =9,8 =5,39 m / s n v 31, 47 Câu 2:
1. Trình bày các vấn đề sau:
a. Hệ quy chiếu quán tính và nguyên lí tương đối Galileo.
b. Hệ quy chiếu không quán tính và lực quán tính ly tâm.
2. Bài toán: Người ta chèo một con thuyền qua sông theo hướng vuông góc với bờ
sông với vận tốc 7,2 km / h . Nước chảy đã mang con thuyền về phía xuôi dòng một khoảng 150 m . Tìm: a. Vận tốc ủ
c a dòng nước đối với bờ sông.
b. Thời gian cần để thuyền qua được sông. Cho biết chiều rộng của sông bằng 0,5 km. Lời giải 1. Lý thuyết
70 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
a. Hệ quy chiếu quán tính là hệ quy ch ế i u mà trên ệ h quy ch ế i u đó, các ị đ nh luật quán tính
của Newton được nghiệm đúng.
- Nguyên lý tương đối Galileo: Mọi hệ quy chiếu chuyển động thẳng ề đ u đối với ệ h quy
chiếu quán tính cũng là hệ quy ch ế i u quán tính hay các đ n
ị h luật Niuton được nghiệm đúng trong hệ quy ch ế
i u chuyển động thẳng đều đối với ệ h quy chiểu quán tính.
Điều đó có nghĩa là: các phương trình động lực học trong các ệ h quy ch ế i u quán tính có
dạng như nhau, các phương trình cơ học ấ
b t biến đối với phép biến đổi Galileo.
b. Trong 1 hệ quy chiếu chuyển động có gia tốc so với 1 hệ quy chiếu quán tính, các định
luật Niuton không được nghiệm đúng nữa là ệ h quy ch ế i u không quán tính.
Lực quán tính ly tâm và lực quán tính xuất h ệ
i n trên 1 vật nằm yên trong ệ h quy ch ế i u
quay so với 1 hệ quy chiếu quán tính. Nó là ệ
h quả của trường gia tốc, xuất hiện trong hệ
quy chiếu phi quán tính. Cũng có thể hiểu lực ly tâm là phản ự l c ủ c a lực hướng tâm tác
động vào vật đang chuyển động theo một đường cong, để giữ cho vật ằ n m cân ằ b ng trong hệ quy ch ế i u.
F = −m ⋅ a hr
Lực quán tính ly tâm có cùng độ lớn nhưng ngược chiều ớ v i lực hướng tâm. 2. Bài toán:
v là vận tốc thuyền so với nước 0
u là vận tốc dòng nước
v là vận tốc thuyền so với bờ
a. Ta có: v = 7.2 km / h = 2m / s 0 BC ut u tan α = = = AB v t v 0 0 BC 150 u Mà = = 0,3 ⇒
= 0,3⇒ u = 0,3.v = 0.6( m / s) 0 AB 500 v0
b. Thời gian cần để qua sông: AB 500 t = = = 250( ) s v 2 0 Câu 3: 1. Lý thuyết
a. Nêu định nghĩa động lượng, thiết lập các định lí ề
v động lượng của chất điểm, ý nghĩa
của động lượng và xung lượng của lực.
b. Trình bày định luật bảo toàn đ n
ộ g lượng của hệ chất điểm cô lập và định luật bảo toàn
động lượng theo một phương ủ c a hệ chất điểm.
Group: Bachkhoa Universe – Góc học tập và thảo luận 71 TAILIEUHUST.COM 2. Bài toán: m
Hai hòn bi có khối lượng m và 1 m = được treo ằ
b ng 2 sợi dây có cùng chiều dài 1 2 2
l = 6(m) vào một điểm. Kéo ệ
l ch hòn bi m cho đến khi dây treo nằm ngang rồi thả ra để 1
nó va chạm vào bi m . Sau va chạm hai hòn bi dính vào nhau và lên tới độ cao cực đại là? 2 Biết g = ( 2 9,8 m / s ) Lời giải 1. Lý thuyết
a. Định nghĩa động l ợ
ư ng :Động lượng của một chất điểm là đại lượng vật lý được xác ị đ nh
bằng tích số giữa khối lượng và vận tốc của chất điểm đó.
Vectơ động lượng: K = mv
- Định lý 1: Theo định luật II Newton, ta có: F = ma . dv d (mv) dK ⇔ m = F ⇔ = F ⇔ = F dt dt dt
Vậy: Đạo hàm động lượng của 1 chất điểm đối với thời gian có giá t ị r bằng lực (hay tổng
hợp lực) tác dụng lên chất điểm đó. B ể
i u thức dK = F dt
- Định lý 2: Theo định lý I: dK 2 K 2 t
= F ⇔ dK = Fdt ⇔ d K = Fdt ∫ ∫ dt 1 K t1
( = F.∆t nếu F không đổi) t2
⇔ ∆K = K − K = Fdt ∫ 2 1 t1 t 2 Fdt ∫
gọi là xung lượng củaa lực F trong khoảng thời gian t → t . 1 2 t1
Vậy: Độ biến thiên động lượng ủ
c a 1 chất điểm trong một khoảng thời gian nào đó có giá
trị bằng xung lượng của lực (hay ổ
t ng hợp lực) tác dụng lên chất điểm trong khoảng thời gian đó. Biểu thức t2 K ∆ = Fdt ∫ 1 t
- Ý nghĩa của động lượng :
+ Động lượng đặc trưng cho chuyền động ề v mặt động lực ọ h c và ậ v n tốc cũng ặ đ c trưng
cho chuyển động về mặt động học.
+ Động lượng đặc trưng cho khả năng truyền chuyền động.
- Ý nghĩa của xung lượng: K ∆ = F. t ∆ .
+ Xung lượng của một lực trong khoảng thời gian ∆t đặc trưng cho tác dụng của lực
trong khoảng thời gian đó.
72 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
b. Định luật bảo toàn của hệ chuyển động cô lập và theo phương.
- Của hế chất điểm (chuyển động ) Theo đ n
ị h lý 2 về động lượng ta có
d (m v +m v +…+m v = F với F là tổng hợp các ngoại lực tác dụng lên hệ. 1 1 2 2 n n ) dt
1. Xét hệ cô lập thì: F = 0 , tức là m v + m v +…+ m v = const. 1 1 2 2 n n ⇒ tổng ộ đ ng lượng ủ
c a 1 hệ cô lập là đại lượng không đổi (được bảo toàn)
2. Theo 1 phương của hệ chất điểm
m v + m v +…+ m v = const 1 1 2 2 n n
Khi đó: Hình chiếu của tổng ộ
đ ng lượng của một hệ lên phương x đó là một đại lượng được bảo toàn. 2. Bài toán: Đặt mốc t ế h năng tại ị
v trí cân bằng của hòn bi 1 trước va chạm.
Áp dụng định luật bảo toàn cơ năng ta có: m v 1 1 0 + m gl =
+ 0 ⇒ v = 2gl (1) 1 2
Ngay sau va chạm cả hai hòn bi có cùng vạn ố
t c v '. Áp dụng định luật bảo toàn động lượng ta có:
m v = (m + m ) m v m v 2 2 1 1 v ' ⇒ v ' = = = v = 2gl (2) 1 1 2 m +m m1 3 3 1 2 m + 1 2 ′2 ′2 Động năng của ệ
h hai hòn bi sau va chạm là: ′ m v m v 3 1 2 1 2 '2 2 W = +
= m v = m v = mgl d 1 1 2 2 4 3 3 Sau khi va c ạ
h m thì hai hòn bi dính vào nhau và tiếp tục chuyển động tròn của ị b 1. Động ′ 3
năng của hệ hai hòn bị chuyển thành thế năng W = m + m gh = m gh 1 ( 1 2 ) 1 2 Của hai hòn bi ở độ cao ố t i đa h ( ố m c thế năng như trên) 2 3 4 W ′ W ′ =
⇔ m gl = m gh ⇒ h = l = 2,667(m) d 1 1 3 2 9 Câu 4:
1. Trình bày các vấn đề sau:
a. Hệ quy chiếu quán tính và nguyên lý tương đối Galileo
b. Hệ quy chiếu không quán tính và lực quán tính ly tâm.
Group: Bachkhoa Universe – Góc học tập và thảo luận 73 TAILIEUHUST.COM 2. Bài toán:
Từ một đỉnh tháp A cao h = 25 m người ta ném một hòn đá lên phía trên theo phương
hợp với phương nằm ngang một, góc α 30° =
với tốc độ v = 15 m / s (hình vẽ). Xác ị đ nh: 0
a. Quỹ đạo của hòn đá, chọn gốc ọ t a độ ở chân tháp.
b. Tốc độ của hỏn đá sau 2 giây kể từ khi ném.
c. Thời gian để hòn đá rơi xuống đất và tầm ném xa tính từ chân tháp. Lấy 2 g = 9,8 m / s Lời giải:
1. Lý thuyết: tương tự câu 2
2. Bài toán: Chọn gốc như hình vẽ V  =V cosα Ta có phương trình v n ậ tốc: x 0 
V =V sinα − gt y 0  x = v t cosα 0
Phương trình chuyển động:  1 2
y = v t sinα − gt + h  0  2 x ⇒ t = V cos α 0 a. Thay x y 1 t = vào y ta có : 2 2
y = h + x tanα −
⋅ x ⇔ y = 25 + x − 0, 029 x V cosα 2 2 2V cos α 3 0 0
Suy ra quỹ đạo là 1 nhánh parabol v =7,5 3 v =7,5 3 m / s b. Ta có x  . Sau t = 2s thì x  2 2
⇒ v = v + v =17,75 m / s v x y  = 7,5− 9,8tv  = 121. − 1 m / s yy
c. Tìm thời gian chạm đất t ta giải phương trình y=0 2 ⇔ 4
− ,9t + 7,5t + 25 = 0 ⇔ t = 3,15s
Tầm xa: L = x(3,15) = 7,5. 3.3,15 = 40,92m Câu 5: Lý thuyết
a. Thiết lập các định Iý về n
độ g lượng của chất điểm. Ý nghĩa của xung lượng của lực.
b. Trình bày định luật bảo toàn động lượng cua hộ chất điểm cô lập và đ n ị h luật bảo toàn động ượ l ng theo một phương ủ c a hệ chất điểm.  Bài toán:
74 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Một bì cát có khối lượng M được treo ằ b ng mợt sợi dây ả m nh không giãn. Bắn ộ m t viên
đạn có khối lượng m theo phương ngang và có tốc độ v vào bì cát. Viên đạn ị b mắc vào
đó và bì cát được nâng lên đến độ cao h so với vị trí ban ầ
đ u. Tính tốc độ y theo các đại lượng m, M,h,g . Lời giải:
1. Lý thuyết: tương tự câu 3 2. Bài toán - Chọn ố
m c thế năng tại v ịtrí A, gọi v’ là vận tốc của hệ bì-đạn ngay sau khi đạn xuyên vào
- Coi hệ bì-cát là hệ cô lập có: động lượng ệ
h trước khi va chạm là K = mv và động lượng 1
hệ sau khi va chạm là K = (m + M )v ' 2
Áp dụng định luật bảo toàn động lượng ta có: K K mv (m M )v′ = ⇒ = + (1 ) 1 2
Cơ năng tại A (sau khi đạn xuyên vào bì): 1 ' 2 W =
⋅ (m + M ).(v ) A 2 Cơ năng tại B: W =(m+M)gh B 1
Theo định luật bảo toàn cơ năng ta có: 2 W W (m M )gh (m M )v′ = ⇔ + = + v′ ⇔ = 2gh (2) A B 2 ′ . m v M.v m + M Từ (1): v = thay vào (2) ta được: = 2gh ⇔ V = ⋅ 2gh m + M m + M m Câu 6: 1. Nêu quan niệm ề
v không gian và thời gian trong cơ ọ
h c Newton. Phép biến đổi
Galileo. Phát biểu nguyên lý tương đối Galileo
2. Bài toán: Một vật A có khối lượng m đặt trên ặ m t p ẳ
h ng nghiêng một góc α nối A
với vật B có khối lượng m bằng một sợi dây mảnh không giãn vắt qua ròng rọc có B khối l ợ
ư ng không đáng kể (hình vẽ). ệ
H số ma sát giữa vật A và ặ m t phẳng nguyên
là k. Bỏ qua ma sát của ròng rọc.
a. Tìm điều kiện của tỉ số mA để vật B đi lên mB b. Tìm gia tốc ủ
c a các vật và lực căng của dây khi đó. Lời giải: 1. Lý thuyết:
Quan niệm về không gian và thời gian:
- Thời gian có tính chất tuyệt đối không phụ thuộc vào hệ quy chiếu
Group: Bachkhoa Universe – Góc học tập và thảo luận 75 TAILIEUHUST.COM
- V ịtrí không gian có tính chất tương đối phụ thuộc vào hệ quy chiếu
- Khoảng không gian có tính chất tuyệt đối không phục thuộc vào hệ quy chiếu
Chứng minh: Xét 2 hệ trục ọ
t a Oxyz quy ước đứng yên, hệ O′x 'y'z' chuyển động tịnh tiến đối với ệ h ′ ′ ′ ′
Oxyz. Ta giả định O x' luôn trượt dọc theo Ox , O y và O z ' song song và cùng
chiều với Oy,Oz . Với mỗi hệ tọa độ ta gắn vào một đồng hồ để chỉ thời gian. Xét một
điểm M có tọa độ không gian và thời gian trong hệ tọa độ Oxyz là t, x, y , z; trong hệ tọa
độ O'x'y'z' là t', x', y', z'. Theo các quan đ ể i m của Newton:
- Thời gian có tính tuyệt đối không phụ thuộc vào ệ h quy ch ế i u: t t′ = (1 ) - V ịtrí của điểm ′ ′
M được xác định tùy theo hệ quy ch ế
i u: x = x ' +OO'; y = y ; z = z (2)
Như vậy: vị trí trong không gian có tính tương đối p ụ
h thuộc vào hệ quy chiếu. Do đó:
chuyển động có tính tương đối tùy thuộc vào hệ quy chiếu.
- Khoảng cách giữa hai điểm bất kì trong không gian là một đại lượng không phụ th ộ u c vào hệ quy ch ế i u. Kho n
ả g cách 2 điểm A,B trong 2 hệ lần lượt là: ′ ′  l x′ x′  = −
x = O O + x o B A  ta lại có A A
⇔ x − x = x′ − x′ ⇔ l =l hay ta có thể nói không B A B A o
l = x − x  ′ ′ B A
x = O O + xB B
gian có tính tuyệt đối, không p ụ h thường vào ệ h quy ch ế i u.
Phép biến đổi Galileo:
Chúng ta xét một trường hợp riêng: chuyển động ủ
c a hệ O' là chuyển động thẳng và đều. Nếu tại t 0,O′ =
trùng với O thì: O O ′ = Vt
V là vận tốc chuyển động của hệ O′ . Theo (1) và (2) ta có: x = x ' +Vt ';
y = y′ ; z = z;t = t′(3) Và ngược ạ
l i: x x′ Vt′ ; y y′ ; z z′ ;t t′ = − = = = (4 )
Các công thức (3) và (4) gọi là phép biến ổ
đ i Galileo: chúng cho ta cách chuyển các ọ t a độ
không gian, thời gian từ hệ quy chiếu O' sang hệ quy chiếu O và ngược lại .
Nguyên lý tương đối Galileo:
+ Phát biểu 1: Mọi hệ quy chiếu chuyển động thẳng đều đối với một hệ quy chiếu quán
tính cũng là hệ quy chiếu quán tính. + Phát biểu 2: Các đ n
ị h luật Newton được nghiệm đúng trong hệ quy chiếu chuyển động
thẳng đều đối với hệ quy chiếu quán tính.
+ Phát biểu 3: Các phương trình động lực học trong các hệ quy chiếu quán tính có dạng như nhau.
76 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 2. Bài toán: Chọn chiều dương ủ c a hệ như hình vẽ.
Phương trình của định luật II Newton với các vật A B là:  A: m g α − k α = T = m a A (sin cos ) A
B :T − m g = m aB B ⇒ m g α − k
α − m g = m + m a A (sin cos ) B ( A B )
a. Điều kiện để B đi lên là: ⇔ ( m + m ) a > 0 ⇔ m .g(sinα − k cosα ) − m .g > 0 A B A B ⇔ m
m (sin α − k cosα ) > m hay B < sinα − k cosα A B mA
m (sin α − k cosα ) − m A B a = ⋅ g  m + m b. Khi đó ta có: A Bm m (
. sin α − k cosα +1)
T = m .(g + a) A B = ⋅ g Bm + mA B Câu 7: 1. Nêu quan niệm ề
v không gian và thời gian trong cơ ọ
h c Newton. Phép biến đổi
Galileo. Phát biểu nguyên lý tương đối Galileo
2. Bài toán: Một người đang chạy với tốc độ v = 2 m / s thì ném tới trước một hòn đá
với tốc độ so với người là v = 5 m / s . Bỏ qua mọi ma sát và chiều cao ủ c a người. 0
a) Tìm góc nghiêng α của vận tốc hòn đá so với người để hòn đá có tầm bay xa cực ạ đ i.
b) Tính tốc độ v′ của hòn đá so với mặt đất trong trường hợp câu a Lời giải
1. Lý thuyết: như câu 6 2. Bài tập:
a. Ta có v′ = v + v (1) 0
Để hòn đá có tầm bay xa nhất thì v′ phải hợp với phương ngang góc 45° nên ′ ' v = v . x y
Chiếu (1) lên 2 phương Ox và Oy : v cos α +v = v sin α 0 0 2 2 2 2 2
⇒ v cosα +v = v 1 −cos α ⇒ 2v cos α + 2vv cosα +v −v = 0 0 0 0 0 0 2   1 vv  cosα  2  ⇒ = − + −  (2) 2  v v  0  0   
Group: Bachkhoa Universe – Góc học tập và thảo luận 77 TAILIEUHUST.COM
Thay số ta được cosα 0, 478 α (61, 45)° = ⇒ = . b) Ta có ′2 2 2
v = v + v + 2vv cos α 0 0
Thay (2) vào biểu thức trên, ta tìm được: ′2 2 2 2
v = v + v 2v − v Thay số được v′ = 6, 2 m / s 0 0 Câu 8:
1. Trình bày định lý về mômen động lượng ủ c a ộ m t chất điểm và ủ c a một hệ chất
điểm đối với gốc tọa độ. ị
Đ nh luật bảo toàn mômen động lượng của chất điểm và hệ chất điểm. 2. Bài toán:
Từ một đỉnh tháp có độ cao h người ta ném một hòn đá có k ố
h i lượng m lên phía trên với
vận tốc v theo phương hơp với phương ngang một góc α . Tìm mô men ngoại lực và mô 0
men động lượng của hòn đá đối với gốc O ở thời điếm t (gốc O chọn tại v ịtrí chân của tháp). Lời giải: 1. Lý thuyết: + Đ n
ị h lý về momen động lượng của một chất điểm đối với gốc tọa độ: Đạo hàm theo thời gian của momen ộ
đ ng lượng đối với O của một chất điểm chuyển động bằng tổng momen đối với dL
O của các lực tác đụng lên chất điểm. Biểu thức: =M / o(F). dt + Đ n
ị h lý về momen động lượng của một hệ chất điểm đối với gốc tọa độ: Đạo hàm theo
thời gian của momen động lượng của một hệ bằng tổng momen các ngoại lực tác ụ d ng lên hệ dL . B ể i u thức: = / o(F ) = ∑ M M dt i + Định luật ả b o toàn:
- Đối với chất điểm: Trong tr ờ ư ng hợp chất đ ể
i m chuyển động luôn luôn chịu tác ụ d ng ủ c a
một lực xuyên tâm F luôn đi qua tâm O cố định. Thì momen động lượng ủ c a chất điểm là
một đại lượng bảo toàn. Biểu thức: M / o(F) = 0 ⇔ L = const - Đối với ệ h chất điểm: ệ H chất điểm cô ậ
l p hoặc chịu tác dụng của các ngoại lực sao cho
tổng momen các ngoại lực ấy ố đ i với điểm ố
g c O bằng 0, thì tổng momen động lượng
của hệ là một đại lượng ả b o toàn.
78 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 2. Bài toán:
- Ngoại lực tác dụng vào hòn đá ch ỉcó trọng lực v = v cosα
Phương trình vận tốc ủ c a hòn đá: x 0 
v = v sin α − t g y 0  x = v cosα 0
Phương trình chuyển động của hòn đá:  1 2
y = h + v t sinα − gt  0  2 x
Momen của ngoại lực: M = r ∧ P |
= r | .| p | .sin(r, p) = r.mg. sin(OMA) = . r m . M g ( P /O) r ⇔ M = mgv t cosα ( / P ) O 0 dL 1 Momen động lượng: = M
⇒ L= mgv .tcosα.dt+ C ∫ 2
= mgv t ⋅ cosα + C ( / P ) O 0 dt 0 2 1
Tại t = 0; L = mv . . h s n i β = mv h cosα 2
⇒ L = mgv t cos α +mv h cos α 0 0 0 0 2 Câu 9:
1. Tính công của lực hấp dẫn khi ộ
m t vật có khối lượng m chuyển động trong trường
hấp dẫn gây bởi một vật có khối lượng M từ vị trí r đến v ịtrí r (Xem các vật như 1 2 chất điểm, có ẽ
v hình). Từ đó suy ra biểu thức tính thế năng của chất điểm trong trường hấp dẫn. 2. Bài toán:
Tính thế năng hấp dẫn của một vật m cách Trái đất (có khối lượng M ) một khoảng I tính
từ tâm trái đất. Từ đó tính thế năng của vật có khối lượng m khi vật m cách bề mặt trái
đất một khoảng h << R , lấy mốc thế năng tại mặt đất bằng không. Lời giải: 1. Lý thuyết:
Công của lực F trong chuyển dời vi phân ds = PQ
mà dA = F.PQ = F.P . Q cos α Nếu ta ẽ
v QH ⊥ OP thì ta có P .
Q cos α = −PH .
Nhưng vì PQ là một chuyển dời vi phân nên ta đặt
OP = r → OH ≈ OQ = r + dr mà
PH = OH − OP = r + dr − r = dr Thay tất cả vào ta có
dA = −F.dr .
Group: Bachkhoa Universe – Góc học tập và thảo luận 79 TAILIEUHUST.COM
Công của lực F trong chuyển dời ủ
c a (m) từ vị trí r đến v ịtrí r trong trường hấp ẫ d n 1 2 r r Mm  1 1  2 M là: 2 A = − Fdr = − G
dr = G .M . ∫ ∫  −  . 2 1 r r2 r r r  2 1 
Dựa vào công thức bên ta thấy công của lực hấp dẫn F không phụ thuộc đường đi mà ch ỉ
phụ thuộc vào vị trí điểm đầu và điểm c ố u i.       + Ta có 1 1 Mm Mm A = GMm − = W  
(r − W r = G − ⋅ + C − G − ⋅ + C t 1 ) t ( 2 )     r r r r  2 1   1   2 
- Tổng quát: Thế năng của Mm (m) tại v
ị trí cách O một khoảng r là: W (r) = −G ⋅ + C với t r
C là hằng số tùy chọn. Đặc biệt W (∞) = C . t 2. Bài toán:
+ Thế năng của một vật m cách Trái đất (M) một khoảng r tính từ tâm trái đất: GMm W( ) r = − + C r
+ Lấy mốc thế năng là mặt đất, biểu thức tính thế năng của chất điểm trong trường hấp
GMm (r − R )
dẫn của trái đất là W = R r GMm
+ Khi r = R + h(h
R) , ta có: r − R = h và 2 rR ≈ R ⇒ W = h = mg h với 2 0 R GM 2 g =
≈ 9,8 m / s là gia tốc trọng trường trên ặ m t đất. 0 2 R Câu 10: 1. Xét chuyển ộ đ ng ủ
c a viên đạn trong trường hấp dẫn ủ
c a trái đất. Tính vận tốc vũ trụ cấp I và cấp II
2. Bài toán: Một vật n ỏ h trượt không ma sát ừ
t đỉnh một bán cầu xuống dưới đất. Cho bán kính 2
R = 3 m, g = 10 m / s . Bỏ qua lực cản của không khí. a. Từ
độ cao nào so với mặt đất vật bắt đầu rời khỏi bán ầ c u.
b. Tìm tốc độ của vật khi bắt đầu rời khỏi bán cầu và tại mặt đất. Lời giải: 1. Lý thuyết:
 Chuyển động trong trường hấp dẫn của trái đất
- Sự phụ thuộc của G theo độ cao :
80 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 Ta có: Mm M M M F = P ⇒ . G = mg ⇒ g = . G = . G = . G hd 2 2 2 2 r r (R + h )  +  2 R h R    R  2 − 2 −  R +h   h   2h  ⇒ g = g = g 1+ ⇒ g = g r − 0   0   0    R   R   R  - Các vận tốc vũ trụ:
Từ 1 điểm A gần mặt đất, người ra bắn 1 vật m với v có thể xảy ra các trường hợp sau: 0
+ v nhỏ thì viện đại rơi xuống đất 0
+ Nếu v đủ lớn thì viện đạn có t ể
h không rơi xuống mặt đất và chuyển động tròn xung 0
quanh trái đất hoặc theo quỹ đạo elip.
+ Nếu v lớn hơn nữa thì vật có thể chuyển động ra xa trái đất 0 Chú ý:
+ Giá trị vận tốc nhỏ nhất để viện đạn vắt đầu chuyển động tròn xung quanh trái đất được
gọi là vận tốc vũ trụ cấp 1
+ Giá trị vận tốc để vật bắt đầu chuyển động ra xa trái đất được gọi là vận tốc vũ trụ cấp 2 2 vy
Tính vận tốc vũ trụ cấp 1: a =
= g ⇒ v ≈ g R n 0 y 0 R
 Tính vận tốc vũ trụ cấp 2: W =W matdat ∞ 2 2 mvMm mvMm ∞  ⇒ + G ∞ − = + G −     2  R  2  ∞  Điều k ệ i n ể
đ vật ra xa vô cùng: v ≥ 0 ∞ 2 mvMm  2G.MR II ⇒ + −G ≥ 0 ⇒ v ≥ = 2g R =   2v II 2 0 2 IR R 2. Bài toán:
a. Chọn mốc thế năng tại ặ m t đất. Xét ạ t i vị trí B
Áp dụng định lý II Newton ta có: F = P + N ,
chiếu lên phương hướng tâm, chiều dương hướng vào tâm ta có: 2 v F = P cos B
α − N = ma = m ⋅ ht ht R
Group: Bachkhoa Universe – Góc học tập và thảo luận 81 TAILIEUHUST.COM 2 2
Vật rời khỏi bán cầu khi N = 0 v h v ⇒ mgcos B B α = m ⋅ ⇔ g ⋅ = 2 ⇔ V = gh R R R B
Áp dụng định luật bảo toàn cơ năng tại A và B 1 3 2 2 mgR = mgh + mv ↔ mgR = mgh ⇔ h = R = 2m 2 B 2 3 Vậy ạ
t i độ cao 2m so với mặt đất vật bắt đầu rời bán ầ c u.
b. Vận tốc khi rời bán cầu: v = gh = 10.2 = 4, 47 m / s B
- Tốc độ khi chạm đất: Áp dụng định luật bảo toàn cơ năng ta có 1 2
W = W ⇔ MgR =
mv ⇔ V = 2gR = 2 1 ⋅ 0.3 = 7, 75 m / s A d 2 d d Câu 11:
1. Tìm biểu thức động năng của chất điểm. Trình bày đ n
ị h lý về động năng của chất điểm. 2. Bài toán:
Một vệ tinh có khối lượng m =150 kg chuyển động trên quỹ đạo tròn có bán kính
R = 7300 km đối với tâm Trái Đất. Tính động năng, cơ năng và tốc độ của vệ tinh trên quỹ đạo. Cho biết −11 G = 6, 67.10 2 2
Nm / kg . Khối lượng Trái Đất 24
M = 5,98.10 kg . Bỏ qua lực cản của không khí. Lời giải: 1. Lý thuyết:
- Định nghĩa: Động năng là phần cơ năng tương ứng với chuyển ộ đ ng ủ c a các vật. Là đại
lượng thể hiện mối phụ thuộc vào ậ v n tốc chuyển ộ đ ng ủ
c a vật thể do công của ngoại lực tác dụng.
- Biểu thức: Có dA = F.ds ⇒ (2) A = Fds ∫ (1) 2   Mà dv (2) dv (2) ds (2) 2 v
F = ma = m ⇒ A = m ds = m dv = mvdv = m d ∫ ∫ ∫ ∫   dt (1) (1) (1) 1 dt dt 2   2 − (2)  mv  ( 2 2 2   2 v ) mv mv mv 2 1 ⇔ A = d = d = − ∫   ∫   2 (1) 2 ( ⇒ = 1 v ) 2 2 2     W mv / 2 d
- Định lý: độ biến thiên động năng của 1 chất điểm trong 1 quãng đường nào đó bằng
công của ngoại lực tác dụng lên chất điểm sinh ra từ quãng đường đó. Biểu thức:
A = W −W d 2 d1
82 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 2. Bài tập: Mm
Thế năng của vệ tinh trong trường hấp ẫ
d n của trái đất là :W (r ) = G − ⋅ t R
(mốc thế năng tại vô cực ) 2   Thế năng của vệ tính: Mm R W = G − ⋅ + . m g . t d R = mg R − t 0 td 0  tdR R    R   6400  td 5 9
= mg .R ⋅ 1 − =150.9,8.6400.10 1 − =1,16.10 J 0 td      R   730  - Vệ tinh chuyển ộ
đ ng tròn, lực hấp dẫn ủ
c a trái đất đóng vai trò là lực hướng tâm 2 Mm V 2 1 Mm mv 1 − F = F ⇒ G ⋅ = m ⋅ ⇒W = G ⋅ = ⇒W = U với U = Mm G − ⋅ hd ht 2 R R d 2 R 2 d 2 R Mm Thay số ta có: U = G − ⋅ = 9 −8, 2.10 J 9
⇒ W = 4,1.10 J R d 1 - Cơ năng của vệ tinh: 9
W = W + U = U = −4,1.10 J d 2 9 2W
- Tốc độ của vệ tinh: 2.4,12.10 d v = = = 7412 m / s m 150 Câu 12:
1. Nêu các đặc điểm động học của chuyển ộ đ ng t n
ị h tiến và chuyển động quay quanh
một trục cố định của vật rắn.
2. Bài toán: Một cột đồng chất có chiều cao h = 5 m đang dựng thẳng đứng th b ì ịđổ
quay quanh chân của nó xu n
ố g mặt phẳng nằm ngang. Xác định:
a. Vận tốc dài của đỉnh cột khi chạm đất.
b. Vị trí của điểm M trên cột sao cho khi M chạm đất thì ậ
v n tốc của nó đúng bằng vận
tốc chạm đất cùa một vật thả tự do từ vị trí M . (cho 2 g = 9.8 m / s ) Lời giải: 1. Lý thuyết:  Đặc đ ể i m động học ủ
c a chuyển động tịnh tiến
- Khi vật rắn chuyển động tịnh tiến, mọi điểm của vật rắn c ó quỹ đạo giống nhau.
- Tại mỗi thời điểm, mọi điểm của vật rắn đều có cùng vận ố t c và gia tốc
- Gọi a là gia tốc chung cho các điểm của vật rắn m , m , ,
… m chịu sự tác dụng của 1 2 n
F ,F ,… ,F song song và cùng chiều. Khi đó ta có: m a = F ; m a = F ;....; m a = F 1 2 n 1 1 2 2 n n
Group: Bachkhoa Universe – Góc học tập và thảo luận 83 TAILIEUHUST.COM
⇒ Khi nghiên cứu chuyển động t n ị h tiến ủ
c a 1 vật rắn, ta chỉ cần nghiên cứu chất điểm
bất kì là được và người ta thường ch n ọ khối tâm.
 Chuyển động quay quanh một trục ố c định của vật rắn
- Do khoảng cách giữa các c ấ
h t điểm của vật rắn không thay đổi nên mọi chất điểm đều chuyển ộ
đ ng tròn và có tâm quay ở trên cùng 1 trục quay.
- Trong cùng 1 khoảng thời gian, mọi điểm trên vật rắn cùng quay được 1 góc. 2 θ ω θ - Tại cùng thời đ ể
i m, mọi chất điểm có cùng ϖ d d d , β i vớ ω = ; β = = 2 dt dt dt - Tại thời đ ể
i m t, vectơ vận tốc dài v và a của chất điểm cách t ụ
r c quay 1 khoảng r , được t v = ω ∧ r ;
xác định bởi công thức: a = β ∧ r 2. Bài toán: 1
- Mốc thế năng tại mặt đất, thế năng của ộ
c t tính tại khối tâm của ộ c t: W = mgh t 2 1 1
Khi rơi xuống, cột có động năng quay 2 2 2 W = Iw = mh w d 2 6
Áp dụng định lý bảo toàn cơ năng 1 1 3 2 2 g W = W ⇔ mgh = mh ω ⇔ω = t d 2 6 w
Vận tốc đỉnh cột khi chạm đất: v = wh = 3gh =12,12 m / s
Vật thả rơi tự do tại M thì vận tốc chạm đất là: v′ = 2 gx M M Khi cột chạm đất: ′ 3g
v = ω x = x M M M h Vì ′ 3g 2 v = v ⇔ 2gx = x
⇔ x = h ≈ 3,33 m M M M M M h 3 Câu 13:
1. Thiết lập phương trình cơ bản của vật rắn quay xung quanh một trục ố c định. Nêu ý
nghĩa của các đại lượng trong phư n
ơ g trình đó. Nêu đặc điểm ủ c a momen quán tính.
2. Bài toán: Một vật m =1 kg đượcc nối với một đầu dây cuốn vào một trụ đặc và được t ả
h rơi xuống như hình vẽ. T ụ
r có bán kính R = 10 cm và có khối lượng
M = 6 kg . Bỏ qua lực ma sát và khôi lượng của dây.
a. Tìm độ lớn gia tốc dài của vật m và lực căng của dây. Cho 2 g = 10 m / s .
84 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 π b. T m
ì công thực hiện bởi lực căng của dây khi trụ quay đượcc một góc (kể từ lúc bắt 4 đầu thả vật) Lời giải: 1. Lý thuyết:
Phương trình cơ bản ủ c a vật ắ
r n quay xung quanh một trục cố định: M = I β
Gọi M là một chất điểm bất kỳ của vật rắn, cách t ụ r c một khoảng r i i
ứng với bán kính vecto OM = r có khối lượng m và chịu tác dụng của i i i ngoại lực tiếp tu ế
y n F . Chất điểm M sẽ chuyển động với vecto gia ti i tốc tiếp tu ế
y n a cho bởi: m .a = F ti i ti ti Nhân có hướng hai ế
v với vecto bán kính r ta được: m .a ∧ r = F ∧ r i i ti i ti i
mà m a ∧ r = M doM = F ∧ r i ti i i ( i ti i )
Lại có a ∧ r = ( r r ) β − ( r.β r = r β − r ⊥ β → r β = ti i i i i ) 2 , . . . 0 i i ( . 0 i i   2
⇒ m.r .β = M . Tính với hệ vật rắn ta có 2 ∑ β = ∑ i m .r . M i ii iiii 2
I = ∑m ⋅r i ii  ⇒ I ⋅ β = (1)M
. Phương trình (1) được gọi là phường trình cơ bản của chuyện M = ∑M ii
động quay của vật rắn xung quanh một trục.
Với: I là momen quán trính của vật rắn đối với trục ∆ .
M là tổng hợp momen của các ngoại lực tác dụng lên vật rắn. β là gia tốc góc.
Đặc điểm của momen quán tính
- Là đại lượng vật lý đặc trưng cho tính bảo toàn trạng thái của hệ trong chuyển động quay
- Momen quán tính phụ thuộc vào khối lượng ủ
c a các thành phần trong hệ và khoảng
cách giữa các thành phần trong hệ đến t ụ r c quay. 2. Bài toán: a. Phương trình đ n
ị h luật II Newton cho vật: P – T = ma Phương trình momen lực: a M
= T.R = Iβ = I T R
Group: Bachkhoa Universe – Góc học tập và thảo luận 85 TAILIEUHUST.COM
mg −T = maT  + a = 9,8 T  = 7,35 N Từ đó ta có hệ:  1 ⇔  ⇒  2 a TR = MR ⋅ 2  T = 3a a = 2, 45 m / s    2 R π
b. Khi trụ quay được 1 góc ⇒ S = R ⋅ϕ = 0,025π (rad) 4
Công của lực căng dây A = T.S = 0,58 J Câu 14:
1. Thiết lập biểu thức tính công của ngoại lực trong chuyển động quay của vật rắn xung quanh một trục ố c định. Suy ra ị đ nh lý ề
v động năng của vật rắn trong chuyển động quay.
2. Bài toán: Một vô lăng dạng đĩa trơn đồng tính có khối lượng m = 40 kg , bán kính
R = 0, 5 m đang quay xung quanh trục đi qua tâm và vuông góc với mặt đĩa với tốc
độ góc n n = 240 vòng/ phút. Tác dụng lên vô lăng một lực hãm. Tìm độ lớn của
mômen hãm trung bình trong các trường hợp:
a. Vô lăng dừng lại trong 40 s .
b. Vô lăng dừng lại sau khi quay được 5 vòng kể từ khi tác dụng lực hãm. Lời giải: 1. Lý thuyết:
Thiết lập biểu t ứ h c:
- Trong trường hợp một vật rắn quay xung quanh một trục ∆ các
lực tác dụng đều là lực tiếp tu ế
y n. Công vi phân của một lực tiếp
tuyến F cho bởi: dA = F .ds . Xong lại có ds =r.dα với dα là góc t t
quay ứng với chuyển dời ds , vậy dA = r.F .dα . t
Theo định nghĩa ta có .rF = M là momen của lực F đối với trục t t
quay ∆ , do đó dA = M .dα
Tích phân hai vế trong một khoảng thời gian hữu h n
ạ , trong đó vận tốc góc ω biến thiên
từ ω đến ω ta được công toàn phần của ngoại l c
ự tác dụng lên vật rắn quay từ vị trí 1 1 2 2 2 ω ω
(ứng với ω ) đến vị tr ị2 ( ứng với ω là: . I . I 2 1 A = − . 2 ) 1 2 2 2
+ Suy ra động năng của vật rắn quay có biểu thức là: . Iω W = d 2
Định lý động năng của vật ắ
r n trong chuyển động quay:
Động năng của vật rắn quay bằng nửa tích của momen quán tính của vật rắn và bình
phương vận tốc góc của vật rắn xung quanh một trục ố c định.
86 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 2. Bài tập: a. Áp dụng đ n
ị h lý về momen động lượng: L ∆ = M t ∆ 2 mR 2π n 1 ⇒ M = 0 − . . = π − ( N / ) m 2 60 ∆t 2 ϖ b. Áp dụng đ n
ị h lý động năng của 1 vật rắn quay ta có: I A = W ∆ = 0 − = M . θ ∆ d 2 2 2 2 Iϖ 1 1 mR  2π n  1 ⇒ M = . = − . . . = 1 − 6   π ( N ) m 2 2π n 2 2  60  2π .5 1 Câu 15:
1. Thiết lập phương trình dao động tắt dần ủ
c a con lắc lò xo dưới tác dụng của lực cản
có độ lớn tỷ lệ với tốc ộ đ . T m
ì công thức tính giảm lượng loga của dao động tắt dần.
2. Bài toán: Một con lắc 10 xo dao động tắt dần với biên độ ban đầu A = 12 cm . Sau 0
2,4 phút biên độ của nó giảm còn 6cm.
a. Tìm hệ số tắt dần.
b. Sau bao lâu biên độ chỉ còn 2 cm . Lời giải: 1. Lý thuyết F = k − x
Các lực tác dụng lên vật: kv  F = r − vc
Áp dụng định luật II Newton ta có: F + F = ma, chiếu lên chiều dương: −kx − rv = ma kv c 2 2 hay d x dx d x r dx k m = −kx− r . ⇔ + ⋅ + x = 0. 2 dt dt 2 dt m dt m 2 Đặt k 2 =ω hay r = d x x d 2β 2 ⇒ +2β ω + x = 0. 0 m m 0 dt dt
Nghiệm của phương trình trên có dạng: −βt x = A e
cos(ωt +ϕ ) đó là phương trình dao đ n ộ g n tắt dần với 2 2 ω = ω − β . 0
Giảm lượng loga: loga tự nhiên của ố s 2 biên ộ
đ dao động liên tiếp cách nhau 1 chu kỳ T . Đặt t A A e β − = ⋅ 10 − βt ⇒ ( A ) t A .e Giảm lượng loga: 0 δ = ln = ln = ln T
eβ ⇒ δ = βT . − β(t+T ) ( A t +T ) . A e
Group: Bachkhoa Universe – Góc học tập và thảo luận 87 TAILIEUHUST.COM 2. Bài tập
a. Biên độ dao động tắt dần có − t A = A e β ⋅ 10
Sau t = 144s, biên độ giảm từ 12cm xuống còn 6cm, thay vào công thức trên ta có: − 1⋅44 3 − 1 6 12.e β ⇒ β 4,8.10 s− = = −
b. Biên độ giảm còn 2cm. Thay vào công thức trên ta có: 3 −4,8 1 ⋅ 0 t 2 2 =12.e ⇒t = 373( s) 2 Câu 16: 1. Trình bày: a. Khái niệm ệ
h nhiệt động và khí lý tưởng.
b. Thiết lập phương trình trạng thái kh ílý tưởng cho 1 mol khí và một khối khí có khối
lượng bất kỳ (có hình vẽ minh họa). 2. Bài toán: Trong một ngày trời ạ
l nh ở nhiệt độ 15°C , thể tích và áp suất của khí bên trong một lốp xe ô tô đo được ầ l n lượt là 3
15dm và 1,70 at. Sau đó, khi xe chạy trện đường cao tốc, nhiệt độ
khí bên trong lốp đo được là 45° C và thể tích cũng tăng lên thành 3 15,9dm . Coi khí bên
trong lốp xe là khí lý tưởng, tính áp s ấ u t lốp xe khi đó. Lời giải: 1. Lý thuyết:
a. Hệ nhiệt động là một hệ cấu tạo bởi 1 số lớn các hạt (phân tử, nguyên từ, …) các hạt này
luôn chuyển động hỗn độn không ngừng và không ngừng trao đổi với nhau khi tương tác.
- Khí lý tưởng là khí tuân theo hoàn toàn chính xác 2 đ n
ị h luật thực nghiệm là Boyle- Mariotte và Gay Lusac, …
+ Hệ khí bỏ qua tưởng tác giữa các phân tử
+ Hệ khí bỏ qua kích thước của các phân tử (các phân tử được coi là chất điểm)
b. Thiết lập phương trình trạng thái ủ c a khí lý tưởng
- Xét quá trình biến đôi một khối khí xác ị đ nh từ trạng thái
(p , V , T sang trạng thái (p , V , T 2 2 2 ) 1 1 1 ) Giả sử có 1 mol kh í ′ ′ V
- Xét quá trình đẳng nhiệt M M ′ có 1
p V = p V ⇔ p = p (1) 1 1 1 1 1 2 1 1 V2 ′
- Xét quá trình đẳng tích p p ′ p M M ′ có 1 2 2 = ⇔ p = T (2) 2 1 1 1 T T T 1 2 2
88 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Từ (1) và (2) ta có: V p p V p V 1 2 1 1 2 2 p = T ⇔ = 1 1 V T T T 2 2 1 2 pV ⇒
= const là phương trình trạng thái khí lý tưởng T pV
- Như vậy đối với 1 mol khí lý tưởng
= R ( R là hằng số không đổi) ⇔ pV = RT T
Đối với một khối khí bất ỳ k có khối lượng m: m v =
(V là thể tích 1 mol khí) µ
Khi đó phương trình trạng thái khí trở thành: m pV = RT µ 2. Bài tập:
Áp dụng phương trình trạng tháu của khí lý tưởng ta có: p V PV PV T 1 1 2 2 1 1 2 = ⇔ p = ⋅ 2 T T T V 1 2 1 2 1, 7.15 318 ⇒ p = ⋅ =1,77 at 2 288 15,9 Câu 17: 1. Trình bày a. Nội dung cơ ả
b n của thuyết động học phân từ khí lý t ở ư ng.
b. Viết phương trình cơ bản của thuyết động học p â
h n tử và phương trình trạng thái của khí lý t ở ư ng. 2. Bài toán:
Một bình dung tích V = 5l ở áp suất p = 8 atm ch
ứa 2 mol khí Oxy (O ). B ế i t khối lượng 2
phân từ của O là µ = 32 g / mol, tính: 2 a. Động năng chuyến ộ
đ ng tịnh tiến trung bình của ộ m t phân tử khí O . 2
b. Trung bình của bình phương vận tốc một phân tử kh íO . 2 Cho biết 5 23 1 1 atm 1, 013.10 P, N 6, 023.10 mol− = = A Lời giải: 1. Lý thuyết:
a. Nội dung cơ bản của thuyết động học phân tử khí lý tưởng
- Các chất khí có cấu tạo gián đoạn và gồm một số rất lớn phân tử
Group: Bachkhoa Universe – Góc học tập và thảo luận 89 TAILIEUHUST.COM - Các phân tử chuyển ộ
đ ng hỗn loạn không ngừng. Khi chuyển ộ đ ng chúng va chạm vào
nhau và va chạm vào thành bình - Cường độ chuyển ộ đ ng ủ
c a phân tử biểu hiện ỏe nhiệt độ của khối khí. Nhiệt độ càng
cao thì các phân tử chuyển động càng mạnh
- Kích thước phân tử rất nhỏ so với khoảng cách giữa chúng
- Các phân tử không tương tác với nhau trừ lúc va chạm b. Phương trình:
- Phương trình cơ bản của thuyết động học phân tử: 2 P = n W 0 3 d
- Phương trình trạng thái của khí lý tưởng: m pV = nRT = RT µ 2. Bài tập: a. n Độ g năng tịnh t ế
i n trung bình của 1 phân tử Oxi là: 5 2 i R i PV 3 8,1, 03.10 .5.10 2 − 1 W = ⋅ ⋅T = ⋅ = ⋅ = 5,05.10 d 23 2 N 2 nN 2 2.6, 023.10 A A b. Ta có: 1 1 2.W . . n N 2 2 d A W = mv ⋅ ⇔ v = d 2 . n N . n µ A −21 23 2W .N 2.5, 05⋅10 6 . d A , 023.10 2 5 = = ⇔ v = 1,9.10 m / s −3 µ 32.10 Câu 18: 1. Trình bày
a. Từ phương trình thuyết động ọ h c phân tử c ấ
h t khí hãy dẫn ra biều thức động năng
chuyển động nhiệt và suy ra công thức tính vận tốc căn quân phương của các phân tử khí.
b. Nêu khái niệm bậc tư do, nội dung định luật phân bố đều theo các bậc tự do, từ đó suy
ra biểu thức nội năng cho một k ố h i khí có khối ượ l ng bất kỳ
2. Bài toán: Một k ố
h i khí Oxy(O được đựng trong một bình chứa hình lập phương 2 )
có kích thước mỗi cạnh bằng 0,10 m, ở áp suất là 5
1, 013.10 Pa và nhiệt độ bằng 27 °C , tính: a. Động ă
n ng chuyển động tịnh tiến trung bình của một phân tử khí O ; 2
b. Số các phân tử khí O có trong bình khí nói trên. 2
90 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 (Cho biết, −23 k = 1, 38.10
J / K , µ = 32 g / mol ). Lời giải: 1. Lý thuyết: 2 a. Từ 3 P
phương trình thuyết động ọ
h c phân tử chất khí P = n W ⇒W = (*) 0 d 3 d 2 n0
Xét một mol khí lý tưởng: PV=RT suy ra P = RT/V. Thay vào (*) ta có: 3 RT W = d 2 V 0 n Mà RT V .n = 3 N ⇒W = . 0 A d 2 N A - Định nghĩa vận ố t c căn quân phương: 2 v = v c Đặ R t 23 k =
= 1,38.10 (J / k ) : hằng số Boltsman NA 3 1 2 3kT ⇒ kT RT kT W = kT = mv ⇒ v = 3 3 3 ⇒ v = = = d 2 2 c c m c m mN µ A
b. Bậc tự do của 1 hệ là số tọa độ c
độ lập cần thiết để mô ả
t trạng thái của hệ trong không gian. Đối với ệ
h khí có phân tử đơn nguyên tử: i = 3. i Đố với l ỡ
ư ng nguyên tử: i = 5. Đối với đa nguyên tử: i = 6 - Định luật phân ố
b đều động năng theo các bậc tự do: Động năng của một phân tử khí
được phân bố đều trên các bậc tự do
- Biểu thức nội năng của khối khí bất ỳ k :
Có động năng trung bình của 1 phân tử là : KT W = i d 2 Nội năng của ộ
m t khối khí có khối lượng bất ỳ k là : i.KT i RT m i
U = W = N.W = N . = . .N ⇒ U = . RT d d A 2 2 N µ 2 A 2. Bài tập: a. Động năng ′ 3 R 3 8, 31 : −21 W = ⋅ ⋅T = ⋅ .300 = 6, 21.10 (J ) d 23 2 N 2 6, 023.10 A P
b. Số phân tử trong bình là: 22 N = n V = .V = 2, 45.10 0 RT Câu 19:
1. Thiết lập
Group: Bachkhoa Universe – Góc học tập và thảo luận 91 TAILIEUHUST.COM
a. Công thức khí áp cho một cột khí lý tưởng ở độ cao h so vớ mặt đất (có hình vẽ minh họa).
b. Biểu thức của định luật phân bố phân tử theo thế năng
2. Bài toán: Ở điều k ệ
i n áp suất bằng 1 at và nh ệ
i t độ 20° C, một người trong trạng thái tĩnh, hít vào hổ
p i một lượng khí có t ể h tích ằ
b ng 0,5 l. Biết rằng trong không
khí số phân tử Oxy chiếm tỷ lệ 21% (coi không khí là khí lý tưởng), tính số phân tử
Oxy trong mỗi lần hít vào, khi người đó ở: a. Trên mặt đất
b. Trên ngọn núi có độ cao h=2000m và nhiệt độ vẫn là 20° C. Biết không khí có
µ = 29 g / mol và R = 8.31 J / mol.K Lời giải 1. Lý thuyết:
a. Công thức khí áp cho một cột khí lý tưởng ở độ cao h so với mặt đất
- Chọn phương Oz hướng lên các điểm như hình vẽ, ta có µ p µ p dp µ g
dp = −ρgdz , trong đó ρ = ⇒ dp = − gdz ⇔ = − dz RT RT p RT
Tích phân hai vế từ O đến h µ gh mgh ( p ) h h dp µ g µgh − − = − dz = − ∫ ∫ ⇔ p(h) = p(o) RT e = p (o) kT e p(O) 0 p RT RT
b. Định luật phân bố theo thế năng: n h n o
n (o) và n (h)là mật độ các phân tử khí tại các áp suất p(o) và p(h) Ta có ( ) ( ) o o = từ o o p(h) p(o) µ gh đó suy ra −
n (h) = n (o) RT e o o µ mgh − Mà mN m = =
nên n (h) = n (o) kT e , Đặt W = mgh R R k o o t
⇒ Mật độ phân tử chất khí đặt trong một trường lực thế phụ thuộc vào thế năng trong trường ự l c thế đó. 2. Bài tập: 4 3 − a. Từ phương trình tr n
ạ g thái của khí lý tưởng ta có: PV 9,81.10 .0, 5.10 n = = = 0,02 mol RT 8,31.293
Số phân tử Oxy hít vào là: 24
N = 0, 21.n.N = 2,53⋅10 ( pt ) A b. Áp suất không khí t i ạ độ cao h = 2000m
92 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 −3 mgh 29 1 ⋅ 0 .9,8.2000 − − 4 kT 8,31.293 4 P( ) h = P .e = 9,8.10 ⋅ e ≈ 7,8 1 ⋅ 0 Pa o mgh 4 −
Số phân tử Oxy hít vào là: 21 7,8.10 21 n = n . kT e = 2,53.10 ⋅ = 2,01 .10 ( pt) 0h 0 4 9,81.10 Câu 20: 1. Trình bày
a. Khái niệm công và nhiệt trong một quá trình cân bằng.
b. Nội dung, biểu thức ,ý nghĩa và hệ quả của nguyên lý 1 nhiệt động lực học.
2. Bài toán: Một khối khí đựng trong một bình c ứ
h a có áp suất không đổi là 2,3.10 Pa
được nén từ thể tích ằ b ng 3 1, 7 m xuống còn 3
1, 2 m . Khi đó, nội năng khối khí giảm đi một lượng bằng 5 1, 4 ⋅10 J . Tính:
a. Công khối khí nhận được khi bị nén.
b. Nhiệt lượng khối khí sinh ra trong quá trình nén. Lời giải: 1. Lý thuyết:
a. Công là đại lượng đặc trưng cho mức độ trao đổi năng lượng thông qua chuyển động có hướng ủ c a hệ
Nhiệt là đại lượng đặc trưng cho mức độ trao đổi năng lượng thông qua mức độ chuyển
động hỗn loạn của các phân tử trong hệ. b.
Nội dung: Trong một quá trình biến đổi, độ biến thiên năng lượng của hệ trong quá
trình biến đổi bằng tổng công và nhiệt ệ
h nhận được trong quá trình đó.  Biểu thức: U ∆ = A + Q W ∆
= A + Q . - Hệ đứng yên W = U ⇒ U ∆ = A + Q Đối với quá trình b ế
i n đổi vô cùng nhỏ dU = dA + dQ .  Ý nghĩa:
- Nếu A > 0,Q > 0 ⇒ U
∆ = U −U > 0 → Nội năng tăng, hệ nhận công và nhiệt. 2 1
- Nếu A < 0,Q < 0 → U
∆ < 0 → Nội năng giảm . → Hệ sinh công A′ , tỏa ra nhiệt Q′ .  Hệ quả: - Đối với ệ h cô lập:
Group: Bachkhoa Universe – Góc học tập và thảo luận 93 TAILIEUHUST.COM
+ Hệ không trao đổi ra môi trường bên ngoài: A = 0 = Q thì ∆U =0 nên nội năng được bảo toàn
+ Hệ cô lập gồm 2 hệ con: Q = 0 ⇒ Q + Q = 0 ⇒ Q = −Q 1 2 1 2
⇒ Kết luận: Trong một ệ
h cô lập gồm 2 hệ con nhiệt lượng do vật này tỏa ra bằng nhiệt
lượng do vật kia thu vào và ngược lại - Đối với ệ
h biến đổi theo chu kỳ: ∆U = 0 ⇒ A+ Q = 0 ⇒ A = Q −
⇒ Kết luận: Trong một chu trình công mà hệ nhận được bằng nhiệt lượng cho 1 hệ bỏ ra và ngược ạ l i ⇒ Không tồn tại đ n ộ g cơ vĩnh cữu loại I 2. Bài toán:
a. Công không khí nhận được (quá trình đẳng áp):
A = −P (V −V = 2
− ,3.10 ⋅ (1,2 −1,7) =1,15.10 ( J) 1 ) 5 5 2
b. Áp dụng nguyên lý I nhiệt động lực học ta có nhiệt khối khí sinh ra là: ′ 5 5 5
Q = −Q = −∆U + A = 1, 4.10 + 1,15.10 = 2, 25.10 Câu 21:
1. Xét một khối khí lý ưở t
ng biến đổi theo quá trình cân bằng đẳng áp:
a. Viết phương trình và vẽ đồ thị của quá trình trong hệ OpV .
b. Thiết lập biểu thức tính công và nhiệt trong quá trình biến đổi đó.
2. Bài toán: Hơ nóng 10g khí Oxy ở nhiệt độ 10 độ C tới thể tích 4 lít trong khi vẫn giữa nguyên áp s ấ u t ở 3at. Tính:
a. Công do khối khí thực hiện
b. Nhiệt lượng mà khối k í h nhận được. Lời giải: 1. Lý thuyết:
a. Quá trình đẳng áp là quá trình biến đổi t ạ r ng thái, trong đó áp
suất của khối khí không đổi P = const Phương trình V V V V 1 2 = const hay n = = = T T T T 1 2 n - Đồ th ịOP : V b.
94 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 - Công: V 2 A = − pdV = p ∫
( V − V . Quy ước: A>0 là nhận công; A<0 là sinh công 1 2 ) 1 V T - Nhiệt: m 2 m m Q = δQ = C dT = C T −T = C ∆ ∫ ∫ p p ( T 2 1 ) p 1 T µ µ µ i + 2 Trong đó C =
R là nhiệt dung mol đẳng áp p 2 2. Bài toán:
a. Công do không khí sinh ra: A′ = A − =P (V V − 2 1 )
Thể tích khí trước khi hơ: m m 1 10 1 3 PV T V R T 8,31.283 2, 5.10 − = ⋅ ⇔ = ⋅ ⋅ ⋅ = ⋅ = (l) 1 1 1 1 9 µ µ P 32 3.9,81.10 4 −3
⇒ A′ = 3.9,81.10 (4 − 2,5) ⋅10 = 441 J
b. Nhiệt độ khối khí sau khi hơ nóng là: V2 T = T ⋅ = 453 2 1 V1 +
Nhiệt lượng khối khí nhận được là: m i 2 10 7 Q = . . . R∆ T =
. .8, 31.(453 − 283) = 1545 J µ 2 32 2 Câu 22:
1. Xét một khối khi lý tưởng biến đổi theo quá trình cân bằng đo n ạ nhiệt:
a. Định nghĩa và thiết lập phương trình liên hệ giữa áp suất và thể tích ủ c a khối khí trong
quá trình biến đổi đó. b. Vẽ dạng đồ th c
ị ủa quá trình trên trục tọa độ OpV. Vì sao trên đồ thị. OpV đường đoạn nhiệt dốc hơn đ ờ ư ng đẳng nhiệt?
2. Bài toán: Một khối khí: đơn nguyên tử, ban đầu có áp suất bằng 5 1, 5.10 Pa và thể tích bằng 3
0, 08 m , được nén đoạn nhiệt đến thể tích 3 0, 04 m . Tính
a. Áp suât khối khí cuối quá trình nén.
b. Công khối khí nhận được trong quá trình. Lời giải: 1. Lý thuyết:
Quá trình đoạn nhiệt là quá trình trong đó hệ không trao đổi nhiệt với mô trường Q = const hay δ Q = 0 a. Ta có:
Group: Bachkhoa Universe – Góc học tập và thảo luận 95 TAILIEUHUST.COM Ta có: m . i R m U = ⋅ T =
C T và δA = − p dV v µ 2 µ m m RT ⇒ dV dT R dV
C dT = − p dV = −
dV Hay C dT = −RT ⇔ + ⋅ = 0 V µ µ V V V T V C V R ⇒ lnT + lnV = const CV − Do R C C P V = = γ − ⇒ T + γ − V = ( γ 1 1 ln ( 1) ln
ln T ⋅V − ) = const C C V V PV γ = const γ  1
⇒ T.V − = const →  1 γ− TP γ  = const
b. Giải thích: Đường đoạn nhiệt dốc hơn ẳ đ ng nhiệt do:
+ Trong quá trình nén đoạn nhiệt (1-2):
δA >0 nên dU > 0 , do đó dT > 0 nghĩa là nhiệt độ khối khí tăng
lên, đường đoạn nhiệt đi lên nhanh hơn đường đẳng nhiệt.
+ Trong quá trình giãn đoạn nhiệt (1-2):
δA <0 nên dU < 0 , do đó dT < 0 nghĩa là nhiệt độ khối khí giảm
và đường đoạn nhiệt đi xuống nhanh hơn đẳng nhiệt
Như vậy trên đồ thị (p,V) đường đoạn nhiệt dốc hơn đường đẳng nhiệt 2. Bài toán: i 2 5 γ + = = = 1, 67 i 3 γ   γ γ V
a. Áp suất khối khí của quá trình nén: 1 5
p V = p V ⇔ p = p ⋅ =   4,77.10 pa 1 1 2 2 2 1  V2 
b. Công mà khối nhận được là: m im mi A = U ∆ = R ( 1 . . . T T − = . .RT − RT = . PV − p V 2 1 )  2 1  ( 2 2 1 1 ) µ 2 2  µ µ 2  3 ⇒ A = . ( 5 5 4,77.10 0
. , 04 −1, 5.10 .0,08 ) =10620( J) 2 Câu 23:
1. Lý thuyết:
a. Phát biểu nguyên lý 2 nhiệt động lực ọ
h c dưới dạng cổ điển ủ c a Clausius và Thomson và
nêu ý nghĩa của nguyên lý.
96 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
b. Thiết Iập biểu thức định lượng ủ c a nguyên lý 2.
2. Bài toán: Trong mỗi chu trình hoạt động, ộ
đ ng cơ của một xe ô tô tải cần một nhiệt lượng bằng 4
10 J để sinh công. bằng 3 2.10 J . Tính:
a. Hiệu suất của động cơ.
b. Nhiệt lượng nhả cho ngụồn lạnh trong mỗi chu trình. Lời giải: 1. Lý thuyết:
a. Phát biểu của Clausius: Nh ệ
i t không thể tự động truyền từ vật lạnh sang ậ v t nóng hơn
- Phát biểu của Thomson: Không thể c ế
h tạo được một máy hoạt động tuần hoàn biến đổi
liên tục nhiệt thành công mà không nhờ làm lạnh một vật và xung quanh không chịu một
sự thay đổi đồng thời nào. Những động cơ như vậy là động cơ vĩnh cửu loại II. - Ý nghĩa:
+ Khắc phục được những hạn chế của nguyên lý I
+ Không thể chế tạo được động cơ vĩnh cửu loại ha i
b. Thiết lập biểu thức định lượng:
Từ biểu thức tính hiệu suất chu trình Các-nô T Q′ 2 2 ⇒ = kết hợp với ị
đ nh nghĩa hiệu suất ta được T Q 1 1 Q Q ′ T T T Q ′ − − Q Q 1 2 1 2 2 2 1 2 ≤ ⇔ ≤ ⇔ + ≤ 0 Q T T Q T T 1 1 1 1 1 2 Giả thiết ệ
h biến đổi theo một chu trình gồm vô số quá trình đẳng nhiệt và đoạn nhiệt ế k
tiếp nhau, tương ứng với nhiệt độ và nhiệt lượng của các nguồn nhiệt bên ngoài là Q T , T , ,
… T ,… và Q ,Q ,…Q ,… khi đó ta c ó i ∑ ≤0 1 2 i 1 2 i i Ti Nếu coi ệ
h tiếp xúc với vô số nguồn nhiệt có nhiệt độ T vô cùng gần nhau và biến thiên
liên tục; mỗi quá trình nhận nhiệt δQ từ nguồn nhiệt, ta có b ể
i u thức định lượng ủ c a nguyên lý II là δ ≤ 0 ∫ Q T
- Dấu “=" ứng với chu trình thuận nghịch
- Dấu "<" ứng với chu trình không thuận nghịch 2. Bài toán:
Group: Bachkhoa Universe – Góc học tập và thảo luận 97 TAILIEUHUST.COM 3 a. Hiệu suất động cơ: A ' 2.10 η = = = 20% 4 Q 10 1
b. Nhiệt nhả cho nguồn lạnh là: ′ ′ 4 3− 3
Q = Q − A = 10 − 2.10 = 8.10 J 2 1 Câu 24:
1. Xét chu trình Carnot thuận nghịch
a. Vẽ đồ thị chu trình trên trục ọ t a độ Op
V và gọi tên các quá trình trong chu trình, chỉ rõ
quá trình nào hệ nhiệt động nhận nhiệt từ nguồn nóng và quá trình nào hệ nhả nhiệt cho nguồn lạnh.
b. Thiết lập biểu thức tính và nêu kết luận về hiệu suất hoạt động cơ nhiệt hoạt đ n ộ g theo chu trình.
2. Bài toán: Một động cơ nhiệt làm việc theo chu trình carnot, trong mỗi chu trình
nhận được 2000 J nhiệt lượng từ nguồn nóng. Nhiệt độ của nguồn nóng là 227° C ,
nhiệt độ của nguồn ạ
l nh là 27° C. Tính: a. Hiệu s ấ u t của động cơ.
b. Công mà động cơ thực hiện trong mỗi chu trình. Lời giải: 1. Lý thuyết:
a. Chu trình cano thuận nghịch ồ
g m 2 quá trình đẳng nhiệt
thuận nghịch và đoạn nhiệt thuận ng ị h ch Đồ thị: - Chu trình Các-nô thuận
+ Quá trình 1-2: Giãn đẳng nhiệt ở T , tác nhân thu nhiệt Q 1 1 từ nguồn nóng
+ Quá trình 2-3: Giãn đoạn nhiệt, t giảm: γ −1 γ −1
T → T :T .V = T .V 1 2 1 2 2 3
+ Quá trình 3-4: Nén đẳng nhiệt ở T , tác nhân tỏa nhiệt Q cho nguồn lạnh 2 2
+ Quá trình 4-1: Nén đoạn nhiệt, nh ệ
i t độ tăng từ T lên T : γ 1 − γ 1 T .V T .V − = 2 1 1 1 2 4 - Chu trình các-nô ngh c
ị h ngược loại với chu trình thuận.
b. Thiết lập biểu thức tính hiệu suất m V ′ m V 2 3 Q = RT ln ; Q = −Q = RT ln 1 1 2 2 2 µ V µ V 1 4
98 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Trong các quá trình đoạn nhiệt γ− γ− γ− γ− 2 − 3 và 4 −1, ta có: 1 1 1 1 TV =T V & TV = T V $ 1 2 2 3 1 1 2 4 γ −1 γ −1 V   V V V Suy ra: 2 3 2 3 = ⇔ =     V V V V  1   4  1 4 m V3 RT ln ′ 2 ⇒ µ
Công thức tính hiêu suất chu trình Các-nô: Q V T 2 4 2 η =1− = 1− hay η = 1− Q m V2 T 1 1 RT ln 1 µ V1
Kết luận: hiệu suất của chu trình Các-nô thuận nghịch đối với khí lý tưởng c ỉ h phụ thuộc
vào nhiệt độ của nguồn nóng và lạnh. Mở rộng thêm: - Phát biểu ị
đ nh luật Cacno: Hiệu suất của tất cả các động cơ thuận nghịch chạy theo chu
trình Cacno với cùng ng ồ
u n nóng và nguồn lạnh đều bằng nhau, không phụ thuộc vào tác
nhân cũng như cách chế tạo máy. H ệ
i u suất của động cơ không thuận nghịch thì nhỏ hơn
hiệu suất của động cơ thuận ng ị h ch.
- Phương hướng thực tế để tăng hiệu suất của động cơ nhiệt: tăng T giảm T và chế tạo 1 2
gần đúng động cơ thuận nghịch. 2. Bài toán: T 27+ 273 a. Hiệu suất động cơ: 2 η =1− = 1− = 40% T 227 + 273 1 ′
b. Công mà động cơ thực hiện trong mỗi chu trình: A η A′ = ⇔
=η.Q = 0, 4.2000 = 800( J) 1 Q1 Câu 25: 1. Trình bày
a. Khái niệm và các tính chất hàm entropi của một ệ h nhiệt động. b. Biểu thức ị
đ nh lượng của nguyên ý
l 2 viết dưới dạng hàm entropi
c. Nội dung nguyên lý tăng entropi . 2. Bài toán:
Tính độ biến thiên entropy khi cho dãn đẳng nhiệt 6 g khí Hydro từ áp suất 1.00kPa đến áp suất 50kPa . Lời giải: 1. Lý thuyết:
Group: Bachkhoa Universe – Góc học tập và thảo luận 99 TAILIEUHUST.COM a.
Khái niệm hàm entropy:
Xét quá trình thuận nghịch từ trạng thái (1) đến t ạ
r ng thái (2) chỉ phụ thuộc vào trạng thái
đầu và trạng thái cuối. Hàm entropy δQ
S là hàm được định nghĩa bởi biểu thức : dS = TTính chất:
- S có giá trị xác định và không phụ thuộc vào quá trình của hệ từ trạng thái này sang trạng tháu khác.
- S là một đại lượng có tính cộng được. - S được xác đ n
ị h sai kém một hằng số cộng δQ S = S + , S ∫
là giá trị entropy tại gốc tính 0 0 T
toán, quy ước S = 0 tại = . 0 T 0 K b. Biểu thức ị
đ nh lượng nguyên lý II v ế i t dưới ạ d ng hàm entropy: (2) δ Q S ∆ ≥ ∫ (1) T
+ Dấu “=” ứng với quá trình thuận nghịch
+ Dấu “>” ứng với quá trình không thuận nghịch với ệ h số cô lập
c. Nội dung nguyên lý tăng entropy: Với quá trình nhiệt động thực tế xảy ra trong một ệ h
cô lập, entropy của hệ luôn luôn tăng. 2. Bài toán: M T m V
Đối với khí lý tưởng: 2 2 S ∆ = ⋅C ln + ⋅ R ⋅ ln V µ T µ V 1 1 V P
Vì quá trình là nén đẳng nhiệt nên 2 1 = V P 1 2 M P 6 100 1 ⇒ ∆S = . . R ln = .8,31.ln =17, 28 J / K µ P 2 50 2 Câu 26: 1. Trình bày
a. Những sự khác biệt trong mô hình khí lý tưởng và khí thực.
b. Khái niệm cộng tích, nội áp và thiết lập phương trình trạng thái cho khí thực trên cơ sở
phương trình trạng thái khí lý tường. 2. Bài toán:
100 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Tính nhiệt độ của 3,5 g khí Ox y chiếm thể tích 3
90 cm ở áp suất 2,8MPa nếu được coi là
khí lý tưởng và khí thực. Rút ra nhận xét về các ế
k t quả nhận được. Cho biết 5 3 2
a = 1,37.10 Jm / kmol ;b = 0,03 3 m / kmol . Lời giải: 1. Lý thuyết: a.
Mô hình khí lý tưởng: - Có kích thước n ỏ h và không đáng kể
- Phân tử không tương tác trừ lúc va chạm
- Thể tích khối khí chính là thể tích dành cho chuyển động nhiệt tự do của các phần tử khí
Mô hình khí thực:
- Khi nén hoặc hạ nhiệt độ, thể tích khối khí giảm; lúc đó các phân tử gần nhau nên không
thể bỏ qua tương tác giữa chúng
- Thể tích riêng của các phân tử cũng chiếm ộ
m t phần đáng kể không thể bỏ qua nó
- Các phân tử khí có tương tác với nhau nên áp suất thực của khối khí giảm đi do tương tác tĩnh điện à
l m giảm tác dụng lên thành bình. b. Khái niệm
Cộng tích: Là hiệu ố
s hiệu chính về thể tích, ký h ệ i u b a
Nội áp: Là số hiệu chính về áp suất, ký h ệ i u p = i 2 vt
1. Thiết lập phương trình t ạ r ng thái khí t ự h c:
Giả sử có 1 mol khí thực
- Thể tích: V là thể tích 1 mol khí thực, thể tích dành cho chuyển động nhiệt. V = V − b t t
- Áp suất: p là áp suất lúc các phân tử khí không hút nhau, p là áp suất khí thực. p = p + p t t i
⇒ Thay vào phương trình trạng thái khí lý tưởng :  a
pV = RT ⇔  p +  V − b = RT t 2 ( t ) Vt   a
Vậy phương trình trạng thái với 1 mol khí thực là p + (V − ) b = RT  2   V  2 Phương trình   trạng thái với 1 k ố h i khí thực bất kỳ: m a m m p + (V − ) b =   RT 2 2  µ V  µ µ
Group: Bachkhoa Universe – Góc học tập và thảo luận 101 TAILIEUHUST.COM 2. Bài toán:
- Mô hình khí lý tưởng:
Từ phương trình trạng thái ta có: µPV T = = 277K mR - Mô hình khí thực: 2
Từ phương trình trạng thái ta có: µ  m a m T = p + (V − ) b =   286 K 2 2 mR  µ V  µ - Nhận xét:
Ở áp suất nhỏ nhiệt độ khối khí tính được dựa trên hai phương trình khác nhau
xấp xỉ nhau nên vẫn có thể áp ụ
d ng mô hình khí lý tưởng cho khí Oxi Câu 27:
1. Thiết lập các định lý về mômen động lượng (2 đ n
ị h lý) của vật rắn quay quanh trục cố định.
2. Bài toán: Một thanh chiều dài l = 0,9( m) , khối lượng M = 6(kg) có thể quay tự do
xung quanh một trục nằm ngang đi qua một đầu của thanh. Một viên đạn khối
lượng m = 0,01( kg) bay theo hướng nằm ngang với vận tốc = 300( m / s) tới xuyên
vào đầu kia của thanh và mắc vào thanh. Vận tốc ố
g c của thanh ngay sau khi viên đạn ậ
đ p vào đầu thanh là bao nhiêu? Lời giải: 1. Lý thuyết: Vật rắn: L = L = r ∧ mv = m r ∧ ∑ ∑ ∑
ω ∧ r ⇒ L = m
Σ ω r r = Σ m r ω ⇒ L = I ω i i .( i i ) ( 2 i i ) i i i i i ( i i ) i . i i i dL d d ω - Định lý 1: = (Iω) = I = β I = µ dt dt dt Vậy: ạ
Đ o hàm mômen động lượng L theo thời gian ằ
b ng tổng mômen lực tác ụ d ng lên dL vật rắn theo trục đó. = µ. dt - Định lý 2: Ta c ó dL = . µ dt
Xét µ tác dụng trong khoảng thời gian t ∆ = t − t 2 1 t2
⇒ ∆L = L − L = µdt ∫ là xung lượng mômen. 2 1 t1
Vậy: Độ biến thiên mômen động lượng của vật rắn quay quanh 1 trục có giá trị bằng xung
lượng của mômen lực tác dụng lên vật rắn trong thời gian ∆t . Nếu µ = const ⇒ L ∆ = µ t ∆ . 2. Bài tập:
102 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Xét hệ trước va chạm: Tổng động lượng cả hệ: p = mv (vì mỗi viên đạn có vận tốc v ) mô
men động lượng trước khi va chạm là: L = r. .
p sinα = 1. p = mvl
Vậy momen quán tính của ệ h vật sau va chạm: L = I ω + I ω sau 1 2
- I là momen chất điểm (viên đạn) đối với trục quay 2 I = ml 1 1 2  l M 2   2
- I là moment quán tính của thanh mảnh Ml'  2  Ml = = = 2 I2 12 12 3 2  Ml
⇒ L = I + I ω = ml +  ω s ( ) 2 1 2  3 
Áp dụng định luật bảo toàn momen động lượng 2   2 Ml mvl v
L = L ⇔ mvl = ml +  ω ⇒ = =1, 658(rad / s) t s 2 3 Ml    M  2 ml + l 1+  3  3m
Câu 28: Một quả cầu khối lượng 2 kg , chuyền động với vận tốc 3 m / s, va chạm xuyên tâm
với một quả cầu thứ hai khối lượng 3 kg đang chuyển động cùng chiều với quả cầu thứ nhất với ậ v n ố
t c 1 m / s . Tìm vận tốc ủ
c a các quả cầu sau va chạm nếu:
a. Va chạm là hoàn toàn đàn hồi.
b. Va chạm là không đàn hồi (mềm). Lời giải:
a. Va chạm hoàn toàn đàn hồi
+ Áp dụng định luật bảo toàn động lượng ta có: ' '
m v + m v = m v + m v 1 1 2 2 1 1 2 2 m v v′ m v′ ⇒ − = − v (1) 1 ( 1 1 ) 2 ( 2 2 ) 2 2 2 ′ 2 m v m v m v m v′
+ Áp dụng bảo toàn cơ năng ta có: 1 1 2 2 1 1 2 2 + = + 2 2 2 2 ⇒ m ( 2 ′2
v − v ) = m ( ′2 2 v − v (2 ) 1 1 1 2 2 2 ) (2) v v′ v′ ⇒ + = + v v′ v′ ⇒ − = 2 m v v′ m 2 v′ ⇒ − = + −v 1 ( 1 1 ) 2 ( 1 2 ) 1 1 2 2 (1) 2 1 6 2v′ 6 3v′ ⇔ − = + −3 3 13 . 1 1 v′ ⇒ = ( m / s) v′ ⇒ = ( m / s) 1 5 2 5 b) Va chạm mềm
Group: Bachkhoa Universe – Góc học tập và thảo luận 103 TAILIEUHUST.COM m v + m v 9
+) m v + m v = (m + m ) 1 1 2 2 V ⇒V = = ( m / s) . 1 1 2 2 1 2 m + m 5 1 2
Câu 29: Một quả cầu ặ
đ c có khối lượng m = 1,4(Kg) , lăn không trượt với vận tốc
V = 10( m / s) thành tường rồi bật ra với ậ
v n tốc V = 8( m / s). Nhiệt lượng tỏa ra trong va 1 2 chạm đó là? Lời giải:
Sau va chạm động năng của vật giảm. Độ giảm động năng này tỏa ra dưới dạng nhiệt. Khi
chuyển động, quả cầu vừa có ộ đ ng năng tịnh t ế i n, vừa có ộ
đ ng năng quay Động năng của
quả cầu đặc, đồng chất, lăn không trượt: 1 1  2  1 1 2 2 2 2 2 2 W = Iω = mR
⋅ω = mR ω = mv dp   2 2  5  5 2 Moment quán tính ủ c a quả cầu ặ đ c ồ đ ng chất: 2 2 I = mR 5 2 mv Động năng tịnh t ế
i n của quả cầu đặc: W = d( tt) 2 1 2 1 2 7 2 ⇒ W = + = mv + mv = mv d Wd q W ( ) d (u ) 5 2 10
Nhiệt lượng tỏa ra do va chạm là: 7 Q = −W = − m v − v = − ⋅ ⋅ − = − J d ( 7 2 2 ) 1, 4 ( 2 2 10 8 35, 25( ) 2 1 ) 10 10 Câu 30:
1. Trình bày định luật phân bố phân tử theo vận tốc Maxwell. Từ đó suy ra công thức tính vận ố
t c có xác suất lớn nhất và vận ố
t c trung bình của phân tử khí (không phải
tích phân). Cho biết ý nghĩa của các loại vận tốc này.
2. Bài toán: Khối lượng riêng ủ c a ộ m t chất khí 2 ρ − = ( 3 5.10
kg / m ) ; vận tốc căn quân phương của các phân ử
t khí này là v = 450( m / s). Áp suất của khối khí tác dụng lên thành bình là: Lời giải: 1. Lý thuyết: 1. Định l ậ u t phân ố
b phân tử theo vận tốc của Maxwel l
+ Thực nghiệm chứng tỏ rằng các phân tử khí có vận tốc rất lớn 0 < v < ∞. Giả sử khí có n phân tử, dn là ố
s phân tử có vận tốc trong khoảng v + dv dn ⇒ dn
(%) là số phần trăm phần tử có vận tốc nằm trong khoảng này hay là xác suất n n tìm thấy p ầ h n tử có vận tốc ằ n m trong kh ả o ng v + dv .
104 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
+F(v) là một hàm phụ thuộc vào v , gọi là hàm phân bố. + dn
F (v)dv là xác suất phân tử có vận tốc trong khoảng ( , v v + d ) v ⇒ F( ) v dv = n ∞ dn ∞ ∞ ⇒ = F( )
v dv ⇒ n = n F(v)dv ∫ ∫ ∫ 0 0 0 n ∞ ⇒
F (v)dv = 1 ∫ là điều k ệ
i n chuẩn hóa của hàm phân ố b . 0 3 2 0 m v 2 m −  
Từ đó Maxwell tìm được: 4 0 2 2 F (v) kT = v ⋅   e π  2kT  + Xét dF( ) v = 2kT 2RT 0 ⇒ F( )
v đạt max tại v = =
= v (xác suất phần tử có v là cao dv xs m µ 0 nhất). → Vận tốc trung bình: ∞ 8 kT 8 kT v =
F (v)vdv = = ∫ 0 m π πµ 0
Vận tốc căn quân phương: ∞ 2 −2 2 3kT 3kT 3 RT v = v =
F (v)v dv = ⇒ v = = ∫ c 0 c m m µ 0 0
+ v < v < v . xs c 2. Bài toán:
Áp dụng phương trình trạng thái khí lí tưởng: PV n PV RT PV P P n = ⇒ = ⇒ = = = RT µ RT µ m m ρ V 2
Vận tốc căn quân phương của các phân tử khí: 3RT RT vc v = ⇒ = c µ µ 3 2 2 P v v c c ⇒ = ⇒ P = ρ ⋅ = ( 2 3375 N / m ) ρ 3 3
Câu 31: Tổng động năng tt trung bình của các phân tử khí N chứa trong 1 khí cầu 2 3 V = 0,02 m là 3
5.10 J và vận tốc căn quân phương của 1 phân tử là 3 2.10 m / s .
a. Tìm khối lượng N chứa trong khí cầu. 2
b. Áp suất khí tác dụng lên thành khí cầu. Lời giải: a. 2 3RT V = µ
Group: Bachkhoa Universe – Góc học tập và thảo luận 105 TAILIEUHUST.COM 3 3 i m m ω 2 2 1 W = U = ⋅ ⋅ RT = V ⇒ m = = ( kg) = 2,5( g) 2 i i 2 µ 2 V 400 b. 3 3 2 ω W = nRT = V ρ ⇒ p = = 1666,67(Pa) 2 2 3 V Câu 32:
1. Định nghĩa trạng thái cân ằ
b ng, quá trình cân bằng. Một quá trình tiến hành như
thế nào có thể xem như là cân bằng? Vì sao?
2. Bài toán: Có hai bình cầu được ố
n i với nhau bằng một ống có khóa, đựng cùng
một chất khí. Áp suất ở bình thứ nhất là 5 2
2.10 N / m , ở bình thứ hai là 6 2 10 N / m .
Mở khóa nhẹ nhàng để hai bình thông với nhau sao cho nhiệt độ khí vẫn không
đổi. Khi đã cân bằng, áp suất ở hai bình là 5 2
4 ⋅10 N / m . Tìm thể tích của bình cầu
thứ hai, nếu biết thể tích của bình cầu thứ nhất là 3 15 dm . Lời giải: 1. Lý thuyết:
- Trạng thái cân bằng là trạng thái trong đó thông số của hệ được hoàn toàn xác định và
sẽ tồn tại mãi mãi nếu không có tác động từ bên ngoài.
- Quá trình cân bằng là quá trình biến đổi gồm một ch ỗ
u i liên tiếp các trạng thái cân bằng.
- Một quá trình được thực hiện ấ
r t chậm, hoặc nói một cách chặt chẽ vô cùng chậm, để có
đủ thời gian thiết lập lại sự cân bằng mới của hệ thì quá trình đó được coi là quá trình cân bằng.
Giải thích: Trong một quá trình biến đổi, hệ chuyển từ trạng thái cân bằng này sang trạng
thái cân bằng tiếp theo thì t ạ r ng thái cân b n
ằ g trước đã bị phá hủy, nó thay đổi theo thời gian. 2. Bài toán
Khi mở khóa cho hai bình thông nhau ta có phương trình trạng thái + p(V +V ) M M 1 2 = RT (1) 1 2 µ M µp V
Từ phương trình trạng thái của khí ở bình 1: 1 1 1 p V = RT , ta có: M = , 1 1 1 µ RT M
Từ phương trình trạng thái của khí ở bình2: 2 µ p V = RT , ta có: p V 2 2 2 2 µ M = . 2 RT ( p − p V 1 )
Thay M và M vào (1) ta có: 1 3 V = =5.10 − . α ( 3 m ) 1 2 p − p2 Câu 33:
106 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
1. Hãy thiết lập công thức tính áp suất của khí quyển phụ thuộc vào đ ộ cao. Từ đó suy ra định luật phân ố b Boltzman.
2. Bài toán: 6,5g hydro ở nhiệt độ 27° C , nhận được nhiệt nên thể tích giãn nở gấp
đôi, trong điều kiện áp s ấ u t không đổi. Tính: a. Công mà khí sinh ra
b. Độ biến thiên nội năng ủ c a k ố h i khí
c. Nhiệt lượng đã cung cấp cho khối khí. Lời giải: 1. Lý thuyết
Xét cột không khí cao dh, diện tích đáy 2 1m , ở
độ cao h . Áp suất đáy dưới p .
⇒ Áp suất đáy trên: p + dp(dp < 0 , do lên cao áp suất giảm) và dp = −dP (do 2 S = 1m )
(trọng lượng cột không khí).
⇒ Số phân tử nằm trong cột dh : d = n S dh = n dh . n 0 0
⇒ Trọng lượng cột dh: dP = d .
n mg = mgn dh hay dp = −mgn dh 0 0 mg dp mg ⇒   dp = − p dh ⇔ = − d . h h h dp mg p mg ⇒ = − dh ⇒ ln ∫ ∫   = − h kT p kT maidat 0 p kTp kT 0 mgh ⇒ = . kT p p e
⇒ Áp suất giảm khi độ cao tăng. 0 −mg −wt - Định luật phân ố
b của Boltzman: n = n . kT kT e = n e . 0h 0, mat dat 0, mat dat 2. Bài toán:
Do quá trình giãn nở là đẳng áp nên ta có: ′ M 3 M i A = p . V ∆ =
RT = 8,1.10 J và U ∆ =
⋅ R (T −T . 2 1 ) 1 µ µ 2 V
Từ phương trình đẳng áp ta có: 2 T = T = 2T. 2 1 1 V1 M i Do đó: 3 U ∆ = ⋅ RT = 20,2 1 ⋅ 0 J µ . 2
Theo nguyên lý thứ nhất của nhiệt động học. ′ 3 Q = U ∆ − A = U
∆ + A = 28,3.10 J
Câu 34: Nén 10 g khí oxy từ điều k ệ
i n tiêu chuẩn đến thể tích 4 lít. Tìm:
a. Áp suất và nhiệt độ của khối khí sau mỗi quá trình nén đẳng nhiệt và đoạn nhiệt.
Group: Bachkhoa Universe – Góc học tập và thảo luận 107 TAILIEUHUST.COM
b. Công cần thiết để nén khí trong mỗi trường hợp. Từ đó, suy ra nên nén theo cách nào là lợi nhất. Lời giải: V
a. Nén đẳng nhiệt: T = T = 273 K và 1 5 2 p = p = 5.10 N / m . 2 1 2 1 V2 γ 1 −  γ V   V  Nén đoạn nhiệt: 1 T = T   = 1 = ⋅  = Γ 520 K và 5 2 p p 9,5.10 N / m 2 2 1 VV 2   2 
b. Công nén khí trong quá trình đẳng nhiệ   t là: M p2 A = RT ⋅ln   =1115J µ p  1  p V − p V
Công nén khí trong quá trình đoạn nhiệt là 2 2 1 1 A = =1500J γ −1
Như vậy nén đẳng nhiệt sẽ có lợi hơn.
Câu 35: Tác nhân của một động cơ nhiệt là một mol khí lí tưởng đơn nguyên tử, t ự h c hiện
một chu trình gồm hai quá trình đằng tích và hai quá trình đẳng áp như hình vẽ. Các điểm
chính giữa của quá trình đẳng áp phía dưới và đường đẳng tích bên trái có cùng nhiệt độ
T , trong khi các điểm chính giữa của quá trình đẳng áp phía trên và đường đẳng tích bên 1
phải có cùng nhiệt độ T . Tìm hiệu suất của chu trình đó. 2 Lời giải: P V T
Từ phương trình trạng thái ta có: 2 2 2 = = (1) P V T 1 1 1
Khi chỉ nhận nhiệt lượng trong quá trình đẳng tích 1-2 và
quá trình đẳng áp 2-3: Q = C ∆T + C T ∆ . v 12 p 23 3 Q = ( 5 p V − p V + p V − p V 2 1 1 1 ) ( 2 2 2 1 ) 2 2 Thay vào (1) ta có: 1 T  5T  2 2 Q = p V  1 −  +3 1 1  2 T T  1  1 
Công khí thực hiện được trong quá trình: A = (p − p V −V 2 1 ) ( 2 1 ) 2  T  Thay (1) vào A ta có: 2 A = p V −1 1 1    T  1 A 2( T − T 2 1 )
⇒ Hiệu suất của chu trình trên là: H = = . Q 5T + 3T 2 1
108 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Câu 36: Một động cơ nhiệt làm việc theo chu trình Cacno, sau mỗi chu trình sinh một công 4
A = 7,35 ⋅10 J . Nhiệt độ của nguồn nóng là 100°C , nhiệt độ của nguồn lạnh là 0°C . Tìm:
a. Hiệu suất của động cơ
b. Nhiệt lượng nhận được của nguồn nóng sau một chu trình
c. Nhiệt lượng nhả cho nguồn lạnh sau một chu trình. Lời giải: T 273 a. Ta có: 2 H =1 − =1 − = 26,81(%) T 373 1 4 b. Ta có: A A 7, 35.10 H = ⇒Q = =
⇒ Q = 274151(J ) 1 1 Q H 0, 2681 1 c. ′ ′
A = Q − Q ⇒ Q = Q − A = 200651(J ) . 1 2 2 1
Câu 37: Tính độ biến thiên entropy khi biến đổi 1g nước ở 0°C thành hơi ở 100°C . Lời giải: + Ta có: S
∆ = ∆S + ∆S 1 2 δ Q mc dT T dT T 373 + Có 2 1 2 −3 S ∆ = = = mc = mcln =10 4 . 200.ln =1,31( J / K) 1 ∫ ∫ ∫ (1) T T T 1 T T 273 1 6 −3 δ + Có Q 1 1 1 2, 26.10 10 . 2 S ∆ = = δQ = Q = = = 6,06( J / K) ∫ ∫ (2) 2 2 2 T T T T Lm 7 3 3 2 2 2 Từ (1) và (2) ⇒ S ∆ = 7,37( J / K)
Group: Bachkhoa Universe – Góc học tập và thảo luận 109 TAILIEUHUST.COM
PHẦN III. MỘT SỐ ĐỀ THI GIỮA KỲ
Đề thi giữa kỳ sẽ do giáo viên dạy lớp ra với hình thức t ắ
r c nghiệm. Một đề có từ 10 – 20
câu hỏi với thời gian thích hợp (tùy giáo viên). Các câu hỏi thường trích từ bộ trắc nghiệm
ở trên và sách bài tập. Chính vì vậy những đề mình nêu dưới đây (đề thi thật) là giúp các
bạn hình dung ra đề thi giữa ỳ
k và luyện tập nên mình ẽ
s không có lời giải ở đây. Các bạn
xem cách làm ở trên nhé. 1. Đề thi giữa ỳ k 1
Câu 1: Một con lắc toán có sợi dây dài 90 cm và cứ sau khoảng thời gian dt = 0.5 phút thì
biên độ giảm 4.5 lần. Giảm lượng loga của con lắc đó bằng bao nhiêu? (cho g = 9.81 m/s2) A. 9,84.10-2 B. 12,2.10-2 C. 2,76.10-2 D. 5,25.10-2
Câu 2: Từ một dộ cao đủ lờn người ta ném một hòn đá theo phương nằm ngang so với mặt đất với ậ
v n tốc bạn đầu 20m/s. Tính gia tốc pháp tuyến của hoàn đá sau lúc ném 0.5 giây (cho g = 9.81 m/s2) A. 3.5 m/s2 B. 9.5 m/s2 C. 12.3 m/s2 D. 7.5 m/s2
Câu 3: Một ô tô chuyển động biến đổi đều lần lượt đi qua 2 điểm A và B cách nhau 36m
trong khoảng thời gian t = 1.5s. ậ V n tốc ủ
c a ô tô ở B là 30m/s. ỏ H i vận ố t c tại A? A. 16 m/s B. 18 m/s C. 20 m/s D. 22 m/s
Câu 4: Một ô tô bắt đầu c ạ h y vào đo n
ạ đường tròn có bán kính 1km và dài 620 m với vận
tốc bạn đầu 54km/h trong thời gian 15s. Tính gia tốc toàn phần của ô tô ở cuối đoạn đường,
coi chuyển động là nhanh dần ề đ u. E. 9.12 m/s2 F. 7.55 m/s2 G. 3.55 m/s2 H. 5.77 m/s2
Câu 5: Một sợi dây mảnh OA dài l = 22cm đầu O cố định, đầu A buộc vào vật nhỏ có thể quay tròn trong mặt p ẳ
h ng đứng xung quanh O. Tại vị trí thấp nhấp cần phải truyền cho vật
vận tốc bé nhất bằng bao nhiêu để vật có t ể
h đi qua điểm cao nhất, lấy g = 9.81 m/s2 A. 3.28 m/s B. 4.23 m/s C. 2.38 m/s D. 5.43 m/s
Câu 6: Một vật bắt đầu trượt xu n
ố g trên một mặt phẳng nghiêng hợp vơi phương ngang
góc 45 độ. Khi trượt được quãng đường s = 40 cm, vật có vận tốc v = 1.5 m/s. Hệ số ma sát
giữa vật và mặt phẳng nghiêng bằng bao nhiêu? Cho g = 9.81 m/s2 A. 0.3 B. 0.4 C. 0.6 D. 0.5
110 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1
Câu 7: Một phi công ngồi trên ghế máy bay nhào lộn theo một đường tròn bán kinh R =
1000 m trong mặt phẳng thẳng đứng. Vận tốc ủ
c a máy bay không đổi v = 540 km/h. Lấy g
= 9.81 m/s2. Tại vị trí thấp nhất của vòng tròn nhào lộn, lực nén của phi công lên ghế ngồi
bằng bao nhiêu biết khối lượng của phi công là 80kg? A. 2585 N B. 4236 N C. 3872 N D. 5324 N
Câu 8: Chất điểm khối lượng m = 30 gam được ném lên từ một điểm O trên mặt đất với vận
tốc ban đầu v0 = 15 m/s theo hướng nghiêng góc a = 45 độ với mặt phẳng nằm ngang. Giá
trị mô men động lượng của chất điểm đối với điểm O tại thời điểm mà chất điểm chạm đất
là: (bỏ qua sức cản không khí, g = 9.81 m/s2) A. 3.5 kgm2/s B. 5.6 kgm2/s C. 7.3 kgm2/s D. 8.2 kgm2/s
Câu 9: Một đĩa tròn khối lượng m = 2.5kg, bán kính R = 0.4m đang quay với vận tốc góc
900 vòng/phút. Tác dụng lên đĩa một momen hãm; đĩa quay chậm ầ d n và sau thời gian dt
= 15 giây thì dừng lại. Tính lực hãm tiếp tuyến? A. -5.51 N B. -4.13N C. -1.34N D. -3.14N
Câu 10: Hai vật có khối lượng m1 = 2.1kg, m2 = 3.3kg được nối với
nhau bằng một sợi dây không dãn và đặt trên mặt bàn nằm ngang.
Dùng một sợi dây khác vắt qua ròng rọc (có khối lượng không đáng
kể) một đầu dây buộc vào vật m2, đầu kia buộc vào vật thứ 3 có khối
lượng m3 = 5.6kg. Hệ được bố trí như hình vẽ. Tính lực căng sợi dây
do vật m3 gây ra. (SBT) A. 23 N B. 17 N C. 27 N D. 12 N
Câu 11: Một khẩu pháo có khối lượng M = 800kg bắn một viên đạn theo phương hợp với
phương ngang một góc 60 độ. Khối lượng của viên đạn m = 7kg, vận tốc ầ đ u nòng v =
380m/s. Khi bắn bệ pháo giật lùi về sau một đoạn s = 45 cm. Lực ả
c n trung bình tác dụn lên
khẩu pháo có giá trị là? A. 4257 N B. 2457 N C. 2547 N D. 5247 N
Câu 12: Người ta chèo một con thuyền qua sông theo hướng vuông góc với vận tốc 3.6
km/h. Nước đã mang con thuyền về phía xuôi dòng một khoảng 120m. Vận tốc ủ c a dòng nước đối ớ
v i bờ sông nhận giá trị bằng bao nhiêu? Cho biết ch ề
i u rộng của sông là S = 0.6km. A. 0.4 m/s B. 0.2 m/s C. 0.6 m/s D. 0.8 m/s
Group: Bachkhoa Universe – Góc học tập và thảo luận 111 TAILIEUHUST.COM
Câu 13: Một ô tô có khối lượng m = 1228kg chạy lên dốc với vận tốc không đổi v = 72km/h.
Mặt đường dốc hợp với mặt phẳng ngang một góc a sao cho sina = 0.05; cosa = 1. Hệ số
ma sát giữa mặt đường và bánh xe là k = 0.05. Lấy g = 9.81 m/s2. Khi đó công suất của động cơ ô tô bằng bao nhiêu? A. 26kW B. 32 kW C. 24 kW D. 30 kW
Câu 14: Một quả cầu có khối lượng m = 0.3 kg được đặt cách đầu một thanh đồng chất một
khoảng a = 0.4 cm sao cho tâm quả cầu nằm trên phương của thanh. Thanh có chiều dài l
= 7cm và khối lượng M = 1kg. Lực hút của thanh lên quả cầu bằng bao nhiêu? Cho hằng số
hấp dẫn vũ trụ G = 6.67.10-11 N.m2/(kg2) A. 7,67.10-8 N B. 6,76.10-8 N C. 6,76.10-8 N D. 7,67.10-8 N
Câu 15: Cho hệ vật được ố
b trí như hình vẽ. Sợi dây không giãn.
Khối lượng của ròng rọc và của sợi dây không đáng kể. Hệ số ma
sát của vật 1 đôi với mặt phẳng nằm ngang k = 0.25. Tính lực căng
của sợi dây khi m1 = 90g, m2 = 120g? A. 0.82 N B. 1.24 N C. 0.63 N D. 0.23 N
Câu 16: Từ đỉnh tháp cao 30m người ta ném một hòn đá lên phía
trên với vận tốc v0 = 20m/s theo phương hợp với phương ngang một góc 45 độ. Thời gian
rơi của hòn đá nhận giá trị nào dưới đây? A. 6.3 s B. 4.3 s C. 3.4 s D. 2.1 s
Câu 17: Một vật có khối lượng m1 = 6kg chuyển động tới va chạm vào vật thứ hai có khối
lượng m = 1kg đang đứng yên. Coi va chạm là xuyên tâm và hoàn toàn đàn hồi. Hỏi vật thứ
nhất truyền cho vật thứ hai bao nhiêu phần trăm ộ
đ ng năng của mình sau va chạm? A. 51 % B. 34% C. 66 % D. 49%
Câu 18: Xác định mô men quán tính của thanh có khối lượng m = 15kg dài L = 90cm đối
với trụ quay đi qua trọng tâm của thanh và hợp với thanh một góc 60 độ. A. 1,20 kg.m2 B. 0,76 kg.m2 C. 0,34 kg.m2 D. 1,43 kg.m2
Câu 19: Một vật rơi tự do từ điểm A ở độ cao 25m (đối với mặt đất) và một viên đạn được
bắn đồng thời từ mặt đất lên cao với vận tốc ban đầu 14m/s theo phương thẳng đứng đi
qua điểm a. Bỏ qua lực cản không khí. Lấy g = 9.81 m/s2. Kh ả
o ng cách giữa viên đạn và vật
rơi sau thời gian 0.8 giây bằng? A. 5.0 m B. 8.0 m
112 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 C. 13.8 m D. 10.3 m
Câu 20: Tác dụng một lực tiếp tuyến Ft = 100N lên một bánh xe đang đứng yên có bán kình
R = 0.3M và có mô men quán tính I = 18kg.m2. Hỏi vận tốc dài tại một điểm trên vành bánh
xe sau khi tác dụng lực 10 giây? A. 5 m/s B. 12 m/s C. 8 m/s D. 3 m/s
2. Đề thi giữa kỳ 2
Câu 1: Một trụ đặc có khối lượng M = 105 kg, bán kính R = 0.5m đang quay xung quanh
trục của nó. Tác dụng lên t ụ
r một lực hãm F = 257.3 N, tiếp tuyến với mặt trụ và vuông góc
với trục quay. Sau thời gian ∆𝜔𝜔 = 2.6s trụ dừng lại. ậ
V n tốc góc của trụ lúc bắt đầu tác dụng lực hãm là: A. 21.8 rad/s B. 25.5 rad/s C. 22.1 rad/s D. 21.2 rad/s
Câu 2: Một vật có khối lượng m1 = 2kg chuyển động với tốc độ v1 = 5m/s tới va chạm
xuyên tâm vào vật có khối lượng m2 = 3kg đứng yên. Va chạm là hoàn toàn mềm. Nhiệt
lượng toả ra trong quá trình va c ạ h m là: A. 34.8 J B. 14.2 J C. 15.0 J D.
Câu 3: Thả rơi tự do một vật nhỏ từ độ cao h = 17.6m. Quãng đường mà vật rơi được trong 0.1s cuối cùng ủ c a thời gian rơi là: A. 2.2 m B. 1.8 m C. 2.4 m D. 1.6m
Câu 4: Một phi công thực hiện vòng tròn nhào lộn trong mặt phẳng đứng. Vận tốc của
máy bay không đổi v = 800 km/h. Giả sử rằng áp lực lớn nhất của phi công lên ghế bằng 5
lần trọng lực của người. Lấy g = 9.8 m/s2. Bán kính q ỹ
u đạo vòng nhào lộn có giá trị bằng: A. 1473.3 m B. 1562.5 m C. 1394.4 m D. 1259.8 m
Câu 5: Một vật nhro có khối lương m buộc vào một sợi dây mảnh chiều dài l = 1.5m; đầu
kia giữ cố định. Cho vật quay trong mặt p ẳ
h ng nằm ngang với tốc độ góc không đổi sao
cho dây hợp với phương thẳng đứng 1 góc 𝛼𝛼 = 30 độ. Cho g = 9.8 m/s2, bỏ qua lực ả c n
không khí. Vận tốc góc có giá trị: A. 2.54 rad/s B. 2.63 rad/s C. 2.75 rad/s D. 2.84 rad/s
Câu 6: Ở đầu một sợi dây dài l = 50 cm có treo một vật ặ n ng. ỏ
H i tại điểm thấp n ấ h t p ả h i
truyền cho vật một vận tốc bé nhất bằng bao nhiêu để vật có t ể h quay tròn trong mặt phẳng đ n ứ g. Lấy g = 9.8 m/s2 A. 4.9 m/s B. 4.4 m/s
Group: Bachkhoa Universe – Góc học tập và thảo luận 113 TAILIEUHUST.COM C. 4.0 m/s D.
Câu 7: Một thanh dài l = 1m, khối lượng M = 6kg có thể quay tự do xung quanh một trục
nằm ngang đi qua một đầu của thanh. Một viên đạn khối lượng m = 10g bay theo hướng nằm ngang với ậ
v n tốc v = 500 m/s tới xuyên vào ầ
đ u kia của thanh và mắc vào thanh. Vận tốc góc ủ
c a thanh ngay sau khi viên đạn đập vào thanh là: A. 2.5 rad/s B. 2.9 rad/s C. 2.8 rad/s D. 2.1 rad/s
Câu 8: Từ một đỉnh tháp cao h = 20m, người ta ném một hòn đá khối lượng 50g theo
phương nghiêng với mặt p ẳ h ng ằ n m ngang, với ậ
v n tốc ban đầu v0 = 18 m/s. Khi rơi tới mặt đất hòn đá có ậ
v n tốc v = 24 m/s. Tính công của lực cản của không khí lên hòn đá. A. -2.7 J B. -1.8 J C. -4.2 J D. -3.5 J
Câu 9: Một con lắc đơn có m = 140g được kéo lệch ra với phương thẳng đứng một góc 𝛼𝛼
= 90 độ, sau đó thả rơi, cho g = 10 m/s2. Lực căng cực đại của dây treo là: A. 4.04 N B. 4.20 N C. 3.27 N D. 3.96 N
Câu 10: Một đĩa tròn đồng chất bán kính R = 20 cm, khối lượng m = 2.2 kg có thể quay
quanh một trục nằm ngang vuông góc với đĩa và cách tâm đĩa một đoạn R/2. Đĩa bắt đầu
quay từ vị trí tương ứng với vị trí cao nhất của tâm đĩa với vận tốc ban đầu bằng 0. Xác
định mômen động lượng ủ c a đĩa đối với t ụ
r c quay khi đĩa đi qua vị trí thấp nhất. A. 0.662 kgm2s-1 B. 0.686 kgm2s-1 C. 0.754 kgm2s-1 D. 0.368 kgm2s-1
Câu 11: Trên một đĩa nằm ngang đang quay, người ta đặt một vật có khối lượng m = 1 kg
cách trục quay r = 50 cm. Hệ số ma sát giữa vật và đĩa bằng k = 0.25. Lực ma sát phải có
độ lớn bằng bao nhiêu ể
đ vật được giữ trên đĩa quay với vận tốc n = 12 vòng/ phút. A. 0.897 N B. 0.612 N C. 0.789 N D. 0.564 N
Câu 12: Một con lắc vật lý được cấu tạo bằng một thanh đồng chất, tiết diện ề đ u có độ
dài bằng l = 50cm và trục quay O của nó cách trọng tâm G một kh ả o ng bằng x. Biết rằng chu kỳ dao động T ủ c a con lắc này là n ỏ
h nhất, x nhận giá trị nào dưới đây: A. 13.7 cm B. 45.6 cm C. 12.1 cm D. 14.4 cm
Câu 13: Trên một trụ rỗng k ố
h i lượng m = 1.2kg, người ta cuộn một
sợi dây không giãn có khối lượng và đường kính nhỏ không đáng kể.
Đầu tự do của dây được gắn trên một giá cố định (hình vẽ). ể Đ trụ rơi
dưới tác dụng của trọng lực. Tìm ứ
s c căng của dây treo. Cho biết rằng gia tốc t ọ
r ng trường có giá trị g = 10m/s A. 6 N B. 7 N
114 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 C. 4 N D. 5 N
Câu 14: Một người ngồi trên ghế Giucopxki và cầm trong tay hai quả tạ, mỗi q ả u có khối
lượng 10 kg. Khoảng cách từ mỗi quả tới trục quay là 0.75m. Ghế quay với vận ố t c góc 2
vòng/s. Hỏi vận tốc của ghế nếu người đó co tay lại để khoảng cách từ mỗi quả tạ đến trục
quay chỉ còn là 20cm, cho biết mômen quán tính của người và ghế đối với trục quay là 2.5 kg.m2 A. 53.7 rad/s B. 52.36 rad/s C. 55.8 rad/s D. 62.4 rad/s 3. Đề thi giữa ỳ k 3
Câu 1: Một vật khối lượng m trượt không ma sát từ đỉnh một mặt cầu xuống dưới. Hỏi từ
khoảng cách nào tính từ chân mặt cầu vật bắt đầu rơi h k ỏi mặt cầu.
Cho bán kình mặt cầu là R = 90cm. A. 0.3 m B. 0.5 m C. 0.6 m D. 0.4 m
Câu 2: Phải ném một vật theo phương thẳng đứng ừ t độ cao h = 30 m
với vân tốc v0 bằng bao nhiêu để nó rơi xuống mặt đất trước 1s so với trường hợp vật tự rơi tự do? G = 10m/s2. A. 13.45 m/s B. 12.25 m/s C. 9.75 m/s D. 8.79 m/s
Câu 3: Một xe lửa bắt đầu chuyển ộ
đ ng nhanh dần đều trên một đường thẳng ngang qua
trước mặt một người quan sát ứ
đ ng ngang toa tàu thứ nhất. Biết rằng toa xe thứ nhất đi
qua trước mặt người quan sát hết thời gian t = 8s. Hỏi toa thứ 8 sẽ đi qua trước mặt người quan sát trong bao lâu? A. 1.20s B. 1.46s C. 3.21s D. 2.16s
Câu 4: Một hòn đá được ném theo phương nằm ngang với vân tốc v0 = 15m/s. Tính gia tốc pháp tuyến ủ
c a hòn đá sau lúc ném 2 giây. (g = 10 m/s2) 𝑚𝑚 𝑚𝑚 A. 2 B. 4 𝑠𝑠2 𝑠𝑠2 𝑚𝑚 𝑚𝑚 C. 6 D. 8 𝑠𝑠2 𝑠𝑠2
Câu 5: Một xe chuyển ộ
đ ng từ đỉnh một dốc phẳng có độ cao h = 80 cm nằm nghiêng
góc 𝛼𝛼 = 30 độ so với mặt nằm ngang và dừng hẳn lại sau khi đã đi được đoạn nằm ngang
CB. Hệ số ma sát giữa xe và mặt đường trên các đoạn DC và CB là k = 0.2. Xác định độ dài quãng đường CB. A. 1.74 m B. 2.61 m C. 2.28 m D. 2.69 m
Group: Bachkhoa Universe – Góc học tập và thảo luận 115 TAILIEUHUST.COM
Câu 6: Từ độ cao h = 30m, một hòn đá được ném lên phía trên với vận tốc v0 = 15m/s
theo phương hợp với mặt phẳng nằm ngang ộ
m t góc bằng 45 độ. Xác đ n ị h vận tốc ủ c a
hòn đá lúc chạm đất. ấ L y g = 10m/s2 A. 34.21 m/s B. 28.72 m/s C. 26.71 m/s D. 33.18 m/s
Câu 7: Một chất điểm k ố
h i lượng m = 0.3 kg được ném lên từ một điểm O với vận tốc v0 =
9m/s theo phương hợp với mặt phẳng nằm ngang một góc 𝛼𝛼 = 30 độ - bỏ qua sức cản
của không khí, cho g = 9.8 m/s2. Mômen ộ
đ ng lượng của chất điểm đối với O khi lên ế đ n độ cao cực đại là: A. 3.226 kgm2/s B. 2.416 kgm2/s C. 1.865 kgm2/s D. 2.054 kgm2/s
Câu 8: Một người kéo xe bằng ộ
m t lực hợp phương ngang một góc 𝛼𝛼 = 30 độ. Xe có khối
lượng m = 250kg và chuyển động ớ
v i vận tốc không đổi. Hệ số ma sát giữa bánh xe và
mặt đường k = 0.2. Lấy g = 10m/s2. Lực kéo có giá trị bằng: A. 517.58 N B. 561.15 N C. 550.71 N D. 543.21 N
Câu 9: Trên một đĩa nằm ngang đang quay, người ta ặ
đ t một vật có khối lượng m = 500g
cách trục quay r = 60 cm. Hệ số ma sát giữa vặt và đĩa bằng k = 0.1. Với vận tốc góc nào
thì vật bắt đầu trượt khỏi đĩa? A. 1.7 rad/s B. 1.3 rad/s C. 2.2 rad/s D. 2.8 rad/s
Câu 10: Một ô tô k ố
h i lượng m = 550kg chuyển động thẳng đều xuống ố d c trên một mặt
phẳng nghiêng, góc nghiêng 𝛼𝛼 so với mặt đất nằm ngang có sin 𝛼𝛼 = 0.0872; cos 𝛼𝛼 = 0.9962. Lực kéo ô tô b n
ằ g Fk = 550N. Hệ số ma sát giữa ô tô và mặt đường là: A. 0.158 B. 0.188 C. 0.208 D. 0.198
Câu 11: Xác định chu kỳ của một con lắc toán chiều dài l = 50cm, biết nó sau khoảng thời
gian t = 6 phút nó mất 99% năng lượng. A. 1.42s B. 1.82s C. 1.66s D. 1.74s
Câu 12: Từ đỉnh một mặt p ẳ
h ng nghiêng cao h = 80cm, người ta cho một vật đồng chất
có hình vành tròn lăn không trượt trên mặt phẳng nghiêng đó. Tìm vận tốc dài ủ c a các vật ở cuối mặt p ẳ h ng nghiêng. A. 2.8 m/s B. 2.2 m/s C. 3.3 m/s D. 3.6 m/s
Câu 13: Một quả cầu ặ
đ c đồng chất có khối lượng m = 2kg, lăn không trượt với vận tốc v1
= 10 m/s đến đập vào thành tường rồi bật ra với vận tốc v2 = 8m/s. Tính nhiệt lượng toả ra trong va chạm đó. A. 54.6 J B. 50.4 J
116 Group: Bachkhoa Universe – Góc học tập và thảo luận
EBOOK VẬT LÝ ĐẠI CƯƠNG 1 C. 48.6 J D. 58.6 J
Câu 14: Tính công cần thiết để làm cho vô lăng hình vành tròn bán kính 1m, khối lượng
500 kg đang đứng yên quay với ậ
v n tốc góc 60 vòng/ phút. A. 9869.6 J B. 8956.2 J C. 9163.5 J D. 9673.7 J
Câu 15: Một hệ gồm trụ đặc đồng chất khối lượng M = 1.54kg và một vật ặ n g khối lượng
m = 800g được nối với nhau bằng một sợi dây và vắt qua ròng rọc như hình vẽ. Bỏ qua
khối lượng của dây, của ròng ọ r c và của khung gắn ớ v i trụ. Tính gia tốc ủ c a vật nặng. Lấy g = 9.8 m/s2 𝑚𝑚 𝑚𝑚 A. 1.16 B. 2.52 𝑠𝑠2 𝑠𝑠2 𝑚𝑚 𝑚𝑚 C. 1.78 D. 2.15 𝑠𝑠2 𝑠𝑠2
Group: Bachkhoa Universe – Góc học tập và thảo luận 117