




































Preview text:
lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Giải bài tập sách ‘‘Bài tập Xác suất và Thống Kê toán’’ trường ĐH KTQD 07/2016 version 2
Bài tập có sự giúp đỡ của SV K52, K53. Có nhiều chỗ sai sót mong được góp ý: nnvminh@yahoo.com
CHƯƠNG 2: BIẾN NGẪU NHIÊN
§1 Biến ngẫu nhiên rời rạc
Bài 2.1 Một xí nghiệp có 2 ô tô vận tải hoạt động. Xác suất trong ngày làm việc các ô tô bị hỏng tương
ứng bằng 0,1 và 0,2. Gọi X là ô tô bị hỏng trong thời gian làm việc. a)
Tìm quy luật phân phối xác suất của X. b)
Thiết lập hàm phân bố xác suất của X và vẽ đồ thị của nó Giải: a)
X là số ô tô bị hỏng trong thời gian làm việc
X là biến ngẫu nhiên rời rạc với các giá trị có thể có X = 0, 1, 2 Ta có: P(X=0) = 0,9. 0,8 = 0,72
P(X=1) = 0,1. 0,8 + 0,9. 0,2 = 0,26 P(X=2) = 0,1. 0,2 = 0,02
Vậy quy luật phân phối xác suất của X là X 0 1 2 P 0,72 0,26 0,02 b)
Theo định nghĩa hàm phân bố xác suất: F(x) = P(XVới x ≤ 0 F(x) = 0
Với 0 < x ≤ 1 F(x) = 0,72
Với 1< x ≤ 2 F(x) = 0,72 + 0,26 = 0,98
Với x > 2 F(x) = 0,72 + 0,26 + 0,02 = 1
Bài 2.2 Một thiết bị gồm 3 bộ phận hoạt động độc lập với nhau. Xác suất trong thời gian t các bộ phận bị
hỏng tương ứng là 0,4; 0,2 và 0,3. a)
Tìm quy luật phân phối xác suất của số bộ phận bị hỏng. b)
Thiết lập hàm phân bố xác suất của X. c)
Tính xác suất trong thời gian t có không quá hai bộ phận bị hỏng. d)
Tìm mốt mo và trung vị md. Giải: 2
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội a)
Gọi X là số bộ phận bị hỏng trong thời gian làm việc t.
X là biến ngẫu nhiên rời rạc với các trị số có thể xảy ra X= 0, 1, 2, 3.
Ta có, P(X = 0) = 0,6.0,8.0,7 = 0,336
P(X = 1) = 0,4.0,8.0,7 + 0,6.0,2.0,7 + 0,6.0,8.0,3 = 0,452
P(X = 2) = 0,4.0,2.0,7 + 0,4.0,8.0,3 + 0,6.0,2.0,3 = 0,188
P(X = 3) = 0,4.0,2.0,3 = 0,024
Vậy quy luật phân phối xác suất của X là X 0 1 2 3 P 0,336 0,452 0,188 0,024 b)
Theo định nghĩa hàm phân bố xác suất F(x) = P (XTa có: F(x) = 0 với x ≤ 0 F(x) = 0,336 với 0 < x ≤ 1 F(x) = 0,788 với 1< x≤2 F(x) = 0,976 với 2< x≤3 F(x) =1 với x>3 c)
Xác suất trong thời gian t không có quá 2 bộ phận bị hỏng: P(X≤2) = 0,976 d)
Từ hàm phân bố xác suất dễ dàng nhận thấy trung vị: md =1
Giá trị Mốt m0 là giá trị có xác suất lớn nhất => mo = 1
Bài 2.3 Có 3 quả cầu trắng và 2 quả cầu đen. Lấy ngẫu nhiên từng quả cầu cho đến khi lấy được quả cầu
trắng. Tìm quy luật phân phối xác suất của số quả cầu được lấy ra.
Giải: Gọi X là “số cầu được lấy ra”
X gồm 3 giá trị 1, 2, 3 (vì đến quả thứ 3 chắc chắn lấy được cầu trắng và kết thúc quá trình lấy). 3
Xác suất lấy được 1 quả cầu: 0,6 5 2 3
Xác suất lấy được 2 quả cầu (quả cầu 1 là đen, quả cầu 2 là trắng): . 0,3 5 4 2 1 3
Xác suất lấy được 3 quả cầu (quả cầu 1 là đen, quả cầu 2 là đen, quả cầu 3 là trắng): . . 0,1 5 4 3
Ta có quy luật phân phối xác suất: 3
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội X 1 2 3 P 0,6 0,3 0,1
Bài 2.4 Xác suất để một người bắn trúng bia là 0,8. Người ấy được phát từng viên đạn để bắn cho đến khi
trúng bia. Tìm quy luật phân phối xác suất của viên đạn bắn trượt.
Giải: Gọi X là số viên đạn bắn trượt: X = {1,2,3,…,n}
Lại có: Gọi A = “Biến cố bắn trúng bia” có P(A) = 0,8 = p và P( ̅) = 0,2 =q. Khi đó: P(X=n) = 0,8.(0,2)n Ta có: X 0 1 2 … n ... P 0,8 0,8.(0,2)1 0,8.(0,2)2 … 0,8.(0,2)n ... Nhận thấy: P(X=n) > 0 Và: 10,2n n 1 P
X n 0,2 .0,8 lim0,8. lim 1 1. n n n 1 0, 2 5 n 0 n 0
Vậy các xác suất trên tạo thành 1 quy luật phân phối xác suất
Bài 2.5 Có 2 lô sản phẩm:
Lô 1: có 8 chính phẩm và 2 phế phẩm
Lô 2: có 7 chính phẩm và 3 phế phẩm
Từ lô thứ nhất lấy ngẫu nhiên 2 sản phẩm bỏ sang lô thứ hai, sau đó từ lô thứ hai lấy ra 2 sản phẩm. a)
Tìm quy luật phân phối xác suất của số chính phẩm được lấy ra. b)
Xây dựng hàm phân bố xác suất của số chính phẩm được lấy Giải: a)
Gọi X là “số chính phẩm được lấy ra từ hộp 2” nhận 3 giá trị 0;1;2
Gọi Hi là “số chính phẩm lấy từ hộp 1 sang hộp 2 là i” với i = 0;1;2 0 2 C . C 1 1 1 C . 16 2 0 C . 28 Ta có: P(H 8 2 8 C2 8 C2 0) = ; P(H = ; P(H = 2 1) = 2) = C 45 2 45 2 45 10 1 C 0 1 C 0 0 2 C . 10 0 2 C . 6 0 2 C . 3 P(X=0|H 7 5 C 8 C4 9 3 C 0) = = ; P(X=0|H = ; P(X=0|H = 2 66 1) = 2 66 2) = 2 66 1 C 2 1 C 2 1 C 2
P X 0 2 P
H P X H i . ( 0 | )i i0 4
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội 1 10 16 6 28 3 190 = . . . = = 0,06397 45 66 45 66 45 66 2970 Tương tự: 1 1 C . 35 1 1 C . 32 1 1 C . 27 P(X=1|H 5 7 C 8 C4 9 3 C 0) = = ; P(X=1|H = ; P(X=1|H = 2 66 1) = 2 66 2) = 2 66 1 C 2 1 C 2 1 C 2 1 35 16 32 28 27 1303 P A 2 1 P
H P X H = . . . = = 0,43872 i . ( 1| )i 45 66 45 66 45 66 2970 i0
P(A=2) = 1 – P(A=0) – P(A=1) = 1 – 0,06397 – 0,43872 = 0,49731 Ta có bảng sau: X 0 1 2 P 0,06397 0,43872 0,49731 b)
Hàm phân phối xác suất của X là: 0 x 0 F x 0,06397 0 x 1 0,50269 1 . x 2 1 x2
Bài 2.6 Hai cầu thủ bóng rổ lần lượt ném bóng vào rổ cho đến khi có người ném trúng với xác suất
ném trúng của từng người lần lượt là 0,3 và 0,4. Người thứ nhất ném trước.
a) Tìm qui luật phân phối xác suất của số lần ném rổ cho mỗi người
b)Tìm qui luật phân phối xác suất của tổng số lần ném rổ của cả 2 người.
Giải: a) Gọi số X1 là số lần ném rổ của người thứ nhất: X1 = 1, 2, 3,…, n,… Khi X 1 n
TH1 người 1 ném cuối thì cả người 1 và người 2 sẽ ném trượt n 1 lần đầu nên n 1 n 1 P( X n) 0, 7 0, 6 .0, 3 1 TH1
TH2 người 2 ném cuối thì cả người 1 ném trượt n lần và người 2 sẽ ném trượt n 1 lần đầu nên n n 1 P( X n) 0, 7 0, 6 .0, 4 1 TH 2 Vậy 1 P( X n) P( X n) P( X n) 0,58.0, 42n 1 1 TH 1 1 TH 2
Vậy qui luật phân phối xác suất của X1 là: X1 1 2 … n ... P 0,58 0,58.0, 42 … 1 0,58.0, 42n ... 5
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Gọi X2 là số lần ném của người thứ 2: X2 =0, 1, 2, 3,…, n,…
Dễ thấy P(X 0) 0,3 2 TH 1
Khi X n 1 2
TH1 người 1 ném cuối thì cả người 1 và người 2 sẽ ném trượt n lần đầu nên
P( X n)
0,7n0,6 .n0,3 2 TH 1
TH2 người 2 ném cuối thì cả người 1 ném trượt n lần và người 2 sẽ ném trượt n 1 lần đầu nên n n 1 P( X n) 0, 7 0, 6 .0, 4 2 TH 2 Vậy n 1 P( X n) P( X n) P( X n) 0,58.0, 6 .0, 7n 2 2 TH 1 2 TH 2
Vậy qui luật phân phối xác suất của X2 là: X2 0 1 2 … n ... P 0,3 0,58.0,7 2 0,58.0,6.0,7 … n 1 0,58.0,6 .0,7n ...
b) Gọi X là tổng số lần ném rổ của 2 người
X nhận các giá trị là 1,2,3,...
Dễ thấy P(X 1) 0,3 .
Xét X 2n 2 có nghĩa người 2 ném cuối. n n 1 n 1 P( X
2n) 0,7 0,6 .0, 4 0, 28.0, 42
Xét X 2n 1 3 có nghĩa người 1 ném cuối.
( 2 1) 0,7n0,6 .n0,3 0,3.0, 42n P X n
Vậy qui luật phân phối xác suất của X là: X 1 3 … 2n+1 ... P 0,3 0,3.0, 42 … 0,3.0, 42n ... X 2 4 … 2n ... P 0,28 0, 28.0, 42 … 1 0, 28.0, 42n ... 6
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.7 Bảng phân phối xác suất của biến ngẫu nhiên X như sau: X -5 2 3 4 P 0,4 0,3 0,1 0,2 a) Tính E(X); V(X) và b) Tìm giá trị mốt m0. Giải: 4 a) E(X)= X P
= -5.0,4+2.0,3+3.0,1+4.0,2 = -0,3. i i i 1 b)
V(X) = E(X2) – E2(X)= (-5)2.0,4+22.0,3+32.0,1+42.0,2-(-0,3)2=15,21.
V (X ) = 3,9. X c)
Vì X là biến ngẫu nhiên rời rạc nên m0 là giá trị của biến ngẫu nhiên tương ứng với xác suất lớn nhất nên m0=-5.
Bài 2.8 Tại một cửa hàng bán xe máy Honda, người ta thống kê được số xe máy X bán ra hàng tuần với
bảng phân bố xác suất như sau: X 0 1 2 3 4 5 6 7 8 9 10 11 P
0,05 0,12 0,17 0,08 0,12 0,20 0,07 0,02 0,07 0,02 0,03 0,05
a) Tìm số xe máy trung bình bán ra mỗi tuần.
b) Tìm phương sai và độ lệch chuẩn của số xe máy bán được mỗi tuần và giải thích ý nghĩa của kết quả nhận được.
Giải: a) Số xe trung bình mỗi tuần bán được là kỳ vọng toán: 11 E( X ) x p 4,33 i i i0 b) Phương sai:
V(X) = E(X2) – E(X)2 = 27.09 – (4.33)2 = 8,3411
Độ lệch chuẩn: V (X ) 2,8881 X
Ý nghĩa: Trung bình cửa hàng bán được 4,33 xe máy mỗi tuần.
2,8881 đánh giá mức độ phân tán của biến ngẫu nhiên. X 7
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.9 Cho X1, X2, X3 là các biến ngẫu nhiên độc lập và có bảng phân phối xác xuất của chúng như sau: X1 0 1 X2 1 2 X3 0 2 P 0.6 0.4 P 0.4 0.6 P 0.8 0.2 Lập X1 X 2 X3 X
Tính E(X ) và V (X ) 3 Giải:
*)Tính E(X ) Ta có: E(X1) = 0.0,6 + 1. 0,4 = 0,4 E(X2) = 0.0,8 + 2.0,2 = 1,6 E(X3) = 0.0,8 + 2.0,2 = 0.4
E X E X E(X ) 1 2 3 0, 4 1,6 0, 4 E(X ) 0,8 3 3 *)Tính V (X )
Ta có: V X E(X ) (EX ) 1 .0, 4 – 0,42 2 2 2 0,24 1 1 1 V X 2 2 2 2 2
E(X ) (EX ) 0,4 .1 0,6.2 1,6 0,24 2 2 2 V X 2 2 2 2
E(X ) (EX ) 2 .0,2 0,4 0,64 3 3 3
V ( X ) V X V (X ) 1 2 3 0, 24 0, 24 0,64 V (X ) 0,12 9 9
Bài 2.10 Thống kê số khách trên 1 ô tô buýt tại một tuyến giao thông thu được các số liệu sau: Số khách trên 1 chuyến 20 25 30 35 40 Tần suất tương ứng 0,2 0,3 0,15 0,1 0,25
Tìm kỳ vọng toán và phương sai của số khách đi mỗi chuyến và giải thích ý nghĩa của kết quả thu được.
Giải: * Gọi X là số khách đi mỗi chuyến, kỳ vọng toán của số khách đi mỗi chuyến là:
E(X) = 0,2.20 + 0,3.25 + 0,15. 30 + 0,1.35 + 0,25.40 = 29,5
Ý nghĩa: Kỳ vọng bằng 29,5 cho biết trung bình có khoảng 29 khách hàng trên 1 chuyến xe.
* Phương sai của số khách đi mỗi chuyến là:
V(X) = E(X2) – E2(X) = 0,2.202 + 0,3.252 + 0,15.302 + 0,1.352 + 0,25.402 – (29,5)2 = 54,75
Độ lệch chuẩn của số khách đi mỗi chuyến là: σ = V(x) = 54,75 ≈ 7,4
Ý nghĩa: Số khách đi các chuyến có sự khác nhau và chênh lệch khá lớn so với số khách trung bình. 8
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.11 Cho X và Y là 2 biến ngẫu nhiên liên tục với E(X)= V(X)= 3; E(Y)= V(Y)= 2 a)
Tính E(Z) và V(Z) biết Z= (3X – 2Y)/5
Z E(Z ) b) Tính E(T) với T= V (Z ) Giải: (3X 2Y )
3E(X ) 2E(Y ) 3.3 2.2 a) Z E(Z ) 1. 5 5 5 2 2 3 2 9.3 4.2 35 7 V (Z) V ( X ) V (Y ) 1, 4 . 5 5 25 25 25 5
Z E(Z ) Z 1 E(Z ) 1 b) T E(T) 0 . V (Z ) 1, 4 1,4
Bài 2.12 Thực hiện 3 lần bắn bia với xác suất trúng bia tương ứng là 0,3; 0,4; 0,6. Tìm kì vọng toán và
phương sai số lần bắn trúng bia.
Giải: Gọi X là số lần bắn trúng bia
X là biến ngẫu nhiên rời rạc với các giá trị có thể xảy ra X = 0, 1, 2, 3.
Ta có P(X = 0) = 0,7.0,6.0,4 = 0,168
P(X = 1) = 0,3. 0,6.0,4 + 0,7.0,4.0,4 + 0,7.0,6.0,6 = 0,436
P(X = 2) = 0,3.0,4.0,4 + 0,3.0,6.0,6 + 0,7.0,4.0,6 = 0,324
P(X = 3) = 0,3.0,4.0,6 = 0,072
Vậy quy luật phân phối xác suất của X là X 0 1 2 3 P 0,168 0,436 0,324 0,072
Kì vọng toán E(X) = 0.0,168 + 1.0,436 + 2.0,324 + 3.0,072 = 1,3
E(X2) = 02.0,168 + 12.0,436 + 22.0,324 + 32.0,072 = 2,38
Phương sai V(X) = E(X2) – (E(X))2 = 0,69.
Bài 2.13 Thống kê lại tất cả 52 cửa hàng bán sản phẩm của công ty trên toàn quốc thu được các số liệu sau:
Số nhân viên bán hàng ở cửa hàng 2 3 4 5
Số cửa hàng tương ứng 10 12 16 14 9
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội a)
Xây dựng bảng phân phối xác suất và hàm phân bố xác suất của số nhân viên bán hàng tại mỗi cửa hàng. b)
Tìm số nhân viên trung bình ở mỗi cửa hàng và phương sai tương ứng Giải: a)
Đặt X là số nhân viên của một cửa hàng, ta có:
Bảng phân phối xác suất: Số nhân viên 2 3 4 5 Tổng Số cửa hàng 10 12 16 14 52 Xác suất 10 5 12 3 16 4 14 7 1 1 P P P P 52 26 2 52 13 3 52 13 4 52 26
Hàm phân bố xác suất của số nhân viên bán hàng tại mỗi cửa hàng: 0 x 2 5 2 x 3 26 11
F x PX x 3 x 4 26 19 4 x 5 26 1 x 5 b)
Số nhân viên trung bình ở mỗi cửa hàng bằng kì vọng: E X 5 3 4 7 95 2. 3. 4. 5. 3,65 26 13 13 26 26 4
Phương sai: V (X ) p [x E X k k 2] k 1 5 2 3 2 4 2 7 2 (2 3,65) (3 3,65) (4 3,65) (5 3,65) , 1 15 26 13 13 26
Bài 2.14 Biến ngẫu nhiên rời rạc X nhận ba giá trị có thể có là x1 = 4 với xác suất P1 = 0,5; x2 = 0,6 với
xác suất P2 = 0,3 và x3 với xác suất P3. Tìm x3 và P3 biết E(X) = 8.
Giải: Ta có P3 = 1 – P1 – P2 = 1 – 0,5 – 0,3 = 0,2
E(X) = 8 = 0,5.4 + 0,6.0,3 + x3.0,2 hay 0,2.x3 = 5,82 Do đó X3 = 29,1.
Bài 2.15 Biến ngẫu nhiên rời rạc X nhận ba giá trị có thể có là x1= -1, x2=0, x3= 1. Tìm các xác suất
tương ứng p , p , 1 2 3
p biết rằng E(X)= 0,1 và E(X2)=0,9.
Giải: Ta có bảng phân phối xác suất của biến ngẫu nhiên rời rạc X là: 10
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội X -1 0 1 P 1 p p 2 3 p E
(X ) 0,1 p +0. p p 0,1 p 0,4 Theo bài ra ta có : 1 2 3 1 p 0,1 (1) 2 2 E
(X ) 0,9 p +0. p p 0,9 p 0,5 1 2 3 3
Vậy p 0, 4; p 0,1; p 0,5 . 1 2 3
Bài 2.16 Biến ngẫu nhiên rời rạc X có qui luật phân phối xác suất như sau: X 1 x x 2 P 1 p 0,7 Tìm x , x , 1 2 1
p biết E(X) = 0,7 và V(X) = 0,21.
Giải: Dễ thấy p 1 p 0,3 . 2 1
E(X ) 0,7 0,3x 0,7x 2,7 x 2 Ta có 1 2 1 . 2 2 2 V
(X ) 0,21 0,3x 0,7x 2,7 0, 21 x 3 1 1 2
Bài 2.17 Có 5 sản phẩm trong đó có 4 chính phẩm và một phế phẩm. Người ta lấy ra lần lượt 2 sản phẩm ( lấy không hoàn lại). a)
Gọi X là: “số phế phẩm có thể gặp phải”. Lập bảng phân phối xác suất của X. b) Tính E(X) và V(X). c)
Gọi Y là: “ số chính phẩm có thể gặp phải”. Lập hệ thức cho biết mối quan hệ giữa Y và X. d) Tính E(Y) và V(Y). Giải: a)
Vì có 5 chính phẩm và 1 phế phẩm nên nếu gọi X là “số phế phẩm có thể gặp phải” thì X= 0 hoặc X=1 4 Gọi X 2 C
0 là biến cố “ không gặp phải phế phẩm nào”: P(X0)= = 0,6. 5 2 C 1 4 C . Gọi X 1 1 C
1 là biến cố “ gặp phải 1 phế phẩm”: P(X1) = = 0,4 5 C2
Ta có bảng phân phối xác suất của X: X 0 1 P 0,6 0,4 b) E(X)= X1P1+X2P2=0,4.
V(X) = E(X2) – E2(X)= 0+12.0,4 – 0,42=0,24. 11
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội c)
Y: “số chính phẩm có thể gặp phải”. Ta có X+Y=2. Vì X nhận 2 giá trị 0, 1 nên tương ứng Y cũng nhận 2 giá trị 2, 1. d)
Ta có bảng phân phối xác suất của biến ngẫu nhiên Y: [ P Y 1] [ P X 1], [ P Y 2] [ P X 0] Y 1 2 P 0,4 0,6
E(Y) = Y1P1+Y2P2= 1.0,4+2.0,6=1,6.
V(Y)= E(Y2) – E2(Y) = 0,4+22.0,6-1,62=0,24.
Bài 2.18 Trở lại bài 2.8. Nếu giá bình quân của mỗi chiếc xe máy bán ra tại cửa hàng đó là 12 triệu đồng
thì doanh thu bình quân hàng tuần của cửa hàng đó là bao nhiêu ?
Giải: Số xe máy bình quân cửa hàng đó bán ra là E(X) = 4,33.
Doanh thu trung bình của cửa hàng = 12.E(X) = 12.4,33 = 51,96 (triệu đồng)
Bài 2.19 Với các số liệu của bài 2.10, giả sử chi phí cho mỗi chuyến xe là 200 ngàn đồng không phụ
thuộc vào số khách đi trên xe thì để công ty xe buýt có thể thu được lãi bình quân cho mỗi chuyến xe là
100 ngàn đồng thì phải quy định giá vé là bao nhiêu?
Giải: * Các số liệu đã cho của bài tập 2.10 như sau:
Thống kê số khách trên 1 ô tô buýt tại một tuyến giao thông thu được các số liệu sau: Số khách trên 1 chuyến 20 25 30 35 40 Tần suất tương ứng 0,2 0,3 0,15 0,1 0,25
* Với câu hỏi của bài tập 2.19,
Ta gọi a là giá vé quy định, theo đề bài:
a.E(X) = 200+100. Suy ra a = 300/E(X) = 300/29,5 = 10,17.
Vậy phải quy định giá vé là 10,17 nghìn đồng.
Bài 2.20 Kinh nghiệm cho thấy là số lượng một loại sản phẩm mà một khách hàng mua có bảng phân phối xác suất như sau: Số lượng sản phẩm 0 1 2 3 Xác suất tương ứng 0,5 0,1 0,2 0,2 a)
Nếu mỗi sản phẩm được bán với giá 110 ngàn đồng và nhân viên bán hàng được hưởng 10% trên
số sản phẩm bán được thì số tiền hoa hồng bình quân mà nhân viên bán hàng được hưởng từ mỗi khách hàng là bao nhiêu. b)
Tìm phương sai của số tiền hoa hồng đó và nêu ý nghĩa của kết quả thu được. 12
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Giải: a) Gọi X là biến ngẫu nhiên số sản phẩm bán được:
Kỳ vọng toán cho số sản phẩm bán được:
E(X) = 0.0,5 + 1.0,1 + 2.0,2 + 3.0,2 = 1,1
Mỗi sản phẩm bán với giá 110 ngàn đồng thì số tiền bình quân thu được từ mỗi khác hàng = 1,1. 110 = 121 ( ngàn đồng )
Nhân viên bán hàng được hưởng 10% trên số sản phẩm bán được.
Số tiền hoa hồng bình quân mà nhân viên bán hàng được hưởng từ mỗi khách hàng là:
121. 0,1 = 12,1 ( ngàn đồng )
b) Phương sai của số lượng sản phẩm bán được: 2 2 2
V ( X ) E(X ) E ( X ) 0,1.1 0, 2.4 0, 2.9 1,1 1, 49
Gọi Y là biến ngẫu nhiên số tiền hoa hồng nhận được thì Y = 10%.110X=11X (đơn vị ngàn)
Phương sai của số tiền hoa hồng:
V(Y) = V(11X) = 112.1,49= 180,29. Ý nghĩa của kết quả:
Số tiền mà nhân viên nhận được hoa hồng khi bán cho 1 khách không đồng đều.
Bài 2.21 Tỉ lệ khách hàng phản ứng tích cực với một chiến dịch quảng cáo là biến ngẫu nhiên có bảng phân phối xác suất sau: X(%) 0 10 20 30 40 50 Px 0,1 0,2 0,35 0,2 0,1 0,05 a)
Chứng tỏ rằng các xác suất Px tạo nên 1 bảng phân phối xác suất b)
Tìm tỉ lệ khách hàng bình quân phản ứng tích cực với quảng cáo đó c)
Tìm xác suất để có trên 20% khách hàng phản ứng tích cực với chiến dịch quảng cáo Giải: a)
Ta thấy: P(X=0)+P(X=10)+P(X=20)+P(X=30)+P(X=40)+P(X=50)=0,1+0,2 +0,35+0,2+0,1+0,05=1.
Do đó các Px tạo nên 1 bảng xác suất. b)
Tỉ lệ bình quân khách hàng phản ứng tích cực với quảng cáo đó chính là kì vọng:
E(X)=0,1.0+0,2.10+0,35.20+0,2.30+0,1.40+0,05.50=21,5. c)
Xác suất để có trên 20% khách hàng phản ứng với chiến dịch quảng cáo là: Pc= 0,2+0,1+0,05=0,35. 13
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.22 Tung cùng một lúc hai con xúc xắc. Gọi X là tổng số chấm thu được. a)
Tìm bảng phân phối xác suất của X b)
Tìm hàm phân bố xác suất của X c)
Giá trị nào của X có khả năng xảy ra nhiều nhất
Giải: X là tổng số chấm thu được. Ta có X là biến ngẫu nhiên rời rạc nhận các giá trị X = 2, 3,…, 12 a) X 2 3 4 5 6 7 8 9 10 11 12 P 1 2 3 4 5 6 5 4 3 2 1 36 36 36 36 36 36 36 36 36 36 36 b) 0 x 2
1/ 36 2 x 3 3 / 36 3 x 4
6/36 4 x 5 10 / 36 5 x 6 15 / 36 6 x 7 F(x) = 21/ 36 7 x 8 26 / 36 8 x 9 30 / 36 9 x 10 33 / 36 10 x 11 35 / 36 11 x 12 1 x 12
c) Từ bảng phân bố xác suất ta thấy m o = 7
Bài 2.23 Qua theo dõi trong nhiều năm kết hợp với sự đánh giá của các chuyên gia tài chính thì lãi suất
đầu tư vào một công ty là biến ngẫu nhiên có bảng phân phối xác suất như sau: X(%) 9 10 11 12 13 14 15 Px 0,05 0,15 0,3 0,2 0,15 0,1 0,05 a)
Tìm xác suất để khi đầu tư vào công ty đó thì sẽ đạt được lãi suất ít nhất là 12% b)
Tìm lãi suất có thể hy vọng khi đầu tư vào công ty đó c)
Mức độ rủi ro khi đầu tư vào công ty đó có thể đánh giá bằng cách nào? Giải: a)
X là lãi suất đầu tư vào công ty ta có 14
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Xác suất để khi đầu tư thu được lãi suất ít nhất 12% là:
P P X 12 P X 12 P X 13 P X 14 P(X 15) 0,2 0,15 0,1 0,05 0,5 a b)
Lãi suất có thể hy vọng khi đầu tư vào công ty là
E(X ) 0,059 0,15 1 0 0,3 1
1 0,212 0,1513 0,1 1 4 0,0515 11,75 c)
Mức độ rủi ro khi đầu tư vào công ty đó có thể đánh giá bằng: 2 2 2 2 2 2 2 2
V ( X ) 9 0, 05 10 0,15 11 0,3 12 0, 2 13 0,15 14 0,115 0, 05 11, 75 2, 2875
V (X ) 2,2875 1,5124 . X
Bài 2.24 Một người đi từ nhà đến cơ quan phải qua 3 ngã tư, xác suất để người đó gặp đèn đỏ tại các ngã
tư tương ứng là 0,2; 0,4 và 0,5. Hỏi thời gian trung bình phải ngừng trên đường là bao nhiêu, biết rằng
mỗi khi gặp đèn đỏ người ấy phải dừng 3 phút.
Giải: Gọi X là số đèn đỏ một người có thể gặp phải thì X là biến ngẫu nhiên rời rạc với các giá trị có thể nhận là {0;1;2;3}
Ta có: P(X=0) = 0,8.0,6.0,5 = 0,24
P(X=1) = 0,2.0,6.0,5 + 0,8.0,4.0,5 + 0,8.0,6.0,5 = 0,46
P(X=2) = 0,2.0,4.0,5 + 0,8.0,4.0,5 + 0,2.0,6.0,5 = 0,26 P(X=3) = 0,2.0,4.0,5 =0,04
Bảng phân phối xác suất của X là: X 0 1 2 3 P 0,24 0,46 0,26 0,04
E(X) = 0.0,24 + 1.0,46 + 2.0,26 + 3.0,04 = 1,1
Gọi Y là thời gian phải dừng đèn đỏ Y = 3X.
Vậy: E(Y) = 3E(X) = 3.1,1 = 3,3 (phút)
Bài 2.25 Có 5000 người xét nghiệm máu để tìm ký sinh trùng sốt rét. Tỷ lệ mắc bệnh ở địa phương theo
thống kê là 10%. Có thể làm xét nghiệm theo 2 phương pháp:
Phương pháp 1: Xét nghiệm từng người
Phương pháp 2: Lấy máu 10 người một trộn lẫn làm một xét nghiệm. Nếu kết quả xét nghiệm là âm tính
(vô trùng) thì thông qua 10 người không ai mắc bệnh. Nếu kết quả xét nghiệm là dương tính (có trùng) thì
chứng tỏ trong 10 người có ít nhất 1 người mắc bệnh. Lúc đó phải làm thêm 10 xét nghiệm lẻ để phát hiện các con bệnh cụ thể. 15
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Hỏi làm theo cách nào lợi hơn?
Giải: Theo phương pháp 1 thì phải làm 5000 xét nghiệm
Theo phương pháp 2 thì gọi X là số xét nghiệm phải làm đối với từng loạt 10 người
X=1 (nếu kết quả xét nghiệm là âm tính) và X=11 (nếu kết quả là dương tính)
P1= P(X=1)=(1 − 0,1) =0,9 (10 người không mắc bệnh)
P2= P(X=11)= 1− P1= 1− 0,9 (có ít nhất 1 người mắc bệnh)
Từ đó E(X) ≈7,5 tức là trung bình phải làm 7,5 xét nghiệm
Vậy tổng số xét nghiệm phải làm là: × 7,5 = 3750 xét nghiệm
Như vậy làm theo phương pháp 2 lợi hơn phương pháp 1 là 25%.
Bài 2.26 Biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau: X 1 4 8 P 0,3 0,1 0,6 Tìm P(|X-E(X)| < 4)?
Giải: Từ bảng phân phối xác suất ta có: E(X)= 1.0,3+4.0,1+8.0,6=5,5
X E( X ) 4 4 X E(X ) 4 1, 5 X 9,5 X 4;8
Suy ra P( X E(X ) 4) P(X 4) P(X 8) 0,1 0,6 0,7 .
§2 Biến ngẫu nhiên liên tục
Bài 2.27 Nhu cầu hàng năm về loại hàng A là biến ngẫu nhiên liên tục X có hàm mật độ xác suất như sau
( đơn vị: ngàn sản phẩm)
k 30 x x (0,30) f x 0 x (0,30) a) Tìm k. b)
Tìm xác suất để nhu cầu về loại hàng đó không vượt quá 12000 sản phẩm một năm. c)
Tìm nhu cầu trung bình hàng năm về loại hàng đó. Giải: 0 30
a) Ta có k 0 và f
xdx =1 = f
xdx + f xdx + f xdx 0 30 30 30 2 = x
f x dx
= k(30 x)dx = 30 k 30x | =450k 0 2 0 0 16
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội Vậy k = 1/450.
b) Xác suất để nhu cầu về loại hàng A không vượt quá 12 ngàn sản phẩm một năm là 12 12 12 2 1 1 P(X 12) = x f
xdx = f xdx = 12 (30 x)dx (30x ) | 0,64 . 0 450 450 2 0 0
c) Nhu cầu trung bình hàng năm về loại hàng đó cũng chính là kỳ vọng của biến ngẫu nhiên X: 30 2 3 1 1 E(X)= x x xf
xdx = .x . 30 x 30 dx 30. | 10. 0 450 450 2 3 0
Bài 2.28 Thời gian xếp hàng chờ mua hàng của khách là biến ngẫu nhiên liên tục với hàm phân bố xác 0 x 0
suất như sau ( đơn vị phút ) 3 2
F (x) ax 3x 2x 0 x 1 1 x 1 a) Tìm hệ số a.
b) Tìm thời gian xếp hàng trung bình
c) Tìm xác suất để trong 3 người xếp hàng thì có không quá 2 người phải chờ quá 0,5 phút
0 x (;0) (1;)
Giải: Ta có f (x) 2 3ax 6x 2 0 x 1
a) Do f(x) là hàm mật độ xác suất của 1 biến ngẫu nhiên nên: 1 2 3 2 1
1 f (x)dx (3ax 6x 2)dx ax 3x 2x | a 1 a 2 . 0 0 1 3 b) 2 4 3 2 1 E( X )
xf (x)dx x(3ax 6x 2)dx
ax 2x x | 0,5 . 0 4 0
c) Xác suất để một người nào đó xếp hàng phải chờ quá 0,5 phút là: P X
P X F 3 2 0.5 = 1 0.5 1
0.5 1 (2.0,5 3.0,5 2.0,5) 0,5.
Xác suất để cả 3 người xếp hàng phải chờ quá 0,5 phút là 3 0.5 nên
Xác suất để có không quá 2 trong 3 người nào đó xếp hàng phải chờ quá 0.5 phút: P =1- 3 0.5 =0,875. c
Bài 2.29 Cho X là biến ngẫu nhiên liên tục có hàm phân bố xác suất sau đây: 1 1 F (x) arctanx . 2
a) Tìm P(0b) Tìm hàm mật độ xác suất của X. 17
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội 1 1 1 1
Giải: a) P (0 arcta 1 n arctan0 2 2 1 1 1 arcta 1
n arctan0 0 . 4 4 ' 1 1 1 1 b) f(x) F’(x)
arctanx arctanx' . 2 2 (1 x )
Bài 2.30 Biến ngẫu nhiên X có hàm phân bố xác suất như sau: x/ x F x 1 e 0 0 x 0
a) Tìm hàm mật độ xác suất của X.
b) Tìm P(0 x ) . x x x .0 1 Giải: a) Ta có: / 1 e / x/ ' e . e . 2 1 x/ e x 0
Hàm mật độ xác suất của X là: f (x) F 'x 0 x 0
b) Ta có: P(0 x ) F ( ) – F 0 / 1 e 1 1 e 1 . e e
Bài 2.31 Biến ngẫu nhiên X liên tục trên toàn trục số và có hàm phân bố xác suất 1 1 ( ) x F x arctan . 2 2 1 Tìm giá trị có thể có
P (X x ) . 1
x thỏa mãn điều kiện 1 4 3
Giải: Ta có P (X x ) P (X x ) 1 P (X x ) 1 1 1 4
Theo định nghĩa hàm phân bố xác suất thì:
P ( X x ) F ( x ) 1 1 Do đó 1 1 x 3 1 1 x 1 ( ) x F x arctan arctan 1 x 2. 1 1 2 2 4 2 4 2 Vậy x 2 . 1
Bài 2.32 Gọi X là biến ngẫu nhiên liên tục trong khoảng (-∞; + ∞) với hàm mật độ xác suất là f (x) . Hãy 1 tính giá trị của f (x)dx
biết rằng P X 1 0,3 . 18
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội 1
Giải: Ta có P X
1 1 P X
1 0,7 mà P X 1 f (x)dx 1 Vậy f (x)dx =0,7.
Bài 2.33 Biến ngẫu nhiên X có hàm phân bố xác suất như sau: 0 x 2 F x 1
x 1 2 x 4 . 2 1 x 4
Tìm xác suất để trong kết quả của phép thử X nhận giá trị: a) Nhỏ hơn 3 b) Trong khoảng [2;3) Giải: 3 a) P [
P x 3] F (3) 1 0,5 a 2 3 2 b) P [
P 2 X 3] F (3) F (2) 1 1 0,5 b 2 2
Bài 2.34 Hàm phân bố xác suất của biến ngẫu nhiên liên tục X có dạng: 0 x 0
F (x) sin2x 0 x . 4 1 x 4
Tìm hàm mật độ xác suất f (x) .
2cos2x x (0, ) Giải: Ta có 4
f (x) F '(x) . 0 x (0, ) 4 0 x 2
Bài 2.35 Biến ngẫu nhiên liên tục X có hàm phân bố xác suất như sau f x cx 1 2 x 4 . 1 x 4 a) Tìm hằng số c b) Tìm E(X) 19
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
c x (2, 4 )
Giải: a) Ta có hàm mật độ xác suất là: f (x) F '(x) 0 x (2,4 )
Theo tính chất của hàm mật độ xác suất, ta có: c 0 và 4 f x 4 1 1
dx cdx cx | 2 . 2 c c 2 2 4 2 1 b) Ta có: x E( X ) xf x 4 dx xdx | 3 . 2 2 4 2
a cos x x ( / 2, / 2 )
Bài 2.36 Biến ngẫu nhiên X có hàm mật độ xác suất f (x) 0 x ( / 2, / 2 ) a) Tìm hệ số a
b) Tìm P(0 X ) 4 c) Tìm E(X)
Giải: a) Do f (x) là hàm mật độ xác suất của nên a cos x 0 x (
/ 2, / 2 ) a 0 , hơn nữa /2 1 f x 1 /2 dx
a cos xdx a sin x | 2 . /2 a a 2 /2 /4 /4 1 1 2
b) P(0 X ) f x /4 dx
cos xdx sin x | . 0 4 2 2 4 0 0 /2 /2 /2 1 1 1 1
c) E(X ) xf x /2 dx x cos xdx xd sin x x sin x | sin xdx 0 /2 . 2 2 2 2 /2 /2 /2
Bài 2.37 Biến ngẫu nhiên liên tục X có hàm phân bố xác suất: 0 x 0 F x 1
k cos x 0
x 2 1 x a) Tìm hệ số k . b)
Tìm P(0 X ) 2 c) Tìm E(X ) . Giải: a)
Vì F (x) liên tục nên ta có: 20
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội 1 lim F
lim kcosx lim 1 x lim F x x x x 2 x 1
kcos 1 1 k . 2 2 1 1 1 1 1 b) P(0 X
) F ( ) F (0) cos( ) cos 0 . 2 2 2 2 2 2 2 2 1
sin x x (0, ) c)
Ta có hàm mật độ xác suất: f (x) F '(x) 2 0 x (0, ) 0
Vậy E(X ) xf
xdx xf
xdx xf
xdx xf
xdx xf xdx 0 0 1 1 1 1 1 . x sinxdx
xd (cosx) xcosx cosxdx sinx . 2 2 2 2 2 2 2 0 0 0 0 0
Bài 2.38 Thu nhập của dân cư 1 vùng là biến ngẫu nhiên liên tục có hàm phân bố xác suất như sau: 0 1 x x 0 x F (x) x ( 0 ) 0 x 0 x
Hãy xác định mức thu nhập sao cho lấy ngẫu nhiên một người ở vùng đó thì thu nhập người này vượt quá
mức trên với xác suất 0,5.
Giải: Gọi a là mức thu nhập sao cho nếu lấy ngẫu nhiên 1 người trong vùng đó thì thu nhập của người
này vượt quá a, với xác suất 0,5.
P( X a) 0,5 P( X a) 1 P(X a) 0,5 F (a) 0 x 0 x 1/ 1/
F (a) 0,5 1 0,5
0,5 a 2 . 0 x 0 x a a Vậy 1/ a 2 x . 0
Bài 2.39 Biến ngẫu nhiên liên tục X có hàm mật độ xác suất như sau: 2 2
cos x x ( / 2, / 2 )
f (x) . 0 x ( / 2, / 2 )
Tìm xác suất để trong 3 phép thử độc lập có 2 lần X nhận giá trị trong khoảng (0, / 4) .
Giải: Xác suất để trong 1 phép thử bất kì, X nhận giá trị trong khoảng (0, / 4) là: /4 /4 2 2 1 cos2x 2 x 1 / 4 1 1 2 P(0 x ) cos xdx dx sin2x . 4 2 2 4 0 4 2 0 0 21
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Theo công thức Bernoulli, xác suất để trong 3 phép thử độc lập có 2 lần X nhận giá trị trong khoảng 2 1 1 1 1 (0; / 4) là: 2 C 1 0, 296 . 3 4 2 4 2 2
x / 9 x(0, 3)
Bài 2.40 Cho hàm số: f (x) . 0 x ( 0,3)
a) Hàm số trên có phải là hàm mật độ xác suất không ?
b) Nếu có thì tìm xác suất để trong 3 phép thử độc lập có ít nhất một lần X nhận giá trị trong khoảng (1;2). 3 2 3 x x 3
Giải: a) Ta có: f x 0 x và f
xdx dx 1
nên f (x) là hàm mật độ xác suất. 9 27 0 0
b) Xác suất để trong một phép thử nào đó X nhận giá trị trong khoảng (1; 2) là: 2 2 2 3 P X f x x x 2 7 (1 2) dx dx 9 27 1 27 1 1 7
nên xác suất để X không nhận giá trị trong khoảng (1;2) là 1 . 27 3 7
Xác suất để trong 3 phép thử độc lập thì cả 3 lần X không nhận giá trị trong khoảng (1;2) là 1 . 27
Xác suất để trong 3 phép thử độc lập có ít nhất 1 lần X nhận giá trị trong khoảng (1;2) là: 3 7 1 1 0,594 . 27
Bài 2.41 Cho hàm phân bố xác suất của biến ngẫu nhiên liên tục x
F x c . b arctg
với ( x ) . a a)
Tìm các hệ số c và b b)
Tìm hàm mật độ xác suất f(x) Giải: a)
Do F (x) là hàm phân bố của 1 biến ngẫu nhiên nên ta có tính chất
0 F c . b c 1/ 2 2
F () 0; F () 1 . F b 1/ 1 c . b 2 22
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội 2 1 1 x 1 1 b) a
f (x) F '(x) ( arctg )' . 2 2 2 a x 2
(x a ) 1 ( ) a
Bài 2.42 Tỷ lệ mắc một loại bệnh trong một vùng dân cư là biến ngẫu nhiên liên tục có hàm mật độ 1
/ 20 x (5, 25) f (x) . 0 x ( 5,25) a) Tính P (| X-10 | >2.5)
b) Tính tỷ lệ mắc bệnh trung bình và phương sai
Giải: a) Vì X là biến ngẫu nhiên liên tục nên ta có
P X 10 2.5 1 P( X 10 2.5) 1– P(10 2,5 X 10 2,5) 12,5 12,5 1 1
– P(7,5 X 12,5) 1
f (x)dx 1 dx 0, 75 . 20 7,5 7,5 5 25 25 2 x x 25
b) E X xf (x)dx xf (x)dx xf (x)dx xf (x)dx dx 15 . 20 40 5 5 25 5 25 3 V X 1 x 25 2 2 2 2 2
x f (x)dx ( xf (x)dx ) x dx 15 15 33,3 . 20 60 5 5
k x (a, b)
Bài 2.43 Biến ngẫu nhiên liên tục X có hàm mật độ xác suất: f (x) . 0 x ( a,b) a) Tìm hệ số k b) Tìm E(X) và V(X) c)
Vẽ đồ thị hàm f(x) và F(x) Giải: a)
Vì f (x) là hàm mật độ nên k 0 và a b b b 1 1
f (x)dx
f (x)dx
f (x)dx
f (x)dx
f (x)dx kdx k(b a) k . b a a b a a b 2 x b 1 2 2 b) b a a b E(x)
xf (x)dx kxdx k . 2 a b a 2 2 a b 3 3 3 2 2 x b Ta có 2 2 2 1 ( ) ( ) . b a a b ab E X x f x dx kx dx k 3 a b a 3 3 a 2 2 2 2 2 2
a b ab (b a)
a b 2ab (b a) V ( X ) 3 4 12 12 23
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
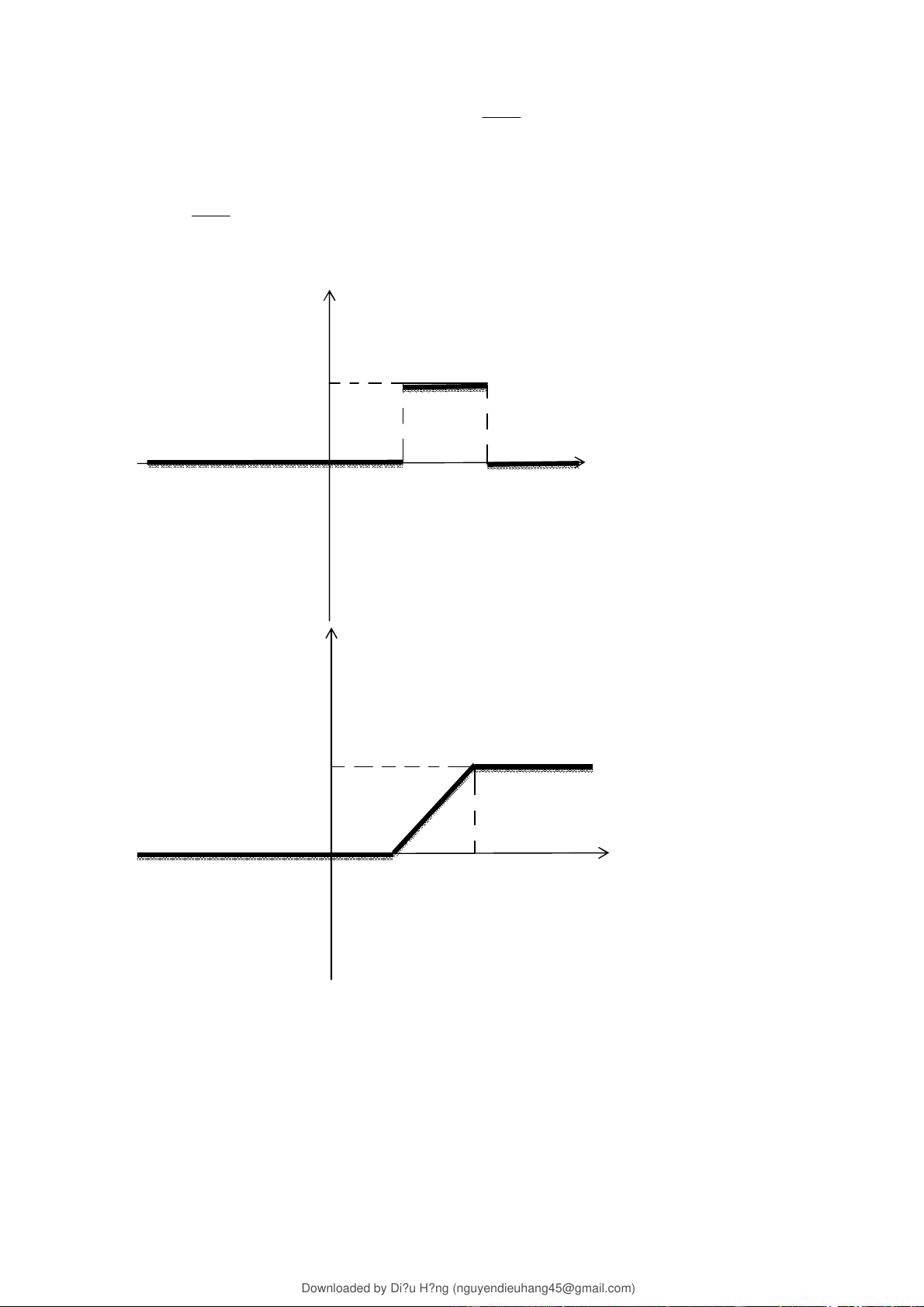
ĐH Ngoại Thương Hà nội x x c) x a
Xét x (a,b) ta có F(x)
f (x)dx kdx b a a 0 x a Vậy ( ) x a F x a
x b b a 1 xb Ta có đồ thị y k y=f(x) 0 a b x y y=F(x) 1 x 0 a b 24
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
csin 2x x (0, / 2 )
Bài 2.44 Biến ngẫu nhiên liên tục X có hàm mật độ xác suất: f (x) . 0 x (0, / 2 ) Tìm hệ số c.
Giải: Do f (x) là hàm mật độ xác xuất của 1 biến ngẫu nhiên nên:
f (x) 0, x
csin 2x 0, x
(0; ) c 0 và 2 2 c 2 1
f (x)dx
c sin 2xdx cos 2x c c 1 . 0 2 0
Bài 2.45 Biến ngẫu nhiên liên tục X có hàm mật độ xác suất: k f x
( x ) x x e e Tìm k . x Giải: 1 Ta có e k 0 và 1 f
xdx k. dx k dx x x 2 x e e e 1 x Ta đi tính e I dx 2 x e 1 Đặt x x
e t e dx dt và đổi cận x t 0 1 A 1 lim lim arctan A I dt dt
lim (arctan A arctan 0) 0 . 2 2 t 1 A t 1 A 0 A 2 2 0 0 Do đó 2 k. 1 k . 2 25
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
§3 Bài tập tổng hợp chương II
Bài 2.46 Theo thống kê dân số thì một người ở độ tuổi 40 sẽ sống thêm 1 năm nữa là 0,995. Một công ty
bán bảo hiểm cho người ở độ tuổi đó với số tiền là 10 ngàn đồng và trong trường hợp người đó chết thì sẽ
bồi thường 1 triệu đồng. Hỏi lợi nhuận trung bình của công ty khi bán một thẻ bảo hiểm.
Giải: Gọi X là lợi nhuận khi bán được một thẻ bảo hiểm (nếu lỗ thì X nhận giá trị âm)
Ta có bảng phân phối xác suất: X 10000 990000 P 0,995 0,005
Số tiền lãi trung bình là: E(X) = 10000.0,995 – 990000.0,005 = 5000
Với mỗi bảo hiểm bán được công ty sẽ lãi trung bình 5000 đồng.
Bài 2.47 Giá hàng ngày trên thị trường thế giới về đường (đơn vị: USD/fao) có bảng phân phối xác suất như sau: X 0,78 0,79 0,8 0,81 0,82 0,83 P 0,05 0,1 0,25 0,4 0,15 0,05 X a)
Tìm xác suất để giá đường vào một ngày nào đó sẽ đạt ít nhất là 0,8USD/fao. b)
Tìm xác suất để giá đường vào một ngày nào đó sẽ thấp hơn 0,82USD/fao. c)
Giả sử giá hàng ngày của đường là độc lập nhau. Tìm xác suất để trong hai ngày liên tiếp giá
đường đều cao hơn 0,8USD/fao. Giải: a)
Gọi Xa: “ giá đường một ngày nào đó đạt ít nhất là 0,8USD/fao”
P(Xa) =P(X≥0,8) = 0,25+0,4+0,15+0,05=0,85. b)
Gọi Xb: “ giá đường một ngày nào đó thấp hơn 0,82USD/fao”
P(Xb)=P(X<0,82)=0,05+0,1+0,25+0,4= 0,8 c)
X1 là biến cố giá đường ngày thứ nhất
X2 là biến cố giá đường ngày thứ hai
P(X1>0,8) = P(X2>0,8) = 0,4 + 0,15 + 0,05 = 0,6
Vì giá hàng ngày của đường độc lập với nhau nên xác suất để giá đường trong hai ngày liên tiếp cao hơn 0,8 USD/fao là:
P(X1>0,8).P(X2>0,8) = 0,6.0,6 = 0,36 26
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.48 Lợi nhuận X thu được khi đầu tư 50 triệu đồng vào một dự án có bảng phân phối xác suất
như sau (đơn vị triệu đồng) X -2 -1 0 1 2 3 Px 0,1 0,1 0,2 0,2 0,3 0,1 a)
Tìm mức lợi nhuận có khả năng nhiều nhất khi đầu tư vào dự án đó. b)
Việc đầu tư vào dự án này có hiệu quả hay không? Tại sao? c)
Làm thế nào để đo được mức độ rủi ro của vụ đầu tư này? Hãy tìm mức độ rủi ro đó. Giải: a)
Mức lợi nhuận có khả năng nhiều nhất khi đầu tư vào dự án đó là Mốt của quy luật phân bố xác suất: mo = 2 b)
Ta có trung bình lợi nhuận:
E(X) = (-2).0,1 + (-1).0,1 + 0.0,2 + 1.0,2 + 2.0,3 + 3.0,1 = 0,8 = 1,6%.50
Có nghĩa dự án có lãi 1,6% thấp so với một dự án lợi nhuận thường 10%-30% do đó không nên đầu tư vào dự án này. c)
Đo mức độ rủi ro của vụ đầu tư này bằng phương sai V(X) hoặc độ lệch chuẩn . X
V(X) = (-2)2.0,1 + (-1)2.0,1 + 02.0,2 + 12.0,2 + 22.0,3 + 32.0,1 - 0,82 = 2,16
V (X ) 1, 47 . X
Bài 2.49 Lợi nhuận thu được từ 1 triệu đồng đầu tư vào công ty A ( X ) và công ty B (X ) có các bảng A B
phân phối xác suất như sau: X -500 -100 100 500 700 A P 0,2 0,3 0,2 0,2 0,1 X A X -200 50 100 B P 0,1 0,6 0,3 X B a)
Nếu dự định đầu tư 10 triệu đồng thì lợi nhuận kỳ vọng khi đầu tư vào công ty A và B là bao nhiêu. 27
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội b)
Nếu dùng hệ số biến thiên như độ đo mức độ rủi ro của đầu tư thì việc đầu tư vào công ty nào rủi ro hơn? Giải: a)
Theo bảng phân phối xác suất thì lợi nhuận của công ty A và B là: E X
500.0,2 100.0,3 100. 0,2 500. 0,1 700. 0,1 60 A E X
200.0,1 50. 0,6 100. 0,3 40 B
Như vậy, nếu đầu tư 10 triệu thì lợi nhuận kỳ vọng sẽ là:
E 10X 10E X 10.60 600 A A
E 10X 10E X 10.40 400 . B B b) Ta có:
V X 2 2 2 2 2 2 500 .0,2
100 .0,3100 .0,2 500 .0, 2 700 .0,1 60 150400 A
V X 150400 387,81 A A V X B 2 2 2 2 200 .0,1 50 . 0,6 100 . 0,3 40 6900
V X 6900 83,06 B B 387,81 A CV A .100% .100% 646,36% E( X ) 60 A 83,06 B CV B
E X B .100% .100% 207,07% 40
Như vậy, đầu tư vào công ty A thì rủi ro cao hơn.
Bài 2.50 Một công ty thuê một luật sư trong một vụ kiện với hai phương án trả công như sau:
Phương án 1: Trả 5 triệu bất kể thắng hay thua kiện.
Phương án 2: Trả 100 ngàn đồng nếu thua kiện và 15 triệu đồng nếu thắng kiện.
Luật sư đã chọn phương án 2. Vậy theo đánh giá của luật sư thì khả năng thắng kiện của công ty tối thiểu là bao nhiêu?
Giải: Gọi X (triệu đồng) là số tiền luật sư nhận được theo phương án 2 và p là khả năng thắng kiện do
luật sư đánh giá ở phương án này. Ta có bảng phân phối xác suất của X là: X 15 0,1 p p 1 p 28
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Ta có: E X 15p 0,1.1– p 14,9 p 0,1.
Do luật sư đã chọn phương án 2 nên theo đánh giá của luật sư thì phương án 2 có lợi nhuận trung bình
cao hơn phương án 1 là 5 triệu.
Nghĩa là: E X 5 14,9 p 0,1 5 p 0,329 .
Vậy theo đánh giá của luật sư thì khả năng thắng kiện tối thiểu của công ty là 0,329.
Bài 2.51 Trên 1 tuyến bay người ta thống kê được rằng có 0.5% hành khách bị mất hành lý và giá trị
trung bình khách hàng đòi bồi thường là 600 ngàn đồng. Công ty hàng không muốn tăng thêm giá vé để
bù đắp cho số tiền phải bồi thường cho số hành lý bị mất. Vậy công ty nên tăng thêm giá vé là bao nhiêu? Tại sao?
Giải: Gọi X (ngàn đồng) là số tiền phải bồi thường cho 1 khách, nó có bảng phân phối xác suất như sau: X 600 0 P 0,005 0,995
nên E(X)= 600. 0,005= 3 (ngàn đồng) là số tiền vé tăng thêm.
Bài 2.52 Số lượng thuyền gỗ X mà một xưởng đóng thuyền có thể làm được trong một tháng có bảng
phân phối xác suất như sau: X 2 3 4 5 6 7 8 Px 0,2 0,2 0,3 0,1 0,1 0,05 0,05 a)
Tìm xác suất để trong tháng tới xưởng đó sẽ đóng được từ 4 đến 7 con thuyền b)
Tìm hàm phân bố xác suất của X c)
Dùng hàm phân bố xác suất hãy tính xác suất để trong tháng tới xưởng sẽ đóng được không quá 6 con thuyền d)
Số thuyền có khả năng nhiều nhất mà xưởng có thể đóng được trong tháng tới là bao nhiêu? e)
Giả sử việc đóng thuyền có chi phí cố định hàng tháng là 25 triệu đồng và chi phí bổ sung cho mỗi
con thuyền là 5 triệu đồng. Hãy tìm chi phí bình quân hàng tháng của xưởng đó. Giải: a)
X là số lượng thuyền gỗ xưởng đó có thể đóng trong tháng tới
P(4 X 7) 0,3 0,1 0,1 0, 05 0,55 b)
Theo định nghĩa hàm phân bố xác suất F(x) = P(X < x) ta có: 29
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội 0 x 2 0,2 2 x 3 0,4 3 x 4 0,7 4 x 5 F(x)= 0,8 5 x 6 0,9 6 x 7 0,95 7 x 8 1 x 1 c)
Xác suất để trong tháng tới xưởng sẽ đóng được không quá 6 con thuyền:
P( X 6) P( X 7) F (7) 0,9 . d)
Số thuyền có khả năng nhiều nhất mà xưởng đó có thể đóng trong tháng tới là: m0=4 e)
Trung bình mỗi tháng xưởng đó đóng được số thuyền là:
EX 2.0, 2 3.0,3 4.0,3 5.0,1 6.0,1 7.0,05 8.0,05 4,05
Chi phí bình quân hàng tháng là:
25 5EX 25 5.4,05 45, 25 (triệu đồng).
Bài 2.53 Số lượng sản phẩm hỏng mà một công nhân có thể làm ra trong một tháng có bảng phân phối xác suất như sau: Số SP hỏng 0 1 2 3 4 5 6 Xác suất tương ứng 0,01 0,09 0,30 0,20 0,20 0,10 0,10 a)
Tìm xác suất để trong một tháng người công nhân đó làm ra không quá 4 sản phẩm hỏng. b)
Giả sử số sản phẩm mà người công nhân đó phải làm bù bằng bình phương số sản phẩm hỏng mà
người đó đã làm trong tháng. Tìm số sản phẩm phải làm bù bình quân mỗi tháng của người công nhân đó. Giải: a)
X là biến ngẫu nhiên số sản phẩm hỏng, ta có:
P( X 4) 0, 01 0, 09 0,30 0, 20 0, 20 0,80 b)
Số sản phẩm hỏng bình quân mà người công nhân làm bù trong 1 tháng nào đó là X2
Số sản phẩm phải làm bù bình quân mỗi tháng là: 2 2 2 2 2 2 2 2
E( X ) 0 .0, 011 .0, 09 2 .0,3 3 .0, 2 4 .0, 2 5 0 . ,1 6 0 . ,1 12,39 . 30
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.54 Số lượng xe ô tô TOYOTA mà một đại lý bán được trong một tuần có bảng phân phối xác suất như sau: Số xe bán được 0 1 2 3 4 5 Xác suất tương ứng 0,1 0,1 0,2 0,2 0,3 0,1 a)
Tìm xác suất để đại lý đó bán được ít nhất 4 xe trong một tuần. b)
Giả sử chi phí cho hoạt động của đại lý bằng căn bậc hai của số xe bán được nhân với 3 triệu. Tìm
chi phí trung bình cho hoạt động của đại lý mỗi tuần.
Giải: a) Xác suất để đại lý đó bán được ít nhất 4 xe trong một tuần là:
P X 4 P X 4 P X 5 0,3 0,1 0, 4 .
b) Chi phí cho hoạt động của đại lý trong một tuần là: Y 3 X .
Chi phí trung bình cho hoạt động của đại lý mỗi tuần là:
E(Y ) 3E( X ) 3.(0.0,11.0,1 2.0, 2 3.0, 2 2.0, 3 5.0,1) 4, 66 triệu.
Bài 2.55 Qua kinh nghiệm, một cửa hàng bán bánh trung thu biết rằng dịp tết trung thu số bánh có thể bán
được có phân phối xác suất như sau:
Số bánh bán được (X) 400 500 600 700 800 900 Xác suất 0,05 0,15 0,41 0,34 0,04 0,01 a)
Tìm trung bình và độ lệch chuẩn của số bánh bán được b)
Nếu cửa hàng đặt mua 600 chiếc thì xác suất bán hết bánh là bao nhiêu, xác suất còn thừa lại là bao nhiêu. c)
Để có thể chắc chắn đến 95% là sẽ đủ bánh bán thì cửa hàng cần đặt mua bao nhiêu chiếc bánh. Giải: a)
E(X)= 400.0.05+500.0,15+600.0,41+700.0,34+800.0,04+900.0,01 = 620 V(X)= 2 400 .0,05+ 2 500 .0,15+ 2 600 .0,41+ 2 700 .0,34+ 2 800 .0,04+ 2 900 .0,01- 2 620 =9000
= V (X ) = 9000 = 94,8683 X b)
Nếu cửa hàng đặt mua 600 chiếc thì xác suất bán hết là:
P(X 600 ) = 1 – P(X 600) 1 - P(X=400) – P(X=500) = 1-0,05-0,15 = 0,8
Xác suất còn thừa lại là:
P(X 600 ) = 1 – P(X 600) = 1 – 0,8 = 0,2 c)
Để chắc chắn tới 95% sẽ đủ bánh bán thì cửa hàng phải đặt mua a cái bánh thỏa mãn
P( X a) 0,95 P( X a 1) 0,95 F (a 1) 0, 95 31
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
mà với 701 x 800 thì F(x) 0,95 F(a 1) , do F(x) là hàm đơn điệu tăng nên
nên ta có a 1 701 a 700 .
Vậy cửa hàng phải đặt ít nhất 700 chiếc bánh.
Bài 2.56 Trong 900000 vé số phát hành có 20 giải 50 triệu, 150 giải 5 triệu và 1600 giải 1 triệu.
Tính số tiền lãi kì vọng của người mua vé số biết giá vé là 5000 đồng.
Giải: Đặt N = 900000.
Gọi X là số tiền lãi, ta có bảng phân phối xác suất của X: X 49995000 4995000 995000 -5000 P 20/N 150/N 1600/N (N-1770)/N Số tiền lãi trung bình: 1 E( X )
(20.49995000 150.4995000 1600.995000 898230.5000) 1 280 . 900000
Bài 2.57 Một nhà kinh doanh muốn đầu tư 10 triệu đồng vào một công ty mà nếu trong năm tới công ty
làm ăn thuận lợi có thể mang lại lãi suất đến 14% còn nếu gặp khó khăn thì lãi suất có thể giảm đến mức
4%. Trong khi đó nếu gửi tiền vào ngân hàng thì lãi suất đảm bảo sau một năm là 8%. Vậy nếu dùng tiền
để đầu tư thì khả năng có lãi hơn gửi ngân hàng là bao nhiêu.
Giải: Gọi X là lãi suất khi đem tiền đầu tư vào công ty.
X là biến ngẫu nhiên liên tục phân phối theo quy luật đều trên đoạn [4;14].
Ta cần tìm xác suất P(X > 8).
Do X phân phối đều trên đoạn [4;14] nên nó có hàm mật độ xác suất dạng 1 /10 x [4;14] f (x) nên 0 x [4;14] 14 1 x 14
Xác suất có lãi hơn gửi ngân hàng là: P X 8 f
xdx dx 0,6 . 10 10 8 8 8
Bài 2.58 Nhu cầu hàng ngày về một loại thực phẩm tươi sống có phân phối xác suất như sau Nhu cầu ( kg) 30 31 32 33 34 35 Xác suất 0,15 0,2 0,35 0,15 0,1 0,05
Mỗi kg thực phẩm mua vào với giá 2,5 ngàn và bán ra với giá 4 ngàn. Nếu bị ế đến cuối ngày thì phải bán
hạ giá còn 1,5 ngàn mới bán hết được. Vậy phải đặt mua hàng ngày bao nhiêu kg thực phẩm để có lãi nhất. 32
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Giải: Gọi số kg thực phẩm mua vào là i
Số kg thực phẩm thị trường cần là X, có bảng phân bố xác suất là: X 30 31 32 33 34 35 P 0,15 0,2 0,35 0,15 0,1 0,05
4X 2,5i 1,5.i X 2,5X i i X
Ta có lợi nhuận thu được: L =
4i 2,5i 1,5i i X
Bảng sau là phân bố xác suất của L đối với từng i (tính bắt đầu từ cột 2 và dòng 3 đến dòng 8): P 0,15 0,2 0,35 0,15 0,1 0,05 E(L) X Lãi trung 30 31 32 33 34 35 i bình 30 45 45 45 45 45 45 45 31 44 46,5 46,5 46,5 46,5 46,5 46,125 32 43 45,5 48 48 48 48 46,75 33 42 44,5 47 49,5 49,5 49,5 46,5 34 41 43,5 46 48,5 51 51 45,875 35 40 42,5 45 47,5 50 52,5 45
Vậy để có lãi nhiều nhất chọn nhập i = 32kg. x e m x x 0
Bài 2.59 Hàm mật độ xác suất của biến ngẫu nhiên liên tục X có dạng: f (x) m! . 0 x 0 Tìm E(X) và V(X).
Giải: Sử dụng hàm Gamma ta có: m x x e dx m! 0
1 m x 1
Ta có: E X 1
xf (x)dx x e dx
(m 1)! m 1 , m! m! 0 m 2 x x e (m 2)!
V X x f (x)dx E(X)2 dx E(X )2 2 2
(m 1) m 1. m! m! 0 33
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.60 Biến ngẫu nhiên liên tục X có hàm phân bố xác suất: 3 0 1 x x x 3 0 F (x) x x 0 . 0 0 x 0 x Tìm E(X) và V(X). 3 3 0x Giải: Ta có: x x 4 0
f (x) F '(x) x . Do đó: 0 x 0 x 3 3 3x 3x 3 0 0 0 . x E X xf x dx x dx . 4 2 x 2x x 2 x 0 0 3 2 3 2 2
2 3x 9x 3x 9x 3 2 2 0 0 0 0 0 . x V X x f x dx E X x dx . 4 x 4 x x 4 4 x 0 0 sinx
x (0, )
Bài 2.61 Biến ngẫu nhiên liên tục của x có hàm mật độ xác suất: f (x) 2
0 x(0, ) a)
Tìm hàm phân bố xác suất F(x) b)
Tìm P(0 X / 4 ) c) Tìm E(X)
Giải: a) Để tìm hàm phân bố xác suất, ta sử dụng tính chất của hàm mật độ xác suất: x F (x) f tdt x
+Với x 0 : F x 0dt 0
+Với 0 x x 0 x sin t 1 F(x)= ( ) t 0 cosx F x f dt dx dt 2 2 0 +Với x x x F(x)= f t 1 dt 0dt
sin tdt 0dt 1 2 34
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội 0 x 0 1
Vậy hàm phân bố xác suất của X có dạng: ( ) cosx F x
0 x . 2
1 x
b) Theo tính chất của hàm phân bố xác suất: P(0 X
) F( ) F 0 1 1 1 2 1 cos 1 cos0 . 4 4 2 4 2 2 4 1 π
c) E(X ) xf xdx x sin xdx . 2 2 0
Bài 2.62 Một công ty cung cấp nguyên vật liệu gửi 5 giấy đòi nợ đến một xí nghiệp yêu cầu thanh toán
tiền cho 5 đợt giao hàng vừa qua với số lượng hàng của các đợt không khác nhau nhiều lắm. Trong số 5
giấy đòi nợ này (mỗi giấy viết riêng cho từng đợt) có 2 giấy ghi sai số tiền phải thanh toán. Do đến hạn
phải trả nợ ngân hàng, công ty yêu cầu xí nghiệp thanh toán ngay cho 3 đợt bất kì trong 5 đợt giao hàng
ngày. Kế toán viên của xí nghiệp lấy ngẫu nhiên cùng một lúc ra 3 giấy để kiểm tra và làm các phiếu chi.
Tính xác suất để trong 3 giấy lấy ra đó có ít nhất một giấy ghi sai số tiền phải thanh toán.
Giải: Gọi A là biến cố trong 3 giấy lấy ra có ít nhất một giấy ghi sai.
A là biến cố trong 3 giấy lấy ra không có giấy nào ghi sai. P( )
A 1 P( A) .
Gọi Ak là giấy lấy ra thứ k bị sai (k=1,2,3). 3 2 1 Ta có A nên P( )
A P(A A A ) P( A )P( A | A )P( A | A A ) . . 0,1. 1 A 2 A 3 A 1 2 3 1 2 1 3 2 3 5 4 3 P( )
A 1 P( A) 0, 9 .
Vậy xác suất để trong 3 giấy lấy ra có ít nhất một giấy ghi sai số tiền thanh toán là 0,9.
Bài 2.63 Xí nghiệp và công ty nói ở bài trên thỏa thuận với nhau nếu kế toán viên của xí nghiệp phát hiện
thấy có giấy đòi nợ nào trong số 3 tờ giấy được lấy ra mà ghi sai số tiền thì xí nghiệp có quyền hoãn trả số
nợ của đợt giao hàng đó. Mỗi giấy hoãn trả sẽ làm thiệt cho công ty khoảng 5 triệu đồng do phải trả lãi nợ quá hạn cho ngân hàng.
Hãy xác định số tiền thiệt hại trung bình có thể xảy ra đối với công ty do phải trả lãi nợ quá hạn.
Giải: Gọi X là số giấy ghi sai trong 3 giấy rút ra: X=0;1;2.
Gọi các biến cố như bài 2.62.
P X 0 P(A) 0,1. 35
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
P X 2 P(A A A A A A A A A ) 1 2 3 1 2 3 1 2 3
P(A )P(A | A )P(A | A A ) P(A )P(A | A )P(A | A A ) P(A )P(A | A )P(A | A A ) 1 2 1 3 1 2 1 2 1 3 1 2 1 2 1 3 1 2 2 1 2 3 1 3 2 1
. .1 . . . . 0,3 . 5 4 5 4 3 5 4 3 P X
1 1 0,1 0,3 0,6 . X 0 1 2 P 0,1 0,6 0,3
E X = 0.0,11.0, 6 2.0,3 1, 2
Số tiền thiệt hại trung bình có thể xảy ra đối với công ty do phải trả nợ quá hạn:
E 5X 5E X 5.1, 2 6 (triệu đồng).
Bài 2.64 Tuổi thọ (tính theo giờ) của 1 loại van điện lắp trong một thiết bị là biến ngẫu nhiên có hàm mật 0 x 100
độ xác suất như sau: f (x) . 2 1 00 / x x 100
Tìm xác suất để có 2 trong số 5 van điện này bị thay thế trong 150h hoạt động đầu tiên biết rằng việc
hỏng của các van điện là độc lập với nhau.
Giải: Gọi X là biến ngẫu nhiên tuổi thọ của một van điện. Xác suất để 1 van điện bất kì bị hỏng trong 150 150 150 100 100 1
150h hoạt động đầu tiên là: P X 150 f x dx dx . 2 x x 3 100 100 1 2
Gọi A là biến cố “Van điện hỏng trong 150h hoạt động đầu tiên”: P( ) A ; P(A) . 3 3
Coi sự hoạt động của mỗi van điện là một phép thử, ta có 5 phép thử độc lập. Theo công thức Bernoulli,
xác suất để 2 trong 5 van điện phải thay thế trong 150h hoạt động đầu tiên là: 2 3 P 2 1 2 2 C . . 0,3292 . 5 5 3 3
Bài 2.65 Tuổi thọ (tính theo giờ) của một trò chơi điện tử bấm tay là một biến ngẫu nhiên có hàm mật độ x/100 ke x 0
xác suất như sau: f (x)
, trong đó k là hằng số. Tính xác suất. 0 x 0 a)
Tuổi thọ của trò chơi này nằm trong khoảng từ 50 đến 150 giờ b)
Tuổi thọ của trò chơi này ít hơn 100 giờ. 36
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Giải: Để f (x) là hàm mật độ thì k 0 và f x x/100 x/100 dx ke dx 1 00ke 100k 1 0 0 1 k . 100 150 150 1 150 a)
P 50 X 150 f x x/100 x/100 1 /2 3/2 dx e dx e e e 0,3834 . 100 50 50 50 100 100 100 1 100 b)
P X 100 f xdx f x x/100 x/100 1 dx e dx e 1 e 0,6321 . 100 0 0 0
Bài 2.66 Tùy theo tình hình kinh tế trong nước mà trong năm tới một công ty thu được mức lãi (tính theo
triệu đơn vị tiền tệ của nước này) khi đầu tư vào hai ngành A và B sẽ như sau:
Tình hình kinh tế Kém phát triển Ổn định Phát triển Mức lãi Ngành A 20 80 120 Ngành B -30 100 140
Theo dự báo thì xác suất để nền kinh tế của nước đang xét trong năm tới sẽ rơi vào các tình trạng
tương ứng trên là 0,3; 0,5 và 0,2.
Vậy công ty nên đầu tư vào ngành nào để cho:
a) Mức lãi kỳ vọng là cao hơn.
b) Độ rủi ro (phương sai của mức lãi) là ít hơn?
Giải: Gọi X , X là biến ngẫu nhiên lãi thu được của công ty nếu đầu tư vào ngành A, ngành B tương A B ứng.
a) Nếu đầu tư vào ngành A thì mức lãi kỳ vọng là:
E( X ) 0,3.20 0,5.80 0, 2.120 70 (triệu). A
Nếu đầu tư vào ngành B thì mức lãi kỳ vọng là:
E( X ) 0,3.( 30)
0,5.100 0, 2.140 69 (triệu) B
Như vậy, đầu tư vào ngành A sẽ có mức lãi kỳ vọng cao hơn.
b) Mức độ rủi ro khi đầu tư vào ngành A là: 2 2 2 2
V ( X ) 0, 3.20 0, 5.80 0, 2.120 70 1300 . A
Mức độ rủi ro khi đầu tư vào ngành B là: 2 2 2 2
V ( X ) 0, 3.(30) 0, 5.100 0, 2.140 69 4429 . B
Như vậy, độ rủi ro của ngành A ít hơn. 37
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.67 Trong một cuộc thi, người ta có hai hình thức sau:
Hình thức thứ nhất là mỗi người phải trả lời hai câu hỏi, mỗi câu trả lời đúng được 5 điểm.
Hình thức thứ hai là nếu trả lời đúng câu thứ nhất mới được trả lời câu thứ hai, nếu không thì
dừng. Trả lời đúng câu thứ nhất được 5 điểm, trả lời đúng câu thứ hai được 10 điểm.
Trong cả hai hình thức thi, các câu trả lời sai đều không được điểm. Giả sử xác suất trả lời đúng mỗi câu
đều là 0,75, việc trả lời mỗi câu là độc lập với nhau.
Theo bạn nên chọn hình thức nào để số điểm trung bình đạt được nhiều hơn?
Giải: * Nếu chọn hình thức 1: Gọi X1 là số điểm có thể đạt được, X1 nhận các giá trị thuộc {0;5;10}
P(X1 = 0) = 0,25.0,25 = 0,0625 (hai câu đều sai)
P(X1 = 10) = 0,75.0,75 = 0,5625 (hai câu đều đúng)
P(X1 = 5) = 1- 0,0625 – 0,5625 = 0,375 (một câu đúng, một câu sai)
E(X1) = 0.0,0625 + 5.0,375 + 10.0,5625 = 7,5
* Nếu chọn hình thức 2: Gọi X2 là số điểm có thể đạt được, X2 nhận các giá trị thuộc {0;5;15}
P(X2 = 0) = 0,25 (sai câu thứ nhất)
P(X2 = 5) = 0,75.0,25 = 0,1875 (đúng câu thứ nhất và sai câu thứ 2)
P(X2 = 15) = 0,75.0,75 = 0,5625 (đúng cả hai câu)
E(X2) = 0.0,25 + 5.0,1875 + 15.0,5625 = 9,375 Ta thấy E(X2) > E(X1)
Vậy nên chọn hình thức 2 để số điểm đạt được trung bình cao hơn.
Bài 2.68 Chủ một cửa hàng sửa chữa điện dân dụng thuê 5 chữa điện dân dụng thuê 5 thợ sửa chữa điện
làm việc 40 giờ một tuần với lương là 800 ngàn/tuần. Để xét xem có cần thuê thêm một thợ nữa không,
ông chủ đã khảo sát nhu cầu X và thu được các số như sau: Nhu cầu X Xác suất 180 - 190 0,03 190 - 200 0,09 200 - 210 0,12 210 - 220 0,15 220 - 230 0,22 230 - 240 0,21 240 - 250 0,13 250 - 260 0,05
Nếu mỗi giờ sửa chữa chủ nhà hàng thu được 30 ngàn thì có nên thuê thêm 1 công nhân nữa không nếu: 38
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội a)
Năm người công nhân cũ chỉ đồng ý làm đúng 40 giờ/tuần. b)
Năm người công nhân cũ đồng ý làm thêm tối đa mỗi người 5 giờ mỗi tuần với tiền công là 25 ngàn/giờ làm thêm.
Giải: Ta coi nhu cầu X là Nhu cầu X (giờ) Xác suất P(x) 185 0,03 195 0,09 205 0,12 215 0,15 225 0,22 235 0,21 245 0,13 255 0,05
a) Có 5 người công nhân cũ chỉ đồng ý làm 40h/tuần, lương phải trả là: 800.5=4000 (ngàn)
* Nếu không thuê thêm công nhân: Gọi Y là lợi nhuận thu được, ta có Y= 30X – 4000
Số giờ tối đa mà cửa hàng đáp ứng được là: 5.40 = 200 (giờ)
Khi đó ta có bảng phân phối xác suất của Y như sau: X 185 195 200 Y 1550 1850 2000 P(Y) 0,03 0,09 0,88
E(Y) = 1550.0,03 + 1850.0,09 + 2000.0,88 = 1973 (nghìn)
* Nếu thuê thêm công nhân, gọi Z là lợi nhuận thu được Z= 30X- 6.800= 30X – 4800.
Số giờ tối đa cửa hàng đáp ứng được: 6.40 = 240 (giờ)
Có bảng phân phối xác suất: X 185 195 205 215 225 235 240 Z 750 1050 1350 1650 1950 2250 2400 P(Z) 0,03 0,09 0,12 0,15 0,22 0,21 0,18
E(Z) = 750.0,03 + 1050.0,09 + 1350.0,12 + 1650.0,15 + 1950.0,22 + 2250.0,21 + 2400.0,18= 1860(nghìn).
Ta thấy E(Y ) E(Z ) do đó không nên thuê thêm người. 39
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
b) * Nếu không thuê người, gọi T là lợi nhuận 3
0X 4000 X 200 T 3 0X 4000 25.
X 200 5X 1000 X 200
Trong đó X là số giờ theo nhu cầu, 4000 (nghìn) là lương ứng với 5 công nhân, (X-200) là số giờ làm
thêm phải trả 25 nghìn/giờ.
Số giờ tối đa của cửa hàng đáp ứng được: 5.45 = 225 (giờ).
Bảng phân phối xác suất: X 185 195 205 215 225 T 1550 1850 2025 2075 2125 P(T) 0,03 0,09 0,12 0,15 0,61
E(T) = 0,03.1550 + 0,09.1850 + 0,12.2025 + 0,15.2075+ 0,61.2125 = 2063,5 (ngàn)
* Khi thuê thêm 1 người công nhân: 30.
X 6.800 30.X 4800 X 240 S 30.X
6.800 25.(X 6.40) 5.X 1200 X 240
Vì 5 công nhân cũ đồng ý làm thêm giờ nên số giờ tối đa mà cửa hàng có thể đáp ứng là: Xmax = 6.40 + 5.5 = 265 (giờ)
Nhưng theo khảo sát, nhu cầu X chỉ lên tối đa tới 260.
Ta có bảng phân phối xác suất S: X 185 195 205 215 225 235 245 255 S 750 1050 1350 1650 1950 2250 2425 2475 P(S) 0,03 0,09 0,12 0,15 0,22 0,21 0,13 0,05
E(S) = 0,03.750 + 0,09.1050 +0,12.1350 + 0,15.1650 + 0,22.1950 + 0,21.2250 + 0,13.2425 + 0,05.2475 = 1867 (ngàn )
Vì E(T) > E(S) nên chủ cửa hàng không nên thuê thêm 1 công nhân 40
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Bài 2.69 Biến ngẫu nhiên X có hàm mật độ xác suất 1
x ( a;a) 2 _ 2
F (x) a x .
0 x( ;aa) Tìm E(X). a Giải: ( ) x x E X dx dx 3 2 3 2 a x a a x a a Đặt u u x u
ta có E(X ) d (u)
du E( X ) . 3 2 3 2 a a u a a u Vậy E(X)= 0.
Bài 2.70 Biến ngẫu nhiên X có hàm phân bố xác suất: 0 x 2 1 1 1 ( ) sin ( x F x
) 2 x 2 . 2 2 1 x 2 a) Tìm P(-1 < X < 1).
b) Tìm hàm mật độ xác suất f (x) . 1 1 1 1 1 1 1 1
Giải: a) Ta có: P 1 X 1 F 1 F 1 1 1 ( sin sin . 2 2 2 2 6 6 3
b) Hàm mật độ xác suất của f (x) là: 1 x 2;2
f (x) F ' x 2
4 x . 0 x 2;2
Bài 2.71* Biến ngẫu nhiên X có hàm mật độ xác suất: 2 kx f x a x e
(k 0;0 x ) a) Tìm hệ số a.
b) Tìm hàm số phân bố xác suất F(x).
Giải: a) Để f (x) là hàm mật độ thì a 0 và 2 kx 2 1 ( ) . kx f x dx ax e dx a x e dx 0 0 0 Xét 2 kx I x e dx 0 41
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội du 2 2 x xdx Đặ u t: kx . Do đó e kx e dx dv v kx e dx k kx kx e e 2 kx 2 2 I x .
.2xdx xe dx .J k 0 k k k 0 0 du dx x u Đặ t: kx . Do đó kx e dx dv v e kx e dx k kx kx kx e e e 1 J . x dx . 2 2 k 0 k k 0 k 0 3 2 Suy ra k I a . 3 k 2
b) Áp dụng công thức tích phân từng phần: 3 2 2 x x x x 2 x k 2 k k k kt 2 kt 2 kt kt 2
F (x) f (t)dt t e dt t de t e e dt 2 2 2 2 0 0 0 0 0 2 x 2 x 2 x k 2 x k k kx 2 kt 2 kx kt 2 kx kt kt x e k te dt x e k tde x e kte k e dt 0 2 2 2 0 0 0 2 2 2 2 k 2 x k k x kx kx kx kt 2 kx kx x k x k 2 2 x e kxe e x e
kxe e 1 1 e . . 0 2 2 2
Bài 2.72 Một ô tô khách chạy trên đoạn đường AB khoảng cách L theo nguyên tắc dừng bánh ở bất kì
chỗ nào khách có yêu cầu. Biết rằng trên quãng đường đó đã có 1 khách lên xe và sau đó 1 đoạn đường đã
xuống xe. Mật độ xác suất của việc lên xe ở điểm x (0 ≤ x ≤ L) tỉ lệ với giá trị x(L – x)2 còn mật độ xác
suất của việc xuống xe tại điểm y với điều kiện là khách đã lên xe tại điểm x (x ≤ y < L) tỉ lệ với giái trị (y
- x)h, h ≥ 0. Tìm xác suất để: a)
Khách lên xe trước điểm Z b)
Khách đã lên xe ở điểm x, sẽ xuống xe sau điểm Z
Giải: a) Gọi X là vị trí khách lên xe, X là một biến ngẫu nhiên.
Ta có hàm mật độ xác suất của việc lên xe: 2
ax(L x) x (0; L) f (x) 0 x (0; L)
Vì X là biến ngẫu nhiên liên tục nên a 0 và 42
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội L L 1 f
xdx ax
L x2 dx 2 2 3
axL 2Lax ax dx 0 0 4 4 4 4 aL 2aL aL aL 12 a 4 2 3 4 12 L
Xác suất để khách lên xe trước điểm Z là: Z Z 2 2 3 4
12 2 12 L Z 2 ( Z Z P X Z F Z f x dx x L x dx ) 4 4 L L 2 3 4 0 0 2 2 3 4 2 6Z L 8Z L 3 Z Z 2 2
(6L 8LZ 3Z ) . 4 4 4 4 L L L L
b) Gọi Y là vị trí khách xuống xe sau khi đã lên xe ở điểm x, Y là biến ngẫu nhiên
Ta có hàm mật độ xác suất của việc xuống xe sau khi đã lên xe ở điểm x: ( )h b y x y ( ; x L) g( y) . 0 y ( ; x L) L h 1 h (L x) h 1
Vì Y là biến ngẫu nhiên liên tục nên b 0 và 1 g
ydy by x dy b b h 1 h 1 (L x) x
Xác suất để khách xuống xe trước điểm Z sau khi đã lên xe ở điểm x là: Z h 1 h 1 h 1 h h 1 (Z x) Z x P Y Z F Y y x dy h 1 h 1 (L x) (L x) h 1 L x x
Vậy xác suất để khách xuống xe sau điểm Z sau khi lên xe ở điểm x là: h 1
1 1 Z x P Y Z P Y Z . L x
Bài 2.73 Trong lô xổ số phát hành có m1 giải giá trị k1,..., mn giải giá trị kn. Tổng số có N vé. Vậy phải
quy định giá vé là bao nhiêu để giải thưởng trung bình cho mỗi vé chỉ bằng nửa giá vé?
Giải: Gọi a là giá vé cần quy định để giải thưởng trung bình cho mỗi vé chỉ bằng nửa giá vé. n
Tổng giải thưởng là: m k i i i 1 n m k a 2 n m k
Theo giả thiết bài ra, ta có: 1 i i 1 i i i i a . N 2 N
Bài 2.74* Một khẩu súng được dùng để bắn thử với cùng một loại đạn. Xác suất trúng đích của mỗi viên
đạn là p . Phép thử kết thúc khi viên đạn đầu tiên trúng đích. Gọi Y là số viên đạn cần bắn (số lần bắn không hạn định). 43
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội a)
Viết quy luật phân phối xác suất của Y . b)
Tìm hàm phân bố xác suất của Y .
Giải: a) Ta tìm xác suất để Y nhận giá trị k : P(Y k) .
Gọi q là xác suất để viên đạn không trúng đích: q 1 p .
Ta phải bắn k viên trong đó k 1 viên đầu không trúng đích và viên cuối trúng đích. Do đó 1 ( ) . ..... . k P Y k q q q p pq .
Vậy Y có bảng phân phối xác suất như sau: Y 1 2 3 …. k … P p pq 2 pq … k 1 pq …
b) Từ bảng phân phối xác của Y ta có hàm phân bố xác suất của Y 0 y 1 p 1 y 2
p(1 q) 2 y 3 F( y) . .. 1 k q p k
y k 1 1 q ...
Bài 2.75 Trong bình có a quả cầu trắng và b quả cầu đen. Một người lấy lần lượt từng quả cầu theo
phương thức có hoàn lại cho đến khí lấy được cầu trắng. Tìm kỳ vọng toán và phương sai của số cầu đen được lấy ra.
Giải: Gọi X là biến ngẫu nhiên số cầu đen được lấy ra. Các giá trị của X là 0, 1,...
Ta đi tìm P(X n) n 0 .
Với mỗi lần lấy thì xác suất lấy được quả cầu trắng là a p
, xác suất lấy được quả cầu đen là a b b q . a b
Nếu X n thì có nghĩa ta lấy được n quả đen liên tiếp và 1 quả cầu trắng cuối cùng, do đó n n
P( X n) . q . q .... . a b ab n q p pq . n 1
a b a b (a b)
Quy luật phân phối xác suất của số cầu đen được lấy ra là: X 0 1 ... n ... P p pq ... n pq ... 44
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội Do đó: E(X ) n n npq p nq n0 n 1 n 1 1 Ta có q n q
. Lấy đạo hàm cả hai vế theo q ta được: 1 nq . 2 2 q q p n (1 ) n 1 1 1 Nhân cả 2 vế với q q được: n nq . 2 p n 1 Từ đó E(X ) q q b p . 2 p p a 2 2 n 2 n 2 E( X ) n n pq n pq p n q n0 n 1 n 1 Từ kết quả q n nq 2 q n (1 ) 1 q q n 1 1
Lấy đạo hàm hai vế theo q ta được: 2 1 n q 3 3 q p n (1 ) 1 q q n (1 )
Nhân cả 2 vế với q ta được: 2 n q 3 p n 1 2 2 q(1 q) q(1 q) E( X ) n p n q p . Do đó 3 2 p p n 1 2 2 2 (1 ) b(a ) ( ) ( ) ( ) q q q q b V X E X E X . 2 2 2 2 p p p a
Bài 2.76 Tìm kì vọng toán và phương sai của số sản phẩm được sản xuất ra giữa hai lần sửa chữa của một
máy nếu xác suất làm ra phế phẩm của máy đó bằng p và máy sẽ được sửa chữa khi làm ra k phế phẩm.
Giải: Gọi X là biến ngẫu nhiên số sản phẩm sản xuất ra giữa hai lần sửa chữa của một máy.
Ta chia việc sản xuất sản phẩm giữa 2 lần sửa chữa của một máy thành k giai đoạn.
Giai đoạn 1 là bắt đầu tới sản phẩm phế phẩm đầu tiên được tạo ra.
Giai đoạn 2 là tiếp theo tới khi sản phẩm phế phẩm thứ 2 được tạo ra. ...
Giai đoạn k là tiếp theo tới khi sản phẩm phế phẩm thứ k được tạo ra.
Gọi X là số sản phẩm của giai đoạn i. Có nghĩa là có X 1 chính phẩm và 1 phế phẩm được tạo ra. i i
X X X ...
là tổng k biến ngẫu nhiên độc lập. 1 2 X k
Đặt q 1 p là xác suất làm ra 1 chính phẩm của máy. 45
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com) lOMoARcPSD|36340008 TS. Nguyễn Văn Minh
ĐH Ngoại Thương Hà nội
Mỗi biến ngẫu nhiên X có bảng phân phối xác suất như sau: i X 1 2 ... n ... i P p pq ... n 1 pq ... 1 p p E( X ) n n npq nq và 2 2 n 1 2 E( X ) n n pq n q i i q q n 1 n 1 n 1 n 1 p p q p p q(1 q) 1 q n 1
theo bài 2.75 ta có E(X ) nq và 2 2 E( X ) n n q i 2 q i 3 2 q p p q q p p n 1 n 1 2 1 q 1 V ( X ) q . i 2 2 2 p p p
Do đó ( ) ( ) E(X ) ... E(X ) k E X E X 1 2 k p q k (1 p)
và V (X ) V (X ) V (X ) ...V (X ) . 1 2 k k 2 2 p p 46
Downloaded by Di?u H?ng (nguyendieuhang45@gmail.com)




