Giải bài tập Môn Công nghệ kỹ thuật điện tử - viễn thông | Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
CHAPTER 1 – 2 – 3 – 4 :ỨNG SUẤT VÀ BIẾN DẠNG lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
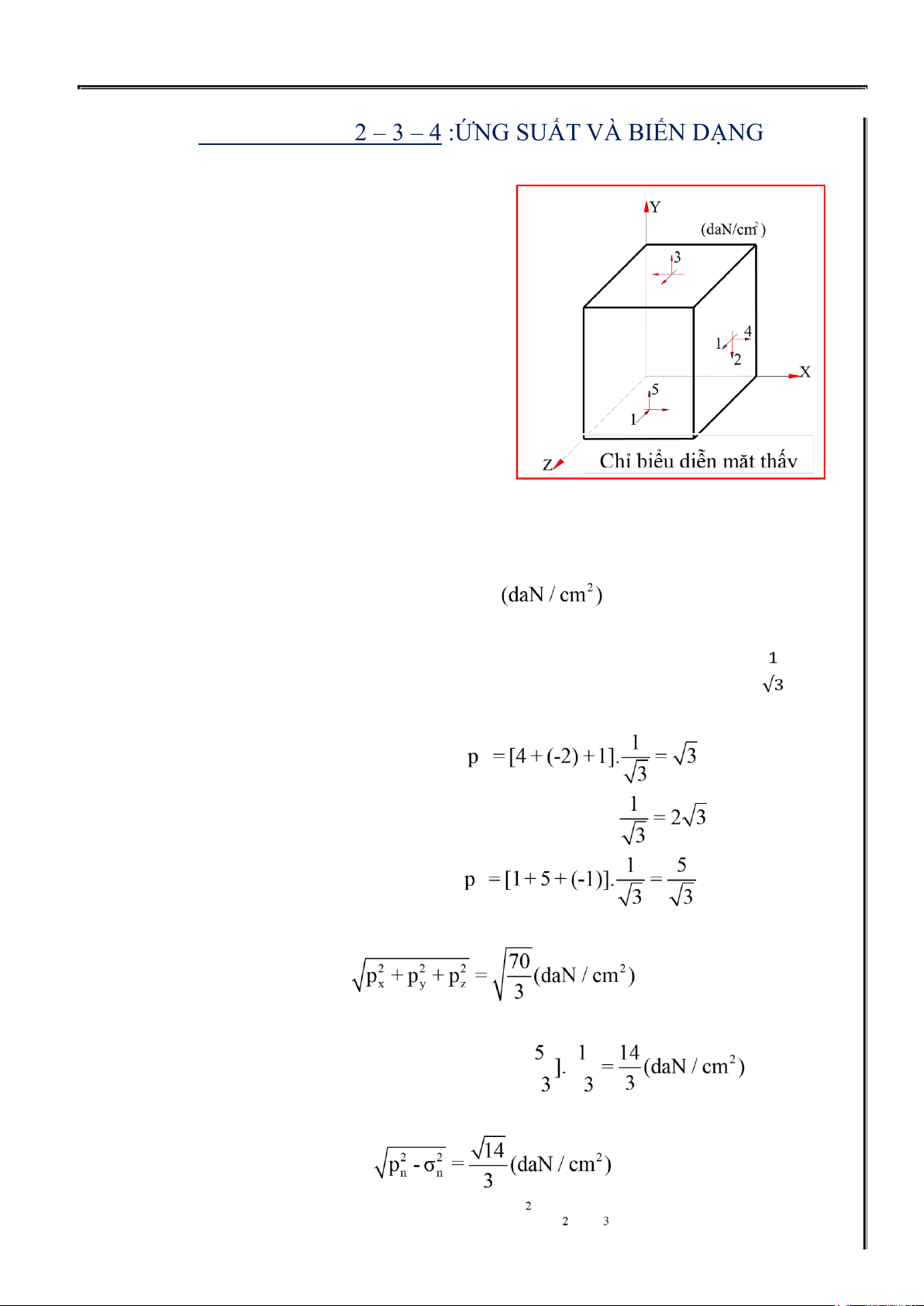
Bài 1:Cho phân tố chịu lực như hình vẽ 1.Lập tenxơ ứng suất ?
2.Tính ứng suất trên mặt nghiêng đều với 3 trục tọa độ ?
3.Tính các thành phần ứng suất chính và xác
định phương chính thứ nhất ?
4.Lập tenxơ cầu và tenxơ ứng suất lệch ? Giải: 1.Từ phân tố ta có
σx = 4,σy = 3,σz = -1,τyz = τzy = 5
τxy = τyx = -2,τxz = τzx =1(daN / cm2)
Ta lập được tenxơ ứng suất sau 4 -2 1 Tσ = -2 3 5 1 5 -1
2.Ta có mặt phẳng nghiêng đều với 3 trục tọa độ là mặt phẳng có l = m = n =
Ta có thành phần ứng suất theo 3 phương
px = σx.l + τyx.m + τzx.n x py = τxy.l + σy.m + τzy.n py =[(-2) +3+5]. pz = τxz.l + τyz.m + σz.n z
→ Ứng suất toàn phần trên mặt phẳng nghiêng pn =
Ứng suất pháp trên mặt nghiêng
σn = px.l + py.m + pz.n =[ 3 + 2 3 +
Ứng suất tiếp trên mặt phẳng nghiêng lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY τn =
3.Ứng suất chính là nghiệm phương trình σ3 - I1σ + I σ - I = 0 Trong đó
I1 = σx + σy + σz = 4 +3+(-1) = 6 (daN / cm2) + +
σx τyxσy τzyσz τxz2 + τ2yz + τzx2 ) I2 =τxy σyτyz σzτzx
σx= σx.σy + σy.σz + σz.σx -(τxy
=12-3-4-(4 + 25+1) = -25 (daN2 / cm4 ) σx τyx τzx I3 =τxy σy
τzy= 4.3.(-1) + 2.[5.1.(-2)]-3.12 -4.52 -(-1).(-2)2 = -131(daN3 / cm6 ) τxz τyz σz
Thay vào phương trình ta có σ3 -6σ2 -25σ +131= 0 σ1 = 6,86 (daN / cm2) 2 ) σ2 = 3,96 (daN / cm σ3 = -4,82 (daN / cm2)
Phương chính thứ nhất là nghiệm của hệ
τxy.l1 +(σy -σ1).m1+τzy.n1 = 0
(-2).l1 + (3-6,86).m1+5.n1 = 0 1.l1 +5.m1 +(-1-6,86).n1 = 0
τxz.l1 + τyz.m1 + (σz -σ1).n1 = 0 l2 + m12 + n12 =1 l12 + m12 + n12 =1 1 -2.l1 -3,86.m1+5.n1 = 0 n1 = 0,573.m1 n1 = 0,573.m1 1.l1 +5.m1 -7,86.n1 = 0 l1 = -0,496.m1 l1 = -0,496.m1 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY l12 + m12 + n12 =1 l12 + m12 + n12 =1 m12 = 0,635 n1 = 0,457 l1 = 0,395 m1 = 0,797 σx +σy +σz 2)
4. Ta có ứng suất pháp trung bình σtb = = = 2 (daN / cm 3 Ta lại có T 0 σ = Tσ + Dσ Trong đó T 0 σ là tenxơ ứng suất cầu 0 0 2 0 0 tb 2 Tσ0 0 tb 0 0 0 0 0 (daN / cm2) 0 tb 2
Dσ là tenxơ ứng suất lệch 0 4 -2 1 2 0 0 4-2 D 0 σ = Tσ Tσ -2 3 5 0 2 0 -2 1 5 -1 0 0 2 1
Bài 2: Cho các thành phần ứng suất
σx = 4,σy = 0,σz = 2,τyz = τxy lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
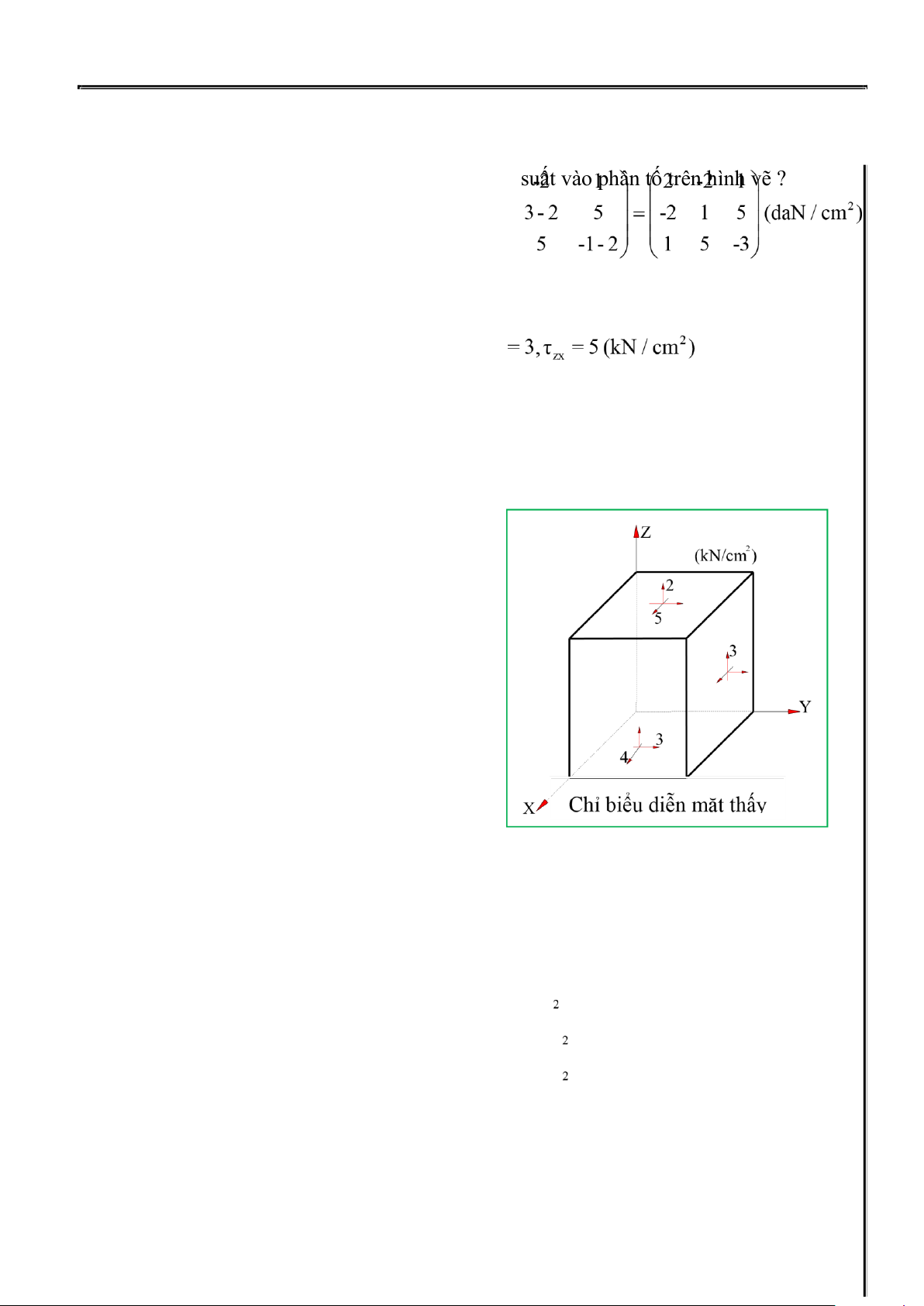
1.Lập tenxơ ứng suất và điền các thành phần ứng suất vào phân tố trên hình vẽ ? lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
3.Phân tố này thuộc trạng thái ứng suất nào ?
2.Xác định các phương chính ? 4.Tính các ứng suất bát diện Giải: 1.Ta có tenxơ ứng suất 4 3 5 Tσ = 30 3 (kN / cm2) 5 3 2
3.Phân tố này thuộc trạng thái ứng suất khối
2.Ta có ứng suất chính là nghiệm của pt σ3 - I1σ2 + I2σ - I3 = 0
Trong đó I1 = 4 + 0 + 2 = 6 (kN/cm2)
I2 = 0 + 0 + 4.2 – (32 + 32 + 52) = -35 (kN2/cm4)
I3 = 0 + 2.3.3.5 – (0 + 4.3.3 + 2.3.3) = 36 (kN3/cm6)
Thay vào ta có σ3 -6σ2 -35σ -36 = 0 σ1 = 9,9 kN / cm σ2 = -1,5 kN / cm σ3 = -2,4 kN / cm
❖ Phương chính 1 là nghiệm của hệ
τxy.l1 +(σy -σ1).m1+τzy.n1 = 0 3.l1 +(0-9,9).m1+3.n1 = 0 5.l1 +3.m1 +(2-9,9).n1 = 0
τxz.l1 + τyz.m1 +(σz -σ1).n1 = 0 l2 + m12 + n12 =1 l12 + m12 + n12 =1 1 3.l1 -9,9.m1+3.n1 = 0 n1 =1,5.m1 n1 =1,5.m1 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY 5.l1 +3.m1 -7,9.n1 = 0 l1 =1,77.m1 l1 =1,77.m1 l12 + m12 + n12 =1 l12 + m12 + n12 =1 m12 = 0,157 n1 = 0,594 l1 = 0,7 m1 = 0,396
❖ Phương chính 2 là nghiệm của hệ
τxy.l2 +(σy -σ2).m 2 +τzy.n2 = 0 3.l2 + (0 +1,5).m 2 +3.n2 = 0 5.l2 +3.m2 + (2 +1,5).n2 = 0
τxz.l2 + τyz.m2 +(σz -σ2).n2 = 0 l2 + m22 + n22 =1 l22 + m22 + n22 =1 2 3.l2 +1,5.m 2 +3.n2 = 0 m2 = 3.n2 m2 = 3.n2 5.l2 +3.m2 +3,5.n2 = 0 l2 = -1,5.n2 l2 = -1,5.n2 l22 + m22 + n22 =1 l12 + m12 + n12 =1 n22 = 0,08 n2 = 0,849 l2 = 0,425 m2 = 0,283
Phương chính 3 là nghiệm của hệ
τxy.l3 + (σy -σ3).m 3+τzy.n3 = 0 3.l3 + (0 + 2,4).m 3+3.n3 = 0
τxz.l3 + τyz.m3 + (σz -σ3).n3 = 0 5.l3 +3.m3 +(2 + 2,4).n3 = 0 l2 + m32 + n32 =1 l32 + m32 + n32 =1 3 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY 3.l3 + 2,4.m 3+3.n3 = 0 m3 = -6.n3 m3 = -6.n3 5.l3 +3.m3 + 4,4.n3 = 0 l3 = 3,8.n3 l3 = 3,8.n3 l32 + m32 + n32 =1 l32 + m32 + n32 =1 n32 = 0,019 n2 = 0,828 l3 = 0,524 m3 = 0,138 4.Ta có ứng
suất toàn phần trên mặt bát diện p2n =32 =
9,92 + (-1,5)2 +(-2,4)2 = 35,34 pn = 5 2 ,9 kN / cm 3 3
Ứng suất pháp bát diện
σ1 + σ2 + σ3 = 9,9-1,5-2,4 = 2 kN / cm2 σbd = 3 3
Ứng suất tiếp bát diện τ 2 2 bd =
pn -σbd = 35,34- 4 = 5,6 kN / cm2
Bài 3: Cho tenxơ ứng suất a 0 0 Tσ = 0 4 -2 (kN / cm2) 0 -2 1
1.Xác định a biết σbd = 2 (kN/cm2) ?
2.Tính các ứng suất chính và phương chính thứ nhất ? Giải:
1.Ta có các bất biến của tenxơ ứng suất I1 = a + 5 kN/cm2
I2 = 4a + 4 + a – (0 + 0 +4) = 5a kN2/cm4 I3 = 0 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
Các ứng suất chính là nghiệm của phương trình σ3 - I1σ2 + I2σ - I3 = 0 Thay số vào ta được
σ3 -(a +5)σ2 +5aσ = 0 σ(σ2 -(a +5)σ +5a) = 0
σ = 0 or σ2 -(a +5)σ +5a = 0 (1)
Giả thiết bài toán ta có đây mà mặt bát diện nên để tồn tại σbd = 2 (kN/cm2) khi chỉ
khi phương trình (1) có 2 nghiệm phân biệt → ∆ = (a +5)2 – 4.5a > 0 ↔ (a -5)2 > 0 luôn đúng
Giả sử phương trình (1) có 2 nghiệmσ1,σ2 theoViet ta có σ1 + σ2 = 5a σ1 + σ2 + σ3 = 5a = 2 a =1,2 Giả thiết σbd = 3 3
Kết luận :Vậy với a = 1,2 thỏa mãn điều kiện bài toán
2.Thay a = 1,2 vào phương trình (1) ta có các ứng suất chính là
σ1 5 kN / cm2,σ2 1,2 kN / cm2,σ3 0 kN / cm2
Phương chính thứ nhất là nghiệm của hệ (σx -σ1).l1 τyx.m1 τzx.n1 (1,2-5).l1 + 0.m1+0.n1 = 0
τxy.l1 + (σy -σ1).m1+τzy.n1 = 0 0.l1 -2.m1 + (1-5).n1 = 0 l12 + m12 + n12 =1 l12 + m12 + n12 =1 l1 0 l1 0 l1 0 -2.m1 -4.n1 = 0 m1 2n1 m1 2n1 l12 + m12 + n12 =1 l12 + m12 + n12 =1 n12 = 0,2 n1 = 0,447 l1 = 0 m1 = 0,894 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
Bài 4: Cho các thành phần ứng suất
12 ql2 qh2 6q 2y + 4q y3;τ = -6q h2 σx = 3 M0 + 8 - 20 y - h3 x h3 xy h3 4 - y2 x h σy = -6h3q y33 - h42 y2 + 12h3 ;τyz = τzx = σz = 0
1.Hãy nghiệm lại phương trình Cauchy xem khi nào thỏa mãn ? 2.Với
điều kiện đó xác định loại trạng thái ứng suất tại điểm M(1,0,-1) ? Giải :
1.Thay các giá trị vào phương trình Cauchy ta có xx yyx zzx 0 0 12 h3q y.x 0 0 0 2 -6q 2 - h2 y 0 0 xy 1 x y z h xyxz yzy zyz 00 0-6 3q0 h4 - y2 h3 y 2 2 x y z
Kết luận :Vậy thành phần ứng suất thỏa mãn phương trình Cauchy khi chỉ khi x 0 1 y 2
2. Với điểm M(1,0,-1) thì ta có x = τyz τzx = σz = 0,τxy = -3q,σy = -q → Đây là trạng lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY 2h 2 thái ứng suất
phẳng (Note ta phải tìm các ứng suất chính trước khi đưa ra kết luận) Bài 5: Cho tenxơ ứng suất sau 1 4 2 Tσ = 4 -1 -2 (daN / cm2) 2 -2 0
1.Xác định các thành phần ứng suất chính ?
2.Lập tenxơ biến dạng tương ứng ? Biết E = 2.104 kN/cm2 = 2.106 daN/cm2,μ = 0,2
3.Tính các biến dạng chính và xác định phương biến dạng chính thứ 2
? 4.Tính độ biến đổi thể tích của phân tố ? Giải:
1. Ta có các bất biến của tenxơ ứng suất I1 = 0 daN/cm2
I2 = -1 –[42 + 22 +(-2)2]= -25 daN2/cm4
I3 = 0 + 2.(-2).2.4 – [ (-1).2.2 +1.(-2).(-2)] = -32 daN3/cm6
Các ứng suất chính là nghiệm của phương trình σ3 - I1σ2 + I2σ - I3 = 0
Thay số vào ta được σ3 -25σ +32 = 0 σ1 = 4,16 daN / cm2 2 σ2 =1,387daN / cm σ3 = -5,547 daN / cm2 2.Ta tính các biến dạng 1 1 -7 εx = E[σx -μ(σy +σz )]= 2.106 [1-0,2.(-1+0)]=6.10 1 1 -7 εy = E[σy -μ(σx +σz )]= 2.106 [-1-0,2.(1+0)]=-6.10 1 1 εz = E[σz -μ(σx + σy )]= 2.106 [0-0,2.(1-1)]=0 E 5 Lại có G = = 8,3.10 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY 2(1+μ) τxy 4 -6 εxy =2G = 2.8,3.105 = 2,4.10 εxz = 2τGxz = 2.8,3.1025 =1,2.10-6
τyz -2 -6 εyz =2G = 2.8,3.105 = - 1,2.10
Ta lập được tenxơ biến dạng sau 6.10-7 2,4.10-6 1,2.10-6 0,6 2,4 1,2 Tε = 2,4.10-6 -6.10-7 -1,2.10-6 2,4 -0,6 -1,2 10-6 1,2.10-6 -1,2.10-6 0 1,2. -1,2 0
3.Ta có biến dạng chính là nghiệm của phương trình ε3 - J1ε2 + J2ε - J3 = 0 Trong đó J1 = εx +εy +εz = 0 εx εyxεy εzyεz εxz + + J2 =εxy εyεyz εzεzx εx
={0,6(-0,6)-[2,42 +1,22 + (-1,2)2]}.10-12 = -9.10-12 εx εyx εzx J3 =εxy εy εzy εxz εyz εz
={2.(-1,2).1,2.2,4-[1,2.1,2.(-0,6) +(-1,2).(-1,2).0,6]}.10-18 = -6,912.10-18
Thay số vào ta có ε3 -9.10-12ε + 6,912.10-18 = 0 ε1 = 2,496.10-6 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY ε2 = 8,32.10-7 ε3 = -3,328.10-6
Phương biến dạng chính thứ 2 là nghiệm của hệ
(εx -ε2).l2 +εyx.m 2 +εzx.n2 = 0
(6-8,32).10-7.l2 + 2,4.10-6.m 2 +1,2.10-6.n2 = 0 εxy
-6.l2 +(-6-8,32).1 0-7.m 2-1,2.10-6.n2 = 0
.l2 + (εy -ε2).m 2 +εzy.n2 = 0 2,4.10 l22 + m22 + n22 =1 l22 + m22 + n22 =1 n2 = -2,036m2 n2 = -2,036m2 l2 = 0,875 l2 = -0,418m2 l2 = -0,418m2 n2 = 0,18 l22 + m22 + n22 =1 m22 = 0,188 m2 = 0,43
4.Độ biến đổi thể tích θ = εx + εy + εz = 0 1 3 0
Bài 6: Cho tenxơ biến dạng sau Tε = 3 -1 4 10-2 0 4 2 1
1.Tính các biến dạng theo phương nghiêng có l = 0,5; n = -0,5; m = 2 ?
2.Tính các biến dạng chính và các phương biến dạng chính
? 3.Lập tenxơ biến dạng cầu và tenxơ biến dạng lệch ? Giải : 1.
εS = l2.εx + m2.εy + n2.εy + τxy.l.m + τyz.m.n + τzx.l.n lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY = 1 2 .1 12 2 .( 1) 21 2 .2 12. 12 .3 12 . 21.4 .10 2 1 4 2 .10 2 2
2.Các biến dạng chính là nghiệm của phương trình ε3 - J1ε2 + J2ε - J3 = 0 Trong đó
J1 = εx + εy + εz = (1-1+ 2).10 2 = 2.10 2 εx + + εyxεy εzyεz εxz J2 =εxy εyεyz εzεzx εx
={1(-1) +(-1).2 + 2.1-[32 +0 + 42]}.10-4 = -26.10-4 εx εyx εzx J3 =εxy εy εzy εxz εyz εz
={1.(-1).2-[4.4.1+3.3.2]}.10-6 = -36.10-6
Thay số vào ta có ε3 -2.10-2ε2 -26.10-4ε +36.10-6 = 0 ε1 = 0,06 ε2 = 0,01 ε3 = -0,05
● Phương biến dạng chính thứ nhất là nghiệm của hệ
(εx -ε1).l1 + εyx.m1+εzx.n1 = 0
(1-6).10-2.l1 +3.10-2.m1+0.n1 = 0
εxy.l1 + (εy -ε1).m1+εzy.n1 = 0
3.10-2.l1 + (-1-6).1 0-2.m1+4.10-2.n1 = 0 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY l2 + m12 + n12 =1 l12 + m12 + n12 =1 1 n1 =1,3m1 n1 =1,3m1 l1 = 0,745 l1 = 0,6m1 l1 = 0,6m1 n1 = 0,344 l 2 2 2 2 1 + m1 + n1 =1 m1 = 0,328 m1 = 0,573
● Phương biến dạng chính thứ 2 là nghiệm của hệ
(εx -ε2 ).l2 + εyx.m 2 +εzx.n2 = 0
(1-1).10-2.l2 +3.10-2.m 2 +0.n2 = 0 εxy 2 y
-2.l2 + (-1-1).1 0-2.m 2 +4.10-2.n2 = 0
.l +(ε -ε2).m 2 +εzy.n2 = 0 3.10 l22 + m22 + n22 =1 l22 + m22 + n22 =1 m2 = 0 m2 = 0 m2 = 0 n2 = -0,75l2 n2 = -0,75l2 n2 = 0,6 l22 + m22 + n22 =1 l22 = 0,64 l2 = 0,8
● Phương biến dạng chính thứ 3 là nghiệm của hệ
(εx -ε3).l3 +εyx.m 3+εzx.n3 = 0 (1+5).10-2.l3 +3.10-2.m 3+0.n3 = 0 εxy.l3 + (εy -ε3).m 3+εzy.n = 0
3.10-2.l3 +(-1+5).1 0-2.m 3+4.10-2.n3 = 0 3 l32 + m32 + n32 =1 l32 + m32 + n32 =1 m3 = -2l3 m3 = -2l3 m3 = 0,78 n3 = -1,25l3 n3 = -1,25l3 n3 = 0,4875 l32 + m32 + n32 =1 l32 = 0,152 l3 = 0,39 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
3.Ta có biến dạng trung bình εx +εy +εz 2.10-2 εtb = = 3 3 Lại có T 0 ε = Tε + Dε (1) Trong đó T 0
ε là tenxơ biến dạng cầu 2 0 3 0 0 Tε0 0 0 10 2 2
Dε là tenxơ biến dạng lệch 0 Từ (1) ta có 3 2 1 0 0 3 0 3 1 0 3 4 3 D 4 10-2 0 2 0 10 2 ε Tε Tε0 = 3 10-2 -1 3 5 3 3 0 4 0 2 4 4 0 2 0 3 3
Bài 7: Một thanh chịu uốn thuần túy có các thành phần biến dạng M M εz = - y;εx = εy = μ y;γxy = γyz = γzx = 0 EJ EJ
1.Các thành phần biến dạng này có thỏa mãn phương trình liên tục không ?
2.Tính các thành phần chuyển vị u, v, w ? Giải: 1.Kiểm tra lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY 2yε2x 2xε2y 0 0 x2γ xyy 0 2zε2y 2yε2z 0 0 2yγ yzz 0 2xε2z 2zε2x 0 0 z2γ zxx 0 2εx 0 γ γ γ 2 y z x yzx zxy xyz 0 2 z2 εxy 0 y γzxy γxyz γyzx 0 2εz 0 γ 2 x y z xyz γyzx γzxy 0
Vậy các thành phần biến dạng thỏa mãn phương trình liên tục
2. Các thành phần chuyển vị là x μ M y u u μ M yx EJ x EJ M v M 2 εy = μ y v μ y EJ y 2EJ M w M εz = - EJ y z w EJ yz lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
Bài 8: Cho các thành phần biến dạng εx = 4.10-2;εy = 0;εz = -
5.10-2;γxy = 4.10-2;γyz = 0;γzx = 6.10-2
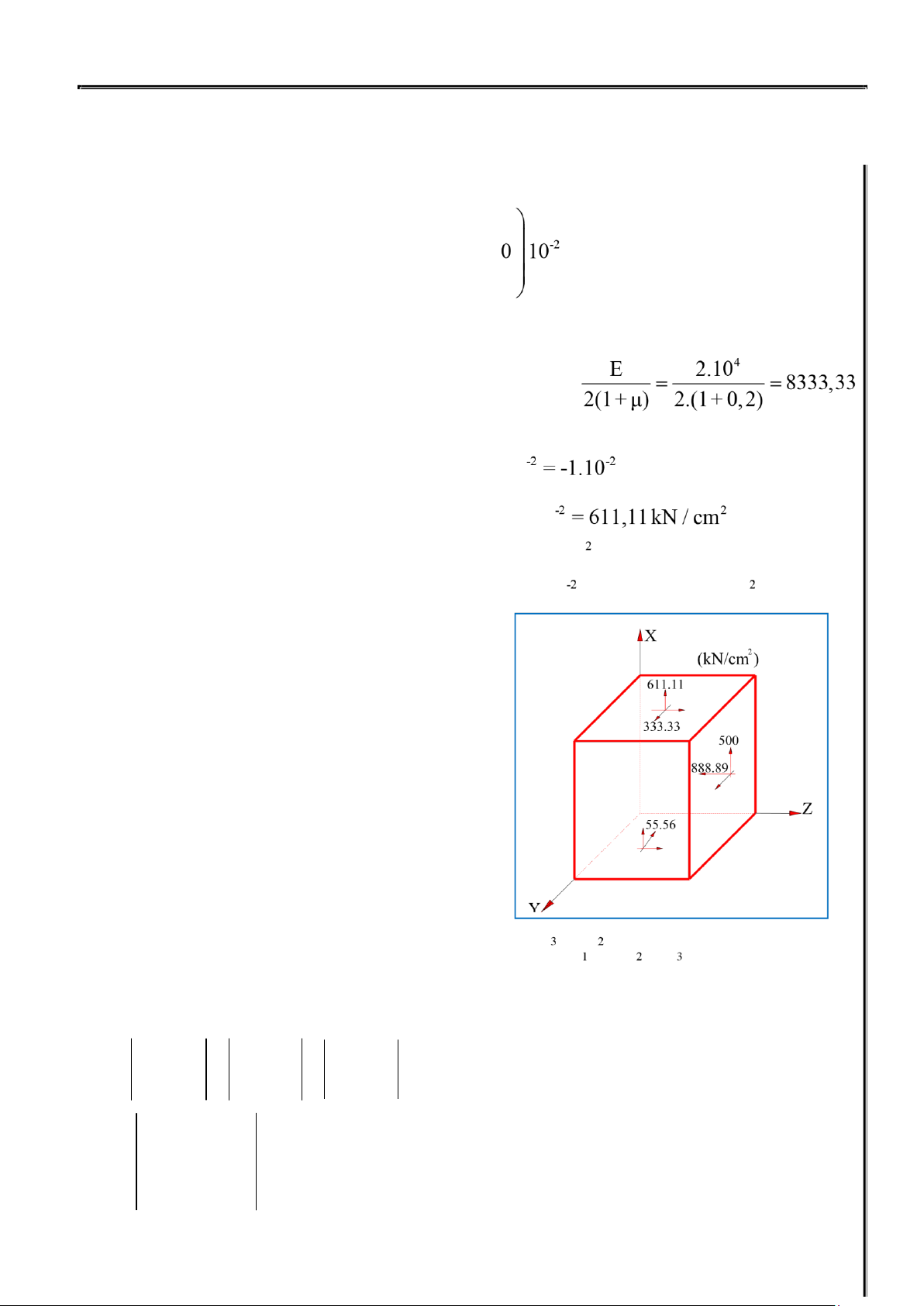
1.Lập tenxơ biến dạng và tenxơ ứng suất tương ứng ,điền các thành phần ứng suất vào phân tố ?
2.Xác định các biến dạng chính và ứng suất chính ?
3.Tính thế năng biến dạng đàn hồi của phân tố ? Biết E = 2.104 kN/cm2 ,μ = 0,2 Giải:
1. Ta có ε = γxy = 4.10-2 = 2.10-2;ε = γyz = 0;ε = γzx = 6.10-2 = 3.10-2 xy yz zx 2 2 2 2 2 lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY
Vậy ta lập được tenxơ biến dạng là + + lOMoAR cPSD| 58675420 NORTH SAINT_AMITABHA ELASTIC THEORY 4 2 3 Tε = 2 0 3 0 -5
Ta có hai hằng số đàn hồi độc lập E.μ 2.104.0,2 λ = = = 5555,56 ;v = G = (1+μ)(1- 2μ) (1+ 0,2)(1-0,4)
Độ biến đổi thể tích θ = εx +εy +εz = (4 +0-5).10 σx = λ.θ + 2.v.εx = 5555,56.(-
1.10-2) + 2.8333,33.4.10 σy = λ.θ + 2.v.εy = 5555,56.(-1.10-2 ) +0 = -55,56 kN
/ cm σz = λ.θ + 2.v.εz = 5555,56.(-1.10-2) + 2.8333,33.(-5.10 ) = -888,89 kN /
cm τxy = v.γxy = 8333,33.4.10-2 = 333,33 kN / cm2 τyz = v.γyz = 0
τzx = v.γzx = 8333,33.6.10-2 = 500 kN / cm2 Vậy ta có tenxơ ứng suất tương ứng sau 611,11 333,33 500 Tσ = 333,33 -55,56 0 (kN / cm2) 500 0 888,89
2.Các biến dạng chính là nghiệm của phương trình ε - J ε + J ε - J = 0 Trong đó
J1 = εx + εy +εz = (4 + 0-5).10 2 = -1.10 2
εx εyxεy εzyεz εxz J2 =εxy εyεyz εzεzx εx
={4.(-5)-[22 +32]}.10-4 = -33.10-4 εx εyx εzx