












































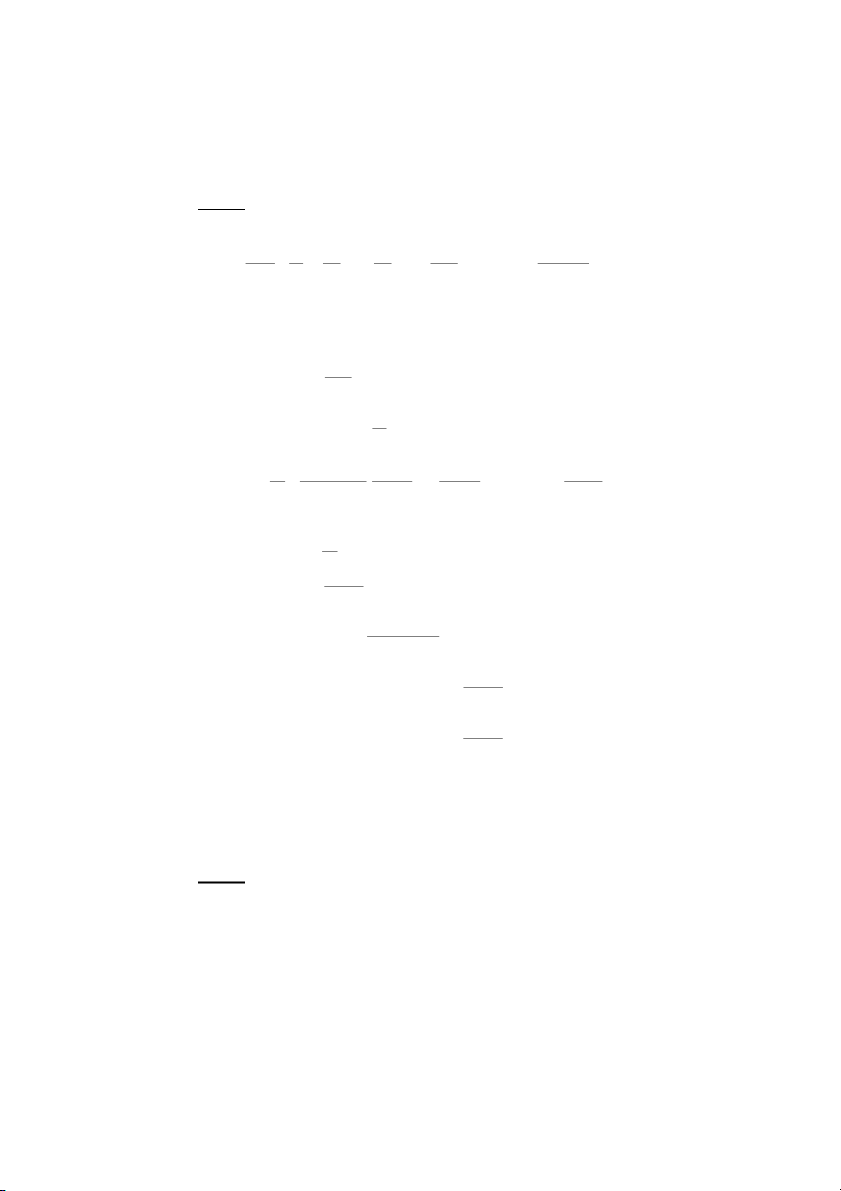

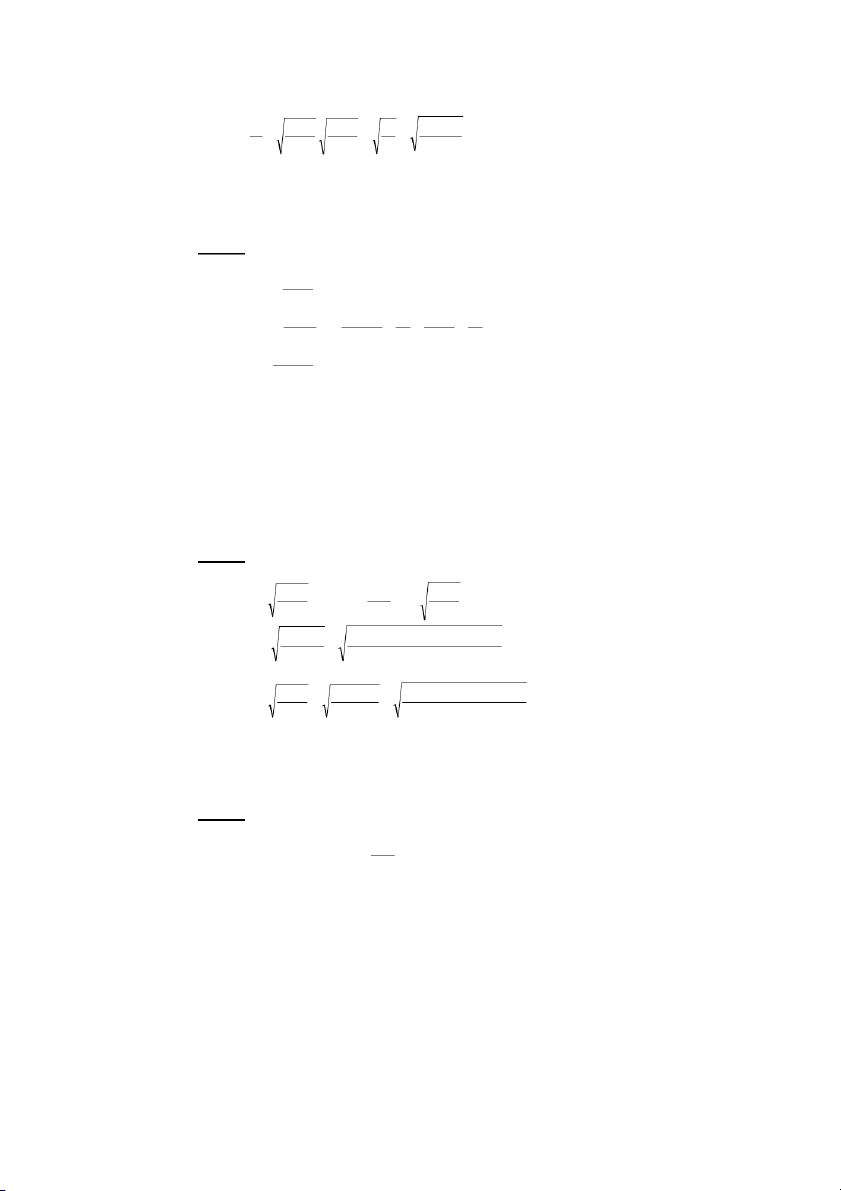






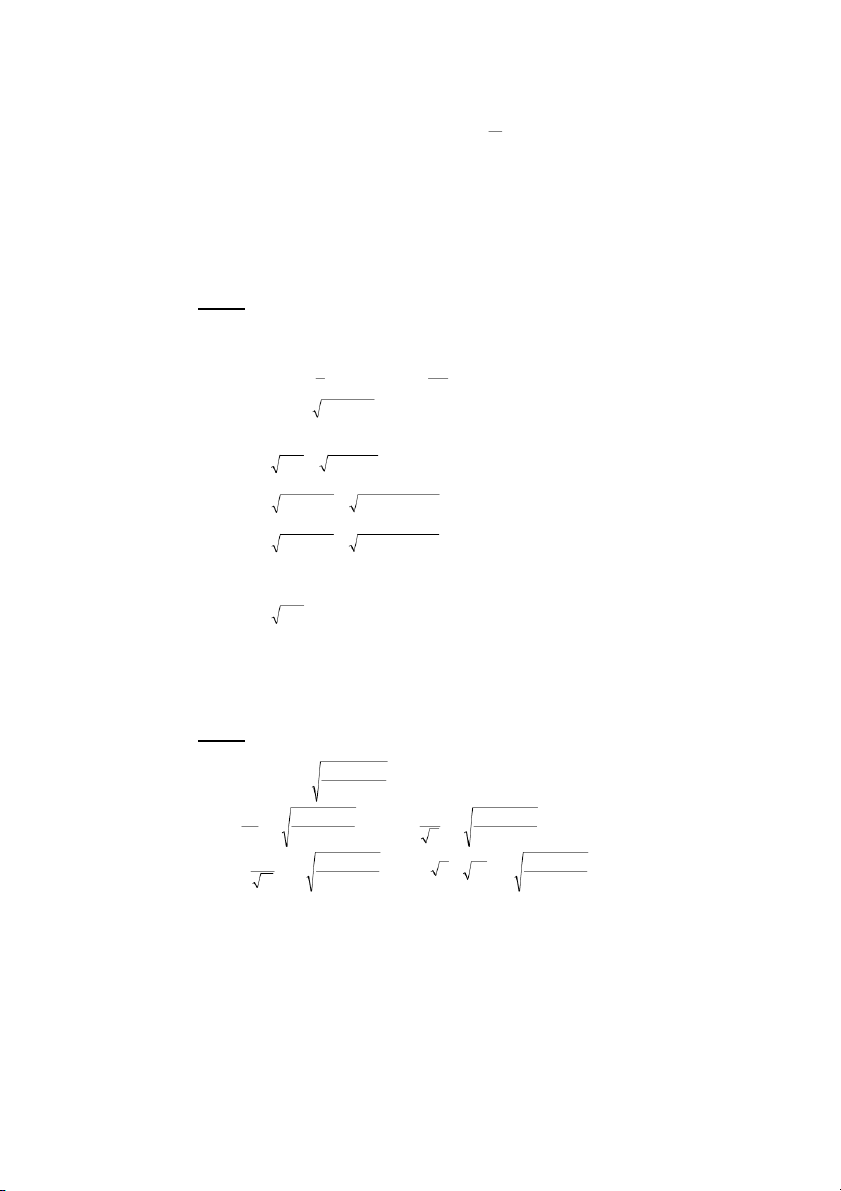


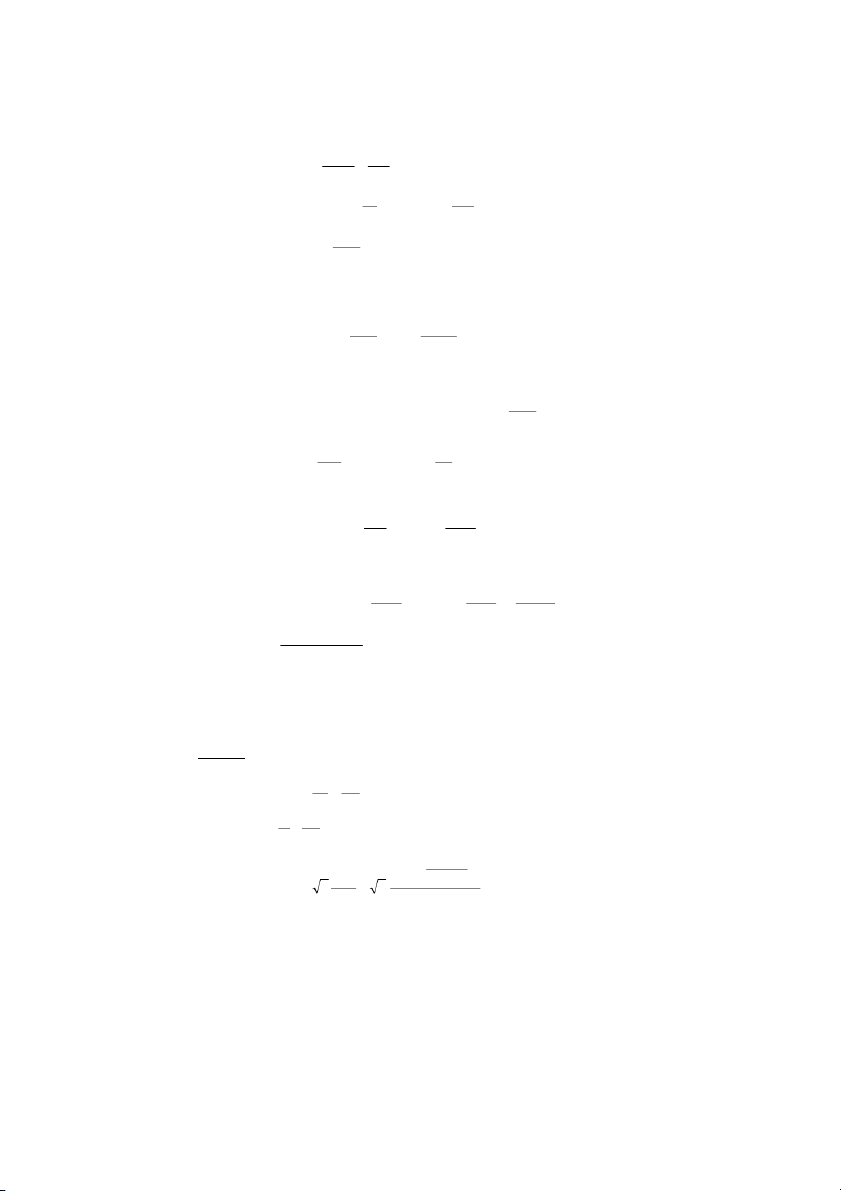

Preview text:
!"ω# $" $ ϕ
!"ω# $"%$ % ϕ%
&'()*+,-! $ϕ . %/ ϕ% π0
/12!345
6$ϕ . "%/# $ ϕ% π5 $ π
ϕ . "%/# $ 5 ϕ% 2
($ϕ . 7'6/8 ϕ%
9:;06<,()*27
-=7>12-6(?3)@
AB07C/D6<+8E7062B-27
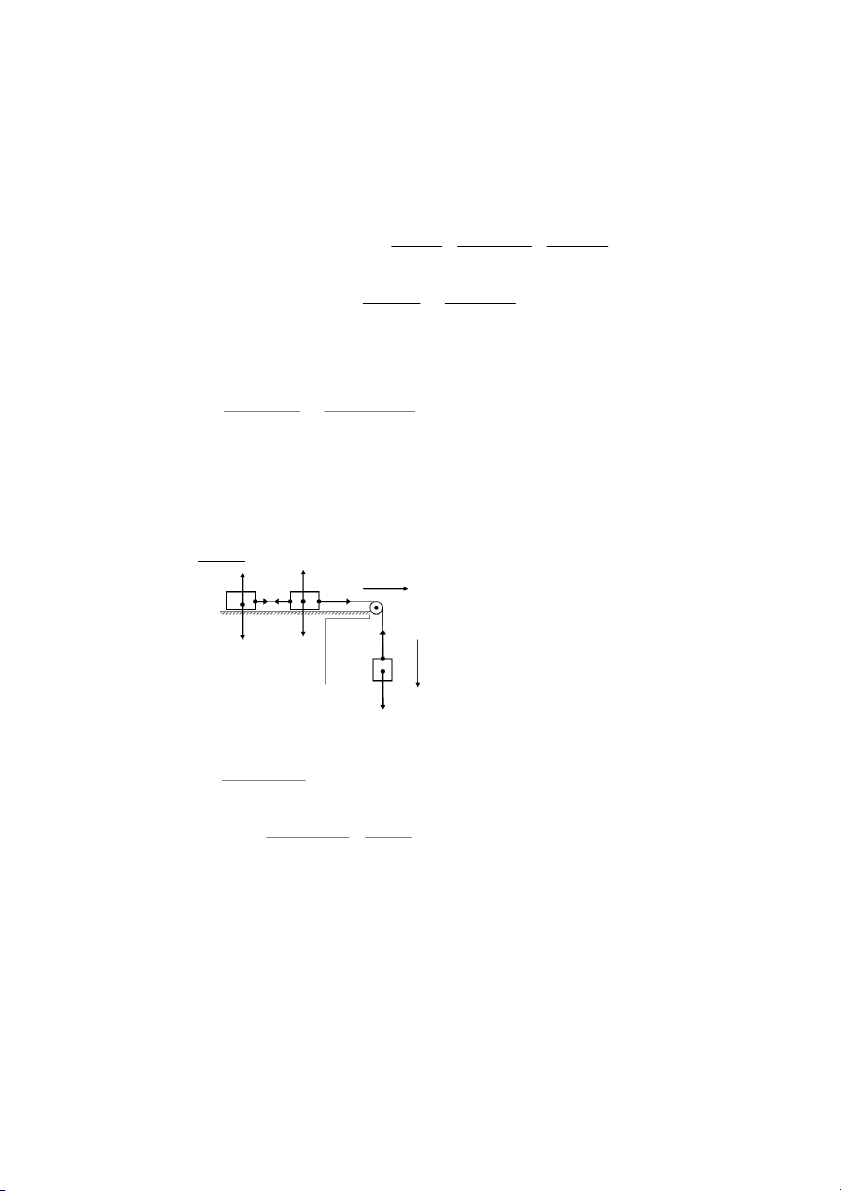
12!8
$Fϕ #%/ ϕ%
πA2" $7
!"ω# $ !"ω# #%/π$ !"ω# $0 ϕ ϕ% ϕ%
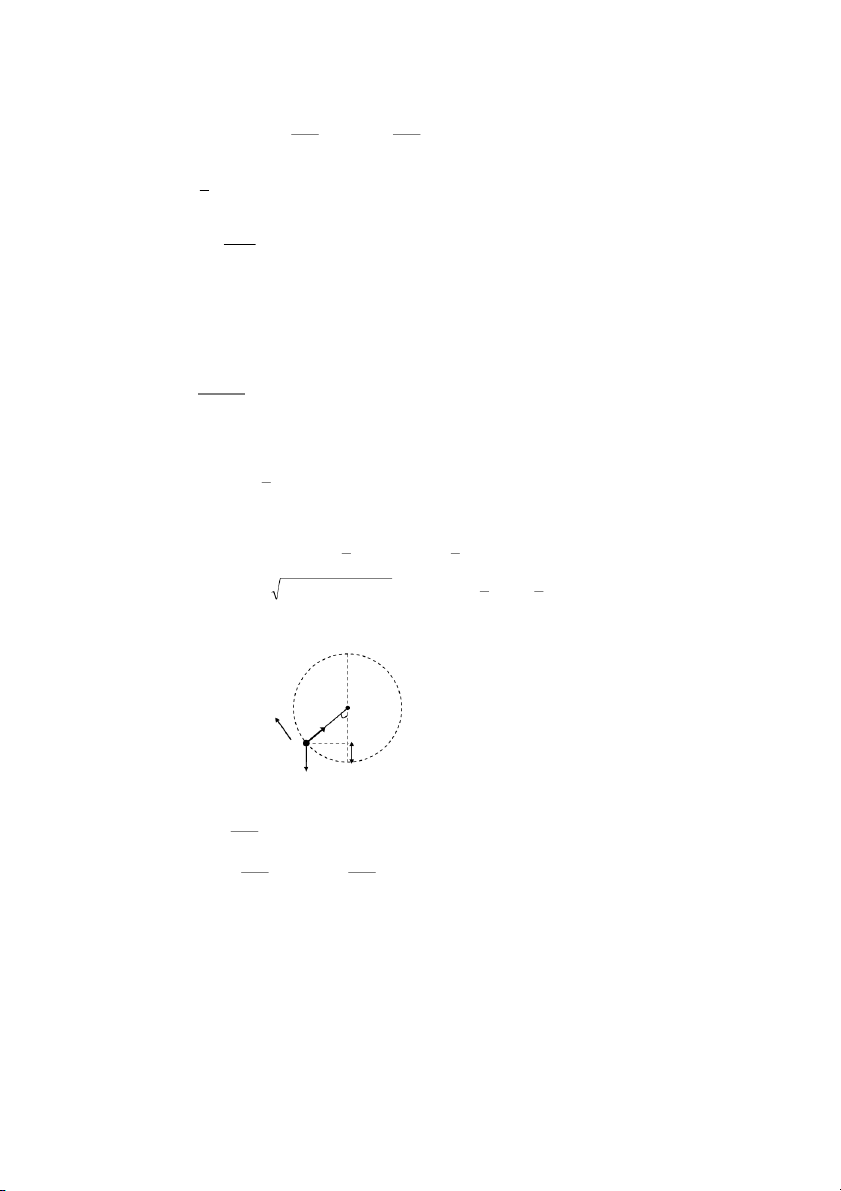
!"ω# $ % ϕ% FG7 x y a = y 2 = x a a a 1 2 1
H. ≤!"ω#ϕ $≤ 4. ≤≤
HB-I$24J6(?6K a y 2 = x AL . ≤≤ a1
6$92M-I$ !" $ !" #%/ !" $ ω#ϕ ω#ϕ% π#π$. ω#ϕ%
FG7N4J6(?6K a y 2 = − x AL
. ≤≤ a1 $F π
ϕ #"%/# $
(?(2N6> ϕ% 2 x 2 y 2 + = 1 a 2 a 2 1 2
26(?+41O-AP071LA2Q;
48
($=/D-" $A2"%$8R3</2!3!
" $A2"%$
x = cosωt.cosϕ −sinωt.sinϕ "S$ 1 1 a1
y = cosωt.cosϕ − sinωt.sinϕ "T$ 2 2 a 2
UV"S$AL!ϕ A2"T$AL.! WA<ALA< % ϕ
x y cosϕ − cosϕ = sin t
ω .sin(ϕ − ϕ )"X$ 2 1 2 1 a a 1 2
9V"S$AL!ϕ A2"T$AL.! WA<ALA< % ϕ x y sinϕ − ϕ = t ω ϕ − ϕ "Y$ 2 sin 1 cos sin( 2 1 ) a a 1 2
Z-"X$A2"Y$WA<ALA< 2 2 x y 2xy + −
cos( ϕ − ϕ ) = sin2 (ϕ − ϕ ) "[$ 2 2 2 1 2 1 a a a a 1 2 1 2
"[$6(?+41O-8
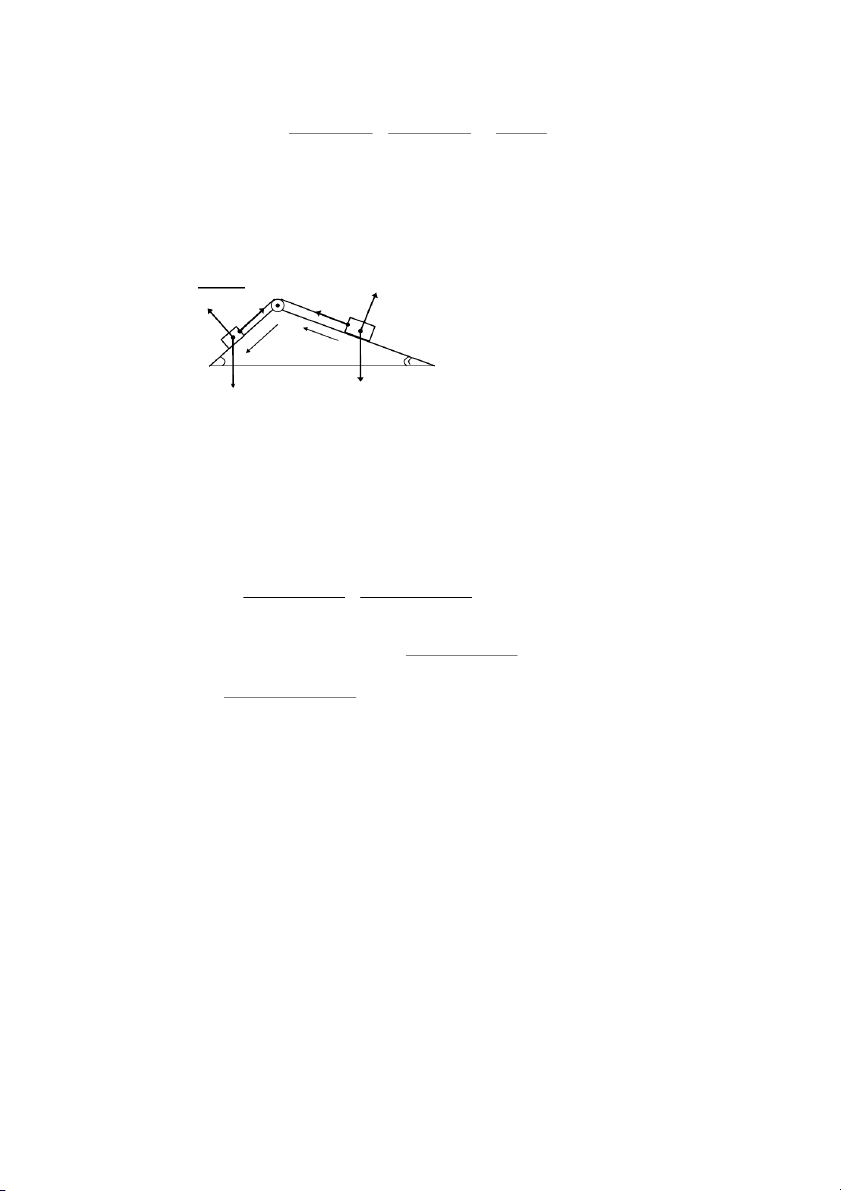
! "!#$%#$#%&!' ϕ ) ( ϕ*
%&+,-./012#3
RPPG\]<\ZALAB3A T^/_+W1G\
ZKA\]ALAB3A S^/_+8 %
FAB36PP4+A]Z0Z]7`
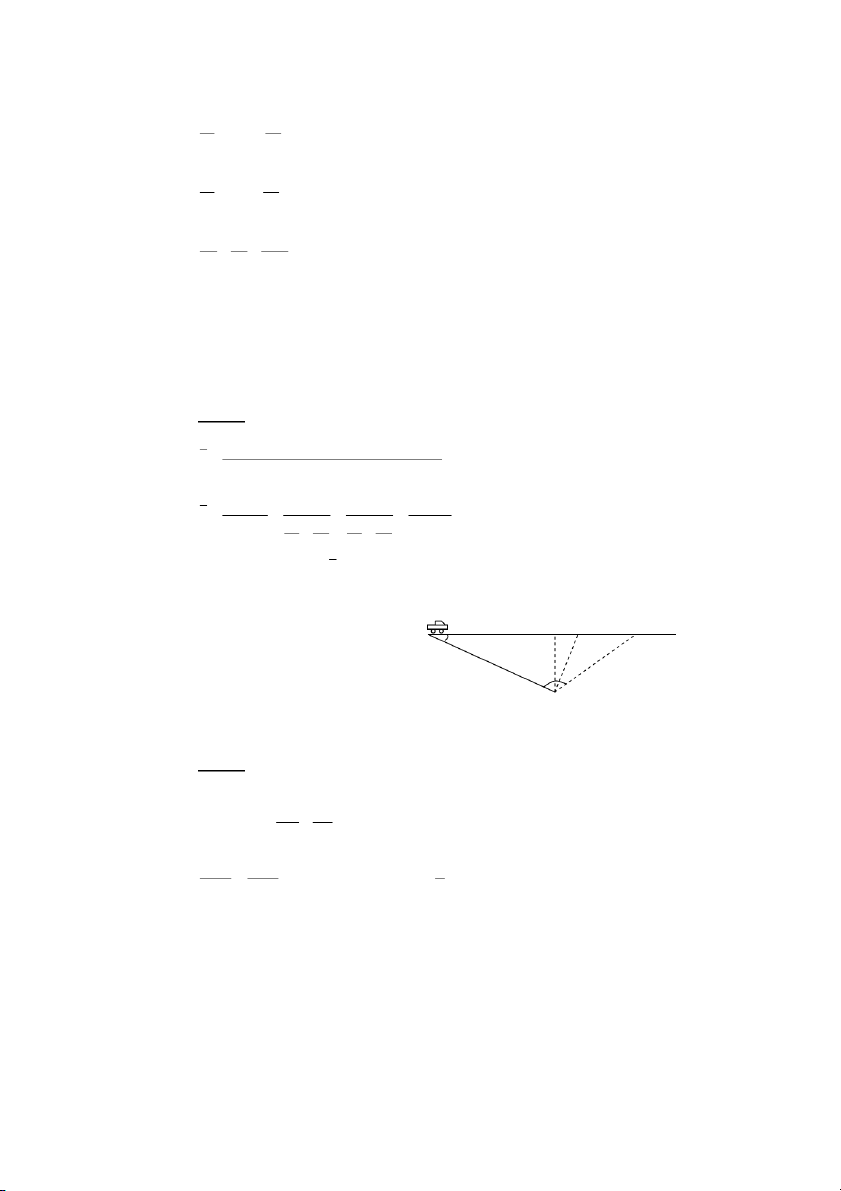
a)C+]Z6;!8F!bOAB36cP> 6 . 4 5 4 + v = 6 5 + +! 4 + . 4 5 0' F, s + s s+ s 2 2v v v 1 2 = = = = = 9,5 m 3 / s. t + t s s 1 1 v + v ( A 1 2 + + v v v v 1 2 1 2
F!3, v = 9 ,5 m 3 / s .
R+> R +J /=X^ +
PP5/PPd f i E Z
%^^ + 6e I β
+ a- PP "f .%$8 Z< PP ]
ALAB3SY/_+8
fQ $ U+ -= c α
L 2 a- N PP` Z< ; R
+ALAB3A ^0g/_+5 % f .%
6$ U+ -= ALAB 3 Q
6;647a-,PP`
$R3a-NPPZ++GRLZ-=6;+
PPG]LZ
MB AB = " $ v v 2 1
hD('1:2!3!]ZR7 MB AB h = , AL sin β = "%$ sin β sin α a
FG" $A2"%$N
h v1 sinα = . = 0 8
, 33αXY^S^jaα %S^ S^j8 a v2
775+0''89:;<0
α = >:; ? <. 56 3 0 ' 0 ≤ α ≤ 123 3 0 ' 0 3 @+ 56 3 0 ' 0 < α < 12303 '
0 5+ 0' '
5?++8h v
C/'+?DE5+'+<F?<.+G0' 1 sin α > . 3 a v2 MD AD 1 h v 1 a v :0 = → AD = sinα . M . D > . . A . D 1 = M . D 8 sinβ sinα sinβ a v h v 2 2 AD MD >
1-05++!8'F95++!5+'F#3 v v 1 2
6$7a-,PPALAB3Qk2;1N2+
<+l121NcPPL"+a-NPP2/P-=+,1C-O
+$0AAB0c-I$@LA2AB3+-=7) h v 1 sinα = . a v2 HALm h v h
α!"α$≤ 4 1 . ≤ 1 v ≥ .v 2 1 a v a 2
h hv v 1 = = 2 5
, m / s = 9km / h 8 2 min a
9N20+-=cLRi0ALRi⊥]R8
RAB,=G/OI6KS^^8fQ!61V
ABLa0<
$nOI614"cLJ>$ALAB3X_!5
6$nOI3"c-J>$ALAB3X_!5
$nOI>48
n/OI0ABK4/OIcAB3/OI8U</O
I 3(L ALAB3 A + 2ABL = C ^
-6B+ 1 v .t + g t 2 . = h 8 0 2 v 2 + 2gh − v
om(-27/<)= t 0 0 = 8 g
n/OI14403(La>40-(6>
2ALAB36IA .X_!0A X_!5aA ^A27/<)= ^ ^ ^ $g0T!5 6$[0S!5 $[0g!8
RAB,=Gf#c-J>EEj"Ep12V
f#$8oq1N7AB>,r14GEpc-J>
ALAB3A 8 ^
$fQAB3A -=6;64ABa-K` ^
6$FO/=@ABL1Na-c+`
$U</P7AB>AB>1L6;64`
oIL1P>M(
$ F+ AB G E < a- 12 2H t = l g
6;+AB%GEj<s0(7 E 1 + f 2 h gt H h
h = v .t − g.t → v = + = g 2 H 0 s 2 0 t 2 H 2
6$n=@AB+L/a-,
Oc)C+!A2!jAB,
"f#$."!#!j$8 Ej x = (H + h) 1 2 1 − gt − v .t − .
g t2 = (H + h) − v .t 0 0 2 2 H+ h = ( 2H − g 2 H.t ) H 2
$ hD ( P > ) A0 0 ! J 6< t 2 2 v − v
= 2.a.sALAB3KM6;A^0.0!
!0</P 0
7!M=KAB 0AB%14<M12 v2 ( H + h 2 ) h = = 8 max 2g 4H
F=M(ABG u0Yr8FO
$vC+2AB,^0 VIA2^0 V3+
8 6$F+I<AB< IA2 38
hD(P> A)C+AB,!+ /G 1N6eI ,= 1 2
s = gt !b7P>)cA+AB, 2
+7/GA'O=12 2h t =
8-(P>2!b=1+ g
,VQ62B-2
$vC+2AB,^0 !I 1 2 1 s = g t. = 9 8 , 0 . 12 , = 0 0 , 49m 8 1 2 2
Ft+AB 2h 2 1 . 9 6 , t = = = 2(s)8 g 9 8 ,
vC+AB,^0 !3q0,Oc)C+,
%.^0 0u!I 1 s = h − g(t − 0, )2 1 1 = 19,6− .9 8 , .(2 − 0 1 , )2 = 1 9 , (m )8 2 2 2
6$FM4
F+AB, I 2s 2.1 t 3 = = = 0 4 , s 5 8 3 g 9 8 ,
F+AB< 3 2 1 . 8 6 , t =t −t =2 − = 0,0 s 5 4 6 (I$J < H" 9 8 ,
FG6]0Z0o4Add+W+=6AB8HB
>c-J>]R)VAdd"f .S$0AB>c(V
ZR0AB>6c(VoR8fQAB2LRL40<6Q)!` ] Z o R f .S
vC+A2 3 AB> ! %w0 0AB>! % %w! ^
AMB 0 ! ^ %w! ^ ! ^ %
AMB 0AB>6! S AMB 0S AMC 8
UB0+<RAB12 s 2 4R s 2 s 2 1 2 3 t = = = = t = t = 1 2 3 a g a a 1 2 3
HB06ABqLR1N8
= r AB c - J > G T^ AL AB 3 A ^
6;647La
$FLτ V!AL+,-ABM(`
6$h τ V!AL+,-ABM(`
9 ^_!%8
hD(P>O+</62X 2 v + 2gh − v 2h t 0 0 =
A2P>+M( t = g g
AB !L0 -= r AB 3 (L AL AB 3 A = C ^
- 2 2h v + g 2 h − v 0 0 2 − = τ → v + 2gh = gτ − + 0 (v g 2 h 0 ) g g
Z-A<-, ( 2 g 2 2gh − g τ g ) − τ g 2 (v + gh 2 + = → = 0 ) τ( τ ) 2v 2gh 0 v 0 0 2( 2gh − τ g )
$AB!L0-(ALτ !7 10. (
1 2 2. 10.40 −10. ) 1 v = = , / 0 2( 2 1 . 0 4 . 0 −10 1 . ) 12 ( 7 m s)
HBAB,rJ>3(L8
6$AB0-(ALτ. !7 −10. ( 1 2 2 1 . 0 4 . 0 +10 . ) 1 v = = − , / 0 2( 2.10.40 1 + 0. ) 8 ( 7 m ) s 1
HBAB,rJ>1448
RABJt<)C+]ZYV8
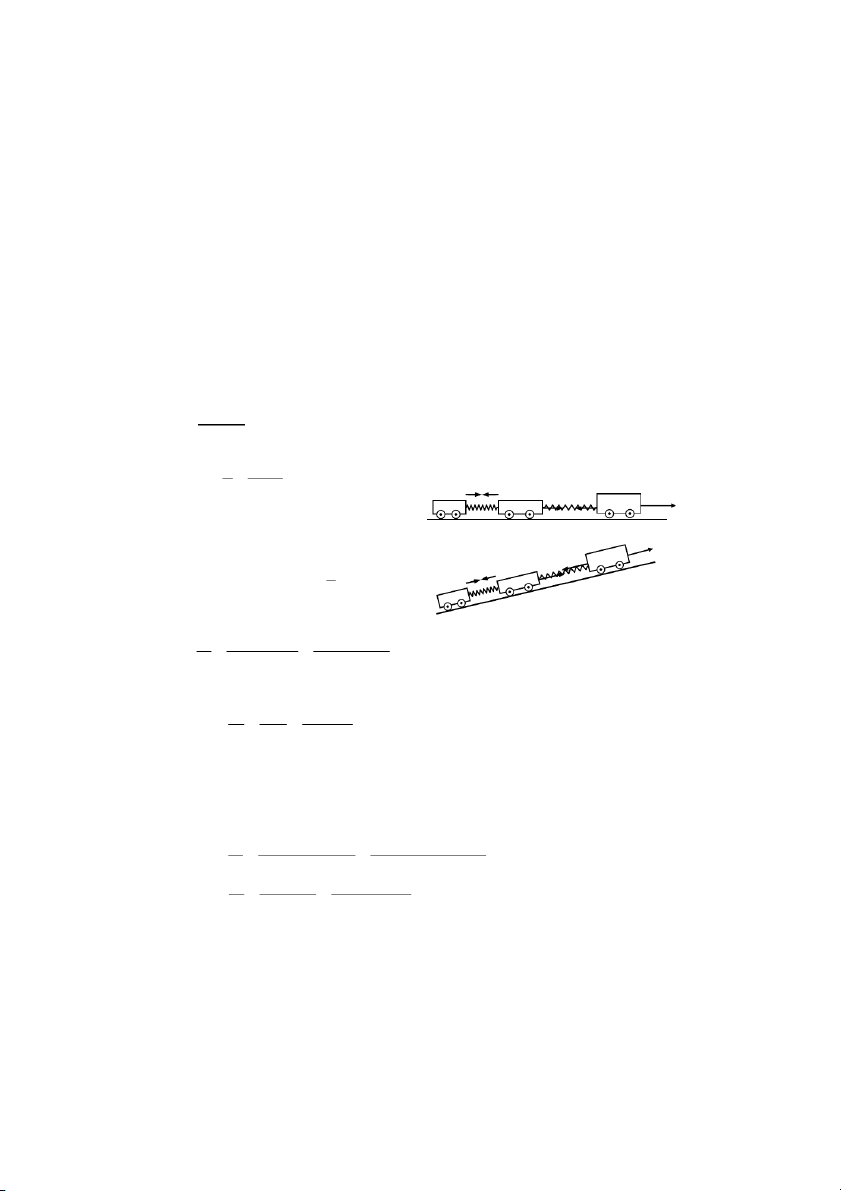
HB3AB/)]6;X_!/)Z6; X_!8F(2)C +]Z8 (
Fc'x03AB v ∆ v − v 15 − 5 5 B A a = = = = ( 2 m / s ) 8 ∆t t 6 3
FG77O)C+]ZcP> 1 2 AB = v t + at A 2
F!3,]ZY^8 *
9:;0AB36J6<t7P>
a606; v + v v A B =
04]Z7(2 2 v + v 5 +15 AB = v.t A B = .t = .6 = 60(m ) 2 2
Rc1D@";4+J$ 0X/8
FD+I0c1D(I0D+!
c1DB(I8HB31Lc1D@76; X^/_+8
Z<;'!3334+6;8FO
$s3c1D8
6$F+c1D<)C+@8
HB36c1D12 v = 50 / 2 = 25km / h8
F+c1D< 0X/212 t = s / v = 15 , / 25 = 0 0 , 6h = 3, 6 B = *(JD 8 v 50km / h max (50 /3, )
s3c1D 6 m / s a = = = = 0 1 , 2 ( 2 9 m / s ) 8 (t / 2) 1 8 , B 1 8 , 6 . s 0
K+!L !8E!HM!/02 2 v − v 50km / h 0 ( )2
%+6+G v 2 − v 2 = 2.a s . 2 a = = = 0 1 , 29m / s 8 0 2s 1 5 , km
1PQ'D0E!.5($R<#
Rc1D6eI(I4+J
)La+)!>ALI>8Z<;c
>)La+)!<+τYV8fQ>!b
)La+)!61V`
-(+,-[8
sm112(2y0 12+I)La+
)!8-(-Jt07
o(2> 1 1 2 2 l = at = aτ 1 2 2
o(2". $ 1 2 (n − ) 1 l = at n 1 − 2
o(2I 1 2 nl = at 8 n 2
FG 7 ! + > ) L a + ) ! ∆t = − = τ − − $8 n t n t n 1 ( n n 1 −
HL[07∆[ 0 g!8
Rd,rc-;ALAB3A^ X_!8FO
3--<A23<-<d!1Nr V8
HB3ABc->!/r !A u0g_!8 s7 v
α@AB3ABA2-J>=C x tgα =
8&c v y Ab648 A ^ A α A A α A 8!α 8!α
FG703--<A23<-<AB1N2O12@2
-I<3
g.v 9 8 , 1 . 5 x a = g sinα = = = 8 2 , m / s n ( 2 ) 2 2 2 2 v + v 15 + 9 8 , x y 2 2 2 2 a = gcos α = g − a =
9,8 − 8,2 = 5, ( 2 4 m/ s ) t n
U+ r )= 67 ALAB 3 A ^_! c - ,- AL a ^
-J;7αT^^8s=!D)=67,rGa8fQ
$1L2)=677,8
6$FI)=678
$F+G1Nr67L1N678
',@1,62a0I1:;07
AB6W/1B-c-
J>A2c-8
oc-J>12J6<tAL
36;0AB36I6;A A 8! ^ ^
α 8oc-12
JALAB3/Pt6;A A 8! ^ α 8
$MA2+AB\14)<AB36Ic
-J>A ^ v 2 0 y v2 2 .sin α y 0 = = = 2, max ( 1 ) m 2g 2g v α
$F+6AB 0 y 2 v . sin t = 2 0 . = = 1, ( 3 s ) g g
6$oP>IABr4 2v si α n v 2 .sin2α L = v t = v 0 0 cos α . = =10m x 0 g g
FG\-f%X+rd14-O4ALAB
3A X_!c-,-ALa-J;7 ^
α S^^8&'
$F+d5
6$n=GV-<yd5
$HB3d1N8 A^ f α z 9
FG\-A4d144, 2 v sinα 0 y ( 2 2 v .sin 0 ) (15 300 ) h = = = = 2 8 , 7m 2g 2g 2 9 . 8 ,
+d v0 2(H + ) h 7 5 , 2 (25 + 2 7 , 8) t y = + = + = 31, ( 5 s) g g 9 8 , 9 8 , FI
L = v cosα t. = 15.cos 30 0.31 , 5 = 4 0 ( 1 m)
HB31N v = g 2 + = . , . + , = , / y (H h) 2 9 8 (25 2 78 ) 23 ( 3 m s) 2 2 2 v = v + v = 23 32 , + .cos = , / y x (15 30 0 ) 26 7 (m s )
C!+?+'%0+8%&HSA3
TNUAV'/9+V&<+Q/W3
X'A !/8U0' x = v t = v cosα t . x 0 1 2 1 2
y = H + v t − g t. = H +v .sin α t. − g t . y 0 2 2
Y<5++!+$+?+'=Z3
Y<"<!<?[/,K+9+Q$!!'</0
%+- !K3
Y</LB<\$97- v = v cosα = const x 0 v = sinα − . y v 0 g t
!#]$(JD^%#_($(<^#*J$2<`D3
FG\-fS^0+rd3ALAB
3A ^_!c-,-ALa-J;7 ^
α S^^8F
$F+dLa/GNr`
6$n=GV-<yd`
$E)*d`
F(q---362 . T8
omzALz;V-8
$ABc2
x = v t = v cosα .t (1) x 0 1 2 1 y = H − v t − g = − α − y .t H v .sin .t g .t 2 0 ( 2 ) 2 2
+0=-^ 0 1
30 −10.sin30 t. − .10 t2 .
= 0 ↔ 30 − 5t − 5t2 = 0 2
om(,+d%!8
6$I{A'OV-640,O8 x =v cosα t. 1 = 0 .co 3 s 00 2 . 1 = 0 m 3 1 ≈ 7 3,m 0
$6<()*A40I-)*
2"-)@A2C/D6<+$
nD+-" $A2"%$6;NG-" $W
A2"%$ x
( 1) → t = v co α s 0 2 1 2 x 1 x
( 2 )→ y = H − v .sinα t . − g t .
= H − v .sinα . − g 0 2 0 v co α s 2 v co α s 0 0 g x2 .
= H − x t.g α − 2v 2 2 cos α 0 x x2 = 30 − −
( /9+ 0 ≤ x ≤10 m 3 ) 3 15
2\;0)*A412-618
fQ-=rABc-,-ALa-J;7α
6;64ALAB36IL0IAB12M8
hD(P>OIAB,r4C1B-,62 . S v2 .sin 2α v2 L 0 0 = ≤ g g v 2
HB!b,IM6; L 0
/!%α 0αTX^8 max = g
n| 1 } K f2 U 12 %0Y[ r8 fQ < t > K & 4c6
/ M"qAB3 6 IA2 7 4$0 /|1 4 !b 126 4`
o6<"f2U$u0[%[_!%5"&4c6$u0g ^_!%8 v2 .sin2α
FG P > I L 0 =
B 0 AL 1M } /P t " A ^ g
/Pt$A27r/Pt"r/7r6;TX^$I9!b\
1'AL3m+8E77',/\1}2
-3&cr6 g 9 7 , 27 L HN = L = 1 . 2 6 , 7 =12 5 , 6(m) XP g HN 9 8 , 10 XP
FAB37
$F))7"F)Ad)
7%T+$8
6$/+A2/-NWW5
$RaF~))F"RaF~))F
Ad%[24$5
($AVF)4)*dAL/6;gg -N8
hD(P>OAB37 2π ω =
A21:/•-=tN3 T
AL12V"!$!b, π
$HB37M)) 2. ω = = 7 2
, 6.10−5(rad / s) 24 3 . 600
6$o/•)/-N12 8n+)<Ad12 %<4AB
37/+A2/-N12 T0X8 ^.X(_!5 0[T8 ^.S(_!
$ol-(P>4AL/•/7AB37
a~)12%0[8 ^.Y(_!5
($oA7/)12gg-N12 0 u8 ^.S(_!
AB3(2)4af2U8
Z<;Axf2U12α% ^8
Fc62 . gAB37M)712
ω[0%Y8 ^.X(_!8Z/O)*f2U"c$12 ω w z α
f62 . u r = Rcosα 8
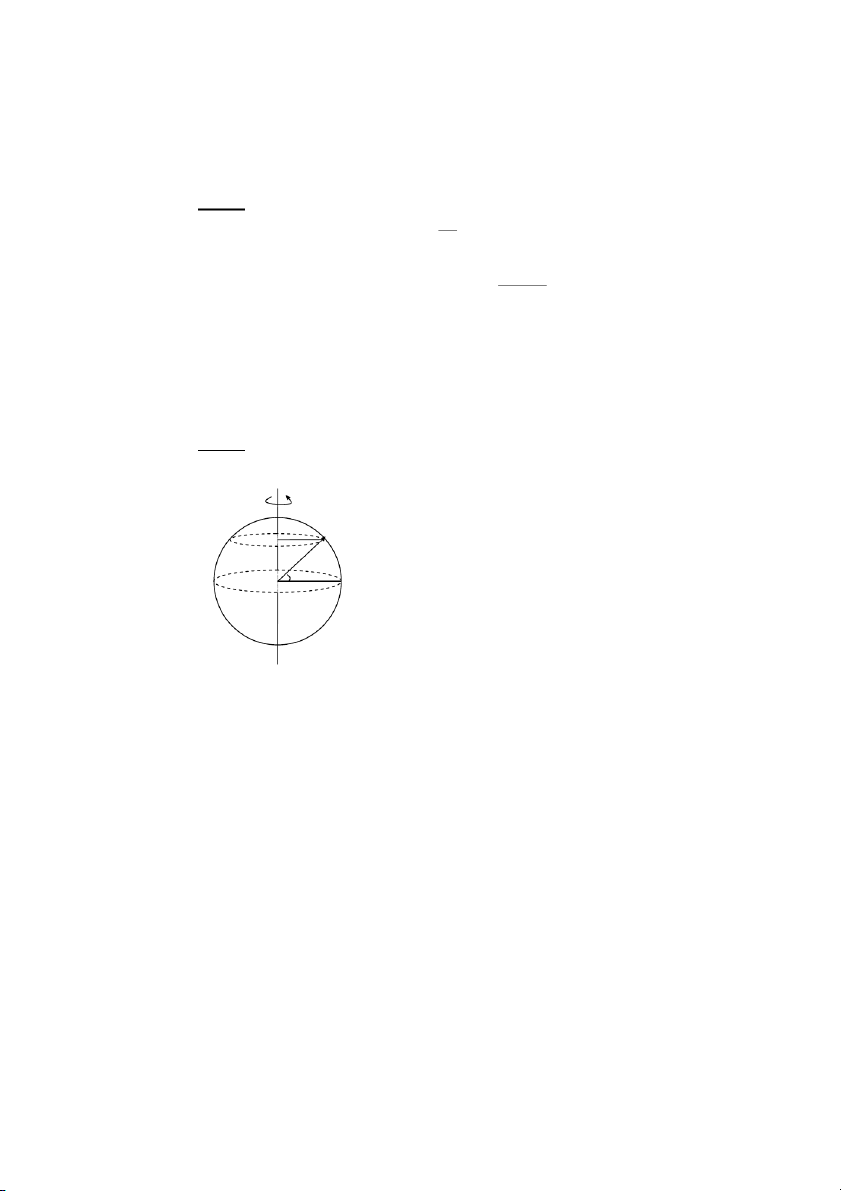
FG77AB3(2f2U12
Aω8ω8w8! α
F!3A2,ATS^_!8
Y 0<%0+ + 8 "B a 7 - ! ' A !' !
b<H"Gc+L/9+7- !'AO%+6+G/9+
DM-!'ϕ!'.5D$/Lω!'/LH0+/$
+!Lβ !'+!L5!Bde!Kf3
R AP 1~ ! / 6e I ) , -N , AB 3 [^^
Ad_-N8FO37AP1~A2!3Ad2AP1~C),-N
<AP1~12(I8
HB37AP1~ω[^^Ad_-N[^^8%π_Y^"(_!$!+τ -NY^!8 R2 ω 1400π / 60 1400π
ωβ 8τ β = = = =1 2 , 2( 2 rad / s ) 8 τ 60 3600
s7),!+τ -N12 1 2 1 ϕ = β τ . = 1 . 2 , 2 6 . 02 = 700π (rad) 2 2
EAB0!3Ad), -N12 ϕ 70 π 0 = = = ]R Z /f 8 *π π 2
R 6 c ) B (I0 ! -N AB 3 7 = GS^^
Ad_-N3 g^Ad_-N8F36cA2!3Ad26cC)
,-N8
Fc'xA3771P372 ω − ω 180 2
. π / 60 − 300 2 . π / 60 0 β = = = 0 − 2 , 1 ( 2 rad / s )8 τ 60
s7),(MA23)MAL)A..!
J6<tN 2 2 ω − ω . π / − . π / 0 ( 2 2 180 2 60 ) (300 2 60) ϕ = = = 24 0 1/ f# 8 2β − 2.0 2 , 1
fa(MA2P>AB376 ω + ω 180 + 300 0 ϕ = .τ = .1 = 240 1/ f# 2 2
R6c76/Ow ^1NI>40!7))
7AL376;S0 T(_!%8fQ0!V>
$HB37A2AB3(24A26`
6$ s 3-- <03 <- < A2 3 2-I 4 A26`
$s7@32-IA26/O6c">ALq4 A26`
$hV>0AB37A2AB3(24A2612 ω = β t. = 31 , 4.1 = 31 , 4 (rad / s ) v = ω.R = 31 , 4.0 1 , = 0 3 , 14 (m / ) s
s3<-<7'/PtA23--< α 1N2
f a = β. R = 31 , 4. 0 1 , = 0,314 ( 2 m/ s t ) 2 2 a = ω R . = 3 1 , 4 .0 1 , = 0 9 , 86 m / s n ( 2 )
od32-I6; 2 2 a = a + a = 1 0
, 3 m / s 8 t n ( 2 )
$s7@32-IA26/O12 α=C a , t 0 314 sin α = = α [^TYj8 a 1 0 , 3
o/)6c6/OX^12^0 V8F
$HB3(2A2AB37A265
6$s3--<@6/O8
HB3(2A2AB374A26 +G H 0+ ! 4 5 f 2 R π 2π 0 . 5 , v = = = = 31 4 , (m / s) 5 ++! ' 4 A < A / f f T 0 1 , v 31 4 , ω = = = 62 8 , (rad / s) R 0 5 ,
6$s3--<{3LV@6/O 2 2 2 a = ω r = ω R . / 2 = 62 8 , .0 5
, / 2 = 986 m / s 8 n ( 2 )
R226eIA2+d06/O /0(2Y^^0
ALAB3XT/_+822<)C+7S^V8FAB3(20
3--<03<-<032-IA23722K3
)C+78o2212(I8
ow / ^^^0A XT/_ X_!0!Y^^0S^!8 ^
hD(P>AJA2d6<t!b
O,1,I<8 1 − − . 2 ( 2 s v t) 2(600 15 3 ) 0 1 0 s = v t + a t a = = = ( 2 m / s )8 0 t t 2 2 2 t 30 3
HB3I3+Ad 1
v = v + a t = 15+ .30 = 25 (m / s) = 90 (km / h )8 0 t 3
s3--<{3LVI 2 2 2 v 25 a = ω R = = = 0 6 , 25 m / s n ( 2 ) R 1000
od32-I12 2 2 2 2 1 5 a = a + a = + = 0 7 , 08 m / s t n ( 2 ) 3 8
s372I
a 1/ 3 t −4 β = = ≈ 3,3. 10 ( 2 rad/ s ) R 1000
HB 3 41c4 D P 6; A %0%8 ^g_!8 FO AB
37A23--<41c<c)*712Add6 /O^0X8 ^.g8
€1cA%0%8 ^g_!%0%8 ^Y_!5w^0X8 ^.g^0X8 ^. ^8
HB37A23LV{3--<1I1,
ωA_wT0T8 ^ Y(_!5
ω% wu0Yg8 ^%%_!%
R+3•)!P7(dL=8U<+•
cLGA'O]!A'OZ"]Z⊥AL(d!P0 .T$!+
^-N!bLA'OoZ/=! %^8U<+•
A-O,(d!+ %0X-N!bLNA'OZ8 %
oAB33AL(dL12/Pt8FO
$Z1!P5
6$HB3A3AL(dL5 Z o
$HB3(dL3AL6+!P5 ! ($s7γ8 R A H γ
FG]<o<+ ^-N0]<Z<+ ]
%0X-N0Zo7(2!Zo %^8 f .T %
V 12 62 t ,- AB 38 F W Z o →
+ q AL (d L AL AB 3 u A2 1 →
!AL(dL"( +•$ALAB 3 v 8 H A γ
ot,-O123AL → → →
6+!PALAB3 ] V = v+ u 8
F+,->62>AL .T0+ f .T6
,->>AL .T68
FcAb07-!
!8 51A8 51"A8! 5A8! γ$8 % γ5 s 120 u = = = 0 2 , (m / s)8 t 600 1 t 10 4
l = v.t = v.cosγ .t → cos 1 γ = = = → γ = 360 5 ' 3 1 2 t2 12 ,5 5 3 u u 0 2 , 1 sinγ = = → v = = = = 0 3 , 3 (m / s)8 5 v sinγ 3 / 5 3
o(d!P l= v.t = 0 3
, 3.( 10. 60) = 200 m8 1
U+•)!PcLAP7AL6+!PAL
AB3[0%/_8UL=CA-OP(d/= X^8
F$HB3(dL3AL6+!P5
6$ F+ I ) , !P8 o 6< !P 6; ^0X/8
Z(d!P1^0X/X^^8! X^0H[0%/_%_!8
FGAb Z o u s s 150 ! = → u = v . = 2 . = 0 6 , 0 (m / s)8 v l l 500 A 1
F+<!!P H AC AB l 500 t = = = = = 250 (s )8 ] V v v 2
-!3$^0Y^_!56$%X^!8
f62 .%[
R66GA'O]LA'OZ8]Z;cLFVPA2
/=S^^/8&'+6<
$nP775
6$o77tcLUZe5
$o77tcLFVP8
o6<AB376;A %^_!0AB363AL/P/OA % Y^^/_8
]ZS^^/07A %^_![%/_0A Y^^/_8 %
$F+66M<-G]<Z l 300 t = = = 0 5 , (h )= 3 0 1 B# 8 v 600 2
6$FM62 .%Y063LA'OZ07-=6<A-O
7α!AL-]Z8F7
V = v 2 − v 2 = 6002 − 722 = 596 / 8 2 1 (km h) ] Z
F+66G]<Z12 α A s 300 t = = = 0 5
, 03 (h ) = 30, 2 B 8 A% V 596
$s7PGFV!P8F+6
f62 .%g I(q12 s 300 t = = = 0 4
, 46 (h ) = 26 , 8 B 8 v + v 600+ 72 2 1
f .XP=68
$o6<O78
6$x@W'A28
$h!AB368
A % S z f .X A % S z f .Xj
$UA2W'=6212(I 8
6$sW'AL+6<+-
8
$Z012AqL8HB3yABG1N
B/8W'AB32(33AB21L"3
6<!37+J$8FGW'07!!3AB ‚ S ‚ 8 %
f .YW'AB38fC6<
4yz]0]Z0Zo0oE8 A ] Z o E z f .Y
z]AB-+^W(IAL 3/1L8
W']Z6<AB!8
W'Zo6ABB(I8
W'oEAB<-B(IAL31L
/Zo8HB(G1328
%. 8Rc7/31,%^^^^/0B(I(L(
1M6;Y^^^U0AB36Ic6; X_!8fQ
$s3c5
6$h61Vc(G15
$+cC,/G1NC</c(GJ8
$s3c,Oc'1BiiUcƒ
„_.Y^^^_%^^^^.^0S_!%8
6$F+/G1NC</(G1 ∆ / Z ) (R = ∆t = = =RZ ( ) D 3 ! ) Z$]
$vC+/G1NC</(G1
!A 8#8%_%888S[X8 ^
%.%8 R y a TuU 6' /…- @ a -J J f%.T
> " %.T$8 9M r-J7 4 ya 12 T[U8
fQ 1MQ I Va y` f !3 ! @
yA2ar-/^0%8
9MV ^[0gU51Mu0gU „U „f „ „ ! !%
f%.T f%.T6
n3y3I1M„ L3(L01M! f
4ayL144"f%.T$0d/3Vy14
41M!1L3(L"f%.T6$8
FGAb201M(q"„ $A2V„ y-=7 f U
'Q „ f F + F
− P = 2× k.N − P = 2. 0,2.147 − 49 = 9, m 1 s ms2 ( 8 ) N „UF + F + P = 2 ×k N . + P = 2 0 . 2 , 1 . 47 + 49 =107 8 , m 1 s ms 2 (N)
%.S8fQ-=(1M6;64142>47
(IA2!+S^V7, 8o6<1M!
26;X†m1,28
sm„121M(1428&rc-01MV3
20c'1BU%06;
„.‡ !
F712/31,A2 s 2 a =
123I8 2 t
FG7! 2 s . m . F = f + ma = 5%mg + 8 ms 2 t
F!3! 0S^!0 X0Y XY^^/,„≈g%^^U8
1C"G%0++L+ !!"%&<=(R$J\#3
%.T8R+(<cALAB3/Pt89NI+/r
cA-OL0!7+}cA-O!8F=+,-02c
,-ALa-J;7α8fQ+,-2+-=a14
c1M1L`Z<;m1,c120!3!@6cA2a +12/8
H<-'1BiiUcƒ1M(A2c8F2-I1M
t ,-< c - J > A2 ; 6; ^. /P 7
c-J>0c-./P73
c-4
F+ ,- /r cA-O L"%. j$ 1M rAP 7 c 14a +12
N + F.sin − P = 0 N = P - F. sin
H2 F.cos α − F = 0 F.cosα = F ms ms
R201M!(14c
„ /U/".„! ! α$ kP F co α s = k(P − F sinα) F = cosα + ksinα U Uj „ α „j „! „j ! f%. j f%. j6
F+,-}cA-O!"%. j6$
Z;-VOM0O,1M!a14c+,- 212
„ /Uj/"#„! ! α$
H21M„jIa142c kP ' F =
cosα − k si α n
wk2„j ‚„8UAB+,-}cA-O!+-=(q 1M1L8
%.X8RAB7/31,X/,a4a-J4,-AL
a-J;7αS^^8f!3!@ABA2a-J46;
/^0%8F3AB4a-J48
F-VO1M(A2ABW S1MJ U
>0 U AP 7 AL a 4 A2 „ ; 4 a ! „ 48 ! z
'1BiiUcƒAB P + N + F α ms = m a .
o< - 2 c - AP 7 AL a
-J4"-z$A2-!!ALa-J
f62%.X
4"-z$, N = Pcos α − Pco α s + N = 0 P si α n − F Psinα − F = ma a = ms ms m
R2„ /8U4 !
P sinα − kP cosα
mg sinα − kmg cosα a = =
= g(sinα − k cosα )8 m m
FαS^^0/^0%0u0gO,S0%T_!%8
[ 7-e!\'$+!L ! /e7UA/0L+ !/3
%.Y8RAB,34a-J4,-ALa-J;
7αTX^8n,,)C+!SY0T0AB,AB3A%_!8&
'!3!@ABA2a-J48
-(P>3AB62%.X7 g si α n − a a
a = g(sinα − k cosα ) k = = t α g − 8 g cosα g cosα
hD(/<>iA3)A..!73AB,2 2 2 2 2 2 12 v − v − 0 v 0 v a = = = 8 2 S . 2S . 2S . 2 v k = tgα − 2.gSc α os
FP!3CαTX^0A%_!0!SY0T^0SYT,/≈^0%8
%.[8R!,(VG,a4a62!-I76Pk
38h,(V6eI,4a62/(2-I6Pk6;
%X†(2(V8&'!3!/@!,(VA2a628 ‡!
f62%.[
sm12m1,=(V0 12m1,-I6Pk8FcI
620(2-I6Pk6;%X†(2(V %X†8
&rc-!,(V0(V'(1M A2‡ 8 !
R3(V6eI,-=7 ‡ ‡ %X†8 ! !
R20‡ /8U/8"[X†$8 !
FG7%X†/8"[X†$ 25 1 k = = ≈ 0 33 , 8 75 3
%.g8 $RPP/31,4+6;0!3!
@6PPA2a+12^0 8FO1M/rPP+,-
$ˆP5
6$ˆP(IAL36;%_!%5
%$olVQ4+,-PPA2
$94(37(3T†56$&3(378
f!3!6;^0 !3+8 →
Ft,-1M(14PPW1M/r F PP0m1M P 0-=
1M--< N a+A21M!a+ f 8 ms U Uj „j „ ‡p! ‡ α !
f62%.g → → → → →
'1BiiUcƒPP12 F + P + N + f = m a ms
om(12c8o<-214-
,
$ nc4+; F − f = ma F = ma + f = ma + kmg ms ms
F!3 ^^^/5/^0 5u0g_!%5A2
$n0^ „ug^U8
6$n(IAL3%_!%„%ug^U8
%$ nc4+(3
$ˆP14(3 F− f − P si α n = ma
F = ma + f + Psin α = ma + kmgcosα +mgsinα ms ms
F70!α^0^T12(3(3!α 1 − 0 042 , ≈ 1 0 ,
F = 1000× 0 + 01,.1000 9 . 8 , 1 . + 1000 9 . 8 , .0 04 , = ( 1372 N )
6$ˆP3(3„"/!α.! α$8 F− f + P si α n = ma
F = ma + f − P sin α = ma + kmgcosα − mg sinα ms ms F!3 F = 1000 ×0 + 0,1.1000. , 9 8.1 −1000.9,8. , 0 04 = 58 ( 8 N)
%.u8R!,(V,Ae)dm7/31,/P/0I
6AB7/31, A2 " ‚ $8&'3ABA2!>~ % %
(V8o!/P/8
-(6;!3 % /8 %
E!,(V /P C0dm/P/31,0/P! 4!,(V
1P~AL1M~(VF5AB!bALq38H ‚ %
4 !1M/r1L 12 3(Ld 6' % % /r1448 F F % %
f62%.u
om(GAB,-AL
yAB"Ab$8'1BiiUcƒGABr4- m : P − T = m a 1 1 1 m : T − P = m a 2 2 2
oA<cA<-4, P − P m − m
P − P = (m + m )a 1 2 1 2 2 a = = g = 3 27 , m / s 1 2 1 2 m + m m + m 1 2 1 2
&c-'1BiiUcƒAB 7 .F 8 m − m 2m m
T = P − m a = m g − m 1 2 . g 1 2 = g 1 1 1 1 m + m m + m 1 2 1 2
FG7O,T = 6 5 , 5 N
%. ^8 R 2 0 ! / -0 AL 3 /P t γ
^0X_!%8 %V!/6eI0+e2A22
B(IL/(GJ8F426)C+!3!
6;/^0^ 8F
$HB31L25
6$F+26/G1N2-L/2(GJ5
$s32B(I5
($vC+2622C,8
FIc
s AL3 ^0X_!%+ %!8
s%B(IAL3 /8^0^ 8u0g^0^ug_! % %
(L(=1M!+∆8 A A %
o7AbW'AB3Ic+48
$HB31LI v = a t = 0 5 , .12 = = max ( 6 m / s) 21, ( 6 km / h) 1 1
6$FIB(I+ v 6 ∆t max = = = 61, ( 2 ) s a 0 098 , 2
Ft+I"/G1N-<1N(G1$ t = t + t ∆ = 12 + 61 2 , = 73, ( 2 s) 8 2 1
$s3I/B(I12 ^0^ug_!%8 %
($vC+IC,6;‰(OŠ,r 1 1 s = v t . = 6 . .73 2 , = 219 6 , max (m ) 2 2 2
%. 8R6=y],a4a-J;8Z=],3AL
6=yZ/ 6;!,(VAe)dm3' "Ab%.X$8
n31,dmA2(V/P/8
$FO1M~(V< %^^5 S^^0!3!@6=]A2 ] Z
a-J;/^0%X8
6$U<tA'O]A2Z1M~(V!b6;64`&c!3
!A‹l8 U% F ‡! % F f%.X
&rAB7/31, 0 ,3AL4%.X8o1M %
(A2ABC,\k4Ab8
o7 A< - ' 1B ii Ucƒ AB 2 r 4 -
N",\6;l47(‰#Š64$ m1 : P − T = m a 1 1 (1) m : T − f = m a ( 2) 2 ms 2
F70 f = k N . = k P . 8 ms 2 2
oA<cA<-" $A2"%$4, P −f m g − k. m g m − k.m P − f = (m + m )a a 1 ms 1 2 1 2 = = = g 1 ms 1 2 m + m m + m m + m 1 2 1 2 1 2
FG-" $! m − km + 1 2 (1 k) m m
T = P − m a = m g − m . g 1 2 = g 1 1 1 1 m + + 1 m 2 m1 m2
%+-?/GMgHQ'e\'$6+/!+f !< /0 (
< !MgHQ'76+3h'$MgHQ'7UA/0/+Nb * < e( *
%#?/GMgHQ'G!%& (1+ k)m m + , , . , A B (1 0 25)0 2 0 3 T = g = ×9 8 , =1 47 , (N) m + m 0 2 , + 0 3 , A B
"F!3/^0%X5 %^^^0%/5 S^^^0S/$ ] Z
%. %8fAB7/31, /0 %/,3AL6;!,(V %
A2,a4a62;8Eq!,(V/Ae)dm0
I(V6A2 A2I/6A2AB>67/31, S/"%. % S
Y$8o!/P/8FO1M~!,(V8 U U% F F % F % % S S f%. Y
Fm1M 122-I1M(c-A212 S
ABALq38F7 m g 3 a = m + m + m 1 2 3
&r4AB 7 m m g 1.3.9 8 , T = m a 1 3 = = = 4 9 , (N) 1 1 m + m + m 1+ 2+ 3 1 2 3
&r4AB 7 − = S m g T m a T = m − 3 2 3 2 3 (g a)
+ + m g ( m m m ) ( 1 2).3 T = m g 3 1 2 3 − = g = 9 . 8 , = 14, ( 7 N) 8 2 3 m + m + m m + m + m 1+ 2+ 3 1 2 3 1 2 3
%. S8\a-J4,-ALa-J;7 α
S^^A2βTX^"%.[$07edm/31,/P/8Eq!,
(VAe)dm0I(V3ALAB]A2Za4a-J48
n31,AB]A2Z6; /8ZQ)=1M!8F3
A21M~(V8 U U F F % β α % f% .[
F 62 20 1 r AB c - a
48E!,(V3AB/P6'C4AB!bALq
38om(Ab"%.$8o1M(
A2ABC,\48
'1BiiUcƒ,<14-AB m : P sin α − T = m a ( ) 1 1 1 1
m : T − P sinβ = m a (2) 2 2 2
oA<cA<-4,
P sinα − P sin β = + 1 2 (m m 1 2 )a sin α − sin β sinα − sin β P P m m a 1 2 1 2 = = g m + m m + m 1 2 1 2
FG-" $!
m sinα − m sin β 1 2
T = P sin α − m a = m gsin α − m . g 1 1 1 1 m + m 1 2 m m . g
. (sinβ + sinα ) 1 2 = m + m 1 2
F'I62C" 6; 0 6; $A26 ] % Z
>3A21M~(V, 2 a = −1 0
, 2m / s 5 T = 59 , N 8
n<)=2>Q;0,AL(CmAL
371L6; 0^%_!%8
ia%0+e$!!!'&/;DWL
f / > %, e3 F $ %0+ 0' ! T +G H
'A8+G+D/9++G.T5++?+e3C'+e$7+
<L+Ea+b?+!L7S+GH.T3
Q L+ S 5+ +?+ e d HU 5 N
7<!D3@+N7<!D$MHU/0
/0+G'A !/c/+NT+GH !UA3@+
N<!D$k0+G !M<!DUA/0+G'A !/$
H7+?DEla+G'A !/3C5
! . +? + "< +G ' A Hm ? +! L ! / %, Q<
%A?++?+++G'A/0+?++%0+3C\+e7!+H+
<0+?+B/05"<0'?++5++?+!+"3C!
+G0'%&1D!+.0<+G%0+/0BB+G
++N<)M!DM0'/m?+HM!eDMn<!DD,K0"M/!+fM/0M?#b%&+<
!9 1K/0 DD0 "M/!+ fM$M+o /0M
?#b+?+/0+?+%0+9P0+3
%. T8R22WI0 ^0A2X03AL
c>M46;@1d38Z<;/'(1M6;
X^^U1dC 8ZQ)!8FOC1d+,-
$226eI601M/rI/PtA2! ^VAB
322L _!5
6$2214(374X†ALAB3/Pt8
C1dVc'1BfN„/8
FG7',!32W F 500N k = = . 5 104 = N / m. F F x c 1 m % % F F „
$ 9M ~ 1d >
7 A d 1M /r = I
8FG'1BiiUcƒ
7F " # $0AL v % a =
8h t
C1d>
f62%. T T ( m + m v ) (10 + 5).103.1 x 1 1 2 = = = = 3 1 . 0−2 m = c 3 m 1 k k t. 5 1 . 0 4 1 . 0
9M~1d>F C1d> % % T m v 5.103.1 x 2 2 = = = = 1 10−2 . m = c 1 m 1 k k t. 5.104 10 .
6$n2I14(38o1M1d-=V6;AL2
-Im1M/r38o T = + 1 (m m 1 2 )g . si α n T = m g.si α n 2 2
F70(37412X†0>12!α^0^X8C1d T + sinα + . . , . , 1 (m m 1 2)g (10 5) 103 9 8 0 05 x = = = = 014 , 7m = 14,7cm 1 k k 5 104 . T m g sinα 5 1 . 03 9 . 8 , 0 . 0 , 5 x 2 2 = = = = 0 0 , 49m = 4 9 , cm 2 k k 5 1 . 04
%. X8RAB7/31,%^^0,cKI!,(V(2 T^5
AB)a-J;ALAB3/Pt!!,(VAa
78s=!D/7(VAL-J>7αSY^8FAB37
ABA21M~(V8 α F 1
f62%. X
HBAAdd76/Ow18!α8 → →
9M(14ABWm1M P A21M~ T "Ab$8Ft,-1M
21221MLVVdAB → → → F = P + T " $ ht
FG%. P mg 0 2 , 9 . 8 , T = = = = 2 4 , 5N cos α cos α cos 360
„8α88α 8
R2„8wω%818!α8ω%8 2
F = mg t.gα = ml si α n ω . 8 ht E7 g ω = = 6 , 5 rad / s l cos α %. Y
AB %.g8ZQ) !0 /31, dmA
+,- 8 % F F F % % f%.g
oN:;!>~(Vm6;06;F8FGAb%.g0
<r4AB 07 .F " $
U<r4AB 07 %
%F. 8 "%$ % % %
hD(Odm3'A2dm;0)C+
-1I)C+AB 0G7/rc % %% "S$
UVA<" $AL%WA<cA<AL"%$! 2( 2m − m )g 1 2 a = 2a = 8 1 2 4m + m 1 2
U< 2g a = 2a = = 3 9 , 2 m / s 8 1 ( 2 2 ) % 5
!'+, !! /01(#!<Mg !HQ' ( 2(2m − m g ) m 3 m g 1 2 1 2 T = P − m a = m g − m = 1 1 1 1 1 4m + m 4m + m 1 2 1 2
%. [8v dm ]/31,/P/0+1W!, (V0
I6A2)=aR 0I/6A2dmZ/31,/P
/8vZ1Ae!,(V/8fI(V3AL)=aR A2R 8wdm % S
]AL26mAB,cA21M/<1d"%.u$8
&'3)=aR A2!3\F41M/<0<R 0R ‚R # S % ≠RS % R 8 S F F F R F % R F S % S R % % f%.u
om(AB%.u8FG3)
A+dA23'3)3AB 2a = a + a "Œ$ 1 2 3
Edm7/31,A21M!Kt76Q)47 T = 2T ; T = 2T ( ) 1 1 1 2
&rc-AB0-'1BiiUcƒ M a = M g − T 1 1 1 1 ( ) 2
M a = T −M g 2 2 2 2 ( ) 3 M a = T − M g 3 3 2 3 ( ) 4
FM-r-6<t ( − − 2) + 2 ( . 3) M 2M g M a
→ M a + 2M a = M − 2M g → a = 1 1 2 2 ( 1 2 ) ( 1 2 ) 1 1 2 2M2 ( − − 2) + 2 (
. 4) → M a + 2M a = (M − M ) (M 2M g M a 1 3) 1 1 g → a = 1 1 3 3 1 3 3 2M 3
F 0 A2"Œ$ % S (M − 2M g− M a M − 2M g − M a 1 2 ) ( ) 1 1 1 3 1 1 2a = + 1 2M 2M 2 3
UV=A<-AL%8R R % S 4M M a = M M g − M 2
M g − M M a + M M g − 2M M g − M M a 2 3 1 1 3 2 3 1 3 1 1 2 2 3 1 2 1
(M M +M M +4M M )a = (M M +M M −4M M )g 1 2 1 3 2 3 1 1 2 2 3 2 3 (M M + M M − 4M M g 1 2 1 3 2 3 ) a = 1 M M + M M + 4M M 1 2 1 3 2 3
hD(/<)=2A26> , S (M M +M M − 4M M 1 2 1 3 2 3 ) (M − 2M − 1 3 ) g g M1 M M + M M + 4M M a 1 2 1 3 2 3 = 3 2M3
(M − 2M )(M M + M M + 4M M )g − M (M M + M M − 4M M ) g 1 3 1 2 1 3 2 3 1 1 2 1 3 2 3 = 2M (M M + M M + 4M M ) 3 1 2 1 3 2 3 M 3 M − M M − 4M M 1 2 1 3 2 3 = g . M M + M M + 4M M 1 2 1 3 2 3 8M M M g FG"%$ 1 2 3 T = M g − M a = 1 1 1 1 M M + M M + 4M M 1 2 1 3 2 3
h!3\1M/< 16M M M g 1 2 3 T = 2T = 1 M M + M M + 4M M 1 2 1 3 2 3
%. g8R<c/31,%^/7/P!4a
-J;8F4c7ad/31,%/"%. ^$0!3!
@dA2c12^0%X89I>+(14d1M6;%U01I
>%.6;%^U89M7-;A2L(mcc8&'
$9M!@dA2c5
6$s3dA2c+,-48
9M!\M@dA2c"‡!$/^0%X8%8u0gT0uU8
„ ‡ ! R ‡ ! f%. ^
.C5 - \ „ %U8 E 7 „ • ‡ d /P ,4 c8 !
F+,-2dA2c,-2AB(ALq
38F7 F 2 2 a = = = 0 0 , 9m / s M + m 20 + 2
sm‡ 121M!@cA2d"%. ^$8&r4c7 ! MF f = M a . = =18 , N ms M + m
)C5-!+„j%^U
F+,-2„j‚"‡ $ 8fd,4c1M!@cA2 !
dN6;1M!1L‡ /T0uU8 !
sm 123d0 123c8 %
U<r4d07
„j.‡ "S$ !
U<r4c7 „ R "T$ ! %
FG"S$A2"T$! ' F−fms 2 a = = 5 , 7 m / s 1 m f ms 2 a = = , 0 2 m 5 / s 2 M
%. u8U+/r/Nym1,ALAB3/Pt6;!,
(V(218n=GI(VLa6;"%. $
$F!3!@/NyA2a"(V,6A2mV/N y$5
6$U<(V6A2I/Ny1L1M!7t/P` →
$sm F121M/ry0α7,-6K(V/rA2a8H/Ny 4
„!α.‡ ^ " $ ! ] „ U 1 α ‡! f%.
2 2
FG" $! l − h f = . F ms l
9MrAP714a+ h N = P − F sin α = P − F l 2 2
E7!3! f F l − h k ms = = N Pl − Fh →
6$hMta1M F12ta-1MU@yA2
a!2/P12t1L1M28E71M!A‹@'l8
%.%^8H<-A46/P/O0
</<1M=/P/O8o6<1M=/P/O|1ALAB3A4
0!3|112/0/31,A46;8
9M=/P/O14A4‡ ./A0/12!3\18
Fc'1BU> dv − kv = m dt dv k = − dt " $ v m
FO-VA<" $, k − t m v = Ce "%$
o12;!3O-V89N^5AA G"%$!oA 8 K k
"%$K2 − t m v = v e "S$ o
sm12)C+2A4,c-7 k − t dx m v = = v e "T$ o dt k h − mv − t x o = e m + B "X$ k
Z12;!3O-V8FG/^0^0! mv B o = k mv k − t
FZA2"X$, o x m 1 e = − k
%.% 8H<-AB</<1M=/P
/O06<;1M=|1ALAB3AB8
9Mt,-a14AB„{/A
Fc'1BU> dv mg − kv = m 8 dt dv k k mg = g − v = − v − " $ dt m m k
a mg u = v −
8" $K2 k du k du k = − u → = − dt "%$ dt m u m
9O-VA<"%$ k k − t − t mg mg m m u = Ce = v − → v = + Ce
"o12;!3O-V$8 k k
F+^0A^ mg C = − k mg k − t v = 1− m e k
vC+2AB,<+"-$ t t mg k 2 k − t mg m g − t x = v.dt = 1 −e m d . t = t . + e m −1 8 2 k 0 0 k k
%.%%8FO1M}63!N14IKd!N
6606<;I7/31, ^0+
d12∆^0^^ V0AB3A4KId12AgYX_!8
s36A4d!N v ∆ v− 0 v a = = = 8 ∆t t ∆ ∆t
9M}63!N14A4 mv F = m a . = = 8650N t ∆
%.%S8Rc/31,%^ALAB36IAXT/_8
&'1M6(14c0<c(G1!+$ -NT^
V56$ ^V5$ V8
92M62%.%%KV121MC8FA‹7P> m v ∆ F = m.| a = | t ∆
F!3%^%^8 ^S/5AXT/_ X_!5 v ∆ | = 0 −v |= 1 m 5
/ s A2
/=+>"tcA'V$!b7,/<)=48
%.%T8RA4/31, ^ALAB3A^%^^_!B-A2
yA24!VA2y18Z<+A4
y6;T8 ^.TV8&'1M=6y14A4A2
41A48
s36A4/4A2y
| ∆v| | 0− v | v | a 0 0 = | = = 8 ∆t t − 0 t
9M=6y14A4 mv 10 1 . 0−3 2 . 00 F = m.| a 0 |= = = 5000(N) t 4 10 −4 .
4VA4 v 2 v 2 0 0 1 1 l = = = v t = 2 . 00 4 . 1 . 0−4 = 4 1 . 0−2 = 8 0 (m) 4cm 2 | a | v0 2 2 2 t
%.%X8 R -V D 7 /3 1, T0XY8 ^.%S AL AB 3 A
Y^_!A2WA226AL74αY^ ^8FO1,1M
A-VD14268
hD('1BiiUcƒ(%,1M-VD(142 612
F.∆t = ∆P = m.∆v = ( m 2 v . .cosα ) = 4 5
, 6.10−26.2 6
. 0.cos 600 = 2 7
, 4.10−24 (N. ) s
%.%Y8Rc/31, XB(IAL371L
6;^0Tu_!%8Z<AB36Ic12A^%[/_8fQ$9MC(14
c56$h61Vc(G18
89MC(14c F = ma = 15 1 . 0 .3 , 0 49 = 7350(N )
o7,
68F+c(G112 v v = v − at = 0 → t o = o a 27 / , 3 6 t = ≈ 15 ( 3 , s) 0,49
%.%[8Fa-J>mzALz;0zJ >8
R,rG7"%0^$"A'r$c-J
>144ALAV3 ^_!8FO6<4Pc1,
3AL3z/=+G1Nr14<1N3NA'O6
I8o/31, /8 9Nr L = L = r × p 1 1
9NABK1r
L = L = r × p = − r × p "p = p − $ 2 2 1 2 1
644c1, L ∆ = L − L = 2 − r × v m 2 1
&rA1L L ∆ = x . v . m . 2 = 2 1 . .10 2 . 40(kg m . 2 = / s )
%.%g88o/31,,r14Gz4a0ALAB
36IA cL47 ^
αALa-J8& 'Pc
1, 3 AL z + AB3 ; 8
Rc1, v2 sin 2 α L = . m v y . = v . m cos α. o x max o 2g mv3 sin2 α .cosα L o = 2g
%8S 8o/31,,r14Gz4aALAB3
IA cL47 ^
αALa-J8 &'+ A23 ALz8
$Pc1M(145
6$Pc1,8
ZQ)!>=/P/O8
8U1M12m1M0cm1M M = mgx = mgv cosα t
. "12c-AB$ p / o o
68Rc1, L = r × p i j k → L = m x y z = m (xv − yv y x ) v v v x y z 1 L = m v cos α . t . − − − o (v sin α gt o ) v sin αt gt 2 v cos α o 2 o 1 2 L = v . g . m . .cos α t . o 2
%.S^8 F4a-J;Ž"%. %$7 /31,
6A2 !,(V/P(C0I/(V,/r) 1yQzAL
AB3/Pt8FO!>~(Vc/=@A2z6<;
/ 0AB312 8 ^ ω^ z f%. %
Z=2c1,7 2 ro mvr = mv r → ω = ω o o o 2 r
9M~F!,(V 4 r 2 2 o T = mω r = mω o 3 r
%.S 8R+/31,X^/>3(I
AL36;T0u_!%8fQ+7=<2A2m1,6/<
+7`
- !3 U+ 7 = ‰Š -I m 1,8 Fm 1, 6 /< 6; TXU
'1BiiUcƒ-(+
N+ m g = m a → N = m (a − g) n n n
m , N 12/31,+A2-=1M2!2(14+"AL1L n
6;m1,+$
F3(I0 a L304 N = m (g − a) < mg
HB+=…A2m1,6/<+ P' = N = m(g − a) P' = 50 ( . 8 , 9 − 9 , 4 ) ≈ 245(N)
%.S%8F+c6<1d0KI1d7c6
AB/31,1I1,6; /0%/A2S/8FO1M~1d
$9N>456$9NM(8
89M~1d1I1,
F u0gU0 F u0YU 0 % % F %u0TU S S
689M~1d+,-M( T + g m = g m → T = 0
fF F F ^ % S
%.SS8R,cKI(V-14-O48
9NI (I ! 7 A2 L/
(G1B(I8fQ)401M~(V-
t<2`o=+4!`
F+,->+=‰aŠ5
F+,->.6+
F+,->6.‰…Š8
'1BiiUcƒ-(/>+ T + g m = a m → T = m(a − g )
n(I14-O40 a L14(7 T =T = m + " $ 1 (g a)
n T = T = mg 2
nB(I14-O40a L3(7 T = T = − 3 ( m g a)
HB41M~(V-c>M=(I
'1BiiUcƒ-(+ N+ m g = m a → N = m − n n n (a g)
m , N 12/31,+A2-=1M2!2(14+"AL1L n
6;m1,+$
s3-" $0m1,+c>M4!b=(I0
+c>M!b=•a•0•6+•0A2•…•8
%.ST8F4x;)0+aAB7/31,
/)X^8f!3!@ABA2x6;/^0%X8fQ
$9M!-=71L6;64AB,@4x<x)
ALAB3 %Ad_-N5
6$HLAB372AB6eI,/Qx`
o1M(A2AB6W1MAB0-=1Mx147"M3
ALm1M$A21M!8'1BUcƒ F = ma = m 2 ω r = 4m 2 π f 2r ms ht
8/P, F ≥ 4m 2 π f 2 r ms 2 2 12 F ≥ . 4 1. 1 , 3 4 . . 5 , 0 = , 0 789 ms (N) 60
68E F ≤ kN = kmg04AB6eI,/Qxc" $07 ms kg m 2 ω r ≥ kmg → ω ≥ r
HB6eI,/ 0 2 , 5 9 . 8 , ω = ≈ 2 2 , (rad / s) 0 5 ,
%.SX8&'1Mr-PA2<6KA2-
Ad21</31,-P6;[X/06/OAd21
6;%^^0A2AB36Ad211P1P/PtA26; SY^/_8
'1BiiUcƒ-(-P mg + N = a m " $
N 12-=1M2<(14-P"6;A2,AL1Mr
-P14<$8
FAd210c-LV0" $,A<2 v2 v2 mg + N = m → N = m 1 − g R R (100)2 N = 75 − 9 8 , = 301 1 ( 5 ) N 200
FM-Ad21 v2 v 2 − mg + N 2 = m → N2 = m + g R R (100)2 N = 75 + 9 8 , = 4485 2 (N ) 200
%.SY8R6-=1M6ALAB3u^^/_8s=<-P7'
,!M~m1,14X1I8F6/OQAd1,267
,8
f,-1M(A2-Pc-LV12„ 8'1BiiUcƒ 2 mv F = ht R
F6")<-)O$-P'(m1MA2
1MLV g m + F = a m ht
Fc62 F v2 | g ht + |≤ g 5 → ≤ 4g m R v2 (250 )2 → R ≥ = ≈ 160 ( 0 m) 4g 4 8 , 9 .
S. 8F6\7a60/31,1I
1,6; 0 0 8&'/3V678 % S
-(+,-%S5 %8
omAb8F "^5 $5 "._%5^$5 a 3 / 2 %
S"_%5^$8E7 s r % G z S m r i i r = i G mi i m x + m x + m x m − m a x 1 1 2 2 3 3 3 2 = = . G m + m + m m + m + m 2 1 2 3 1 2 3 + + m y m y m y m 3 a . 1 1 2 2 3 3 1 y = = G m + m + m 2 m + m + m 1 2 3 ( 1 2 3 )
HL 0 % a
3 5>s;O@ % S x = 0,y = G G 4
+-V>AL7\a/31,%8
S.%8F4xdW6/Ow7/r1ydQ6/O5
V1y/r;Vx6;w_%8&'A'O/3V x48 w z z w_% z% r r 1 2
f62S. %
o7xd6I12WxdQ"-I6'/r$06
/O07/3V;z 01e-AL-Ixd1!/1L6'/r"-I,P %
6;($07mV;z 8f41227mVA2
NVzx6I8
&r)<73;Vxd8smAcA'O/3V
x/r1y0xC/r1yA2-Ix6'/r1I1,12 , c a, ,
b 8F7
c = 0, b = R / 2 8 F7 M.c = m a + m b 1 2
ρ .πR2 .0 = ρ (πR2 −πr2) a . + ρπr2 b
. " 7 ρ 12 B /3 1, x$8 r2 r2 b Rr 2 b a = − b = − . . = − . R2 − r2 (R 2 2 − ) b r b 2 (R 2 − r 2 ) b
HB0/3VxC6'/r;VzA-O3(AL1y/r 2 Rr x = b = 2( 2 2 R − r )
S.S8o76!N/31, ^7/P!4+
8F46!N7e/}6/31,X8s=!D/}6=
c-+8H47/31, ^^/A27AB3Id12X^^_!8
&'AB36!N!/6e06<;
$9NI6!N>45
6$FL/6e06!NALAB3 g/_c6e5
$FL/6e06!NALAB3 g/_,6e8
sm/31,!NA2A41I1,12RA20AB36!NLA2
!/6e0A46e/Qd1I1,12A0AjA2A 8&rA46e, ^
6I8
Fc'1B6=21, (M + m)v = ' Mv + ( m ' v −v ) 0
(M+ m)v' = (M + m)v+ mv 0 m v' = v + v 0 M + m
$Z!N>4A^0A X^^"_!$ ^ 100 v' = 0 + 5 . 00 ≈ 3 3 , ( 1 m / s) 15 1 . 03 + 100
Z!N,6eALAB3S0S "_!$8
6$Z!Nc6eAg"/_$X"_!$0A .X^^"_!$ ^ v' = 5 − 3 3 , 1 = 1 6 , ( 9 m / s)
Z!Nq6eALAB3 0Yu"_!$8
$Z!N,6eAX"_!$0A X^^"_!$ ^ v' = 5 + 3 3 , 1 = 8 3 , ( 1 m / s )
Z!N,6eALAB3g0S "_!$8
S.T8RcKI/P!ALAB3A _!4a
+;"S.S$8F26c7/31,R ^/8R)=I/3
1,%/6c,1ALAB3;A [_!8 %
h/a-c0)=I;B-8fQ!7cc
20ALAB36;64`
Fc'1B6=21, A % A fS.S
Mv − mv = + 1 2 (M m)v Mv − mv − 10.1 2.7 v 1 2 = = ≈ 0 − 3 , ( 3 m / ) s M + m 10 + 2
"o(AB3126Ic$
HB0cALAB3^0SS"_!$,AL6I c8
S.X8R/}6/P76-B3B0=(L7αTX^
!ALa-J;8H47/31, ^/A27AB36IA ^
%^^_!867/31,RX^^/8fQAB3B!N<6Q) !`
smAB3B!N12A8E6Q)!46=21,c
- Mv + mv co α s = 0 0 mv 0 α cos 10.cos 45 v 0 = − = − ≈ 2 − 82 , (m / s) M 500
S.Y8R=?1NI>40!7-/Oa-O!ALAB3
/PtS^^_!3AL=?8FyV01,/O-6;µu^8
n31,t6I=?6;R %[^8fQ ^
$h61V=?LAB3AT^_!5
6$ n /3 1, t = ? 12 u^ AB 3 = ? 12 6 4`
ZQ)!>=/P/OA21MNF8
&r + 0 /3 1, d 1 = ? 12 R0 AB 3 12 A8 h
/=+Q(=?-74/31,(R0AB312A#(A0
-I/O-7AB312"A.$8
Fc'1B6=21,
M.v = (M −dM)( v + dv ) + dM.( v − u )
M d . v − dM u . = 0 v M dv dM dv dM = = 0 M0 u M u M v M M 0 0 = ln = ln u M M − t µ 0
HB3=?+Vc6> M M v = u 0 ln = u 0 l n "Œ$ M M − t µ 0
$F+AB3=?AB3AT^_!8FG6>"Œ$! v M v M 0 0 exp = t = 1 −exp − u M − µt u µ 0 40 270 t = 1− exp− . ≈ 0 3 , 75 (s) 300 90
6$HB3=?//31,dRu^ M 270 v = v 0 ln = 300.ln ≈ 330(m / s) 0 M 90
S.[8FPc1,F3AL)478&cF
12Ia0W76/OwYT^^/07/31,4
6ρX0X_S8
RPc1,)=IaW)+/O12 2 2π 4π 4π L = Iω = MR 2 . = .ρ . R 3 R 2 . 5 T T 5 3 5 16 2 π ρR5 16 2 π 5500 (.6 4 , 1 . 06 ) = = . ≈ 7 2 , 1 . 033 (kg m 2 . / s) 15 T 15 24.3600
S.g8RxdW/31,^0S/076/Ow^0T0)
ALAB37ω X^^Ad_-N8F(14xPcC5x)B
(IA2!+∆%^V(G18FPcC78
3AL))3'ALPc1M/Pt0AB3
76<tc+AL37 ω − ω M 0 β = = I t . π 2 1500 2 , . , . ∆ L ( I ω − ω ω 0 ) 2 0 3 0 4 mR 0 60 M = = = − = − ≈ 0 − 1 , ( 9 N m . ) t t 2t 2 2 . 0
S.u8Ra0W/31, ^^/06/Ow^0X)
)78F(141MC„%TS0TU0<-<ALa
A2AP7AL)8h+∆S 0TV0(G18FOAB37
1N6eI(1MC8
n(1MC„14a0Pc1MC1
) ω − ω M β = 0 = t I Mt FRt 2Ft ω =ω − = − = − 0 2
I mR / 2 mR 2 (.− 243, ) 4 .31 4 , = − ≈ 30 ( 0 rad / s) 100 0 . 5 ,
S. ^8Ry7/31,X^/0+/O 0)ALAB3g^^
Ad_-N8F (A21MC<-<ALa A2AP7AL
)8h%-NS[V0(G18F
$RPcC56$9MC<-<8 F7 2 800 2 . π 2 50 5 , 0 . . L ∆ I (ω − ω ω 0 ) mR M 60 = = = − = − ≈ − , 6 67 (N m . ) ∆t ∆t t 157 M mRω , 6 67 F = = − = − = 1 − , 3 34( N) R t 5 , 0
S. 8RW(21^0X^7)M()
;)I8RA4/31,^0^ /6c
-;ALAB3AT^^_!L4A2I/A2eA2
8FAB37!/A4B-A28Z<;Pc
)O3AL)6;X/%8
-('1B6=2Pc1,{A4 mvl = I' ω = ( 2 I + ml )ω mvl
0,01. 400.0 5 , ω = = ≈ 0, ( 4 rad / ) s I + ml2 5 + 0 0 , 1 0 . 52 ,
S. %8RxdW/31, ^^/)ALAB37 ^ ω
Ad_-N8R+/31, Y^/>Kr-x8fQAB37x/ %
+A2>KVx8o+8
-('1B6=2Pc1,+{x I ω = I ω 1 1 2 2
2 2 I 0 5 , m . R + m R m + 2m 1 1 2 1 2 ω = ω = ω = ω 2 1 2 1 1 I 0 5 , m . R m 2 1 1 100 + 2 6 . 0 ω = 1
. 0 = 22 "Ad_-N$ 2 100
S. S8&'Pc)OW(2/31,3
AL!V
$F)@A2AL7α275
6$F!!ALA2(5
$FAP7ALA2@(8
$F!!+,-2AL+,-))@A2
AP 7 AL 8 F + ,-0 4 0
/=G7<)-!31I/Pt12!1I r = r.sinα 1 2 2 2 dm r . = dm r . sin α 1 r2dm = 2 sin α .r 2 d . m 1 2 1 I = I .sin α 2 2 = ml sin α 1 12
6$&r)qAL0m40/=G7
<)1P6;/P04Pc)O3AL)q
AL126;^8hD('1:fc.hcc 2 2
I = 0 + md = md
$hD('1:fc.hcc 1 2 2 I = ml + md 12
S. T8Rx6;W"/31,4-g0u ^S/_S$76(26T8 ^.
S06/OwX8 ^.%8x6'/r1yd6/Ow_%S.T8F
Pc)OxC6'/r3ALAP7ALxA2)Vz x8
sm i 12 Pc ) O x 6' /r AL ) ^
∆ ) V A2
AP7ALx5i A2i 12Pc)O-I6'/r3AL) %
)V-I6'/rA2AP7ALx8F 2 2 2 4 MR ρ.b. R π .R π bR ρ I = = = 0 2 2 2 π R 2 . 2 ρ b . . R 2 . 4 πρ
FM m R bR 4 I = I = = = 1 2 2 2 8 32
Fc'1:hcc{fc0Pc)O-I6'/rAL )∆12
4 2 2 4 πρ π πρ bR R R 3 bR I' = I' = + b ρ . = 1 2 32 4 2 32
RPc)Oi xC6'/r3AL / ∆12 4 4 πρ bR 3πρ bR
I = I − I' −I' = − 2. k 0 1 2 2 32 4 3 3 − 4 5πρbR 5π 8 . 9 , 1 . 0 4 . 1 . 0 .0 0 , 5 4 = = ≈ 2 2 , 1 . 0 − ( 2 kg m . ) 16 16
S. X8FPc)OF3AL)7<16/O
F12wYT^^/A2/31,46F6;-X0X8 ^. S/8S8
F7I4Pc)OF3AL)712 5 2 2 2 4π 3 2 8πρR I = mR = ρ. R R . = 5 5 3 15 8π 3 = .5 5 , .10 ( . 6 4 , .10 )5 6 37 ≈ 9 9 , .10 ( 2 kg m . ) 15
S. Y8 F ( 14 6 c6 /O w ^0X A2 7 Pc ) O i
%^/8%01M<-<ALA26„ ^^U8F
$s36c5
6$HB3(24A26!/(1M ^V6<;
1NI6c>48
s376c12 M Ft R 100 5 , 0 . β = = = = 5 , 2 ( 2 rad / s ) I I 20
HB34A26c! ^!12 v = R ω = (βt)R = 2 5 , .10 0 . 5 , = 12 5 , (m / s )
S. [8R6c6/OwX^)(L(Pc1MR
ug^U8fQ-=y-(14A261M6;64
6c)B(IAL37β.%0X(_!%8Z<!3!/^0%X0Pc
)O6c3AL)iX^/8%"S8X$8
sm1M2y-(14A26c12„89M!VCc!b
7-<-<AL6cA27t1L6;%/„"(-$8 F7 M − M − M 2kFR ms β = = I I M − Iβ 980 − 50 ( . − 2 5 , ) F = = = 442 ( 0 ) N 2kR
2.0,25.0 5 ,
S. g8R\7/31,,a4a-J;"
S.Y$8RPc)O\3AL76;i8U+/r\
6;1M8fQ →
$ s7 α @ 1M F A2 a -J ; -= 6; 6 4 \
73A-O1M/r5 →
6$9M F -=71L6;64\/P,`o!3!
@\A2a-J6;/8 Fn F F t
$R3\73A-O1M/r0\-=)c/
WW8n7 F co α
s (R −r cosα )− F si α n r . si α n > 0 FR co α s − Fr > 0 r cos α > R
6$F7- Fcosα − F = γ m = m β R ms
mg − N − F sinα = 0 FR co α s − Fr = (I + 2 mR )β N = mg− Fsinα F(Rcos α − r) I cos α + mRr F = Fcosα − mR = F ms I + 2 mR I + 2 mR
\/P,I7 N ≥ 0 F ≤ kN ms mg F ≤ sinα I cosα − mRr F ≤ k (mg − F si α n ) I + mR 2 kmg ( 2 I + mR ) F ≤
I (cosα + k sin α) + mR(r + kR sin α)
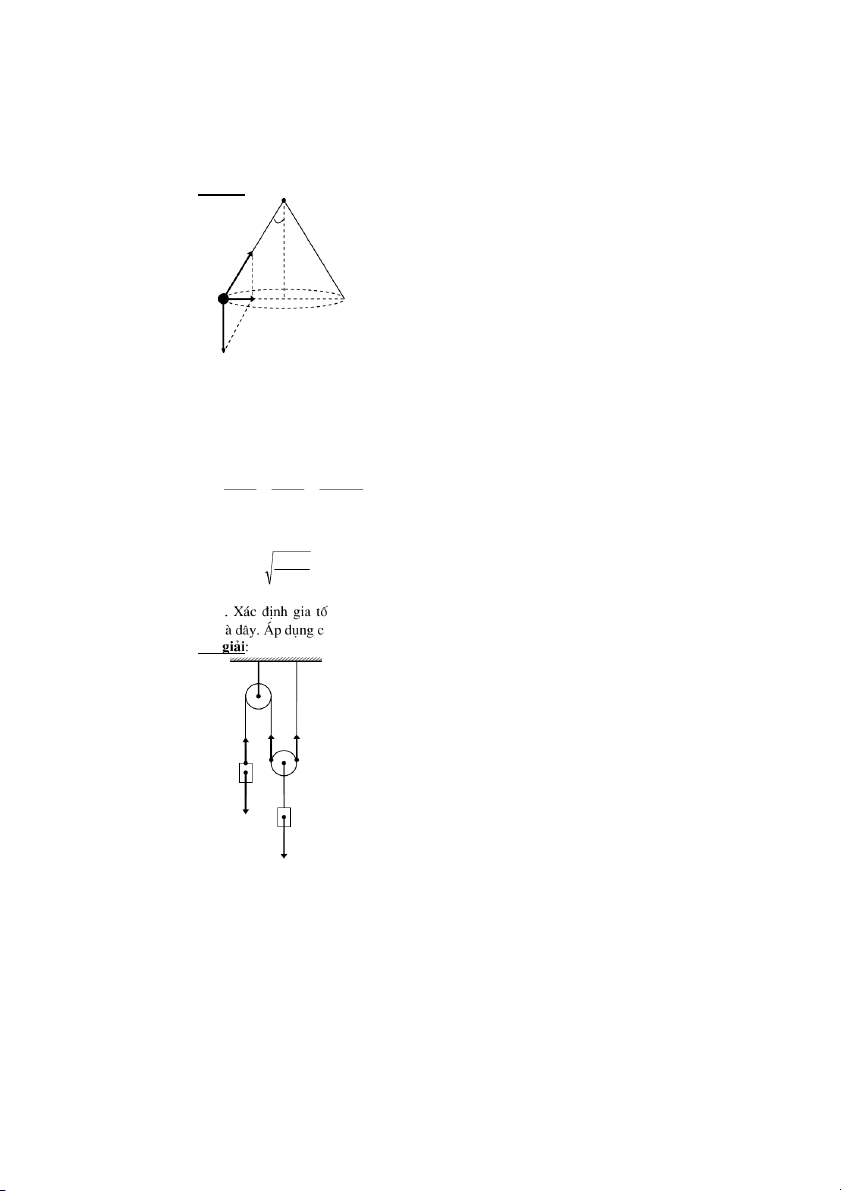
S8 u.F4y/31, /0+!,(V/PC
7/31,A2+/OQ/P/8IM((V,e4
3'"S.[$8(L(m1,8F3A2
!>~(Vc8
F
F AG ) AG 8 sm F 12 !> ~ (V8 F< 1B- - 1M A2
Pc1M07 mg − T = γ m TR = β I = β 2 mR
Ra/0G314@AB3(2A2AB3707 v = R ω γ = βR
F7- mg − T = mγ 2 γ m = mg T = m β R = γ m T = mγ g 9 8 , γ = = = 4 9 , (m / s 2 ) 2 2 mg 1 9 . 8 , T = = = 4, ( 9 ) N 2 2
S.%^8fAB7/31,1I1,6; A2 " ‚ $0,3AL % %
6;!,(VAe)dm"/31,dm6;$"S.g$8F
$s3AB5
6$h>~F A2F (Vc8odm12xd5!/P %
/8-(6;!3 %/0 /5 /8 %
F<1B--1MA2Pc1M m g − T = m γ 1 1 1 1 T −m g = m γ 2 2 2 2 2 ( γ T − T = β = . 1 2 ) mR R I 3 2 R
F% % F %
E?γ =γ = γ = γ 07- 1 2 3 T = m g T m g 1 1( − γ ) = 1 1 ( − γ ) T m g T m g 2 = 2 ( + γ ) 2 = 2( + γ ) m T − T = γ m 1 2 γ = (m − m g m m 1 2 ) − ( + 1 2 ) γ 2 2 m1(4m2 + ) m g T = 1 2m 2m m T γ 1 = m 1(g − ) + + 1 2 m2(4m + m 1 ) g T = m γ 2 2 (g + ) T = 2 2m + 2m + m 1 2 (2m γ 1 + 2m 2 + m ) = 2 (m1 − m 2 ) g ( 2 m − m 1 2 )g γ = 2m + 2m + m 1 2
S.% 8RWaW/31,R%0XT/A2ABa
/31,^0X/,3AL6;!,(VAe)dm"S.u$8ZQ
)/31,(V0dmA2/eAL8F3ABaA2
!>~(V8
smF12!>~(V0G-1MA2Pc1M07! mg − T = γ m mg − T = γ m MR 2 2 γ 3 TR = β I = + MR T = Mγ 2 R 2 , . , 3 mg 0 5 9 8 γ = = ≈ 11 , 4(m / s2 ) mg = m + M γ 3 , , . , 2 0 5 + m + 1 5 2 54 M 2 3 T = Mγ 3 T = Mγ = 1 5 , 2 . 5 , 4.11 , 4 ≈ 4 3 , 3(N) 2 2
S.%%8RAB]/31,,4a-J4A212)6
c76/Ow"S. ^$8RPc)O
6 c 3 AL ) 6; i8 n3 1, F (V
/P/8F376c` F
„!
smF12!>~(V07- TR = β I
T − mgsinα + kmgsinα = γ m = m β R I β − m β R
= mg sinα − kmg cosα R mgR( si α n − k cosα ) β = 2 I − mR
HL/12!3!a-J4
#U< k > tgα 0KV6; β = 0 8 #U< mgR si α n
k = 0 β = 8 2 I − mR
S.%S8R7(21 ));)
I89NI0KA'O;0!7,="S. $8
F371N6eI=A21N)A'OJ>8
RPc1M(m1MV))/47!AL
-J>12
M = F(l / 2 ).sinα sinα si α HB M mgl g 3 n β = = = I 1 2 l2 2l 2. ml + m 12 4
#FA'O6I 3g 8 , 9 . 3 = 900: β = = = 14 7 , ( 2 m/ s ) 2l 2.1
#FA'O)A'OJ> = 0: β = 0 .
S.%T8RxdW6/Ow /31,7))
;AP7ALxA2Vxw_%8x6eI)GA'
O> ALA' OVx ALAB3 I6; ^8& 'Pc
1,x3AL)/x)A'O-8
RPc)Ox3AL)12 2 2 1 R mR 2 3 I = mR + m = 2 2 4
-('1B6=2~1, 2 2 1 ω 2 (I ) L mgR = Iω = = 2 I 2 I 2 2 3 m 6 gR 3 L = 2mgRI = = mR gR 4 2
→ →
S.%X8R7t1,6; K A2Pc1, L 3 → →
ALz8& 'Pc 1, 3AL zj6< OO' r 8 0
F+,-2Pc1,/P-z`
RPc1,3ALzj12 L = r m v r r m v O' ∧ = O'i i i ( + Oi OO' ) ∧ i i i i = r ∧ m v + r m v Oi i i ∧ 0 i i i i
= r ∧ m v + r ∧ m v Oi i i 0 i i i i = L + r ∧ K O 0
RPc1,/P-A2z L = L ⇔ r ∧ K = 0 ⇔ K = 0 O ' O 0 →
S.%Y8o>;Pc1, L 3AL z → → → → →
e1AL )<n76K L L # 12Pc ^
r • P 07 L 0 ^ →
1,3AL/3V0 r 12Ar6/O/3V3ALz 0 →
n0P 12t1,8
FM62S.%X0z6;mVs0A2zj6;zn07 L = L + ∧ O rO P
T. 8fQ6-=7P!6;6406<;67
/3 1, S^^^/0/6 14 / -= -N8 ZQ ) !> = /P/O8
R3 6 14 0 6 -= 3 P e P = m 1M ]
∆ 8FG7!P!6 A mg∆h = t ∆ ∆t
FS^^^/0 / ^^^0∆ -NY^!A2A26>4
O,Tu^/‘8
T.%8FOPI</r1dC%^06<;1M/r|1AL
C1dA231dC -=I1MS^U8
f!32W1d6; k = N 30 / c 1 m = 3000N / m
oP1M/r x ∆ x ∆ 2 ∆ ] ( ) F dx . = (k x . ) k x dx . = 0 2 0 0
HL/S^^^U_5∆%^^0%]Y^’8
T.S8RPP/31,0/e3(37AB3
/PtAXT/_84(312T†8fQPP-=7P!6
4714,(34qALAB3XT/_8
H/e3(30PP7AB3/Pt4-=7/ ‡ ! ! α8
c14(31M/r„ PP-=6; /
„ ‡ #8! / !
α%88!α
oP!PP/14(3ALAB3A,OcP> A F S . k P = = = F . v = ( . 2 mg. sin ).v k t t " $ = 2.1000.9 8 , .0 04 , .15 ≈11, kW 8
T.T8RPP/31,%01c14(374T†8f!3!12^0^g8 F
$oPM6KPP4)C+(2S/5
6$ oP! PP0 6<; + < )C+ 4 T -N8
9M/r-=V6;AL2-I8!αm1MA21M ! F = mg.sin α + f = mg.sinα + k m
. gcos α ≈ mg.sin α +k m . g 8 k ms
oP/r4)C+(2S/ A = F S
. = mg (.sinα + k) S . = 2000.9 8 , ( . 0 04 , + 0 08 , ).3000 = 7 06 , .106(J )8 k
oP!
A 7 0 , 6.106 P = = = 2 94 , .104 W = 29 4 , kW t 4. 60
T.X8R22/31,X^4+;ALAB
3/Pt6;SY/_8oP!I12%%^0g/‘8F!3!@
2A2+8
n4+;01M/rII-=V6;
AL1M! F = f = k.mg 8 k ms
oP!I7'cP> A F S . P k = = = F v . = k m . g v . k t t 3 P 220 8 , .10 k = = = 0 045 , mgv 50.103 9 . 8 , 10 .
T.Y8U++'P!6;<6'Ab T.T8
F<6'W2/…-0/…-aA28R2…-,eAL
d03d7cmABv8FmAB,m!7V6;AL1M
!A2@d;8&'P!<!3Ad)
12Y^Ad_-N0(2d/GV1 0m1,
AB6;vTu^U8Fm1,d/P/8
sm‡ 12M!@2/…-A28F7/V ! 6; Ql f r . = Q l . 8 ‡ ms ! r 1 v
oP! Q l. P = f . v = . ( π . . = π
0 12!3Ad) ms [ 2 n)r] 2 Qnl r
V8 P = 2.π 49 . 0 1 . 1 . = 3 08 , 10 3 . W
T.[8RP! X/‘-1+(V]Z"
T.X$8Z/O-1%X0 AB 3 ) -1 %^ Ad_-N89M ~
4](V1L-P1M~(LZ8F1M~76<
;(V!!AL8
oP!-1
„8A“"F .F $8”8% ] Z π88
FG/F %F !F %8F P 8 ] Z ] Z π r. n . 3 F!3 15 10 . T = 2T = = 9556(N) A B π 0 . 25 , 2 . F] 1 F Z
T.g8R <c /31,%^^^^/ B(I (L(
1M !6;Y^^^U8 h+c(G 18HB36Ic12 XT/_8FO
$oP1M!5
6$vC+2cC,/G1N71M!(L/c (GJ8
EMc'1:~0P=1M!12=~cG
'6IA^0(70P271LO6;~6Ic 1 2 1 A | = ∆E |= m v . =
. 20000. 152 = 2,25. 106 J 8 ms K 2 2
vC+2c(,/G1NCc</c(GJ A , . ms 2 25 106 S = = = 375(m ) f 6000 ms
T.u8FOPI<22/31,g8 ^X/
$F~3GA SY/_<A XT/_3 %
6$EG1<AB36I12[%/_8
F!b-('1:~6<4~AB6;P(
1M(A2AB(7
$oP12c~AB3GA SY/_ ^_!<A XT/_ X_! % 1 2 1 2 1 5 2 1 A = ∆E = m v . − m.v =
.8.10 .15 −
.8.105.10 2 = 5.10 7 J K 2 1 2 2 2 2
6$oP12c=AB3GA^[%/_%^_!<A^_! 1 2 1 2 1 A = ∆E = m.v − m.v
= 0− .8.105.202 = −1 6 , .108 J K 2 2 0 2
oP212P="PV$8
T. ^8R/}-/31,RTX^/=c-;8
-7/31,X/0AB3IdATX^_!8n6e06-BA-O
!!TX8F1MC6(14-8
smH12AB3B1q/}-8EMA2'1B6=21,-
(-7 m M V . + m v . = 0 V = − v . M
R A H
9MC/}-!P12=~/}- 1 2 F S . = M V . .< 2 FG7 M V2 . m2 v2 . F = = .< 2 S . 2 s. M . 5 2 4 . 50 2 = = 12500 (N ) 2 0 . 4 , 5 4 . 50
T. 8RA4 /31, ^/6 ALAB3 A ^^_!a-
6=y(2A2e!VA26=y!T8F
$9M=66=y14A45
6$HB3A4!//Q6=y\(2(%8
$FA‹!D('1:A~7,- 2 − m 02 . mv2 − mv2 10 1 . 00 F c s 0 . = − → F 0 c = − = − = −125 ( 0 N) 2 2 s 2 2.0 0 , 4
6$H47/=~4!VA26=yTL(G18U<6=y\
(2%!/4)6=y0A4A‹d<-ALAB3
Aj•A8Fc'1:A~ 2 2 − ]j mv' mv 0 − = Fc d 0 2 2 2F d 2 −1250 .0 0 , 2 c 2 ( )
! Aj 2 + v = + 100 ≈[ _!8 0 m 10
T. %8 R c 4 G \ (3 -J Eo 7 " T.Y$ A2
(GJ1!/C,;oZ8o]Z!5]o 5!3!
@cA2a+4EoA2oZ6;8
FO!3!A23c4+EoA2Zo8 E α o ] Z ! 1
.F\a-J4c7<~‘ 8oO<~2C(q
eP] A2] 1M!4+EoA2oZ8E7‘] # %
] 07P1M!4EoA2oZ12 % ] /8"8!
α$8Eo/815
] /"!.1$8 %
FG7! h
mgh = kmgl + kmg(s − l) = kmgs / 8 s
.VO1MA2-('1BU>0,-
!α."‡ $ 8 0 " $ ! Eo Eo
./8oZ "%$
FG" $!
!α./8"8!α$8 Eo h h l a
=g (sinα −k cosα ) = g . . CD − 2 2 2 2 l + h s l + h gh l = 1 − Z > l 2 + h 2 s odG"%$ h a = −kg = − g . < 0 CB s -!3 h gh l h k = ; a = 1− ; a = −kg = − .g 8 DC CB s h2 + l2 s s
T. S8 R AB /3 1, , /P ! G \ a I3(L
"T.[$8fQG/=∆2"OG\aI$AB6eI/QaI8
o6/OaIwu^8 ∆ w w fT.`
F)AB,4aI0AB'(1Mm1M
ABA2-=1Mw aI8Ft,-1M22-I2-I
--<7Ad1MLVdAB02-I<-
<-V,(IAB8
&r2-I--< m v 2 . m v2 . m v2 . P − R = m a . = R = P − = mg cosα − n n ht R n n R R
Ra/0c'1B6=2~=<~AB6;~
~AB8 1 ∆ A%8 2 2mg∆h R − ∆h 2m ∆ g h ∆ 3 h R cosα n = mg − = mg − = m g − 1 R R R R
HB \ 7 , m 12 6 4 a I < 7 d - 14 a I 1M
"6;-=1MwaI$0> 12w≥^8hM+/Qa I6e I= / w ^8f 3∆h R R = mg 1 − = 0 h ∆ = = 30c . m n R 3
T. T8RAB/31, /,4a-J4,-ALa
;7α!!α^0 8h/,<a-J40ABd
<-4a-J;1 ^L(G18f!3
!!3)/^0^X8FAB3ABK3a-J
4893m+ ^_!%8 ] 9 α Z f o ! 1
E(1M!‡ ./0AB,4a-JZoAL !
3./88smA12AB3ABK3a-J40c'1:
~7 1 1 f l . = 0 − mv2 kmg l . = mv 2 ms 2 2
→ v = 2kgl = 2.0,05.10.10 ≈ 3 1 , ( 6 m / s)
T. X8FG\-%^0+rd/31,X^c
-4ALa-J;0ALAB36IA g_!8nL ^
ad7AB3A%T_!8FOP1M=/P/O14d8
om3O<~;a8F+I4d7~ 1 W = mv 2 + mgh t 2 0
F+da77~ 1 2 W ' = mv t 2
wk2~1N!d6;~6Id4
P!1M0(7
W' = W + A A = W' −W C C m
A = ( v2 − v2 ) − mgh C 0 2 0 0 , 5 =
(242 −182 )− 0 0,5 9. 8, 2.0 = −3, ( 5 J) 2
T. Y8RAB/31, ^/,G\a-J4%^
38nLV(3AB7AB3 X_!8FOP!8
oP!6K1M!6;6<4~AB 1 2 1 A = W − W =
mv − mgh = .10.15 2 − 10.9 8 , .20 = −83 C D! 9 ( 5 J) 2 2
T. [8I!,(Vz]0(21S^7cABa"T.g$8fQ
-]-=ABAB36r6;64AB7
)da-JJ>8
v Z B F z 1 v ] A
F]AB,~ 1 2
mv 8h7AB6eId A 2
14-O48F< ~AB ~(I0~ "(7AB3$ AB= (I "T.g$8
R3ABda-JJ>0AB3A AB Z
Z-=1L12!,(V1P6'~"F≥^$8 → → →
H Z AB ' ( m 1M P = mg A2 1M ~ T " L c
-J>$1MLVdAB04 mv2 F B = = mg + T 8 ht l
HBAB3QZAB7)d A Z gl 8 " $
Ra/0c'1B6=2~ "∆‘ $ ." $ 0 ]Z ∆‘ ]Z
! v2 = v 2 + 4gl 8 A B
HB AB 3Q I AB ] 7 ) d a -J
J> ( v 2 ) =( v 2 ) + 4gl , v = g 5 l = 3 8 , m / s A min B min Amin
T. g8R1em1,,/r/Q-J>7α
u^^0!71e,=8o>;!>~(Vc6;S/
1e)A'OV6;8 F A
n)A'OV6;0,-1M@!>~(VA2m1M1e
1MLV28
mv 2 mv 2 T − P = m.a = T = + mg ht l l
-('1B6=2~7 1 mv2 = mgl 2
FG7!!>~F 2mgl T = + mg = m 3 g = P 3 l
T. u8 R )= I /3 1, ^0 / , e K I … (2 1
0%[/31,/P/8f)a-JJ>)I
/8F)=I7AB3A T0 S_!8 ^
$F !M- <~A2 ~ )=Ic7 α,-6K
A2-J>8om3O<~A'O-)=I8
6$&'1M(F)=I14c7 α8FFA'O
-A2)=I8
om3O<~A'O-])=I8n)=IKo0
,-AL-J>7α
$<~A2~)=I12
‘ 18" .! o α$5 ‘ 1 2 mv 2
Fc'1B6=2~7
‘ #‘ "‘ $ #"‘ $ 8 ^ ^
f mg (l1− cos α) 1 2 + mv = mg (.2. ) 1 2 l + mv 0 2 2 1 1
v = 2gl (.1 + cosα ) 2 + v 5 ‘
mv 2 + mgl(1+ cos α ) 0 2 mv 2 2 0 Z z v F α o o ]
6$1MLVAB,)<'6Km1MA21MF mv 2 F = = T − mg co α s ht l mv2 mv2 → T = + mgcosα 0 = + 2m (
g 1 +cosα ) + mgcosα l l
v 2 F m 0 + g 3 cos α + 2g l 2 v2 4 1,3
F-0α^ T = m 0 + g 5 = 0 1 , . + 5 9 . 8 , = 6 2 , ( 4 ) N l 1 2 , 7 v2 4 1,32
F0α g^^0 T = m 0 −g = 0 1 , . − .9 8 , = 0 3 , 6 ( 3 N) 8 l 1 2 , 7
o=A'O0AB/r~8
T.%^8AB3A4+(q1eD87126
cKI!,(V"T.u$8nA44A26076'e7A26
,V14278FAB31N7!e-4A268
Z</31,A4120/31,612R8
V1262A8R3=70-('1B6=2
1,A2 ' 1B 6=2~8 sm A A2H1I 1, 12AB 3 L/ 4A2
6!/74A28 α R A
'1B6=21,
A"R#$H8 " $
'1B6=2~
"#R$ V2 "#R$8 V = g 2 h "%$ 2
FG" $A2"%$!A m+ M m + M V . = . g 2 h 8 m m
0R0!bO,AB3AA48
T.% 8R3|/31,R7MA2m4c,B6;
N/31,8|,eKI>(2 1m1,
/P/"T. ^$8n73|04c630N6'6B(L-
!4c8fQAB36B6rN-=6;643|7
),=Ad)cz8
smA0H1I1,12AB3NA2AB33|8
-('1B6=21,7 R8H8A
Fc/<)=62T. [03|7d)
czAB3H7-2-==C/ V ≥ gl 5
M V . M 5gl v = ≥ m m z 1 R H A
T.%%8Rd6/31,/P!4+C7
(AbT. 8fd6,=/P7AB36IG%w0/O
L6Q/P/8fQ
$2d6+/Q+C`
6$1L2d6!b,!/+/Q+C`
$&c62B-T. S0T. gd6+/Q+C/1Mrd614C
6;/P8FG/4! ] o Z f % f 8! mv2 α 0 " $ fT.%% R
-('1B6=2~)]Z"Z12d6++
C$7f 5 "T.Sj$8 R 3
6$HB3d6Z,!G" $ A 2Rg ^
8h/++C06c-61\o8HB 3
3;Ko"A $ A ! $ A ! ^
α0AB3J>"A ^
α .8 -('
1B6=2~)]o0! f 50 8 % R 27
T.%S8R)=I/31,%/0ALAB3S_!0A4
VAL)=I>/31,S/qAL)=I>
ALAB3 _!8FAB3)=I!A<
$H12222W8
6$H12/P2W"$8 A % A% #
$H2W
H @ AB V c ' 1B 6= 2 1, A2 6= 2
~8F7-6=2
m v '+ m v ' = m v + m v " $ 1 1 2 2 1 1 2 2 1 1 1 1 2 2 2 2 m v ' + m v ' = m v + m v "%$ 1 1 2 2 1 1 2 2 2 2 2 2
o=!314)< AA<014)< !A<d %
1-4 m v −v = m v − v "S$ 1 ( '1 1 ) 2 ( ' 2 2 ) m v ' −v = m v − v ' "T$ 1( 2 2 1 1 ) 1 ( 2 2 2 2 )
E!A0ABtAB3471"T$A<A<AL"S$ ,
v '+ v = v ' + v "X$ 1 1 2 2
UVA<"X$AL WA<cA<AL"S$, %
m v ' + v + m v ' −v = 2m v 2 ( 1 1 ) 1( 1 1 ) 2 2 2m v + (m − m )v 2 2 1 2 1 → v ' = "Y$ 1 m + m 1 2
92M"atAd\!3 A2%$N 2m v + (m − m )v 1 1 2 1 2 v ' = "[$ 2 m + m 1 2
-(AL %/0 S/0A S_!0A _!A2"Y$A2"[$O, % %
Aj ^0Y_!5Aj %0Y_!8 %
6$H
hA0AB!b7qAB3A Aj Aj A8 %
H2Vc'1B6=21,
m v '+ m v ' = m v + m v (m + m v = m v + m v 1 2 ) 1 1 2 2 1 1 2 2 1 1 2 2 + m v m v 1 1 2 2 v = m + m 1 2
F'/31,A2AB3C,Aj Aj A 0g_!8 %
T.%T8f)=I,cKI!,(V!!(26;8fI/
!,(V,6A2!)=I<-NALA2V
Nq;4+;"T. %$8n31,)=I1I
1,6;%^^A2 ^^8v=I>,V14T0XA2=38
fQ!A0)=I,V1464<
$H12222W56$H128 %
F622!bAB(='1B6=2~1e
62T. g0T.%^A262AA4V62T.%S8
UL/)=I A2)=I%77AB312 v = 2gh 1
hA0)=I7AB312A j5A jA2N!b14 A2 % % 2 2
>6; v ' v ' h 1 = 5 h 2 = 8 1 2g 2 2g
$ U< A @ AB 12 2 W0 - ( P > 62 T.%S AL
%^^% 5A ^ 1 5 4
8FG7, % % v ' = v v ' = v 1 1 2 1 3 3 v 2 ' 1 v 2 1 1 v 2 ' 16 v 2 16 h 1 1 = = = h = 4 . 5 , = 0 5 , 5 h 2 1 = = . = h = 8 2 ( 8 cm) 1 (cm) 2g 9 2g 9 9 2g 9 2g 9
6$U<A@AB12
Aj Aj %A _S8 % v 2 ' 4 v 2 4 h = h 1 1 = = . = .h = 8 1 2 ( 2 cm) 2g 9 2g 9
T.%X8RAB/31, LAA2AB>>
40/31, 8oA124VA2222W8fQ!3-I~ %
~6IAB>CAB>!A`
-(+,-$ %56$ u%8
-(P>A2W7,62%.%SAL v ≠ 0;v =0 1 2
O,AB3)=I>%!A 2m v 1 1 v ' = 2 m + m 1 2
FG7!|!3-I~~2AB CAB% 2 2 W' d m v ' m 4m 4m m 2 2 2 2 1 1 2 η = = = = 8 2 2 2 W m v m ( m + m ) ( m + m ) d1 1 1 1 1 2 1 2
n % η ^^†8
n u % ηSY†
T.%Y8RxWa%^U01~/P,4a-J;
ALAB3AT_!8F~x8
xW7Pc)O 1 2 I =
m.R "ALw126/Ox$8 2
nx1~/P,4!2;07/ v = ω R 8
~x6W~'<A2~) ‘ 1 1 1 1 1 1 1 3 2 2 2 2 2 2 2 2 2 mv + I ω . = mv + m R . ω . = mv + m R . ω = mv 2 2 2 2 2 2 4 4
T.%[8FOPI<12AP1~A2d+/O 0
/31,X^^/0>4)LAB3 %^Ad_-N8
RPc)OAP1~A2d 2 I = mR . 8
HB3)AP1~12 %^Ad_-N" %^8%π($_"Y^V$Tπ"(_!$8
oP12AP1~)O6;~~")$AP1~ ] 1 2 1 1 2 2 1 ∆‘ 2 2 I ω . = . m d . ω . = 5 . 00 1 .
(.4π ) = 10000(J)= 10kJ 2 2 4 8
T.%g8R)=IaW7/31, /01~/P,ALAB3
A ^_!<B-A22+W6BALAB3A g_!8FO1,= %
A78
h A ~ AB =8 = a 2 = (L (
v.∆‘ 8nOIN:;)=IAG7~'<AG7
~)8~))=Ia0W01~/P, ‘ 1 2 1 2 2 2 1 2 2 1 2 ) I.ω = m . R .ω = m.R .ω = m.v 2 2 5 5 5 2
E7ƒ ƒ #ƒ 1 mv 7 2 2 8 ) mv + = mv 5 2 10
HB01,=(A 7 Q = −∆ W = − − = − . . − = , d ( m v 2 2 2 1 ) 7 v 1 (82 102 ) 25 2(J ) 10 10
T.%u8 R W 7 X0 KA' O J > 6' t
38&'
$HB3(2\/75
6$H'OR4!/RAB37N6;
AB3AB=M(GA'OR8 mgh
$A'OJ>07<~ƒ
8ntLa<~ 2
26<2~)KA'O‘ 1 i
ω% 07i12Pc 2
)O3AL)3i mh2 0 ω12AB371N 3 8
-('1B6=2~ 1 mgh mh 2 g 3 I 2 . ω . = 2 ω . = mgh ω = 2 2 3 h
FG7!AB3(2\1NAω gh 3 = 3 10 . 5 . = 12 2 , _!8
6$sm12R/KA'OJ>8-(P>O
AB3ABM(07AB3R/ v 2gx 8 M
Fc/I62 g 3 2 ω g 2 x x. = g 2 x
h ^_SS0SS8 h 3
T.S^8FG\a-J4^0X0+ABW
7(/1~/P,4a-J478FAB3(2
ABK3a-J4<
$HB7()=Ia5
6$HB12xd5
$HB12A2d8
"s=!DAB36IAB6;/P$8
s= !D ; 7 AB a 1~ /P ,0 /P AB 3 I G \ a
-J478RPc)OAB7A<6;i/88w%0
7/12;!3-A2AB8nAB1~/P,ALAB
3(2AAB7~) ‘ 1 1 1 2 2 2 2 8 ) I ω . = kmR ω = kmv 2 2 2
~2-IAB ‘ 1 2 1 2 1
‘)#‘ kmv + mv = (k 1 + ) 2 mv 8 2 2 2
Fc'1B6=2~0~ABKVa-J46;
=<~AB 1 ( g 2 h k +1 )mv 2 = mgh v = 8 2 k +1
-(/<)=t)2AL^0X0AB7(
$)=Ia/%_X8 g 2 h 10gh 10 9 . 8 , 0 . 5 , v = = = = 2 6 , 5(m / s ) 2 / 5 + 1 7 7
6$xa/ _%8 g 2 h g 4 h 4.9 8 , .0 5 , v = = = = 2 5 , 6(m / s ) 1/ 2+ 1 3 3
$)=Ia/ 8 g 2 h v = = gh = 9 8 , 0 . 5 , = 2 2 , 1(m / s ) 1 +1
T.S 8o76;P"a$06;"y$q,=G
\a-J48oN7q6/OwYA2q/31,
^0X/8Ra,)r!38fQ
$HB3'<K3a-J47//P`
6$RPc)Oy5
$h61V1~/P,LVa-J4`o6<
\a-J4^0X074αS^^0/31,4P
- %Y^^/_SA2- S^^/_S8 %
$EMA2/<)=62T.S^0AB2a"!3Pc)O
Q$AB3(2NVa421L8E706220
7/<1B;0/3a6;P!b1~/36;8
6$UC6<0Pc)O/3PA2,' 2 2 2 +
6;P>>i mR R
R1 07w 126/O ,I = m 2 2 2
8
H/31,6;4ρ 9 9
πw% ρ% π "w% . 2
R $07912 1
(20ρ A2 12/31,4PA28 ρ%
2 (ρ −ρ R 2 1 ) 2 ρ 2 . $w% % R " ρ ρ R = 1 % 1 ρ2 2 2
FG7O, R + R 2ρ − ρ 2 ρ − ρ I = m 1 = 2 1 2 m . R 0" 2 1 k = $8 2 2 2ρ 2 ρ 2 2
HB3P/1~LV(3"c62T.S^$ g 2 h g 4 h v = = 8 Al 1 / 2 +1 3
HB3/1~LV(3 g 2 h g 2 h 4ρ g . h g 4 h 2 v = = = <
= v "A ρ < ρ $ Pb Al 1 2 k + 1 2ρ − ρ ρ − ρ 2 1 4 3 2 1 + 1 2ρ 2
$EMA2/<)=AAB3AB1~/P,62T.S^ 1 (k +1)mv2 = mgh 2
F2c+A<-2, (k + )
1 mv .v' = mgh' (k + )
1 mv.v' = mg (v sinα) g si α n a = v' = k +1 v ( g 2 h)/ (k + ) 1 2h (.k +1) t = = = a
g sin α /( k + ) 2 1 g sin α
F70^0X0αS^^0
-(/3P0/ _%
2. 0, 5.(1/ 2+ ) 1 t = = 0 7 , 8(s) 9 8 2 , .sin 300 2 2 1 . 1300 − 2600 100
-(/30 ρ − ρ 2 1 k = = 2ρ 2 1 . 1300 113 2 2.0 5
, .(100 / 113 + ) 1 t = = 0 8 , ( 8 s) 9 8 2 , .sin 300
T.S%8R+W4<sP-/A2I)=0y)=7
/31, ^/8n=Gy)=L)12^0[X8s<)ALAB3
ω Ad_!8fQP(+MA2AB3<<+71
/=Gy)=<)\d12^0%^06<Pc)O
+A2<3AL)12i %0X/8%8 ^
RPc)O+A2)=1N6IA21N! 2 2 I = I + 2.m.d
= 2,5+ 2. 10. 0,75 = 13,75 kgm 1 0 1 ( 2 ) 2 2 I = I + 2 m . d . = 2 5
, + 2.10.0 2 , = 3 3 , 0 kgm 2 0 2 ( 2 )
n))7~A2Pc1,12 L = I ω 1 1 1 ‘ 1 2 1 I ω
= . 13,75. π = 8 1 1 (2 )2 27 ( 5 ) J 2 2
EPc1,,6=24AB37)!/+
1=C6> I 13 7 , 5 I ω = L = L = I 1 ω ω = ω = .2π = 8 3 , 3π / 2 2 2 1 1 1 2 1 (rad s ) I 3 3 , 2
Fc'1:A~0+CI3P6; ] 1 1
∆‘ ‘ .‘ 2 2 % I ω − I ω 2 2 1 1 2 2 1
= . 3,3(.8, π )2 1 33 − .13 7 , 5 ( . 2π )2 = 87 ( 1 ) J 2 2
X. 8F1MNRaF+14AB7/31, ;4aF
06<;/31,RaF+R 0u[8 ^S^/A2/=6Ga
<VRaF+12 Tu8 ^Y/8
-(P>'1BAAB-(‹ 3 − 30 mM − 10 9 , 1 . 7.10 F = G 11 6 = , 6 67.10 ≈ . 9 , 5 10− 2 2 (N ) r ( 9 14 . 9 10 )
X.%8n=@FA2RaF~12SgT^^^/8n31,F
12X0uY8 ^%[ A2RaF~12[0SX8 ^%X8&'A'O71MN
RaF~A2F14V6;8
sm/=G71MNRaF~A2FV6;
<VF12"k2•1$8F7 M m M m F = F G E = G M E M 2 2 x (l − x) M 2 2 − = E (l x ) M M x M l − x M = x M E l 384000 x = = ≈ 345600(km) 1 + M / M 25 27 + M E 1 3 , 7 5.10 /( , 5 96.10 )
X.S8 R )= I /31, a #. I
W J 4
-/r(28F7(210 z ] /3
1,%8F1MN14)=I8
o2@(Q0/71MN714/31, 12 m .dm m .m .dx 1 1 2 dF = − G = G
(l + a − x)2
l(l + a − x)2
9MNt14)=I12 l Gm m l dx Gm m 1 1 2 1 2 F = dF = − = . 2 l
l + a − x l
l + a − x 0 ( ) 0 Gm m 1 1 Gm m 1 2 = . 1 2 − = l
a l + a a (l + a )
X.T8f)=I7q6/O/31,41I1,6;- A2- ,a %
P+1Q7/31,412- 8fQ/2 ^
$f)=IN5
6$f)=I}8
o6</OLP+1Q1L!AL/OL)=IA2 - ‚- 8 %
&r)=I>
#9M-(‹@)=I12 2 m m G 4π 4π ρ ρ 16 6 π GR 1 2 3 3 1 2 F = G = .ρ . R .ρ R = k "AL k = $ 1 2 2 1 2 2 r r 3 3 r 9
#E/OLP+1L)=I4//P7
)=I>01M-(‹P+14)=>c-/
M41‹8U<6L-I1Q0-Id1!b(1M
-(‹q1L,AL 1M-(‹(-IV8KV0
-I12-I1Q6'<6K)=I>8FMK4l7 ρ ρ 1 0 F = k 2 2 r
#U<m„ 12(0t,-1M(14)=I 6; ρ1
F = F − F = k ρ − ρ 1 2 ( 2 2 0 ) r
s3(14)=I 12 F kρ ρ − ρ 3 ρ − ρ 4 3 G π R 1( 2 0 ) 2 0 a = = . = K
"AL K = $ 2 3 2 m r 4πρ R r 3 1 1
#FM0<mLA-O)=I 12(01Mt,-
(14)=I%12 ρ2 F' = k (ρ − ρ 2 1 0) r ρ − ρ 1 0 a '= K 2 r
s33@N ρ + ρ −2ρ 1 2 0
a = a + a'= K 0 2 r
$f)=I1I ρ + ρ
a + a'> 0 ⇔ ρ + ρ − 2 ρ > 0 1 2 ⇔ ρ < 1 2 0 0 2
6$f)=I ρ + ρ
a + a'< 0 ⇔ ρ + ρ − 2ρ < 0 1 2 ⇔ ρ > 1 2 0 0 2
X.X8F)=I6;6/Ow+/r1yI8Ra
1y<-NAL a)=IA2)V78n31,)=I
L//r1y6;R8F4-yV)=IA21y0+a
d6Q/31,V)=I("X.%$8F1M-(‹2
)=I"C/r1y$(14d68
9M-(‹)=IC/r1yN6;1M-(‹V6K
)=I/r1yA2-I6'/r8
9M-(‹)=I/r1y14d6 Mm F = G 1 2 d
9M-(‹-I6'/r14d6 3 4π R m.ρ. M 'm 3 2 m 4π Mm 3 F = G = . G = G .ρ R = G 2 2 2 2 r R R 3 2(2d − R )2 d − 8 d − 2 2
HB01M-(‹)=IC/r1y14d6 2 2 1 1
7 d − 8dR+ 2 R
F = F − F = GMm − = GMm 1 2 2 2 d ( 2 2d −R ) ( 2 2d − )2 R
X.Y8FAB3(2F))RaF+06<;/31,
Ra F+ 12 R %8 ^S^/ A2 /= 6 @ F A2 Ra F+ ( 0X8 ^g/8
9MLV F )RaF+O121M- (‹ F = F hd ht M 2 E M S v G = M 2 E d d GM , 6 67.10 1 − 1 . 2 . 1030 v S = = ≈ 1 . 3 04 (m s / )= 3 ( 0km s / ) d . 5 , 1 1011
X.[8FAB3(2AVF6<;)*A
12d8HK6 ^^^/8oA\'=K1M
NFA2K401M=/P/O/P/8o6/O
FwYS[^/8
9B-1BM62X.YAV)F0 7 − 11 24 G. M GM , 6 67.10 , 5 . 9 . 6 10 v E E = = = ≈ 3 , 7 4 . 4 103(m / ) s = , 7 3 ( 4 km / . ) s d R + h 10 6 + , 6 3 . 7 106
X.g8 f 2 ) ) Ra F+ AL )* I N 12
@Add6/O1I1,6;w X^8 ^Y/0"F$A2w ^g8 ^Y/ %
"h/$8F|!3AB3(2278
hD(1B-1BA2O62X.Y07 GM GM v S = ; v S = 1 2 d d 1 2
6 v GM d d 10 . 8 10 1 = S . 2 2 = = ≈ 8 , 0 5 v d GM d 15 . 0 106 2 1 S 1
X.u8n31,RaF~ Q /31,F g 1I0+ /O Ra
F~6;S_ +/OF8fQ+4aaY^^14
RaF~!ba648
Fc'1BAAB-(‹ M m E P = G 2 RE M m k M m k M m k P ' = G M = G 1 E 1 = G E 1 = P R 2 2 2 2 2 M (k2RE) k R k 2 E 2 1 / 81 P '= .600 ≈ 100 2 (N ) (3/11)
X. ^876;AP<"AP<$/e-m
4a+-714A‰3'Š">4aA!
/P3AL a$8R3AB-= A2
a-JOGFV!PALAB376;AB3F
))78
fCOAB3(2A2A78Z</F)
) 7 12 F %S + XY -N T V8 Z /O O F 12 w YS[g/8
sm/=GA<VF12(0AB3(2A12 3 GM 2π d d E v = T = = 2π d v GM E 2 2 1 − 1 24 T GM (86164) , 6 . 67.10 9 , 5 . 6.10 d 3 E = = ≈ 42 1 , 26.106 3 (m) = 4212 ( 6 ) km 4 2 π 4 2 π
HB0AB3(2A2A12 −11 24 GM 2π GM 2π 6 , 6 . . 7 10 9 , 5 . 6.10 v E E 3 = = = ≈ , 3 07.103 3 (m / s ) d T 86164
h = d − R = 42126 − 6378 = 35748(k ) m
X. 8FAB3Al-ii3ALRaF~"x12AB341D
-7G6aRaF~I-=777/Q!>NRaF~$8
s3m+46aRaF~ M M g = G M 2 R M
HB3Al-,OcP>
G 2 M , 6 . 2 67.10 1 − 1 3 , 7 . 5.1022 v = 2g R M = = ≈ 3 ,
2 8.103 (m / s) M M M R (3 /1 ) 1 3 , 6 . 7.106 M
X. %8U+41D0AVI4F,14 X^^/8
$F3m+K75
6$=-7ALAB36;64c-AP7AL6
/OF)*7)F12+d8n7/
)A)F6;64`
96/OF6;YX^^/03m+46aF
6;u0g_!%8ZQ)!>=/P/O8
$s3m+,OcP> 2 2 2 M R M R 6500 g = G = .G = g = . 8 , 9 ≈ , 8 45 m /s 2 2 0 ( )2 r r R R + h 6500+ 500
6$)*A12+d01M-(‹N6;1MLV F = F hd ht M m v2 GM GM R 2 G E = m v E E = = . 2 2 r r R + h R R + h g R2 6 . 8 , 9 500 . 2 106 v 0 = = ≈ ,
7 69.103 (m / s) = , 7 6 ( 9 km / s) R+ h 700 . 0 10 3
o/•)A12 3 3 18 2 r π (R + h) 7 .10 T = = 2π = 2π ≈ 572 ( 0 s ) ≈ 1h 3 ' 5 2 v g R 5 , 6 . 8 , 9 . 2 1012 0
X. S8RmAB4a'!>NRaF+8H64"RaF+K
‰(LVŠ$1M74AL1MNF062"RaF+K4‰\
IŠ$1M7G6L1MNF8HAB064mAB-=a
62077N/P`F!`
nPN0ARaF+N=F1‹AB46aF8
Y. 8HB-=7AB364/OL7c-
=%1I8
/OLABc-=%1I0I7 2 l v = 1− = k = 5 , 0 2 l c 0 2 2 v = c ( 2 1 − k ) v = c 1 − k2 = 3 1 . 08. 1 − 0 52 , ≈ 2 6 , 1 . 08(m / ) s
Y.%8Rxd6/OwJALAB3Ac-!
!ALax8fQ)<eALF0x7(`
xd/JALAB3Ac-!!ALa
x!b6'r2c1-8nOLc-6'1/
/OLc-AP7,@48sm-+64x
)<eAL712 2 2 2
x' +y' = R 2
Ra/ v x = x ' 1 − ; y = y' 2 c
HB0-+64)<eALF 2 x 2 2 + y = R 2 v 1− 2 c
V12-+c1-8
Y.S8o77WW3"W6$3AL
AbY. 893O+121NWW]j)3(WW]8fQ3AL
+)!>4!AL7WW]/WW\+7
<2`HA'O/0=WW8
H'O/WW(O3!MW+!
]j ] fY.
Y.T8f4•PAlALAB36;^0uX1IAB3
!8fQ/=+cWW+)!>4F>AL
/=‰+!3ŠV4•P8
hD(P>A+ t ∆ 1 ∆ t'= = ≈ ( 2 , 3 s) v 2 1 − , 0 952 1 − c2
Y.X8n31,α~464<~AB37G^<^0u
1IAB3!8
U<~AB30/31,l~14 m0 m = 1− (v / c)2 1 1 m ∆ = m − m = − 1 = , 1 . 4 67.10− . − 1 0 m 27 0 1 − (v / c)2 2 1 − 9 , 0 −27 ≈ . 6 , 8 10 (kg )
Y.Y8n31,41c6;1I/31,\78F
~41c48
~ c1c 6;~ 1, 2-I1N A2 1N >4 W = m ∆ c2 . = ( m 2 − m = 0 0 ) 2 2 c m c 0 3 − 1 16 1 − 4 = . 1 , 9 10 1 . 9 . 0 ≈ . 2 , 8 10 (J)
Y.[8n-VVu%–%SX~1,=-7/=%^^
RcH8Ft/31,/-V /18
U~1,=-7\1BAL/3 2 E = ∆mc E E N 1 − 3 26 . 200.1 6 , . 10 .6 0 , 25.10 ∆m 0 = = = ≈ 0 2 , 1 ( 4 kg / kmo ) l c 2 c 2 9 1 . 016
Y.g8FAB34•P<~1,2-I4•P76;
^1I~1,\78
U~1,2-I4•P6;/1I~1,\ 2 m c 0 2 W = = km c 0 2 v 1 − 2 c 2 v 1 2 2 1 1 − = v = c 1 − 2 2 c k 2 k 1 8 1 v = c 1 − = 3.10 1− ≈ 2 9 , 85 1 . 08 (m / s) k2 102
Y.u8$Ry-NRaF+6>~1,6;Y0X8 ^% /‘8U<6>
Ra F+ 12 /P t + /3 1, 7 = D 12 6 4`
6$s=O!M</31,RaF+1/Pt8
$hMt/31,-A2!Mt~1, 2 E ∆ = ∆mc 2 30 16 ∆ ∆ E mc 0 5 , 1 . 9 , 7 1 . 0 .9 1 . 0 t = = = ≈ 3 7 , 9 1 . 018 (s) P P 6 5 , .1021.3 6 , .106 11 t ≈ , 1 . 2 10 "~$
6$RaF+AG~1,AGB~1,G6428U<-I~
1,BA26;-I0~1,RaF+/Pt04/31,Ra
F+/Pt8
Y. ^8&'‰+!3Šτ4•Pµ7~1,‘ ^ucH"
)<-dO$5+!34•P\12τ %0%8 ^.Y!0/3 ^
1,4•Pµ12%^Y0[ " 12/31,41c$8 c c
‰F+!3Š4•P)<-dO,'
cP> τ m τ m c2 Wτ 109 1 . 6 , 1 . 0 1 − 9 2 . 2 , 1 . 0 6 − 0 v 0 v 0 τ = = = τ = = ≈ 21 , .10−5 2 0 (s) 2 m 2 −31 16 v mc mc 206 7 , 9 . 1 , .10 .9 1 . 0 1 − c2
[. 8FAB3=(d/Ooz%3(‹6<;>D+/3
1,/O=)<(36;^0X /8n31,4/O
6;[0X/_S8+/O36;%8o/O121Q1:K8
sm/31,/O=)<(3A'+12µ8 F7 m ρ V . ρ S . l µ = = = = S ρ v t t t µ 0 5 , 1 1 v = = . ≈ 0 1 , ( 2 m / s) S ρ 1800 2 2 1 . 0−2 7 5 , .π 2
[.%871y+/O( 8+/O6
E^0X8F!M-AB3MLK6A2M
L8-(6;!3+,-^0%8
smh A2h%12<(6A21y5A A2A%12AB3=L
!aLA2=)=1y8n70c-Zc1 2 2
v + 2gh = v 1 2
Ra/0(O14(d= v S = v S 1 1 2 2 2 2 S v 1 = v2 = v2 + 2gh 2 S 1 1 2 D4 v2 1+ = 2gh 1 d4 2gh 2gh d2 v = ≈ = 2gh
( do d D ) 1 1 + (D / d)4 (D / d)4 D2
n^0%0AB3ML12 2 0 0 , 1 v = 2.9 8 , .0,2 ≈ 7 9 , 2.10−4 / 1 (m s) 0 5 ,
[.S8F4627a6L02671yQ;6
A2ML 8RML6,@/Pt8 %
fQL3a621y96;64"c-;
$`s=62+,-
$ %XA2 Y5 %
6$ YA2 %X8 %
HB3L/)1y
v = 2gh 0 2
h//Q1y0-IDLABrALAB
36I6;A 8 ^
F+G//Q1y</12 2 h t 1 = g
FIL12 2h1 L = v t = 2gh . = 2 h h 0 2 1 2 g $
%X0 Y % L = 2 25.16 = 4 ( 0 ) cm 6$
Y0 %X % L = 2 16 2 . 5 = 4 ( 0 cm )
[.T8U+a6L72J>4a62;8
F4267(q1yQ8o1yq;4+J>8s=!D
<(6!AL<(1y!>L6 /Pt8
$o>;AB3L4a626;8
6$o>;3L3q4a62
/=G1y<>L6-=6;/=G1y/< a628
$R3L--=1yA'O2`
&r1yKA'Oa62/= A2aL12 8 %
HB3L//Q1y12 v = 2gh 0 2
$hD('1B6=2~1,-IL!//Q6 1 1 2 2 mv = mv + mgh = mgh + mgh 0 1 2 1 2 2 v = g
2 (h + h ) = 2gH 1 2
HLf12>L!ALa628
wk2;AB3La62/P-A2A'O1y8
6$FG/<)=62[.S07 L = 2 h h = 2 − 1 2 ( h H h) ' L = 2 ' h (H − ' h )
LA2q L = ' L ( h H − h ) = ' h ( H − ' h )
H( h − h' ) − ( h 2 − h 2 ' ) = 0
( h − h' )( H − h − h' ) = 0 Eh ≠ ' h H =h + ' h hay h = H − ' h
$hD(6J>oP! L = 2 h(H − ) h ≤ H
E‰Š=/A2\/ H
h = H − h h = 8 2
[.X8s@ IL6'1yQ8R>LKI
I f S^8 fQ L = ) 1y AL AB 3 6; 6 4
+,-!
$sIL>45
6$sI,V14
$sIAL3 0%_!%144W3(L8
($sIc-;AL3 0%_!%8
HB 3 L = /Q I - A2 - ! r- 14 I8 n I
AL3L144a3(L!b-!-r-
14I8F7 1 ma P + v2 ρ = P + g ρ h + = P + g ρ h + a ρ h 0 2 0 S 0 v = 2(g + a)h
"(Lc-m1M$
ŒU<I>4a,V14
^ v = 2gh = 2.9 8 , 0 . 3 , ≈ 2 4 , ( 2 m / ) s
ŒU<IAL3 0%_!%L144 v = ( 2 g + a)h = 2 (.9 8 , +1, ) 2 0 3 , ≈ 2, ( 57 m / ) s
A2/3L3(L v = ( 2 g − a)h = 2 (.9 8 , −1 2 , )0 3 , ≈ 2 2 , ( 7 m / ) s
ŒU<IAL3 0%_!%c-0-!-\
42I4/P7(12tAB3L=!AL
/I8 v = gh 2 ≈ 2, ( 42 m / s)
[.Y8R60(Oh>IL8671y
(Oh 8fQ
$h61VLK6=<`
6$ML-+<2/K1y8ZQ)L L8
hD(6>AB3L>LCOK62[.%07 2gh v = 1 + (S / S )2 1 dh 2gh dh 2g = − = − dt dt 1 +(S / S )2 h 1 + (S / S )2 1 1 h dh t ' 2g = − dt 2 − = − 2 ( h h 0 ) 2g t h' 1+ / + / h 0 (S S1) 1 (S S )2 1 0
2 1 2g h = 2 h − t 0 4 1 + (S/ S )2 1
F+L6=<12 2 2h 1 [ + 0 (S / S1) ] τ = g
ŒU< S S 7 1 S 2h0 τ = S g 1 2 S g 1 h = h − t. 0 S 2
[.[8F V+7,^0%1OLA268fQK6-=7
1y+/O6;64>L6/PtA276; "/G1y$8
>L6/Pt01,LtA2-=6;1,L= dV = dV 1 2 k d . t = vSdt = S 2gh d . t 3 k 0 2 , 1 . 0− 5 S = = ≈ 4 5 , 2 1 . 0 − ( 2 m ) 2gh 2 9 . 8 , 1 . S 4
4.4,52.10−5 d = = ≈ 7 6 , 1 . 0 3 − (m) π π
[.g8U+('3(mc>ILALAB
3Ag0S_!"[.%$8fQ>L(V1438
-('1BZc1 1 1 2 2
P + ρv = P + ρgh + ρv = P + ρg h + h 0 0 0 ( 0 ) 2 2 2 2 v 8 3 , 3 h = = ≈ 3 5 , 4(m ) 2g 2 9 . 8 ,
[.u8 U+ t /P /O ) 3 ]Z " [.S$8 o> y -N 7 X 1O
/P/O=)38EO<(-I]6;%%0-IQZA2
-I366;^0X%8F >L∆ 3 68Z</31,
4/P/O6; 0S%/_S8
U+t/P/O)3]Z"[.S$8o>y-N7 X1O/P
/O=)38EO<(-I]6;%%0-IQZA2
-I366;^0X%8F>L∆368Z</31,4
/P/O6; 0S%/_S8
smρ 0 1I1,12/31,4/P/OA2L5h 0h 12(O ρ% %
<(3"h ‚h $0H12O/O,t)3 V8 %
-('1BZc1 1 1 2 2 P +
ρ v + ρ gh + ρ gh = P +
ρ v + ρ gh' +ρ gh' 1 1 1 1 2 2 1 2 1 1 2 2 2 2 1 V2 V2 ρ − − ρ g h ∆ + ρ g h ∆ = 0 1 2 2 1 2 2 S S 1 2 2 ρ V 1 1 ∆h = 1 − 2(ρ ρ g S S 2 − 1 ) 2 2 2 1 2 1 3 , 2 0 . 0 , 15 1 1 = − ≈ 5 7 , .10 4 − (m) = 0 5 , ( 7 mm) 2 (1000 1 − 3 , 2 ) 9 . 8 , 0 2 , 5 1 . 0 4 − 4 1 . 0 4 −
[. ^8F46a-<-JA2;+a67/r
1y Q K -O 3 " [.T$8 E O 1y 6; A2 6; h
^^^%8R1y/r!601y//rKX^8Z>LL
f ^^8F36!/K1y8ZQ)!@
A268n31,6Q/P/8Z<(O<(6 h ^0X%8
&1M(146/K1y12 dp dm v . −dm v . v ρ S 2 dt − v ρ S 2 dt 1 1 2 2 1 2 F = = = dt dt dt = ρ ( S 2gh − 2gh = ρ 1 2 ) 2 ghS −6 ρ F 2 ghS S 2 gh
2.1000.10 . 9 8 , .0 5 , −2 γ = = = = =1 9 , 6 1 . 0 ( 2 m / s ) M ρ HS S H 0 5 , 1 . 1 1
[. 8R62J>))7"•$AL
AB37ω8Z>I1Q8
$&'(a1Q68
6$s=!D-!V66;- 0-!1Q14/ ^
68n31,41Q12 8 ^
$s=!D1Q612L8F-! ∆-L14a64
6!6/6)ALAB37 ω %0Y(_!A2/6
>48Z/O612w^0X8
$n6)0y-VD6a1Q/31,
'(t,-1M
#1M)O1Vω%8
#m1M8
Ra1Q6'4A2;V6;/7J7ALt,-1M8
4,'6K7 2 2 mω r ω r tgα = = mg g 2 F17 dz ω r tgα = dz = dr dr g 2 2 ω r z = z + 0 2g
HB0(a1Q12-6P1Pd)•8
6$-!46>AL6/O12 2 2 2 2 ω r ρω r
P = ρgz = g ρ z + = P + 0 0 2 g 2
$o1Q2a7(2(Q R 2 ω r2 dV = 2πr d . r.z
V = dV = 2 r π . z 0 + dr 2 0 g R 2 πω 2 ω V = 2 z π r r R π z R 0 + 4 = 2 2 0 + 4 g 4 g 0
n6/P)0-!612 V 2 ω R2 P ρ ρ ρ 1 = gh = g = g 2 z0 + R π 4 g
HB0-!L14a64!6/6)A2/
6>412 2 2 2 2 2 2 ω R ω R ρω R
∆P = P − P = ρg z + − g ρ z + = 2 1 0 0 2 g 4 g 4 2 2 100 . 0 12 6 , 5 , 0 . 4 = ≈ 10 ( 2 N / m ) 4
[. %8R3(‹7u^^7L="[.X$8&'1M
(2314Ly3<<(312A27(O
6;hT%011,L=)312v%T1O_-N8 F7 dp dm F = = (v − v 2 )1 dt dt E Q dm v = v = 0 = Q
ρ A2 v ⊥ v 4 1 2 S dt 1 2 2 24.10−3 1000. 2 ρ 60 Q F = 2 = 2. ≈ 5 , 0 64(N ) S 4.10−4
Hc1M,-AL-7TX^A2LA-O1k3