Giải chi tiết file tổng hợp đề thi môn Vật lý đại cương I | Đại học Bách Khoa Hà Nội

Giải chi tiết file tổng hợp đề thi môn Vật lý đại cương I | Đại học Bách Khoa Hà Nội. Tài liệu được biên soạn giúp các bạn tham khảo, củng cố kiến thức, ôn tập và đạt kết quả cao kết thúc học phần. Mời các bạn đọc đón xem!

9 5 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

TỔNG HỢP ĐỀ THI MÔN VẬT LÝ ĐẠI CƯƠNG I

Câu 1: Một cột đồng chất có chiều cao

 

8h m

, đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ

xuống. Gia tốc trọng trường

 

9,8 /m s

. Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây ?

 

16,836 /m s

 

14,836 /m s

 

15,336 /m s

 

14,336 /m s

Giải

Ở vị trí thẳng đứng, cột có thế năng:

W mg

Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất:

W I





Trong đó: là moment quán tính của cột đối với trục quay gốc của cột: I

I 



là vận tốc góc của cột lúc chạm đất.

Áp dụng định luật bảo toàn cơ năng:

gmhh





Vận tốc dài:

 

. 3 3.9,8.8 =15,336 /v h gh m s



  

Câu 2: Ở thời điểm ban đầu một chất điểm có khối lượng

 

1m kg

có vận tốc

 

20 /v m s

. Chất điểm chịu

lực cản

F rv 

( biết

2r ln

là vận tốc chất điểm). Sau

2,2s

vận tốc của chất điểm là:

 

4,353 /m s

 

3,953 /m s

 

5,553 /m s

 

3,553 /m s

Giải

Lực cản:

F ma mv m

  

Mặt khác:

dv dv r

F rv m rv dt

dt v m

       

Lấy tích phân:

 

.2,2

. 20. 4,353 /

v t

r ln

dv r v r

dt ln t v v e e m s

v m v m



        

 

Câu 3: Một chát điểm dao động điều hòa với chu kì

 

2T s

, pha ban đầu







. Năng lượng toàn phần

 

2,6.10W J





và lực tác dụng lên chất điểm lúc lớn nhất

 

2.10F N





. Phương trình dao động nào sau đây

là đúng chất điểm trên:

 

2,9. 2

sin t cm



 



 

 

 

2,7.

sin t cm



 



 

 

 

2,6.

sin t cm



 



 

 

 

2,8. 2

sin t cm



 



 

 

Giải

Lực tác dụng lên chất điểm lúc lớn nhất:

F kA

Cơ năng:

   

1 1 2

. . 0,026 2,6

2 2

E kA F A A m cm

     

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Ta có:

 

2 2

2 /

T rad s

 

  

    

Phương trình dao động của chất điểm:

 

2,6.

x cos t cm



 

 

 

 

Câu 4: Một chất điểm chuyển động có phương trình:

x asin t

y bcos t













. Cho

 

30a b cm 

và

 

10 /rad s

 



Gia tốc chuyển động của chất điểm có giá trị bằng:

 

296,1 /m s

 

301,1 /m s

 

281,1 /m s

 

281,1 /m s

Giải

Ta có:

 

sin t

x a sin t

y b cos t

cos t











 



 













Mà

     

2 2

1 1

x y

sin t cos t R a b

a b

 

   

      

   

   



PT chuyển động tròn

Mặt khác:

 

v x R cos t

v y

v x

v y R sin t

 



 

 





 



 

 

  





Mà

       

 

2 2

2 2 2 2 2 2

x y

v v v y x R sin t cos t R

     

       



Gia tốc chuyển động của chất điểm (chuyển động tròn):

 

2 2 2

2 2

0,3. 10 296,1 /

v R

a R m s

R R



 

    

Câu 5: Khối lượng của

 

1 kmol

chất khí là

 

30 /kg kmol





và hệ số Poat xông của chất khí là-

1, 4





. Nhiệt

dung riêng đẳng áp của khí bằng (cho hằng số khí

 

8,31.10 / .R J kmol K

 

995,5 / .J kg K

 

982,5 / .J kg K

 

930,5 / .J kg K

 

969,5 / .J kg K

Giải

Hệ số Poat xông của chất khí là -

1,4



 

Với

và

lần lượt là nhiệt dung mol đẳng áp và nhiệt dung mol đẳng tích

Mặt khác:

p v v p

C C R C C R    

p p

v p

C C

C C R



    

 

Nhiệt dung riêng đẳng áp của khí:

 

1,4.8,31.10

969,5 / .

1 30 1,4 1

c J kg K



  

   

 

Câu 6: Một động cơ nhiệt hoạt động theo chu trình Carnot thuận nghịch giữa 2 nguồn điện có nhiệt độ

 

400 K

và

 

100 K

. Nếu nó nhận 1 lượng nhiệt

 

6 kJ

của nguồn nóng trong mỗi chu trình thì công mà nó sinh ra trong

mỗi chu trình là:

 

4,5 kJ

 

2,5 kJ

 

1,5 kJ

 

6,5 kJ

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

2 2

1 1 1

1 ' 1 4,5

T T

A Q kJ

T Q T



 

      

 

 

Câu 7: Một ống thủy tinh nhỏ khối lượng

 

120M g

bên trong có vài giọt ête được đậy bằng 1 nút cố định có

khối lượng

 

10m g

. Ống thủy tinh được treo ở đầu một sợi dây không giãn, khối lượng không đáng kể, chiều

dài

 

60l cm

(hình vẽ). Khi hơ nóng ống thủy tinh ở vị trí thấp nhất, ête bốc hơi và nút bật ra. Để ống có thể

quay được cả vòng xung quanh điểm treo O , vận tốc bật bé nhất của nút là: (Cho

 

10 /g m s

)

mỗi chu trình là:

 

69,127 /m s

 

64,027 /m s

 

70,827 /m s

 

65,727 /m s

Giải

Tại v trí A, vị ận tốc tại đây phải đủ ớn để l dây thẳng đứng và căng đét

0T 

2 2

A A

v v

P T m T m mg v gl

l l

       

Vận tốc nhỏ nhất tại A để ống quay tròn:

Amin

v gl

Đối với ống thủy tinh:

Áp dụng định luật bảo toàn cơ năng:

2 2 2 2

1 1 1 1

2 2 2 2

B dB tB B B

W W W MV Mv Mgh MV Mv Mg l       

2 2

V v gl  

Vận tốc tối thiểu để đạt đỉnh:

4 5 5

B min

v gl V gl gl gl V gl      

Áp dụng định luật bảo toàn động lượng:

 

65,727 /

min

min min min

M gl

mv MV v m s

m m

    

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 8: Một khối khí Hidro bị nén đến thể tích bằng

lúc đầu khi nhiệt độ không đổi. Nếu vận tốc trung bình

của phân tử hidro lúc đầu là

thì vận tốc trung bình sau khi nén là

Giải:

Công thức tính vận tốc trung bình của phân tử khí:

8kT







Vận tốc trung bình của phân tử khí chỉ phụ thuộc vào nhiệt độ

 

T const

Nếu vận tốc trung bình của phân tử hidro lúc đầu là

thì vận tốc trung bình sau khi nén không đổi

Câu 9: Một mol khí hidro nguyên tử được nung nóng đẳng áp, thể tích gấp 8 lần. Entrôpie của nó biến thiên một

lượng bằng (cho hằng số khí

 

8,31 / .R J mol K

)

 

43,2 /J K

 

43,7 /J K

 

44,2 /J K

 

44,7 /J K

Giải

Độ biến thiên Entropy:



Qúa trình đẳng áp:

Q nC dT n RdT





 

Thay vào và lấy tích phân từ trạng thái 1 ứng với

đến trạng thái 2 ứng với

2 2 2

i dT i i

S n R n RlnT n Rln

TT T

  

    



Điều kiện của quá trình đẳng áp

 

p const

2 2

1 1

T V



 

43,2 /

S n Rln J K



   

(khí

: 3H i 

)

Câu 10: : Một tụ đặc trưng khối lượng

 

100M kg

, bán kính

 

0,5R m

đang quay xung quanh trục của nó.

Tác dụng lên trụ một lực hãm

 

257,3F N

tiếp tuyến với mặt trụ và vuông góc với trục quay. Sau thời gian

 

2,6t s 

, trụ dừng lại. vận tốc của góc trụ lúc bắt đầu lực hãm là

 

25,966 /rad s

 

26,759 /rad s

 

0,167 /rad s

 

0,626 /rad s

Giải

Gia tốc góc của trụ đặc:

0 0

t t

  





  

 

Moment hãm tiếp tuyến với mặt trụ:

. .

M F R I



 

Moment quán tính đối với trụ đặc:

I M

 

. . 10.292 /

F R M rad s

 

    

Vận tốc của góc trụ lúc bắt đầu lực hãm là

 

. 26,759 /t rad s

 

  

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 11: Một quả cầu đồng chất khối lượng

đặt cách đầu một thanh đồng chất một đoạn bằng a trên phương

kéo dài của thanh. Thanh có chiều dài

, khối lượng

. Lực hút của thanh lên quả cầu là

 

1 2

m m

a a l

 

1 2

m m

a a l

1 2

m m

1 2

m m

Giải

Dạng thanh nên chia thanh thành từng đoạn nhỏ có kích thước

và

có khối lượng

, cách đầu O của thanh một khoảng x

Giờ xác định dm theo dx, đối với thanh dài thì ta chú ý đến khối lượng

trên một đơn vị độ dài



dm dx dx



 

Bài yêu cầu xác định lực hút, tức là sẽ phải sử dụng công thức liên quan

tới lực hấp dẫn giữa qủa cầu và đoạn

   

1 1 2

2 2

m dm m m dx

dF G G

l a x l l a x

 

   

Lấy tích phân, hi quét từ trái sang phải biến

thay đổi từ 0 đến

 

   

1 2 1 2 1 2 1 2

1 1

m m dx Gm m Gm m Gm m

F G

l l a x l a l a a l a

l l a x

 

     

 

   

  



Câu 12: Thả rơi tự do một vật nhỏ từ độ cao

 

17,6h m

. Quãng đường mà vật rơi được trong

 

0,1 s

cuối cùng

của thời gian rơi là:

 

1,608 m

 

1,808 m

 

2,208 m

 

2,408 m

Giải

Thời gian rơi của vật:

 

1,9

t s

 

Quãng đường vật rơi trong 0,1 giây cuối là:

     

2 2

0,1

1 1 1

0,1 0,1 1,808

2 2 2

t t

s s s gt g t g t t m



 

         

 

Công thức tổng quát cho quãng đường rơi trong n giây cuối là

 

s g t t n

 

   

 

với



Câu 13: Có

 

18M g

khí đang chiếm thể tích

 

4V l

ở nhiệt độ

22t C

. Sauk hi hơ nóng đẳng á, khối

lượng riêng của nó bằng

 

4 3

6.10 /g cm







. Nhiệt độ của khối khí sau khi hơ nóng là:

 

2213 K

 

2113 K

 

2013 K

 

1913 K

Giải

Trước khi hơ nóng:

Áp dụng phương trình TT khí lý tưởng:

1 1

pV RT





 

Sau khi hơ nóng:

2 2 2

RTm m

pV RT p RT



  

   

 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Lấy

 

1 1

1 2

2 1

2213

mT mT

V T K

T V

 

    

Câu 14: Một trụ đặc khối lượng

 

70M kg

có thể quay xung quanh một trục nằm ngang trùng với trục của

trụ. Một sợi dây không giãn được quấn nhiêu vòng vào trụ, đùa tự do của dây có treo một vật nắng khố lượng

 

20m kg

. Để hệ tự chuyện động, sức căng của sợi dây là ( lấy

 

9,8 /g m s

)

 

132,19 N

 

121 N

 

124,73 N

 

113,54 N

Giải

Thiếu hình

Dưới tác d ng c a trong lụ ủ ực

lên vật nặng, hệ trụ + vật nặng chuyển động: trụ quay, vật nặng chuyển động tịnh

tiến (hệ vừa có phần quay vừa có phần tịnh tiến). Vì vậy không thể áp dụng định luật II Newton hay phương trình

cơ bản của chuyển động quay cho toàn bộ hệ. Gọi



là gia tốc góc của trụ, a là gia tốc dài của vật nặng. Vì

chuyển động của vật nặng và chuyển động của một điểm trên mặt trụ có cùng gia tốc nên ta có hệ thức:

.a R





 

(

là bán kính của trụ)

Gọi

và

là sức căng của dây tại A, ta có:

'T T 

(tức là

'T T

)

 

Với

tác dụng lên đoạn dây nối với vật nặng, còn

tác dụng lên đoạn dây nối với trụ

Áp dụng định luật II Newton riêng cho vật nặng, ta có:

P T ma 

Chọn chiều dương cùng chiều chuyển động với vật nặng

Chiếu phương trình trên lên phương chuyển động

mg T ma 

 

Áp dụng phương trình cơ bản của chuyển động quay cho riêng trụ đặc, ta có

'RT I





Với I là moment quán tính của trụ đặc:

I 

 

Từ

     

1 ; 2 ; 3

và

 

m M

T m g a















 



Câu 15: Ở đầu sợi dây

chiều dài

có treo một vật nặng

. Để vật quay tròn trong mặt phẳng thẳng đứng

thì tại điểm thấp nhất phải truyền cho vật một vật tốc theo phương nằm ngang có độ lớn là ( cho gia tóc trọng

trường bằng g)

5gl

2gl

Giải

Chọn chiều dương và gốc tọa độ như hình vẽ:

Sức căng T cực tiểu khi vật lên đến điểm cao nhất PT Newton II tại điểm cao

nhất B:

min

mg T m

 

Áp dụng ĐLBT cơ năng:

2 2

1 1

2 2

A B

mv mv mgl 

1 1

2 2

A min

mv mgl lT mgl   

Để vật quay tròn trong mặt phẳng thẳng đứng thì tại điểm thấp nhất thì điều kiện

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

1 5

0 5

2 2

min A

T mv mgl v gl    

min

v gl 

Câu 16: Có 1g khí Hydro

 

đựng trong một bình có thể tích

 

5 l

. Mật độ phân tử của chất khí đó là: (cho

hằng số khí

 

8,31.10 / .R J kmol K

; hằng số Boltzmann

 

1,38.10 /k J K





)

6,022.10

phân t ử/

5,522.10

phân tử/

4,522.10

phân tử/

7,022.10

phân tử/

Giải

Số phân tử khí của chất khí đó là

. .

A A

N n N N



 

Hằng số Boltzmann

 

1,28.10 / .

RT R R m R

k J K N N

V N k k





      

Mật độ phân tử của chất khí đó là

' 6,022.10

N mR p

V k V kT



   

Câu 17: Một con lắc đơn có

 

120m g

được kéo lệch với phương thẳng đứng một góc





, sau đó thả rơi

cho

 

10 /g m s

. Lực căng cực đại của dây treo là

 

4,791 N

 

3,997 N

 

3,6 N

 

4,394 N

Giải

Chuyển động c a vủ ật m là chuyển động tròn đều trên quỹ đạo có bán kính

Áp d nh lu t bụng đị ậ ảo toàn cơ năng:

2 1 1

d t tmax

mgl mgl

W W W W mv

cos cos

 

     

 

 

2v gl cos cos

 

  

Chọn chi ng xu ng và g c thều dương hướ ố ố ế năng tại vị trí cân b ằng

Vật chịu tác d ng c a các lụ ủ ực: Lực căng dây

 

, trọng lực

Áp dụng định luật II Newton:

P T ma 

Chiếu (1) lên chiều dương hình vẽ:

. .

T P m a T mgcos m



    

(trọng lực đóng vai trò lực hướng tâm)

   

0 0

2 3 2T mgcos mg cos cos mg cos cos

    

     

 

0 3 3.0,12.10. 90 3,6

max max

T T mgcos cos N

 

     

Câu 18: Có hai bình khí cùng thể tích, cùng nội năng. Bình 1 chứa khí Heli

 

, bình 2 chứa Nito

 

. Coi

các khí lí tưởng. Gọi

1 2

,p p

là áp suất tương ứng của bình 1,2. Ta có:

1 2

p p

1 2

p p

1 2

p p

1 2

p p

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Vì hai bình khí có cùng thể tích



quá trình đẳng tích

Biến thiên nội năng trong qua trình đẳng tích:

. . .

2 2 2

m i i i

U RT nRT PV



   

Khí Heli

3i 

và khí Nito

5i 

Ta có:

1 1

1 1 1 1

2 2 1 1 1 2

2 2 2 2 1 2

2 2 2 1

1 2 1 2

. . .

2 2

5 5

. . . 1 .

2 2 3 3

;

i i

U n RT PV

i i i P P i

U n RT PV P P

i P P i

V V V U U U



  



         





      





Câu 19: Một chất điểm khối lượng

 

0,2m kg

được ném lên từ O với vận tốc

 

7 /v m s

theo phương hợp

với mặt phẳng nằm ngang với một góc





, bỏ qua sức cản của không khí, cho

 

9,8 /g m s

. Mômen

động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là:

 

0,052 /kgm s

 

0,758 /kgm s

 

0,218 /kgm s

 

0,488 /kgm s

Giải

Chọn hệ trục Oxy như hình vẽ ọa độ. Gốc t tại v trí b u ném, chiị ắt đầ ều

dương hướng xu ng, cùng chi u v i gia tố ề ớ ốc

Gia tốc:

a g









 





Vận tốc:

0 0

. .

x x x

y y y

v v a t v cos

v v a t v sint gt



  







   





Phương trình chuyển động của chất điểm:

: . .

: .

x x

y y

Ox x v cos t

Ox x v t a t

Oy y v sin t gt

Oy y v t a t







 





 



 

 

 

 







Tại vị trí cao nhất của chuyển động chất điểm:

0 .

v sint

v v sint gt t

    

Và

2 2 2 2

0 0 0

0 0

1 1 1

. .

2 2 2

v sin v sin v sin

y h v sin t gt v sin

g g g

  

 

     

Động lượng

tại thời điểm t bất kì:

 

x y x y

p t p i p j mv i mv j   

Xét tích có hướng của hai vector:

1 2 3

u u i u j u k  

và

1 2 3

v v i v j v k  

1 2 3

2 3 1 3

1 2

1 2 3

u v u u u i j k

v v v v

v v

v v v

   

Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới

trục z coi như bằng 0

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

. 0 . .

0 0

x y x y

r v v v i j k v y v x k

y x x y

x y

     

Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển

động chất điểm là:

 

0 0 0 0

. . . . . .

x y

L v y v x v cos t m v sin gt mv cos v si n t gt

   

 

     

 

 

 

2 2 3 2

2 2

0 0

1 1

0,758 /

2 2 2

v sin v sin

mgv t cos mgv cos m cos kgm s

g g

 

  

   

Câu 20: Một tàu điện sau khi suất phát chuyển động trên đường nằm ngang với gia tốc

 

0,7 /a m s

. 11 giây

sau khi bắt đâu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng hẳn. Hệ số ma sát trên

quãng đường

0,01k 

. Cho

 

10 /g m s

. Thời gian chuyển động của toàn bộ tàu là

 

92,8 s

 

84,8 s

 

88 s

 

86,4 s

Giải

Tầu chuyển động theo hai giai đoạn:

Giai đoạn 1: chuyển động với gia tốc

 

0,7 /a m s

với thời gian

 

11t s

Giai đoạn 2: chuyển động chậm dần đều với gia tốc

 

. 0,01.10 0,1 /a k g m s  

dưới tác dụng cản của lực

ma sát trong thời gian

t

Vận tốc lớn nhất của tàu:

 

1 1

. 0,7.11 7,7 /

max

v a t m s  

Tầu chuyển động chậm dần đều trong thời gian:

 

7,7

0,1

max

t s

   

Tổng thời gian chuyển động của tầu (kể từ lúc xuất phát đến khi tầu dừng lại)

 

2 1

77 11 88t t t s     

Câu 21: Một phi công thực hiện vòng tròn nhào lộn trong mặt phẳng đứng. Vận tốc của máy bay không đổi

 

900 /v km h

. Giả sử rằng áp lực lớn nhất của phi công lên ghế bằng 5 lần trọng lực của người. Lấy

 

10 /g m s

. Bán kính quỹ đạo vòng nhào lộn có giá trị bằng:

 

1562,5 m

 

1584,1 m

 

1594,4 m

 

1573,3 m

Giải

Áp d nh lu t II Newton cho phi công: ụng đị ậ

mg N ma 

là phản lực mà ghế tác dụng lên phi công (bằng và ngược chiều với lực nén của phi công lên ghế).

Áp lực lớn nhất tại điểm thấp nhất

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Tại điểm thấp nhất của vòng nhào lộn, theo phương hướng tâm,

 

được viết thành:

2 2ht

mg N ma mg N m

      

Theo bài ra, ta có:

5 5N P mg 

 

2 2

5 1562,5

v v

mg mg m R m

R g

      

Câu 22: Một con lắc lò xo

 

10m g

, dao động điều hòa với đô dời

 

8 5

x cos t cm



 

 

 

 

. Kí hiệu

là lực

cực đại tác dụng lên con lắc và

là năng lượng của con lắc. Kết luận nào dưới đây đúng:

   

0,3 , 0,9.10F N W J



 

   

0,3 , 0,8.10F N W J



 

   

0,2 , 0,8.10F N W J



 

   

0,2 , 0,9.10F N W J



 

Giải

Theo bài ra, ta có:

 

   

2 2

5 / ; 0,01. 5 2,5 /

rad s k m K m

    

     

Ta có:

 

2 2 3

2,5.0,08 0, 2

1 1

.2,5.0,08 8.10

2 2

F kA N

W kA J



  





  





Câu 23: Một đoàn tàu khối lượng 30 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng

 

12 /km h

. Công suất đầu máy là

 

200 kW

. Gia tốc trọng trường bằng

 

9,8 /m s

. Hệ số ma sát bằng:

23,4.10



20,41.10



22,4.10



21,41.10



Giải

Đổi

   

12 / /

v km h m s 

Ta có:

 

200.10

. 600

P F v F N

    

Mà

 

6000

6000 20,41.10

30.10 .9,8

F F mg N

 



      

Câu 24: Một thanh chiều dài

 

0,9l m

, khối lượng

 

6M kg

có thể quay tự do xung quanh một trục nằm

ngang đi qua một đầu của thanh. Một viên đạn khối lượng

 

0,01m kg

bay theo hương nằm ngang với vận tốc

 

300 /v m s

tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc gốc của thanh ngay sau khi viên đạn

đập vào đầu thanh là:

 

2,429 /rad s

 

1,915 /rad s

 

1,144 /rad s

 

1,658 /rad s

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có mỗi

viên đạn có tốc độ và khối lượng

mang một động lượng

p mv

Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách

từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm

quay tới viên đạn chính là độ dài

Vậy mômen động lượng trước khi va chạm là:

. . .

L r p sin l p mvl



  

Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với

cùng vận tốc góc



. Vậy moomen quán tính của hệ vật sau va chạm:

1 2s

L I I

 

 

Với

là moment chất điểm (viên đạn) đối với trục quay

I ml

là moment quán tính của thanh mảnh

2 2

12 12 3

Ml Ml

 

 

 

  

Hay

 

1 2

L I I ml

 

 

   

 

 

Áp dụng định luật bảo toàn động lượng

 

1,658 /

t s

Ml mvl v

L L mvl ml rad s

MMl

 

 

       

 

 

 



 

 

Câu 25: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

50 kW

. Nhiệt độ của nguồn nóng là

127 C

, nhiệt độ của nguồn lạnh là

31 C

. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:

 

12200 kJ

 

12600 kJ

 

12500 kJ

 

12300 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 50 625

304

400

A A

Q kJ

T Q



      





Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút:

 

1 1

625

. .60 12500

Q Q t kJ  

Câu 26: Thả rơi tự do 1 vật nhỏ tư độ cao

 

19,6h m

. Quãng đường mà vật rơi được trong 0,1 giây cuối của

thời gian rơi là: (cho

 

9,8 /g m s

)

 

1,911 m

 

1,711 m

 

1,311 m

 

1,511 m

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Thời gian rơi của vật:

 

t s

 

Quãng đường vật rơi trong 0,1 giây cuối là:

     

2 2

0,1

1 1 1

0,1 0,1 1,911

2 2 2

t t

s s s gt g t g t t m



 

         

 

Công thức tổng quát cho quãng đường rơi trong n giây cuối là

 

s g t t n

 

   

 

với



Câu 27: Một khối khí ôxy

 

bị nung nóng từ nhiệt độ

 

240 K

đến

267 C

. Nếu vận tốc trung bình của phân

tử ôxy lúc đầu là v thì lúc sau là:

1,35v

1,55v

1,5v

1,6v

Giải

Công thức tính vận tốc trung bình của phân tử khí:

8kT





Hay

2 2

1 1

267 273

1,5

240

v T













   











Câu 28: Một con lắc toán có sợi dây

 

1l m

, cứ sau

0,8t 

phút thì biên độ giao động giảm 2 lần. Giảm

lượng loga của con lắc dố bằng giá trị nào sau đây ( cho

 

9,8 /g m s

)

3,489.10



2,898.10



2,701.10



3,292.10



Giải

Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:

F F kx rv   

Phương trình cơ bản của chuyển động trong trường hợp này là

ma kx rv  

Hay:

2 2

d x dx d x r dx k

m r kx x

dt dt dt m dt m

      

 

Đặt





(hệ số tắt dần)

Phương trình

 

trở thành

2 0

d x dx

x x

dt dt

 

  

 

gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi

 



, nghiệm phương trình

này có dạng:

 

x A e cos t



 



 

Đây là biểu thức độ dời của dao động tắt dần. Hằng số



gọi là tần số của dao động tắt dần:

2 2

  

 

Chu kỳ

của dao động tắt dần là:

2 2

2 2 2

  



 



  



Giảm lượng loga của con lắc:

2 2



  

 

 



TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Theo bài ra, ta có:

. .48

1 1

0,01444

2 2

e e

 



  

     

và

9,8



  



2 2 2

2 2

. 0,01444. 2,898.10

9,8 0,0144

 

 

 



   

 

Câu 29: Một mol khí hidro nguyên tử được nung nóng đẳng áp, thể tích tăng gấp 2 lần. Entrôpie của nó biến

thiên một lượng bằng ( cho hằng số khí

 

8,31 / .R J mol K

)

 

14,4 /J K

 

15,9 /J K

 

14,9 /J K

 

15,4 /J K

Giải

Độ biến thiên Entropy:



Qúa trình đẳng áp:

Q nC dT n RdT





 

Thay vào và lấy tích phân từ trạng thái 1 ứng với

đến trạng thái 2 ứng với

2 2 2

i dT i i

S n R n RlnT n Rln

TT T

  

    



Điều kiện của quá trình đẳng áp

 

p const

2 2

1 1

T V



 

14,4 /

S n Rln J K



   

(khí

: 3H i 

)

Câu 30: Một động cơ nhiệt làm việc theo chu trình Carnot với nhiệt độ nguồn nóng là

100 C

. Trong mỗi một

chu trình tác nhân nhận của nguồn nóng một nhiệt lượng

 

10 kcal

và thực hiện công

 

15 kJ

. Nhiệt độ của nguồn

lạnh là:

 

236,72 K

 

235,72 K

 

239,72 K

 

238,72 K

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

2 2

2 1

1 1 1 1 1

' ' ' 15

1 1 1 373. 1 239,34

10.4,186

T TA A A

T T K

T Q T Q Q



 

           

 

 

Câu 31: Ở thời điểm ban đầu một chất điểm có khối lượng

 

1m kg

có vận tốc

 

19 /v m s

. Chất điểm chịu

lực cản

F rv 

( biết

2r ln

là vận tốc chất điểm). Sau

 

1,8 s

vận tốc của chất điểm là:

 

4,656 /m s

 

4,256 /m s

 

5,456 /m s

 

5,056 /m s

Giải

Lực cản:

F ma mv m

  

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Mặt khác:

dv dv r

F rv m rv dt

dt v m

       

Lấy tích phân:

 

. 5,456 /

v t

dv r v r

dt ln t v v e m s

v m v m



       

 

Câu 32: Một khẩu pháo có khối lượng

 

480M kg

bắn một viên đạn theo phương làm với mặt ngang một góc





. Khối lượng của viên đạn

 

5m kg

, vận tốc đầu nòng

 

400 /v m s

. Khi bắn bệ pháo giật lùi về phía

sau một đoạn

 

54s cm

. Lực cản trung bình tác dụng lên quả pháo có giá trị:

 

2129 N

 

1929 N

 

2229 N

 

2029 N

Giải

Theo định lu t bậ ảo toàn động lượng thì vận t c giố ật lùi c a kh u pháo là: ủ ẩ

 

. . 5.400. 60 25

480 12

m v cos cos

V m s



     

Dấu

" "

chứng tỏ pháo giật lùi, ngược chiều dương)

Áp dụng công thức:

 

2 2 2

' 2 4,0187 /

V V aS a m s

      

Lực cản trung bình tác dụng lên quả pháo:

 

4,0187.480 1929

F Ma N    

Câu 33: Một con lắc toán có sợi dây

 

65l m

. Biết rằng sau thời gian





phút, nó mất

99%

năng lượng.

giảm lượng lôga của con lắc nhận giá trị nào dưới đây (cho

 

9,8 /g m s

)

0,975.10



1,125.10



1,035.10



1,065.10



Giải

Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:

F F kx rv   

Phương trình cơ bản của chuyển động trong trường hợp này là

ma kx rv  

Hay:

2 2

d x dx d x r dx k

m r kx x

dt dt dt m dt m

      

 

Đặt





(hệ số tắt dần)

Phương trình

 

trở thành

2 0

d x dx

x x

dt dt

 

  

 

gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi

 



, nghiệm phương trình

này có dạng:

 

x A e cos t



 



 

Đây là biểu thức độ dời của dao động tắt dần. Hằng số



gọi là tần số của dao động tắt dần:

2 2

  

 

Chu kỳ

của dao động tắt dần là:

2 2

2 2 2

  



 



  



Giảm lượng loga của con lắc:

2 2



  

 

 



Theo bài ra, ta có:

2 . 2 .6.60 3

0,01 0,01 6,396.10

e e

 







   

     

và

9,8 49

65 325



  



TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

3 2

2 2

. 6,396.10 . 1,035.10

6,396.10

325

 

 

 

 



   



Câu 34: Hai khối khí

và

có cùng mật độ số hạt. Nhiệt độ của khối khí

là

120 C

, nhiệt độ của khối

khí

là

60 C

. Áp suất của

và

theo thứ tự là

và

. Ta có:

1 2

0,98P P

1 2

1,18P P

1 2

0,88P P

1 2

1,28P P

Giải

Số phân tử khí của chất khí đó là

. .

A A

N n N N



 

Hằng số Boltzmann

 

1,28.10 / .

RT R R m R

k J K N N

V N k k





      

Mật độ phân tử của chất khí đó là

N mR p

V k V kT



  

Vì hai khối khí

và

có cùng mật độ số hạt và nhiệt độ thay đổi



áp suất thay đổi



Qúa trình đẳng tích

Áp dụng PT trạng thái quá trình đẳng tích:

1 1

1 2

2 2

120 273

1,18

60 273

P T

P P

P T



   



Câu 35: Một bánh xe có bán kính

 

12R cm

lúc đầu đứng yên sau đs quay quanh trục cảu nó với gia tốc góc

 

3,14 /rad s





. Sau giây thứ nhất gia tốc toàn phần của một điểm trên vành bánh là:

 

120,17 /cm s

 

126,17 /cm s

 

130,17 /cm s

 

124,17 /cm s

Giải

Sau giây th nh t, v n t c góc và vứ ấ ậ ố ận t c dài c a mố ủ ột điểm tren vành bánh là:

 

. 3,14.1 3,14 /t rad s

 

  

và

 

3,14.0,12 0,3768 /v R m s



  

Gia tốc tiếp tuyến có giá trị không đổi còn gia tốc pháp tuyến lúc này:

 

. 3,14.0,12 0,3768 /

a R m s



  

và

 

2 2 2

. 3,14 .0,12 1,18352 /

a R m s



  

Gia tốc toàn phần:

 

2 2 2

124,17 /

t n

a a a m s  

Câu 36: Một chất điểm bắt đầu trượt từ đỉnh mặt phẳng nghiêng góc



so với phương nằm ngang (xem hình

vẽ). Hệ số ma sát giữa vật và mặt phẳng nghiêng là

; khối lượng của vật là m ( lấy

 

9,81 /g m s

). Cho

   

2,5 , 0,2, 8 , 30m kg k h m



   

. Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O là:

 

62,107 Nm

 

52,234 Nm

 

45,652 Nm

 

55,525 Nm

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Chọn h c tệ trụ ọa độ Oxy như hình vẽ ều dương cùng chiề ển độ , chi u chuy ng của vật

Vật chịu tác d ng c a các lụ ủ ực: trọng lực

, phản lực

và lực ma sát

Áp dụng định luật II Newton, ta có:

P N f ma  

 

Chiếu

 

lên trục

:Ox

N P N Pcos mgcos

 

    

Chiếu

 

lên trục

:Oy

t ms ms

P sin f

P f ma P sin f ma a





      

Mà

 

. .

f k N k mgcos F mg sin kcos

  

    

Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O chính là công của lực

tác dụng lên điểm O

   

. . . . . 30 55,525

A F h cos mg sin k cos h cos N

  

   

Câu 37: Một vật khối lượng m bắt đầu trượt không ma sát từ đỉnh một mặt cầu bán kính

 

2R m

xuống dưới.

Vật rời khỏi mặt cầu với vị trí cách đỉnh mặt cầu một khoảng là:

 

0,807 m

 

0,737 m

 

0,667 m

 

0,877 m

Giải

Chọn chi u chuy ng c a v t ều dương cùng chiề ển độ ủ ậ

Vật chịu tác d ng c a các lụ ủ ực: trọng lực

, phản lực

Áp dụng định luật II Newton, ta có:

P N ma 

 

Vì chuyển động tròn nên gia tốc ở đây đóng vai trò là gia tốc hướng tâm

Chiếu

 

lên phương chuyển động:

2 2

v v

Psin N ma m N Psin m

R R

 

     

Theo hình vẽ, ta có:

R h

sin



 



Khi vật di chuyển xuống dưới thì thế năng của vật giảm dần và biến thành động năng. Như vậy độ biến thiên

thế năng phải bằng độ biến thiên động năng của vật:

 

t d

W W mgR mg R h mv mg h         

Để vật rời khỏi mặt cầu thì

 

0 0 2 0 0,667

mv R h R

N Psin mg mg h h m

R R



 

           

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 38: Một chất điểm dao động điều hòa với chu kì

 

1, 4 s

và biên độ

 

8 cm

. Vận tốc chất điểm trên tại vị trí

mà ly độ bằng

biên độ bằng giá trị nào dưới đây:

 

0,311 /m s

 

0,321 /m s

 

0,331 /m s

 

0,341 /m s

Giải

Áp dụng phương trình về mối liên hệ của

, ,A x v

 

2 2

2 2 2 2 2 2 2

2 2

0,08 0,04 0,311 /

2 1,4

v A

A x v A x A m s

 



   

         

   

   

Câu 39: Một ống thủy tinh nhỏ khối lượng

 

130M g

bên trong có vài giọt ête được đậy bằng 1 nút cố định

có khối lượng

 

10m g

. Ống thủy tinh được treo ở đầu một sợi dây không giãn, khối lượng không đáng kể,

chiều dài

 

65l cm

(hình vẽ). Khi hơ nóng ống thủy tinh ở vị trí thấp nhất, ête bốc hơi và nút bật ra. Để ống có

thể quay được cả vòng xung quanh điểm treo O , vận tốc bật bé nhất của nút là: (Cho

 

10 /g m s

)

 

72,411 /m s

 

70,711 /m s

 

74,111 /m s

 

79,211 /m s

Giải

Tại v trí A, vị ận tốc tại đây phải đủ ớn để l dây thẳng đứng và căng đét

0T 

2 2

A A

v v

P T m T m mg v gl

l l

       

Vận tốc nhỏ nhất tại A để ống quay tròn:

Amin

v gl

Đối với ống thủy tinh:

Áp dụng định luật bảo toàn cơ năng:

2 2 2 2

1 1 1 1

2 2 2 2

B dB tB B B

W W W MV Mv Mgh MV Mv Mg l       

2 2

V v gl  

Vận tốc tối thiểu để đạt đỉnh:

4 5 5

B min

v gl V gl gl gl V gl      

Áp dụng định luật bảo toàn động lượng:

 

74,111 /

min

min min min

M glMV

mv MV v m s

m m

    

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 40: Một khối khí ôxy

 

biến đổi trạng thái sao cho khối lượng riêng của nó giảm 1,5 lần và tốc độ trung

bình của các phân tử giảm 1,5 lần. Trong quá trình đó, áp suất mà khí ôxy tác dụng lên thành bình thay đổi như

thế nào?

A. Giảm

3,375

lần

B. Giảm

1, 225

lần

C. Giảm

2,25

lần

D. Giảm

1,837

lần

Giải

Theo bài ra, ta có:

n const

 

Ở trạng thái

1 1

p V



và ở trạng thái 2:

2 2

p V



2 1 2

1 2 1

p V T

 

Công thức tính vận tốc trung bình của phân tử khí:

8kT





Hay

2 2

1 1

v T









 



 



 

 









và

1 1

1 2

2 2

2 1

m V

m V V







 







2 1 2 2 2

1 2 1 1 1

. .

p V T v



 

   

 

 

Câu 41: Một vệ tinh có khối lượng

 

150m kg

chuyển động trên quỹ đạo tròn bán kính

 

7,4.10r m

quanh

Trái Đất. Cho khối lượng trái đất

 

5,98.10M kg

. Hằng số hấp dẫn

 

11 2 2

6,67.10 . /G N m kg





. Tốc độ vệ

tinh trên quỹ đạo đó là:

 

7,042 /km s

 

6,742 /km s

 

7,342 /km s

 

6,442 /km s

Giải

Lực hấp dẫn giữa trái đất và vệ tinh là lực gây ra gia tốc hướng tâm cho vệ tinh nên:

   

7342 / 7,342 /

hd ht ht

GMm v GM GM

F F ma m v v m s km s

r r r r

         

Câu 42: Một máy nhiệt lí tưởng làm việc theo chu trình Carnot, sau mỗi chu trình thu được 600 calo từ nguồn

nóng có nhiệt độ

127 C

. Nhiệt độ nguồn lạnh là

27 C

. Công do máy sinh ra sau một chu trình

 

627,9 J

 

647,9 J

 

637,9 J

 

657,9 J

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

2 2

1 1 1

' 300

1 ' 1 600.4,186. 1 627,9

400

T TA

A Q J

T Q T



 

        

 

 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 43: Có 1g khí Hidro

 

đựng trong một bình có thể tích 6 lít. Mật dộ phan tử của chất khí đó là ( cho

hằng số khí

 

8,31.10 / .R J kmol K

; hằng số Boltzmann

 

1,38.10 /k J K





)

3,158.10

ph ân tử/

4,518.10

phân tử/

6,018.10

phân tử/

5,018.10

phân tử/

Giải

Số phân tử khí của chất khí đó là

. .

A A

N n N N



 

Hằng số Boltzmann

 

1,28.10 / .

RT R R m R

k J K N N

V N k k





      

Mật độ phân tử của chất khí đó là

' 5,018.10

N mR

V k V



  

phân tử/

Câu 44: Một chất điểm khối lượng

 

0,3m kg

được ném lên từ O với vận tốc

 

9 /v m s

theo phương hợp

với mặt phẳng nằm ngang một góc





– bỏ qua sức cản của không khí, cho

 

9,8 /g m s

. Mômen động

lượng của chất điểm đối với O tại vị trí cao nhất của chuyện động chất điểm là:

 

3,226 /kgm s

 

2,416 /kgm s

 

2,956 /kgm s

 

2,146 /kgm s

Giải

Chọn hệ trục Oxy như hình vẽ. Gốc t t i v trí b u ném, chiọa độ ạ ị ắt đầ ều

dương hướng xu ng, cùng chi u v i gia tố ề ớ ốc

Gia tốc:

a g









 





Vận tốc:

0 0

. .

x x x

y y y

v v a t v cos

v v a t v sint gt



  







   





Phương trình chuyển động của chất điểm:

: . .

: .

x x

y y

Ox x v cos t

Ox x v t a t

Oy y v sin t gt

Oy y v t a t







 





 



 

 

 

 







Tại vị trí cao nhất của chuyển động chất điểm:

0 .

v sint

v v sint gt t

    

Và

2 2 2 2

0 0 0

0 0

1 1 1

. .

2 2 2

v sin v sin v sin

y h v sin t gt v sin

g g g

  

 

     

Động lượng

tại thời điểm t bất kì:

 

x y x y

p t p i p j mv i mv j   

Xét tích có hướng của hai vector:

1 2 3

u u i u j u k  

và

1 2 3

v v i v j v k  

1 2 3

2 3 1 3

1 2

1 2 3

u v u u u i j k

v v v v

v v

v v v

   

Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới

trục z coi như bằng 0

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

. 0 . .

0 0

x y x y

r v v v i j k v y v x k

y x x y

x y

     

Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển

động chất điểm là:

 

0 0 0 0

. . . . . .

x y

L v y v x v cos t m v sin gt mv cos v si n t gt

   

 

     

 

 

 

2 2 3 2

2 2

0 0

1 1

2,416 /

2 2 2

v sin v sin

mgv t cos mgv cos m cos kgm s

g g

 

  

   

Câu 45: Một khối ôxy

 

ở nhiệt độ

20 C

. Để nâng vận tốc căn quân phương của phân tử lên gấp đôi, nhiệt

độ của khí là:

899 C

919 C

929 C

889 C

Giải

Công th c tính v n tứ ậ ốc căn quần phương:



(với k là hằng số Boltzmann)

Mặt khác:

R RT

k v

m N









  











Ta có:

 

1 1 2

2 1 2

2 2 1

1172 899

v T v

T T K t C

v T v









 



      



 

 









Câu 46: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

45 kW

. Nhiệt độ của nguồn nóng là

127 C

, nhiệt độ của nguồn lạnh là

31 C

. Nhiệt lượng tác nhân nhận ở nguồn nóng trong một phút có giá trị:

 

10950 kJ

 

11050 kJ

 

11250 kJ

 

11350 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 45

1 187,5

304

400

A A

Q kJ

T Q



      





Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút:

 

1 1

. 187,5.60 11250Q Q t kJ  

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 47: Một ô tô khối lượng

 

550m kg

chuyển động thẳng đều xuống dốc trên một mặt phẳng nghiêng, góc

nghiêng



so với mặt đất nằm ngang có

0,00872; 0,9962sin cos

 

 

. Lực kéo ô tô bằng

 

550

F N

, cho

 

10 /g m s

. Hệ số ma sát giữa ô tô và mặt đường là:

0,158

0,188

0,208

0,198

Giải

Chọn trục Oxy như hình vẽ. Chiều dương cùng chiều chuyển động với ô tô

Ô tô chịu tác dụng của các lực: lực kéo

của động cơ ô tô, trọng lực

, phản lực tiếp tuyến

của mặt

đường và lực ma sát của mặt đường

Áp dụng định luật II Newton, ta có

F P N f   

(vì ô tô chuyển động thẳng đều)

Chiếu phương trình này nên phương chuyển động của ô tô, ta được:

k ms

F f Psin



  

. 0,188

k ms

F mgsin

F f Psin k N Psin kmgcos mgsin k

mgcos



   





         

Câu 48: Có ba vật đồng chất, cùng khối lượng: cầu đặc, trụ đặc và trụ rỗng cùng được thả lăn không trượt từ đỉnh

một mặt phẳng nghiêng. Vật nào tới chân mặt phẳng nghiêng lớn nhất:

A. Cả 3 vật B.Trụ đặc Trụ rỗng Quả cầu đặc C. D.

Giải

Moment quán tính của trụ đặc:

I 

Moment quán tính của trụ rỗng:

I mR

Moment quán tính của cầu đặc:

I 

Vì

2 2

5 2

mR mR

I I I mR     

quả cầu đặc tới chân mặt phẳng nghiêng nhanh nhất

Câu 49: Cho một chu trình Carnot thuận nghịch, đột biến trên entropi trong quá trình đẳng nhiệt có hệ số là

 

1 /S kcal K 

; hiệu suất nhiệt độ giữa 2 đường đẳng nhiệt là

   

300 ;1 4,18T K cal J  

. Nhiệt lượng đã

chuyển hóa thành công trong chu trình đang xét là:

 

12,54.10 J

 

12,04.10 J

 

13,54.10 J

 

11,04.10 J

Giải

Nhiệt lượng đã chuyển hóa thành công trong chu trình đang xét là

 

3 5

. 10 .300.4,18 12,54.10A S T J    

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 50: Thả rơi tự do một vật nhỏ từ độ cao

 

17,6h m

. Thời gian cần thiết để vật đi hết

 

1 m

cuối của độ

cao

là: ( cho

 

9,8 /g m s

)

 

5,263.10 s



 

5,463.10 s



 

5,863.10 s



 

4,863.10 s



Giải

Thời gian rơi của vật:

 

2 2.17,6

1,895

9,8

t s

  

Thời gian để vật đi được 1m đầu:

 

2 ' 2.1

' 0,45

9,8

t s

  

Thời gian để vật đi hết 1m cuối:

 

16,6

2.16,6

" 1,895 5,463.10

9,8

tong

t t t s



    

Câu 51: Một đoàn tàu khối lượng

tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng

 

36 /km h

. Công suất đầu máy là

 

245 kW

. Gia tốc trọng trường bằng

 

9,8 /m s

. Hệ số ma sát bằng:

5,000.10



5,997.10



3,006.10



2,009.10



Giải

Ta có:

 

245.10

. 24500

P F v F N

    

Mà

F F mg



 



Hệ số ma sát:

24500

0,05

9,8.50.10



  

Câu 52: Một đĩa trong khối lượng

 

155M kg

đỡ một người có khối lượng

 

51m kg

. Lúc đầu người đứng

ở mép và đĩa quay với vận tốc góc





(vòng/phút) quanh trục đi qua tâm đĩa. Vận tốc góc của đĩa khi người

đi vào đúng tâm của đĩa là ( coi người như 1 chất điểm)

 

2,006 /rad s

 

2,276 /rad s

 

1,736 /rad s

 

0,926 /rad s

Giải

Bài này áp d nh lu t bụng đị ậ ảo toàn động lượng

Giai đoạn trước: mômen động lượng của hệ sẽ là:

1 1truoc dia nguoi

L I I

 

 

Mômen quán tính đĩa đặc như đã biết là:

dia

I 

Mômen quán tính của người (chất điểm) là:

nguoi

I mR

truoc

L mR



 

  

 

 

Giai đoạn sau: để ý là khi người đi vào tâm đĩa thì coi như khoảng cách từ người tới tâm đĩa là 0. Điều này kéo

theo mômen quán tính của người với tâm đĩa coi như bằng 0.

Moment động lượng của hệ lúc này là

2 2

sau dia

L I

 

 

Áp dụng định luật bảo toàn động lượng:

2 2

1 2

2 2

truoc sau

MR mR

L L mR

 

 

   

 

 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

0,5 155.0,5 51

. 1,736 /

0,5 0,5.155 3

M m

rad s



 

 

   

Câu 53: Giả sự lực cản của nước tác dụng lên xà lan tỉ lệ với tốc độ của xà lan đối với nước. Một tàu kéo cung

cấp công suất

250P 

mã lực ( 1 mã lực

 

746 W

) cho xà lan khi chuyển động với tốc độ

 

0,25 /v m s

Công suất cần thiết để kéo xà lan với tốc độ

 

0,75 /v m s

là

2240

mã lực B.

2220

mã lực C.

2250

mã lực D.

2270

mã lực

Giải

Lực c n c c tả ủa nướ ỉ lệ với tốc độ của xà lan với nước:

 

F kv k const 

Ta có:

2 2

1 1

1 1 2

2 1

2 2 1

2 2

2250

F k v

F v v

F F

F v v

F k v





   



    



   





   



(mã lực)

Câu 54: Một động cơ nhiệt làm việc theo chu trình Carnot bằng không khí lấy ở áp suất ban đầu

 

7,0P at

Thể tích ban đầu của không khí

 

2V dm

. Sau lần giãn đẳng nhiệt lần thứ nhất nó chiếm thể tích

 

5V dm

và sau khi giãn đoạn nhiệt thể tích của khí là

 

8,1V dm

. Áp suất khí sau khi giãn đoạn nhiệt có giá trị

bằng;

 

12,98.10 Pa

 

10,98.10 Pa

 

13,98.10 Pa

 

15,98.10 Pa

Giải

Giai đoạn 1: quá trình đẳng nhiệt

 

T const

Áp dụng phương trình TT của quá trình đẳng nhiệt:

 

1 1

1 1 2 2 2

7.2

2,8

PV PV P at

    

Giai đoạn 2: Qúa trình đoạn nhiệt

Áp dụng phương trình TT cho quá trình đoạn nhiệt:

   

1,4

4 4

2 2 3 3 3 2

2,8. 1,425 1,425.9,8.10 13,98.10

8,1

PV PV P P at Pa



 

 

      

 

 

Câu 55: Một viên bi có khối lượng

, vận tốc

bắn thẳng góc vào một bức tương phẳng. Sau khi va chạm

viên bi bay ngược trở lại với vận tốc bằng

. Gội động năng ban đầu của viên bi là

, độ biến thiên động

năng và động lượng của viên bi là

W

và

p

; ta có

W

và

 

2 2p mE 

W  

và

 

3 2

p 

W  

và

 

5 2

p 

W  

và

 

9 2

p 

Giải

Độ biến thiên động năng:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

2 2 2 2

2 1

1 1 1 4 1 9 1 9

. . .

2 2 2 5 2 25 2 25

sau t

W W W mv mv m v mv mv E

 

          

 

 

Câu 56: Một ô tô có khổi lượng

2,1m 

tấn chuyển động trên đoạn đường nằm ngang với vận tốc không đổi

 

54 /v km h

. Công suất của ô tô bằng

 

9,8 kW

. Lấy

 

9,8 /g m s

. Hệ số ma sát giữa bánh xe và mặt

đường có giá trị bằng;

0,305.10



0,281.10



0,317.10



0,341.10



Giải

Ta có:

 

9,8.10 1960

15 3

P F v F N

    

Mà

F F mg



 



Hệ số ma sát:

1960

0,0317

9,8.2,1.10



  

Câu 57: Nhiệt độ của một khối plasma khí coi là khí lí tưởng trên mặt trời là

 

2,6.10 K



. Vận tốc căn quân

phương của các điện tử tự do trong khối khí đó. (

   

31 23

9,1.10 , 1, 38.10 /

m kg k J K

 

 

) là:

 

11,876.10 /m s



 

10,876.10 /m s



 

13,876.10 /m s



 

12,876.10 /m s



Giải

Công th c tính v n tứ ậ ốc căn quần phương:

 

10,876.10 /

v m s



 

(với k là hằng số Boltzmann)

Câu 58: Một bánh xê bắt đầu quay quanh một trục cố định đi qua tâm vành bánh và vuông góc với mặt phẳng

bánh xe, có góc quay xác định bằng biểu thức:





; trong đó

 

0,125 / ;a rad s t

là thời gian. Điểm

trên

vành bánh xe sau

 

2 s

có vận tốc dài

 

2 /v m s

. Gia tốc toàn phần của điểm

khi đó có giá trị bằng:

 

2 2 /m s

 

2 5 /m s

 

5 /m s

 

2 /m s

Giải

Theo bài ra, ta có:

 

2 2 2

1 1

2 0,25 /

2 2

at t a a rad s

   

      

Vận tốc góc:

 

. 0, 25.2 0,5 /t rad s

 

  

Vận tốc dài:

 

0,5

v R R m



    

Gia tốc tiếp tuyến và gia tốc pháp tuyến lúc này:

 

. 4.0,25 1 /

a R m s



  

và

 

2 2 2

. 0,5 .4 1 /

a R m s



  

Gia tốc toàn phần:

 

2 2 2

2 /

t n

a a a m s  

Câu 59: Một tàu điện khi xuất phát chuyển động trên đường nằm ngang với gia tốc

 

0,9 /a m s

, 13s sau khi

bắt đầu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng lại hẳn. Hệ số ma sát trên đường

0,01k 

. Cho

 

10 /g m s

. Thời gian chuyển động toàn bộ của tàu là:

 

130 s

 

126,8 s

 

125,2 s

 

128,4 s

Giải

Tầu chuyển động theo hai giai đoạn:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Giai đoạn 1: chuyển động với gia tốc

 

0,9 /a m s

với thời gian

 

13t s

Giai đoạn 2: chuyển động chậm dần đều với gia tốc

 

. 0,01.10 0,1 /a k g m s  

dưới tác dụng cản của lực

ma sát trong thời gian

t

Vận tốc lớn nhất của tàu:

 

1 1

. 0,9.13 11,7 /

max

v a t m s  

Tầu chuyển động chậm dần đều trong thời gian:

 

11,7

117

0,1

max

t s

   

Tổng thời gian chuyển động của tầu (kể từ lúc xuất phát đến khi tầu dừng lại)

 

2 1

13 117 130t t t s     

Câu 60: Khối lượng của một mol chất khí là

 

32 /kg kmol





và hệ số Poat xông của chất khí là -

1, 4





. Nhiệt

lượng rung riêng đẳng áp của khí bằng ( cho hằng số khí

 

8,31.10 / .R J kmol K





 

921,91 / .J kg K

 

934,91 / .J kg K

 

869,91 / .J kg K

 

908,91 / .J kg K

Giải

Ta có:

1,4 3,5

p p

v p

C C

C R

C C R



    



Nhiệt lượng rung riêng đẳng áp của khí:

 

3,5

908,91 / .

c J kg K



  

Câu 61: Một xi lanh có pit –tông có thể di động được. Trong xi lanh đựng một khối khí lí tưởng. Vỏ xi lanh -

không dẫn nhiệt. Nếu áp suất không khí trong xi lanh tăng 2 lần thì nội năng của khí thay đổi như thế thế nào?

( gọi



là hệ số Poatxông)

A.Tăng





lần Tăng B.





lần C. Tăng





lần Tăng D.





lần

Giải

Theo nguyên lý 1:

. . . .

m i

U n C T RT



 

Phương trình trạng thái của quá trình đoạn nhiệt:

1 1

1 2

1 1 2

2 1

. .

T P

T P T P

T P



 



 



 

 

  

 

 

Ta có:

1 1 1

1 1 2

2 2 1

1 2 2

. .

m i

U nC T RT

U T P

m i

U T P

U nC T RT









 



 



   



 

 



 





Câu 62: Một người kéo xe bằng một hợp lực với phương ngang một góc





. Xe có khối lượng

 

240m kg

và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường

0,26k 

. Lấy

 

10 /g m s

Lực kéo có giá trị bằng:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

622,59 N

 

626,49 N

 

614,79 N

 

618,69 N

Giải

Chọn chi u chuy ều dương cùng chiề ển động

Khi xe chuy ng, ch u tác d ng c a các lển độ ị ụ ủ ực: Trọng lực

, phản lực

, lực kéo

và lực ma sát

Vì xe chuyển động với vận tốc không đổi nên

0a 

Áp dụng định luật II Newton, ta có:

ms k

P N f F   

 

Chiếu

 

lên trục Oy:

. 0

N F sin P



  

Chiếu

 

lên trục Ox:

. 0 .

k ms k ms

F cos f F cos f

 

   

Mà lực ma sát tác dụng lên xe:

 

. .

ms k

f k N k P F sin



  

Hay

   

. . . 626,49

k k k

F cos k P F sin F N

cos k sin

 

    



Câu 63: Một vật cố khối lượng

 

10m kg

bắt đầu trượt từ đỉnh dốc một mặt phẳng nghiêng cao

 

20h cm

Khi tới chân dốc có vận tốc

 

15 /v m s

. Cho

 

10 /g m s

. Công của lực ma sát là

 

867,7 J

 

853,1 J

 

875 J

 

860,4 J

Giải

Chọn mặt đất làm gốc tính thế năng

 

W 

, chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu

tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường,

hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát:

2 1 0

2 2

mvmv

A W W mgh mgh

  

     

  

 

Thay số:

   

0 0

0, 0,2 , 15 / , 0v h m v m s h   

 

875

A mv mgh J   

Câu 64: Một đĩa tròn đồng chất bán kính

 

0,15R m

, có thể quay xung quanh một trục nằm ngang vuông góc

với đĩa và cách tâm đĩa một đoạn

. Đĩa bắt đầu quay từ vị trí cao nhất của tâm đĩa với vận tốc đầu bằng 0. Vận

tốc khi tâm đĩa ở vị trí thấp nhất là (

 

9,8 /g m s

)

 

13,199 /rad s

 

49,915 /rad s

 

12,226 /rad s

 

50,888 /rad s

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Tại vị trí cao nhất và vị trí thấp nhất khoảng cách giữa hai khối tâm là

Chọn mốc thế năng là vị trí thấp nhất

cho tiện. Như vậy ở vị trí cao nhất năng lượng của đĩa tròn dưới dạng thế năng và có dạng:

W mgR

Tại vị trí thấp nhất năng lượng của đĩa có dạng động năng (thế năng bằng ) và có dạng:0





Moment quán tính của thanh đối với trục quay:

1 3

2 2 4

R mR

I mR m

 

  

 

 

Áp dụng định luật bảo toàn năng lượng:

 

2 2 2

1 1 3 3 8

13,199 /

2 2 4 8 3

mR g

mgR I g R rad s

   

      

Câu 65: Khối lượng riêng của một chất khí

 

2 3

5.10 /kg m







; vận tốc căn quân phương của các phân tử khí

này là

 

450 /v m s

. Áp suất của khối khí tác dụng lên thành bình là:

 

3575 /N m

 

3675 /N m

 

3475 /N m

 

3375 /N m

Giải

Áp dụng PT trạng thái khí lí tưởng:

PV m PV RT PV P P

RT RT m

  

      

Vận tốc căn quân phương của các phân tử khí:

RT RT

 

  

 

2 2

. 3375 /

3 3

C C

v v

P N m



    

Câu 66: Một ô tô bắt đầu chạy vào đoạn đường vòng bán kính

 

1,3R km

và dài

 

600 m

với vận tốc

 

54 /v km h

. Ô tô chạy hết quãng đường trong thời gian

 

17t s

. Coi chuyển động là nhanh dần đều, gia

tốc toàn phần của ô tô cuối đoạn đường vòng bằng:

 

2,869 /m s

 

4,119 /m s

 

3,369 /m s

 

3,119 /m s

Giải

Áp dụng công thức:

S v t a t 

để tính gia tốc tiếp tuyến.

   

 

2 2

2 2 600 15.17

2,386 /

S v t

a m s

 

   

Vận tốc dài của đoàn tàu cuối quãng đường tròn được tính theo công thức:

 

. 15 2,386.17 55,562 /

v v a t m s    

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Dùng công thức:

 

2 2

55,562

2,375 /

1,3.10

a m s

  

để tính gia tốc pháp tuyến của đoàn tàu.

Gia tốc toàn phần của đoàn tàu được tính theo công thức:

 

2 2 2 2 2

2,386 2,375 3,366 /

t n

a a a m s    

Câu 67: Cộng tích đối với 1 mol chất khí thực là đại lượng có giá trị bằng:

A. Một phần ba của thể tích lớn nhất mà một mol chất lỏng ( tương ứng với chất khí đang xét) có thể có được

B. Bằng thể tích nhỏ nhất của mol khí

C. Bằng tổng các thể tích riêng của các phân tử mol khí

D. Bằng thể tích tới hạn của mol khí

Câu 68: Một khối khí ôxy

 

có khối lượng riêng là

 

0,59 /kg m





. Số Avôgađrô

 

6,023.10 /N J kmol

. Tỷ số áp suất khí và động năng tịnh tiến trung bình của phân tử khí là:

 

6,873.10 /Pa J

 

8,993.10 /Pa J

 

8,463.10 /Pa J

 

7,403.10 /Pa J

Giải

Dạng phương trình thuyết động lực học phân tử:

p n mv

Trong đó:

là mật độ phân tử trong 1 đơn vị thể tích

 



 

 

tổng số phân tử khí có trong thể tích

là khối lượng phân tử khí

vận tốc toàn phương TB của 1 phân tử khí

Có

0 0 0

1 2 2

3 3 2 3

p n mv n n W  

 

2 2 2

7,403.10 /

3 3 3

p N N

n Pa J





    

Câu 69: Một chất điểm dao động điều hòa với chu kì

 

2T s

, pha ban đầu







. Năng lượng toàn phần

 

2,6.10W J





và lực tác dụng lên chất điểm lúc lớn nhất

 

2.10F N





. Phương trình dao động nào sau đây

là đúng của chất điểm trên:

 

6,873.10 /Pa J

 

8,993.10 /Pa J

 

8,463.10 /Pa J

 

7,403.10 /Pa J

Giải

Lực tác dụng lên chất điểm lúc lớn nhất:

F kA

Cơ năng:

   

1 1 2

. . 0,026 2,6

2 2

E kA F A A m cm

     

Ta có:

 

2 2

2 /

T rad s

 

  

    

Phương trình dao động của chất điểm:

 

2,6. 2,6.

3 3

x cos t sin t cm

 

   

   

   

   

Câu 70: Hai quả cầu

và

được treo ở hai đầu sợi dây mảnh không dãn dài bằng nhau. Hai đầu kia của các

sợi dây được buộc vào một cái giá sao cho các quả cầu tiếp xúc với nhau và tâm của chúng cùng nằm trên một

đường nằm ngang. Khối lượng của các quả cầu

 

165

m g

và

 

750

m g

. Kéo quả cầu A lệch khỏi vị trí

cân bằng đến độ cao

 

6h cm

và thả ra. Sau va chạm, quả cầu B được nâng lên độ cao là: (coi va chạm là hoàn

toàn không đổi, cho

 

9,8 /g m s

)

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

7,617 mm

 

1,951 mm

 

2,958 mm

 

7,804 mm

Giải

Trường hợp a: va chạm hoàn toàn đàn hồi

Định luật bảo toàn động lượng:

1 1 1 1 2 2

m v m V m V 

Chiếu lên trục ta có: giả sử sau khi va chạm mỗi vật chạy về 1 hướng

1 1 1 1 2 2

m v m V m V  

 

Định luật bảo toàn cơ năng: thế năng của vật

chính bằng động năng của nó trước khi va chạm và bằng tổng

động năng của vật

và

sau khi va chạm:

2 2 2

1 1 1 1 2 2

2 2 2

m v m V m V

m gh   

 

1 1 1 1 2 2 1 1 1 2 2

m v m V m V m v V m V     

 

2 2 2

1 1 1 1 2 2

2 2 2

m v m V m V

m gh m v V m V     

Lấy

 

1 1 2

v V V  

và

1 1

m v

m gh v gh  

Thay ngược lại vào

 

để tìm mối quan hệ giữa

và

   

2 1

1 1 1 2 1 1 1 1

2 1

m m

m v V m v V V v

m m



    



Tượng tự tìm được mỗi quan hệ giữa

và

2 1

1 2

V v

m m





Sau va chạm, quả cầu B được nâng lên độ cao là

   

2 1 2

7,804.10 7,804

2 2

V m m

h m mm

g g





   

Câu 71: Một phi công đang lái máy bay thực hiện vòng tròn nhào lộn trong một mặt phẳng đứng với vận tốc

 

700 /km h

. Giả thiết phi công có thể chịu đựng sự tăng trọng lượng lên 3 lần. Bán kính nhỏ nhất của vòng tròn

nhào lộn mà máy bay có thể đạt được là ( cho

 

9,8 /g m s

)

 

1979 m

 

1929 m

 

2029 m

 

1779 m

Giải

Áp d nh lu t II Newton cho phi công: ụng đị ậ

mg N ma 

là phản lực mà ghế tác dụng lên phi công (bằng và ngược chiều với lực nén của phi công lên ghế).

Áp lực lớn nhất tại điểm thấp nhất

Tại điểm thấp nhất của vòng nhào lộn, theo phương hướng tâm,

 

được viết thành:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

2 2ht

mg N ma mg N m

      

Theo bài ra, ta có:

3 3N P mg 

 

2 2

1750

3 1929

2 2.9,8

v v

mg mg m R m

R g

 

 

 

       

Câu 72: Một động cơ nhiệt có hiệu suất

 

10 %

và nhả nhiệt cho một nguồn có nhiệt độ

 

450 K

. Nó nhận nhiệt

từ một nguồn có nhiệt độ ít nhất là:

 

479 K

 

514 K

 

507 K

 

500 K

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

 

2 2

450

1 0,1 500

1 1 0,1

T T

T K



       

 

Câu 73: Một trụ đặc khối lượng

 

80M kg

có thể quay xung quanh một trục nằm ngang trùng với trục của trụ.

Một sợi dây không giãn được quấn nhiều vòng vào trụ, đầu tự do của dây có treo một vật nặng khối lượng

 

10m kg

. Để hệ tự chuyển động, sức căng của sợi dây là ( lấy

 

9,8 /g m s

 

78,4 N

 

70,94 N

 

82,13 N

 

67,21 N

Giải

Thiếu hình

Dưới tác d ng c a trong lụ ủ ực

lên vật nặng, hệ trụ + vật nặng chuyển động: trụ quay, vật nặng chuyển động tịnh

tiến (hệ vừa có phần quay vừa có phần tịnh tiến). Vì vậy không thể áp dụng định luật II Newton hay phương trình

cơ bản của chuyển động quay cho toàn bộ hệ. Gọi



là gia tốc góc của trụ, a là gia tốc dài của vật nặng. Vì

chuyển động của vật nặng và chuyển động của một điểm trên mặt trụ có cùng gia tốc nên ta có hệ thức:

.a R





 

(

là bán kính của trụ)

Gọi

và

là sức căng của dây tại A, ta có:

'T T 

(tức là

'T T

)

 

Với

tác dụng lên đoạn dây nối với vật nặng, còn

tác dụng lên đoạn dây nối với trụ

Áp dụng định luật II Newton riêng cho vật nặng, ta có:

P T ma 

Chọn chiều dương cùng chiều chuyển động với vật nặng

Chiếu phương trình trên lên phương chuyển động

mg T ma 

 

Áp dụng phương trình cơ bản của chuyển động quay cho riêng trụ đặc, ta có

'RT I





Với I là moment quán tính của trụ đặc:

I 

 

Từ

     

1 ; 2 ; 3

và

 

24 78,4

m M

T m g N

m M

T m g a







 

    



 



 



 



TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 74: Một khối khí nitơ

 

biến đổi trạng thái sao cho áp suất của nó tăng 2 lần và vận tốc căn quân phương

của các phân tử tăng

lần . Trong quá trình đó , khối lượng riêng của khối khí nitơ thay đổi như thế nào?

A. Giảm

lần Tăng B.

2 2

lần C.Tăng

lần D. Không đổi

Giải

Công thức tính khối lượng riêng của chất khí:

m p

V RT





 

Ta có:

1 1

1 1 2

2 2 1

2 2

p T















 











Công thức tính vận tốc căn quân phương của phân tử khí:

3kT



Hay

2 2

1 1

v T







 



 



 

 









1 1 2

2 2 1

. 1

p v



 

  

 

 

Câu 75: Một con lắc đơn có

 

110m g

được kéo ra lệch với phương thẳng đứng một góc





, sau đó thả

rơi, cho

 

10 /g m s

. Lực căng cực đại của dây treo là:

 

3,3 N

 

3,697 N

 

2,109 N

 

4,094 N

Giải

Chuyển động c a vủ ật m là chuyển động tròn đều trên quỹ đạo có bán kính

Áp d nh lu t bụng đị ậ ảo toàn cơ năng:

2 1 1

d t tmax

mgl mgl

W W W W mv

cos cos

 

     

 

 

2v gl cos cos

 

  

Chọn chi ng xu ng và g c thều dương hướ ố ố ế năng tại vị trí cân b ằng

Vật chịu tác d ng c a các lụ ủ ực: Lực căng dây

 

, trọng lực

Áp dụng định luật II Newton:

P T ma 

Chiếu (1) lên chiều dương hình vẽ:

. .

T P m a T mgcos m



    

(trọng lực đóng vai trò lực hướng tâm)

   

0 0

2 3 2T mgcos mg cos cos mg cos cos

    

     

 

0 3 3,3

max max

T T mgcos N

 

    

Câu 76: Cộng tích đối với 1 mol chất khí thực là đại lượng có giá trị bằng:

A. Phản lực của thành bình lên phân tử khí

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

B. Lực đẩy giữa các phân tử khí

C. Lực hút của thành bình lên phân tử khí

D. Lực hút giữa các phân tử khí

Xét tại đỉnh vật chịu tác dụng của 2 lực là lực căng

và trọng lực

, và hai lực này đóng vai trò là lực hướng

tâm luôn

Áp dụng định luật II Newton, ta có:

P T ma 

Chiếu lên trục thẳng đứng chiều dương hướng xuống dưới:

2 2

B B

v v

P T ma m T m mg

l l

     

Để ý tại vị trí A vật được cấp năng lượng dưới dạng động năng, tại vị trí B thì động năng này đã được chuyển

một phần thành thế năng và động năng tại B. Do đó ta có:

     

2 2 2 2

1 1

.2 4

2 2

A B B Ad A d B t B

W W W mv mv mg l mv mv mgl       

Thay vào phương trình trên, ta được:

2 2

A A

mv mgl v

T mg m g

l l

 



   

 

 

Để vật quay tròn trong mặt phẳng thẳng đứng thì

0 5 0 5

T g v gl

     

Câu 77: Có

 

18M g

khí đang chiếm thể tích

 

4V l

ở nhiệt độ

22t C

. Sau khi hơ nóng đẳng áp, khối

lượng riêng của nó bằng

 

4 3

6.10 /g cm







. Nhiệt độ của khối khí sau khi đun nóng là:

 

2513 K

 

2113 K

 

2213 K

 

2013 K

Giải

Trước khi hơ nóng:

Áp dụng phương trình TT khí lý tưởng:

1 1

pV RT





 

Sau khi hơ nóng:

2 2 2

RTm m

pV RT p RT



  

   

 

Lấy

 

1 1

1 2

2 1

2213

mT mT

V T K

T V

 

    

Câu 78: Một thanh đồng chất chiều dài

có thể quay quanh một trục nằm ngang đi qua một đầu của thanh và

vuông góc với thanh. Vận tốc góc cực tiểu phải truyền cho thanh ở vị trí cân bằng để nó đến được vị trí nằm

ngang là:

. B.

. C.

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Chọn mốc thế năng tại vị trí thấp nhất của thanh

Tại vị tri thấp nhất

 

max dmax

v v W W mv   

Tại vị trí cao nhất

 

tmax

v W W mgl   

Áp dụng định luật bảo toàn năng lượng:

mv mgl v gl  

Vận tốc góc cực tiểu phải truyền cho thanh ở vị trí cân bằng để nó đến được vị trí nằm ngang là

2v g

l l



 

Câu 79: Một quả cầu đặc có khối lượng

 

1,5m kg

, lăn không trượt với vận tốc

 

10 /v m s

đến đập vào

thành tường rồi bật ra với vận tốc

 

8 /v m s

. Nhiệt lượng tỏa ra trong va chạm đó là:

 

41,74 J

 

39,77 J

 

43,71 J

 

37,8 J

Giải:

Sau va chạm động năng của vật giảm. Độ giảm động năng này tỏa ra dưới dạng nhiệt

Khi chuyển động, quả cầu vừa có động năng tịnh tiến, vừa có động năng quay

Động năng của quả cầu đặc, đồng chất, lăn không trượt:

2 2 2 2 2 2

1 1 2 1 1

2 2 5 5 5

W I mR mR mv

  

 

   

 

 

Moment quán tính của quả cầu đặc đồng chất:

I mR

Động năng tịnh tiến của quả cầu đặc:

 

d tt

W 

   

2 2 2

1 1 7

5 2 10

d q d tt

W W W mv mv mv    

Nhiệt lượng tỏa ra do va chạm:

   

 

2 2 2 2

2 1

7 7

.1,5. 10 8 37,8

10 10

Q W m v v J         

Câu 80: : Thả rơi tự do một vật nhỏ từ độ cao

 

17,6h m

. Quãng đường mà vật rơi được trong

 

0,1 s

cuối của

thời gian rơi là:

 

9,8 /g m s

 

1,608 m

 

1,808 m

 

2,208 m

 

2,408 m

Giải

Thời gian rơi của vật:

 

1,9

t s

 

Quãng đường vật rơi trong 0,1 giây cuối là:

     

2 2

0,1

1 1 1

0,1 0,1 1,808

2 2 2

t t

s s s gt g t g t t m



 

         

 

Công thức tổng quát cho quãng đường rơi trong

giây cuối là

 

s g t t n

 

   

 

với



Câu 81: Một con lắc toán có sợi dây dài là

, và cứ sau

5t 

phút thì biên độ giao động giảm 2 lần. Giảm lượng

lôga của con lắc đó là

0,023





. Cho gia tốc trọng trường

 

9,8 /g m s

. Hỏi

bằng giá trị nào dưới đây:

 

2,554 m

 

2,044 m

 

1,704 m

 

2,214 m

Giải

Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:

F F kx rv   

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Phương trình cơ bản của chuyển động trong trường hợp này là

ma kx rv  

Hay:

2 2

d x dx d x r dx k

m r kx x

dt dt dt m dt m

      

 

Đặt





(hệ số tắt dần)

Phương trình

 

trở thành

2 0

d x dx

x x

dt dt

 

  

 

gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi

 



, nghiệm phương trình

này có dạng:

 

x A e cos t



 



 

Đây là biểu thức độ dời của dao động tắt dần. Hằng số



gọi là tần số của dao động tắt dần:

2 2

  

 

Theo bài ra, ta có:

. .300 3

1 1

7,7.10

2 2

e e

 



   

     

Giảm lượng loga của con lắc:

 

0,023 2,987T T s



 



    

Chu kỳ

của dao động tắt dần là:

   

2 2

2 2 2

2,987 2, 214T s l m

  



 



     



Câu 82: Tổng động năng tịnh tiến trung bình của các phân tử khí Nito

 

chứa trong một khí cầu bằng

 

5.10W J





và vận tốc căn quân phương của phân tử khí đó là

 

2.10 /

v m s

. Khối lượng khí nitơ trong

khí cầu là:

 

2,84.10 kg



 

2,5.10 kg



 

3,01.10 kg



 

2,33.10 kg



Giải

Tổng động năng tịnh tiến trung bình của các phân tử khí Nito

 

là

 

2 3

1 2 2.5.10

2,5.10

2.10

W mv m kg



    

Câu 83: Một vật nhỏ có khối lượng m buộc vào đầu sợi dây mảnh chiều dài

 

1,5l m

, đầu kia giữ cố định. Cho

vật quay trong mặt phẳng nằm ngang với vận tốc góc không đổi sao cho sợi dây hợp với phương thẳng đứng một

góc





. Cho

 

10 /g m s

, bỏ qua lực cản không khí. Tốc độ góc có giá trị:

 

2,575 /rad s

 

2,775 /rad s

 

3,075 /rad s

 

2,675 /rad s

Giải

Chọn mốc thế năng tại vị trí căn bằng, chiều dương hướng xuống

Trong quá trình dao động, vật chịu tác dụng của các lực: trọng lực

 

, lực căng dây

 

và lực hướng tâm

Áp dụng định luật II Newton, ta có:

P T F  

 

Chiếu

 

lên trục Ox:

0 0

. 30 0 . 30

ht ht

F T sin F T sin   

Chiếu

 

lên trục Oy:

0 . 30

P Tcos P Tcos mg T cos T

cos

 

       

0 0

. 30 . 30

F T sin mg tan mg   

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Mà

2 2 0

. . . 30

ht ht

F ma m R m l sin

 

  

 

2 0 2

1 2

. . 30 . 2,775 /

3 3 3

mg g g

m l sin l rad s

  

     

Câu 84: Cộng tích đối với một mol chất khí thực là đại lượng có giá trị bằng:

A. Bằng thể tích nhỏ nhất của một mol khí

B. Bằng tổng các thể tích riêng của các phân tử mol khí

C. Một phần ba của thể tích lớn nhất mà một mol chất lỏng ( tương ứng với chất khí đang xét) có thể có được

D. Bằng thể tích tới hạn của mol khí

Câu 85: Một thanh chiều dài

 

0,6l m

, khối lượng

 

3M kg

có thể quay tự do xung quanh một trục nằm

ngang đi qua một đầu của thanh. Một viên đạn khối lượng

 

0,01m kg

bay theo phương nằm ngang với vận

tốc

 

300 /v m s

tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc góc của thanh ngay sau khi viên

đạn đập vào thanh là:

 

4,95 /rad s

 

4,436 /rad s

 

5,721 /rad s

 

5,207 /rad s

Giải

Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có mỗi

viên đạn có tốc độ và khối lượng

mang một động lượng

p mv

Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách

từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm

quay tới viên đạn chính là độ dài

Vậy mômen động lượng trước khi va chạm là:

. . .

L r p sin l p mvl



  

Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với

cùng vận tốc góc



. Vậy moomen quán tính của hệ vật sau va chạm:

1 2s

L I I

 

 

Với

là moment chất điểm (viên đạn) đối với trục quay

I ml

là moment quán tính của thanh mảnh

2 2

12 12 3

Ml Ml

 

 

 

  

Hay

 

1 2

L I I ml

 

 

   

 

 

Áp dụng định luật bảo toàn động lượng

 

4,95 /

t s

Ml mvl v

L L mvl ml rad s

 

 

       

 

 

 



 

 

Câu 86: Một con lắc vật lý được cấu tạo bằng một thanh đồng chất tiết diện đều có độ dài bằng

và trục quay O

của nó cách trọng tâm

một khoảng bằng

. Biết rằng chu kỳ dao động

của con lắc này là nhỏ nhất,

nhận

giá trị nào dưới đây?

4 3

2 3

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Chu kỳ dao động

của con lắc:

mgd





Với

1 2

I I I 

với

là moment quán tính của thánh và

là moment quán tính của chất điểm đối với trục quay

1 2

I I I mx   

( ở đây

d x

)

2 2

12 12

2 2

l l

m x x

mgx gx

 

   

 

   

   

  

2 2

' 0 2 0

12 2 3

max x

l l l

T T x x x

 

        

 

 

Câu 87: Một ôtô chuyển động biến đổi đều lần lượt đi qua hai điểm

và

cách nhau

 

25S m

trong khoảng

thời gian

 

1,6t s

, vận tốc ô tô ở

là

 

12 /m s

. Vận tốc của ôtô ở

nhận giá trị nào sau đây:

 

18,25 /m s

 

18,75 /m s

 

19,25 /m s

 

20,75 /m s

Giải

Áp dụng công thức

 

2 2

2 2 . 19,25 /

B A

B A B A A B

v v

S S

v v aS S v v v v m s

t t t



         

Câu 88: Một vật có khối lượng

 

2m kg

chuyển động với tốc độ

 

6 /v m s

tới va chạm xuyên tâm vào vật

có khối lượng

 

3m kg

đứng yên. Va chạm là hoàn toàn mềm. Nhiệt lượng tỏa ra trong quá trình va chạm là

 

21,3 J

 

21,6 J

 

22,2 J

 

22,5 J

Giải

Vì va chạm là hoàn toàn mềm nên

   

1 1

1 1 1 2 2 2

1 2

2.6

. . 2,4 /

2 3

m v

m v m m v v m s

m m

     

 

Nhiệt lượng tỏa ra trong quá trình va chạm là:

   

2 2

1 1 1 2 2

1 1

. . . . 21,6

2 2

truoc sau

Q W W m v m m v J     

Câu 89: Một người đẩy xe một lực hướng xuống theo phương hợp với phương ngang một góc





. Xe có

khối lượng

 

230m kg

và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường

0,23k 

. Lấy

 

9,81 /g m s

. Lực đẩy của người có giá trị bằng:

 

693,28 N

 

690,98 N

 

686,38 N

 

697,88 N

Giải

Chọn chi u chuy ều dương cùng chiề ển động

Khi xe chuy ng, ch u tác d ng c a các lển độ ị ụ ủ ực: Trọng lực

, phản lực

, lực đẩy

và lực ma sát

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Vì xe chuyển động với vận tốc không đổi nên

0a 

Áp dụng định luật II Newton, ta có:

' ' 0

P N f F   

 

Chiếu

 

lên trục Oy:

' '. 0N F sin P



  

Chiếu

 

lên trục Ox:

'. ' 0 '. '

ms ms

F cos f F cos f

 

   

Mà lực ma sát tác dụng lên xe:

 

' . ' '.

f k N k P F sin



  

Hay

   

'. . '. ' 690,98

F cos k P F sin F N

cos k sin

 

    



Câu 90: Một đĩa trong khối lượng

 

165M kg

đỡ một người có khối lượng

 

53m kg

. Lúc đầu người đứng

ở mép và đĩa quay với vận tốc góc





(vòng/phút) quanh trục đi qua tâm đĩa. Vận tốc góc của đĩa khi người

đi vào đúng tâm của đĩa là ( coi người như 1 chất điểm)

 

1,99 /rad s

 

2,53 /rad s

 

2,26 /rad s

 

1,72 /rad s

Giải

Bài này áp d nh lu t bụng đị ậ ảo toàn động lượng

Giai đoạn trước: mômen động lượng của hệ sẽ là:

1 1truoc dia nguoi

L I I

 

 

Mômen quán tính đĩa đặc như đã biết là:

dia

I 

Mômen quán tính của người (chất điểm) là:

nguoi

I mR

truoc

L mR



 

  

 

 

Giai đoạn sau: để ý là khi người đi vào tâm đĩa thì coi như khoảng cách từ người tới tâm đĩa là 0. Điều này kéo

theo mômen quán tính của người với tâm đĩa coi như bằng 0.

Moment động lượng của hệ lúc này là

2 2

sau dia

L I

 

 

Áp dụng định luật bảo toàn động lượng:

2 2

1 2

2 2

truoc sau

MR mR

L L mR

 

 

   

 

 

 

0,5 165.0,5 53

. 1,72 /

0,5 0,5.165 3

M m

rad s



 

 

   

Câu 91: Một ô tô khối lượng

1,5m 

tấn đang đi trên đường phẳng nằm ngang với tốc độ

 

21 /m s

bỗng nhiên

phanh lại. Ô tô dừng lại sau khi trượt thêm

 

25 m

. Độ lớn trung bình của lực ma sát là:

 

13,53.10 N

 

13,23.10 N

 

12,63.10 N

 

14,13.10 N

Giải

Gia tốc:

 

2 2

0 21

8,82 /

2 2.25

v v

a m s



   

Độ lớn trung bình của lực ma sát là:

 

8,82.1,5.1000 13230

F ma N    

Câu 92: Một động cơ nhiệt làm việc theo chu trình Carnot bằng không khí lấy ở áp suất ban đầu

 

7,0P at

Thể tích ban đầu của không khí

 

2V dm

. Sau lần giãn đẳng nhiệt lần thứ nhất nó chiếm thể tích

 

5V dm

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

và sau khi giãn đoạn nhiệt thể tích của khí là

 

8,1V dm

. Áp suất khí sau khi giãn đoạn nhiệt có giá trị

bằng;

 

14,98.10 Pa

 

13,98.10 Pa

 

11,98.10 Pa

 

16,98.10 Pa

Giải

Giai đoạn 1: quá trình đẳng nhiệt

 

T const

Áp dụng phương trình TT của quá trình đẳng nhiệt:

 

1 1

1 1 2 2 2

7.2

2,8

PV PV P at

    

Giai đoạn 2: Qúa trình đoạn nhiệt

Áp dụng phương trình TT cho quá trình đoạn nhiệt:

   

1,4

4 4

2 2 3 3 3 2

2,8. 1,425 1, 425.9,8.10 13,98.10

8,1

PV PV P P at Pa



 

 

      

 

 

Câu 93: Hơ nóng 1 mol khí lí tưởng lưỡng nguyên tử từ nhiệt độ

đến

bằng hai quá trình đẳng áp và đẳng

tích. Gọi biến thiên entropi trong mỗi quá trình đẳng áp, đẳng tích lần lượt là

S

và

S

Khi đó:

1,8

P V

S S  

1,4

P V

S S  

1,6

P V

S S  

2,0

P V

S S  

Giải

Độ biến thiên Entropy:



Qúa trình đẳng áp:

Q nC dT n RdT





 

Thay vào và lấy tích phân từ trạng thái 1 ứng với

đến trạng thái 2 ứng với

2 2 2

i dT i i

S n R n RlnT n Rln

TT T

  

    



Tương tự, ta có độ biến thiên entropy của quá trình đẳng tích;

S n Rln

 

Với khí lưỡng nguyên t thì ử

5i 

2 5 2

2 2

1,4

2 2

 



   



A. ∆𝑆p = 1,8 ∆𝑆v B. p = 1,4 v C. p = 1,6 ∆𝑆 ∆𝑆 ∆𝑆 ∆𝑆v D. p = 2,0 v ∆𝑆 ∆𝑆

Câu 94: Kỷ lục đẩy tạ ở Hà Nội là

 

14,07 m

. Nếu tổ chức đẩy tạ ở Xanh Pêtecbua trong điều kiện tương tự (cùng

vận tốc ban đầu và góc nghiêng) thì kỉ lục sẽ là: (cho gia tốc trọng trường ở Hà Nội là

 

9,727 /g m s

, ở Xanh

Pêtecbua là

 

9,810 /g m s

, bỏ qua chiều cao của người đẩy)

 

16,951 m

 

12,951 m

 

15,951 m

 

13,951 m

Giải

Từ công thức tầm xa:

. 2v sin





ta thấy với lực đẩy không đổi (để

không đổi) và góc ném không đổi (ném

xa nhất khi góc ném bằng

) thì tầm xa L tỷ lệ nghịch với gia tốc trọng trường g. Do đó, có thể xác định kỷ

lục đẩy tạ tại thành phố Xanh Pêtecbua là

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

9,727

. .14,07 13,951

9,81

XP HN

L L m

  

Câu 95: Một ô tô khối lượng

 

450m kg

chuyển động thẳng đều xuống dốc trên một mặt phẳng nghiêng, góc

nghiêng



so với mặt đất nằm ngang có

0,0872; 0,9962sin cos

 

 

. Lực kéo ô tô bằng

 

450

F N

, cho

 

10 /g m s

. Hệ số ma sát giữa ô tô và mặt đường là:

0,218

0,188

0,168

0,178

Giải

Chọn trục Oxy như hình vẽ. Chiều dương cùng chiều chuyển động với ô tô

Ô tô chịu tác dụng của các lực: lực kéo

của động cơ ô tô, trọng lực

, phản lực tiếp tuyến

của mặt

đường và lực ma sát của mặt đường

Áp dụng định luật II Newton, ta có

F P N f   

(vì ô tô chuyển động thẳng đều)

Chiếu phương trình này nên phương chuyển động của ô tô, ta được:

k ms

F f Psin



  

. 0,188

k ms

F mgsin

F f Psin k N Psin kmgcos mgsin k

mgcos



   





         

Câu 96: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

55 kW

. Nhiệt độ của nguồn nóng là

127 C

, nhiệt độ của nguồn lạnh là

31 C

. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:

 

14050 kJ

 

13650 kJ

 

13550 kJ

 

13750 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 55 1375

304

400

A A

Q kJ

T Q



      





Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút:

 

1 1

1375

. .60 13750

Q Q t kJ  

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 97: Một thanh đồng chất có độ dài

, khối lượng

. Đối với trục quay nào dưới đây mô mem quán tính

của thanh là nhỏ nhất

A. Song song và cách thanh một khoảng bằng

B. Đi qua khối tâm và vuông góc với thanh

C. Vuông góc và đi qua một đầu thanh

D. Đi qua khối tâm và làm với thanh một góc







Câu 98: Một thanh mảnh đồng chất có độ dài

có thể quay quanh một trục đi qua đầu thanh và vuông góc với

thanh. Lúc đầu thanh ở vị trí nằm ngang, cho thanh rơi xuống. Vận tốc dài ở đầu dưới của thanh khi thanh rơi

tới vị trí thẳng đứng là

2gl

3gl

Giải

Chọn mốc thế năng tại vị trí thấp nhất của thanh

Tại vị tri thấp nhất

 

max dmax

v v W W mv   

Tại vị trí cao nhất

 

tmax

v W W mgl   

Áp dụng định luật bảo toàn năng lượng:

mv mgl v gl  

Câu 99: Một ô tô bắt đầu chạy vào đoạn đường vòng bán kính

 

1,1R km

và dài

 

600 m

với vận tốc

 

54 /v km h

. Ô tô chạy hết quãng đường trong thời gian

 

19t s

. Coi chuyển động là nhanh dần đều, gia

tốc toàn phần của ô tô cuối đoạn đường vòng bằng:

 

2,737 /m s

 

2,987 /m s

 

3,237 /m s

 

3,487 /m s

Giải

Áp dụng công thức:

S v t a t 

để tính gia tốc tiếp tuyến.

   

 

2 2

2 2 600 15.19

1,745 /

S v t

a m s

 

   

Vận tốc dài của đoàn tàu cuối quãng đường tròn được tính theo công thức:

 

. 15 1,745.19 48,155 /

v v a t m s    

Dùng công thức:

 

2 2

48,155

2,108 /

1,1.10

a m s

  

để tính gia tốc pháp tuyến của đoàn tàu.

Gia tốc toàn phần của đoàn tàu được tính theo công thức:

 

2 2 2 2 2

1,745 2,108 2,737 /

t n

a a a m s    

Câu 100: Một vật có khối lượng

 

2m kg

chuyển động với tốc độ

 

7 /v m s

tới va chạm xuyên tâm vào

vật có khối lượng

 

3m kg

đứng yên. Va chạm là hoàn toàn mềm. Nhiệt lượng tỏa ra trong quá trình va chạm

là

 

30,3 J

 

29,7 J

 

30 J

 

29,4 J

Giải

Vì va chạm là hoàn toàn mềm nên

   

1 1

1 1 1 2 2 2

1 2

2.7

. . 2,8 /

2 3

m v

m v m m v v m s

m m

     

 

Nhiệt lượng tỏa ra trong quá trình va chạm là:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

   

2 2

1 1 1 2 2

1 1

. . . . 29,4

2 2

truoc sau

Q W W m v m m v J     

Câu 101: 4: Gọi

và

lần lượt là khối lượng và bán kính của Trái Đất.

là hằng số hấp dẫn vũ trụ,

và

lần lượt là gia tốc trọng trường ở độ cao

và mặt đất. Công thức nào dưới đây đúng với h bất kỳ:

 

R h







g g

 

 

 

 

 



 

 



Giải

Gia tốc trọng trường ở độ cao h:

 

R h





Câu 102: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

10 kW

. Nhiệt độ của nguồn nóng là

100 C

, nhiệt độ của nguồn lạnh là

0 C

. Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút có giá trị:

 

1,438.10 kJ

 

1,638.10 kJ

 

1,738.10 kJ

 

1,338.10 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 10

1 37,3

273

373

A A

Q kJ

T Q



      



Gọi

là nhiệt lượng mà tác nhân nhả cho nguồn lạnh:

 

1 1

' 37,3 10 27,3Q Q A kJ    

Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là

 

. 60.27,3 1638Q Q t kJ  

Câu 103: Một khối khí lí tưởng có thể tích

 

6V m

dãn nở đẳng nhiệt từ áp suất

 

2 at

đến

 

1 at

. Lượng

nhiệt đã cung cấp cho quá trình này là:

 

9,16.10 J

 

10,16.10 J

 

8,16.10 J

 

5,16.10 J

Giải

Trong quá trình đẳng nhiệt:

0U 

mà

0U A Q Q A      

Công của quá trình đẳng nhiệt

1 1

A PdV PV ln

 



Áp dụng PT trạng thái của quá trình đẳng nhiệt:

2 1

1 2

V P



Hay

 

4 4 5

1 1

2.6. 2.9,8.10 8,318.9,81.10 8,16.10

A PV ln ln J Q

    

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 104: Một khẩu pháo có khối lượng

 

600M kg

bắn một viên đạn theo phương làm với mặt ngang một góc





. Khối lượng của viên đạn

 

5m kg

, vận tốc đầu nòng

 

400 /v m s

. Khi bắn bệ pháo giật lùi về phía

sau một đoạn

 

42s cm

. Lực cản trung bình tác dụng lên quả pháo có giá trị:

 

1784,1 N

 

1984,1 N

 

2284,1 N

 

1884,1 N

Giải

Theo định lu t bậ ảo toàn động lượng thì vận t c giố ật lùi c a kh u pháo là: ủ ẩ

 

. . 5.400. 60 5

600 3

m v cos cos

V m s



     

Dấu

" "

chứng tỏ pháo giật lùi, ngược chiều dương)

Áp dụng công thức:

 

2 2 2

' 2 3,31 /

V V aS a m s

      

Lực cản trung bình tác dụng lên quả pháo:

 

3,31.600 1984,1

F Ma N    

Câu 105: Từ đỉnh đồi cao, một quả pháo được bắn chếch lên phía trên một góc





so với phương nằm

ngang với vận tốc đầu nòng là

 

400 /v m s

. Sau khi bắn một khoảng thời gian

 

5t s

, góc



giữa hướng

của vận tốc quả pháo và hướng của gia tốc toàn phần thỏa mãn giá trị nào dưới đây ( bỏ qua sức cản không khí.

Gia tốc trọng trường bằng

 

9,8 /g m s

1,894tg



 

2,894tg



 

2,094tg



 

2,294tg



 

Giải

Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí pháo bắt đầu bắn, chiều dương hướng xuống, cùng chiều với

gia tốc

Gia tốc:

a g









 





Vận tốc:

0 0

. .

x x x

y y y

v v a t v cos

v v a t v sint gt



  







   





Phương trình chuyển động của chất điểm:

: . .

: .

x x

y y

Ox x v cos tOx x v t a t

Oy y v sin t gt

Oy y v t a t







 





 



 

 

 

 







Theo hình vẽ, ta có:

tan





Tại thời điểm

 

5 :t s

400. 30

2,294

. 5

. 5 400. 30 9,8.5

v v cos

v cos

cos

tan

v v sin g

v sin g sin













   



 

 





TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Mặt khác:

2,294tan tan

 

  

(do

180

 

 

)

Câu 106: Một vật coi là chất điểm có khối lượng m bắt đầu trượt từ đỉnh mặt phẳng nghiêng góc



so với

phương nằm ngang (xem hình vẽ). Hệ số ma sát giữa vật và mặt phẳng nghiêng là

. Moomen động lượng của

chất điểm đối với điểm O tại thời điểm

có giá trị là:

 

mghtsin sin kcos

  



 

mghtcos sin kcos

  



 

mghtcos cos ksin

  



 

mght sin kcos

 



Giải

Chọn h c tệ trụ ọa độ Oxy như hình vẽ ều dương cùng chiề ển độ , chi u chuy ng của vật

Vật chịu tác d ng c a các lụ ủ ực: trọng lực

, phản lực

và lực ma sát

Áp dụng định luật II Newton, ta có:

P N f ma  

 

Chiếu

 

lên trục

:Ox

N P N Pcos mgcos

 

    

Chiếu

 

lên trục

:Oy

t ms ms

P sin f

P f ma P sin f ma a





      

Mà

 

. .

f k N k mgcos F mg sin kcos

  

    

Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O chính là công của lực

tác dụng lên điểm O

 

. . .

A F h cos mghcos sin k cos

   

  

Câu 107: Một thanh chiều dài

 

0,7l m

, khối lượng

 

4M kg

có thể quay tự do xung quanh một trục nằm

ngang đi qua một đầu của thanh. Một viên đạn khối lượng

 

0,01m kg

bay theo hương nằm ngang với vận tốc

 

300 /v m s

tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc gốc của thanh ngay sau khi viên đạn

đập vào đầu thanh là:

 

2,676 /rad s

 

3,19 /rad s

 

2,933 /rad s

 

3,961 /rad s

Giải

Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có

mỗi viên đạn có tốc độ và khối lượng

mang một động lượng

p mv

Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách

từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm

quay tới viên đạn chính là độ dài

Vậy mômen động lượng trước khi va chạm là:

. . .

L r p sin l p mvl



  

Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với

cùng vận tốc góc



. Vậy moomen quán tính của hệ vật sau va chạm:

1 2s

L I I

 

 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Với

là moment chất điểm (viên đạn) đối với trục quay

I ml

là moment quán tính của thanh mảnh

2 2

12 12 3

Ml Ml

 

 

 

  

Hay

 

1 2

L I I ml

 

 

   

 

 

Áp dụng định luật bảo toàn động lượng

 

3,19 /

t s

Ml mvl v

L L mvl ml rad s

MMl

 

 

       

 

 

 



 

 

Câu 108: Theo thuyết động học phân tử của chất khí, với mọi chất khí mà phân tử có hai nguyên tử ở cùng

nhiệt độ thì kết luận nào sau đây đúng

A. Mọi phân tử của chúng có cùng một động năng trung bình

B. Các phân tử khí nhẹ có năng lượng trung bình cao hơn so với các phân tử khí nặng

C. Các phân tử khí nhẹ có năng lượng trung bình thấp hơn so với các phân tử khí nặng

D. Mọi phân tử của chúng có cùng một vận tốc trung bình

Câu 109: Một đoàn tàu khối lượng 2 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng

 

54 /v km h

. Công suất đầu máy là

 

10 kW

. Gia tốc trọng trường bằng

 

9,8 /m s

. Hệ số ma sát bằng:

0,376.10



0,564.10



0,328.10



0,34.10



Giải

Đổi

   

54 / 15 /v km h m s 

Ta có:

 

10.10 2000

15 3

P F v F N

    

Mà

 

2000

0,034

3 2.10 .9,8

F F mg N

 

      

Câu 110: Một đoàn tàu khối lượng 40 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng

 

24 /km h

. Công suất đầu máy là

 

225 kW

. Gia tốc trọng trường bằng

 

9,8 /m s

. Hệ số ma sát bằng:

bằng:

11,6.10



10,6.10



7,613.10



8,61.10



Giải

Đổi

   

24 / /

v km h m s 

Ta có:

 

225.10

. 33750

P F v F N

    

Mà

 

33750

33750 0,086

40.10 .9,8

F F mg N

 

      

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 111: Một viên bi có khối lượng

, vận tốc

bắn thẳng góc vào một bức tương phẳng. Sau khi va chạm

viên bi bay ngược trở lại với vận tốc bằng

. Gội động năng ban đầu của viên bi là

, độ biến thiên động

năng và động lượng của viên bi là

W

và

p

; ta có

W

và

 

2 2p mE 

W  

và

 

3 2

p 

W  

và

 

5 2

p 

W  

và

 

9 2

p 

Giải

Độ biến thiên động năng:

2 2 2 2

2 1

1 1 1 4 1 9 1 9

. . .

2 2 2 5 2 25 2 25

sau t

W W W mv mv m v mv mv E

 

          

 

 

Câu 112: Một chất điểm bắt đầu trượt từ đỉnh mặt phẳng nghiêng góc



so với phương nằm ngang (xem hình

vẽ). Hệ số ma sát giữa vật và mặt phẳng nghiêng là

; khối lượng của vật là m ( lấy

 

9,81 /g m s

). Cho

   

2,3 , 0,2, 9 , 30m kg k h m



   

. Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O là:

 

64,05 Nm

 

57,468 Nm

 

60,759 Nm

 

67,341 Nm

Giải

Chọn h c tệ trụ ọa độ Oxy như hình vẽ ều dương cùng chiề ển độ , chi u chuy ng của vật

Vật chịu tác d ng c a các lụ ủ ực: trọng lực

, phản lực

và lực ma sát

Áp dụng định luật II Newton, ta có:

P N f ma  

 

Chiếu

 

lên trục

:Ox

N P N Pcos mgcos

 

    

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Chiếu

 

lên trục

:Oy

t ms ms

P sin f

P f ma P sin f ma a





      

Mà

 

. .

f k N k mgcos F mg sin kcos

  

    

Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O chính là công của lực

tác dụng lên điểm O

   

. . . . . 30 57,468

A F h cos mg sin k cos h cos N

  

   

Câu 113: Một viên bi nhỏ

 

10m g

rơi theo phương thẳng đứng không vận tốc ban đầu trong không khí, lực

cản của không khí

F rv 

(tỷ lệ ngược chiều v i v n t c), ớ ậ ố

là h s cệ ố ản. V n t c cậ ố ực đại mà viên bi đạt được

bằng

 

50 /

max

v m s

. Cho gia tốc trọng trường

 

10 /g m s

. Hệ số cản có giá trị:

 

4,353 /m s

 

3,953 /m s

 

5,553 /m s

 

3,553 /m s

Giải

Lực cản:

F ma mv m

  

Mặt khác:

dv dv r

F rv m rv dt

dt v m

       

Lấy tích phân:

 

.2,2

. 20. 4,353 /

v t

r ln

dv r v r

dt ln t v v e e m s

v m v m



        

 

Câu 114: Một động cơ nhiệt có hiệu suất

 

25 %

và nhả nhiệt cho một nguồn có nhiệt độ

 

600 K

. Nó nhận

nhiệt từ một nguồn có nhiệt độ ít nhất là:

 

786 K

 

821 K

 

807 K

 

800 K

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Hay

 

2 2

600

1 0,25 800

1 1 0,25

T T

T K



      

 

Câu 115: Một cột đồng chất có chiều cao

 

11h m

, đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ

xuống. Gia tốc trọng trường

 

9,8 /m s

. Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây

 

16,983 /m s

 

19,483 /m s

 

17,983 /m s

 

17,483 /m s

Giải

Ở vị trí thẳng đứng, cột có thế năng:

W mg

Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất:

W I





Trong đó: là moment quán tính của cột đối với trục quay gốc của cột: I

I 



là vận tốc góc của cột lúc chạm đất.

Áp dụng định luật bảo toàn cơ năng:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

1 3

2 2 3

h mh g

 

  

Vận tốc dài:

 

. 3 3.9,8.11 =17,983 /v h gh m s



  

Câu 116: Một người đứng cách con đường thẳng một khoảng

 

50h m

để chờ ô tô. Khi thấy đầu ô tô còn cách

mình một đoạn

 

200a m

thì người ấy bắt đầu chạy (thẳng, đều, theo một hướng nào đó) ra đường để đón gặp

ô tô. Biết vận tốc ô tô là

 

36 /v km h

. Để có thể gặp được ô tô, người ấy phải chả với vận tốc nhỏ nhất vmin

bằng bao nhiêu?

 

2,5 /m s

 

3,25 /m s

 

3 /m s

 

2,75 /m s

Giải

Muốn gặp đúng ô tô tại B thì thời gian người chạy từ M tới M phải bằng thời gian ô tô chạy từ A tới B:

2 1

MB AB

v v



 

Sử dụng đinh lý hàm sin trong tam giác ABM, ta có:

MB AB

sin sin

 



với

sin





 

Từ

 

và

 

sin

a v



 

Để có thể gặp được ô tô với vận tốc nhỏ nhất thì lúc này người chạy đến đường cũng là lúc xe ô tô đi tới (người

gặp đúng ô tô mà không phải chờ đợi lãng phí thời gian), vì vậy, giữa hướng chạy và vận tộc của người phải có

quan hệ:

sin

a v





Vì với mọi



thì

 

1sin





nên

2 1

. 1 .

vh h

sin v v

a v a



   

   

2,5 / 9 /

min

v m s km h

   

Lúc này, người phải chạy theo hướng

,MI

với

MI AM

Câu 117: Một khối khí lí tưởng có thể tích

 

5V m

dãn nở đẳng nhiệt từ áp suất

 

4 at

đến

 

2 at

. Lượng

nhiệt đã cung cấp cho quá trình này là:

 

11,6.10 J

 

16,6.10 J

 

13,6.10 J

 

14,6.10 J

Giải

Trong quá trình đẳng nhiệt:

0U 

mà

0U A Q Q A      

Công của quá trình đẳng nhiệt

1 1

A PdV PV ln

 



TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Áp dụng PT trạng thái của quá trình đẳng nhiệt:

2 1

1 2

V P



Hay

 

4 4 5

1 1

2.6. 2.9,8.10 8,318.9,81.10 13,6.10

A PV ln ln J Q

    

Câu 118: Một quả cầu đặc có khối lượng

 

1,4m kg

, lăn không trượt với vận tốc

 

10 /v m s

đến đập vào

thành tường rồi bật ra với vận tốc

 

8 /v m s

. Nhiệt lượng tỏa ra trong va chạm đó là

 

41,19 J

 

39,22 J

 

37,25 J

 

35,28 J

Giải:

Sau va chạm động năng của vật giảm. Độ giảm động năng này tỏa ra dưới dạng nhiệt

Khi chuyển động, quả cầu vừa có động năng tịnh tiến, vừa có động năng quay

Động năng của quả cầu đặc, đồng chất, lăn không trượt:

2 2 2 2 2 2

1 1 2 1 1

2 2 5 5 5

W I mR mR mv

  

 

   

 

 

Moment quán tính của quả cầu đặc đồng chất:

I mR

Động năng tịnh tiến của quả cầu đặc:

 

d tt

W 

   

2 2 2

1 1 7

5 2 10

d q d tt

W W W mv mv mv    

Nhiệt lượng tỏa ra do va chạm:

   

 

2 2 2 2

2 1

7 7

.1,4. 10 8 35,28

10 10

Q W m v v J         

Câu 119: Một con lắc toán có sợi dây

 

1l m

, cứ sau

1t 

phút thì biên độ giao động giảm 2 lần. Giảm lượng

loga của con lắc dố bằng giá trị nào sau đây ( cho

 

9,8 /g m s

)

1,728.10



2,319.10



2,713.10



1,702.10



Giải:

Theo bài ra, ta có:

. .60

1 1

0,01155

2 2

e e

 



  

     

Chu kỳ

của dao động tắt dần là:

2 2

2 2 2

  



 



  



Giảm lượng loga của con lắc:

2 2

. 0,01155. 0,02319

9,8

0,01155

 

  

 

   



Câu 120: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

11 kW

. Nhiệt độ của nguồn nóng là

100 C

, nhiệt độ của nguồn lạnh là

0 C

. Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút có giá trị:

 

2,002.10 kJ

 

1,802.10 kJ

 

1,502.10 kJ

 

1,702.10 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 11

1 41,03

273

373

A A

Q kJ

T Q



      



Gọi

là nhiệt lượng mà tác nhân nhả cho nguồn lạnh:

 

1 1

' 41,03 11 30,03Q Q A kJ    

Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là

 

' 3

. 60.30,03 1,802.10Q Q t kJ  

Câu 121: Một tàu điện sau khi suất phát chuyển động trên đường nằm ngang với gia tốc

 

0,7 /a m s

. 10 giây

sau khi bắt đâu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng hẳn. Hệ số ma sát trên

quãng đường

0,01k 

. Cho

 

10 /g m s

. Thời gian chuyển động của toàn bộ tàu là

 

66,8 s

 

74,8 s

 

80 s

 

68,4 s

Giải

Tầu chuyển động theo hai giai đoạn:

Giai đoạn 1: chuyển động với gia tốc

 

0,7 /a m s

với thời gian

 

10t s

Giai đoạn 2: chuyển động chậm dần đều với gia tốc

 

. 0,01.10 0,1 /a k g m s  

dưới tác dụng cản của lực

ma sát trong thời gian

t

Vận tốc lớn nhất của tàu:

 

1 1

. 0,7.10 7 /

max

v a t m s  

Tầu chuyển động chậm dần đều trong thời gian:

 

0,1

max

t s

   

Thời gian chuyển động của toàn bộ tàu là

 

2 1

70 10 80t t t s     

Câu 122: Một người đẩy xe một lực hướng xuống theo phương hợp với phương ngang một góc





. Xe có

khối lượng

 

240m kg

và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường

0,24k 

. Lấy

 

9,81 /g m s

. Lực đẩy của người có giá trị bằng:

 

764,31 N

 

752,81 N

 

755,11 N

 

757,41 N

Giải

Chọn chi u chuy ều dương cùng chiề ển động

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Khi xe chuy ng, ch u tác d ng c a các lển độ ị ụ ủ ực: Trọng lực

, phản lực

, lực đẩy

và lực ma sát

Vì xe chuyển động với vận tốc không đổi nên

0a 

Áp dụng định luật II Newton, ta có:

' ' 0

P N f F   

 

Chiếu

 

lên trục Oy:

' '. 0N F sin P



  

Chiếu

 

lên trục Ox:

'. ' 0 '. '

ms ms

F cos f F cos f

 

   

Mà lực ma sát tác dụng lên xe:

 

' . ' '.

f k N k P F sin



  

Hay

   

'. . '. ' 757,42

F cos k P F sin F N

cos k sin

 

    



Câu 123: Một hòn đá được ném theo phương ngang từ độ cao đủ lớn với vận tốc

 

12 /v m s

. Gia tốc pháp

tuyến của hòn đá sau giây thứ 2 có giá trị bằng (lấy

 

9,8 /g m s

)

 

4,617 /m s

 

5,117 /m s

 

5,867 /m s

 

4,867 /m s

Giải

Vận t c c a vố ủ ật theo phương thẳng đứng sau khi ném

 

2.9,8 19,6 /

v gt m s  

Góc



giữa vận tốc của vật và phương thẳng đứng thỏa mãn:





. Xem hình vẽ

Từ đó, gia tốc pháp tuy n và gia t c tiế ố ếp tuyến c a v t lúc này chính là nh ng ph n chi u c a gia t c g: ủ ậ ữ ầ ế ủ ố

 

2 2 2 2

9,8.12

. 5,117 /

12 19,6

x y

g v

a g sin m s

v v



   

 

Câu 124: Tổng động năng tịnh tiến trung bình của các phân tử khí Nito

 

chứa trong một khí cầu bằng

 

5,6.10W J





và vận tốc căn quân phương của phân tử khí đó là

 

2.10 /

v m s

. Khối lượng khí nitơ trong

khí cầu là:

 

2,8.10 kg



 

2,97.10 kg



 

3,31.10 kg



 

2,46.10 kg



Giải

Tổng động năng tịnh tiến trung bình của các phân tử khí Nito

 

là

 

2 3

1 2 2.5,6.10

2,8.10

2.10

W mv m kg



    

Câu 125: Một động cơ làm việc theo chu trình Carnot với tác nhân là không khí. Nhiệt độ ban đầu là

127 C

;

thể tích của không khí sau lần giãn đẳng nhiệt

 

5V dm

và sau khi giãn đoạn nhiệt nó chiếm thể tích

 

8,1V dm

. Hiệu suất của động cơ có giá trị:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

15,549%

13,549%

17,549%

11,549%

Giải

Giai đoạn 1: quá trình đẳng nhiệt

   

1 2

400T const T T K   

Giai đoạn 2: Qúa trình đoạn nhiệt

Áp dụng phương trình TT cho quá trình đoạn nhiệt:

 

1,4 1

1 1

2 2 3 3 3 2

400. 329,8

8,1

T V T V T T K



 



 

 

    

 

 

Hiệu suất của động cơ:

329,8

1 1 0,15549 15,549%

400



     

Câu 126: Một tụ đặc trưng khối lượng

 

105M kg

, bán kính

 

0,6R m

đang quay xung quanh trục của nó.

Tác dụng lên trụ một lực hãm

 

257,3F N

tiếp tuyến với mặt trụ và vuông góc với trục quay. Sau thời gian

 

2,6t s 

, trụ dừng lại. vận tốc của góc trụ lúc bắt đầu lực hãm là:

 

21,237 /rad s

 

20,444 /rad s

 

1,404 /rad s

 

0,611 /rad s

Giải

Gia tốc góc của trụ đặc:

0 0

t t

  





  

 

Moment hãm tiếp tuyến với mặt trụ:

. .

M F R I



 

Moment quán tính đối với trụ đặc:

I M

 

. . 8,168 /

F R M rad s

 

    

Vận tốc của góc trụ lúc bắt đầu lực hãm là

 

. 21,237 /t rad s

 

  

Câu 127: Khối lượng riêng của một chất khí

 

2 3

8.10 /kg m







; vận tốc căn quân phương của các phân tử khí

này là

 

600 /v m s

. Áp suất của khối khí tác dụng lên thành bình là:

 

9900 /N m

 

9800 /N m

 

9500 /N m

 

9600 /N m

Giải

Áp dụng PT trạng thái khí lí tưởng:

PV m PV RT PV P P

RT RT m

  

      

Vận tốc căn quân phương của các phân tử khí:

vRT RT

 

  

 

2 2

. 9600 /

3 3

C C

v vP

P N m



    

Câu 128: Một khối khí ôxy

 

bị nung nóng từ nhiệt độ

 

320 K

đến

287 C

. Nếu vận tốc trung bình của

phân tử ôxy lúc đầu là v thì lúc sau là:

1,35v

1,55v

1,5v

1,6v

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Công thức tính vận tốc trung bình của phân tử khí:

8kT





Hay

2 2

1 1

267 273

1,323

240

v T













   











Câu 129: Một ô tô khối lượng

1,6m 

tấn đang đi trên đường phẳng nằm ngang với tốc độ

 

22 /m s

bỗng nhiên

phanh lại. Ô tô dừng lại sau khi trượt thêm

 

25 m

. Độ lớn trung bình của lực ma sát là:

 

16,388.10 N

 

15,488.10 N

 

15,788.10 N

 

16,088.10 N

Giải

Gia tốc:

 

2 2

0 22

9,68 /

2 2.25

v v

a m s



   

Độ lớn trung bình của lực ma sát là:

 

9,68.1,6.1000 15488

F ma N    

Câu 130: Một xe lửa gồm nhiều toa được đặt trên các lò xo của hệ thống bánh xe. Mỗi lò xo của to axe chịu một

trọng lượng

 

5.10P N

nén lên nó. Xe lửa bị rung động mạnh nhất khi nó chạy với tốc độ

 

26 /v m s

qua

các chỗ nối của đường ray. Độ dài mỗi thanh ray bằng

 

12,5l m

. Hệ số đàn hồi của các lò xo nhận giá trị nào

dưới đây (cho

 

9,8 /g m s

)

 

82,64.10 N

 

88,64.10 N

 

87,4.10 N

 

84,14.10 N

Giải

Con lắc dao động mạnh nhất khi xảy ra cộng hưởng (chu kỳ dao động riêng của vật trùng chu kỳ qua các chỗ nối

của đường ray):

 

12,5

0,48

T s

  

Mặt khác:

   

5.10

5.10 5102,04

9,8

P N mg m kg

     

Mà

   

2 2

4 . 4 .5102,04

2 0,48 87,4.10 /

0,48

m m

T s k N m

k T

 



     

Câu 131: Ở thời điểm ban đầu một chất điểm có khối lượng

 

1m kg

có vận tốc

 

16 /v m s

. Chất điểm

chịu lực cản

F rv 

( biết

2r ln

là vận tốc chất điểm). Sau

vận tốc của chất điểm là:

 

2,8 /m s

 

4,4 /m s

 

4 /m s

 

3,2 /m s

Giải

Lực cản:

F ma mv m

  

Mặt khác:

dv dv r

F rv m rv dt

dt v m

       

Lấy tích phân:

 

. 16. 4 /

v t

r ln

dv r v r

dt ln t v v e e m s

v m v m



        

 

Câu 132: Nguyên lý thứ nhất của nhiệt động học khẳng định rằng

A. Nội năng của một hệ nhiệt động luôn luôn được bảo toàn

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

B. Không thể chế tạo được động cơ vĩnh cửu loại 1

C. Không thể chế tạo được động cơ vĩnh cửu loại 2

D. Một hệ nhiệt động cô lập không thể hai lần đi qua cùng một trạng thái

Câu 133: Một hạt chuyển động trong mặt phẳng xy từ điểm 1 có bán kính véctơ

 

2r i j m 

đến điểm 2 có

bán kính véctơ

 

2 3r i j m 

và

là các vector n vđơ ị trong t ecac. H t chuyọa độ Đ ạ ển động dưới tác

dụng của lực có biểu thức

 

3 4F i j N 

. Công th c hi n b i lự ệ ở ực đó là:

 

5 J

 

17 J

 

23 J

 

17 J

Giải

Công th c hi n b i l là: ự ệ ở ực đó

 

     

1 2

. . 3 2 1 4 3 2 17F r r A A A J         

Câu 134: Chất điểm bắt đầu chuyển động trên đường tròn bán kính

 

2R m

. Vận tốc của chất điểm phụ thuộc

vào quãng đường đi được S theo công thức

 

1/2

; 2 / ;v a S a m s 

.Góc



giữa vector vận tốc

và gia tốc

toàn phần



sau 3s c xáđượ c định b ởi

8,6tg





9tg





9,2tg





9,6tg





Giải

Theo bài ra, ta có

2 4v a S S v S   

Áp dụng công thức:

 

2 2

2 /

v v a S

a m s







  









 

. 2.3 6 /

v a t m s   

 

2 2

18 /

a m s

   

Góc



giữa vector vận tốc

và gia tốc toàn phần



sau 3s:



  

Câu 135: Một động cơ làm việc theo chu trình Carnot với tác nhân là không khí. Nhiệt độ ban đầu là

127 C

; thể

tích của không khí sau lần giãn đẳng nhiệt

 

5,5V dm

và sau khi giãn đoạn nhiệt nó chiếm thể tích

 

8,6V dm

. Hiệu suất của động cơ có giá trị:

16,373%

22,373%

18,373%

20,373%

Giải

Giai đoạn 1: quá trình đẳng nhiệt

   

1 2

400T const T T K   

Giai đoạn 2: Qúa trình đoạn nhiệt

Áp dụng phương trình TT cho quá trình đoạn nhiệt:

 

1,4 1

1 1

2 2 3 3 3 2

5,5

400. 334,51

8,6

T V T V T T K



 



 

 

    

 

 

Hiệu suất của động cơ :

334,51

1 1 0,16373 16,373%

400



     

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 136: Một con lắc toán có sợi dây

 

55l m

. Biết rằng sau thời gian





phút, nó mất

99%

năng lượng.

giảm lượng lôga của con lắc nhận giá trị nào dưới đây (cho

 

9,8 /g m s

)

0,975.10



1,125.10



1,035.10



1,065.10



Giải

Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:

F F kx rv   

Phương trình cơ bản của chuyển động trong trường hợp này là

ma kx rv  

Hay:

2 2

d x dx d x r dx k

m r kx x

dt dt dt m dt m

      

 

Đặt





(hệ số tắt dần)

Phương trình

 

trở thành

2 0

d x dx

x x

dt dt

 

  

 

gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi

 



, nghiệm phương trình

này có dạng:

 

x A e cos t



 



 

Đây là biểu thức độ dời của dao động tắt dần. Hằng số



gọi là tần số của dao động tắt dần:

2 2

  

 

Chu kỳ

của dao động tắt dần là:

2 2

2 2 2

  



 



  



Giảm lượng loga của con lắc:

2 2



  

 

 



Theo bài ra, ta có:

2 . 2 .6.60 3

0,01 0,01 6,396.10

e e

 







   

     

và

9,8 49

55 275



  



 

2 2

. 6,396.10 . 0,0952

6,396.10

275

 

 

 



   



Câu 137: Một vệ tinh có khối lượng

 

150m kg

chuyển động trên quỹ đạo tròn bán kính

 

7,6.10r m

quanh

Trái Đất. Cho khối lượng trái đất

 

5,98.10M kg

. Hằng số hấp dẫn

 

11 2 2

6,67.10 . /G N m kg





. Tốc độ vệ

tinh trên quỹ đạo đó là:

 

6,344 /km s

 

6,644 /km s

 

7,244 /km s

 

6,944 /km s

Giải

Lực hấp dẫn của trái đất cũng đóng vai trò là lực hướng tâm:

 

2 2

. .

. . . . 7,244 /

hd ht ht

M m M m v GM

F F G m a G m v km s

r r r r

       

Câu 138: Một chất điểm dao động điều hòa với chu kì

 

1,6 s

và biên độ

 

7 cm

. Vận tốc chất điểm trên tại vị

trí mà ly độ bằng

biên độ bằng giá trị nào dưới đây:

 

0,218 /m s

 

0,248 /m s

 

0,208 /m s

 

0,238 /m s

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Áp dụng phương trình về mối liên hệ của

, ,A x v

 

2 2

2 2 2 2 2 2 2

2 2

0,07 0,035 0, 238 /

2 1,6

v A

A x v A x A m s

 



   

         

   

   

Câu 139: Một khối khí ôxy

 

có khối lượng riêng là

 

0,56 /kg m





. Số Avôgađrô

 

6,023.10 /N J kmol

. Tỷ số áp suất khí và động năng tịnh tiến trung bình của phân tử khí là:

 

5,967.10 /Pa J

 

7,557.10 /Pa J

 

8,617.10 /Pa J

 

7,027.10 /Pa J

Giải

Dạng phương trình thuyết động lực học phân tử:

p n mv

Trong đó:

là mật độ phân tử trong 1 đơn vị thể tích

 



 

 

tổng số phân tử khí có trong thể tích

là khối lượng phân tử khí

vận tốc toàn phương TB của 1 phân tử khí

Có

0 0 0

1 2 2

3 3 2 3

p n mv n n W  

 

2 2 2

7,027.10 /

3 3 3

p N N

n Pa J





    

Câu 140: Từ đỉnh tháp cao

 

18 m

người ta ném 1 hòn đá khối lượng

 

58m g

theo phương nghiêng với mặt

phẳng nằm nagng một góc





, với vận tốc ban đầu

 

16 /v m s

. Khi rơi tới đất hòn đá có vận tốc

 

21 /v m s

. Công của lực cản của không khí lên hòn đá là: ( cho

 

10 /g m s

)

 

5,775 J

 

2,975 J

 

3,675 J

 

5,075 J

Giải

Công của lực cản của không khí lên hòn đá là:

 

22 2 2

0,058.21 0,058.16

0,058.10.18 5,075

2 2 2 2

mvmv

A mgh J

   

       

 

  

Câu 141: Một động cơ nhiệt có hiệu suất

 

25 %

và nhả nhiệt cho một nguồn có nhiệt độ

 

900 K

. Nó nhận

nhiệt từ một nguồn có nhiệt độ ít nhất là:

 

1200 K

 

1193 K

 

1221 K

 

1214 J

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

 

2 2

900

1 0,25 1200

1 1 0,25

T T

T K



       

 

Câu 142: Một động cơ nhiệt làm việc theo chu trình Carnot với nhiệt độ nguồn nóng là

90 C

. Trong mỗi một

chu trình tác nhân nhận của nguồn nóng một nhiệt lượng

 

10 kcal

và thực hiện công

 

15 kJ

. Nhiệt độ của nguồn

lạnh là:

 

235,32 K

 

230,32 K

 

231,32 K

 

232,32 K

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

2 2

2 1

1 1 1 1 1

' ' ' 15

1 1 1 363. 1 232,92

10.4,186

T TA A A

T T K

T Q T Q Q



 

           

 

 

Câu 143: Một khẩu pháo có khối lượng

 

450M kg

bắn một viên đạn theo phương làm với mặt ngang một

góc





. Khối lượng của viên đạn

 

5m kg

, vận tốc đầu nòng

 

400 /v m s

. Khi bắn bệ pháo giật lùi về

phía sau một đoạn

 

55s cm

. Lực cản trung bình tác dụng lên quả pháo có giá trị:

 

2320,2 N

 

1920,2 N

 

2220,2 N

 

2020,2 N

Giải

Theo định lu t bậ ảo toàn động lượng thì vận t c giố ật lùi c a kh u pháo là: ủ ẩ

 

. . 5.400. 60 20

450 9

m v cos cos

V m s



     

Dấu

" "

chứng tỏ pháo giật lùi, ngược chiều dương)

Áp dụng công thức:

 

2 2 2

' 2 4,49 /

V V aS a m s

      

Lực cản trung bình tác dụng lên quả pháo:

 

4,49.450 2020,2

F Ma N    

Câu 144: Khối lượng riêng của một chất khí

 

2 3

9.10 /kg m







; vận tốc căn quân phương của các phân tử khí

này là

 

400 /v m s

. Áp suất của khối khí tác dụng lên thành bình là:

 

4800 /N m

 

5100 /N m

 

4700 /N m

 

4600 /N m

Giải

Áp dụng PT trạng thái khí lí tưởng:

PV m PV RT PV P P

RT RT m

  

      

Vận tốc căn quân phương của các phân tử khí:

vRT RT

 

  

 

2 2

. 4800 /

3 3

C C

v vP

P N m



    

Câu 145: Một động cơ nhiệt hoạt động theo chu trình Carnot thuận nghịch giữa 2 nguồn điện có nhiệt độ

 

800 K

và

 

200 K

. Nếu nó nhận 1 lượng nhiệt

 

8 kJ

của nguồn nóng trong mỗi chu trình thì công mà nó sinh ra trong

mỗi chu trình là:

 

4 kJ

 

5 kJ

 

3 kJ

 

6 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

2 2 2

1 1 1 1 1

' ' 200

1 1 ' 1 8. 1 6

800

T T TA A

A Q kJ

T Q T Q T



 

           

 

 

Câu 146: Một quả cầu có khối lượng

 

100m g

được gắn vào đầu sợi dây có khối lượng không đáng kể. Một

đầu dây gắn vào điểm O cố định. Sợi dây có chiều dài

 

50l cm

. Cho vật chuyển động tròn quanh O trong mặt

phẳng đứng. Tại vị trí cao nhất B quả cầu có vận tốc

 

3,2 /

v m s

. Lấy

 

9,81 /g m s

. Sức căng của sợi dây

tại vị trí thấp nhất A có giá trị

 

9,953 N

 

7,953 N

 

6,953 N

 

5,953 N

Giải

Chọn mốc thế năng tại vị trí A

Ta có:

2 2 2 2

1 1

0 2

2 2

A B A B B A B B

W W mv mv mgh v v gh       

29,86

v 

Áp dụng định luật II Newton tại điểm A chiếu lên phương dây treo, ta có:

 

2 2

6,953

A A

mv mv

T P mg N

l l

    

Câu 147: Một đĩa tròn đồng chất bán kính

 

0,2R m

, có thể quay xung quanh một trục nằm ngang vuông góc

với đĩa và cách tâm đĩa một đoạn

. Đĩa bắt đầu quay từ vị trí cao nhất của tâm đĩa với vận tốc đầu bằng 0. Vận

tốc khi tâm đĩa ở vị trí thấp nhất là (

 

9,8 /g m s

)

 

36,725 /rad s

 

11,431 /rad s

 

37,698 /rad s

 

12,404 /rad s

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Tại vị trí cao nhất và vị trí thấp nhất khoảng cách giữa hai khối tâm là

Chọn mốc thế năng là vị trí thấp nhất

cho tiện. Như vậy ở vị trí cao nhất năng lượng của đĩa tròn dưới dạng thế năng và có dạng:

W mgR

Tại vị trí thấp nhất năng lượng của đĩa có dạng động năng (thế năng bằng ) và có dạng:0





Moment quán tính của thanh đối với trục quay:

1 3

2 2 4

R mR

I mR m

 

  

 

 

Áp dụng định luật bảo toàn năng lượng:

 

2 2 2

1 1 3 3 8

11,431 /

2 2 4 8 3

mR g

mgR I g R rad s

   

      

Câu 148: Hai quả cầu

và

được treo ở hai đầu sợi dây mảnh không dãn dài bằng nhau. Hai đầu kia của các

sợi dây được buộc vào một cái giá sao cho các quả cầu tiếp xúc với nhau và tâm của chúng cùng nằm trên một

đường nằm ngang. Khối lượng của các quả cầu

 

165

m g

và

 

750

m g

. Kéo quả cầu A lệch khỏi vị trí

cân bằng đến độ cao

 

6h cm

và thả ra. Sau va chạm, quả cầu B được nâng lên độ cao là: (coi va chạm là hoàn

toàn không đổi, cho

 

9,8 /g m s

)

 

1,764 mm

 

7,991 mm

 

7,804 mm

 

1,951 mm

Giải

Trường hợp a: va chạm hoàn toàn đàn hồi

Định luật bảo toàn động lượng:

1 1 1 1 2 2

m v m V m V 

Chiếu lên trục ta có: giả sử sau khi va chạm mỗi vật chạy về 1 hướng

1 1 1 1 2 2

m v m V m V  

 

Định luật bảo toàn cơ năng: thế năng của vật

chính bằng động năng của nó trước khi va chạm và bằng tổng

động năng của vật

và

sau khi va chạm:

2 2 2

1 1 1 1 2 2

2 2 2

m v m V m V

m gh   

 

1 1 1 1 2 2 1 1 1 2 2

m v m V m V m v V m V     

 

2 2 2

1 1 1 1 2 2

2 2 2

m v m V m V

m gh m v V m V     

Lấy

 

1 1 2

v V V  

và

1 1

m v

m gh v gh  

Thay ngược lại vào

 

để tìm mối quan hệ giữa

và

   

2 1

1 1 1 2 1 1 1 1

2 1

m m

m v V m v V V v

m m



    



Tượng tự tìm được mỗi quan hệ giữa

và

2 1

1 2

V v

m m





TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Sau va chạm, quả cầu B được nâng lên độ cao là

   

2 1 2

7,804.10 7,804

2 2

V m m

h m mm

g g





   

Câu 149: Một vật cố khối lượng

 

12m kg

bắt đầu trượt từ đỉnh dốc một mặt phẳng nghiêng cao

 

24h cm

Khi tới chân dốc có vận tốc

 

15 /v m s

. Cho

 

10 /g m s

. Công của lực ma sát là

 

1520 J

 

1544,6 J

 

1537,3 J

 

1508,1 J

Giải

Chọn mặt đất làm gốc tính thế năng

 

W 

, chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu

tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường,

hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát:

2 1 0

2 2

mvmv

A W W mgh mgh

  

     

  

   

Thay số:

   

0 0

0, 0,2 , 15 / , 0v h m v m s h   

 

1321,2

A mv mgh J   

Câu 150: Một chất điểm có khối lượng

 

230m g

được ném lên từ điểm O trên mặt đất với vận tốc

 

13 /v m s

theo phương hợp với phương ngang một góc





. Bỏ qua sức cản của không khí, lấy

 

9,81 /g m s

. Mômen động lượng của chất điểm đối với điểm O sau

 

1 s

kể từ khi ném có giá trị là:

 

13,22 . /kg m s

 

13,739 . /kg m s

 

12,701 . /kg m s

 

11,144 . /kg m s

Giải

Chọn hệ trục Oxy như hình vẽ ọa độ. Gốc t tại vị trí b u ném, chiắt đầ ều

dương hướng xu ng, cùng chi u v i gia tố ề ớ ốc

Gia tốc:

a g









 





Vận tốc:

0 0

. .

x x x

y y y

v v a t v cos

v v a t v sint gt



  







   





Phương trình chuyển động của chất điểm:

: . .

: .

x x

y y

Ox x v cos t

Ox x v t a t

Oy y v sin t gt

Oy y v t a t







 





 



 

 

 

 







TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Động lượng

tại thời điểm t bất kì:

 

x y x y

p t p i p j mv i mv j   

Xét tích có hướng của hai vector:

1 2 3

u u i u j u k  

và

1 2 3

v v i v j v k  

1 2 3

2 3 1 3

1 2

1 2 3

u v u u u i j k

v v v v

v v

v v v

   

Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới

trục z coi như bằng 0

 

. 0 . .

0 0

x y x y

r v v v i j k v y v x k

y x x y

x y

     

Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển

động chất điểm là:

 

0 0 0 0

. . . . . .

x y

L v y v x v cos t m v sin gt mv cos v si n t gt

   

 

     

 

 

 

2 0 2 2

1 1

.0,23.9,81.13. 30 .1 12,701 /

2 2

mgv t cos cos kgm s



  

Câu 151: Một động cơ làm việc theo chu trình Carnot với tác nhân là không khí. Nhiệt độ ban đầu là

127 C

;

thể tích của không khí sau lần giãn đẳng nhiệt

 

6V dm

và sau khi giãn đoạn nhiệt nó chiếm thể tích

 

9,1V dm

. Hiệu suất của động cơ có giá trị:

17,347%

11,347%

9,347%

15,347%

Giải

Giai đoạn 1: quá trình đẳng nhiệt

   

1 2

400T const T T K   

Giai đoạn 2: Qúa trình đoạn nhiệt

Áp dụng phương trình TT cho quá trình đoạn nhiệt:

 

1,4 1

1 1

2 2 3 3 3 2

400. 338,61

9,1

T V T V T T K



 



 

 

    

 

 

Hiệu suất của động cơ:

338,61

1 1 0,15347 15,347%

400



     

Câu 152: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

12 kW

. Nhiệt độ của nguồn nóng là

100 C

, nhiệt độ của nguồn lạnh là

0 C

. Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút có giá trị:

 

2,266.10 kJ

 

1,966.10 kJ

 

1,866.10 kJ

 

1,766.10 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 12

1 44,76

273

373

A A

Q kJ

T Q



      



Gọi

là nhiệt lượng mà tác nhân nhả cho nguồn lạnh:

 

1 1

' 44,76 12 32,76Q Q A kJ    

Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là

 

. 60.32,76 1965,6Q Q t kJ  

Câu 153: Một xe lửa gồm nhiều toa được đặt trên các lò xo của hệ thống bánh xe. Mỗi lò xo của to axe chịu một

trọng lượng

 

5.10P N

nén lên nó. Xe lửa bị rung động mạnh nhất khi nó chạy với tốc độ

 

26 /v m s

qua

các chỗ nối của đường ray. Độ dài mỗi thanh ray bằng

 

12,5l m

. Hệ số đàn hồi của các lò xo nhận giá trị nào

dưới đây (cho

 

9,8 /g m s

)

 

82,64.10 /N m

 

88,64.10 /N m

 

87,4.10 /N m

 

84,14.10 /N m

Giải

Con lắc dao động mạnh nhất khi xảy ra cộng hưởng (chu kỳ dao động riêng của vật trùng chu kỳ qua các chỗ nối

của đường ray):

 

12,5

0,48

T s

  

Mặt khác:

   

5.10

5.10 5102,04

9,8

P N mg m kg

     

Mà

   

2 2

4 . 4 .5102,04

2 0,48 87,4.10 /

0,48

m m

T s k N m

k T

 



     

Câu 154: Một thanh chiều dài

 

1l m

, khối lượng

 

7M kg

có thể quay tự do xung quanh một trục nằm

ngang đi qua một đầu của thanh. Một viên đạn khối lượng

 

0,01m kg

bay theo hương nằm ngang với vận tốc

 

300 /v m s

tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc gốc của thanh ngay sau khi viên đạn

đập vào đầu thanh là:

 

2,051 /rad s

 

1,28 /rad s

 

1,794 /rad s

 

1,023 /rad s

Giải

Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có

mỗi viên đạn có tốc độ và khối lượng

mang một động lượng

p mv

Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách

từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm

quay tới viên đạn chính là độ dài

Vậy mômen động lượng trước khi va chạm là:

. . .

L r p sin l p mvl



  

Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với

cùng vận tốc góc



. Vậy moomen quán tính của hệ vật sau va chạm:

1 2s

L I I

 

 

Với

là moment chất điểm (viên đạn) đối với trục quay

I ml

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

là moment quán tính của thanh mảnh

2 2

12 12 3

Ml Ml

 

 

 

  

Hay

 

1 2

L I I ml

 

 

   

 

 

Áp dụng định luật bảo toàn động lượng

 

1,28 /

t s

Ml mvl v

L L mvl ml rad s

 

 

       

 

 

 



 

 

Câu 155: Một vật nhỏ có khối lượng m buộc vào đầu sợi dây mảnh chiều dài

 

1,2l m

, đầu kia giữ cố định.

Cho vật quay trong mặt phẳng nằm ngang với vận tốc góc không đổi sao cho sợi dây hợp với phương thẳng đứng

một góc





. Cho

 

10 /g m s

, bỏ qua lực cản không khí. Tốc độ góc có giá trị:

 

3,202 /rad s

 

2,902 /rad s

 

3,402 /rad s

 

3,102 /rad s

Giải

Chọn mốc thế năng tại vị trí căn bằng, chiều dương hướng xuống

Trong quá trình dao động, vật chịu tác dụng của các lực: trọng lực

 

, lực căng dây

 

và lực hướng tâm

Áp dụng định luật II Newton, ta có:

P T F  

 

Chiếu

 

lên trục Ox:

0 0

. 30 0 . 30

ht ht

F T sin F T sin   

Chiếu

 

lên trục Oy:

0 . 30

P Tcos P Tcos mg T cos T

cos

 

       

0 0

. 30 . 30

F T sin mg tan mg   

Mà

2 2 0

. . . 30

ht ht

F ma m R m l sin

 

  

 

2 0 2

1 2

. . 30 . 3,102 /

23 3 3

mg g g

m l sin l rad s

  

     

Câu 156: Từ đỉnh đồi cao, một quả pháo được bắn chếch lên phía trên một góc





so với phương nằm

ngang v i v n t u nòng là ớ ậ ốc đầ

 

450 /v m s

. Sau khi b n mắ ột kho ng th i gian ả ờ

 

5t s

, góc 𝜑 giữa hướng

của vận tốc quả pháo và hướng của gia tốc toàn phần thỏa mãn giá trị nào dưới đây ( bỏ qua sức cản không khí.

Gia tốc trọng trường bằng

 

9,8 /g m s

1,614tg



 

1,814tg



 

2,214tg



 

2,014tg



 

Giải

Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí pháo bắt đầu bắn, chiều dương hướng xu ng, cùng chi u vố ề ới

gia tốc

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Gia tốc:

a g









 





Vận tốc:

0 0

. .

x x x

y y y

v v a t v cos

v v a t v sint gt



  







   





Phương trình chuyển động của chất điểm:

: . .

: .

x x

y y

Ox x v cos t

Ox x v t a t

Oy y v sin t gt

Oy y v t a t







 





 



 

 

 

 







Theo hình vẽ, ta có:

tan





Tại thời điểm

 

5 :t s

2,214

. 4

v v cos

v cos

tan

v v sin g

v sin g













  



 







Mặt khác:

2,214tan tan

 

   

(do

180

 

 

)

Câu 157: Một động cơ nhiệt có hiệu suất

 

20 %

và nhả nhiệt cho một nguồn có nhiệt độ

 

500 K

. Nó nhận

nhiệt từ một nguồn có nhiệt độ ít nhất là:

 

639 K

 

625 K

 

618 K

 

604 K

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

 

2 2

500

1 0,2 625

1 1 0,2

T T

T K



       

 

Câu 158: Hai hòn bi có khối lượng

và

m 

được treo bằng 2 sợi dây có cùng chiều dài

 

6l m

vào

một điểm. Kéo lệch hòn bi

cho đến khi dây treo nằm ngang rồi thả ra để nó va chạm vào bi

. Sau va chạm

hai hòn bi dính vào nhau và lên tới độ cao cực đại là: ( cho

 

9,8 /g m s

)

 

2,827 m

 

2,907 m

 

2,667 m

 

2,747 m

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Áp dụng định luật bảo toàn cơ năng ( cho hệ gồm hòn bi và Trái Đất ; chọn mốc tính thế năng tại vị trí cân 1

bằng của hòn bi 1 trước va chạm ) ta tính được vận tốc của hòn bi v 1 trước va chạm:

1 1

0 0 2

m v

m gl v gl    

 

Ngay sau va chạm cả hai hòn bi có cùng vận tốc

. Áp dụng định luật bảo toàn động lượng ta có:

 

1 1

1 1 2

1 2

2 2

' ' 2

3 3

m v m v

m v m m v v v gl

m m

      



 

Động năng của hệ hai hòn bi sau va chạm là:

2 2

1 2

1 1

' ' 3 1 2

' '

2 2 4 3 3

m v m v

W m v m v mgl    

Sau va chạm hai hòn bi dính vào nhau và tiếp nối chuyển động tròn ban đầu của hòn bi . Động năng 1

của

hệ hai hòn bi chuyển động thành thế năng

 

1 2 1

W m m gh m gh  

của hai hòn bi ở độ cao tối đa

( chọn

mốc tính thế năng như trên) :

 

1 1

2 3 4

' ' 2,667

3 2 9

d t

W W m gl m gh h l m     

Câu 159: Từ đỉnh đồi cao một hòn đá được ném theo phương nằm ngang với vận tốc

 

15 /v m s

. Bỏ qua sức

cản không khí, cho

 

9,8 /g m s

, gia tốc tiếp tuyến của hòn đá sau lúc ném 1 giây là:

 

5,36 /m s

 

3,86 /m s

 

4,86 /m s

 

6,36 /m s

Giải

Vận t c c a vố ủ ật theo phương n m sau khi ném ằ

 

1.9,8 9,8 /

v gt m s  

Góc



giữa vận tốc của vật và phương thẳng đứng thỏa mãn:





. Xem hình vẽ

Từ đó, gia tốc pháp tuy n và gia t c tiế ố ếp tuyến c a v t lúc này chính là nh ng ph n chi u c a gia t c g: ủ ậ ữ ầ ế ủ ố

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

2 2 2 2

9,8.15

. 8,204 /

15 9,8

x y

g v

a g sin m s

v v



   

 

 

2 2 2 2 2

9,8 8, 204 5,36 /

t n

a g a m s    

Câu 160: Có

 

22M g

khí đang chiếm thể tích

 

4V l

ở nhiệt độ

27t C

. Sauk hi hơ nóng đẳng á, khối

lượng riêng của nó bằng

 

4 3

6.10 /g cm







. Nhiệt độ của khối khí sau khi hơ nóng là:

 

2850 K

 

2750 K

 

2950 K

 

3050 K

Giải

Trước khi hơ nóng:

Áp dụng phương trình TT khí lý tưởng:

1 1

pV RT





 

Sau khi hơ nóng:

2 2 2

RTm m

pV RT p RT



  

   

 

Lấy

 

1 1

1 2

2 1

2750

mT mT

V T K

T V

 

    

Câu 161: Hai khối khí

và

có cùng mật độ số hạt. Nhiệt độ của khối khí

là

60 C

, nhiệt độ của khối

khí

là

30 C

. Áp suất của

và

theo thứ tự là

và

. Ta có:

1 2

0,899P P

1 2

1,199P P

1 2

1,399P P

1 2

1,099P P

Giải

Số phân tử khí của chất khí đó là

. .

A A

N n N N



 

Hằng số Boltzmann

 

1,28.10 / .

RT R R m R

k J K N N

V N k k





      

Mật độ phân tử của chất khí đó là

N mR p

V k V kT



  

Vì hai khối khí

và

có cùng mật độ số hạt và nhiệt độ thay đổi



áp suất thay đổi



Qúa trình đẳng tích

Áp dụng PT trạng thái quá trình đẳng tích:

1 1

1 2

2 2

60 273

1,099

30 273

P T

P P

P T



   



Câu 162: Một cột đồng chất có chiều cao

 

7h m

, đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ

xuống. Gia tốc trọng trường

 

9,8 /m s

. Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây ?

 

13,846 /m s

 

15,846 /m s

 

15,346 /m s

 

14,346 /m s

Giải

Ở vị trí thẳng đứng, cột có thế năng:

W mg

Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất:

W I





Trong đó: là moment quán tính của cột đối với trục quay gốc của cột: I

I 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ



là vận tốc góc của cột lúc chạm đất.

Áp dụng định luật bảo toàn cơ năng:

gmhh





Vận tốc dài:

 

. 3 3.9,8.8 =14,346 /v h gh m s



  

Câu 163: Một chất điểm chuyển động có phương trình:

x asin t

y bcos t













. Cho

 

35a b cm 

và

 

10 /rad s

 



Gia tốc chuyển động của chất điểm có giá trị bằng:

 

214,7 /m s

 

236,7 /m s

 

231,7 /m s

 

246,7 /m s

Giải

Ta có:

 

sin t

x a sin t

y b cos t

cos t











 



 













Mà

     

2 2

1 1

x y

sin t cos t R a b

a b

 

   

      

   

   



PT chuyển động tròn

Mặt khác:

 

v x R cos t

v y

v x

v y R sin t

 



 

 





 



 

 

  





Mà

       

 

2 2

2 2 2 2 2 2

x y

v v v y x R sin t cos t R

     

       



Gia tốc chuyển động của chất điểm (chuyển động tròn):

 

2 2 2

2 2

0,3. 10 345,44 /

v R

a R m s

R R



 

    

Câu 164: Một con lắc toán có sợi dây

 

1l m

. Biết rằng sau thời gian





phút,thì biên độ giảm 2 lần. giảm

lượng lôga của con lắc nhận giá trị nào dưới đây (cho

 

9,8 /g m s

)

3,312.10



2,898.10



3,115.10



3,903.10



Giải

Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:

F F kx rv   

Phương trình cơ bản của chuyển động trong trường hợp này là

ma kx rv  

Hay:

2 2

d x dx d x r dx k

m r kx x

dt dt dt m dt m

      

 

Đặt





(hệ số tắt dần)

Phương trình

 

trở thành

2 0

d x dx

x x

dt dt

 

  

 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

 

gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi

 



, nghiệm phương trình

này có dạng:

 

x A e cos t



 



 

Đây là biểu thức độ dời của dao động tắt dần. Hằng số



gọi là tần số của dao động tắt dần:

2 2

  

 

Chu kỳ

của dao động tắt dần là:

2 2

2 2 2

  



 



  



Giảm lượng loga của con lắc:

2 2



  

 

 



Theo bài ra, ta có:

. .7.60 3

1 1

1,65.10

2 2

e e

 



   

     

và

9,8



  



 

3 2

2 2 2

2 2

. 1,65.10 . 3, 312.10

9,8 1,65.10

 

 

 

 



   



Câu 165: Khối lượng của

 

1 kmol

chất khí là

 

26 /kg kmol





và hệ số Poat xông của chất khí là-

1, 4





Nhiệt dung riêng đẳng áp của khí bằng (cho hằng số khí

 

8,31.10 / .R J kmol K

 

1118,7 / .J kg K

 

1079,7 / .J kg K

 

1131,7 / .J kg K

 

1144,7 / .J kg K

Giải

Hệ số Poat xông của chất khí là -

1,4



 

Với

và

lần lượt là nhiệt dung mol đẳng áp và nhiệt dung mol đẳng tích

Mặt khác:

p v v p

C C R C C R    

p p

v p

C C

C C R



    

 

Nhiệt dung riêng đẳng áp của khí:

 

1,4.8,31.10

1118,7 / .

1 26 1, 4 1

c J kg K



  

   

 

Câu 166: Kỷ lục đẩy tạ ở Hà Nội là

 

12,67 m

. Nếu tổ chức đẩy tạ ở Xanh Pêtecbua trong điều kiện tương tự

(cùng vận tốc ban đầu và góc nghiêng) thì kỉ lục sẽ là: (cho gia tốc trọng trường ở Hà Nội là

 

9,727 /g m s

ở Xanh Pêtecbua là

 

9,810 /g m s

, bỏ qua chiều cao của người đẩy)

 

9,563 m

 

12,563 m

 

11,563 m

 

14,563 m

Giải

Từ công thức tầm xa:

. 2v sin





ta thấy với lực đẩy không đổi (để

không đổi) và góc ném không đổi (ném

xa nhất khi góc ném bằng

) thì tầm xa L tỷ lệ nghịch với gia tốc trọng trường g. Do đó, có thể xác định kỷ

lục đẩy tạ tại thành phố Xanh Pêtecbua là

 

9,727

. .12,67 12,563

9,81

XP HN

L L m

  

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 167: Một trụ rỗng có khối lượng

 

44M kg

, đường kính

 

1,4d m

, đang quay xung quanh trục của nó

với tần số

600n 

vòng/phút. Tác dụng vào trụ một lực hãm tiếp tuyến với mặt trụ và vuông góc v i tr c quay. ớ ụ

Sau th i gian ờ

2,5t 

𝑝ℎú𝑡, trụ dừng lại. Độ lớn của lực hãm tiếp tuyến nhận giá trị nào dưới đây

 

10,522 N

 

12,901 N

 

12,108 N

 

14,487 N

Giải

Gia tốc góc của trụ đặc:

 

0 0

20 2

2,5.60 15

rad s

t t

  

 

 



     

 

Moment hãm tiếp tuyến với mặt trụ:

. .

M F R I



 

Moment quán tính đối với trụ rỗng:

I MR

 

. . 44.0,7. 12,901

t t

F R MR F MR N



 

     

Câu 168: Một chất điểm khối lượng

 

0,1m kg

được ném lên từ O với vận tốc

 

5 /v m s

theo phương hợp

với mặt phẳng nằm ngang với một góc





, bỏ qua sức cản của không khí, cho

 

9,8 /g m s

. Mômen

động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là:

 

0,132 /kgm s

 

0,138 /kgm s

 

0,678 /kgm s

 

0,948 /kgm s

Giải

Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại v trí b u ném, chiị ắt đầ ều

dương hướng xu ng, cùng chi u v i gia tố ề ớ ốc

Gia tốc:

a g









 





Vận tốc:

0 0

. .

x x x

y y y

v v a t v cos

v v a t v sint gt



  







   





Phương trình chuyển động của chất điểm:

: . .

: .

x x

y y

Ox x v cos t

Ox x v t a t

Oy y v sin t gt

Oy y v t a t







 





 



 

 

 

 







Tại vị trí cao nhất của chuyển động chất điểm :

0 .

v sint

v v sint gt t

    

Và

2 2 2 2

0 0 0

0 0

1 1 1

. .

2 2 2

v sin v sin v sin

y h v sin t gt v sin

g g g

  

 

     

Động lượng

tại thời điểm t bất kì:

 

x y x y

p t p i p j mv i mv j   

Xét tích có hướng của hai vector:

1 2 3

u u i u j u k  

và

1 2 3

v v i v j v k  

1 2 3

2 3 1 3

1 2

1 2 3

u v u u u i j k

v v v v

v v

v v v

   

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới

trục z coi như bằng 0

 

. 0 . .

0 0

x y x y

r v v v i j k v y v x k

y x x y

x y

     

Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển

động chất điểm là:

 

0 0 0 0

. . . . . .

x y

L v y v x v cos t m v sin gt mv cos v si n t gt

   

 

     

 

 

 

2 2 3 2

2 2

0 0

1 1

0,138 /

2 2 2

v sin v sin

mgv t cos mgv cos m cos kgm s

g g

 

  

   

Câu 169: Thả rơi tự do một vật nhỏ từ độ cao

 

18,8h m

. Quãng đường mà vật rơi được trong

 

0,1 s

cuối

cùng của thời gian rơi là:

 

1,471 m

 

1,671 m

 

1,871 m

 

2,471 m

Giải

Thời gian rơi của vật:

 

1,96

t s

 

Quãng đường vật rơi trong 0,1 giây cuối là:

     

2 2

0,1

1 1 1

0,1 0,1 1,871

2 2 2

t t

s s s gt g t g t t m



 

         

 

Công thức tổng quát cho quãng đường rơi trong n giây cuối là

 

s g t t n

 

   

 

với



Câu 170: Một đoàn tàu khối lượng 60 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng

 

48 /km h

. Công suất đầu máy là

 

260 kW

. Gia tốc trọng trường bằng

 

9,8 /m s

. Hệ số ma sát bằng:

1,322.10



4,313.10



0,325.10



3,316.10



Giải

Đổi

   

48 / /

v km h m s 

Ta có:

 

260.10

. 19500

P F v F N

    

Mà

 

19500

19500 3,316.10

60.10 .9,8

F F mg N

 



      

Câu 171: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

8 kW

. Nhiệt độ của nguồn nóng là

100 C

, nhiệt độ của nguồn lạnh là

0 C

. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:

 

1,01.10 kJ

 

1,31.10 kJ

 

1,21.10 kJ

 

1,51.10 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 8

1 29,84

273

373

A A

Q kJ

T Q



      



Gọi

là nhiệt lượng mà tác nhân nhả cho nguồn lạnh:

 

1 1

' 29,84 8 21,84Q Q A kJ    

Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là

 

. 21,84.60 1310,4Q Q t kJ  

Câu 172: Một bánh xe có bán kính

 

10R cm

lúc đầu đứng yên sau đs quay quanh trục cảu nó với gia tốc góc

 

3,14 /rad s





. Sau giây thứ nhất gia tốc toàn phần của một điểm trên vành bánh là:

 

109,47 /cm s

 

105,47 /cm s

 

103, 47 /cm s

 

107,47 /cm s

Giải

Sau giây th nh t, v n t c góc và vứ ấ ậ ố ận t c dài c a mố ủ ột điểm tren vành bánh là:

 

. 3,14.1 3,14 /t rad s

 

  

và

 

3,14.0,1 0,314 /v R m s



  

Gia tốc tiếp tuyến có giá trị không đổi còn gia tốc pháp tuyến lúc này:

 

. 3,14.0,1 0,314 /

a R m s



  

và

 

2 2 2

. 3,14 .0,1 0,98586 /

a R m s



  

Gia tốc toàn phần:

   

2 2 2 2

1,0347 / 103,47 /

t n

a a a m s cm s   

Câu 173: Một đĩa tròn đồng chất bán kính

 

0,1R m

, có thể quay xung quanh một trục nằm ngang vuông góc

với đĩa và cách tâm đĩa một đoạn

. Đĩa bắt đầu quay từ vị trí cao nhất của tâm đĩa với vận tốc đầu bằng 0. Vận

tốc khi tâm đĩa ở vị trí thấp nhất là (

 

9,8 /g m s

)

 

74,349 /rad s

 

16,166 /rad s

 

73,376 /rad s

 

15,193 /rad s

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Tại vị trí cao nhất và vị trí thấp nhất khoảng cách giữa hai khối tâm là

Chọn mốc thế năng là vị trí thấp nhất

cho tiện. Như vậy ở vị trí cao nhất năng lượng của đĩa tròn dưới dạng thế năng và có dạng:

W mgR

Tại vị trí thấp nhất năng lượng của đĩa có dạng động năng (thế năng bằng ) và có dạng:0





Moment quán tính của thanh đối với trục quay:

1 3

2 2 4

R mR

I mR m

 

  

 

 

Áp dụng định luật bảo toàn năng lượng:

 

2 2 2

1 1 3 3 8

16,166 /

2 2 4 8 3

mR g

mgR I g R rad s

   

      

Câu 174: Tác dụng lên một bánh xe bán kính

 

0,7R m

và có mômen quán tính

 

20 .I kg m

một lực tiếp

tuyến với vành

 

115F N

. Vận tốc dài của một điểm trên vành bánh sau khi tác dụng lực

 

15 s

là ( biết rằng

lúc đầu bánh xe đứng yên)

 

40,292 /m s

 

48,172 /m s

 

42,262 /m s

 

38,322 /m s

Giải

Moment lực không đổi theo thời gian chuy ng: ển độ

 

115.0,7

. . 4,025 /

F R

M F R I rad s

 

     

Vận tốc góc:

 

. 4,025.15 60,375 /t rad s

 

  

Vận tốc dài của một điểm trên vành bánh:

 

. 42,263 /v R m s



 

Câu 175: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

60 kW

. Nhiệt độ của nguồn nóng là

127 C

, nhiệt độ của nguồn lạnh là

31 C

. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:

 

14700 kJ

 

15000 kJ

 

15100 kJ

 

15200 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 60

1 250

304

400

A A

Q kJ

T Q



      



TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ



Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút:

 

1 1

. 250.60 15000Q Q t kJ  

Câu 176: Một ống thủy tinh nhỏ khối lượng

 

100M g

bên trong có vài giọt ête được đậy bằng 1 nút cố định

có khối lượng

 

10m g

. Ống thủy tinh được treo ở đầu một sợi dây không giãn, khối lượng không đáng kể,

chiều dài

 

54,3 /m s

(hình vẽ). Khi hơ nóng ống thủy tinh ở vị trí thấp nhất, ête bốc hơi và nút bật ra. Để ống

có thể quay được cả vòng xung quanh điểm treo O , vận tốc bật bé nhất của nút là: (Cho

 

10 /g m s

)

mỗi chu trình là:

 

55,1 /m s

 

50 /m s

 

48,3 /m s

 

54,3 /m s

Giải

Tại v trí A, vị ận tốc tại đây phải đủ ớn để l dây thẳng đứng và căng đét

0T 

2 2

A A

v v

P T m T m mg v gl

l l

       

Vận tốc nhỏ nhất tại A để ống quay tròn:

Amin

v gl

Đối với ống thủy tinh:

Áp dụng định luật bảo toàn cơ năng:

2 2 2 2

1 1 1 1

2 2 2 2

B dB tB B B

W W W MV Mv Mgh MV Mv Mg l       

2 2

V v gl  

Vận tốc tối thiểu để đạt đỉnh:

4 5 5

B min

v gl V gl gl gl V gl      

Áp dụng định luật bảo toàn động lượng:

 

57,01 /

min

min min min

M glMV

mv MV v m s

m m

    

Câu 177: Từ đỉnh đồi cao, một quả pháo được bắn chếch lên phía trên một góc





so với phương nằm

ngang với vận tốc đầu nòng là

 

600 /v m s

. Sau khi bắn một khoảng thời gian

 

4t s

, góc



giữa hướng

của vận tốc quả pháo và hướng của gia tốc toàn phần thỏa mãn giá trị nào dưới đây ( bỏ qua sức cản không khí.

Gia tốc trọng trường bằng

 

9,8 /g m s

1,992tg



 

2,894tg



 

2,094tg



 

2,294tg



 

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí pháo bắt đầu bắn, chiều dương hướng xuống, cùng chiều với

gia tốc

Gia tốc:

a g









 





Vận tốc:

0 0

. .

x x x

y y y

v v a t v cos

v v a t v sint gt



  







   





Phương trình chuyển động của chất điểm:

: . .

: .

x x

y y

Ox x v cos tOx x v t a t

Oy y v sin t gt

Oy y v t a t







 





 



 

 

 

 







Theo hình vẽ, ta có:

tan





Tại thời điểm

 

5 :t s

1,992

. 4

v v cos

v cos

tan

v v sin g

v sin g













  



 







Mặt khác:

1,992tan tan

 

   

(do

180

 

 

)

Câu 178: Một tàu điện khi xuất phát chuyển động trên đường nằm ngang với gia tốc

 

0,6 /a m s

 

13 s

khi bắt đầu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng lại hẳn. Hệ số ma sát trên

đường

0,01k 

. Cho

 

10 /g m s

. Thời gian chuyển động toàn bộ của tàu là:

 

68,4 s

 

70 s

 

74,8 s

 

66,8 s

Giải

Tầu chuyển động theo hai giai đoạn:

Giai đoạn 1: chuyển động với gia tốc

 

0,6 /a m s

với thời gian

 

13t s

Giai đoạn 2: chuyển động chậm dần đều với gia tốc

 

. 0,01.10 0,1 /a k g m s  

dưới tác dụng cản của lực

ma sát trong thời gian

t

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Vận tốc lớn nhất của tàu:

 

1 1

. 0,6.13 7,8 /

max

v a t m s  

Tầu chuyển động chậm dần đều trong thời gian:

 

7,8

0,1

max

t s

   

Tổng thời gian chuyển động của tầu (kể từ lúc xuất phát đến khi tầu dừng lại)

 

2 1

78 13 91t t t s     

Câu 179: Từ đỉnh tháp cao

 

18 m

người ta ném 1 hòn đá khối lượng

 

52m g

theo phương nghiêng với mặt

phẳng nằm ngang một góc





, với vận tốc ban đầu

 

16 /v m s

. Khi rơi tới đất hòn đá có vận tốc

 

20 /v m s

. Công của lực cản của không khí lên hòn đá là: ( cho

 

10 /g m s

)

 

5,616 J

 

4,916 J

 

43,516 J

 

7,016 J

Giải

Công của lực cản của không khí lên hòn đá là:

 

22 2 2

0,058.21 0,058.16

0,058.10.18 5,616

2 2 2 2

mvmv

A mgh J

   

       

   

  

Câu 180: Giả sự lực cản của nước tác dụng lên xà lan tỉ lệ với tốc độ của xà lan đối với nước. Một tàu kéo cung

cấp công suất

245P 

mã lực ( 1 mã lực

 

746 W

) cho xà lan khi chuyển động với tốc độ

 

0,25 /v m s

Công suất cần thiết để kéo xà lan với tốc độ

 

0,75 /v m s

là

2225

mã lực B.

2205

mã lực C.

2235

mã lực D.

2215

mã lực

Giải

Lực c n c c tả ủa nướ ỉ lệ với tốc độ của xà lan với nước:

 

F kv k const 

Ta có:

2 2

1 1

1 1 2

2 1

2 2 1

2 2

2205

F k v

F v v

F F

F v v

F k v





   



    



   





   



mã lực

Câu 181: Tác dụng lên một bánh xe bán kính

 

0,9R m

và có mômen quán tính

 

20 .I kg m

một lực tiếp

tuyến với vành

 

125F N

. Vận tốc dài của một điểm trên vành bánh sau khi tác dụng lực

 

15 s

là ( biết rằng

lúc đầu bánh xe đứng yên)

 

71,997 /m s

 

70,027 /m s

 

75,937 /m s

 

77,907 /m s

Giải

Moment lực không đổi theo th i gian chuy ng: ờ ển độ

 

125.0,9

. . 5,625 /

F R

M F R I rad s

 

     

Vận tốc góc:

 

. 5,625.15 84,375 /t rad s

 

  

Vận tốc dài của một điểm trên vành bánh:

 

. 75,937 /v R m s



 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Câu 182: Một chất điểm chuyển động có phương trình:

x asin t

y bcos t













. Cho

 

25a b cm 

và

 

10 /rad s

 



Gia tốc chuyển động của chất điểm có giá trị bằng:

 

256,7 /m s

 

246,7 /m s

 

231,7 /m s

 

241,7 /m s

Giải

Ta có:

 

sin t

x a sin t

y b cos t

cos t











 



 













Mà

     

2 2

1 1

x y

sin t cos t R a b

a b

 

   

      

   

   



PT chuyển động tròn

Mặt khác:

 

v x R cos t

v y

v x

v y R sin t

 



 

 





 



 

 

  





Mà

       

 

2 2

2 2 2 2 2 2

x y

v v v y x R sin t cos t R

     

       



Gia tốc chuyển động của chất điểm (chuyển động tròn):

 

2 2 2

2 2

0,3. 10 246,7 /

v R

a R m s

R R



 

    

Câu 183: Tổng động năng tịnh tiến trung bình của các phân tử khí Nito

 

chứa trong một khí cầu bằng

 

5,7.10W J





và vận tốc căn quân phương của phân tử khí đó là

 

2.10 /

v m s

. Khối lượng khí nitơ trong

khí cầu là:

 

2,68.10 kg



 

2,85.10 kg



 

3,19.10 kg



 

2,34.10 kg



Giải

Tổng động năng tịnh tiến trung bình của các phân tử khí Nito

 

là

 

2 3

1 2 2.5.10

2,85.10

2.10

W mv m kg



    

Câu 184: Một động cơ nhiệt làm việc theo chu trình Carnot bằng không khí lấy ở áp suất ban đầu

 

7,0P at

Thể tích ban đầu của không khí

 

3,5V dm

. Sau lần giãn đẳng nhiệt lần thứ nhất nó chiếm thể tích

 

6,5V dm

và sau khi giãn đoạn nhiệt thể tích của khí là

 

9,5V dm

. Áp suất khí sau khi giãn đoạn nhiệt

có giá trị

bằng;

 

22,736.10 Pa

 

21,736.10 Pa

 

24,736.10 Pa

 

19,736.10 Pa

Giải

Giai đoạn 1: quá trình đẳng nhiệt

 

T const

Áp dụng phương trình TT của quá trình đẳng nhiệt:

 

1 1

1 1 2 2 2

7.3,5

3,77

6,5

PV PV P at

    

Giai đoạn 2: Qúa trình đoạn nhiệt

Áp dụng phương trình TT cho quá trình đoạn nhiệt:

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

   

1,4

4 4

2 2 3 3 3 2

6,5

3,77. 2,22 2,22.9,8.10 21,72.10

9,5

PV PV P P at Pa



 

 

      

 

 

Câu 185: Một trụ đặc khối lượng

 

60M kg

có thể quay xung quanh một trục nằm ngang trùng với trục của

trụ. Một sợi dây không giãn được quấn nhiêu vòng vào trụ, đùa tự do của dây có treo một vật nắng khố lượng

 

40m kg

. Để hệ tự chuyện động, sức căng của sợi dây là ( lấy

 

9,8 /g m s

)

 

156,81 N

 

171,73 N

 

168 N

 

175,46 N

Giải

Thiếu hình

Dưới tác d ng c a trong lụ ủ ực

lên vật nặng, hệ trụ + vật nặng chuyển động: trụ quay, vật nặng chuyển động tịnh

tiến (hệ vừa có phần quay vừa có phần tịnh tiến). Vì vậy không thể áp dụng định luật II Newton hay phương trình

cơ bản của chuyển động quay cho toàn bộ hệ. Gọi



là gia tốc góc của trụ, a là gia tốc dài của vật nặng. Vì

chuyển động của vật nặng và chuyển động của một điểm trên mặt trụ có cùng gia tốc nên ta có hệ thức:

.a R





 

(

là bán kính của trụ)

Gọi

và

là sức căng của dây tại A, ta có:

'T T 

(tức là

'T T

)

 

Với

tác dụng lên đoạn dây nối với vật nặng, còn

tác dụng lên đoạn dây nối với trụ

Áp dụng định luật II Newton riêng cho vật nặng, ta có:

P T ma 

Chọn chiều dương cùng chiều chuyển động với vật nặng

Chiếu phương trình trên lên phương chuyển động

mg T ma 

 

Áp dụng phương trình cơ bản của chuyển động quay cho riêng trụ đặc, ta có

'RT I





Với I là moment quán tính của trụ đặc:

I 

 

Từ

     

1 ; 2 ; 3

và

 

   

5,6 /

40. 9,8 5,6 168

a m s

m M

T N

T m g a





 



 

 

  

 



 



Câu 186: Một viên bi nhỏ

 

14m g

rơi theo phương thẳng đứng không vận tốc ban đầu trong không khí, lực

cản của không khí

F rv 

(tỷ l c chi u vệ ngượ ề ới v n t c), ậ ố

là h sệ ố cản. V n t c c i mà viêậ ố ực đạ n bi đạt được

bằng

 

60 /

max

v m s

. Cho

 

10 /g m s

. Hệ số cản có giá trị:

 

2,333.10 /Ns m



 

2,363.10 /Ns m



 

2,353.10 /Ns m



 

2,343.10 /Ns m



Giải

Theo bài ra, ta có:

c max

F rv P mg  

(Do vật rơi tự do)



Hệ số cản:

 

14.10 .10

2,333.10 /

r Ns m



  

Câu 187: Một phi công thực hiện vòng tròn nhào lộn trong mặt phẳng đứng. Vận tốc của máy bay không đổi

 

940 /v km h

. Giả sử rằng áp lực lớn nhất của phi công lên ghế bằng 5 lần trọng lực của người. Lấy

 

10 /g m s

. Bán kính quỹ đạo vòng nhào lộn có giá trị bằng:

 

1740,5 m

 

1682,9 m

 

1672,1 m

 

1715,3 m

Giải

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Áp d nh lu t II Newton cho phi công: ụng đị ậ

mg N ma 

là phản lực mà ghế tác dụng lên phi công (bằng và ngược chiều với lực nén của phi công lên ghế).

Áp lực lớn nhất tại điểm thấp nhất

Tại điểm thấp nhất của vòng nhào lộn, theo phương hướng tâm,

 

được viết thành:

2 2ht

mg N ma mg N m

      

Theo bài ra, ta có:

5 5N P mg 

 

2 2

5 1740,5

v v

mg mg m R m

R g

      

Câu 188: Một máy nhiệt lí tưởng làm việc theo chu trình Carnot, sau mỗi chu trình thu được 605 calo từ nguồn

nóng có nhiệt độ

127 C

. Nhiệt độ nguồn lạnh là

27 C

. Công do máy sinh ra sau một chu trình

 

613,13 J

 

643,13 J

 

663,13 J

 

633,13 J

Giải

Hiệu suất theo chu trình Carnot:



 

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

2 2

1 1 1

' 300

1 ' 1 605.4,186. 1 633,13

400

T TA

A Q J

T Q T



 

        

 

 

Câu 189: Một vật có khối lượng

 

2m kg

chuyển động với tốc độ

 

6,5 /v m s

tới va chạm xuyên tâm vào

vật có khối lượng

 

3m kg

đứng yên. Va chạm là hoàn toàn mềm. Nhiệt lượng tỏa ra trong quá trình va chạm

là

 

26,25 J

 

25,65 J

 

25,35 J

 

25,95 J

Giải

Vì va chạm là hoàn toàn mềm nên

   

1 1

1 1 1 2 2 2

1 2

2.6,5

. . 2,6 /

2 3

m v

m v m m v v m s

m m

     

 

Nhiệt lượng tỏa ra trong quá trình va chạm là:

   

2 2

1 1 1 2 2

1 1

. . . . 25,35

2 2

truoc sau

Q W W m v m m v J     

Câu 190: Một cột đồng chất có chiều cao

 

10h m

, đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ

xuống. Gia tốc trọng trường

 

9,8 /m s

. Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây ?

 

17,146 /m s

 

15,646 /m s

 

18,146 /m s

 

17,646 /m s

Giải

Ở vị trí thẳng đứng, cột có thế năng:

W mg

Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất:

W I





TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Trong đó: là moment quán tính của cột đối với trục quay gốc của cột: I

I 



là vận tốc góc của cột lúc chạm đất.

Áp dụng định luật bảo toàn cơ năng:

gmhh





Vận tốc dài:

 

. 3 3.9,8.8 =17,146 /v h gh m s



  

Câu 191: Một bánh xe có bán kính

 

14R cm

lúc đầu đứng yên sau đs quay quanh trục cảu nó với gia tốc góc

 

3,14 /rad s





. Sau giây thứ nhất gia tốc toàn phần của một điểm trên vành bánh là:

 

142,87 /cm s

 

140,87 /cm s

 

144,87 /cm s

 

138,87 /cm s

Giải

Sau giây th nh t, vứ ấ ận t c góc và v n t c dài c a mố ậ ố ủ ột điểm tren vành bánh là:

 

. 3,14.1 3,14 /t rad s

 

  

và

 

3,14.0,14 0,4396 /v R m s



  

Gia tốc tiếp tuyến có giá trị không đổi còn gia tốc pháp tuyến lúc này:

 

. 3,14.0,14 0,4396 /

a R m s



  

và

 

2 2 2

. 3,14 .0,14 1,380344 /

a R m s



  

Gia tốc toàn phần:

   

2 2 2 2

1,4487 / 144,87 /

t n

a a a m s cm s   

Câu 192: Một người đẩy xe một lực hướng xuống theo phương hợp với phương ngang một góc





. Xe có

khối lượng

 

210m kg

và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường

0,21k 

. Lấy

 

9,81 /g m s

. Lực đẩy của người có giá trị bằng:

 

566,16 N

 

563,86 N

 

561,56 N

 

568,46 N

Giải

Chọn chi u chuy ều dương cùng chiề ển động

Khi xe chuy ng, ch u tác d ng c a các lển độ ị ụ ủ ực: Trọng lực

, phản lực

, lực đẩy

và lực ma sát

Vì xe chuyển động với vận tốc không đổi nên

0a 

Áp dụng định luật II Newton, ta có:

' ' 0

P N f F   

 

Chiếu

 

lên trục Oy:

' '. 0N F sin P



  

Chiếu

 

lên trục Ox:

'. ' 0 '. '

ms ms

F cos f F cos f

 

   

Mà lực ma sát tác dụng lên xe:

 

' . ' '.

f k N k P F sin



  

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Hay

   

'. . '. ' 568,47

F cos k P F sin F N

cos k sin

 

    



Câu 193:

Một ôtô chuyển động biến đổi đều lần lượt đi qua hai điểm

và

cách nhau

 

20S m

trong khoảng thời

gian

 

2t s

, vận tốc ô tô ở

là 12 m/s. Vận tốc của ôtô ở

nhận giá trị nào sau đây:

 

8,5 /m s

 

6,5 /m s

 

8 /m s

 

7 /m s

Giải

Ta có:

 

2 2

8 /

A B

A B A B

B A

v v

S S

v v v v m s

t tv v









      













Câu 194: Một vật khối lượng m bắt đầu trượt không ma sát từ đỉnh một mặt cầu bán kính

 

3,4R m

xuống

dưới. Vật rời khỏi mặt cầu với vị trí cách đỉnh mặt cầu một khoảng là:

 

1,603 m

 

0,923 m

 

1,273 m

 

1,333 m

Giải

Chọn chi u chuy ng c a v t ều dương cùng chiề ển độ ủ ậ

Vật chịu tác d ng c a các lụ ủ ực: trọng lực

, phản lực

Áp dụng định luật II Newton, ta có:

P N ma 

 

Vì chuyển động tròn nên gia tốc ở đây đóng vai trò là gia tốc hướng tâm

Chiếu

 

lên phương chuyển động:

2 2

v v

Psin N ma m N Psin m

R R

 

     

Theo hình vẽ, ta có:

R h

sin



 



Khi vật di chuyển xuống dưới thì thế năng của vật giảm dần và biến thành động năng. Như vậy độ biến thiên

thế năng phải bằng độ biến thiên động năng của vật:

 

t d

W W mgR mg R h mv mg h         

Để vật rời khỏi mặt cầu thì

 

0 0 2 0 1,333

mv R h R

N Psin mg mg h h m

R R



 

           

Câu 195: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất

 

40 kW

. Nhiệt độ của nguồn nóng là

127 C

, nhiệt độ của nguồn lạnh là

31 C

. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:

 

10000 kJ

 

9900 kJ

 

9800 kJ

 

10300 kJ

Giải

Hiệu suất theo chu trình Carnot:



 

TUẤN TEO TÓP

CLB HỖ TRỢ HỌC TẬP – I HỌC BÁCH KHOA HN ĐẠ

Với

1 2

;T T

lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh

Mặt khác:





Với

là công sinh ra trong mỗi chu trình và

là nhiệt lượng nhận được trong mỗi chu trình

Hay

 

1 1

' ' 40 500

304

400

A A

Q kJ

T Q



      





Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút:

 

1 1

500

. .60 10000

Q Q t kJ  

Câu 196: Một vật cố khối lượng

 

13m kg

bắt đầu trượt từ đỉnh dốc một mặt phẳng nghiêng cao

 

26h cm

Khi tới chân dốc có vận tốc

 

15 /v m s

. Cho

 

10 /g m s

. Công của lực ma sát là

 

867,7 J

 

853,1 J

 

875 J

 

860,4 J

Giải

Chọn mặt đất làm gốc tính thế năng

 

W 

, chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu

tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường,

hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát:

2 1 0

2 2

mvmv

A W W mgh mgh

  

     

  

 

Thay số:

   

0 0

0, 0,2 , 15 / , 0v h m v m s h   

 

1428,7

A mv mgh J   

Câu 197: Một khối ôxy

 

ở nhiệt độ

22 C

. Để nâng vận tốc căn quân phương của phân tử lên gấp đôi, nhiệt

độ của khí là:

877 C

907 C

927 C

897 C

Giải

Công th c tính v n tứ ậ ốc căn quần phương:



(với k là hằng số Boltzmann)

Ta có:

   

2 2

1 1 2 1

2 1

2 2 1 1

22 273 1180

T v v v

T T K

T v v v







     



      



     

     









| 1/80

| | Tải xuống

Preview text:

TUẤN TEO TÓP
TỔNG HỢP ĐỀ THI MÔN VẬT LÝ ĐẠI CƯƠNG I
Câu 1: Một cột đồng chất có chiều cao h  8m , đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ
xuống. Gia tốc trọng trường  2
9,8 m / s  . Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây ?
A. 16,836 m / s 
B. 14,836 m / s 
C. 15,336m / s
D. 14,336 m / s  Giải
Ở vị trí thẳng đứng, cột có thế năng: h W  mg . t 2 1
Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất: 2 W  I d 2 2 mh
Trong đó: I là moment quán tính của cột đối với trục quay gốc của cột: I  3
 là vận tốc góc của cột lúc chạm đất.
Áp dụng định luật bảo toàn cơ năng: 2 h 1 mh 2 g 3 mg .      2 2 3 h
Vận tốc dài: v  .
 h  3gh  3.9,8.8 =15,336m / s
Câu 2: Ở thời điểm ban đầu một chất điểm có khối lượng m  
1 kg có vận tốc v  20 m / . Chất điểm chịu 0  s
lực cản F  rv ( biết r  ln2 , v là vận tốc chất điểm). Sau 2, 2s vận tốc của chất điểm là: e
A. 4,353m / s
B. 3,953 m / s 
C. 5,553m / s 
D. 3,553 m / s  Giải dv
Lực cản: F  ma  mv'  m e dt Mặt khác: dv dv r F  r  v  m  r  v    dt e dt v m v t r ln2 dv r v r  t  .2,2 Lấy tích phân: m 1
  dt  ln
  t  v  v .e  20.e  4,353 m /   0  s v m v m v 0 0 0 
Câu 3: Một chát điểm dao động điều hòa với chu kì T  2 , pha ban đầu   . Năng lượng toàn phần 0  s 3  5  3
W  2,6.10 J  và lực tác dụng lên chất điểm lúc lớn nhất F  2.10
. Phương trình dao động nào sau đây 0 N 
là đúng chất điểm trên:     2 
A. 2,9.sin 2t  
 cm B . 2,7.sin t   cm  3   3      2 
C . 2, 6.sin t  
cm D .2,8.sin 2t   c  m  3   3  Giải
Lực tác dụng lên chất điểm lúc lớn nhất: F  kA 0 1 1 2E Cơ năng: 2 E 
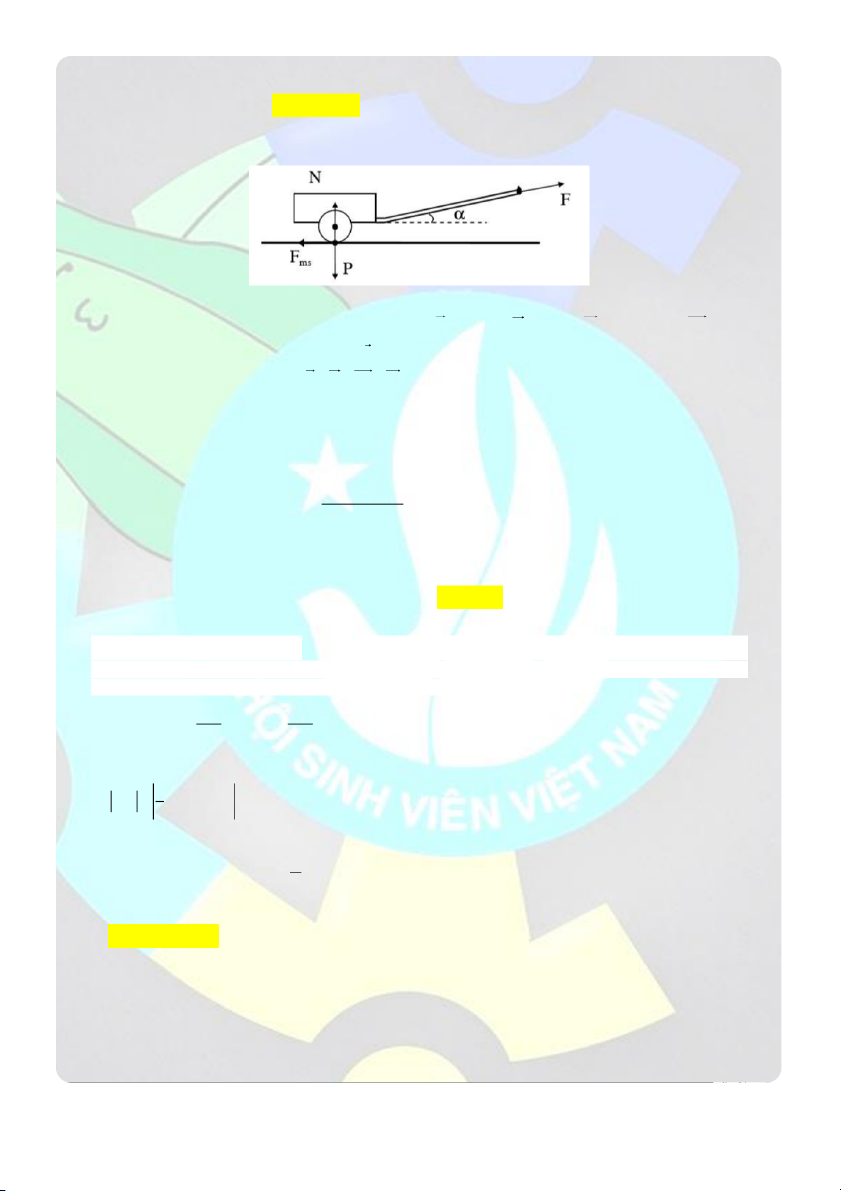
kA  .F .A  A   0,026 m  2,6 0   cm  2 2 F0
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN
TUẤN TEO TÓP 2 2
Ta có: T  2      2 rad / s  T 2  
Phương trình dao động của chất điểm: 
x  2,6.cos  t    cm   3  x  asin t 
Câu 4: Một chất điểm chuyển động có phương trình: 
. Cho a  b  30 cm  và   10 rad / s. y  bcos t  
Gia tốc chuyển động của chất điểm có giá trị bằng: A.  2 296,1 m / s  B.  2 301,1 m / s  C.  2 281,1 m / s  D.  2 281,1 m / s  Giải  a  
x  a.sin   t   sin   t  Ta có: x   
y  b.cos   t   co  s  t   b   y  2 2     Mà 2   2     1 x y sin t cos t        
1 R  a  b a   b   PT chuyển động tròn
v  x'  Rcos t  v   y x    Mặt khác: x   
v  y'  R sin t v   x    y   y 
Mà v  v v  y 2     x 2 2 2 2 2  R   2 sin  t   2 cos t   R x y   2 2 2 
 Gia tốc chuyển động của chất điểm (chuyển động tròn): v R a    R   2 2   2 0,3. 10 296,1 m / s ht  R R
Câu 5: Khối lượng của 1kmol  chất khí là   30kg / kmol và hệ số Poat-xông của chất khí là   1, 4 . Nhiệt
dung riêng đẳng áp của khí bằng (cho hằng số khí 3
R  8, 31.10 J / km . ol K  ):
A. 995,5 J / kg.K B. 982, 
5 J / kg.K C. 930, 
5 J / kg.K D. 969, 
5 J / kg.K Giải C
Hệ số Poat-xông của chất khí là p   1,4 Cv
Với C và C lần lượt là nhiệt dung mol đẳng áp và nhiệt dung mol đẳng tích p v
Mặt khác: C  C  R  C  C  R p v v p C C  p p R      C  p C C  R  1 v p 3 C  p R 1, 4.8,31.10
Nhiệt dung riêng đẳng áp của khí: c     969,5 J kg K p  / .      1 301,4   1
Câu 6: Một động cơ nhiệt hoạt động theo chu trình Carnot thuận nghịch giữa 2 nguồn điện có nhiệt độ 400 K 
và 100 K  . Nếu nó nhận 1 lượng nhiệt 6kJ  của nguồn nóng trong mỗi chu trình thì công mà nó sinh ra trong mỗi chu trình là:
A. 4,5kJ  B. 2,5kJ  C. 1,  5 kJ D. 6,5kJ  Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và Q là nhiệt lượng nhận được trong mỗi chu trình 1 T A '  T  Hay 2 2  1 
 A'  Q 1    4,5 1 kJ  1 T 1 Q  1 T 
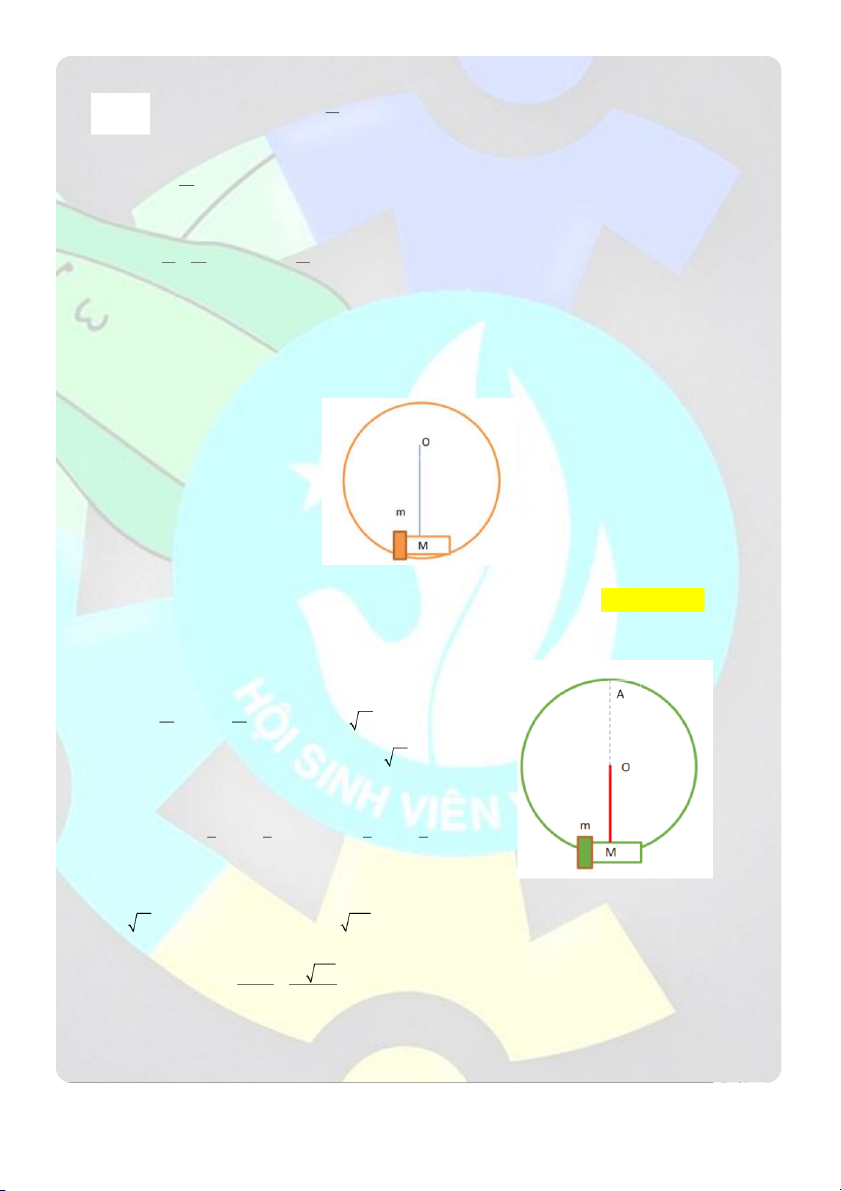
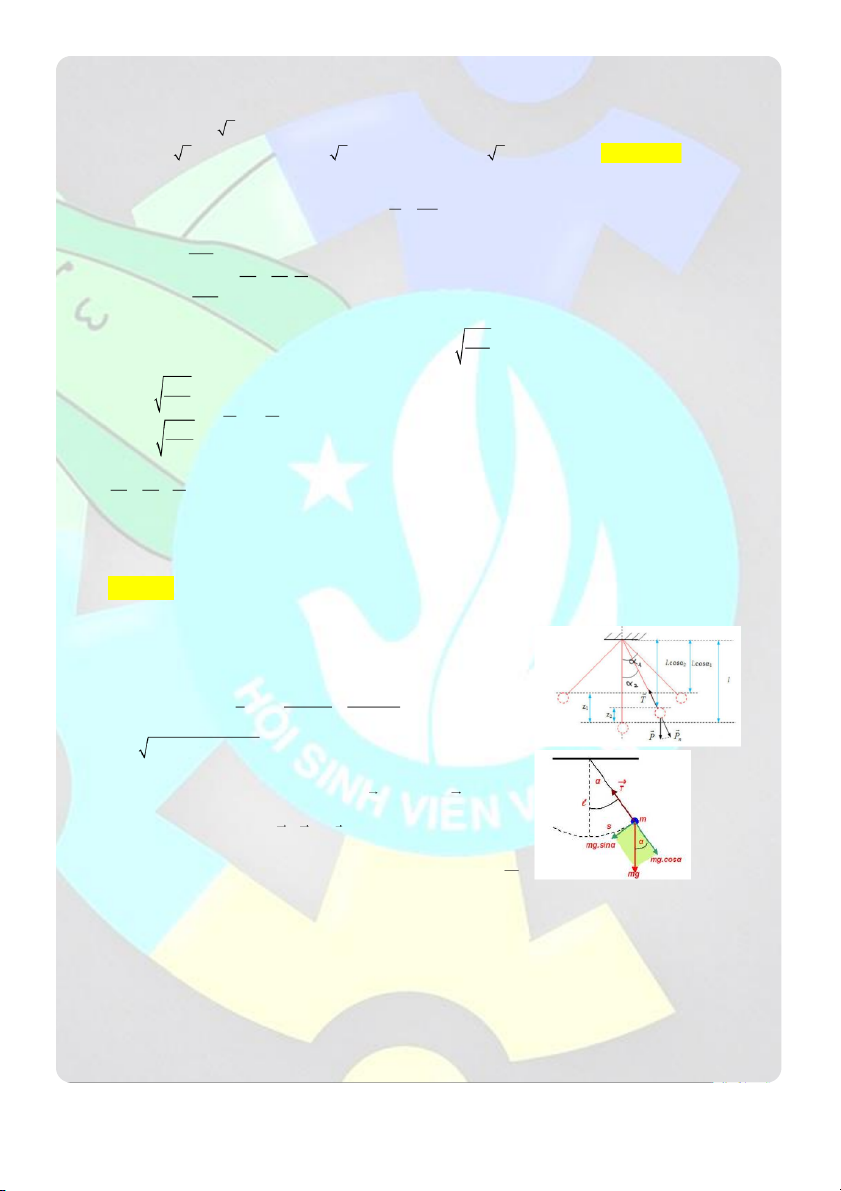
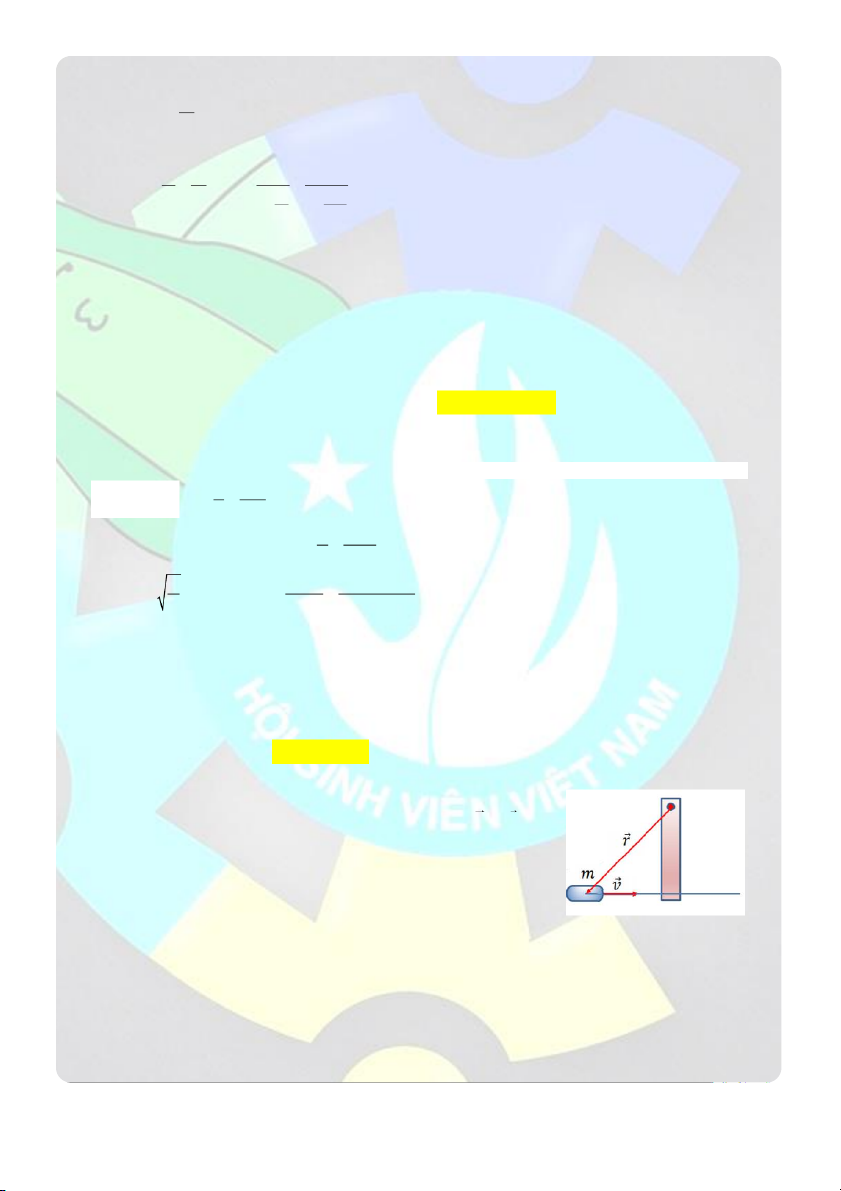
Câu 7: Một ống thủy tinh nhỏ khối lượng M  120 g  bên trong có vài giọt ête được đậy bằng 1 nút cố định có
khối lượng m  10 g . Ống thủy tinh được treo ở đầu một sợi dây không giãn, khối lượng không đáng kể, chiều
dài l  60cm (hình vẽ). Khi hơ nóng ống thủy tinh ở vị trí thấp nhất, ête bốc hơi và nút bật ra. Để ống có thể
quay được cả vòng xung quanh điểm treo O , vận tốc bật bé nhất của nút là: (Cho g   2 10 m / s  ) mỗi chu trình là:
A. 69,127 m / s
B. 64,027 m / s
C. 70,827 m / s
D. 65,727  m / s Giải
Tại vị trí A, vận tốc tại đây phải đủ lớn để dây thẳng đứng và căng đét  T  0 2 2 v v A A
P T  m T  m
 mg  0 v  gl A l l
Vận tốc nhỏ nhất tại A để ống quay tròn: v  gl Amin
Đối với ống thủy tinh:
Áp dụng định luật bảo toàn cơ năng: 1 2 1 2 1 2 1 2
W  W W  MV  Mv  Mgh  MV 
Mv  Mg 2l B dB tB 2 2 B 2 2 B 2 2
 V  v  4gl B
Vận tốc tối thiểu để đạt đỉnh: 2 v 
gl  V  gl  4gl  5gl  V  5gl B min
Áp dụng định luật bảo toàn động lượng: MV M 5 gl min mv  MV  v    65,727 m s min min min  /  m m
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 1
Câu 8: Một khối khí Hidro bị nén đến thể tích bằng
lúc đầu khi nhiệt độ không đổi. Nếu vận tốc trung bình 2
của phân tử hidro lúc đầu là V thì vận tốc trung bình sau khi nén là V A. 2V B. 4V C. V D. 2 Giải: 8
Công thức tính vận tốc trung bình của phân tử khí: kT v  m
Vận tốc trung bình của phân tử khí chỉ phụ thuộc vào nhiệt độ T  const
Nếu vận tốc trung bình của phân tử hidro lúc đầu là V thì vận tốc trung bình sau khi nén không đổi
Câu 9: Một mol khí hidro nguyên tử được nung nóng đẳng áp, thể tích gấp 8 lần. Entrôpie của nó biến thiên một
lượng bằng (cho hằng số khí R  8,3 
1 J / mo .lK )
A. 43, 2 J / K 
B. 43, 7 J / K 
C. 44,2 J / K 
D. 44,7 J / K  Giải dQ
Độ biến thiên Entropy: dS  T i  2
Qúa trình đẳng áp: Q nC dT  n RdT p 2
Thay vào và lấy tích phân từ trạng thái 1 ứng với 1
T đến trạng thái 2 ứng với 2 T T2 i  2 dT i  2  2 T i 2 2 T  S   n R  n RlnT  n Rln  2 T 2 T 2 T T 1 1 1 T V
Điều kiện của quá trình đẳng áp  p  const : 2 2  1 T 1 V i  2 2 V  S   n Rln
 43,2J / K  (khí H : i  3) 2 2 1 V
Câu 10: : Một tụ đặc trưng khối lượng M  100 kg , bán kính R  0,5m đang quay xung quanh trục của nó.
Tác dụng lên trụ một lực hãm F  257,3 N  tiếp tuyến với mặt trụ và vuông góc với trục quay. Sau thời gian t   2,6 
s , trụ dừng lại. vận tốc của góc trụ lúc bắt đầu lực hãm là
A. 25, 966rad / s
B. 26,759rad / s
C. 0,167 rad / s
D. 0,626 rad / s Giải   
Gia tốc góc của trụ đặc: 0 0     t t
Moment hãm tiếp tuyến với mặt trụ: M  F .R  I. t 2
Moment quán tính đối với trụ đặc: R I  M 2 2 R 2.
 F .R  M . Ft    10.292 rad s t  2 /  2 MR
Vận tốc của góc trụ lúc bắt đầu lực hãm là   . t   26,759 rad / 0  s 
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 11: Một quả cầu đồng chất khối lượng 1
m đặt cách đầu một thanh đồng chất một đoạn bằng a trên phương
kéo dài của thanh. Thanh có chiều dài l , khối lượng 2
m . Lực hút của thanh lên quả cầu là m m m m m m m m A. 1 2 G B. 1 2 G C. 1 2 G D. 1 2 G
a a  l 
a a  l  2 a al Giải
Dạng thanh nên chia thanh thành từng đoạn nhỏ có kích thước dx và
có khối lượng dm , cách đầu O của thanh một khoảng x
Giờ xác định dm theo dx, đối với thanh dài thì ta chú ý đến khối lượng
trên một đơn vị độ dài : m2
dm   dx  dx l
Bài yêu cầu xác định lực hút, tức là sẽ phải sử dụng công thức liên quan
tới lực hấp dẫn giữa qủa cầu và đoạn dm m dm m m dx 1 1 2 dF  G 
l  a  x G 2
l l  a  x 2
Lấy tích phân, hi quét từ trái sang phải biến x thay đổi từ 0 đến l l m m dx Gm m l Gm m  1 1  1 2 1 2 1 2 G 1 m 2 m  F  G       
l l  a  x2
l l a x 0     0   l a l a a l a 
Câu 12: Thả rơi tự do một vật nhỏ từ độ cao h  17,  6 
m . Quãng đường mà vật rơi được trong 0,1s  cuối cùng của thời gian rơi là:
A. 1, 608 m B. 1,808m C. 2,208m D. 2,408m Giải 2 Thời gian rơi của vật: h t  1  ,9  s g
Quãng đường vật rơi trong 0,1 giây cuối là: 1 1 s   s  s
 gt  g t 
 g t  t    m t t  2 1 0,1  0,12 2 2 1,808 0,1   2 2 2   1 2
Công thức tổng quát cho quãng đường rơi trong n giây cuối là 2 h s g t  t n2      t  2   với g
Câu 13: Có M  18 g  khí đang chiếm thể tích V  4 l  ở nhiệt độ 0
t  22 C . Sauk hi hơ nóng đẳng á, khối
lượng riêng của nó bằng 4     3 6.10
g / cm . Nhiệt độ của khối khí sau khi hơ nóng là:
A. 2213 K
B. 2113 K 
C. 2013 K 
D. 1913 K  Giải Trước khi hơ nóng: m
Áp dụng phương trình TT khí lý tưởng: p  1 1 V 1 RT     Sau khi hơ nóng: m m R 2 T p 2 2 V  R 2 T  p  R 2 T     V   2
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 1 Lấy m 1 T m 1 T  V   T   2213 K 1 2   2 T   2 1 V
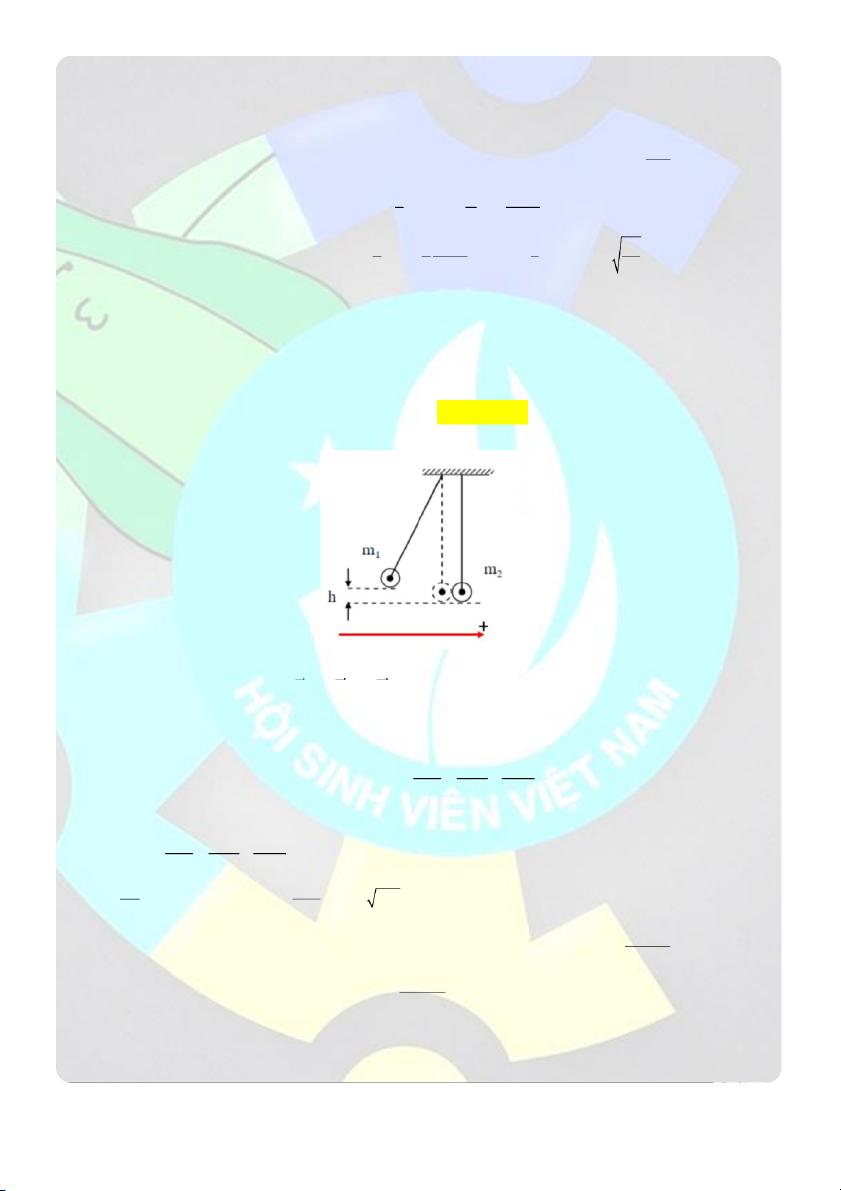
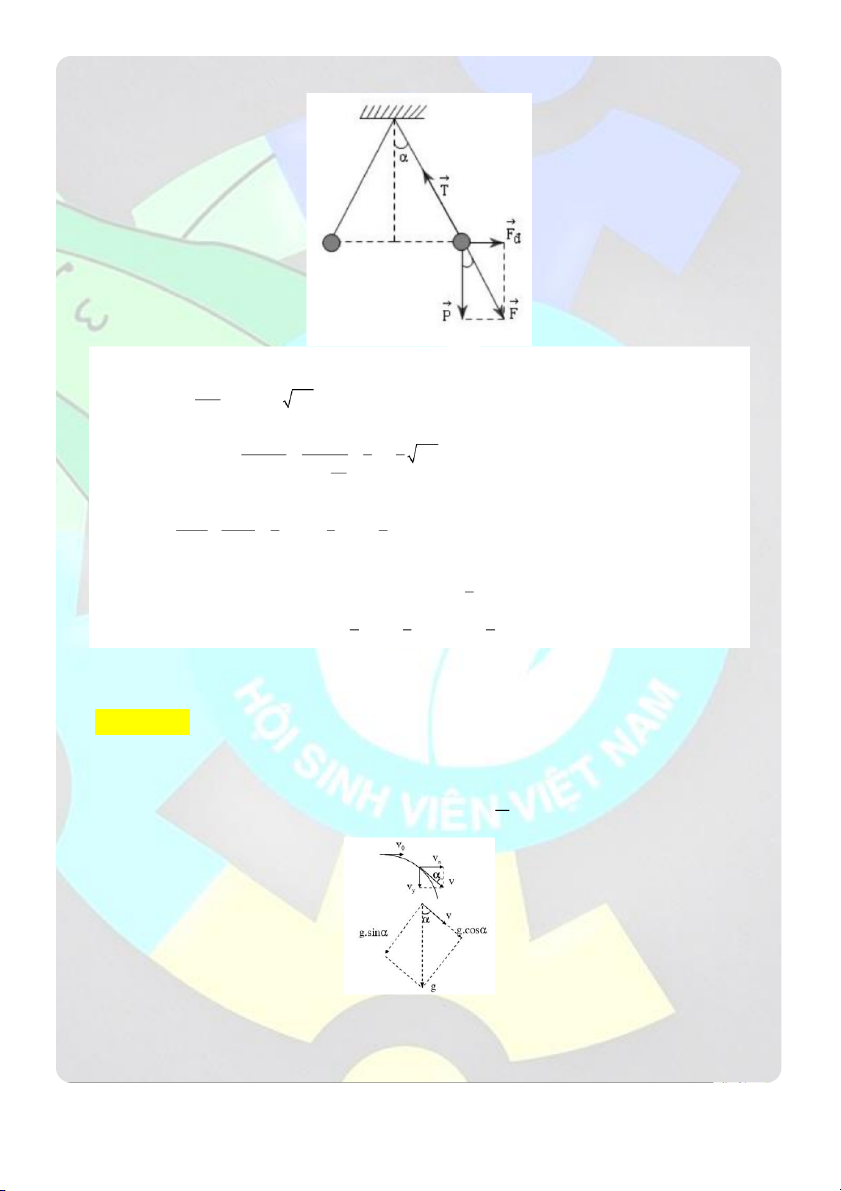
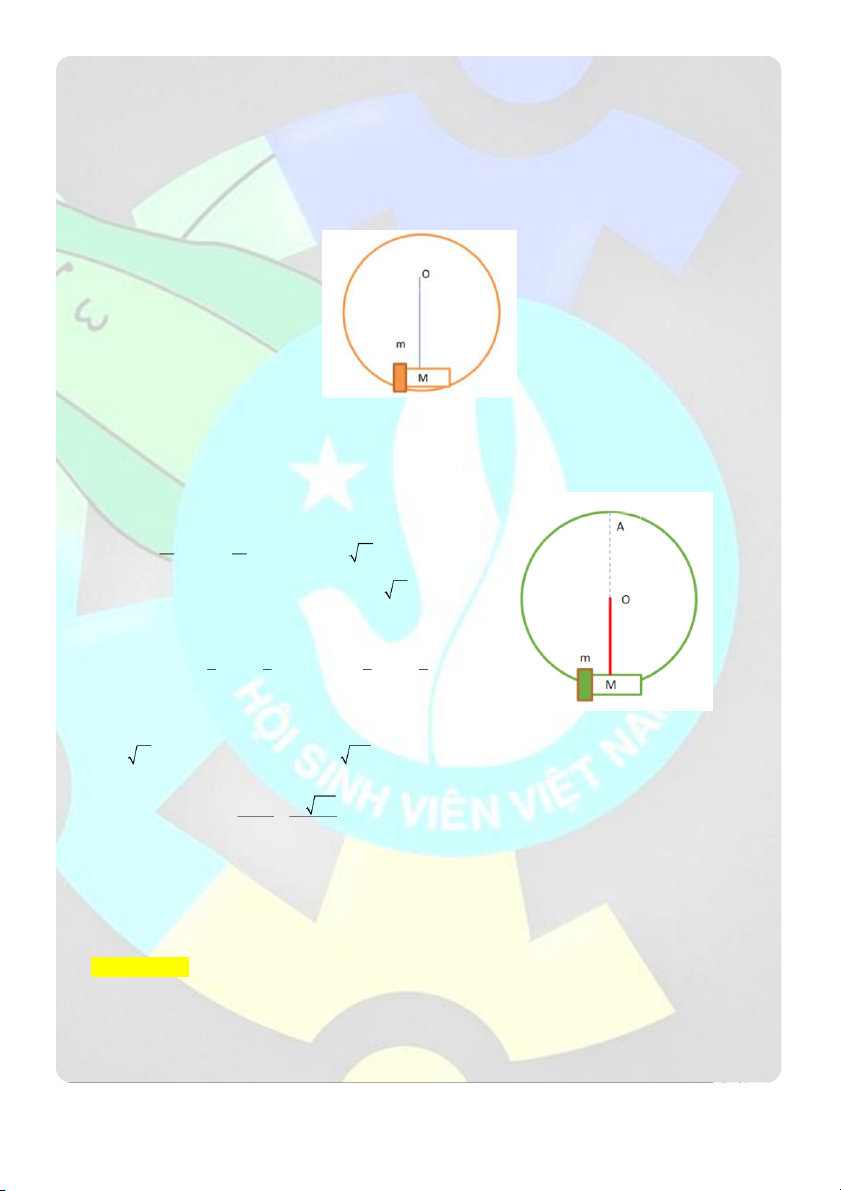
Câu 14: Một trụ đặc khối lượng M  7 
0 kg có thể quay xung quanh một trục nằm ngang trùng với trục của
trụ. Một sợi dây không giãn được quấn nhiêu vòng vào trụ, đùa tự do của dây có treo một vật nắng khố lượng
m  20 kg . Để hệ tự chuyện động, sức căng của sợi dây là ( lấy g   2 9,8 m / s  )
A. 132,19 N  B. 121N  C. 124,7  3 N
D. 113,54  N  Giải Thiếu hình Dưới tác d n ụ g c a
ủ trong lực P lên vật nặng, hệ trụ + vật nặng chuyển động: trụ quay, vật nặng chuyển động tịnh
tiến (hệ vừa có phần quay vừa có phần tịnh tiến). Vì vậy không thể áp dụng đị
nh luật II Newton hay phương trình
cơ bản của chuyển động quay cho toàn bộ hệ. Gọi  là gia tốc góc của trụ, a là gia tốc dài của vật nặng. Vì
chuyển động của vật nặng và chuyển động của một điểm trên mặt trụ có cùng gia tốc nên ta có hệ thức: a  .
 R 1 (R là bán kính của trụ)
Gọi T ' và T là sức căng của dây tại A, ta có: T  T
 ' (tức là T  T ' ) 2
Với T tác dụng lên đoạn dây nối với vật nặng, còn T ' tác dụng lên đoạn dây nối với trụ
Áp dụng định luật II Newton riêng cho vật nặng, ta có: P  T  ma
Chọn chiều dương cùng chiều chuyển động với vật nặng
Chiếu phương trình trên lên phương chuyển động mg T  ma   3
Áp dụng phương trình cơ bản của chuyển động quay cho riêng trụ đặc, ta có RT '  I  2
Với I là moment quán tính của trụ đặc: MR I    4 2  2mg a  
Từ 1; 2; 3 và 4  2m M T   m  g a 
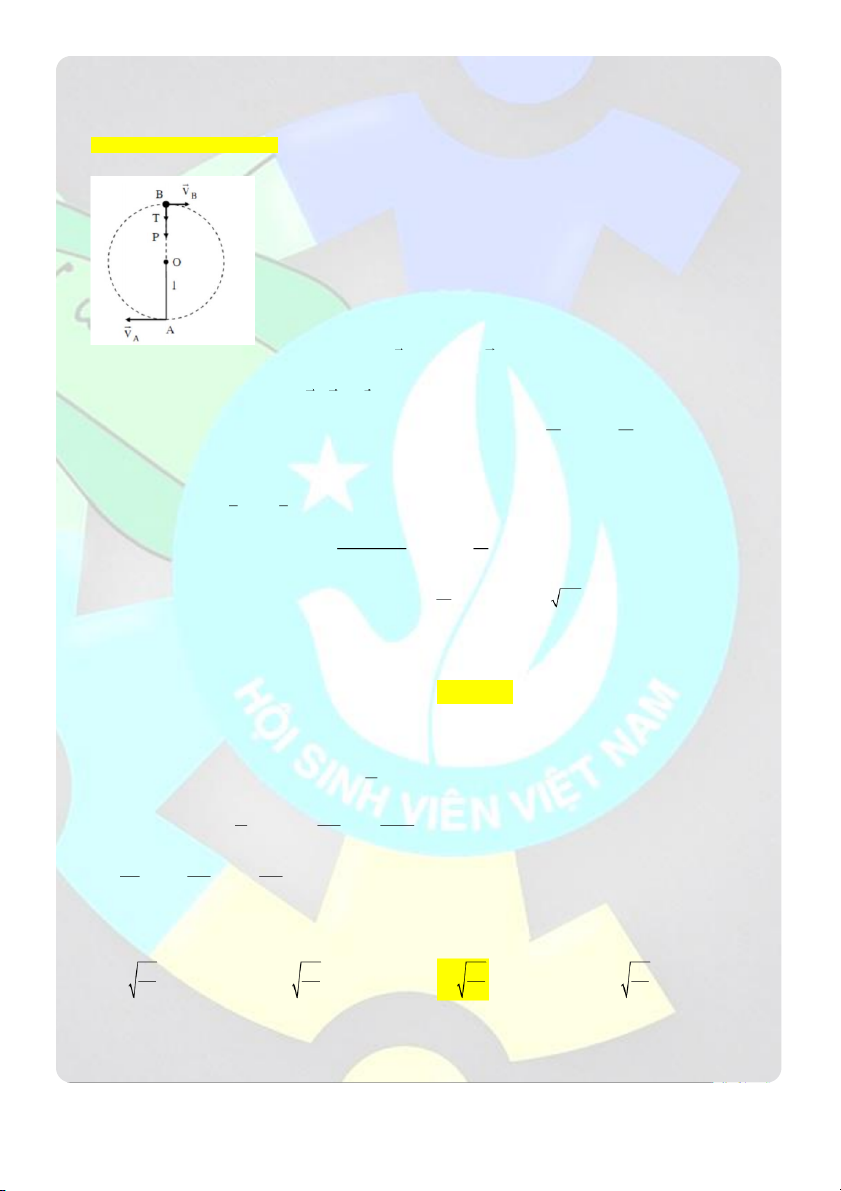
Câu 15: Ở đầu sợi dây OA chiều dài l có treo một vật nặng m . Để vật quay tròn trong mặt phẳng thẳng đứng
thì tại điểm thấp nhất phải truyền cho vật một vật tốc theo phương nằm ngang có độ lớn là ( cho gia tóc trọng trường bằng g) 5 l A. 5gl B. gl C. D. 2gl g Giải
Chọn chiều dương và gốc tọa độ như hình vẽ:
Sức căng T cực tiểu khi vật lên đến điểm cao nhất PT Newton II tại điểm cao 2 v nhất B: B mg T  m min l 1 1 Áp dụng ĐLBT cơ năng: 2 2 mv  mv 2 mgl 2 A 2 B 1 2 1
 mv  mgl  lT 2mgl 2 A 2 min
Để vật quay tròn trong mặt phẳng thẳng đứng thì tại điểm thấp nhất thì điều kiện
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 1 5 2 T
 0  mv  mgl  v  5gl min 2 A 2  v  5gl min
Câu 16: Có 1g khí Hydro H đựng trong một bình có thể tích 5l  . Mật độ phân tử của chất khí đó là: (cho 2  hằng số khí 3
R  8, 31.10  J / kmol.K ; hằng số Boltzmann 2  3 k  1,38.10 J / K ) A. 25 6,022.10 phân tử / 3 m B . 25 5, 522.10 phân tử/ 3 m C. 25 4,522.10 phân tử/ 3 m D . 25 7, 022.10 phân tử/ 3 m Giải
Số phân tử khí của chất khí đó là  . m N n N  .N A A  RT R  R m R Hằng số Boltzmann 23 k  
 1,28.10  J / K  N   N  . A V N k  k A N mR p
Mật độ phân tử của chất khí đó là 25 n'     6,022.10 V k .V kT
Câu 17: Một con lắc đơn có m  120 g  được kéo lệch với phương thẳng đứng một góc 0
  90 , sau đó thả rơi cho g   2
10 m / s  . Lực căng cực đại của dây treo là A. 4,  791 N 
B. 3,997 N
C. 3, 6 N 
D. 4,394 N  Giải Chuyển động c a
ủ vật m là chuyển động tròn đều trên quỹ đạo có bán kính l
Áp dụng định luật bảo toàn cơ năng: 1 2 mgl mgl
W W W W  mv   d t tmax 2
1 cos 1 cos0 
v  2gl cos  cos 0 
Chọn chiều dương hướng xuống và gốc thế năng tại vị trí cân bằng Vật chịu tác d ng c ụ a
ủ các lực: Lực căng dây T  , trọng lực P
Áp dụng định luật II Newton: P  T  ma 2
Chiếu (1) lên chiều dương hình vẽ:   .     .v T P m a T mgcos m n l
(trọng lực đóng vai trò lực hướng tâm)
T  mgcos  2mg cos cos  mg 3cos 2  0   cos 0  0 T    0  T
 3mgcos  3.0,12.10.co 9 s 0  3, 6 N max 0 max  
Câu 18: Có hai bình khí cùng thể tích, cùng nội năng. Bình 1 chứa khí Heli He , bình 2 chứa Nito N . Coi 2 
các khí lí tưởng. Gọi p ,1 p là áp suất tương ứng của bình 1,2. Ta có: 2 3 2 5 A.  B. p  p C. p  p D. p  p 1 p 2 p 1 2 5 1 2 5 1 2 3 Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Vì hai bình khí có cùng thể tích  quá trình đẳng tích
Biến thiên nội năng trong qua trình đẳng tích: m   . i . i  . i U RT nRT  PV  2 2 2
Khí Heli  i  3 và khí Nito  i  5  1 i 1 i U  . n .RT  . 1 1 1 1 PV  2 2   i i i P P i 5 5 Ta có: 2 2 1 1 1 2 U  . n .RT  .PV 1  .      2 2 2 2 1 P 2 P 2 2 i P P i 3 3 2 2 2 1 V
  V  V ;     1 2 U 1 U 2 U  
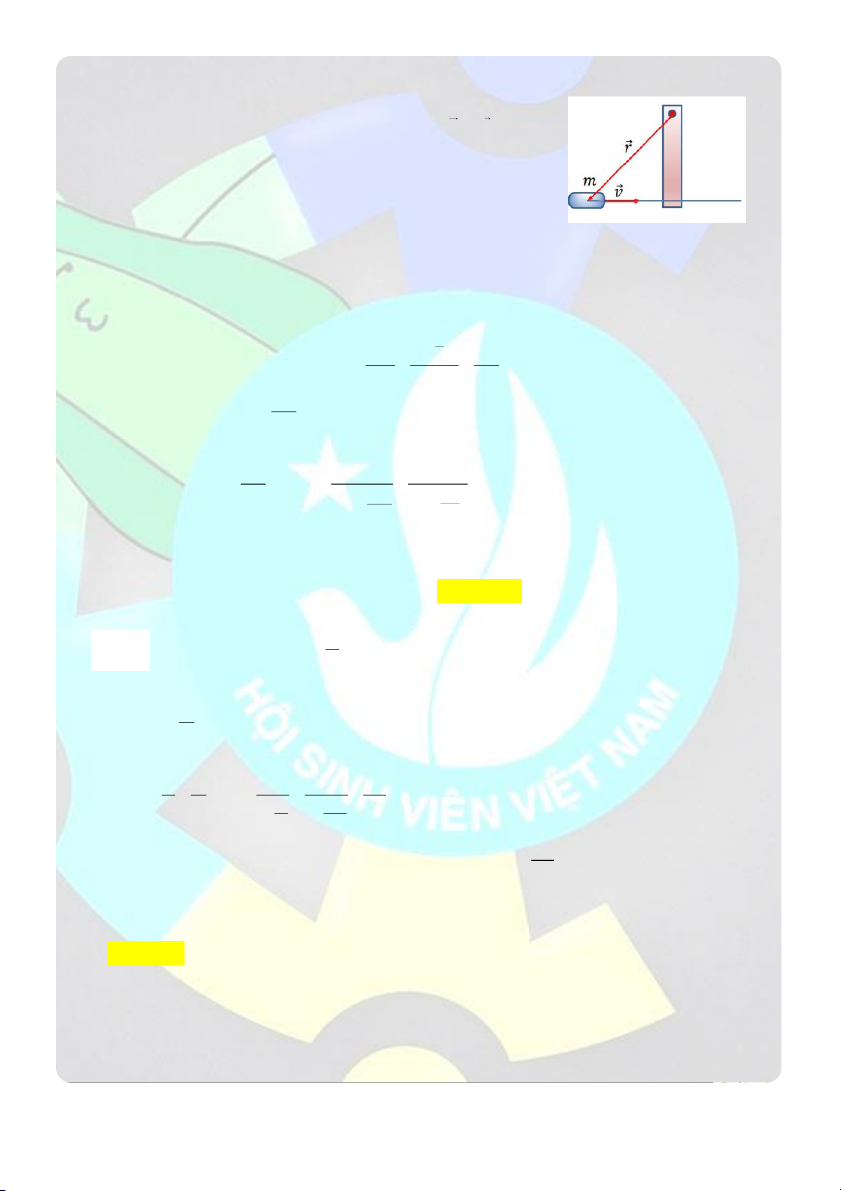
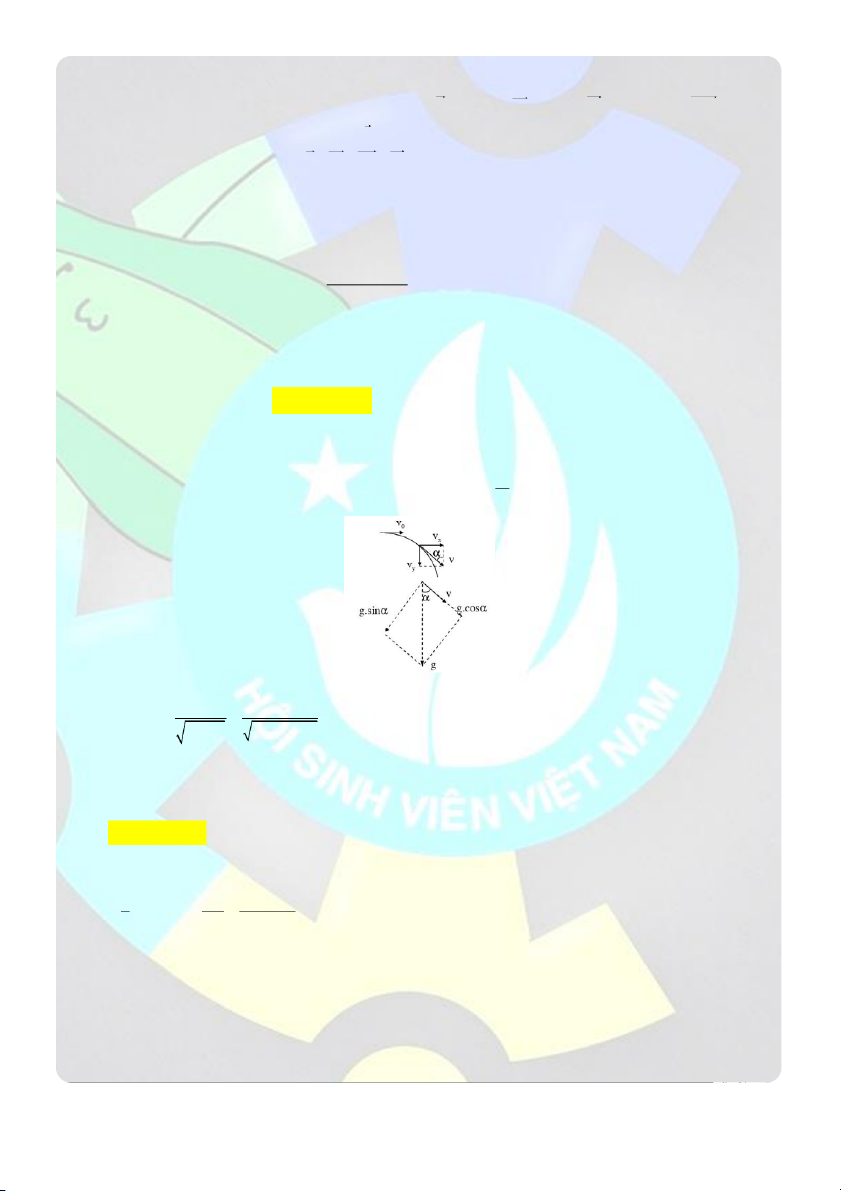
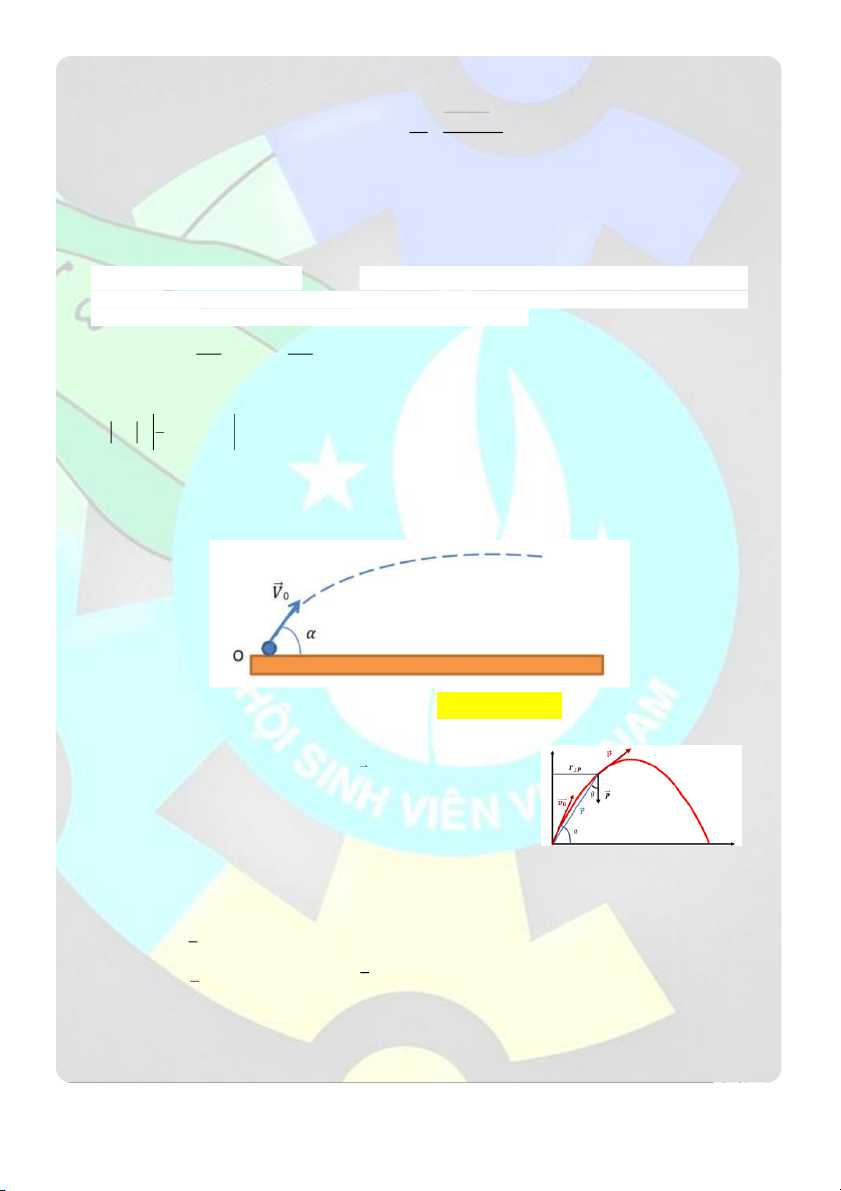
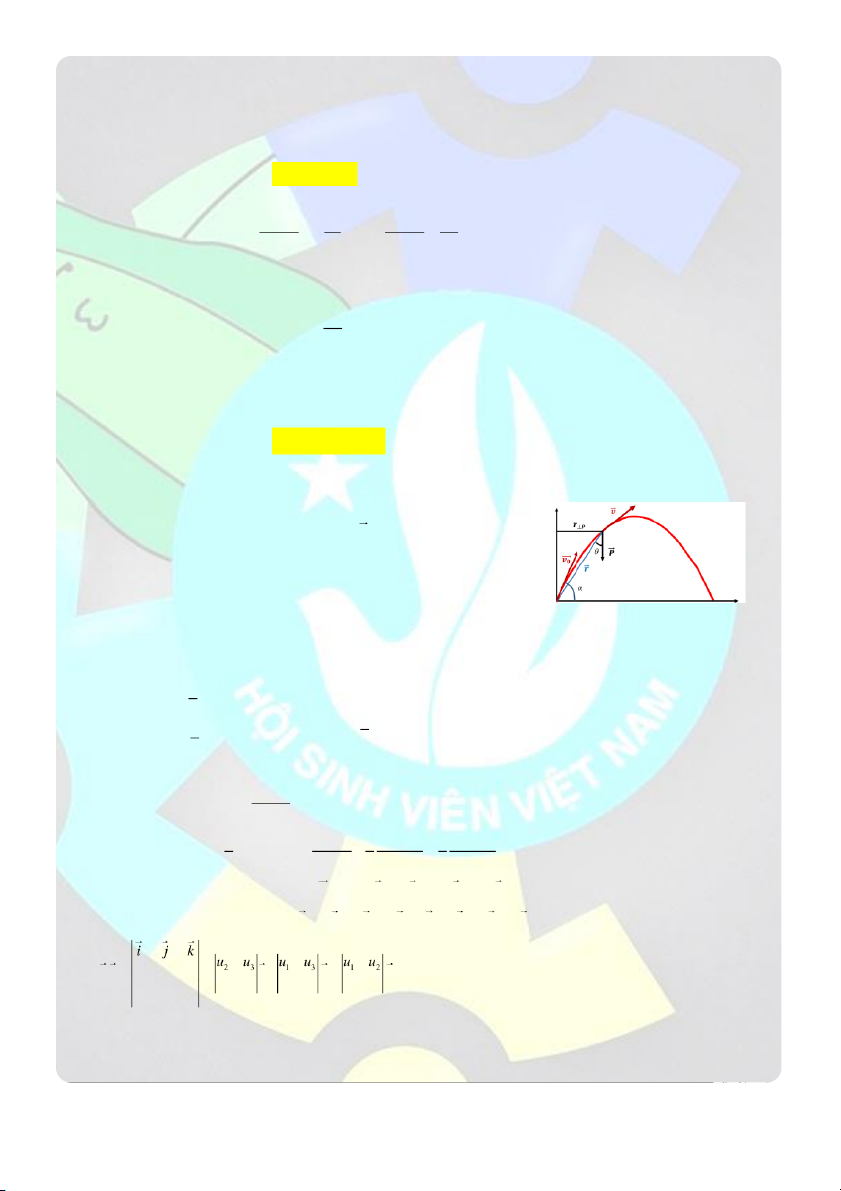
Câu 19: Một chất điểm khối lượng m  0, 2 kg  được ném lên từ O với vận tốc v  7 m / theo phương hợp 0  s 
với mặt phẳng nằm ngang với một góc 0
  30 , bỏ qua sức cản của không khí, cho g   2
9,8 m / s  . Mômen
động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là: A.  2
0,052 kgm / s B.  2
0,758 kgm / s C.  2
0, 218 kgm / s D.  2
0, 488 kgm / s Giải
Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí bắt đầu ném, chiều
dương hướng xuống, cùng chiều với gia tốc g a  0  Gia tốc: x  a   g  y 
v  v  a .t  v .cos   Vận tốc: x 0 x x 0 
v  v  a t  v .sint  gt  y 0 y y 0 
Phương trình chuyển động của chất điểm:  1 2
Ox :x  v t  a t
Ox :x  v .cos .t 0 x x 0  2     1 2 1    2 Oy : y v sin .t gt   0
Oy :y  v  0 t a t  y y 2  2
Tại vị trí cao nhất của chuyển động chất điểm: v . 0  0  . sint v
v sint  gt  t  y 0 g 2 2 2 2 1 v sin 1 v sin  1  Và 2 v sin 0 0 0
y  h  v sin .t 
gt  v sin .   0 0 2 g 2 g 2 g
Động lượng p tại thời điểm t bất kì: 
p t  p i  p j  mv i  mv j x y x y
Xét tích có hướng của hai vector: u  u i  u j  u k và v  v i  v j  v k 1 2 3 1 2 3 . u v  u u u  i  j  k 1 2 3 v v v v v v 2 3 1 3 1 2 v v v 1 2 3
Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới trục z coi như bằng 0
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP r.v  v v  i  j 
k  v y  v x k x y 0  x. y .  y 0 x 0 x y x y 0
Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là:  
L  v .y  v .x  v cos .t .m v sin  gt  mv cos v si n t   gt x y .  1 2 . 0 0 0  0 2    2 2 3 2 1   2 1 0 v sin 0 v sin
 mgv t cos  mgv cos  m
cos  0,758 kgm / 0 0 s 2  2  2 2 g 2g 2
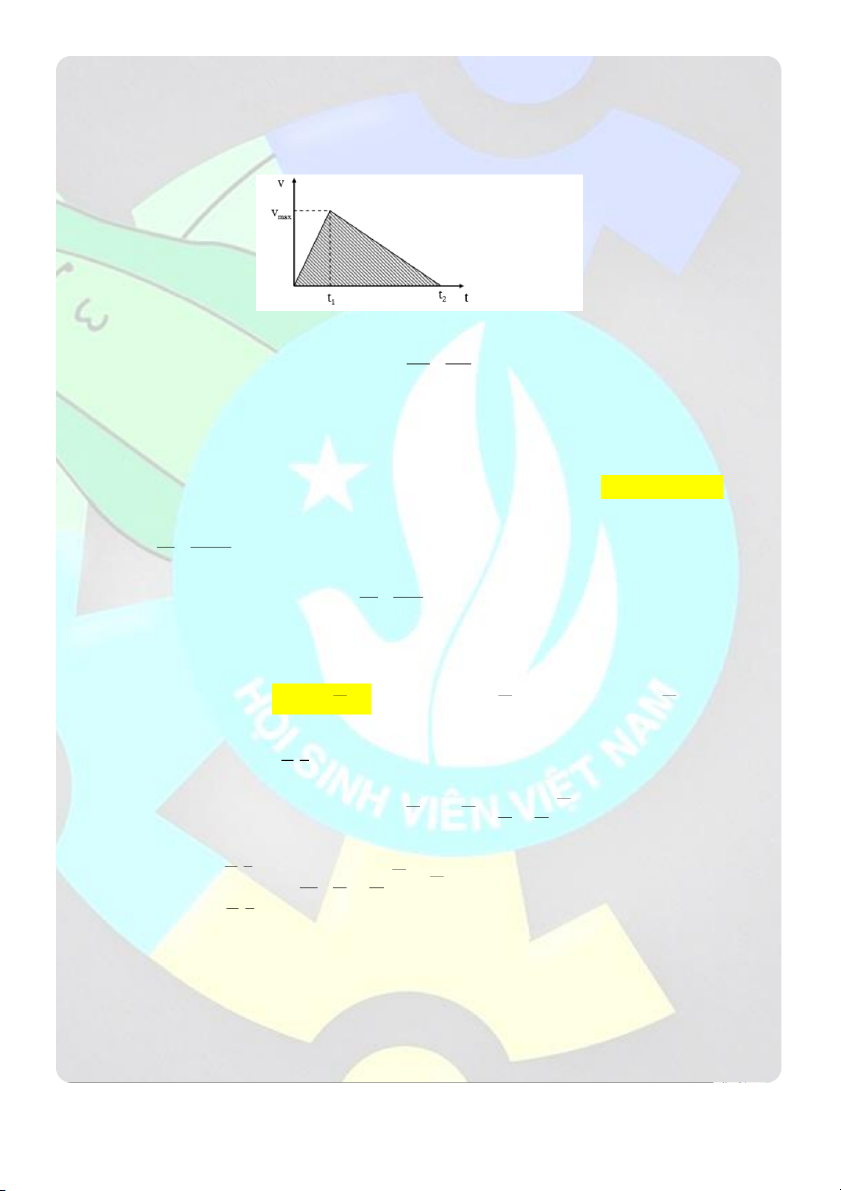
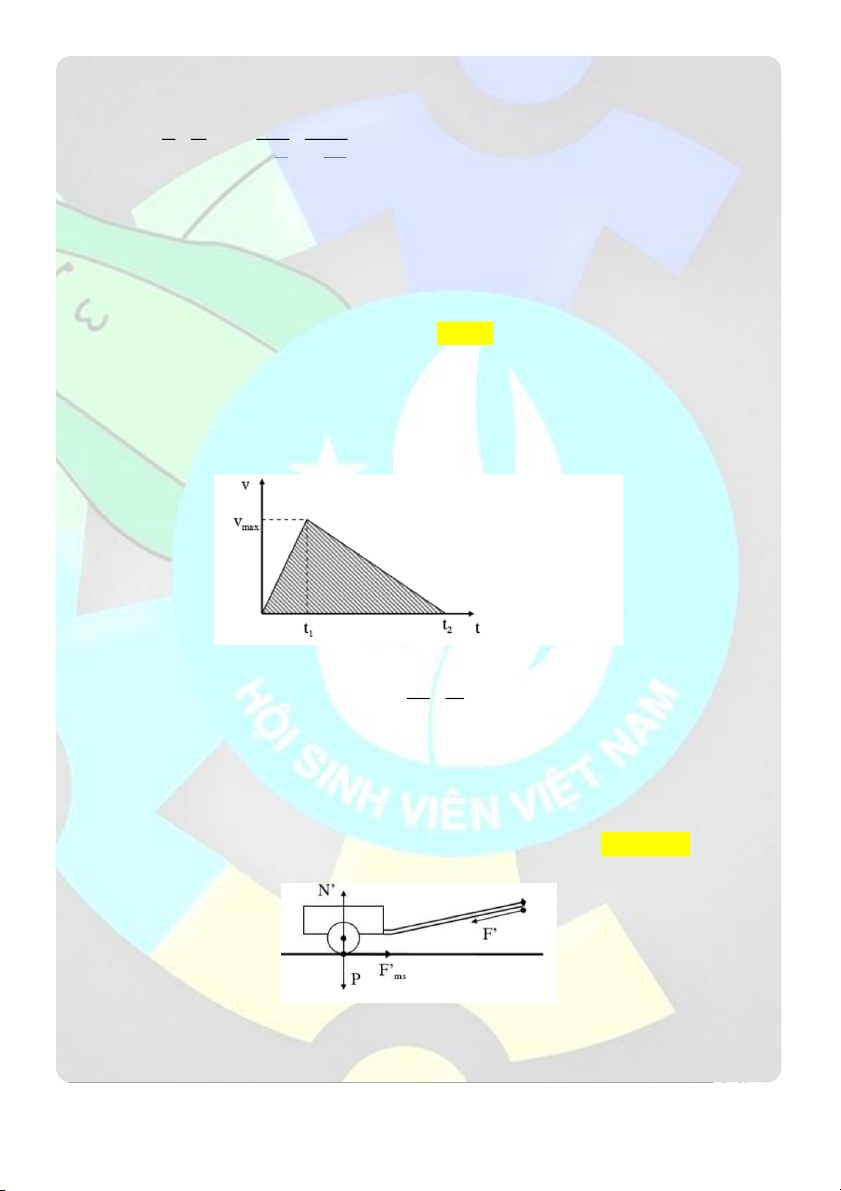
Câu 20: Một tàu điện sau khi suất phát chuyển động trên đường nằm ngang với gia tốc a  0,7 m / s  . 11 giây
sau khi bắt đâu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng hẳn. Hệ số ma sát trên
quãng đường k  0, 01. Cho g   2
10 m / s  . Thời gian chuyển động của toàn bộ tàu là
A. 92,8 s B. 84,8 s C. 8  8  s D. 86, 4  s Giải
Tầu chuyển động theo hai giai đoạn:
Giai đoạn 1: chuyển động với gia tốc a  0,7 2 m /
với thời gian t  11 1 s  1 s 
Giai đoạn 2: chuyển động chậm dần đều với gia tốc a  k.g  0,01.10  0,  2 1 m /
dưới tác dụng cản của lực 2 s 
ma sát trong thời gian t 
Vận tốc lớn nhất của tàu: v
 a .t 0,7.11 7,7 m/ s max 1 1   v 7,7
Tầu chuyển động chậm dần đều trong thời gian: max t     77 s a 0,1 2
Tổng thời gian chuyển động của tầu (kể từ lúc xuất phát đến khi tầu dừng lại) t  t  t  77 11  88 2 1  s
Câu 21: Một phi công thực hiện vòng tròn nhào lộn trong mặt phẳng đứng. Vận tốc của máy bay không đổi
v  900 km / h  . Giả sử rằng áp lực lớn nhất của phi công lên ghế bằng 5 lần trọng lực của người. Lấy g   2
10 m / s . Bán kính quỹ đạo vòng nhào lộn có giá trị bằng:
A. 1562,5m
B. 1584,1 m 
C. 1594, 4 m
D. 1573,3 m  Giải
Áp dụng định luật II Newton cho phi công: mg  N  ma
N là phản lực mà ghế tác dụng lên phi công (bằng và ngược chiều với lực nén của phi công lên ghế).
Áp lực lớn nhất tại điểm thấp nhất
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Tại điểm thấp nhất của vòng nhào lộn, theo phương hướng tâm,   1 được viết thành: 2 v
mg  N  ma  mg  N  m 2 ht 2 R
Theo bài ra, ta có: N  5P  5 2 mg 2 2 v v  mg  5mg  m  R  1562,5 m  R 4 g   
Câu 22: Một con lắc lò xo m  10 g  , dao động điều hòa với đô dời x  8cos 5 t  
cm . Kí hiệu F là lực  2  0
cực đại tác dụng lên con lắc và W là năng lượng của con lắc. Kết luận nào dưới đây đúng: A. F 0,  3 N 2 ,W 0,9.10  
B. F  0,3 N  2 ,W  0,8.10 0 J  0  J
C. F  0,2 N 2 ,W  0,8.10 D. F 0,2 N  2 ,W 0,9.10   0 J  0  J Giải
Theo bài ra, ta có:     2 rad s  k 2 5 / ; 
 k  m  0,01.5 2  2,5K / m m
F  kA  2,5.0,08  0,2 0  N  Ta có:  1 1 2 2  3 W
  kA  .2,5.0,08  8.10 J   2 2
Câu 23: Một đoàn tàu khối lượng 30 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng
12 km / h  . Công suất đầu máy là 200 kW . Gia tốc trọng trường bằng  2
9,8 m / s  . Hệ số ma sát bằng: A. 2 23, 4.10 B. 2 20, 41.10 C. 2 22, 4.10 D. 2 21, 41.10 Giải 10
Đổi v  12km / h  m / s 3 3 P 200.10
Ta có: P  F.v  F    600 N  v 10 3 F 6000 Mà F F mg 6000 N          ms   ms 2 20, 41.10 3 mg 30.10 .9,8
Câu 24: Một thanh chiều dài l  0,9 m  , khối lượng M  
6 kg có thể quay tự do xung quanh một trục nằm
ngang đi qua một đầu của thanh. Một viên đạn khối lượng m  0, 
01 kg  bay theo hương nằm ngang với vận tốc
v  300 m / s  tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc gốc của thanh ngay sau khi viên đạn đập vào đầu thanh là:
A. 2, 429 rad / s
B. 1,915 rad / s
C. 1,144 rad / s
D. 1, 658rad / s Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có mỗi
viên đạn có tốc độ và khối lượng m mang một động lượng p  mv
Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách
từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm
quay tới viên đạn chính là độ dài l
Vậy mômen động lượng trước khi va chạm là: L  r.p.sin  l.p  mvl t
Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với
cùng vận tốc góc  . Vậy moomen quán tính của hệ vật sau va chạm:
L  I   I  s 1 2
Với I là moment chất điểm (viên đạn) đối với trục quay 2 I  ml 1 1 2  l  2 M   2 Ml '  2  Ml
I là moment quán tính của thanh mảnh    2 I 2 12 12 3 2  Ml 
Hay L  I  I   ml     s   2 1 2 3  
Áp dụng định luật bảo toàn động lượng 2   2 Ml mvl v
L  L  mvl  ml      
 1,658 rad / s t s   2    3  2 Ml   ml  l 1 M    3  3m 
Câu 25: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 50 kW . Nhiệt độ của nguồn nóng là 0
127 C , nhiệt độ của nguồn lạnh là 0
31 C. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:
A. 12200 kJ 
B. 12600 kJ 
C. 12500 kJ 
D. 12300 kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 50 625 Hay 2  1   Q    kJ 1   T Q T 304 2 3 1 1 1 1 T 400 1 625
 Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút: '
Q  Q .t  .60 12500 1 1 kJ 3
Câu 26: Thả rơi tự do 1 vật nhỏ tư độ cao h  19,6 m . Quãng đường mà vật rơi được trong 0,1 giây cuối của
thời gian rơi là: (cho g   2 9,8 m / s  )
A. 1,911m B. 1,  711 m C. 1,311m D. 1,511m Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 Thời gian rơi của vật: h t  2 s  g
Quãng đường vật rơi trong 0,1 giây cuối là: 1 1 s   s  s
 gt  g t 
 g t  t    m t t  2 1 0,1  0,12 2 2 1,911 0,1   2 2 2   1 2
Công thức tổng quát cho quãng đường rơi trong n giây cuối là h s g t  t n2 2      t  2   với g
Câu 27: Một khối khí ôxy 
bị nung nóng từ nhiệt độ 240 K  đến 0 267 2 O 
C . Nếu vận tốc trung bình của phân
tử ôxy lúc đầu là v thì lúc sau là: A. 1, 35v B. 1, 55v C. 1, 5v D. 1, 6v Giải
Công thức tính vận tốc trung bình của phân tử khí: 8kT v  m  8kT1   1v  m v T 267  273 Hay 2 2      1,5  8kT v T 240 1 1 2  2 v  m
Câu 28: Một con lắc toán có sợi dây l  1m  , cứ sau t  0,8 phút thì biên độ giao động giảm 2 lần. Giảm
lượng loga của con lắc dố bằng giá trị nào sau đây ( cho g   2 9,8 m / s  ) A. 2 3, 489.10 B. 2 2,898.10 C. 2 2,701.10 D. 2 3, 292.10 Giải
Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:
F  F  kx  rv C
Phương trình cơ bản của chuyển động trong trường hợp này là ma  kx  rv 2 2 Hay: d x dx d x r dx k m  r  kx    x  0 1 2 2 dt dt dt m dt m Đặt r   (hệ số tắt dần) 2m 2 d x dx
Phương trình 1 trở thành 2 x  2  x  0 2 2 0 dt dt
2 gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi    , nghiệm phương trình 0 này có dạng:  t x     0 A e cos  t 
Đây là biểu thức độ dời của dao động tắt dần. Hằng số  gọi là tần số của dao động tắt dần: 2 2      0 2 2 2
Chu kỳ T của dao động tắt dần là: T    2 2     g 2 0   l 2
Giảm lượng loga của con lắc:   T   .  2 2    0
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP x g 9,8   t 1   1 Theo bài ra, ta có: . .48  e   e     0,01444 và 2     9,8 A 2 2 0 l  1 0 2 2 2  . 0,01444. 2,898.10     2 2 2    9,8 0,0144 0
Câu 29: Một mol khí hidro nguyên tử được nung nóng đẳng áp, thể tích tăng gấp 2 lần. Entrôpie của nó biến
thiên một lượng bằng ( cho hằng số khí R  8,31 J / mol.K  )
A. 14,4 J / K 
B. 15, 9  J / K 
C. 14,9 J / K 
D. 15, 4 J / K  Giải Độ biến thiên Entropy: dQ dS  T i 2 Qúa trình đẳng áp:  
Q  nC dT  n RdT p 2
Thay vào và lấy tích phân từ trạng thái 1 ứng với 1
T đến trạng thái 2 ứng với 2 T T2 i  2 dT i  2  2 T i 2 2 T  S   n R  n RlnT  n Rln  2 T 2 T 2 T T 1 1 1 T V
Điều kiện của quá trình đẳng áp  p  const : 2 2  1 T 1 V i  2 2 V  S   n Rln
14, 4J / K  (khí H : i  3) 2 2 1 V
Câu 30: Một động cơ nhiệt làm việc theo chu trình Carnot với nhiệt độ nguồn nóng là 0
100 C . Trong mỗi một
chu trình tác nhân nhận của nguồn nóng một nhiệt lượng 10 kcal  và thực hiện công15kJ  . Nhiệt độ của nguồn lạnh là:
A. 236,72 K 
B. 235, 72  K 
C. 239,72 K 
D. 238, 72  K  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' T A' A' 15 Hay 2 2      1    1  T  T 1  373. 1    239, 34 2 1 K    T Q T Q Q    10.4,186 1 1 1 1 1 
Câu 31: Ở thời điểm ban đầu một chất điểm có khối lượng m  
1 kg có vận tốcv  19 m / . Chất điểm chịu 0  s
lực cản F  rv ( biết r  ln2 , r  ln2 là vận tốc chất điểm). Sau 1,8s vận tốc của chất điểm là: e
A. 4,656m / s
B. 4, 256 m / s
C. 5, 456 m / s
D. 5,056 m / s Giải Lực cản:   ' dv F ma mv  m e dt
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP Mặt khác: dv dv r F  r  v  m  r  v    dt e dt v m v t r  Lấy tích phân: t dv r v r
  dt  ln
  t  v  v . m e  5,456 m /   0  s v m v m v 0 0 0
Câu 32: Một khẩu pháo có khối lượng M  480kg bắn một viên đạn theo phương làm với mặt ngang một góc 0
  60 . Khối lượng của viên đạn m  5kg , vận tốc đầu nòng v  400m / s . Khi bắn bệ pháo giật lùi về phía
sau một đoạn s  54 cm . Lực cản trung bình tác dụng lên quả pháo có giá trị: A. 2  129 N  B. 1  929 N  C. 2  229 N  D. 2  029 N  Giải
Theo định luật bảo toàn động lượng thì vận tốc giật lùi c a ủ khẩu pháo là: 0 . m . v cos 5.400.c 60 os 25 V       m / s  M 480 12
Dấu " " chứng tỏ pháo giật lùi, ngược chiều dương) 2 Áp dụng công thức: 2 2 V
V V  aS  a      2 ' 2
4,0187 m / s  2S
Lực cản trung bình tác dụng lên quả pháo: F  Ma   4,0187.480 1929 N C  
Câu 33: Một con lắc toán có sợi dây l  65m . Biết rằng sau thời gian   6 phút, nó mất 99% năng lượng.
giảm lượng lôga của con lắc nhận giá trị nào dưới đây (cho g   2 9,8 m / s  ) A. 2 0,975.10 B. 2 1,125.10 C. 2 1, 035.10 D. 2 1, 065.10 Giải
Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:
F  F  kx  rv C
Phương trình cơ bản của chuyển động trong trường hợp này là ma  kx  rv 2 2 Hay: d x dx d x r dx k m  r  kx    x  0 1 2 2 dt dt dt m dt m Đặt r   (hệ số tắt dần) 2m 2 Phương trình  d x dx 1 trở thành 2 x  2  x  0 2 2 0 dt dt
2 gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi    , nghiệm phương trình 0 này có dạng:  t x     0 A e cos  t 
Đây là biểu thức độ dời của dao động tắt dần. Hằng số  gọi là tần số của dao động tắt dần: 2 2      0 2 2 2
Chu kỳ T của dao động tắt dần là: T    2 2     g 2 0   l 2
Giảm lượng loga của con lắc:   T   .  2 2    0  g 9,8 49 Theo bài ra, ta có: 2   . t  2   .6.60 3   e  0,01 e
 0,01   6,396.10 và 2      0 l  65 325 0
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 3 2 2    .  6,396.10 . 1,035.10 2 2    49 6,396.10 2 3 0 325
Câu 34: Hai khối khí 2
O và H có cùng mật độ số hạt. Nhiệt độ của khối khí 2 2 O là 0
120 C , nhiệt độ của khối khí H là 0 60 2 C . Áp suất của 2
O và H theo thứ tự là 2 1 P và 2 P . Ta có:
A. P  0,98P
B. P  1,18P
C. P  0,88P
D. P  1, 28P 1 2 1 2 1 2 1 2 Giải m
Số phân tử khí của chất khí đó là N  . n N  .N A A  Hằng số Boltzmann RT R 2  3    1,28.10  /  R m     . R k J K N N A V N k  k A N mR p
Mật độ phân tử của chất khí đó là n'    V k  .V kT Vì hai khối khí  áp suất thay đổi 2
O và H có cùng mật độ số hạt và nhiệt độ thay đổi 2  Qúa trình đẳng tích P T 120 273
Áp dụng PT trạng thái quá trình đẳng tích: 1 1    P 1,18 1 2 P P T 60  273 2 2
Câu 35: Một bánh xe có bán kính R  12 c 
m lúc đầu đứng yên sau đs quay quanh trục cảu nó với gia tốc góc    2
3,14 rad / s . Sau giây thứ nhất gia tốc toàn phần của một điểm trên vành bánh là: 2 2 2 2
A. 120,17 cm / s 
B. 126,17 cm / s 
C. 130,17cm / s 
D. 124,17 cm / s  Giải
Sau giây thứ nhất, vận tốc góc và vận tốc dài c a
ủ một điểm tren vành bánh là:
  .t  3,14.1 3,14 rad / s  và v R 3,14.0,12 0,3768m / s
Gia tốc tiếp tuyến có giá trị không đổi còn gia tốc pháp tuyến lúc này: a   R    2 .
3,14.0,12 0,3768 m / s và 2 2 a   R    2 .
3,14 .0,12 1,18352 m / s n  t  Gia tốc toàn phần: 2 2 a  a  a  m s t n  2 124,17 / 
Câu 36: Một chất điểm bắt đầu trượt từ đỉnh mặt phẳng nghiêng góc  so với phương nằm ngang (xem hình
vẽ). Hệ số ma sát giữa vật và mặt phẳng nghiêng là k ; khối lượng của vật là m ( lấy g   2
9,81 m / s  ). Cho m  kg k  h    0 2,5 , 0, 2,
8 m ,  30 . Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O là:
A. 62,107 Nm
B. 52, 234 Nm
C. 45,652  Nm
D. 55, 525 Nm Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP Chọn hệ tr c
ụ tọa độ Oxy như hình vẽ, chiều dương cùng chiều chuyển động của vật Vật chịu tác dụng c a
ủ các lực: trọng lực P , phản lực N và lực ma sát f ms
Áp dụng định luật II Newton, ta có: P  N  f  ma   1 ms
Chiếu 1 lên trục Ox : N  P 0  N  Pcos  mgcos n .   Chiếu  P sin f
1 lên trục Oy : P  f ma  P. ms sin  f ma  a  t ms ms m
Mà f  k.N  k.mgcos  F  mg sin  kcos ms  
Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O chính là công của lực F tác dụng lên điểm O
A  F h cos  mg  sin  k cos  0 . . . . . h co 3
s 0  55,525 N F  
Câu 37: Một vật khối lượng m bắt đầu trượt không ma sát từ đỉnh một mặt cầu bán kính R  2 m xuống dưới.
Vật rời khỏi mặt cầu với vị trí cách đỉnh mặt cầu một khoảng là:
A. 0,807m
B. 0,737 m
C. 0,667 m
D. 0,877 m Giải
Chọn chiều dương cùng chiều chuyển động c a ủ vật Vật chịu tác dụng c a
ủ các lực: trọng lực P , phản lực N
Áp dụng định luật II Newton, ta có: P  N  ma 1
Vì chuyển động tròn nên gia tốc ở đây đóng vai trò là gia tốc hướng tâm 2 2
Chiếu 1 lên phương chuyển động: v v
Psin  N  ma  m
 N  Psin m ht R R R  h 
Theo hình vẽ, ta có: sin  R
Khi vật di chuyển xuống dưới thì thế năng của vật giảm dần và biến thành động năng. Như vậy độ biến thiên 2
thế năng phải bằng độ biến thiên động năng của vật: W 
W  mgR  mg R  h   mv 2   mv  2mg h  t d 2 2  
Để vật rời khỏi mặt cầu thì  0 mv     0 R h   2   0 R N Psin mg mg h  h    0,667m  R R 3
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 38: Một chất điểm dao động điều hòa với chu kì 1, 4 s  và biên độ 8cm . Vận tốc chất điểm trên tại vị trí 1
mà ly độ bằng biên độ bằng giá trị nào dưới đây: 2 A. 0,  311 m / s B. 0,  321 m / s C. 0,  331 m / s D. 0,  341 m / s Giải
Áp dụng phương trình về mối liên hệ của , A x, v : 2 2  v  2  A  2 2 2 2 2 2 2 2 A  x 
 v  A  x  A   0,08  0,04  0,31     1 m/ s    T  2  1, 4
Câu 39: Một ống thủy tinh nhỏ khối lượng M  130 g  bên trong có vài giọt ête được đậy bằng 1 nút cố định
có khối lượng m  10 g . Ống thủy tinh được treo ở đầu một sợi dây không giãn, khối lượng không đáng kể,
chiều dài l  65cm (hình vẽ). Khi hơ nóng ống thủy tinh ở vị trí thấp nhất, ête bốc hơi và nút bật ra. Để ống có
thể quay được cả vòng xung quanh điểm treo O , vận tốc bật bé nhất của nút là: (Cho g   2 10 m / s  ) A. 72,  411 m / s B. 70,  711 m / s
C. 74,111 m / s D. 79,  211 m / s Giải
Tại vị trí A, vận tốc tại đây phải đủ lớn để dây thẳng đứng và căng đét  T  0 2 2 v v A A
P T  m  T  m
 mg  0  v  gl A l l
Vận tốc nhỏ nhất tại A để ống quay tròn: v  gl Amin
Đối với ống thủy tinh:
Áp dụng định luật bảo toàn cơ năng: 1 2 1 2 1 2 1 2
W  W W  MV  Mv  Mgh  MV 
Mv  Mg 2l B dB tB 2 2 B 2 2 B 2 2
 V  v  4gl B
Vận tốc tối thiểu để đạt đỉnh: 2 v 
gl  V  gl  4 gl  5 gl  V  5 gl B min
Áp dụng định luật bảo toàn động lượng: MV M 5 gl min mv  MV  v    74,111 m s min min min  /  m m
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 40: Một khối khí ôxy 
biến đổi trạng thái sao cho khối lượng riêng của nó giảm 1,5 lần và tốc độ trung 2 O 
bình của các phân tử giảm 1,5 lần. Trong quá trình đó, áp suất mà khí ôxy tác dụng lên thành bình thay đổi như thế nào? A. Giảm 3, 375 lần
B. Giảm 1, 225 lần
C. Giảm 2, 25 lần
D. Giảm 1,837 lần Giải Theo bài ra, ta có: pV n   const RT p V p V p V T Ở trạng thái 1: 1 1 n  và ở trạng thái 2: 2 2 n  2 1 2   . R p V T 1 T RT2 1 2 1 8
Công thức tính vận tốc trung bình của phân tử khí: kT v  m  8k 1 T v  2  1  m  v  T m   V  Hay 2 2 V      và 1 1 1 2     8 T      1 v  1 T k m V V 2  2 2 2 1 2 v  m 2 p V T  v  8 2 1 2 2 2   .  .    p V T  v   27 1 2 1 1 1
Câu 41: Một vệ tinh có khối lượng m  150kg  chuyển động trên quỹ đạo tròn bán kính 6
r  7, 4.10 m  quanh
Trái Đất. Cho khối lượng trái đất 24
M  5,98.10  k 
g . Hằng số hấp dẫn 1  1 G   2 2 6,67.10
N.m / kg . Tốc độ vệ
tinh trên quỹ đạo đó là:
A. 7,042 km / s
B. 6,742km / s
C. 7,342km / s
D. 6, 442 km / s Giải
Lực hấp dẫn giữa trái đất và vệ tinh là lực gây ra gia tốc hướng tâm cho vệ tinh nên: 2 GMm v 2 GM GM F 
 F  ma  m  v   v 
 7342m / s  7,342km / s hd ht ht  2 r r r r
Câu 42: Một máy nhiệt lí tưởng làm việc theo chu trình Carnot, sau mỗi chu trình thu được 600 calo từ nguồn nóng có nhiệt độ 0
127 C . Nhiệt độ nguồn lạnh là 0
27 C . Công do máy sinh ra sau một chu trình
A. 627,9 J 
B. 647,9 J 
C. 637,9 J 
D. 657,9 J  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  T1
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   Q1
Với A' là công sinh ra trong mỗi chu trình và Q là nhiệt lượng nhận được trong mỗi chu trình 1 T A'  T   300  Hay 2 2  1 
 A '  Q 1  600.4,186. 1    627,9 1    J T Q T    400  1 1 1
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 43: Có 1g khí Hidro H đựng trong một bình có thể tích 6 lít. Mật dộ phan tử của chất khí đó là ( cho 2  hằng số khí 3
R  8, 31.10  J / kmol.K ; hằng số Boltzmann 2  3 k  1,38.10 J / K  ) A. 25 3,158.10 phân tử/ 3 m B. 25 4,518.10 phân tử/ 3 m C. 25 6,018.10 phân tử/ 3 m D. 25 5,018.10 phân tử/ 3 m Giải
Số phân tử khí của chất khí đó là  . m N n N  .N A A  RT R  R m R Hằng số Boltzmann 23 k  
 1,28.10  J / K  N   N  . A V N k  k A
Mật độ phân tử của chất khí đó là N mR 25 n'    5,018.10 phân tử/ 3 m V  . k V
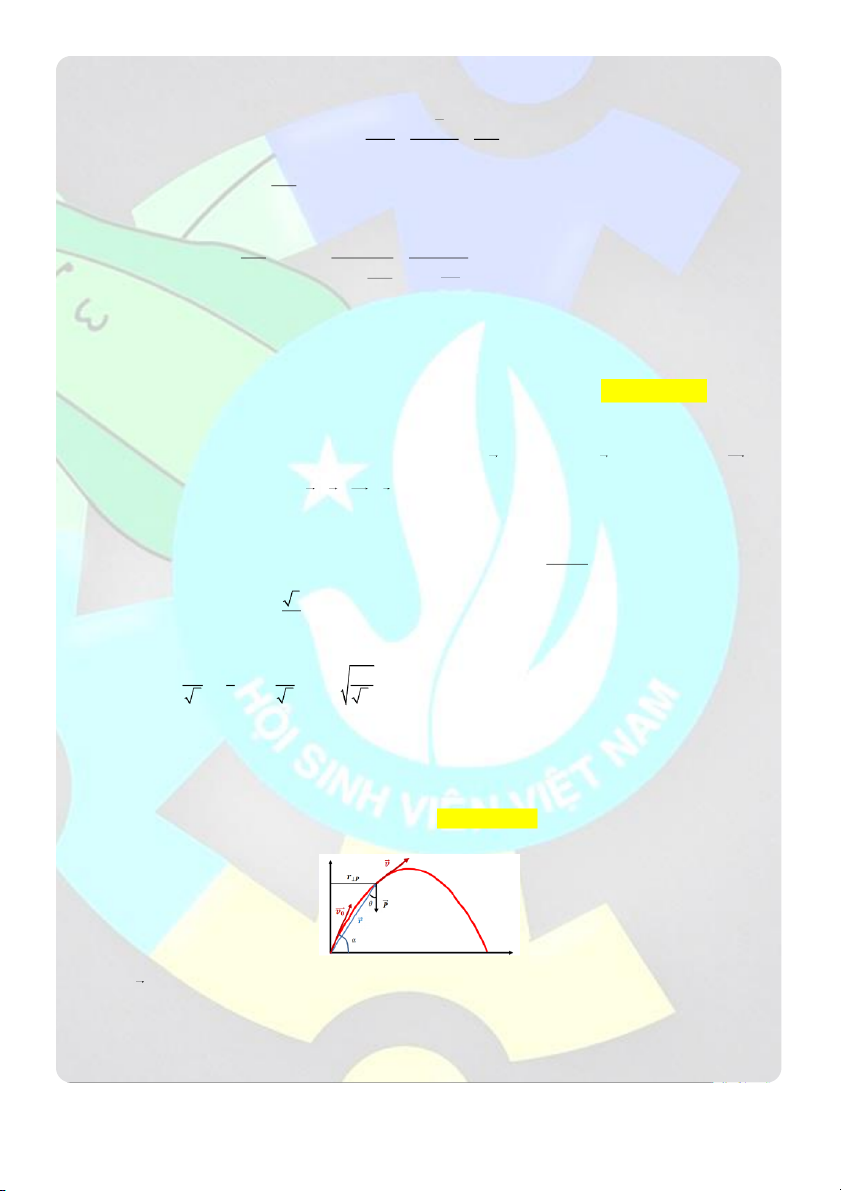
Câu 44: Một chất điểm khối lượng m  0, 
3 kg được ném lên từ O với vận tốc v  9 m / theo phương hợp 0  s
với mặt phẳng nằm ngang một góc 0   30
– bỏ qua sức cản của không khí, cho g   2
9,8 m / s  . Mômen động
lượng của chất điểm đối với O tại vị trí cao nhất của chuyện động chất điểm là: A.  2
3, 226 kgm / s B.  2
2, 416 kgm / s C.  2
2,956 kgm / s D.  2
2,146 kgm / s Giải
Chọn hệ trục Oxy như hình vẽ. Gốc tọa
độ tại vị trí bắt đầu ném, chiều
dương hướng xuống, cùng chiều với gia tốc g a  0 Gia tốc:  x  a    g y 
v  v  a .t  v .cos Vận tốc:  x 0 x x 0  v
  v  a t  v .sint  gt y 0 y y 0 
Phương trình chuyển động của chất điểm:  1 2
Ox :x  v t  a t
Ox :x  v .cos .t 0 x x 0  2     1 2 1    2 Oy : y v sin .t gt   0
Oy :y  v  0 t a t  y y 2  2
Tại vị trí cao nhất của chuyển động chất điểm: v . 0  0  . sint v
v sint  gt  t  y 0 g 2 2 2 2 1 v sin 1 v sin  1 v sin  Và 2 0 0 0
y  h  v sin .t 
gt  v sin .   0 0 2 g 2 g 2 g
Động lượng p tại thời điểm t bất kì: 
p t  p i  p j  mv i  mv j x y x y
Xét tích có hướng của hai vector: u  u i  u j  u k và v  v i  v j  v k 1 2 3 1 2 3 . u v     1 u 2 u 3 u i j k 2 v 3 v 1 v 3 v 1 v 2 v 1 v 2 v 3 v
Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới trục z coi như bằng 0
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP r.v  v v  i  j 
k  v y  v x k x y 0  x. y .  y 0 x 0 x y x y 0
Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là:  
L  v .y  v .x  v cos.t.m v sin  gt  mv cos v si n t   gt x y .  1 2 . 0 0 0  0 2    2 2 3 2 1 2 1   0 v sin 0 v sin
 mgv t cos  mgv cos  m
cos  2, 416 kgm / 0 0 s 2  2  2 2 g 2g
Câu 45: Một khối ôxy  ở nhiệt độ 0 20 2 O 
C . Để nâng vận tốc căn quân phương của phân tử lên gấp đôi, nhiệt độ của khí là: A. 0 899 C B. 0 919 C C. 0 929 C D. 0 889 C Giải 3
Công thức tính vận tốc căn quần phương: kT v 
(với k là hằng số Boltzmann) C m  m n      R 3RT Mặt khác: k   v  C N   A   . m N A    3R 1 T   1 v 2     Ta có: 1 v 1 T v2   
 T  T    1172 K  t  899 C 2 1   0 2  3RT 2 v 2 T  1 v  2  2 v   
Câu 46: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 45 kW . Nhiệt độ của nguồn nóng là 0
127 C , nhiệt độ của nguồn lạnh là 0
31 C. Nhiệt lượng tác nhân nhận ở nguồn nóng trong một phút có giá trị:
A. 10950 kJ 
B. 11050 kJ 
C. 11250 kJ 
D. 11350 kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 45 Hay 2  1   Q    187,5 kJ 1   T Q T 304 2 1 1 1 1 T 400 1
 Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút: '
Q  Q .t  187,5.60  11250 1 1 kJ 
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 47: Một ô tô khối lượng m  550 kg chuyển động thẳng đều xuống dốc trên một mặt phẳng nghiêng, góc
nghiêng  so với mặt đất nằm ngang có sin  0,00872;cos  0,9962 . Lực kéo ô tô bằng F  55  0 N , cho k  g   2
10 m / s . Hệ số ma sát giữa ô tô và mặt đường là: A. 0,158 B. 0,188 C. 0, 208 D. 0,198 Giải
Chọn trục Oxy như hình vẽ. Chiều dương cùng chiều chuyển động với ô tô
Ô tô chịu tác dụng của các lực: lực kéo F của động cơ ô tô, trọng lực P , phản lực tiếp tuyến N của mặt
đường và lực ma sát của mặt đường f ms
Áp dụng định luật II Newton, ta có F  P  N  f  0 (vì ô tô chuyển động thẳng đều) ms
Chiếu phương trình này nên phương chuyển động của ô tô, ta được: F  f  Psin  0 k ms  
 F  f Psin  k . F mgsin k
N  Psin  kmgcos mgsin  k   0,188 k ms mgcos
Câu 48: Có ba vật đồng chất, cùng khối lượng: cầu đặc, trụ đặc và trụ rỗng cùng được thả lăn không trượt từ đỉnh
một mặt phẳng nghiêng. Vật nào tới chân mặt phẳng nghiêng lớn nhất: A. Cả 3 vật B.Trụ đặc C.Trụ rỗng D. Quả cầu đặc Giải 2
Moment quán tính của trụ đặc: mR I  2
Moment quán tính của trụ rỗng: 2 I  mR 2 2
Moment quán tính của cầu đặc: mR I  5 2 2 2 Vì mR mR 2 I   I 
 I  mR  quả cầu đặc tới chân mặt phẳng nghiêng nhanh nhất 5 2
Câu 49: Cho một chu trình Carnot thuận nghịch, đột biến trên entropi trong quá trình đẳng nhiệt có hệ số là
S  1kcal / K  ; hiệu suất nhiệt độ giữa 2 đường đẳng nhiệt là T
  300K ;1cal  4,18 J  . Nhiệt lượng đã
chuyển hóa thành công trong chu trình đang xét là: A. 5 12,54.10 J  B. 5 12,04.10  J  C. 5 13,54.10  J  D. 5 11, 04.10  J  Giải
Nhiệt lượng đã chuyển hóa thành công trong chu trình đang xét là 3 5 A  S  . T
  10 .300.4,18  12,54.10  J 
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 50: Thả rơi tự do một vật nhỏ từ độ cao h  17, 6 m . Thời gian cần thiết để vật đi hết 1m  cuối của độ
cao h là: ( cho g   2 9,8 m / s ) A. 2 5, 263.10  2  2 2  s 
B. 5, 463.10 s
C. 5,863.10  s
D. 4,863.10 s  Giải 2h 2.17,6
Thời gian rơi của vật: t   1  ,895 s g 9,8 2h ' 2.1
Thời gian để vật đi được 1m đầu: t '    0,45 s g 9,8 2.16, 6
Thời gian để vật đi hết 1m cuối: 2 t " t t 1,895 5, 463.10      s tong 16,6   9,8
Câu 51: Một đoàn tàu khối lượng 50 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng 3  6 km / 
h . Công suất đầu máy là 245 kW  . Gia tốc trọng trường bằng  2
9,8 m / s . Hệ số ma sát bằng: A. 2 5,000.10 B. 2 5,997.10 C. 2 3, 006.10 D. 2 2,009.10 Giải 3 P 245.10
Ta có: P  F.v  F    24500 N  v 10
Mà F  F  mg ms F 24500 Hệ số ma sát: ms     0,05 3 mg 9,8.50.10
Câu 52: Một đĩa trong khối lượng M  155kg  đỡ một người có khối lượng m  5 
1 kg . Lúc đầu người đứng
ở mép và đĩa quay với vận tốc góc   10 (vòng/phút) quanh trục đi qua tâm đĩa. Vận tốc góc của đĩa khi người 1
đi vào đúng tâm của đĩa là ( coi người như 1 chất điểm)
A. 2,006rad / s
B. 2, 276 rad / s
C. 1, 736 rad / s
D. 0,926 rad / s Giải
Bài này áp dụng định luật bảo toàn động lượng
Giai đoạn trước: mômen động lượng của hệ sẽ là: L  I   I  truoc dia 1 nguoi 1 2
Mômen quán tính đĩa đặc như đã biết là: MR I  dia 2
Mômen quán tính của người (chất điểm) là: 2 I  mR nguoi 2  MR  2  L  mR  truoc   1  2 
Giai đoạn sau: để ý là khi người đi vào tâm đĩa thì coi như khoảng cách từ người tới tâm đĩa là 0. Điều này kéo
theo mômen quán tính của người với tâm đĩa coi như bằng 0. 2
Moment động lượng của hệ lúc này là mR L  I    sau dia 2 2 2 2 2  MR  mR
Áp dụng định luật bảo toàn động lượng: 2 L  L   mR      truoc sau 1 2  2  2
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 0,5M  m 155.0, 5  51       .  1,736 rad / 2  s 0,5M 0,5.155 3
Câu 53: Giả sự lực cản của nước tác dụng lên xà lan tỉ lệ với tốc độ của xà lan đối với nước. Một tàu kéo cung
cấp công suất P  250mã lực ( 1 mã lực  74 
6 W ) cho xà lan khi chuyển động với tốc độ v  0,25 m / . 1  s 1
Công suất cần thiết để kéo xà lan với tốc độ v  0,75 m / là 2  s A. 2240 mã lực B. 2220 mã lực C. 2250 mã lực D. 2270 mã lực Giải
Lực cản của nước tỉ lệ với tốc độ của xà lan với nước: 2
F  kv k  const  2 2 2 F   . k v F  v   v  Ta có: 1 1 1 1 2  
    F  F    2250 (mã lực) 2 1 2
F  k.v  2 F  2 v   1 v 2 2 
Câu 54: Một động cơ nhiệt làm việc theo chu trình Carnot bằng không khí lấy ở áp suất ban đầu P  7, 0 . 1 at
Thể tích ban đầu của không khí V  2 3
. Sau lần giãn đẳng nhiệt lần thứ nhất nó chiếm thể tích V  5  3 2 dm  1 dm 
và sau khi giãn đoạn nhiệt thể tích của khí làV  8,1 3
. Áp suất khí sau khi giãn đoạn nhiệt có giá trị 3 dm  3 P bằng; A. 4 12,98.10  4 4 4 Pa 
B. 10,98.10 Pa 
C. 13,98.10  P  a
D. 15,98.10  Pa Giải
Giai đoạn 1: quá trình đẳng nhiệt T  const  PV 7.2
Áp dụng phương trình TT của quá trình đẳng nhiệt: 1 1
PV  PV  P    2,8 1 1 2 2 2 at  V 5 2
Giai đoạn 2: Qúa trình đoạn nhiệt
Áp dụng phương trình TT cho quá trình đoạn nhiệt:  1,4   V   5  2
PV  PV  P  P  2,8.
 1,425 at  1,425.9,8.10  13,98.10 2 2 3 3 3 2     4 4 Pa   V 8,1  3   
Câu 55: Một viên bi có khối lượng m , vận tốc v bắn thẳng góc vào một bức tương phẳng. Sau khi va chạm 4
viên bi bay ngược trở lại với vận tốc bằng v . Gội động năng ban đầu của viên bi là E , độ biến thiên động 5
năng và động lượng của viên bi là W và p  ; ta có 1
A. W và p    mE  2 2 2 1 3E 32mE 2 B. W    và p   4 2 5E  mE12 5 2 C. W    và p   9 3 9E  mE 12 9 2 D. W    và p   25 5 Giải
Độ biến thiên động năng:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 1 2 1 2 1  4  1 2 9 1 2 9 W 
 W W  mv  mv  . . m v  mv     . mv   E sau t 2 1 2 2 2 5  2 25 2 25
Câu 56: Một ô tô có khổi lượng m  2,1 tấn chuyển động trên đoạn đường nằm ngang với vận tốc không đổi v  54 km /
. Công suất của ô tô bằng 9,8kW  . Lấy g   2
9,8 m / s  . Hệ số ma sát giữa bánh xe và mặt 0  h
đường có giá trị bằng; A. 1 0,305.10 B. 1 0, 281.10 C. 1 0,317.10 D. 1 0,341.10 Giải 3 P 9,8.10 1960
Ta có: P  F.v  F    N  v 15 3
Mà F  F  mg ms 1960 Hệ số ma sát: Fms 3     0,0317 3 mg 9,8.2,1.10
Câu 57: Nhiệt độ của một khối plasma khí coi là khí lí tưởng trên mặt trời là 6
2,6.10  K  . Vận tốc căn quân
phương của các điện tử tự do trong khối khí đó. (  31 m  kg  23 9,1.10
, k 1, 38.10  J / K ) là: e  A. 6 11,876.10  6  6 6 m / s 
B. 10,876.10 m / s 
C. 13,876.10  m / s
D. 12,876.10 m / s  Giải 3
Công thức tính vận tốc căn quần phương: kT 6 v 10,876.10  
m / s (với k là hằng số Boltzmann) C  m
Câu 58: Một bánh xê bắt đầu quay quanh một trục cố định đi qua tâm vành bánh và vuông góc với mặt phẳng
bánh xe, có góc quay xác định bằng biểu thức: 2   2
at ; trong đó a  0,125 rad / s ;t là thời gian. Điểm A trên
vành bánh xe sau 2s có vận tốc dài v  2m / s . Gia tốc toàn phần của điểm A khi đó có giá trị bằng: A.  2 2 2 m / s  B.  2 2 5 m / s  C.  2 5 m / s  D.  2 2 m / s  Giải 1 1 Theo bài ra, ta có: 2 2
  at   t  a      2a  0,25 2 rad / s  2 2
Vận tốc góc:   .t  0, 25.2  0,5 rad / s  v 2
Vận tốc dài: v  R  R    4m  0,5
Gia tốc tiếp tuyến và gia tốc pháp tuyến lúc này: 2 2 2 a   R    2 .
4.0, 25 1 m / s và a   .R  0,5 .4 1 m/ s n  t  Gia tốc toàn phần: 2 2
a  a  a   2 2 m / s t n  2
Câu 59: Một tàu điện khi xuất phát chuyển động trên đường nằm ngang với gia tốc a  0,9m / s  , 13s sau khi
bắt đầu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng lại hẳn. Hệ số ma sát trên đường
k  0, 01. Cho g   2
10 m / s  . Thời gian chuyển động toàn bộ của tàu là: A. 130 s
B. 126,8 s 
C. 125, 2 s
D. 128, 4 s  Giải
Tầu chuyển động theo hai giai đoạn:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Giai đoạn 1: chuyển động với gia tốc a  0,9 2 m /
với thời gian t 13 1 s  1 s 
Giai đoạn 2: chuyển động chậm dần đều với gia tốc a  k.g  0,01.10  0,  2 1 m /
dưới tác dụng cản của lực 2 s 
ma sát trong thời gian t 
Vận tốc lớn nhất của tàu: v
 a .t 0,9.13 11,7 m/ s max 1 1   v 11,7
Tầu chuyển động chậm dần đều trong thời gian: max t     117 s  a 0,1 2
Tổng thời gian chuyển động của tầu (kể từ lúc xuất phát đến khi tầu dừng lại) t  t  t  13 117  130 2 1 s
Câu 60: Khối lượng của một mol chất khí là   3 
2 kg / kmol và hệ số Poat-xông của chất khí là  1, 4 . Nhiệt
lượng rung riêng đẳng áp của khí bằng ( cho hằng số khí 3
R  8,31.10  J / kmo .lK  ): A. 921, 
91 J / kg.K  B. 934, 
91 J / kg.K C. 869, 
91 J / kg.K D. 908, 
91 J / kg.K Giải C C Ta có: p p    1
 ,4  C 3,5R p C C  R v p Cp 3,5R
Nhiệt lượng rung riêng đẳng áp của khí: c    908,9 J kg K p  1 / .   32
Câu 61: Một xi lanh có pit –tông có thể di động được. Trong xi-lanh đựng một khối khí lí tưởng. Vỏ xi lanh
không dẫn nhiệt. Nếu áp suất không khí trong xi lanh tăng 2 lần thì nội năng của khí thay đổi như thế thế nào?
( gọi  là hệ số Poatxông) 1   A.Tăng 1 2 lần B. Tăng 2  lần C. Tăng 1 2 lần D. Tăng 1 2 lần Giải Theo nguyên lý 1:  . . m  . i U n C T .RT v  2  1   1   1      T P 
Phương trình trạng thái của quá trình đoạn nhiệt: 1 2 T .P  T .   1 1 2 P   2 T  1 P   m i  1
U  nC .T  .  1 RT  v 1 1  1   2     Ta có: U 1 1 T 2 P        2  m i U 2 2 T   1 P U  nC T  RT  v . . 1 2 2   2
Câu 62: Một người kéo xe bằng một hợp lực với phương ngang một góc 0
  30 . Xe có khối lượng m  240 kg
và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường k  0, 26 . Lấyg   2 10 m / s  .
Lực kéo có giá trị bằng:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
A. 622,59 N 
B. 626,49 N 
C. 614,79 N 
D. 618, 69  N  Giải
Chọn chiều dương cùng chiều chuyển động
Khi xe chuyển động, chịu tác d ng c ụ
ủa các lực: Trọng lực P , phản lực N , lực kéo F và lực ma sát f k ms
Vì xe chuyển động với vận tốc không đổi nên a  0
Áp dụng định luật II Newton, ta có: P  N  f  F  0 1 ms k
Chiếu 1 lên trục Oy: N  F .sin  P  0 k
Chiếu 1 lên trục Ox: F .cos  f  0  F .cos  f k ms k ms
Mà lực ma sát tác dụng lên xe: f  k.N  k  P  F .sin ms k  Hay . kP
F cos  k P  F sin  F   N k . . k  626,49 k  
cos  k .sin
Câu 63: Một vật cố khối lượng m  10kg  bắt đầu trượt từ đỉnh dốc một mặt phẳng nghiêng cao h  20cm .
Khi tới chân dốc có vận tốc 2 v  1  5 m / 
s . Cho g  10m / s  . Công của lực ma sát là
A. 867,7 J  B. 853,  1 J C. 875 J 
D. 860, 4 J  Giải
Chọn mặt đất làm gốc tính thế năng W 
, chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu t 0
tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường,
hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát: 2 2  mv   m  0 v A  W  W   mgh   mgh f 2 1    0  ms  2  2  
Thay số: v  0,h  0,2 m ,v  15 m / s , h  0 0 0     1 2  A  mv  mgh  J f 875 ms 0   2
Câu 64: Một đĩa tròn đồng chất bán kính R  0,15m , có thể quay xung quanh một trục nằm ngang vuông góc
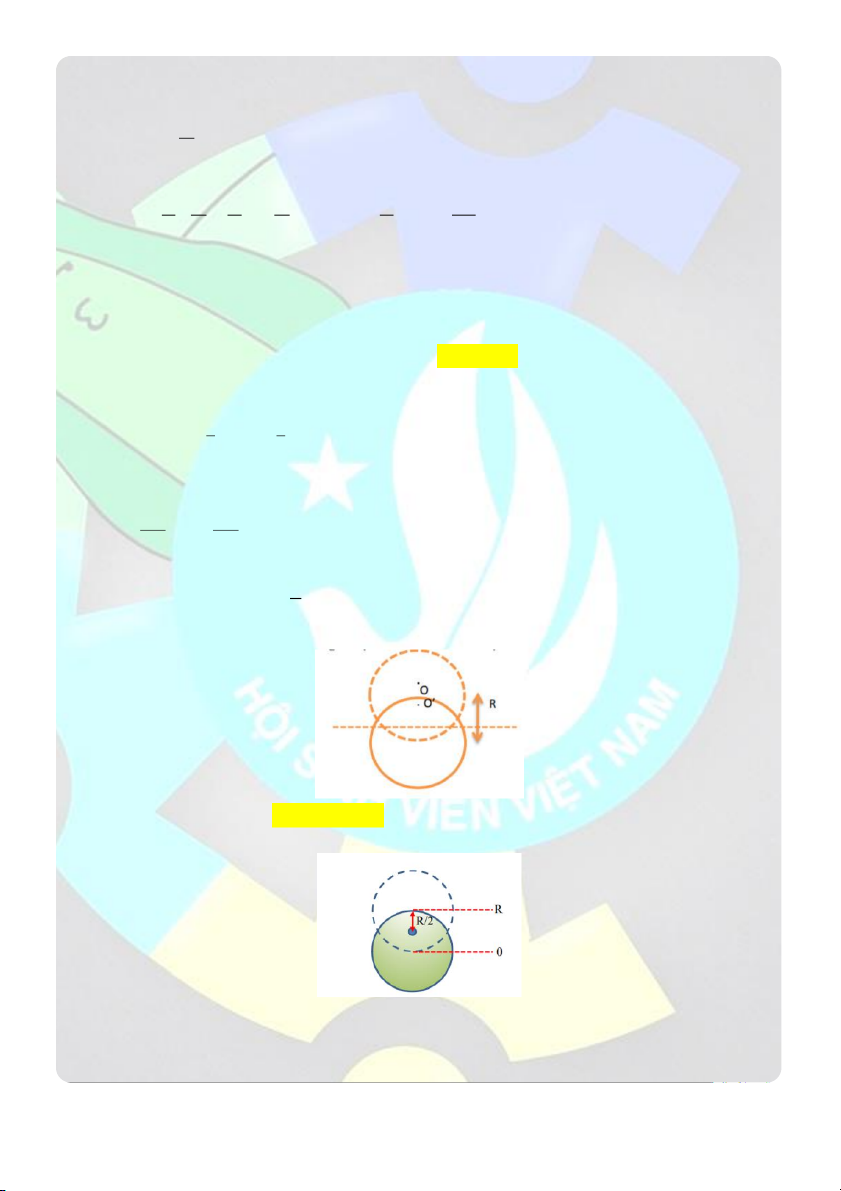
với đĩa và cách tâm đĩa một đoạn R . Đĩa bắt đầu quay từ vị trí cao nhất của tâm đĩa với vận tốc đầu bằng 0. Vận 2
tốc khi tâm đĩa ở vị trí thấp nhất là ( g   2 9,8 m / s  )
A. 13,199 rad / s
B. 49,915rad / s
C. 12, 226 rad / s
D. 50,888 rad / s Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Tại vị trí cao nhất và vị trí thấp nhất khoảng cách giữa hai khối tâm là R. Chọn mốc thế năng là vị trí thấp nhất
cho tiện. Như vậy ở vị trí cao nhất năng lượng của đĩa tròn dưới dạng thế năng và có dạng: W  mgR t 2 
Tại vị trí thấp nhất năng lượng của đĩa có dạng động năng (thế năng bằng ) 0 và có dạng: I W  d 2 2 2 1  R 3mR
Moment quán tính của thanh đối với trục quay: 2 I  mR  m  2  2    4 2 1 1 3mR 3 8
Áp dụng định luật bảo toàn năng lượng: 2 2 2 g mgR  I 
  g  R   
 13,199rad / s  2 2 4 8 3R
Câu 65: Khối lượng riêng của một chất khí 2     3 5.10
kg / m  ; vận tốc căn quân phương của các phân tử khí
này là v  450m / s . Áp suất của khối khí tác dụng lên thành bình là: A.  2 3575 N / m  B.  2 3675 N / m  C.  2 3475 N / m  D.  2 3375 N / m  Giải
Áp dụng PT trạng thái khí lí tưởng: PV m PV RT PV P P n        RT  RT  m m  V 2 3RT RT v
Vận tốc căn quân phương của các phân tử khí: C v    C   3 2 2 P v v C C    P     2 . 3375 N / m   3 3
Câu 66: Một ô tô bắt đầu chạy vào đoạn đường vòng bán kính R  1,3 k 
m và dài 600 m  với vận tốc v  54 km /
. Ô tô chạy hết quãng đường trong thời gian t  17 s  . Coi chuyển động là nhanh dần đều, gia 0  h
tốc toàn phần của ô tô cuối đoạn đường vòng bằng: A.  2 2,869 m / s  B.  2 4,119 m / s  C.  2 3,369 m / s  D.  2 3,119 m / s  Giải 1 Áp dụng công thức: 2 S  v t 
a t để tính gia tốc tiếp tuyến. 0 2 t 2S  v t 2 600 15.17 0     a    2,38 m s t  2 6 / 2 2  t 17
Vận tốc dài của đoàn tàu cuối quãng đường tròn được tính theo công thức:
v  v  a .t 15  2,386.17  55, 562 m / 0 s t  
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 2 v 55,562
Dùng công thức: a  
 2,375 m s để tính gia tốc pháp tuyến của đoàn tàu. n  2 / 3  R 1,3.10
Gia tốc toàn phần của đoàn tàu được tính theo công thức: 2 2 2 2
a  a  a     2 2,386 2,375 3,366 m / s t n 
Câu 67: Cộng tích đối với 1 mol chất khí thực là đại lượng có giá trị bằng:
A. Một phần ba của thể tích lớn nhất mà một mol chất lỏng ( tương ứng với chất khí đang xét) có thể có được
B. Bằng thể tích nhỏ nhất của mol khí
C. Bằng tổng các thể tích riêng của các phân tử mol khí
D. Bằng thể tích tới hạn của mol khí
Câu 68: Một khối khí ôxy 
có khối lượng riêng là    3
0,59 kg / m  . Số Avôgađrô 2 O  26
N  6,023.10  J / kmol . Tỷ số áp suất khí và động năng tịnh tiến trung bình của phân tử khí là: A. 24 6,873.10  24 24 24 Pa / J
B. 8,993.10  Pa / J
C. 8, 463.10  Pa / J 
D. 7, 403.10  Pa / J  Giải 1 2
Dạng phương trình thuyết động lực học phân tử: p  0 n mv 3  N Trong đó: 
n là mật độ phân tử trong 1 đơn vị thể tích n  0  0   V 
N tổng số phân tử khí có trong thể tích V
m là khối lượng phân tử khí 2
v vận tốc toàn phương TB của 1 phân tử khí 2 2  Có 1 2 mv 2 p 2 2 N 2 N p  n mv  n .  n W 24   n    7, 403.10 Pa / 0  J  0 0 0 3 3 2 3 d W 3 3 V 3  d 
Câu 69: Một chất điểm dao động điều hòa với chu kì T  2 , pha ban đầu   . Năng lượng toàn phần 0 s 3 5
W  2,6.10 J  và lực tác dụng lên chất điểm lúc lớn nhất  3 F  2.10
. Phương trình dao động nào sau đây 0  N
là đúng của chất điểm trên: A. 24 6,873.10  24 24 24 Pa / J
B. 8,993.10  Pa / J
C. 8, 463.10  Pa / J 
D. 7, 403.10  Pa / J  Giải
Lực tác dụng lên chất điểm lúc lớn nhất:  0 F kA 1 1 2 Cơ năng: 2 E
E  kA  .F .A  A 
 0,026 m  2,6 cm 0     2 2 0 F 2 2
Ta có: T  2      2 rad / s  T 2      
Phương trình dao động của chất điểm: x  2,6.cos t 
 2,6.sin t      cm   3   3 
Câu 70: Hai quả cầu A và B được treo ở hai đầu sợi dây mảnh không dãn dài bằng nhau. Hai đầu kia của các
sợi dây được buộc vào một cái giá sao cho các quả cầu tiếp xúc với nhau và tâm của chúng cùng nằm trên một
đường nằm ngang. Khối lượng của các quả cầu m  165 g và m  750 g . Kéo quả cầu A lệch khỏi vị trí B   A  
cân bằng đến độ cao h  6cm và thả ra. Sau va chạm, quả cầu B được nâng lên độ cao là: (coi va chạm là hoàn
toàn không đổi, cho g   2 9,8 m / s  )
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
A. 7, 617 mm B. 1,95  1 mm
C. 2,958mm
D. 7,804mm Giải
Trường hợp a: va chạm hoàn toàn đàn hồi
Định luật bảo toàn động lượng: m   1v1 m1 1 V m2V2
Chiếu lên trục ta có: giả sử sau khi va chạm mỗi vật chạy về 1 hướng    1 1 m 1 v 1 m 1 V 2 m 2 V
Định luật bảo toàn cơ năng: thế năng của vật m chính bằng động năng của nó trước khi va chạm và bằng tổng 1 2 2 2 động năng của vật 1 m 1 v 1 m 1 V 2 m 2 V 2 1 m và 2 m sau khi va chạm: 1 m gh      2 2 2 1: m       1v1 m1 1 V m2V2 m1 v1 1
V  m2V2 2 2 2  m v m V m V 2 : 1 1 1 1 2 2       1 m gh 1 m  2 2 1 v 1 V  2 2 m 2 V 2 2 2 2 2 m v Lấy 1 1 m gh   v  2
  v V V và gh 1 1 1 2 1 1 2 
Thay ngược lại vào  
1 để tìm mối quan hệ giữa m m V và
m v  V  m v  V  V  v 1 v : 1  1 1  2  1 1  2 1 1 1 1 m  2 1 m 2
Tượng tự tìm được mỗi quan hệ giữa m V và V  v 2 v : 1 1 2 1  1 m 2 m 2m1 v 2 1 
Sau va chạm, quả cầu B được nâng lên độ cao là 2 V 1 m 2 m  3 h    m  mm B 7,804.10   7,804   2g 2g
Câu 71: Một phi công đang lái máy bay thực hiện vòng tròn nhào lộn trong một mặt phẳng đứng với vận tốc
700km / h . Giả thiết phi công có thể chịu đựng sự tăng trọng lượng lên 3 lần. Bán kính nhỏ nhất của vòng tròn
nhào lộn mà máy bay có thể đạt được là ( cho g   2 9,8 m / s  )
A. 1979 m 
B. 1929 m  C. 2029  m
D. 1779 m  Giải
Áp dụng định luật II Newton cho phi công: mg  N  ma
N là phản lực mà ghế tác dụng lên phi công (bằng và ngược chiều với lực nén của phi công lên ghế).
Áp lực lớn nhất tại điểm thấp nhất
Tại điểm thấp nhất của vòng nhào lộn, theo phương hướng tâm,   1 được viết thành:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 v mg       2 N ma mg N m ht 2 R
Theo bài ra, ta có: N  3P  3 2 mg 2  1750  2 2   v v  9   m
 g  3mg  m  R   1929m R 2g 2.9,8
Câu 72: Một động cơ nhiệt có hiệu suất 10 % và nhả nhiệt cho một nguồn có nhiệt độ 450 K  . Nó nhận nhiệt
từ một nguồn có nhiệt độ ít nhất là: A. 479 K  B. 514 K  C. 507 K  D. 500 K  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 T T 450 2 2   1  0,1T    500 K 1   T 1 1 0,1 1
Câu 73: Một trụ đặc khối lượng M  80kg  có thể quay xung quanh một trục nằm ngang trùng với trục của trụ.
Một sợi dây không giãn được quấn nhiều vòng vào trụ, đầu tự do của dây có treo một vật nặng khối lượng
m  10 kg  . Để hệ tự chuyển động, sức căng của sợi dây là ( lấyg   2
9,8 m / s  ):
A. 78, 4 N 
B. 70,94 N 
C. 82,13 N  D. 67, 2  1 N  Giải Thiếu hình Dưới tác d n ụ g c a
ủ trong lực P lên vật nặng, hệ trụ + vật nặng chuyển động: trụ quay, vật nặng chuyển động tịnh
tiến (hệ vừa có phần quay vừa có phần tịnh tiến). Vì vậy không thể áp dụng định luật II Newton hay phương trình
cơ bản của chuyển động quay cho toàn bộ hệ. Gọi  là gia tốc góc của trụ, a là gia tốc dài của vật nặng. Vì
chuyển động của vật nặng và chuyển động của một điểm trên mặt trụ có cùng gia tốc nên ta có hệ thức: a  .
 R 1 (R là bán kính của trụ)
Gọi T ' và T là sức căng của dây tại A, ta có: T  T
 ' (tức là T  T ' ) 2
Với T tác dụng lên đoạn dây nối với vật nặng, còn T ' tác dụng lên đoạn dây nối với trụ
Áp dụng định luật II Newton riêng cho vật nặng, ta có: P  T  ma
Chọn chiều dương cùng chiều chuyển động với vật nặng
Chiếu phương trình trên lên phương chuyển động mg T  ma   3
Áp dụng phương trình cơ bản của chuyển động quay cho riêng trụ đặc, ta có RT '  I  2 MR
Với I là moment quán tính của trụ đặc: I    4 2  2mg a    2mg 
Từ 1; 2; 3 và 4 
2m M  T  m g   78, 4   N         2m M  T m g a
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 74: Một khối khí nitơ N biến đổi trạng thái sao cho áp suất của nó tăng 2 lần và vận tốc căn quân phương 2 
của các phân tử tăng 2 lần . Trong quá trình đó , khối lượng riêng của khối khí nitơ thay đổi như thế nào? A. Giảm 2 lần B Tăng . 2 2 lần C.Tăng 2 lần D. Không đổi Giải 
Công thức tính khối lượng riêng của chất khí: m p    V RT   1 T : p   1 1   RT  Ta có: 1 p T 1 1 2    .    2 p 2 2 p 1 : T T   2 2  RT  2 3
Công thức tính vận tốc căn quân phương của phân tử khí: kT v  m  3k 1 T v  2 1    Hay m 2 v 2 T       3 v T kT  1  1 2 v  2  m 2    1 1 p 2   . v 1     2 2 p  1 v 
Câu 75: Một con lắc đơn có m  110 g  được kéo ra lệch với phương thẳng đứng một góc 0   90 , sau đó thả rơi, cho g   2
10 m / s  . Lực căng cực đại của dây treo là:
A. 3, 3 N
B. 3, 697 N
C. 2,109 N 
D. 4,094 N  Giải Chuyển động c a
ủ vật m là chuyển động tròn đều trên quỹ đạo có bán kính l
Áp dụng định luật bảo toàn cơ năng: 1 2 mgl mgl
W W W W  mv   d t tmax 2
1 cos 1 cos0 
v  2gl cos  cos 0 
Chọn chiều dương hướng xuống và gốc thế năng tại vị trí cân bằng Vật chịu tác d ng c ụ a
ủ các lực: Lực căng dây T  , trọng lực P
Áp dụng định luật II Newton: P  T  ma 2
Chiếu (1) lên chiều dương hình vẽ:   .     .v T P m a T mgcos m n l
(trọng lực đóng vai trò lực hướng tâm)
T  mgcos  2mg cos cos  mg 3cos  2  0   cos 0  T    0  T
 3mgcos  3,3 N max 0 max  
Câu 76: Cộng tích đối với 1 mol chất khí thực là đại lượng có giá trị bằng:
A. Phản lực của thành bình lên phân tử khí
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
B. Lực đẩy giữa các phân tử khí
C. Lực hút của thành bình lên phân tử khí
D. Lực hút giữa các phân tử khí
Xét tại đỉnh vật chịu tác dụng của 2 lực là lực căng T và trọng lực P , và hai lực này đóng vai trò là lực hướng tâm luôn
Áp dụng định luật II Newton, ta có: P  T  ma 2 2
Chiếu lên trục thẳng đứng chiều dương hướng xuống dưới: v v B B P T  ma m T m mg ht l l
Để ý tại vị trí A vật được cấp năng lượng dưới dạng động năng, tại vị trí B thì động năng này đã được chuyển
một phần thành thế năng và động năng tại B. Do đó ta có: 1 2 1 2 2 2 W  W W
 mv  mv  mg l  mv  mv  mgl d A d B t B .2 4 2 A 2 B B A 2 2 mv  4mgl  v 
Thay vào phương trình trên, ta được: A A T   mg  m  5g   l l   2 v
Để vật quay tròn trong mặt phẳng thẳng đứng thì T  0 A 
 5g  0  v  5gl A l
Câu 77: Có M  18 g  khí đang chiếm thể tích V  4l  ở nhiệt độ 0
t  22 C . Sau khi hơ nóng đẳng áp, khối
lượng riêng của nó bằng 4     3 6.10
g / cm . Nhiệt độ của khối khí sau khi đun nóng là:
A. 2513 K
B. 2113 K 
C. 2213 K 
D. 2013 K  Giải Trước khi hơ nóng:
Áp dụng phương trình TT khí lý tưởng: m p  1 1 V R 1 T  m m RT Sau khi hơ nóng: 2 p     2 2 V R 2 T p R 2 T  V   2 1 mT mT Lấy 1 1  V   T   2213 1 2  K 2 T   2 1 V
Câu 78: Một thanh đồng chất chiều dài l có thể quay quanh một trục nằm ngang đi qua một đầu của thanh và
vuông góc với thanh. Vận tốc góc cực tiểu phải truyền cho thanh ở vị trí cân bằng để nó đến được vị trí nằm ngang là: 3 6 2 9 g g g g A. . B . . C. D. l l l l Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Chọn mốc thế năng tại vị trí thấp nhất của thanh 1
Tại vị tri thấp nhất v  v W  W  mv max  2 dmax 2
Tại vị trí cao nhất v   0  W W  mgl tmax 1
Áp dụng định luật bảo toàn năng lượng: 2
mv  mgl  v  2gl 2 v 2
Vận tốc góc cực tiểu phải truyền cho thanh ở vị trí cân bằng để nó đến được vị trí nằm ngang là g    l l
Câu 79: Một quả cầu đặc có khối lượng m  1,5kg  , lăn không trượt với vận tốc v  10 m / đến đập vào 1  s
thành tường rồi bật ra với vận tốc v  8 m /
. Nhiệt lượng tỏa ra trong va chạm đó là: 2  s
A. 41, 74 J 
B. 39,77  J  C. 43,  71 J  D. 37,  8 J Giải:
Sau va chạm động năng của vật giảm. Độ giảm động năng này tỏa ra dưới dạng nhiệt
Khi chuyển động, quả cầu vừa có động năng tịnh tiến, vừa có động năng quay 1 1  2  1 1
Động năng của quả cầu đặc, đồng chất, lăn không trượt: 2 2 2 2 2 2 W  I  mR
.  mR   mv dq 2 2 5    5 5 2
Moment quán tính của quả cầu đặc đồng chất: 2 I  mR 5 2
Động năng tịnh tiến của quả cầu đặc: mv W  d tt  2 1 2 1 2 7 2
 W  W +W
 mv  mv  mv d d q  d tt  5 2 10 7 7
Nhiệt lượng tỏa ra do va chạm: Q  W    m v  v      J d  2 2 .1,5  2 2 . 10 8 37,8 2 1    10 10
Câu 80: : Thả rơi tự do một vật nhỏ từ độ cao h  17, 6 m . Quãng đường mà vật rơi được trong 0,1s cuối của
thời gian rơi là: g   2 9,8 m / s 
A. 1, 608 m B. 1,808m C. 2,208m D. 2,408m Giải 2 Thời gian rơi của vật: h t  1  ,9  s g
Quãng đường vật rơi trong 0,1 giây cuối là: 1 1 s   s  s
 gt  g t 
 g t  t    m t t  2 1 0,1  0,12 2 2 1,808 0,1   2 2 2   1 2
Công thức tổng quát cho quãng đường rơi trong h
n giây cuối là s   g t
  t n2 2  t  2   với g
Câu 81: Một con lắc toán có sợi dây dài là l , và cứ sau t  5 phút thì biên độ giao động giảm 2 lần. Giảm lượng
lôga của con lắc đó là  0,023 . Cho gia tốc trọng trường g   2
9,8 m / s  . Hỏi l bằng giá trị nào dưới đây:
A. 2,554m
B. 2,044 m
C. 1, 704 m D. 2,214m Giải
Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:
F  F  kx  rv C
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Phương trình cơ bản của chuyển động trong trường hợp này là ma  kx  rv 2 2 Hay: d x dx d x r dx k m  r  kx    x  0 1 2 2 dt dt dt m dt m Đặt r   (hệ số tắt dần) 2m 2 Phương trình  d x dx 1 trở thành 2 x  2  x  0 2 2 0 dt dt
2 gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi    , nghiệm phương trình 0 này có dạng:  t x     0 A e cos  t 
Đây là biểu thức độ dời của dao động tắt dần. Hằng số  gọi là tần số của dao động tắt dần: 2 2      0 x   t 1   1 Theo bài ra, ta có: . .300 3  e   e     7,7.10 A 2 2 0 
Giảm lượng loga của con lắc:   T   0,023 T   2,987 s   2 2 2
Chu kỳ T của dao động tắt dần là: T   
 2,987 s  l  2,214m 2 2     g 2 0   l
Câu 82: Tổng động năng tịnh tiến trung bình của các phân tử khí Nito 
chứa trong một khí cầu bằng 2 N  3  3
W  5.10  J  và vận tốc căn quân phương của phân tử khí đó là v  2.10  m / s . Khối lượng khí nitơ trong e  khí cầu là: A. 3 2,84.10 kg B.  3 2,5.10  kg C. 3 3, 01.10  kg D. 3 2,33.10  kg Giải
Tổng động năng tịnh tiến trung bình của các phân tử khí Nito N là 2  3 1 2 2W 2.5.10 3 W mv m 2,5.10      kg e 2 2   2 ve  3 2.10 
Câu 83: Một vật nhỏ có khối lượng m buộc vào đầu sợi dây mảnh chiều dài l  1,5 m  , đầu kia giữ cố định. Cho
vật quay trong mặt phẳng nằm ngang với vận tốc góc không đổi sao cho sợi dây hợp với phương thẳng đứng một góc 0
  30 . Cho g   2
10 m / s  , bỏ qua lực cản không khí. Tốc độ góc có giá trị:
A. 2,575rad / s
B. 2,775rad / s
C. 3, 075 rad / s
D. 2,675rad / s Giải
Chọn mốc thế năng tại vị trí căn bằng, chiều dương hướng xuống
Trong quá trình dao động, vật chịu tác dụng của các lực: trọng lực P, lực căng dây T  và lực hướng tâm F ht
Áp dụng định luật II Newton, ta có: P T  F  0 1 ht
Chiếu 1 lên trục Ox: 0 0
F T .sin30  0  F  T.si 3 n 0 ht ht mg
Chiếu 1 lên trục Oy: 0 P T
 cos 0  P Tcos mg T.cos30 T  0 co 3 s 0 0 0 3
 F  T.sin30  mg.tan30  mg ht 3
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP Mà 2 2 0
F  ma  m .R  m .l.si 3 n 0 ht ht 2 0 mg 1 2 g 2  . . 30    . g m l sin l    
 2,775 rad / s  3 2 3 3l
Câu 84: Cộng tích đối với một mol chất khí thực là đại lượng có giá trị bằng:
A. Bằng thể tích nhỏ nhất của một mol khí
B. Bằng tổng các thể tích riêng của các phân tử mol khí
C. Một phần ba của thể tích lớn nhất mà một mol chất lỏng ( tương ứng với chất khí đang xét) có thể có được
D. Bằng thể tích tới hạn của mol khí
Câu 85: Một thanh chiều dài l  0,6 m  , khối lượng M  
3 kg có thể quay tự do xung quanh một trục nằm
ngang đi qua một đầu của thanh. Một viên đạn khối lượng m  0,0 
1 kg bay theo phương nằm ngang với vận
tốc v  300 m / s  tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc góc của thanh ngay sau khi viên đạn đập vào thanh là: A. 4,  95 rad /  s
B. 4, 436 rad / s
C. 5,721rad / s
D. 5, 207 rad / s Giải
Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có mỗi
viên đạn có tốc độ và khối lượng m mang một động lượng p  mv
Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách
từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm
quay tới viên đạn chính là độ dài l
Vậy mômen động lượng trước khi va chạm là: L  r.p.sin  l.p  mvl t
Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với
cùng vận tốc góc  . Vậy moomen quán tính của hệ vật sau va chạm:
L  I   I  s 1 2
Với I là moment chất điểm (viên đạn) đối với trục quay 2  1 I1 ml 2  l  2 M   2 Ml '  2  Ml
I là moment quán tính của thanh mảnh    2 I 2 12 12 3 2   Hay Ml
L  I  I   ml     s   2 1 2 3  
Áp dụng định luật bảo toàn động lượng 2   2 Ml mvl v
L  L  mvl  ml        rad s t s   4,95 / 2    3  2 Ml   ml  l 1 M    3  3m 
Câu 86: Một con lắc vật lý được cấu tạo bằng một thanh đồng chất tiết diện đều có độ dài bằng l và trục quay O
của nó cách trọng tâm G một khoảng bằng x . Biết rằng chu kỳ dao động T của con lắc này là nhỏ nhất, x nhận
giá trị nào dưới đây? l l l l A. B. C. D. 3 2 4 3 2 3 Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Chu kỳ dao động T của con lắc:  2 I T  mgd
Với I  I  I với 1 2
I là moment quán tính của thánh và 1
I là moment quán tính của chất điểm đối với trục quay 2 2 ml 2 I  I    ( ở đây  ) 1 I2 mx d x 12 2 2     2 l 2 l m x  x       12   12   T  2  2 mgx gx 2   2 2 l l l T
 T '  0  2 x  x     0  x   max x  12  12 2 3
Câu 87: Một ôtô chuyển động biến đổi đều lần lượt đi qua hai điểm A và B cách nhau S  25m trong khoảng
thời gian t  1, 6 s  , vận tốc ô tô ở B là 12m / s . Vận tốc của ôtô ở A nhận giá trị nào sau đây:
A. 18, 25m / s
B. 18, 75 m / s 
C. 19, 25 m / s
D. 20,75m / s Giải v  v 2S 2 Áp dụng công thức 2 2
v v 2aS 2 . S B A S  v v   v  v 1  9,25 m s B A B A A B  /  t t t
Câu 88: Một vật có khối lượng m  2
chuyển động với tốc độ v  6 m /
tới va chạm xuyên tâm vào vật 1  s 1 kg
có khối lượng m  3
đứng yên. Va chạm là hoàn toàn mềm. Nhiệt lượng tỏa ra trong quá trình va chạm là 2 kg 
A. 21, 3 J 
B. 21, 6 J 
C. 22, 2 J 
D. 22,5 J  Giải m .v 2.6
Vì va chạm là hoàn toàn mềm nên m .v m m  1 1 .v  v    2,4 m / 1 1 1 2 2 2  s m  m 2  3 1 2
Nhiệt lượng tỏa ra trong quá trình va chạm là: 1 1 2 Q  W
W  .m .v  m  m v  J truoc sau .  2 . 21,6 1 1 1 2 2   2 2
Câu 89: Một người đẩy xe một lực hướng xuống theo phương hợp với phương ngang một góc 0   30 . Xe có
khối lượng m  230 kg và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường
k  0, 23 . Lấy g   2
9,81 m / s  . Lực đẩy của người có giá trị bằng:
A. 693, 28 N B. 690,  98 N C. 686,  38 N D. 697,  88 N Giải
Chọn chiều dương cùng chiều chuyển động
Khi xe chuyển động, chịu tác d ng c ụ
ủa các lực: Trọng lực P , phản lực N ' , lực đẩy F ' và lực ma sát f ' ms
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Vì xe chuyển động với vận tốc không đổi nên a  0
Áp dụng định luật II Newton, ta có: P  N ' f  F ' 0   1 ms
Chiếu 1 lên trục Oy: N ' F '.sin  P  0
Chiếu 1 lên trục Ox: F '.cos  f '  0  F '.cos  f ' ms ms
Mà lực ma sát tác dụng lên xe: f '  k.N '  k P  F '.sin ms  Hay '.
  .   '.   ' kP F cos k P F sin F   690,98 N 
cos  k.sin
Câu 90: Một đĩa trong khối lượng M  165kg  đỡ một người có khối lượng m  53 kg . Lúc đầu người đứng
ở mép và đĩa quay với vận tốc góc   10 (vòng/phút) quanh trục đi qua tâm đĩa. Vận tốc góc của đĩa khi người 1
đi vào đúng tâm của đĩa là ( coi người như 1 chất điểm)
A. 1,99 rad / s  B. 2,5  3 rad / s
C. 2, 26 rad / s 
D. 1, 72 rad / s  Giải
Bài này áp dụng định luật bảo toàn động lượng
Giai đoạn trước: mômen động lượng của hệ sẽ là: L  I   I  truoc dia 1 nguoi 1 2
Mômen quán tính đĩa đặc như đã biết là: MR I  dia 2
Mômen quán tính của người (chất điểm) là: 2 I  mR nguoi 2  MR  2  L  mR  truoc   1  2 
Giai đoạn sau: để ý là khi người đi vào tâm đĩa thì coi như khoảng cách từ người tới tâm đĩa là 0. Điều này kéo
theo mômen quán tính của người với tâm đĩa coi như bằng 0. 2
Moment động lượng của hệ lúc này là mR L  I    sau dia 2 2 2 2 2  MR  mR
Áp dụng định luật bảo toàn động lượng: 2 L  L   mR      truoc sau 1 2 2 2   0,5M  m 165.0, 5  53       .  1,72 rad / 2  s 0,5M 0,5.165 3
Câu 91: Một ô tô khối lượng m  1, 5 tấn đang đi trên đường phẳng nằm ngang với tốc độ 21m / s bỗng nhiên
phanh lại. Ô tô dừng lại sau khi trượt thêm 25m . Độ lớn trung bình của lực ma sát là: A. 3 13,53.10  3 3 3 N 
B. 13, 23.10 N 
C. 12,63.10  N 
D. 14,13.10  N  Giải 2 2 2 2 v  v 0 21 Gia tốc: 0 a    8,82 2 m / s  2s 2.25
Độ lớn trung bình của lực ma sát là: F  ma  8,82.1,5.1000  13230 N ms  
Câu 92: Một động cơ nhiệt làm việc theo chu trình Carnot bằng không khí lấy ở áp suất ban đầu P  7, 0 . 1 at
Thể tích ban đầu của không khí 3 V  2 3
. Sau lần giãn đẳng nhiệt lần thứ nhất nó chiếm thể tích V  5 2 dm  1 dm 
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
và sau khi giãn đoạn nhiệt thể tích của khí làV  8,1 3 . Áp suất khí sau khi giãn đoạn nhiệt có giá trị 3 dm  3 P bằng; A. 4 14,98.10  4 4 4 Pa 
B. 13,98.10  Pa
C. 11,98.10  Pa
D. 16,98.10 Pa  Giải
Giai đoạn 1: quá trình đẳng nhiệt T  const  PV 7.2
Áp dụng phương trình TT của quá trình đẳng nhiệt: 1 1
PV  PV  P    2,8 1 1 2 2 2 at  V 5 2
Giai đoạn 2: Qúa trình đoạn nhiệt
Áp dụng phương trình TT cho quá trình đoạn nhiệt:  1,4     V  5  2
PV  PV  P  P  2,8.
 1,425 at  1,425.9,8.10  13,98.10 2 2 3 3 3 2     4 4 Pa   V    8,1 3 
Câu 93: Hơ nóng 1 mol khí lí tưởng lưỡng nguyên tử từ nhiệt độ 1 T đến 2
T bằng hai quá trình đẳng áp và đẳng
tích. Gọi biến thiên entropi trong mỗi quá trình đẳng áp, đẳng tích lần lượt là S và S Khi đó: P V A. S   1,8 S  B. S  1,4 S 
C. S  1, 6S D. S   2,0 S  P V P V P V P V Giải Độ biến thiên Entropy: dQ dS  T i  2
Qúa trình đẳng áp: Q nC dT  n RdT p 2
Thay vào và lấy tích phân từ trạng thái 1 ứng với 1
T đến trạng thái 2 ứng với 2 T T2 i  2 dT i  2 T  2 i 2 T2  S   n R  n RlnT  n Rln  P 2 T 2 T 2 T T 1 1 1 i T
Tương tự, ta có độ biến thiên entropy của quá trình đẳng tích; 2 S   n Rln V 2 1 T i 2 5 2 S 
Với khí lưỡng nguyên t t ử hì i  5 P 2 2    1,4 S  i 5 V 2 2
A. ∆𝑆p = 1,8 ∆𝑆v B. ∆𝑆p = 1,4 ∆𝑆v C. ∆𝑆p = 1,6 ∆𝑆v D. ∆𝑆p = 2,0 ∆𝑆v
Câu 94: Kỷ lục đẩy tạ ở Hà Nội là14,07 m  . Nếu tổ chức đẩy tạ ở Xanh Pêtecbua trong điều kiện tương tự (cùng
vận tốc ban đầu và góc nghiêng) thì kỉ lục sẽ là: (cho gia tốc trọng trường ở Hà Nội là g  9,72  2 7 m / , ở Xanh 1 s 
Pêtecbua là g  9,810  2 m /
, bỏ qua chiều cao của người đẩy) 2 s 
A. 16,951m
B. 12,951m  C. 15,  951 m
D. 13,951m Giải 2 v .sin2 Từ công thức tầm xa: 0 L 
ta thấy với lực đẩy không đổi (để v không đổi) và góc ném không đổi (ném 0 g
xa nhất khi góc ném bằng 0
45 ) thì tầm xa L tỷ lệ nghịch với gia tốc trọng trường g. Do đó, có thể xác định kỷ
lục đẩy tạ tại thành phố Xanh Pêtecbua là
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP g 9,727 HN L  .L  .14,07 13,95 m XP HN  1  g 9,81 XP
Câu 95: Một ô tô khối lượng m  450 kg chuyển động thẳng đều xuống dốc trên một mặt phẳng nghiêng, góc
nghiêng  so với mặt đất nằm ngang có sin  0,0872;cos  0,9962 . Lực kéo ô tô bằng F  45  0 N , cho k  g   2
10 m / s . Hệ số ma sát giữa ô tô và mặt đường là: A. 0,218 B. 0,188 C. 0,168 D. 0,178 Giải
Chọn trục Oxy như hình vẽ. Chiều dương cùng chiều chuyển động với ô tô
Ô tô chịu tác dụng của các lực: lực kéo F của động cơ ô tô, trọng lực P , phản lực tiếp tuyến N của mặt
đường và lực ma sát của mặt đường f ms
Áp dụng định luật II Newton, ta có F  P  N  f  0 (vì ô tô chuyển động thẳng đều) ms
Chiếu phương trình này nên phương chuyển động của ô tô, ta được: F  f  Psin  0 k ms  
 F  f Psin  k. F mgsin k
N  Psin  kmgcos mgsin  k   0,188 k ms mgcos
Câu 96: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 5 
5 kW  . Nhiệt độ của nguồn nóng là 0
127 C , nhiệt độ của nguồn lạnh là 0
31 C. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:
A. 14050 kJ 
B. 13650 kJ 
C. 13550 kJ 
D. 13750 kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  T1
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 55 1375 Hay 2  1   Q    kJ 1   T Q T 304 2 6 1 1 1 1 T 400 1 1375
 Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút: '
Q  Q .t  .60 13750 1 1 kJ  3
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 97: Một thanh đồng chất có độ dài l , khối lượng m . Đối với trục quay nào dưới đây mô mem quán tính của thanh là nhỏ nhất
A. Song song và cách thanh một khoảng bằng l
B. Đi qua khối tâm và vuông góc với thanh
C. Vuông góc và đi qua một đầu thanh 
D. Đi qua khối tâm và làm với thanh một góc   2
Câu 98: Một thanh mảnh đồng chất có độ dài l có thể quay quanh một trục đi qua đầu thanh và vuông góc với
thanh. Lúc đầu thanh ở vị trí nằm ngang, cho thanh rơi xuống. Vận tốc dài ở đầu dưới của thanh khi thanh rơi
tới vị trí thẳng đứng là A. 2gl B. gl C. 3gl D. 0 Giải
Chọn mốc thế năng tại vị trí thấp nhất của thanh 1
Tại vị tri thấp nhất v  v  W  W  mv max  2 dmax 2
Tại vị trí cao nhất v   0  W W  mgl tmax 1
Áp dụng định luật bảo toàn năng lượng: 2
mv  mgl  v  2gl 2
Câu 99: Một ô tô bắt đầu chạy vào đoạn đường vòng bán kính R  1,  1 k 
m và dài 600 m  với vận tốc v  54 km /
. Ô tô chạy hết quãng đường trong thời gian t  19 s  . Coi chuyển động là nhanh dần đều, gia 0  h
tốc toàn phần của ô tô cuối đoạn đường vòng bằng: A.  2 2,737 m / s  B.  2 2,987 m / s  C.  2
3, 237 m / s  D.  2
3, 487 m / s  Giải 1 Áp dụng công thức: 2 S  v t 
a t để tính gia tốc tiếp tuyến. 0 2 t 2S  v t 2 60015.19 0     a   1,745 m s t  2 / 2 2  t 19
Vận tốc dài của đoàn tàu cuối quãng đường tròn được tính theo công thức:
v  v  a .t  15  1, 745.19  48,155 m / 0 s t   2 2 v 48,155
Dùng công thức: a  
 2,108 m s để tính gia tốc pháp tuyến của đoàn tàu. n  2 / 3  R 1,1.10
Gia tốc toàn phần của đoàn tàu được tính theo công thức: 2 2 2 2
a  a  a    m s t n  2 1, 745 2,108 2,737 / 
Câu 100: Một vật có khối lượng m  2
chuyển động với tốc độ v  7 m /
tới va chạm xuyên tâm vào 1  s 1  k  g
vật có khối lượng m  3
đứng yên. Va chạm là hoàn toàn mềm. Nhiệt lượng tỏa ra trong quá trình va chạm 2 kg  là
A. 30,3 J 
B. 29, 7  J  C. 3  0 J
D. 29, 4 J  Giải m .v 2.7
Vì va chạm là hoàn toàn mềm nên m .v m m  1 1 .v  v    2,8 m / s 1 1 1 2 2 2   m  m 2  3 1 2
Nhiệt lượng tỏa ra trong quá trình va chạm là:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 1 1 2 Q  W
W  .m .v  . m  m v  J truoc sau   2 . 29, 4 1 1 1 2 2   2 2
Câu 101: 4: Gọi M và R lần lượt là khối lượng và bán kính của Trái Đất. G là hằng số hấp dẫn vũ trụ, g và
g lần lượt là gia tốc trọng trường ở độ cao 0
h và mặt đất. Công thức nào dưới đây đúng với h bất kỳ:  2  1 h GM   2    GM GM  R  A. g  B. g  C.  1 h g g  D. g   2 0   2 R  h2 R  R  R Giải GM
Gia tốc trọng trường ở độ cao h: g   R h2
Câu 102: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 10 kW  . Nhiệt độ của nguồn nóng là 0
100 C , nhiệt độ của nguồn lạnh là 0
0 C . Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút có giá trị: A. 3 1, 438.10 kJ  B. 3 1, 638.10 kJ  C. 3 1, 738.10  kJ D. 3 1,338.10 kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  T1
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 10 Hay 2  1   Q    37,3 1 kJ  T Q T 273 2 1 1 1 1 T 373 1 Gọi ' '
Q  Q  A '  37,3 10  27,3 1
Q là nhiệt lượng mà tác nhân nhả cho nguồn lạnh: 1 1 kJ 
Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là '
Q  Q .t  60.27,3  1638 1 kJ 
Câu 103: Một khối khí lí tưởng có thể tích V   3
6 m  dãn nở đẳng nhiệt từ áp suất 2at đến 1at  . Lượng
nhiệt đã cung cấp cho quá trình này là: A. 5 9,16.10  5 5 5 J 
B. 10,16.10 J 
C. 8,16.10  J 
D. 5,16.10  J Giải
Trong quá trình đẳng nhiệt: U  0 mà U
  0  A  Q  Q   A V 2
Công của quá trình đẳng nhiệt 2 V A  PdV   1 P 1 V ln V V 1 1 V P
Áp dụng PT trạng thái của quá trình đẳng nhiệt: 2 1  1 V 2 P P Hay 1 4 4 5 A PV ln  2.6.l 2
n .9,8.10  8,318.9,81.10  8,16.10  1 1  J Q 2 P
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 104: Một khẩu pháo có khối lượng M  600kg  bắn một viên đạn theo phương làm với mặt ngang một góc 0
  60 . Khối lượng của viên đạn m  5kg , vận tốc đầu nòng v  400m / s . Khi bắn bệ pháo giật lùi về phía
sau một đoạn s  42 cm  . Lực cản trung bình tác dụng lên quả pháo có giá trị: A. 1  784,  1 N B. 1  984,  1 N C. 2  284,  1 N  D. 1  884,  1 N Giải
Theo định luật bảo toàn động lượng thì vận tốc giật lùi c a ủ khẩu pháo là: 0 . m . v cos 5.400.cos60 5 V    
  m / s M 600 3
Dấu "" chứng tỏ pháo giật lùi, ngược chiều dương) 2 V Áp dụng công thức: 2 2
V V  aS  a      2 ' 2 3,31 m / s  2S
Lực cản trung bình tác dụng lên quả pháo: F  Ma   3,31.600  1984,1 N C  
Câu 105: Từ đỉnh đồi cao, một quả pháo được bắn chếch lên phía trên một góc 0
  30 so với phương nằm
ngang với vận tốc đầu nòng là v  400 m /
. Sau khi bắn một khoảng thời gian t  5s , góc  giữa hướng 0  s 
của vận tốc quả pháo và hướng của gia tốc toàn phần thỏa mãn giá trị nào dưới đây ( bỏ qua sức cản không khí.
Gia tốc trọng trường bằng g   2 9,8 m / s 
A. tg  1,894
B. tg  2,894
C. tg  2,094
D. tg  2, 294 Giải
Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí pháo bắt đầu bắn, chiều dương hướng xuống, cùng chiều với gia tốc g a  0  Gia tốc: x  a    g y 
v  v  a .t  v .cos  Vận tốc: x 0 x x 0  v
  v  a t  v .sint  gt y 0 y y 0 
Phương trình chuyển động của chất điểm:  1 2
Ox : x  v t  a t
Ox : x  v .cos.t  0x x 0  2     1 2 1   2 Oy : y v sin .    0 : t gt Oy y  v  0 t a t y y  2  2 Theo hình vẽ, ta có: vx tan  vy 0
v  v .cos   x v .cos 400.co 3 s 0 Tại thời điểm 0
t  5 s : 0   tan    2,294 0 v
  v .sin  5g v sin  g sin  y . 5 400. 30 9,8.5 0  0
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Mặt khác: tan   t
 an  2,294 (do 0    180 )
Câu 106: Một vật coi là chất điểm có khối lượng m bắt đầu trượt từ đỉnh mặt phẳng nghiêng góc  so với
phương nằm ngang (xem hình vẽ). Hệ số ma sát giữa vật và mặt phẳng nghiêng là k . Moomen động lượng của
chất điểm đối với điểm O tại thời điểm t có giá trị là:
A. mghtsin sin  kcos  B. mghtcos  sin kcos 
C. mghtcos  cos  ksin D. mght sin  kcos Giải Chọn hệ tr c
ụ tọa độ Oxy như hình vẽ, chiều dương cùng chiều chuyển động của vật Vật chịu tác dụng c a
ủ các lực: trọng lực P , phản lực N và lực ma sát f ms
Áp dụng định luật II Newton, ta có: P  N  f  ma   1 ms
Chiếu 1 lên trục Ox : N  P 0  N  Pcos  mgcos n . P sin  f
Chiếu 1 lên trục Oy : P  f ma  P. ms sin  f ma  a  t ms ms m
Mà f  k.N  k.mgcos  F  mg sin  kcos ms  
Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O chính là công của lực F tác dụng lên điểm O A  . F .
h cos  mghcos  sin  . k cos F 
Câu 107: Một thanh chiều dài l  0,7 m , khối lượng M  
4 kg có thể quay tự do xung quanh một trục nằm
ngang đi qua một đầu của thanh. Một viên đạn khối lượng m  0,0 
1 kg bay theo hương nằm ngang với vận tốc
v  300 m / s  tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc gốc của thanh ngay sau khi viên đạn đập vào đầu thanh là:
A. 2,676rad / s
B. 3,19 rad / s
C. 2,933rad / s  D. 3,  961 rad /  s Giải
Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có
mỗi viên đạn có tốc độ và khối lượng m mang một động lượng p  mv
Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách
từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm
quay tới viên đạn chính là độ dài l
Vậy mômen động lượng trước khi va chạm là: L  r.p.sin  l.p  mvl t
Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với
cùng vận tốc góc  . Vậy moomen quán tính của hệ vật sau va chạm:
L  I   I  s 1 2
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Với I là moment chất điểm (viên đạn) đối với trục quay 2 I  ml 1 1 2  l  2 M   2 Ml '  2 Ml 
I là moment quán tính của thanh mảnh    2 I 2 12 12 3 2  Ml 
Hay L  I  I   ml     s   2 1 2  3 
Áp dụng định luật bảo toàn động lượng 2   2 Ml mvl v
L  L  mvl  ml          3,19 rad / s t s 2   3 2 Ml     ml  l 1 M    3  3m 
Câu 108: Theo thuyết động học phân tử của chất khí, với mọi chất khí mà phân tử có hai nguyên tử ở cùng
nhiệt độ thì kết luận nào sau đây đúng
A. Mọi phân tử của chúng có cùng một động năng trung bình
B. Các phân tử khí nhẹ có năng lượng trung bình cao hơn so với các phân tử khí nặng
C. Các phân tử khí nhẹ có năng lượng trung bình thấp hơn so với các phân tử khí nặng
D. Mọi phân tử của chúng có cùng một vận tốc trung bình
Câu 109: Một đoàn tàu khối lượng 2 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng v  54 km /
. Công suất đầu máy là 10 kW . Gia tốc trọng trường bằng  2
9,8 m / s  . Hệ số ma sát bằng: 0  h A. 1 0,376.10 B. 1 0,564.10 C. 1 0,328.10 D. 1 0,34.10 Giải
Đổi v  54 km / h 15 m / 0    s 3 P 10.10 2000
Ta có: P  F.v  F    N  v 15 3 2000 2000 F
Mà F  F  mg  N      ms   ms 3 0,034 3 3 mg 2.10 .9,8
Câu 110: Một đoàn tàu khối lượng 40 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng
24 km / h  . Công suất đầu máy là 225 kW . Gia tốc trọng trường bằng  2
9,8 m / s  . Hệ số ma sát bằng: bằng: A. 2 11, 6.10 B. 2 10, 6.10 C. 2 7, 613.10 D. 2 8,61.10 Giải 20
Đổi v  24km / h  m / s 3 3 P 225.10
Ta có: P  F.v  F    33750 N  v 15 F 33750
Mà F  F  mg  33750 N      ms   ms 0, 086 3 mg 40.10 .9,8
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 111: Một viên bi có khối lượng m , vận tốc v bắn thẳng góc vào một bức tương phẳng. Sau khi va chạm 4
viên bi bay ngược trở lại với vận tốc bằng v . Gội động năng ban đầu của viên bi là E , độ biến thiên động 5
năng và động lượng của viên bi là W và p  ; ta có 1
A. W và p    mE  2 2 2 1 3E 32mE 2 B. W    và p   4 2 1 5E  5 2mE 2 C. W    và p   9 3 1 9E 9 2mE  2 D. W    và p   25 5 Giải
Độ biến thiên động năng: 2 1 2 1 2 1  4  1 2 9 1 2 9 W 
 W W  mv  mv  . . m v  mv     . mv   E sau t 2 1 2 2 2 5  2 25 2 25
Câu 112: Một chất điểm bắt đầu trượt từ đỉnh mặt phẳng nghiêng góc  so với phương nằm ngang (xem hình
vẽ). Hệ số ma sát giữa vật và mặt phẳng nghiêng là k ; khối lượng của vật là m ( lấy g   2
9,81 m / s  ). Cho m  kg k  h   m 0 2,3 , 0, 2, 9
,  30 . Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O là:
A. 64,05 Nm
B. 57, 468 Nm
C. 60,759 Nm
D. 67,341 Nm Giải Chọn hệ tr c
ụ tọa độ Oxy như hình vẽ, chiều dương cùng chiều chuyển động của vật Vật chịu tác dụng c a
ủ các lực: trọng lực P , phản lực N và lực ma sát f ms
Áp dụng định luật II Newton, ta có: P  N  f  ma   1 ms
Chiếu 1 lên trục Ox : N  P 0  N  Pcos  mgcos n
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP . P sin  f
Chiếu 1 lên trục Oy : P  f ma  P. ms sin  f ma  a  t ms ms m
Mà f  k.N  k.mgcos  F  mg sin  kcos ms  
Mômen tổng hợp các vật tắc dụng lên chất điểm đối với O chính là công của lực F tác dụng lên điểm O
A  F h cos  mg  sin  k cos  0 . . . . . h c 30 os  57,468 N F  
Câu 113: Một viên bi nhỏ m  10 g rơi theo phương thẳng đứng không vận tốc ban đầu trong không khí, lực
cản của không khí F  rv (tỷ lệ ngược chiều với vận tốc), r là hệ số cản. Vận tốc cực đại mà viên bi đạt được c bằng v
 50 m / s . Cho gia tốc trọng trường g   2
10 m / s  . Hệ số cản có giá trị: max 
A. 4,353m / s
B. 3,953 m / s
C. 5,553 m / s
D. 3,553 m / s Giải Lực cản:   ' dv F ma mv  m e dt Mặt khác: dv dv r F  r  v  m  r  v    dt e dt v m v t r ln2 dv r v r  t  .2,2 Lấy tích phân: m 1
  dt  ln
  t  v  v .e  20.e  4,353 m /   0  s v m v m v 0 0 0
Câu 114: Một động cơ nhiệt có hiệu suất 25 %  và nhả nhiệt cho một nguồn có nhiệt độ 600 K . Nó nhận
nhiệt từ một nguồn có nhiệt độ ít nhất là:
A. 786 K  B. 82  1 K C. 807 K  D. 800 K  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  T1
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 T T 600 Hay 2 2  1  0,25  T    800 1 K T 1 1 0,25 1
Câu 115: Một cột đồng chất có chiều cao h  11m  , đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ
xuống. Gia tốc trọng trường  2
9,8 m / s  . Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây
A. 16,983m / s
B. 19, 483 m / s  C. 17,98  3 m /  s
D. 17, 483 m / s  Giải h
Ở vị trí thẳng đứng, cột có thế năng: W  mg . t 2 1
Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất: 2 W  I d 2 2 mh
Trong đó: I là moment quán tính của cột đối với trục quay gốc của cột: I  3
 là vận tốc góc của cột lúc chạm đất.
Áp dụng định luật bảo toàn cơ năng:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 h 1 mh 3 2 g mg  .     2 2 3 h
Vận tốc dài: v  .
 h  3gh  3.9,8.11 =17,983m / s 
Câu 116: Một người đứng cách con đường thẳng một khoảng h  50m để chờ ô tô. Khi thấy đầu ô tô còn cách
mình một đoạn a  20  0 
m thì người ấy bắt đầu chạy (thẳng, đều, theo một hướng nào đó) ra đường để đón gặp
ô tô. Biết vận tốc ô tô là v  36 km / h  . Để có thể gặp được ô tô, người ấy phải chả với vận tốc nhỏ nhất vmin bằng bao nhiêu? A. 2,  5 m / s
B. 3, 25 m / s
C. 3m / s  D. 2,  75 m /  s Giải
Muốn gặp đúng ô tô tại B thì thời gian người chạy từ M tới M phải bằng thời gian ô tô chạy từ A tới B: MB AB  1 2 v 1 v
Sử dụng đinh lý hàm sin trong tam giác ABM, ta có: MB AB  với h sin  2 sin sin a h Từ 1 và 2 1
 sin  . v a v2
Để có thể gặp được ô tô với vận tốc nhỏ nhất thì lúc này người chạy đến đường cũng là lúc xe ô tô đi tới (người
gặp đúng ô tô mà không phải chờ đợi lãng phí thời gian), vì vậy, giữa hướng chạy và vận tộc của người phải có quan hệ: h 1 sin  . v a v2 h v h
Vì với mọi  thì sin   1 nên 1 sin  . 1 v  . 2 v1 a v a 2 hv1  v 
 2,5 m / s 9 km / 2 h min     a
Lúc này, người phải chạy theo hướng MI, với MI  AM 3
Câu 117: Một khối khí lí tưởng có thể tích V  5m  dãn nở đẳng nhiệt từ áp suất 4at đến 2at . Lượng
nhiệt đã cung cấp cho quá trình này là: A. 5 11, 6.10  5 5 5 J 
B. 16,6.10 J 
C. 13, 6.10  J 
D. 14,6.10 J  Giải
Trong quá trình đẳng nhiệt: U  0 mà U
  0  A  Q  Q   A V 2
Công của quá trình đẳng nhiệt V2 A  PdV   1 P 1 V ln V V 1 1
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Áp dụng PT trạng thái của quá trình đẳng nhiệt: 2 V 1 P  1 V 2 P Hay 1 P 4 4 5 A PV ln  2.6.l 2
n .9,8.10  8,318.9,81.10  13,6.10 1 1  J  Q 2 P
Câu 118: Một quả cầu đặc có khối lượng m  1, 4 kg , lăn không trượt với vận tốc v  10 m / đến đập vào 1  s
thành tường rồi bật ra với vận tốc v  8 m /
. Nhiệt lượng tỏa ra trong va chạm đó là 2  s
A. 41,19 J 
B. 39, 22 J 
C. 37, 25 J 
D. 35, 28 J  Giải:
Sau va chạm động năng của vật giảm. Độ giảm động năng này tỏa ra dưới dạng nhiệt
Khi chuyển động, quả cầu vừa có động năng tịnh tiến, vừa có động năng quay 1 1  2  1 1
Động năng của quả cầu đặc, đồng chất, lăn không trượt: 2 2 2 2 2 2 W  I  mR
.  mR   mv dq 2 2 5    5 5 2
Moment quán tính của quả cầu đặc đồng chất: 2 I  mR 5 2
Động năng tịnh tiến của quả cầu đặc: mv W  d tt  2 1 2 1 2 7 2
 W  W + W
 mv  mv  mv d d q dtt 5 2 10 7 7
Nhiệt lượng tỏa ra do va chạm: Q  W    m v  v      J d  2 2 .1, 4  2 2 . 10 8 35, 28 2 1    10 10
Câu 119: Một con lắc toán có sợi dây l  1m  , cứ sau t  1 phút thì biên độ giao động giảm 2 lần. Giảm lượng
loga của con lắc dố bằng giá trị nào sau đây ( cho g   2 9,8 m / s  ) A. 2 1, 728.10 B. 2 2,319.10 C. 2 2,713.10 D. 2 1, 702.10 Giải: x    t 1   1 Theo bài ra, ta có: . .60  e   e     0,01155 A 2 2 0 2 2 2
Chu kỳ T của dao động tắt dần là: T    2 2     g 2 0   l 2 2
Giảm lượng loga của con lắc:   T  .   0,01155.  0,02319 2 2    9,8 2 0 0,01155 1
Câu 120: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 11kW  . Nhiệt độ của nguồn nóng là 0
100 C , nhiệt độ của nguồn lạnh là 0
0 C . Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút có giá trị: A. 3 2,002.10  kJ B. 3 1,802.10 kJ  C. 3 1,502.10  kJ  D. 3 1, 702.10 kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 11 Hay 2  1   Q    41,03 kJ 1   T Q T 273 2 1 1 1 1 T 373 1 Gọi '
Q là nhiệt lượng mà tác nhân nhả cho nguồn lạnh: '
Q  Q  A '  41, 03 11  30,03 1 1 kJ 1
Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là ' 3
Q  Q .t  60.30,03  1,802.10 1  kJ 2
Câu 121: Một tàu điện sau khi suất phát chuyển động trên đường nằm ngang với gia tốc a  0,7 m / s  . 10 giây
sau khi bắt đâu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng hẳn. Hệ số ma sát trên
quãng đường k  0, 01. Cho g   2
10 m / s  . Thời gian chuyển động của toàn bộ tàu là
A. 66,8 s B. 74,8 s C. 8  0  s D. 68, 4  s Giải
Tầu chuyển động theo hai giai đoạn:
Giai đoạn 1: chuyển động với gia tốc a  0,7 2 m /
với thời gian t  10 1 s 1 s 
Giai đoạn 2: chuyển động chậm dần đều với gia tốc a  k.g  0,01.10  0,  2 1 m /
dưới tác dụng cản của lực 2 s 
ma sát trong thời gian t 
Vận tốc lớn nhất của tàu: v
 a .t  0,7.10  7 m/ s max 1 1   v 7
Tầu chuyển động chậm dần đều trong thời gian: max t     70s a 0,1 2
Thời gian chuyển động của toàn bộ tàu là t  t  t  70 10  80 2 1  s
Câu 122: Một người đẩy xe một lực hướng xuống theo phương hợp với phương ngang một góc 0   30 . Xe có
khối lượng m  240 kg và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường 2
k  0, 24 . Lấy g  9,8 
1 m / s  . Lực đẩy của người có giá trị bằng: A. 764,3  1 N 
B. 752,81 N  C. 755,1  1 N D. 757, 4  1 N  Giải
Chọn chiều dương cùng chiều chuyển động
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Khi xe chuyển động, chịu tác d ng c ụ
ủa các lực: Trọng lực P , phản lực N ' , lực đẩy F ' và lực ma sát f ' ms
Vì xe chuyển động với vận tốc không đổi nên a  0
Áp dụng định luật II Newton, ta có: P  N ' f  F ' 0   1 ms
Chiếu 1 lên trục Oy: N ' F '.sin  P  0
Chiếu 1 lên trục Ox: F '.cos  f '  0  F '.cos  f ' ms ms
Mà lực ma sát tác dụng lên xe: f '  k.N '  k P  F '.sin ms  Hay '.
  .   '.   ' kP F cos k P F sin F   757,42 N 
cos  k.sin
Câu 123: Một hòn đá được ném theo phương ngang từ độ cao đủ lớn với vận tốc v  12 m / . Gia tốc pháp 0  s
tuyến của hòn đá sau giây thứ 2 có giá trị bằng (lấy g   2 9,8 m / s  ) A.  2 4,617 m / s  B.  2 5,117 m / s  C.  2 5,867 m / s  D.  2 4,867 m / s  Giải Vận tốc c a
ủ vật theo phương thẳng đứng sau khi ném 2s : v  gt  2.9,8 19,6 m / s y 
Góc  giữa vận tốc của vật và phương thẳng đứng thỏa mãn: v x tg  . Xem hình vẽ vy
Từ đó, gia tốc pháp tuyến và gia tốc tiếp tuyến c a
ủ vật lúc này chính là những phần chiếu c a ủ gia tốc g: . g v 9,8.12 a  g . x sin    5,117 m s n  2 /  2 2 2 2 v  v 12 1  9,6 x y
Câu 124: Tổng động năng tịnh tiến trung bình của các phân tử khí Nito N
chứa trong một khí cầu bằng 2  3 3
W  5, 6.10 J  và vận tốc căn quân phương của phân tử khí đó là v  2.10  m / s . Khối lượng khí nitơ trong e  khí cầu là: A. 3 2,8.10  3  3  3 kg 
B. 2,97.10  kg
C. 3,31.10 kg 
D. 2, 46.10  kg Giải
Tổng động năng tịnh tiến trung bình của các phân tử khí Nito N là 2  3 1 2 2W 2.5, 6.10 3 W mv m 2,8.10      kg e   2 2 ve  3 2.10 2
Câu 125: Một động cơ làm việc theo chu trình Carnot với tác nhân là không khí. Nhiệt độ ban đầu là 0 127 C ;
thể tích của không khí sau lần giãn đẳng nhiệt V  5  3 2
dm  và sau khi giãn đoạn nhiệt nó chiếm thể tích V  8,1 3 3
dm . Hiệu suất của động cơ có giá trị:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP A. 15,549% B. 13,549% C. 17,549% D. 11,549% Giải
Giai đoạn 1: quá trình đẳng nhiệt T  const   T  T  400 K 1 2  
Giai đoạn 2: Qúa trình đoạn nhiệt
Áp dụng phương trình TT cho quá trình đoạn nhiệt:  1  1,4 1     1   1  V  5  2 T V  T V
 T  T    400.  329,8 K 2 2 3 3 3 2     V    8,1 3  T 329,8
Hiệu suất của động cơ: 3  1  1   0,15549 15,549% T 400 2
Câu 126: Một tụ đặc trưng khối lượng M  105kg  , bán kính R  0,6m đang quay xung quanh trục của nó.
Tác dụng lên trụ một lực hãm F  257,3 N  tiếp tuyến với mặt trụ và vuông góc với trục quay. Sau thời gian t   2,6 
s , trụ dừng lại. vận tốc của góc trụ lúc bắt đầu lực hãm là:
A. 21, 237 rad / s
B. 20, 444 rad / s
C. 1, 404 rad / s D. 0,61  1 rad / s Giải   
Gia tốc góc của trụ đặc: 0 0     t t
Moment hãm tiếp tuyến với mặt trụ: M  F .R  I. t 2
Moment quán tính đối với trụ đặc: R I  M 2 2 R 2.
 F .R  M . Ft      8,168 rad s t  2 /  2 MR
Vận tốc của góc trụ lúc bắt đầu lực hãm là   . t   21,237 rad / 0  s 
Câu 127: Khối lượng riêng của một chất khí 2     3 8.10
kg / m  ; vận tốc căn quân phương của các phân tử khí
này là v  600 m / s  . Áp suất của khối khí tác dụng lên thành bình là: A.  2 9900 N / m  B.  2 9800 N / m  C.  2 9500 N / m  D.  2 9600 N / m  Giải PV m PV RT PV P P
Áp dụng PT trạng thái khí lí tưởng: n        RT  RT  m m  V 2 3
Vận tốc căn quân phương của các phân tử khí: RT RT vC v    C   3 2 2 P v v C C    P     2 . 9600 N / m   3 3
Câu 128: Một khối khí ôxy 
bị nung nóng từ nhiệt độ 320 K  đến 0 287 2 O 
C . Nếu vận tốc trung bình của
phân tử ôxy lúc đầu là v thì lúc sau là: A. 1, 35v B. 1, 55v C. 1, 5v D. 1, 6v Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 8
Công thức tính vận tốc trung bình của phân tử khí: kT v  m  8k 1 T   1 v  m v T 267  273 Hay 2 2      1,323  8 v T kT 240 1 1 2 v  2  m
Câu 129: Một ô tô khối lượng m  1, 6 tấn đang đi trên đường phẳng nằm ngang với tốc độ 22 m / s  bỗng nhiên
phanh lại. Ô tô dừng lại sau khi trượt thêm 25m . Độ lớn trung bình của lực ma sát là: A. 3 16,388.10 N  B. 3 15, 488.10 N  C. 3 15,788.10  N  D. 3 16,088.10  N  Giải 2 2 2 2 v  v 0 22 Gia tốc: 0 a    9,68 2 m / s  2s 2.25
Độ lớn trung bình của lực ma sát là: F  ma  9,68.1, 6.1000  15  488 N ms 
Câu 130: Một xe lửa gồm nhiều toa được đặt trên các lò xo của hệ thống bánh xe. Mỗi lò xo của to axe chịu một trọng lượng 4
P  5.10 N nén lên nó. Xe lửa bị rung động mạnh nhất khi nó chạy với tốc độ v  26m / s qua
các chỗ nối của đường ray. Độ dài mỗi thanh ray bằng l  12,5m. Hệ số đàn hồi của các lò xo nhận giá trị nào
dưới đây (cho g   2 9,8 m / s  ) A. 4 82,64.10  4 4 4 N
B. 88,64.10  N
C. 87, 4.10  N 
D. 84,14.10  N Giải
Con lắc dao động mạnh nhất khi xảy ra cộng hưởng (chu kỳ dao động riêng của vật trùng chu kỳ qua các chỗ nối S 12,5
của đường ray): T    0,48 s v 26 4 P 5.10 Mặt khác: 4
P  5.10 N   mg  m    5102,04kg  g 9,8 2 2 m 4 .m 4 .5102,04 Mà T  2  0,48s 4  k  
 87,4.10 N / m 2 2   k T 0, 48
Câu 131: Ở thời điểm ban đầu một chất điểm có khối lượng m  
1 kg có vận tốc v 16 m / . Chất điểm 0  s
chịu lực cản F  rv ( biết r  ln2 , v là vận tốc chất điểm). Sau 2s vận tốc của chất điểm là: e
A. 2,8 m / s
B. 4,4 m /  s
C. 4 m / s
D. 3, 2 m / s Giải dv
Lực cản: F  ma  mv'  m e dt Mặt khác: dv dv r F  r  v  m  r  v    dt e dt v m v t r l 2 n dv r v r  t  .2 Lấy tích phân: m 1
  dt  ln
  t  v  v .e 16.e  4 m /   0  s v m v m v 0 0 0
Câu 132: Nguyên lý thứ nhất của nhiệt động học khẳng định rằng
A. Nội năng của một hệ nhiệt động luôn luôn được bảo toàn
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
B. Không thể chế tạo được động cơ vĩnh cửu loại 1
C. Không thể chế tạo được động cơ vĩnh cửu loại 2
D. Một hệ nhiệt động cô lập không thể hai lần đi qua cùng một trạng thái
Câu 133: Một hạt chuyển động trong mặt phẳng xy từ điểm 1 có bán kính véctơ r  i  2 đến điểm 2 có 1  jm
bán kính véctơ r  2i  3 , đơ
ị trong tọa độ Đecac. Hạt chuyển động dưới tác 2 
j m i và j là các vector n v
dụng của lực có biểu thức F  3i  4 j N  . Công thực hiện bởi lực đó là: A. 5 J 
B. 17 J C. 2  3 J  D. 17 J  Giải
Công thực hiện bởi lực đó là:
F.r .r  A  3 2 1  4 3
  2  A  A  17 1 2      J 
Câu 134: Chất điểm bắt đầu chuyển động trên đường tròn bán kính R  2 m . Vận tốc của chất điểm phụ thuộc
vào quãng đường đi được S theo công thức v  a S a   1/2 ;
2 m / s; .Góc  giữa vector vận tốc v và gia tốc
toàn phần  sau 3s được xác định bởi
A. tg  8,6 B. tg  9
C. tg  9, 2
D. tg  9,6 Giải Theo bài ra, ta có 2
v  a S  2 S  v  4S v  0 0  Áp dụng công thức: 2 2 v  v  2  0 a S  t a  2 m s  t  2 /  
 v  a .t  2.3  6m / s t  2 2 v 6  a   18 m s n  2 /  R 2 a 18
Góc  giữa vector vận tốc v và gia tốc toàn phần  sau 3s: n tg    9 a 2 t
Câu 135: Một động cơ làm việc theo chu trình Carnot với tác nhân là không khí. Nhiệt độ ban đầu là 0 127 C ; thể
tích của không khí sau lần giãn đẳng nhiệt V  5,5 3 2
dm  và sau khi giãn đoạn nhiệt nó chiếm thể tích V  8,6 
3 . Hiệu suất của động cơ có giá trị: 3 dm  A. 16,373% B. 22,373% C. 18,373% D. 20,373% Giải
Giai đoạn 1: quá trình đẳng nhiệt T  const   T  T  400 K 1 2  
Giai đoạn 2: Qúa trình đoạn nhiệt
Áp dụng phương trình TT cho quá trình đoạn nhiệt:  1  1,4 1     1   1  V  5,5  2 T V  T V  T  T  400.  334,51 2 2 3 3 3 2   K    V    8,6 3  T 334,51
Hiệu suất của động cơ: 3  1  1   0,16373 16,373% T 400 2
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 136: Một con lắc toán có sợi dây l  55m. Biết rằng sau thời gian   6 phút, nó mất 99% năng lượng.
giảm lượng lôga của con lắc nhận giá trị nào dưới đây (cho g   2 9,8 m / s  ) A. 2 0,975.10 B. 2 1,125.10 C. 2 1, 035.10 D. 2 1, 065.10 Giải
Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:
F  F  kx  rv C
Phương trình cơ bản của chuyển động trong trường hợp này là ma  kx  rv 2 2 Hay: d x dx d x r dx k m  r   kx    x  0 1 2 2 dt dt dt m dt m Đặt r   (hệ số tắt dần) 2m 2 d x dx
Phương trình 1 trở thành 2 x  2  x  0 2 2 0 dt dt
2 gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi    , nghiệm phương trình 0 này có dạng:  t x     0 A e cos  t 
Đây là biểu thức độ dời của dao động tắt dần. Hằng số  gọi là tần số của dao động tắt dần: 2 2      0 2 2 2
Chu kỳ T của dao động tắt dần là: T    2 2     g 2 0   l 2
Giảm lượng loga của con lắc:   T   .  2 2    0  g 9,8 49 Theo bài ra, ta có: 2   . t  2   .6.60 3   e  0,01 e
 0,01   6,396.10 và 2      0 l  55 275 0 2 3 2    .  6,396.10 .  0,0952 2 2    49 6,396.10 2 3 0 275
Câu 137: Một vệ tinh có khối lượng m  15 
0 kg chuyển động trên quỹ đạo tròn bán kính 6
r  7, 6.10  m quanh
Trái Đất. Cho khối lượng trái đất 24
M  5,98.10  k 
g . Hằng số hấp dẫn 11 G   2 2 6,67.10
N.m / kg . Tốc độ vệ
tinh trên quỹ đạo đó là:
A. 6,344km / s
B. 6,644 km / s
C. 7, 244 km / s
D. 6,944km / s Giải
Lực hấp dẫn của trái đất cũng đóng vai trò là lực hướng tâm: 2 M .m M .   .  .  . m  .v GM F F G m a G m  v 
 7,244 km / s hd ht 2 ht 2   r r r r
Câu 138: Một chất điểm dao động điều hòa với chu kì 1, 6 s  và biên độ 7 cm . Vận tốc chất điểm trên tại vị 1
trí mà ly độ bằng biên độ bằng giá trị nào dưới đây: 2
A. 0, 218m / s
B. 0, 248m / s
C. 0, 208 m / s
D. 0, 238m / s Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Áp dụng phương trình về mối liên hệ của , A x, v : 2 2       2 2 v 2 2 2 2 A 2 2 2 A  x 
 v  A  x  A   0,07  0,035  0, 238     m/ s   T  2  1,6
Câu 139: Một khối khí ôxy 
có khối lượng riêng là    3
0,56 kg / m  . Số Avôgađrô 2 O  26
N  6,023.10  J / kmol  . Tỷ số áp suất khí và động năng tịnh tiến trung bình của phân tử khí là: A. 24 5,967.10  24 24 24 Pa / J 
B. 7,557.10  Pa / J 
C. 8,617.10 Pa / J 
D. 7,027.10  Pa / J  Giải 1 2
Dạng phương trình thuyết động lực học phân tử: p  0 n mv 3  N Trong đó: 
n là mật độ phân tử trong 1 đơn vị thể tích  0 n  0   V 
N tổng số phân tử khí có trong thể tích V
m là khối lượng phân tử khí 2
v vận tốc toàn phương TB của 1 phân tử khí 2 1 2 2 mv 2 p 2 2 N 2  Có N p  n mv  n .  n W 24   n    7,027.10 Pa / 0  J  0 0 0 3 3 2 3 d W 3 3 V 3  d
Câu 140: Từ đỉnh tháp cao 18m người ta ném 1 hòn đá khối lượng m  5 
8 g theo phương nghiêng với mặt
phẳng nằm nagng một góc 0
  30 , với vận tốc ban đầu v  16 m / . Khi rơi tới đất hòn đá có vận tốc 0  s
v  21 m / s  . Công của lực cản của không khí lên hòn đá là: ( cho g   2 10 m / s  )
A. 5,775 J B. 2  ,97  5 J
C. 3, 675 J 
D. 5,075 J  Giải
Công của lực cản của không khí lên hòn đá là: 2 2 2 2  mv mv   0,058.21 0, 058.16  0 A     mgh     J c 0, 058.10.18 5, 075      2 2   2 2 
Câu 141: Một động cơ nhiệt có hiệu suất 25 %  và nhả nhiệt cho một nguồn có nhiệt độ 900 K . Nó nhận
nhiệt từ một nguồn có nhiệt độ ít nhất là:
A. 1200 K 
B. 1193 K  C. 122  1 K 
D. 1214 J  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 T T 900 2 2   1  0,25  T    1200 1  K T 1 1 0, 25 1
Câu 142: Một động cơ nhiệt làm việc theo chu trình Carnot với nhiệt độ nguồn nóng là 0
90 C . Trong mỗi một
chu trình tác nhân nhận của nguồn nóng một nhiệt lượng 10 kcal  và thực hiện công15kJ  . Nhiệt độ của nguồn lạnh là:
A. 235, 32  K 
B. 230,32 K 
C. 231,32 K 
D. 232,32 K 
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP Giải
Hiệu suất theo chu trình Carnot: 2  1 T  T1
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' T A'  A'   15  Hay 2 2  1   1  T  T 1  363. 1    232,92 2 1 K    T Q T Q Q    10.4,186 1 1 1 1 1 
Câu 143: Một khẩu pháo có khối lượng M  450kg  bắn một viên đạn theo phương làm với mặt ngang một góc 0
  60 . Khối lượng của viên đạn m  
5 kg , vận tốc đầu nòng v  400 m / s  . Khi bắn bệ pháo giật lùi về
phía sau một đoạn s  55 cm . Lực cản trung bình tác dụng lên quả pháo có giá trị: A. 2  320,2 N  B. 1  920,2 N  C. 2  220,2 N  D. 2  020,2 N  Giải
Theo định luật bảo toàn động lượng thì vận tốc giật lùi c a ủ khẩu pháo là: 0 . m . v cos 5.400.co 6 s 0 20 V       m / s  M 450 9
Dấu " " chứng tỏ pháo giật lùi, ngược chiều dương) 2 V Áp dụng công thức: 2 2
V V  aS  a      2 ' 2 4, 49 m / s  2S
Lực cản trung bình tác dụng lên quả pháo: F  Ma  4,49.450  2020,  2 N C 
Câu 144: Khối lượng riêng của một chất khí 2     3 9.10
kg / m  ; vận tốc căn quân phương của các phân tử khí
này là v  400m / s . Áp suất của khối khí tác dụng lên thành bình là: A.  2 4800 N / m  B.  2 5100 N / m  C.  2 4700 N / m  D.  2 4600 N / m  Giải PV m PV RT PV P P
Áp dụng PT trạng thái khí lí tưởng: n        RT  RT  m m  V 2 3
Vận tốc căn quân phương của các phân tử khí: RT RT vC v    C   3 2 2 P v v C C    P     2 . 4800 N / m   3 3
Câu 145: Một động cơ nhiệt hoạt động theo chu trình Carnot thuận nghịch giữa 2 nguồn điện có nhiệt độ 800 K 
và 200 K  . Nếu nó nhận 1 lượng nhiệt 8kJ  của nguồn nóng trong mỗi chu trình thì công mà nó sinh ra trong mỗi chu trình là: A. 4kJ  B. 5kJ  C. 3kJ  D. 6kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' T A'  T   200  Hay 2 2 2  1    1
 A'  Q 1   8. 1  6 1   kJ T Q T Q T    800 1 1 1 1 1
Câu 146: Một quả cầu có khối lượng m  100 g  được gắn vào đầu sợi dây có khối lượng không đáng kể. Một
đầu dây gắn vào điểm O cố định. Sợi dây có chiều dài l  50cm . Cho vật chuyển động tròn quanh O trong mặt
phẳng đứng. Tại vị trí cao nhất B quả cầu có vận tốc v  3, 2 m/ s . Lấy g   2
9,81 m / s  . Sức căng của sợi dây n 
tại vị trí thấp nhất A có giá trị A. 9,95  3 N B. 7,95  3 N C. 6,95  3 N
D. 5, 953 N  Giải
Chọn mốc thế năng tại vị trí A 1 1 Ta có: 2 2 2 2 W  W  mv  0 
mv  mgh  v  v  2gh A B 2 A 2 B B A B B 2  v  29,86 A
Áp dụng định luật II Newton tại điểm A chiếu lên phương dây treo, ta có: 2 2 mv mv A A T  P  mg   6,953N  l l
Câu 147: Một đĩa tròn đồng chất bán kính R  0, 2 m  , có thể quay xung quanh một trục nằm ngang vuông góc R
với đĩa và cách tâm đĩa một đoạn
. Đĩa bắt đầu quay từ vị trí cao nhất của tâm đĩa với vận tốc đầu bằng 0. Vận 2
tốc khi tâm đĩa ở vị trí thấp nhất là ( g   2 9,8 m / s  )
A. 36,725 rad / s
B. 11, 431rad / s C. 37,  698 rad /  s
D. 12, 404 rad / s  Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Tại vị trí cao nhất và vị trí thấp nhất khoảng cách giữa hai khối tâm là R. Chọn mốc thế năng là vị trí thấp nhất
cho tiện. Như vậy ở vị trí cao nhất năng lượng của đĩa tròn dưới dạng thế năng và có dạng: W  mgR t 2 
Tại vị trí thấp nhất năng lượng của đĩa có dạng động năng (thế năng bằng ) 0 và có dạng: I W  d 2 2 2 1  R 3
Moment quán tính của thanh đối với trục quay: 2 mR I  mR  m  2  2    4 2 1 1 3mR 3 8
Áp dụng định luật bảo toàn năng lượng: 2 2 2 g mgR  I 
  g  R     11,43  1 rad / s 2 2 4 8 3R
Câu 148: Hai quả cầu A và B được treo ở hai đầu sợi dây mảnh không dãn dài bằng nhau. Hai đầu kia của các
sợi dây được buộc vào một cái giá sao cho các quả cầu tiếp xúc với nhau và tâm của chúng cùng nằm trên một
đường nằm ngang. Khối lượng của các quả cầu m  165 g và m  750 g . Kéo quả cầu A lệch khỏi vị trí B   A  
cân bằng đến độ cao h  6cm và thả ra. Sau va chạm, quả cầu B được nâng lên độ cao là: (coi va chạm là hoàn
toàn không đổi, cho g   2 9,8 m / s  )
A. 1, 764 mm B. 7,99  1 mm
C. 7,804mm D. 1,95  1 mm Giải
Trường hợp a: va chạm hoàn toàn đàn hồi
Định luật bảo toàn động lượng: m   1v1 m1 1 V m2V2
Chiếu lên trục ta có: giả sử sau khi va chạm mỗi vật chạy về 1 hướng    1 1 m 1 v 1 m 1 V 2 m 2 V
Định luật bảo toàn cơ năng: thế năng của vật m chính bằng động năng của nó trước khi va chạm và bằng tổng 1 2 2 2 động năng của vật m v m V m V m sau khi va chạm: 1 1 1 1 2 2 m gh    2 1 m và 2 1 2 2 2
1: m v  mV  m V  m v V  m V 1 1 1 1 2 2 1  1 1  2 2 2 2 2 2 : 1 m 1 v 1 m 1 V 2 m 2 V m gh     m v V  m V 1 1  2 2 1 1  2 2 2 2 2 2 2 2 Lấy 1 m 1 v m gh   v  2
  v V V và gh 1 1 1 2 1 1 2 m m
Thay ngược lại vào  
1 để tìm mối quan hệ giữa V và      1 v : 1 m  1 v 1 V  2 m  1 v 1 V  2 1 1 1 V 1 v m  2 1 m 2m
Tượng tự tìm được mỗi quan hệ giữa V và V  v 2 v : 1 1 2 1  1 m 2 m
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 1 m v 2 1 
Sau va chạm, quả cầu B được nâng lên độ cao là 2 V 1 m 2 m  3 h    7,804.10 m  mm B   7,804  2g 2g
Câu 149: Một vật cố khối lượng m  1 
2 kg bắt đầu trượt từ đỉnh dốc một mặt phẳng nghiêng cao h  24cm .
Khi tới chân dốc có vận tốc v  1  5 m /  s . Cho g   2
10 m / s  . Công của lực ma sát là
A. 1520 J 
B. 1544,6 J  C. 1537,  3 J 
D. 1508,1 J  Giải
Chọn mặt đất làm gốc tính thế năng W  0 , chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu t 
tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường,
hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát: 2 2  mv   m  0 v A
 W  W    mgh   mgh f 2 1 0  ms  2   2 
Thay số: v  0,h  0,2 m ,v  15 m / s , h  0 0 0     1 2  A 
mv  mgh  1321, 2 J f 0   ms 2
Câu 150: Một chất điểm có khối lượng m  230 g được ném lên từ điểm O trên mặt đất với vận tốc v  13 m /
theo phương hợp với phương ngang một góc 0
  30 . Bỏ qua sức cản của không khí, lấy 0  s g   2
9,81 m / s . Mômen động lượng của chất điểm đối với điểm O sau 1s  kể từ khi ném có giá trị là: 2 2 2 2
A. 13, 22 kg.m / s 
B. 13, 739kg.m / s C. 12,70 
1 kg.m / s
D. 11,144 kg.m / s  Giải
Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí bắt đầu ném, chiều
dương hướng xuống, cùng chiều với gia tốc g a  0 Gia tốc:  x  a    g y 
v  v  a .t  v .cos   Vận tốc: x 0 x x 0 
v  v  a t  v .sint  gt  y 0 y y 0 
Phương trình chuyển động của chất điểm:  1 2
Ox :x  v t  a t
Ox :x  v .cos .t 0 x x 0  2     1 2 1    2 Oy : y v sin .t gt   0
Oy :y  v  0 t a t  y y 2  2
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Động lượng p tại thời điểm t bất kì: 
p t  p i  p j  mv i  mv j x y x y
Xét tích có hướng của hai vector: u  u i  u j  u k và v  v i  v j  v k 1 2 3 1 2 3 . u v     1 u 2 u 3 u i j k 2 v 3 v 1 v 3 v 1 v 2 v 1 v 2 v 3 v
Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới trục z coi như bằng 0 r.v  v v 0  i  j 
k  v y  v x k x y  . . x y  y 0 x 0 x y x y 0
Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là:  
L  v y  v x  v cos t m v sin  gt  mv cos v si n t   gt x . y . . . .  1 2  . 0 0 0 0   2  1 2 1 0 2
 mgv t cos  .0, 23.9,81.13.co 3 s 0 .1  12,70  2 1 kgm / s 0  2 2
Câu 151: Một động cơ làm việc theo chu trình Carnot với tác nhân là không khí. Nhiệt độ ban đầu là 0 127 C ;
thể tích của không khí sau lần giãn đẳng nhiệt V  6  3
và sau khi giãn đoạn nhiệt nó chiếm thể tích 2 dm  V  9,1
3 . Hiệu suất của động cơ có giá trị: 3 dm  A. 17,347% B. 11,347% C. 9,347% D. 15,347% Giải
Giai đoạn 1: quá trình đẳng nhiệt T  const   T  T  400 1 2 K 
Giai đoạn 2: Qúa trình đoạn nhiệt
Áp dụng phương trình TT cho quá trình đoạn nhiệt:  1 1,41    1   1  V  6  2 T V  T V
 T  T    400.  338,61 K 2 2 3 3 3 2     V    9,1 3  T 338, 61
Hiệu suất của động cơ: 3  1  1   0,15347 15,347% T 400 2
Câu 152: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 12 kW  . Nhiệt độ của nguồn nóng là 0
100 C , nhiệt độ của nguồn lạnh là 0
0 C . Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút có giá trị: A. 3 2, 266.10 kJ  B. 3 1,966.10 kJ  C. 3 1,866.10  kJ  D. 3 1, 766.10 kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  T1
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 12 Hay 2  1   Q    44,76 kJ 1   T Q T 273 2 1 1 1 1 T 373 1 Gọi '
Q là nhiệt lượng mà tác nhân nhả cho nguồn lạnh: '
Q  Q  A '  44,76 12  32,76 1 1 kJ 1
Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là '
Q  Q .t  60.32, 76  1965, 6 1  kJ
Câu 153: Một xe lửa gồm nhiều toa được đặt trên các lò xo của hệ thống bánh xe. Mỗi lò xo của to axe chịu một trọng lượng 4
P  5.10 N nén lên nó. Xe lửa bị rung động mạnh nhất khi nó chạy với tốc độ v  26m / s qua
các chỗ nối của đường ray. Độ dài mỗi thanh ray bằng l  12,5m. Hệ số đàn hồi của các lò xo nhận giá trị nào
dưới đây (cho g   2 9,8 m / s  ) A. 4 82, 64.10  4 4 4 N /  m
B. 88, 64.10  N /  m
C. 87, 4.10  N / m
D. 84,14.10  N /  m Giải Giải
Con lắc dao động mạnh nhất khi xảy ra cộng hưởng (chu kỳ dao động riêng của vật trùng chu kỳ qua các chỗ nối S 12,5
của đường ray): T    0,48 s v 26 4 P 5.10 Mặt khác: 4
P  5.10 N   mg  m    5102,04kg  g 9,8 2 2 m 4 .m 4 .5102,04 Mà T  2  0,48s 4  k  
 87,4.10 N / m 2 2   k T 0, 48
Câu 154: Một thanh chiều dài l  1m  , khối lượng M  7 kg có thể quay tự do xung quanh một trục nằm
ngang đi qua một đầu của thanh. Một viên đạn khối lượng m  0,0 
1 kg bay theo hương nằm ngang với vận tốc
v  300 m / s  tới xuyên vào đầu kia của thanh và mắc vào thanh. Vận tốc gốc của thanh ngay sau khi viên đạn đập vào đầu thanh là: A. 2,  051 rad / s
B. 1, 28 rad / s 
C. 1, 794 rad / s
D. 1, 023rad / s Giải
Xét hệ trước va chạm: trước khi va chạm dễ thấy là thanh thì đứng yên. Có
mỗi viên đạn có tốc độ và khối lượng m mang một động lượng p  mv
Muốn tìm mômen động lượng thì phải tìm ra được tâm quay và khoảng cách
từ tâm quay tới phương của vận tốc, nhìn thì biết ngay khoảng cách từ tâm
quay tới viên đạn chính là độ dài l
Vậy mômen động lượng trước khi va chạm là: L  r.p.sin  l.p  mvl t
Xét hệ sau va chạm: Sau khi va chạm thì cả thanh và đạn sẽ chuyển động với
cùng vận tốc góc  . Vậy moomen quán tính của hệ vật sau va chạm:
L  I   I  s 1 2
Với I là moment chất điểm (viên đạn) đối với trục quay 2 I  ml 1 1
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2  l  2 M   2 Ml '  2 Ml 
I là moment quán tính của thanh mảnh    2 I 2 12 12 3 2   Hay Ml
L  I  I   ml   s   2 1 2  3   
Áp dụng định luật bảo toàn động lượng 2   2 Ml mvl v
L  L  mvl  ml          1, 28 rad s t s  /  2  3  2 Ml   ml  l 1 M    3  3m 
Câu 155: Một vật nhỏ có khối lượng m buộc vào đầu sợi dây mảnh chiều dài l  1, 2 m , đầu kia giữ cố định.
Cho vật quay trong mặt phẳng nằm ngang với vận tốc góc không đổi sao cho sợi dây hợp với phương thẳng đứng một góc 0
  30 . Cho g   2
10 m / s  , bỏ qua lực cản không khí. Tốc độ góc có giá trị:
A. 3, 202rad / s
B. 2,902 rad / s
C. 3, 402 rad / s D. 3,10  2 rad /  s Giải
Chọn mốc thế năng tại vị trí căn bằng, chiều dương hướng xuống
Trong quá trình dao động, vật chịu tác dụng của các lực: trọng lực P, lực căng dây T  và lực hướng tâm F ht
Áp dụng định luật II Newton, ta có: P T  F  0 1 ht
Chiếu 1 lên trục Ox: 0 0
F T .sin30  0  F  T.si 3 n 0 ht ht Chiếu  mg 1 lên trục Oy: 0 P T
 cos 0  P Tcos mg T.cos30 T  0 co 3 s 0 3 0 0
 F  T.sin30  mg.tan30  mg ht 3 Mà 2 2 0
F  ma  m .R  m .l.si 3 n 0 ht ht mg 1 g 2 2 0 2  . . 30    . g m l sin l    
 3,102 rad / s  3 2 3 3l
Câu 156: Từ đỉnh đồi cao, một quả pháo được bắn chếch lên phía trên một góc 0
  30 so với phương nằm
ngang với vận tốc đầu nòng là v  450 m /
. Sau khi bắn một khoảng thời gian t  5s, góc 0  s 𝜑 giữa hướng
của vận tốc quả pháo và hướng của gia tốc toàn phần thỏa mãn giá trị nào dưới đây ( bỏ qua sức cản không khí.
Gia tốc trọng trường bằng g   2 9,8 m / s  A. tg  1  , 614
B. tg  1,814 C. tg  2  ,214 D. tg  2  ,014 Giải
Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí pháo bắt đầu bắn, chiều dương hướng xuống, cùng chiều với gia tốc g
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP a  0 Gia tốc:  x  a    g y 
v  v  a .t  v .cos Vận tốc:  x 0 x x 0  v
  v  a t  v .sint  gt y 0 y y 0 
Phương trình chuyển động của chất điểm:  1 2
Ox : x  v t  a t
Ox : x  v .cos.t 0x x 0  2     1 2 1    2 Oy : y v sin .t gt   0
Oy : y  v  0 t a t  y y 2  2 v Theo hình vẽ, ta có: x tan  vy
v  v .cos    x v . Tại thời điểm cos
t  5 s : 0 0  tan   2,214
v  v . sin  4 g v sin    g y . 4  0 0
Mặt khác: tan  t  an  2  ,214 (do 0    180 )
Câu 157: Một động cơ nhiệt có hiệu suất 20 %  và nhả nhiệt cho một nguồn có nhiệt độ 500 K . Nó nhận
nhiệt từ một nguồn có nhiệt độ ít nhất là:
A. 639 K  B. 625 K  C. 618 K  D. 604 K  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 T T 500 2 2   1  0,2 T    625 1 K T 1   1 0, 2 1 m
Câu 158: Hai hòn bi có khối lượng l  6 vào 1 m và 1 m 
được treo bằng 2 sợi dây có cùng chiều dài m 2 2
một điểm. Kéo lệch hòn bi 1
m cho đến khi dây treo nằm ngang rồi thả ra để nó va chạm vào bi m . Sau va chạm 2
hai hòn bi dính vào nhau và lên tới độ cao cực đại là: ( cho g   2 9,8 m / s )
A. 2,827m
B. 2,907 m
C. 2,667 m
D. 2,747 m Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Áp dụng định luật bảo toàn cơ năng ( cho hệ gồm hòn bi và 1
Trái Đất ; chọn mốc tính thế năng tại vị trí cân
bằng của hòn bi 1 trước va chạm ) ta tính được vận tốc v của hòn bi 1 trước va chạm: 1 m 1 0 v  m gl 
 0  v  2 1 1 gl 2
Ngay sau va chạm cả hai hòn bi có cùng vận tốc v '. Áp dụng định luật bảo toàn động lượng ta có:
m v   m  m  m v m v 2 2 1 1 v ' v '   v  2 2 1 1 2 gl m  m m1 3 3 1 2  1 m 2
Động năng của hệ hai hòn bi sau va chạm là: 2 2 m v ' m v ' 3 1 2 1 2 2 2 W '  
 m v '  m v  mgl d 1 1 2 2 4 3 3
Sau va chạm hai hòn bi dính vào nhau và tiếp nối chuyển động tròn ban đầu của hòn bi 1. Động năng W ' của d 3
hệ hai hòn bi chuyển động thành thế năng W '  m  m gh  m gh của hai hòn bi ở độ cao tối đa h ( chọn t  1 2  1 2 2 3 4
mốc tính thế năng như trên) : W ' W '  m gl  m gh  h  l  2,667 m d t 1 1   3 2 9
Câu 159: Từ đỉnh đồi cao một hòn đá được ném theo phương nằm ngang với vận tốc v  15 m / . Bỏ qua sức 0  s
cản không khí, cho g   2
9,8 m / s  , gia tốc tiếp tuyến của hòn đá sau lúc ném 1 giây là: A.  2 5, 36 m / s  B.  2 3,86 m / s  C.  2 4,86 m / s  D.  2 6,36 m / s  Giải Vận tốc c a
ủ vật theo phương nằm sau khi ném 1s : v  gt  1.9,8  9,8m / s y 
Góc  giữa vận tốc của vật và phương thẳng đứng thỏa mãn: v x tg  . Xem hình vẽ vy
Từ đó, gia tốc pháp tuyến và gia tốc tiếp tuyến c a
ủ vật lúc này chính là những phần chiếu c a ủ gia tốc g:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP g.v 9,8.15 a  g . x sin    8,204 m s n  2 /  2 2 2 2 v  v 15 9,8 x y 2 2 2 2 a  g  a     2 9,8 8, 204 5,36 m / s t n 
Câu 160: Có M  2 
2 g khí đang chiếm thể tích V  4 l  ở nhiệt độ 0
t  27 C . Sauk hi hơ nóng đẳng á, khối
lượng riêng của nó bằng 4     3 6.10
g / cm . Nhiệt độ của khối khí sau khi hơ nóng là:
A. 2850 K B. 2750 K C. 2950 K D. 3050 K Giải Trước khi hơ nóng:
Áp dụng phương trình TT khí lý tưởng: m pV  RT 1 1 1   Sau khi hơ nóng: m m R 2 T pV  RT  p  RT  2 2 2 2  V   2 1 Lấy m 1 T m 1 T  V   T   2750 K 1 2   2 T   2 1 V
Câu 161: Hai khối khí 2
O và H có cùng mật độ số hạt. Nhiệt độ của khối khí 2 O là 0 60 2
C , nhiệt độ của khối khí H là 0 30 2 C . Áp suất của 2
O và H theo thứ tự là 2 1 P và 2 P . Ta có:
A. P  0,899P
B. P  1,199P
C. P  1,399P
D. P  1, 099P 1 2 1 2 1 2 1 2 Giải
Số phân tử khí của chất khí đó là  . m N n N  .N A A  Hằng số Boltzmann RT R 2  3    1,28.10  /  R m     . R k J K N N A V N k  k A
Mật độ phân tử của chất khí đó là ' N mR p n    V k  .V kT Vì hai khối khí  áp suất thay đổi 2
O và H có cùng mật độ số hạt và nhiệt độ thay đổi 2  Qúa trình đẳng tích P T 60 273
Áp dụng PT trạng thái quá trình đẳng tích: 1 1    P 1,099 1 2 P P T 30 273 2 2
Câu 162: Một cột đồng chất có chiều cao h  7 m , đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ
xuống. Gia tốc trọng trường  2
9,8 m / s  . Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây ?
A. 13,846 m / s 
B. 15,846 m / s
C. 15,346 m / s
D. 14,346 m / s  Giải h
Ở vị trí thẳng đứng, cột có thế năng: W  mg . t 2 1
Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất: 2 W  I d 2 2 mh
Trong đó: I là moment quán tính của cột đối với trục quay gốc của cột: I  3
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
 là vận tốc góc của cột lúc chạm đất.
Áp dụng định luật bảo toàn cơ năng: h 1 mh2 2 g 3 mg .      2 2 3 h
Vận tốc dài: v  .h  3gh  3.9,8.8 =14,346m / s x  asin t 
Câu 163: Một chất điểm chuyển động có phương trình: 
. Cho a  b  35cm v
à   10 rad /  s . y  bcos t  
Gia tốc chuyển động của chất điểm có giá trị bằng: A.  2 214,7 m / s  B.  2 236,7 m / s  C.  2
231, 7 m / s  D.  2 246,7 m / s  Giải  a  
x  a.sin  t sin t  Ta có: x   
y  b.cos   t   c  os  t   b   y  2 2     Mà 2   2     1 x y sin t cos t        
1 R  a  b   a   b   PT chuyển động tròn
v  x'  Rcos t  v   y x    Mặt khác: x    v 
 y'  Rsin t v    x   y    y
Mà v  v  v  y2  x2 2 2 2 2  R   2 sin  t   2  cos t   R x y  
 Gia tốc chuyển động của chất điểm (chuyển động tròn): 2 2 2 v R  a    R    2 2   2 0,3. 10 345, 44 m / s ht  R R
Câu 164: Một con lắc toán có sợi dây l  1m  . Biết rằng sau thời gian   7 phút,thì biên độ giảm 2 lần. giảm
lượng lôga của con lắc nhận giá trị nào dưới đây (cho g   2 9,8 m / s  ) A. 2 3,312.10 B. 2 2,898.10 C. 2 3,115.10 D. 2 3,903.10 Giải
Thiết lập phương trình dao động tắt dần của con lắc lò xo. Trong trường hợp này, hợp lực tác dụng lên quả cầu:
F  F  kx  rv C
Phương trình cơ bản của chuyển động trong trường hợp này là ma  kx  rv 2 2 d x dx d x r dx k Hay: m  r   kx    x  0 1 2 2 dt dt dt m dt m r Đặt   (hệ số tắt dần) 2m 2 Phương trình  d x dx 1 trở thành 2 x  2  x  0 2 2 0 dt dt
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
2 gọi là phương trình vi phân của dao động tắt dần. Theo toán học giải tích, khi    , nghiệm phương trình 0 này có dạng:  t x     0 A e cos  t 
Đây là biểu thức độ dời của dao động tắt dần. Hằng số  gọi là tần số của dao động tắt dần: 2 2      0 2 2 2
Chu kỳ T của dao động tắt dần là: T    2 2     g 2 0   l 2
Giảm lượng loga của con lắc:   T   .  2 2    0 x g 9,8   1    1 Theo bài ra, ta có: . t .7.60 3  e   e     1,65.10 và 2     9,8 0 A 2 2 l  1 2  2 3 2    . 1,65.10 .  3,312.10 2 2    9,8  1,65.10 2 3 0
Câu 165: Khối lượng của 1 kmol  chất khí là   26 kg / kmol  và hệ số Poat-xông của chất khí là  1, 4 .
Nhiệt dung riêng đẳng áp của khí bằng (cho hằng số khí 3
R  8, 31.10  J / kmo . l K  ):
A. 1118, 7 J / kg.K 
B. 1079,7 J / k . g K 
C. 1131,7 J / kg.K 
D. 1144,7 J / k . g K  Giải C
Hệ số Poat-xông của chất khí là p   1,4 Cv
Với C và C lần lượt là nhiệt dung mol đẳng áp và nhiệt dung mol đẳng tích p v
Mặt khác: C  C  R  C  C  R p v v p C C  p p R      C  p C C  R  1 v p 3 C  p R 1, 4.8,31.10
Nhiệt dung riêng đẳng áp của khí: c     1118,7 J kg K p  / .      1 261,4   1
Câu 166: Kỷ lục đẩy tạ ở Hà Nội là 12,67 m  . Nếu tổ chức đẩy tạ ở Xanh Pêtecbua trong điều kiện tương tự
(cùng vận tốc ban đầu và góc nghiêng) thì kỉ lục sẽ là: (cho gia tốc trọng trường ở Hà Nội là g  9,72  2 7 m / , 1 s 
ở Xanh Pêtecbua là g  9,810 2 m /
, bỏ qua chiều cao của người đẩy) 2 s 
A. 9,563 m
B. 12,563m C. 11,56  3  m
D. 14,563m Giải 2 v .sin2 Từ công thức tầm xa: 0 L 
ta thấy với lực đẩy không đổi (để v không đổi) và góc ném không đổi (ném 0 g
xa nhất khi góc ném bằng 0
45 ) thì tầm xa L tỷ lệ nghịch với gia tốc trọng trường g. Do đó, có thể xác định kỷ
lục đẩy tạ tại thành phố Xanh Pêtecbua là g 9,727 HN L  .L  .12,67 12,563 m XP HN   g 9,81 XP
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Câu 167: Một trụ rỗng có khối lượng M  44kg , đường kính d  1, 4 m , đang quay xung quanh trục của nó
với tần số n  600 vòng/phút. Tác dụng vào trụ một lực hãm tiếp tuyến với mặt trụ và vuông góc với tr c ụ quay.
Sau thời gian t  2,5 𝑝ℎú𝑡, trụ dừng lại. Độ lớn của lực hãm tiếp tuyến nhận giá trị nào dưới đây
A. 10,522 N  B. 12,90  1 N  C. 12,10  8 N
D. 14,487 N  Giải    20 2
Gia tốc góc của trụ đặc: 0 0         2 rad / s  t t 2,5.60 15
Moment hãm tiếp tuyến với mặt trụ: M  F .R  I. t
Moment quán tính đối với trụ rỗng: 2 I  MR 2 2
 F .R  MR .  F  MR  44.0,7. 12,90 N t t  1  15
Câu 168: Một chất điểm khối lượng m  0, 
1 kg được ném lên từ O với vận tốc v  5 m / theo phương hợp 0  s
với mặt phẳng nằm ngang với một góc 0
  30 , bỏ qua sức cản của không khí, cho g   2
9,8 m / s  . Mômen
động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là: A.  2
0,132 kgm / s B.  2
0,138 kgm / s C.  2
0,678 kgm / s D.  2
0,948 kgm / s Giải
Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí bắt đầu ném, chiều
dương hướng xuống, cùng chiều với gia tốc g a  0  Gia tốc: x  a    g y 
v  v  a .t  v .cos  Vận tốc: x 0 x x 0  v
  v  a t  v .sint  gt y 0 y y 0 
Phương trình chuyển động của chất điểm:  1 2
Ox :x  v t  a t
Ox :x  v .cos .t 0 x x 0  2     1 2 1   2 Oy : y
v sin .t  gt   0
Oy :y  v  0 t a t y y  2  2
Tại vị trí cao nhất của chuyển động chất điểm: v . 0  0  . sint v
v sint  gt  t  y 0 g 2 2 2 2 1 v sin 1 v sin  1 v sin  Và 2 0 0 0
y  h  v sin .t 
gt  v sin .   0 0 2 g 2 g 2 g
Động lượng p tại thời điểm t bất kì: 
p t  p i  p j  mv i  mv j x y x y
Xét tích có hướng của hai vector: u  u i  u j  u k và v  v i  v j  v k 1 2 3 1 2 3 . u v     1 u 2 u 3 u i j k 2 v 3 v 1 v 3 v 1 v 2 v 1 v 2 v 3 v
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Áp dụng vào bài toán của chúng ta và chú ý các thành phần liên quan tới trục z coi như bằng 0 r.v  v v 0  i  j 
k  v y  v x k x y  . . x y  y 0 x 0 x y x y 0
Mômen động lượng của chất điểm đối với O tại vị trí cao nhất của chuyển động chất điểm là:  
L  v .y  v .x  v cos.t.m v sin  gt  mv cos v si n t   gt x y .  1 2 . 0 0 0  0 2    2 2 3 2 1   2 1 v sin v sin 0 0
 mgv t cos  mgv cos  m
cos  0,138 kgm / 0 0 s 2  2  2 2 g 2g
Câu 169: Thả rơi tự do một vật nhỏ từ độ cao h  18,8 m . Quãng đường mà vật rơi được trong 0,1 s cuối
cùng của thời gian rơi là: A. 1, 47  1 m B. 1, 67  1 m C. 1,871m D. 2,47  1 m Giải 2 Thời gian rơi của vật: h t  1  ,96 s g
Quãng đường vật rơi trong 0,1 giây cuối là: 1 1 s   s  s  gt  g         t 2 1 0,1 g t t 0,12 2 2 1,871 m t t 0,1   2 2 2   1 2
Công thức tổng quát cho quãng đường rơi trong n giây cuối là h s g t  t n2 2      t  2   với g
Câu 170: Một đoàn tàu khối lượng 60 tấn chuyển động trên đường ray nằm ngang với vận tốc không đổi bằng
48 km / h . Công suất đầu máy là 260 kW  . Gia tốc trọng trường bằng  2
9,8 m / s . Hệ số ma sát bằng: A. 2 1,322.10 B. 2 4,313.10 C. 2 0,325.10 D. 2 3,316.10 Giải 40
Đổi v  48km / h  m / s 3 3 P 260.10
Ta có: P  F.v  F   19500 N  v 40 3 F 19500 Mà F F mg 19500 N          ms   ms 2 3,316.10 3 mg 60.10 .9,8
Câu 171: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 8kW . Nhiệt độ của nguồn nóng là 0
100 C , nhiệt độ của nguồn lạnh là 0
0 C . Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị: A. 3 1, 01.10 kJ  B. 3 1,31.10 kJ  C. 3 1, 21.10 kJ  D. 3 1,51.10 kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 8 Hay 2  1   Q    29,84 kJ 1   T Q T 273 2 1 1 1 1 T 373 1 Gọi '
Q là nhiệt lượng mà tác nhân nhả cho nguồn lạnh: '
Q  Q  A '  29,84  8  21,84 1 1 kJ  1
Nhiệt lượng tác nhân nhả cho nguồn lạnh, trong một phút là '
Q  Q .t  21,84.60  1310, 4 1 kJ 
Câu 172: Một bánh xe có bán kính R  1  0 c 
m lúc đầu đứng yên sau đs quay quanh trục cảu nó với gia tốc góc    2
3,14 rad / s . Sau giây thứ nhất gia tốc toàn phần của một điểm trên vành bánh là: 2 2 2 2
A. 109, 47 cm / s 
B. 105, 47 cm / s 
C. 103, 47 cm / s 
D. 107, 47 cm / s  Giải
Sau giây thứ nhất, vận tốc góc và vận tốc dài c a
ủ một điểm tren vành bánh là:
  .t  3,14.1 3,14 rad / s  và v R 3,14.0,1 0,314m / s
Gia tốc tiếp tuyến có giá trị không đổi còn gia tốc pháp tuyến lúc này: a   R   m s và 2 2 a   R   m s n  2 . 3,14 .0,1 0,98586 /  t  2 . 3,14.0,1 0,314 /  Gia tốc toàn phần: 2 2
a  a  a  m s  cm s t n  2   2 1, 0347 / 103, 47 / 
Câu 173: Một đĩa tròn đồng chất bán kính R  0,1m  , có thể quay xung quanh một trục nằm ngang vuông góc R
với đĩa và cách tâm đĩa một đoạn
. Đĩa bắt đầu quay từ vị trí cao nhất của tâm đĩa với vận tốc đầu bằng 0. Vận 2
tốc khi tâm đĩa ở vị trí thấp nhất là ( g   2 9,8 m / s  )
A. 74,349 rad / s
B. 16,166 rad / s 
C. 73,376rad / s
D. 15,193 rad / s  Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Tại vị trí cao nhất và vị trí thấp nhất khoảng cách giữa hai khối tâm là R. Chọn mốc thế năng là vị trí thấp nhất
cho tiện. Như vậy ở vị trí cao nhất năng lượng của đĩa tròn dưới dạng thế năng và có dạng: W  mgR t 2 
Tại vị trí thấp nhất năng lượng của đĩa có dạng động năng (thế năng bằng ) 0 và có dạng: I W  d 2 2 2 1  R 3mR
Moment quán tính của thanh đối với trục quay: 2 I  mR  m  2  2    4 2 1 1 3mR 3 8
Áp dụng định luật bảo toàn năng lượng: 2 2 2 g mgR  I 
  g  R     16,  166 rad /  s 2 2 4 8 3R 2
Câu 174: Tác dụng lên một bánh xe bán kính R  0,7 m và có mômen quán tính I  20 kg.m  một lực tiếp
tuyến với vành F  115
. Vận tốc dài của một điểm trên vành bánh sau khi tác dụng lực 15 s  là ( biết rằng 1  N
lúc đầu bánh xe đứng yên)
A. 40,292m / s
B. 48,172 m / s
C. 42, 262 m / s
D. 38,322 m / s Giải
Moment lực không đổi theo thời gian chuyển động: F .R 115.0, 7 1
M  F .R  I .      4,025 rad / 1  2 s  I 20
Vận tốc góc:   .t  4,025.15  60,375rad / s
Vận tốc dài của một điểm trên vành bánh: v  .
 R  42,263m / s
Câu 175: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 60 kW  . Nhiệt độ của nguồn nóng là 0
127 C , nhiệt độ của nguồn lạnh là 0
31 C. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:
A. 14700kJ 
B. 15000kJ 
C. 15100 kJ
D. 15200kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  T1
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 60 Hay 2  1   Q    250 1 kJ  T Q T 304 1 1 2 1 1 T 400 1
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
 Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút: '
Q  Q .t  250.60  15000 kJ 1 1  
Câu 176: Một ống thủy tinh nhỏ khối lượng M  100 g  bên trong có vài giọt ête được đậy bằng 1 nút cố định
có khối lượng m 10 g . Ống thủy tinh được treo ở đầu một sợi dây không giãn, khối lượng không đáng kể, chiều dài 54, 
3 m / s (hình vẽ). Khi hơ nóng ống thủy tinh ở vị trí thấp nhất, ête bốc hơi và nút bật ra. Để ống
có thể quay được cả vòng xung quanh điểm treo O , vận tốc bật bé nhất của nút là: (Cho g   2 10 m / s  ) mỗi chu trình là:
A. 55,1m / s B. 5  0 m /  s
C. 48, 3 m / s  D. 54,  3 m / s Giải
Tại vị trí A, vận tốc tại đây phải đủ lớn để dây thẳng đứng và căng đét  T  0 2 2 v v A A
P T  m T  m
 mg  0  v  gl A l l
Vận tốc nhỏ nhất tại A để ống quay tròn: v  gl Amin
Đối với ống thủy tinh:
Áp dụng định luật bảo toàn cơ năng: 1 2 1 2 1 2 1 2
W  W W  MV  Mv  Mgh  MV 
Mv  Mg 2l B dB tB 2 2 B 2 2 B 2 2
 V  v  4gl B
Vận tốc tối thiểu để đạt đỉnh: 2 v 
gl  V  gl  4 gl  5 gl  V  5 gl B min
Áp dụng định luật bảo toàn động lượng: MV M 5 gl min mv  MV  v    57,01 m s min min min  /  m m
Câu 177: Từ đỉnh đồi cao, một quả pháo được bắn chếch lên phía trên một góc 0
  30 so với phương nằm
ngang với vận tốc đầu nòng là v  600 m /
. Sau khi bắn một khoảng thời gian t  4 s , góc  giữa hướng 0  s
của vận tốc quả pháo và hướng của gia tốc toàn phần thỏa mãn giá trị nào dưới đây ( bỏ qua sức cản không khí.
Gia tốc trọng trường bằng g   2 9,8 m / s 
A. tg  1,992
B. tg  2,894 C. tg  2  ,094
D. tg  2, 294 Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Chọn hệ trục Oxy như hình vẽ. Gốc tọa độ tại vị trí pháo bắt đầu bắn, chiều dương hướng xuống, cùng chiều với gia tốc g a  0  Gia tốc: x  a   g  y
v  v  a .t  v .cos  Vận tốc: x 0 x x 0  v
  v  a t  v .sint  gt y 0 y y 0 
Phương trình chuyển động của chất điểm:  1 2
Ox : x  v t  a t
Ox : x  v .cos.t  0x x 0  2     1 2 1   2 Oy : y v sin .    0 : t gt Oy y  v  0 t a t y y  2  2 Theo hình vẽ, ta có: vx tan  vy
v  v .cos   x v . Tại thời điểm cos
t  5 s : 0 0   tan  1,992 v
  v .sin  4g v sin  g y . 4 0  0
Mặt khác: tan  tan   1,992 (do 0    180 )
Câu 178: Một tàu điện khi xuất phát chuyển động trên đường nằm ngang với gia tốc a   2
0,6 m / s , 13 s  sau
khi bắt đầu chuyển động người ta tắt động cơ và tàu chuyển động cho đến khi dừng lại hẳn. Hệ số ma sát trên
đường k  0, 01 . Cho g   2
10 m / s  . Thời gian chuyển động toàn bộ của tàu là: A. 68, 4  s B. 70 s  C. 74,8s D. 66,8 s Giải
Tầu chuyển động theo hai giai đoạn:
Giai đoạn 1: chuyển động với gia tốc a  0,6 2 m /
với thời gian t 13 1 s  1 s 
Giai đoạn 2: chuyển động chậm dần đều với gia tốc a  k.g  0,01.10  0,1 2 m /
dưới tác dụng cản của lực 2 s 
ma sát trong thời gian t 
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Vận tốc lớn nhất của tàu: v
 a .t 0,6.13  7,8 m/ s max 1 1   v 7,8
Tầu chuyển động chậm dần đều trong thời gian: max t     78s a 0,1 2
Tổng thời gian chuyển động của tầu (kể từ lúc xuất phát đến khi tầu dừng lại) t  t  t   78 13  91 2 1 s
Câu 179: Từ đỉnh tháp cao 18m người ta ném 1 hòn đá khối lượng m  5 
2 g theo phương nghiêng với mặt
phẳng nằm ngang một góc 0
  30 , với vận tốc ban đầu v 16 m /
. Khi rơi tới đất hòn đá có vận tốc 0  s
v  20 m / s  . Công của lực cản của không khí lên hòn đá là: ( cho g   2 10 m / s  )
A. 5,616 J B. 4,   916 J
C. 43,516 J 
D. 7, 016 J  Giải
Công của lực cản của không khí lên hòn đá là: 2 2 2 2  mv mv   0,058.21 0,058.16  0 A    mgh 
 0,058.10.18  5,616 J c        2 2   2 2 
Câu 180: Giả sự lực cản của nước tác dụng lên xà lan tỉ lệ với tốc độ của xà lan đối với nước. Một tàu kéo cung
cấp công suất P  245 mã lực ( 1 mã lực  74 
6 W ) cho xà lan khi chuyển động với tốc độ v  0,25 m / . 1  s 1
Công suất cần thiết để kéo xà lan với tốc độ v  0,75 m / là 2  s A. 2225mã lực B. 2205mã lực C. 2235 mã lực D. 2215 mã lực Giải
Lực cản của nước tỉ lệ với tốc độ của xà lan với nước: 2
F  kv k  const  2 2 2 F   . k v F  v   v  Ta có: 1 1 1 1 2  
    F  F    2205 mã lực 2 1 2
F  k.v  2 F  2 v   1 v 2 2  2
Câu 181: Tác dụng lên một bánh xe bán kính R  0,9m và có mômen quán tính I  20 kg.m  một lực tiếp
tuyến với vành F  125
. Vận tốc dài của một điểm trên vành bánh sau khi tác dụng lực 15 s  là ( biết rằng 1  N
lúc đầu bánh xe đứng yên)
A. 71,997m / s
B. 70,027 m / s
C. 75,937 m / s
D. 77,907 m / s Giải
Moment lực không đổi theo thời gian chuyển động: F .R 125.0,9 1
M  F .R  I .      5,625 rad / 1  2 s  I 20
Vận tốc góc:   .t  5,625.15 84, 375rad / s
Vận tốc dài của một điểm trên vành bánh: v  .
 R 75,937 m / s
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP x  asin t 
Câu 182: Một chất điểm chuyển động có phương trình: 
. Cho a  b  2  5 c  m v
à   10 rad /  s . y  bcos t  
Gia tốc chuyển động của chất điểm có giá trị bằng: 2 2 2 2
A. 256,7m / s 
B. 246,7m / s 
C. 231, 7 m / s 
D. 241, 7 m / s  Giải  a  
x  a.sin  t sin t  Ta có: x      .       b y b cos t cos t   y 2 2  x   y  Mà 2 sin  t   2  cos  t    1       
1 R  a  b   a   b   PT chuyển động tròn
v  x  R  cos t     x '   v y Mặt khác: x   
v  y  R  sin t v     x y '   y   Mà 2 2 v 
v  v  y2  x2 2 2  R   2 sin  t   2  cos t   R x y   2 2 2   v R
Gia tốc chuyển động của chất điểm (chuyển động tròn): 2 a    R    2   2 0,3. 10 246, 7 m / s ht  R R
Câu 183: Tổng động năng tịnh tiến trung bình của các phân tử khí Nito N
chứa trong một khí cầu bằng 2  3 3
W  5, 7.10  J  và vận tốc căn quân phương của phân tử khí đó là v  2.10  m / s . Khối lượng khí nitơ trong e  khí cầu là: 3  3   3 3 
A. 2,68.10 kg 
B. 2,85.10  kg
C. 3,19.10  kg
D. 2,34.10  kg Giải
Tổng động năng tịnh tiến trung bình của các phân tử khí Nito N là 2  3 1 2 2W 2.5.10 3 W mv m 2,85.10      kg e 2 2   2 ve  3 2.10 
Câu 184: Một động cơ nhiệt làm việc theo chu trình Carnot bằng không khí lấy ở áp suất ban đầu P  7, 0 . 1 at
Thể tích ban đầu của không khí V  3,  3 5
. Sau lần giãn đẳng nhiệt lần thứ nhất nó chiếm thể tích 1 dm  3 V  6,5 
3 và sau khi giãn đoạn nhiệt thể tích của khí là V  9,5
. Áp suất khí sau khi giãn đoạn nhiệt 3 dm  2 dm  có giá trị 3 P bằng; A. 4 22,736.10  P  a B. 4 21, 736.10  Pa C. 4 24,736.10  Pa D. 4 19,736.10  Pa Giải
Giai đoạn 1: quá trình đẳng nhiệt T  const  PV 7.3,5
Áp dụng phương trình TT của quá trình đẳng nhiệt: 1 1
PV  PV  P    3,77 1 1 2 2 2 at  V 6,5 2
Giai đoạn 2: Qúa trình đoạn nhiệt
Áp dụng phương trình TT cho quá trình đoạn nhiệt:
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP  1,4     V  6,5 2
PV  PV  P  P    3,77.
 2,22 at  2,22.9,8.10  21,72.10 Pa 2 2 3 3 3 2     4 4   V   9,5 3 
Câu 185: Một trụ đặc khối lượng M  6 
0 kg có thể quay xung quanh một trục nằm ngang trùng với trục của
trụ. Một sợi dây không giãn được quấn nhiêu vòng vào trụ, đùa tự do của dây có treo một vật nắng khố lượng 2
m  40kg  . Để hệ tự chuyện động, sức căng của sợi dây là ( lấy g  9,8 m / s  )
A. 156,81 N 
B. 171, 73 N  C. 168 N 
D. 175, 46 N  Giải Thiếu hình Dưới tác d n ụ g c a
ủ trong lực P lên vật nặng, hệ trụ + vật nặng chuyển động: trụ quay, vật nặng chuyển đ ộng tịnh
tiến (hệ vừa có phần quay vừa có phần tịnh tiến). Vì vậy không thể áp dụng định luật II Newton hay phương trình
cơ bản của chuyển động quay cho toàn bộ hệ. Gọi  là gia tốc góc của trụ, a là gia tốc dài của vật nặng. Vì
chuyển động của vật nặng và chuyển động của một điểm trên mặt trụ có cùng gia tốc nên ta có hệ thức: a  .
 R 1 (R là bán kính của trụ)
Gọi T ' và T là sức căng của dây tại A, ta có: T  T
 ' (tức là T  T ' ) 2
Với T tác dụng lên đoạn dây nối với vật nặng, còn T ' tác dụng lên đoạn dây nối với trụ
Áp dụng định luật II Newton riêng cho vật nặng, ta có: P  T  ma
Chọn chiều dương cùng chiều chuyển động với vật nặng
Chiếu phương trình trên lên phương chuyển động mg  T  ma   3
Áp dụng phương trình cơ bản của chuyển động quay cho riêng trụ đặc, ta có RT '  I  2
Với I là moment quán tính của trụ đặc: MR I    4 2  2mg a  a  5,6    2 m / s 
Từ 1; 2; 3 và 4  2m  M        T  m  g a  T 40  . 9,8 5,  6 16  8 N 
Câu 186: Một viên bi nhỏ m  1 
4 g rơi theo phương thẳng đứng không vận tốc ban đầu trong không khí, lực
cản của không khí F  rv (tỷ lệ ngư c
ợ chiều với vận tốc), r là hệ số cản. Vận tốc cực đại mà viên bi đạt được c bằng 2 v  
60 m / s . Cho g  10m / s  . Hệ số cản có giá trị: max  A. 3
2,333.10  Ns / m B. 3
2,363.10  Ns / m C. 3
2,353.10 Ns / m D. 3
2,343.10  Ns / m Giải
Theo bài ra, ta có: F  rv
 P  mg (Do vật rơi tự do) c max 3 mg 14.10 .10  Hệ số cản: 3 r 2,333.10     Ns / m v 60
Câu 187: Một phi công thực hiện vòng tròn nhào lộn trong mặt phẳng đứng. Vận tốc của máy bay không đổi
v  940 km / h  . Giả sử rằng áp lực lớn nhất của phi công lên ghế bằng 5 lần trọng lực của người. Lấy g   2
10 m / s . Bán kính quỹ đạo vòng nhào lộn có giá trị bằng:
A. 1740,5m
B. 1682,9 m
C. 1672,1m
D. 1715,3 m  Giải
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Áp dụng định luật II Newton cho phi công: mg  N  ma
N là phản lực mà ghế tác dụng lên phi công (bằng và ngược chiều với lực nén của phi công lên ghế).
Áp lực lớn nhất tại điểm thấp nhất
Tại điểm thấp nhất của vòng nhào lộn, theo phương hướng tâm,   1 được viết thành: 2 v mg       2 N ma mg N m ht 2 R
Theo bài ra, ta có: N  5P  5 2 mg 2 2 v v  m
 g  5mg  m  R  1740,5m R 4g
Câu 188: Một máy nhiệt lí tưởng làm việc theo chu trình Carnot, sau mỗi chu trình thu được 605 calo từ nguồn nóng có nhiệt độ 0
127 C . Nhiệt độ nguồn lạnh là 0
27 C . Công do máy sinh ra sau một chu trình
A. 613,13 J 
B. 643,13 J 
C. 663,13 J 
D. 633,13 J  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A'  T   300  Hay 2 2  1 
 A '  Q 1  605.4,186. 1    633,13 1   J  T Q T    400 1 1 1 
Câu 189: Một vật có khối lượng m  2
chuyển động với tốc độ v  6,5 m / tới va chạm xuyên tâm vào 1  s 1 kg
vật có khối lượng m  3
đứng yên. Va chạm là hoàn toàn mềm. Nhiệt lượng tỏa ra trong quá trình va chạm 2 kg  là
A. 26, 25 J 
B. 25, 65 J 
C. 25, 35 J 
D. 25, 95 J  Giải m .v 2.6, 5
Vì va chạm là hoàn toàn mềm nên m .v m m  1 1 .v  v    2,6 m / 1 1 1 2 2 2  s m  m 2  3 1 2
Nhiệt lượng tỏa ra trong quá trình va chạm là: 1 2 1 Q  W W  m v  m  m v  J truoc sau . . .  2 . 25,35 1 1 1 2 2   2 2
Câu 190: Một cột đồng chất có chiều cao h  10 m  , đang ở vị trí thẳng đứng ( chân cột tì lên mặt đất ) thì bị đổ
xuống. Gia tốc trọng trường  2
9,8 m / s  . Vận tốc dài của đỉnh cột khi nó chạm đất bằng giá trị nào dưới đây ?
A. 17,146 m / s 
B. 15,646 m / s 
C. 18,146 m / s
D. 17, 646 m / s  Giải
Ở vị trí thẳng đứng, cột có thế năng: h W  mg . t 2 1
Khi đổ tới mặt đất thì thế năng này biến thành động năng quay của cột ở vị trí chạm đất: 2 W  I d 2
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP 2 mh
Trong đó: I là moment quán tính của cột đối với trục quay gốc của cột: I  3
 là vận tốc góc của cột lúc chạm đất.
Áp dụng định luật bảo toàn cơ năng: h 1 mh2 2 g 3 mg  .     2 2 3 h
Vận tốc dài: v  .h  3gh  3.9,8.8 =17,146m / s
Câu 191: Một bánh xe có bán kính R  1  4 c 
m lúc đầu đứng yên sau đs quay quanh trục cảu nó với gia tốc góc    2
3,14 rad / s . Sau giây thứ nhất gia tốc toàn phần của một điểm trên vành bánh là: A.  2
142,87 cm / s  B.  2
140,87 cm / s  C.  2
144,87 cm / s  D.  2
138,87 cm / s  Giải
Sau giây thứ nhất, vận tốc góc và vận tốc dài c a
ủ một điểm tren vành bánh là:
  .t  3,14.1 3,14 rad / s  và v R 3,14.0,14 0,4396m / s
Gia tốc tiếp tuyến có giá trị không đổi còn gia tốc pháp tuyến lúc này: a   R    2 .
3,14.0,14 0, 4396 m / s và 2 2 a   R    2 .
3,14 .0,14 1, 380344 m/ s n  t  Gia tốc toàn phần: 2 2
a  a  a   2 m s    2 1, 4487 / 144,87 cm / s t n 
Câu 192: Một người đẩy xe một lực hướng xuống theo phương hợp với phương ngang một góc 0   30 . Xe có
khối lượng m  21 
0 kg và chuyển động với vận tốc không đổi. Hệ số ma sát giữa bánh xe và mặt đường
k  0, 21 . Lấy g   2
9,81 m / s . Lực đẩy của người có giá trị bằng: A. 566,1  6 N
B. 563,86 N 
C. 561,56 N
D. 568, 46 N  Giải
Chọn chiều dương cùng chiều chuyển động
Khi xe chuyển động, chịu tác d ng c ụ
ủa các lực: Trọng lực P , phản lực N ' , lực đẩy F ' và lực ma sát f ' ms
Vì xe chuyển động với vận tốc không đổi nên a  0
Áp dụng định luật II Newton, ta có: P  N ' f  F ' 0   1 ms
Chiếu 1 lên trục Oy: N ' F '.sin  P  0
Chiếu 1 lên trục Ox: F '.cos  f '  0  F '.cos  f ' ms ms
Mà lực ma sát tác dụng lên xe: f '  k.N '  k P  F '.sin ms 
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP kP
Hay F '.cos  k. P  F '.sin  F '   568,47 N 
cos  k.sin Câu 193:
Một ôtô chuyển động biến đổi đều lần lượt đi qua hai điểm A và B cách nhau S  20 
m trong khoảng thời
gian t  2 s , vận tốc ô tô ở B là 12 m/s. Vận tốc của ôtô ở A nhận giá trị nào sau đây:
A. 8, 5 m / s B. 6,  5 m / s
C. 8m / s
D. 7 m / s Giải  v  v A B a   t 2S 2 Ta có: S   v  v   v   v  m s A B A B 8  /  2 2 v  v t t  B A a   2S
Câu 194: Một vật khối lượng m bắt đầu trượt không ma sát từ đỉnh một mặt cầu bán kính R  3, 4 m  xuống
dưới. Vật rời khỏi mặt cầu với vị trí cách đỉnh mặt cầu một khoảng là:
A. 1, 603 m  B. 0,92  3  m
C. 1, 273m D. 1,333m Giải
Chọn chiều dương cùng chiều chuyển động c a ủ vật Vật chịu tác dụng c a
ủ các lực: trọng lực P , phản lực N
Áp dụng định luật II Newton, ta có: P  N  ma 1
Vì chuyển động tròn nên gia tốc ở đây đóng vai trò là gia tốc hướng tâm 2 2 Chiếu  v v
1 lên phương chuyển động: Psin  N  ma  m
 N  Psin m ht R R   Theo hình vẽ, ta có: R h sin  R
Khi vật di chuyển xuống dưới thì thế năng của vật giảm dần và biến thành động năng. Như vậy độ biến thiên 2 mv
thế năng phải bằng độ biến thiên động năng của vật: W 
W  mgR  mg R  h    mv  mg h  t d   2 2 2 2 mv R h R
Để vật rời khỏi mặt cầu thì N 0 Psin       0 mg  2mg h   0 h   1,  333 m R R 3
Câu 195: Một động cơ nhiệt làm việc theo chu trình Carnot có công suất 40 kW  . Nhiệt độ của nguồn nóng là 0
127 C , nhiệt độ của nguồn lạnh là 0
31 C. Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút có giá trị:
A. 10000kJ 
B. 9900 kJ
C. 9800 kJ
D. 10300kJ  Giải
Hiệu suất theo chu trình Carnot: 2  1 T  1 T
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN TUẤN TEO TÓP
Với T ;1T lần lượt là nhiệt độ nguồn nóng và nhiệt độ nguồn lạnh 2 A ' Mặt khác:   1 Q
Với A' là công sinh ra trong mỗi chu trình và 1
Q là nhiệt lượng nhận được trong mỗi chu trình T A' A' 40 500 Hay 2  1   Q    kJ 1   T Q T 304 2 3 1 1 1 1 T 400 1  500
Nhiệt lượng tác nhân nhận của nguồn nóng trong một phút: '
Q  Q .t  .60 10000 1 1 kJ  3
Câu 196: Một vật cố khối lượng m  1 
3 kg bắt đầu trượt từ đỉnh dốc một mặt phẳng nghiêng cao h  26cm .
Khi tới chân dốc có vận tốc v  
15 m / s . Cho g   2
10 m / s  . Công của lực ma sát là
A. 867,7 J  B. 853,  1 J C. 875 J 
D. 860, 4 J  Giải
Chọn mặt đất làm gốc tính thế năng W  0 , chiều chuyển động của vật trên mặt dốc là chiều dương. Do chịu t 
tác dụng của lực ma sát (ngoại lực không phải là lực thế), nên cơ năng của vật không bảo toàn. Trong trường,
hợp này, độ biến thiên cơ năng của vật có giá trị bằng công của lực ma sát: 2 2  mv   m  0 v A  W  W   mgh   mgh f 2 1    0  ms  2  2  
Thay số: v  0,h  0, 2 m , v 15 m / s , h  0 0 0     1 2  A 
mv  mgh  1428, 7 J f 0   ms 2
Câu 197: Một khối ôxy  ở nhiệt độ 0 22 2 O 
C . Để nâng vận tốc căn quân phương của phân tử lên gấp đôi, nhiệt độ của khí là: A. 0 877 C B. 0 907 C C. 0 927 C D. 0 897 C Giải 3
Công thức tính vận tốc căn quần phương: kT v 
(với k là hằng số Boltzmann) C m  3k 1 T v  2 2 1  m T  v   v   2  Ta có: 1 1 2  
    T  T    22  273 1 v   1180 2 1  K  3kT T2 v  2 v   1 v   1  2  2 v  m
CLB HỖ TRỢ HỌC TẬP – ĐẠI HỌC BÁCH KHOA HN

Giải chi tiết file tổng hợp đề thi môn Vật lý đại cương I | Đại học Bách Khoa Hà Nội

Thông tin :

Tài liệu liên quan:

Giải bài tập ma trận nghịch đảo

Giáo trình Vật lý đại cương I | Đại học Bách Khoa Hà Nội

Tuyển tập 204 câu hỏi trắc nghiệm môn Vật lý đại cương I | Đại học Bách Khoa Hà Nội

Cách giải các dạng bài tập chương 1: Động lực học | Vật lý đại cương I | Đại học Bách Khoa Hà Nội

Tuyển tập các câu hỏi ôn tập giữa kì môn Vật lý đại cương I | Đại học Bách Khoa Hà Nội