




Preview text:
TRƯỜNG TRUNG HỌC PHỔ THÔNG TÔN THẤT TÙNG
GIẢI NHANH MỘT SỐ BÀI TOÁN TO VẬ V T Ậ LÝ L 12 BẰNG BẰN MÁY MÁ TÍNH
CASIO FX 570ES/VN - VINACAL 2016
TỔ VẬT LÝ - CÔNG NGHỆ
Copyright © by 2016 TỔ VẬT LÝ CÔNG NGHỆ
TRƯỜNG THPT TÔN THẤT TÙNG
Tài liệu được biên soạn nhằm mục đích làm tài liệu giảng dạy cho các đối tượng học
sinh mong muốn rèn luyện khả năng tư duy và giải nhanh một số dạng toán VẬT LÝ
12 bằng máy tính. Nội dung biên soạn bám sát chương trình sách giáo khoa của Bộ
Giáo dục và Đào tạo và được phân loại thành các dạng toán từ cơ bản đến nâng cao.
Các nội dung trong tài liệu bao gồm
• Ứng dụng chức năng SOLVE để tìm nhanh một số đại lượng.
• Viết nhanh phương trình dao động - biểu thức điện áp và cường độ dòng điện.
• Tổng hợp hai hay nhiều dao động điều hòa.
• Ứng dụng chức năng TABLE MODE 7
• Tìm nhanh quãng đường vật thực hiện trong dao động điều hòa.
• Tìm nhanh các đại lượng R, L, C trong hộp kín.
Tài liệu được sưu tầm và biên soạn lần đầu tiên nên không tránh khỏi việc còn nhiều
sai sót. Mọi ý kiến xin vui lòng đóng góp về địa chỉ email: tolycn.thptttt@gmail.com
Lưu hành nội bộ - Đà Nẵng, Tháng 11/2016
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng
ỨNG DỤNG SỐ PHỨC VÀ MÁY TÍNH
GIẢI NHANH MỘT SỐ BÀI TOÁN VẬT LÝ 12
I ĐỊNH NGHĨA SỐ PHỨC - CÁC PHÉP TÍNH TRÊN SỐ PHỨC
1 Định nghĩa số phức
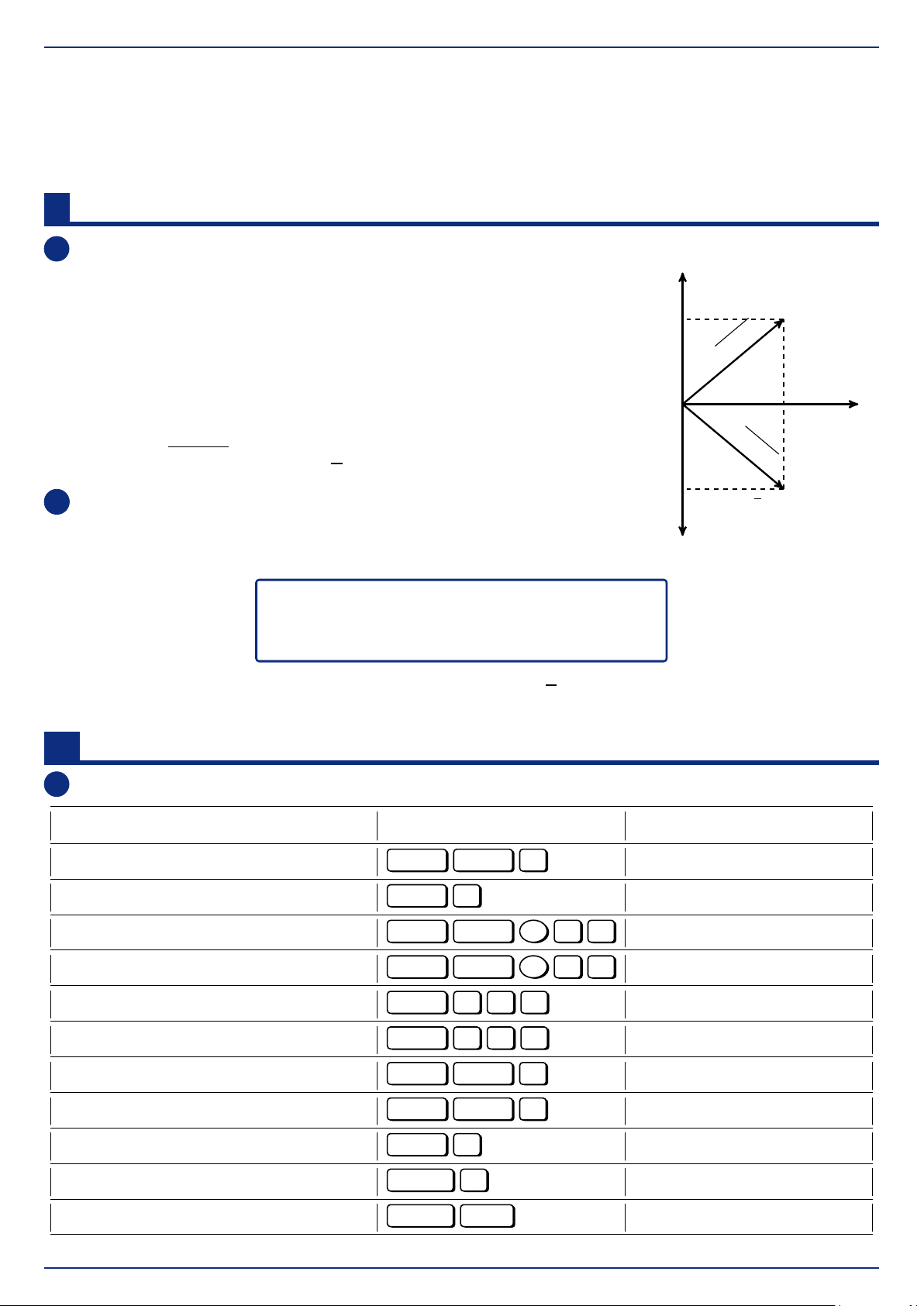
• Số phức là số được viết dưới dạng a + bi, trong đó a, b Trục ảo
là những số thực và số i thoả i2 = −1. z = a + bi b 2
• Kí hiệu là z = a + bi với a là phần thực, b là phần ảo, i là b 2 + a đơn vị ảo. p r =
• Số phức được biểu diễn dưới dạng lượng giác r
z = a + bi = r(cosϕ + isinϕ) = p Trục thực a 2+ p b b với r = a2 + b2 và tanϕ = 2 a –b
2 Biểu diễn hàm điều hòa dưới dạng số phức z = a − bi
Xét hàm điều hòa x = Acos(ωt + ϕ). Biểu diễn x bằng vectơ quay, tại t = 0 ta có ¯ ¯ ( − → − → ¯ A ¯ = OM = A x = Acos(ωt + ϕ) ⇔ A : ¯ ¯ ϕ −−→ = (Ox, OM) ½ a = Acosϕ Ta thấy:
. Tại t = 0 ta biểu diễn x bởi x = a + bi = A(cosϕ + isinϕ) = Aeiϕ b A sin ϕ
II CÁC THAO TÁC CƠ BẢN TRONG TÍNH TOÁN BẰNG MÁY TÍNH
1 Các thao tác nhập xuất trên máy Casio Fx570ES/VN Chọn chế độ Nút bấm Màn hình hiển thị
Chỉ định dạng nhập / xuất toán SHIFT MODE 1 Math
Thực hiện phép tính số phức MODE 2 CMPLX
Hiển thị dạng tọa độ cực SHIFT MODE H 3 2 A∠ϕ
Hiển thị dạng tọa độ Đề các SHIFT MODE H 3 1 a + bi
Chuyển từ a + bi sang A∠ϕ SHIFT 2 4 = A∠ϕ
Chuyển từ A∠ϕ sang a + bi SHIFT 2 3 = a + bi
Chọn đơn vị đo góc là Rad SHIFT MODE 4 R
Chọn đơn vị đo góc là độ SHIFT MODE 3 D Nhập kí hiệu góc ∠ SHIFT (–) ∠ Nhập ẩn số X ALPHA ) X
Nhập dấu = trong biểu thức ALPHA CALC =
TỔ VẬT LÝ - CÔNG NGHỆ Trang 3
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH Tìm nhanh ẩn số X SHIFT CALC = X =
2 Bảng nhập xuất một số hằng số dùng cho Vật lý 12 Hằng số Vật lý Nút bấm Giá trị hiển thị Khối lượng prôton mp SHIFT 7 0 1 1, 67262158.10−27 Khối lượng nơtron SHIFT 7 0 2 1.674927351.10−27 Khối lượng electron SHIFT 7 0 3 9.10938291.10−31 Bán kính Bo SHIFT 7 0 5 5.291772109.10−11 Hằng số Plăng (h) SHIFT 7 0 6 6.62606957.10−34 Điện tích êlectron (e) SHIFT 7 2 3 1.602176565.10−19 Hằng số Rydberg RH SHIFT 7 1 6 10973731.57
Lưu ý: Khi nhập xuất các số liệu này thường máy tính chỉ trả về dạng kí hiệu (Ví
dụ: mn; me;e;...). Để hiển thị giá trị chúng ta nhấn = sẽ thấy các giá trị số của các đại lượng trên.
III PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI NHANH
Dạng 1: TÌM NHANH MỘT ĐẠI LƯỢNG BẰNG CHỨC NĂNG SOLVE
Chức năng SOLVE giúp người dùng có thể tìm nhanh một đại lượng chưa biết.
Việc sử dụng chức năng này giống như chúng ta đang giải một phương trình.
Thông thường chúng ta phải thực hiện nhiều
thao tác giải như nhân chéo, chuyển vế đổi Thao tác nhập xuất
dấu, mới ra nghiệm cần tìm. Việc này thường • Xác định đa thức cần tính toán
chiếm khá nhiều thời gian trong việc làm bài • Nhập ẩn số X: ALPHA )
thi trắc nghiệm. Chưa kể đến việc nhân chia • Nhập dấu =: ALPHA CALC
sai cho kết quả không như ý muốn.
• Thực hiện giải: SHIFT CALC = VÍ DỤ MINH HỌA Ví dụ 1
Gia tốc trọng trường tại nơi có con lắc đơn, khi biết chu kỳ T = 2(s) và chiều dài của
con lắc đơn dao động nhỏ là 1 m là A. g = 9,78 m/s2. B. g = 9,87 m/s2. C. g = 9,96 m/s2. D. g = 9,69 m/s2. Hướng dẫn giải s `
Chu kì của con lắc đơn được tính theo công thức: T = 2π
. Thực hiện nhập dữ liệu g r 1
vào máy tính theo cấu trúc 2 = 2π X
• Nhập máy tính: 2 ALPHA CALC 2π p 1 H ALPHA )
• Bấm SHIFT CALC = Kết quả hiển thị X = 9,869604401
Vậy gia tốc trọng trường g ≈ 9,87 m/s2.Đáp án B.
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 4
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng Ví dụ 2
Một mạch dao động gồm một tụ điện có điện dung C và một cuộn cảm có độ tự cảm
L. Mạch dao động có tần số riêng 100kHz và tụ điện có C = 5nF. Độ tự cảm lúcủa mạch dao động là: A. 5.10−5H. B. 5.10−4H. C. 5.10−3H. D. 2.10−4H. Hướng dẫn giải 1
Tần số riêng của mạch dao động: f = p
. Thực hiện nhập dữ liệu vào máy tính 2π LC 1 cấu trúc 100000 = p 2π 5.10−9X
• Nhập dữ liệu: 100000 ALPHA CALC
1 H 2πp5.10−9 ALPHA )
• Bấm SHIFT CALC = Kết quả hiển thị X = 5,0660 × 10−4
Vậy độ tự cảm L ≈ 5.10−4 H. Đáp án B. Ví dụ 3
Một vật dao động điều hoà trên quỹ đạo dài 40cm. Khi ở vị trí x = 10 cm vật có vận p
tốc 20π 3 cm/s. Chu kì dao động của vật là A. 1 s. B. 0,5 s. C. 0,1 s. D. 5 s. Hướng dẫn giải à p !2 µ ¶2 ³ v ´2 vT 20π 3T
Xuất phát từ công thức liên hệ: A2 = x2 + ω ⇔202 =x2+ = 102 + 2π 2π p
• Nhập: 20 x2 ALPHA CALC 10 x2 + ( 20π 3 ALPHA ) H 2π ) x2 =
• Bấm SHIFT CALC = Kết quả hiển thị X = 1. Đáp án A. Ví dụ 4
Khi treo vật nặng có khối lượng m vào lò xo có độ cứng k1 = 60 N/m thì vật dao động p với chu kì
2s Khi treo vật nặng đó vào lò xo có độ cứng k2 = 0,3 N/cm thì vật dao
động điều hoà với chu kì là A. 4 s. B. 2 s. C. 0,5 s. D. 3 s. Hướng dẫn giải s T1 k2
Các em tự chứng minh công thức: =
với T là ẩn số X cần tìm T 2 2 k1 p p • Nhập: 2 H ALPHA ) I ALPHA CALC 30 H 60
• Bấm SHIFT CALC = Kết quả hiển thị X = 2. Đáp án B. Ví dụ 5
Điện áp xoay chiều đặt vào hai đầu một đoạn mạch R, L, C không phân nhánh.
Điện áp hiệu dụng hai đầu mạch là 100V, hai đầu cuộn cảm thuần L là 120V, hai
bản tụ C là 60V. Điện áp hiệu dụng hai đầu R là: A. 80 V. B. 140 V. C. 260 V. D. 20 V. Hướng dẫn giải
Hiệu điện thế hiệu dụng hai đầu đoạn mạch: U2 = U2R + (UL − UC)2. Với UR là biến số X.
• Nhập: 100 x2 ALPHA CALC ALPHA ) x2 + ( 120 – 60 ) x2
• Bấm SHIFT CALC = Kết quả hiển thị X = 80 hay UR = 80V. Đáp án A.
TỔ VẬT LÝ - CÔNG NGHỆ Trang 5
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH BÀI TẬP VẬN DỤNG
Câu 1. Trong thực hành, để đo gia tốc trọng trường, một học sinh dùng một con lắc
đơn có chiều dài dây treo 80 cm. Khi cho con lắc dao động điều hòa, học sinh này thấy
con lắc thực hiện được 20 dao động toàn phần trong thời gian 36 s. Theo kết quả thí
nghiệm trên, gia tốc trọng trường tại nơi học sinh làm thí nghiệm bằng: A. g = 9,748 m/s2. B. g = 9,874 m/s2. C. g = 9,847 m/s2. D. g = 9,783 m/s2.
Câu 2. Trên một sợi dây dài 1m, hai đầu cố định, có sóng dừng với 2 bụng sóng. Bước
sóng của sóng trên dây là: A. 1 m. B. 2 m. C. 0,5 m. D. 0,25 m.
Câu 3. Một sóng cơ có tần số 50 Hz truyền theo phương Ox có tốc độ 30 m/s. Khoảng
cách giữa hai điểm gần nhau nhất trên phương Ox mà dao động của các phần tử môi π
trường tại đó lệch pha nhau bằng 3 A. 20 cm. B. 10 cm. C. 5 cm. D. 60 cm.
Câu 4. Người ta truyền một công suất 500 kW từ một trạm phát điện đến nơi tiêu
thụ bằng đường dây một pha. Biết công suất hao phí trên đường dây là 10 kW, điện
áp hiệu dụng ở trạm phát là 35 kV. Coi hệ số công suất của mạch truyền tải điện
bằng 1. Điện trở tổng cộng của đường dây tải điện là A. 55Ω. B. 38Ω. C. 49Ω. D. 52Ω.
Câu 5. Công thoát êlectron của một kim loại là 4,14 eV. Giới hạn quang điện của kim loại này là A. 0,6 µm. B. 0,3 µm. C. 0,4 µm. D. 0,2 µm.
Câu 6. Một con lắc lò xo có khối lượng vật nhỏ là m1 = 300 gam dao động điều hòa với
chu kì 1s. Nếu thay vật nhỏ có khối lượng m bằng vật nhỏ có khối lượng m thì con 1 2
lắc dao động với chu kì 0,5s. Giá trị m bằng 2 A. 100 gam. B. 150 gam. C. 25 gam. D. 75 gam.
Dạng 2: GIÁ TRỊ TỨC THỜI TRONG HÀM ĐIỀU HÒA
t Li độ tức thời trong dao động điều hòa - Độ lêch pha
Xét một vật dao động điều hòa có phương trình dao động (li độ): x = Acos(ωt + ϕ)
• Tại thời điểm t1 vật có li độ x1
• Hỏi tại thời điểm t2 = t1 + ∆t vật có li độ x =?
Hướng dẫn: Độ lệch pha giữa x và x : ∆ϕ = ω.∆t. Suy ra li độ của vật tại thời điểm 1 2 t là 2 ½ ³ ´ ´ dấu + nếu x x 1 ↓
2 = A cos ± cos−1³ x1 + ∆ϕ với A dấu − nếu x1 ↑
Nếu đề không nói đang tăng hay đang giảm, ta lấy dấu (+). x Thao tác trên máy: 1 H
A cos ± SHIFT cos + ∆ϕ ) = A I
t Điện áp - Cường độ dòng điện tức thời
Tương tự xét mạch điện RLC mắc nối tiếp có biểu thức điện áp và cường độ dòng
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 6
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng
điện qua mạch lần lượt là u = U0 cos(ωt + ϕu); i = I0 cos(ωt + ϕi)
Điện áp và cường độ dòng điện qua mạch tại thời điểm t2 = t1 + ∆t được xác định bằng công thức µ µ u ¶ ¶ ½ 1 dấu + nếu u u 1 ↓ = U0 cos ± cos−1 + ∆ϕ với U0 dấu − nếu u1 ↑ µ µ i ¶ ¶ ½ 1 dấu + nếu i i 1 ↓ = I0 cos ± cos−1 + ∆ϕ với I0 dấu − nếu i1 ↑
Việc thao tác trên máy tính hoàn toàn tương tự như trên.
Lưu ý: Ngoài ra bài toán trên còn được áp dụng tốt cho các bài toán sóng cơ học.
Việc áp dụng hoàn toàn tương tự. VÍ DỤ MINH HỌA Ví dụ 1 µ 3π¶
Một vật dao động điều hòa có phương trình x = 10cos 4πt − (cm). Khi t = t1 vật 8
thì vật có li độ x = x1 = −6 cm và đang tăng. Vậy tại thời điểm t = t1 + 0,125 s vật có li độ A. 8 cm. B. 6 cm. C. – 6 cm. D. – 8 cm. Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. π
Độ lệch pha giữa x và x : ∆ϕ = 4π.0,125 =
rad. Li độ của vật tại thời điểm t = t 1 2 1 + 0, 125 s: 2 µ π¶ x2 = 10cos −cos−1 −6 + 10 2 −6 H SHIFT ×10x H
10 cos − SHIFT cos ) + ) = 10 I 2 I
Màn hình hiển thị giá trị: 8. Hay x2 = 8 cm. Đáp án A. Ví dụ 2 µ 3π¶
Một vật dao động điều hòa có phương trình x = 5cos 4πt + (cm). Khi t = t1 vật 8
thì vật có li độ x = x1 = −3 cm và đang tăng. Vậy tại thời điểm t = t1 + 0,25 s vật có li độ A. –3 cm. B. 3 cm. C. – 6 cm. D. 6 cm. Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian.
Độ lệch pha giữa x và x : ∆ϕ = 4π.0,25 = π rad. Li độ của vật tại thời điểm t = t 1 2 1 + 0, 25 s: µ µ −3¶ ¶ x2 = 5cos cos−1 + π 5 −3 H
5 cos – SHIFT cos ) + SHIFT ×10x ) = 5 I
Màn hình hiển thị giá trị: 3. Hay x2 = 3 cm. Đáp án B.
TỔ VẬT LÝ - CÔNG NGHỆ Trang 7
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH Ví dụ 3 ³ π´
Cho dòng điện xoay chiều i = 4cos 8πt +
(A), vào thời điểm t dòng điện có cường 6 1
độ i1 = 0,7A. Hỏi sau đó 3s thì dòng điện có cường độ i là bao nhiêu? 2 A. 4 A. B. 0,7 A. C. – 4 A. D. –0,7 A. Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian.
Độ lệch pha: ∆ϕ = 8π.3 = 24π rad. Cường độ dòng điện i là 2 µ µ 0, 7¶ ¶
• i2 = i1 = 0,7A (vì i cùng pha với i ) Hoặc: i cos−1 1 2 2 = 4 cos + 24π 4 0, 7 H 4 cos SHIFT cos )
+ 24 SHIFT ×10x ) = 4 I
Màn hình hiển thị giá trị: 0,7. Hay i2 = 0,7 A. Đáp án B. Ví dụ 4
(CĐ 2013) Điện áp ở hai đầu đoạn mạch là u = 160cos(100πt) (V) (t tính bằng giây).
Tại thời điểm t , điện áp ở hai đầu đoạn mạch có giá trị là 80V và đang giảm. đến 1
thời điểm t2 = t1 + 0,015 s, điện áp ở hai đầu đoạn mạch có giá trị bằng p p A. 40 3 V. B. 80 3 V. C. 40 V. D. 80 V. Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 3π
Độ lệch pha giữa u và u : ∆ϕ = 100π.0,015 =
rad. Điện áp sau thời điểm đó 0,015s: 1 2 2 µ µ 80 ¶ 3π¶ u = 160cos cos−1 + 160 2 p 80 H 3 SHIFT ×10x 200 2 I cos SHIFT cos ) + ) = 160 I 2 I p p
Màn hình hiển thị giá trị: ≈ −100 2. Hay u = 80 3 V. Đáp án B. Ví dụ 5 p ³ π´
(ĐH 2010) Tại thời điểm t, điện áp điện áp u = 200 2cos 100πt − (V) có giá trị 2 p 1
100 2 Vvà đang giảm. Sau thời điểm đó
s, điện áp này có giá trị là bao nhiêu? 300 p p A. 200 V. B. 100 2 V. C. −100 2 V. D. –200 V. Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 1 π 1
Độ lệch pha giữa u và u : ∆ϕ = 100π. =
rad. Điện áp sau thời điểm đó s: 1 2 300 3 300 p p à à ! ! 100 2 π u = 200 2cos cos−1 p + 200 2 3 p p 100 2 H SHIFT ×10x 200 2 I cos SHIFT cos p ) + ) = 200 2 I 3 I p p
Màn hình hiển thị giá trị: ≈ 100 2. Hay u = 100 2 V. Đáp án B.
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 8
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng
Dạng 3: VIẾT NHANH PHƯƠNG TRÌNH DAO ĐỘNG - BIỂU THỨC ĐIỆN
ÁP VÀ CƯỜNG ĐỘ DÒNG ĐIỆN
t Phương trình dao động của vật dao động điều hòa v0
Phương trình dao động của một vật dao động điều hòa có dạng: x = x0 − i ω Thao tác trên máy tính • Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị
dạng tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. v0 • Nhập x0 + (–)
ENG Suy ra phương trình dao động của vật ω
t Biểu thức hiệu điện thế, cường độ dòng điện của mạch RLC mắc nối tiếp
• Xác định tổng trở phức của đoạn mạch: Z = R + (ZL − ZC)i
• Nếu bài toán yêu cầu viết biểu thức u (điện áp, hiệu điện thế), ta chỉ việc thay
vào các biểu thức sau và bấm máy tính uR = i.R; uL = i.ZL; uC = i.ZC
• Nếu bài toán yêu cầu viết biểu thức i (cường độ dòng điện) qua mạch uR uL uC u U0∠ϕ U0 SHIFT (–) ϕ i = = = = = = R ZL ZC z R + (ZL − ZC)i R + ( Z – L ZC ) ENG VÍ DỤ MINH HỌA Ví dụ 1
Vật m dao động điều hòa với tần số 0,5Hz, tại gốc thời gian nó có li độ x0 = 4cm, vận
tốc v0 = 12,56cm/s, lấy π = 3,14. Hãy viết phương trình dao động. Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian.
• Tính ω = 2πf = π rad/s. Tại t = 0 ta có x0 = 4; v0 = 12,56 cm/s. 12, 56 p 1 • Nhập 4 + (–)
ENG Màn hình hiển thị 4 2∠ − π 3, 14 4 p ³ π´
Vậy phương trình dao động của vật: x = 4 2cos πt − (cm) 4 Ví dụ 2
Vật m gắn vào đầu một lò xo nhẹ, dao động điều hòa với chu kỳ 1s. người ta kích
thích dao động bằng cách kéo m khỏi vị trí cân bằng ngược chiều dương một đoạn
3 cm rồi buông. Chọn gốc tọa độ ở VTCB, gốc thời gian lúc buông vật, hãy viết phương trình dao động. Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 2π • Tính ω =
= 2π rad/s. Tại t = 0 ta có x0 = 3; v0 = 0 cm/s. T 0 • Nhập −3 +
ENG Màn hình hiển thị 3∠π 2π
TỔ VẬT LÝ - CÔNG NGHỆ Trang 9
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Vậy phương trình dao động của vật: x = 3cos(2πt + π)(cm) Ví dụ 3 1 10−4
Cho đoạn mạch xoay chiều có R = 40 Ω; L = H; C
F mắc nối tiếp, điện áp 2 π = 0,6π p
đầu mạch u = 100 2cos(100πt)(V), Cường độ dòng điện qua mạch là ³ π´ ³ π´ A. i = 2,5cos 100πt + (A).
B. i = 2,5cos 100πt − (A). 4 4 ³ π´ ³ π´
C. i = 2,0cos 100πt − (A). D. i = 2,0cos 100πt + (A). 4 4 Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 1
• Ta có: ZL = Lω = 100 Ω; ZC = ω = 60 Ω ⇒ ZL−ZC = 40 Ω. Cường độ dòng điện qua C mạch p u U0∠ϕ 100 2∠0 i = = = Z R + (ZL − ZC)i 40 + 40i p 5 1 • Nhập
100 2 I SHIFT (–) 0 H 40 + 40 END Màn hình hiển thị ∠ − π 2 4 ³ π´
Vậy biểu thức cường độ dòng điện: i = 2,5cos 100πt − (A). Đáp án B. 4 Ví dụ 4 1
Cho hiệu điện thế giữa hai đầu đoạn mạch xoay chiều chỉ có cuộn thuần cảm L = H π p ³ π´ là: u = 220 2cos 100πt +
(V). Biểu thức cường độ dòng điện trong mạch là 3 ³ π´ p ³ π´ A. i = 3cos 100πt + (A).
B. i = 2,2 2cos 100πt − (A). 6 6 ³ π´ p ³ π´ C. i = 3cos 100πt − (A).
D. i = 2,2 2cos 100πt + (A). 4 4 Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 1
• Cảm kháng: ZL = ωL = 100ππ = 100Ω. Cường độ dòng điện qua mạch p u U 220 2 0∠ϕu ∠π i = = = 3 Z R + (ZL − ZC)i 100i p π
• Nhập 220 2 I SHIFT (–) ÷ 100 ENG = 3 p 11 2 1 p ³ π´ Màn hình hiển thị:
∠ − π ⇒ i = 2,2 2cos 100πt − (A). 5 6 6 Ví dụ 5 p 10−4
Cho hiệu điện thế hai đầu tụ C là u = 100 2cos100πt. Biết C = F. Biểu thức π
cường độ dòng điện qua mạch là p p A. i = 2cos100πt(A).
B. i = 2cos(100πt + π)(A). p ³ π´ p ³ π´ C. i = 2cos 100πt + (A). D. i = 2cos 100πt − (A). 2 2
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 10
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 1 1 • Dung kháng: ZC = ω =
= 100Ω. Cường độ dòng điện qua mạch C 10−4 100π. π p u U0∠ϕu 100 2∠0 i = = = Z R + (ZL − ZC)i −100i p
• Nhập 100 2 I SHIFT (–) 0 ÷ −100 ENG = 1 p ³ π´
Màn hình hiển thị: 1, 4142 . . . ∠ π ⇒ i = 2cos 100πt + (A). Đáp án C. 2 2 Ví dụ 6 1
Cho mạch điện xoay chiều gồm cuộn dây thuần cảm L = H và điện trở thuần π
R = 100Ω mắc nối tiếp. Nếu đặt vào hai đầu đoạn mạch một điện áp xoay chiều có
biểu thức u = 200cos100πt(V) thì biểu thức cường độ dòng điện trong mạch là p ³ π´ ³ π´ A. i = 2cos 100πt − (A). B. i = 2cos 100πt − (A). 4 4 ³ π´ ³ π´ C. i = cos 100πt − (A). D. i = cos 100πt + (A). 2 4 Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 1
• Cảm kháng: ZL = ωL = .100π π
= 100Ω. Cường độ dòng điện qua mạch u U0∠ϕu 200∠0 i = = = Z R + (ZL − ZC)i 100 + 100i
• Nhập 200 SHIFT (–) 0 ÷ ( 100 + 100 ENG ) = p 1 p ³ π´ Màn hình hiển thị:
2∠ − π ⇒ i = 2cos 100πt − (A). Đáp án A. 4 4 Ví dụ 7 3
Cho mạch điện xoay chiều AB gồm cuộn dây thuần cảm L = H, điện trở thuần 5π 10−4
R = 40Ω và tụ điện có điện dung C =
F mắc nối tiếp. Để cường độ dòng điện qua p π
mạch có biểu thức i = 2cos(100πt)(V) thì biểu thức điện áp đặt vào hai đầu AB phải là ³ π´ ³ π´ A. u = 80cos 100πt + (V). B. u = 80cos 100πt − (V). 4 4 p ³ π´ p ³ π´ C. u = 80 2cos 100πt + (V).
D. u = 80 2cos 100πt − (V). 4 4 Hướng dẫn giải
Bấm MODE 2 và SHIFT MODE H 3 2
để tính toán dạng số phức và hiển thị dạng
tọa độ cực. SHIFT MODE 4 để hiển thị đơn vị đo góc Radian. 3 1 1 • Ta có: ZL = ωL = .100π = 60Ω; ZC = =
= 100Ω. Điện áp đặt vào hai 5π ωC 10−4 100π π
TỔ VẬT LÝ - CÔNG NGHỆ Trang 11
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH đầu đoạn mạch AB p
u = i.Z = (I0∠ϕi) × (R + (ZL − ZC)i) = 2∠0 × (40 + (60 − 100)i) p • Nhập
2 I SHIFT (–) 0 x ( 40 u (60-100) ENG ) = 1 ³ π´
Màn hình hiển thị: 80∠ − π ⇒ uAB = 80cos 100πt − (V). Đáp án B. 4 4 BÀI TẬP VẬN DỤNG
Câu 1. Cho một doạn mạch điện gồm điện trở R = 50Ω mắc nối tiếp với một cuộn dây 0, 5 p ³ π´ thuần cảm L =
H. Đặt vào hai đầu đoạn mạch điện áp u 2 cos 100πt (V). π = 100 − 4
Dòng điện qua đoạn mạch là p ³ π´ p A. i = 2 2cos 100π − (A).
B. i = 2 2cos(100π) (A). 4 p ³ π´ C. i = 2 2cos 100π − (A). D. i = 2cos(100π) (A). 2 p
Câu 2. Mắc điện áp u = 200 2cos100πt (V) vào hai đầu đoạn mạch gồm tụ điện có 10−4 điện dung
F nối tiếp với điện trở thuần 100Ω. Biểu thức cường độ dòng điện qua π mạch là p ³ π´ ³ π´ A. i = 2cos 100πt + (A). B. i = 2cos 100πt + (A). 4 4 ³ π´ p ³ π´ C. i = 2cos 100πt − (A). D. i = 2cos 100πt − (A). 4 4 100
Câu 3. Mạch điện RLC có R = 100Ω, L = 0,381H, C =
µF. Nếu cường độ dòng điện 2π p ³ π´
trong mạch là i = 2cos 100πt +
(A) thì biểu thức điện áp là 4 ³ π´ ³ π´ A. u = 100cos 100πt + (V). B. u = 200cos 100πt + (V). 4 4 ³ π´ ³ π´
C. u = 200cos 100πt − (V).
D. u = 100cos 100πt − (V). 4 2
Câu 4. Cuộn dây có điện trở 50Ω có hệ số tự cảm 0,636H mắc nối tiếp với một điện p
trở 100Ω, cường độ dòng điện chạy qua mạch: i = 2cos(100πt) (A) thì biểu thức điện áp hai đầu cuộn dây là p µ 76π¶ µ 76π¶ A. 50 34 cos 100πt + (V). B. 50 cos 100πt + (V). 180 180 p µ 76π¶ p µ 53π¶ C. 50 34 cos 100πt − (V). D. 250 2 cos 100πt + (V). 180 180
Câu 5. Cho mạch điện RLC như hình vẽ. Điện trở R = 50Ω, cuộn thuần cảm C 3 10−4 R L L = H, C = F A B 5π π E F ³ π´
Hiệu điện thế uEB = 80cos 100πt −
(V). Biểu thức của điện áp uAB có dạng 3 p ³ π´ ³ π´
A. uAB = 80 2cos 100πt − (V).
B. uAB = 80cos 100πt − (V). 3 4 p ³ π ´ ³ π ´
C. uAB = 80 2cos 100πt − (V).
D. uAB = 80cos 100πt − (V). 12 12
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 12
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng
Dạng 4: CỘNG TRỪ HAI HÀM SỐ ĐIỀU HÒA
Bấm MODE 2 và SHIFT MODE 4 để tính toán dưới dạng số phức và đơn vị Radian.
t Tổng hợp hai dao động điều hòa
Xét một vật thực hiện hai dao động điều hòa cùng phương, cùng tần số có phương
trình lần lượt là x1 = A1 cos(ωt + ϕ1) và x2 = A2 cos(ωt + ϕ2). Phương trình dao động
tổng hợp của vật có dạng
x = x1 + x2 = A1 cos(ωt + ϕ1) + A2 cos(ωt + ϕ2)
• Phương trình tổng hợp: x = A =
1 SHIFT (–) ϕ1 + A2 SHIFT (–) ϕ2
t Biết phương trình dao động tổng hợp và một dao động thành phần, xác
định phương trình dao động còn lại
Xét vật thực hiện hai dao động điều hòa cùng phương, cùng tần số, biết
phương trình dao động tổng hợp x = Acos(ωt + ϕ) và dao động thành phần
x1 = A1 cos(ωt + ϕ1). Phương trình dao động của thành phần thứ hai x =
2 = A2 cos(ωt + ϕ2) = x − x1 = A SHIFT (–) ϕ
– A1 SHIFT (–) ϕ1
t Tìm biểu thức điện áp toàn mạch
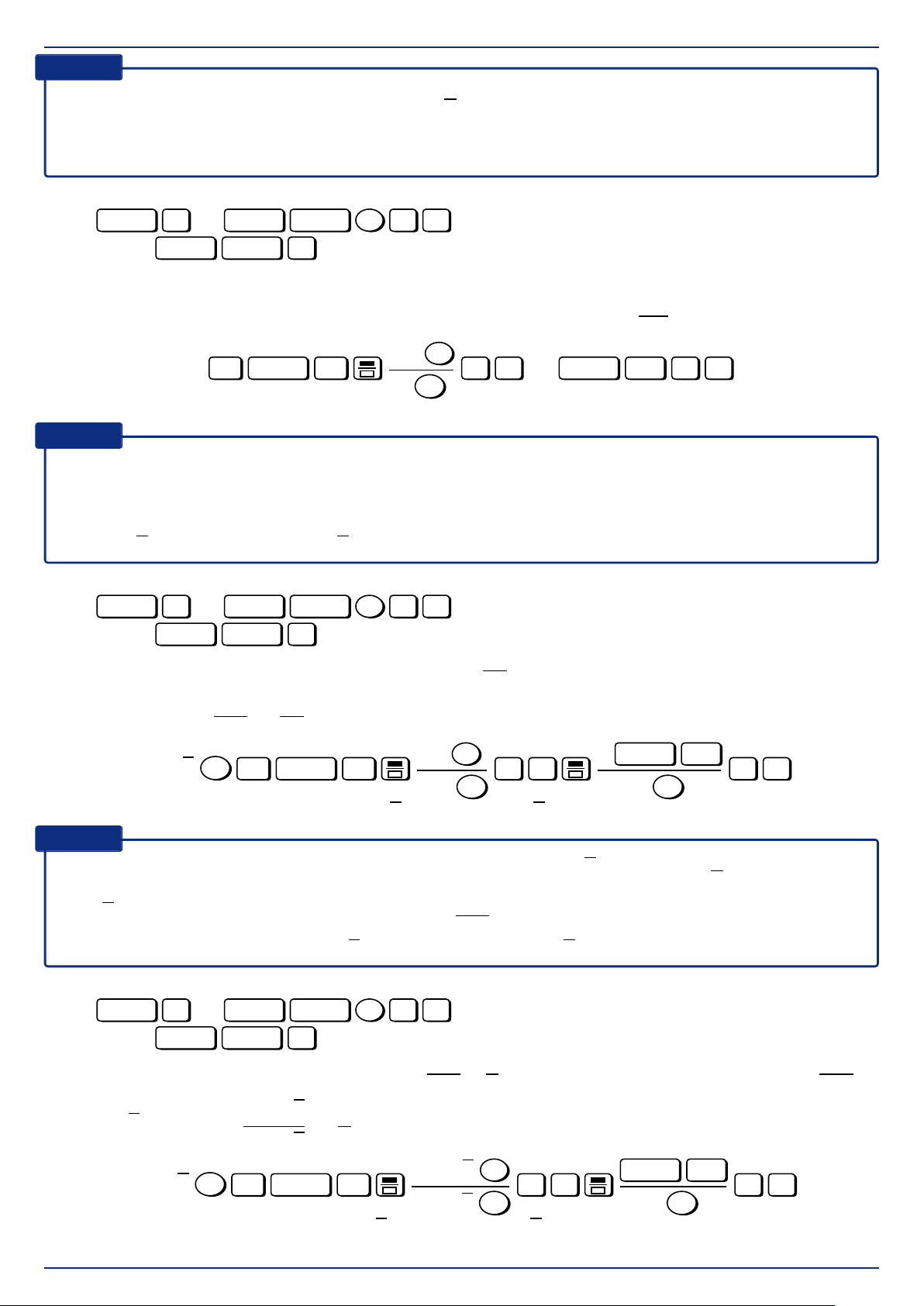
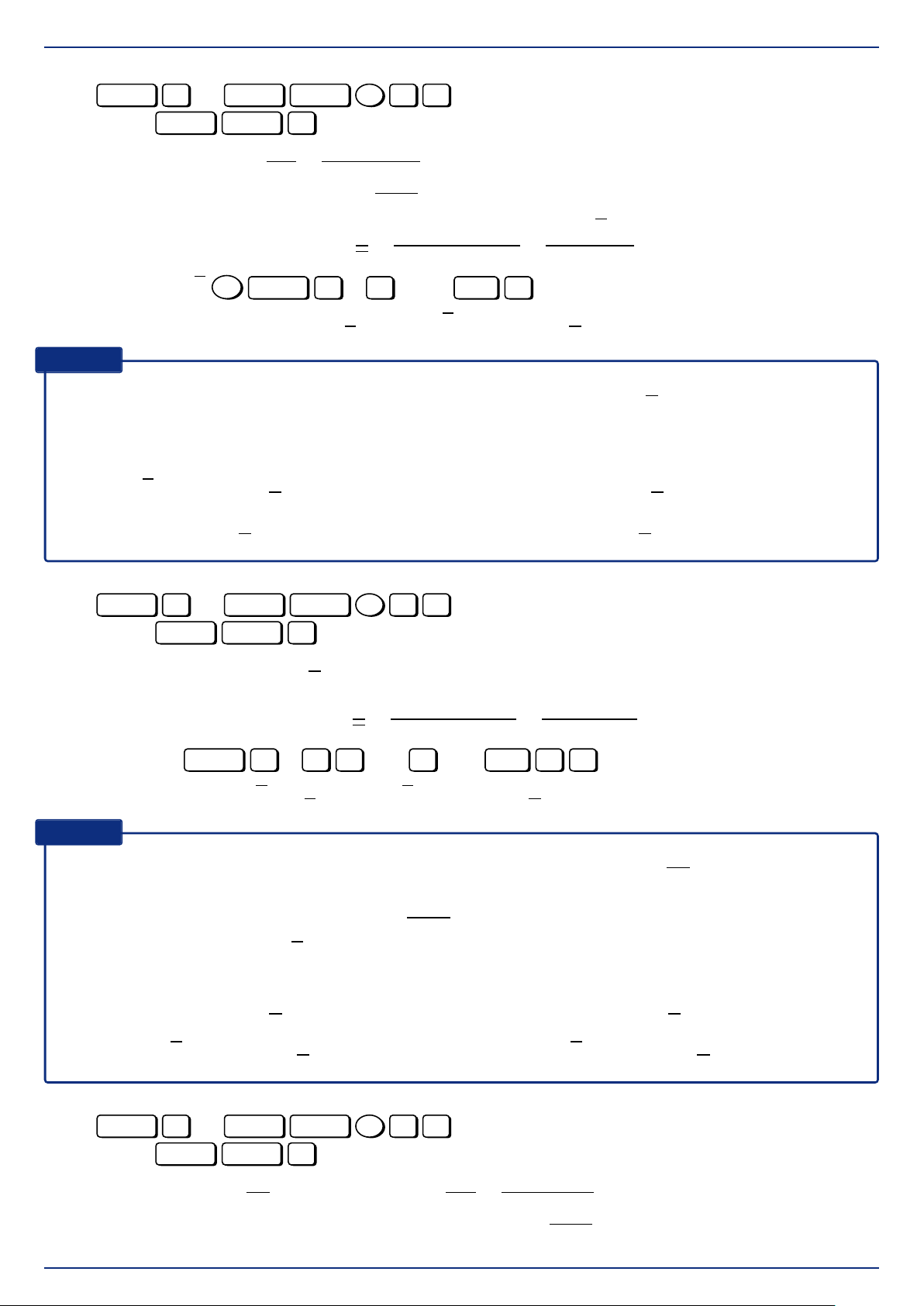
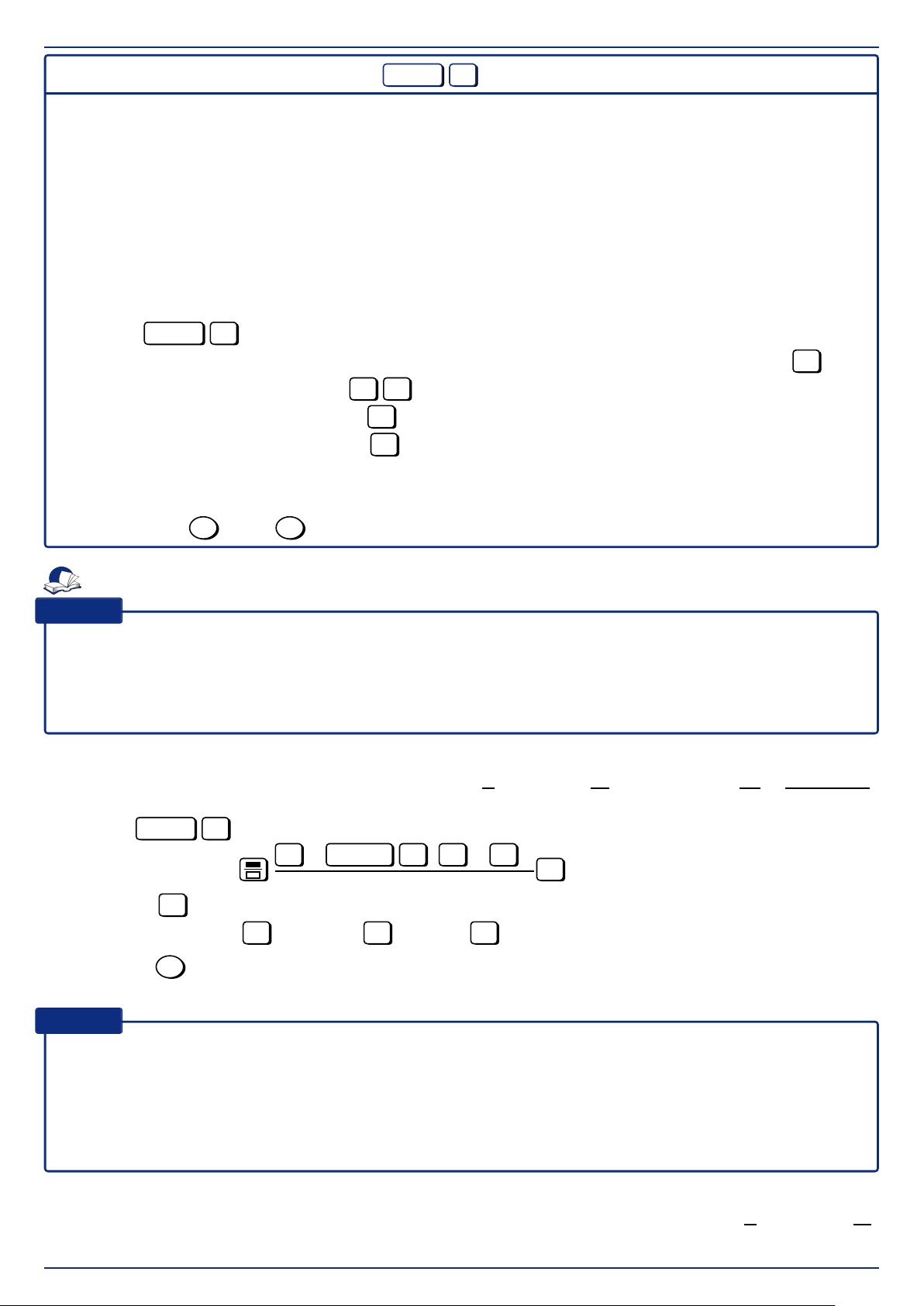
Xét đoạn mạch AB như hình vẽ, giả sử ta có biểu C R L A B
thức điện áp giữa hai đầu các đoạn mạch AM và M MB lần lượt là uAM = U1 cos(ωt + ϕ1); uMB = U2 cos(ωt + ϕ2)
Vì đoạn mạch AM mắc nối tiếp với đoạn mạch MB nên: uAB = uAM + uMB.
• Biểu thức điện áp đoạn mạch AB: u =
AB = U1 SHIFT (–) ϕ1 + U2 SHIFT (–) ϕ2 VÍ DỤ MINH HỌA Ví dụ 1
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số có ³ π´
phương trình: x1 = 5cos πt +
(cm); x2 = 5cosπt(cm). Dao động tổng hợp của vật có 3 phương trình p ³ π´ p ³ π´ A. x = 5 3cos πt − (cm). B. x = 5 3cos πt + (cm). 4 6 ³ π´ ³ π´ C. x = 5cos πt + (cm). D. x = 5cos πt − (cm). 4 3 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian p π 15 5 3
• Nhập 5 SHIFT (–)
+ 5 SHIFT (–) 0. Bấm = Kết quả hiển thị + i 3 2 2 p 1 • Bấm SHIFT 2 3 =
Kết quả thu được 5 3∠ π 6 p ³ π´
Vậy phương trình dao động tổng hợp của vật là x = 5 3cos πt + (cm). Đáp án B. 6
TỔ VẬT LÝ - CÔNG NGHỆ Trang 13
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH Ví dụ 2
Dao động tổng hợp của hai dao động điều hòa cùng phương có biểu thức p ³ π´ ³ π´ x = 5 3cos 6πt +
cm. Dao động thứ nhất có biểu thức x1 = 5cos 6πt + cm. Biểu 2 3
thức dao động thứ hai có biểu thức p µ ¶ ³ π´ p 3π A. x2 = 5 2cos 6πt − cm. B. x2 = 5 2cos 6πt + cm. 4 4 µ ¶ ³ π´ 2π C. x2 = 5cos 6πt − cm. D. x2 = 5cos 6πt + cm. 3 3 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian. Nhấn SHIFT 2 3 =
để hiển thị kết quả tính theo tọa độ cực. p
• Nhập 5 3 I SHIFT (–) (π/2) – 5 SHIFT (–) (π/3) = Kết quả: 5∠2π/3 µ 2π¶
Vậy phương trình dao động tổng hợp là: x = 5cos 6πt + cm. Đáp án D. 3 Ví dụ 3
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số p ³ π´
có phương trình x1 = 3 3cos ωt −
(cm) và x2 = cosωt(cm). Phương trình dao động 2 tổng hợp của vật là p µ ¶ ³ π´ p 3π A. x = 2 2cos ωt − (cm). B. x = 2 2cos ωt + (cm). 4 4 ³ π´ ³ π´ C. x = 2cos ωt − (cm). D. x = 2cos ωt + (cm). 3 3 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian. Nhấn SHIFT 2 3 =
để hiển thị kết quả tính theo tọa độ cực. p
• Nhập 3 3 I SHIFT (–) (−π/2) + 1 SHIFT (–) (0) = Kết quả: 2∠ − π/3 ³ π´
Vậy phương trình dao động tổng hợp là: x = 2cos ωt − cm. Đáp án C. 3 Ví dụ 4
Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số có p ³ π´
phương trình x1 = 3cos πt −
cm, x2 = cos(πt)cm. Phương trình dao động tổng hợp 2 của vật làp ³ π´ p ³ π´ A. x = 2 2cos πt − cm. B. x = 2 2cos πt + cm. 4 4 ³ π´ ³ π´ C. x = 2cos πt − cm. D. x = 2cos πt + cm. 3 3 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian. Nhấn SHIFT 2 3 =
để hiển thị kết quả tính theo tọa độ cực. p • Nhập
3 I SHIFT (–) (−π/2) + 1 SHIFT (–) (0) = Kết quả: 2∠ − π/3 ³ π´
Vậy phương trình dao động tổng hợp là: x = 2cos πt − cm. Đáp án C. 3
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 14
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng Ví dụ 5
Một vật dao động điều hòa xung quanh vị trí cân bằng dọc theo trục Ox có li độ 4 ³ π´ 4 ³ π´ x = p cos 2πt + + p cos 2πt +
(cm). Biên độ và pha ban đầu của dao động là 3 6 3 2 π π p π 8 π A. 4 cm; rad. B. 2 cm; rad. C. 4 3 cm; rad. D. p cm; rad. 3 6 3 3 3 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian 4 π 4 π p • Nhập p SHIFT (–)
+ p SHIFT (–) . Bấm = Kết quả hiển thị 2+2 3i 3 I 6 3 2 1 • Bấm SHIFT 2 3 =
Kết quả thu được 4∠ π 3 π
Biên độ và pha ban đầu của dao động là 4 cm; rad. Đáp án B. 3 Ví dụ 6
(ĐH-2010) Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần µ 5π¶
số có phương trình li độ x = 3cos πt −
(cm). Biết dao động thứ nhất có phương 6 ³ π´
trình li độ x1 = 5cos πt +
(cm). Dao động thứ hai có phương trình li độ là 6 µ ¶ ³ π´ 5π A. x2 = 8cos πt + (cm). B. x2 = 2cos πt − (cm). 6 6 µ 5π¶ ³ π´ C. x2 = 8cos πt − (cm). D. x2 = 2cos πt + (cm). 6 6 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian (–) 5π π p
• Nhập 3 SHIFT (–)
– 5 SHIFT (–)
. Bấm = Kết quả hiển thị −4 3 − 4i 6 6 5 • Bấm SHIFT 2 3 =
Kết quả thu được 8∠ − π 6 µ 5π¶
Vậy phương trình dao động tổng hợp của vật là x = 8cos πt − (cm). Đáp án C. 6 Ví dụ 7 Một chất điểm dao động điều hoà có phương trình dao động tổng µ 5π¶ hợp x = 2cos πt +
(cm) với các dao động thành phần cùng phương là 12 ³ π´
x1 = A1 cos(πt + ϕ1)(cm) và x2 = 5cos πt +
(cm), Biên độ và pha ban đầu của dao 6 động 1 là: 2π π p π π A. 5 cm; ϕ1 = . B. 10 cm; ϕ1 = .
C. 5 2 cm; ϕ1 = . D. 5 cm; ϕ1 = . 3 2 4 3 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian
• Phương trình của dao động thứ nhất: x1 = A1∠ϕ1 = x − x2 = A∠ϕ − 5∠ϕ2
TỔ VẬT LÝ - CÔNG NGHỆ Trang 15
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH 5π π 2 • Nhập 2 SHIFT (-) – 5 SHIFT (-) =
Kết quả hiển thị: 5∠ π 12 6 3 2π
Vậy biên độ và pha ban đầu của dao động 1 là 5 cm và ϕ1 = . Đáp án A. 3 Ví dụ 8
Nếu đặt vào hai đầu một đoạn mạch điện chứa một điện trở thuần và một tụ điện p ³ π´
mắc nối tiếp một điện áp xoay chiều có biểu thức u = 100 2cos ωt − (V), khi đó 4
điện áp giữa điện trở thuần có biểu thức uR = 100cosωt. Biểu thức điện áp hai đầu tụ điện sẽ bằng ³ π´ p ³ π´ A. uC = 100cos ωt − . B. uC = 100 2cos ωt + . 2 4 ³ π´ p ³ π´ C. uC = 100cos ωt + . D. uC = 100 2cos ωt + . 4 2 Hướng dẫn giải Nhấn MODE 2 và SHIFT MODE 4
để tính toán theo số phức và đổi sang đơn vị Radian π
• Biểu thức điện áp: u = uR + uC ⇒ uC = u − uR,− = −45◦ 4 p
• Nhập: 100 2 I SHIFT (–) ( (–) 45 ) –
0 SHIFT (–) 0 =
Kết quả hiển thị: 100∠ − π/2. Vậy biểu thức điện áp giữa hai đầu tụ điện có dạng: ³ π´ uC = 100cos ωt − . Đáp án A. 2 BÀI TẬP VẬN DỤNG
Câu 1. Cho các dao động thành phần lần lượt có phương trình
x1 = 3cosπt (cm); x2 = 3sinπt (cm); x3 = 2cosπt (cm); x4 = 2sinπt (cm)
Phương trình dao động tổng hợp của bốn dao động trên là p ³ π´ p ³ π´ A. x1 = 5 2cos πt − (cm). B. x2 = 5 2cos πt + (cm). 4 4 ³ π´ ³ π´ C. x3 = 5cos πt − (cm). D. x4 = 5cos πt + (cm). 4 4
Câu 2. Một vật thực hiện đồng thời hai dao động cùng phương, cùng tần số với p ³ π´
x1 = 4 3cos10πt (cm) và x2 = 4cos 10πt −
(cm), t tính bằng giây. Vận tốc của vật tại 2 thời điểm t = 2s p p
A. v = 20 2π(cm/s). B. v = 40 2π(cm/s). C. v = 40π(cm/s). D. v = 20π(cm/s).
Câu 3. Một vật thực hiện đồng thời hai dao động cùng phương với phương trình lần µ ¶ ³ π´ 5π lượt là x1 = A1 cos 20t + (cm) và x2 = 3cos 20t +
(cm). Biết vận tốc dao động cực 6 6
đại của vật là 140 cm/s. Giá trị của A1 là A. A1 = 10cm. B. A1 = 9cm. C. A1 = 8cm. D. A1 = 7cm.
Câu 4. Một vật có khối lượng 100g thực hiện đồng thời hai dao động điều hòa cùng µ 5π¶
phương có phương trình x1 = 3sin20t(cm) và x2 = 2cos 20t − (cm). Năng lượng dao 6 động của vật là A. W = 0,038J. B. W = 0,38J. C. W = 3,8J. D. W = 38J.
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 16
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng
Dạng 5: CHỨC NĂNG TABLE MODE 7
Chức năng TABLE của các máy Casio FX500 hoặc VINACAlúcó thể giúp chúng ta
giải quyết nhanh các bài toán liên quan đến sóng âm, sóng dừng, giao thoa sóng hoặc sóng ánh sáng
Nguyên tắc hoạt động: Ban đầu chúng ta có một hàm số f(x) với x là các số
nguyên dương. Khi thay x vào hàm số f(x), ứng với mỗi giá trị của x ta sẽ có giá trị hàm f(x) tương ứng.
t Từ công thức tính ta suy ra đại lượng f(x) biến thiên mà đề cho
t Nhập dữ liệu vào máy tính
• Bấm MODE 7 để mở chức năng Table
• Màn hình hiển thị f(X) =, nhập biểu thức vừa suy ra ở bước trên. Bấm =
– Hiển thị: Start? Nhập 1 =
Đây là giá trị ban đầu của X
– Hiển thị: End? Nhập 30 = Đây là giá trị kết thúc của X.
– Hiển thị: Step? Nhập a = (a là một số, thường chọn 1, 2,. . . ) Đây là bước
nhảy, máy tính sẽ tự động cộng thêm a vào các giá trị X tiếp theo khi thay
vào hàm f(X) theo thứ tự X, X + a,X + a + a,...
t Bấm phím H hoặc N để dò tìm kết quả thỏa mãn yêu cầu bài toán. VÍ DỤ MINH HỌA Ví dụ 1
Sợi dây dài ` = 1m được treo lơ lững trên một cần rung. Cần rung dao động theo
phương ngang với tần số thay đổi từ 100Hz đến 120Hz. Tốc độ truyền sóng trên
dây là 8m/s. Trong quá trình thay đổi tần số thì quan sát được mấy lần sóng dừng A. 5. B. 4. C. 6. D. 15. Hướng dẫn giải λ v v (2X + 1)8
Điều kiện có sóng dừng trên dây: ` = (2k + 1) = (2k + 1) ⇒ f = (2k + 1) 4 4f 4` = 4
• Bấm MODE 7 để mở chức năng Table, màn hình hiển thị f(X) = ( 2 ALPHA ) + 1 ) 8 • Nhập biểu thức
= Màn hình hiển thị g(X) =, chúng 4
ta bấm = để bỏ qua bước nhập g(X)
• Nhập Start? 20 = End? 30 = Step? 1 =
Bấm phím H để dò tìm kết quả thỏa mãn yêu cầu bài toán, thấy tại X = 25 → 29 thì
giá trị f(X) tương ứng là 102 → 118, thỏa mãn điều kiện 100 ≤ f ≤ 120. Đáp án A. Ví dụ 2
Một sóng hình sin truyền theo phương Ox từ nguồn O với tần số 20 Hz, có tốc độ
truyền sóng nằm trong khoảng từ 0,7 m/s đến 1 m/s. Gọi A và B là hai điểm nằm
trên Ox, ở cùng một phía so với O và cách nhau 10cm. Hai phần tử môi trường luôn
dao động ngược pha. Tốc độ truyền sóng là A. 100 cm/s. B. 85 cm/s. C. 90 cm/s. D. 80 cm/s. Hướng dẫn giải λ v
Vì hai phần tử A và B luôn dao động ngược pha. Điều kiện: d = (2k + 1) = (2k + 1) . 2 2f
TỔ VẬT LÝ - CÔNG NGHỆ Trang 17
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH d.2f 0, 1.2.20 4 4 Suy ra: v = = = ⇒ f(X) = 2k + 1 2k + 1 2k + 1 2X + 1
• Bấm MODE 7 để mở chức năng Table, màn hình hiển thị f(X) = 4 H • Nhập biểu thức =
Màn hình hiển thị g(X) =, chúng ta 2 ALPHA ) + 1 I
bấm = để bỏ qua bước nhập g(X)
• Nhập Start? 1 = End? 10 = Step? 1 =
Bấm phím H để dò tìm kết quả thỏa mãn yêu cầu bài toán, thấy tại X = 2 thì giá trị
f(X) tương ứng là 0.8. Đáp án D. Ví dụ 3
Một sợi dây đàn hồi rất dài có đầu A dao động với tần số f và theo phương vuông
góc với sợi dây. Biên độ dao động là 4 cm, vận tốc truyền sóng trên dây là 4 m/s.
Xét một điểm M trên dây và cách A một đoạn 28 cm, người ta thấy M luôn luôn dao
động vuông pha với A. Tìm bước sóng λ. Biết rằng tần số f có giá trị trong khoảng từ 22 Hz đến 26 Hz A. 12 cm. B. 8 cm. C. 14 cm. D. 16 cm. Hướng dẫn giải λ v v
Ta có hai điểm vuông pha nhau thì d = (2k + 1) = (2k + 1) ⇒ f = (2k + 1) . Thay các 4 4f 4d 4 2X + 1
giá trị đã cho ta có: f = (2X + 1) = 4.0, 28 0, 28
• Bấm MODE 7 để mở chức năng Table, màn hình hiển thị f(X) = 2 ALPHA ) + 1 H • Nhập biểu thức =
Màn hình hiển thị g(X) =, chúng ta 0, 28 I
bấm = để bỏ qua bước nhập g(X)
• Nhập Start? 1 = End? 10 = Step? 1 =
Bấm phím H để dò tìm kết quả thỏa mãn yêu cầu bài toán, thấy tại X = 3 thì giá trị v
f(X) tương ứng là 25. Suy ra λ = = 16cm Đáp án D. f Ví dụ 4
Trong thí nghiệm giao thoa sóng nước người ta quan sát 2 điểm MN trên đoạn
thẳng nối 2 nguồn thấy M dao động với biên độ cực đại, N không dao động và MN
cách nhau 3cm. Biết tần số dao động của nguồn bằng 50Hz, vận tốc truyền sóng
trong khoảng 0, 9m/s ≤ v ≤ 1,6m/s. Vận tốc truyền sóng là A. 1,00 m/s. B. 1,20 m/s. C. 1,50 m/s. D. 1,33 m/s. Hướng dẫn giải (k + 0,5)v MN.2f 3 3
Theo bài ta có: MN = (k + 0,5)i = ⇒ v = = ⇒ f(X) = 2f k + 0,5 k + 0,5 X + 0,5
• Bấm MODE 7 để mở chức năng Table, màn hình hiển thị f(X) = 3 H • Nhập biểu thức =
Màn hình hiển thị g(X) =, chúng ta ALPHA ) I + 0,5
bấm = để bỏ qua bước nhập g(X)
• Nhập Start? 1 = End? 10 = Step? 1 =
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 18
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
Trường THPT Tôn Thất Tùng
Bấm phím H để dò tìm kết quả thỏa mãn yêu cầu bài toán, thấy tại X = 2 thì giá trị
f(X) tương ứng là 1, 2. Đáp án B. Ví dụ 5
(ĐH-2009) Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng
ánh sáng trắng có bước sóng từ 0,38 µm đến 0,76 µm. Tại vị trí vân sáng bậc 4 của
ánh sáng đơn sắc có bước sóng 0,76 µm còn có bao nhiêu vân sáng nữa của các ánh sáng đơn sắc khác? A. 3. B. 8. C. 7. D. 4. Hướng dẫn giải k1λ1 4.0, 76 3, 04
Xuất từ điều kiện hai vân sáng trùng nhau: k1λ1 = k2λ2 ⇒ λ2 = = = . k2 k2 k2 Đặt 3, 04 f(X) =
với 0, 38 µm ≤ f(X) ≤ 0,76 µm X
• Bấm MODE 7 để mở chức năng Table, màn hình hiển thị f(X) = 3, 04 H • Nhập biểu thức =
Màn hình hiển thị g(X) =, chúng ta bấm ALPHA ) I =
để bỏ qua bước nhập g(X)
• Nhập Start? 1 = End? 10 = Step? 1 =
Bấm phím H để dò tìm kết quả thỏa mãn yêu cầu bài toán, thấy tại X = 5 → 8 thì giá
trị f(X) tương ứng là 0, 608 → 0,38. Vậy có 4 giá trị của k thỏa mãn. Đáp án D. Ví dụ 6
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 2 mm,
khoảng cách từ mặt phẳng chứa 2 khe đến màn quan sát là 2 m. Nguồn phát ánh
sáng gồm các bức xạ đơn sắc có bước sóng trong khoảng 0,40 µm đến 0,76 µm. Trên
màn, tại điểm cách vân trung tâm 3,3 mm có bao nhiêu bức xạ cho vân tối? A. 6 bức xạ. B. 4 bức xạ. C. 3 bức xạ. D. 5 bức xạ. Hướng dẫn giải λD axt 2.3, 3 3, 3
Điều kiện cho vân tối: xt = (k + 0,5) ⇒ λ = = ⇒ f(X) = a (k + 0,5)D (k + 0,5)2 k + 0,5
• Bấm MODE 7 để mở chức năng Table, màn hình hiển thị f(X) = 3, 3 H • Nhập biểu thức =
Màn hình hiển thị g(X) =, chúng ta ALPHA ) + 0,5 I
bấm = để bỏ qua bước nhập g(X)
• Nhập Start? 1 = End? 10 = Step? 1 =
Bấm phím H để dò tìm kết quả thỏa mãn yêu cầu bài toán, thấy tại X = 4 → 7 thì giá
trị f(X) tương ứng là 0, 733 → 0,44. Vậy có 4 giá trị của k thỏa mãn. Đáp án B. Ví dụ 7
(ĐH-2010) Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng
ánh sáng trắng có bước sóng từ 380 nm đến 760 nm. Khoảng cách giữa hai khe là
0,8 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2 m. Trên
màn, tại vị trí cách vân trung tâm 3 mm có vân sáng của các bức xạ với bước sóng
A. 0,48 µm và 0,56 µm.
B. 0,40 µm và 0,60 µm.
TỔ VẬT LÝ - CÔNG NGHỆ Trang 19
Trường THPT Tôn Thất Tùng
GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 BẰNG MÁY TÍNH
C. 0,40 µm và 0,64 µm.
D. 0,45 µm và 0,60 µm. Hướng dẫn giải λD axs 1, 2 1, 2
Điều kiện có vân sáng: xs = k ⇒ λ = = ⇒ f(X) = a kD k X
• Bấm MODE 7 để mở chức năng Table, màn hình hiển thị f(X) = 1, 2 H • Nhập biểu thức =
Màn hình hiển thị g(X) =, chúng ta bấm = ALPHA ) I
để bỏ qua bước nhập g(X)
• Nhập Start? 1 = End? 10 = Step? 1 =
Bấm phím H để dò tìm kết quả thỏa mãn yêu cầu bài toán, thấy tại X = 2,3 thì giá
trị f(X) tương ứng là 0, 6; 0, 4. Đáp án B.
Dạng 6: QUÃNG ĐƯỜNG VẬT THỰC HIỆN TRONG DAO ĐỘNG ĐIỀU HÒA
t Quãng đường vật đi được từ thời điểm t đến thời điểm t 1 2
Xét một vật dao động điều hòa có phương trình x = Acos(ωt + ϕ). Để xác định quãng
đường vật đi được từ thời điểm t đến t ta sử dụng công thức 1 2 t2 t2 Z Z · t ¸ 2 − t1 S = |v|.dt = m.4A + ¯ ¯−ωA sin(ωt + ϕ)¯¯.dt với m = T t1 t1+mT phần nguyên
Thao tác nhập dữ liệu vào máy tính m.4A + R
SHIFT hyp Aω × sin ω ALPHA ) + ϕ ) H t = 1 + mT N t2
t Khoảng thời gian ngắn nhất để vật đi từ điểm có li độ x đến x 1 2 ¯ x x ¯ ∆ 2 1 t = ¯arccos − arccos ¯ : ω ¯ A A ¯
• Nhấn SHIFT hyp để màn hình hiển thị biểu tượng trị tuyệt đối | | ¯ x1 x2 ¯
• Nhập dữ liệu: ¯ SHIFT cos – SHIFT cos ¯ ÷ ω = ¯ A A ¯
Lưu ý: Việc tính tích phân cho kết quả khá lâu, các em có thể đọc đề và làm câu
tiếp theo để máy tính thực hiện và cho kết quả. VÍ DỤ MINH HỌA Ví dụ 1 ³ π´
Một vật dao động điều hoà dọc theo trục Ox với phương trình: x = 3cos 4πt − (cm) 3 13
(t đo bằng giây). Quãng đường vật đi được từ thời điểm t1 = s đến thời điểm 6 23 t2 = s là 6 A. 40 cm. B. 57,5 cm. C. 40,5 cm. D. 56 cm. Hướng dẫn giải · ¸ ³ π´ 2π t2 − t1
• Vận tốc của vật: v = −3.4πsin 4πt − ; T = = 3. 3 ω = 0,5s ⇒ T
Sưu tâm và biên soạn: GV Lê Khánh Loan Trang 20



