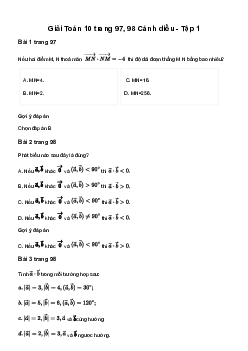



Preview text:
Giải Toán 10 Bài 5: Tích của một số với một vectơ
Luyện tập Toán 10 Bài 5 Cánh diều Luyện tập 1
Hai đường trung tuyến AM và BN cắt nhau tại G. Tìm các số a, b biết: Gợi ý đáp án Ta có:
là hai vecto cùng hướng và Suy ra . Vậy Ta có:
là hai vecto ngược hướng và Suy ra . Vậy . Luyện tập 2
Cho ba điểm A, B, C. Chứng minh Gợi ý đáp án Ta có: Luyện tập 3
Cho I là trung điểm của đoạn thẳng AB và điểm M tùy ý. Chứng minh rằng Gợi ý đáp án
Do I là trung điểm của AB nên Khi đó: Vậy
Giải Toán 10 trang 92 Cánh diều - Tập 1 Bài 1 trang 92
Cho hình thang MNPQ, MN / / PQ, MN=2 PQ. Phát biểu nào sau đây là đúng? Gợi ý đáp án Chọn đáp án C Bài 2 trang 92 Cho đoạn thẳng
a. Xác định điểm C thoả mãn
b. Xác định điểm D thoả mãn Gợi ý đáp án a. b. Bài 3 trang 92
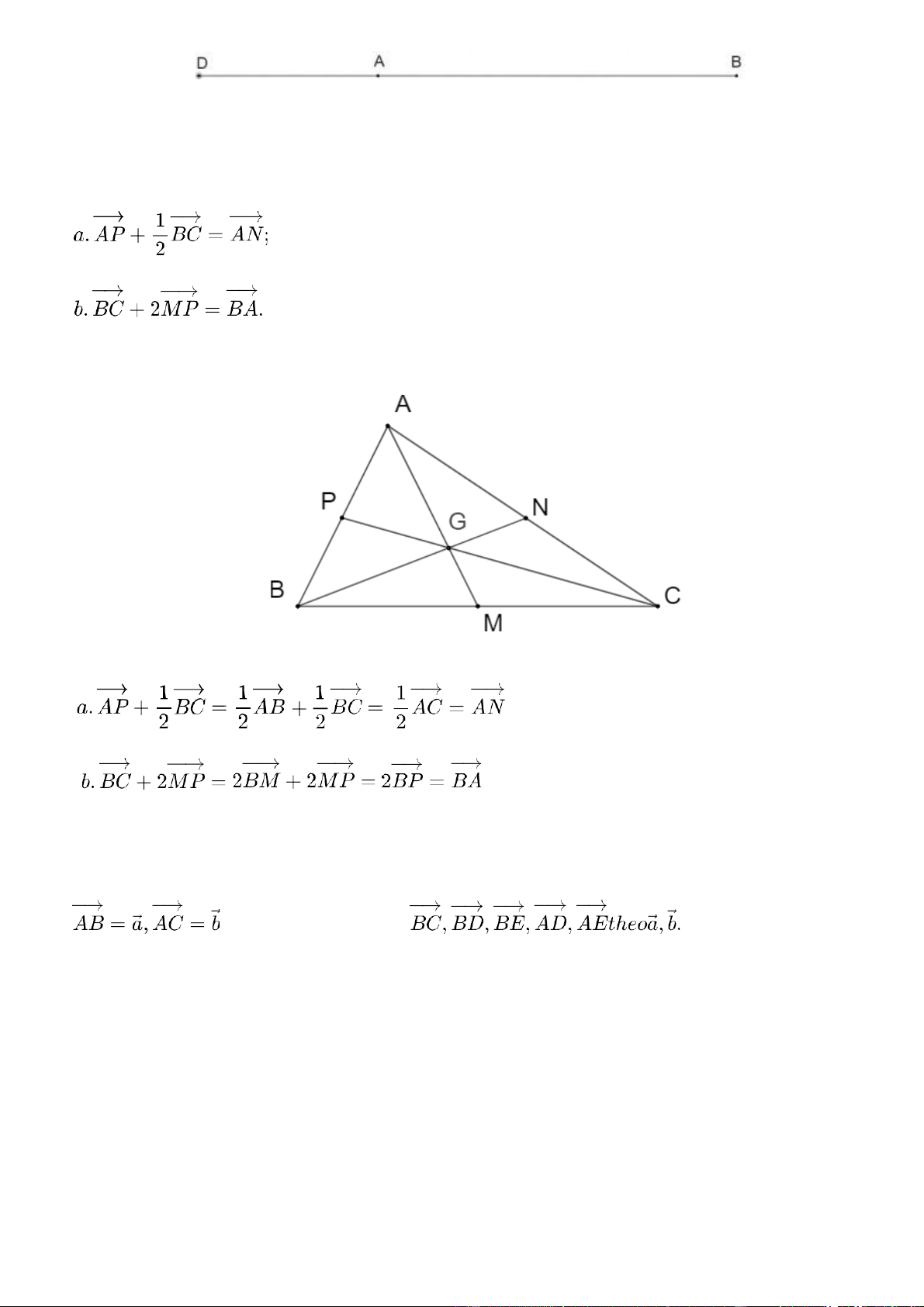
Cho tam giác ABC có M,N,P lần lượt là trung điểm của BC, CA, AB. Chứng minh: Gợi ý đáp án (đpcm). (đpcm). Bài 4 trang 92
Cho tam giác A B C. Các điểm D, E thuộc cạnh B C thoả mãn B D=D E=E C (Hình 62). Giả sử . Biểu diễn các vectơ Gợi ý đáp án Bài 5 trang 92
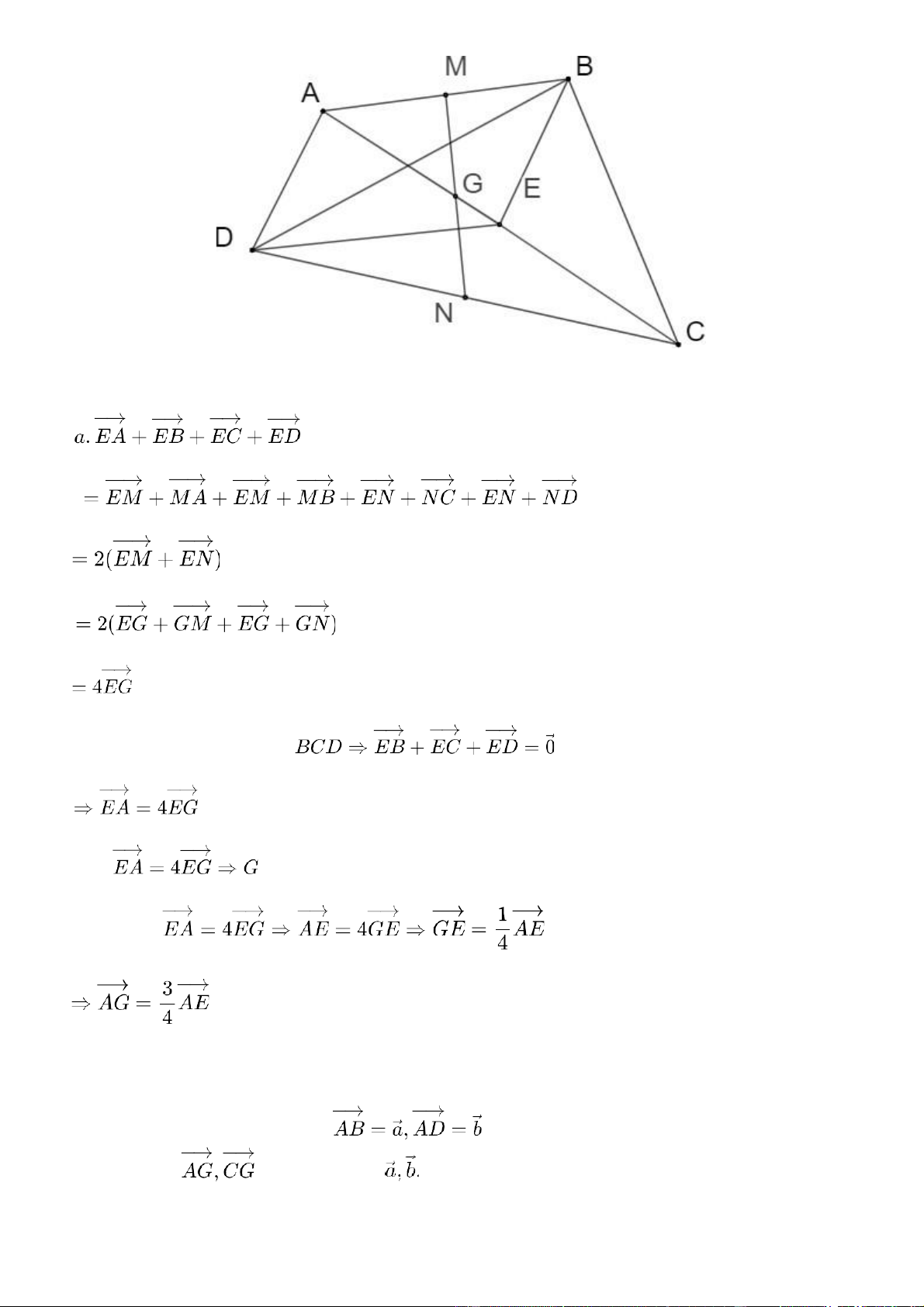
Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm
của đoạn thẳng MN,E là trọng tâm tam giác BCD. Chứng minh:
c. Điểm G thuộc đoạn thẳng A E và Gợi ý đáp án (Đpcm)
b. E là trọng tâm tam giác c. Vì thuộc đoạn thẳng A E Mặt khác: Bài 6 trang 92
Cho hình bình hành ABCD. Đặt
. Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ Gợi ý đáp án Bài 7 trang 92
Cho tam giác ABC. Các điểm D, E, H thoả mãn a. Biểu thị mỗi vectơ theo hai vectơ
b. Chứng minh D, E, H thẳng hàng. Gợi ý đáp án a. b. Ta có: Vậy D, E, H thẳng hàng.