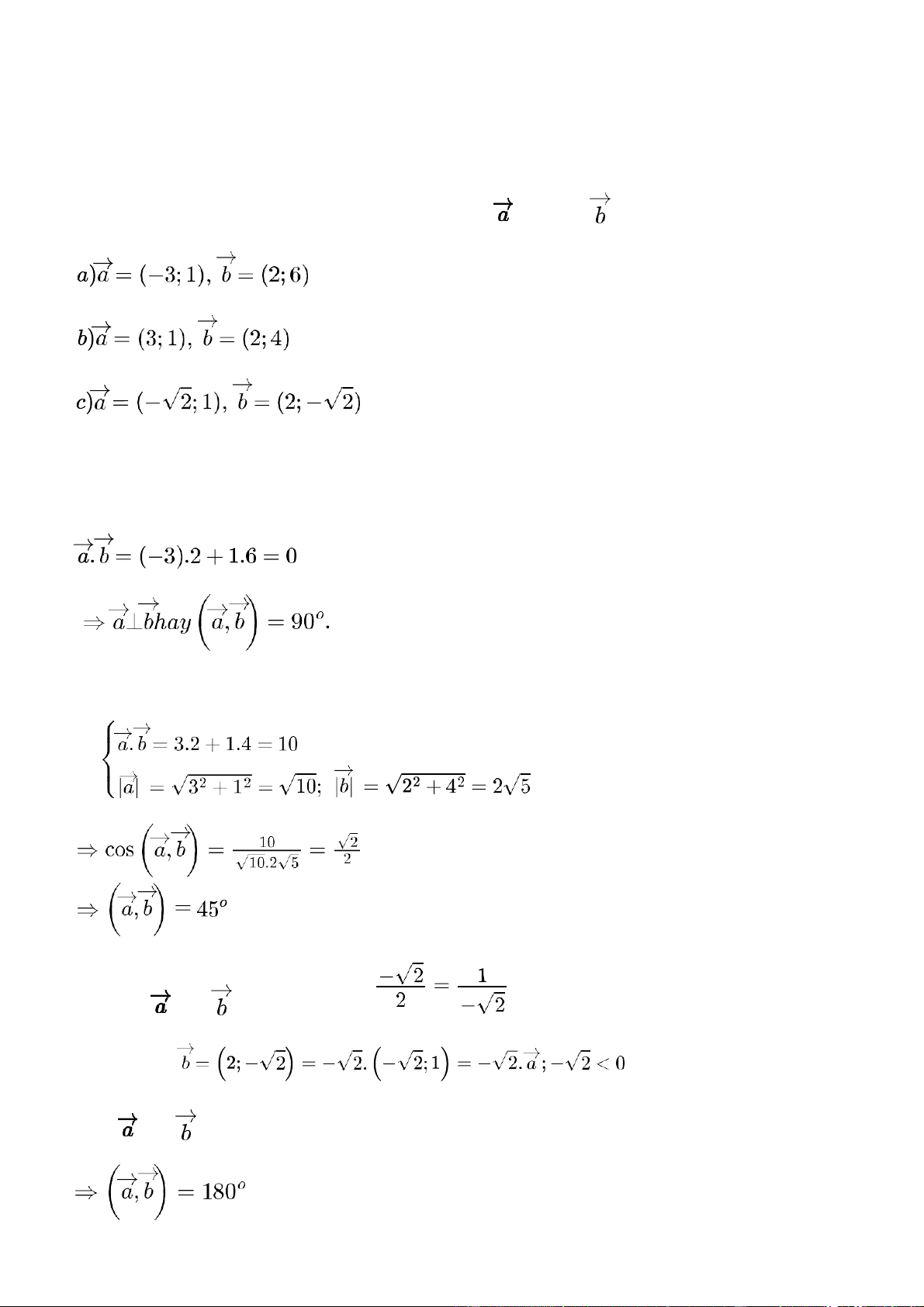





Preview text:
Giải Toán 10 trang 70 Kết nối tri thức Tập 1 Bài 4.21 trang 70
Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ và
trong mỗi trường hợp sau: Gợi ý đáp án a) b) c) Dễ thấy: và cùng phương do Hơn nữa: Do đó: và ngược hướng. Bài 4.22 trang 70 Tìm điều kiện của để: Gợi ý đáp án a) Ta có: Nói cách khác: cùng hướng. b) Ta có: Nói cách khác: ngược hướng. Bài 4.23 trang 70
Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2), B(-4; 3). Gọi M (t; 0) là một điểm thuộc trục hoành. a) Tính theo t. b) Tính t để Gợi ý đáp án a)
Ta có: A (1; 2), B(-4; 3) và M (t; 0) b) Để hay thì
Vậy t = -1 hoặc t = -2 thì Bài 4.24 trang 70
Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A (-4; 1), B (2;4), C (2; -2) a) Giải tam giác
b) Tìm tọa độ trực tâm H của tam giác ABC. Gợi ý đáp án a) Ta có:
Áp dụng định lí cosin cho tam giác ABC, ta có: Vậy tam giác ABC có: b)
Gọi H có tọa độ (x; y)
Lại có: H là trực tâm tam giác ABC và và Do đó à
Mà: \overrightarrow {BC} = (0; - 6) Và Vậy H có tọa độ Bài 4.25 trang 70
Chứng minh rằng với mọi tam giác ABC, ta có: Gợi ý đáp án Đặt Mà ì ê Do đó hay (đpcm) Bài 4.26 trang 70
Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có: Gợi ý đáp án Ta có:
(do G là trọng tâm tam giác ABC)
\begin{array}{l} = 3{\overrightarrow {MG} ^2} + {\overrightarrow {GA} ^2} +
{\overrightarrow {GB} ^2} + {\overrightarrow {GC} ^2}\\ = 3M{G^2} + G{A^2} + G{B^2} + G{C^2}\end{array} (đpcm).




