Giải Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông | Kết nối tri thức
Giải Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông | Kết nối tri thức được trình bày khoa học, chi tiết giúp cho các bạn học sinh chuẩn bị bài một cách nhanh chóng và đầy đủ đồng thời giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình. Thầy cô và các bạn xem, tải về ở bên dưới.
Chủ đề: Chương 4: Tam giác bằng nhau (KNTT)
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Giải Toán 7 bài 15: Các trường hợp bằng nhau của tam
giác vuông sách Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 15 - Luyện tập Luyện tập 1
Quay lại tình huống mở đầu, ta thấy mỗi chiếc cột với bóng của nó tạo thành hai cạnh góc
vuông của một tam giác vuông. Hai tam giác vuông này có hai cặp cạnh tương ứng bằng nhau
và hai góc ở đỉnh chiếc cột của hai tam giác vuông này cũng bằng nhau. Vậy lí do mà bạn Tròn đưa ra có đúng không? Gợi ý đáp án:
Lí do mà bạn Tròn đưa ra là đúng. Vì hai tam giác vuông này bằng nhau (g-c-g) Luyện tập 2
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các
tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB. Gợi ý đáp án:
Xét hai tam giác vuông OBM và OAM có: OM chung
(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng) Luyện tập 3
Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra
ba cặp tam giác vuông bằng nhau trong hình. Gợi ý đáp án:
Do A, B, C nằm trên đường tròn tâm O => OA = OB = OC = R
Xét tam giác AOP vuông tại P và tam giác BOP vuông tại P ta có: OA = OB (giả thiết) PO là cạnh chung
=> ∆AOP = ∆BOP (cạnh huyền cạnh – cạnh góc vuông)
Xét tam giác AON vuông tại N và tam giác CON vuông tại N ta có: OA = OC (giả thiết) ON là cạnh chung
=> ∆AON = ∆CON (cạnh huyền cạnh – cạnh góc vuông)
Xét tam giác BOM vuông tại M và tam giác COM vuông tại M ta có: OB = OC (giả thiết) OM là cạnh chung
=> ∆BOM = ∆COM (cạnh huyền cạnh – cạnh góc vuông)
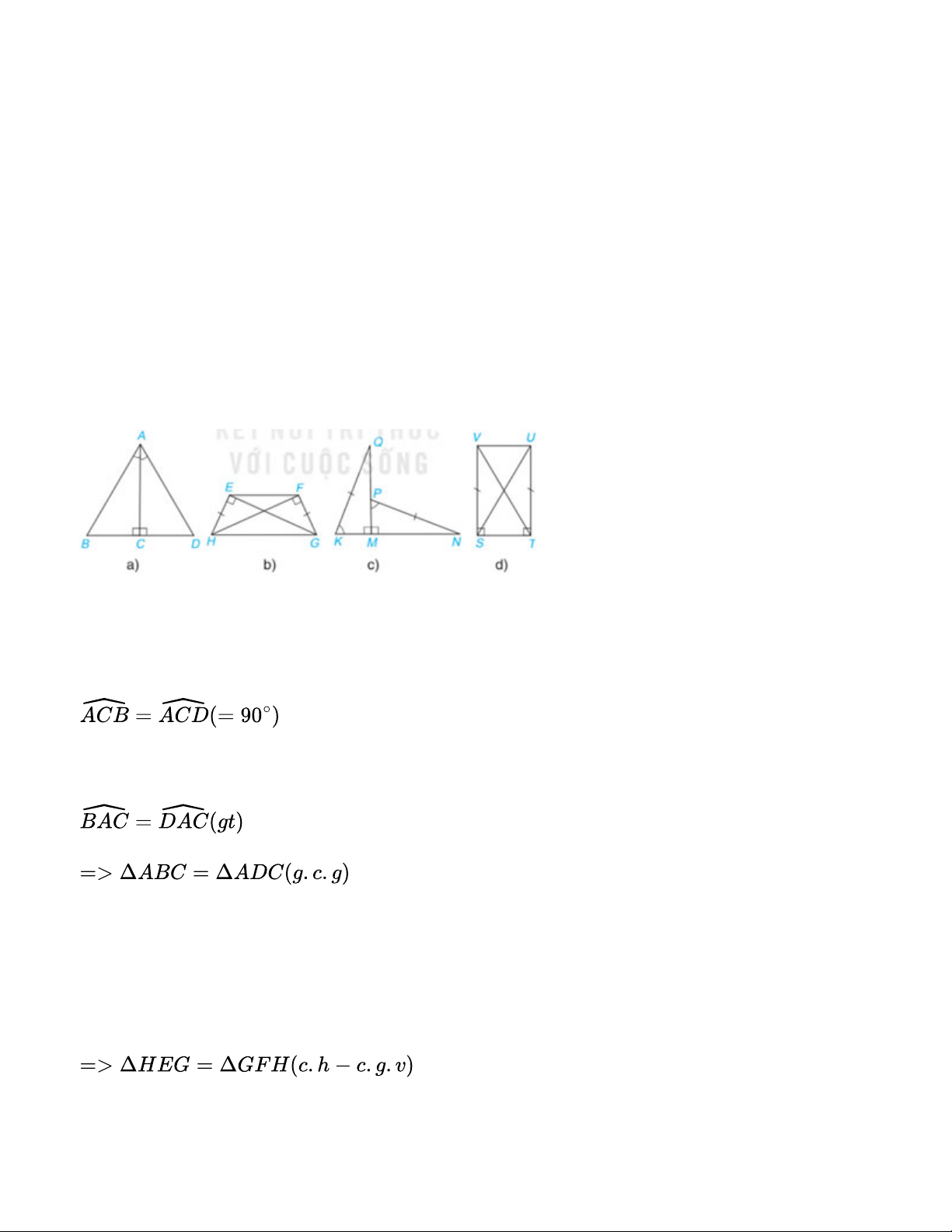
Giải Toán 7 Kết nối tri thức với cuộc sống trang 79 tập 1 Bài 4.20
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao? Gợi ý đáp án:
a) Xét 2 tam giác vuông ABC và ADC có: AC chung
b) Xét 2 tam giác vuông HEG và GFH có: HE=GF(gt) HG chung
c) Xét 2 tam giác vuông QMK và NMP có: QK=NP
(cạnh huyền – góc nhọn)
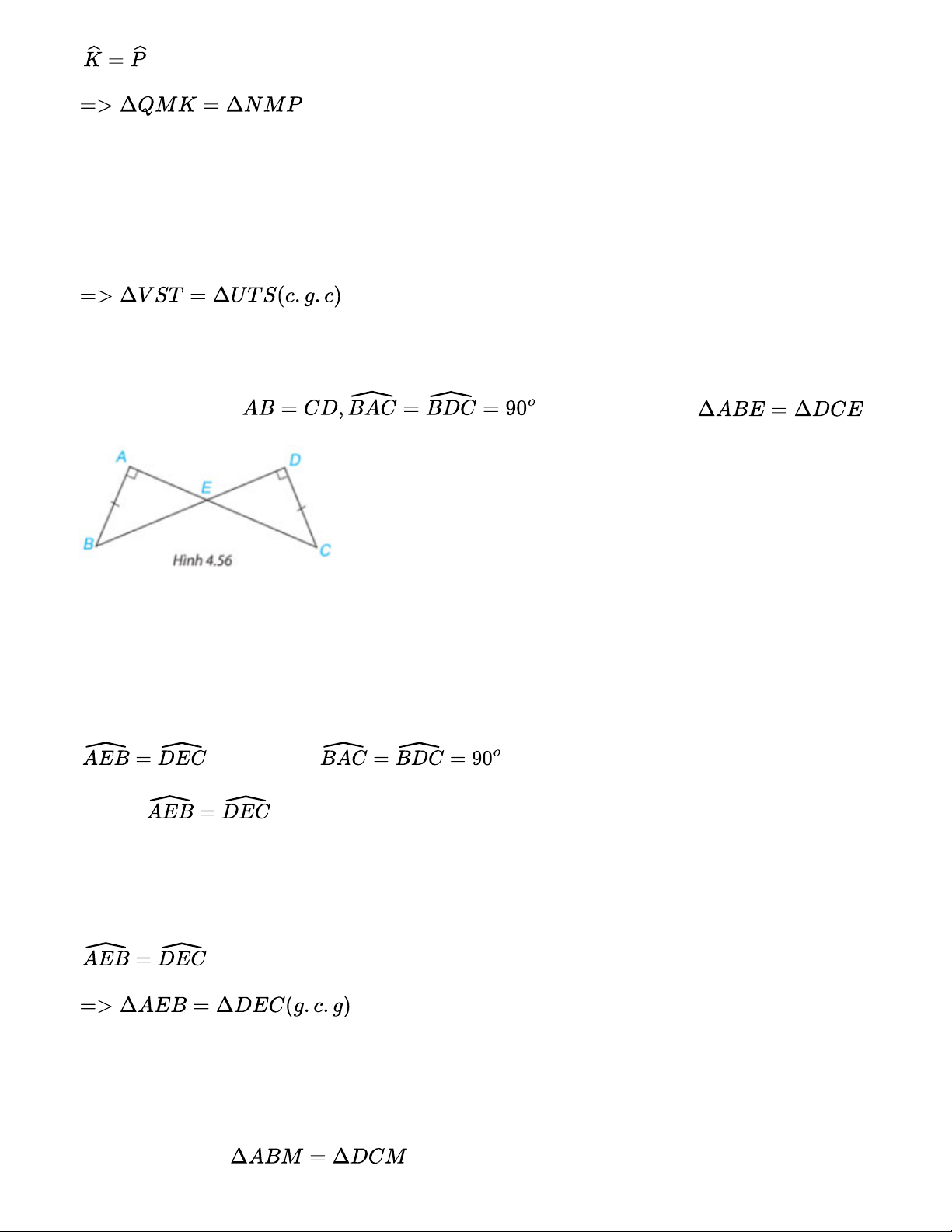
d) Xét 2 tam giác vuông VST và UTS có: VS=UT ST chung Bài 4.21 Cho hình 4.56, biết . Chứng minh rằng . Gợi ý đáp án:
Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AED và DEC có: (đối đỉnh) và . Suy ra:
Xét 2 tam giác vuông AEB và DEC có: AB=DC Bài 4.22
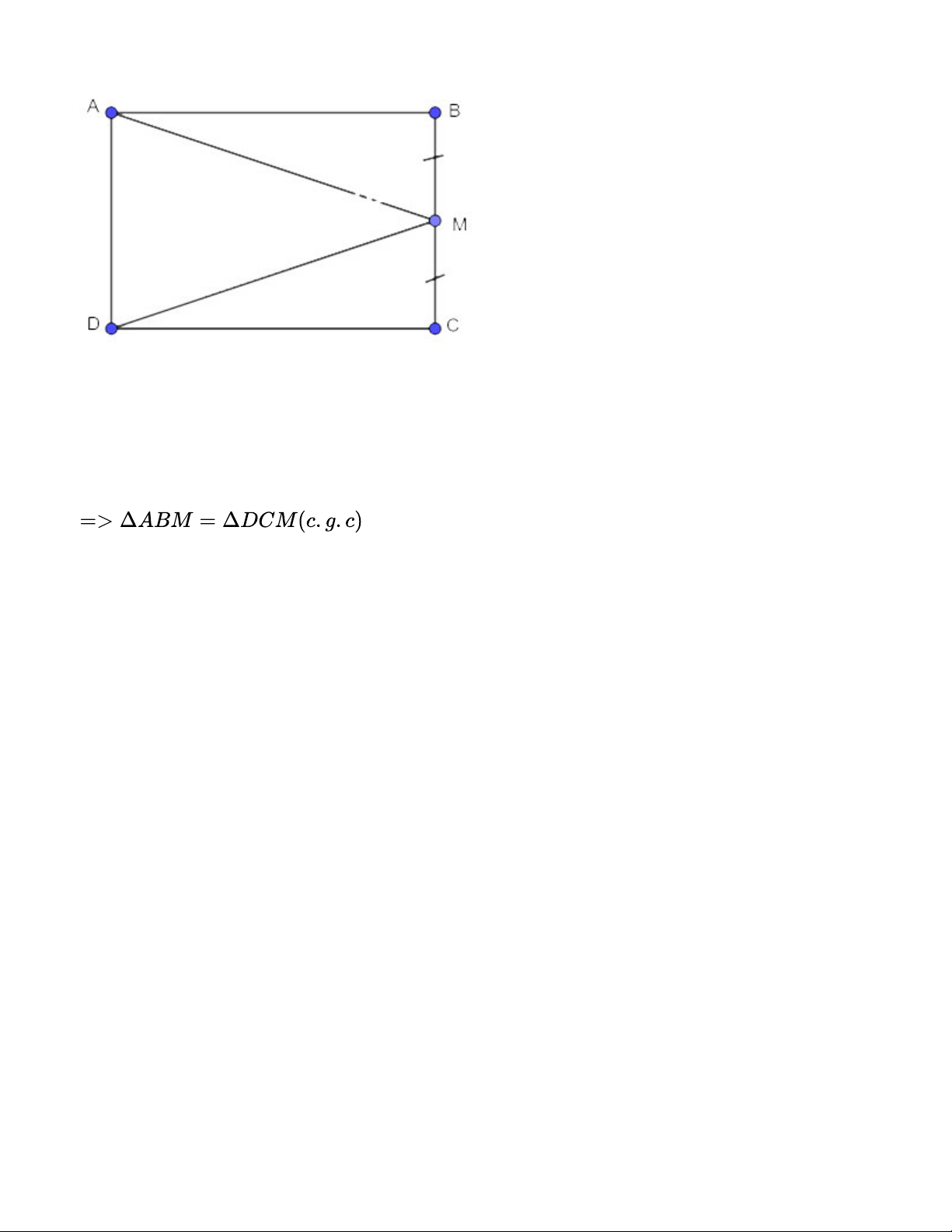
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Chứng minh rằng . Gợi ý đáp án:
Xét 2 tam giác vuông ABM và DCM có:
AB=DC (tính chất hình chữ nhật) BM=CM (gt)