Giải Toán 7 bài Luyện tập chung trang 74 Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống trang 74 tập 1 Bài 4.16
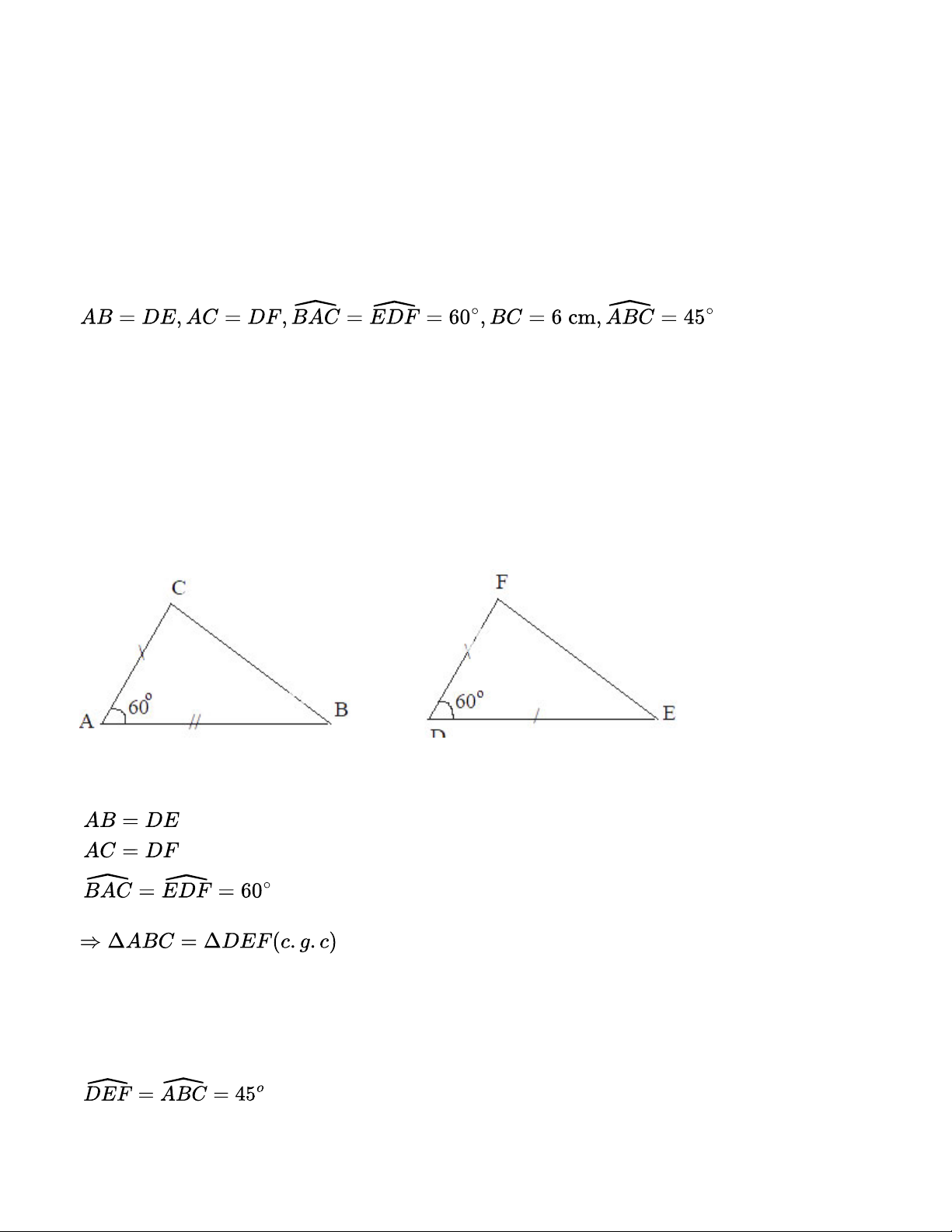
Cho hai tam giác ABC và DEF thoả mãn . Tính độ dài cạnh
EF và số đo các góc ACB, DEF, EFD. Phương pháp giải:
Chứng minh hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh.
Từ đó suy ra các cặp cạnh và các cặp góc tương ứng bằng nhau. Gợi ý đáp án:
Xét hai tam giác ABC và DEF có: Do đó: EF = BC = 6cm Bài 4.17
Cho hai tam giác ABC và DEF thoả mãn . Tính độ dài cạnh DF. Phương pháp giải:
Chứng minh hai tam giác bằng nhau theo trường hợp góc - cạnh - góc. Gợi ý đáp án:
Xét hai tam giác ABC và DEF có: (2 cạnh tương ứng) Mà AC = 6 cm Bài 4.18
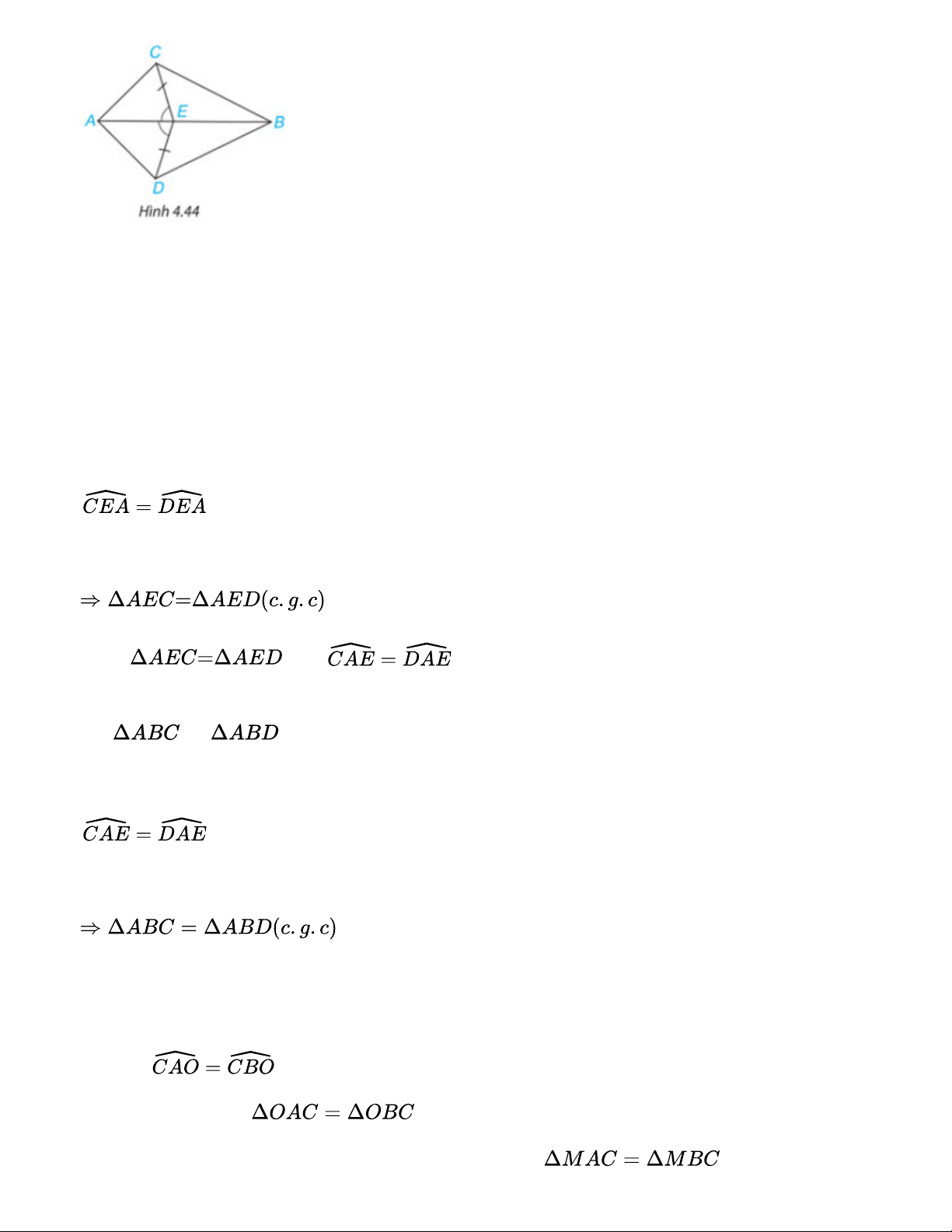
Cho Hình 4.44, biết EC = ED và . Chứng minh rằng: Phương pháp giải:
Chứng minh hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh. Gợi ý đáp án:
a) Xét hai tam giác AEC và AED có EC = ED AE chung b) Do nên
(2 góc tương ứng) và AC=AD (2 cạnh tương ứng). Xét và có: AB chung AC=AD Bài 4.19
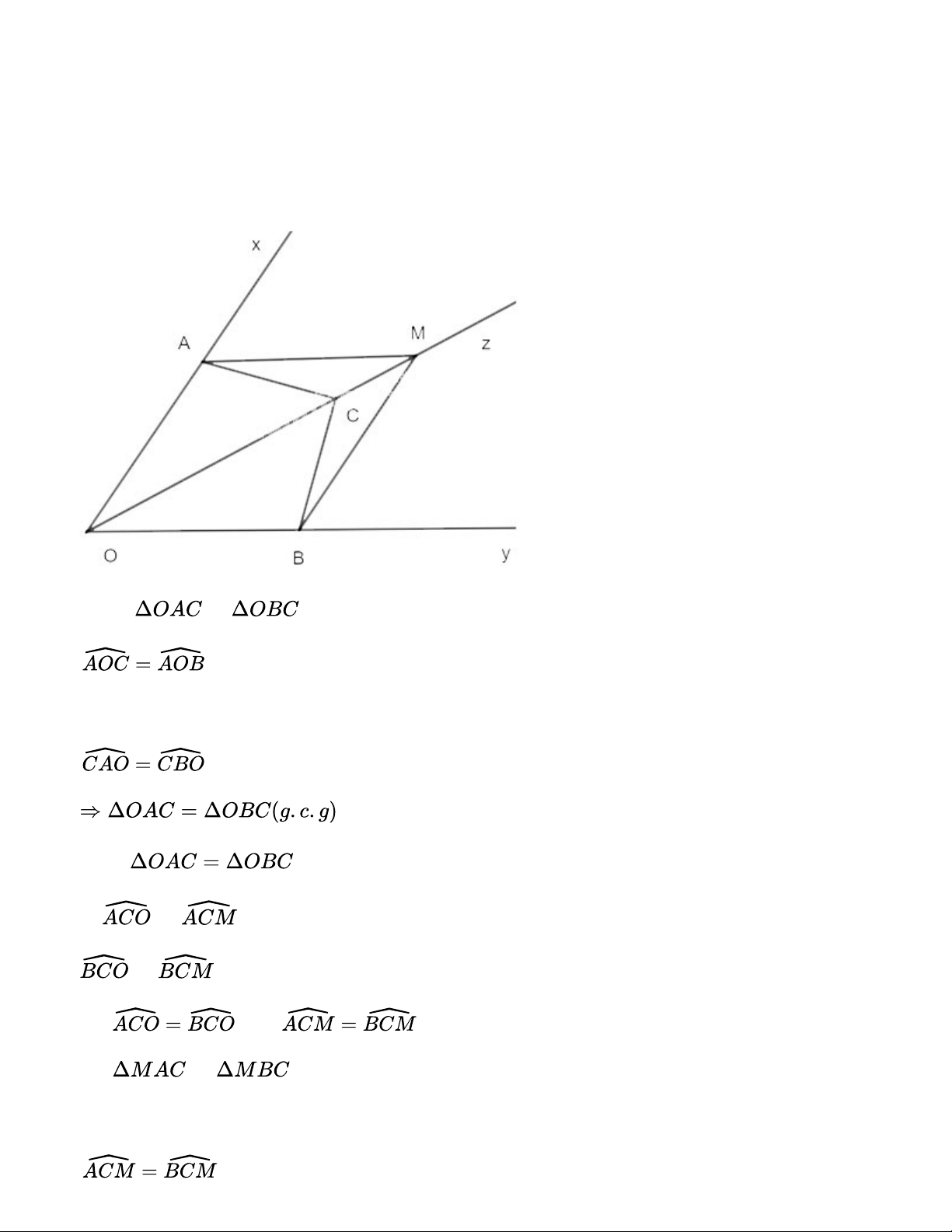
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho . a) Chứng minh rằng .
b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng . Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
b) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh. Gợi ý đáp án: a) Xét và có: (Oz là phân giác góc xOy) OC chung b) Do
nên AC=BC (2 cạnh tương ứng) Vì và kề bù và kề bù Mà nên Xét và có: AC=BC CM chung
Lý thuyết Luyện tập chung trang 74
1. Hai tam giác bằng nhau
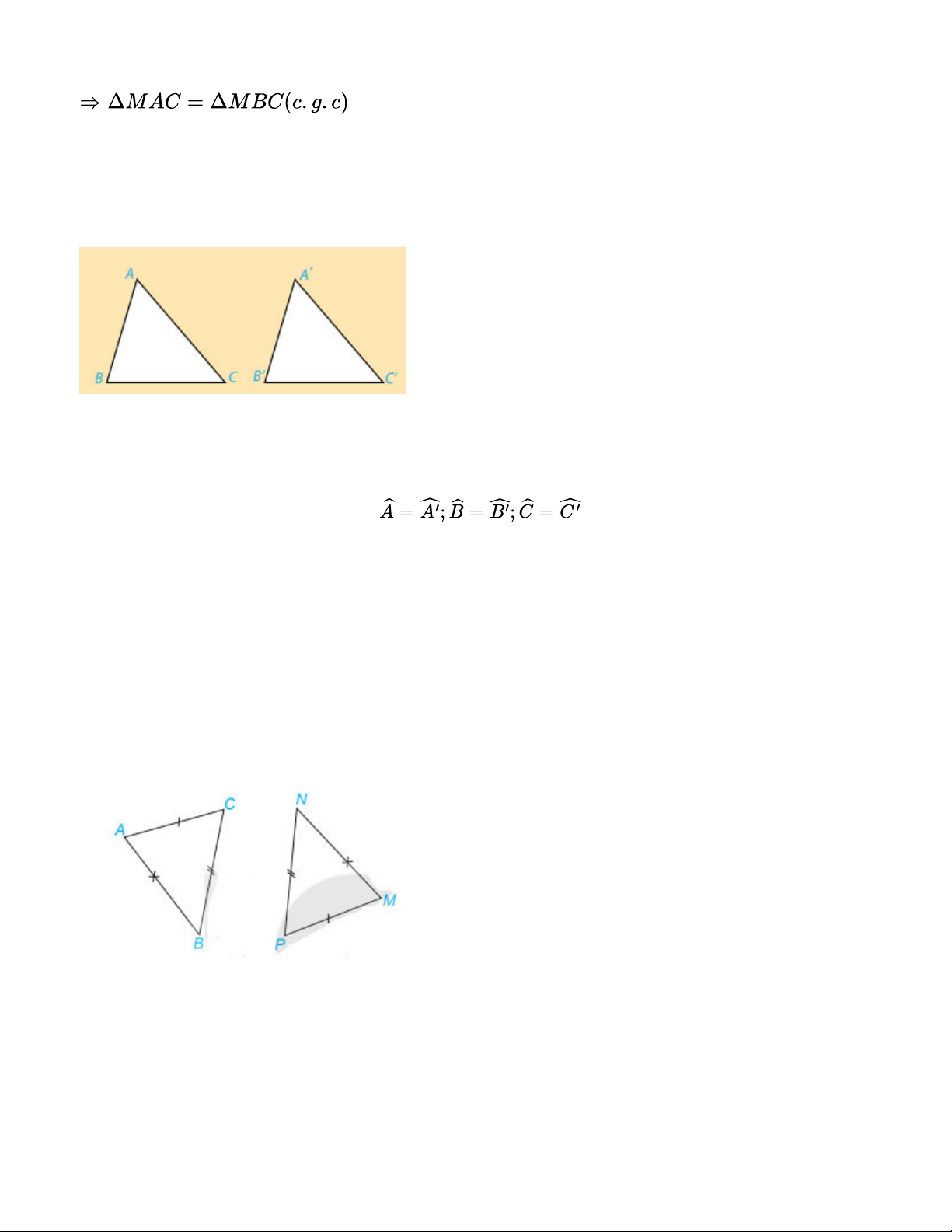
Hai tam giác ABC và A’B’C’ bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các
góc tương ứng bằng nhau, tức là:
AB = A’B’ ; AC = A’C’ ; BC = B’C’ và
Ta viết: ΔABC=ΔA′B′C′
Nếu 2 tam giác bằng nhau, ta suy ra tất cả các cạnh, các góc tương ứng bằng nhau.
2. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh (c.c.c)
Nếu 3 cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau. Ví dụ: Xét ΔABC và ΔMNP AB = MN BC = NP AC = MP Vậy ΔABCΔ = ΔMNP (c.c.c)