











































Preview text:
Chủ đề 1 HÀM SỐ LƯỢ NG GIÁC (2 tiết - 1,2 ) I. MỤC ĐÍCH YÊU CẦU:
1.Về kiến thức: Học sinh nắm rõ hơn các kiến thức đã được học trong phần bài học.
2.Về kỹ năng: Học sinh thành thạo hơn trong việc giải bài tập.
3.Về tư duy, thái độ: Rèn luyện tư duy linh hoạt thông qua việc giải toán. II. CHUẨN BỊ:
Giáo viên: Chuẩn bị một số bài tập về hàm số lượng giác.
Học sinh: Học kỹ lí thuyết, xem lại các ví dụ và bài tập đã giải.
III. PHƯƠNG PHÁP: Về cơ bản sử dụng phương pháp dạy học gợi mở vấn đề. Tuần 2- Tiết 1 IV. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới: HÀM SỐ LƯỢNG GIÁC
Hoạt động1: Tìm tập xác định của hàm số.
Hoạt động của GV
Hoạt động của HS
Ghi bảng
Hỏi: Tập xác định của Hs trả lời: Bài 1: hàm số
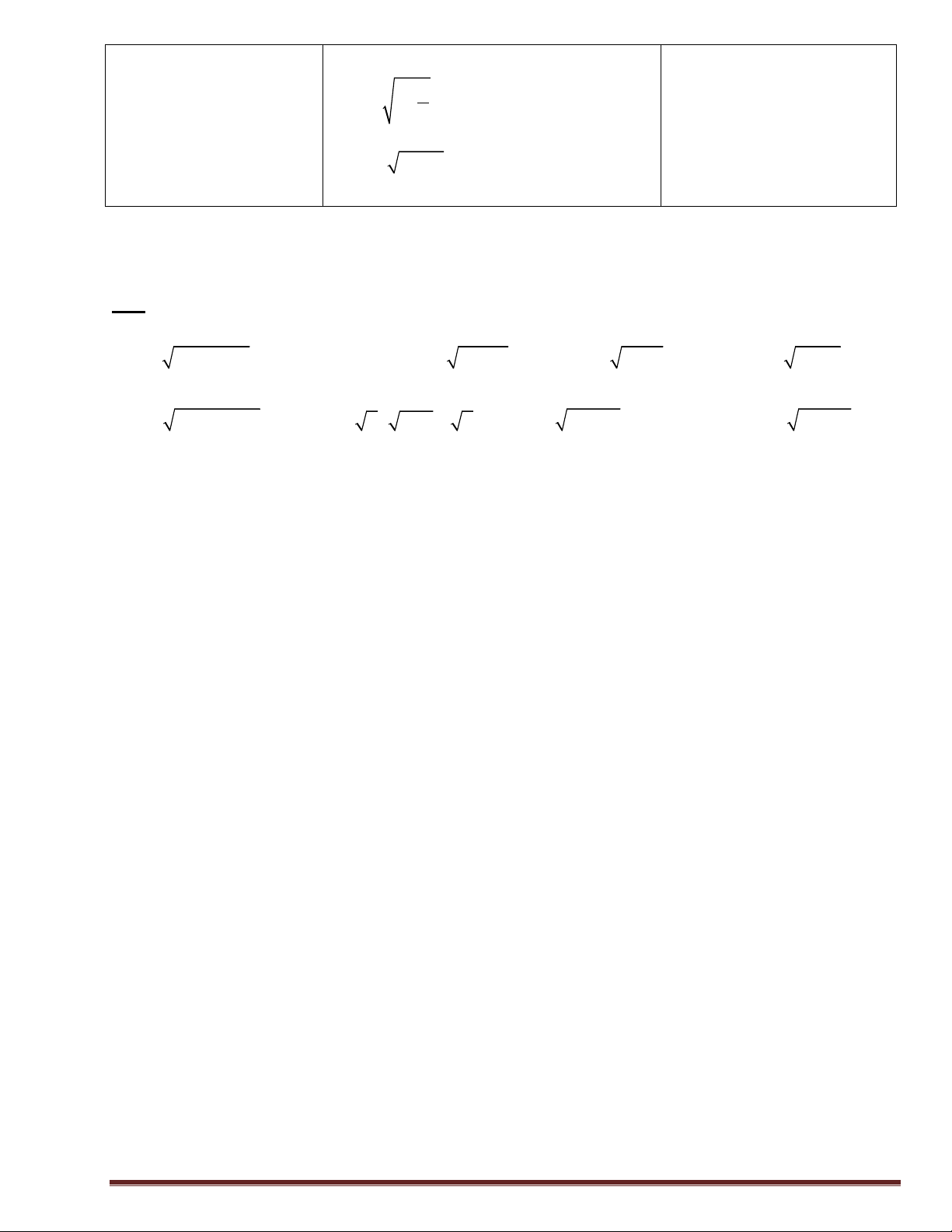
-Là tập hợp tất cả các số thực x sao Tìm tập xác định của hàm số: y=f(x) là gì? cho hàm số có nghĩa 1- sin x + x Các biểu thức tanf(x), 1) y = 1 sin ; 2) y = ; cos x 1- sin x f (x) - tanf(x) có nghĩa khi
cotf(x), f (x) , p p
3) y = cot(x + ); 4) y = tan(2x - ); g(x) p f (x) ¹ + kp 3 6 có nghĩa khi nào? 2 2x p
Gv yêu cầu Hs áp dụng - cotf(x) có nghĩa khi f (x) ¹ kp 5) y = sin(
); 6) y = cot(x - ); x -1 4
tìm tập xác định của các - f (x) có nghĩa khi f (x) ³ 0
7) y = tan(2x +1); 8) y = cos x; hàm số f (x) -
có nghĩa khi g(x) ¹ 0 4 p 9) y = cos
; 10) y = cot(2x - ). g(x) 5x 6
Hs xung phong lên bảng giải bài.
Hoạt động2: Tìm GTLN và GTNN của các hàm số.
Hoạt động của GV
Hoạt động của HS
Ghi bảng
Gv: Để làm những bài toán về -Hs lắng nghe và ghi nhớ
Bài 2Tìm GTLN và GTNN của tìm GTLN và GTNN của các các hàm số:
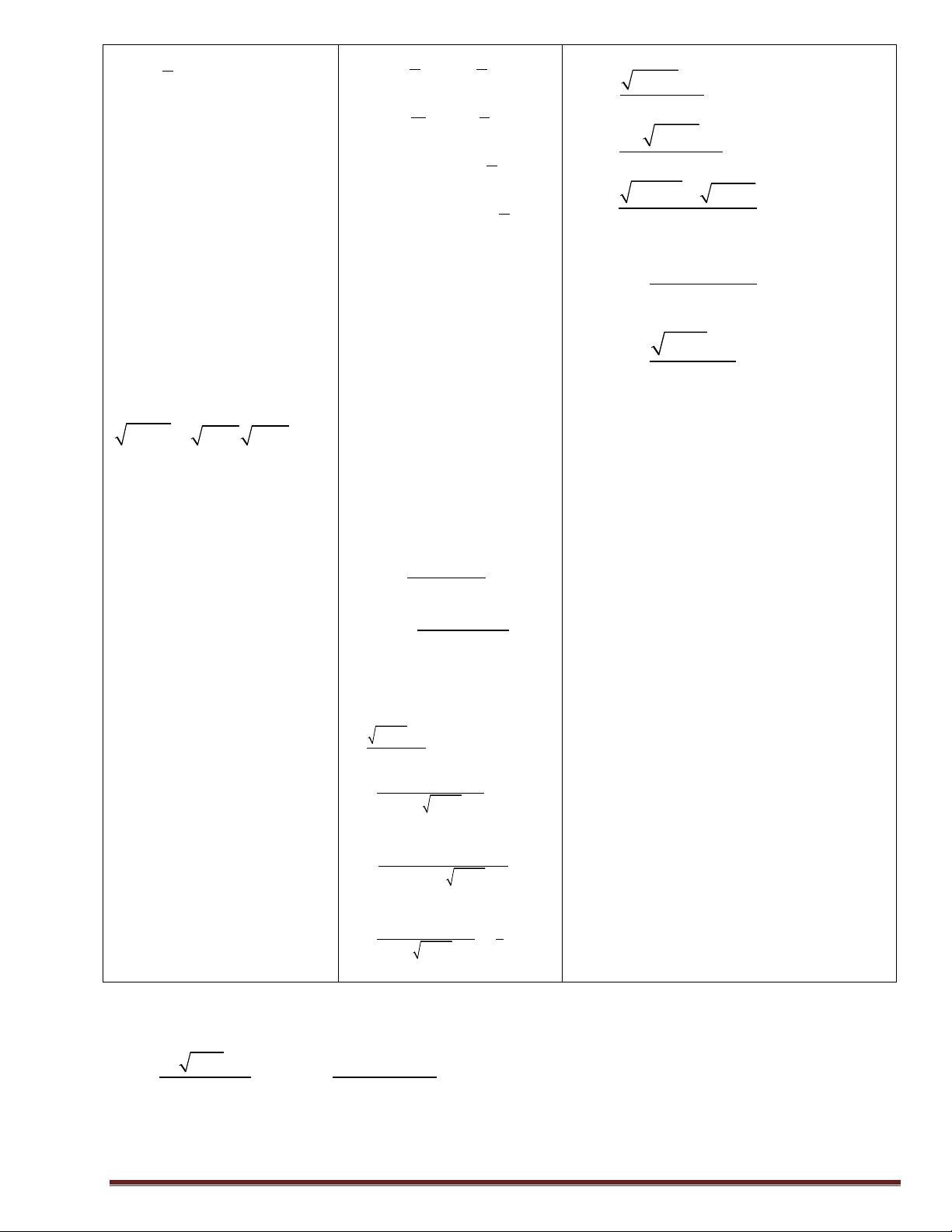
hàm số có liên quan đến sinx, æ p ö 1) y = 2cos x - =1
cosx ta thường áp dụng hệ ç ÷ è 3 ø quả: a " Î ! : 1 - £ sina £1và 2 1+ 4cos x 1 - £ cosa £1
2) y = 2 + 3cos x 3) y = 3
Gv: Với câu 5 và câu 6 ta phải Trả lời: = + -
dùng công thức lượng giác 2 2 2 4) y 1 sin x 3 5) 4sin .
x cos x = sin 2x
nào để biến đổi đưa về một 2 2 = - 2 5) y 3 4sin . x cos x
6) 2sin x - cos 2x = 1- 2cos 2x hàm số lượng giác. 2
6) y = 2sin x - cos 2x
V. CỦNG CỐ – DẶN DÒ: Học bài – Xem lại ví dụ – Đọc phần tiếp theo – Làm bài tập Sbt Rút kinh nghiệm Page 1
Tuần dạy - Tiết 2 VI. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới: HÀM SỐ LƯỢNG GIÁC (tt)
Hoạt động3: Xác định tính chẵn lẻ của các hàm số.
Hoạt động của GV
Hoạt động của HS
Ghi bảng
-Gv nhắc lại định nghĩa về
-Hàm số y=f(x) với tập xác Bài 3:
hàm số chẵn và hàm số lẻ.
định D gọi là hàm số chẵn
Xác định tính chẵn lẻ của các hàm số: nếu x
" ÎD thì -x ÎD và
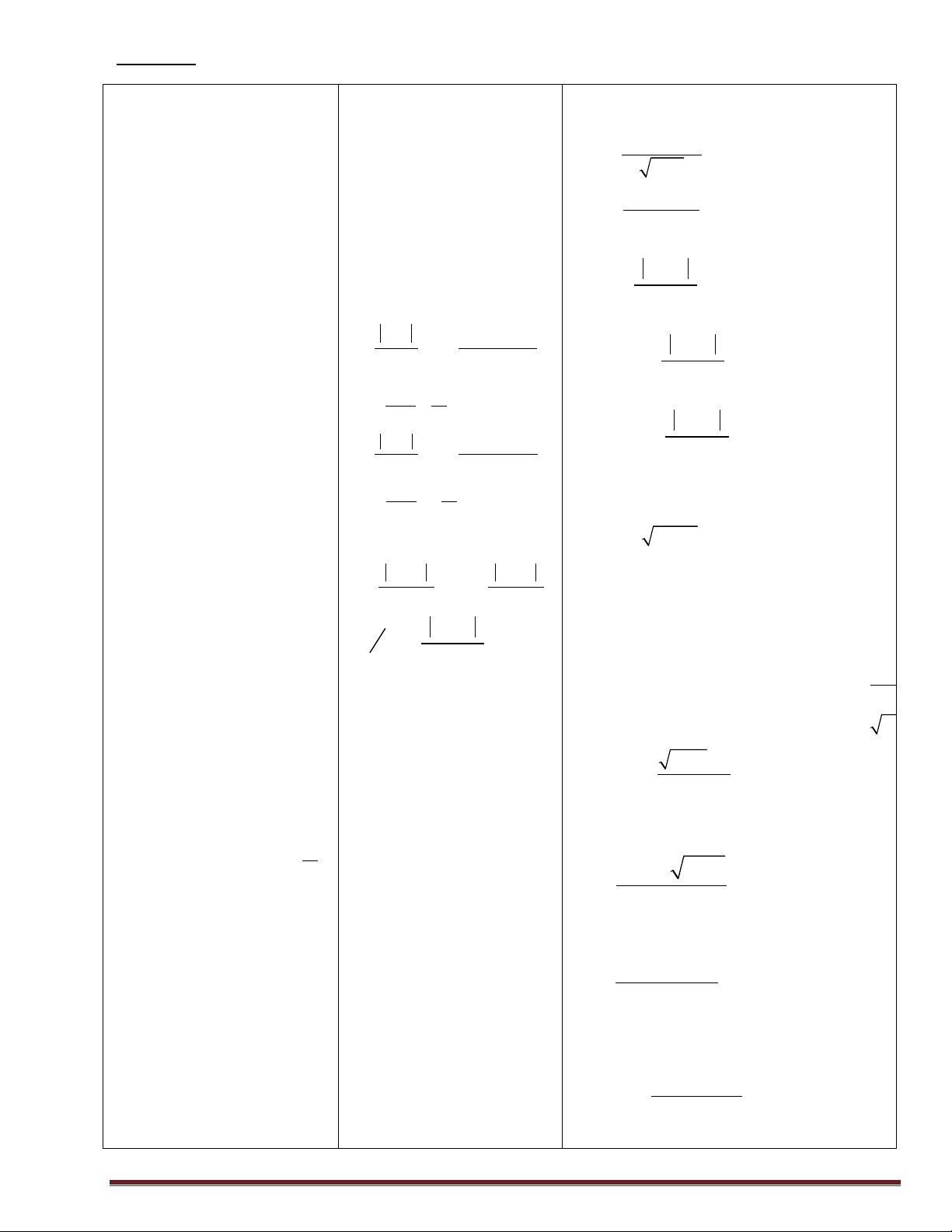
1) y = tan x + 2sin x f(-x)=f(x) 2
2) y = cos x + sin x
3) y = sin x + cos x
-Hàm số y=f(x) với tập xác 4) y = sin . x cos3x
-Gv yêu cầu Hs lên bảng giải. định D gọi là hàm số lẻ nếu 5) y = sin x+cot x x
" ÎD thì -x ÎD và 6) y = . x sin x f(-x)=-f(x). 7) y = .
x cos 2x -Hs lên bảng giải. 3
8) y = x sin 2x
9) y = x - sin x
10) y = sin 2x
Hoạt động4: Xác định chu kỳ của hàm số.
Hoạt động của GV
Hoạt động của HS
Ghi bảng
-Gv: Hãy xác định chu kì tuần -Hs phát biểu: Bài 4:
hoàn của các hàm số: sinx; cosx; -Chu kì tuần hoàn của hàm số
Xác định chu kỳ của hàm số: tanx? sin, cos là 2p . 1) y = cos 6x
-Chu kì tuần hoàn của hàm số 2) y = sin 3x tan, cot là p . x
-Vậy chu kì tuần hoàn của hàm
-Hs xác định chu kì tuần hoàn 3) y = tan 3 số là? của các hàm số
VII. CỦNG CỐ – DẶN DÒ:
-Nắm các kiến thức về tập xác định, tính chẵn lẻ, sự biến thiên, đồ thị và GTLN, GTNN của một hàm số lượng giác.
-Làm thêm các bài tập trong Sbt Rút kinh nghiệm Page 2
Ngày soạn: 10/ 9 / 2016
Chủ đề 2 PHƯƠNG TRÌNH LƯỢNG GIÁC (4 tiết- 3, 4, 5, 6)
I. MỤC ĐÍCH YÊU CẦU:
1.Về kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của phương trình lượng giác và bước
đầu hiểu được một số kiến thức mới về phương trình lượng giác trong chương trình nâng cao chưa được
đề cập trong chương trình chuẩn.
2.Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về phương trình lượng giác. Thông qua việc rèn
luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số
kiến thức mới trong chương trình nâng cao.
3.Về tư duy, thái độ:Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II. CHUẨN BỊ:Giáo viên: Giáo án, các bài tập và phiếu học tập,…
Học sinh: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III. PHƯƠNG PHÁP: Về cơ bản sử dụng phương pháp dạy học gợi mở vấn đề. Tuần dạy Tiết 3
IV. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
Ôn tập kiến thức cũ bằng cách đưa ra hệ thống câu hỏi sau:
-Nêu các phương trình lượng giác cơ bản sinx = a, cosx = a, tanx = a va cotx = a và công thức nghiệm.
-Dạng phương trình bậc nhất đối với hàm số lượng giác và cách giải.
-Phương trình bậc hai đối với một hàm số lượng giác.
-Phương trình bậc nhất đối với sinx và cosx và cách giải (phương trình a.sinx + b.cosx = c)
3/ Bài mới:
I. Phương trình lượng giác cơ bản
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ1( ): (Bài tập về
Bài tập 1: Giải các phương
phương trình lượng giác cơ trình sau: bản)
HS thảo luận để tìm lời giải… p
GV nêu đề bài tập 14 trong a)sin 4x = sin ; 5 SGK nâng cao. GV phân
HS nhận xét, bổ sung và ghi chép æ x + p ö 1 công nhiệm vụ cho mỗi sửa chữa… b)sin = - ; ç ÷
nhóm và yêu cầu HS thảo è 5 ø 2
luận tìm lời giải và báo x c) os c = os c 2; cáo. 2 GV gọi HS nhận xét, bổ æ p ö 2 sung (nếu cần) d) os c x + = . ç ÷
GV nêu lời giải đúng và
HS trao đổi và cho kết quả: è 18 ø 5 cho điểm các nhóm. p p p p a)x =
+ k , x = + k ; 20 2 5 2 11p 29p b)x = - + 10 k p , x = + 10 k p. 6 6 c)x = 2 ± 2 + k4p; p 2 d)x = a ± - + k2p , í v i cosa = . 18 5 Page 3
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ2: (Bài tập về tìm
Bài tập 2: tìm nghiệm của các
nghiệm của phương trình
phương trình sau trên khoảng trên khoảng đã chỉ ra)
HS xem nội dung bài tập 2, thảo đã cho:
GV nêu đề bài tập 2 và viết luận, suy nghĩ và tìm lời giải… a)tan(2x – 150) =1 với - lên bảng.
HS nhận xét, bổ sung và ghi chép
1800GV cho HS thảo luận và sửa chữa… 1 p
tìm lời giải sau đó gọi 2 HS HS trao đổi và rút ra kết quả: b)cot3x = - vÌ i - < x < 0. 3 2
đại diện hai nhóm còn lại a)-1500, -600, 300;
lên bảng trình bày lời giải. 4p p GV gọi HS nhận xét, bổ b) - ; - . 9 9 sung (nếu cần)
GV nêu lời giải đúng….
V. CỦNG CỐ – DẶN DÒ:
Hỏi: Giải các phương trình: 3p 0 a) tan 3x = tan ;
b) tan(x -15 ) = 5; 5 æ x ö 2p 0 c) cot + 20 = - 3; d) cot 3x = tan . ç ÷ è 4 ø 5 Rút kinh nghiệm : Page 4 Tuần dạy Tiết 4 VI. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1: (Bài tập về
Bài tập 1: Giải các phương trình phương trình bậc hai sau: đối với một hàm số 2
a) 2cos x - 3cos x +1 = 0 lượng giác)
HS suy nghĩ và trả lời… 2
b)sin x + sin x +1 = 0 GV để giải một phương trình bậc hai 2
c) 3 tan x - (1+ 3)tan x +1= 0. đối với một hàm số HS chú ý theo dõi.
lượng giác ta tiến hành như thế nào?
HS thảo luận theo nhóm để tìm lời giải GV nhắc lại các bước
và cử đại diện báo cáo. giải.
HS nhận xét, bổ sung và sửa chữa, ghi GV nêu đề bài tập 1, chép. phân công nhiệm vụ
HS trao đổi và cho kết quả: cho các nhóm, cho các p p ± + p
nhóm thảo luận để tìm a) x=k2 ;x= k2 . 3 lời giải. p GV gọi HS đại diện b) x= - + k2p ; 2 các nhóm trình bày lời p p giải. c) x =
+ kp , x = + kp. Gọi HS nhận xét, bổ 4 6 sung (nếu cần) GV nêu lời giải đúng… HĐ2 ( ): (Bài tập về
HS suy nghĩ và trả lời…
Bài tập 2: Giải các phương trình
phương trình bậc nhất HS nêu cách giải đối với phương trình sau: đối với sinx và cosx)
bậc nhất đối với sinx và cosx… a)3cosx + 4sinx= -5; Phương trình bậc nhất b)2sin2x – 2cos2x = 2 ;
đối với sinx và cosx có HS thảo luận theo nhóm và cử đại diện c)5sin2x – 6cos2x = 13. dạng như thế nào? báo cáo.
-Nêu cách giải phương HS nhận xét, bổ sung và sửa chữa ghi
trình bậc nhất đối với chép. sinx và cosx.
HS trao đổi và rút ra kết quả:
GV nêu đề bài tập 2 và a + + p vÌ i co a 3 s = vµ si a 4 yêu cầu HS thảo luận a) (2k 1) , n = 5 5 tìm lời giải. 5p 13p Gọi HS nhận xét, bổ b) x = + kp , x = ; sung (nếu cần) 24 24 c) V´ nghi÷m.
VII. CỦNG CỐ – DẶN DÒ: Học bài – Xem lại ví dụ – Đọc phần tiếp theo – Làm bài tập SGK Rút kinh nghiệm Page 5 Tuần dạy - Tiết 5
VIII. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ1(Phương trình bậc nhất đối với
Bài tập 1: Giải các phương trình
sinx và cosx; phương trình đưa về sau:
phương trình bậc nhất đối với sinx a)3sinx + 4cosx = 5; và cosx) b)2sinx – 2cosx = 2 ;
HĐTP 1: (phương trình bậc nhất
HS các nhóm thảo luận và 1 đối với sinx và cosx)
tìm lời giải sau đó cử đại c)sin2x +sin2x = 2
GV nêu đề bài tập và ghi lên bảng.
biện trình bày kết quả của d)5cos2x -12sin2x =13.
GV cho HS các nhóm thảo luận tìm nhóm. lời giải.
HS các nhóm nhận xét, bổ
GV gọi đại diện các nhóm trình bày sung và sửa chữa ghi chép.
kết quả của nhóm và gọi HS nhận xét, bổ sung (nếu cần)
GV hướng dẫn và nêu lời giải đúng.
HĐTP 2: Phương trình đưa về
phương trình bậc nhất đối với sinx và cosx)
GV nêu đề bài tập 2 và cho HS các
Bài tập 2: Giải các phương trình
nhóm thảo luận tìm lời giải.
HS các nhóm xem nội dung sau:
GV gọi HS trình bày lời giải và
các câu hỏi và giải bài tập a)3sin2x nhận xét (nếu cần) theo phân công của các
GV phân tích hướng dẫn (nếu HS
nhóm, các nhóm thảo luận, +8sinx.cosx+ (8 3 - 9) cos2x = 0;
nêu lời giải không đúng) và nêu lời
trao đổi để tìm lời giải. b)4sin2x + 3 3 sin2x-2cos2x=4 giải chính xác.
Các nhóm cử đại diện lên bảng trình bày. 1 c)sin2x+sin2x-2cos2x = ;
Các phương trình ở bài tập 2 còn HS nhận xét, bổ sung và 2
được gọi là phương trình thuần nhất sửa chữa ghi chép. d)2sin2x+ (3+ 3)sinx.cssx
bậc hai đối với sinx và cosx. HS chú ý theo dõi trên
GV: Ngoài cách giải bằng cách đưa bảng… + ( 3 - ) 1 cos2x = -1.
về phương trình bậc nhất đối với
sinx và cosx ta còn có các cách giải khác.
GV nêu cách giải phương trình
thuần nhất bậc hai đối với sinx và cosx: a.sin2x+bsinx.cosx+c.cos2x=0 HS chú ý theo dõi trên bảng…
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ1:(Phương trình bậc
HS các nhóm thảo luận để tìm lời
Bài tập1: Giải các phương trình:
nhất đối với sinx và cosx
giải các câu được phân công sau
và phương trình đưa về
đó cử đại diện báo cáo.
phương trình bậc nhất
HS nhận xét, bổ sung và sửa chữa
đối với sinx và cosx) ghi chép.
GV cho HS các nhóm thảo HS trao đổi và rút ra kết quả: Page 6
Hoạt động của GV
Hoạt động của HS
Ghi bảng
luận để tìm lời giải sau đó 5p = - + p
a) 3 cos x + sin x = 2 - ; cử đại diện báo cáo. a) x
k2 , k Î Z. 6
b) cos3x - sin 3x = 1; æ p ö p b) os c 3x + = os c ç ÷ 1
c)4sin x + 3cos x = 4(1+ tan x) - . è 4 ø 4 cos x GV gọi HS nhận xét, bổ p p
Û 3x + = ± + k2p , k ÎZ sung (nếu cần) 4 4 Vậy… c)( os
c x -1)(4sinx + 3 os c x -1) = 0 é os c x = 1 Þ ê
GV nêu lời giải đúng … ë4sinx + 3 os c x = 1 éx = 2kp ê Þ 4 3 1 ê sinx + os c x = ë5 5 5 1
Þ x -a = ±arccos + k2p 5 1
Û x = a ± arccos + k2p. 5 Vậy …
HĐ2: (Các phương trình
HS các nhóm thảo luận để tìm lời
Bài tập 2. Giải các phương trình sau: dạng khác)
giải các câu được phân công sau a)cos2x – sinx-1 = 0;
GV nêu đề bài 2 và ghi lên đó cử đại diện báo cáo. b)cosxcos2x = 1+sinxsin2x; bảng.
HS nhận xét, bổ sung và sửa chữa c)sinx+2sin3x = -sin5x;
GV cho HS các nhóm thảo ghi chép. d)tanx= 3cotx luận tìm lời giải.
GV gọi HS đại diện các
nhóm lên bảng trình bày lời giải. GV phân tích và nêu lời giải đúng…
IX. CỦNG CỐ – DẶN DÒ: Học bài – Xem lại ví dụ – Đọc phần tiếp theo – Làm bài tập SGK Rút kinh nghiệm Page 7 Tuần dạy - Tiết 6 X. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1:
HS các nhóm thảo luận đẻ tìm lời giải các Bài tập: GV nêu các bài tập và
bài tập như được phân công.
1)Giải các phương trình sau: ghi lên bảng, hướng
HS đại diện các nhóm trình bày lời giải a)cos2x – sinx – 1 = 0
dẫn giải sau đó cho HS (có giải thích). b)tanx = 3.cotx các nhóm thảo luận và
HS nhận xét, bổ sung và sửa chữa ghi 1 gọi HS đại diện các chép.
c)sinx.sin2x.sin3x = sin 4x 4 nhóm lên bảng trình
HS trao đổi và rút ra kết quả: bày lời giải.
a) cos 2x - sin x -1 = 0 GV gọi HS các nhóm
Û sin x(2sin x +1) = 0 khác nhận xét và bổ sung (nếu cần) ésin x = 0 ê Û 1 Û ... ê = - sin x ë 2 b) tanx = 3.cotx ĐK: cosx ¹ 0 và sinx ¹ 0 Ta có: tanx = 3.cotx GV nêu lời giải đúng 3 nếu HS không trình 2 Û tan x = Û tan x = 3 bày đúng lời giải. tan x Û tan x = ± 3 p
Þ x = ± + kp ,k Î! 3 Vậy…
c) HS suy nghĩ và giải … HĐ2:
HS các nhóm thảo luận để tìm lời giải và Bài tập: GV nêu đề một số bài
của đại diện lên bảng trình bày lời giải
Giải các phương trình sau:
tập và ghi đề lên bảng (có giải thích)
a) cot x - cot 2x = tan x +1 sau đó phân công
HS nhận xét, bổ sung và sửa chữa ghi 2
b) cos x = 3sin 2x + 3 nhiệm vụ cho các chép. nhóm
HS trao đổi và rút ra kết quả: c) cos .
x tan 3x = sin 5x GV cho các nhóma a)ĐK: sinx≠0 và cosx≠0
thảo luận và gọi HS đại cos x cos 2x sin x
diện lên bảng trình bày Þ - = +1 sin x sin 2x cos x lời giải. 2 2
Þ 2cos x - cos 2x = 2sin x + sin 2x GV gọi HS nhận xét, bổ sung (nếu cần) 2 2
Þ 2(cos x - sin x) - cos 2x = sin 2x
GV nhận xét và nêu lời Þ cos 2x = sin 2x Þ tan 2x =1 giải chính xác (nếu HS Þ không trình bày đúng ... lời giải)
b) Ta thấy với cosx = 0 không thỏa mãn
phương trình. với cosx≠0 chia hai vế của
phương trình với cos2x ta được: 1=6tanx+3(1+tan2x) Û 3tan2x+6tanx+2 = 0 Page 8
Hoạt động của GV
Hoạt động của HS
Ghi bảng 3 - ± 3 Û tan x = Û ... 3 c) cos .
x tan 3x = sin 5x 1 Û ( x + x) 1 sin 4 sin 2
= (sin8x + sin 2x) 2 2
Þ sin 8x = sin 4x é p
x = k , k Î ê ! 2 Þ ê p p
êx = + k ,k Î ê ! ë 12 6
XI. CỦNG CỐ – DẶN DÒ:
-Nêu lại công thức nghiệm các phương trình lượng giác cơ bản, các phương trình lượng giác thường gặp
và cách giải các phương trình lượng giác thường gặp.
-Xem lại các bài tập đã giải và các cách giải các phương trình luợng giác cơ bản và thường gặp.
-Làm thêm các bài tập trong phần ôn tập chương trong sách bài tập. Rút kinh nghiệm Page 9
Ngày soạn: 2 / 10 / 2016
Chủ đề 3 CHỦ ĐỀ :PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG (2 tiết- 7, 8 ) I.Mục tiêu:
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của phép dời hình và phép đồng
dạng trong mặt phẳng và bước đầu hiểu được một số kiến thức mới về phép dời hình và phép đồng dạng
trong chương trình nâng cao chưa được đề cập trong chương trình chuẩn.
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về phép dời hình và phép đồng dạng. Thông qua
việc rèn luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu
một số kiến thức mới trong chương trình nâng cao.
3)Về tư duy và thái độTích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III.Tiến trình giờ dạy:-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. Tuần dạy - Tiết 7
+Ôn tập kiến thức:Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu khái niệm phép dời hình, các phép tịnh tiến, , phép quay (là những phép dời hình)
+Nêu các tính chất của các phép dời hình,… +Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1:
HS thảo luận theo nhóm Cử đại
HĐTP1:(Bài tập về
diện lên bảng trình bày Bài tập 1:
chứng minh một đẳng Vì O’A’=OA, O’B’=OB,
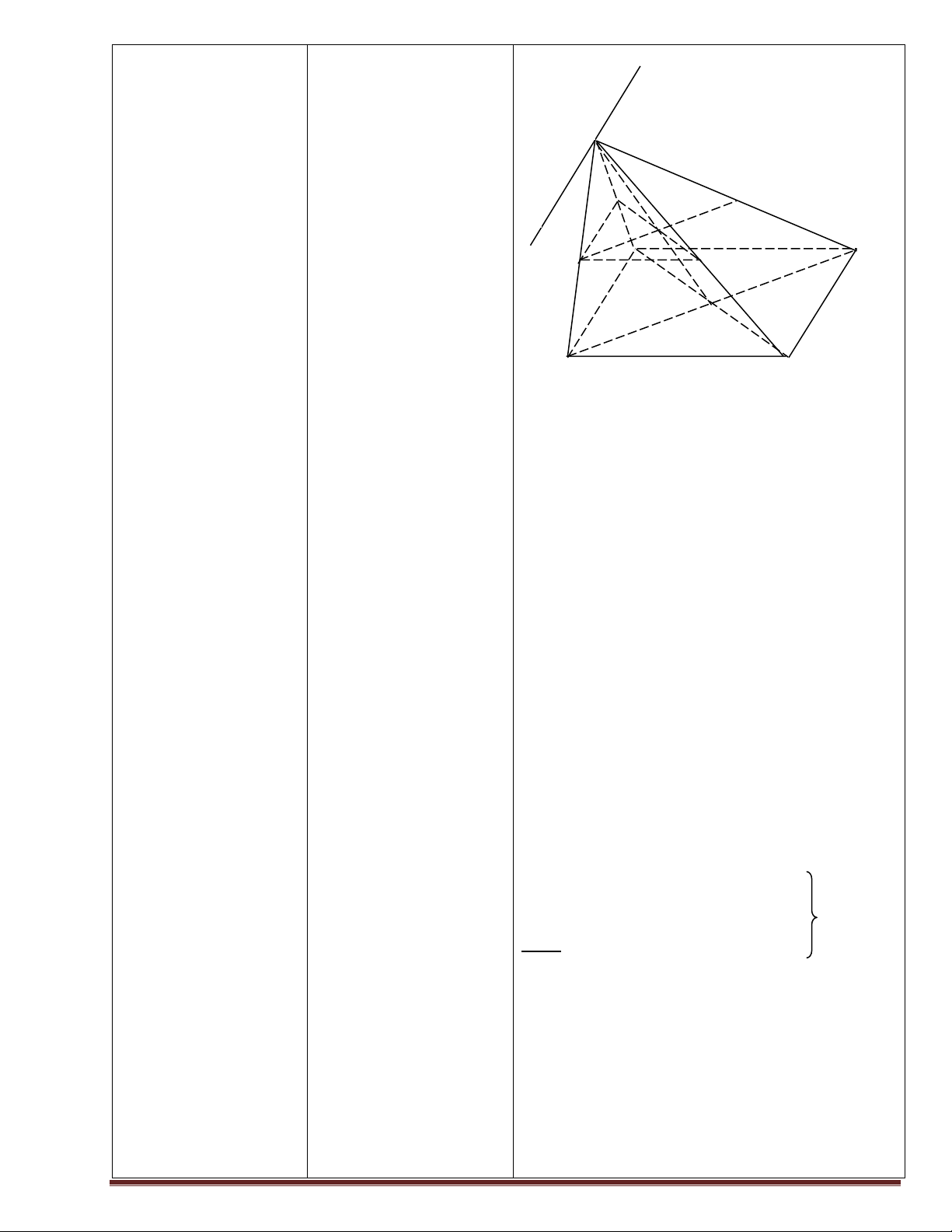
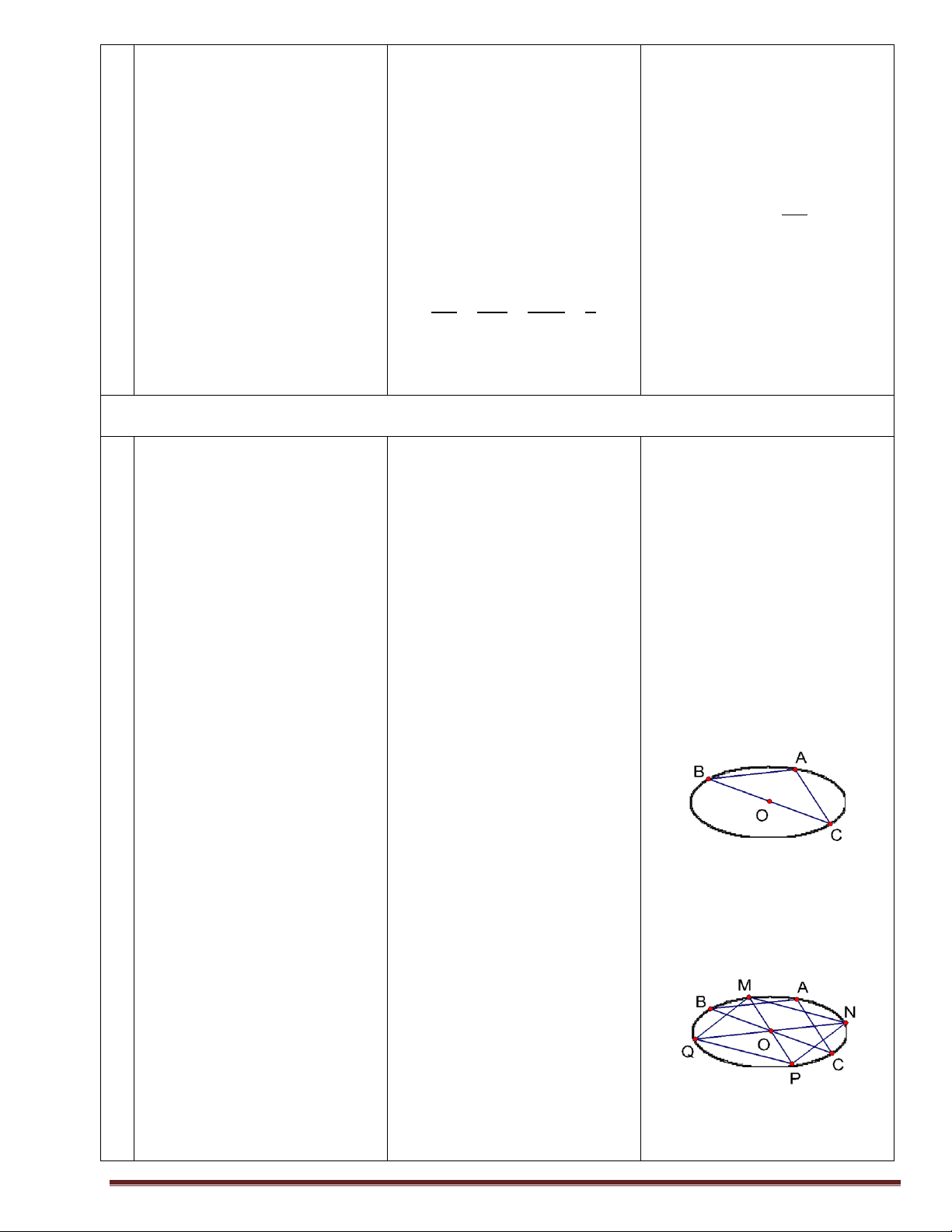
Chứng minh rằng nếu phép dời hình biến
thức bằng cách sử !!!"2
A’B’=AB và AB2= AB nên ta có: 3 điểm O, A, B lần lượt thành 3 điểm O’,
dụng kiến thức phép !!!!!" !!!" A’, B’ thì ta có: 2 2 dời hình)
A' B' = AB Þ A' B' = AB !!!!!" !!!!!" !!!" !!!" )
a O' A'.O' B' = O . A OB GV nêu đề và ghi lên !!!!!" !!!!!" 2 !!!" !!!" 2 !!!!!" !!!!!" !!!" !!!"
Þ (O'B'-O' A') = (OB-OA) bảng. Cho HS thảo )
b O' B' = t.O' A' Û OB = t.OA luận theo nhóm để tìm !!!!!"2 !!!!!" !!!!!" !!!!!"2
với t là một số tùy ý. lời giải.
Þ O' B' - 2O' B'.O' A' + O' A' !!!" !!!" !!!" !!!"
GV gọi HS đại diện lên 2 2 = OB - 2 . OB OA + OA
bảng trình bày lời giải. !!!!!" !!!!!" !!!" !!!" Gọi HS nhận xét, bổ
Þ O' A'.O' B' = O . A OB sung (nếu cần) GV nhận xét, nêu lời )T
b ı c©u a) vµ Æfinh ngh‹a ta c„ : giải đúng (nếu HS !!!!" !!!!" !!!!" !!!!" " O'B'=tO'A' Û O'B'-tO'A'=0 không trình bày đúng Bài tập 2: !!!!!" !!!!!" lời giải)
Trong mặt phẳng tọa độ Oxy cho điểm
Û (O'B'-t.O'A')2 = 0
I(2;-3) và đường thẳng d có phương trình !!!!!" !!!!!" !!!!!" !!!!"
HĐTP2: (Bài tập về 2 2
3nx + 2y -1 = 0. Tìm tọa độ của điểm I’
Û O' B' - 2tO' B'.O' A' + t O' A' = 0
phép đối xứng tâm)
vàn phương trình của đường thẳng d’ lần !!!"2 !!!" !!!" !!!" GV nêu đề bài tập và Û OB - 2t . OB OA 2 + t OA = 0
lượnt là ảnh của I và d qua phép đối xứng ghi lên bảng, cho HS !!!" !!!" 2 tâm O.
Û (OB-t.OA)
các nhóm thảo luận để = 0 tìm lời giải. !!!" !!!" " Gy: I’(-2; 3)
Û OB- t.OA = 0 Gọi HS đại diện nhóm
d' đối xứng với d qua tâm O nên phương !!!" !!!" lên bảng trình bày lời
Û OB = t.OA
trình của đường thẳng d có dạng: 3x + 2y Page 10 giải. + c= 0 Gọi HS nhận xét, bổ
HS các nhóm thảo luận để tìm lời Lấy M(1; -1) thuộc đường thẳng d khi đó sung (nếu cần)
giải và cử đại diện lên bảng trình
điểm đối xứng của M qua O là M’(-1;1)
bày lời giải (có giải thích)
thuộc đường thẳng d’. GV nhận xét, bổ sung
HS nhận xét, bổ sung và sửa chữa Suy ra: 3(-1) +2.1 +c = 0 và nêu kết quả đúng ghi chép. Û c = 1 (nếu HS không trình
HS trao đổi và rút ra kết quả:
Vậy đường thẳng d’ có phương trình: 3x bày đúng kết quả) + 2y +1 = 0 HĐ2: Bài tập 3:
HĐTP1: (Bài tập về
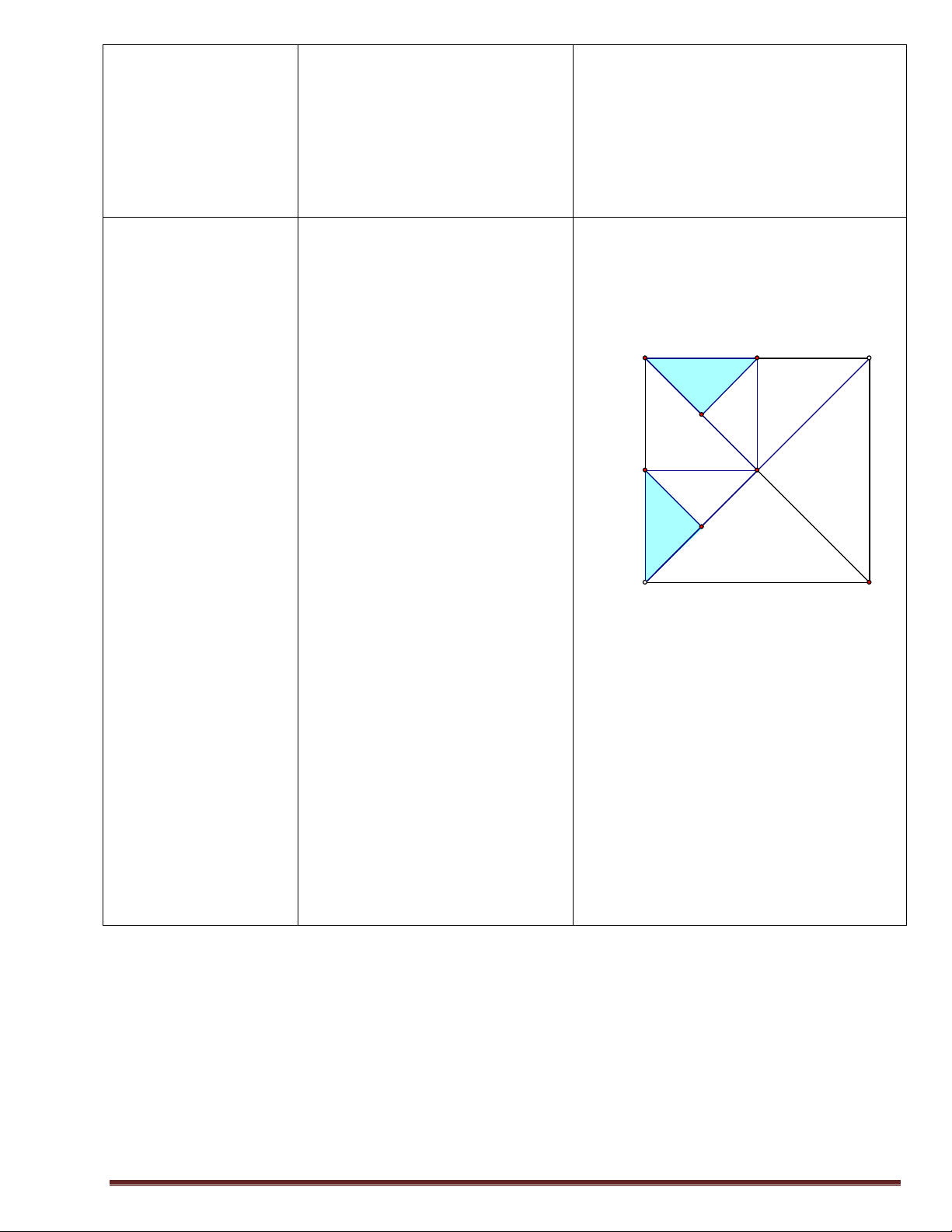
Cho hình vuông ABCD tâm O, M là trung phép quay)
HS thảo luận theo nhóm để tìm lời điẻm của AB, N là trung điểm của OA. GV nêu đề và ghi lên
giải và cử đại diện lên bảng trình
Tìm ảnh của tam giác AMN qua phép bảng. Cho HS các bày lời giải. quay tâm O góc quay
nhóm thảo luận để tìm
HS nhận xét, bổ sung và sửa chữa A M B lời giải. ghi chép. Gọi HS đại diện nhóm
HS trao đổi để rút ra kết quả: lên bảng trình bày lời
Phép quay tâm O góc quay 900 giải.
biến A thành D, biến M thành M’ N Gọi HS nhận xét, bổ
là trung điểm của AD, biến N sung (nếu cần)
thành N’ là trung điểm của OD. GV nhận xét, bổ sung
Do đó nó biến tam giác AMN M' O và nêu lời giải đúng thành tam giác DM’N’. (nếu HS không trình bày đúng lời giải) N' D C 900.
HĐTP2: (Bài tập về phép tịnh tiến)
HS các nhóm thảo luận để tìm lời Bài tập 4: GV nêu đề và ghi lên giải.
Trong mp Oxy cho đường thẳng d có
bảng, cho HS các nhóm HS đại diện trình bày lời giải trên phương trình 3x – y – 3 = 0. Viết phương
thảo luận tìm lời giải bảng (có giải thích)
trình của đường thẳng d’ là ảnh của
và gọi HS đại diện lên
HS nhận xét, bổ sung và sửa chữa đường thẳng d qua phéo dời hình có được
bảng trình bày kết quả ghi chép.
bằng cách thực hiện liên tiếp phép đối của nhóm.
xứng tâm I(1;2) và phép tịnh tiến theo ! Gọi HS nhận xét, bổ
HS trao đổi và rút ra kết quả … vectơ v = ( 2; - ) 1 sung (nếu cần). GV nhận xét, bổ sung và nêu kết quả đúng (nếu HS không trình bày đúng kết quả)
HĐ3: Củng cố và hướng dẫn học ở nhà:
*Củng cố:-Nêu lại định nghĩa các phép dời hình và tính chất của nó.
*Áp dụng: Giải bài tập sau: ! !
Chứng minh rằng phép tịnh tiến theo vectơ v ¹ 0 là kết quả của việc thực hiện liên tiếp hai phép đối
xứng qua hai trục song song với nhau.
*Hướng dãn học ở nhà:-Xem lại các bài tập đã Page 11 Tuần dạy - Tiết 8 +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu khái niệm phép đồng dạng, phép vị tự,…
+Nêu các tính chất của các phép đồng dạng,… +Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1: Bài tập1:
HĐTP1: (Bài tập về phép
Trong mp Oxy cho đường thẳng d có vị tự)
HS các nhóm thảo luận để tìm lời phương trình 3x + 2y – 6 = 0. Hãy
GV nêu đề và ghi lên bảng, giải và cử đại diện lên bảng trình
viết phương trình của đường thẳng d’
cho HS các nhóm thảo luận bày kết quả của nhóm (có giải
là ảnh của d qua phép vị tự tâm O tỉ số để tìm lời giải. thích). k = -2
Gọi HS đại diện trình bày
HS nhận xét, bổ sung và sửa chữa lời giải. ghi chép…
Gọi HS nhận xét, bổ sung
HS trao đổi để rút ra kết quả: (nếu cần)
Qua phép vị tự đường thẳng d’
GV nhận xét và nêu kết quả song song hoặc trùng với d nên
đúng (nếu HS không trình
phương trình của nó có dạng bày đúng kết quả) 3x+2y+c =0 Lấy M(0;3) thuộc d. Gọi
M’(x’,y’) là ảnh của M qua phép
vị tự tâm O, tỉ số k = -2. Ta có: !!!!" !!!!" !!!!"
OM = (0,3),OM ' = 2 - OM ìx' = 0
HĐTP2: (Bài tập áp dụng Þ í về phép vị tự) îy' = 2 - .3 = 6 - Bài tập 2:
GV nêu đề và ghi lên bảng, Do M’ thuộc d’ nên ta có:
Trong mp Oxy cho đường thẳng d có
cho HS các nhóm thảo luận 2(-6) +c = 0. Do đó c = 12
phương trình 2x + y – 4 = 0.
để tìm lời giải và gọi HS
Vậy phương trình của đường
a)Hãy viết phương trình của đường
đại diện lên bảng trình bày
thẳng d’ là: 3x + 2y + 12 = 0.
thẳng d1 làảnh của d qua phép vị tự kết quả của nhóm. tâm O tỉ số k = 3.
Gọi HS nhận xét, bổ sung
HS các nhóm thảo luận để tìm lời b)hãy viết phương trình của đường (nếu cần)
giải vàcử đại diện lên bảng trình
thẳng d2 là ảnh của d qua phép vị tự
GV nhận xét và nêu kết quả bày kết quả của nhóm mình (có
tâm I(-1; 2) tỉ số k = -2.
đúng (nếu HS không trình giải thích) bày đúng kết quả)
HS nhận xét, bổ sung và sửa chữa ghi chép.
HS trao đổi để rút ra kết quả… HĐ2: Bài tập 3:
HĐTP1: (Bài tập về phép
Trong mp Oxy cho đường thẳng d có đồng dạng)
HS các nhóm thảo luận để tìm lời phương trình x + y -2 = 0. Viết
GV nêu đề và ghi lên bảng
giải và cử đại diện lên bảng trình
phương trình đường thẳng d’ là ảnh và cho HS các nhóm thảo
bày lời giải của nhóm (có giải
của d qua phép đồng dạng có được
luận để tìm lời giải và gọi thích).
bằng cách thực hiện liên tiếp phép vị
đại diện nhóm lên bảng
HS nhận xét, bổ sung và sửa chữa 1
trình bày kết quả của nhóm. ghi chép.
tự tâm I(-1;-1) tỉ số k = và phép 2
Gọi HS nhận xét, bổ sung
HS trao đổi để rút ra kết quả: quay tâm O góc quay -450. (nếu cần)
Gọi d1 là ảnh của d qua phép vị tự GV nhận xét, bổ sung và Page 12
nêu kết quả đúng (nếu HS 1
không trình bày dúng kết
tâm I(-1;-1) tỉ số k = . Vì d1 2 quả)
song song hoặc trùng với d nên
phương trình của nó có dạng: x + y +c = 0
Lấy M(1;1) thuộc đường thẳng d =
thì ảnh của nó qua phép vị tự nói trên là O thuộc d 1. Vậy phương trình của d 1 là: x+y=0. Ảnh của d 1 qua phép quay
HĐTP2: (Bài tập áp
tâm O góc quay -450 là đường Bài tập 4: dụng)
thẳng Oy có phương trình: x = 0.
Trong mp Oxy cho đường tròn (C) có
GV nêu đề bài tập và ghi
phương trình (x-1)2 +(y-2)2 = 4. Hãy
lên bảng, cho HS các nhóm HS thảo luận theo nhóm để rút ra viết phương trình đường tròn (C’) là
thảo luận để tìm lời giải và kết quả và cử đại diện lên bảng
ảnh của (C) qua phép đồng dạng có
gọi HS đại diện nhóm lên
trình bày lời giải (có giải thích)
được bằng cách thực hiện liên tiếp
bảng trình bày lời giải.
HS nhận xét, bổ sung và sửa chữa phép vị tự tâm O tỉ số k = -2 và phép GV gọi HS nhận xét, bổ ghi chép. đối xứng trục Ox. sung (nếu cần)
HS trao đổi để rút ra kết quả:… GV nhận xét, bổ sung và
nêu lời giải đúng (nếu HS
không trình bày đúng lời giải )
HĐ3: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại định nghĩa các phép dời hình, phép đồng dạng và tính chất của nó.
*Áp dụng: Giải bài tập sau:
Trong mp Oxy cho đường thẳng d có phương trình 3x – 2y -6 = 0.
a) Viết phương trình của đường thẳng d1 là ảnh của d qua phép đối xứng trục Oy;
b) Viết phương trình của đường thẳng d2 là ảnh của d qua phép đối xứng qua đường thẳng D có phương trình x+y-2 = 0.
*Hướng dãn học ở nhà:
-Xem lại các bài tập đã giải trong tiết TCH1 và TCH2.
- Ôn tập lại và ghi nhớ các định nghĩa của phép dời hình và phép đồng dạng. Page 13
Ngày soạn: 22 / 10 / 2016
Chủ đề 4 TỔ HỢP VÀ XÁC SUẤT (4 tiết 9,10,11,12)
I. MỤC ĐÍCH YÊU CẦU:
1.Về kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của tổ hợp và xác suất và bước
đầu hiểu được một số kiến thức mới về tổ hợp và xác suất chưa được đề cập trong chương trình chuẩn.
2.Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về tổ hợp và xác suất. Thông qua việc rèn
luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số
kiến thức mới trong chương trình nâng cao.
3.Về tư duy, thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán. II. CHUẨN BỊ:
Giáo viên: Giáo án, các bài tập và phiếu học tập,…
Học sinh: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp. III. PHƯƠNG PHÁP:
Về cơ bản sử dụng phương pháp dạy học gợi mở vấn đề. Tiết 9 IV. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới:
Ôn tập kiến thức cơ bản của chủ đề: Quy tắc cộng, quy tắc nhân, hoán vị, chỉnh hợp, tổ hợp.
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ1(Ôn tập kiến thức cũ I. Ôn tập:
về quy tắc cộng, quy tắc
nhân, hoán vị, chỉnh hợp,
tổ hợp và rèn luyện kỹ nămg giải toán)
HS nêu lại lý thuyết đã học…
HĐTP1: (Ôn tập kiến thức cũ)
GV gọi HS nêu lại quy tắc
cộng, quy tắc nhân, hoán vị,
chỉnh hợp, tổ hợp và công thức nhị thức Niu-tơn.
HS các nhóm thảo luận và ghi lời
HĐTP2: (Bài tập áp dụng) giải vào bảng phụ.
GV nêu đề bài tập 1 và cho
Đại diện lên bảng trình bày lời
II.Bài tập áp dụng:
HS các nhóm thảo luận tìm giải.
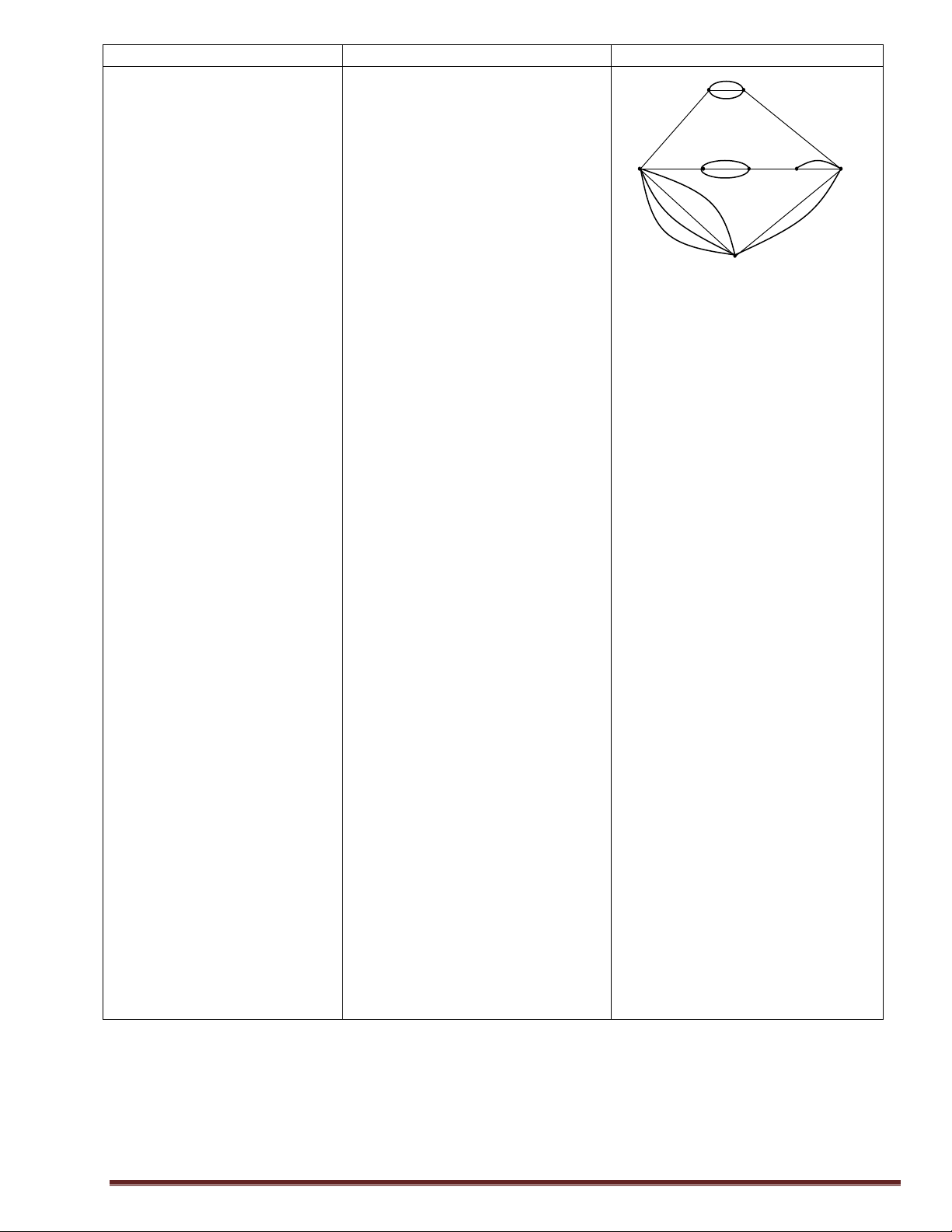
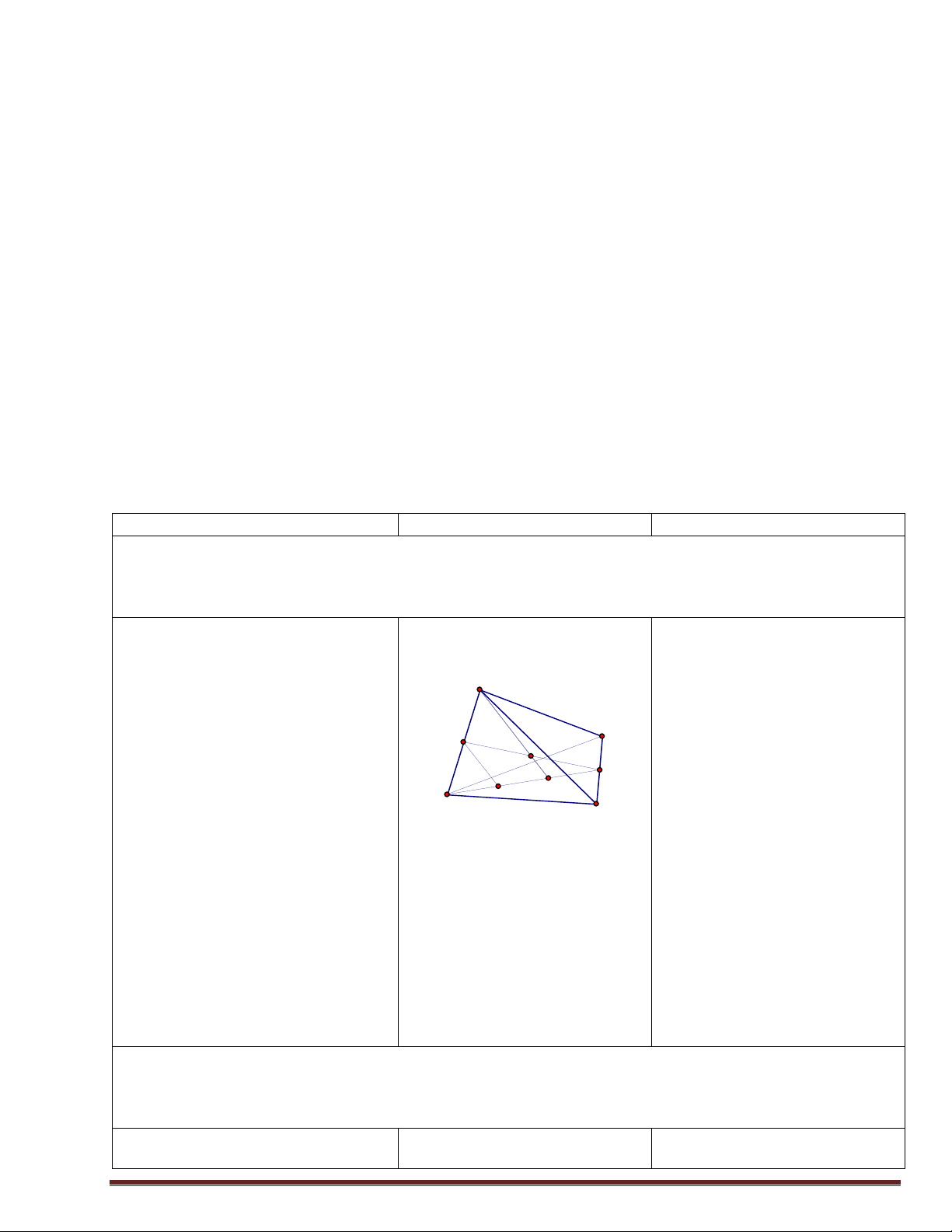
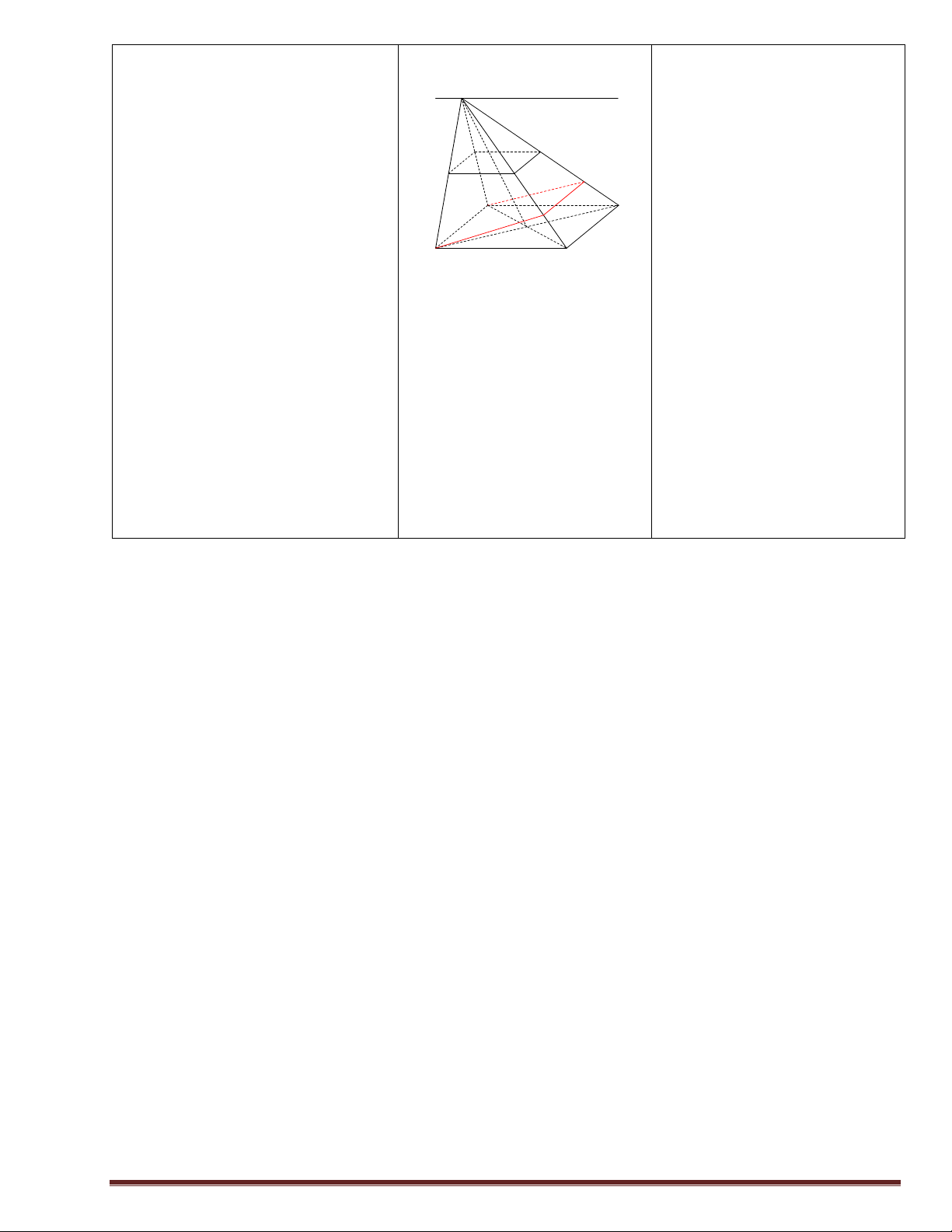
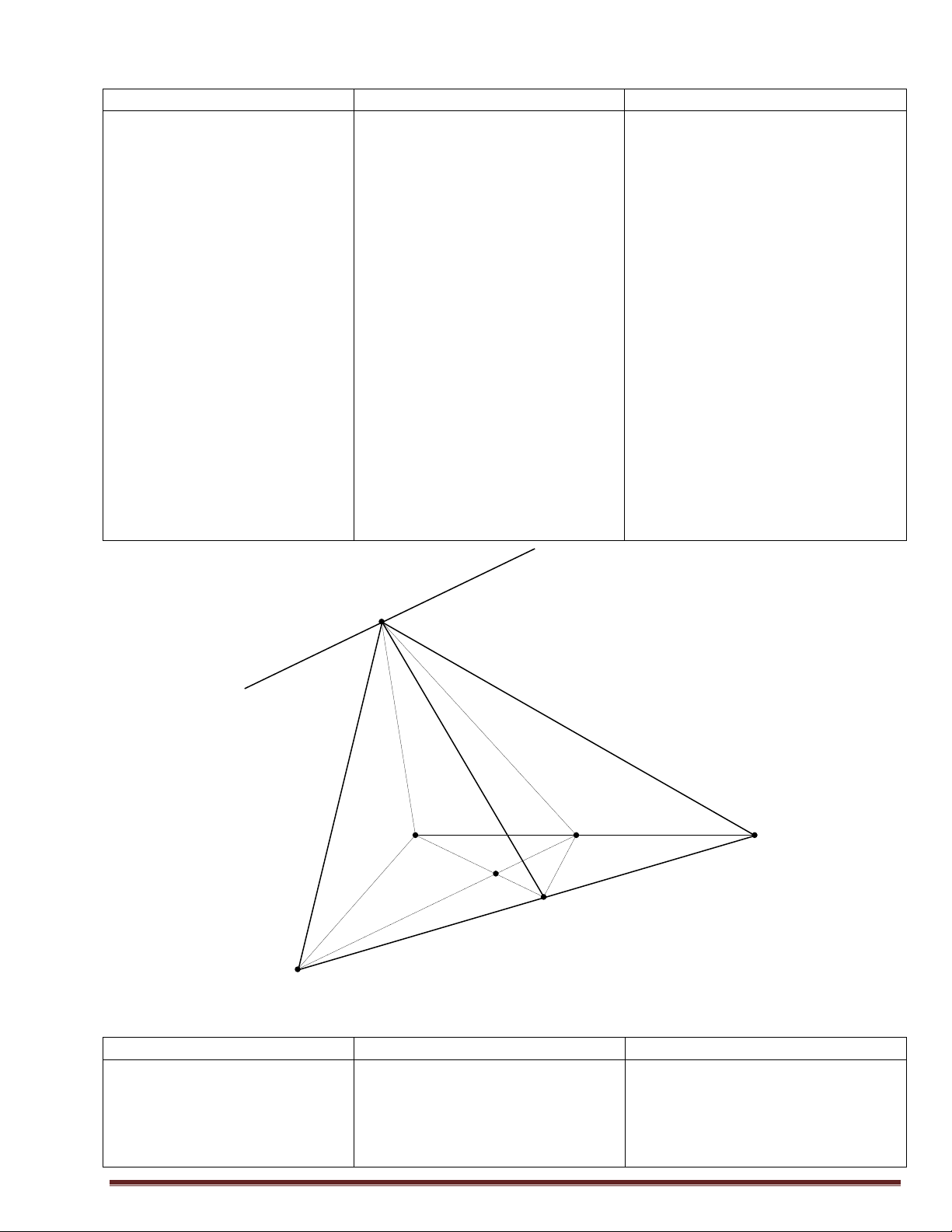
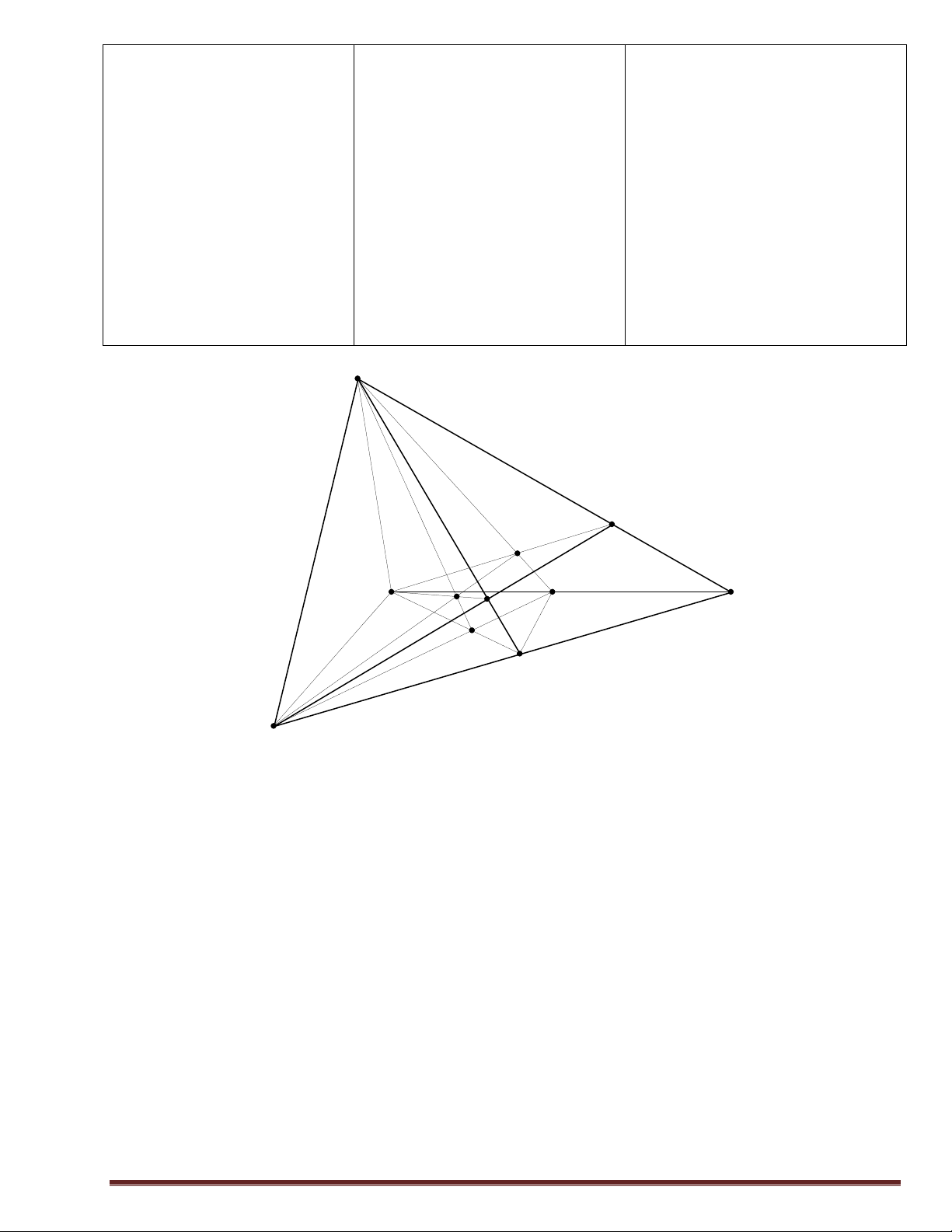
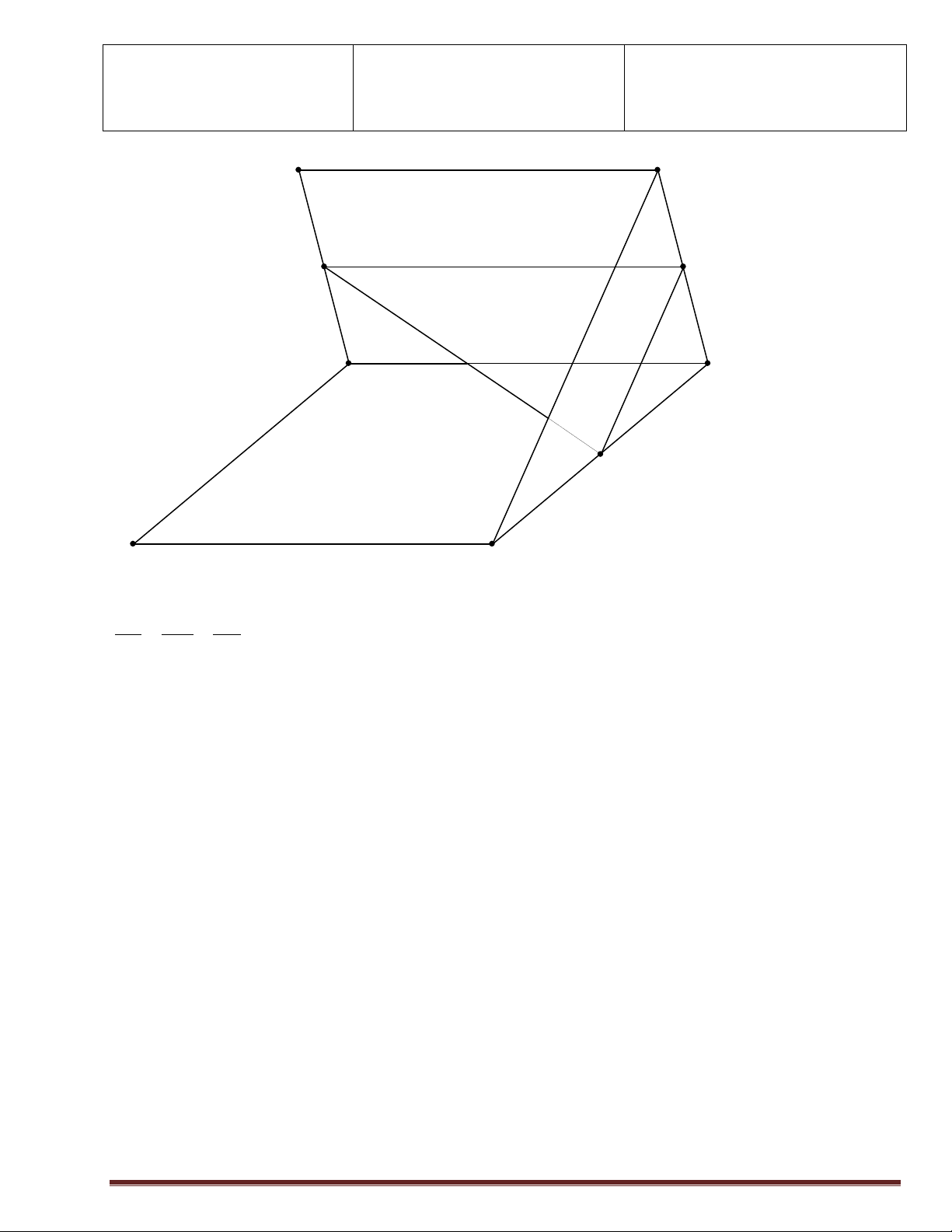
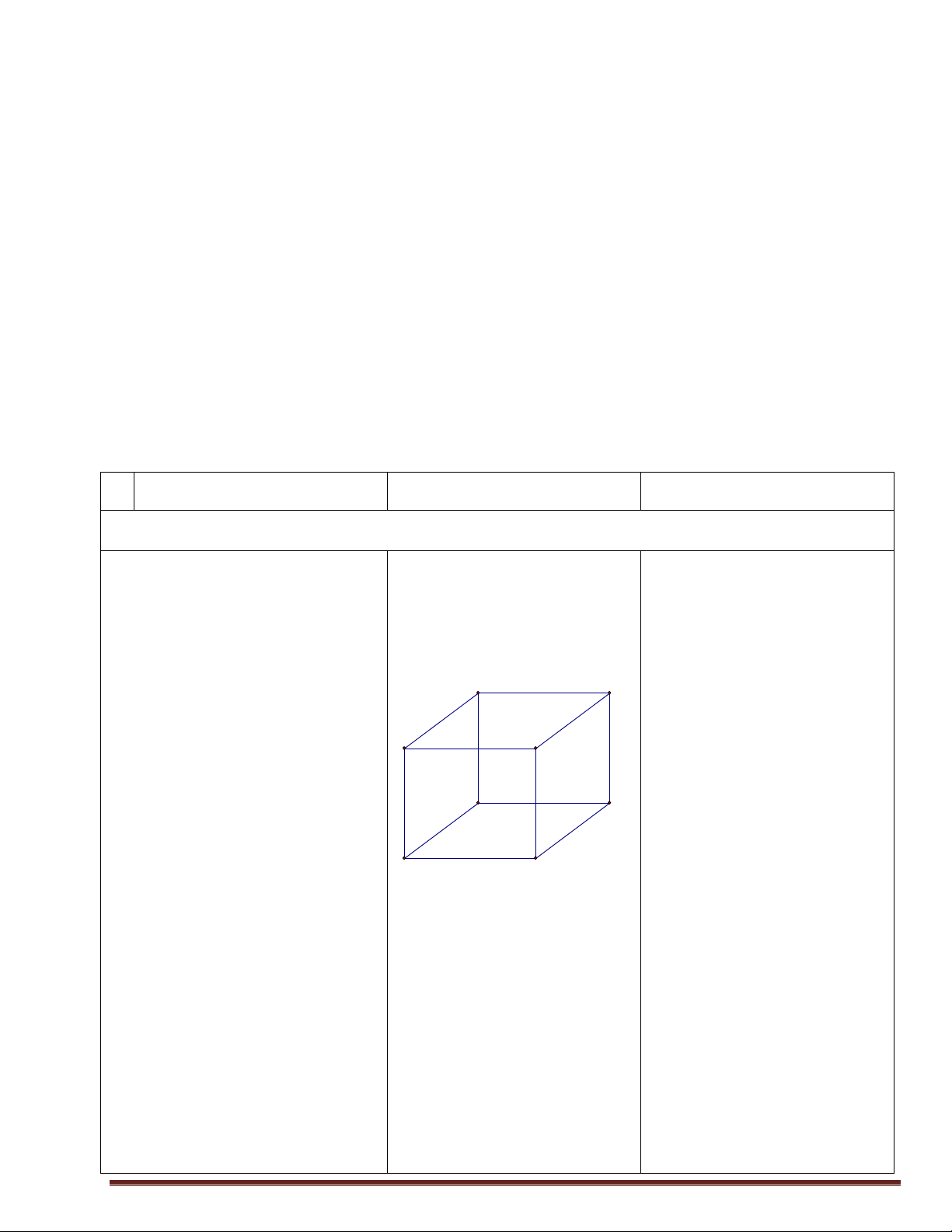
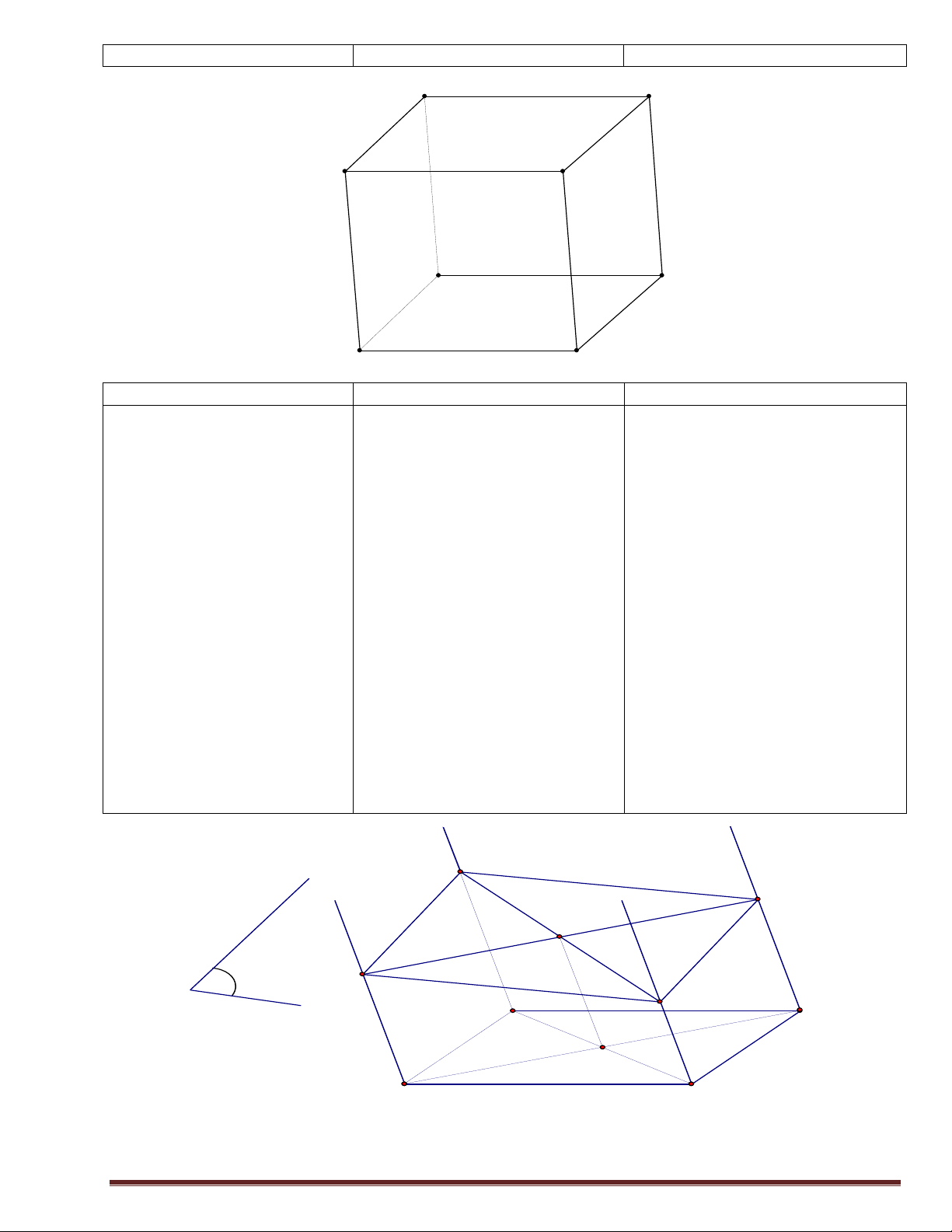
Bài tập1: Cho mạng giao thông lời giải.
HS nhận xét, bổ sung, sửa chữa như hình vẽ:
Gọi HS đại diện lên bảng và ghi chép. trình bày lời giải.
HS trao đổi và rút ra kết quả:
Gọi HS nhận xét, bổ sung
Ký hiệu A, B, C lần lượt là các (nếu cần)
tập hợp các cách đi từ M đến N
GV nhận xét và nêu lời giải
qua I, E, H. Theo quy tắc nhân ta chính xác (nếu HS không có: n(A) =1 x 3 x 1 =3
trình bày đúng lời giải) n(B) = 1x 3 x 1 x 2 = 6 n(C) = 4 x 2 = 8 Page 14
Hoạt động của GV
Hoạt động của HS
Ghi bảng
Vì A, B, C đôi một không giao I D
nhau nên theo quy tắc cộng ta có
số cách đi từ M đến N là: n(A∪B∪C)=n(A) +n(B) +n(C) =3+6+8=17 M E F G N
HS các nhóm thảo luận để tìm lời
HĐTP3: (Bài tập về áp giải.
dụng quy tắc nhân)
HS đại diện lên bảng trình bày
GV nêu đề bài tập 2 và cho lời giải. H
HS các nhóm thảo luận để
HS nhận xét, bổ sung, sửa chữa tìm lời giải. và ghi chép.
Gọi HS đại diện trình bày lời HS trao đổi và rút ra kết quả: giải.
a) Có 4 cách chọn hệ số a vì a≠0.
GV gọi HS nhận xét, bổ sung Có 5 cách chọn hệ số b, 5 cách (nếu cần)
chọn hệ số c, 4 cách chọn hệ số
Bài tập 2: Hỏi có bao nhiêu đa
GV nhận xét và nêu lời giải
d. Vậy có: 4x5x5x5 = 500 đa thức bậc ba: chính xác (nếu HS không thức.
P(x) =ax3+bx2+cx+d mà ác hệ số trình bày đúng)
b) Có 4 cách chọn hệ số a (a≠0). a, b, c, d thuộc tập
-Khi đã chọn a, có 4 cách chọn b. {-3,-2,0,2,3}. Biết rằng:
-Khi đã chọn a và b, có 3 cách a) Các hệ số tùy ý; chọn c.
b) Các hệ số đều khác nhau.
-Khi đã chọn a, b và c, có 2 cách chọn d. Theo quy tắc nhân ta có: 4x4x3x2=96 đa thức.
HS thảo luận và cử đại diện lên
bảng trình bày lời giải (có giải
Bài tập 3. Để tạo những tín hiệu,
HĐTP4: (Bài tập về áp thích)
người ta dùng 5 lá cờ màu khác
dụng công thức số các hoán HS nhận xét, bổ sung, sửa chữa
nhau cắm thành hàng ngang. Mỗi
vị, số các chỉnh hợp) và ghi chép.
tín hiệu được xác định bởi số lá
GV nêu đề bài tập 3 (hoặc
HS trao đổi và cho kết quả:
cờ và thứ tự sắp xếp. Hỏi có có
phát phiếu HT), cho HS các
a)Nếu dùng cả 5 lá cờ thì một tín thể tạo bao nhiêu tín hiệu nếu:
nhóm thảo luận và gọi đại
hiệu chính là một hoán vị của 5
a) Cả 5 lá cờ đều được dùng;
diện lên bảng trình bày lời
lá cờ. Vậy có 5! =120 tín hiệu
b) Ít nhất một lá cờ được dùng. giải. được tạo ra.
Gọi HS nhận xét, bổ sung
b)Mỗi tín hiệu được tạo bởi k lá (nếu cần)
cờ là một chỉnh hợp chập k của 5
GV nhận xét và nêu lời giải
phần tử. Theo quy tắc cộng, có chính xác. tất cả: 1 2 3 4 5
A + A + A + A + A = 325 tín 5 5 5 5 5 hiệu.
V. CỦNG CỐ – DẶN DÒ: Học bài – Xem lại ví dụ – Đọc phần tiếp theo – Làm bài tập SGK Rút kinh nghiệm Tiết 10 VI. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm. Page 15
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ1: (Ôn tập kiến thức và bài I.Ôn tập: tập áp dụng)
HĐTP: (Ôn tập lại kiến thức
về tổ hợp và công thức nhị
thức Niu-tơn, tam giác Pascal,
xác suất của biến cố…)
GV gọi HS nêu lại lý thuyết về
HS nêu lại lý thuyết đã học…
tổ hợp, viết công thức tính số các Viết các công thức tính số các tổ
tổ hợp, viết công thức nhị thức
hợp, công thức nhị thức Niu- Niu-tơn, tam giác Pascal. tơn,…
GV gọi HS nhận xét, bổ sung
Xác suất của biến cố… (nếu cần) HS nhận xét, bổ sung …
HĐ2: (Bài tập áp dụng công
thức về tổ hợp và chỉnh hợp)
II. Bài tập áp dụng: HĐTP1:
GV nêu đề và phát phiếu HT
Bài tập 1: Từ một tổ gồm 6
(Bài tập 1) và cho HS thảo luận
bạn nam và 5 bạn nữ, chọn tìm lời giải.
HS các nhóm thảo luận và tìm
ngẫu nhiên 5 bạn xếp vào bàn
Gọi HS đại diện lên bảng trình
lời giải ghi vào bảng phụ.
đầu theo những thứ tự khác bày lời giải.
HS đại diện nhóm lên bảng trình nhau. Tính xác suất sao cho
Gọi HS nhận xét, bổ sung (nếu bày lời giải.
trong cách xếp trên có đúng 3 cần)
HS nhận xét, bổ sung, sửa chữa bạn nam.
GV nhận xét, và nêu lời giải và ghi chép.
chính xác (nếu HS không trình
HS trao đổi và rút ra kết quả; bày đúng lời giải)
Mỗi một sự sắp xếp chỗ ngồi
cho 5 bạn là một chỉnh hợp chập
5 của 11 bạn. Vậy không gian mẫu W gồm 5 A (phần tử) 11
Ký hiệu A là biến cố: “Trong
cách xếp trên có đúng 3 bạn nam”.
Để tính n(A) ta lí luận như sau: -Chọn 3 nam từ 6 nam, có 3
C cách. Chọn 2 nữ từ 5 nữ, có 6 2 C cách. 5
-Xếp 5 bạn đã chọn vào bàn đầu
theo những thứ tự khác nhau, có
5! Cách. Từ đó thưo quy tắc nhan ta có: n(A)= 3 2 C .C .5! 6 5
Vì sự lựa chọn và sự sắp xếp là
ngẫu nhiên nên các kết quả đồng khả năng. Do đó: 3 2 C .C .5! 6 5 P( ) A = » 0, 433
HĐTP2: (Bài tập về tính xác 5 A11
suất của biến cố) Page 16
Hoạt động của GV
Hoạt động của HS
Ghi bảng
GV nêu đề và phát phiếu HT 2
HS các nhóm thảo luận và ghi
Bài tập2: Một tổ chuyên môn
và yêu cầu HS các nhóm thảo
lời giải vào bảng phụ, cử đại
gồm 7 thầy và 5 cô giáo, trong luận tìm lời giải.
diện lên bảng trình bày lời giải
đó thầy P và cô Q là vợ chồng.
Gọi HS đại diện các nhóm lên (có giải thích)
Chọn ngẫu nhiên 5 người để
bảng trình bày kết quả của
HS nhận xét, bổ sung, sửa chữa
lập hội đồng chấm thi vấn đáp. nhóm. và ghi chép.
Tính xác suất để sao cho hội
HS trao đổi và rút ra kết quả:
đồng có 3 thầy, 3 cô và nhất
Gọi HS nhận xét, bổ sung (nếu
Kết quả của sự lựa chọn là một
thiết phải có thầy P hoặc cô Q cần)
nhóm 5 người tức là một tổ hợp nhưng không có cả hai.
chập 5 của 12. Vì vậy không gian mẫu W gồm:
GV nhận xét và nêu lời giải 5 C = 792 phần tử. 12
chính xác (nếu HS không trình
Gọi A là biến cố cần tìm xác bày đúng lời giải)
suất, B là biến cố chọn được hội
đồng gồm 3 thầy, 2 cô trong đó
có thầy P nhưng không có cô Q.
C là biến cố chọn được hội đông
gồm 3 thầy, 2 cô trong đó có cô Q nhưng không có thầy P. Như vậy: A=B∪ C và n(A)=n(B)+ n(C) Tính n(B):
-Chọn thầy P, có 1 cách.
-Chọn 2 thầy từ 6 thầy còn lại, có 2 C cách. 6
-Chọn 2 cô từ 4 cô, có 2 C cách 4 Theo quy tắc nhân: n(B)=1. 2 C . 2 C =90 6 4 Tương tự: n(C)= 3 1 1.C .C = 80 6 4 Vậy n(A) = 80+90=170 và: n( ) A 170 P( ) A = = n(W) 792
VII. CỦNG CỐ – DẶN DÒ:
Bài tập: Sáu bạn, trong đó có bạn H và K, được xếp ngẫu nhiên thành hàng dọc. Tính xác suất sao cho:
a) Hai bạn H và K đứng liền nhau;
b) Hai bạn H và K không đứng liền nhau. Rút kinh nghiệm - Tiết 11
VIII. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng Page 17
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ1: (Ôn tập lại lý thuyết về xác suất)
HS suy nghĩ và trả lời các câu hỏi… Bài tập 1: HĐTP1:
HS các nhóm thảo luận để tìm lời giải Lấy ngẫu nhiên một thẻ từ một Gọi HS nhắc lại: và ghi vào bảng phụ
hộp chứa 20 thẻ được đánh số
-Công thức tính xác suất;
Hs đại diện lên bảng trình bày lời giải. từ 1 tới 20. Tìm xác suất để thẻ
-Các tính chất của xác suất;
HS trao đổi và rút ra kết quả: được lấy ghi số:
-Hai biến cố độc lập? Không gian mẫu: a)Chẵn; -Quy tắc nhân xác suất; W = {1,2,..., } 20 Þ n(W) = 20 b)Chia hết cho 3;
HĐTP2: (Bài tập áp dụng)
Gọi A, B, C là các biến cố tương ứng c)Lẻ và chia hết cho 3.
GV nêu đề bài tập 1 và ghi
của câu a), b), c). Ta có: lên bảng:
a)A = {2,4,6,..., } 20 Þ n ( A) = Nêu câu hỏi: 10
-Để tính xác suất cảu một 10 1 Þ P ( A) = =
biến cố ta phải làm gì? 20 2
-Không gian mẫu, số phần tử
b)B = {3,6,9,12,5, } 18 Þ n (B) = 6
của không gian mẫu trong bài tập 1. 6 3 Þ P (B) = = = 0,3
GV cho HS các nhó thảo luận 20 10
và gọi HS đại diện lên bảng 3 trình bày lời giải. c)C = {3,9, } 15 Þ P(C) = = 0,15 20
Gọi HS nhận xét, bổ sung …
GV nhận xét và nêu lời giải HS suy nghĩ trả lời: đúng.
P ( AÈ B) = P ( A) + P (B) Bài tập 2:
Một lớp học có 45 HS trong HĐTP3:
đó 35 HS học tiếng Anh, 25
Nếu hai biến cố A và B xung
HS học tiếng Pháp và 15 HS
khắc cùng liên quan đến phép P ( A È B) = P ( A) + P (B) - P ( A Ç B) học cả Anh và Pháp. Chọn
thử thì ta có điều gì?
ngẫu nhiên một HS. Tính xác
Vậy nếu hai biến cố A và B
suất của các biến cố sau:
bất kỳ cùng liên quan đến
HS các nhóm thảo luận và tìm lời
a)A: “HS được chọn học tiếng
một phép thử thì ta có công giải… Anh” thức tính xác suất
b)B: “HS được chọn chỉ học
P ( AÈ B)? tiếng Pháp”
HĐTP4: (Bài tập áp dụng)
c)C: “HS được chọn học cả
GV nêu đề bài tập 2 và cho Anh lẫn Pháp”
HS các nhóm thảo luận tìm
d)D: “HS được chọn không lời giải.
học tiếng Anh và tiếng Pháp”.
Gọi Hs đại diện trình bày lời
giải, gọi HS nhận xét, bổ
sung và nêu lời giải đúng.
IX. CỦNG CỐ – DẶN DÒ:
Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên hai người. Tìm xác suất sao cho trong hai người đó:
a)Cả hai người đó đều là nữ;b)Không có nữ nào; c)Ít nhất một người là nữ; d)Có đúng một người là nữ. Rút kinh nghiệm Tiết 12 X. TIẾN TRÌNH BÀI HỌC :
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. Page 18
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1: (Ôn tập) Bài tập1: GV gọi HS nêu lại công
HS suy nghĩ và trả lời…
Khai triển (x – a)5 thành thức nhị thức Niu-tơn, tổng các đơn thức. công thức tam giác Pascal…
HS các nhóm thảo luận và cử đại diện lên
HĐTP1: (Bài tập áp
bảng trình bày lời giải (có giải thích). dụng)
HS đại diện các nhóm lên bảng trình bày
GV nêu các bài tập và ghi lời giải. lên bảng.
HS nhận xét, bổ sung và sửa chữa ghi GV phân công nhiệm vụ chép… cho các nhóm và cho các
HS trao đổi và rút ra kết quả:
nhóm thảo luận để tìm lời Theo công thức nhị thức Niu-tơn ta có:
giải, gọi HS đại diện các 5 5
(x - a) = éx + ë (-a)ù nhóm lên bảng trình bày û lời giải.
= x + 5x (-a) +10x (-a)3 +10x (-a)2 5 4 3 2 + ... GV gọi HS nhận xét, bổ 5 4 3 2 2 3 4 5 = - + - + - sung và sửa chữa ghi x 5x a 10x a 10x a 5xa a chép. GV nhận xét và nêu lời
HS các nhóm thảo luận để tìm lời giải. giải chính xác (nếu HS
Bài tập 2: Tìm số hạng
HS đại diện nhóm lên bảng trình bày lời
không trình bày đúng lời không chứa x trong khai giải (có giải thích) giải). 6
HS trao đổi và rút ra kết quả: æ 1 ö triễn: 2x -
Số hạng tổng quát trong khai triển là: ç 2 ÷
HĐTP2: (Bài tập về tìm è x ø k
một số hạng trong khai -k k æ 1 ö C 2x . - 6 ( )6
triển nhị thức Niu-tơn) ç 2 ÷ è x ø GV nêu đề và ghi lên 6 = C 2 - 1 k k k - k - x 6 ( ) 6 3 bảng.
GV cho HS các nhóm thảo Ta phải tìm k sao cho: 6 – 3k = 0, nhận
luận để tìm lời giải và gọi được k = 2
HS đại diện lên bảng trình Vậy số hạng cần tìm là …. 240. bày lời giải. GV gọi HS nhận xét, bổ sung (nếu cần)
HĐ2: (Bài tập áp dụng) Bài tập3:
HĐTP1: (Bài tập về tìm
Tìm số hạng thứ 5 trong
số hạng thứ k trong khai 10 æ 2 ö triển nhị thức)
HS các nhóm xem đề và thảo luận tìm lời khai triễn x + , mà ç ÷
GV nêu đề và ghi lên bảng giải. è x ø và cho HS các nhóm thảo
HS đại diện các nhóm lên bảng trình bày
trong khai triễn đó số mũ
luận tìm lời giải, gọi HS
lời giải (có giải thích) của x giảm dần.
đại diện nhóm có kết quả
HS trao đổi và rút ra kết quả:
nhanh nhất lên bảng trình
Số hạng thứ k + 1 trong khai triễn là: bày lời giải. k k -k æ 2 ö
Gọi HS nhận xét, bổ sung 10 t = C x k 1 + 10 ç ÷ è x (nếu cần). ø
GV nêu lời giải chính xác 4 - æ 2 4 10 4 ö 2 Þ = = (nếu HS không trình bày t C x 3360x 5 10 ç ÷ è x ø đúng lời giải) 2 HĐTP2: (Tìm n trong VÀ t y = 3360x 5 Page 19
Hoạt động của GV
Hoạt động của HS
Ghi bảng
khai triễn nhị thức Niu-
HS các nhóm thảo luận để tìm lời giải và tơn)
cử đại diện lên bảng trình bày lời giải. GV nêu đề và ghi lên
HS nhận xét, bổ sung và sửa chữa ghi bảng, cho HS các nhóm chép.
Bài tập4: Biết hệ số trong
thảo luận tìm lời giải.
HS trao đổi và rút ra kết quả: khia triễn (1+ 3 )n x là 90. Gọi HS đại diện nhóm
Số hạng thứ k + 1 của khai triễn là:
trình bày lời giải và gọi Hãy tìm n t = C 3 k k x k 1 + n (
) .Vậy số hạng chứa x2 là:
HS nhận xét, bổ sung (nếu cần)
t = C 3x = C 9x 3 n ( )2 2 2 2 n Theo bài ra ta có: 2
C 9 =90 Û n = 5 n HĐTP3:
HS các nhóm thảo luận để tìm lời giải và Bài tập1:
GV nêu đề bài tập và ghi
cử đại diện lên bảng trình bày lời giải.
Trong khai triển của (1+ax)n lên bảng và cho HS các
HS trao đổi và rút ra kết quả:
ta có số hạng đầu là 1, số
nhóm thảo luận tìm lời Ta có ( + )n 1 2 2 2
1 ax = 1+ C ax + C a x + ...
hạng thứ hai là 24x, số hạng giải. n n
thứ ba là 252x2. Hãy tìm a
GV gọi HS đại diện nhóm Theo bài ra ta có: và n.
lên bảng trình bày lời giải. ìna = 24 1 C ìï a = 24 ï
Gọi HS nhận xét, bổ sung n í Þ ín n -1 a 2 2 ( ) 2 (nếu cần) C ï a = 252 î ï = 252 n î 2 GV nhận xét, bổ sung và
nêu lời giải đúng (nếu HS ìa = 3 Þ í không trình bày đúng) în = 8
HS các nhóm thảo luận và cử đại diện lên HĐTP4:
bảng trình bày lời giải
GV nêu đề bài tập 2 và Số hạng chứa x7 là cho HS các nhóm thảo 2 ( 0 2 1 1 2 2 0 C .C b - + C aC b - + C a C x 3 6 3 6 3 6 ) 7
luận để tìm lời giải. ( ) ( ) S Bài tập 2:
Gọi HS đại diện các nhóm ố hạng chứa x8 là: Trong khai triển của
lên bảng trình bày lời giải. ( 0 1 C C b - + C aC x ( + )3 ( - )6 x a x b 3 6 ( ) 1 0 3 6 ) 8 .Theo bài ra ta , hệ số x7 là
Gọi HS nhận xét, bổ sung (nếu cần) có:
-9 và không có số hạng chứa 2 2 x8. Tìm a và b. 15
ì b -18ab + 3a = 9 - ìa = 2b í Þ GV nhận xét, bổ sung và í 2 î 6 - b + 3a = 0 b î = 1
nêu lời giải đúng (nếu HS
không trình bày đúng lời éìa = 2 giải) êíb êî = 1
GV ra thêm bài tập tương Þ êì = -
tự và hướng dẫn giải sau a 2 êí đó rọi HS các nhóm lên ê b ëî = 1 -
bảng trình bày lời giải.
XI. CỦNG CỐ – DẶN DÒ : Xem lại các bài tập đã giải, làm các bài tập 3.2, 3.4, 3.5 trong SBT/65. Rút kinh nghiệm
Ngày soạn: 12 / 1 1 / 2016
Chủ đề 5 ĐƯÒNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN
(5 tiết 13,14,15,16,17) I.Mục tiêu: Page 20
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản về qua hệ song song trong không
gian và bước đầu hiểu được một số kiến thức mới về quan hệ song song trong không gian .
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về qua hệ song song. Thông qua việc rèn luyện
giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số kiến
thức mới trong chương trình nâng cao.
3)Về tư duy và thái độ:Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III.Tiến trình giờ dạy: Tiết 13:
Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu lại các tính chất thừa nhận
+Nêu lại phương pháp tìm giao điểm của một đường thẳng và một mặt phẳng, tìm giao tuyến của hai mặt
phẳng, chứng minh ba điểm thẳng hàng,… 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Ghi bảng
Hoạt động 1: Luyện tập vận dụng tính chất hai đường thẳng song song
(Chứng minh 3 điểm thẳng hàng)
1. Cho tứ diện ABCD. Gọi M,
N lần lượt là trung điểm của A
các cạnh AB, CD và G là trung điểm của MN. D M
a) Tìm giao điểm A¢ của AG và G (BCD). N B M' A' C Đ1. A¢ = AG Ç BN.
b) Qua M kẻ đường thẳng Mx
// AA¢ và Mx cắt (BCD) tại M¢. 1. Xác định A¢?
Chứng minh B, M¢, A¢ thẳng
Đ2. Chứng minh chúng là 3 hàng và BM¢ = M¢A¢ = A¢N.
điểm chung của 2 mặt phẳng.
H2. Nêu cách chứng minh 3 điểm thẳng hàng? c) Chứng minh GA = 3GA¢.
Hoạt động 2: Luyện tập vận dụng tính chất hai đường thẳng song song
(Tìm giao tuyến của hai mặt phẳng)
2. Cho hình chóp S.ABCD, đáy Page 21
• GV hướng dẫn giúp HS giải quyết ABCD là hình bình hành. vấn đề. S x
a) Tìm giao tuyến của (SAC) và (SBD). H K
b) Tìm giao tuyến của (SAD) I J F và (SBC). A D E
c) Gọi H, I, J, K lần lượt là O B C
trung điểm các cạnh SA, SB, SC, SD. Chứng minh rằng Đ3. HIJK là hình bình hành. + Tìm hai điểm chung.
d) Lấy E Î SC (E ¹ S, E ¹ C).
+ Tìm một điểm chung và Tìm thiết diện của hình chóp S.ABCD khi cắt bởi (ABE). phương của giao tuyến.
H3. Nêu các cách tìm giao tuyến của hai mặt phẳng?
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách vận dụng các tính chất của hai đường thẳng song song để giải toán.4. BÀI TẬP VỀ NHÀ:
- Bài tập thêm SBT, CKT (GV hướng dẫn, dặn dò).
- Đọc trước bài “Đường thẳng và mặt phẳng song song”.
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Page 22 Tiết 14
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1:
GV gọi HS nêu lại vị trí tương Bài tập1:
đối của đường thẳng và mặt HS suy nghĩ trả lời…
Cho hình chóp S.ABCD có đáy
phẳng, vị trí tương đối của hai
ABCD là hình thang (AB//CD và
đường thẳng, cách xác định
AB>CD). Tìm giao tuyến của các một mặt phẳng. cặp mặt phẳng.
HĐTP1: (Bài tập về tìm giao a)(SAC) và (SBD)
tuyến của hai mặt phẳng) b)(SAD) và (SBC)
GV nêu đề bài tập áp dụng và c)(SAB) và (SCD) ghi lên bảng.
HS các nhóm thảo luận để tìm lời (Xem hình vẽ 1)
Cho HS các nhóm thảo luận để giải và cử đại diện lên bảng trình
tìm lời giải và gọi HS đại diện bày lời giải của nhóm (có giải
lên bảng trình bày lời giải. thích)
GV gọi HS nhận xét, bổ sung
HS nhận xét, bổ sung và sửa chữa (nếu cần) ghi chép.
GV nhận xét, bổ sung và nêu
HS trao đổi để rút ra kết quả…
lời giải đúng (nếu HS không
trình bày đúng lời giải)
HS chú ý theo dõi trên bảng để
tiếp thu kiến thức và phương pháp giải… d S D A I O C B Hình vẽ 1
Hoạt động của GV
Hoạt động của HS Ghi bảng
HĐTP2: (Bài tập về tìm giao Bài tập 2:
điểm của một đường thẳng
Cho hình chóp S.ABCD có đáy và mặt phẳng)
ABCD là một tứ giác sao cho AD
GV nêu đề, ghi lên bảng và vẽ HS thảo luận để tìm lời giải và cử và BC cắt nhau tại E, m làđiểm hình.
đại diện lên bảng trình bày lời thuộc đoạn thẳng SC. Page 23
Cho HS thảo luận để tìm lời
giải của nhóm (có giải thích)
a)Tìm giao điểm N của SD và
giải và gọi HS đại diện lên
HS nhận xét, bổ sung và sửa chữa (MAB);
bảng trình bày lời giải. ghi chép.
b)Gọi I là giao điểm cảu AM và
Gọi HS nhận xét, bổ sung (nếu HS trao đổi để rút ra kết quả:…
BN. Khi M di động trên đoạn SC cần)
thì điểm I chạy trên đường nào? (xem hình vẽ 2)
HS chú ý theo dõi trên bảng để
tiếp thu phương pháp giải…
GV nhận xét và nêu lời giải
đúng (nếu HS không trình bày đúng lời giải). S F N D E A M I O C B Hình 2
HĐ2: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại phương pháp tìm giao tuyến, giao điểm, chứng minh 3 điểm thẳng hàng.
*Hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải và làm thêm các bài tập trong SBT trang 64: BT2.10; 2.12. Page 24 Tiết 15 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Ghi bảng
Hoạt động 1: Luyện tập chứng minh đường thẳng và mặt phẳng song song D C
1. Cho hai hbh ABCD và O M ABEF không cùng nằm
• GV hướng dẫn HS cách vẽ hình. A B I trong một mặt phẳng. N O’ E F
a) Gọi O, O’ lần lượt là tâm của các hbh ABCD và Đ1. ABEF. Chứng minh đường
H1. Nêu cách chứng minh đt song OO¢ // DF Þ OO¢ // (ADF)
thẳng OO’ song song với các song mp ?
mặt phẳng (ADF) và (BCE). OO¢ // CE Þ OO¢ // (BCE)
b) Gọi M và N lần lượt là các
trọng tâm của các tam giác ABD và ABE. Chứng minh IM IN 1 = = Þ MN // DE
đường thẳng MN // (CEF). ID IE 3 Þ MN // (CEF)
Hoạt động 2: Luyện tập tìm thiết diện của hình chóp A
2. Cho tứ diện ABCD. Trên Q M
cạnh AB lấy một điểm M. D B Cho (P) là mp qua M, song P N C song với AC và BD. Đ1. MN // PQ // AC
a) Tìm giao tuyến của (P) với các mặt của tứ diện. MQ // NP // BD
b) Thiết diện của tứ diện cắt Þ MNPQ là hbh. bởi (P) là hình gì? S
H1. Nêu tính chất của các giao tuyến ? P
3. Cho hình chóp S.ABCD Q
có đáy ABCD là một tứ giác
lồi. Gọi O là giao điểm của N
hai đường chéo AC và BD. A D
Xác định thiết diện của hình O B
chóp cắt bởi mặt phẳng (P) M C đi qua O, song song với AB
và SC. Thiết diện đó là hình Đ2. gì? • (P)Ç(ABCD) = MN Page 25
• GV hướng dẫn HS cách xác định (P) // AB Þ MN // AB thiết diện. • (P)Ç(SBC) = MQ (P) // SC Þ MQ // SC • (P)Ç(SAB) = PQ (P) // AB Þ PQ // AB
H2. Ta cần xác định giao tuyến của
(P) với mặt nào trước ? Þ MN // PQ Þ MNPQ laø hình thang.
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách chứng minh đường thẳng song song với mặt phẳng.
– Các ứng dụng rút ra từ các tính chất.
4. BÀI TẬP VỀ NHÀ:
- Bài tập thêm SBT, CKT (GV hướng dẫn, dặn dò).
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... . Page 26 Tiết 16 +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+Nêu các vị trí tương đối của đường thẳng và mặt phẳng.
+Nêu các định lí 1, 2, 3 và hệ quả.
+Nêu phương pháp để chứng minh đường thẳng song song với mặt phẳng; … +Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1:
GV HĐTP1: (Bài tập về
chứng minh đường thẳng HS suy nghĩ trả lời…
song song với mặt phẳng) Bài tập1:
GV nêu đề bài tập áp dụng và
HS các nhóm thảo luận để tìm lời Cho hình chóp S.ABCD, trên các ghi lên bảng.
giải và cử đại diện lên bảng trình
cạnh SA và SC lần lược lấy hai
Cho HS các nhóm thảo luận để bày lời giải của nhóm (có giải SE SF
tìm lời giải và gọi HS đại diện thích) điểm E và F sao cho = . SA SC
lên bảng trình bày lời giải.
HS nhận xét, bổ sung và sửa chữa Chứng minh EF song song với mặt
GV gọi HS nhận xét, bổ sung ghi chép. phẳng ABCD. (nếu cần)
HS trao đổi để rút ra kết quả…
GV nhận xét, bổ sung và nêu
lời giải đúng (nếu HS không
HS chú ý theo dõi trên bảng để
trình bày đúng lời giải)
tiếp thu kiến thức và phương pháp giải… S E F D A C B
Hoạt động của GV
Hoạt động của HS Ghi bảng
HĐTP2: (Bài đường thẳng
song song với mặt phẳng) Bài tập 2:
Cho hình chóp S.ABCD có đáy
GV nêu đề, ghi lên bảng và vẽ HS thảo luận để tìm lời giải và cử ABCD là một hình thang với hình.
đại diện lên bảng trình bày lời
AB//CD ; goi G, G’ lần lượt là
Cho HS thảo luận để tìm lời
giải của nhóm (có giải thích)
trong jtâm của các tam giác SAD, Page 27
giải và gọi HS đại diện lên
HS nhận xét, bổ sung và sửa chữa SBC. Chứng minh đường thẳng
bảng trình bày lời giải. ghi chép.
GG’ song song với mặt phẳng
Gọi HS nhận xét, bổ sung (nếu HS trao đổi để rút ra kết quả:… (SAB). cần)
HS chú ý theo dõi trên bảng để
tiếp thu phương pháp giải…
GV nhận xét và nêu lời giải
đúng (nếu HS không trình bày đúng lời giải). S G' B C G D A
HĐ2: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại phương pháp chứng minh đường thẳng song song với mặt phẳng.
*Hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải và làm thêm các bài tập sau:
BT1.Cho tứ diện ABCD, gọi E là trung điểm của cạnh BD, I và J lần lượt là trung điểm các đoạn CE và
CA. chứng minh đường thẳng IJ song song với mặt phẳng (ABD)
BT2. Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD và CD > AB. Một mp(P) đi qua AB
và cát các cạnh SC, SD lần lượt tại M và N. Chứng minh MN//mp(ABCD) Page 28 Tiết 17. +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu điều kiện cần và đủ để hai mp song song;
+Nêu lại phương pháp chứng minh hai mặt phẳng song song.
+Nhắc lại định lí Ta-Lét trong không gian,… +Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng
HĐ1: Bài tập về xác định
Bài tập 1: (SGK trang 71)
giao điểm của một đường thẳng và mp.
HS xem đề và thảo luận nhóm
GV gọi một HS nêu đề bài tập Cử đại diện lên bảng trình bày lời 1 trong SGK trang 71 và cho giải (có giải thích)
HS cá nhóm thảo luận và ghi
HS nhận xét, bổ sung và sửa chữa
lời giải vào bảng phụ. ghi chép.
GV gọi HS đại diện lên bảng
HS các nhóm trao đổi để rút ra trình bày lời giải. kết quả:…
GV gọi HS nhận xét, bổ sung (nếu cần)
GV nhận xét và nêu lời giải đúng.
HS chú ý theo dõi trên bảng…
(GV nên vẽ hình trước khi HS lên bảng) B' b c C' d a A' B C D' A D
GV hướng dẫn: Chứng minh hai mp (a,AD) và (b,BC) song song với nhau.
Hoạt động của GV
Hoạt động của HS Ghi bảng
HĐ2: Bài tập về chứng minh
đường thẳng song song với
Bài tập: Cho hình bình hành mp:
HS thảo luận theo nhóm để tìm
ABCD và ABEF nằm trong hai mp
GV nêu đề và ghi lên bảng
lời giải và cử đại diện lên bảng
phân biệt. Gọi M, N là hai điểm di (hoặc phát phiếu HT)
trình bày (có giải thích).
động trên hai đoạn thẳng AD và GV cho HS các nhóm thảo AM NB
luận để tìm lời giải và gọi HS BE sao cho: = MD NE
đại diện nhóm lên bảng trình
Chứng minh rằng MN luôn song bày.
song với một mp cố định.
Gọi HS nhận xét, bổ sung (nếu HS nhận xét, bổ sung và sửa chữa Page 29 cần) ghi chép.
GV nhận xét, bổ sung và nêu
HS trao đổi để rút ra kết quả:…
lời giải đúng (nếu HS không
trình bày đúng lời giải) D C P M A B N F E
LG: Trong mp (ABCD), qua M kẻ đường thẳng song song với AB cắt BC tại P, ta có: PB MA NB = = ™ n n PN / / CE . PC MD NE
Ta có: (MNP)//(DCE) (vì MP//DC và PN//CE)
Mà MN nằm trong (MNP) nên MN song song với (DCE) (cố định)
HĐ3: Củng cố và hướng dẫn học ở nhà:
-Gọi HS nhắc lại phương pháp tìm giao tuyến của hai mp, cách tìm giao điểm của một đường thẳng với
một mp, cách chứng minh một đường thẳng song song với một mp, phương pháp chứng minh hai đường
thẳng song song. Hai mp song song,…
-Xem lại các bài tập đã giải; làm thêm các bài tập sau:
Bài tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
a)Hãy xác định giao tuyến của hai mp (SAB) và (SCD) và giao tuyến của hai mp (SAC) và (SBD).
b)Một mp (a ) thay đổi qua BC cắt cạnh SA tại A’(A’ không trùng với S và A và cắt cạnh SD tại D’. Tứ
giác BCD’A’ là hình gì?
c)Gọi I là giao điểm của BA’ và CD’, J là giao điểm của CA’ và BD’. Với (a ) như câu b) thì I và J chạy trên các đường nào?
Bài tập 2: Cho tứ diện ABCD có AB = CD. Gọi M, N là hai điểm thay đổi trên hai cạnh AB và CD sao
cho BM = CN. Chứng minh rằng MN luôn luôn song song với một mặt phẳng cố định. Page 30
Ngày soạn: 2 / 12 / 2016
Chủ đề 6: DÃY SỐ - CẤP SỐ CỘNG - CẤP SỐ NHÂN (4 tiết: 18,19,20,21)
I. MỤC ĐÍCH YÊU CẦU:
1.Về kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của dãy số, cấp số cộng, cấp số
nhân và bước đầu hiểu được một số kiến thức mới về dãy số, cấp số cộng, cấp số nhân chưa được đề cập
trong chương trình chuẩn.
2.Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về dãy số, cấp số cộng, cấp số nhân.
Thông qua việc rèn luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn
và tìm hiểu một số kiến thức mới trong chương trình nâng cao.
3.Về tư duy, thái độ::
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán. II. CHUẨN BỊ:
Giáo viên: Giáo án, các bài tập và phiếu học tập,…
Học sinh: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III. PHƯƠNG PHÁP: Về cơ bản sử dụng phương pháp dạy học gợi mở vấn đề. Tiết 18 IV. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+Nêu phương pháp quy nạp toán học.
+Nêu định nghĩa dãy số, dãy số tăng, giảm, dãy số bị chặn trên, bị chặn dưới và bị chặn,…
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1: Phương pháp
HS nêu các bước chứng minh một bài quy nạp toán học. toán bằng pp quy nạp.
Bài tập: Chứng minh rằng:
HĐTP1: (Ôn tập lại pp 1.2 +2.5+3.8+ …+n(3n-1) quy nạp toán học) =n2(n+1) với * n Î • (1). GV gọi một HS nêu lại các bước chứng minh bằng pp quy nạp toán
HS thảo luận để tìm lời giải và cử đại học.
diện lên bảng trình bày lời giải có giải
Áp dụng pp chứng minh thích.
quy nạp để giải các bài
HS nhận xét, bổ sung và sửa hữa ghi tập sau. chép. GV nêu đề và ghi lên
HS trao đổi và rút ra kết quả: bảng và cho HS các Với n = 1, VT = 1.2 = 2
nhóm thảo luận để tìm VP = 12(1+1) = 2 lời giải.
Do đó đẳng thức (1) đúng với n=1. Gọi HS đại diện nhóm Đặt VT = Sn. lên bảng trình bày lời
Giả sử đẳng thức (1) đúng với n = k, giải. k ³ 1, tức là: Gọi HS nhận xét, bổ Sk = 1.2 +2.5+3.8+…+k(3k-1) sung (nếu cần) =k2(k+1)
GV nhận xét, bổ sung và Ta phải chứng minh (1) cũng đúng với nêu lời giải chính xác n = k +1, tức là:
(nếu HS không trình bày Sk+1= (k+1)2(k+2) Page 31
Hoạt động của GV
Hoạt động của HS
Ghi bảng đúng lời giải
Thật vậy, theo giả thiết quy nạp ta có: Sk+1=Sk+(k+1)[3(k+1)-1] HĐTP2: =k2(k+1)+(k+1)(3k+2)
GV nêu đề bài tập 2 và =(k+1)(k2+3k+2)=(k+1)2(k+2) cho HS các nhóm thảo
Vậy đẳng thức (1) đúng với mọi Bài tập 2: luận tìm lời giải. * n Î • . Chứng minh rằng: GV gọi HS đại diện
n7 – n chia hết cho 7 với mọi nhóm lên bảng trình bày * n Î • . lời giải. Gọi HS nhận xét, bổ
HS thảo luận để tìm lời giải… sung (nếu cần)
HS nhận xét, bổ sung và sửa chữa ghi
GV nhận xét, hướng dẫn chép…
và phân tích tìm lời giải nếu HS không trình bày đúng lời giải
HS chú ý theo dõi trên bảng…
HĐ2: Ôn tập về dãy số HS nhắc lại khái niệm dãy số và nêu Bài tập 3:
và bài tập áp dụng.
khái niệm dãy số tăng, giảm, bị chặn,
Xét tính tăng, giảm hay bị chặn HĐTP1:
các nhóm thảo luận để tìm lời giải.
của các dãy số xác dịnh bởi số
GV gọi HS nhắc lại khái HS đại diện các nhóm lên bảng trình hạng tổng quát sau:
niệm dãy số và dãy số
bày lời giải (có giải thích)
a) un = n2; b) un= = 1- n +1 , hữu hạn.
HS nhận xét, bổ sung và sửa chữa ghi 1
Cho biết khi nào thì một chép. c) u = ; d) 2 u = os c n ; n + n dãy số tăng, giảm, bị
HS thảo luận và nêu kết quả: n 2 2
chặn trên, dưới và bị a)Ta có: n e) u = chặn. n 2 u
= n +1 > n = u , n " n +1 n 1 + ( )2 2
GV nêu đề bài tập và ghi n lên bảng, cho HS các Vậy un là dãy tăng. 1
nhóm thảo luận tìm lời b)u c) u = n= = 1 - n +1 n n + 2 giải như đã phân công. Ta có: u - u = n 1 + n 1 1 Gọi HS đại diện lên Ta có: 0 < un < < , n "
= (1- n + 2)-(1- n +1) n + 2 2
bảng trình bày lời giải.
gọi HS nhận xét, bổ sung 1 1 -
Dãy số (un) bị chặn trên bởi (nếu cần) = n +1 - n + 2 = < 0 2 n +1 + n + 2 GV nhận xét và nêu lời bị chặn dưới bởi 0. Þ u < u
giải đúng (nếu HS không n 1 + n Vậy (un) bị chặn.
trình bày đúng lời giải)
Vậy dãy (un) là dãy giảm.
V. CỦNG CỐ – DẶN DÒ: 2n -1
Bài tập: Chứng minh dãy số xác định bởi số hạng tổng quát sau là dãy tăng: u = n 3n +1 Page 32 Tiết 19 VI. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+Nêu định nghĩa cấp số cộng.
+Viết công thức tính số hạng tổng quát khi biết số hạng đầu và công sai.
+Nêu tính chất của cấp số cộng.
+Viết các công thức tính tổng của n số hạng đầu của một cấp số cộng.
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1: Bài tập1: HĐTP1:(Tìm n và
HS các nhóm thảo luận để tìm lời
Một cấp số cộng có số hạng thứ
công sai của một cấp giải.
nhất là 5, số hạng cuối là 45 và tổng số cộng)
HS đại diện lên bảng trình bày lời
số là 400. Tìm n và công sai. GV nêu đề và ghi lên giải (có giải thích)
bảng, cho HS các nhóm HS nhận xét, bổ sung và sả chữa ghi
thảo luận tìm lời giải, chép. gọi HS đại diện lên
HS trao đổi và nêu kết quả:
bảng trình bày lời giải. n(u + u 1 n ) GV gọi HS nhận xét, S =
Û 2S = n u + u n n ( 1 n ) 2 bổ sung (nếu cần) 2S 2.400 n Û n = = = 16 GV nhận xét, bổ sung u + u 5 + 45 1 n và nêu lời giải đúng u - u 8
u = u + n -1 n d Û d = = n 1 ( ) 1 (nếu HS không trình n -1 3 bày đúng lời giải)
HS thảo luận để tìm lời giải và cử đại
diện lên bảng trình bày lời giải (có
HĐTP2: (Bài tập về giải thích) Bài tập 2: tìm số hạng uk)
HS nhận xét, bổ sung và sửa chữa
Một cấp số cộng có số hạng thứ 54 GV nêu đề và ghi lên ghi chép.
và thứ 4 lần lượt là -61 và 64. Tìm bảng. Cho HS các
HS trao đổi và rút ra kết quả: số hạng thứ 23. nhóm thảo luận và tìm u
= u + n -1 d n 1 ( ) lời giải. Gọi HS đại diện lên
Û u = u + 53d(1) 54 1
bảng trình bày lời giải.
Û u = u + 3d(2) 4 1 Gọi HS nhận xét, bổ
Gi∂i h÷ ph≠¨ ng tr◊nh (1), (2) ta Æ≠Óc: sung (nếu cần) 143 5 u = , d = - GV nhận xét và nêu lời 1 2 2 giải chính xác (nếu HS 33 không trình bày đúng)
Þ u = u + 22d = 23 1 2 HĐ2: Bài tập 3: HĐTP1:(Tìm các số
HS các nhóm thảo luận để tìm lời
Chèn 20 số vào giữa số 4 và 67,
hạng còn lại của một giải.
biết rằng dãy số đó là một cấp số
cấp số cộng khi biết số HS đại diện nhóm lên bảng trình bày cộng.
hạng đầu và số hạng
lời giải (có giải thích) cuối…)
HS nhận xét, bổ sung và sửa chữa GV nêu đề bài tập và ghi chép. Page 33
Hoạt động của GV
Hoạt động của HS
Ghi bảng ghi lên bảng, cho HS
HS trao đổi và rút ra kết quả:
thảo luận tìm lời giải.
Ta xem số 4 là số hạng đầu và số 67 Gọi HS đại diện nhóm
như là số hạng cuối. Như vậy cấp số lên bảng trình bày lời
cộng phải tìm có tất cả 22 số hạng. giải. Ta c„ : u
= u + n -1 d n 1 ( ) Gọi HS nhận xét, bổ Û 67 = 4 + 21d sung (nếu cần) GV nêu nhận xét, và Û d = 3
trình bày lời giải đúng
Vậy cấp số cộng được tạo thành là: (nếu HS không trình
4, 7, 10, … , 61, 64, 67 và 20 số cần bày đúng lời giải)
chèn là: 7, 10, 13, …, 58, 61, 64.
HS thảo luận theo nhóm để tìm lời Bài tập 4:
HĐTP2: (Bài tập về
giải và cử đại diện lên bảng trình bày Tìm tổng của một cấp số cộng gồm
tính tổng của n số
lời giải (có giải thích) các số:
hạng đầu của một cấp HS nhận xét, bổ sung và sửa chữa 1 3 số cộng) ghi chép.
5 ,6 ,8... Æ’n sË hπng th¯ 17. 2 4 GV nêu đề và ghi lên
HS trao đổi và rút ra kết quả: bảng, cho HS thảo luận é (n - )1d ù tìm lời giải. Ta cã : S = n u ê + n 1 ú 2 Gọi HS đại diện lên ë û
bảng trình bày lời giải. é 1 (17 - ) 1 5 ù 263 Û S = 17 5 ê + . ú = Gọi HS nhận xét, bổ n 2 2 4 2 ë û sung (nếu cần) GV nhận xét và nêu lời giải chính xác (nếu HS không trình bày đúng lời giải)
VII. CỦNG CỐ – DẶN DÒ:
*Áp dụng: Giải bài tập sau:
Có bao nhiêu số của một cấp số cộng -9; -6; -3; … để tổng số các số này là 66. Page 34 Tiết 20 -21
VIII. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+Nêu định nghĩa cấp số nhân.
+Viết công thức tính số hạng tổng quát khi biết số hạng đầu và công bội.
+Nêu tính chất các số hạng của cấp số nhân.
+Viết các công thức tính tổng của n số hạng đầu của một cấp số nhân.
3/ Bài mới:
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1: Bài tập 1:
HĐTP1: (Chèn các số
HS các nhóm thảo luận để tìm lời
Hãy chèn 4 số của một cấp số
vào giữa hai số đã cho giải.
nhân vào giữa hai số 160 và 5.
của một cấp số nhân)
HS đại diện lên bảng trình bày lời GV nêu đề và ghi lên giải (có giải thích) bảng. Cho HS các nhóm
HS nhận xét, bổ sung và sửa chữa
thảo luận để tìm lời giải. ghi chép.
Gọi HS đại diện lên bảng
HS trao đổi để rút ra kết quả: trình bày lời giải.
Ta xem số 160 như là số hạng đầu
Gọi HS nhận xét, bổ sung và số 5 như là số hạng thứ 6 của một (nếu cần). cấp số nhân. Ta có: 5
u = u .q 6 1 u u 1 5 6 6 5 Û q = Þ q = 5 = u u 32 1 1 1 1 5 = = 5 GV nhận xét và nêu lời 2 2 giải chính xác (nếu HS
Suy ra các số hạng của cấp số nhân
không trình bày đúng lời là: giải) 160, 80, 40, 20, 10, 5
Vậy các số cần chèn là: 80, 40, 20. 10.
HĐTP2: (Tính tổng của
n số hạng của một cấp số HS thảo luận theo nhóm để tìm lời nhân)
giải và cử đại diện lên bảng trình
GV nêu đề và ghi lên bảng bày lời giải. Bài tập 2: (hoặc phát phiếu HT)
HS nhận xét, bổ sung và sửa chữa
Tìm tổng của một cấp số nhân
GV cho HS thảo luận theo ghi chép.
gồm 7 số hạng mà các số hạng
nhóm để tìm lời giải.
HS trao đổi để rút ra kết quả: 2 3
Gọi HS đại diện nhóm lên Cấp số nhân có công bội là: đầu là: , 1 - , ,... 3 2 bảng trình lời giải. 3 q = - . Ta có:
Gọi HS nhận xét, bổ sung 2 (nếu cần)
GV nhận xét và trình bày
lời giải chính xác (nếu HS
không trình bày đúng lời giải) Page 35
Hoạt động của GV
Hoạt động của HS
Ghi bảng 1 n - q S = u n 1 1- q 7 æ 3 ö 1- - 2 ç ÷ è 2 ø 463 Þ S = . 7 3 3 96 1+ 2 HĐ2:
HĐTP1: (Bài tập về tìm
các số hạng của một cấp
số nhân khi biết tổng và
HS các nhóm thảo luận để tìm lời Bài tập 3:
tích của các số đó).
giải và cử đại diện lên bảng trình
Tìm 3 số hạng của một cấp số GV ghi đề và ghi lên
bày lời giải (có giải thích)
nhân mà tổng số là 19 và tích là bảng. Cho HS thảo luận
HS nhận xét, bổ sung và sửa chữa 216.
theo nhóm và gọi HS đại ghi chép.
diện nhóm lên bảng trình
HS trao đổi và rút ra kết quả: bày. Giải: GV gọi HS nhận xét, bổ
Gọi 3 số hạng liên tiếp của cấp số sung (nếu cần) nhân là: a
, a, aq (vÌ i q lµ c´ ng bÈi) q Theo giả thiết ta có: ìa GV nhận xét và nêu lời . . a aq = 216 (1) ï
giải đúng (nếu HS không ïq í
trình bày đúng lời giải) a ï + + = a aq 19 (2) ï îq
Từ (1) ta có a = 6. Thay vào (2) ta được: 6q2- 13q + 6 = 0 3 2
Û q = ho∆c q = 2 3
Vậy 3 số hạng cần tìm là: 4, 6, 9 hay 9, 6, 4.
HĐTP2: (Bài tập về tìm
số hạng đầu của một cấp HS các nhóm thảo luận để tìm lời Bài tập 4:
số nhân khi biết công
giải và cử đại diện lên bảng trình
Tìm số hạng đầu của một cấp số
bội, tổng và số hạng
bày lời giải (có giải thích)
nhân biết rằng công bội là 3, tổng cuối)
HS nhận xét, bổ sung và sửa chữa
số là 728 và số hạng cuối là 486.
GV nêu đề và ghi lên bảng ghi chép. hoặc phát phiếu HT.
HS trao đổi và rút ra kết quả: GV cho HS các nhóm thảo
luận để tìm lời giải.
GV gọi HS đại diện nhóm
lên bảng trình bày lời giải.
Gọi HS nhận xét, bổ sung (nếu cần) GV nhận xét, bổ sung và
nêu lời giải đúng (nếu HS Page 36
Hoạt động của GV
Hoạt động của HS
Ghi bảng
không trình bày đúng lời 1 n - q giải) S = u (1) n 1 1- q n 1 -
u = u .q (2) n 1 u Tı (2) n Þ u = 1 n 1 q - u 1 n - q Thay vµo (1) n Þ S = . (3) n n 1 q - 1- q
Theo giải thiết Sn=728, un=486,q=3 n ( ) 486 1- 3 3 Þ 728 = . n 1 3 - 1- 3 n- 486 1 5 Û 3 = = 243 = 3 2
Û n -1 = 5 Û n = 6 u 486 486 Þ u n = = = = 2 1 n 1 - 5 q 3 243
IX. CỦNG CỐ – DẶN DÒ:
*Áp dụng: Giải bài tập sau:
Tìm công bội của một csn có số hạng đầu là 7 số hạng cuối là 448 và tổng số các số hạng là 889. Rút kinh nghiệm Page 37
Ngày soạn: 22 / 1 / 2017 Chủ đề 7
GIỚI HẠN DÃY SỐ (4tiết: 22,23,24,25)
I. MỤC ĐÍCH YÊU CẦU:
1.Về kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của giới hạn và bước đầu hiểu
được một số kiến thức mới về giới hạn trong chương trình nâng cao chưa được đề cập trong chương trình chuẩn.
2.Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về giới hạn. Thông qua việc rèn luyện giải
toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số kiến thức
mới trong chương trình nâng cao.
3.Về tư duy, thái độ::
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán. II. CHUẨN BỊ:
Giáo viên: Giáo án, các bài tập và phiếu học tập,…
Học sinh: Ôn tập kiến thức cũ, làm bài tập trước khi đến lớp.
III. PHƯƠNG PHÁP: Về cơ bản sử dụng phương pháp dạy học gợi mở vấn đề. IV. TIẾN TRÌNH BÀI HỌC: Tiết 22,23
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
-Nêu các định nghĩa về giới hạn hữu hạn của dãy số và các giới hạn đặc biệt.
-Nêu các định lí về giới hạn hữu hạn, tổng của cấp số nhân lùi vô hạn,…
-Giới hạn vô cực và các giới hạn đặc biệt về giới hạn vô cực.
*Bài tập: Luyện tập tính giới hạn hữu hạn của dãy số
Hoạt động của GV
Hoạt động của HS
Ghi bảng Bµito¸n 1 1 Bµito¸n 1 2 - 2 a,: lim n = = 2 2n -1 2 a,lim 2n -1 -3n + 2n- 4 + 2 1 1 a,lim b,lim n + 2 n n + 2 2 2n +1
Gîi ý: chia c¶ tö vµ mÉu cho n - + 2 - 4 n n 2 3 3 + 5.4 4n - n +1 2 -3 c, lim d,lim n n n n 2 b,: lim = -3n + 2n- 4 4 + 2 3n - 2 b,lim 1 2 2 2n +1 2 + 2 n Bµi to¸n 2
Gîi ý: chia c¶ tö vµ mÉu cho n2 c, lim a, lim(-n3 + 3n2 + n +4) 3n + 5.4n c, lim b, lim(3 n2 +5 n -2) 4n + 2n c,lim( 2
n - n - n )
Gîi ý:chia c¶ tö vµ mÉu cho 4n
3. Tìm các giới hạn sau: Page 38 2 4n - n +1 3 2 n 2n +1 4n - n -1 d,lim n n ( ) + 5.1 a) lim ;b) lim ; 3 + 5.4 3n - 2 = 4 lim = 3n - 2 3 + 2 2n 4n + 2n 1+ 2 ( )n
Gîi ý: chia c¶ tö vµ mÉu cho n 4 4n + 6.5n c) lim ; 5 n n lim = 5 5 + 3 1 Bµi to¸n 2 2 3n +1 + n 1 1 d) lim . n 4 - + 1- 2 2n a, lim(-n3 + 3n2 + n +4) 2 d= lim n n = (3 n - 2 b, lim(3 n2 +5 n -2) ) n 1 1 c,lim( 2
n - n - n ) 4 - + 2 n n = 2 lim - 2 3 3 n
Gîi ý : ý a,b lµm b×nh th-êng
con ý C th× ta nh©n c¶ tö vµ a, lim(-n3 + 3n2 + n +4)
mÉu víi biÓu thøc liªn hîp 3 1 4 : lim n3(-1+ + + ) = - 2 3 n n n ¥ b, lim(3 n2 +5 n -2) 5 - 2 ¥ lim [n2(3+ )] = + 2 n n
H1. Nêu cách biến đổi và qui c,lim( 2n -n -n) = tắc cần sử dụng? 2 2 n - n - n lim = 2 n - n + n -n lim 2 n - n + n 1 - 1 = lim = - 1 2 1- +1 n Luyện tập:
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ1: Bài tập về tính
HS các nhóm thảo luận để tìm lời
Bài tập 1: Tính các giới hạn sau:
giới hạn của các dãy số: giải và cử đại diện lên bảng trình 3n -1 2
GV nêu đề bài tập và gọi bày (có giải thích). A = lim
H = lim( n + 2n - n) n + 2 HS các nhóm thảo luận n - 2 3n - 5.4n
để tìm lời giải, gọi HS đại HS các nhóm nhận xét, bổ sung và N = lim O = lim n
diện lên bảng trình bày. sửa chữa ghi chép. 3n + 7 1- 4 GV gọi HS nhận xét, bổ
HS các nhóm trao đổi để rút ra kết sung (nếu cần). quả: … GV nhận xét, bổ sung và Page 39
Hoạt động của GV
Hoạt động của HS
Ghi bảng nêu lời giải đúng. 1 3 - 3n -1 = lim = lim n A = 3 n + 2 n 1+ 2 2
H = lim( n + 2n - n) 2 2
n + 2n - n 2 = lim = = 1 2
n + 2n + n 2 1+ +1 n
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ2: Bài tập về tính
Bài tập 2: Đặt limun = a. Ta Bài tập 2:
giới hạn của một dãy số
Cho dãy số (un) xác định bởi: u = 2 + u
cho bởi công thức truy n 1 + n u ìï = 2 hồi:
Þ limu = lim 2 + u 1 n 1 + n í
GV nêu đề bài tập và cho u ï = 2 + u ³ Þ = + î vÌ i n 1 n 1 + n HS các nhóm thảo luận có: a 2 a
Biết (un) có giới hạn khi n ® +¥ , hãy
để tìm lời giải, gọi HS đại 2 Þ a - a - 2 = 0 tìm giới hạn đó.
diện lên bảng trình bày. Þ a = 1 - ho∆c a = 2
Gọi HS nhận xét, bổ sung Bài tập 3: ³ (nếu cần).
Vì un >0 nên limun = a 0 . Vậy
Cho dãy số (un) xác định bởi công thức GV nhận xét, bổ sung và limun= 2 truy hồi:
nêu lời giải đúng (nếu HS *Lưu ý: Trong lời giải trên, ta đã ì 1
không trình bày đúng lời
áp dụng tính chất sau đây: u = ï 1 giải) ï 2
“Nếu lim un = a thì lim un+1 = a” í 1
(Có thể chứng minh bằng định u ï = vÌ i n ³ 1 +
Bài tập 3: (Xem lời giải n 1 nghĩa ï 2 - u î n ví dụ 10 trong sách bài
Dãy số (un) có giới hạn hay không khi tập trang 146)
n ® +¥ ? Nếu có, hãy tính giới hạn đó.
Bài tập 3: (Xem lời giải ví dụ 10 trong sách bài tập trang 146)
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ3: Bài tập về tính
HS các nhóm thảo luận để tìm lời giải Bài tập 4:
tổng của cấp số nhân
và cử đại diện lên bảng trình bày lời giải Tính tổng: lùi vô hạn: (có giải thích). 1 1
GV nêu đề bài tập, cho HS nhận xét, bổ sung và sửa chữa S = 2 - 2 +1- + -... 2 2
HS các nhóm thảo luận ghi chép.
tìm lời giải và gọi HS
HS các nhóm trao đổi và rút ra kết quả: … đại diện các nhóm lên
Bài tập 4:Dãy số vô hạn:
bảng trình bày lời giải. 1 1 GV gọi HS nhận xét, 2, - 2,1, -
, ,...là một cấp số nhân 2 2 bổ sung (nếu cần) GV nhận xét và nêu lời - 2 1 với công bội q = = - . giải đúng (nếu HS 2 2 không trình bày đúng 1 1 lời giải). Vì q = - = < 1 2 2
nên dãy số này là một cấp số nhân lùi vô hạn. Do đó ta có: Page 40 1 1 S = 2 - 2 +1- + -... 2 2 . 2 2 2 = 1 2 +1 1+ 2
: Củng cố:Nhấn mạnh:– Cách vận dụng các qui tắc tìm giới hạn của dãy số.
4. BÀI TẬP VỀ NHÀBài tập thêm SBT, CKT (GV hướng dẫn, dặn dò). 3 6n - 2n +1 2 n + 4n - 5 2 2n - n 2 n +1 - n +1 1) lim 2) lim 3) lim 4, lim 3 n - 2n 3 2 3n + n + 7 2 1- 3n 3n + 2 n 4 5) ( 3 lim 3n - 7n + ) 11 6) 4 2 lim 2n - n + n + 2 7) lim 8) 2 lim n + n +1 - n ( ) n n 2.3 + 4
IV RÚT KINH NGHIỆM, BỔ SUNG:
......................................................................................................................................................... Page 41 Tiết 24,25
Tiếp theo: Luyện tập tính giới hạn vô cực của dãy số
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1:
*Giới hạn đặc biệt:
HĐTP1: Ôn tập lí thuyết ) lim k a n = +¥ vÌ i k nguy™ n d≠¨ ng;
về giới hạn vô cực
GV nhắc lại các giới hạn
HS chú ý theo dõi để lĩnh hội kiến thức… ) lim n b q = +¥ n’ u q > 1.
đặc biệt và Một vài quy
tắc tìm giới hạn vô cực *Định lí: QUY TẮC 1: Nếu limu
a)N’ u lim u = a vµ n= n ±¥ và limv u n= ¥ thì
lim v = ±¥ th◊ lim n = 0; n lim(u v nvn) được cho bởi n bảng sau:
b)N’ u lim u = a > 0,lim v = 0 n n u limu vµ v > 0 n " th◊ lim n = + ; ¥ n limvn lim(unvn) n vn +¥ +¥ +¥
c)N’ u lim u = +¥ vµ n +¥ -¥ -¥ = > th◊ = +¥ lim v a 0 lim u v . n n n -¥ +¥ -¥
(Xem các giới hạn đặc biệt -¥ -¥
+¥ HS các nhóm thảo luận để tìm lời giải và
ghi lời giải vào bảng phụ, cử đại diện lên
cuả hàm số và các công QUY TẮC 2: Nếu limu
bảng trình bày lời giải (có giải thích)
thức về giới hạn hàm số): n= ±¥ và limv
HS nhận xét, bổ sung và sửa chữa ghi n= L ¹0 thì chép. lim(unvn) được cho bởi
HS trao đổi và rút ra kết quả:…Đ1. bảng sau:
2. Tính các giới hạn sau: ( 3 n - 2 lim 2n + n - ) limu a) 1 3 2 n dấu của lim(unvn)
a) lim(n - 2n + n -1) ; L 2 1 1 = 3 lim n (1- + - )=+¥. b) - 3 n + 2 lim( 5n - 3) ; 2 3 +¥ + +¥ n n n æ 2 2 ö +¥ - -¥ b) c) lim ç n - ÷ ; è n +1 ø -¥ + -¥ - 3 n + 2 lim( 5n - 3) = ... = -¥ . d) (- 2 lim n + n n + ) 1 . -¥ - +¥ æ 2 2 ö c) lim ç n - ÷ = ... = +¥ . è n +1 ø QUY TẮC 3: Nếu
limun=L¹0, limvn=0 và d) (- 2 lim n + n n + ) 1 = ... = -¥
vn>0 hoặc vn<0 kể từ một
số hạng nào đó trở đi thì un lim được cho bởi bảng vn sau: Page 42 dấu của dấu của un lim L vn vn + + +¥ + - -¥ - + -¥ - - +¥ HĐTP2: Bài tập áp
HS các nhóm thảo luận để tìm lời giải .
2. Tính các giới hạn sau: dụng:
GV nêu đề bài tập (hoặc 3 2
lim(n + 2n - n +1) a. 3 2
lim(n + 2n - n +1)
phát phiếu HT) và cho HS a. é 2 1 1 ù
các nhóm thảo luận để tìm 3 = lim n (1+ - + ) ê 2 2 3 ú
b. lim(-n + 5n - 2)
lời giải và gọi HS đại diện ë n n n û lên bảng trình bày. 2 - -
Gọi HS nhận xét, bổ sung 3 c. lim( n n n) ì lim n = +¥ ï (nếu cần) vì í 2 1 1 GV nhận xét, bổ sung và lim(1+ - + ) = 1 > 0 ï 2 2 3
d. lim( n - n + n) î n n n
nêu lời giải đúng (nếu HS
không trình bày đúng lời 3 2
Þ lim(n + 2n - n +1) = +¥ giải) é 5 2 2 2 ù
b. lim(-n + 5n - 2) = lim n ( 1 - + - ) ê 2 n n ú ë û
H1. Nêu cách biến đổi và 2 ì = +¥ qui tắc cần sử dụng? lim n ï vì í 5 2 - + - = - < lim( 1 ) 1 0 ï 2 î n n 2
Þ lim(-n + 5n - 2) = -¥ c. 2
lim( n - n - n) 2 2
( n - n - n)( n - n + n) = lim 2 n - n + n -n 1 - 1 = lim = lim = - 2 n - n + n 1 2 1- +1 n é 1 ù d. 2
lim( n - n + n) = lim ên( 1- +1)ú n ë û Page 43 ì lim n = +¥ ï í 1 lim( 1- +1) = 2 > 0 ï î n 2
Þ lim( n - n + n) = +¥
Củng cố:Nhấn mạnh:– Cách vận dụng các qui tắc tìm giới hạn của dãy số.
4. BÀI TẬP VỀ NHÀBài tập thêm SBT, CKT (GV hướng dẫn, dặn dò).
Bài:Tính các giới hạn sau: 2
a) lim(3n + n -1) 4 2 b) lim( 2
- n + n - n + 3) c ( 2
) lim 3n + nsin 2n) 2
d) lim 3n + n -1 ) lim (2.3n 5.4n e - ) 2
f ) lim 3n +1 - 2n 2
g) lim n +1 - n h ( 2 ) lim
n - n + n) i ( 2 ) lim
3n - 6n +1 - 7n) k)lim n ( n -1 - n) l ( 2 ) lim
n - 3n - n) m (3 3 2 ) lim
n + n - n)
RÚT KINH NGHIỆM, BỔ SUNG: Page 44
Ngày soạn: 2 / 2 / 2017 Chủ đề 8
GIỚI HẠN HÀM SỐ (6tiết: 26,27,28,29,30,31) I. MỤC TIÊU:
+ Về kiến thức : Giúp học sinh nắm được định nghĩa giới hạn của hàm số tại một điểm, giới hạn của
hàm số tại vô cực, giới hạn vô cực của hàm số và các định lí về giới hạn hữu hạn của hàm số.
+ Về kỹ năng : Tăng cường rèn luyện kỹ năng giải toán về giới hạn. Thông qua việc rèn luyện giải toán
HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số kiến thức mới
trong chương trình nâng cao.
3)Về tư duy và thái độ:Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:
-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập kiến thức cũ, làm bài tập trước khi đến lớp.
III.Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức:. Tiết: 26,27
Hoạt động của GV
Hoạt động của HS
Ghi bảng
HĐ: GIỚI HẠN HỮU HẠN
Nhận xét: lim x = x ; lim c = c o
CỦA HS TẠI MỘT ĐIỂM: x® ® o x x o x
HS thảo luận theo nhóm để
1. Định nghĩa1: cho khoảng tìm lời giải và cử đại diện
K, x Î K , hs y = f ( x) xđ lên bảng trình bày lời giải o
Bài tập 1: tìm g.h sau: (có giải thích)
trên K hoặc trên K {xo} . HS nhận xét, bổ sung và 2 2x + 3x 2 x + 3x + 2 sửa chữa ghi chép. . a lim ; .l b im x 1 ®- x 1 ® -
lim f ( x) = L Û (" 4x x 2 dãy
HS trao đổi để rút ra kết x® o x quả:… ( 2 2 x lim x = x x - 2x x - 4x + 3 n ) : , ta có n o .l c im ; d.lim ; n®¥ x®0 x 1 x ® x -1
lim f ( x = L 2 n ) ) x + 3x + 2 x - 2 n®¥ . e lim ; f .lim 2 x 1 ®- x®0 x +1 x - 3x + 2
Hoạt động của GV
Hoạt động của HS
Ghi bảng
.Bài tập 2: Xác định dạng vô định HS các thảo luận theo 2 x + x - 2
nhóm và cử đại diện lên a) lim ; 3 x 2 ®- x + 8
bảng trình bày lời giải (có giải thích) 2 2 3 + 4x + 1+ x b) lim ; HS nhận xét, bổ sung và x®-¥ 5x + 2 sửa chữa ghi chép) 3 æ 1 1 ö
HS trao đổi và rút ra kết c) lim - ; ç ÷
x®0 x è x + 2 2 ø quả:… d) lim
x + x + - x x®+¥ ( 2 1 ).
HĐ 1: Tìm hiểu về giới hạn Page 45 æ 0 ö 0 1
Bài tập 3: Tính các giới hạn sau: dπng của hàm số : a)Dạng KQ: - ; ç ÷ è 0 ø 0 4 2x + 3 - 3 a) lim ;
GV nêu đề hoặc phát phiếu ¥ 3 b)Dạng KQ: - ; x®3 x - 3 HT, cho HS các nhóm thảo ¥ 5 2 x - 4
luận để tìm lời giải và gọi 3 b) lim ; 3 2
HS đại diện lên bảng trình c)Dạng 0.¥ KQ: - ;
x®2 x - x - x - 2 4 bày lời giải. 2 1 2x +1 - 3x + 3
Gọi HS nhận xét, bổ sung d)Dạng ¥ - ¥ KQ: . c) lim . x®2 x - 2 (nếu cần) 2
Bài tập4 : Tính các giới hạn sau:
GV nhận xét, bổ sung và nêu 2 (x + 3) - 27
lời giải đúng (nếu HS không 1/ lim
trình bày đúng lời giải) x 0 ® x HĐ 2: *Hướng dẫn: 3 3- x -1
a)Nhân lượng liên hiệp tử Ph©n tÝch tö vµ mÉu 2/ lim x®2 x - 2 số; thµnh tÝch ®Ó gi¶i -íc b)Phân tích: nh©n tö chung. 2
x - 4 = x - 2 x + 2 NÕu u(x) hay v(x) cã chøa 3 2
x - x - x - 2 = ( x - 2)( 2 x + x bi + Õ
)1 n sè d-íi dÊu c¨n th× cã
thÓ nh©n c¶ tö vµ mÉu víi c)Thêm vào 3 và -3 trên biÓu thøc liªn hîp.
tử.HĐ: Rèn luyện kỹ năng giải toán: (x + 2 3) - 27
*Xác định dạng vô định và lim x®0 x tính giới hạn. 3 x + 2 9x +
GV nêu đề bài tập (hoặc 27x = lim phát phiếu HT) x®0 x GV cho HS thảo luận theo = 2 lim(x + x + 27x) = 27
nhóm và gọi HS đại diện lên x®0
bảng trình bày lời giải. .
Gọi HS nhận xét, bổ sung 9- 5x - 2 (nếu cần) lim ® 2 x 1 x -1
GV nhận xét, bổ sung và nêu 5- 5x
lời giải đúng (nếu HS không = lim ® 2 (x - 2 x 1 1) ( 9- 5x + 2)
trình bày đúng lời giải) 5(1- = x) lim x®1 (x -1)(x +1)( 9 - 5x + 2) - = 5 = - 5 lim . x®1 (x +1)( 9 - 5x + 2) 9
*Củng cố:-Nêu lại cách tính giới hạn của các dạng vô định thường gặp,...
Bài tập : Cho hàm số: Xem l¹i c¸c d¹ng v« ®Þnh vµ c¸ch kh- d¹ng v« ®Þnh 3 3x x -1 + 2 x - 8 a, lim , b lim x®¥ x®2 x - 6 (x - 2)(1- 2x)
-Xem lại các bài tập đã giải, làm thêm các bài tập RÚT KINH NGHIỆM, Page 46 Tiết 28,29
HĐ: Tính giới hạn bằng Bài tập 1:
cách sử đụng định nghĩa
HS thảo luận theo nhóm và Tìm các giới hạn sau:
giới hạn một bên:
cử đại diện lên bảng trình 2 x - 4x + 3
GV nêu đề (hoặc phát phiếu
bày kết quả (có giải thích). a) lim ; x 1- ® 1- x
HT), cho HS thảo luận theo HS nhận xét, bổ sung và 2
nhóm và gọi HS đại diện sửa chữa ghi chép. 3x + x +1 b) lim . trình bày lời giải.
HS trao đổi để rút ra kết x®2+ x - 2
Gọi HS nhận xét, bổ sung quả:… Bài tập 2: (nếu cần) KQ: x - 5
GV nhận xét, bổ sung và nêu a) 0; b) +¥ : 1/ lim + 2 ® -
lời giải đúng (nếu HS không x 5 x 25
trình bày đúng lời giải). x - 5 x - 5 lim = lim x - 5 + 2 +
x®5 x - 25 x®5 (x - 5)(x + 5) 2/ lim . - 2 x®5 x - 25 = 1 = 1 lim + x®5 x + 5 10 x - 5 Hái cã $ lim ? x - 5 5- x 2 lim = lim x®5 x - 25 - 2 - x®5 x - 25 x®5 (x - 5)(x + . 5) -1 1 = lim = -
Bài tập 3:Tính lim f ( x); lim f ( x) biết - - + x®5 x + 5 10 x®2 x®2 ì
ï 3x + 3 - 2 khi x ³ 2 Do f ( x) = í 3 2 x - 5 x - 5 ïî2x - 2x khi x ! 2 lim ¹ lim + 2 - 2 ® - ® - x 5 x 25 x 5 x 25
Bài tập 4: Tính lim f ( x) biết: - $ x 5 x 1 ® lim nªn . 2 x®5 x - 25 2 ì x - x 3
ì x -1 khi x ³1 ï khi x ! 1 . a f ( x) = í ; .
b f ( x) = í x -1 î + 1 x khi x " 1 ï
î 3x +1 +1 khi x £1 ì 2 - x -1 ï khi x ³ 1 .
c f ( x) = í x -1 1 ïî + 2x khi x "1
Bài tập 5: Tìm các giới hạn sau ¥
CH : nªu c¸ch khö d¹ng Chia c¶ tö vµ mÉu cho ¥ k 5x + 3 1- x x ,víi k lµ sè mò cao nhÊt lim ? cña biÕn sè x.(Hay ph©n x®-¥ 1- x tÝch tö vµ mÉu thµnh
Bài tập 6Tìm các giới hạn sau 1/ tÝch chøa nh©n tö n x råi 1 gi¶n -íc). lim 3 2 x®-¥ 3x - x + 2 +/ NÕu u(x) vµ v(x) cã
chøa biÕn x trong dÊu c¨n, 3 th× ®-a k x ra ngoµi (k lµ 3x + x +1 2/ lim . bËc cao nhÊt cña x trong 2 x®-¥ x + 3x -1
c¨n) tr-íc khi chia c¶ tö vµ Page 47 mÉu cho lòy thõa cña x.
Gîi ý: chia c¶ tö vµ mÉu cho x3 1 3 1- 5+ x 3 1 5x + 3 1- x x lim = lim = 0. = x 1/ lim lim 3 2 x®-¥ x 3x - x + 2 ®-¥ 1 2 x®-¥ 1- x x®-¥ 1 -1 3- + 3 x x x 1 1 5+ 3 - 2 x x = lim = -5 . 1 æ 1 2 ö x®-¥ 1 - V◊ lim = 0 ,lim 3 3 . 3 ç - + 3 ÷ = 1 x x®-¥ x®¥ x è x x ø 3 æ 1 1 ö 3 x ç3+ + 2 3 ÷ 3x + x + 1 è x x ø 2/ lim = lim ®-¥ 2 x x + 3x - x®¥ 1 2 æ 3 1 ö x ç1+ - 2 ÷ è x x ø + 1 + 1 3 2 3 = × x x lim x = - ¥ x®-¥ + 3 - 1 1 2 x x
*Củng cố:-Nêu lại cách tính giới hạn của các dạng vô định thường gặp,... -Giải bài tập sau: ì2 n’ u x £ 4 - ï
Bài tập : Cho hàm số: f ( x) 2
= í 25- x n’ u -4 < x £ 3 ï4 n’ u x > 3 ïî
a) Tính lim f ( x), lim f ( x), lim f (x), lim f (x). x 4- x 4- x 3- x 3+ ®- ®+ ® ®
b)Tìm các khoảng liên tục của f(x).
*Hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải, làm thêm các bài tập 3.5, 3.6 và 3.7 sách bài tập trang 164 và 165. RÚT KINH NGHIỆM, Page 48
Tiết 30,31: hµm sè liªn tôc I.Môc tiªu::
VÒ KiÕn thøc: Häc sinh n¾m ®-îc ph-¬ng ph¸p xÐt tÝnh liªn tôc cña hµm sè trªn tËp x¸c ®Þnh cña nã vµ t¹i mét ®iÓm.
VÒ kü n¨ng:Häc sinh n¾m ®-îc c¸c b-íc gi¶i bµi to¸n chøng minh ph-¬ng tr×nh cã nghiÖm.
t- duy vµ th¸i ®é:TÝch cùc ho¹t ®éng, tr¶ lêi c©u hái. BiÕt quan s¸t vµ ph¸n ®o¸n chÝnh x¸c.Lµm cho
HS høng thó trong häc tËp m«n To¸n.
KiÓm tra bµi cò : KÕt hîp víi bai häc Bµi míi :
Hoạt động của GV
Hoạt động của HS
Ghi bảng HĐ1:
Bài tập 1: Tìm số thực m sao cho
GV nêu đề bài tập (hoặc phát
HS thảo luận theo nhóm và cử hàm số:
phiếu HT), cho HS thảo luận
đại diện lên bảng trình bày lời 2 3 ì x n’ u x < 2
theo nhóm và gọi HS đại diện giải… f ( x) = í î n’ u ³
lên bảng trình bày lời giải. HS nhận xét bổ sung … 2mx x 2
Khi nào thì hàm số f(x) liên
Hàm số f(x) liên tục tại x = 2 liên tục tại x =2 tục tại x = 2? nếu:
Gọi HS nhận xét, bổ sung (nếu lim f (x) = lim f (x) = f (2) cần) x 2- x 2+ ® ®
GV nhận xét, bổ sung và nêu
HS trao đổi để rút r kết quả:…
lời giải đúng (nếu HS không 11 với m = thì f(x) liên tục tại
trình bày đúng lời giải) 4 x = 2. HĐ2: Bài tập 2:
GV nêu đề (hoặc phát phiếu
HS thảo luận theo nhóm để tìm Chứng minh rằng phương trình: HT), cho HS các nhóm thảo
lời giải và cử đại diện lên bảng x3-2x2+1= 0 có ít nhất một nghiệm
luận để tìm lời giải và gọi HS
trình bày (có giải thích) âm.
đại diện lên bảng trình bày.
GV hướng dẫn: Sử dụng định
lí:”Nếu f(x) liên tục trên [a;b]
và f(a).f(b) < 0 thì tồn tại điểm cÎ( ;
a b) sao cho f(c) = 0”.
Gọi HS nhận xét, bổ sung (nếu HS nhận xét, bổ sung và sửa cần) chữa ghi chép…
GV nhận xét, bổ sung và nêu
HS trao đổi để rút ra kết quả:…
lời giải đúng (nếu HS không Đặt f(x) = x3-2x2+1
trình bày đúng lời giải)
Do f(x) liên tục trên ! nên f(x) liên tục trên [-1;0].
Mặt khác, vì f(0)=1.f(-1)=-2<0 nêu tồn tại một số c Î( 1; - 0)sao cho f(c) = 0. Vậy
phương trình có ít nhất một nghiệm âm.
Bµi 7(143) XÐt tÝnh liªn tôc cña
Bµi 7(143) XÐt tÝnh liªn tôc hµm sè sau trªn R Page 49
Hoạt động của GV
Hoạt động của HS
Ghi bảng
cña hµm sè sau trªn R LG: 2 ì x - x - 2 ï ; x > 2 2 ì x - x - 2 f(x)= í x - 2 ï ;
x > 2 TËp x¸c ®Þnh: D=R. f(x)= í x - 2 5 ïî - x ; x £ 2 5 ïî - x ; x £ 2 2 x - x - 2 Víi x>2 ta cã f(x)= x - 2 HD:
lµ hµm ph©n thøc h÷u tØ nªn
H·y nªu c¸c b-íc xÐt tÝnh liªn
nã liªn tôc trªn(2;+ ¥ ).
tôc cña hµm sè trªn tËp x¸c
Víi x<2 ta cã f(x) = 5-x lµ hµm ®Þnh cña nã.
®a thøc nªn nã liªn tôc trªn(-
Víi bµi nµy ta cÇn chia lµm ¥ ;2) mÊy tr-êng hîp, lµ nh÷ng T¹i x=2 ta cã: tr-êng hîp nµo? f(2)= 5-2=3 T¹i sao? 2 x - x - 2
Chó ý : Víi hµm sè cho ë d¹ng lim f (x) = lim + +
nµy ®Ó tÝnh giíi h¹n cña f(x) x®2 x®2 x - 2
t¹i x= 2 cÇn ph¶i tÝnh giíi h¹n
ph¶i vµ giíi h¹n tr¸i t¹i x=2. (x +1)(x - 2) = lim = lim (x +1) x 2+ ® x 2+ ® Bµi14(144) x - 2 =3 Bµi14(144)
T×m m ®Ó f(x) liªn tôc t¹i x=
T×m m ®Ó f(x) liªn tôc t¹i x= 3. 3. BiÕt r»ng f(x) =
lim f (x) = lim (5 - x) = 3 x 2- ® x 2- ® BiÕt r»ng f(x) = ì 3 - x ï ; x ¹ 3 ì 3 - x í x +1 - 2
Do ®ã : lim f (x) = ï ; x ¹ 3 x 2+ ® í x +1 - 2 ïîm ; x = 3
lim f (x) = f(2) ïîm ; x = 3 x 2- ® HD: Þf(x) liªn tôc t¹i x=2.
Hµm sè f(x) liªn tôc t¹i x=x 0
VËy hµm sè liªn tôc trªn !
Û lim f (x) = f (x ) 0 x®x LG: 0
Do ®ã ta ph¶i tÝnh f(3) vµ Ta cã: f(3)=m; lim f (x) x®3 3 - x lim f (x) = lim x®3 x®3 x +1 - 2
Sau ®ã gi¶i ph-¬ng tr×nh Èn m.
(3 - x)( x +1 + 2) = lim x®3
( x +1 - 2)( x +1 + 2)
(3 - x)( x +1 + 2) = lim = x®3 + - x 1 4 Page 50
Hoạt động của GV
Hoạt động của HS
Ghi bảng
(3 - x)( x +1 + 2) lim ® x 3 x - 3
Bµi 8(143) Chøng minh r»ng pt sau = lim( x +1 + 2) =4 x®3
cã Ýt nhÊt ba nghiÖm trong kho¶ng (-2;5).
Do ®ã: Hµm sè f(x) liªn tôc t¹i x=3 x5-3x4+5x-2=0
Bµi 8(143) Chøng minh r»ng
Û lim f (x) = f (3) x®3
pt sau cã Ýt nhÊt ba nghiÖm trong kho¶ng (-2;5). Û m=4. x5-3x4+5x-2=0 HD:
Ta ph¶i chØ ra hai sè a vµ b XÐt f(x) = x5-3x4+5x-2 tho¶ m·n: Ta cã: f(-2) = -72; f(1)= 1; -2 f(2)= -8; vµ f(3)=13.
f(a).f(b)<0 vµ f(b).f(5)<0
Þf(-2).f(1)<0; f(1).f(2)<0 vµ
Khi ®ã ph-¬ng tr×nh f(x)= 0 f(2).f(3)<
cã Ýt nhÊt ba nghiÖm trong
mµ f(x) lµ hµm liªn tôc nªn nã
kho¶ng (-2;5) trong ®ã mçi
liªn tôc trªn c¸c ®o¹n: [-2;1]; nghiÖm thuéc mét trong cac [1;2]; [2;3]. kho¶ng:(-2;a); (a;b); (b;5).
Do ®ã ph-¬ng tr×nh f(x) = 0
cã Ýt nhÊt ba nghiÖm trong
kho¶ng (-2;5) trong ®ã mçi nghiÖm thuéc mét kho¶ng (- 2;1); (1;2); (2;3).
Cñng cè: C¸ch gi¶i bµi to¸n xÐt tÝnh liªn tôc cña hµm sè trªn tËp x¸c ®Þnh.
C¸ch gi¶i bµi to¸n chøng minh ph-¬ng tr×nh cã Ýt nhÊt mét nghiÖm
Bài tập: Chứng minh rằng phương trình (3m2 – 5)x3 – 7x2 + 1 = 0 luôn có nghiệm âm với mọi giá trị của m.
HD: Chứng minh hàm số f(x) = (3m2 – 5)x3 – 7x2 + 1 liên tục trên [-1; 0]… RÚT KINH NGHIỆM,
Ngày soạn: 5 / 2 / 2017
Chủ đề 9 VÉC TO TRONG KHÔNG GIAN (2tiết:32-33) I. MỤC TIÊU: Page 51
Kiến thức: Củng cố: Các định nghĩa: vectơ trong không gian, hai vectơ cùng phương, cùng hướng,
ngược hướng, độ dài của vectơ, hai vectơ bằng nhau, vectơ – không.
- Định nghĩa về sự đồng phẳng của ba vectơ và điều kiện để ba vectơ đồng phẳng.
Kĩ năng: Biết thực hiện phép cộng, phép trừ vectơ trong không gian, phép nhân vectơ với một số, biết sử
dụng qui tắc ba điểm, qui tắc hình hộp để tính toán.
Thái độ: Liên hệ được với nhiều vấn đề trong thực tế với bài học.
- Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về vectơ.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định lớp, kiểm tra sĩ số lớp, khởi động tiết học.
2. Kiểm tra bài cũ: (Trong quá trình luyện tập) 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Ghi bảng
Hoạt động 1: Tìm hiểu khái niệm ba vectơ đồng phẳng !!!" !!!" !!!" 1. Cho hình hộp
Ta cã: AC = AD + DC ; 1. Cho hình hộp !!!" !!!" !!!"
ABCD.A’B’C’D’. Chứng minh DB = DA + DC ; a) !!!" !!!!" !!!" !!!!"
!!!" !!!!!" !!!!" !!!" !!!" !!!" !!!!" rằng:
BA' = CD ' = CD + CC ' ;
AB + B 'C ' + DD ' = AB + AD + AA' = AC ' !!!!" !!!!" !!!" !!!" !!!!" !!!!" !!!!"
C ' D = C 'C + CD !!!!" !!!!!" !!!!!" !!!"
a) AB + B 'C ' + DD ' = AC ' ;
b) BD - D ' D - B ' D ' = BB ' !!!" !!!!" !!!!!" !!!" A B !!!" !!!" !!!" !!!!" "
b) BD - D ' D - B ' D ' = BB ' ;
AC + BA' + DB + C ' D = 0 . !!!" !!!" !!!" !!!!" "
c) AC + BA' + DB + C ' D = 0 . D C B' A' D' C'
!!!" !!!!!" !!!!" !!!" !!!" !!!" !!!!"
AB + B 'C ' + DD ' = AB + AD + AA' = AC '
2. Cho hình bình hành ABCD. !!!!" !!!!!" !!!!!" !!!"
b) BD - D ' D - B ' D ' = BB '
Gọi S là một điểm nằm ngoài
mặt phẳng chứa hình bình Bµi 3 (91) Đ. hành. Chứng minh rằng: !!" !!" !!" !!" !!" !!!"
Cho h×nh b×nh hµnh ABCD. Gäi S SA + SC
SA + SC = SB + SD . !!" !!" !!!" !!!"
lµ mét ®iÓm n»m ngoµi mÆt
= (SB + BA) + (SD + !!" !!!" !!" !!! D "C)
ph¼ng chøa h×nh b×nh hµnh.
3. Cho hình tứ diện ABCD.
= (SB + SD) + (BA + !!" !!!" DC) Chøng minh r»ng:
Gọi M, N lần lượt là trung !!" !!!" !!" !!!" = SB + SD
điểm của AB và CD. Chứng
SA + SC = SB + SD Page 52
HD: Sö dông tÝnh chÊt trung minh rằng: ®iÓm cña ®o¹n th¼ng. Đ. a) !!!!" 1 !!!" !!!"
a) MN = (AD + BC);
Gäi O lµ giao ®iÓm cña hai ®-êng !!!" !!!" 2 chÐo AC vµ BD. 1 (AD+BC) 2 !!!!" !!!" !!!" !!!" !!!!" !!!" 1
b) MN = (AC + BD). Bµi 5 (92)
é AM + MN + ND ù 1 ( ) 2 = ê ú !!!" !!!!" !!!"
Cho tø diÖn ABCD. H·y x¸c ®Þnh 2 ê+(BM + MN + ë NC )úû
4. Cho hình tứ diện ABCD. ®iÓm E, F sao cho:
Gọi G là trọng tâm của tam
b) ) Theo tÝnh chÊt cña trung ®iÓm !!!" !!!" !!!" !!!"
giác ABC. Chứng minh rằng:
a) AE = AB + AC + AD cña ®o¹n th¼ng ta cã: !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!" !!" !!!" !!" !!" !!"
DA + DB + DC = 3DG .
b) AF = AB + AC - AD
IA + IC = 2IM ; IB + ID = 2IN
Gäi G lµ träng t©m tam gi¸c CBD !!!" !!" " HD:
vµ: IM + IN = 0 ; !!!" !!!" !!!" !!!" A
Ta cã: AB + AC + AD = 3AG Do ®ã: !!!" !!!"
Do ®ã AF = 3AG . B D !!" !!" !!" !!" !!!" !!!" " + + + = + = G
IA IB IC ID 2(IM IN ) 0 M
b) Gäi M lµ trung ®iÓm cña BC ta N cã: F C !!!" !!!" !!!!" !!!"
AB + AC = 2AM = AP b)Ta cã: Þ P !!!" !!" !!" !!!" !!" !!"
!!!" !!!" !!!" !!!" !!!" !!!" !!!"
PA = PI + IA = + - = - =
; PB = PI + IB AF AB AC AD AP AD DP E !!!" !!" !!" !!!" !!" !!"
PC = PI + IC ; PD = PI + ID 5. (Bµi 7 (92) !!" !!" !!" !!" "
Bµi 7 Cmr: IA + IB + IC + ID = 0 Do ®ã: b) Cmr: !!!" !!!" !!!" !!!" !!" + + + = !!" !!" !!" !!" " a) Cmr:
PA PB PC PD 4PI
IA + IB + IC + ID = 0 !!" !!!" !!!" !!!" !!!" c) Cmr: 1
PI = (PA + PB + PC + PD) Hay: !!" !!!" !!!" !!!" !!!" 4 1 !!" !!!" !!!" !!!" !!!"
PI = (PA + PB + PC + PD) 1
• GV hướng dẫn giúp HS giải quyết PI = (PA + PB + PC + PD) 4 4 vấn đề
Củng cố :. C¸c quy t¾c vÒ phÐp to¸n cña vÐct¬.
§ TÝnh chÊt trung ®iÓm cña ®o¹n th¼ng vµ träng t©m cña tam gi¸c.
4) BTVN Lµm l¹i c¸c bµi ®· ch÷a
Lµm tiÕp c¸c bµi:4,6,8,9,10 (92)
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
Ngày soạn: 15 / 2 / 2017
Chủ đề 9 VÉC TƠ TRONG KHÔNG GIAN (2tiết:34-35) I. MỤC TIÊU:
Kiến thức: Củng cố:Khái niệm góc giữa hai vectơ và tích vô hướng của hai vectơ trong không gian. Page 53
- Khái niệm hai đường thẳng vuông góc với nhau trong không gian.
Kĩ năng: Luyện tập:Xác định góc giữa hai đường thẳng trong không gian.
- Cách chứng minh hai đường thẳng vuông góc.
Thái độ: Liên hệ được với nhiều vấn đề trong thực tế với bài học.
- Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hai đường thẳng vuông góc.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định lớp, kiểm tra sĩ số lớp, khởi động tiết học.
2. Kiểm tra bài cũ: (Trong quá trình luyện tập). H. Đ. 3. Giảng bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Ghi bảng
Hoạt động 1: Luyện tập cách xác định góc giữa hai vectơ trong không gian Đ1.
1. Cho hlp ABCD.EFGH. Hãy
xác định góc giữa các cặp !!!" !!!" !!!" !!!"
§ ( AB, EG) = ( AB, AC) = ∑ CAB vectơ sau: = 450.
H1. Nêu cách xác định góc giữa hai !!!" !!!" ∑ !!!" !!!" 0 vectơ ?
(AB, EG) = FEG = 45 a) AB va¯EG !!!" !!!" !!!" !!!" !!!" !!!" HD:
§ ( AF, EG) = ( AF, AC) = b) AF va¯EG ∑
§Ó t×m gãc gi÷a hai vÐct¬ bÊt k×, CAF . !!!" !!!" !!!" !!!" c) AB va¯DH
ta ®-a vÒ t×m gãc gi÷a hai vÐct¬
. ( AF, EG) = 600.
míi cã chung gèc vµ thø tù cïng !!!" !!!!" !!!" !!!" =
h-íng víi hai vÐct¬ ban ®Çu. § ( AB, DH ) (AB, AE) = ∑ EAB = 900
2. Cho tứ diện ABCD. CMR: !!!" !!!!"
V ( AB, DH ) = 900. !!!" !!!" !!!" !!!" !!!" !!!" B C a) A .
B CD + AC.DB + AD.BC = 0 A D G b) Nếu AB ^ CD và AC ^ DB F E H thì AD ^ BC. !!!" !!!" ∑ 0
(AB, DH) = HDC = 90
3. Cho S là diện tích của DABC. Chứng minh: Đ2.
H2. Nêu định nghĩa và tính chất !!!" !!!" !!!" !!!" !!!" 1 !!!"2 !!!"2 !!!" !!!" 2
của tích vô hướng của hai vectơ ? - . AB CD = .( AB AD - AC) S = AB .AC ( . AB AC) 2 !!!" !!!" !!!" !!!" !!!"
AC.DB = AC.(AB - AD) Page 54 !!!" !!!" !!!" !!!" !!!"
AD.BC = AD.(AC - AB)
H3. Nhắc lại công thức tính diện Đ3. tích tam giác ? 1 S = . AB AC.sin A 2
H4. Nhắc lại công thức tính góc giữa hai vectơ? Đ4. !!!" !!!" . AB AC cos A = !!!" !!!" AB . AC
Hoạt động 2: Luyện tập chứng minh hai đường thẳng vuông góc trong không gian C’
4. Trong KG cho hai tam giác Q P
đều ABC và ABC¢ có chung
cạnh AB và nằm trong hai mp A B
khác nhau. Gọi M, N, P, Q lần M N C
lượt là trung điểm của AC, CB, BC¢, AC¢. CMR: !!!" !!!!" Đ1. . AB CC ' = 0 a) AB ^ CC¢.
b) MNPQ là hình chữ nhật.
Đ2. MNPQ là hình bình hành
H1. Nêu cách chứng minh hai đt vuông góc? và MN ^ MQ. !!" !!!"
5. Cho hình chóp S.ABC có
H2. Nêu cách chứng minh MNPQ Đ3. . SA BC = 0 ∑ ∑ ∑ = = là hình chữ nhật?
ASB BSC CSA và SA = SB = SC. CMR: SA ^ BC, SB ^ AC, SC ^ AB.
H3. Nêu cách chứng minh SA ^ BC ?
6. Cho tứ diện ABCD có AB = AC = AD và ∑ ∑ BAC = BAD = 600. Chứng minh: Đ4. a) AB ^ CD. !!!" !!!" a) . AB CD = 0
b) Nếu M, N là trung điểm của AB và CD thì MN ^ AB và Page 55
H4. Nêu cách chứng minh? !!!!" 1 !!!" !!!" !!!" MN ^ CD.
b) MN = (AD + AC - AB) 2 !!!!" !!!" !!!!" !!!"
Þ MN.AB = 0 , MN.CD = 0
Hoạt động 3: Củng cố Nhấn mạnh:
– Cách xác định góc giữa hai vectơ.
– Cách chứng minh hai đường thẳng vuông góc.
4. BÀI TẬP VỀ NHÀ:
- Đọc trước bài "Đường thẳng vuông góc với mặt phẳng".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Page 56
Ngày soạn: 5/ 3 / 2017
Chủ đề 10 ĐẠO HÀM (9iết : 36 ® 44)
I. MỤC TIÊU: Qua chủ đề này HS cần:
1.Về kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của đạo hàm và bước đầu hiểu được
một số kiến thức mới về đạo hàm.
2.Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về đạo hàm. Thông qua việc rèn luyện giải toán
HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số kiến thức mới
trong chương trình nâng cao.
- Hiểu và áp dụng được cách tính đạo hàm bằng định nghĩa vào giải bài tập.
- Nắm được các công thức tính đạo hàm cơ bản.
- Tính được đạo hàm cấp hai, vi phân của một hàm số.
3.Về tư duy, thái độ:Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán. II. CHUẨN BỊ:
Giáo viên: Giáo án, các bài tập và phiếu học tập,…
Học sinh: Ôn tập kiến thức cũ, làm bài tập trước khi đến lớp.
III. PHƯƠNG PHÁP: Về cơ bản sử dụng phương pháp dạy học gợi mở vấn đề. IV. TIẾN TRÌNH BÀI HỌC:
1/ Ổn định lớp: Kiểm tra sĩ số học sinh, chia lớp thành 6 nhóm.
2/ Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
Tiết : 36, 37:Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
-Nêu các công thức tính đạo hàm tổng, hiệu, tích, thương, các công thức tính đạo hàm thường gặp, đạo
hàm của các hàm số lượng giác,... -+Bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính đạo hàm bằng định nghĩa
H1. Nêu các bước tính đạo Đ1.
1. Tính đạo hàm của các hàm số sau hàm bằng định nghĩa ?
tại các điểm đã chỉ ra bằng định
B1: Cho xo số gia Dx, tính Dy nghĩa: tương ứng. 2
a) y = x + x tại x B2: Lập tỷ số Dy/Dx 0 = 1 y D 1 B3: Tìm lim b) y = tại x0 = 2 x x D ®0 x D x +1 a) y¢(1) = 3 c) y = tại x0 = 0 x -1 1 b) y¢(2) = - d) y = 7 - 2x tại x0 = 3. 4 c) y¢(0) = – 2 Page 57 d) y¢(3) = –1.
2. Chứng minh hàm số
Đ2. Hàm số có đạo hàm tại x0 2 ( ìï x -1) ne·u x ³ 0 thì liên tục tại x f (x) = í 2 0. ïî-x ne·u x < 0
H2. Nêu tính chất liên quan
không có đạo hàm tại điểm x = 0
giữa đạo hàm và tính liên tục
nhưng có đạo hàm tại điểm x = 2 của hàm số ?
Đ3. lim f (x) ¹ lim f (x) x 0+ x 0- ® ®
H3. Xét tính liên tục của hàm Þ f(x) không liên tục tại x=0 số tại x = 0 ?
Þ f(x) không có đạo hàm tại x = 0. Dy Đ4. lim = 2 D ® Dx x 0 Þ f¢(2) = 2. Dy
H4. Tại x = 2, tính lim Dx®0 Dx
Hoạt động của GV
Hoạt động của HS Ghi bảng
Bµi 1: Cho hµm Bài 3 2
1: y' = x + x - 2
HS thảo luận và cử đại diện lên 3 2 x x sè: y = + - 2x
bảng trình bày lời giải. 3 2 HS nhận xét, bổ sung ... ( ) 3 2
a ) y' x = 0 Û x + x - 2 = 0 Û x = 1
Víi nh÷ng gi¸ trÞ nµo cña x th× ( ) 3 2 b ) y' x = 2
- Û x + x - 2 = 2 -
a) y’(x) = 0b) y’(x)= -2c) y’(x)
HS chú ý theo dõi trên bảng để Û x = 0 =10 lĩnh hội kiến thức... ( ) 3 2
c ) y' x = 10 Û x + x - 2 = 10 Û x = 0 Bài 2:
f ' ( x) = 2( x + 2)( x + 3)2 ( 2
3x + 11x + 9)
Bµi 2: T×m f’(-1), f’(-2),f’(-3) Page 58 biÕt: ( ) 1
f ' x = 2 x +1 2 3 Bài i 3:
f ( x) = ( x + 1)( x + 2) ( x + 3) 1
Þ f ' (3) = 4
Bµi 3: Cho hµm sè
f (3) + ( x - 3) f ' (3)
f ( x) = x + 1 = + + ( - ) 1 3 1 x 3 2 3 + 1
TÝnh f (3) + ( x - 3) f ' (3) x - 3 = 2 + 4
Bµi 4: Cho hai hµm sè ( ) 1 f ' x = vµ 2 ( ) 1 cos x f x = tanx v
µ g (x) = 1- x ( ) 1 g' x = Bài : (1- x)2 f ' (0)
Þ f ' (0) = 1; g' (0) = 1 t›nh g' (0)
f ' (0) =1 g' (0)
Bài tập 1:Tìm công thức tính đạo
hàm của các hàm số sau bằng cách sử dụng định nghĩa: )
a y = f (x) = ax + ; b 2 )
b y = ax + bx + ; c ax + b ) c y = ; cx + d ) c y = x.
Trong miền xác định của mỗi hàm số. HĐ2: Bài tập 2:
GV gọi HS lên bảng ghi lại các
HS lên bảng ghi lại công thức.
Dùng công thức tính đạo hàm của
công thức tính đạo hàm của các các hàm số sau: hàm số thường gặp. x +1 Nêu bài tập áp dụng:
HS thảo luận theo nhóm để tìm ) a y = x - 2;
Cho HS thảo luận và gọi HS đại x - 2
lời giải và cử đại diện lên bảng
diện lên bảng trình bày lời giải. ) b y = x tan ; x
Gọi HS nhận xét, bổ sung (nếu
trình bày (có giải thích) ) c y = ( 2 x - ) 1 ( 3 5- 4x ) cần) .
GV nhận xét, chỉnh sửa và bổ HS nhận xét, bổ sung . sung...
Chú ý theo dõi trên bảng để lĩnh hội kiến thức.
HĐ3:Củng cố và hướng dẫn học ở nhà: Page 59
*Củng cố:- Nêu lại ba bước tính đạo hàm bằng định nghĩa, các công thức tính đạo hàm tổng, hiệu, tích,
thương; Các công thức tính đạo hàm thường gặp.
*Áp dụng:Dùng công thức, hãy tính đạo hàm của các hàm số sau: ) a y = ( 2 x + 2)( 2 1- 3x ) 2 ; )
b y = x + 4x +1; 5 ) c y = sin . x o c s2 ;
x d)y = ( 2 x + x + ) 1 x +1.
*Hướng dẫn học ở nhà:-Xem lại các bài tập đã giải.
- Học thuộc các công thức tính đạo hàm thường gặp.
- Ôn tập lại phương trình tiếp tuyến của một đường cong khi biết tiếp điểm. hệ số góc, song song với một
đường thẳng, vuông góc với một đường thẳng,... Rút kinh nghiệm: Page 60 Tiết 38,39
*Tiến trình giờ dạy:-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.+ *
H1. Nêu quy tắc cần sử Đ1.
1. Tính đạo hàm của các hàm số dụng? sau: 2 tan x 2x = + a) y ' 2 2 2 cos x sin x a) 2 2
y = tan x - cot x 1 x b) y ' = - sin . x b) y = cos . 2 (1+ x) 1+ x 1+ x
Hoạt động 2: Vận dụng đạo hàm của các hàm số lượng giác
H1. Nêu các bước giải toán ? Đ1.
2. Giải phương trình f¢(x) = 0 với: + Tính f¢(x). a) f(x) = 3cosx + 4sinx + 5x
+ Giải phương trình f¢(x) = 0. b) f(x) = 1 – sin(p + x) +
H2. Nhắc lại cách giải PTLG a) f¢(x) = –3sinx + 4cosx + 5 æ 2p + x ö + 2 cosç ÷ . è 2 ø 3 4
f¢(x) = 0Û sin x - cos x = 1 5 5 p
3. Chứng minh hàm số sau có đạo Û sin(x -j) = sin
hàm không phụ thuộc vào x 2 x 6 6 2 2
y = sin x + cos x + 3sin x.cos x b) f(x) = 1 + sinx – 2 cos 2 Þ x f¢(x) = cos x + sin H3. Biến đổi y? 2 x æ p ö
f¢(x) = 0 Û sin = sin ç x - ÷ 2 è 2 ø Đ3. y = 1 Þ y¢ = 0
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1: f’(x) =
Bài tập 1:Dùng công thức, tính đạo
GV gọi HS lên bảng viết lại
hàm của các hàm số sau: æ p ö æ æ p öö
công thức đạo hàm của các ( x) 'cot 3x - + x cot 3x - ç ÷ ç ç ÷ è 4 ø æ p è è 4 ÷ ö hàm số lượng giác. a. f(x) = øø x cot 3x - ; ç ÷ è 4 ø
GV nêu đề bài tập và cho HS Page 61
thảo luận tìm lời giải. b. g(x) = cos2x GV gọi HS nhận xét, bổ +cos2æ 2p ö æ 2p 2 ö + x + cos - x sung (nếu cần). = ç ÷ ç ÷ è 3 ø è 3 ø
GV chỉnh sửa và bổ sung. 1 æ p ö 3 x cot 3x - - ç ÷
c. h(x) = sin(cos2x).cos(sin2x) 2 x è 4 ø æ p ö
Bài 2: T×m ®¹o hµm c¸c 2 sin 3x - ç ÷ è 4 ø hµm sè sau
sau khi t×m g’(x) cã nhËn xÐt g× vÒ hµm g(x) a) = ( - )3 7 2 y x 5x b. t-¬ng tù g’(x)
Gîi ý: ¸p dông c«ng thøc: y’x = y’u. u’x
Bài 2: T×m ®¹o hµm c¸c hµm sè sau = - 2cosxsinx – b) = ( 2 + )( 2 y x 1 5 - 3x ) 2cos a) = ( - )3 7 2 y x 5x æ 2p ö æ 2p ö æ 2p ö æ 2p ö 2x + x sin + x + 2cos - x sin - x ç ÷ ç ÷ ç ÷ ç ÷ c) y = è 3 ø è 3 ø è 3 ø è 3 ø 2 x -1 b) = ( 2 + )( 2 y x 1 5 - 3x ) = - sin2x - 3 - 5x d) y = 2x 2 æ 4p ö æ 4p ö c) y = x - x +1 sin + 2x + sin - 2x ç ÷ ç ÷ 2 x -1 è 3 ø è 3 ø 3 æ n ö 3 - 5x e) y = m + ç ÷ 4p y = 2 = - sin2x + 2cos sin(-2x) = - d) è x ø 2 3 x - x +1 sin2x + sin2x = 0 HD: 3 æ n ö c.h’(x)=- e) y = m + ç ÷ 2 a) ¸p dông c«ng thøc: è x ø
2cos(cos2x)cosxsinxcos(sin2x)– (un)' = n. un-1 . u' 2sin(cos2x)sin(sin2x)sinxcosx
Bài 3: T×m ®¹o hµm c¸c hµm sè sau b) ¸p dông c«ng thøc:
= -sin2xcos(cos2x)cos(sin2x)– 2 = - + sin2xsin(cos2x)sin(sin2x) a) y x x x 1 ( uv)' = u' v + u v' 2 = - - = -sin2x b) y 2 5x x
c) vµ d) ¸p dông c«ng thøc:
[cos(cos2x)cos(sin2x)+sin(cos2x) 3 x = sin(sin2x)] c) y 2 - u
u 'v - uv ' a x ( ) ' = 2 = -sin2xcos(cos2x – v v 1 + x = sin2x) d)y 1 - x e) ¸p dông c«ng thøc: = -sin2xcos(cos2x) (un)' = n. un-1 . u'
v× g’(x) = 0 nªn g(x) lµ mét Bài tập :
Dùng công thức, tính đạo hàm của các vµ c«ng thøc
hµm b»ng. b»ng c¸ch chän x = hàm số sau: 1 u - ' n -nu ' 3 ( ) ' = Þ ( )' = 0, ta thÊy g(0) = x 3 2 2 = u u u u 2 ) a y o c s ; 3 ) b y = xsin ; x
Bài 3: T×m ®¹o hµm c¸c 3 vËy g(x) = víi mäi x. hµm sè sau 2 2 ) c y = tan x +1.
Bài 2: T×m ®¹o hµm c¸c hµm sè sau Page 62 2
a) y = x - x x + 1 a) y' = (x - 5x )'(x - 5x )2 7 2 7 2 2 b) y = 2 - 5x - x = (7x -10x)(x - 5x )2 6 7 2 3 x c) y = 2 a - x 1 + x d)y = b) y = ( 2 x + ) 1 ( 2 5 - 3x ) 1 - x 4 2 = 3x - + 2x + 5 3 HD: y' = 12 - x + 4x
a) ¸p dông linh ho¹t c¸c c«ng (2x)'( 2x - )1 -(2x)( 2 x - ) 1 ' thøc c) y' = (x - )2 2 1 uv)' = u' v + u v' 2( 2 x - ) 1 - (2x) 2 2x 2x - - 2 = = b) ¸p dông c«ng thøc: (x - )2 1 (x - )2 2 2 1 u ' ( u ) ' = 2 2 u 5x - 6x - 2 d) y' = (x -x + )2 2 1
c) vµ d) ¸p dông c«ng thøc: 2 6n - æ n ö u
u 'v - uv ' e) y = m + ( ) ' = ç ÷ 3 2 2 v v x è x ø u '
vµ c«ng thøc: ( u ) ' =
Bµi 3: T×m ®¹o hµm c¸c hµm sè sau 2 u a) 2 y = x - x x +1 Bài 5: Cho 3 2 y = x - 3x + 2 . 2
Þ y ' = (x - x x +1)'= 2x - T×m x để
x' x - x ( x )' a) y’>0 x 3 x x b) y’<3 = 2x - - = 2x - 2 x 2
HD: TÝnh y' sau ®ã gi¶i c¸c
bÊt ph-¬ng tr×nh Èn x t-¬ng b) øng. 2 y = 2 - 5x - x 2 (2 - 5x - x ) ' Þ y ' = = 2 2 2 - 5x - x 2 - x - 5 2 2 2 - 5x - x 5 - - 2x VËy y' = 2 2 2 - 5x - x Page 63 2 x ( 2 2 3a - 2x ) 3 - x c) y' = ( = a - x ) ; d)y' 3 2( 1- x )3 2 LG: 3 2 y = x - 3x + 2 2 y = 3x - 6x 2
a)y' > 0 Û 3x - 6x > 0 Û x Î( ; -¥ 0) È (2;+¥) 2 b)y' < 3 Û 3x - 6x < 3 2 Û x - 2x -1< 0 Û 1- 2 < x <1+ 2
HĐ3:Củng cố và hướng dẫn học ở nhà:
*Củng cố:- Nêu lại các công thức tính đạo hàm tổng, hiệu, tích, thương; Các công thức tính đạo hàm
thường gặ, các công thức đạo hàm của các hàm số lượng giác.
*Áp dụng:Dùng công thức, hãy tính đạo hàm của các hàm số sau: - x ) a y = (x + ) 2 1 3 2 2 5 1 ; )
b y = x - 2x + 3; ) c y = sin . x o
c s 2x +1;d)y = ( 2 x + 2x + ) 2 1 x +1. x
*Hướng dẫn học ở nhà:-Xem lại các bài tập đã giải.
- Học thuộc các công thức tính đạo hàm thường gặp.
- Ôn tập lại cách tính đạo hàm cấp hai của một hàm s Page 64 Tiết 40,41
*Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
Ôn tập kiến thức cũ ... *Bài mới:
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính đạo hàm cấp hai
• GV hướng dẫn giúp HS giải Đ. 1. quyết vấn đề. a) 622080. a) Cho 6
f (x) = (x +10) . Tính f ''(2) . p b) f ''(- ) = 9 - , f ''(0) = 0 , p
b) Cho f (x) = sin 3x . Tính f ''(- ) , 2 2 p 9 f ''( ) = - . p
f ''(0) , f ''( ) . 18 2 18
2. Tính đạo hàm cấp hai của các hàm số sau:
• GV hướng dẫn giúp HS giải Đ. 1 quyết vấn đề. a) y = ; 1- x 2 a) y '' = . 3 1 ( - x) 1 b) y = ; 1- x 3 b) y '' = . 5 4 1 ( - x) c) y = tan x ; 2 x c) y = sin '' . 3 cos x d) y '' = 2 - cos 2x . d) 2 y = cos x . Page 65
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1: Bài tập 1:
GV nhắc lại định nghĩa đạo
HS thảo luận theo nhóm để
Tính đạo hàm cấp hai của các hàm số
hàm cấp hai của một hàm số.
tìm lời giải và cử đại diện lên sau: GV nêu bài tập và cho HS bảng. 2 ) a y = sin2 ; x ) c y = sin ; x thảo luận theo nhóm. 2
Gọi HS đại diện trình bày lời
HS nhận xét, bổ sung và sửa ) b y = o c s2 ;
x d)y = o c s ; x giải. chữa ghi chép. ) e y = x tan . x
Gọi HS nhận xét, bổ sung
HS chú ý theo dõi trên bảng (nếu cần)
để lĩnh hội kiến thức.
GV nhận xét, chỉnh sửa và bổ sung. HĐ2: Bài tập 2:
GV nêu đề bài tập và cho HS
HS thảo luận và cử đại diện 2 x + 2x + 2 thảo luận theo nhóm.
lên bảng trình bày lời giải. a)Cho hàm số: y = 2
Gọi HS đại diện lên bảng
HS nhận xét, bổ sung và sửa
Chứng minh rằng: 2y.y’’ – 1 =y’2 trình bày lời giải. chữa ghi chép.
b)Cho hàm số y = x3 + 2x2 + x – 5. Giải
Gọi HS nhận xét, bổ sung.
bất phương trình y’ < 0.
GV nhận xét, chỉnh sửa và bổ HS chú ý theo dõi để lĩnh hội sung. kiến thức... HĐ3:
Củng cố và hướng dẫn học ở nhà: *Củng cố:
*Áp dụng: Cho hàm số y = cos22x. a) Tính y”, y”’.
b) Tính giá trị của biểu thức: A= y’’’ +16y’ + 16y – 8.
*Hướng dẫn học ở nhà:- Xem lại các bài tập đã giải. Ôn tập lại cách tính vi phân của một hàm số.
* Làm bài tập sau:Cho hàm số: 2
y = x + x +1 .
a) Tìm hệ thức giữa y’ và y;
b) Tìm hệ thức giữa y’’, y’ và y. HD: a) Tính y’ 2
Þ 2y' x +1- y = 0b)Tính y” Þ y ( 2 4 ' x + ) 1 + 4xy'- y = 0 Page 66 Tiết 42
*Tiến trình giờ dạy:-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức:Ôn tập kiến thức cũ ... *Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1:
*Ta gọi vi phân của hàm số y = f(x),
GV nhắc lại khái niệm vi phân của HS chú ý theo dõi để lĩnh ký hiệu là: dy hoặc df(x), là tích của một hàm số hội kiến thức...
đạo hàm hàm số với vi phân dx của biến số y = f (x)
GV nêu bài tập áp dụng và cho HS HS thảo luận thoe nhóm
Þ dy = df (x) = y'dx = f '(x)dx
thảo luận tìm lời giải.
để tìm lời giải và cử đại
Gọi HS đại diện lên bảng trình
diện lên bảng trình bày. bày. HS nhận xét, bổ sung và
Gọi HS nhận xét, bổ sung (nếu sữa chữa ghi chép... cần)
GV nhận xét, chỉnh sửa bổ sung. HĐ2: Đ.
1. Tìm vi phân của các hàm số sau:
GV nêu các công thức tính vi phân
của các hàm số tổng, hiệu, tích, a) dy = 1 dx . a) y = x ; thương: 2 x )
a y = u + v Þ dy = du + dv )
b y = uv Þ dy = udv + vdu b) y = ( 2 x + x + )( 2 4 1 x - x ); u udv - vdu ) c y = Þ dy = b) 2 v v 2
dy = [(2x + 4)(x - x )
• GV hướng dẫn giúp HS giải quyết 2 æ 1 ö
+(x + 4x +1) 2x - ç ÷]dx. vấn đề. è 2 x ø 2 tan x c) y = 2 tan x ; c) dy = dx . 2 cos x d) cos x 2
(x - 1) sin x + 2x cos x d) y = . dy = dx 1- 2 x (1 - 2 2 x ) .
Hoạt động 2: Luyện tập ứng dụng vi phân vào phép tính gần đúng Đ. Đặt y x = 2 ( )
a + x . 2. Chứng minh rằng với |x| rất bé so
với a>0 (|x| £ a) ta có: ' Ta có: x • 2
GV hướng dẫn giúp HS giải quyết
a + x » a + (a>0). 2a Page 67 vấn đề. 1 y '(x) = . 2 2 a + x
Áp dụng công thức trên, hãy tính Từ đó, gần đúng các số sau:
Dy = y(x) - y(0) » y '(0)x a) 146 ; Þ 2
a + x » a + 1 x . 2a b) 34 ; Áp dụng: c) 120 . a) 12,08. b) 5,83. c) 10,95. HĐ2:
GV nêu các công thức tính vi phân HS chú ý theo dõi trên Bài tập 1:
của các hàm số tổng, hiệu, tích,
bảng để lĩnh hội kiến
Tính vi phân của các hàm số sau: thương: thức... 2 ) a y = x +1; )
a y = u + v Þ dy = du + dv 2 )
b y = uv Þ dy = udv + vdu )
b y = x + x +1; u udv - vdu ) c y = o c s2 ; x ) c y = Þ dy = 2 v v 1 d)y = cot . 2 x +1 Bài tập áp dụng:
Cho Hs thảo luận và gọi HS đại
diện lên bảng trình bày lời giải. HS thảo luận theo nhóm
Gọi HS nhận xét, bổ sung (nếu
để tìm lời giải và cử đại cần).
diện lên bảng trình bày...
GV nhận xét, chỉnh sửa và bổ sung. HS nhận xét, bổ sung và sửa chữa ghi chép...
Bài tập 2: Tính vi phân của các hàm số sau: )
a y = sin x + cos ; x 1 2 ) b y = x +1 + ; 2 x + 3 )
c y = tan x + sin(2x + ) 3 ; 1 d)y = - .t anx 2 2x
4Củng cố và hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải.
- Nắm chắc các công thức tính đạo hàm đã học,... Rút kinh nghiệm Page 68 Tiết 43,44
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
-Nêu các công thức phương trình tiếp tuyến tại một điểm, nêu phương trình đường thẳng đi qua một điểm và có hệ số góc k;
phương trình đường thẳng song song với một đường thẳng đã cho, vuông góc với một đường thẳng đã cho.
*Bài tập: Viết phương trình đường thẳng đi qua điểm M0(x0; y0) Biết rằng đường thẳng: a) Có hệ số góc k;
b) Song song với đường thẳng (d): ax + b y + c = 0;
c) Vuông góc với đường thẳng (d’): y = k’x + b. *Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ1:
HS viết các công thức trên bảng... Bài tập 1:
GV gọi HS lên bảng viết lại công
Dùng công thức, tính đạo hàm của các hàm số
thức đạo hàm của các hàm số lượng sau: giác.
HS thảo luận theo nhóm và cử đại x 3
GV nêu đề bài tập và cho HS thảo
diện lên bảng trình bày... ) a y = o c s ;
luận tìm lời giải. HS nhận xét, bổ sung 3
GV gọi HS nhận xét, bổ sung (nếu
Chú ý theo dõi trên bảng để lĩnh hội ) b y = xsin ; x cần). kiến thức...
GV chỉnh sửa và bổ sung. 2 ) c y = tan x +1. HĐ2: Bài tập 1:
GV gọi HS lên bảng viết hương
HS lên bảng ghi lại phương trình
Cho đường cong (C) có phương trình: y=x3 +
trình tiếp tuyến của một đường cong tiếp tuyến tại một điểm. 4x +1
(C) có phương trình: y = f(x) tại
a) Viết phương trình tiếp tuyến với đương cong
điểm có hoành độ x0.
(C) tai điểm có hoành độ x0 = 1;
GV nêu bài tập áp dụng:
b) Tiếp tuyến có hệ số góc k = 31;
Cho HS thảo luận theo nhóm và gọi
c) Song song với đường thẳng: y = 7x + 3;
HS đại diện lên bảng trình bày lời
HS thảo luận theo nhóm để tìm lời
d) Vuông góc với đường thẳng: giải.
giải và cử đại diện lên bảng trình 1
Gọi HS nhận xét, bổ sung . bày lời giải. y = - x - 5.
GV nhận xét, chỉnh sửa và bổ sung.
HS nhận xét, bổ sung và sửa chữa 16 ghi chép... Page 69
-----------------------------------&------------------------------------ Ngày: 17/10/2016 Chủ đề CĐ - HH2 (T4)
ĐƯÒNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN I.Mục tiêu:
Qua chủ đề này HS cần:
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản về qua hệ song song trong
không gian và bước đầu hiểu được một số kiến thức mới về quan hệ song song trong không gian .
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về qua hệ song song. Thông qua việc rèn
luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số
kiến thức mới trong chương trình nâng cao.
3)Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:
-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III.Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu pp tìm giao tuyến của 2 mp (nêu 2 phương pháp khi hai mp có 1 điểm chung và khi 2 mp song song)
+Nêu lại phương pháp chứng minh đường thẳng song song mặt phẳng.
*Áp dụng: Giải bài tập 2 về nhà.
GV gọi HS nhận xét. bổ sung và giáo viên nêu lời giải đúng (nếu HS không trình bày đúng lời giải). +Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng
HĐ1: Bài tập về xác định
Bài tập1: Cho hình lập phương
thiết diện và chứng minh
ABCD.A’B’C’D’.Gọi M, N, P lần
đường thẳng song song với
lượt là trung điểm của AB, B’C’, mp: DD’.
GV nêu đề và ghi lên bảng,
HS thảo luận theo nhóm để tìm
a)Hãy xác định thiết diện tạo bởi
cho HS các nhóm thảo luận để lời giải và cử đại diện lên bảng
hình lập phương đã cho và mp
tìm lời giải và ghi lời giải vào
trình bày (có giải thích). (MNP)
bảng phụ. Gọi HS đại diện lên
b)Chứng minh rằng đường thẳng
bảng trình bày lời giải.
MN song song với mp (BDC’).
Gọi HS nhận xét, bổ sung (nếu cần).
GV nhận xét, bổ sung và nêu
HS nhận xét, bổ sung và sửa chữa
lời giải đúng (nếu HS không ghi chép. Page 70
trình bày đúng lời giải).
HS trao đổi để rút ra kết quả:… D C A B D' C' A' B'
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ2:
Bài tập2: Từ 4 điểm của hình bình GV: Để chứng minh hai mp HS suy nghĩ trả lời …
hành ABCD vẽ bốn nửa đường
song song với nhau ta phải
thẳng song song cùng chiều Ax, chứng minh như thế nào?
By, Cz, Dt. Một mp (a )cắt 4 nửa
Để chứng minh hai đường
đường thẳng Ax, By, Cz, Dt tại A’,
thẳng song song với nhau ta B’, C’, D’. phải ta phải làm gì?
HS thảo luận theo nhóm để tìm
a)Chứng minh hai mp (Ax, By) và
lời giải và cử đại diện lên bảng
(Cz, Dt) song song với nhau.
trình bày (có giải thích).
b)Chứng minh tứ giác A’B’C’D’ là
GV nêu đề và ghi lên bảng, hình bình hành.
cho HS các nhóm thảo luận để
c)Gọi O, O’ lần lượt là tâm các
tìm lời giải và ghi lời giải vào
hình bình hành ABCD, A’D’C’D’.
bảng phụ. Gọi HS đại diện lên
Chứng minh đường thẳng OO’
bảng trình bày lời giải.
HS nhận xét, bổ sung và sửa chữa song song với đường thẳng AA’ và
Gọi HS nhận xét, bổ sung (nếu ghi chép. AA’ +CC’ =BB’ +DD’. cần).
HS trao đổi để rút ra kết quả:…
GV nhận xét, bổ sung và nêu
lời giải đúng (nếu HS không
trình bày đúng lời giải). t z D' C' x y O' A' a D B' C O A B a)(Ax,By)//(Cz,Dt): Ta có: Page 71 ìïAx//Dt (gt) í
ïîAB / /DC (Hai cπnh ÆËi cÒa h◊nh b◊nh hµnh) Þ ( , Ax B ) y / /(C , z Dt). )
b A' B' C' D ' lµ h◊nh b◊nh hµnh Ta c„ : (
ìï Ax,By) / / (C ,zDt) í
Þ A' B'/ /C' D ' a ï Ç î
(Ax,By) = A' B', a Ç (C ,
z Dt ) = C' D ' ¯n
Ch g minh t≠¨ n
g t˘ ta c„ : A'D'//B'C'
VÀy t¯ gi∏c A'B'C'D' lµ h◊nh b◊nh hµnh. c)OO'//AA'; AA'+CC'=BB'+DD'
Theo t›nh ch t cÒa h◊nh b◊nh hµnh th◊ O lµ trung Æi”m cÒa Æπ
o n AC, BD vµ O' lµ trung Æi”m cÒa Æπ o n thºng A'C', B'D'.
Tứ giác AA’C’C có AA’//CC’ nên là hình thang, OO’ là đường trung bình của hình thang này do đó: + CC = AA ' ' OO' ; 2 BB + DD
Chứng minh tương tự ta có: OO = ' ' ' 2
Vậy AA’ + CC’ = BB’ + DD’.
HĐ3: Củng cố và hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải và làm thêm các bài tập:
Bài tập 1: Cho đỉnh S nằm ngoài hình bình hành ABCD. Xét mp a
( ) qua AD cắt SB, SC lần lượt tại M
và N. Chứng minh AMND là hình thang.
Bài tập 2: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và BD. Gọi P là điểm tùy ý trên
cạnh AB sao cho P ¹ A và P ¹ B. Xét I = PD Ç AN và J =PC Ç AM.
Chứng minh rằng: IJ // CD.
-----------------------------------&------------------------------------ +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu pp tìm giao tuyến của 2 mp (nêu 2 phương pháp khi hai mp có 1 điểm chung và khi 2 mp song song)
+Nêu lại phương pháp chứng minh đường thẳng song song mặt phẳng. +Bài mới:
Hoạt động của GV
Hoạt động của HS Ghi bảng HĐ2:
BT1: Cho h×nh chãp S. ABCD cã ®¸y lµ h×nh GV: Nêu pp tìm giao HS suy nghĩ trả lời …
b×nh hµnh. M, N trung ®iÓm SA, SB, K Î SC. tuyến của 2 mp. GV: Để chứng minh
a) T×m giao tuyÕn cña (SAB) vµ (SCD), (SAC) hai mp song song với
HS thảo luận theo nhóm vµ (SBD) nhau ta phải chứng
để tìm lời giải và cử đại minh như thế nào?
diện lên bảng trình bày
b) MN song song víi nh÷ng mÆt ph¼ng nµo ? Để chứng minh hai (có giải thích). đường thẳng song song
c) T×m giao ®iÓm cña (MNK) vµ SD?
với nhau ta phải ta phải làm gì?
d) NÕu K lµ trung ®iÓm SC th× (MNK) song Page 72 song víi mÆt ph¼ng nµo GV: Nêu pp tìm giao HS nhận xét, bổ sung và điểm của mp và đt. sửa chữa ghi chép. GV nêu đề và ghi lên
HS trao đổi để rút ra kết S
bảng, cho HS các nhóm quả: a)* AB Ì (SAB)
thảo luận để tìm lời (1)
giải và ghi lời giải vào Q bảng phụ. Gọi HS đại M CD Ì (SCD) (2)
diện lên bảng trình bày x lời giải. I AB // CD (tÝnh chÊt A N D Gọi HS nhận xét, bổ K hbh) sung (nếu cần). GV nhận xét, bổ sung S Î (SAB) Ç (SCD) (3) O và nêu lời giải đúng (nếu HS không trình Từ (1), (2) và (3)Þ Sx bày đúng lời giải). B C lµ giao tuyÕn cña (SAB) vµ (SCD) víi Sx // AB // CD ) * AC Ç BD = 0
b) * D SAB: M lµ trung ®iÓm SA vµ N lµ
trung ®iÓm SB Þ MN lµ ®êng trung b×nh cña O Î AC Ì (SAC)
D SAB Þ MN // AB v× AB // CD Þ MN // CD O Î BD Ì (SBD)
* MN // AB (CMT) vµ AB Ì (ABCD) Þ O Î (SAC) Ç (SBD) Þ MN // (ABCD) v× S Î (SAC) Ç (SBD)
* MN // CD (CMT) vµ CD Ì (SCD) VËy SO = (SAC) Ç (SBD… Þ MN // (SCD)
d) NÕu K lµ trung c) * Trong (SAC): SO Ç MK = I ®iÓm SD, mµ N lµ trung ®iÓm SB Þ KN * Trong (SBD): NI Ç SD = Q lµ ®êng trung b×nh D * SD Ì (SBD) SBC Þ KN // BC
(SBD) Ç (MNK) = NI mµ NI Ç SD = Q * KN Ç MN = N Þ Q = (MNK) Ç SD KN, MN Ì (MNK) Þ (MNK) // (ABCD)
BT2: Cho h×nh chãp S.ABCD cã ®¸y ABCD lµ
h×nh b×nh hµnh. T×m giao tuyÕn cña c¸c cÆp KN // BC, BC Ì mÆt ph¼ng sau ®©y: (ABCD) Þ KN // (SABCD) a, (SAC) vµ (SBD) Mµ MN // (ABCD) b, (SAB) vµ (SCD) Gi¶i:
a, Giao tuyÕn cña (SAC) vµ (SBD): Page 73
- Trong mÆt ph¼ng (ABCD) gäi O = AC Ç BD.
- Hai mÆt ph¼ng (SAC) vµ (SBD) cã S vµ O lµ
2 ®iÓm chung nªn giao tuyÕn cña 2 mÆt ph¼ng nµy lµ ®-êng th¼ng SO.
b, Giao tuyÕn cña (SAB) vµ (SCD):
- Ta cã AB Ì (SAB) vµ DC Ì (SCD) mµ AB //
CD nªn theo ®Þnh lý giao tuyÕn cña 3 mÆt
ph¼ng th× giao tuyÕn cña (SAB) vµ (SCD) lµ ®-êng th¼ng d // AB // CD.
- (SAB) vµ (SCD) cã 1 ®iÓm chung lµ S.
- VËy giao tuyÕn cña (SAB) vµ (SCD) lµ ®-êng
th¼ng ®i qua S vµ song song víi AB.
C, T×m giao ®iÓm cña ®-êng th¼ng vµ mÆt
ph¼ng: T×m mét mÆt ph¼ng chøa ®-êng th¼ng
®· cho vµ cã giao víi mÆt ph¼ng kia. Sau ®ã
t×m giao tuyÕn cña 2 mÆt ph¼ng. Giao ®iÓm
cña ®-êng th¼ng ®· cho vµ giao tuyÕn chÝnh lµ
giao ®iÓm cña ®-êng th¼ng vµ mÆt ph¼ng ®· cho.
HĐ3: Củng cố và hướng dẫn học ở nhà:
-Gọi HS nhắc lại phương pháp tìm giao tuyến của hai mp, cách tìm giao điểm của một đường thẳng với
một mp, cách chứng minh một đường thẳng song song với một mp, phương pháp chứng minh hai đường
thẳng song song. Hai mp song song,…
-Xem lại các bài tập đã giải; làm thêm các bài tập sau:
BT1: Cho tø diÖn ABCD. Gäi M, N lÇn l-ît lÊy trªn c¸c c¹nh AC vµ BC sao cho MN kh«ng
song song víi AB. Gäi O lµ mét ®iÓm thuéc miÒn trong cña tam gi¸c ABD. T×m giao ®iÓm cña AB vµ AD víi mÆt ph¼ng (OMN)
BT2: Cho tø diÖn ABCD. Trªn c¸c ®o¹n CA, CB, BD cho lÇn l-ît c¸c ®iÓm M, N, P sao cho MN
kh«ng song song víi AB, NP kh«ng song song víi CD. T×m thiÕt diÖn cña mÆt ph¼ng t¹o bëi (MNP) vµ tø diÖn ABCD.
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
LUYỆN TẬP §4 (1/1)
(§4. Hai mặt phẳng song song) I. MỤC TIÊU:
Kiến thức: Củng cố:
- Định nghĩa và tính chất của hai mặt phẳng song song.
- Điều kiện để hai mặt phẳng song song. Kĩ năng: Page 74
- Nắm được cách chứng minh mặt phẳng song song với mặt phẳng đã cho.
- Vận dụng để chứng minh đường thẳng song song với mặt phẳng. Thái độ:
- Liên hệ được với nhiều vấn đề trong thực tế với bài học.
- Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về hình học không gian.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định lớp, kiểm tra sĩ số lớp, khởi động tiết học.
2. Kiểm tra bài cũ: (Trong quá trình luyện tập). H. Đ. 3. Giảng bài mới: TL
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập chứng minh hai mặt phẳng song song 1. Cho hình hộp ABCD.A¢B¢C¢D¢.
H1. Nêu điều cần chứng minh Đ1. A¢D // B¢C, A¢B // D¢C ? a) CMR (BDA¢) // (B¢D¢C). 20' Þ (BDA¢) // (B¢D¢C).
b) CMR đường chéo AC¢ đi qua trọng tâm G
H2. Xác định các trọng tâm G 1 và G2 của hai 1 tam giác BDA¢ và B¢D¢C. và G Đ2. G 2 của các tam giác BDA¢ 1 = AC¢ Ç A¢O và B¢D¢C ? G c) Chứng minh G 2 = CO¢ Ç AC¢ 1 và G2 chia
đoạn AC¢ thành ba phần bằng nhau.
H3. Tính AG1, G1G2, G2C¢ ?
d) Gọi O và I lần lượt là tâm
của các hình bình hành ABCD
Đ3. AG1 = G1G2 = G2C¢ =
và AA¢C¢C. Xác định thiết diện
của mp(A¢IO) với hình hộp đã AC ' = cho. 3 Page 75 D C O A B G1 D’ G2 C’ O’ A’ B’
Hoạt động 2: Luyện tập vận dụng tính chất của hai mặt phẳng song song
2. Cho hai hình bình hành ABCD và ABEF không cùng
H1. Nêu cách chứng minh hai Đ1. CB // AD, BE // AF
thuộc một mặt phẳng. Trên mặt phẳng song song ? 17' Þ (CBE) //(ADF)
AC, BF lần lượt lấy các điểm M , N sao cho AM BN 1 = = . AC BF 3
H2. Nêu cách chứng minh
Hai đường thẳng song song với M¢N¢ // DF ?
Đ2. Dùng định lí Thales đảo AB kẻ từ M và N cắt AD, AF trong mặt phẳng.
lần lượt tại M’, N’. AM ' AM 1 = = Chứng minh rằng: AD AC 3 AN ' BN 1 a) (CBE) // (ADF) = = AF BF 3 b) M’N’ // DF Þ AM ' AN ' =
Þ M’N’ // DF c) NM // (DEF) AD AF F E N’ N A B M’ M D C
Hoạt động 3: Củng cố • Nhấn mạnh:
5' – Cách vận dụng định nghĩa và
tính chất để chứng minh hai mp song song, đt song song mp, hai đt song song.
– Cách vẽ hình, cách trình bày Page 76 lời giải.
4. BÀI TẬP VỀ NHÀ:
- Bài tập thêm SBT, CKT (GV hướng dẫn, dặn dò).
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
.........................................................................................................................................................
(Bài tập cần làm: 2, 3, 4 tr 71.) Page 77
CHƯƠNG II. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG ÔN TẬP CHƯƠNG II ... I. MỤC TIÊU: Kiến thức:
- Củng cố các tính chất của phép chiếu song song.
- Các khái niệm về hình chóp, hình lăng trụ, hình hộp, hình chóp cụt. Kĩ năng:
- Biết tìm hình chiếu của điểm trong không gian trên mặt phẳng chiếu theo phương của một
đường thẳng cho trước.
- Biết biểu diễn các hình đơn giản. Thái độ:
- Liên hệ được với nhiều vấn đề trong thực tế với bài học.
- Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hình vẽ minh hoạ.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về phép chiếu song song.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định lớp, kiểm tra sĩ số lớp, khởi động tiết học.
2. Kiểm tra bài cũ: (Trong quá trình luyện tập). H. Đ. 3. Giảng bài mới: TL
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Vận dụng tính chất phép chiếu song song để giải toán
H1. Nêu tính chất trọng tâm Đ1. Giao điểm 3 đường trung 1. DABC có hình chiếu song tam giác ? tuyến.
song là DA¢B¢C¢. CMR trọng
tâm của DABC có hình chiếu 15' song song là trọng tâm
H2. Nêu tính chất của phép Đ2. Bảo toàn tỉ số độ dài hai DA¢B¢C¢. chiếu cần sử dụng ?
đoạn thẳng cùng phương. Page 78
H3. Xác định phép chiếu ?
Đ3. Xét phép chiếu song song 2. Cho hình hộp theo phương BC¢
lên ABCD.A¢B¢C¢D¢. Tìm điểm I mp(ABCD). Khi đó:
trên đường chéo B¢D và điểm J
trên đường chéo AC sao cho IJ D ! D, I ! J, B¢ ! B¢¢ ID // BC¢. Tính tỉ số .
Þ J là giao điểm của B¢¢D và IB ' AC. ID JD AD 1 = = = IB ' JB ' B ' C 2
Hoạt động 2: Vận dụng tính chất phép chiếu song song để vẽ hình biểu diễn
H1. Xác định phép chiếu ? Đ1.
3. Hãy chọn phép chiếu song
song để hình chiếu của một tứ
– Phương chiếu d là phương diện là một hình bình hành.
của một trong ba đường thẳng 25'
đi qua trung điểm của hai cạnh
đối diện của tứ diện.
– Mặt chiếu là mp tuỳ ý cắt d. Đ2.
4. Vẽ hình biểu diễn của một H2. Nêu cách vẽ ?
– Vẽ elip tâm O. Lấy B, C Î tam giác vuông nội tiếp trong
(E) sao cho B, O, C thẳng một đường tròn. hàng, A Î (E), A ¹ B, C.
– DABC là hình biểu diễn của
một tam giác vuông nội tiếp trong một đường tròn.
5. Vẽ hình biểu diễn của một Đ3. Từ bài 4).
hình vuông nội tiếp trong một đường tròn.
– Qua O vẽ hai dây MP và NQ
lần lượt song song với AC và
AB. Khi đó tứ giác MNPQ là H3. Nêu cách vẽ ?
hình biểu diễn của một hình
vuông nội tiếp trong đường tròn.
6. Vẽ hình biểu diễn của một Page 79 lục giác đều. Đ4.
– Vẽ hình bình hành OABC
– Lấy các điểm D, E, F lần lượt
đỗi xứng với các điểm A, B, C qua O. H4. Nêu cách vẽ ?
Þ ABCDEF là hình biểu diễn
của một lục giác đều.
Hoạt động 3: Củng cố • Nhấn mạnh:
3' – Cách vẽ hình biểu diễn của
một số hình thường gặp.
4. BÀI TẬP VỀ NHÀ:
- Đọc trước bài "Vectơ trong không gian".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN.
QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
LUYỆN TẬP §1 (1/1) IAN.
QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
LUYỆN TẬP §3 (1/1) I. MỤC TIÊU: Page 80
Kiến thức: Củng cố:
- Định nghĩa đường thẳng vuông góc với mặt phẳng.
- Các dấu hiệu nhận biết đường thẳng vuông góc với mặt phẳng.
- Định lí ba đường vuông góc.
Kĩ năng: Luyện tập:
- Cách chứng minh đường thẳng vuông góc với mặt phẳng.
- Cách sử dụng định lí ba đường vuông góc và biết xác định góc giữa đường thẳng và mặt phẳng. Thái độ:
- Liên hệ được với nhiều vấn đề trong thực tế với bài học.
- Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về đường thẳng vuông góc với mặt phẳng.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định lớp, kiểm tra sĩ số lớp, khởi động tiết học.
2. Kiểm tra bài cũ: (Trong quá trình luyện tập). H. Đ. 3. Giảng bài mới: TL
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập tính góc giữa đường thẳng và mặt phẳng
3. Cho hình chóp SABCD có
đáy ABCD là hình vuông cạnh
H1. Xác định góc giữa đt và Đ1. a. SA ^ (ABCD) và SA = mp ? 20' a) ∑ 0 SCA = 60 a 6 . Tính góc giữa: S a) SC và (ABCD) b) ∑ 1 tan CSB = a 6 H 7 b) SC và (SAB) A B
c) Vẽ AH ^SB ÞAH ^ (SBC) c) AC và (SBC) O D a C ∑ 21 sin ACH = 7
H2. Xác định góc giữa MN và (ABCD) ?
4. Cho hình chóp SABCD có
đáy ABCD là hình vuông cạnh Đ2. ∑ 0 MNH = 60 a, tâm O. SO ^ (ABCD). Gọi 20'
M, N lần lượt là trung điểm của Page 81 các cạnh SA và BC. Biết Þ a 10 a 30 MN = , MH = ∑ 0
H3. Xác định góc giữa MN và 2 4
(MN,(ABCD)) = 60 . (SBD) ? a 30 a) Tính MN và SO. Þ SO = 2MH = S 2 b) Tính góc giữa MN và M
Đ3. Vẽ ME ^ SO, NF ^ BO (SBD). A B H ∑ ∑ = O N
Þ (MN,(SBD)) (MN, EF) D a C a 2 ME = 4 Þ ∑ 5 sin(MN,(SBD)) = 5 M F E I N
Hoạt động 2: Củng cố • Nhấn mạnh:
3' – Cách xác định góc giữa
đường thẳng và mặt phẳng.
4. BÀI TẬP VỀ NHÀ:
- Đọc trước bài "Hai mặt phẳng vuông góc".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Page 82
Tiết chương trình : CĐ14, CĐ15. Ngày soạn : ... Ngày dạy : ...
CHƯƠNG III. VECTƠ TRONG KHÔNG GIAN.
QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
LUYỆN TẬP §4 (1,2/2) I. MỤC TIÊU:
Kiến thức: Củng cố:
- Định nghĩa góc giữa hai mặt phẳng.
- Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau.
- Định nghĩa và tính chất của hình lăng trụ đứng, chiều cao của hình lăng trụ đứng.
- Định nghĩa hình chóp đều, hình chóp cụt đều và các tính chất của các hình đó. Kĩ năng:
- Biết vận dụng các định lí về hai mặt phẳng vuông góc để giải các bài toán hình học không gian. Thái độ:
- Liên hệ được với nhiều vấn đề trong thực tế với bài học.
- Phát huy tính độc lập, sáng tạo trong học tập. II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức về hai mặt phẳng vuông góc.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định lớp, kiểm tra sĩ số lớp, khởi động tiết học.
2. Kiểm tra bài cũ: (Trong quá trình luyện tập)
H. (Một số câu hỏi trong các hoạt động). Đ. 3. Giảng bài mới: TL
Hoạt động của Giáo viên
Hoạt động của Học sinh Nội dung
Hoạt động 1: Luyện tập xác định góc giữa hai mặt phẳng
1. Cho tứ diện ABCD có
DABC vuông ở B. Chứng minh
15' H1. Nêu các cách xác định góc Page 83 giữa hai mặt phẳng ? Đ1. AB ^ BC, DB ^ BC rằng ∑
ABD là góc giữa hai mặt phẳng (ABC) và (DBC). D Þ ∑ ABD = ∑ ((ABC),(DBC)) A C B
H2. Nêu cách xác định góc giữa hai mặt phẳng ? 25'
2. Cho hình chóp SABCD có S
đáy ABCD là hình vuông cạnh a, SA ^ (ABCD) và SA = a 3 A
a 3 . Tính góc giữa các cặp D Đ2. mặt phẳng sau: O B a a) SB ^ BC, AB ^ BC C a) (SBC) và (ABC). Þ ∑ ((SBC),(ABC)) = ∑ SBA =600 b) (SBD) và (ABD). b) SO ^ BD, AO ^ BD c) (SAB) và (SCD). Þ ∑ ((SBD),(ABD)) = ∑ SOA ∑ tan SOA = 6 c) ∑ 0 DSA = 30
Hoạt động 2: Luyện tập chứng minh hai mặt phẳng vuông góc
H1. Nêu cách chứng minh hai Đ1.
3. Cho hình chóp SABCD có mặt phẳng vuông góc?
đáy ABCD là hình thoi cạnh a 20' a) AC ^ BD, AC ^ SO và có SA = SB = SC = a. CMR S Þ AC ^ (SBD) a) (ABCD) ^ (SBD). a Þ (ABCD) ^ (SBD) b) DSBD vuông. A B b) OS = OB = OD O D a C Þ DSBD vuông Page 84
H2. Nêu cách chứng minh hai mặt phẳng vuông góc? b B C
4. Cho hình hộp chữ nhật a ABCD.A¢B¢C¢D¢ có AB = a, 20' D c A BC = b, CC¢ = c. B’ C’ Đ2.
a) CMR (ADC¢B¢) ^ (ABB¢A¢) A’ D’ a) AD ^ AB, AD ^ AA¢
b) Tính độ dài đường chéo AC¢ Þ AD ^ (ABB¢A¢) theo a, b, c. Þ (ADC¢B¢) ^ (ABB¢A¢) b) 2 2 2 2
AC ' = AB + BC + CC ' = a2 + b2 + c2
Hoạt động 3: Củng cố • Nhấn mạnh:
3' – Cách xác định góc giữa hai mặt phẳng.
– Cách chứng minh hai mặt 3' phẳng vuông góc.
4. BÀI TẬP VỀ NHÀ:
- Đọc trước bài "Khoảng cách".
IV. RÚT KINH NGHIỆM, BỔ SUNG:
.........................................................................................................................................................
.........................................................................................................................................................
......................................................................................................................................................... Page 85




