


















































Preview text:
Giáo án Tự chọn 11
Tiết 1. ÔN TẬP CÔNG THỨC LƯỢNG GIÁC I. Mục tiêu.
Qua bài học học sinh cần nắm được:
1/ Về kiến thức
• Củng cố khái niệm các giá trị lượng giác của 1 cung
• Nắm được các công thức lượng giác cơ bản, cung có liên quan đặc biệt .
2/ Về kỹ năng
• Biết vận dụng các công thức lgiác, bảng dấu để tính các gtlg còn lại.
• Biết tính gtlg của các cung hơn 900 nhờ vào gtrị đặc biệt và mối liên quan đặc biệt.
3/ Về tư duy, Về thái độ
• Nhớ, Hiểu, Vận dụng
• Cẩn thận, chính xác.
• Tích cực hoạt động; rèn luyện tư duy khái quát, tương tự.
II) Trọng tâm: giá trị lượng giác của một cung bất kỳ, quan hệ giữa các giá trị lượng giác. III. Chuẩn bị.
1) Chuẩn bị của GV: ngoài Giáo án, SGK, STK, còn có phiếu học tập, …
2) Chuẩn bị của HS: Ngoài Sách GK, thước, viết, còn có bảng phụ, phiếu trả lời và chuẩn bị kiến thức đã học các lớp dưới
IV. Tiến trình bài học và các hoạt động.
1. Ổn định lớp:
2. Kiểm tra bài cũ: Nhắc lại công thức lượng giác
Hoạt động của thầy và trò Nội dung I.
Quan heä giöõa caùc giaù trò löôïng giaùc:
1. Coâng thöùc löôïng giaùc cô baûn: 2 2 sin a + cos a = 1
Hoạt động 1: cho 3 3p 1 p sina = - , p < a < , tính các 2 1+ tan a = , a ¹ + kp , kÎ Z 5 2 2 cos a 2 giá trị lượng giác. 1 2 1+ cot a =
, a ¹ kp k Î Z 2 ( ) 4 a § cosa = - sin 5 p 3 tana.cota = 1, a ¹ k , k Î Z tana = 2 4
2. Giaù trò löôïng giaùc cuûa caùc cung coù lieân quan 4 cot = ñaëc bieät: 3
a) Cung ñoái nhau: a vaø - a
Hoạt động2: Giáo viên gọi học sinh
b) Cung buø nhau: a vaø (p - a)
lên bảng vẽ hình minh hoạ và nêu
c) Cung hôn keùm p: a vaø (p + a )
giá trị lượng giác của các cung có p
liên quan đặc biệt trên.
d) Cung phuï nhau: a vaø -a : 2
Hoạt động 3: tính p Ví duï: Cho 0 < a < . æ 11p ö 31p cos - , tan ,sin ( 0 1380 - ç ÷ ) 2 è 4 ø 6
a) Tính sin (a -p ) theo sina
§ Hoïc sinh leân baûng döïa æ p a ö +
vaøo giaù trò löôïng giaùc b) Tính cot ç ÷ theo cota è 2 ø cuûa caùc cung coù lieân Giaûi:
quan ñaëc bieät ñeå laøm. a) sin (a -p ) = -sina æ p ö b) cot a + = - tana ç ÷ è 2 ø 1
Giáo án Tự chọn 11
Hoạt động của thầy và trò Nội dung
Hoạt động 4: không dùng máy tính, hãy
I. Công thức cộng: æ p ö
sin (a ± b) = sin a cosb ± cos asin b tính cos - ç ÷ è 12 ø
cos (a ± b) = cos a cosb ! sin asin b æ p ö p cos - = cos ç ÷ tan a ± tan b è 12 ø 12 tan (a ± b) = 1! tan a tan b 2 æ p p ö (1+ 3) = cos - = ç ÷
với điều kiện các biểu thức đều có nghĩa è 3 4 ø 4
Hoạt động 5: Chứng minh rằng:
(a +b) (a -b) 2 2 sin sin
= sin a - sin b II.
Công thức nhân đôi:
§ Học sinh sử dụng công thức cộng làm sin 2a = 2sin a cos a bài. 2 2 2 2
cos 2a = cos a - sin a = 2cos a -1 = 1- 2sin a
Hoạt động 6: Từ công thức nhân đôi hãy 2 tan a tan 2a = 2 suy ra công thức của 2 2 2
sin a,cos a, tan a ? 1- tan a 1+ cos 2a 2 cos a = 1 2
Ví dụ: tính sin 2a nếu sin a - cos a = 5 1- cos 2a 2 sin a = Giải: 2 1 sin a - cos a = 1- cos 2a 2 tan a = 5 1+ cos 2a 1 2 2
Û sin a + cos a - 2sin a cos a = 25 1 24 Û sin 2a =1- = 25 25
4. Củng cố và luyện tập: p p p p Câu 1: cos sin + cos sin bằng: 6 3 3 6 1 a) 1 b) 0 c) – 1 d) 2 æ 5p ö æ 9p ö æ 5p ö æ 9p ö Câu 2: biểu thức cos -a + sin -a - cos +a - sin +a bằng: ç ÷ ç ÷ ç ÷ ç ÷ è 12 ø è 12 ø è 12 ø è 12 ø
a) 2(sina + cosa ) c) 2cosa c) 2sina d) 0 2
Giáo án Tự chọn 11 Tiết 2: PHÉP TỊNH TIẾN I. Mục tiêu:
Qua T này tiết học này HS cần: 1. Về Kiến thức:
Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của phép tịnh tiến 2. Về kỹ năng:
Tăng cường rèn luyện kỹ năng giải toán về dựng hình là ảnh hoặc tạo ảnh của một hình qua ptt cho
trướ, sử dụng biểu thức tọa độ để tìm tọa độ của điểm, viết phương trình của đường thẳng, phương trình của đường tròn.
3. Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị:
1. GV: Giáo án, các bài tập ,…
2. HS: Ôn tập kiến thức cũ, làm bài tập trước khi đến lớp.
III. Tiến trình giờ dạy:
1. Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu khái niệm phép tịnh tiến, các tính chất và biểu thức tọa độ của ptt. 2. Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung HĐTP1. (Dựng hình) Bài tập 1.
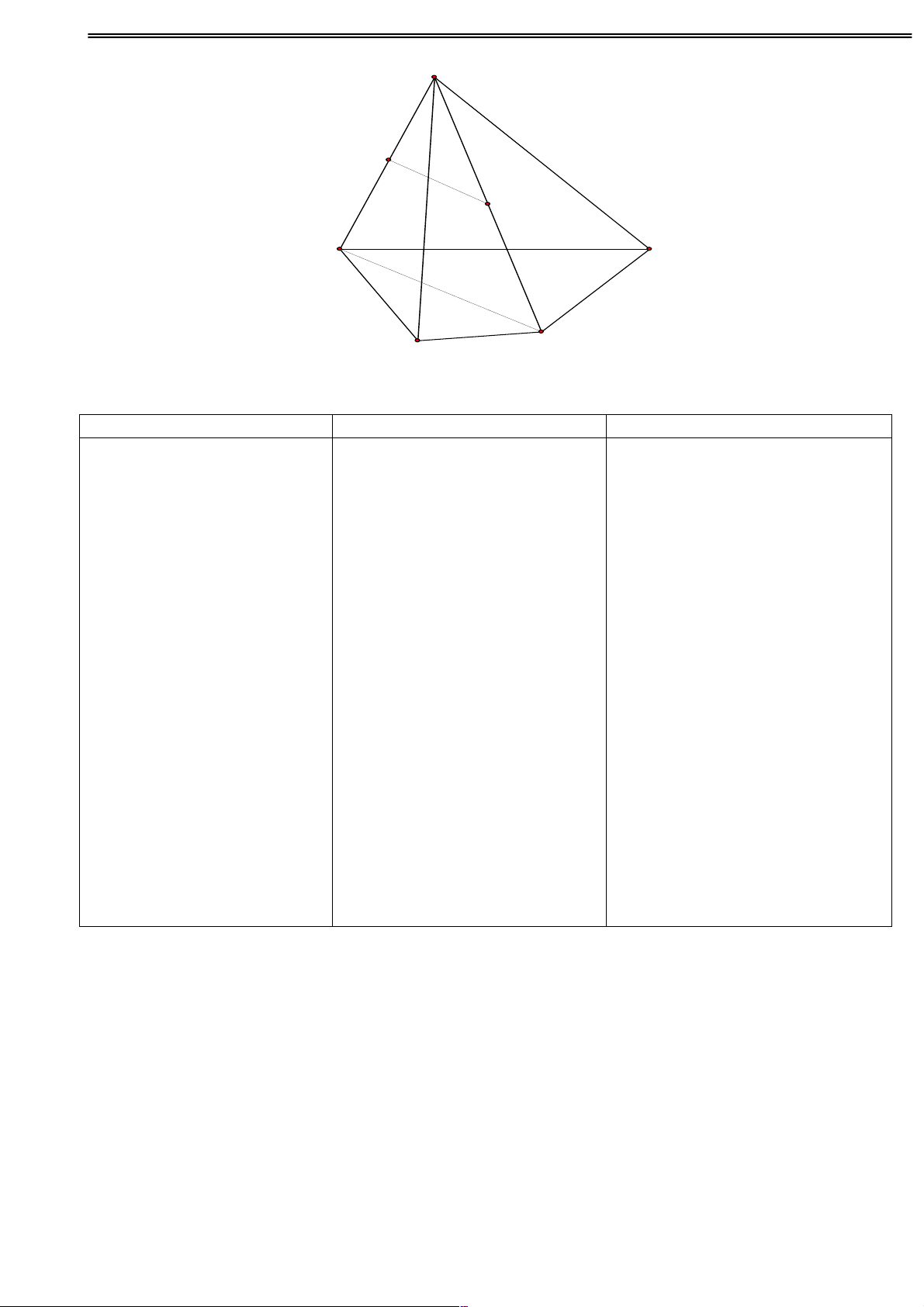
Cho tam giác ABC đều, G là trọng tâm. Dựng
ảnh của tam giác ABC qua phép tịnh tiến theo véctơ !!!" AG
HĐTP2: (Bài tập tọa Bài tập 2: độ)
Trong mp Oxy cho điểm M(0;-2), đường
GV nêu đề và ghi lên
thẳng d có phương trình 3x – y – 3 = 0 và
bảng, cho HS các nhóm
đường tròn ©: x2 + y2 = 1.
thảo luận tìm lời giải và
a) Tìm tọa độ điểm M’ là ảnh điểm M qua ptt !
gọi HS đại diện lên bảng
HS các nhóm thảo luận để theo vectơ v = (2;- ) 3 b)Viết phương
trình bày kết quả của tìm lời giải. nhóm.
HS đại diện trình bày lời
trình của đường thẳng d’ là ảnh của đường
thẳng d qua phép tịnh tiến theo vectơ
Gọi HS nhận xét, bổ sung giải trên bảng (có giải thích) ! (nếu cần).
HS nhận xét, bổ sung và sửa v = (2;- ) 3
GV nhận xét, bổ sung và chữa ghi chép.
c)Viết phương trình của đường tròn (C’) là
nêu kết quả đúng (nếu HS
ảnh của đường tròn © qua phép tịnh tiến theo !
không trình bày đúng kết HS trao đổi và rút ra kết quả vectơ v = (2;- ) 3 quả) … Lời giải gợi ý:
a)M’(x’;y’) là ảnh điểm M qua ptt theo vectơ ! v = (2;- ) 3 Ta có x’ = 0+2=2 Hướng dẫn câu c) y’=-2+(-3)=-5 b)
Để vẽ 1 đường tròn ta cần
có được yếu tố nào?
d’ là ảnh của đường thẳng d qua phép tịnh ! Để viết Phương trình
tiến theo vectơ v = (2;- ) 3
đường tròn ta cần tìm gì?
ta có d’//d hoặc d’º d. Sau khi có tâm và bán Do đó d’ có pt dạng : kính viết pt ntn?
Học sinh xác định tâm và 3x – y + t = 0 3
Giáo án Tự chọn 11
Để tìm được tâm và bán
bán kính của (C).
Lấy điểm K(1;0) thuộc d, K’(x’;y’) là ảnh của
kính của (C’) ta cần làm
Từ đó tìm tâm và bán kính
K qua ptt trên thì K’(3;-3) và K’ thuộc d’ nên gì?
(C’) suy ra Phương trình
thay vào Phương trình ta được t = -12 (C’).
Vậy Phương trình d’ là: 3x – y – 12 = 0 . Củng cố:
- Nhắc lại các kiến thức đã ôn tâp.
BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong mặt phẳng Oxy, cho điểm M(–2; 1). Tìm tọa độ của điểm N sao cho M là ảnh của N qua phép !
tịnh tiến vector v = (–3; 2). A. (1; –1) B. (1; 3) C. (–1; –1) D. (–1; 1) !
Câu 2. Trong mp Oxy cho v = (2;1) và điểm A(4;5). Hỏi A là ảnh của điểm nào trong các điểm sau đây qua !
phép tịnh tiến v : A. (1;6) B. (2;4) C. (4;7) D. (3;1).
Câu 3. Cho ñöôøng thaúng (d): x - 2y = 3. Phöông trình ñöôøng thaúng (d’) laø aûnh cuûa (d) qua pheùp !
tònh tieán vectô v = (5; 2) - laø: a) x – 2y + 3 = 0
b) x – 2y – 10 = 0 c) 2x – y – 3 = 0 d) x – 2y – 12 = 0 !"
Câu 4. Cho v ( 4;
- 2) và đường thẳng D ': 2x - y -5 = 0. Hỏi D ' là ảnh của đường thẳng D nào qua T!": v
A/. D : 2x - y -13 = 0 . B/. D : x - 2y - 9 = 0 . C/. D : 2x + y -15 = 0 . D/. D : 2x - y -15 = 0 .
Câu 5. Cho hình bình hành ABCD, Khi đó :
A. B = T!!!" (C)
B. B = T!!!" (C) AD DA
C. B = T!!!" ( A)
D. B = T!!!" (C) . CD AB
Câu 6. Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x² + y² – 2x + 4y – 4 = 0. Tìm ảnh của (C) !
qua phép tịnh tiến vectơ v = (–2; 5)
A. (x – 3)² + (y – 3)² = 4
B. (x – 3)² + (y + 7)² = 9
C. (x + 1)² + (y – 3)² = 4 D. (x + 1)² + (y + 7)² = 9 4
Giáo án Tự chọn 11
TIẾT 3. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN I.Mục tiêu 1) Kiến thức
Học sinh nắm chắc về các phương trình lượng giác CƠ BẢN – CÔNG THỨC NGHIỆM . 2) Kĩ năng
- HS có kĩ năng giải các bài tập về một số phương trình lượng giác CƠ BẢN
- áp giải một số dạng bài tập co liên quan 3) Thái độ
HS có sự ham hiểu biết , đức tính cẩn thận , chính xác II. Trọng tâm:
Học sinh nắm chắc về các phương trình lượng giác thường gặp . III. Chuẩn bị:
1)Thầy: SGK, SGV, SBT
2)Trò: Ôn lại các kiến thức về phương trình lượng giác thường gặp
IV.Tiến trình bài học 1) Ổn định lớp 2) Kiểm tra miệng
Nêu cách giải pt: sinx = a , cosx=a, tanx=a
3) Tiến trình bài học
Hoạt động của GV và HS Nội dung
Hoạt động1 :Giải phương trình Giải phương trình 2sinx - 3 = 0 1. 2sinx - 3 = 0 Nêu cách giải pt sinx = a Û sinx = 3 /2 ì p = + p p x k2 ï Û ï sinx = sin Û 3 í 3 2p ïx =
+ k2p ,k Î Z ïî 3 Hoạt động2 2. 3 tanx + 1 = 0 Giải phương trình Û tanx = -1/ 3 3 tanx + 1 = 0 p Nêu cách giải pt tanx = a Û tanx = tan(- ) 6 Hoạt động 3
Û x = -p /6 + k p , kÎ Z Giải phương trình 3. cosx = -1/ 2 = 2 cosx + 1 = 0 p p Û 3 cosx = - cos = cos Nêu cách giải pt cosx = a 4 4 p Û 3 x= ±
+ k2p ,k Î Z Hoạt động 4 4 Giải phương trình 4. 3cotx + 1 = 0 3cotx + 1 = 0 Û cotx = - 1/3
Nêu cách giải pt cotx = a
Û x = arccot(-1/3) + kp , k Î !
Hoạt động của GV và HS Nội dung
Hoạt động 5 :Giải phương trình Giải phương trình x 1 x 1 cos = - 1. cos = - 2 2 2 2 Nêu cách giải pt cosx = a x p 2p Û cos = - cos = cos 2 3 3 5
Giáo án Tự chọn 11 x p p
Û = ± 2 + k2 ( k Î! ) là nghiệm 2 3
Hoạt động 6: Giải phương trình 3 sin 3x = 3 2. sin 3x = 2 2 Nêu cách giải pt sinx = a ì p = + p p x k2 ïï Û sin3x = sin Û 3 í (k Î !)
Hoạt động 7 Giải phương trình 3 2p ïx = + k2p cos7x = 0 ïî 3 3. cos7x = 0 p Û 7x = + kp 2 p p Û x =
+ k (k Î !) là nghiệm
Hoạt động 4 Giải phương trình 14 7 p p 2 2 4. cos( x - ) = cos( x - ) = 3 2 3 2 p p Û cos( x - ) = cos 3 4 ì 7p x = + k2p
Hoạt động 5 Giải phương trình ï Û ï 12 í (k Î !) là nghiệm 3 Sin(2x + 5) = p ï = + p 2 x k2 ïî 12 3
5. sin(2x + 5) = ( pt vô nghiệm) 2
4) Câu hỏi và bài tập củng cố:
- Câu hỏi 1: Công thức tìm nghiệm pt lượng giác cơ bản theo sin, cos, tan và cot * Đáp án câu hỏi 1: SGK
BÀI TẬP TRẮC NGHIỆM
Câu 1: Phương trình lượng giác .tan x = - 3 có nghiệm là : p p p p A. x = + kp B. x = - + k2p C. x = + kp D. x = - + kp 3 3 6 3 x 3
Câu 2: Giải phương trình lượng giác : cos = - có nghiệm là 2 2 5p p p p A. x = ± + 5
k2p B. x = ± + 5 k2p C. x = ± + 5 k4p D. x = ± + k4p 3 6 6 3 æ 2x p ö
Câu 3: Phương trình : sin - = 0 có nhghiệm là : ç ÷ è 3 3 ø 5p k3p p p k p A. x = ± +
B. x = kp C. x = + 3 kp D. x = + 2 2 3 2 2
Câu 4: Giải phương trình : 2
tan x = 3 có nghiệm là : p p p A. x = ± + p k B. x = ± + kp C. vô nghiệm D. x = + kp 3 6 6 1
Câu 5: Phương trình lượng giác: cot x = có nghiệm là: 3 p p p A. x = + kp B. x = + kp C. x = + k2p D.Vô nghiệm 6 3 3 6
Giáo án Tự chọn 11
Tiết 4. BÀI TẬP KHÁI NIỆM PHÉP DỜI HÌNH VÀ HAI HÌNH BẰNG NHAU I. MỤC TIÊU Qua bài học HS cần: 1. Về kiến thức:
- Củng cố cho học sinh kiến thức về các phép biến hình như phép tịnh tiến, phép quay
- Tính chất chung của các phép dời hình. 2. Về kỹ năng:
- Dùng phép biến hình để chứng minh một số tính chất hình học, dựng hình
3. Về tư duy và thái độ:
- Về tư duy: Biết quan sát và phán đoán chính xác, biết quy lạ về quen.
- Về thái độ: Cẩn thận, chính xác, tích cực hoạt động, trả lời các câu hỏi.
II. CHẨN BỊ CỦA GV VÀ HS
GV: Phiếu học tập, giáo án, các dụng cụ học tập.
HS: Chuẩn bị bài tập phép đối xứng tâm và phép quay của SGK và SBT, chuẩn bị bảng phụ (nếu cần).
III. PHƯƠNG PHÁP DẠY HỌC
Về cơ bản là gợi mở, vấn đáp và kết hợp với điều khiển hoạt động nhóm.
IV. TIẾN TRÌNH BÀI HỌC 1. Ổn định tổ chức: - Kiểm tra sĩ số. 2. Kiểm tra bài cũ:
Câu hỏi: Các phép biến hình đã học có tính chất chung nào ? 3. Bài mới:
+Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung
HĐ1:(Bài tập về chứng
minh một đẳng thức bằng
cách sử dụng kiến thức
HS thảo luận theo nhóm để tìm lời
phép dời hình) giải. Bài tập 1:
GV nêu đề và ghi lên bảng.
Cử đại diện lên bảng trình bày lời Chứng minh rằng nếu phép dời hình
Cho HS thảo luận theo giải.
biến 3 điểm O, A, B lần lượt thành 3
nhóm để tìm lời giải.
HS nhận xét, bổ sung và sửa chữa điểm O’, A’, B’ thì ta có:
GV gọi HS đại diện lên ghi chép.
B = T!!!" ( A)
bảng trình bày lời giải.
HS trao đổi để rút ra kết quả: CD
với t là một số tùy ý.
Gọi HS nhận xét, bổ sung
Vì O’A’=OA, O’B’=OB, (nếu cần)
A’B’=AB và AB2=B=T!!!"(C) AD nên ta có:
GV nhận xét, nêu lời giải
đúng (nếu HS không trình
bày đúng lời giải) HĐ2: Bài tập 2: HĐTP1:
Cho hình vuông ABCD tâm O, M là
GV nêu đề và ghi lên bảng.
trung điẻm của AB, N là trung điểm
Cho HS các nhóm thảo luận HS thảo luận theo nhóm để tìm lời của OA. Tìm ảnh của tam giác AMN để tìm lời giải.
giải và cử đại diện lên bảng trình qua phép quay tâm O góc quay 900.
Gọi HS đại diện nhóm lên bày lời giải.
bảng trình bày lời giải.
HS nhận xét, bổ sung và sửa chữa
Gọi HS nhận xét, bổ sung ghi chép. (nếu cần)
HS trao đổi để rút ra kết quả:
GV nhận xét, bổ sung và
Phép quay tâm O góc quay 900
nêu lời giải đúng (nếu HS
biến A thành D, biến M thành M’
không trình bày đúng lời
là trung điểm của AD, biến N giải)
thành N’ là trung điểm của OD.
Do đó nó biến tam giác AMN HĐTP2:
thành tam giác DM’N’. 7
Giáo án Tự chọn 11
GV nêu đề và ghi lên bảng, Bài tập 3:
cho HS các nhóm thảo luận
Trong mp Oxy cho đường thẳng d có
tìm lời giải và gọi HS đại
HS các nhóm thảo luận để tìm lời phương trình 3x – y – 3 = 0. Viết
diện lên bảng trình bày kết giải.
phương trình của đường thẳng d’ là quả của nhóm.
HS đại diện trình bày lời giải trên ảnh của đường thẳng d qua phéo dời
Gọi HS nhận xét, bổ sung
bảng (có giải thích)
hình có được bằng cách thực hiện liên (nếu cần).
HS nhận xét, bổ sung và sửa chữa tiếp phép quay tâm O góc quay 90 và
GV nhận xét, bổ sung và ghi chép.
phép tịnh tiến theo vectơ v=(1,3)
nêu kết quả đúng (nếu HS
không trình bày đúng kết
HS trao đổi và rút ra kết quả … quả) HĐTP3:
HS các nhóm thảo luận để tìm lời Bài tập 4. Trong mặt phẳng Oxy, cho !"
GV nêu đề và ghi lên bảng, giải. v = (2;5) và đường tròn
cho HS các nhóm thảo luận HS đại diện trình bày lời giải trên 2 2
tìm lời giải và gọi HS đại
bảng (có giải thích)
(C):(x - 2) +( y - ) 1 = 25 . Gọi (C ')
diện lên bảng trình bày kết
HS nhận xét, bổ sung và sửa chữa là ảnh của (C) qua phép tịnh tiến T!" , quả của nhóm. ghi chép. v
Gọi HS nhận xét, bổ sung
(C '') là ảnh của (C ') qua phép quay (nếu cần).
HS trao đổi và rút ra kết quả Q
. Viết phương trình (C '').
GV nhận xét, bổ sung và ( ,90o O )
nêu kết quả đúng (nếu HS
không trình bày đúng kết quả)
HĐ3: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại định nghĩa các phép dời hình và tính chất của nó.
*Áp dụng: Giải bài tập sau:
*Hướng dãn học ở nhà:
-Xem lại các bài tập đã giải.
- Ôn tập lại và ghi nhớ các định nghĩa của phép dời hình 8
Giáo án Tự chọn 11
PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP TIẾT 5 I.Mục tiêu:
Qua chủ đề này HS cần:
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của phương trình lượng giác và
bước đầu hiểu được một số kiến thức mới về phương trình lượng giác trong chương trình nâng cao chưa
được đề cập trong chương trình chuẩn.
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về phương trình lượng giác. Thông qua việc
rèn luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số
kiến thức mới trong chương trình nâng cao.
3)Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:
-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
*Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Bài mới: (Một số phương trình lượng giác thường gặp)
Hoạt động của GV
Hoạt động của HS Nội dung
HĐ1( ): (Bài tập về phương
Bài tập 1: Giải các phương trình sau:
trình bậc hai đối với một hàm a) 2cos2x-3cosx+1=0; số lượng giác)
HS suy nghĩ và trả lời… b)sin2x+sinx+1=0;
GV để giải một phương trình 2 )
c 3 tan x - (1+ 3)t anx+1=0.
bậc hai đối với một hàm số
lượng giác ta tiến hành như HS chú ý theo dõi. thế nào?
GV nhắc lại các bước giải.
HS thảo luận theo nhóm để
GV nêu đề bài tập 1, phân
tìm lời giải và cử đại diện báo
công nhiệm vụ cho các nhóm, cáo.
cho các nhóm thảo luận để
HS nhận xét, bổ sung và sửa tìm lời giải. chữa, ghi chép.
GV gọi HS đại diện các nhóm HS trao đổi và cho kết quả: trình bày lời giải. p
Gọi HS nhận xét, bổ sung a)x=k2 p ;x= ± + 2 k . p 3 (nếu cần) p
GV nêu lời giải đúng… b)x= - + 2 k ; p 2 p p c) x = + k , p x = + k . p 4 6
HĐ2 ( ): (Bài tập về phương
Bài tập 2: Giải các phương trình sau:
trình bậc nhất đối với sinx và a)3cosx + 4sinx= -5; cosx) b)2sin2x – 2cos2x = 2 ;
Phương trình bậc nhất đối với HS suy nghĩ và trả lời… c)5sin2x – 6cos2x = 13.
sinx và cosx có dạng như thế nào?
-Nêu cách giải phương trình
HS nêu cách giải đối với
bậc nhất đối với sinx và cosx. phương trình bậc nhất đối với
GV nêu đề bài tập 2 và yêu sinx và cosx…
cầu HS thảo luận tìm lời giải.
Gọi HS nhận xét, bổ sung
HS thảo luận theo nhóm và cử (nếu cần) đại diện báo cáo.
HS nhận xét, bổ sung và sửa
GV nêu lời giải đúng… chữa ghi chép. 9
Giáo án Tự chọn 11
HS trao đổi và rút ra kết quả: 3 4 ) a a + (2k +1) , p Ìv i cosa= µ v sina= 5 5 5p 13p ) b x = + k , p x = ; 24 24 ) c ´ V nghi÷m. *Củng cố ( ):
Củng cố lại các phương pháp giải các dạng toán.
*Hướng dẫn học ở nhà( ):
-Xem lại các bài tập đã giải.
-Làm thêm các bài tập sau: Bài tập 1: a)tan(2x+1)tan(5x-1)=1; p b)cotx + cot(x + )=1. 3 Bài tập 2: a)2cos2x + 2 sin4x = 0; b)2cot2x + 3cotx +1 =0. 10
Giáo án Tự chọn 11
TIẾT 6. LUYỆN TẬP PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP I.Mục tiêu 1) Kiến thức
Học sinh nắm chắc về các phương trình lượng giác thường gặp . 2) Kĩ năng
- HS có kĩ năng giải các bài tập về một số phương trình lượng giác thườnggặp
- áp giải một số dạng bài tập co liên quan 3) Thái độ
HS có sự ham hiểu biết , đức tính cẩn thận , chính xác II. Trọng tâm
Học sinh nắm chắc về các phương trình lượng giác thường gặp . III. Chuẩn bị:
1)Thầy: SGK, SGV, SBT
2)Trò: Ôn lại các kiến thức về phương trình lượng giác thường gặp IV. Tiến trình:
1) Ổn định lớp(1 phút)
2) Kiểm tra miệng (5 phút)
Nêu các công thức cộng ( 8 đ) sin(a+b)=sinacosb+sinbcosa sin(a-b)=sina.cosb-sinb.cosa cos(a+b)=cosa.cosb-sina.sinb cos(a-b)=cosa.cosb+sina.sinb 3) Bài mới
Hoạt động của GV và HS Nội dung Họat động 1: Gỉai phương trình sau:
GV: Cho học sinh nhận dạng pt, a=?, b=?, 1. sinx - 3 cosx = 1. c=? HS: Trả lời
GV: Cho hs giải tại chổ, gọi một hs lên bảng Û (- )2 3 +1 .sin(x+a) = 2 (1) giải HS: Lên bảng trình bày 1 3 với cosa= , sina= - .
GV: Đánh giá và chỉnh sửa. 2 2 p Từ đó lấy a= - 3 é 5p = + p p x k2 2 ê 12 (1) Û sin(x - ) = Û ê 3 2 11p êx =
+ k2p ,(k Î Z) ê ë 12 2. 2cos2x – sin2x = 1 Û -sin2x+2cos2x=1 1 - 2 Hoạt động 2: Giải pt
Û 5 sin (2x +a )=1(vớicosa= ,sina= )
Cho Hs giải GV nhận xét, sửa sai và cho 5 5 điểm
3. 2sin2x -5sinx.cosx – cos2x = -2
Ta nhaän thaáy cosx = 0 coù khoâng phaûi laø Hoạt động 3
nghieäm cuûa phöông trình .
GV yêu cầu HS xét xem cosx = 0 có phải là Neân cosx ¹ 0 thì ta coù theå chia 2 veá cuûa
nghiệm của phương trình không ?
phöông trình cho cos2x ta ñöôïc
+ Nếu cosx ¹ 0 thì ta có thể chia 2 vế của 2 2
2 tan x - 5tan x -1 = -
phương trình cho cos2x để đưa phương trình 2 cos x
đã cho về thành phương trình bậc hai đối 2 2
Û 2 tan x - 5tan x -1 = 2( - 1+ tan x) với tanx. 11
Giáo án Tự chọn 11 2 1 = ?
Û 4 tan x - 5tan x +1 = 0 2 cos x é p é =
Gv yêu cầu HS giải bài tập. tan x 1 x = + kp ê ê 4
GV yêu cầu học sinh lên bảng giải cả lớp Û 1 Û ê k Î ! êtan x = 1 ê
quan sát và nêu nhận xét. ë 4 x = arctan + kp êë 4 Bài tập 4
-Đa ra bài tập 4 , yêu cầu học sinh đọc đề , nêu
Giải phương trình 2sinx(3+sinx )+2cosx(cosx-1) hớng giải =0
-Thực hiện theo yêu cầu của gv Û 6sinx -2cosx =-2
-Tóm tắt lại hớng giải , yêu cầu học sinh thực Û 3sinx –cosx =-1 hiện Û 2 2 3 + (- ) 1 sin(x+a )=-1
-Thực hiện yêu cầu của gv
-Nhận xét, chữa bài trên bảng ? Û 1 sin(x+a )=-
-Quan sát , rút ra nhận xét 10
-Nhận xét, chữa bài của học sinh , củng cố kiến é 1 thức
êx + a = ar sin(- ) + k p 2 10
-Nghe, ghi , chữa bài tập , củng cố kiến thức Û ê ê 1 êx + a = p - arcsin(- ) = k p 2 ë 10 é 1 êx = arcsin(- ) - a + k2p Û ê 10 ê 1 êx = p - arcsin(-
) - a + k2p , k Î Z ë 10 3 1 Với cosa = ;sina = - 10 10
4) Câu hỏi, bài tập củng cố:
- Câu hỏi 1: Công thức tìm nghiệm pt lượng giác cơ bản theo sin, cos, tan và cot. BÀI TẬP TRẮC NGHIỆM
Câu 1: Giải phương trình 3 sin 2x - cos2x + 1 = 0 éx = kp éx = kp éx = 2kp éx = kp A. ê p (kÎ!) B. ê 2p (kÎ!) C. ê 2p (kÎ!) D. ê 2p (kÎ!) êx = + kp êx = + 2kp êx = + 2kp êx = + kp êë 3 êë 3 êë 3 êë 3
Câu 2. Nghiêm của pt 3.cos2x = – 8.cosx – 5 là: p
A. x = kp B. x = p + k2p C. x = k2p D. x = ± + k2p 2
Câu 3: Nghiệm của phương trình 2
2cos x + sin x +1 = 0 (với k Î ! ) là p p
A. x = - + k2p B. x = + k2p
C. x = kp
D. x = k2p 2 2
Câu 4: Phương trình sin x + cos x = 2 sin 5x (với k Î ! ) có nghiệm là: p p p p π π π π p p p p p p p p A.
+ k , + k B. + k , + k C. + k , + k D. + k , + k 16 2 8 3 4 2 6 3 12 2 24 3 18 2 9 3
Bài 5. Giải phương trình os
c 2x + cos x + 1 = 0 A. p 2p p p x 2 = + k2p ,x = ± + kp
B. x = + kp ,x = + k2p 2 3 2 3 C. p 2p 7 p p x 2 = + k3p ,x = ± + k p
D. x = + kp ,x = ± + k2p 2 3 2 2 3 12
Giáo án Tự chọn 11
Tiết 7 . PHÉP VỊ TỰ I. Mục tiêu:
Qua chủ đề này HS cần: 1. Về Kiến thức:
Làm cho HS hiểu sâu sắc hơn và vận dụng được định nghĩa phép vị tự để vẽ hình, vận dụng được các
tính chất để giải bài tập.. 2. Về kỹ năng:
Tăng cường rèn luyện kỹ năng giải toán về phép vị tự: Vẽ hình, tìm tọa độ của điểm, tìm tâm vị tự của hai đường tròn.
3. Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị:
1. GV: Giáo án, các bài tập và phiếu học tập,…
2. HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III. Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
1. Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu khái niệm phép đồng dạng, phép vị tự,…
+Nêu các tính chất của các phép đồng dạng,… 2. Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung HĐ1: Bài tập1:
HĐTP1: (Bài tập về phép
HS các nhóm thảo luận để tìm lời giải Trong mp Oxy cho đường thẳng d vị tự)
và cử đại diện lên bảng trình bày kết
có phương trình 3x + 2y – 6 = 0.
GV nêu đề và ghi lên bảng,
quả của nhóm (có giải thích).
Hãy viết phương trình của đường
cho HS các nhóm thảo luận
HS nhận xét, bổ sung và sửa chữa ghi thẳng d’ là ảnh của d qua phép vị
để tìm lời giải. chép…
tự tâm O tỉ số k = -2
Gọi HS đại diện trình bày
HS trao đổi để rút ra kết quả: lời giải.
Qua phép vị tự đường thẳng d’ song
Gọi HS nhận xét, bổ sung
song hoặc trùng với d nên phương (nếu cần)
trình của nó có dạng 3x+2y+c =0
GV nhận xét và nêu kết quả
Lấy M(0;3) thuộc d. Gọi M’(x’,y’) là
đúng (nếu HS không trình
ảnh của M qua phép vị tự tâm O, tỉ số bày đúng kết quả) k = -2. Ta có: !!!!" !!!!" !!!!"
OM = (0,3),OM ' = 2 - OM ìx' = 0 Þ í îy' = 2 - .3 = 6 -
Do M’ thuộc d’ nên ta có: 2(-6) +c = 0. Do đó c = 12
Vậy phương trình của đường thẳng d’ là: 3x + 2y + 12 = 0. Bài tập 2:
HĐTP2: (Bài tập áp dụng
Trong mp Oxy cho đường thẳng d về phép vị tự)
HS các nhóm thảo luận để tìm lời giải có phương trình 2x + y – 4 = 0.
GV nêu đề và ghi lên bảng,
vàcử đại diện lên bảng trình bày kết
a)Hãy viết phương trình của
cho HS các nhóm thảo luận
quả của nhóm mình (có giải thích)
đường thẳng d1 làảnh của d qua
để tìm lời giải và gọi HS đại HS nhận xét, bổ sung và sửa chữa ghi phép vị tự tâm O tỉ số k = 3.
diện lên bảng trình bày kết chép.
b)hãy viết phương trình của quả của nhóm.
HS trao đổi để rút ra kết quả…
đường thẳng d2 là ảnh của d qua
Gọi HS nhận xét, bổ sung
phép vị tự tâm I(-1; 2) tỉsố k = -2. (nếu cần) 13
Giáo án Tự chọn 11
GV nhận xét và nêu kết quả
đúng (nếu HS không trình bày đúng kết quả)
HĐ2 (Bài tập về ứng Bài tập 3:
dụng phép vị tự vào việc
Cho đường tròn (O;R), B,C cố
tìm quỹ tích)
HS các nhóm thảo luận để tìm lời giải định trên (O), A là một điểm thay
GV nêu đề và ghi lên bảng
và cử đại diện lên bảng trình bày lời đổi trên (O).
và cho HS các nhóm thảo
giải của nhóm (có giải thích).
a) Tìm quỹ tích trọng tâm tam
luận để tìm lời giải và gọi
HS nhận xét, bổ sung và sửa chữa ghi giác ABC.
đại diện nhóm lên bảng chép.
b) Tìm quỹ tích trực tâm H của
trình bày kết quả của nhóm. tam giác ABC.
Gọi HS nhận xét, bổ sung (nếu cần)
GV nhận xét, bổ sung và nêu
kết quả đúng (nếu HS không
trình bày dúng kết quả)
3: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại phương pháp giải bài toán sử dụng phép vị ự.
BÀI TẬP TRẮC NGHIỆM
Caâu 1:Cho tam giaùc ABC troïng taâm G,M laø trung ñieåm BC.Trong caùc meänh ñeà sau ñaây, meänh ñeà naøo sai
a)Pheùp vò töï taâm G tæ soá k = -2 bieán ñieåm A thaønh ñieåm M.
b)Pheùp vò töï taâm G tæ soá k = -2 bieán ñieåm M thaønh ñieåm A. 3
c)Pheùp vò töï taâm A tæ soá k = bieán ñieåm G thaønh ñieåm M. 2 1
d)Pheùp vò töï taâm M tæ soá k = bieán ñieåm A thaønh ñieåm G. 3
Câu 2 : Cho tg ABC, G là trọng tâm , gọi A’, B’, C’ lần lượt là trung điểm của BC, AC, AB. Khi đó phép vị
tự biến tg A’B’C’ thành tgABC là. A. V(G,-2) B. V(G, -1/2) C. V(G, 2) D. V(G,1/2)
Câu 3: Nếu A’(-3;10) là ảnh của A qua phép vị tự tâm I(1;4) tỉ số k=2/3 thì tọa độ của A là A. (-5;13) B. (7;-5) C. (-5/3;8) D. (3;1)
4: Trong mp Oxy cho đường thẳng d:x+y-2=0. Hỏi qua phép V
biến d thành đt nào trong các đt sau: (O, 2 - ) A.2x+2y-4=0 B.x+y+4=0 C.x+y-4=0 D.2x+2y=0 14
Giáo án Tự chọn 11
Tiết 8. HOÁN VỊ - CHỈNH HỢP – TỔ HỢP I.Mục tiêu:
a. Kiến thức: Giúp học sinh nắm:
- Phát biểu được các khái niệm hoán vị, chỉnh hợp, tổ hợp.
- Viết được biểu thức tính số các hoán vị, số các chỉnh hợp và số các tổ hợp
- Viết được biểu thức biểu diễn hai tính chất cơ bản của k C n b. Kĩ năng:
- Vận dụng kiến thức về hoán vị, chỉnh hợp, tổ hợp để giải các bài toán liên quan. c. Thái độ:
- Cẩn thận, chính xác trong tính toán, lập luận. II. Trọng tâm:
- Viết được biểu thức tính số các hoán vị, số các chỉnh hợp và số các tổ hợp
- Viết được biểu thức biểu diễn hai tính chất cơ bản của k C n
III. Chuẩn bị:
1)Thầy: SGK, SGV, SBT
2)Trò: công thức tính hoán vị, chỉnh hợp, tổ hợp IV. Tiến trình:
1) Ổn định lớp: (1 phút)
2) Kiểm tra miệng: (5 phút)
Hãy trình bày khái niệm và công thức hoán vị, chỉnh hợp, tổ hợp?
3) Tiến trình bài học:
Hoạt động của giáo viên và học sinh Nội dung bài học
Hoạt động 1: Ôân lại lý thuyết A. Lý thuyết:
GV: Hệ thống lại kiến thức B. Bài tập:
Bài 1: Có bao nhiêu cách xếp bốn bạn A, B, C, D
vào bốn chiếc ghế kê thành hàng ngang? Giải
Mỗi cách xếp cho ta một hoán vị của bốn bạn và
ngược lại. Vậy số cách xếp là P4=4!=24 (cách)
Bài 2: Có bao nhiêu số nguyên dương gồm 5 chữ số
Hoạt động 2: Giải bài tập
khác không và khác nhau (đôi một) ?
GV: Yêu cầu HS giải bài 1 5 9! HS: Giải … Giải A = = 9.8.7.6.5 = 15120 (số) 9 4!
GV: HD (nếu cần) nêu định nghĩa, công thức Bài 3: Cần phân công ba bạn từ 1 tổ có 10 bạn để hoán vị
trực nhật. Hỏi có bao nhiêu cách phân công khác nhau?
GV: Yêu cầu HS giải bài 2 Giải HS: Giải …
Kết quả của sự phân công là một nhóm gồm ba bạn,
GV: HD (nếu cần) nêu định nghĩa, công thức tức là một tổ hợp chập 3 của 10 bạn. Vậy số cách chỉnh hợp phân công là: 10!
GV: Yêu cầu HS giải bài 3 3 C = =120 (cách) 10 3!(10 - 3)! HS: Giải …
GV: HD (nếu cần) nêu định nghĩa, công thức tổ hợp Hđ2
Hoạt động của gv và HS
Nội dung kiến thức Hoạt động 1:
Bài tập 1 Có bao nhiêu cách để xếp 5 hs
- Đưa ra bài tập số 1, yêu cầu học sinh đọc kỹ đề bài, suy
nam và 5 học sinh nữ vào 10 chiếc ghế nghĩ, nêu hướng giải.
được kê thành một hàng sao cho hs nam
- Rõ yêu cầu của gv, suy nghĩ , thực hiện .
và nữ ngồi xen kẽ. Giải 15
Giáo án Tự chọn 11
Đánh số các ghế từ 1 đến 10
- Tóm tắt lại hướng giải, yêu cầu học sinh thực hiện.
TH1 : Hs nam ngồi vào các ghế lẻ : có 5! Cách
- Nắm được hướng giải, làm bài tập theo hướng dẫn .
HS nữ ngồi vào ghế chẵn : có 5! Cách Vậy có 5!.5! cách
- Nhận xét kết quả bài toán ?
TH 2 : HS nữ ngồi vào các ghế lẻ : có 5!
- Quan sát bài toán, rút ra nhận xét. Cách
HS Nam ngồi vào ghế chẵn : có 5!
- Nghe, ghi, chữa bài tập Cách Vậy có 5!.5! cách
- Nhận xét, chữa bài tập cho hs
Vậy số cách xếp chỗ ngồi là 5!.5!+5!.5!= Hoạt động
Bài tập 2 Có bao nhiêu cách chọn 5
- Đưa ra bài tập 2, yêu cầu học sinh nghiên cứu đề, suy bóng đèn từ 9 bóng đèn mầu khác nhau nghĩ, nêu hướng giải.
để lắp vào 1 dãy gồm 5 vị chí khác
- Thực hiện theo yêu cầu của gv, nêu hướng giải . nhau. Giải
- Tóm tắt hướng giải, yêu cầu học sinh thực hiện.
Mỗi cách lắp bóng đèn là một chỉnh
- Rõ yêu cầu, thực hiện giải bài tập theo hướng đã định hợp chập 5 của 9.
Vậy số cách lắp bóng là :
- Nhận xét, chữa bài tập cho hs. 5 ! 9
- Nhận nhiệm vụ, giải bài tập theo yêu cầu. A = =15120 9 9 ( - )! 5
4) Câu hỏi, bài tập củng cố:
Cho HS trình bày định nghĩa, định lí: hoán vị, chỉnh hợp, tổ hợp.
5) Hớng dẫn học sinh tự học BT TN
Câu 1: Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có
bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau? A. 34560 B. 17280 C. 120960 D. 744
Câu 2: Lấy hai con bài từ cỗ bài tú lơ khơ 52 con. Số cách lấy là: A. 104 B. 450 C. 1326 D. 2652
Câu 3: Một lớp có 15 học sinh nam và 20 học sinh nữ. Có bao nhiêu cách chọn 5 bạn học
sinh sao cho có đúng 3 học sinh nữ. A. 110790 B. 119700 C. 117900 D. 110970
Câu 4: Trong không gian cho 10 điểm phân biệt trong đó không có bốn điểm nào đồng
phẳng. Từ các điểm trên ta lập được bao nhiêu vectơ khác nhau, không kể vectơ-không? A. 20 B. 60 C. 100 D. 90
Câu 5: Một tổ công nhân có 12 người. Cần chọn 3 người làm tổ trưởng, tổ phó, thành viên.
Hỏi có bao nhiêu cách chọn. A. 1230 B. 12! C. 220 D. 1320 16
Giáo án Tự chọn 11 TIẾT 9
PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG I.Mục tiêu:
Qua chủ đề này HS cần:
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của phép dời hình và phép đồng
dạng trong mặt phẳng và bước đầu hiểu được một số kiến thức mới về phép dời hình và phép đồng dạng
trong chương trình nâng cao chưa được đề cập trong chương trình chuẩn.
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về phép dời hình và phép đồng dạng. Thông
qua việc rèn luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu
một số kiến thức mới trong chương trình nâng cao.
3)Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:
-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III.Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu khái niệm phép đồng dạng, phép vị tự,…
+Nêu các tính chất của các phép đồng dạng,… +Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung HĐ1: Bài tập1:
HĐTP1: (Bài tập về phép vị HS các nhóm thảo luận để tìm lời Trong mp Oxy cho đường thẳng d có tự)
giải và cử đại diện lên bảng trình phương trình 3x + 2y – 6 = 0. Hãy
GV nêu đề và ghi lên bảng,
bày kết quả của nhóm (có giải
viết phương trình của đường thẳng d’
cho HS các nhóm thảo luận thích).
là ảnh của d qua phép vị tự tâm O tỉ
để tìm lời giải.
HS nhận xét, bổ sung và sửa chữa số k = -2
Gọi HS đại diện trình bày ghi chép… lời giải.
HS trao đổi để rút ra kết quả:
Gọi HS nhận xét, bổ sung
Qua phép vị tự đường thẳng d’ (nếu cần)
song song hoặc trùng với d nên
GV nhận xét và nêu kết quả
phương trình của nó có dạng
đúng (nếu HS không trình 3x+2y+c =0
bày đúng kết quả)
Lấy M(0;3) thuộc d. Gọi M’(x’,y’)
là ảnh của M qua phép vị tự tâm
O, tỉ số k = -2. Ta có: !!!!" !!!!" !!!!"
OM = (0,3),OM ' = 2 - OM ìx' = 0 Þ í îy' = 2 - .3 = 6 -
Do M’ thuộc d’ nên ta có:
2(-6) +c = 0. Do đó c = 12
Vậy phương trình của đường
thẳng d’ là: 3x + 2y + 12 = 0.
HĐTP2: (Bài tập áp dụng
về phép vị tự)
HS các nhóm thảo luận để tìm lời 17
Giáo án Tự chọn 11
GV nêu đề và ghi lên bảng,
giải vàcử đại diện lên bảng trình Bài tập 2:
cho HS các nhóm thảo luận bày kết quả của nhóm mình (có
Trong mp Oxy cho đường thẳng d có
để tìm lời giải và gọi HS đại giải thích)
phương trình 2x + y – 4 = 0.
diện lên bảng trình bày kết
HS nhận xét, bổ sung và sửa chữa a)Hãy viết phương trình của đường quả của nhóm. ghi chép.
thẳng d1 làảnh của d qua phép vị tự
Gọi HS nhận xét, bổ sung
HS trao đổi để rút ra kết quả…
tâm O tỉ số k = 3. (nếu cần)
b)hãy viết phương trình của đường
GV nhận xét và nêu kết quả
thẳng d2 là ảnh của d qua phép vị tự
đúng (nếu HS không trình
tâm I(-1; 2) tỉ số k = -2.
bày đúng kết quả) HĐ2: Bài tập 3:
HĐTP1: (Bài tập về phép
HS các nhóm thảo luận để tìm lời Trong mp Oxy cho đường thẳng d có đồng dạng)
giải và cử đại diện lên bảng trình phương trình x + y -2 = 0. Viết
GV nêu đề và ghi lên bảng
bày lời giải của nhóm (có giải
phương trình đường thẳng d’ là ảnh
và cho HS các nhóm thảo thích).
của d qua phép đồng dạng có được
luận để tìm lời giải và gọi
HS nhận xét, bổ sung và sửa chữa bằng cách thực hiện liên tiếp phép vị
đại diện nhóm lên bảng ghi chép. 1
trình bày kết quả của nhóm. HS trao đổi để rút ra kết quả:
tự tâm I(-1;-1) tỉ số k = và phép 2
Gọi HS nhận xét, bổ sung
Gọi d1 là ảnh của d qua phép vị tự quay tâm O góc quay -450. (nếu cần) 1
GV nhận xét, bổ sung và
tâm I(-1;-1) tỉ số k = . Vì d1 song 2
nêu kết quả đúng (nếu HS
song hoặc trùng với d nên phương
không trình bày dúng kết
trình của nó có dạng: x + y +c = quả) 0
Lấy M(1;1) thuộc đường thẳng d=
thì ảnh của nó qua phép vị tự nói
trên là O thuộc d1.
Vậy phương trình của d1 là:
x+y=0. Ảnh của d1 qua phép quay
tâm O góc quay -450 là đường
thẳng Oy có phương trình: x = 0.
HĐTP2: (Bài tập áp dụng) Bài tập 4:
GV nêu đề bài tập và ghi lên HS thảo luận theo nhóm để rút ra Trong mp Oxy cho đường tròn (C) có
bảng, cho HS các nhóm
kết quả và cử đại diện lên bảng
phương trình (x-1)2 +(y-2)2 = 4. Hãy
thảo luận để tìm lời giải và
trình bày lời giải (có giải thích)
viết phương trình đường tròn (C’) là
gọi HS đại diện nhóm lên
HS nhận xét, bổ sung và sửa chữa ảnh của (C) qua phép đồng dạng có
bảng trình bày lời giải. ghi chép.
được bằng cách thực hiện liên tiếp
GV gọi HS nhận xét, bổ
HS trao đổi để rút ra kết quả:…
phép vị tự tâm O tỉ số k = -2 và phép sung (nếu cần)
tịnh tiến theo vec tơ v=(3,-5)
GV nhận xét, bổ sung và
nêu lời giải đúng (nếu HS
không trình bày đúng lời giải )
HĐ3: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại định nghĩa các phép dời hình, phép đồng dạng và tính chất của nó.
*Hướng dãn học ở nhà:
-Xem lại các bài tập đã giải trong tiết TCH1 và TCH2.
- Ôn tập lại và ghi nhớ các định nghĩa của phép dời hình và phép đồng dạng. 18
Giáo án Tự chọn 11
Tiết 10 : CÔNG THỨC NHỊ THỨC NIUTƠN
I.Chuẩn kiến thức kỹ năng 1.Kiến thức
- Nhằm củng cố, khắc sâu các kiến thức về tổ hợp và công thức nhị thức Niutơn. 2.Kĩ năng.
- Biết làm các dạng bài tập liên quan đến tổ hợp và khai triển nhị thức.
- Đặc biệt là một số bài tập có liên quan đến thực tế . 3. Tư duy_ Thái độ
- Liên hệ được với nhiều vấn đề trong thực tiễn.
- Cẩn thận chính xác trong việc làm và trình bày lời giải.
II . Chuẩn bị phơng tiện dạy học.
1)Thầy: SGK, SGV, SBT
2)Trò: Nắm chắc các công thức tính tổ hợp , chỉnh hợp , hoán vị.
- Các kiến thức về công thức nhị thức.
III.Gợi ý phơng pháp dạy học
-Sử dụng phơng pháp tổng hợp
IV.Tiến trình bài học A.Các Hoạt động
- Hoạt động 1 : Ôn tập lí thuyết .
- Hoạt động 2 : Ôn tập và làm các dạng bài tập về tổ hợp và xác suất.
B. Phần thể hiện trên lớp . 1.ổn định lớp. 2.Bài mới
HĐ2: (Bài tập áp Bài tập3: dụng)
Tìm số hạng thứ 5 trong khai
HĐTP1: (Bài tập về 10 æ 2 ö
tìm số hạng thứ k
HS các nhóm xem đề và thảo triễn x + , mà trong khai ç x ÷ è ø
trong khai triển nhị
luận tìm lời giải.
triễn đó số mũ của x giảm dần. thức)
HS đại diện các nhóm lên bảng
GV nêu đề và ghi lên trình bày lời giải (có giải thích) bảng và cho HS các
HS nhận xét, bổ sung và sửa
nhóm thỏa luận tìm lời chữa ghi chép.
giải, gọi HS đại diện
HS trao đổi và rút ra kết quả:
nhóm có kết quả nhanh Số hạng thứ k + 1 trong khai
nhất lên bảng trình bày triễn là: lời giải. -k æ 2 k k 10 ö
Gọi HS nhận xét, bổ t = C x k 1 + 10 ç x ÷ è ø sung (nếu cần). 4
GV nêu lời giải chính - æ 2 4 10 4 ö 2 Þ t = C x = 3360x 5 10 ç ÷ xác (nếu HS không è x ø
trình bày đúng lời giải ) 2 À
V y t = 3360x 5
Bài tập4: Biết hệ số trong khia n
triễn (1+ 3x) là 90. Hãy tìm n
HS các nhóm thảo luận để tìm
lời giải và cử đại diện lên bảng 19
Giáo án Tự chọn 11
HĐTP2: (Tìm n trong trình bày lời giải.
khai triễn nhị thức
HS nhận xét, bổ sung và sửa Niu-tơn) chữa ghi chép.
GV nêu đề và ghi lên
HS trao đổi và rút ra kết quả:
bảng, cho HS các nhóm Số hạng thứ k + 1 cảu khai
thảo luận tìm lời giải. triễn là:
Gọi HS đại diện nhóm t = C 3 k k x k 1 + n ( ) .Vậy số hạng
trình bày lời giải và gọi chứa x2 là: HS nhận xét, bổ sung (nếu cần)
t = C 3x = C 9x 3 n ( )2 2 2 2 n
GV nhận xét, nêu lời Theo bài ra ta có:
giải chính xác (nếu HS 2 C 9=90 Û n = 5 n không trình bày dúng lời giải) 3. Củng cố:
*Hướng dẫn học ở nhà:
- Xem lại kiến thức đã học và những bài tập đã làm BTTN
Câu 1: Hệ số của x6 trong khai triển (2-3x)10 là: 6 4 6 C .2 .( 3 - ) 6 6 4 C .2 .( 3 - ) 4 6 4 C .2 .( 3 - ) 6 4 6 A. 10 B. 10 C. 10 D. C - .2 .3 10
Câu 2: Hệ số của x5 trong khai triển (2x+3)8 là: 3 3 5 C .2 .3 3 5 3 C .2 .3 5 5 3 C - .2 .3 5 3 5 C .2 .3 A. 8 B. 8 C. 8 D. 8 13
Câu 3: Hệ số của x7 trong khai triển æ 1 ö x - là : ç ÷ è x ø 4 A. C - 4 C 3 C - 3 C 13 B. 13 C. 13 D. 13 40 æ 1 ö
Câu 4: Số hạng của x31 trong khai triển x + là : ç ÷ 2 è x ø A. 37 31 C - x B. 3 31 C x C. 2 31 C x D. 4 31 C x 40 40 40 40 6 æ 2 ö
Câu 5: Số hạng không chứa x trong khai triển 2 x + là : ç ÷ è x ø A. 4 2 2 C B. 2 2 2 C C. 4 4 2 C D. 2 4 2 C 6 6 6 6 20
Giáo án Tự chọn 11
Tiết 11. XÁC SUẤT CỦA BIẾN CỐ I. Mục tiêu:
Qua chủ đề này HS cần: 1. Về Kiến thức:
Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của tổ hợp và xác suất và bước đầu
hiểu được một số kiến thức mới về tổ hợp và xác suất chưa được đề cập trong chương trình chuẩn. 2. Về kỹ năng:
Tăng cường rèn luyện kỹ năng giải toán về tổ hợp và xác suất. Thông qua việc rèn
luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm
hiểu một số kiến thức mới trong chương trình nâng cao.
3. Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II. Chuẩn bị:
1. GV: Giáo án, các bài tập và phiếu học tập,…
2. HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III.Tiến trình tiết dạy:
1. Kiểm tra bài cũ: Kết hợp với điều khiển hoạt động nhóm. 2. Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung
HĐ1: (Ôn tập kiến thức I.Ôn tập:
và bài tập áp dụng)
HĐTP: (Ôn tập lại kiến
thức về tổ hợp và công
thức nhị thức Niu-tơn,
tam giác Pascal, xác suất của biến cố…)
HS nêu lại lý thuyết đã học… HĐTP1:
Viết các công thức tính số
GV nêu đề và phát phiếu
các tổ hợp, công thức nhị
HT (Bài tập 1) và cho HS thức Niu-tơn,…
thảo luận tìm lời giải.
Xác suất của biến cố…
Gọi HS đại diện lên bảng
trình bày lời giải.
HS nhận xét, bổ sung …
Gọi HS nhận xét, bổ sung
II. Bài tập áp dụng: (nếu cần)
GV nhận xét, và nêu lời
Bài tập 1: Từ một tổ gồm 6
giải chính xác (nếu HS
bạn nam và 5 bạn nữ, chọn
không trình bày đúng lời
ngẫu nhiên 5 bạn xếp vào bàn giải
HS các nhóm thảo luận và
đầu theo những thứ tự khác
tìm lời giải ghi vào bảng
nhau. Tính xác suất sao cho phụ.
trong cách xếp trên có đúng 3
HĐTP2: (Bài tập về tính HS đại diện nhóm lên bảng bạn nam.
xác suất của biến cố)
trình bày lời giải.
HS nhận xét, bổ sung, sửa 21
Giáo án Tự chọn 11
GV nêu đề và phát phiếu chữa và ghi chép.
HT 2 và yêu cầu HS các
HS trao đổi và rút ra kết quả;
nhóm thảo luận tìm lời 3 2 C .C .5!
Bài tập2: Một tổ chuyên môn 6 5 giải. P( ) A = » 0,433 5 A
gồm 7 thầy và 5 cô giáo,
Gọi HS đại diện các nhóm 11
trong đó thầy P và cô Q là vợ
lên bảng trình bày kết quả HS các nhóm thảo luận và
chồng. Chọn ngẫu nhiên 5 của nhóm.
ghi lời giải vào bảng phụ, cử người để lập hội đồng chấm
Gọi HS nhận xét, bổ sung đại diện lên bảng trình bày thi vấn đáp. Tính xác suất để (nếu cần)
lời giải (có giải thích)
sao cho hội đồng có 3 thầy, 3
GV nhận xét và nêu lời
HS nhận xét, bổ sung, sửa
cô và nhất thiết phải có thầy P
giải chính xác (nếu HS chữa và ghi chép.
hoặc cô Q nhưng không có cả
không trình bày đúng lời
HS trao đổi và rút ra kết quả: hai. giải) HĐ2
Hoạt động của GV
Hoạt động của HS Nội dung
HĐ1: (Ôn tập lại lý thuyết về xác suất) HĐTP1: Gọi HS nhắc lại:
-Công thức tính xác suất;
-Các tính chất của xác suất;
-Hai biến cố độc lập? Bài tập 1: -Quy tắc nhân xác suất;
HS suy nghĩ và trả lời các Lấy ngẫu nhiên một thẻ từ … câu hỏi…
một hộp chứa 20 thẻ được
HĐTP2: (Bài tập áp dụng) HS các nhóm thảo luận để đánh số từ 1 tới 20. Tìm
GV nêu đề bài tập 1 và ghi
tìm lời giải và ghi vào
xác suất để thẻ được lấy lên bảng: bảng phụ ghi số: Nêu câu hỏi:
Hs đại diện lên bảng trình a)Chẵn;
-Để tính xác suất cảu một bày lời giải. b)Chia hết cho 3;
biến cố ta phải làm gì?
HS trao đổi và rút ra kết c)Lẻ và chia hết cho 3.
-Không gian mẫu, số phần quả:
tử của không gian mẫu Không gian mẫu: trong bài tập 1. W = {1,2,...,2 } 0 Þ n(W) = 20
GV cho HS các nhó thảo
Gọi A, B, C là các biến cố
luận và gọi HS đại diện lên tương ứng của câu a), b),
bảng trình bày lời giải.
Gọi HS nhận xét, bổ sung …
GV nhận xét và nêu lời giải đúng.
3.( Củng cố và hướng dẫn học ở nhà) *Củng cố:
-Nêu công thức tính xác suất của một biến cố trong phép thử.
-Nêu lại thế nào là hai biến cố xung khắc.
-Áp dụng giải bài tập sau 22
Giáo án Tự chọn 11
Tiết 12 ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG & MP. I. MỤC TIÊU : 1.Về kiến thức: Giúp học sinh:
Củng cố 4 tiên đề hình học không gian.
Thông qua bài tập, từng bước hướng dẫn học sinh cách biểu diễn hình không gian và
cách chứng minh bài tập hình không gian. Kỹ năng xác định giao tuyến của hai mặt phẳng,
giao điểm đường thẳng với mp, bài toán tìm thiết diện.
Cách chứng minh 3 điểm thẳng hàng.
Giáo dục tính chính xác, chặt chẽ, logic.
2.Về kỹ năng:
Vận dụng tốt các tiên đề để giải các bài tập đơn giản.
Áp dụng được lý thuyết để làm được các bài tập sgk.
3.Về tư duy, thái độ:
Tích cực, lý thú trong tiếp thu kiến thức mới.
Giáo dục tư duy logic, trí tưởng tượng không gian, tập trung, cẩn thận khi làm bài tập. II . CHUẨN BỊ:
Giáo viên: Soạn bài và xem lại giáo án trước giờ lên lớp.
Học sinh: Làm các bài tập trước khi đến lớp, ghi lại những vấn đề cần trao đổi.
III. TIẾN TRÌNH DẠY HỌC:
2.Kiểm tra bài cũ: (5’)
Nêu cách tìm giao tuyến 2 mp?
Nêu cách tìm giao điểm của đt với mp? 3.Bài mới: 25’
Hoạt động 3: (BT9 sgk) Bài 9: Cho HS đọc kỹ đề BT 9
+HS đọc đề và vẽ hình. sgk và vẽ hình. Cho hình chóp S.ABCD có
H1: Nhắc lại thế nào là đáy là hình bình hành +HS trả lời. hình chóp? ABCD. Trong mp đáy vẽ đt
Cho HS đọc kỹ đề và vẽ (d) đi qua A và không song hình bài tập này.
song với các cạnh của hình +HS đọc và vẽ hình.
Nhắc lại cách tìm giao bình hành, d cắt BC tại E.
điểm của đt với mp cho Gọị C’ là một điểm trên SC. HS nắm rõ hơn.
Cho HS tìm cách giải a. Tìm giao điểm M của CD câu và mp(C’AE). 9a. +HS thảo luận tìm ra
b. Tìm thiết diện hình chóp cách giải. với mp(C’AE). Giải:
Gọi HS lên bảng trình b) Gọi F = ' MC Ç SD bày câu 9a?
Gv sửa bài cho HS hiểu. Từ đó ta có thiết diện cần 23
Giáo án Tự chọn 11
H2: Nêu cách tìm thiết tìm là tứ giác AEC’F. diện? +HS trình bày. Hướng dẫn HS làm tiếp 9b +HS chú ý lắng nghe và Nhắc kỹ lại các kiến thấu hiểu. thức cho HS khắc sâu hơn. +HS trả lời. Bài 10: a) Gọi N = SM Ç CD S F Ta có : N = CD Ç (SBM) ' C
Hoạt động 4: (BT 10 b) Gọi O = AC Ç BN. D C d sgk) M Ta có : (SBM) Ç (SAC) =
Gọi 4 hs lần lượt giải 4 E SO. câu. A B c) Gọi I = SO Ç BM. Ta có: I = BM Ç (SAC). d) Gọi R = AB Ç CD, P = 20’ MR Ç SC. Ta có: P = SC Ç (ABM) Þ PM = (SCD) Ç (ABM). IV. CỦNG CỐ, DẶN DÒ: 24
Giáo án Tự chọn 11
Tiết 13 ÔN TẬP CHƯƠNG 2 I. Mục tiêu: 1. Kiến thức:
- Củng cố về hoán vị, chỉnh hợp, tổ hợp.
- Củng cố khai triển nhị thức Newton.
- Củng cố xác suất của các biến cố. 2. Kỹ năng:
- Vận dụng về hoán vị, chỉnh hợp, tổ hợp.
- Khai triển nhị thức Newton.
- Tính xác suất của các biến cố
3. Thái độ: Cẩn thận, chính xác. II.
Chuẩn bị của giáo viên và học sinh:
1. Chuẩn bị của giáo viên:
a. Phương tiện: Hệ thống câu hỏi liên quan đến chương II mà học sinh đã học.
b. Phương pháp: Luyện tập , đàm thoại , giải quyết vấn đề
2. Chuẩn bị của học sinh: Làm bài tập “Ôn tập chương II”.
III. Tiến trình bài dạy:
1. Bài cũ: Kiểm tra trong ôn tập 2. Bài mới: Hoạt động 1:
Hoạt động của giáo viên
Hoạt động của học sinh
Có bao nhiêu số tự nhiên gồm bốn chữ Gọi số cần tìm có dạng abcd
số được tạo thành từ các chữ số: a)Có: 4
6 = 1296 số có 4 chữ số có thể giống 1,2,3,5,7,9 sao cho: nhau.
a) Các chữ số có thể giống nhau. b) Có: 4
A = 360 số có 4 chữ số khác nhau. 6
b) Các chữ số khác nhau. c) d: có 5 cách chọn
c) Số đó là số lẻ có các chữ số khác abc có 3 A = 60 cách chọn
nhau. d) Các chữ số khác nhau và 5
Có: 5.60 = 300 số lẻ có 4 chữ số khác nhau
chữ số 3,7 luôn đứng cạnh nhau
d) Để 3,7 đứng cạnh nhau có: 3 cách chọn
Hoán đổi vị trí 3, 7 có: 2! = 2 cách Còn 2 số còn lại có: 2 A = 12 cách chọn 4
Có: 3.2.12 = 72 số có 4 chữ số và 3, 7 đứng cạnh nhau Hoạt động 2:
Hoạt động của giáo viên
Hoạt động của học sinh 12 æ 5
a)Số hạng tổng quát của khai triển là: Cho khai triển: 2 ö A = x - ç ÷ è x ø ( ) k 12-k æ 5 2 ö - = ( 5 - ç ÷ )k k k 24-3k C x C x 12 12 a) Tìm số hạng chứa 3 x è x ø
b) Tìm số hạng đứng giữa của khai Theo đề: 24-3k 3 x
= x Û 24 - 3k = 3 Û k = 7 triển. Số hạng có chứa 3 x là: C ( 5 - )7 7 3 3 x = 61875 - 000x 12
b) Vì n = 12 nên khai triển có 13 số hạng
vậy số hạng đứng giữa khai triển là: C 5 - x = 14437500x 12 ( )6 6 6 6 Hoạt động 3: 25
Giáo án Tự chọn 11
Hoạt động của giáo viên
Hoạt động của học sinh
Túi I có: 4 bi đen, 2 bi trắng. Túi II có: 3 a) n(W) 1 1 = C .C = 45 5 9
bi đen, 5 bi trắng. Lấy đồng thời 2 bi,
b) Gọi A là biến cố lấy được 2 bi cùng màu mỗi túi 1 bi. đỏ: a) Tính n(W) . n( A) 1 1 = C .C =12 3 4
c) Tính xác suất sao cho 2 bi lấy ra cùng Xác suất để A xảy ra là: màu n A 12 4
b) Tính xác suất sao cho 2 bi lấy ra cùng P( A) ( ) = = = n(W) 45 15
màu đen d) Tính xác suất sao cho 2 bi lấy ra khác màu
c) Gọi B là biến cố lấy được 2 bi cùng màu: n(B) 1 1 1 1
= C .C + C .C = 22 3 4 2 5 n B
Xác suất để B xảy ra là: P(B) ( ) 22 = = n(W) 45
d) Gọi C là biến cố lấy ra 2 bi khác màu, C
là biến cố đối của B nên xác suất để C xảy ra là:
P (C) = - P (B) 22 23 1 = 1- = 45 45
3. Củng cố: nhắc lại các kiến thức đã học về xác suất BTTN
Câu 1: Gieo một con súc sắc 2 lần. Số phần tử của không gian mẫu là? A. 6 B.12 C.18 D.36
Câu 2: Gieo một đồng tiền liên tiếp 3 lần. Tính xác suất của biến cố A: “ lần đầu tiên xuất hiện mặt sấp” 1 A. P( ) A = 3 B. P( ) A = 7 C. P( ) A = 1 D. P( ) A = 2 8 8 4
Câu 3: Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được 1 7 8 1 chọn đều là nữ. A. B. C. D. 15 15 15 5
Câu 4: Một bình chứa 16 viên bi, với 7 viên bi trắng, 6 viên bi đen, 3 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi.
Tính xác suất lấy được cả 3 viên bi đỏ. 1 1 1 143 A. B. C. D. 560 16 28 280
Câu 5: Công thức nào sau đây dùng để tính xác suất của biến cố A : n(A) n( ) W n(A) n(A) A. P (A) = 1 - B. P (A) = C. P (A) = D. P (A) = n( ) W n(A) n(B ) n( ) W
Câu 6: Một tổ học sinh gồm có 6 nam và 4 nữ. Chọn ngẫu nhiên 3 em. Tính xác suất 3 em được chọn có ít nhất 1 nữ. 5 1 1 1 A. B. C. D. 6 6 30 2
Câu 7: Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy 3 hoa có đủ cả ba màu? A. 240 B. 210 C. 18 D. 120
Câu 8: Một lớp học có 40 học sinh gồm 25 nam và 15 nữ. Chọn 3 học sinh tham gia vệ sinh công cộng toàn
trường, hỏi có bao nhiêu cách chọn 3 học sinh trog đó có 1 học sinh nam và 2 học sinh nữ? A. 5250 B. 4500 C.2625 D.1500 26
Giáo án Tự chọn 11
Tiết 15 : Đường thẳng song song với mặt phẳng
I.Chuẩn kiến thức kỹ năng 1.Kiến thức
- Nhằm củng cố , khắc sâu và nâng cao các kiến thức về đường thẳng và mặt phẳng trong không gian 2.Kĩ năng.
- Biết làm các dạng bài tập liên quan đến đường thẳng và mặt phẳng.
- Rèn luyện khả năng vẽ hình không gian. 3. Tư duy_ Thái độ
- Liên hệ được với nhiều vấn đề trong thực tiễn. - óc tư duy lô gíc.
- Cẩn thận chính xác trong việc làm và trình bày lời giải.
II . Chuẩn bị phơng tiện dạy học.
1)Thầy: SGK, SGV, SBT, Giáo án
2)Trò: Nắm chắc cách biểu diễn một hình không gian trên mặt phẳng .
- Các tính chất và các định lí về đường thẳng và mặt phẳng trong không gian.
III.Gợi ý phơng pháp dạy học
-Sử dụng phơng pháp tổng hợp
IV.Tiến trình bài học A.Các Hoạt động
Gồm 7 hoạt động là nhằm giải quyết các dạng bài toán về hình học không gian.
B. Phần thể hiện trên lớp . 1.ổn định lớp. 2.Bài mới
Hoạt động của GV
Hoạt động của HS Nội dung HĐ1:
GV HĐTP1: (Bài tập về chứng minh đường
HS suy nghĩ trả lời…
thẳng song song với mặt Bài tập1: phẳng)
HS các nhóm thảo luận để Cho hình chóp S.ABCD, trên
GV nêu đề bài tập áp
tìm lời giải và cử đại diện
các cạnh SA và SC lần lược
dụng và ghi lên bảng.
lên bảng trình bày lời giải
lấy hai điểm E và F sao cho
Cho HS các nhóm thảo
của nhóm (có giải thích) SE SF = . Chứng minh EF
luận để tìm lời giải và gọi HS nhận xét, bổ sung và sửa SA SC
HS đại diện lên bảng trình chữa ghi chép. song song với mặt phẳng bày lời giải.
HS trao đổi để rút ra kết ABCD.
GV gọi HS nhận xét, bổ quả… sung (nếu cần)
GV nhận xét, bổ sung và
HS chú ý theo dõi trên bảng
nêu lời giải đúng (nếu HS để tiếp thu kiến thức và
không trình bày đúng lời phương pháp giải… giải) 27
Giáo án Tự chọn 11 S E F D A C B
Hoạt động của GV
Hoạt động của HS Nội dung
HĐTP2: (Bài đường thẳng
song song với mặt phẳng) Bài tập 2:
Cho hình chóp S.ABCD có đáy
GV nêu đề, ghi lên bảng và
HS thảo luận để tìm lời giải và ABCD là một hình thang với vẽ hình.
cử đại diện lên bảng trình bày
AB//CD ; goi G, G’ lần lượt là
Cho HS thảo luận để tìm lời lời giải của nhóm (có giải
trong jtâm của các tam giác
giải và gọi HS đại diện lên thích)
SAD, SBC. Chứng minh đường
bảng trình bày lời giải.
HS nhận xét, bổ sung và sửa
thẳng GG’ song song với mặt
Gọi HS nhận xét, bổ sung chữa ghi chép. phẳng (SAB). (nếu cần)
HS trao đổi để rút ra kết quả:…
HS chú ý theo dõi trên bảng để
tiếp thu phương pháp giải…
GV nhận xét và nêu lời giải
đúng (nếu HS không trình bày đúng lời giải).
HĐ2: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại phương pháp chứng minh đường thẳng song song với mặt phẳng.
*Hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải và làm thêm các bài tập sau: 3.Củng cố
- Ôn tập lại các kiến thức chính về đường thẳng và mặt phẳng và quan hệ song song trong không gian. 28
Giáo án Tự chọn 11
Tiết 16 : DÃY SỐ –CẤP SỐ CỘNG-CẤP SỐ NHÂN
I.Chuẩn kiến thức kỹ năng 1.Kiến thức
- Nhằm củng cố , khắc sâu và nâng cao các kiến thức về dãy số , cấp số cộng , cấp số nhân. 2.Kĩ năng.
- Biết làm các dạng bài tập liên quan đến dãy số.
- áp dụng làm các bài tập có liên quan. 3. Tư duy_ Thái độ
- Liên hệ được với nhiều vấn đề trong thực tiễn. - óc tư duy lô gíc.
- Cẩn thận chính xác trong việc làm và trình bày lời giải.
II . Chuẩn bị phương tiện dạy học.
1)Thầy: SGK, SGV, SBT, Giáo án
2)Trò: Ôn tập các kiến thức đã học về Dãy số, cấp số cộng , cấp số nhân . Đồ dùng học tập.
III.Gợi ý phơng pháp dạy học
-Sử dụng phơng pháp tổng hợp
IV.Tiến trình bài học A.Các Hoạt động
Gồm 6 hoạt động là nhằm giải quyết các dạng bài toán về dãy số.
B. Phần thể hiện trên lớp . 1.ổn định lớp. 2.Bài mới Hoạt động 1
Bài tập 3 : Xét tính tăng giảm của các dãy số sau : a) 2 u = 3n -1 n b) n +1 u = n n -1 c) ( 1)n 2n -
GV hướng dẫn học sinh làm ý a) Hoạt động của GV Hoạt động cuả HS Câu hỏi 1
Nêu định nghĩa dãy số tăng , dãy +.HS đứng tại chỗ trả lời. số giảm ? Câu hỏi 2
Xét hiệu u - u + = ? +. Ta có n 1 n u - u n 1
3 + -1- 3n +1 = 2.3n + = >0 . n 1 n
Vậy dãy số là dãy số tăng.
+. HS lên bảng trình bày lời giải câu b
Đáp án : Là dãy số tăng +. Hs lên bảng làm ý c
Đáp án : Không tăng không giảm. Hoạt động 4
Bài tập 4 : Tính số tiếng chuông báo giờ của một đồng hồ chạy từ 0h đến 12 giờ . Biết số
tiếng chuông bằng số giờ. 29
Giáo án Tự chọn 11
GV gợi ý để học sinh làm Hoạt động của GV Hoạt động của HS Câu hỏi 1
Số tiếng chuông có lập thành
+. Là một cấp số cộng có u1 = 1 và d= 1. một CSC không ? Câu hỏi 2
áp dụng công thức tính tổng của n + áp dụng công thức S = n.(u +u )
số hạng đầu CSC hãy tính số tiếng 1 12 2
chuông đồng hồ theo yêu cầu đề bài. 12 Þ S = (1+12) = 78 tiếng chuông 12 2 Hoạt động 5
Bài tập 5 : Cho cấp số nhân (un) có công bội q .
a) Cho biết u1 = 2 , u7 = 1457
b) Cho biết u1 = 1/2 , u5 = 1/35
c) Cho biết u1 = -3 , q=2/3 . Tìm u6
GV gợi ý để học sinh lên bảng làm. Hoạt động của GV Hoạt động của HS Câu hỏi 1
Nêu công thức số hạng tổng +. 1 u u . n q - = n 1 quát? Câu hỏi 2 a) q= 3
áp dụng mỗi học sinh làm một ý b) q =1/2 theo yêu câu của bài. c) -2/243 Hoạt động 6
Bài tập 6 : Tìm u1 và q của một cấp số nhân biết : u ì - u = 72 a) 4 2 í u - u = 144 î 5 3 GV gợi ý học sinh làm Hoạt động của GV Câu hỏi 1
Hãy phân tích các số hạng theo
+. áp dụng công thức số hạng tổng quát số hạng đầu ? 1 u u . n q - = n 1 Ta có :
u = u .q , 2
u = u .q , 3
u = u .q , 4
u = u .q 2 1 3 1 2 1 5 1 Câu hỏi 2 +. Thay vào ta có HPT Giải HPT tìm u1 và d ? 3 u
ìï q -u .q = 72 1. 1 í 4 2 u
ï .q - u .q =144 î 1 1
Giải HPT trên có u =12,q = 2 . 1 u ì = 192 b) 6 í u = 384 î 7 Giải : HS lên bảng làm.
Đs: u = 6,q = 2 1 3.Củng cố 30
Giáo án Tự chọn 11
- Nhắc lại các công thức về số hạng tổng quát và công thức tính tổng của Cấp số cộng và cấp số nhân. 4.Bài tập
- Hoàn thành các bài tập đã chữa vào vở.
Tiết 16 Bài tập ôn tập chương2
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+ Nêu pp tìm giao tuyến của 2 mp (nêu 2 phương pháp khi hai mp có 1 điểm chung và khi 2 mp song song) 31
Giáo án Tự chọn 11
+Nêu lại phương pháp chứng minh đường thẳng song song mặt phẳng.
*Áp dụng: Giải bài tập 2 về nhà.
GV gọi HS nhận xét. bổ sung và giáo viên nêu lời giải đúng (nếu HS không trình bày đúng lời giải). +Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung
HĐ1: Bài tập về xác định
Bài tập1: Cho hình lập
thiết diện và chứng minh
phương ABCD.A’B’C’D’.Gọi
đường thẳng song song
M, N, P lần lượt là trung điểm với mp:
của AB, B’C’, DD’.
GV nêu đề và ghi lên
HS thảo luận theo nhóm để
a)Hãy xác định thiết diện tạo
bảng, cho HS các nhóm
tìm lời giải và cử đại diện lên bởi hình lập phương đã cho và
thảo luận để tìm lời giải
bảng trình bày (có giải mp (MNP)
và ghi lời giải vào bảng thích).
b)Chứng minh rằng đường
phụ. Gọi HS đại diện lên
thẳng MN song song với mp
bảng trình bày lời giải. (BDC’).
Gọi HS nhận xét, bổ sung (nếu cần).
GV nhận xét, bổ sung và
HS nhận xét, bổ sung và sửa
nêu lời giải đúng (nếu HS chữa ghi chép.
không trình bày đúng lời
HS trao đổi để rút ra kết giải). quả:… D C A B D' C' A' B'
Hoạt động của GV
Hoạt động của HS Nội dung 32
Giáo án Tự chọn 11 HĐ2:
Bài tập2: Từ 4 điểm của hình GV: Để chứng minh hai HS suy nghĩ trả lời …
bình hành ABCD vẽ bốn nửa mp song song với nhau ta
đường thẳng song song cùng
phải chứng minh như thế
chiều Ax, By, Cz, Dt. Một mp nào?
(a )cắt 4 nửa đường thẳng Ax,
Để chứng minh hai đường
By, Cz, Dt tại A’, B’, C’, D’. thẳng song song với nhau
HS thảo luận theo nhóm để a)Chứng minh hai mp (Ax, ta phải ta phải làm gì?
tìm lời giải và cử đại diện lên By) và (Cz, Dt) song song với
bảng trình bày (có giải nhau. thích). b)Chứng minh tứ giác
GV nêu đề và ghi lên
A’B’C’D’ là hình bình hành.
bảng, cho HS các nhóm
c)Gọi O, O’ lần lượt là tâm
thảo luận để tìm lời giải các hình bình hành ABCD,
và ghi lời giải vào bảng
A’D’C’D’. Chứng minh
phụ. Gọi HS đại diện lên
HS nhận xét, bổ sung và sửa đường thẳng OO’ song song
bảng trình bày lời giải. chữa ghi chép.
với đường thẳng AA’ và AA’
Gọi HS nhận xét, bổ sung
HS trao đổi để rút ra kết +CC’ =BB’ +DD’. (nếu cần). quả:…
GV nhận xét, bổ sung và
nêu lời giải đúng (nếu HS
không trình bày đúng lời giải). t z D' C' x y O' A' a D B' C O A B
HĐ3: Củng cố và hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải và làm thêm các bài tập:
Bài tập 1: Cho đỉnh S nằm ngoài hình bình hành ABCD. Xét mp a ( ) qua AD cắt SB, SC lần
lượt tại M và N. Chứng minh AMND là hình thang.
Bài tập 2: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và BD. Gọi P là điểm
tùy ý trên cạnh AB sao cho P ¹ A và P ¹ B. Xét I = PD Ç AN và J =PC Ç AM.
Chứng minh rằng: IJ // CD.
Tiết 17 . ÔN TẬP KIẾN THỨC VỀ CẤP SỐ CỘNG VÀ BÀI TẬP ÁP DỤNG *Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức 33
Giáo án Tự chọn 11
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+Nêu định nghĩa cấp số cộng.
+Viết công thức tính số hạng tổng quát khi biết số hạng đầu và công sai.
+Nêu tính chất của cấp số cộng.
+Viết các công thức tính tổng của n số hạng đầu của một cấp số cộng. +Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung HĐ1: Bài tập1: HĐTP1:(Tìm n và
HS các nhóm thảo luận để tìm
Một cấp số cộng có số hạng
công sai của một cấp lời giải.
thứ nhất là 5, số hạng cuối là số cộng)
HS đại diện lên bảng trình bày
45 và tổng số là 400. Tìm n
GV nêu đề và ghi lên
lời giải (có giải thích) và công sai.
bảng, cho HS các nhóm HS nhận xét, bổ sung và sả
thảo luận tìm lời giải, chữa ghi chép.
gọi HS đại diện lên
HS trao đổi và nêu kết quả:
bảng trình bày lời giải. n(u + u 1 n ) S =
Û 2S = n u + u n n ( 1 n)
GV gọi HS nhận xét, bổ 2 sung (nếu cần) 2S 2.400 n Û n = = = 16 u + u 5+ 45 1 n
GV nhận xét, bổ sung u - u 8
và nêu lời giải đúng
u = u + n- d Û d = = n ( ) n 1 1 1 n-1 3 (nếu HS không trình
HS thảo luận để tìm lời giải và bày đúng lời giải)
cử đại diện lên bảng trình bày
lời giải (có giải thích)
HĐTP2: (Bài tập về
HS nhận xét, bổ sung và sửa tìm số hạng uk) chữa ghi chép. Bài tập 2:
GV nêu đề và ghi lên
HS trao đổi và rút ra kết quả:
Một cấp số cộng có số hạng bảng. Cho HS các
thứ 54 và thứ 4 lần lượt là -
u = u + n -1 d n 1 ( )
nhóm thảo luận và tìm
61 và 64. Tìm số hạng thứ 23. lời giải. Û u = u + 53 ( d 1) 54 1
Gọi HS đại diện lên Û u = u + 3 ( d 2) 4 1
bảng trình bày lời giải. Gi∂i h÷ ph≠¨ ng tr◊nh (1), (2) ta Æ≠Óc:
Gọi HS nhận xét, bổ 143 5 u = ,d = - sung (nếu cần) 1 2 2 33
Þ u = u + 22d =
GV nhận xét và nêu lời 23 1 2
giải chính xác (nếu HS không trình bày đúng) HĐ2: Bài tập 3: HĐTP1:(Tìm các số
HS các nhóm thảo luận để tìm
Chèn 20 số vào giữa số 4 và
hạng còn lại của một lời giải.
67, biết rằng dãy số đó là một
cấp số cộng khi biết số HS đại diện nhóm lên bảng cấp số cộng.
hạng đầu và số hạng
trình bày lời giải (có giải thích) cuối…)
HS nhận xét, bổ sung và sửa
GV nêu đề bài tập và chữa ghi chép.
ghi lên bảng, cho HS
HS trao đổi và rút ra kết quả:
thảo luận tìm lời giải.
Ta xem số 4 là số hạng đầu và 34
Giáo án Tự chọn 11
Gọi HS đại diện nhóm
số 67 như là số hạng cuối. Như
lên bảng trình bày lời
vậy cấp số cộng phải tìm có tất giải. cả 22 số hạng.
Gọi HS nhận xét, bổ
Ta c„ : u = u + n -1 d n 1 ( ) sung (nếu cần) Û 67 = 4+ 21d
GV nêu nhận xét, và Û d = 3
trình bày lời giải đúng
Vậy cấp số cộng được tạo thành (nếu HS không trình
là: 4, 7, 10, … , 61, 64, 67 và 20 bày đúng lời giải)
số cần chèn là: 7, 10, 13, …, 58, 61, 64. Bài tập 4:
HĐTP2: (Bài tập về
HS thảo luận theo nhóm để tìm Tìm tổng của một cấp số
tính tổng của n số
lời giải và cử đại diện lên bảng cộng gồm các số:
hạng đầu của một cấp trình bày lời giải (có giải thích) 1 3
5 ,6 ,8... Æ’n sË hπng th¯ 17. số cộng)
HS nhận xét, bổ sung và sửa 2 4
GV nêu đề và ghi lên chữa ghi chép.
bảng, cho HS thảo luận HS trao đổi và rút ra kết quả: tìm lời giải. é (n- ) 1 d ù
Gọi HS đại diện lên c
Ta „ : S = nêu + n 1 ú
bảng trình bày lời giải. 2 ë û
Gọi HS nhận xét, bổ é 1 (17- ) 1 5ù 263 Û S = 17ê5 + . ú = sung (nếu cần) n 2 2 4 2 ë û
GV nhận xét và nêu lời
giải chính xác (nếu HS không trình bày đúng lời giải)
HĐ3: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại định nghĩa cấp số cộng, nêu công thứ tính số hạng tổng quát, tính chấp về các số
của một cấp số cộng, công thức tính tổng n số hạng đầu cảu một cấp số cộng.
*Áp dụng: Giải bài tập sau:
Có bao nhiêu số của một cấp số cộng -9; -6; -3; … để tổng số các số này là 66.
*Hướng dãn học ở nhà:
-Xem lại các bài tập đã giải.
- Ôn tập lại và ghi nhớ các định nghĩa và công thức đã học về cấp số cộng.
- Ôn tập lại định nghix cấp số nhân và các công thức.
-----------------------------------&------------------------------------
Tiết 18. ÔN TẬP KIẾN THỨC VỀ CẤP SỐ NHÂN VÀ BÀI TẬP ÁP DỤNG *Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức 35
Giáo án Tự chọn 11
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
+Nêu định nghĩa cấp số nhân.
+Viết công thức tính số hạng tổng quát khi biết số hạng đầu và công bội.
+Nêu tính chất các số hạng của cấp số nhân.
+Viết các công thức tính tổng của n số hạng đầu của một cấp số nhân. +Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung HĐ1: Bài tập 1:
HĐTP1: (Chèn các số
Hãy chèn 4 số của một cấp số
vào giữa hai số đã cho HS các nhóm thảo luận để tìm nhân vào giữa hai số 160 và
của một cấp số nhân) lời giải. 5.
GV nêu đề và ghi lên
HS đại diện lên bảng trình bày
bảng. Cho HS các nhóm lời giải (có giải thích)
thảo luận để tìm lời giải. HS nhận xét, bổ sung và sửa
Gọi HS đại diện lên chữa ghi chép.
bảng trình bày lời giải.
HS trao đổi để rút ra kết quả:
Gọi HS nhận xét, bổ
Ta xem số 160 như là số hạng sung (nếu cần).
đầu và số 5 như là số hạng thứ
6 của một cấp số nhân. Ta có: 5
u = u .q 6 1 u u 1 5 6 6 5 Û q = Þ q = 5 = u u 32 1 1 1 1 5 = =
GV nhận xét và nêu lời 5 2 2
giải chính xác (nếu HS
Suy ra các số hạng của cấp số
không trình bày đúng lời nhân là: giải) 160, 80, 40, 20, 10, 5
Vậy các số cần chèn là: 80, 40, 20. 10.
HS thỏa luận theo nhóm để tìm
lời giải và cử đại diện lên bảng
trình bày lời giải.
HS nhận xét, bổ sung và sửa HĐTP2: (Tính tổng chữa ghi chép. Bài tập 2:
của n số hạng của một HS trao đổi để rút ra kết quả:
Tìm tổng của một cấp số nhân cấp số nhân)
Cấp số nhân có công bội là:
gồm 7 số hạng mà các số
GV nêu đề và ghi lên 3 q = - . Ta có: hạng đầu là: 2 3 , 1 - , ,...
bảng (hoặc phát phiếu 2 3 2 HT) 1 n - q S = u
GV cho HS thảo luận n 1 1- q
theo nhóm để tìm lời 7 æ 3 ö giải. 1- - 2 ç 2÷ è ø 463
Gọi HS đại diện nhóm Þ S = . 7 3 3 96 +
lên bảng trình lời giải. 1 2
Gọi HS nhận xét, bổ 36
Giáo án Tự chọn 11 sung (nếu cần) GV nhận xét và trình bày lời giải chính xác
(nếu HS không trình bày đúng lời giải) HĐ2:
HĐTP1: (Bài tập về
tìm các số hạng của
một cấp số nhân khi
HS các nhóm thảo luận để tìm Bài tập 3:
biết tổng và tích của
lời giải và cử đại diện lên bảng Tìm 3 số hạng của một cấp số các số đó).
trình bày lời giải (có giải
nhân mà tổng số là 19 và tích
GV ghi đề và ghi lên thích) là 216.
bảng. Cho HS thảo luận HS nhận xét, bổ sung và sửa
theo nhóm và gọi HS đại chữa ghi chép.
diện nhóm lên bảng
HS trao đổi và rút ra kết quả: trình bày. Giải:
GV gọi HS nhận xét, bổ Gọi 3 số hạng liên tiếp của cấp sung (nếu cần) số nhân là:
a , ,aa q (vÌ i ql µ ´c n gbÈi) q Theo giả thiết ta có: ìa =
GV nhận xét và nêu lời . . a aq 216 (1) ïïq
giải đúng (nếu HS í a ï
không trình bày đúng lời + a+ aq = 19 (2) ï îq giải)
Từ (1) ta có a = 6. Thay vào (2) ta được: 6q2- 13q + 6 = 0 3 2
Û q = ho∆c q = 2 3
Vậy 3 số hạng cần tìm là: 4, 6, 9 hay 9, 6, 4.
HS các nhóm thảo luận để tìm
lời giải và cử đại diện lên bảng Bài tập 4:
HĐTP2: (Bài tập về
trình bày lời giải (có giải
Tìm số hạng đầu của một cấp
tìm số hạng đầu của thích)
số nhân biết rằng công bội là
một cấp số nhân khi
HS nhận xét, bổ sung và sửa
3, tổng số là 728 và số hạng
biết công bội, tổng và chữa ghi chép. cuối là 486. số hạng cuối)
HS trao đổi và rút ra kết quả: GV nêu đề và ghi lên bảng hoặc phát phiêus HT. GV cho HS các nhóm
thảo luận để tìm lời giải. GV gọi HS đại diện 37
Giáo án Tự chọn 11
nhóm lên bảng trình bày 1 n - q S = u (1) lời giải. n 1 1- q
Gọi HS nhận xét, bổ n 1
u = u .q - (2) sung (nếu cần) n 1 u
GV nhận xét, bổ sung và Tı (2) n Þ u = 1 n 1 q -
nêu lời giải dúng i(nếu n HS không trình bày u 1- q Thay µ v o (1) n Þ S = . (3) n - đúng lời giải) n 1 q 1- q Theo giải thiết Sn=728, un=486,q=3 n ( ) 486 1- 3 3 Þ 728 = . n 1 3 - 1- 3 n- 486 1 5 Û 3 = = 243 = 3 2
Û n -1 = 5 Û n = 6 u 486 486 Þ u n = = = = 2 1 n 1 - 5 q 3 243
HĐ3: Củng cố và hướng dẫn học ở nhà: *Củng cố:
-Nêu lại định nghĩa cấp số cộng, nêu công thứ tính số hạng tổng quát, tính chấp về các số
của một cấp số nhân, công thức tính tổng n số hạng đầu của một cấp số nhân.
*Áp dụng: Giải bài tập sau:
Tìm công bội của một cấp số nhân có số hạng đầu là 7 số hạng cuối là 448 và tổng số các số hạng là 889.
*Hướng dãn học ở nhà:
-Xem lại các bài tập đã giải.
- Ôn tập lại và ghi nhớ các định nghĩa và công thức đã học về cấp số cộng, cấp số nhân 38
Giáo án Tự chọn 11 Tiết 20, 21
GIỚI HẠN CỦA DÃY SỐ I . Mục tiêu :
+ Kiến thức : Giúp học sinh
- Nắm được định nghĩa dãy số II .Chuẩn bị:
+ Giáo viên : bài tập, sách giáo khoa.
III .Phương pháp: Gợi mở , vấn đáp , hoạt động nhóm .
IV.Tiến trình bài học:
1. Kiểm tra bài cũ : Nêu cách tính giới hạn của các dãy số. 2. Bài mới : Tg Hoạt động của giáo
Hoạt động của học sinh Ghi bảng. viên 39
Giáo án Tự chọn 11 T 1 1) Tính giới hạn sau: 13’ HĐ 1: Sử dụng CSC, 1 + 2 + 3 + ! + n CSN vào tính giới a) lim ĐS: 1/2 2 n + 2 hạn của dãy số.
+Học sinh ghi đề bài tập. +Giáo viên ghi đề 1 +Học sinh làm việc theo lên bảng, cho học nhóm theo sự phân công. sinh hoạt động nhóm HĐ 2:Sử dụng định
+Học sinh lên bảng trình lí 1 của giới hạn 0
bày ý tưởng.( áp dụng tổng vào bài tập. n số hạng của CSC,CSN). 3) Tính các giới hạn: +Cho học sinh đứng 2 n + n + 8’ tại chỗ giải thích ý 3 2 5 a/ lim = 3/7 tưởng. 7 2 n - n + 3 +Cho học sinh xung 2 n + 1 + 4n phong lên bảng. b/ lim = 5/3 3n - 2 HĐ 3: Sử dụng các
+Học sinh nêu lại phương
c/ lim ( n2 + 2n+ 2 - n) tính chất của giới
pháp tính giới hạn: Lưu ý hạn hữu hạn vào bài
xét bậc ở tử và mẫu. sin n d/ lim = 0 . tập. n +Hãy nêu phương
17’ pháp tính giới hạn của dãy số có dạng: P(n)
*Bài tập trắc nghiệm: ở cuối trang. . Q(n) *Ôn tập củng cố: + Phương pháp tính +Học sinh nhắc lại các giới hạn của dãy số
dạng toán cơ bản vừa học. có dạng:
+Học sinh đứng tại chỗ trả P(n) 7’ . lời. Q(n) +Bài tập trắc nghiệm(dự kiến) 40
Giáo án Tự chọn 11 T 2
Bài 4 : Tính các giới hạn sau : 17’ 2 3 7n 3 - n 6n 2 - n + 1 HĐ 4:Sử dụng các a / lim ĐS : 7 b / lim ĐS : 3 2 3 n - 2 2n - n định lí về giới hạn +Học sinh làm việc theo 2 2n + 1 n - 1 vào bài tập. nhóm: c / lim ĐS : 0 d / lim ĐS :1 3 n - 3n + 3 n + 1 +Giáo viên ghi đề Tổ 1 làm câu a, c. bài tập 4 trên bảng. Tổ 2 làm câu b,d. Bài 5)Tính tổng +Cho học sinh làm Tổ 3,4 làm câu 5. sau: S = æ 1 1 ö æ 1 1 ö æ 1 1 ö ç - ÷ + ç - ÷ + + - ! ç ÷ + ! việc theo nhóm. Học sinh xung phong lên è 2 3 ø è 22 32 ø è n n 2 3 ø *Giáo viên hướng
bảng trình bày lời giải. dẫn học sinh bài 5: 8’ 1 1 S= + + .. 2
+Áp dụng tổng vô hạn của
Bài 7: Tìm tổng các cấp số nhân vô hạn sau: 2 2
một cấp số nhân có công 1 1 1 -( + + ..). 2 bội nhỏ hơn 1. a) 8, 4, 2, 1, , . . .; 3 3 2 HĐ 5: Sử dụng các 2 +1 1 1 quy tắc về giới hạn , , ,.... vào bài tập 6. 2 -1 2 - 2 2 12’ +Học sinh xung phong lên +Giáo viên cho học
Bài 8: Tìm các giới hạn sau: bảng trình bày và giải sinh xung phong lên 2 3 n -11n +1 thích ý tưởng. a) lim ĐS:+ ¥ bảng trình bày lời 2 n - 2 giải. 1 b) lim ĐS:- ¥ +Học sinh chú ý vào 2 2 n + - n + 2 4 phương pháp giải. n(3 n3 lim
+ n2 - n)ĐS:+ ¥ HĐ 6: Tính tổng của cấp số nhân lùi vô hạn. +Yêu cầu học sinh 8’ nhắc lại công thức tính tổng của CSN lùi vô hạn.
+học sinh lên bảng trình
HĐ 7: Tính giới hạn bày lời giải. của dãy số có giới hạn vô cực. +Cho học sinh xung *Dự kiến: phong lên bảng giải thích cách làm.
+Học sinh lên bảng trình bày lời giải. *Ôn tập củng cố: Tìm các giới hạn sau 2 3 n -11n +1 c) lim ĐS:+ ¥ 2 n - 2 1 d) lim ĐS:- ¥ 2 n + 2 2 - n + 4 n(3 n3 lim + n2 - n)ĐS 41
Giáo án Tự chọn 11 Tiết 22
LUYỆN TẬP HAI MẶT PHẲNG SONG SONG I. Mục tiêu +Về kiến thức:
- Hiểu được các kiến thức về hai mặt phẳng song song
- Hiểu và vận dụng được các định nghĩa, tính chất, định lí trong bài +Về kĩ năng:
- Biết chứng minh hai mặt phẳng song song
- Biết cách vận dụng định lí Thalès, định lí Thalès đảo
- Biết vẽ các hình lăng trụ, hình hộp, hình chóp cụt +Về tư duy, thái độ:
- Về tư duy: phát triển trí tưởng tượng không gian và tư duy logic, biết quy lạ về quen
- Về thái độ: tích cực hoạt động, trả lời câu hỏi II. Chuẩn bị
GV : Giáo án, phiếu học tập, thước kẻ.
HS : Kiến thức về ĐL 1, 2, 3 bài đường thẳng song song với mặt phẳng; ĐL 1, tính chất 2, ĐL Thalès thuận
và đảo bài hai mặt phẳng song song
III. Phương pháp: Gợi mở, vấn đáp.
IV. Tiến trình bài dạy
1. Ổn định lớp: (1’) Kiểm tra sĩ số, tác phong 2. Bài mới
HĐ3: Củng cố định lí Thalès và định lí Thalès đảo
20’ HĐTP1: (Bài đường Bài tập 1
thẳng song song với
Cho hình chóp S.ABCD có đáy ABCD là mặt phẳng)
một hình thang với AB//CD ; goi G, G’ lần
HS thảo luận để tìm lời giải
lượt là trong jtâm của các tam giác SAD, GV nêu đề, ghi lên
và cử đại diện lên bảng trình
SBC. Chứng minh đường thẳng GG’ song bảng và vẽ hình.
bày lời giải của nhóm (có giải song với mặt phẳng (SAB). Cho HS thảo luận để thích)
tìm lời giải và gọi HS
HS nhận xét, bổ sung và sửa S
đại diện lên bảng trình chữa ghi chép. bày lời giải.
HS trao đổi để rút ra kết Gọi HS nhận xét, bổ quả:… sung (nếu cần) G' B C G GV nhận xét và nêu lời giải đúng (nếu HS D không trình bày đúng lời giải).
HS chú ý theo dõi trên bảng
để tiếp thu phương pháp giải A 20’ HĐTP2 Gợi ý : G 1G2 // MN , G1G3 // H: haõy veõ hình ? MP , H: Chứng minh mà G 1G2 và G1G3 cắt nhau (G
Bài2 : Cho tứ diện ABCD. Ba điểm M, N, 1G2G3) // (BCD)? trong mp (G
P lần lượt trung điểm BC, CD, DB. G 1G2G3) , MN và MP cắt 1, G2,
nhau trong mp(BCD). Từ đó G3 lần lượt trọng tâm D ABC, D ACD, suy ra đpcm . D ADB.
a. Chứng minh (G1G2G3) // (BCD) H: Tìm thiết diện của
b. Tìm thiết diện của tứ diện ABCD
tứ diện ABCD với Gợi ý :
với (G1G2G3). Tính diện tích thiết (G
diện biết diện tích D BCD là S
1G2G3). Tính diện Thiết diện là (EFG)
tích thiết diện biết diện Diện tích 42
Giáo án Tự chọn 11 tích D BCD là S? A 2 2 dt(EFG) æ SG ö æ 2 ö 1 = = E G3 ç ÷ ç ÷ dt G (BCD) è SM ø è 3 ø G1 B G2 4 4 F P dt(EF D G) = dt(BCD) = S 9 9 M N C
HĐ3: Củng cố toàn bài
V. Củng cố: (5’)
- Trình bày phương pháp chứng minh 2 đường thẳng song song, đường thẳng song song với mặt phẳng, 2 mặt phẳng song song
Bài1:Cho hai hình vuông ABCD và ABEF ở trong hai mp phân biệt. trên các đường chéo AC và BF lần
lượt lấy các điểm M và N sao cho AM=BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’ CM: a)(ADF)//(BCE) b)M’N’//DF c)(DEF)//(MM’N’N) và NM//(DEF)
Bài 2:Cho tứ diện ABCD trong đó AB=AC=CD=a; M là một điểm trên cạnh AC với AM=x (0mp đi qua Mvà song song với AB và CD
a)Xác định thiết diện của mp(a ) với tứ diện ABCD. thiết diện là hình gì?
b)Tính diện tích thiết diện theo a và x. xác định x để diện tích này lớn nhất Tiết 23,24
LUYỆN TẬP GIỚI HẠN CỦA HÀM SỐ. A. MỤC TIÊU:
- Hiểu được định nghĩa, giới hạn của hàm số tại một điểm: giới hạn hữu hạn, giới hạn vô cực.
- Biết tính giới hạn ( hữu hạn hay vô cực) của một số hàm số
B. SỰ CHUẨN BỊ CỦA THẦY VÀ TRÒ
1. Chuẩn bị của GV: bảng phụ, dụng cụ dạy học, giáo án.
2. Chuẩn bị của HS: bài cũ, dụng cụ học tập.
C.PHƯƠNG PHÁP DẠY HỌC:
- PPDH gợi mở vấn đáp, đan xen hoạt động nhóm.
D. TIẾN TRÌNH BÀI HỌC
Hoạt động 1: ôn tập lại kiến thức cũ : Hoạt động 2: Bài mới. TIẾT1 Tg
Hoạt động của giáo viên
Hoạt động của học sinh Ghi bảng. 43
Giáo án Tự chọn 11 .
Bài 1 : Tính giới hạn
15’ +Giáo viên hướng dẫn học sinh +Học sinh chú ý và đứng tại chỗ 3 2 x - 5x +1 giải bài tập 1.
trả lời câu hỏi của giáo viên. a) lim = 3 2 x®¥ x - 2
(x - )12(7x - 2)2
HĐ 1:Sử dụng phương pháp giải 49 b) lim = ¥ x®¥ (2x + )14 16 các dạng vô định . ¥
16’ +Giáo viên ghi đề trên bảng và +Học sinh làm việc theo nhóm.
cho học sinh hoạt động nhóm theo tổ.
Bài 2 : Tính giới hạn
+Giáo viên cho học sinh nhận a) lim x( 2 x + 5 - x) 5 =
xét tính đúng sai của bài toán. x®+¥ 2 lim( x + 1 - x ) . b/.
+Học sinh chú ý phương pháp x®¥ biến đổi bài toán. Bài giải HĐ dự kiến.
Bài 3:Tìm các giới hạn:
Giáo viên ghi đề bài trên bảng 2
x + x + 2 + 3x
12’ và cho học sinh đứng tại chỗ
+Học sinh biến đổi tương tự như a/. lim , x®±¥ 2 x + - x +
nêu phương pháp giải các bài
trong bài tập về dãy số. 4 1 1 toán
ĐS:4( khi x ® +¥ ); -2/3 ( khi x ® -¥ ). b/. lim ( 2 3 3 x +1 - x -1 ) x®±¥
ĐS:0( khi x ® +¥ ); + ¥ ( khi x ® -¥ ). c/. lim( 3 2 3
x + 3x - x ).ĐS: 1. x®¥ *Ôn tập củng cố: 2’ ¥
+Phương pháp khử dạng vô định . ¥
+Yêu cầu học sinh làm lại các bài tập đã học và bài tập làm thêm. Bài tập 2x + 7 - 3 2
x - 3x + 2x d) lim e) lim f) 2 3 3 lim ( x +1 - x -1) 3 2 x ® 1 x - 4x + 3 x®-¥ 3x -1 x ® + ¥ 2 x - 3x + 3 g) lim h) cos x - cos x 3 lim - 2 x®- 2 x + x - 2 2 x®0 2x Tiết 2: I.Mục tiêu:
- Hiểu được định nghĩa, giới hạn của hàm số tại một điểm: giới hạn hữu hạn, giới hạn vô cực. 0
- Biết tính giới hạn ( hữu hạn hay vô cực) của một số hàm số đặc biệt phương pháp khử dạng vô định 0 II.Chuẩn bị:
+Chuẩn bị của GV: bảng phụ, dụng cụ dạy học, giáo án. III.Phương pháp:
- PPDH gợi mở vấn đáp, đan xen hoạt động nhóm. IV. Bài mới: Hoạt động 2: Bài mới.
Tg Hoạt động của giáo viên
Hoạt động của học sinh Ghi bảng 44
Giáo án Tự chọn 11
8’ HĐ 1: Sử dụng phương pháp 2 x - 3x + 2 0 lim x®2 x - 2 khử dạng vô định 0 (x - 2)(x - )
+Giáo viên nêu bài tập 1,2
+Học sinh chú ý và đứng 1 = lim Bài 1: Tìm .
và gợi ý cho học sinh biết tại chỗ trả lời. x®2 x - 2 phương pháp giải.. = lim(x - ) 1 = 1
HĐ 2: Tính giới hạn có giới hạn x®2 hữu hạn.
Bài 2 : Tính giới hạn
10’ +Cho học sinh làm việc theo a) lim( 3 x + 5 2 x +10x) = 0 x®0 nhóm. +Học sinh làm việc theo 2 x + x - nhóm và đại diện nhóm 2 15 b) lim = 8
+Yêu cầu học sinh lên bảng lên bảng trình bày. x®3 x - 3 trình bày. 2 2 x + 3x +1 1 c) lim = +Học sinh khác nhận xét + 2 x® 1 - x -1 2
+Giáo viên hướng dẫn lại cho
lời giải của bạn mình. Bài 3:Tính ghạn học sinh. ( 2 x + h)3 3 - 2x
HĐ 3: Sử dụng phương pháp 2 a) lim = 6x , +Học sinh làm bài tập 0 h®0 h
7’ khử dạng vô định vào bài tập theo nhóm. 4 4 - 0 x a 3 b) lim = 4a . có chứa tham số. x®a x - a
+Giáo viên giao bài 4 a: tổ 1,2;
Bài 4 : Tính giới hạn +Học sinh làm việc theo bài 4b cho tổ 3,4. 2 x - 3x + 2 nhóm và đại diện nhóm a) lim = + 2
lên bảng trình bày lời giải. x®2 (x - 2) +¥
+Giáo viên cho học sinh lên 2 2 x - 3x +
bảng trình bày lời giải. 1 10’ b) lim = +¥ 2 x - 3x + 2 + x® 3 1 _ x - 2 x - x +1 a) lim
HĐ 4:Nhân lượng liên hợp để + x®2 (x - 2)2 Giải 2 x - 3x + 2 0
đưa về dạng vô định . (x - )( 2 x - = ) 1 lim a) lim+ 2 0 + x®2 (x - 2) x® (x - 2)2 2
+Giáo viên phân công mỗi tổ x -1 (x - )( 2 x - = ) 1 làm một câu. = lim lim+ 2 + x®2 (x - 2) x®2 (x - 2) x - 8’ . = +¥ = 1 lim + x®2 (x - 2) = +¥ *Ôn tập củng cố:
+Phương pháp khử dạng vô định.
+Yêu cầu học sinh về nhà làm lại các bài tập đã học.
Bài tập Tính các giới hạn sau : n + 2 sin n a) lim ( + ) b) lim ( 2 x +1 + x) n n +1 2 x->-¥ Tiết 25,26 HÀM SỐ LIÊN TỤC. 45
Giáo án Tự chọn 11 I. MỤC TIÊU : Học sinh biết :
+Củng cố khái niệm hàm số liên tục tại một điểm, liên tục trên một khỏang.
+Phân loại các điểm gián đoạn. II . CHUẨN BỊ
Giáo viên : Soạn bài và xem lại giáo án trước giờ lên lớp.
III. TIẾN TRÌNH DẠY HỌC
1. Ổn định lớp và kiểm tra bài cũ : Phát biểu định nghĩa hàm số liên tục ? 2. Bài mới : Hoạt động bài mới.
Tg Hoạt động của giáo viên
Hoạt động của học sinh Ghi bảng.
10’ HĐ 1:Xét tính liên tục của hàm
Bài tập 1:Xét tính liên tục của hàm số : số tại một điểm. +Học sinh nhaqức lại ì 2 x -1
+Giáo viên yêu cầu học sinh kiến thức. ï , x ¹ f (x) = 1 í x -1 tại x = 1.
nhắc lại định nghĩa hàm số 0 ïa, x =
liên tục tại một điểm. î 1
Bài tập 2 Cho hàm số f(x) chưa xác 8’ định tại x = 0 : lim f (x) 2 - 2 f (x) x x x®0 a) = b) b) Vì x 2
+Yêu cầu học sinh giải thích x + = 2x lim = ¥ 2 x + 2x cách làm của mình. x® 2 0 x f (x) = Có thể gán cho f(0) giá 2 nên không thể gán f(0) x
bất cứ giá trị nào để hàm trị bằng bao nhiêu để hàm số f(x) trở
số f(x) liên tục tại x = 0. thành liên tục tại x = 0. Bài giải 2 x - 2x
a) lim f (x) = lim = 2 - để hàm x®0 x®0 x
HĐ 2:Xét tính liên tục của hàm
số liên tục tại x = 0 thì f (0) = 2 - . số trên khoảng . Ta có
+yêu cầu học sinh nhắc lại tính 2 x -1
chất của hàm số liện tục trên lim x 1+ ® 1- x
Bài tập 3: Hãy chọn a để hàm số 7’ khoảng đoạn. = lim(- x - ) = - ì 2 x - 1 1 2 , x ³ x 1+ ® ï y = 1
+Giáo viên hướng dẫn lại cho í 1 - x liên tục trên R .
và lim(2x + a) = 2 + a . ï các học sinh x - ®1
î2x + a, x <1
Để hàm số liên tục trên
Bài tập 4: Xét tính liên tục của hàm số R thì sau : 2 + a = 2 - Û a = 4 - . ì 3 x - 2 x + 2x - 2 x
a) f (x) ï , ¹ = 1 í x -1 ï ,4 x = î 1 ì 2 x - x - 6 2 10 ï x( , x 3x 0 x - ) - ¹ 3
+Học sinh nêu đáp số và
b) f (x) ïï = a, x = lên bảng trình bày lời í 0 . ï 10’ giải. ïb, x = 3 ïî 46
Giáo án Tự chọn 11 *Ôn tập củng cố:
+Yêu cầu học sinh nhắc lại xét tính liên tục tại một điểm, liên tục trên khoảng.
+Yêu cầu học sinh về nhà làm lại các bài tập và chuẩn bị bài tập cho tiết học sau.
Tiết 2: Về sự tồn tại nghiệm của phương trình.
*Ổn định lớp, kiểm diện sĩ số. *Bài mới:
Tg Hoạt động của giáo viên
Hoạt động của học sinh Ghi bảng. 5’
HĐ 1: Kiểm tra hệ quả của
Hệ qủa : Hàm số f liên tục trên [a;b] hàm số liên tục.
và f (a) f (b) < 0 thì tồn tại ít nhất +Giáo viên yêu cầu học
+Học sinh nhắc lại kiến thức c Î ( ;
a b): f (c) =
sinh đứng tại chỗ trả lời. cơ bản. một điểm 0 . 8’
HĐ 2: vận dụng hệ quả về
sự tồn tại nghiệm của + a) f (0) f ( ) 1 = 6 - < 0 Û
phương trình vào bài tập.
Bài tập1: Chứng minh rằng phương
phương trình có ít nhất một trình : nghiệm trên ( ) 1 ; 0 . +Giáo viên yêu cầu học a) 3 2
x + 2x - 2 = 0 có ít nhất một
sinh lên bảng trình bày và nghiệm .
giải thích cách làm của b) 4 4 x + 2 2
x - x - 3 = 0 có ít nhất +Học sinh xong phong lên mình. (- )
bảng trình bày và giải thích hai nghiệm trên khoảng 1 ; 1 . cách làm của mình. 10 ’
HĐ 3: Tìm số nghiệm của phương trình: +Học sinh chú ý.
Bài tập 4:Chứng tỏ rằng các phương +Giáo viên cho học sinh +Hàm số f(x)= ax2+b x+c
trình sau luôn luôn có nghiệm.
nêu ý tưởng lời giải. liên tục trên R. a/. cosx+mcos2x=0. HĐ 4:Chứng minh một +f(0)=c; b/.m(x-1)3(x+2)+ 2x+3=0.
phương trình có nghiệm với f(1/3)= 1/9( a+3b+9c).
Bài tập 5:Cho phương trình ax2+b
mọi giá trị của tham số m. Suy ra: f(0)+ 18f(1/3)= x+c=0 +Yêu cầu học sinh phát 2a+6b+19c.
Với a ¹ 0 và 2a+6b+19c=0. Chứng 8’ hiện và chứng minh bài +Nếu f(0)=0 hay f(1/3)=0
minh rằng phương trình luôn có toán đúng hướng. phương trình f(x)=0 có nghiệm thuộc [0;1/3]. nghiệm thuộc [0;1/3]. Giải: +Nếu f ( ) 0 ¹ 0 và f 1 ( / ) 3 ¹ 0 suy ra: f(0).f(1/3) <0. *Ôn tập củng cố: 2’
+Nêu phương pháp chứng minh về sự tồn tại nghiệm của phương trình. +Bài tập trắc nghiệm: ìax+3 ,x ³1
Bài 1.Cho hàm số f (x) = í
đ ể hàm số liên tục tai x=1 giá trị a bằng: 2
îx + x -1, x < 1 A.-2 B.-1 C.0 D.1 2 ìx - 4 ï khi x > 2
Bài 2:Cho hàm số y = í x - 2
. Giá trị a để hàm số liên tục tại x = 2 là: 5 ïî x + a khix £ 2 A. a = -10 B. a = 10 C.a = 6 D. a= -6
Bài 3) Tìm a,b để hàm số sau liên tục trên R 47
Giáo án Tự chọn 11 ìx2 < x khi 1 ï f(x) = íax + 1 khi b £ x £ 3 ï î4 - x khi x > 3
b) Chứng minh rằng phương trình: x3 – 3x2 + 3 = 0 có 3 Tiết 27
QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN I.Mục tiêu:
Qua chủ đề này HS cần:
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản về quan hệ vuông góc trong
không gian và bước đầu hiểu được một số kiến thức mới về quan hệ vuông góc trong không gian trong
chương trình chưa được đề cập trong chương trình chuẩn.
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về quan hệ vuông góc trong không gian.
Thông qua việc rèn luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và
tìm hiểu một số kiến thức mới trong chương trình nâng cao.
3)Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác. 48
Giáo án Tự chọn 11
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:
-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
.III Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm.
+Ôn tập kiến thức:
GV nêu câu hỏi để ôn tập kiến thức cũ… *Bài mới:
Hoạt động của GV
Hoạt động của HS Nội dung
10 HĐ1: Ôn tập kiến thức về 1)Ôn tập:
quan hệ vuông góc trong không gian:
1)Phép toán về vectơ trong không gian:
Gọi HS nhắc lại kiến thức bằng HS chú ý theo dõi và suy
cách đưa ra hệ thống câu hỏi:
nghĩ trả lời các câu hỏi đặt +Quy tắc 3 điểm; ra … +Quy tắc hình bình hành; +Hiệu của 2 vectơ; + Quy tắc hình hộp;
+Điều kiện đồng phẳng của 3
HS nhận xét, bổ sung và ghi vectơ trong không gian. chép … 2)Quan hệ vuông góc:
+Góc giữa hại đường thẳng;
+Hai đường thẳng vuông góc;
+Đường thẳng vuông góc với
mặt phẳng; Phương pháp chứng
minh 2 đường thẳng vuông góc,
2 mặt phẳng vuông góc,…
+Khoảng cách giữa hai đường
thẳng chép nhau, giữa đường
thẳng và mặt phẳng song song,…
15 HĐ2: Bài tập áp dụng: Bài tập 1:
Sử dụng các quy tắc của vectơ
Cho hình chóp S.ABCD có đáy
để biến đổi vế này thành vé
ABCD là hình chữ nhật. Chứng
kia của một đẳng thức vectơ: minh rằng: !!" !!" !!" !!!"
GV nêu đề bài tập và cho HS )
a SA + SC = SB + SD
các nhóm thảo luận để tìm lời
HS thảo luận theo nhóm để !!"2 !!"2 !!"2 !!!"2
giải và gọi HS đại diện lên
tìm lời giải và cử đại diện )
b SA + SC = SB + SD bảng trình bày.
lên bảng trình bày lời giải
Gọi HS nhận xét, bổ sung (nếu (có giải thích) cần)
HS nhận xét, bổ sung và sửa
GV nhận xét, bổ sung và nêu lời chữa ghi chép…
giải đúng (nếu HS không trình
HS trao đổi theo nhóm để bày đúng lời giải) rút ra kết quả:…. b)Phân tích: !!"2 !!" !!!"
SA = (SO+ OA)2 = ... !!" !!"2 !!!"2
Tương tự: SC , SB , SD ,...
15 HĐ3: Bài tập áp dụng: Bài tập 2:
Chứng minh hai đường thẳng
Cho tứ diện ABCD có hai cặp
vuông góc nhau trong không
cạnh đối diện AB và CD, AC và 49
Giáo án Tự chọn 11 gian:
HS thảo luận theo nhóm dể
DB vuông góc với nhau. Chứng
GV nêu đề bài tập và cho HS
tìm lời giải và cử đại diện
minh rằng cặp cạnh đối diện còn
các nhóm thảo luận để tìm lời
lên bảng trình bày (cóa giải
lại là AD và BC cũng vuông góc
giải và gọi HS đại diện lên thích) với nhau. bảng.
HS nhận xét, bổ sung và sửa
Gọi HS nhận xét, bổ sung (nếu chữa ghi chép… cần).
HS trao đổi rút ra kết quả:
GV nhận xét, bổ sung và nêu lời ….
giải đúng (nếu HS không trình bày đúng lời giải)
HD: Sử dụng hiệu hai vectơ…
HĐ4: Củng cố và hướng dẫn học ở nhà(5) *Củng cố:
-Nhắc lại phương pháp chứng minh hai đường thẳng vuông góc, đường thẳng vuông góc mặt phẳng, …
*Hướng dẫn học ở nhà:
- Xem lại các bài tập đã giải, làm thêm bài tập sau: Bài tậpVN:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng (ABCD). Hình chiếu
vuông góc của A trên SB, SD lần lượt là H, K.
a) Chứng minh cá mặt bên của hình chóp S.ABCD là các tam giác vuông.
b) Chứng minh AH và AK cùng vuông góc với SC.
b) Mặt phẳng (AHK) cắt đoạn thẳng SC tại I, chứng minh HK vuông góc với AI. Tiết 28,29
LUYỆN TẬP QUAN HỆ VUÔNG GÓC I. Mục tiêu
- Củng cố kiến thức về quan hệ vuông góc giữa hai đường thẳng ,giữa đường thẳng và mặt phẳng
- Nắm được cách chứng minh đường thẳng vuông góc đường thẳng ,đường thẳng vuông góc mặt phẳng
II Phương pháp tiết dạy :
Gợi mở thảo luận nhóm
III. Tiến trình giờ dạy: 1.Ổn định lớp .
2 Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. 3.Bài mới: Tiết 1 Tg Hoạt động của GV Hoạt động của HS Nội dung 50
Giáo án Tự chọn 11 10 HĐ1: 1. Ôn tập: HĐTP1:Ôn tập lí thuyết: GV gọi HS nhắc lại
định nghĩa đường thẳng
2. Bài tập1: (Bài tập VN) vuông góc với mặt
Cho hình chóp S.ABCD có đáy ABCD là hình
phẳng, định lí 3 đường
vuông, SA vuông góc với mặt phẳng (ABCD). vuông góc,…
Hình chiếu vuông góc của A trên SB, SD lần Gọi HS nêu phương lượt là H, K. pháp chứng minh đường
a) Chứng minh các mặt bên của hình chóp thẳng d vuông góc với
S.ABCD là các tam giác vuông. mặt phẳng (a )
b) Chứng minh AH và AK cùng vuông góc với SC.
b) Mặt phẳng (AHK) cắt đoạn thẳng SC tại I, HS suy nghĩ trả lời câu
chứng minh HK vuông góc với AI. S hỏi … I K HĐTP2: Bài tập áp HS nhận xét, bổ sung H D dụng: … A
GV gọi HS đại diện các B C nhóm lên bảng trình bày
lời giải bài tập về nhà. HS đại diện lên bảng
a) các mặt bên của hình chóp là các tam giác Gọi HS nhận xét, bổ trình bày lời giải (có vuông: sung (nếu cần). giải thích) Ta có: GV nhận xét, bổ sung HS nhận xét, bổ sung SA ^ ( ABCD) Þ SA ^ A ,
B SA ^ AD Þ Hai và nêu lời giải đúng và sửa chữa ghi chép…
tam giác SAB, SAD vuông tại A; (nếu HS không trình 30’ bày đúng lời giải) b) AH ^ S , C AK ^ SC : HS suy nghĩ nêu HĐ2: Chứng minh phương pháp chứng ìAH ^ SB Þ AH ^ (SBC) Ta cã : í
đường thẳng vuông góc minh đường thẳng îAH ^ BC Þ AH ^ SC với mặt phẳng: vuông góc với mặt
Chứng minh tương tự ta cũng có: AK ^ S . C HĐTP1: phẳng… c) HK ^ AI Để chứng minh đường Để chứng minh đường
Hai tam giác vuông SAB và SAD bằng nhau thẳng a vuông góc với thẳng a vuông góc với
(vì cạnh SA chung, AB = AD) nên những đoạn a mặt phẳng a ( ) ta phải mặt phẳng ( ) ta có 2
tương ứng trong hai tam giác cũng bằng nhau, cách sau: làm gì? do đó ta có: +Chứng minh a vuông
GV gọi HS đứng tại chỗ góc với hai đường ìSH = SK SH SK í Þ = Þ HK // . BD trả lời câu hỏi. thẳng cắt nhau nằm îSB = SD SB SD Gọi HS bổ sung (nếu trong mặt phẳng a ( ) ; ìBD ^ SA cần) +Chứng minh a song í îBD ^ AC song với một đường thẳng b vuông góc với
Þ BD ^ (SAC); HK ^ BD , HK ^ (SAC) Þ HK ^ AI a ( ) . Tiết 2 HS thảo luận theo nhóm
để tìm lời giải và cử đại HĐTP2: Bài tập áp dụng:
diện lên bảng trình bày (có giải thích)
GV nêu đề bài tập (hoặc
15’ phát phiếu HT) và cho HS nhận xét, bổ sung và sửa chữa ghi chép… HS cac nhóm thảo luận để tìm lời giải.
HS trao đổi và rút ra kết quả:… Gọi HS đại diện lên Bài tập 2:
bảng trình bày lời giải.
Cho tư diện S.ABC có SA vuông góc với mặt Gọi HS nhận xét, bổ sung (nếu cần)
phẳng (ABC) và tam giác ABC vuông tại B. 51
a) Chứng minh đường thẳng BC vuông góc GV nhận xét, bổ sung với mặt phẳng (SAB); và nêu lời giải đúng
b) Gọi AH là đường cao của tam giác SAB. (nếu HS không trình bày đúng lời giải).
Chứng minh AH vuông góc với mặt phẳng
Giáo án Tự chọn 11
Bài 1(hướng dẫn 10’). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O, SA=a 2 . SA
vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của A trên SB, SC, SD.
a. CMR: AD ^ (SAB) và CD ^ (SAD) b. OI // (SAB)
c. (AHK) là mặt phẳng trung trực của đoạn thẳng SC
Bài tập 2:Cho tứ diện OABC có ba cạnh OA,OB,OC đôi một vuông góc nhau.Gọi H là hình chiếu của O lên mp(ABC) a/CM: BC ^(OAH)
b/Tính góc giữa hai đường thẳng AC vàOB 1 1 1 1 c/CM: = + + 2 2 OH OA 2 2 OB OC
d/Gọi a,b,d lần lượt là góc giữa các đường thẳng OA,OB,OC với mp(ABC). CM: sin2a + sin2b + sin2d =1 Bài tập 1:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Mặt SAB là tam giác cân tại S và mặt phẳng (SAB)
vuông góc với mặt phẳng (ABCD). Gọi I là trung điểm của đoạn thẳng AB. Chứng minh rằng:
a)BC và AD cùng vuông góc với mặt phẳng (SAB).
b)SI vuông góc với mặt phẳng (ABCD). Bài tập 3:
Cho hình thoi ABCD tâm O; gọi S là một điểm trong không gian sao cho hai mặt phẳng (SAC) và (SBD)
vuông góc với nhau. Chứng minh SO vuông góc với mặt phẳng (ABCD).
Bài 4: . (4 điểm ) Cho hình chóp S.ABCD có SA ^ (ABCD) và SA = a 2 đáy ABCD là hình thang
vuông tại A và B có AB = BC = a ; AD = a 2
a) Chứng minh rằng: tam giác SCD vuông.
b) Tính khoảng cách từ A đến mặt phẳng (SBC). .
c) Từ điểm I là trung điểm của AD ta dựng IJ vuông góc với SD (JÎ SD). Chứng minh: SD vuông
góc với mặt phẳng (CIJ)
d) Tính góc giữa hai mặt phẳng (SAD) và (SCD).
Bài 5: . (3 điểm ) Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và ∑ 0
BAD = 60 . Gọi O là giao 3a
điểm của AC và BD. Đường thẳng SO ^ (ABCD) và SO =
. Gọi E là trung điểm của BC, F là trung điểm 4 của BE.
a) Chứng minh (SOF) ^ (SBC).
b) Tính các khoảng cách từ O và A đến (SBC). Bài 6.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O; gọi I, J lần lượt là trung điểm các cạnh AB, BC.
Biết SA = SC, SB = SD. Chứng minh rằng:
a) Đường thẳng SO vuông góc với mặt phẳng (ABCD).
b) Đường thẳng IJ vuông góc với mặt phẳng (SBD).
HĐ3: Củng cố và hướng dẫn học ở nhà (5/) *Củng cố:
-Nhắc lại phương pháp chứng minh 2 đường thẳng vuông góc, đường thẳng vuông góc mặt phẳng,…
*Hướng dẫn học ở nhà:
- Xem lại các bài tập đã giải, xem lại phương pháp chứng minh 2 mặt phẳng vuông góc với nhau. - Làm bài tập sau:
-----------------------------------&------------------------------------ 52
Giáo án Tự chọn 11 TIẾT 30
LUYỆN TÂP QUAN HỆ VUÔNG GÓC I. Mục tiêu +Về kiến thức:
- Định nghĩa đường thẳng vuông góc với mặt phẳng, định lý 3 đường vuông góc
- Góc giữa đường thẳng và mặt phẳng +Về kĩ năng:
- Rèn luyện kỹ năng vẽ hình
- Thành thạo dạng toán chứng minh: hai đường thẳng vuông góc, đường thẳng vuông góc với mặt phẳng +Về tư duy, thái độ:
- Rèn luyện trí tưởng tượng không gian cho học sinh.
- Tích cực hoạt động, có tinh thần hợp tác.
- Thái độ học tập nghiêm túc II. Chuẩn bị
GV : SGK, dụng cụ dạy học, bảng phụ và giáo án
HS : làm bài tập trước khi đến lớp
III. Phương pháp: Gợi mở, vấn đáp, luyện tập
IV. Tiến trình bài dạy
1. Ổn định lớp: (1’) Kiểm tra sĩ số, tác phong 2. Bài mới:
*HĐ1: Rèn luyện kỹ năng vẽ hình và giải toán 53
Giáo án Tự chọn 11 5’
Bài tập Cho tứ diện OABC có ba cạnh
OA,OB,OC đôi một vuông góc nhau.Gọi
H là hình chiếu của O lên mp(ABC) a/CM: BC ^(OAH)
b/Tính góc giữa hai đường thẳng AC vàOB
-Đọc đề, tóm tắt giả thiết và 1 1 1 1 h/d HS vẽ hình -HS thực hiện c/CM: = + + 2 2 OH OA 2 2 OB OC
d/Gọi a,b,d lần lượt là góc giữa các
đường thẳng OA,OB,OC với mp(ABC). CM: sin2a + sin2b + sin2d =1 O
8’ -Nêu các pp chứng minh
đường thẳng vuông góc với mặt phẳng? - HS trả lời câu hỏi A B -Trong bài toán này em dùng pp nào? H A' Gợi ý: .BC vuông góc với đoạn C nào trong mp(OAH)? a/CM:BC ^(OAH)
.BC còn vuông góc với -HS trả lời đoạn nào trong (OAH)? -HS khác nhận xét
-Nhận xét, đánh giá, chính xác hoá -Gọi HS nêu cách làm -HS trả lời
-HS dùng đ/n để xác định -Cho HS xung phong giải -H/dẫn:
và tính góc giữa hai đường ^
thẳng AC và OB sẽ bế tắc? BC OH ü
ý Þ BC ^ (OAH )
7’ -Không nên sử dụng cách
OA ^ (OBC) Þ BC ^ OAþ
này, nên dựa vào câu a để -HS xung phong giải.
b/Tính góc giữa hai đường thẳng AC và
-HS liên hệ đến hệ thức nào -HS đứng tại chỗ trình OB đã học? bày -Nhìn vào hình vẽ xem OH
7’ là đường cao của tam giác
-H/dẫn: AC ^ (OBH) Þ AC ^ OB
vuông nào? Từ đó ta cần -HS thực hiện
Vậy góc giữa AC và OB bằng 900
dựng thêm đường phụ nào 1 1 1 1 không? c/CM: = + + 2 2 OH OA 2 2 OB OC -Cho biết kết quả -H/dẫn: -HS trả lời 1 D OAA' vuông tại O ( với = ? 2 OH A' = AH Ç BC)
-Liên hệ giữa hệ thức vừa 1 1 1 ü
nêu với vế phải của hệ thức = + 8’ a 2 2 2 OH OA ' OA ïï
cần chứng minh. Em cần -Học sinh xđ góc trên ý Þ đpcm
phải làm gì để hoàn thành hình vẽ 1 1 1 ï = + 2 2 2 ï yêu cầu của bài toán? ' OA OB OC þ
-Gọi HS xác định góc a ? -HS trả lời
d/CM: sin2a + sin2b + sin2d = 1 (ttự xđ góc b và d) 2 2 OH OH -H/dẫn: sin2a = ; sin2b = và -Gọi HS tính sin2a = ? 2 2 OA OB 2 OH
*Gợi ý: Dựa vào kết quả sin2d = 2 54 OC của câu c
Do đó: sin2a + sin2b + sin2d= = ( ) =1(đpcm)
Giáo án Tự chọn 11
* Củng cố - Dặn dò: Xem kỹ bài toán trên, đồng thời qua bài tập này chúng ta rút ra một số pp CM thường
dùng khi giải các bài tập liên quan Bài tập
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ^ (ABCD) và SA = a.
a) Chứng minh: (SAB) ^ (SBC)
b) Tính góc giữa hai mặt phẳng (SAD) và (SCD)
c) Tính khoảng cách từ điểm A đến mặt phẳng (SBD)
d) Tính khoảng cách giữa hai đường thẳng AC và SB
Bài 2 : Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và SC =
a 2 . Gọi H và K lần lượt là trung điểm của AB và AD. a. Chứng minh SH ^ (ABCD) b. Chứng minh AC ^ SK c. Chứng minh CK ^ SD. Tiết 31 ,32
Luyện tập Đạo Hàm I.Mục tiêu:
Qua chủ đề này HS cần:
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản của đạo hàm và bước đầu hiểu
được một số kiến thức mới về đạo hàm.
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về đạo hàm. Thông qua việc rèn luyện giải
toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và tìm hiểu một số kiến thức mới
trong chương trình nâng cao.
- Hiểu và áp dụng được cách tính đạo hàm bằng định nghĩa vào giải bài tập.
- Nắm được các công thức tính đạo hàm cơ bản.
- Tính được đạo hàm cấp hai, vi phân của một hàm số.
3)Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:
-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập kiến thức cũ, làm bài tập trước khi đến lớp. III.Các tiết dạy:
Tiết 1: Ôn tập kiến thức về đạo hàm cơ bản và bài tập áp dụng.
Tiết 2: Ôn tập kiến thức về đạo hàm cơ bản và bài tập áp dụng(tt) Tiết 1
*Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
-Nêu các công thức tính đạo hàm tổng, hiệu, tích, thương, các công thức tính đạo hàm thường gặp, đạo hàm
của các hàm số lượng giác,... p
*Bài tập: Tính các đạo hàm bằng cách sử dụng định nghĩa: y = t anx, tai x = . 4 -+Bài mới: 55
Giáo án Tự chọn 11 TG Hoạt động của Hoạt động của Nội dung GV HS 10’ HĐ1: Bài tập 1: GV nêu lại ba HS thảo luận và
Tìm công thức tính đạo hàm của các hàm số sau bằng bước tính đạo cử đại diện lên
cách sử dụng định nghĩa: hàm bằng định bảng trình bày lời )
a y = f (x) = ax + ; b nghĩa... giải. 2 )
b y = ax + bx + ; c Bài tập áp dụng: HS nhận xét, bổ GV cho HS thảo sung ... ax + b ) c y = ; luận theo nhóm và cx + d gọi HS đại diện ) c y = x. lên bảng trình bày
Trong miền xác định của mỗi hàm số. lời giải. Gọi HS nhận xét, HS chú ý theo bổ sung. dõi trên bảng để GV nhận xét, bổ lĩnh hội kiến
sung và chỉnh sửa. thức... GV nêu công thức đạo hàm của các hàm số đã ra trong bài tập 1. 20’ HĐ2: Bài tập 2: GV gọi HS lên HS lên bảng ghi
Dùng công thức tính đạo hàm của các hàm số sau: bảng ghi lại các lại công thức. x +1 công thức tính a) y = x - 2; x - 2 đạo hàm của các
b) y = x tan ; x hàm số thường HS thảo luận theo gặp. nhóm để tìm lời c) y = ( 2 x - ) 1 ( 3 5 - 4x ). Nêu bài tập áp giải và cử đại dụng: diện lên bảng
Cho HS thảo luận trình bày (có giải
và gọi HS đại diện thích) lên bảng trình bày lời giải. HS nhận xét, bổ Gọi HS nhận xét, sung . bổ sung (nếu cần) GV nhận xét, Chú ý theo dõi chỉnh sửa và bổ
trên bảng để lĩnh sung... hội kiến thức. Bài tập 3 10’
Dùng công thức, hãy tính đạo hàm của các hàm số sau: ) a y = ( 2 x + 2)( 2 1- 3x ) 2 ; )
b y = x + 4x +1; 5 ) c y = sin . x o c s2 ;
x d)y = ( 2 x + x + ) 1 x +1. HĐ3:
Củng cố và hướng dẫn học ở nhà: *Củng cố:
- Nêu lại ba bước tính đạo hàm bằng định nghĩa, các công thức tính đạo hàm tổng, hiệu, tích, thương; Các
công thức tính đạo hàm thường gặp.
*Hướng dẫn học ở nhà: 56
Giáo án Tự chọn 11
-Xem lại các bài tập đã giải.
- Học thuộc các công thức tính đạo hàm thường gặp.
- Ôn tập lại phương trình tiếp tuyến của một đường cong khi biết tiếp điểm. hệ số góc, song song với một
đường thẳng, vuông góc với một đường thẳng,...
-----------------------------------&----------------------------------- Tiết 2
*Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
Ôn tập kiến thức cũ bằng các đưa ra hệ thống câu hỏi sau:
-Nêu các công thức phương trình tiếp tuyến tại một điểm, nêu phương trình đường thẳng đi qua một điểm và
có hệ số góc k; phương trình đường thẳng song song với một đường thẳng đã cho, vuông góc với một đường thẳng đã cho.
*Bài tập: Viết phương trình đường thẳng đi qua điểm M0(x0; y0) Biết rằng đường thẳng: a) Có hệ số góc k;
b) Song song với đường thẳng (d): ax + b y + c = 0;
c) Vuông góc với đường thẳng (d’): y = k’x + b. *Bài mới: TG
Hoạt động của GV
Hoạt động của HS Nội dung 10’ HĐ1:
HS viết các công thức trên Bài tập 1:
GV gọi HS lên bảng viết lại bảng...
Dùng công thức, tính đạo hàm của
công thức đạo hàm của các các hàm số sau: hàm số lượng giác. x 3
GV nêu đề bài tập và cho HS HS thảo luận theo nhóm và ) a y = o c s ; 3
thảo luận tìm lời giải.
cử đại diện lên bảng trình ) b y = xsin ; x
GV gọi HS nhận xét, bổ sung bày... (nếu cần). HS nhận xét, bổ sung 2 ) c y = tan x +1.
GV chỉnh sửa và bổ sung.
Chú ý theo dõi trên bảng để lĩnh hội kiến thức... 20’ HĐ2: Bài tập 1:
GV gọi HS lên bảng viết
HS lên bảng ghi lại phương
Cho đường cong (C) có phương
hương trình tiếp tuyến của
trình tiếp tuyến tại một điểm. trình: y=x3 + 4x +1 một đường cong (C) có
a) Viết phương trình tiếp tuyến với
phương trình: y = f(x) tại
đương cong (C) tai điểm có hoành điểm có hoành độ x0. độ x0 = 1;
GV nêu bài tập áp dụng:
b) Tiếp tuyến có hệ số góc k = 31;
Cho HS thảo luận theo nhóm HS thảo luận theo nhóm để
c) Song song với đường thẳng: y =
và gọi HS đại diện lên bảng
tìm lời giải và cử đại diện lên 7x + 3; trình bày lời giải.
bảng trình bày lời giải.
d) Vuông góc với đường thẳng:
Gọi HS nhận xét, bổ sung .
HS nhận xét, bổ sung và sửa 1
GV nhận xét, chỉnh sửa và chữa ghi chép... y = - x - 5. 16 bổ sung.
- 3HS nắm thông tin và vận Bài tập 2: 10’
dụng thực hành giải bài tập.
Viết PTTT của dồ thị hàm số: y = – - GV cho HS xác định 3
- Các HS còn lại quan sát, x2 -3 , biết:
dạng tiếp tuyến cụ thể. Rồi
thực hành, nhận xét bài giải.
a) Tiếp tuyến có hoành độ x bằng 1.
lần lượt gọi 2HS lên bảng
- Chính xác hoá về kiến thức. b) Tiếp tuyến có hệ số góc bằng 2. giải.
b) Tiếp tuyến đi qua A(-1; 0 - GV nhấn mạnh phương
pháp giải từng dạng toán tiếp tuyến. HĐ3:(5’)
Củng cố và hướng dẫn học ở nhà: *Củng cố: 57
Giáo án Tự chọn 11
- Nêu lại các công thức tính đạo hàm tổng, hiệu, tích, thương; Các công thức tính đạo hàm thường gặ, các
công thức đạo hàm của các hàm số lượng giác. *Áp dụng:
Dùng công thức, hãy tính đạo hàm của các hàm số sau: - x ) a y = (x + ) 2 1 3 2 2 1 ; )
b y = x - 2x + 3; x 5 ) c y = sin . x o
c s 2x +1; d)y = ( 2 x + 2x + ) 2 1 x +1.
*Hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải.
- Học thuộc các công thức tính đạo hàm thường gặp.
- Ôn tập lại cách tính đạo hàm cấp hai của một hàm số.
-----------------------------------&------------------------------------ Tiết 33,34
LUYỆN TẬP HÌNH HỌC KHÔNG GIAN KHOẢNG CÁCH I.Mục tiêu:
Qua chủ đề này HS cần:
1)Về Kiến thức: Làm cho HS hiểu sâu sắc hơn về kiến thức cơ bản về quan hệ vuông góc trong
không gian và bước đầu hiểu được một số kiến thức mới về quan hệ vuông góc trong không gian trong
chương trình chưa được đề cập trong chương trình chuẩn.
2)Về kỹ năng: Tăng cường rèn luyện kỹ năng giải toán về quan hệ vuông góc trong không gian.
Thông qua việc rèn luyện giải toán HS được củng cố một số kiến thức đã học trong chương trình chuẩn và
tìm hiểu một số kiến thức mới trong chương trình nâng cao.
3)Về tư duy và thái độ:
Tích cực hoạt động, trả lời câu hỏi. Biết quan sát và phán đoán chính xác.
Làm cho HS hứng thú trong học tập môn Toán.
II.Chuẩn bị củaGV và HS:
-GV: Giáo án, các bài tập và phiếu học tập,…
-HS: Ôn tập liến thức cũ, làm bài tập trước khi đến lớp.
III Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
GV nêu câu hỏi để ôn tập kiến thức cũ… *Bài mới: Tg
Hoạt động của GV
Hoạt động của HS Nội dung 20 HĐ1: Bài tập1: GV gọi HS nêu cách
Cho hình lập phương ABCD.A’B’C’D’
dựng khoảng cách từ
HS suy nghĩ và trả lời ... cạnh a.
một điểm đến một
a)Chứng minh rằng khoảng cách từ các
đường thẳng, đến một
điểm B,C,D,A’,B’,D’ đến đường chéo mặt phẳng.
AC’ bằng nhau. Hãy tính khoảng cách
Nêu bài tập áp dụng.
HS thảo luận và cử đại diện đó.
GV cho HS thảo luận
lên bảng trình bày lời giải.
b)Tính khoảng cách từ đỉnh A đến mặt theo nhóm.
HS nhận xét, bổ sung và sửa phẳng (A’BD) của hình lập phương.
Gọi HS đại diện lên chữa ghi chép...
bảng trình bày lời giải.
GV gọi HS nhận xét, bổ HS chú ý theo dõi trên bảng sung.
để lĩnh hội kiến thức... GV nhận xét, bổ sung và sửa chữa. 58
Giáo án Tự chọn 11 20 HĐ2: Bài tập 2:
GV: Gọi HS nêu cách
HS suy nghĩ và trả lời ...
Cho hình tứ diện OABC có OA, OB, OC
dụng: +Khoảng cách
đôi một vuông góc và OA = OB = OC =
giữa đường thẳng và
a. Gọi I là trung điểm của cạnh BC. Tìm
mặt phẳng song song;
khoảng cách giữa AI và OC đồng thời
+ Khoảng cách giữa
xác định đường vuông góc chung của hai
hai đường thẳng chéo đường thẳng đó. nhau.
Để tính khoảng cách giữa
Để tính khoảng cách
hai đường thẳng chéo nhau
giữa hai đường thẳng a và b ta tính: chéo nhau a và b ta
+ Khoảng cách giữa a và
phải tính như thế nào?
mặt phẳng (a ) chứa b và song song với a.
+ Tính khoảng cách giữa hai
mặt phẳng song song lần
lượt chứa a và b.
HS thảo luận và cử đại diện
lên bảng trình bày lời giải (có giải thích)
GV nêu đề bài tập áp
HS nhận xét, bổ sung ...
dụng và cho HS thảo
luận theo nhóm để tìm
lời giải và gọi HS đại
HS chú ý theo dõi trên bảng
diện lên bảng trình bày. để lĩnh hội kiến thức. Gọi HS nhận xét, bổ sung (nếu cần). GV nhận xét, và chỉnh sửa bổ sung.
HĐ3: Củng cố và hướng dẫn học ở nhà (5) *Củng cố:
- Nhắc lại cách xác định khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng; khoảng cách
giữa đường thẳng và mặt phẳng song song và khoảng cách giữa hai đường thẳng chéo nhau, đường vuông
góc chung của hai đường thẳng chéo nhau.
*Hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải, ôn tập lại các phương pháp chứng minh, cách xác định khoảng cách trong quan hệ vuông góc. *Giải bài tập sau:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, có cạnh SA vuông góc với mặt phẳng (ABCD)
và SA = a. Tính khoảng cách giữa hai đường thẳng: a) SB và AD; b) BD và SC. Tiết 2
*Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
GV nêu câu hỏi để ôn tập kiến thức cũ… *Bài mới: Tg
Hoạt động của GV
Hoạt động của HS Nội dung 20 HĐ1: Bài tập 1: Sửa bài tập 1 HS đại diện lên bảng
Cho hình chóp S.ABCD có đáy GV vẽ hình lên bảng.
trình bày lời giải (có giải ABCD là hình chữ nhật. Mặt SAB là
GV gọi HS đại diện các nhóm thích)
tam giác cân tại S và mặt phẳng 59
Giáo án Tự chọn 11
lên bảng trình bày lời giải các
(SAB) vuông góc với mặt phẳng
bài tập 1 và 2 đã ra trong tiết 4. HS nhận xét, bổ sung và
(ABCD). Gọi I là trung điểm của
Gọi HS nhận xét, bổ sung (nếu sửa chữa ghi chép.
đoạn thẳng AB. Chứng minh rằng: cần)
a)BC và AD cùng vuông góc với
GV nhận xét, chỉnh sửa và bổ mặt phẳng (SAB). sung.
b)SI vuông góc với mặt phẳng
HS chú ý theo dõi để lĩnh (ABCD). Bài tập 2 ( tương tự). hội kiến thức... Bài tập 2:
Cho hình thoi ABCD tâm O; gọi S là 10
một điểm trong không gian sao cho
hai mặt phẳng (SAC) và (SBD)
vuông góc với nhau. Chứng minh
SO vuông góc với mặt phẳng (ABCD). 100 HĐ2: Bài tập 3
Sửa bài tập đã ra trong tiếp HS đại diện lên bảng
Cho hình chóp S.ABCD có đáy 5:
trình bày lời giải (có giải ABCD là hình vuông cạnh a, có
GV gọi HS đại diện lên bảng thích)
cạnh SA vuông góc với mặt phẳng trình bày lời giải. HS nhận xét, bổ sung ...
(ABCD) và SA = a. Tính khoảng
Gọi HS nhận xét, bổ sung
cách giữa hai đường thẳng:
GV nhận xét, chỉnh sửa và bổ
Chú ý theo dõi trên bảng a) SB và AD; sung .
để lĩnh hội kiến thức... b) BD và SC.
HĐ3: Củng cố và hướng dẫn học ở nhà (5) *Củng cố:
- Phương pháp chứng minh đường thẳng vuông góc với mặt phẳng.
- Phương pháp chứng minh hai mặt phẳng vuông góc; Xác định và tính được góc giữa hai đường thẳng, giữa
đường thẳng và mặt phẳng, giữa hai mặt phẳng,...
- Cách xác định khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng; khoảng cách giữa
đường thẳng và mặt phẳng song song và khoảng cách giữa hai đường thẳng chéo nhau, đường vuông góc
chung của hai đường thẳng chéo nhau.
*Hướng dẫn học ở nhà:
-Xem lại các bài tập đã giải, ôn tập lại các phương pháp chứng minh, cách xác định khoảng cách, góc trong quan hệ vuông góc, 60
Giáo án Tự chọn 11 Tiết 35,36
BÀI TẬP ĐẠO HÀM HÀM SỐ LƯỢNG GIÁC -ĐAO HÀM CẤP CAO
I. Mục đích, yêu cầu:
- Giúp HS vận dụng thành thạo các quy tắc tìm đạo hàm của các hàm số lượng giác.
- Giúp HS củng cố kĩ năng vận dụng các công thức tìm đạo hàm của những hàm số thường gặp.
- Giúp HS ôn tập một số kiến thức về lượng giác.
-Bài tập áp dụng (tt),đạo hàm cấp cao
II. Chuẩn bị phương tiện dạy học:
+ Giáo viên: Giáo án, bài tập chọn lọc.
+ Học sinh: Vở bài tập.
III. Phương pháp dạy học: Phương pháp vấn đáp, gợi mở.
IV. Tiến trình dạy học: 1. Ổn định lớp: 2. Kiểm tra bài cũ:
Gọi 2 HS lên bảng viết các công thức tính đạo hàm của các hàm số lượng giác. GV gọi 1 HS nhận xét
phần trả lời của bạn. Sau đó GV xem phần trả lời của HS và chỉnh sửa để cho điểm phù hợp.
Tiết 1: Bài tập áp dụng, đao hàm hàm số lượng giác.
Tiết 2: Bài tập áp dụng (tt),đạo hàm cấp cao 3. Bài mới: Tiết 1 TG
Hoạt động của giáo viên
Hoạt động của học sinh Nội dung ghi bảng 61
Giáo án Tự chọn 11
20’ Nhắc lại công thức tính đạo hàm ?
Bài 1:Tìm đạo hàm của các hàm số
HĐ 1:Đạo hàm của hàm số +Học sinh lên bảng trình bày sau: lượng giác. lời giải. a) y = 5sinx - 3cosx. Gọi HS lên bảng. sinx+cosx
GV gợi ý lại các quy tắc tính b) y = . sinx-cosx u
+Học sinh khác nhận xét kết đạo hàm
, u - v, u.v, các quả của bạn mình. c) y = xcotx. v d) y = 1 + 2 t anx .
công thức tính đạo hàm u , 2 + e) y = sin 1 x . sinu Đáp án: a) y’ = 5cosx + 3sinx 2 - b) y’ = . 2 (sinx - cosx) e.y’= ( 1 2 + x )'.cos( 1 2 + x ) x c) y’ = cotx - .
+Giáo viên hướng dẫn lại cho 2 sin x học sinh dưới lớp. 1 d) y’ = . 2 + cos x 1 2 t anx 2 x cos 1+ x e) y’ = . 2 1+ x 15’ Bài 2: f '(1)
-Nghe và thực hiện.
HĐ 2:Tính đạo hàm của hàm a) Tính biết f(x) = x2 và
-Các HS còn lại nhận xét và g '(1) số tại x0. bổ sung . x p g(x) = 4x + sin . Gọi 2 HS lên bảng. 2
GV gợi ý tính f’(x), g’(x) từ b) Tính f’(π) nếu
đó dẫn đến f’ (1), g’(1) và kết sinx - cosx
+Học sinh lên bảng trình bày quả bài toán.
và giải thích cách làm của f(x) = . cosx - xsinx mình. Đáp án:
a) f’(x) = 2x ¨ f’(1) = 2. p x p g’(x) = 4 + cos ¨ g’(1) = 4. 2 2 f '(1) 1 ¨ = . g '(1) 2 b) f’(π) = -π2. 10’
Bài 3:Giải phương trình y’(x) = 0 biết:
+Học sinh xung phong lên a) y = 3cosx + 4sinx + 5x.
HĐ 3:Giải phương trình lượng b) y = sin2x - 2cosx. bảng trình bày và nêu giác.
phương pháp giải phương a) y’ = - 3sinx + 4cosx + 5 Nghiệm phương trình x = trình lượng giác.
GV gợi ý. Tính y’, cho y’=0. p
GV nhắc lại cách giải các j + + k2p 4 với sinφ = ,k Î Z .
phương trình lượng giác và 2 5 b) y’ = -4sin2x + 2sinx + 2
các công thức lượng giác có Nghiệm phương trình liên quan đến bài toán. é p x = + k2p ê 2 ê -p ê 62 x = + k2 ( p k Î Z) ê 6
GV gợi ý: Tính y’ và áp dụng ê 7p ê
các công thức liên quan đến x = + k2p êë 6
Giáo án Tự chọn 11
V. Củng cố và công việc ở nhà: 1 . Củng cố:
+ Viết lại các công thức tính đạo hàm của các hàm số lượng giác.
+ Nhắc lại các dạng bài tập đã làm.
2. Công việc ở nhà:
BT1: Tính đạo hàm các hàm số sau: 2008 a) y = b) y = (x – 2) 2 x +1 2 2 x + a 2 - x + 4x - 5
BT2: Cho hàm số y = f(x) = x - 2 a) Tính f’(-2)
b) Giải bất phương trình f’(x) > 0 . 1
BT3: Viết phương trình tiếp tuyến của đồ thị hàm số y = , biết: x
a) Tiếp tuyến có tung độ bằng -1. 1
b) Tiếp tuyến có hệ số góc bằng - . 4
c) Tiếp tuyến đi qua A(0,1) Tiết 2
*Tiến trình giờ dạy:
-Ổn định lớp, chia lớp thành 6 nhóm.
-Kiểm tra bài cũ: Đan xen với các hoạt động nhóm. +Ôn tập kiến thức:
Ôn tập kiến thức cũ ... *Bài mới: TG
Hoạt động của GV
Hoạt động của HS Nội dung HĐ1: Bài tập 1:
GV nhắc lại định nghĩa đạo
Tính đạo hàm cấp hai của các hàm số
20’ hàm cấp hai của một hàm sau: số.
HS thảo luận theo nhóm để a) y = sin 2 ; x GV nêu bài tập và cho HS
tìm lời giải và cử đại diện b) y = os c 2 ; x thảo luận theo nhóm. lên bảng. 2
Gọi HS đại diện trình bày c) y = sin ; x lời giải. HS nhận xét, bổ sung và 2 d) y = os c ; x
Gọi HS nhận xét, bổ sung sửa chữa ghi chép.
e) y = x tan . x (nếu cần)
HS chú ý theo dõi trên bảng
GV nhận xét, chỉnh sửa và
để lĩnh hội kiến thức. bổ sung. 20’ HĐ2: Bài tập 2:
GV nêu đề bài tập và cho
HS thảo luận và cử đại diện 2 x + 2x + 2 HS thảo luận theo nhóm.
lên bảng trình bày lời giải. a)Cho hàm số: y = 2
Gọi HS đại diện lên bảng HS nhận xét, bổ sung và
Chứng minh rằng: 2y.y’’ – 1 =y’2 trình bày lời giải. sửa chữa ghi chép.
b)Cho hàm số y = x4 -6x2 + 12x -1. Giải
Gọi HS nhận xét, bổ sung.
bất phương trình y// < 0.
GV nhận xét, chỉnh sửa và
HS chú ý theo dõi để lĩnh bổ sung. hội kiến thức... HĐ3(5’)
Củng cố và hướng dẫn học ở nhà: *Củng cố: *Áp dụng: Cho hàm số y = cos22x. a) Tính y”, y”’.
b) Tính giá trị của biểu thức: A= y’’’ +16y’ + 16y – 8. 63
Giáo án Tự chọn 11
*Hướng dẫn học ở nhà:
- Xem lại các bài tập đã giải.
- Ôn tập lại cách tính vi phân của một hàm số. * Làm bài tập sau: Cho hàm số: 2
y = x + x +1 .
a) Tìm hệ thức giữa y’ và y;
b) Tìm hệ thức giữa y’’, y’ và y. HD: a) Tính y’ 2
Þ 2y' x +1- y = 0 b)Tính y” Þ y ( 2 4 ' x + ) 1 + 4xy'- y = 0
-----------------------------------&------------------------------------ Tiết 36 ÔN TẬP CUỐI NĂM 64
Giáo án Tự chọn 11 65




