


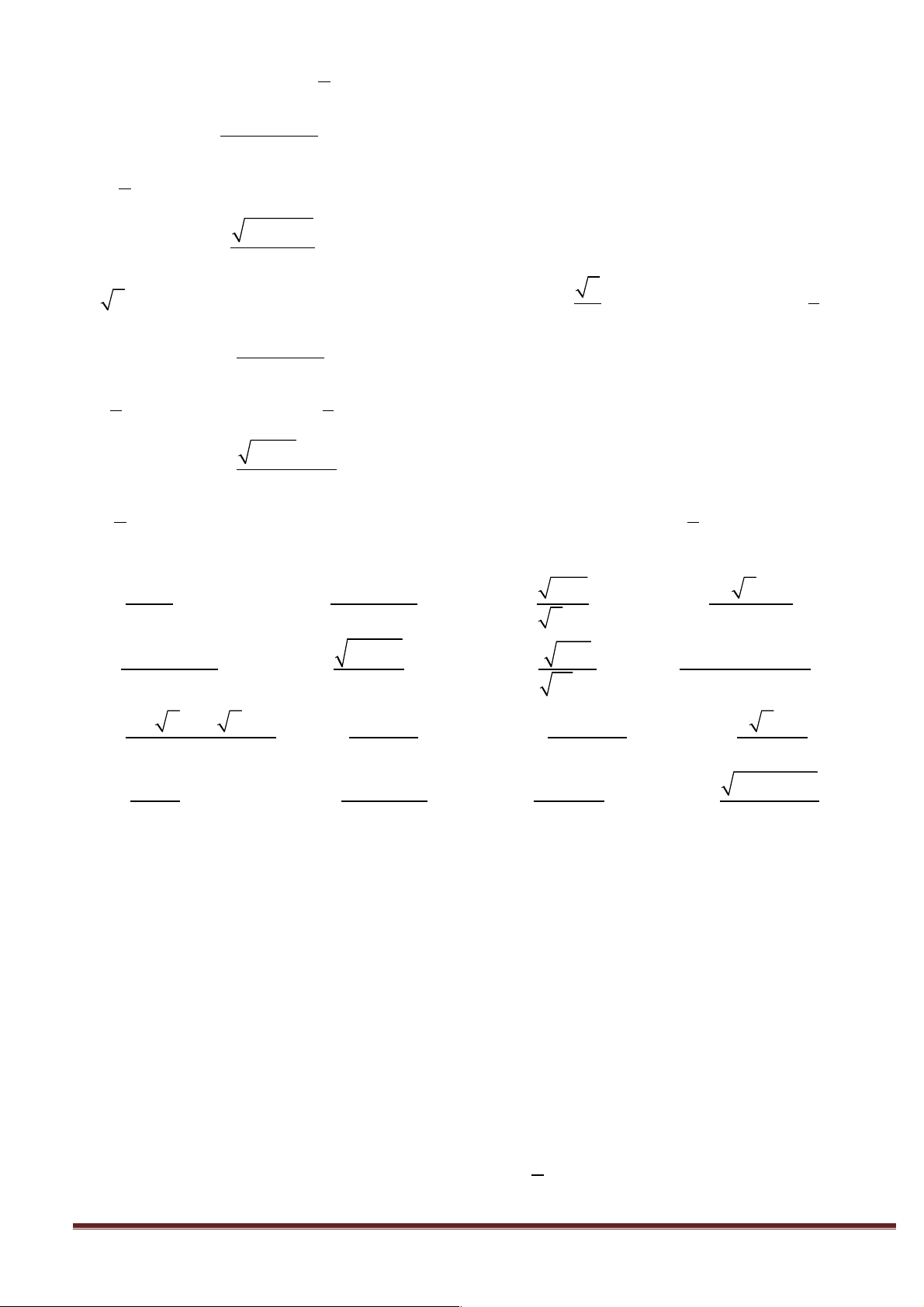


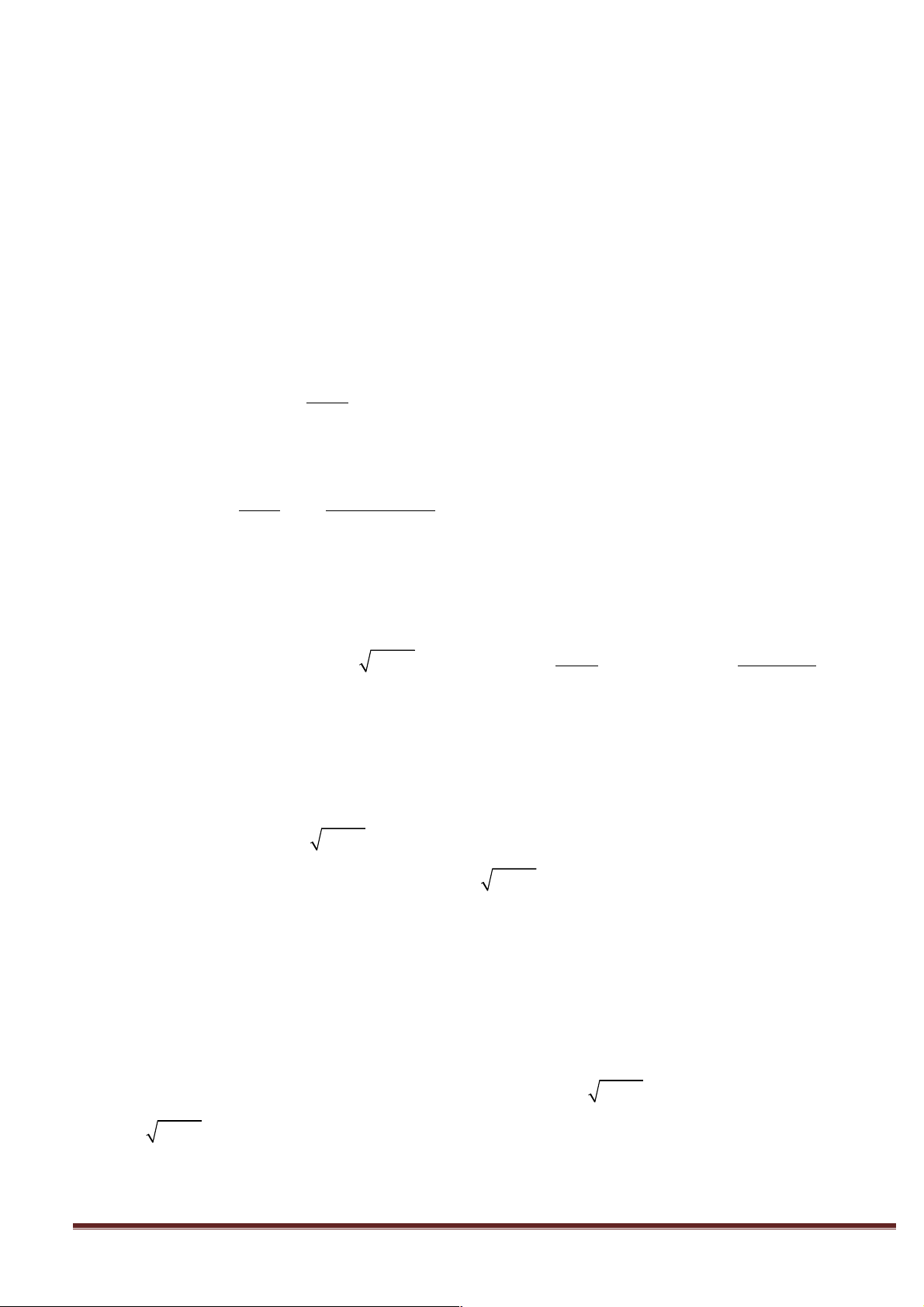




















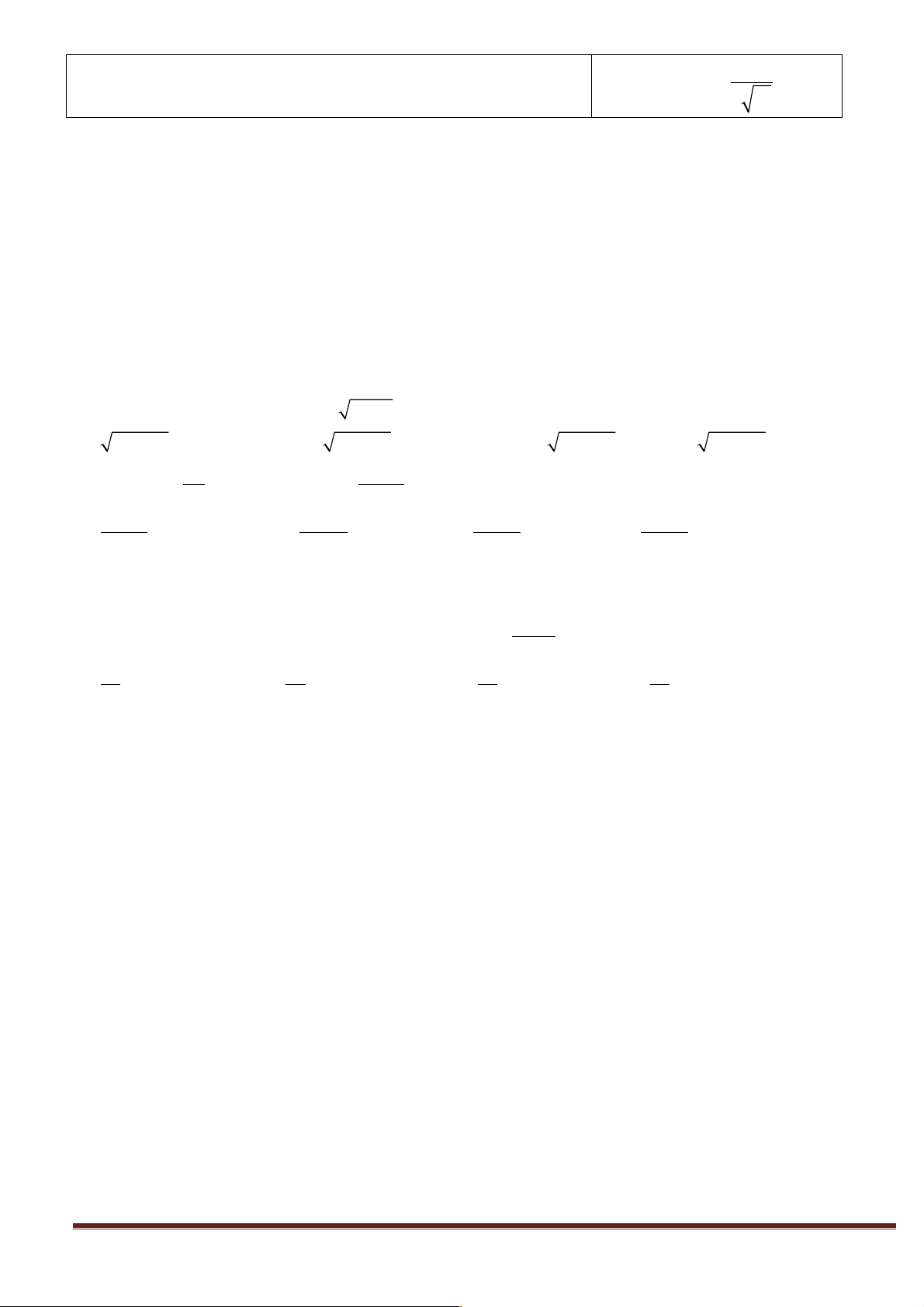





Preview text:
Ngày soạn: 19/1/2019 GIỚI HẠN CỦA DÃY SỐ A. Mục tiêu:
1. Về kiến thức: Qua bài học này, học sinh cần biết được:
- Định nghĩa giới hạn hữu hạn của dãy số.
- Các định lí về giới hạn hữu hạn của dãy số.
2. Về kỹ năng: Học sinh cần rèn luyện các kỉ năng sau:
- Rèn luyện tính cẩn thận chính xác trong tính toán, lập luận.
- Biết vận dụng định lí vào bài tập .
- Xây dựng tư duy logic, linh hoạt, biết quy lạ thành quen, phát triển tư duy logic toán học.
- Biết sử dụng máy tính.
3. Về thái độ:
- Chủ động tích cực tiếp thu kiến thức mới.
- Tích cực và tương tác tốt trong hoạt động nhóm.
- Thái độ hứng thú trong học tập.
4.Định hướng phát triển năng lực:
- Rèn luyện năng lực tự học, năng lực hợp tác, năng lực giao tiếp, năng lực quan sát, năng lực phát hiện và
giải quyết vấn đề, năng lực tính toán, năng lực vận dụng kiến thức vào cuộc sống,…
B. Chuẩn bị của giáo viên và học sinh: 1. Giáo viên:
- Giáo án, đồ dùng dạy học.
- Các bảng phụ (hoặc trình chiếu) và các phiếu học tập. 2. Học sinh:
- Đồ dùng học tập :sgk,máy tính...
- Đọc bài trước ở nhà. C. Phương pháp:
- Gợi mở, vấn đáp.
- Phát hiện và giải quyết vấn đề.
- Tổ chức hoạt động nhóm.
D.Chuổi các hoạt động học:
I. HOẠT ĐỘNG 1:KHỞI ĐỘNG- GIỚI THIỆU(5 phút):
1.Mục tiêu: Giúp HS hình dung được khái niệm giới hạn của dãy số.
2. Phương thức: Vấn đáp, giải quyết tình huống.
3. Năng lực cần đạt: - Giải quyết vấn đề. - Năng lực quan sát.
- Năng lực vận dụng kiến thức vào cuộc sống. 4. Cách tiến hành:
a.Chuyển giao nhiệm vụ-Hình thành khái niệm.
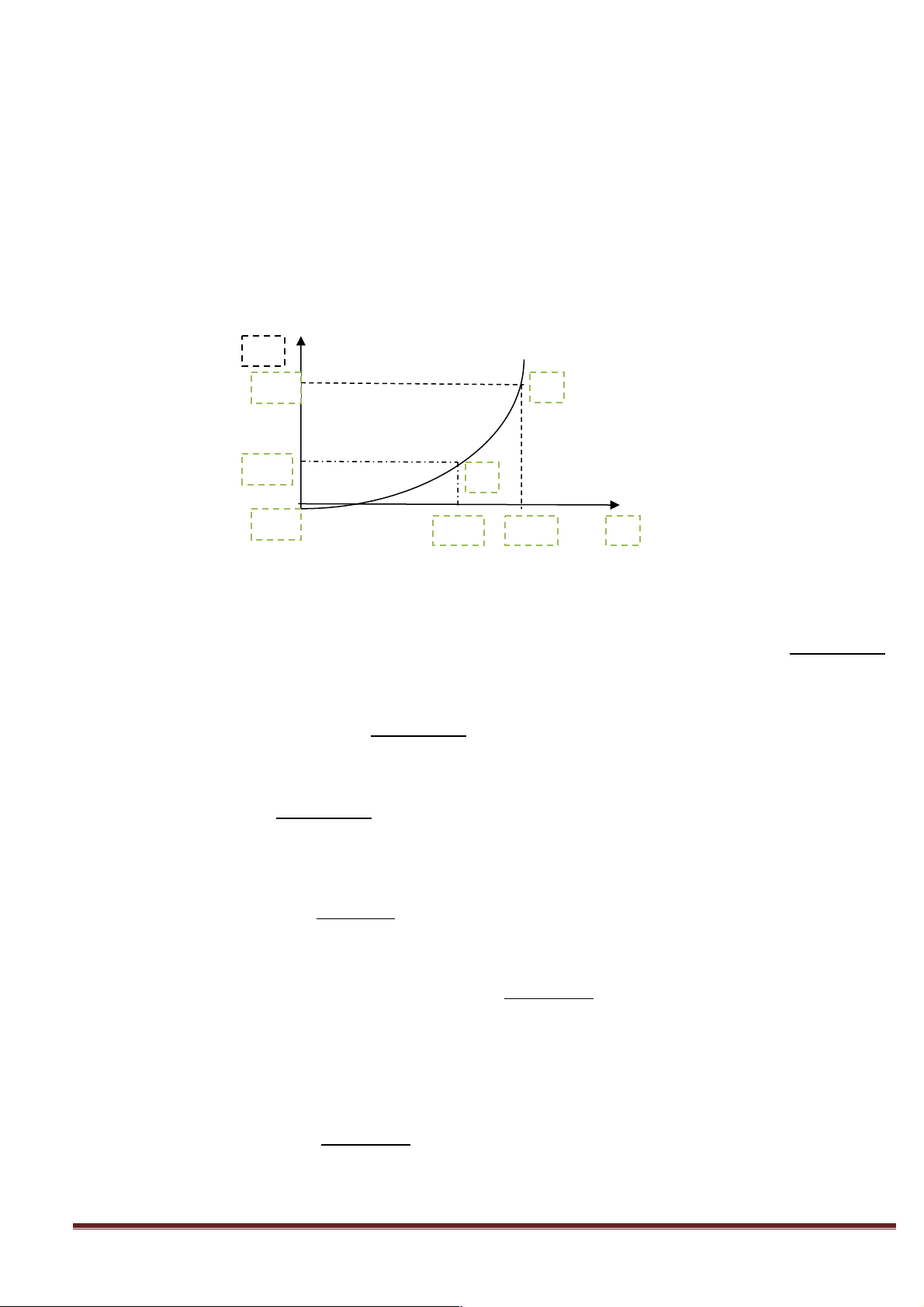
Câu hỏi:Em hãy quan sát các hình dưới đây và nêu những hiểu biết của em về các hình Hình 1 Hình 2
b.Thực hiện nhiệm vụ: Trang 1
- HS quan sát hình vẽ, hình dung , tưởng tượng.
- HS làm việc cá nhân, trao đổi với bạn bên cạnh về kết quả thực hiện.
- GV gợi ý khi cần thiết.
c.Báo cáo thảo luận:
- Kết quả của HS
- HS nhận xét tại chỗ.
d.Kết luận-Đánh giá-Cho điểm: Trả lời câu hỏi:
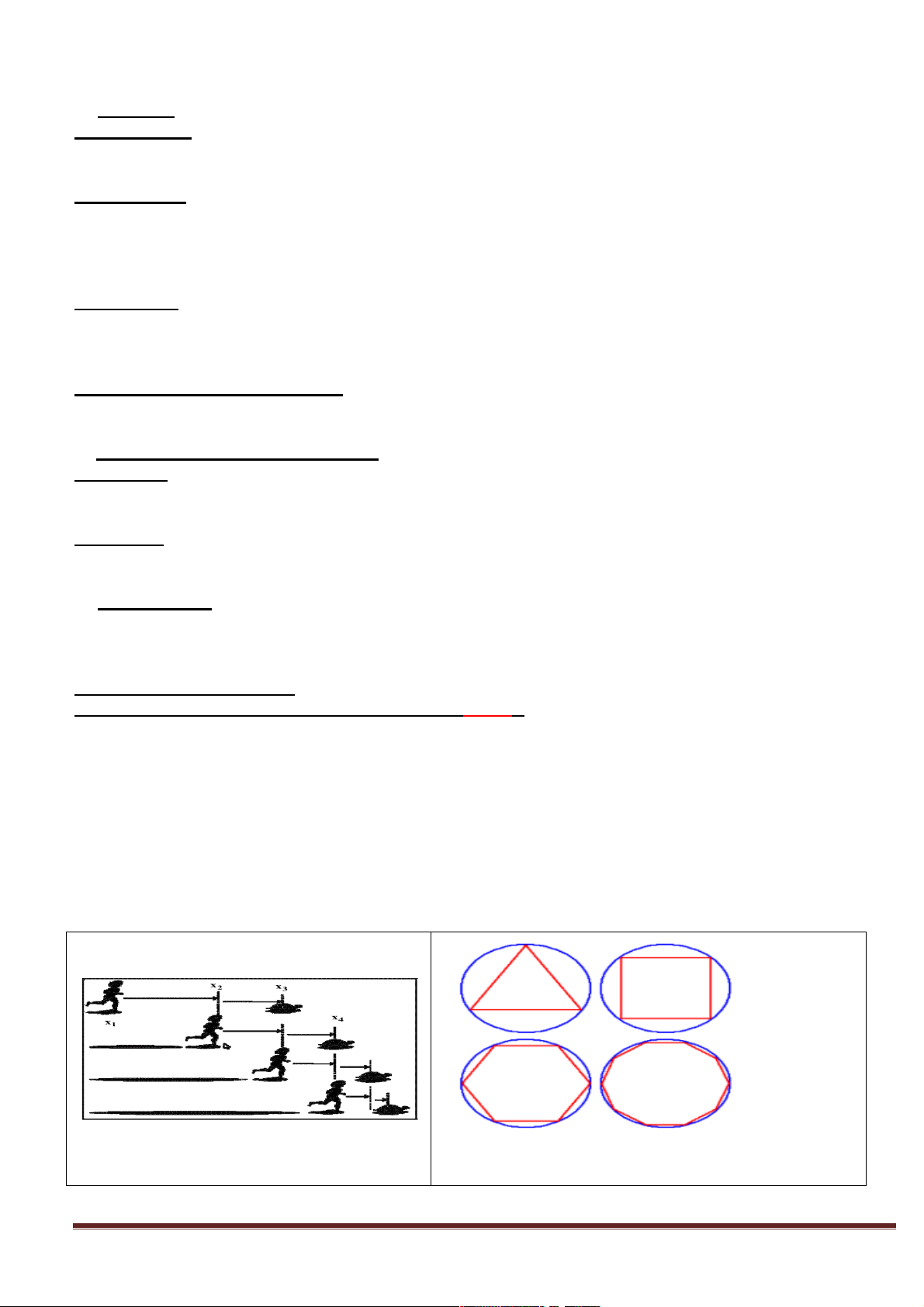
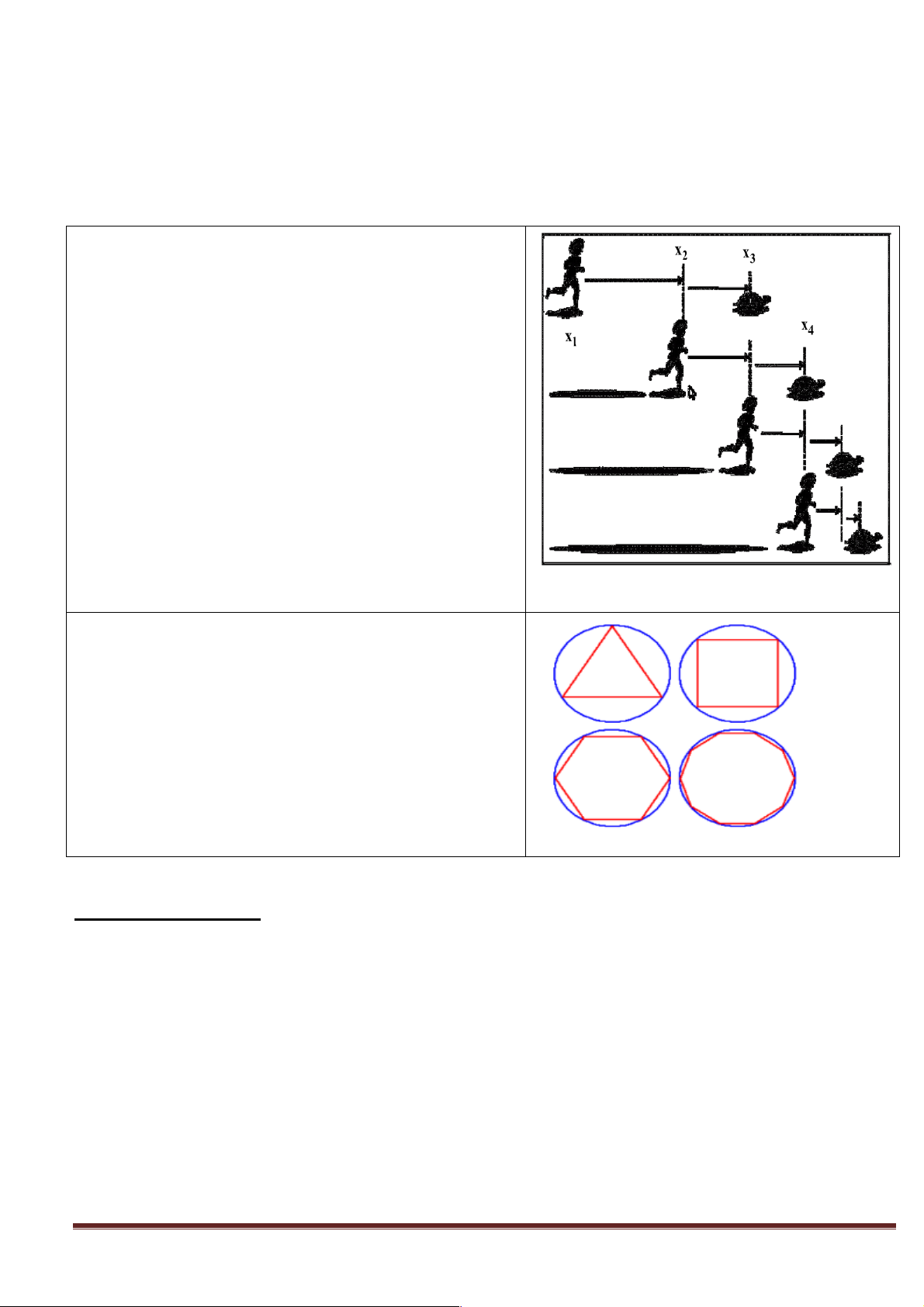
Hình 1 nói về một nghịch lí của Zê- Nông.
Nghịch lí này nói về câu chuyện: A-sin chạy đua cùng rùa.
Một ngày nọ, thần A-sin chạy thi với một con rùa. Do
được mệnh danh là thần về tốc độ nên A-sin nhường rùa
một đoạn, A-sin ở tại x , rùa ở tại x . Cả hai xuất phát 1 2
cùng một lúc, theo cùng một hướng và nhiệm vụ của thần
A-sin là phải đuổi kịp con rùa.
Chỉ trong nháy mắt, không mấy khó khăn, A-sin đến được
x . Thế nhưng dù rùa chạy chậm thì vận tốc của nó vẫn 2
lớn hơn 0 và nó đi đến được x . Tiếp tục, A-sin đuổi đến 3
x thì rùa đến x , A-sin đuổi đến x thì rùa đến x ,… 3 4 4 5
Cứ tiếp tục như thế, các điểm này luôn luôn tồn tại và như
thế thì A-sin, một vị thần về tốc độ lại không đuổi kịp một
con rùa. Điều này là vô lý theo lẽ thường tình, nhưng hoàn
toàn không có gì mâu thuẫn trong lập luận trên, vậy điều gì đang diễn ra? Hình 1
Hình 2 nói về một nghịch lí có tên là nghịch lí đường tròn.
Nghịch lí này: Xét một đường tròn và một đa giác đều nội
tiếp đường tròn ấy (Hình bên). Số cạnh đa giác tăng từ 3
Bạn có nhận xét gì về đa giác n cạnh ấy nếu như số cạnh
cứ không ngừng tăng lên, tăng mãi mãi đến vô tận?
Rõ ràng, khi số cạnh không ngừng tăng lên thì đa giác sẽ
càng ngày càng trở thành hình tròn mà nó nội tiếp. Điều
này cũng không quá khó để tưởng tượng. Khi ấy ta nói giới
hạn của đa giác khi n tiến tới vô tận sẽ là đường tròn. Hình 2
Học sinh tự nghiên cứu ở nhà: Bằng những hiểu biết của mình, em hãy tìm xem những lập luận ở trên đúng hay sai? Vì sao?
* GV giới thiệu bài học:
Các nội dung trên liên quan bài toán giới hạn mở đầu về Giải tích.Nội dung của chương này xoay quanh
hai khái niệm cơ bản là giới hạn và liên tục, là cơ sở cho việc nghiên cứu các nội dung khác của giải
tích(Đạo hàm, Tích phân,…).Đặc biệt cho phép giải quyết các bài toán của khoa học và thực tiễn, mà ta
không thể giải quyết được nếu chỉ dùng các kiến thức của Đại số.Đó chính là những bài toán liên quan
tới sự vô hạn.Giới hạn của dãy số là nội dung mà chúng ta nghiên cứu trong tiết học hôm nay.
II. HOẠT ĐỘNG 2: NỘI DUNG BÀI HỌC (HÌNH THÀNH KIẾN THỨC)
1. Mục tiêu: Học sinh biết được khái niệm giới hạn của dãy số.
- Nắm vững khái niệm dãy số có giới hạn 0; giới hạn hữu hạn của dãy số.
2. Phương thức: Hỏi đáp, gợi mở, giao bài tập.
3. Năng lực cần đạt:
- Năng lực tự học - hợp tác - giao tiếp – vận dụng kiến thức vào cuộc sống. 4.Cách tiến hành:
4.1.Nội dung 1:Dãy số có giới hạn 0:(10 phút) a.Tiếp cận: Trang 2
a.1.Chuyển giao nhiệm vụ- Hình thành khái niệm:
Em hãy thử tưởng tượng tình huống sau: Có một cái bánh. Nếu chia đều cho hai người ăn thì mỗi
người được bao nhiêu phần? Nếu chia đều cho cả lớp 40 người ăn thì mỗi người được bao nhiêu phần? Nếu
chia đều cho cả trường 1500 học sinh thì mỗi HS được bao nhiêu phần? Nếu chia đều cho cả huyện 1 triệu
người ăn thì mỗi người được bao nhiêu phần? Nếu chia đều cho cả thế giới 7,5 tỉ người ăn thì mỗi người được bao nhiêu phần?
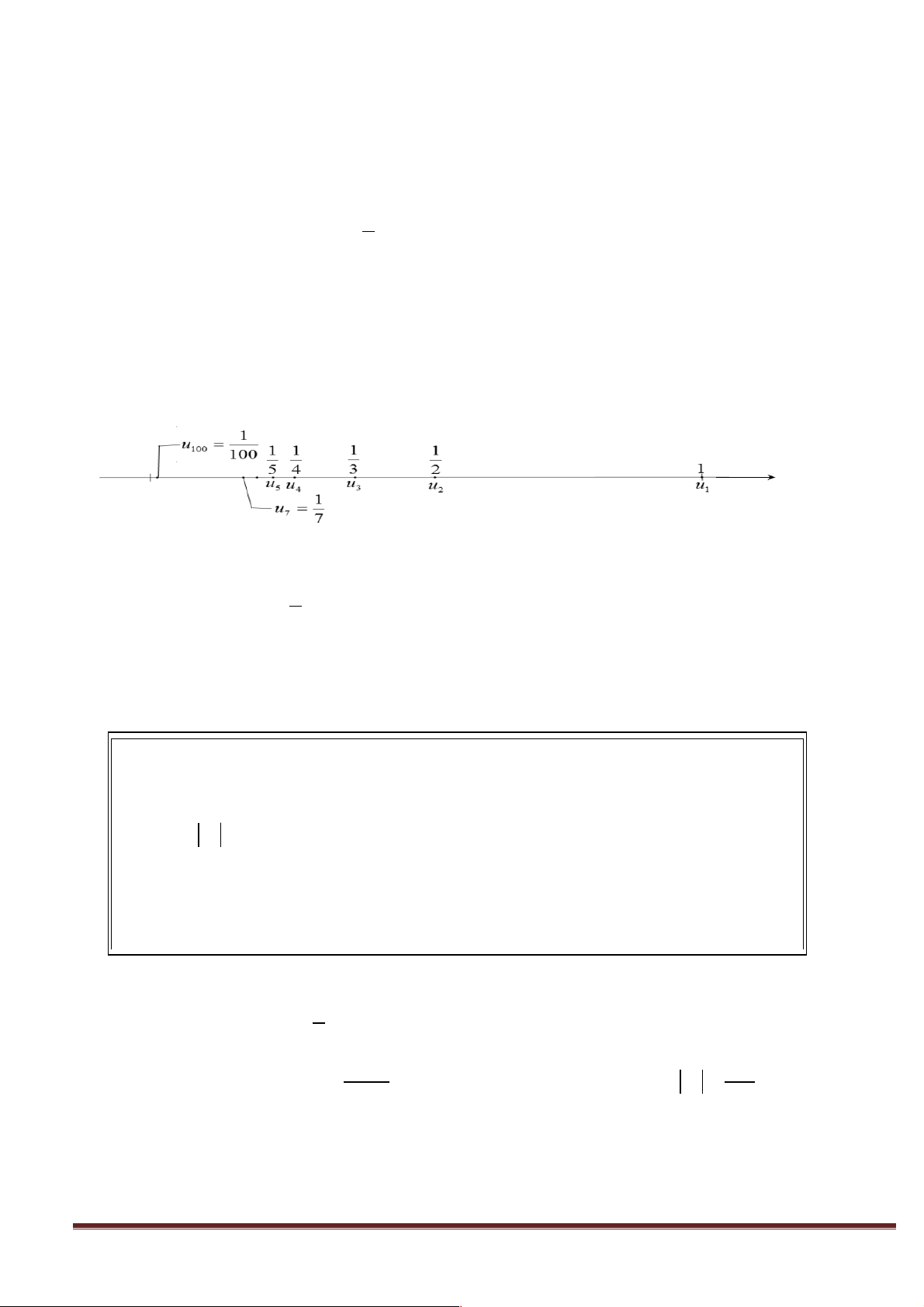
Khi số người được chia tăng lên càng lớn thì số bánh mỗi người nhận được như thế nào? 1
? Ta hình thành dãy số (u u = n ) với . n n
- Em hãy biểu diễn vài giá trị của dãy số trên trục số?
- Nhận xét xem khoảng cách từ u đến 0 thay đổi như thế nào khi n càng lớn ? n
- Bắt đầu từ số hạng
u thứ mấy thì khoảng cách từ u tới 0 nhỏ hơn 0,01 ? 0,001? n n
a.2.Thực hiện nhiệm vụ:
- HS suy nghĩ và trả lời câu hỏi của GV.
a.3.Báo cáo thảo luận:
- GV biểu diễn dãy (Un) trên trục số cho HS quan sát. - HS trả lời tại chỗ - Kết quả của HS 1 - GV: dãy số (u u = n ) với
là dãy số giảm, bị chặn dưới bởi số 0, khi n càng tăng thì dãy số càng dần về 0. n n
a.4.Kết luận-Đánh giá-Cho điểm:
- GV:Gọi HS nhận xét, đính chính trả lời của HS và đưa ra kết quả chính xác nhất.
- HS tiếp thu khái niệm mới.
b.Hình thành định nghĩa dãy số có giới hạn 0:(Nội dung ghi bảng- trình chiếu)
I. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ: 1.Định nghĩa:
a.Định nghĩa 1:Ta nói rằng dãy số (un ) có giới hạn là 0 khi n dần tới dương vô
cực, nếu u có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở n đi.
Khi đó ta viết: lim u = 0 hoặc u ® 0 khi n ® + . ¥ n n®+¥ n
Quy ước thay cho lim u ta viết tắt limu và hiểu ngầm n ® + . ¥ n n®+¥ n
c.Cũng cố:(Nội dung ghi bảng - trình chiếu - bảng phụ) 1
Ví dụ 1: Dãy số (u u = n ) với
ta xét ở trên thỏa được định nghĩa trên nên nó có giới hạn là 0. n n (- )1n 1
Ví dụ 2: Cho dãy số (u u = . n u < . n n ) với Kể từ số hạng thứ trở đi thì ta có Hãy chọn số n 2 n 0 n 100 0 nhỏ nhất.
A. n = 10.
B. n = 101.
C. n = 100.
D. n = 11. 0 0 0 0
4.2.Nội dung 2:Dãy số có giới hạn hữu hạn:(10 phút) a.Tiếp cận: Trang 3
a.1.Chuyển giao nhiệm vụ- Hình thành khái niệm: 3n +1
Ví dụ 3:: Cho dãy số (vn), với vn =
.Chứng minh rằng, dãy số u = v - 3 có giới hạn là 0. n n n
a..2.Thực hiện nhiệm vụ:
- HS suy nghĩ trao đôi với bạn bên cạnh về kết quả thực hiện
a..3.Báo cáo thảo luận:
- Gọi 1 HS lên bảng trình bày LG. - Kết quả của HS
a.4.Kết luận-Đánh giá-Cho điểm:
- GV:Gọi HS nhận xét, đính chính trả lời của HS và đưa ra kết quả chính xác nhât. + 3n 1
Ví dụ 3:: Cho dãy số (vn), với vn =
.Chứng minh rằng, dãy số u = v - 3 có giới n n n hạn là 0. Giải: n + Ta có : lim (v - 3 1 3) = lim ( - 1 3) = lim = 0 n n®+¥ n®+¥ n n®+¥ n
Vậy lim u = 0 (đpcm) n n®+¥
- GV: Trong ví dụ trên ta nói dãy số (vn) có giới hạn là 3. - GV: HD HS bấm máy tính: 3X +1 +Nhập X + CALC 6 10 = + CALC 9 10 = + Kết quả 3
- HS: Khái quát hóa định nghĩa.
- HS tiếp thu khái niệm mới.
b.Hình thành định nghĩa dãy số có giới hạn hữu hạn:(Nội dung ghi bảng) (v n ® +¥ n )
b.Định nghĩa 2:Ta nói rằng dãy số
có giới hạn là số L khi nếu lim(v - L = lim v = L lim v = L v ® L n ® +¥ n ) 0.Kí hiệu: hoặc hoặc khi . n n n n®+¥ c. Cũn g cố: c.1.Chu
yển giao nhiệm vụ:
Phiếu HT1:(Nội dung ghi bảng – trình chiếu – bảng phụ)
Câu hỏi 1: Tìm giới hạn của các dãy số sau: 2n -1 - n + - n + a/ u = 5 3 . b/ v = 3 2 c/ w = n n n n n n
Câu hỏi 2: Chọn mệnh đề sai. 1 n æ ö æ 1 ö n n + A. lim = 0. B. lim - 3 = 3. - C. lim( 2) = 1 0. D. lim = 1. ç ÷ ç ÷ è 3 ø 10 è n ø n
Bài tập tương tự: ( HS làm ở nhà )Tìm các giới hạn sau: n - 5 - n + 3 - n + 2 a/ u = 5 3 . b/ v = c/ w = n n n n +1 n 2n +1
c..2.Thực hiện nhiệm vụ: Trang 4 - HS thảo luận nhóm. - GV: Hỗ trợ HS
+ Các em có thể bấm máy tính để dự đoán kết quả, sau đó sử dụng định nghĩa 2 để tìm giới hạn.
c.3.Báo cáo thảo luận:
- Đại diện HS lên bảng trình bày kết quả thực hiện. - Kết quả của HS
c.4.Kết luận-Đánh giá-Cho điểm:
- GV:Gọi HS nhận xét, đính chính trả lời của HS và đưa ra kết quả chính xác nhất.
Lời giải- Phiếu HT1:(Nội dung ghi bảng)
Đáp số-Câu hỏi 1: Tìm giới hạn của các dãy số sau: æ n - ö - a/ (u - = - = = Þ u = n ) 2 1 1 lim 2 lim 2 lim 0 lim 2 . ç ÷ n è n ø n æ - n + ö b/ (v + = + = = Þ v = - n ) 5 3 3 lim 5 lim 5 lim 0 lim 5 ç ÷ n è n ø n æ - n + ö c/ ( + = + = = Þ w = - n ) 3 2 2 lim w 3 lim 3 lim 0 lim 3 ç ÷ n è n ø n
Câu hỏi 2: Chọn mệnh đề sai. 1 n æ ö æ 1 ö n n + A. lim = 0. B. lim - 3 = 3. - C. lim( 2) = 1 0. D. lim = 1. ç ÷ ç ÷ è 3 ø 10 è n ø n
4.3. Nội dung 3: Một vài giới hạn đặc biệt :(3 phút) a.Tiếp cận:
- Từ kết quả câu hỏi 2, GV cho HS tiếp thu kiến thức mới.
b.Hình thành giới hạn đặc biệt :(Nội dung ghi bảng – trình chiếu – bảng phụ)
2. Một vài giới hạn đặc biệt : 1 1 a) lim = 1
0 với k nguyên dương; b) lim = 0 và lim = 0 ; k n n 3 n c) lim n
q = 0 nếu q <1; d) Nếu u = c (c là hằng số) thì limu = c . n n
4.4. Nội dung 4:Định lí về giới hạn hữu hạn :(7 phút) a.Tiếp cận:
a.1.Chuyển giao nhiệm vụ- Hình thành khái niệm:
- GV: Từ kết quả của câu hỏi 1 trong phiếu HT1, em hãy tìm lim(u + v limu + lim v n
n ) rồi so sánh với n n .
a..2.Thực hiện nhiệm vụ:
- HS thảo luận với bạn bên cạnh để tìm câu trả lời.
a..3.Báo cáo thảo luận:
Ta có limu = 2 ; lim v = 5
- ; lim(u + v ) = lim w = 3 - n n n n n
- Ghi nhận kết quả: lim(u + v limu + lim v n n ) = . n n
GV: Việc tìm giới hạn bằng định nghĩa khá phức tạp nên người ta thường áp dụng các công thức giới
hạn đặc biệt nêu trên và định lí sau đây. a.4.Kết luận:
- GV: Nhấn mạnh, dãy u ;v đều phải có giới hạn hữu hạn.Phát biểu tương tự các nội dung còn lại trong n n định lí.
- HS tiếp thu khái niệm mới.
b.Hình thành định lí về giới hạn hữu hạn :(Nội dung ghi bảng – trình chiếu) Trang 5
II. Định lí về giới hạn hữu hạn : Định lí 1:
a. Nếu limu = a và lim v = b thì n n
+ lim(u + v = a + b
lim(u - v = a - b n n ) n n ) + u a
+ lim(u .v = a b lim n = (b ¹ 0) n n ) . + v b n
b. Nếu u ³ 0 với mọi n và limu = a thì a ³ 0 và lim u = a . n n n c.Cũng cố:
c.1.Chuyển giao nhiệm vụ:
Phiếu HT2:(Nội dung ghi bảng)
Câu hỏi 3: Tìm các giới hạn sau: 2 5n - n 2 1+ 9n A = lim B = lim 2 1- n 3 - 2n
Bài tập tương tự: ( HS làm ở nhà )Tìm các giới hạn sau: 2 4n - n 2 2n - n 2 1+ 3n 2n + 3 C = lim D = lim E = lim F = lim 2 1- n 3 1- n 3 - 2n 2 1+ 2n
c..2.Thực hiện nhiệm vụ:
- HS thảo luận nhóm.
- GV: Hỗ trợ HS khi cần.
+ Các em bấm máy tính để kiểm tra kết quả
c.3.Báo cáo thảo luận:
- Đại diện HS lên bảng trình bày kết quả thực hiện. - Kết quả của HS
c.4.Kết luận-Đánh giá-Cho điểm:
- GV:Gọi HS nhận xét, đính chính trả lời của HS và đưa ra kết quả chính xác nhất.
Lời giải- Phiếu HT2:(Nội dung ghi bảng- trình chiếu)
Đáp số-Câu hỏi 3: Giải : 2 æ 1 ö 1 æ 1 ö n 5 - 1 ç ÷ 5 - lim 5 - ç ÷ lim5 - lim è n ø n è n ø 5 - 0 A = lim = lim = n = = = 5 - æ 1 ö 1 1 2 æ 1 ö - n -1 -1 lim -1 0 1 ç lim - lim1 2 ÷ 2 ç 2 ÷ è n ø n è n ø 2 n 2 æ 1 ö 1 1 n + 9 ç ÷ + + 2 n 9 9 2 2 è n ø = lim = lim n = lim n B = - 3/2 æ 3 ö æ 3 ö 3 n - 2 n - 2 - 2 ç ÷ ç ÷ è n ø è n ø n
III. LUYỆN TẬP:(7 phút)
1.Chuyển giao nhiệm vụ:
Phiếu HT3:(Nội dung ghi bảng – bảng phụ - trình chiếu) 3n - 2 Câu hỏi 4:Tìm lim ? 2n +1 Trang 6 3 A. -2 B. C. 1 D. 0 2 2 3 - n + n - 3 Câu hỏi 5:Tìm lim ? 4 2n +1 3 A. - B. -3 C. 0 D. 1 2 2 2n - 3n Câu hỏi 6:Tìm: lim ? 2 1- 5n 2 A. 2 B. 0 C. - 3 D. 5 5 2n + 5n Câu hỏi 7: Tìm lim ? 3.2n + 4.5n 1 1 A. B. C. 1 D. 2 4 3 2 n +1 - 2n Câu hỏi 8: Tìm lim ? 2n +1 1 A. - 1 B. -¥ C. 0 D. 2 2
Câu hỏi 9 :Tính các giới hạn sau:(Bài tập về nhà) 2n -1 2 2n +1 n +1 2n n + 3 1. lim 2. lim 3. lim 4. lim n +1 3 n - 4n + 9 n +1 2 n + n +1 3 6n + 2n +1 3 2 3 n + n n +1 2 3 (2n -1) (5n +1) 5. lim 6. lim 7. lim 8. lim 3 2n + 4n - 9 2n +1 2 n +1 2 2 (n +1) (3n +5)
(2n n +1)( n + 3) 2 n - n +1 2 3n + n +1 n n +1 9. lim 10. lim 11. lim 12. lim (n +1)(n + 2) 2 - 2n -3 3 2n -1 2 n + n 6n -1 2 3n + n - 5 3n + 5.4n 2 9n - n +1 13. lim 14. lim 15. lim 16. lim 3n + 2 2 2n +1 4n + 2n 4n - 2
2.Thực hiện nhiệm vụ:
- HS thảo luận nhóm.
- GV: Hỗ trợ HS khi cần.
+ Các em bấm máy tính để kiểm tra kết quả
3.Báo cáo thảo luận:
- Đại diện HS lên bảng trình bày kết quả thực hiện. - Kết quả của HS
4.Kết luận-Đánh giá-Cho điểm:
- GV:Gọi HS nhận xét, đính chính trả lời của HS và đưa ra kết quả chính xác nhất.
Lời giải- Phiếu HT3:(Nội dung ghi bảng) 4B; 5C;6C;7A;8A
IV.VẬN DỤNG VÀ MỞ RỘNG:(3 phút)
1.Vận dụng vào thực tế:(Bài tập HS nghiên cứu ở nhà tiết sau nộp bài, ghi điểm cộng)
Bài toán: Để trang hoàng cho căn hộ của mình chú chuột Mickey tô màu cho một bức tường hình vuông có 1
cạnh là 1m, các bức tô như sau: tô hình vuông cạnh nhỏ là m , tô tiếp hình vuông có cạnh bằng một nữa 2
cạnh hình vuông vừa tô...và cứ tô tiếp mãi. Hỏi diện tích mà chú chuột tô được là bao nhiêu? Trang 7 Lời giải:
Gọi u là hình vuông được tô màu thứ n n 1 1 1
Khi đó u = ;u = ;...;u =
. Tổng diện tích tô đến hình vuông thứ n là: 1 2 4 16 n 4n 1 1 1 u 1 n - q 1 ( ) u u 1 1 1 1
S = u + u + ... + u = + + ...+ = = - . n
q với u = ;q = . n 1 2 n 2 4 4 4n 1- q 1- q 1- q 1 4 4
Vì quy trình tô màu của Mickey có thể tiến ra vô hạn nên phần diện tích được tô là: é 1 1 ù ê æ 1 n ö ú 1 4 4 S = lim S = lim - . = n ê 1 1 ç ÷ ú è 4 ø 3 ê1- 1- ú ë 4 4 û
2. Mở rộng, tìm tòi:(Học sinh nghiên cứu một tuần)
a.Sử dụng các kiến thức đã học, em hãy giải thích các nghịch lí đã nêu trong phần giới thiệu.
b.Trong tiết học hôm nay ta đề cập đến giới hạn hữu hạn của dãy số, thế thì dãy số như thế nào gọi là có giới
hạn không hữu hạn(vô hạn; vô cực)?
c.Trong định lí về giới hạn hữu hạn, nếu có ít nhất một trong hai dãy số u hay v dần ra vô cực ( ±¥ ) thì ta n n
làm thế nào?Chẳng hạn, tìm các giới hạn sau: 1. 2
lim( n +1 - n) 2. 2 4
lim(1+ n - n +3n +1) 3. 2 2
lim(n n +1 - n n - 2) 4. 2
lim( n + n +1 - n) 5. 2 2
lim n( n +1 - n - 2 ) 6. 3 2 3
lim( n - 2n - n - n)
NỘI DUNG PHÁT CHO HỌC SINH: Phiếu HT1:
Câu hỏi 1: Tìm giới hạn của các dãy số sau: 2n -1 - n + - n + a/ u = 5 3 . b/ v = 3 2 c/ w = n n n n n n 2 1- 2n
Câu hỏi 2: Gọi l = lim . Tìm l. 2 n
A. l = 2. B. l = 2. -
C. l = 0.
D. l = 1.
Bài tập tương tự: ( HS làm ở nhà )Tìm các giới hạn sau: n - 5 - n + 3 - n + 2 a/ u = 5 3 . b/ v = c/ w = n n n n +1 n 2n +1 Phiếu HT2:
Câu hỏi 3: Tìm các giới hạn sau: Trang 8 2 5n - n 2 1+ 9n A = lim B = lim 2 1- n 3 - 2n
Bài tập tương tự: ( HS làm ở nhà )Tìm các giới hạn sau: 2 4n - n 2 2n - n 2 1+ 3n 2n + 3 C = lim D = lim E = lim F = lim 2 1- n 3 1- n 3 - 2n 2 1+ 2n Phiếu HT3: 3n - 2 Câu hỏi 4:Tìm lim ? 2n +1 3 A. -2 B. C. 1 D. 0 2 2 3 - n + n - 3 Câu hỏi 5:Tìm lim ? 4 2n +1 3 A. - B. -3 C. 0 D. 1 2 2 2n - 3n Câu hỏi 6:Tìm: lim ? 2 1- 5n 2 A. 2 B. 0 C. - 3 D. 5 5 2n + 5n Câu hỏi 7: Tìm lim ? 3.2n + 4.5n 1 1 A. B. C. 1 D. 2 4 3 2 n +1 - 2n Câu hỏi 8: Tìm lim ? 2n +1 1 A. - 1 B. -¥ C. 0 D. 2 2
Câu hỏi 9 :Tính các giới hạn sau:(Bài tập về nhà) 2n -1 2 2n +1 n +1 2n n + 3 1. lim 2. lim 3. lim 4. lim n +1 3 n - 4n + 9 n +1 2 n + n +1 3 6n + 2n +1 3 2 3 n + n n +1 2 3 (2n -1) (5n +1) 5. lim 6. lim 7. lim 8. lim 3 2n + 4n - 9 2n +1 2 n +1 2 2 (n +1) (3n +5)
(2n n +1)( n + 3) 2 n - n +1 2 3n + n +1 n n +1 9. lim 10. lim 11. lim 12. lim (n +1)(n + 2) 2 - 2n -3 3 2n -1 2 n + n 6n -1 2 3n + n - 5 3n + 5.4n 2 9n - n +1 13. lim 14. lim 15. lim 16. lim 3n + 2 2 2n +1 4n + 2n 4n - 2
Bài tập HS nghiên cứu ở nhà tiết sau nộp bài, ghi điểm cộng:
Bài toán: Để trang hoàng cho căn hộ của mình chú chuột Mickey tô màu cho một bức tường hình vuông có 1
cạnh là 1m, các bức tô như sau: tô hình vuông cạnh nhỏ là m , tô tiếp hình vuông có cạnh bằng một nữa 2
cạnh hình vuông vừa tô...và cứ tô tiếp mãi. Hỏi diện tích mà chú chuột tô được là bao nhiêu? Trang 9
Học sinh nghiên cứu một tuần:
a.Sử dụng các kiến thức đã học, em hãy giải thích các nghịch lí đã nêu trong phần giới thiệu.
b.Trong tiết học hôm nay ta đề cập đến giới hạn hữu hạn của dãy số, thế thì dãy số như thế nào gọi là có giới
hạn không hữu hạn(vô hạn; vô cực)?
c.Trong định lí về giới hạn hữu hạn, nếu có ít nhất một trong hai dãy số u hay v dần ra vô cực ( ±¥ ) thì ta n n
làm thế nào?Chẳng hạn, tìm các giới hạn sau: 1. 2
lim( n +1 - n) 2. 2 4
lim(1+ n - n +3n +1) 3. 2 2
lim(n n +1 - n n - 2) 4. 2
lim( n + n +1 - n) 5. 2 2
lim n( n +1 - n - 2 ) 6. 3 2 3
lim( n - 2n - n - n)
Ngày soạn: 10/2/2019 CHỦ ĐỀ: GIỚI HẠN CỦA HÀM SỐ
I. Mục tiêu của bài (chủ đề) 1. Kiến thức:
- Học sinh biết khái niệm giới hạn hữu hạn của hàm số tại một điểm, giới hạn một bên, giới hạn hữu hạn của
hàm số tại vô cực, giới hạn vô cực của hàm số.
- Học sinh hiểu được định lí về giới hạn hữu hạn, định lí về giới hạn một bên, một vài giới hạn đặc biệt và
các quy tắc về giới hạn vô cực. 2. Kỹ năng:
- Học sinh biết cách tính giới hạn hàm số tại một điểm, tính giới hạn hàm số tại vô cực
- Học sinh phân biệt được các dạng vô định của giới hạn hàm số. 3. Thái độ:
- Tích cực, chủ động và hợp tác trong hoạt động nhóm.
- Say mê hứng thú trong học tập và tìm tòi nghiên cứu liên hệ thực tiễn.
4. Đinh hướng phát triển năng lực:
- Năng lực hợp tác: Tổ chức nhóm học sinh hợp tác thực hiện các hoạt động.
- Năng lực tự học, tự nghiên cứu: Học sinh tự giác tìm tòi, lĩnh hội kiến thức và phương pháp giải quyết bài tập và các tình huống.
- Năng lực giải quyết vấn đề: Học sinh biết cách huy động các kiến thức đã học để giải quyết các câu hỏi.
Biết cách giải quyết các tình huống trong giờ học.
- Năng lực thuyết trình, báo cáo: Phát huy khả năng báo cáo trước tập thể, khả năng thuyết trình.
II. Chuẩn bị của giáo viên và học sinh 1. Giáo viên:
- Thiết kế hoạt động học tập hợp tác cho học sinh tương ứng với các nhiệm vụ cơ bản của bài học.
- Tổ chức, hướng dẫn học sinh thảo luận, kết luận vấn đề. 2. Học sinh:
- Mỗi học sinh trả lời ý kiến riêng và phiếu học tập. Mỗi nhóm có phiếu trả lời kết luận của nhóm sau khi đã
thảo luận và thống nhất.
- Mỗi cá nhân hiểu và trình bày được kết luận của nhóm bằng cách tự học hoặc nhờ bạn trong nhóm hướng dẫn.
- Mỗi người có trách nhiệm hướng dẫn lại cho bạn khi bạn có nhu cầu học tập.
III. Chuỗi các hoạt động học
1. GIỚI THIỆU (HOẠT ĐỘNG TIẾP CẬN BÀI HỌC) (thời gian) Trang 10
Quan sát các hình ảnh (máy chiếu)
Lớp chia thành các nhóm (nhóm có đủ các đối tượng học sinh, không chia theo lực học) và tìm câu trả lời cho
các câu hỏi H1, H2, H3. Các nhóm viết câu trả lời vào bảng phụ.
H1. . Em có nhận xét gì về hình ảnh sau?
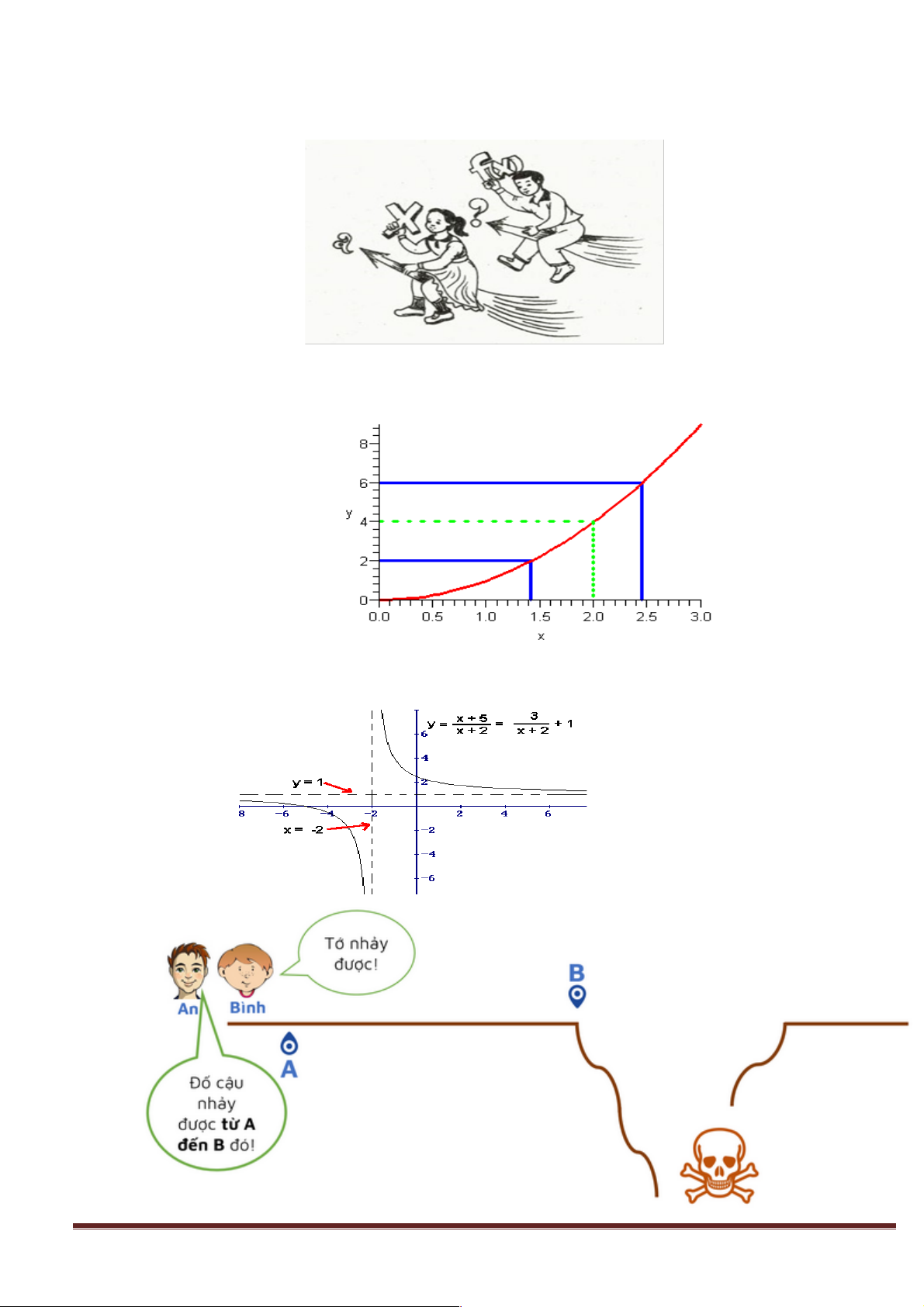
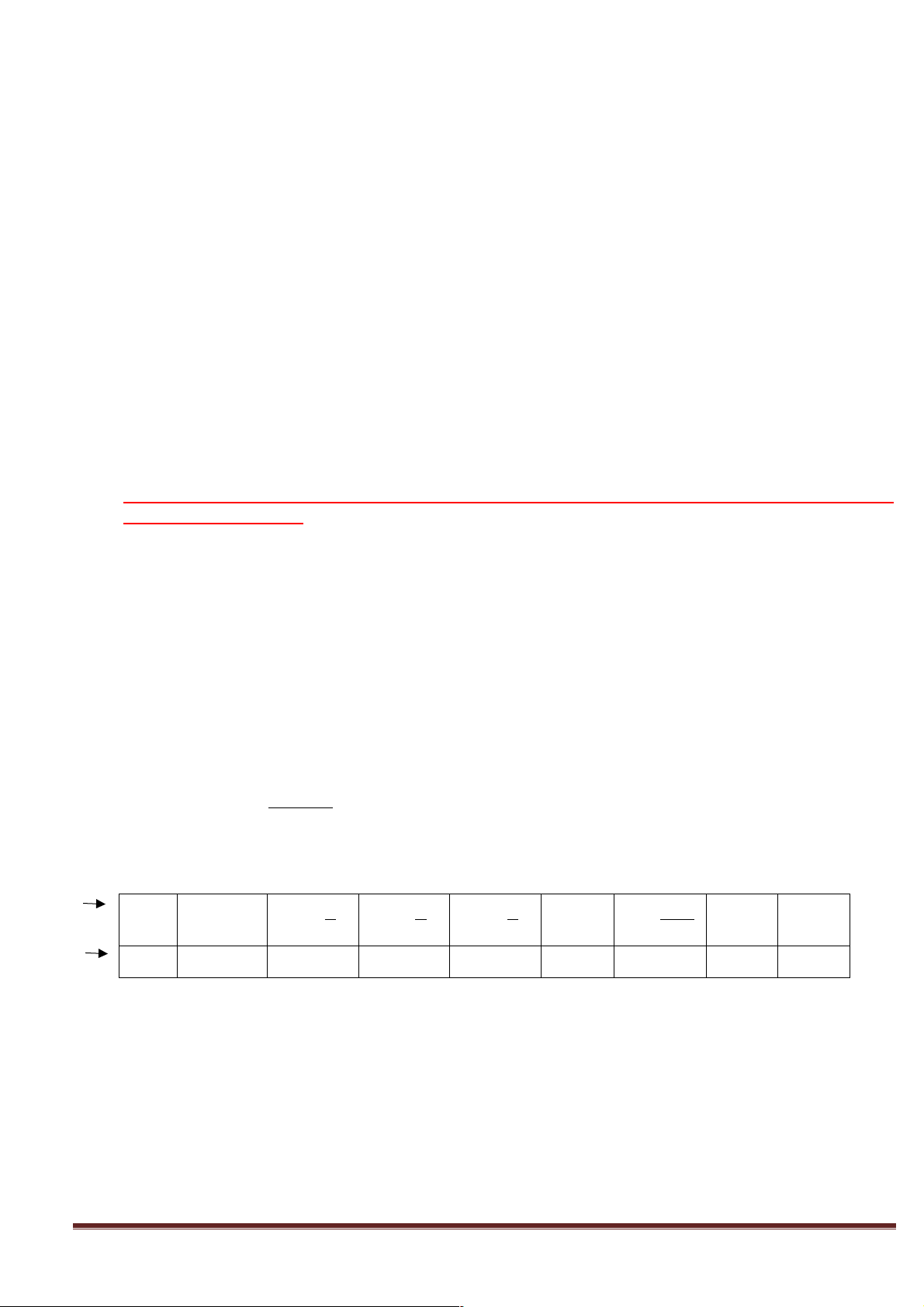
H2.Quan sát hình ảnh dưới đây, em có nhận xét gì về giá trị hàm số y = f (x) khi x dần đến 2?
H 3. Quan sát hình ảnh dưới đây, em có nhận xét gì về giá trị hàm số y = f (x) khi x dần đến -2? Trang 11
An rõ ràng không thể bắt Bình nhảy ngay tới B vì Bình sẽ chết, không lẽ An muốn Bình chết, đúng
không? Tuy nhiên, để chứng minh khả năng của mình mà không bị chết, Bình có thể nhảy tới điểm gần
B bao nhiêu cũng được, miễn sao không chạm vào B. Gần bao nhiêu thì tùy An chọn!” + Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi H1, H2, H3. Viết kết quả vào bảng phụ.
- Giáo viên quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm không hiểu nội dung các câu hỏi + Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi.
- HS quan sát các phương án trả lời của các nhóm bạn.
- HS đặt câu hỏi cho các nhóm bạn để hiểu hơn về câu trả lời.
- GV quan sát, lắng nghe, ghi chép.
+ Đánh giá, nhận xét, tổng hợp:
- GV nhận xét thái độ làm việc, phương án trả lời của các nhóm, ghi nhận và tuyên dương nhóm có
câu trả lời tốt nhất. Động viên các nhóm còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo.
Qua các hoạt động giáo viên dẫn dắt vào bài:
Giới hạn cho ta một dự đoán chắc chắn về giá trị hàm số khi biến tiếp cận một đại lượng nào đó:
“Giới hạn của hàm số”
2. NỘI DUNG BÀI HỌC (HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC)
2.1 Đơn vị kiến thức 1 (thời gian )
a) Tiếp cận (khởi động)
HTKT 1. Giới hạn hữu hạn của hàm số tại một điểm. Định nghĩa 1. * Mục tiêu:
- Học sinh biết được khái niệm giới hạn hữu hạn của hàm số tại một điểm.
- Áp dụng để tính được giới hạn hàm số tại một điểm.
* Nội dung, phương thức tổ chức: + Chuyển giao:
L. Chia lớp thành 4 nhóm. Nhóm 1, 2 hoàn thành câu hỏi số 1; Nhóm 3, 4 hoàn thành câu hỏi số 2. Các nhóm
viết câu trả lời vào bảng phụ. 2 2x - 2x
Xét hàm số f (x) = . x -1
1. Cho biến x những giá trị khác nhau lập thành dãy số ( x x ® n ) ,
1 như trong bảng sau. Tính các giá n
trị của f (x) 3 4 5 n + x x = 2 x = x = x = 1 x = 1 2 3 4 …. n ….. 1 2 3 4 n
f (x) f (x ) = ? f (x ) = ? f (x ) = ? f (x ) = ? f (x ) = ? 1 2 3 4 …. n ….. ?
Ta thấy rằng tương ứng với các giá trị của dãy ( xn ) là các giá trị
f (x ), f (x ), f (x ), f (x ),..., f (x ),...cũng lập thành dãy ký hiệu là ( f ( xn )) 1 2 3 4 n
+ Tìm giới hạn dãy số ( f ( xn )) .
2. Với mọi dãy số ( x x ¹ 1 x ®1 ( f (xn)) n ) sao cho , thì dãy số tương ứng
có giới hạn bằng bao nhiêu n n ? + Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi trong phiếu học tập. Viết kết quả vào bảng phụ. Trang 12
- Giáo viên quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm không hiểu nội dung các câu hỏi. + Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi.
- HS quan sát các phương án trả lời của các nhóm bạn.
- HS đặt câu hỏi cho các nhóm bạn để hiểu hơn về câu trả lời.
+ Đánh giá, nhận xét, tổng hợp:
- Trên cơ sở câu trả lời của học sinh, GV kết luận, và dẫn dắt học sinh hình thành khái niệm giới hạn hữu hạn của hàm số. b) Hình thành Định nghĩa 1: SGK
+ Củng cố, luyện tập
- Yêu cầu học sinh làm Ví dụ 1 2 x -1
- Ví dụ 1 . Cho hàm số f (x) =
. Chứng minh rằng lim f (x) = 2 - x +1 x 1 ®-
Giải :Hàm số xác định trên R \{ -1} Giả sử ( x x ¹ 1 - x ® 1 - n ® +¥
n ) là một dãy số bất kỳ, thảo mãn và khi n n 2 x -1 x - x + n ( n )1( n )1
Ta có lim f (x ) = lim = lim = lim x -1 = 2 - n x +1 x + n ( n ) ( n ) 1
Do đó lim f (x) = 2 - x 1 ®-
Nhận xét: lim x = x , lim c = c o x® ® o x x o x
c) Củng cố : Tính các giới hạn sau 6x -1 2 x - 3x + 2
a. I = lim (4x - 3) b. 2
J = lim ( x + 5 - 4) c. lim d. lim x®2 x®2 x 3 ® x + 5 x 2 ®- x - 2
2.2 Đơn vị kiến thức 2 (thời gian )
HTKT 2. Giới hạn hữu hạn của hàm số tại một điểm. Định lí về giới hạn hữu hạn
* Mục tiêu: Học sinh biết được nội dung định lí 1. Thông quá đó biết áp dụng nội dung định lí vào để tính
giới hạn tại một điểm.
* Nội dung, phương thức tổ chức: + Chuyển giao: Câu hỏi 1. Tính 2
M = lim (4 x+ x + 5 - 7) . x®2
Câu hỏi 2. Tính I+J. Biết I = lim (4x - 3) , 2
J = lim ( x + 5 - 4) x®2 x®2
So sánh giá trị của M và I+J?
Yêu cầu học sinh thảo luận theo nhóm và trả lời các câu hỏi + Thực hiện
- Các nhóm thảo luận đưa ra các đáp án trả lời cho các câu hỏi H1, H2. Viết kết quả vào bảng phụ.
- Giáo viên quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm không hiểu nội dung các câu hỏi. + Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi. Đại diện các nhóm trình bày. - Dự kiến câu trả lời: 2
M = lim (4 x+ x + 5 - 7) = 4
I = lim (4x - 3) = 5 x®2 x®2 2
J = lim ( x + 5 - 4) = 1 - x®2 Vậy M = I+J
+ Đánh giá, nhận xét, tổng hợp:
- Trên cơ sở câu trả lời của học sinh, Giáo viên đưa ra nội dung định lí 1. Trang 13 Định lí 1:
a) Nếu lim f (x) = L và lim g(x) = M thì: x® ® 0 x x 0 x
lim [ f (x) + g(x)] = L + M x® 0x
lim [ f (x) - g(x)] = L - M x® 0x
lim [ f (x).g(x)] = . L M x® 0x f (x) L lim = (nếu M ¹ 0)
x® 0x g(x) M
b) Nếu f(x) ³ 0 và lim f (x) = L thì L ³ 0 và lim f (x) = L x® ® 0 x x 0 x
c) Nếu lim f (x) = L thì lim f (x) = L x® ® 0 x x 0 x
+ Củng cố, luyện tập 1. lim 2
(4x - 2x+5) 2. lim(3x - 2 x +10) 3. (3x -4x+5)3 lim x 1 ® x 1 ® x®3 8x+1 3 x +7x - 5 4. lim 5. lim 6. 2 lim(3x+1)(-4x +8) . 2 x 1 ® 4x - 6 4 x®-1 2x +1 x 1 ®
Yêu cầu học sinh: tính giới hạn trên
2.3 Đơn vị kiến thức 3 (thời gian)
HTKT 3. Giới hạn một bên
* Mục tiêu: Học sinh hiểu được định nghĩa giới hạn một bên và nội dung định lí 2
* Nội dung, phương thức tổ chức: + Chuyển giao:
L. Học sinh nhận phiếu học tập. Yêu cầu học sinh thảo luận theo nhóm và trả lời câu hỏi sau
Em nhận xét gì về hai hình ảnh trên? (Hình ảnh hàng người chạy (theo 1 hướng) về đích) 5
ì x + 2 khi x ³1
Cho hàm số f (x) = í 2 îx khi x < 1 3 4 5 n + x x = 2 x = x = x = 1 x = 1 2 3 4 …. n ….. 1 2 3 4 n
f (x) f (x ) = ? f (x ) = ? f (x ) = ? f (x ) = ? f (x ) = ? 1 2 3 4 …. n ….. ?
Câu hỏi? Em có nhận xét gì về giá trị của dãy f (x ) khi x ®1 và x ³ 1? n n n + Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi.
- Các nhóm viết kết quả dự đoán của nhóm mình lên bảng phụ. + Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi. Trang 14
- Giáo viên nhận xét, kết luận và phát biểu Định nghĩa 2, Định lí 2
b) Định nghĩa 2(SGK)
Định lí 2: lim f (x) = L Û lim f (x) = lim f (x) = L x® - + 0 x x® ® 0 x x 0 x c) Củng cố.
Ví dụ. Trả lời các câu hỏi trắc nghiệm sau . 2 ìx - 3x +1 khi x < 2
Câu 1. Cho hàm số: f ( x) = í
, tìm lim f ( x). 5 î x - 3 khi x ³ 2 x 2- ® A.11 B. 7 C. 1 - D. 13 - 3
ìï2x - 2x khi x ³1
Câu 2. Cho hàm số f ( x) = í
, tìm lim f ( x) . 3
ïîx -3x khi x <1 x 1- ® A. 4 - B. 3 - C. 2 - D. 2 2 ì x +1 ï khi x < 1
Câu 3. Cho hàm số: f ( x) = í 1- x
, tìm lim f ( x) . ï x 1- ®
î 2x - 2 khi x ³1 A. 1 - B. 0 C.1 D. +¥ 2 ìx + 2x -1 khi x < 1 ï
Câu 4. Cho hàm số f ( x) = í
, tìm lim f ( x). 2 ïî 3x +1 khi x ³ 1 x 1 ® A. -¥ B. 2 C. 4 D. +¥
2.4 Đơn vị kiến thức 4 (thời gian)
HTKT 4. Giới hạn hữu hạn của hàm số tại vô cực. * Mục tiêu:
- Học sinh biết định nghĩa giới hạn hữu hạn của hàm số tại vô cực.
-Biết vận dụng định nghĩa vào việc giải một số bài toán đơn giản về giới hạn của hàm số.
.* Nội dung, phương thức tổ chức: + Chuyển giao:
L1. Chia lớp thành 4 nhóm. Nhóm 1, 2 hoàn thành Phiếu học tập số 1; Nhóm 3, 4 hoàn thành Phiếu
học tập số 2. Các nhóm nhận phiếu học tập và viết câu trả lời vào bảng phụ. 1
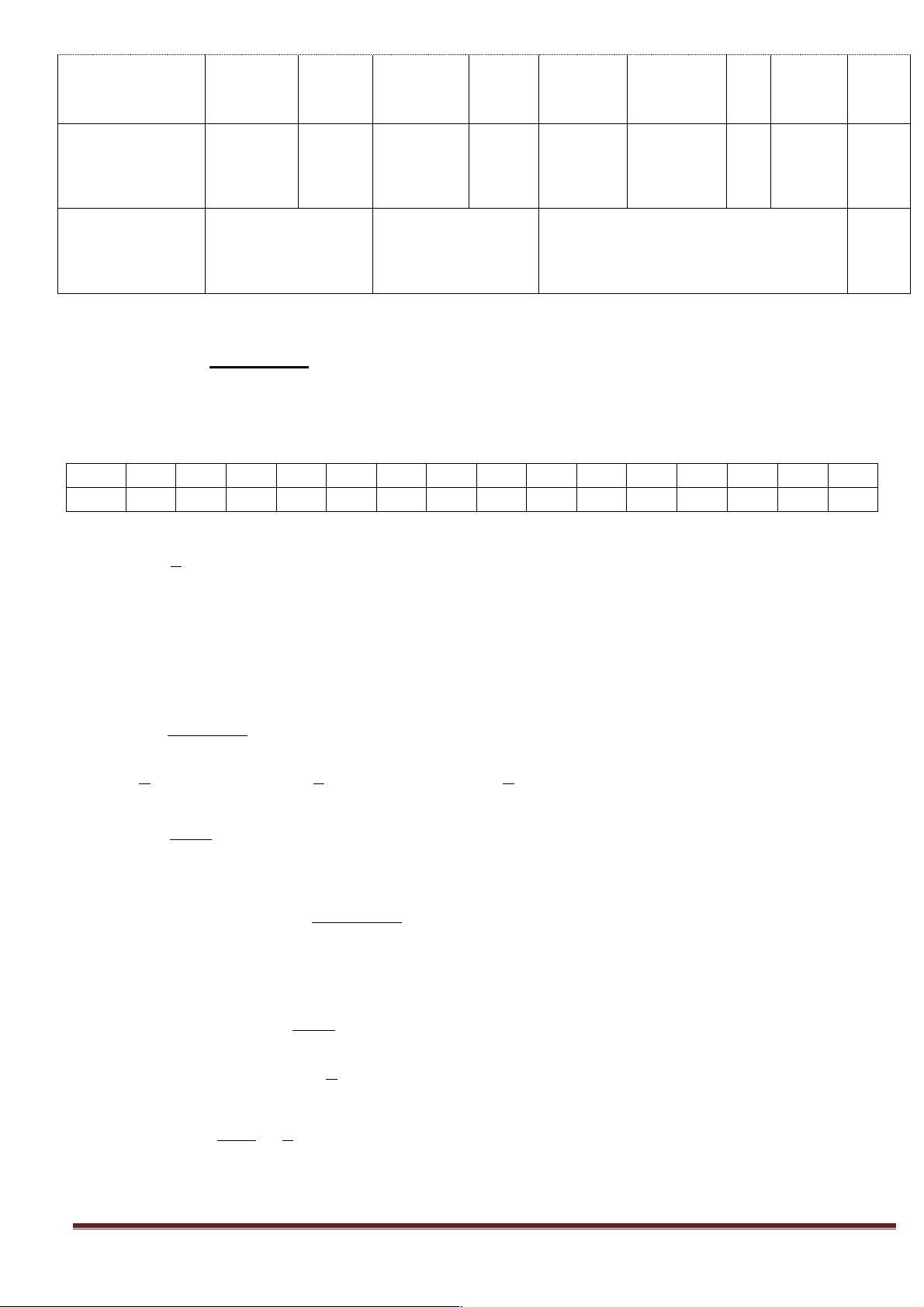
Câu hỏi :Cho hàm số f (x) =
có đồ thị như hvẽ x - 2 6 4 2 -5 5 -2 -4
PHIẾU HỌC TẬP SỐ 1
Tính giá trị của hàm số với những giá trị của x cho trong bảng x = 3 x = 4 x = 5 ...... x ® +¥ f (3) = ? f (4) = ? f (5) = ? ......... f (+¥) = ? Trang 15
PHIỂU HỌC TẬP SỐ 2
Tính giá trị của hàm số với những giá trị của x cho trong bảng x = 0 x = 3 - x = 7 - ...... x ® -¥ f (0) = ? f ( 3 - ) = ? f ( 7 - ) = ? ......... f (-¥) = ? + Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi trong phiếu học tập. Viết kết quả vào bảng phụ.
- Giáo viên quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm không hiểu nội dung các câu hỏi.
+ Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi.
- HS quan sát các phương án trả lời của các nhóm bạn.
- HS đặt câu hỏi cho các nhóm bạn để hiểu hơn về câu trả lời.
+ Đánh giá, nhận xét, tổng hợp:
- Trên cơ sở câu trả lời của học sinh, GV kết luận: Định nghĩa giới hạn hữu hạn của hàm số tại vô cực
Hoạt động của GV
Hoạt động của HS
Định nghĩa giới hạn hữu hạn của hàm số tại vô cực HS: Ghi nhận kiến thức.
a. Định nghĩa 3 : SGK/T 128 3x + 2
Ví dụ 1: Cho hàm số f (x) = .
a. Định nghĩa 3 : SGK/T 128 x -1 3x + 2
Tìm lim f (x) và lim f (x) . 1
Ví dụ 1: Cho hàm số f (x) = . x®-¥ 2 x®+¥ lim
x + x - x = x -1 x®+¥ ( ) 2
Tìm lim f (x) và lim f (x) .
H: Tìm tập xác định của hàm số trên ? x®-¥ x®+¥ Giải:
H: Học sinh giải thích ntn?
Hàm số đã cho xác định trên (- ¥ ; 1) và trên (1; + ¥ ).
Giả sử ( x ) là một dãy số bất kỳ, thoả mãn x < 1 n n và x ® - ¥ . n 2 3 + 3x + 2 x
Ta có lim f (x ) = lim n = lim n = 3 n x - 1 1 n 1 - x n x + 3 2
Vậy lim f (x) = lim = 3 x®-¥ x®-¥ x -1
Giả sử ( x ) là một dãy số bất kỳ, thoả mãn x > 1 n n và x ® + ¥ . n Ta có: 2 3 + 3x + 2 x lim f (x ) = lim n = lim n = 3 n x - 1 1 n 1 - x n 3x + 2
Vậy lim f (x) = lim = 3 x®+¥ x®+¥ x - 1 b. Chú ý: b. Chú ý: Trang 16
+) Với c, k là các hằng số và k nguyên dương, ta
Với c, k là các hằng s 3x + ố v
1 à k nguyên dương, luôn có : lim = 0 lim c = ? 2 x®-¥ x - 2 c x®±¥
lim c = c ; lim = 0. k c x®±¥ x®±¥ x lim = ? k
+) Định lý 1 về giới hạn hữu hạn của hàm số khi x®±¥ x
x ® x vẫn còn đúng khi x ® +¥ hoặc x ® -¥ 0
H: Khi x ® +¥ hoặc x ® -¥ thì có nhận xét gì về định lý 1 ? 5 2 x - 3x
Ví dụ 2: Tìm lim
HS: Định lý 1 vẫn c 2 òn đúng. 2 x®+¥ x + 2 5x + 3x +1 5 + Củng cố, l li uy m ện tập: = 2 x®-¥
Giải: Chia cả tử và mẫu cho 2 x , ta có:
- Từ định nghĩa, 2hã x y -nê 2 u phươ 2 ng pháp tìm giới hạn 3 3
hữu hạn của hàm số tại vô cực? 2 5 - lim 5 ( - ) x - 5 3x lim = lim x = x®+¥ x =
Học sinh làm các ví dụ 2,3,4,5. 2 x®+¥ x + 2 x®+¥ 2 2 1 + lim 1 ( + ) 2 x 2 x®+¥ x 3 -
H: Giải như thế nào? lim 5 lim x®+¥ x®+¥ x 5 - 0 = 2 = 5
H: Chia cả tử và mẫu cho x , ta được gì? 2 1 + 0 lim 1 + lim 2 x®+¥ x®+¥ x Kết quả ? Ví dụ 3:
Gọi HS lên bảng làm Ví dụ 4: Ví dụ 5: - Quy tắc tìm : f ( x) æ ¥ ö lim . ç ÷
x®±¥ g ( x) è ¥ ø
2.5 Đơn vị kiến thức 5 (thời gian)
HTKT 5. Giới hạn vô cực của hàm số .Một vài giới hạn đặc biệt .
* Mục tiêu: Học sinh biết, hiểu định nghĩa giới hạn vô cực. Từ đó áp dụng làm các bài tập tìm giới hạn vô cực đặc biệt
* Nội dung, phương thức tổ chức: + Chuyển giao: 1
L1: Tính giới hạn: lim x®2 x - 2
L2. Yêu cầu học sinh thảo luận theo nhóm và trả lời các câu hỏi sau.
H1. Khi x ® 2 thì x - 2 ® ? 1 H2. ® ? x - 2 1 H3. lim = ? x®2 x - 2 Trang 17 + Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi H1, H2, H3. Nhóm nào xong trước
được quyền trả lời trước, các nhóm khác nghe nhận xét, bổ sung nếu thiếu.
- Giáo viên quan sát, theo dõi các nhóm. Giải thích câu hỏi nếu các nhóm không hiểu nội dung các câu hỏi.
+ Báo cáo, thảo luận
- Đại diện nhóm trình bày.
- Dự kiến câu trả lời:
TL1. . Khi x ® 2 thì x - 2 ® 0 1 TL2. ® +¥ x - 2 1 TL3. lim = +¥ x®2 x - 2
+ Đánh giá, nhận xét, tổng hợp:
- Trên cơ sở câu trả lời của học sinh, GV kết luận hàm số có giới hạn vô cực khi x ® x . 0
- GV kết luận hàm số có giới hạn vô cực khi x ® ¥ .
Hoạt động của GV
Hoạt động của HS
III. Giới hạn vô cực của hàm số :
III. Giới hạn vô cực của hàm số :
1. Giới hạn vô cực:
1. Giới hạn vô cực:
Định nghĩa 4:
Định nghĩa 4:
Cho hàm số y = f(x) xác định trên khoảng (a;
- Giáo viên : gọi học sinh đứng tại chỗ đọc định +∞). nghĩa 4 SGK
Ta nói hàm số y = f(x) có giới hạn là - ∞ khi
x ® +¥ nếu với dãy số (xn) bất kì, xn > a và
- Giáo viên hướng dẫn học sinh ghi định nghĩa x ® +¥ , ta có f (x ) ® -¥ . n n bằng kí hiệu.
Kí hiệu: lim f (x) = -¥ hay f (x) ® -¥ khi x®+¥
- lim f (x) = +¥ thì lim (- f (x)) = ? x ® +¥ . x®+¥ x®+¥ Nhận xét :
lim f (x) = +¥ Û lim (- f (x)) = -¥
- Giáo viên đưa đến nhận xét. x®+¥ x®+¥
2. Một vài giới hạn đặc biệt: a) k
lim x = +¥ với k nguyên dương.
- Giáo viên gọi học sinh tính các gới hạn sau: x®+¥ k * 5 lim x , 5 lim x , 6 lim x
b) lim x = -¥ nếu k là số lẻ x®-¥ c®+¥ c®-¥ c®-¥ k
- Giáo viên đưa đến một vài gới hạn đặc biệt.
c) lim x = +¥ nếu k là số chẵn. x®-¥
+ Củng cố, luyện tập
2.6 Đơn vị kiến thức 6 (thời gian)
HTKT 6. Một vài quy tắc về giới hạn vô cực.
* Mục tiêu: Học sinh biết được quy tắc về giới hạn vô cực: giới hạn của tích, thương .
* Nội dung, phương thức tổ chức: + Chuyển giao:
1. Học sinh nhận phiếu học tập. Yêu cầu học sinh thảo luận theo nhóm và trả lời câu hỏi sau trong phiếu học tập số 3.
PHIẾU HỌC TẬP SÔ 3 Trang 18
- Nêu nội dung qui tắc tìm giới hạn tích f(x).g(x).
- Tìm giới hạn lim ( 3 x - 2x) x®+¥ Yêu cầu học sinh:
- Dưới sự hướng dẫn của Giáo viên học sinh phát biểu quy tắc tìm giới hạn của tích .
- Vận dụng tìm giới hạn ở phiếu học tập số 03 + Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi.
- Các nhóm viết kết quả dự đoán của nhóm mình lên bảng phụ.
+ Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi.
- Giáo viên nhận xét, kết luận và phát biểu qui tắc tìm giới hạn tích f(x).g(x).
Hoạt động của GV
Hoạt động của HS
3. Một vài quy tắc về giới hạn vô cực.
HS: Ghi nhận kiến thức.
3. Một vài quy tắc về giới hạn vô cực.
a. Qui tắc tìm giới hạn tích f(x).g(x).
a. Qui tắc tìm giới hạn tích f(x).g(x).
Nếu lim f (x) = L ¹ 0 và lim g(x) = +¥ ( hoặc - x® x x® 0 x0
∞ ) thì lim f (x).g(x) được tính theo quy tắc cho x® x0 trong bảng sau:
lim f (x) lim g(x) lim f (x).g(x) x® x0 x® x0 x® x0 L > 0 + ∞ + ∞ - ∞ - ∞ L < 0 + ∞ - ∞ - ∞ + ∞ Ví dụ : Tìm ( 3 lim x - 3x) x®±¥
2. Học sinh nhận phiếu học tập. Yêu cầu học sinh thảo luận theo nhóm và trả lời câu hỏi sau trong phiếu học tập số 4.
PHIẾU HỌC TẬP SÔ 4 f (x)
- Nêu nội dung qui tắc tìm giới hạn thương . g(x) 2x +1
- Tìm giới hạn lim 2 x® 2 - (x + ) 2 Yêu cầu học sinh:
- Dưới sự hướng dẫn của Giáo viên học sinh phát biểu quy tắc tìm giới hạn của thương .
- Vận dụng tìm giới hạn ở phiếu học tập số 04 + Thực hiện
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi.
- Các nhóm viết kết quả dự đoán của nhóm mình lên bảng phụ.
+ Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi. f (x)
- Giáo viên nhận xét, kết luận và phát biểu qui tắc tìm giới hạn thương . g(x)
Hoạt động của GV
Hoạt động của HS
3. Một vài quy tắc về giới hạn vô cực.
HS: Ghi nhận kiến thức. Trang 19
3. Một vài quy tắc về giới hạn vô cực.
a. Qui tắc tìm giới hạn tích f(x).g(x).
a. Qui tắc tìm giới hạn tích f(x).g(x). f (x) f (x)
b. Quy tắc tìm giới hạn của thương
b. Quy tắc tìm giới hạn của thương g(x) g(x)
lim f (x) lim g(x) Dấu của g(x) x® x0 x® x0 f (x) lim
x® x0 g(x) L ± ∞ Tuỳ ý 0 L > 0 0 + + ∞ - - ∞ L < 0 + - ∞ - + ∞
Chú ý: Các quy tắc trên vẫn đúng cho các trường hợp + -
x ® x , x ® x , x ® +¥, x ® -¥ 0 0 2x - 4 2x - 4 Ví dụ : Tìm a) lim b) lim x 1- ® x -1 x 1+ ® x -1
3. LUYỆN TẬP (thời gian)
* Mục tiêu: Giúp học sinh củng cố kiến thức và rèn luyện cho học sinh kĩ năng biến đổi và tính toán.
* Nội dung, phương thức tổ chức: + Chuyển giao:
1. HS nhận phiếu học tập gồm các câu hỏi trắc nghiệm và tự luận
2. Học sinh hoạt động cá nhân, trả lời các câu hỏi trắc nghiệm và hoạt động nhóm làm các câu hỏi tự luận.
PHIẾU HỌC TẬP SỐ 5 Câu 1. lim ( 2
3x - 3x - 8) bằng x 2 ®-
A.5 B. 7 C. 9 D. +¥ 2 x - 3x + 2 Câu 2: lim bằng x 1 ® x -1
A. -1 B. 1 C. 2 D. +¥ 2 ìx - 3x +1 khi x < 2
Câu 3. Cho hàm số: f ( x) = í
, tìm lim f ( x). 5 î x - 3 khi x ³ 2 x 2- ® A.11 B. 7 C. 1 - D. 13 - 3
ìï2x - 2x khi x ³1
Câu 4. Cho hàm số f ( x) = í
, tìm lim f ( x) . 3
ïîx -3x khi x <1 x 1- ® A. 4 - B. 3 - C. 2 - D. 2 2 x +1 Câu 5. lim bằng x 1+ ® x -1 A. +¥ B. 2 C.1 D. -¥ 2 ìx + 2x -1 khi x < 1 ï
Câu 6. Cho hàm số f ( x) = í
, tìm lim f ( x). 2 ïî 3x +1 khi x ³ 1 x 1 ® A. -¥ B. 2 C. 4 D. +¥ Trang 20 2 2x - 3x +1 Câu 8. lim bằng 2 x 1 ® 1- x
A.1/2 B. 1/4 C. -1/4 D.-1/2 2 x -12x + 35 Câu 9. lim bằng x®5 5x - 25 1 2 2 A. B. C. - D. +¥ 5 5 5
Câu 10. lim ( x +1 - x - 3) bằng x®+¥ A. -¥ B. 2 C. 0 D. +¥
PHIẾU HỌC TẬP SỐ 6 ( có thể BTVN)
Bài tập 1. Tính các giới hạn sau: 2 x - 3x + 2 1. lim ( 2 x - x + 7) 2. lim x 1 ®- x 1 ® x -1 x + 5 - 3 3 2 3x - 2x + 2 3. lim 4. lim x®4 4 - x x 1 ®- x - 2 4x +1 - 3 2 1+ x -1 5. lim 6. lim 2 x®2 x - 4 x®0 x
Bài tập 2. Tính các giới hạn sau: 2 x - 3x + 2 2 2x - 3x + 1 2 x - 4x + 3 1. lim 2. lim 3. lim x® (x - 2)2 2 3 2 x 1
® x - x - x + 1 x 3 ® x - 3 6 5
4x - 5x + x 3 1 - x -1 3 x + 1 4. lim 5. lim 6. lim x® (1- x)2 1 x®0 3x x 1 ®- 2 x + 3 - 2
Bài tập 3. Tính các giới hạn sau: 2 2 2 3x - 5x +1
(x - )1 .(7x + 2) ( 2 2x + ) 1 (5x + 3) 1. lim 2. lim 3. lim 2 x®¥ x - 2 x®¥ (2x + )4 1 x®¥ ( 3 2x - ) 1 ( x + ) 1 4. 2 lim
x - 4x - x x®¥ ( )
Bài tập 4. Tính các giới hạn sau: 1. é 2 lim x x 5 x ù + - 2. 2 lim
x - x + 3 + x x®±¥ ( ) x®+¥ ê ë ( )úû + Thực hiện
- Học sinh làm việc cá nhân và khoanh đáp án vào phiếu trả lời trắc nghiệm và làm việc nhóm vào
bảng phụ với câu hỏi tự luận.
- Giáo viên theo dõi, đảm bảo tất cả học sinh đều tự giác làm việc.
+ Báo cáo, thảo luận Trang 21
- GV đưa ra đáp án cho từng câu hỏi, các nhóm thống kê số học sinh làm đúng từng câu.
- GV yêu cầu học sinh trình bày cách làm cụ thể cho từng câu hỏi.
- GV nhận xét và lựa chọn cách làm nhanh nhất cho từng câu trắc nghiệm.
4. VẬN DỤNG VÀ MỞ RỘNG (
4.1 Vận dụng vào thực tế (thời gian)
4.2 Mở rộng, tìm tòi (mở rộng, đào sâu, nâng cao,…) (thời gian)
Học sinh nghiên cứu và là các bài tập sau?
*Bài toán 1: Theo dự đoán tỉ lệ tuổi thọ con người của một nước đang phát triển, sau x năm kể từ bây giờ là: 138x + 236 T(x) =
năm . Hỏi tuổi thọ của con người sẽ đạt được tới mức Giới hạn là bao nhiêu? 2x + 5 Bài tập thêm:
Vận dụng linh hoạt các kiến thức đã học về giới hạn hữu hạn của hàm số tại một điểm và kỹ năng biến đổi
toán học, yêu cầu học sinh tính các giới hạn sau. 2018 x + x - 2 m x -1 1. lim 2. lim 2016 x 1 ® x + x - 2 1 n x® x -1
(1+ 5x)(1+ 9x) -1
(1+ x)(1+ 2x)(1+ 3x) -1 3. lim 4. lim x®0 x x®0 x 2 x + x + ... n + x - n n
x - nx + n -1 5. lim 6. lim x 1 ® x -1 2 x 1 ® (x -1)
ìm - 2x khi x ³1
7. Cho hàm số f ( x) = í
. Tìm m đề tồn tại giới hạn lim f ( x). 2
îx - 3 khi x <1 x 1 ® 3 2 x +1 - 8 - x 2 x 8. lim 9. lim x®0 x x®0
1+ x sin 3x - cos 2x 3 2 3 2
8x + x + 6x + 9 - 9x + 27x + 27
( 2x +1998) 7 1-2x -1998 10. lim 11. lim 3 x®0 x x®0 x + Thực hiện
- Học sinh làm việc cá nhân giải bài vào vở bài tập.
- Giáo viên theo dõi, đảm bảo tất cả học sinh đều tự giác làm việc. + Báo cáo, thảo luận
- GV yêu cầu học sinh trình bày cách làm cụ thể cho từng bài.
- GV nhận xét và bổ sung lựa chọn cách làm hay, nhanh nhất cho từng bài.
Ngày soạn: 24/2/2019 CHỦ ĐỀ : HÀM SỐ LIÊN TỤC
I. Mục tiêu của bài: 5. Kiến thức:
- Biết được định nghĩa hàm số liên tục tại một điểm.
- Biết được định nghĩa hàm số liên tục trên một đoạn, khoảng cũng như các định lí cơ bản. 6. Kỹ năng:
- Vận dụng định nghĩa xét tính liên tục của hàm số tại một điểm.
- Xét tính liên tục của hàm số trên một khoảng, đoạn. Vận dụng định lí chứng minh sự tồn tại nghiệm của một phương trình. 7. Thái độ:
- Tích cực hoạt động, phát huy sự sáng tạo, tìm tòi.
- Rèn luyện tính cẩn thận, chính xác trong tính toán, trình bày. Trang 22
8. Đinh hướng phát triển năng lực:
(Năng lực tự học, năng lực hợp tác, năng lực giao tiếp, năng lực quan sát, năng lực phát hiện và giải quyết
vấn đề, năng lực tính toán, năng lực vận dụng kiến thức vào cuộc sống ...)
II. Chuẩn bị của giáo viên và học sinh 1. Giáo viên:
- Giáo án, phiếu học tập,bảng phụ.
- Máy chiếu, bảng phụ trình bày nhóm 2. Học sinh:
- Chuẩn bị trước bài học, sách giáo khoa, máy tính cầm tay.
III. Chuỗi các hoạt động học
1. GIỚI THIỆU (3 phút)
Giáo viên trình chiếu hai hình ảnh cho học sinh quan sát. Hình 1 Hình 2
Hình 1 cho ta thấy cây cầu thông suốt, các phương tiện giao thông qua lại liên tục.
Hình 2 cho ta thấy cây cầu bị gãy, giao thông bị gián đoạn hay không liên tục.
Trong cuộc sống thì cụm từ “liên tục” được sử dụng rất nhiều, vậy trong toán học khái niệm liên tục được
hiểu như thế nào, ta đi vào bài học: “ Hàm số liên tục”. 2. NỘI DUNG BÀI HỌC
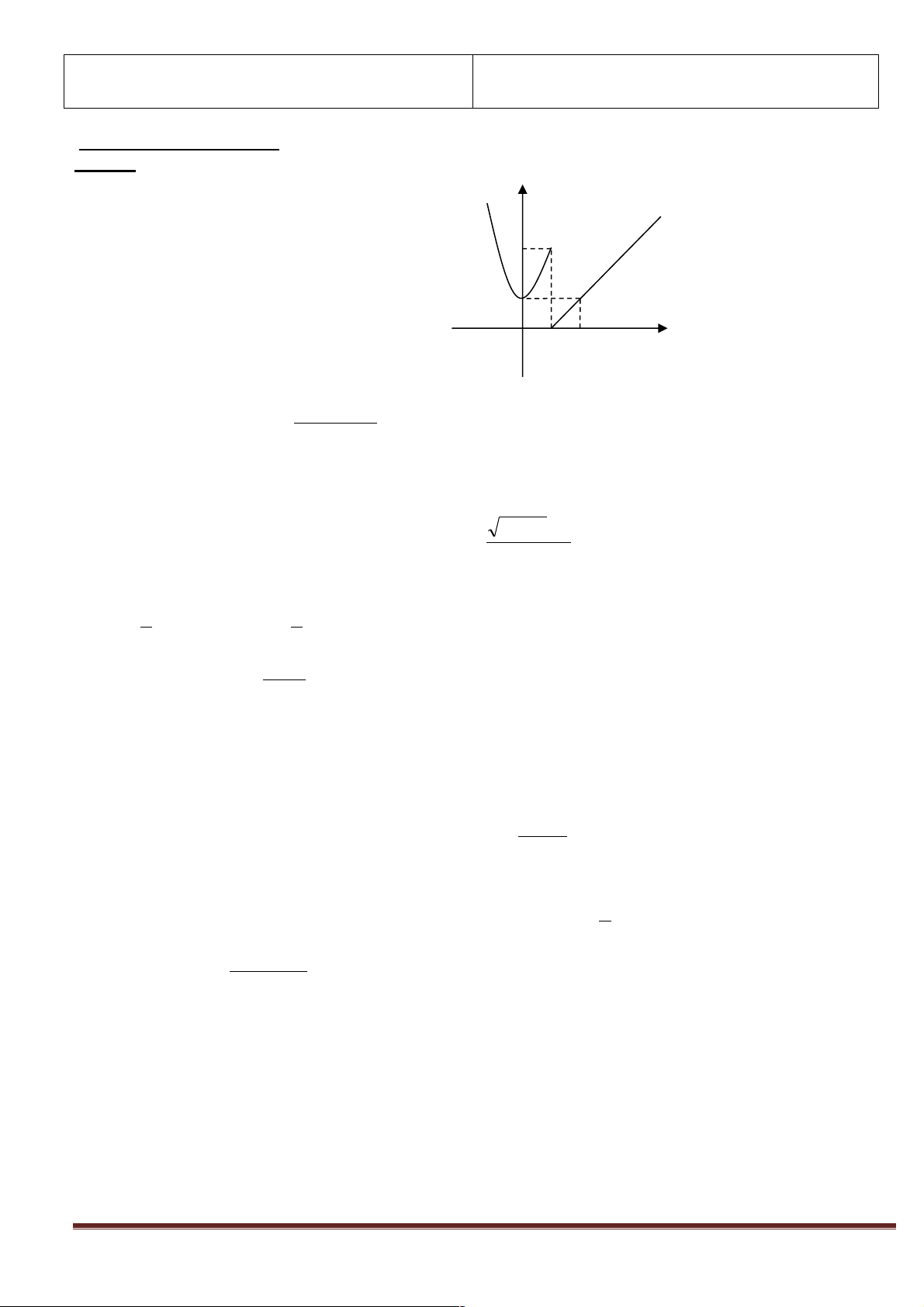
2.1 Hàm số liên tục tại một điểm( 30 phút) y a) Tiếp cận Gợi ý
Bài toán 1: Cho hàm số 2 y = f (x) = x + Tìm TXĐ.
+ Tính f (1) ; tính lim f (x) và so sánh chúng. 1 x 1 ®
+ Nhận xét về đồ thị của hàm số tại điểm x =1. x O 1 + TXĐ: D = R . + f (1) = lim f (x) = 1. x 1 ®
+ Đồ thị hàm số là đường liền nét tại x =1.
Bài toán 2: Cho hàm số Trang 23 Ï 2 x Ô + 2 khi x £ 1 Ô Ô y y g(x) Ô = = Ì . Ô Ô 4 khi x 4 Ô > 1 Ô Ó + Tìm TXĐ. 2
+ Tính g(1) ; tính lim g(x) (nếu có) và so sánh chúng. xÆ1 + TXĐ: D = R .
+ Nhận xét về đồ thị của hàm số tại điểm x =1. + g(1) = 3; x lim g(x) = 3 O π lim 1 g(x) = 4 x 1- x 1+ Æ Æ
fi không tồn tại lim g(x) . xÆ1
+ Đồ thị hàm số không liền nét tại x = 1.
+ Dẫn dắt hình thành kiến thức: Qua hai bài toán trên nhận thấy hàm số y = f (x l
) iên tục tại x = 1; hàm số y = g(x
) không liên tục tại x = 1 hay gián đoạn tại x = 1. Hãy phát biểu định nghĩa hàm số liên tục tại một điểm.
b) Hình thành kiến thức
Định nghĩa 1: Cho hàm số y = f (x) xác định trên khoảng K và x K
Œ .Hàm số y = f (x) được gọi là 0
liên tục tại x nếu lim f (x) = f (x ). 0 0 xÆ x0
Hàm số y = f (x) không liên tục tại x được gọi là gián đoạn tại điểm đó. 0 c) Củng cố Gợi ý
Câu 1. Nêu các bước xét tính liên tục của hàm số tại
- Tìm tập xác định, xét xem x có thuộc TXĐ 0 điểm x ? 0 hay không. - Tính f (x ) và lim f (x). 0 xÆ x0
- So sánh f (x ) và lim f (x). 0 xÆ x0
+ Nếu f (x ) = lim f (x) fi Hàm số liên 0 xÆ x0 tục tại x . 0
+ Nếu f (x ) π lim f (x) fi Hàm số 0 x + 1 xÆ x0
Câu 2: Xét tính liên tục của hàm số f (x) = tại gián đoạn tại x . x 0 x = 2. 0 TXĐ: D = R \ { } 0 ; 2 D Œ .
Câu 3: Xét tính liên tục của hàm số 3 Ï 2 Ta có f (2) = = lim f (x) x Ô - x - 6 Ô Ô 2 xÆ 2 Ô khi x π 3 f (x) = Ì tại x = 3. x - 3 0
Do đó hàm số liên tục tại x = 2. Ô 0 2x Ô Ô + 1 khi x = 3. TXĐ: D = R. Ô Ó
Ta có f (3) = 7 π lim f (x) = 5 xÆ 3
Do đó hàm số gián đoạn tại x = 3. 0
2.2 Hàm số liên trên một khoảng (15 phút) a) Tiếp cận Gợi ý 1. Cho hàm số 2 y = f (x) = x Trang 24 + Ta đã biết hàm số 2
y = f (x) = x liên tục tại x = 1. + Hàm số liên tục tại x = 0, x = 2.
+ Xét tính liên tục của hàm số tại các điểm
+ Đồ thị hàm số là một đường liền nét. x = 0, x = 2.
+ Hàm số liên tục tại mọi điểm thuộc khoảng
+ Đồ thị hàm số y = f (x) có không liền nét tại điểm (- • ; +• ) nào trên (- • ; +• ) không?
+ Đoán xem y = f (x) có liên tục tại mọi điểm thuộc khoảng (- • ; +• ? )
Đồ thị hàm số không liền nét tại x = 1. Ï 2 x Ô + 2 khi x £ 1 Ô
Vì hàm số không liên tục tại x = 1 nên nói nó Ô Ô
liên tục tại mọi điểm thuộc khoảng
2. Cho hàm số y = g(x) = Ì . Ô (- • ; +• ) là sai. 4 khi x Ô Ô > 1 Ô Ó
+ Ta đã biết hàm số g(x) không liên tục tại x = 1.
+ Đồ thị hàm số có không liền nét tại điểm nào thuộc khoảng (- • ; +• ) không?
+ Ta nói hàm số liên tục tại mọi điểm thuộc khoảng (- • ; +• ) đúng hay sai?
Hàm số y = f (x) liên tục tại mọi điểm thuộc (- • ; +• , đồ t )
hị là một đường liền nét nên y = f (x) là
hàm số liên tục trên khoảng (- • ; +• . )
Hàm số y = g(x) không liên tục tại x = 1, đồ thị không liền nét tại x = 1 nên y = g(x) không liên tục trên khoảng (- • ; +• . )
b) Hình thành kiến thức: Định nghĩa 2: H
y àm số y = f (x)x được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.
Hàm số y = f (x) được gọi là liên tục trên đoạn [a; b ]nếu nó liên tục trên khoảng (a; b ) và
lim f (x) = f (a), lim f (x) = f (b). x a+ Æ x b- Æ
Nhận xét: Đồ thị hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó. Hàm số liên tục trên khoảng Hàm số không liên tục trên khoảng a b a b O O c) củng cố Gợi ý
Đồ thị hàm số nào dưới đây không liên tục trên khoảng (a;b ?. )
Đáp án C: Đồ thị hàm số không
liền nét tại một điểm thuộc khoảng (a;b . ) Trang 25
2.3 Một số định lí cơ bản
2.3.1: Định lí 1(10 phút) a)Định lí 1:
a) Hàm số đa thức liên tục trên toàn bộ tập số thực R.
b) Hàm số phân thức hữu tỉ( thương của hai đa thức) và các hàm số lượng giác liên tục trên từng khoảng
của tập xác định của chúng. b) Củng cố:
1: Hàm số nào dưới đây liên tục trên toàn bộ tập số Đáp án B: vì 2 x + 3 ≥ 3; " x R Œ thực R ? + x +1 x 1 fi f (x) = A. 2
f (x) = t anx + x - 3. B. f (x) = .
có tập xác định R. 2 2 + x + 3 x 3
Do đó nó liên tục trên toàn R. ì2x+1 khi x ¹ 2 1 C. f (x) = í .D. f (x) = 10 î khi x=2 2 cot x + 3
2.Xét tính liên tục của hàm số sau trên tập xác định TXĐ: D = R. 2
+ Với x > 2 : f (x) là phân thức hữu tỉ nên liên ìx - 4 ï khi x > 2 của nó f (x) = í (2; +• ). x - 2 . tục ï
+ Với x < 2 : f (x) là đa thức bậc nhất nên liên î2x + 1 khi x £ 2 tục (- • ; 2).
+ Với x = 2 : lim f (x) = lim (2x + ) 1 = 5 x 2- x 2- Æ Æ Ê 2 x Á 4ˆ - ˜ lim f (x) = lim Á ˜ Á ˜ = 4 Á Ë - ˜ xÆ 2+ xÆ 2+ x 2 ¯
fi không tồn tại lim f (x) . xÆ 2
Do đó hàm số không liên tục tại x = 2.
Vậy f (x) liên tục trên khoảng (- • ; 2) và (2; +• ).
2.3.2: Định lí 2(10 phút) a) Tiếp cận Gợi ý Cho hai hàm số 2 f (x) = x - x + 1 và
a) Hàm số f (x) và g(x) là các hàm đa thức liên g(x) = x + 1.
tục trên R nên liên tục tại x =1.
b) các hàm số f (x) + g(x) ; f (x) - g(x) ;
a) Xét tính liên tục của hàm số f (x) và g(x) tại x = 1. f (x) 0 f (x).g(x) ; f (x).g(x) ; tại x = 1.
b) Xét tính liên tục các hàm số f (x) + g(x) ; g(x) 0 f (x)
f (x) - g(x) ; f (x).g(x) ; f (x).g(x) ; tại g(x) Trang 26 x = 1. 0
Hãy phát biểu định lý 2. b) Hình thành kiến thức
Định lí 2: Giả sử y = f (x) và y = g(x) là hai hàm số liên tục tại điểm x . Khi đó 0
a) Các hàm số y = f (x) + g(x) , y = f (x) - g(x) và y = f (x).g(x) liên tục tại x ; 0 f (x) b) Hàm số y =
liên tục tại x nếu g(x ) π 0 . g(x) 0 0 c) củng cố Gợi ý Cho hàm số 2 y = f (x) = x - x và
Các hàm số đều liên tục tại x = 2. y = g(x) = x - 1.
Xét tính liên tục của các hàm số y = f (x) ,
y = g(x) , y = f (x) + g(x) , y = f (x) - g(x) ; f (x) y = f (x).g(x) ; y = tại x = 2. g(x) 0
2.3.3 Định lí 3(10 phút) a) Tiếp cận:
Cho hàm số y = f (x) có đồ thị như hình bên dưới. y f(b ) a b
a) Hàm số liên tục trên đoạn [a; b .] x
b) f (a) < 0; f(b) > 0 fi f(a).f(b) < 0 O
c) Đồ thị cắt trục hoành. f(a
a) Hàm số y = f (x) có liên tục trên đoạn [a; b ] không?
b) Nhận xét dấu của f (a) và f(b).
c) Đồ thị hàm số có cắt trục hoành không?
Nhận thấy khi hàm số y = f (x) liên tục trên đoạn [a; b ,] f (a) và f(b) khi đó đồ thị hàm số luôn cắt trục
hoành tại ít nhất một điểm thuộc khoảng (a; b . )
Số giao điểm của đồ thị y = f (x) và trục hoành là số nghiệm của phươngtrình f (x) = 0.
b) Hình thành định lí 3
Định lí 3: Nếu hàm số y = f (x) liên tục trên đoạn [a; b ]và f (a).f (b) < 0 , thì phương trình f (x) = 0
có ít nhất một nghiệm trên khoảng (a; b . ) c) củng cố:
Chứng minh rằng phương trình 3 2
x - 2x -1 = 0 có *) Tập xác định: R
ít nhất một nghiệm trong khoảng (2;3).
*) Hàm số f ( x) 3 2
= x - 2x -1 liên tục trên R nên nó liên tục trên [2;3]. *) f (2) = 1
- ; f (3) = 8 Þ f (2). f (3) < 0
Suy ra phương trình f ( x) = 0 có ít nhất một Trang 27
nghiệm nằm trong khoảng (2;3)
3. LUYỆN TẬP (15 phút)) Trắc nghiệm khách quan: TNKQ:
Câu 1. Cho hàm số y = f (x) có đồ thị như hình bên dưới không liên tục tại điểm có hoành độ bằng bao y nhiêu ? 3 x 1 O 1 2
A. x = 1. B. x = 3. C. x = 0. D. x = 2. 2 ì x + 2x - 3 ï khi x ¹ 1
Câu 2. Cho hàm số f (x) = í x -1
. Tìm m để hàm số liên tục tại điểm x = 1. ï 0 î2 khi x =1
A. m = 3 . B. m = 5 . C. m = 4 . D. m = 6. ì
ï 3x + 4 -1 khi x ¹ -1
Câu 3. Tìm giá trị của tham số m để hàm số f (x) = í x +1
liên tục tại x = - 1. ï îm khi x = -1 3 1 A. m = . B. m = . C. m = - 1. D. m = 3. 2 2 x - 3
Câu 4: Cho hàm số y =
. Mệnh đề nào dưới đây đúng? x + 1
A. Hàm số đã cho gián đoạn tại x = 1.
B. Hàm số đã cho liên tục trên toàn R.
C. Hàm số đã cho liên tục trên khoảng (- • ;- ) 1 và ( - 1;+ • ).
D. Hàm số đã cho gián đoạn tại x = 3. Ï 3 x Ô - 1 Ô Ô khi x π 1
Câu 5: Tìm giá trị thực của tham số m để hàm số f (x) = Ì liên tục trên R. x - 1 Ô2 Ô Ô m + 1 khi x = 1 Ô Ó 3 A. m = 1. B. m = 0. C. m = . D. m = 3. 2 2x
Câu 6: Cho f (x) =
và g(x) = sin x . Xét tính liên tục của hai hàm số y = f (x) và y = g(x) 2 x - x + 3 trên toàn trục số.
A. Hàm số y = f (x) không liên tục trên toàn trục số, hàm số y = g(x) liên tục trên toàn trục số.
B. Cả hai hàm số y = f (x) và y = g(x) đều liên tục trên toàn trục số.
C. y = f (x) liên tục trên toàn trục số, y = g(x) chỉ liên tục trên đoạn [- ] 1 ; 1 .
D. Cả hai hàm số y = f (x) và y = g(x) đều không liên tục trên toàn trục số.
Câu 7: Cho phương trình 4 2 2x - 5x + x +1 = 0.
Mệnh đề nào dưới đây đúng?
A. Phương trình có ít nhất hai nghiệm trong khoảng (0;2). Trang 28
B. Phương trình không có nghiệm trong khoảng ( 1; - ) 1 .
C. Phương trình không có nghiệm trong khoảng ( 2; - 0).
D. Phương trình chỉ có 1 nghiệm trong khoảng ( 2; - ) 1 . Tự luận: Ï 3 x Ô - 8 Ô Ô khi x π 2
Câu 1: Xét tính liên tục của hàm số f (x) = Ì x - 2 . Ô5 Ô Ô khi x = 2 Ô Ó
Cần thay số 5 bởi số nào để hàm số f (x) liên tục tại x = 2. 0 2 ì5- ax nêu x > 2
Câu 2: Định a để hàm số liên tục: f (x) = í trên R. îx +1 nêu x £ 2
Câu 3: Chứng minh rằng phương trình 3 2
2x - 5x + x + 1= 0 có ít nhất hai nghiệm.
4. VẬN DỤNG VÀ MỞ RỘNG:
Câu 1: Chứng minh phương trình 2
x sin x + x cos x +1 = 0 có ít nhất một nghiệm x Î 0;p 0 ( ) . 2 ìx -1 ï khi x < 3 và x ¹ 1 x -1 ïï
Câu 2: Xét tính liên tục của hàm f (x) = 4 khi x = 1 í
trên tập xác định của nó. ï ï ïî x +1 khi x ³ 3. Trang 29
Ngày soạn: 3/3/2019 ÔN TẬP CHUYÊN ĐỀ 4 A. Mục tiêu:
1. Về kiến thức: Học sinh biết được:
- Các dạng giới hạn và cách tìm giới hạn của dãy số, hàm số.
- Khái niệm và các định lý về hàm số liên tục
2. Về kỹ năng: Học sinh cần rèn luyện các kỉ năng sau:
- Rèn luyện tính cẩn thận chính xác trong tính toán, lập luận.
- Biết vận dụng định lí vào bài tập .
- Xây dựng tư duy logic, linh hoạt, biết quy lạ thành quen, phát triển tư duy logic toán học.
- Biết sử dụng máy tính.
3. Về thái độ:
- Chủ động tích cực tiếp thu kiến thức mới.
- Tích cực và tương tác tốt trong hoạt động nhóm.
- Thái độ hứng thú trong học tập.
4.Định hướng phát triển năng lực:
- Rèn luyện năng lực tự học, năng lực hợp tác, năng lực giao tiếp, năng lực quan sát, năng lực phát hiện và
giải quyết vấn đề, năng lực tính toán, năng lực vận dụng kiến thức vào cuộc sống,…
B. Chuẩn bị của giáo viên và học sinh: 1. Giáo viên:
- Giáo án, đồ dùng dạy học.
- Các bảng phụ và các phiếu học tập. 2. Học sinh:
- Đồ dùng học tập :sgk,máy tính... C. Phương pháp:
- Gợi mở, vấn đáp.
- Tổ chức hoạt động nhóm.
D.Chuổi các hoạt động học:
Giải bài tập trắc nghiệm .
Phát phiếu học tâp 1 - Chuyển giao nhiệm vụ
Nhóm 1:câu 1,5. Nhóm 2:câu 2,6. Nhóm 3: câu 3,7. Nhóm 4: câu 4,8
Câu 1. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Nếu lim u = +¥ , thì limu = +¥ .
B. Nếu lim u = +¥ , thì limu = -¥ . n n n n
C. Nếu limu = 0 , thì lim u = 0.
D. Nếu limu = -a , thì lim u = a . n n n n n 2 - 5 -2
Câu 2. Kết quả đúng của lim là: n n 3 + 5 . 2 5 5 25 A. – . B. 1. C. . D. – . 2 2 2 2 - n + 2n +1
Câu 3. Kết quả đúng của lim là 3 4 n + 2 Trang 30 3 2 1 1 A. – . B. – . C. – . D. . 3 3 2 2 3 4 n - n
Câu 4. Giới hạn dãy số (un) với un = là: 4n - 5 3 A. –¥. B. +¥. C. . D. 0. 4 n n 3 - 2 . 4 1 - - 3 Câu 5. lim bằng : n n 2 . 3 + 4 A. +¥. B. –¥. C. 0. D. 1. n3 - 2n + 5
Câu 6. Chọn kết quả đúng của lim : 3 + n 5 2 A. 5. B. . C. –¥. D. +¥. 5
Câu 7. Giá trị đúng của lim ( 2 n -1 - 3 2 n + 2 ) là: A. +¥. B. –¥. C. –2. D. 0. æ np 2 ö
Câu 8. lim çn sin - 3 2n ÷ bằng: è 5 ø A. +¥. B. 0. C. –2. D. –¥.
- Học sinh thực hiện nhiệm vụ.
- Học sinh lên bảng trình bày.
- Giáo viên nhận xét chỉnh sửa.
Phát phiếu học tâp 2 - Chuyển giao nhiệm vụ
Nhóm 1:câu 1,5. Nhóm 2:câu 2,6. Nhóm 3: câu 3,7. Nhóm 4: câu 4,8 5 Câu 1. bằng : lim 3x + 2 x®+¥ 5 A. 0. B. 1. C. . D. +¥. 3 2 x + 2x +1
Câu 2. Chọn kết quả đúng trong các kết quả sau của là: lim x® 1 - 2 3 x + 2 1 A. –¥. B. 0. C. . D. +¥. 2 2 2x -1 Câu 3. bằng : lim 2 x®-¥ 3 - x 1 1 A. –2. B. – . C. . D. 2. 3 3 1+ 3x Câu 4. bằng : lim x®-¥ 2 2 x + 3 - 3 2 2 3 2 2 A. . B. . C. . D. – . 2 2 2 2 Trang 31 x - 3
Câu 5. Giá tri đúng của lim x® x - 3 3 A. Không tồn tại. B. 0. C. 1. D. +¥. 2 x - x +1 Câu 6. bằng : lim 2 + x® x - 1 1 A. –¥. B. –1. C. 1. D. +¥.
Câu 7. Chọn kết quả đúng trong các kết quả sau của (4 5 x - 3 3 x + x ) 1 là: lim + x®-¥ A. –¥. B. 0. C. 4. D. +¥. x -1
Câu 8. Cho hàm số f (x) = (x + ) 2
. Chọn kết quả đúng của f ( ) : 4 2 x + x +1 lim x x®+¥ 1 A. 0. B. . C. 1. D. Không tồn tại. 2
- Học sinh thực hiện nhiệm vụ.
- Học sinh lên bảng trình bày.
- Giáo viên nhận xét chỉnh sửa.
Phát phiếu học tâp 3 - Chuyển giao nhiệm vụ
Nhóm 1:câu 1,5. Nhóm 2:câu 2,6. Nhóm 3: câu 3,7. Nhóm 4: câu 4,8
Câu 1. Cho hàm số f (x) 2
= x - 4 . Chọn câu đúng trong các câu sau:
(I) f(x) liên tục tại x = 2.
(II) f(x) gián đoạn tại x = 2.
(III) f(x) liên tục trên đoạn [- ; 2 2].
A. Chỉ (I) và (III). B. Chỉ (I). C. Chỉ (II).
D. Chỉ (II) và (III). ì 2x + 8 - 2 ï , x > 2 -
Câu 2. Cho hàm số f (x) = í x + 2
. Tìm khẳng định đúng trong các khẳng định sau: ï , x = 2 - î0 (I) f (x) = 0 . lim x®( 2)+ -
(II) f(x) liên tục tại x = –2.
(III) f(x) gián đoạn tại x = –2.
A. Chỉ (I) và (III). B. Chỉ (I) và (II). C. Chỉ (I) . D. Chỉ (III).
Câu 3. Tìm khẳng định đúng trong các khẳng định sau:
I. f(x) liên tục trên đoạn [a;b] và f(a).f(b) > 0 thì tồn tại ít nhất số c Î (a;b) sao cho f(c) = 0.
II. f(x) liên tục trên (a;b] và trên [b;c) nhưng không liên tục trên (a;c). A. Chỉ I đúng. B. Chỉ II đúng.
C. Cả I và II đúng. D. Cả I và II sai.
Câu 4. Tìm khẳng định đúng trong các khẳng định sau:
I. f(x) liên tục trên đoạn [a;b] và f(a).f(b) < 0 thì phương trình f(x) = 0 có nghiệm.
II. f(x) không liên tục trên [a;b] và f(a).f(b) ³ 0 thì phương trình f(x) = 0 vô nghiệm. A. Chỉ I đúng B. Chỉ II đúng.
C. Cả I và II đúng. D. Cả I và II sai. Trang 32 ì 2 x - 3 ï , x ¹ 3
Câu 5. Cho hàm số f (x) = í x - 3
. Tìm khẳng định đúng trong các khẳng định sau: ï , x = 3 î2 3
I. f(x) liên tục tại x = 3 .
II. f(x) gián đoạn tại x = 3 .
III. f(x) liên tục trên R. A. Chỉ (I) và (II).
B. Chỉ (II) và (III).
C. Chỉ (I) và (III).
D. Cả (I),(II),(III) đều đúng.
Câu 6. Tìm khẳng định đúng trong các khẳng định sau:
I. f(x) = x5 – 3x2 +1 liên tục trên R. 1 II. f (x) =
liên tục trên khoảng (–1;1). 2 x -1
III. f (x) = x - 2 liên tục trên đoạn [2;+¥). A. Chỉ I đúng. B. Chỉ (I) và (II).
C. Chỉ (II) và (III).
D. Chỉ (I) và (III). 2 x +1
Câu 7. Cho hàm số f (x) =
. f(x) liên tục trên các khoảng nào sau đây ? 2 x + 5x + 6 A. (–3;2). B. (–3;+¥) C. (–¥; 3). D. (2;3).
Câu 8. Cho hàm số f(x) = x3 – 1000x2 + 0,01 . phương trình f(x) = 0 có nghiệm thuộc khoảng nào trong các khoảng sau đây ? I. (–1; 0). II. (0; 1). III. (1; 2). A. Chỉ I. B. Chỉ I và II. C. Chỉ II. D. Chỉ III.
- Học sinh thực hiện nhiệm vụ:
Thảo luận và hoàn thành phiếu học tập - Báo cáo kết quả:
Đại diện các nhóm trình bày kết quả. - Nhận xét đánh giá:
Giáo viên nhấn mạnh các dạng toán thường gặp trong bài này, đồng thời chú ý cách giải nhanh bằng máy tính. Trang 33
MA TRẬN ĐỀ KIỂM TRA CHƯƠNG GIỚI HẠN
NĂM HỌC: 2018-2019 Môn: Toán- Khối 11 (Thời gian làm bài: 45 phút)
Hìnhthức: Trắc nghiệm 50% + Tự luận 50% Cấp độ Nhận biết Thông hiểu Vận dụng Cộng Cấp độ thấp Cấp độ cao Chủ đề TNKQ TL TNKQ TL TNKQ TL TN TL KQ
Giới hạn của dãy Câu 1 Câu 11 Câu 3 số Câu 2 Câu 4 Số câu 2 1 2 5 Số điểm 1.0đ 1.0đ 1.0đ 3.0đ Tỉ lệ % 10% 10% 10% 30% Giới hạn hàm số Câu 5 Câu Câu 7 Câu Câu 9 Câu 6 12a Câu 8 12b Số câu 1 1 2 1 1 7 Số điểm 1.0đ 1đ 1.0đ 1.0đ 0.5đ 4.5đ Tỉ lệ % 10% 10% 10% 10% 5% 45% Hàm số liên tục Câu 10 Câu 13 Câu 14 Tìm m để Chứng hàm số minh pt liên tục tại có 1 điểm nghiệm Trang 34 Số câu 1 1 1 3 Số điểm 0.5đ 1.0đ 1.0đ 2.5đ Tỉ lệ % 5% 10% 10% 25% Số câu 4 2 4 1 2 1 1 15 Số điểm 2.0đ 2.0đ 2.0đ 1.0đ 1.0đ 1.0đ 1.0đ 10đ Tỉ lệ % 20% 20% 20% 10% 10% 10% 10% 100% Tổng số câu 6 5 4 10 Tổng số điểm 4.0đ 3.0đ 3.0đ 10đ
Tỉ lệ % 40% 30% 30% 100%
TRƯỜNG THPT NGUYỄN THÁI BINH
ĐỀ KIỂM TRA 1 TIẾT TỔ TOÁN
MÔN: GIẢI TÍCH 11 CHƯƠNG IV
Họ, tên thí sinh:..................................................................... Lớp: .............................Mã đề: I. TRẮC NGHIỆM:
Học sinh chọn 1 đáp án đúng ở mỗi câu điền vào bảng sau CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ĐA
Câu 1: Trong các khẳng định sau, khẳng định nào Sai? A. c lim = 0 (c là hằng số).
B. lim c = c (c là hằng số). xÆ+ • x xÆ+ • lim x = x . D. lim k x = + • . 0 C. xÆx xÆ- • 0 Câu 2: lim ( 2
x - 2x + 3) có giá trị là bao nhiêu? x 1 ®- A. 4. B. 1. C. 6. D. 2. 2 Câu 3: x - 3x + 2 lim
có giá trị là bao nhiêu? x®2 2x - 4 A. 1 - . B. 1 . C. 3 . D. +¥ . 2 2 2 2 Câu 4: x +1 lim
có giá trị là bao nhiêu? x 1+ ® x -1 A. 2. B. -¥ . C. 1. D. +¥ . Ï 2 Ô- x - x + 2 Ô Câu 5: Ô khi x π - 2
Cho hàm số f (x) Ô = Ì x + 2
. Hàm số gián đoạn tại x = - 2 khi Ôb Ô Ô khi x = - 2 Ô Ó A. b π 3 . B. b = - 3 . C. b π - 3 . D. b = 3 . Câu 6: 5n +1
Giá trị của A = lim bằng 1- 2n 5 A. +¥ . B. - . C. -¥ . D. 5. 2 n Ê ˆ Á Ê ˆ Câu 7: 2017 3 Tìm ˜ limÁ - Á ˜ Á Á ˜ + 2017˜˜ 2 Á Ë n 7 Á ˜ Ë ¯ ˜˜¯ A. 2017. B. 0. C. + • D. - • . Trang 35 n 1 -
Câu 8: Kết quả đúng của 5 - 4 lim là: 2n + 4.4n 1 1 . B. - . C. 1. D. 1 - . A. 16 16
Câu 9: Chọn khẳng định đúng. A. lim n
q = 0 nếu q < 1. B. lim n
q = 0 nếu q < 1. C. lim n
q = 0 nếu q > 1. D. lim n
q = 0 nếu q > 1. 2 Câu 10: x + 2 - 4 - x a a lim =
( là phân số tối giản).Tính p = 2a - b ? x 1 ® x -1 b b p = 4 . p = 16 . p = 7 . p = 1. A. B. C. D. II. TỰ LUẬN:
Câu 11. Tính giới hạn n +1 lim . 3n + 2 2 x - 3x + 2
Câu 12. Tính các giới hạn: a) lim( 2
x - 2x + 3). b) lim x®3 x®2 2x - 4 ÏÔ 1- x Ô khi x π 1
Câu 18. Tìm m để hàm số Ô f (x) Ô = Ì x + 3 - 2 liên tục tại x=1. Ô Ô 2 2 x
Ô - 6x + m khi x = 1 Ô Ó
Câu 19. Chứng minh rằng phương trinh 4 2018 4
(m + m + 1)x
+ x - 16 = 0 luôn có nghiệm với mọi m. ----------- HẾT --------- CHUYÊN ĐỀ 5
Ngày soạn: 10/3/2019 CHỦ ĐỀ:ĐỊNH NGHĨA VÀ Ý NGHĨA ĐẠO HÀM
I. Mục tiêu của bài (chủ đề) Kiến thức:
- Hiểu rõ định nghĩa đạo hàm tại một điểm.
- Hiểu rõ đạo hàm của một hàm số tại một điểm là một số xác định.
- Nắm vững ý nghĩa hình học và vật lí của đạo hàm.
- Hiểu rõ mối quan hệ giữa tính liên tục và sự tồn tại đạo hàm. 9. Kỹ năng:
- Biết cách tính đạo hàm tại một điểm bằng định nghĩa của các hàm số thường gặp.
- Vận dụng tốt vào viết phương trình tiếp tuyến. 10. Thái độ:
- Tư duy các vấn đề của toán học một cách lôgic và hệ thống.
11. Đinh hướng phát triển năng lực:
- Năng lực hợp tác: Tổ chức nhóm học sinh hợp tác thực hiện các hoạt động.
- Năng lực tự học, tự nghiên cứu: Học sinh tự giác tìm tòi, lĩnh hội kiến thức và phương pháp giải quyết bài tập và các tình huống.
- Năng lực giải quyết vấn đề: Học sinh biết cách huy động các kiến thức đã học để giải quyết các câu hỏi.
Biết cách giải quyết các tình huống trong giờ học.
- Năng lực thuyết trình, báo cáo: Phát huy khả năng báo cáo trước tập thể, khả năng thuyết trình.
II. Chuẩn bị của giáo viên và học sinh 1. Giáo viên:
- Thiết kế hoạt động học tập hợp tác cho học sinh tương ứng với các nhiệm vụ cơ bản của bài học. Trang 36
- Tổ chức, hướng dẫn học sinh thảo luận, kết luận vấn đề. 2. Học sinh:
- Mỗi học sinh trả lời ý kiến riêng và phiếu học tập. Mỗi nhóm có phiếu trả lời kết luận của nhóm sau khi đã
thảo luận và thống nhất.
- Mỗi cá nhân hiểu và trình bày được kết luận của nhóm bằng cách tự học hoặc nhờ bạn trong nhóm hướng dẫn.
- Mỗi người có trách nhiệm hướng dẫn lại cho bạn khi bạn có nhu cầu học tập.
III. Chuỗi các hoạt động học:
1. GIỚI THIỆU (HOẠT ĐỘNG TIẾP CẬN BÀI HỌC) (10’) * Mục tiêu:
+ Tạo sự chú ý cho học sinh để vào bài mới.
+ Tạo tình huống để học sinh tiếp cận với khái niệm “đạo hàm”.
* Nội dung, phương thức tổ chức: + Chuyển giao:
L1. Quan sát các hình ảnh (máy chiếu)
L2. Lớp chia thành các nhóm (nhóm có đủ các đối tượng học sinh, không chia theo lực học) và tìm
câu trả lời cho các câu hỏi H1, H2, H3. Các nhóm viết câu trả lời vào bảng phụ.
H1. Theo em ở bức ảnh dưới đây chú công an giao thông đang làm gì?
H2. Vận tốc của vận động viên tại các thời điểm khác nhau có bằng nhau không? Có tính được vận
tốc tại thời điểm t cụ thể được không? 0
H3. Một dòng điện chạy trong dây dẫn. Tính thời gian và cường độ dòng điện chạy qua dây dẫn tại
thời điểm t0 đến t? Tính cường độ trung bình của dòng điện? Hình 1 Hình 2 + Thực hiện Trang 37
- Các nhóm thảo luận đưa ra các phương án trả lời cho các câu hỏi H1, H2, H3. Viết kết quả vào bảng phụ. + Báo cáo, thảo luận
- Các nhóm HS treo bảng phụ viết câu trả lời cho các câu hỏi.
- HS quan sát các phương án trả lời của các nhóm bạn.
- HS đặt câu hỏi cho các nhóm bạn để hiểu hơn về câu trả lời.
- GV quan sát, lắng nghe, ghi chép.
+ Đánh giá, nhận xét, tổng hợp:
- GV nhận xét thái độ làm việc, phương án trả lời của các nhóm, ghi nhận và tuyên dương nhóm có
câu trả lời tốt nhất. Động viên các nhóm còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo.
- Dự kiến các câu trả lời:
TL1. Hình 1 chú công an đang bắn tốc độ các loại xe.
TL2 Vận động viên trong hình 1 chạy trên quãng đường được tính theo công thức S = f (t) s S1 N S0 M O t0 t1 t
Giả sử tại thời điểm t , vận động viên ở vị trí M có S = f (t ) ; tại thời điểm t (t > t ) , vận động viên ở vị 0 0 0 1 1 0
trí N có S = f (t ) . Khi đó, trong khoảng thời gian từ t đến t , quãng đường vận động viên chạy được là 1 1 0 1
f (t ) - f (t )
MN = f (t ) - f (t ) . Vậy vận tốc trung bình của vận động viên trong khoảng thời gian đó là 1 0 . 1 0 t - t 1 0
(1)Nếu t - t càng nhỏ thì tỉ số (1) càng phản ánh chính xác hơn sự nhanh chậm của VĐV tại thời điểm t . 1 0 0
f (t ) - f (t )
Từ đó, người ta xem giới hạn của tỉ số 1 0
khi t dần đến t là vận tốc tức thời tại thời điểm t của t - t 1 0 0 1 0
VĐV, kí hiệu là v(t ). 0
f (t ) - f (t ) Nói cách khác, 1 0 v(t ) = lim . 0 ® 1 t t0 t - t 1 0
Bài toán tìm vận tốc tức thời
Quãng đường s của chuyển động là một hàm số của thời gian t s = s(t)
s(t) - s(t )
Giới hạn hữu hạn (nếu có) 0 lim
đgl vận tốc tức thời của chuyển động tại thời điểm t0. t®t t - t 0 0
TL 3. Đ1. Thời gian: t – t0. Cường độ: Q(t) – Q(t0)
Q(t) - Q(t )
Đ 2. Cường độ trung bình của dòng điện: I 0 tb = t - t0
• GV dẫn dắt tương tự như bài toán tìm vận tốc tức thời.
Bài toán tìm cường độ tức thời
Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t Q = Q(t)
Q(t) - Q(t )
Giới hạn hữu hạn (nếu có) 0 lim
đgl cường độ tức thời của dòng điện tại thời điểm t0. t®t t - t 0 0 * Sản phẩm:
+ Các phương án giải quyết được ba câu hỏi đặt ra ban đầu. Trang 38
+ Đưa ra được dự đoán: “Định nghĩa đạo hàm”.
- Tùy vào chất lượng câu trả lời của HS, GV có thể đặt vấn đề: Nhiều vấn đề của toán học, vật lí, hóa học,
f (x) - f (x )
sinh học, ... dẫn đến bài toán tìm giới hạn: 0 lim
Trong toán học người ta gọi giới hạn trên là đạo x® 0 x x - x0
hàm của hàm số tại điểm x (nếu giới hạn này là hữu hạn). Đó chính là nội dung bài học “Định nghĩa và ý 0 nghĩa đạo hàm”.
2. NỘI DUNG BÀI HỌC (HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC)
*Mục tiêu: Học sinh nắm được 4 đơn vị kiến thức của bài.
*Nội dung: Đưa ra các phần lý thuyết và có ví dụ ở mức độ NB, TH.
*Kỹ thuật tổ chức: Thuyết trình, Tổ chức hoạt động nhóm.
*Sản phẩm: HS nắm được định lý, các hệ quả và giải các bài tập mức độ NB,TH.
I.Đạo hàm của hàm số tại một điểm:
I.1. Định nghĩa đạo hàm của hàm số tại một điểm: * Mục tiêu:
- Học sinh biết được khái niệm của hàm số liên tục tại một điểm.
- Áp dụng để xét tính liên tục của một số hàm số tại một điểm cho trước.
- Hình thành cách tính đạo hàm bằng định nghĩa.
* Nội dung, phương thức tổ chức:
a) Tiếp cận (khởi động)(10’)
Vận tốc tức thời
Cường độ dòng điện tức thời
Tốc độ phản ứng hóa học tức thời
s(t) - s(t )
Q(t) - Q(t )
C(t) - C(t ) 0 v(t ) = lim 0 I (t ) = lim 0 v(t ) = lim 0 0 0 t®t ® ® 0 t - t t t t - t t t t - t 0 0 0 0 0 ĐẠO HÀM
f (x) - f (x ) 0 f '(x ) = lim 0 x® 0 x x - x0
+ Chuyển giao:
NV: * Học sinh đọc định nghĩa SGK.
* Học sinh giải quyết 2 hoạt động: HÐI.1.1; HÐI.1.2.
* Từ việc so sánh kết quả của 2 hoạt động, đưa ra cách tính đạo hàm y D
bằng định nghĩa ( dùng trực tiếp định nghĩa hoặc dùng lim ). x D ®0 x D Hoạt động Gợi ý HÐI.1.1
f (x) - f (x ) 0
f (x) - f (x ) lim Cho hàm số 2
y = f (x) = x . Tính 0 lim ? x® 0 x x - x0 x® 0 x x - x0 2 2 x - x HÐI.1.2 0 = lim x®x x - x Đặt x
D = x - x là số gia của đối số tại x . 0 0 0 0
= lim(x + x ) = 2x y
D = f (x) - f (x ) = f (x + x
D ) - f (x ) : số gia 0 0 x®x 0 0 0 0
tương ứng của hàm số. !y a.Tính lim ? !y x D ®0 !x lim = 2x 0
f (x) - f (x ) !y x D ®0 !x b.So sánh kết quả 0 lim và lim
f (x) - f (x ) !y x® D ® 0 0 x x - x x 0 !x 0 lim = lim
c. Nêu các buớc tính đạo hàm bằng định nghĩa của x® D ® 0 x x - x x 0 !x 0 Trang 39
hàm số y = f (x) ?
+ Thực hiện: Học sinh suy nghĩ và làm ví dụ vào giấy nháp.
+ Báo cáo, thảo luận: Chỉ định một học sinh bất kì trình bày lời giải, các học sinh khác thảo luận để hoàn thiện lời giải.
+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa lời
giải, từ đó nêu cách tính đạo hàm bằng định nghĩa và đạo hàm trên một khoảng. HS viết bài vào vở.
b) Hình thành kiến thức(5’)
Từ kết quả bài toán 1, ta suy ra cách tính đạo hàm bằng định nghĩa:
I.2. Các bước tính đạo hàm bằng Định nghĩa :
Bước 1: Giả sử x
D là số gia của đối số tại x , tính y
D = f (x + x D ) - f (x ). 0 0 0 y D Bước 2: Lập tỉ số . x D y D Bước 3: Tìm lim . x D ®0 x D c) Củng cố(7’) Củng cố. Gợi ý
Tính đạo hàm của các hàm số sau bằng a) Gọi x
D là số gia tại điểm x0 = 1, ta có: định nghĩa
a) y = f (x) = 2x - 3 tại điểm x0 =1 y D = f ( x
D +1) - f (1) = 2( x D +1) - 3 +1 = 2Dx y D = = Suy ra: lim lim 2 2 x D ®0 x D ®0 x D x +1 b) y = tại x Vậy, y’(1) = 2. 0 = 0 x -1 b) Gọi x
D là số gia tại điểm x0 = 0, ta có: D = (D ) - ( x D + x D y f x f 0) 1 2 = + = 1 x D -1 x D -1 y D 2 Suy ra: lim = lim = 2 - x D ®0 x D ®0 x D x D -1 Vậy, y’(0) = -2.
I.3.QUAN HỆ GIỮA SỰ TỒN TẠI CỦA ĐẠO HÀM VÀ TÍNH LIÊN TỤC CỦA HÀM SỐ.
+ Mục tiêu: Học sinh biết được mối liên hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số
+ Nội dung, phương thức tổ chức:
a)Tiếp cận (khởi động)(5’)
+) HĐ1: Khởi động. • Xét hàm số 2 ì
x +1 ne·u x ³ 0 f (x) = í îx ne·u x < 0
H1. Tính lim f (x) ? x®0
H2. Nếu hàm số y = f (x) gián đoạn tại x thì nó có đạo hàm tại điểm đó 0 Trang 40 không?
H3. Nếu một hàm số liên tục tại 1 điểm có thể khẳng định được hàm số đó có
đạo hàm tại điểm đó hay không?
+ Chuyển giao:
NV: * Học sinh đọc định nghĩa SGK.
* Học sinh giải quyết 3 câu hỏi:H1, H2, H3.
+ Thực hiện: Học sinh suy nghĩ và trả lời vào giấy nháp.
Đ1. lim f (x) = 1, lim f (x) = 0 x 0+ x 0- ® ®
Þ không tồn tại lim f (x) x®0
Đ 2. Þ không có f¢(0).
Đ 3. Nếu hàm số y = f (x) gián đoạn tại x thì nó không có đạo hàm tại điểm đó. 0
Nếu một hàm số liên tục tại 1 điểm chưa thể khẳng định được hàm số đó có đạo
hàm tại điểm đó hay không.
+ Báo cáo, thảo luận: Chỉ định một học sinh bất kì trình bày lời giải, các học sinh khác thảo luận để hoàn thiện lời giải.
+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa lời
giải, từ đó nêu định lí về quan hệ giữa đạo hàm và liên tục. HS viết bài vào vở.
b)Hình thành kiến thức(3’)
Định lí. Nếu hàm số f(x) có đạo hàm tại x0 thì nó liên tục tại điểm đó. Chú ý:
a) Nếu y = f(x) gián đoạn tại x0 thì nó không có đạo hàm tại x0.
b) Nếu y = f(x) liên tục tại x0 thì có thể không có đạo hàm tại x0. c) Củng cố:(5’) +) HĐ3: Củng cố. GỢI Ý ìx, x ³ 0
Ví dụ 1. Cho hàm số f (x) = í . Xét î-x, x < 0
tính liên tục của hàm số đã cho, tính đạo hàm tại x=0.
I.4.Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM.(20’) * Mục tiêu:
- Học sinh biết được ý nghĩa hình học của đạo hàm.
- Biết vận dụng công thức để viết phương trình tiếp tuyến của đồ thị hàm số.
* Nội dung, phương thức tổ chức:
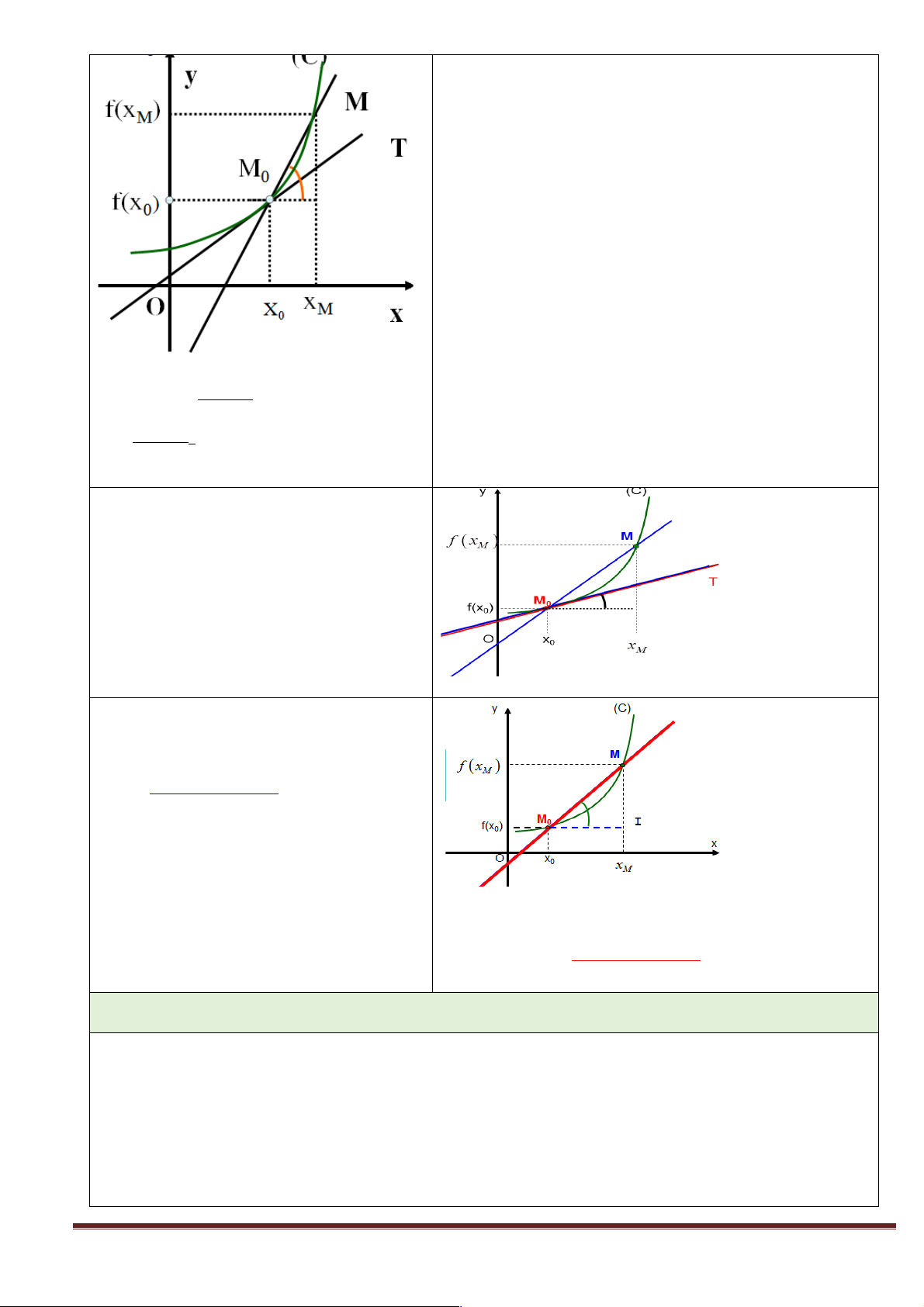
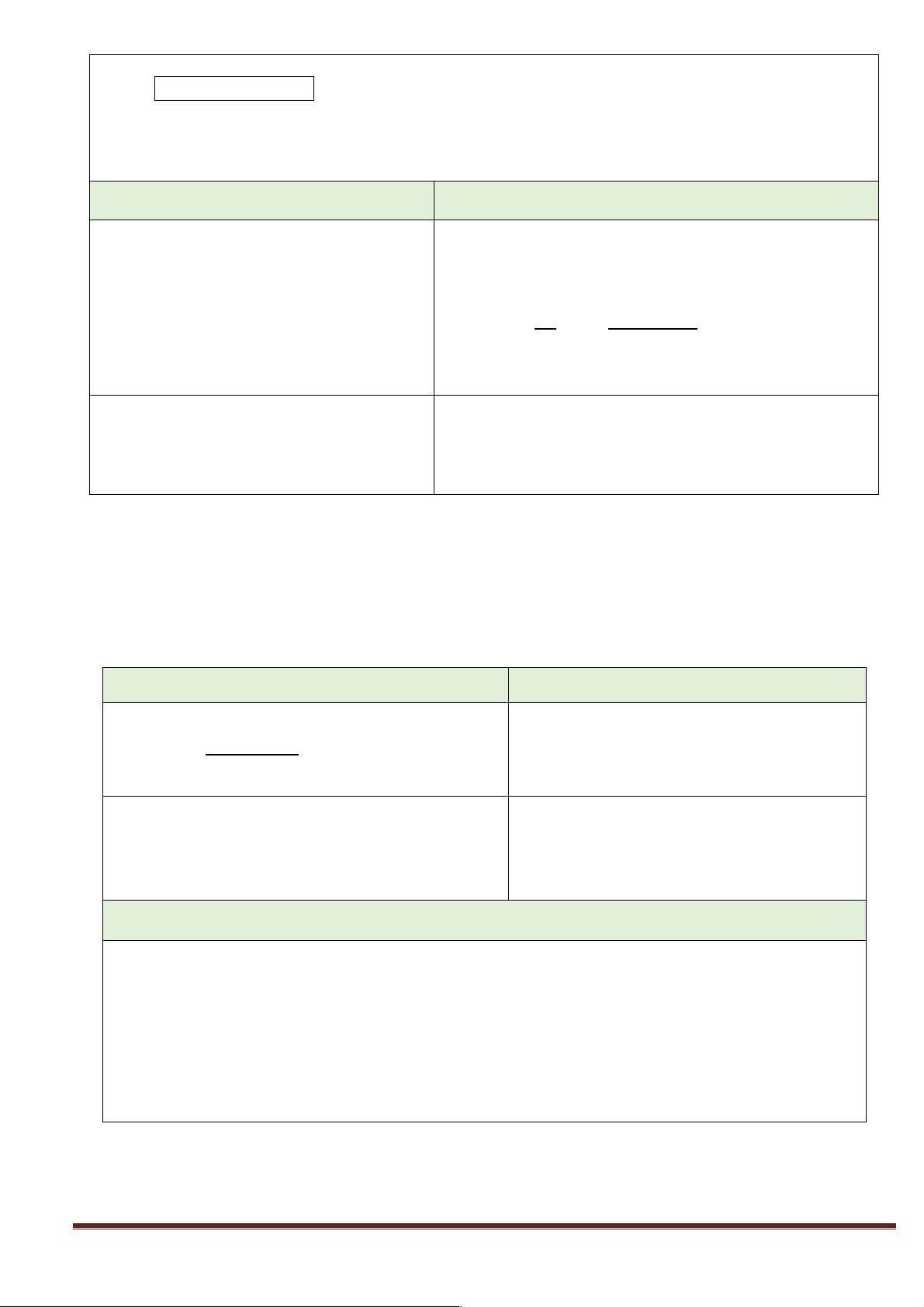
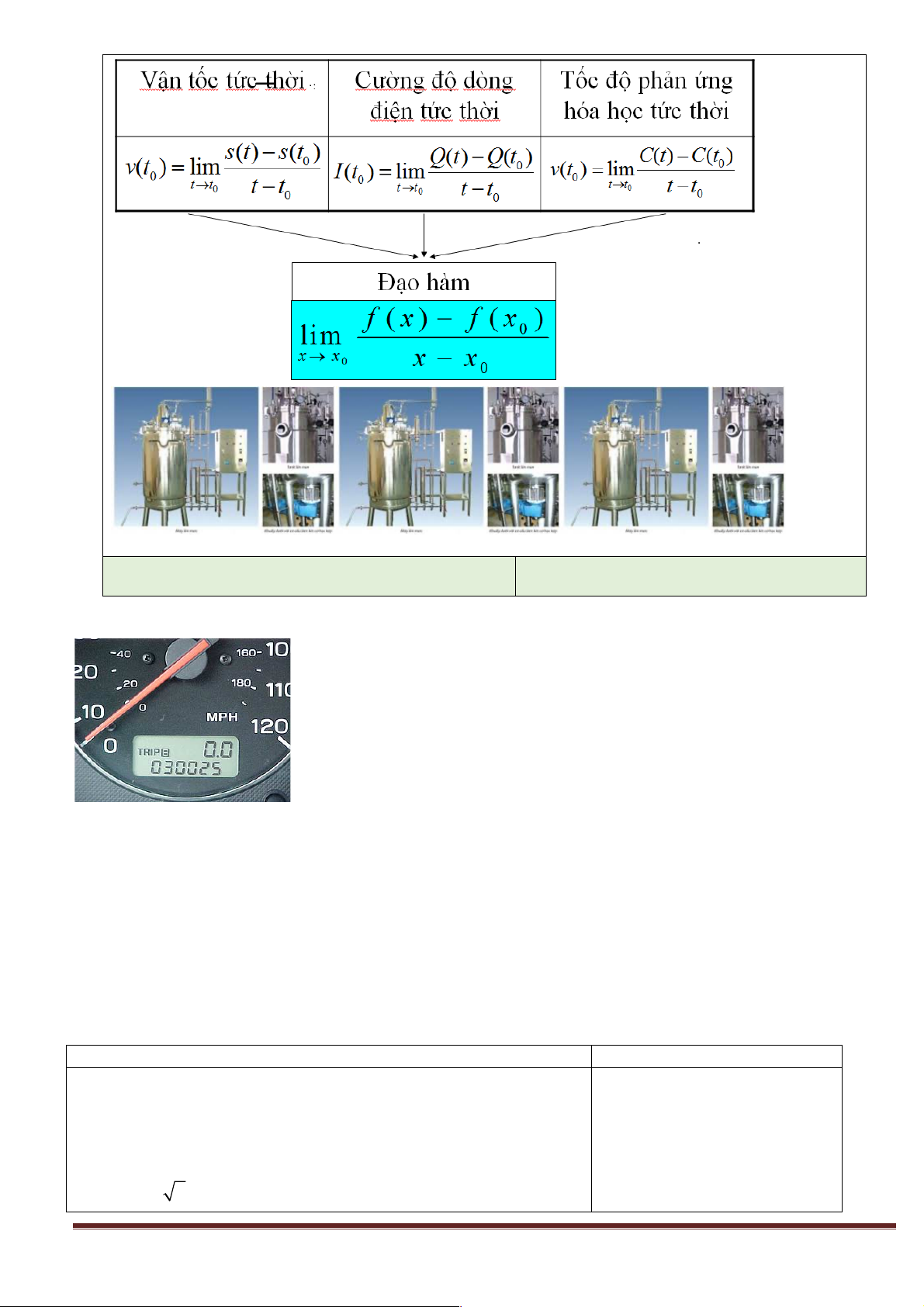
+) HĐ1: Khởi động. GỢI Ý HĐ1.1. Trang 41
Cho hàm số f(x) có đồ thị (C), một điểm
M0(x0; f(x0)) cố định thuộc (C).
Với mọi điểm M(xM;f(xM)) di động trên (C), khác M0.
Đường thẳng M0M gọi là một cát tuyến của (C).
HĐ1.2. Khi x ¦ x0 thì M di chuyển trên (C) tại điểm M0.
Ta coi đường thẳng M0T đi qua M0 là vị
trí giới hạn của cát tuyến M0M khi M
chuyển dọc theo (C) đến M0.
Đường thẳng M0T gọi là tiếp tuyến của (C)
tại M0 và M0 gọi là tiếp điểm
HĐ1.3. Gọi kMlà hệ số góc của cát tuyến
M0M, k0 là hệ số góc của tiếp tuyến M0T. Thì f (x - f x M ) ( 0) k = M x - x M 0
Giả sử f(x) có đạo hàm tại x0. Khi đó ( f x - f x f ' x = lim = lim k = k 0 ) ( M ) ( 0) M 0 xM®x0 x - x x ®x M 0 M 0
+) HĐ2: Hình thành kiến thức.
Cho đường cong (C) và M0 Î (C). M là điểm di động trên (C). Vị trí giới hạn M0T (nếu có) của cát
tuyến M0M đgl tiếp tuyến của (C) tại M0. Điểm M0 đgl tiếp điểm.
Chỳ ý: Không xét tiếp tuyến song song hoặc trùng với Oy.
b) Ý nghĩa hình học của đạo hàm Định lí 2:
Đạo hàm của y = f(x) (C) tại điểm x0 là hệ số góc của tiếp tuyến M0T của (C) tại điểm M0(x0; f(x0)).
c) Phương trình tiếp tuyến Trang 42
Định lý 3: Phương trình tiếp tuyến của (C): y = f(x) tại điểm M0(x0; f(x0)) là
y – y0 = f¢(x0).(x – x0) trong đó y0 = f(x0). +) HĐ3: Củng cố. GỢI ớ
HĐ3.1. Tìm hệ số góc của tiếp tuyến của HĐ 3.1 : Gọi x
D là số gia tại điểm x0 = -2, ta có: đồ thị hàm số 2
y = -x + 3x - 2 tại điểm có 2 y D = f ( x D - 2) - f ( 2)
- = -(Dx - 2) + 3(Dx - 2) - 2 +12 hoành độ -2. 2 = -D x + 7Dx 2 y D -D x + 7 x D Suy ra: lim = lim = lim (- x D + 7) = 7 x D ®0 x D ®0 x D ®0 x D x D Vậy, y’(-2) = 7. HĐ3.2: Cho hàm số 2
y = -x + 3x - 2 . Viết HĐ3.2: Gọi M (x ; y ) là tiếp điểm 0 0
pttt của đồ thị hàm số trên tại điểm có Ta có x = 2 - Þ y = 12 - 0 0 hoành độ -2.
Hệ số góc tiếp tuyến k=7.
Vậy phương trình tiếp tuyến y=7(x+2)-12=7x+2.
I.5. Ý NGHĨA VẬT LÍ CỦA ĐẠO HÀM.(10’) * Mục tiêu:
- Học sinh biết được ý nghĩa vật lí của đạo hàm.
- Biết vận dụng công thức để tính vận tốc tức thời, cường độ tức thời tại thời điểm t0.
* Nội dung, phương thức tổ chức:
+) HĐ1: Khởi động. GỢI Ý
HĐ1.1. Theo định nghĩa
f (t) - f (t ) V(t ) = 0 lim = s'(t ) 0 t® 0 t0 t - t0
HĐ1.2. Điện lượng Q = Q (t
) cường độ dòng I(t ) = Q '(t )
điện I (t ) = ? 0 0 0
+) HĐ2: Hình thành kiến thức.
Đạo hàm là một khái niệm Toán học có xuất xứ từ những bài toán thực tiễn, kĩ thuật khác nhau như
Cơ học, Vật lí, Hình học, Hóa học, Sinh học... Trang 43 +) HĐ3: Củng cố. GỢI Ý
Ví dụ 1:Lúc 10 giờ khởi hành, công tơ mét chỉ quãng đường xe đã đi trước đó là 30025 km, lúc 10 giờ 6
phút, công tơ mét chỉ 30029 km, kim tốc độ sẽ chỉ ở vạch bao nhiêu? A. 20. B. 30. C. 40. D. 50.
Ví dụ 2. Một chất điểm chuyển động có phương trình 2
s = t (t: tính bằng giây; s tính bằng mét). Vận tốc
của chất điểm tại thời điểm 2 (giây) là:
A. 2m/s. B. 3m/s. C. 4m/s. D. 5m/s.
II: ĐẠO HÀM TRÊN MỘT KHOẢNG.(15’)
- Mục tiêu: Tiếp cận định nghĩa đạo hàm trên một khoảng. Hình thành định nghĩa đạo hàm trên một khoảng.
- Nội dung, phương thức tổ chức:Tổ chức cho học sinh hoạt động nhóm.
+ Chuyển giao:
NV: * Học sinh làm ví dụ.
* Từ đó HS đọc đạo hàm bằng định nghĩa đạo hàm của hàm số trên một khoảng
HÐ1.2.1: Khởi động (Tiếp cận). Gợi ý Cho các hàm số sau a. 2
y = f (x) = x tính đạo hàm bằng định nghĩa tại điểm x
a. y '(x ) = 2x 0 0 0
b. y = c tính đạo hàm bằng định nghĩa tại điểm x , với c là 0
b. y '(x ) = 0 hằng số 0
c. y = x tính đạo hàm bằng định nghĩa tại điểm x > 0 , 0 Trang 44 1
c. y '(x ) = 0 2 x0
+ Thực hiện: Học sinh suy nghĩ và làm ví dụ vào giấy nháp.
+ Báo cáo, thảo luận: Chỉ định một học sinh bất kì trình bày lời giải, các học sinh khác thảo luận để hoàn thiện lời giải.
+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Trên cơ sở câu trả lời của học sinh, giáo viên chuẩn hóa lời
giải, từ đó nêu định nghĩa và đạo hàm trên một khoảng , quy tắc tính đạo hàm của 4 hàm số thường gặp. HS viết bài vào vở.
II.1.Định nghĩa: Đạo hàm trên một khoảng
Hàm số y = f (x) được gọi là có đạo hàm trên khoảng ( ;
a b) nếu nó có đạo hàm tại mọi điểm x trên khoảng
đó.Khi đó, ta gọi hàm số f ' : ( ; a b) ® !
x ! f '(x)
là đạo hàm của hàm số y = f (x) trên khoảng ( ;
a b), kí hiệu là y ' hay f '(x).
3. LUYỆN TẬP (25’)
Câu 1: Số gia của hàm số f ( x) = 2x -1 ứng với số gia x
D của đối số x tại x = 5 là: 0 A. 9 + 2 x D - 4 B. 9 + 2 x D - 3 C. 9 + 2 x D - 5 D. 9 + 2 x D -1 y D 2 x + x Câu 2: Tỉ số
của hàm số f ( x) = ứng với số gia x
D của đối số x tại x =1là: x D x - 2 0 5 + x D 6 + x D 5 + x D 4 + x D A. B. C. D. x D -1 x D -1 x D - 2 x D -1
Câu 3: Phương trình tiếp tuyến của đồ thị hàm số f ( x) 2
= -x + 3x - 2 tại điểm có hoành độ x = 2 là: 0
A. y = -x + 3
B. y = -x +1
C. y = -x + 2 D. y = -x - 2 x +
Câu 4: Hệ số góc của tiếp tuyến với đồ thị hàm số f ( x) 2 1 =
tại điểm có hoành độ x = 2 là: x + 4 0 9 5 1 7 A. B. C. D. 36 36 36 36
Câu 5: Phương trình tiếp tuyến của đồ thị hàm số ( ) 2
f x = x , biết tiếp tuyến đó đi qua điểm M 0; 1 - ) là:
A. y = 3x -1 và y = 3
- x -1 B. y = 4x -1 và y = 4 - x -1
C. y = 2x -1 và y = 2
- x -1 D. y = x -1 và y = -x -1
4. VẬN DỤNG VÀ MỞ RỘNG
4.1 Vận dụng vào thực tế (10’)
Bài toán: Một bình nuôi cấy vi sinh vật được giữ ở nhiệt độ 00C. Tại thời điểm t=0 người ta cung cấp nhiệt
cho nó. Nhiệt độ tăng lên và được ước tính bởi hàm số 3 0
f (t) = (t -1) +1( C) ( f (t) là nhiệt độ của bình nuôi cấy ở thời điểm t)
a) Tính tốc độ tăng nhiệt trung bình của bình nuôi cấy trên trong khoảng thời gian từ lúc t = 0,5s đến thời 0
điểm t ' sau đó 1 giây.
b) Tính tốc độ tăng nhiệt độ trung bình của bình nuôi cấy trên trong khoảng thời gian từ lúc t = 1, 25s đến 0
thời điểm t ' sau đó 1 giây.
c) Trong 2 thời điểm trên, thời điểm nào nhiệt độ bình nuôi cấy tăng nhanh hơn.
a. Mở rộng, tìm tòi (mở rộng, đào sâu, nâng cao,…) (10’)
* Mục tiêu: Nắm đượcquan hệ giữa đạo hàm và tính liên tục của hàm số. Học sinh biết được một số
chuyển động có vận tốc lớn . * Nội dung:
- ND1: Quan hệ giữa đạo hàm và tính liên tục của hàm số. .
- ND2: Giới thiệu một số chuyển động có vận tốc lớn.
* Kỹ thuật tổ chức: Hoạt động cá nhân, hoạt động nhóm.HS viết báo cáo.
* Sản phẩm: Kiến thức về quan hệ giữa đạo hàm và tính liên tục, một số chuyển động có vận tốc lớn . Trang 45 * Tiến trình
HÐ củng cố, tìm tòi Gợi ý
1.NC Quan hệ giữa sự tồn tại của đạo hàm 1. Nếu hàm số y = f (x) có đạo hàm tại x thì nó liên tục 0
và tính liên tục của hàm số? tại điểm đó
2. Nếu hàm số y = f (x) có đạo hàm tại x thì nó không 0
có đạo hàm tại điẻm đó
3. Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.
+Vận tốc âm thanh: khoảng 343m/s.
+ Vận tốc chuyển động của vệ tinh cách trái đất 200km:22km/s
+ Vận tốc chuyển động của trái đất quanh mặt trời : 30km/s
+ vận tốc của ánh sáng : 300000km/s
+ Vận tốc của máy bay Airbus: 270m/s
+ Vận tốc tên lửa đưa người lên vũ trụ: khoảng 11km/s
Hình ảnh phóng vệ tinh vinasat 1
Ngày soạn: 24/3/2019 CHỦ ĐỀ: QUY TẮC TÍNH ĐẠO HÀM I. MỤC TIÊU
1. Kiến thức: Học sinh nắm được quy tắc tính đạo hàm của tổng, hiệu, tích , thương các hàm số; hàm
hợp và đạo hàm của hàm hợp; nắm được các công thức đạo hàm của các hàm số thường gặp. Phải xác định
được hàm số đã cho thuộc dạng công thức nào?
2. Kĩ năng: Tìm được đạo hàm của các hàm số thường gặp
3. Thái độ: Nghiêm túc trong học tập, coi trọng môn học. Trang 46
4. Định hướng phát triển năng lực:
+ Năng lực chung: Tự học; giải quyết vấn đề; sáng tạo; tự quản lý; giao tiếp; hợp tác; sử dụng CNTT; sử
dụng ngôn ngữ; tính toán.
+ Năng lực chuyên biệt: Vận dụng các tri thức Toán; giải một số bài toán có tính thực tiễn điển hình; vận
dụng tri thức Toán, phương pháp tư duy Toán vào thực tiễn. Giao tiếp, sử dụng ngôn ngữ toán.
II. CHUẨN BỊ CỦA GIÁO VIÊN VÀ HỌC SINH: 1. Giáo viên:
- Thiết bị dạy học: thước , phấn.
- Phiếu học tập của học sinh. 2. Học sinh:
- Ôn lại kiến thức về định nghĩa đạo hàm. - Bảng phụ.
III. CHUỖI CÁC HOẠT ĐỘNG: 1. GIỚI THIỆU: (1p)
Chào các em, về tính đạo hàm bằng định nghĩa nhìn chung là phức tạp. Đối với một số hàm thường gặp ta
có các qui tắc và các công thức cho phép ta tính đạo hàm của chúng nhanh hơn. Như vậy các qui tắc và công
thức đó là gì? Đó chính là nội dung bài học của chúng ta ngày hôm nay:“Qui tắc tính đạo hàm”
2. NỘI DUNG BÀI HỌC:
Hoạt động 1: Tiếp cận đạo hàm của các hàm số thường gặp. (7p)
1. Mục tiêu: Nắm bắt được các hàm số thường gặp, cách tính đạo hàm của các hàm số thường gặp.
2. Phương pháp/Kĩ thuật dạy học: Phát vấn.
3. Hình thức tổ chức hoạt động: Nêu vấn đề.
4. Phương tiện dạy học: 5. Sản phẩm:
Bài toán 1:Hãy tính đạo hàm của hàm số 2
y = f (x) = x tại x0 bằng 2.
=> Bài toán này học sinh có thể dự đoán được đạo hàm của hàm số 10 y = f (x) = x
Từ những bài toán đó, hình thành nên công thức tính đạo hàm của hàm số = (x) = xn y f
Hoạt động 2: Tìm hiểu đạo hàm của các hàm số thường gặp. (15p)
1. Mục tiêu: Học sinh nắm bắt được công thức tính đạo hàm của các hàm số thường gặp
2. Phương pháp/Kĩ thuật dạy học: Giải quyết vấn đề. Vấn đáp.
3. Hình thức tổ chức hoạt động: Nhiệm vụ được giao cho cả lớp. HS thực hiện công việc theo nhóm.
4. Phương tiện dạy học: bảng, phấn, thước.
5. Sản phẩm: Thực hiện yêu cầu.
Nội dung kiến thức
Hoạt động của giáo viên
Hoạt động của học sinh Vd 1:
+Nêu quy tắc tính đạo hàm bằng + Hs trả lời.
a) Dùng định nghĩa tính đạo hàm định nghĩa. của hàm số 2
y = f (x) = x tại x0
+ Gv nhận xét câu trả lời của hs. tùy ý.
+ Gv nêu vd 1a. yêu cầu hs làm
+ Học sinh thảo luận và tính toán,
b) Hãy tính đạo hàm của hàm số
nhanh (thảo luận 2 bạn cùng bàn) đưa ra kết quả. 2
y = f (x) = x tại x
+ Gv phân lớp thành hai nhóm 0 bằng 2.
lớn. một nhóm làm ví dụ 1b, 1
c) Dùng định nghĩa tính đạo hàm
nhóm làm ví dụ 1c. (vẫn hoạt động + Hs thực hiện. của hàm số 3
y = f (x) = x tại x0
theo nhóm nhỏ là hai bạn cùng tùy ý. bàn)
+ Hs dự đoán : y = ( 10 ) 9 ' x ' = 10.x
+ Gv yêu cầu học sinh có thể dự
đoán được đạo hàm của hàm 10
+ Hs lắng nghe và ghi nhận công
số y = f (x) = x tại điểm x0 tùyý. Định lí 1: Hàm số thức.
→ ta có công thức : (xn)’=nxn-1 n
y = x ( n Î ,
• n > 1) có đạo hàm (kxn)’=k.nxn-1
tại mọi x Î ! và ( n x ) n 1 ' . n x - = . + Hs thực hiện.
+ Gv yêu cầu hs tính đạo hàm của Nhận xét:
hàm hằng và hàm số y = x . + Hs ghi nhận. Trang 47
+ Đạo hàm của hàm hằng bằng 0. + Gv đưa ra nhận xét.
+ Đạo hàm của hàm số y = x bằng 1
+ (kxn)’=k.nxn-1(k là hằng số) + Hs thực hiện.
Vd 2: Tính đạo hàm của hàm số + Gv yêu cầu hs (nhóm) tính đạo
y = x tại điểm tại x
hàm của hàm số y = x tại điểm 0 dương. + Hs ghi nhận.
Định lí : Hàm số y = x có đạo tại x0 tùyý.
+ Gv yêu cầu ba nhóm trình bày hàm dương và
kết quả và đưa ra nhận xét. ¢ y’ = ( x ) 1 = , (x > 0) 2 x
Hoạt động 3: Đạo hàm tổng, hiệu, tích, thương. (22p)
1. Mục tiêu: Nắm chắc đạo hàm của tổng ,hiệu, tích, thương.
2. Phương pháp/Kĩ thuật dạy học: dạy học nhóm.
3. Hình thức tổ chức hoạt động: Nhiệm vụ được giao cho cả lớp. HS thực hiện công việc theo nhóm.
4. Phương tiện dạy học: bẳng, phấn, thước.
5. Sản phẩm: Bài báo cáo kết quả hoạt động nhóm.
Nội dung kiến thức
Hoạt động của GV
Hoạt động của HS
Vd4: Giả sử u = u(x), v = v(x) là
+ Gv gợi ý cho hs sử dụng định
+ Hs thực hiện theo nhóm.
các hàm số có đạo hàm tại điểm x
nghĩa để làm vd4. Sau đó học
thuộc khoảng xác định. Chứng
sinh làm việc theo nhóm và giải
minh : (u + v)’ = u’ + v’(đọc SGK) vd 4. + Hs trình bày.
Định lí : Giả sử u = u(x), v = v(x)
+ Gv yêu cầu 2 nhóm bất kì lên
+ hs lắng nghe và ghi nhận.
là các hàm số có đạo hàm tại điểm trình bày. Sau đó nhận xét .
+ Hs lắng nghe và nghi nhận.
x thuộc khoảng xác định. Ta có:
+ Gv nêu định lý và chú ý.
(u + v)’ = u’ + v’ (1)
(u - v)’ = u’ - v’ (2)
(u.v)’ = u’v + v’u (3) ' æ u ö
u 'v - v 'u =
(v = v(x) ¹ 0) (4) ç ÷ 2 è v ø v
+ Hs làm bài tập theo nhóm. 1 ¢ æ ö v ' + Chú ý : = - ç ÷ 2
+ Gv ghi ví dụ 5. yêu cầu hs sử è v ø v
dụng kiến thức đã học về đạo
+ Có thể mở rộng thêm đạo hàm
hàm để giải.( hs giải theo nhóm + Hs thực hiện
của tổng, hiệu, tích cho u1.u2,..., un hai người)
VD 5: Tính đạo hàm của các hàm
+ Gv yêu cầu 4 nhóm bất lỳ lên số sau:
giải, trình bày cụ thể đã sử dụng
a) y = 5x3 – 2x5- 3x +4
công thức gì để giải sau đó nhận b) y = -x3 x .
xét bài giải của học sinh 1- 3x c) y = 2x + 5
Hoạt động 4: Đạo hàm của hàm hợp (T2-3) (20p)
1. Mục tiêu: Nắm chắc cách tính đạo hàm của hàm hợp.
2. Phương pháp/Kĩ thuật dạy học: dạy học nhóm.
3. Hình thức tổ chức hoạt động: Nhiệm vụ được giao cho cả lớp. HS thực hiện công việc theo nhóm.
4. Phương tiện dạy học: bảng, phấn, thước.
5. Sản phẩm: Bài báo cáo kết quả hoạt động nhóm
Nội dung kiến thức
Hoạt động của GV
Hoạt động của HS + Khái niệm hàm hợp.
+ Giáo viên giới thiệu khái niệm + Hs lắng nghe và ghi nhận.
+ Định lí: Nếu hàm số u = g(x) có
hàm hợp. Hướng dẫn hs giải ví dụ.
đạo hàm tại x là u ' và hàm số x
Đặt u = 1 – 2x thì y = u3, y’u = 3u2 + Hs theo dõi. Trang 48
y = f (u) có đạo hàm tại u là y ' , u’x = - 2. u
thì hàm hợp y = f ( g(x)) có đạo
Áp dụng công thức đạo hàm của
hàm tại x là y ' = y ' .u ' x u x
hàm hợp tính được y’x = -6(1 –
Ví dụ: Tính đạo hàm của hàm số y 2x)2. = (1 – 2x)3 + Gv nêu định nghĩa. + Hs thực hiện.
Bài 3 trang 162 SGK
+ Gv yêu cầu các nhóm làm bài
Tính đạo hàm của các hàm số sau: 3 7 2
tập 3 vào bảng phụ và lần lượt hai
a) y = (x - 5x ) ; + Hs ghi nhận.
nhóm một lên treo bảng, một b) y = ( 2 x + ) 1 ( 2 5 - 3x );
nhóm trình bày, sau đó so sánh kết 2x 3 - 5x c) y = ; d) ; 2 2 quả. x -1 x - x +1 3 + Gv nhận xét. æ n ö
e) y = m + ç 2 ÷ è x ø 3. LUYỆN TẬP (55p)
Hoạt động 5: Luyện tập
1. Mục tiêu: vận dụng kiến thức đạo hàm vào làm bài tập
2. Phương pháp/Kĩ thuật dạy học: dạy học nhóm
3. Hình thức tổ chức hoạt động: Nhiệm vụ được giao cho cả lớp. HS thực hiện công việc theo nhóm.
4. Phương tiện dạy học: phiếu học tập, máy chiếu.
5. Sản phẩm: Bài báo cáo kết quả hoạt động nhóm.
Nội dung kiến thức
Hoạt động của GV
Hoạt động của HS
Câu 1: Bằng định nghĩa tính đạo hàm
+ GV yêu cầu hs nhắc lại các
- Thực hiện nhiệm vụ học tập của hàm số 2
y = 7 + x - x tại x = 1
bước tính đạo hàm tại một điểm 0 bằng định nghĩa.
- Chuyển giao nhiệm vụ học tập: - Nhận xét, đánh giá. - Trao đổi thảo luận.
- Theo dõi, hướng dẫn, giúp đỡ
- Các nhóm thảo luận. Đại diện HS thực hiện nhiệm vụ nhóm trả lời.
- Đánh giá kết quả thực hiện
- Các nhóm khác nhận xét. nhiệm cụ của HS
Câu 2: Tìm đạo hàm của các hàm số:
- Chuyển giao nhiệm vụ học tập: - Thực hiện nhiệm vụ học tập 5 a y = x ( 2 ) 3 8 - 3x ) phát phiếu học tập 1 3 - Nhận xét, đánh giá. b) y =
+ a (a là hằng số)
- Theo dõi, hướng dẫn, giúp đỡ - Trao đổi thảo luận. 2 x HS thực hiện nhiệm vụ
- Các nhóm thảo luận. Đại diện 2 x - 2x +1 c) y =
- Đánh giá kết quả thực hiện nhóm trả lời. x +1 nhiệm vụ của HS
- Các nhóm khác nhận xét.
d) y = (x2 + 1)(3 – 2x2)
- Chuyển giao nhiệm vụ học tập: - Thực hiện nhiệm vụ học tập
+ Gv phát phiếu học tập 3: phát phiếu học tập - Trao đổi thảo luận. - Nhận xét, đánh giá.
- Các nhóm thảo luận. Đại diện
- Theo dõi, hướng dẫn, giúp đỡ nhóm trả lời. HS thực hiện nhiệm vụ
- Các nhóm khác nhận xét.
- Đánh giá kết quả thực hiện nhiệm vụ của HS
4. VẬN DỤNG VÀ MỞ RỘNG:
4.1 . VẬN DỤNG VÀO THỰC TẾ: (15p) Trang 49
1. Các em đều biết, khi ngồi trên xe máy mà nhìn đồng hồ công-tơ-mét thì sẽ biết rằng xe đang di chuyển
với vận tốc bao nhiêu. Nhưng, các chú công an giao thông không … ngồi trên xe chúng ta mà tại thời điểm
bóp cò, cái súng tốc độ ấy lại biết xe chúng ta đang chạy với tốc độ bao nhiêu. Cái súng ấy đã hoạt động như
thế nào? Cơ sở toán học của nó là gì?
- Đạo hàm cho ta biết tốc độ thay đổi của một đại lượng so với đại lượng khác ở vài vị trí hay điểm riêng biệt
(nên ta gọi là "tốc độ thay đổi tức thời").
- Như ta đã biết, vận tốc chính là thương số giữa quãng đường và thời gian vật đi hết quãng đường đó, nhưng
điều này chỉ đúng khi vận tốc là hằng số cố định (hay vật chuyển động đều). Ta cần một công thức khác khi
vận tốc thay đổi theo thời gian.
- Nếu ta có biểu thức cho s (quãng đường) theo t (thời gian) thì vận tốc ở bất kỳ thời điểm nhỏ t nào được tính s D bởi: v = lim t D ®0 t D y D f (x + x D ) - f (x ) Mà ta đã học: 0 0 f '(x ) = lim = lim 0 x D ®0 x D ®0 x D x D
2. Số lượng vi khuẩn sau t giờ trong 1 thí nghiệm ở phòng thí nghiệm đã được kiểm soát là: n = f (t). Ý
nghĩa của đạo hàm f '(5) là gì? Đơn vị của nó là gì?
- Ý nghĩa của đạo hàm f '(5) là sự thay đổi số lượng vi khuẩn theo thời gian tại thời điểm t = 5 . - Đơn vị là con/giờ. Trang 50




