Giáo Án Dạy Thêm Hình 8 Chủ Đề Diện Tích Đa Giác

CHỦ ĐỀ 10. DIỆN TÍCH ĐA GIÁC
A/ KIẾN THỨC CẦN NHỚ
1/ Mỗi đa giác có một diện tích xác định. Diện tích đa giác là một số dương có các tính chất sau:
+ Hai tam giác bằng nhau thì có diện tích bằng nhau.
+ Nếu một đa giác được chia thành những đa giác không có điểm trong chung thì diện tích của
nó bằng tổng diện tích của những đa giác đó.
+ Hình vuông cạnh có độ dài bằng 1 thì có diện tích là 1.
2. Các công thức tính diện tích đa giác
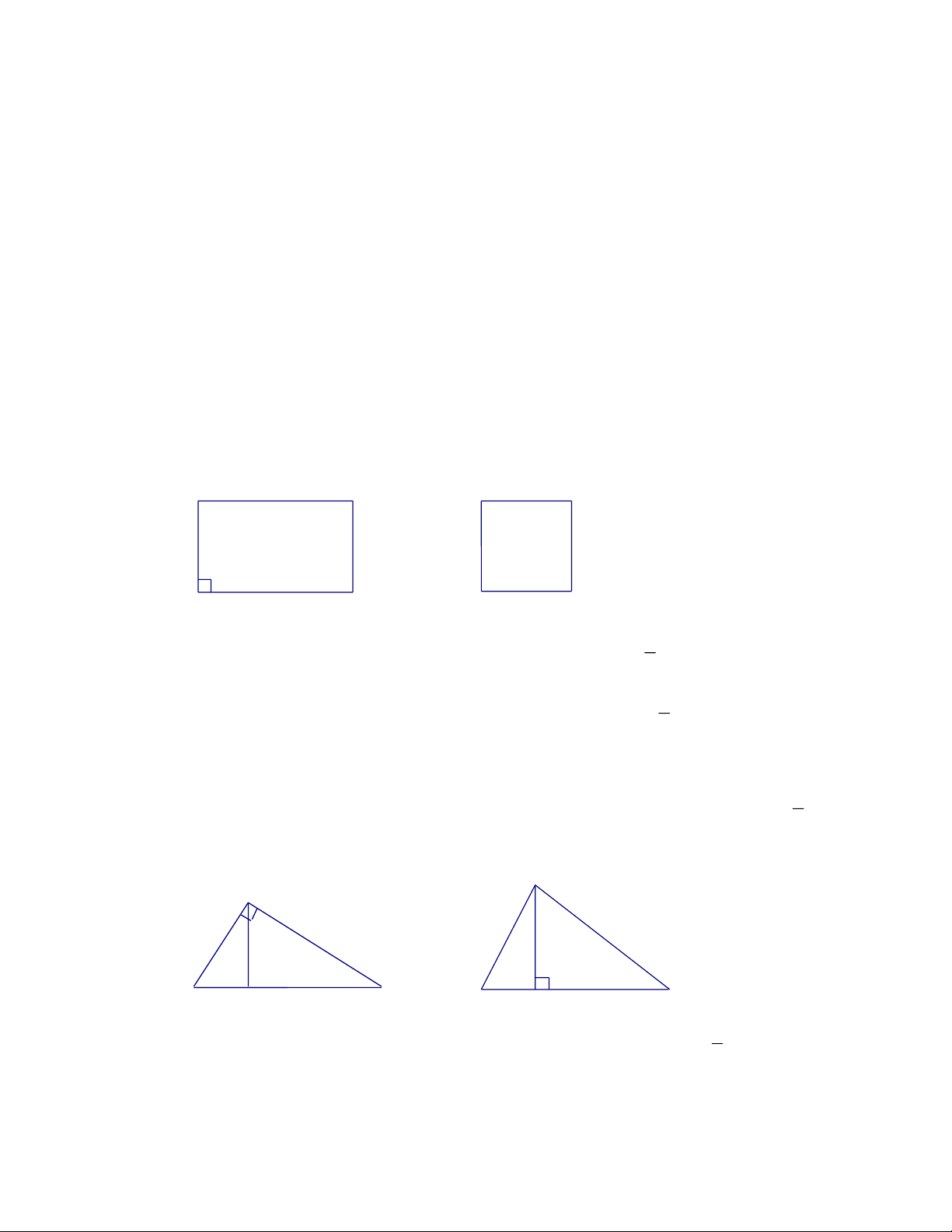
+ Diện tích hình chữ nhật bằng tích hai kích thước của nó S = a.b .
(a, b là kích thước hình chữ nhật)
+ Diện tích hình vuông bằng bình phương cạnh của nó S = a2.
(a là độ dài cạnh hình vuông) b a a a 1
Chú ý: Diện tích hình vuông có đường chéo dài bằng d là 2 d . 2 1
+ Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông S = . a b . 2
(a , b là độ dài hai cạnh góc vuông) 1
+ Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó S = . a h . 2
(a, h là độ dài cạnh và đường cao tương ứng) b a h h a c 1
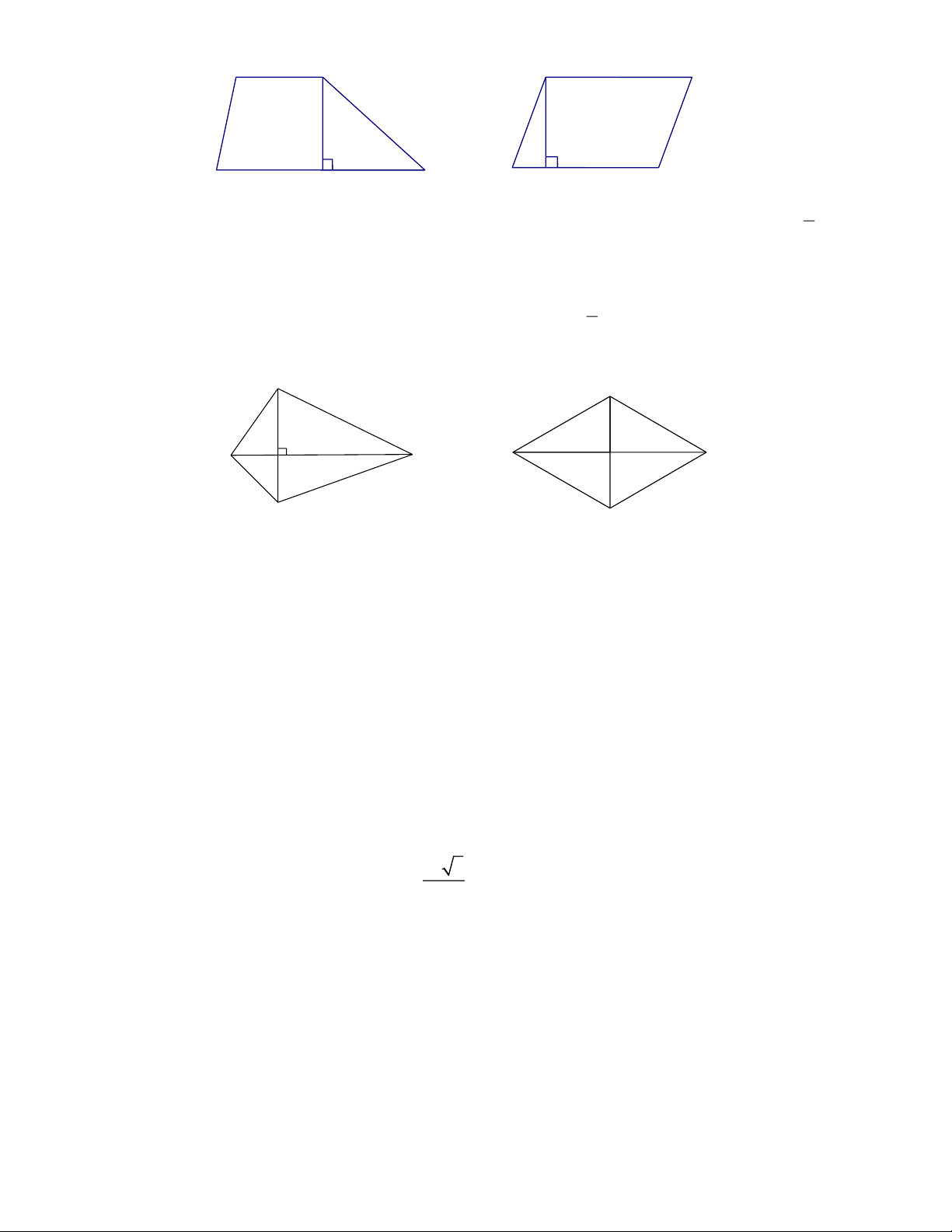
+ Diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao: S = (a + b).h 2
( a, b là độ dài hai đáy, h là độ dài đường cao).
+ Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó: S = a.h
(a, h là độ dài một cạnh và đường cao tương ứng). Trang 1 h h b a 1
+ Diện tích tứ giác có hai đường chéo vuông góc bằng nửa tích hai đường chéo: S = .d .d 1 2 2
(d1 ; d2 là độ dài hai đường chéo tương ứng). 1
+ Diện tích hình thoi bằng nửa tích hai đường chéo S = .d .d 1 2 2
(d1 ; d2 là độ dài hai đường chéo tương ứng). d d 2 2 d d 1 1 3. Bổ sung
+ Hai tam giác có chung một cạnh (hoặc một cặp cạnh bằng nhau) thì tỉ số diện tích bằng tỉ số
hai đường cao ứng với cạnh đó
+ Hai tam giác có chung một đường cao(hoặc một cặp đường cao bằng nhau) thì tỉ số diện tích
bằng tỉ số hai cạnh ứng với đường cao đó.
+ Tứ giác ABCD là hình thang( AB // CD). Hai đường chéo AC và BD cắt nhau tại O thì S = S . AOD BOC
+ Trong cách hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
+ Hai hình chữ nhật có cùng chiều cao thì tỉ số diện tích bằng tỉ số hai đáy. 2
+ Tam giác đều cạnh a có diện tích là a 3 . 4
B/ BÀI TẬP VẬN DỤNG.
I/ MỘT SỐ VÍ DỤ.
Ví dụ 1. Cho hình chữ nhật ABCD có AB = 12 cm, AD = 6,8 cm. Gọi H, I, E, K là các trung điểm
tương ứng của BC, HC, DC, EC.
a) Tính diện tích tam giác DBE.
b) Tính diện tích tứ giác EHIK. Giải Trang 2 Tìm cách giải.
Dễ dàng tính được diện tích hình chữ nhật ABCD. Mặt khác, đề bài xuất hiện nhiều yếu tố trung
điểm nên chúng ta có thể vận dụng tính chất : hai tam giác có chung đường cao thì tỉ số diện tích bằng
tỉ số hai cạnh đáy ứng với đường cao đó. Từ đó rút ra nhận xét: đường trung tuyến của tam giác chia
tam giác ấy thành hai phần có diện tích bằng nhau.
Từ nhận xét quan trọng đó, chúng ta lần lượt tính được diện tích các tam giác BCD, BCE, DBE, BEH, ECH, HKC, CKI, ....
Trình bày lời giải A B
a) ABCD là hình chữ nhật nên 1 1 1 2 S = .S = .AB.AD= .12.6,8 = 40,8cm . BCD ABCD H 2 2 2
E là trung điểm của CD, suy ra: I 1 2 S = S = .S = 20,4cm . C D E K BDE BCE BCD 2
b) H là trung điểm BC 1 1 2  S = .S = .20,4 =10,2cm . CHE BCE 2 2 K là trung điểm CE 1 2  S = .S = 5,1cm . HKC CHE 2 I là trung điểm CH 1 2  S = .S = 2,55cm . CKI HKC 2 Vậy 2 S = S − S =10,2 − 2,55 = 7,65cm . EHIK CHE CIK
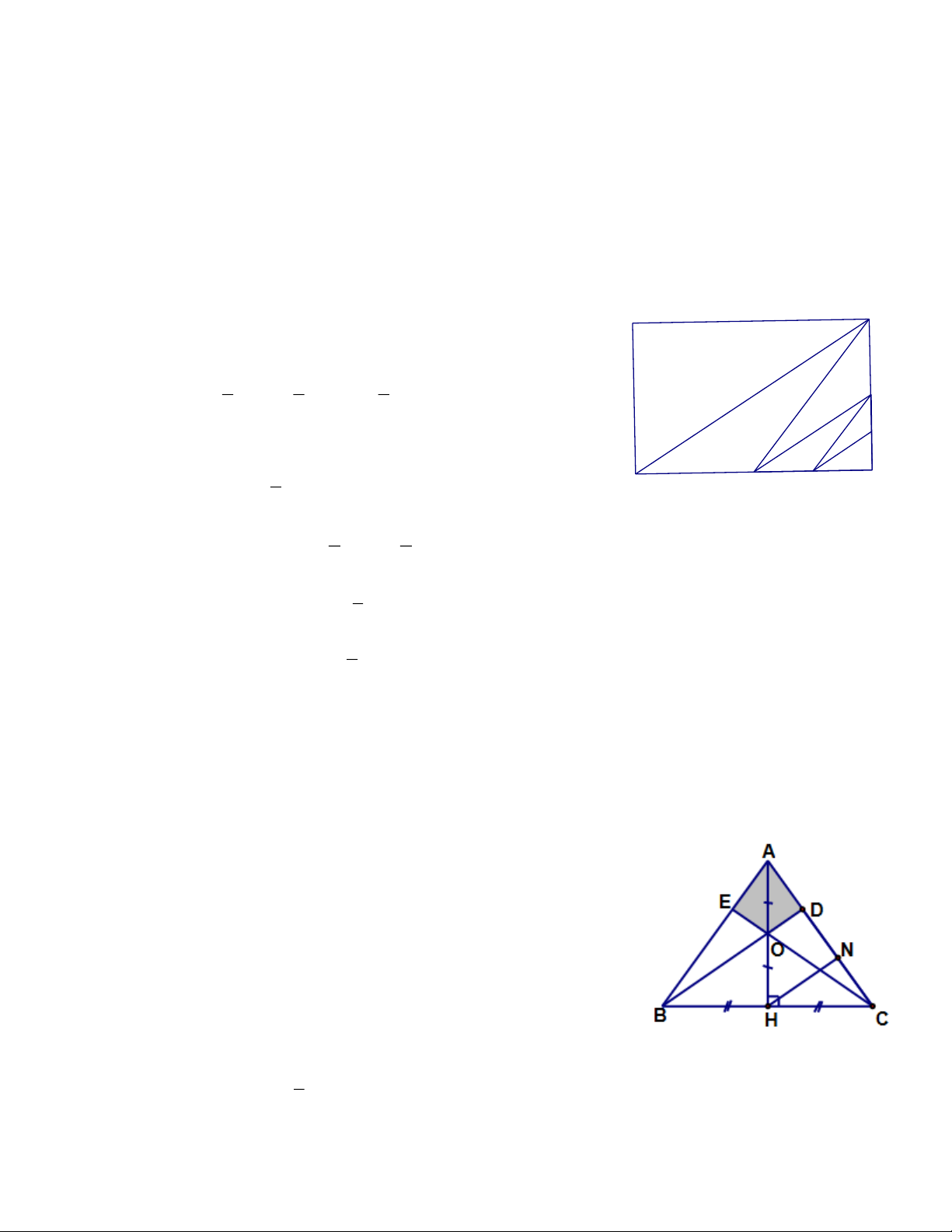
Ví dụ 2. Cho tam giác ABC cân ở A, AB = AC = 5cm, BC = 6cm. Gọi O là trung điểm của đường cao
AH. Các tia BO và CO cắt cạnh AC và AB lần lượt ở D và E. Tính SADOE ? Tìm cách giải.
Để tính diện tích đối với bài tập này học sinh phải. nhận thấy S
ABC đã biết nên ta cần tìm mối quan hệ về SADOE với SABC. Lại có H và
O là những điểm đặc biệt trên các đoạn AC, AH nên ta dễ dàng tìm
được mối quan hệ đó bằng cách lấy thêm điểm N là trung điểm của DC.
Trình bày lời giải
Gọi N là trung điểm của CD. 1 => AD = DN = NC = AC. 3 Trang 3 S AD 1 => AOD =
= (Chung chiều cao hạ từ O xuống AC) S AC 3 AOC 1 => SAOD = SAHC (1) 6 S AO 1 AOC =
= (Chung chiều cao hạ từ C xuống AH) S AH 2 AHC 1
Mà SAHC = SABC (Chung chiều caoAH) (2) 2 1 Từ (1) và (2) => SAOD = SABC . Mà SAOE = SAOD 12 1 => SADOE = 2 SAOD = SABC. 6
Áp dụng đlí Pitago vào AHC vuông tại H => AH = 4cm AH.BC 4.6 => S 2 ABC = = = 12cm 2 2 1
Vậy SADOE = .12 = 2 cm2. 6
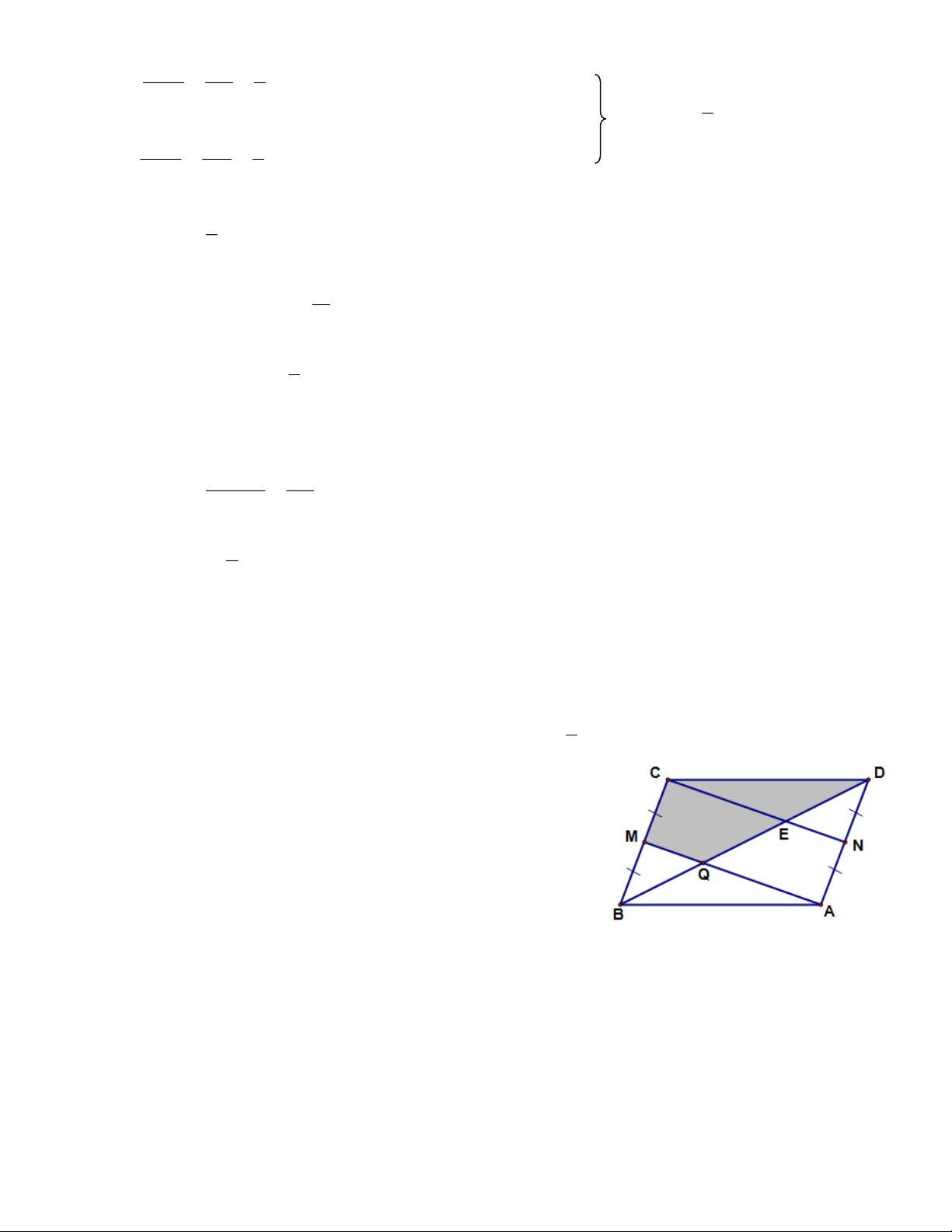
Ví dụ 3. Cho hbh ABCD có diện tích bằng 1. Gọi M là trung điểm của BC, AM cắt BD ở Q. Tính diện tích MQDC ? Tìm cách giải. 1
Hs cần nhận thấy SABCD = 1 nên dễ dàng suy ra SBCD = . 2
Để tính SMQDC thì phải thông qua SBCD và SBMQ .
Do đó ta cần phải tìm mối quan hệ của SBMQ với SBCD .
Để tìm được mối liên hệ đó ta phải xét xem Q nằm trên BD
có ở vị trí đặc biệt không bằng cách lấy thêm điểm N là trung điểm của AD.
Trình bày lời giải
Lấy N là trung điểm của AD.
Chỉ ra AMCN là hình bình hành => AM // CN
=> QB = QE ; ED = QE ( Định lí đường trung bình) => BQ = QE = ED Trang 4 1 1
=> SBMQ = SBCQ ; SQBC = SBCD. 2 3 1 => SBMQ = SBCD 6 5 5 5 => SMQDC = SBCD = SABCD = 6 12 12 1
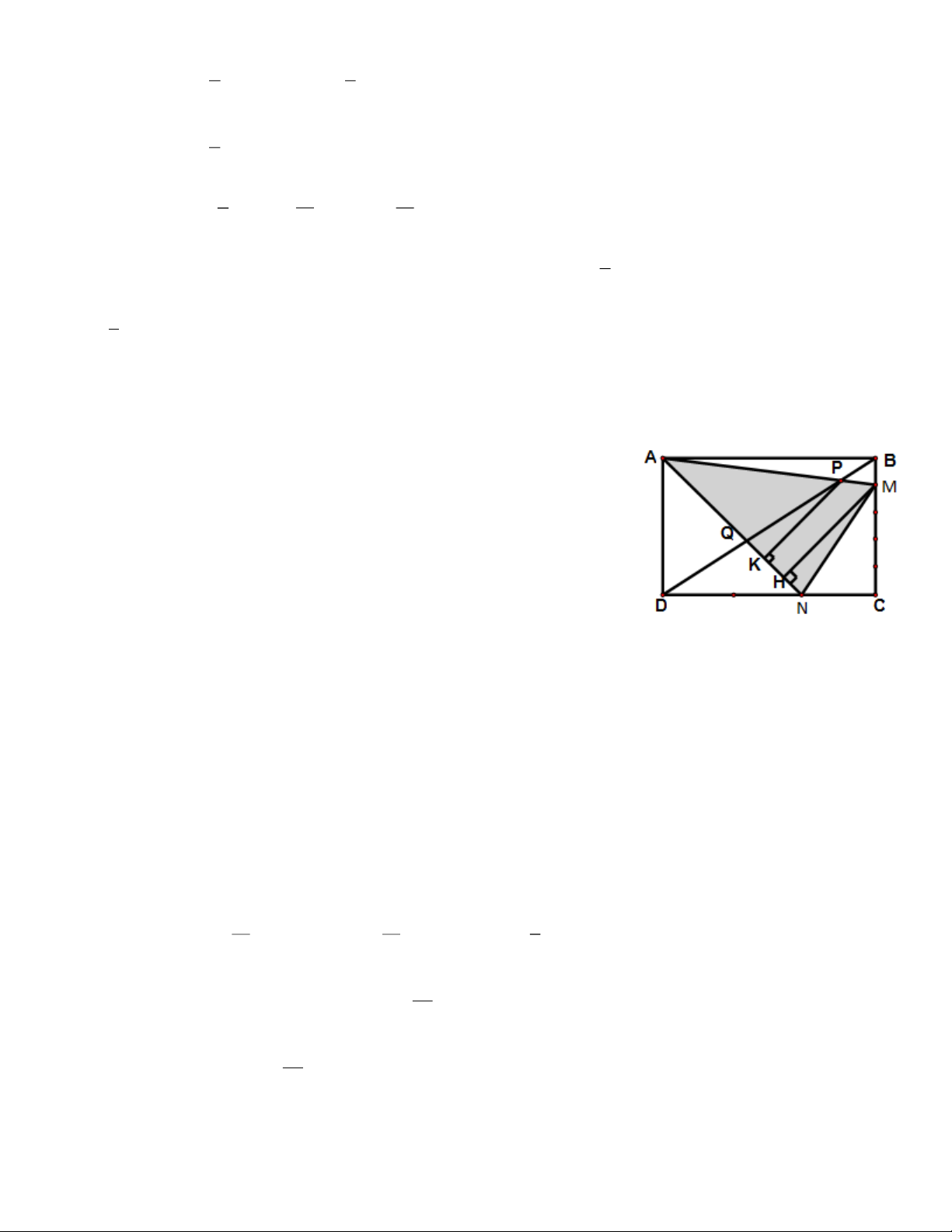
Ví dụ 4. Cho hình chữ nhật ABCD, trên cạnh BC lấy M: BM = BC. Trên cạnh CD lấy N sao cho 5 1 CN = CD. 3 a) Tính SAMN theo SABCD.
b) BD cắt AM ở P, BD cắt AN ở Q. Tính SMNQP theo SABCD. Tìm cách giải.
(a) hs dễ dàng nhận ra phải sử dung tính chất 1: Nếu một đa
giác được chia thành các đa giác không có điểm chung thì diện tích
của nó bằng tổng diện tích của các đa giác đó ( tính cộng).
Nên để tính diện tích của AMN ta có:
SAMN = SABCD - SABN - SCMN - SADN
(b) Tính SMNQP theo SABCD cần phải tìm mối liên hệ SMNPQ với SAMN vì các đỉnh của tứ giác nằm trên cạnh của  AMN.
Muốn tìm mối liên hệ đó rõ ràng phải thông qua  APQ.
Ta nhận thấy  APQ và  AMN có hai đáy cùng thuộc một đường thẳng nên ta phải kẻ thêm
đường vuông góc PK và MH. Từ đó suy ra lời giải của bài toán.
Trình bày lời giải
a) SAMN = SABCD - SABN - SCMN - SADN 1 2 1 SABM = SABCD ; SCMN = SABCD; SADN = SABCD. 10 15 3 13
Do đó ta tính được : SAMN = SABCD 60 13 Vậy SMNPQ = SABCD 60 Trang 5 1 PK.AQ SAPQ PK AQ
b) Kẻ MH ⊥ AN ; PK ⊥ AN => 2 = = . S 1 MH AN AMN MH.AN 2 PK AP
Vì PK// MH ( cùng vuông góc với AN) => = .(Theo định lí Ta let). MH AM AP AD 5 AP 5 Ddcm = = => = PM BM 1 AM 6 AQ AB 3 AQ 3 Vì DN // AB => = = => = . QN DN 2 AN 5 S AP AQ 5 3 1 1 13 Do đó APQ = .
= . = => SAPQ = SMNPQ = SAMN = SABCD S AM AN 6 5 2 2 60 AMN
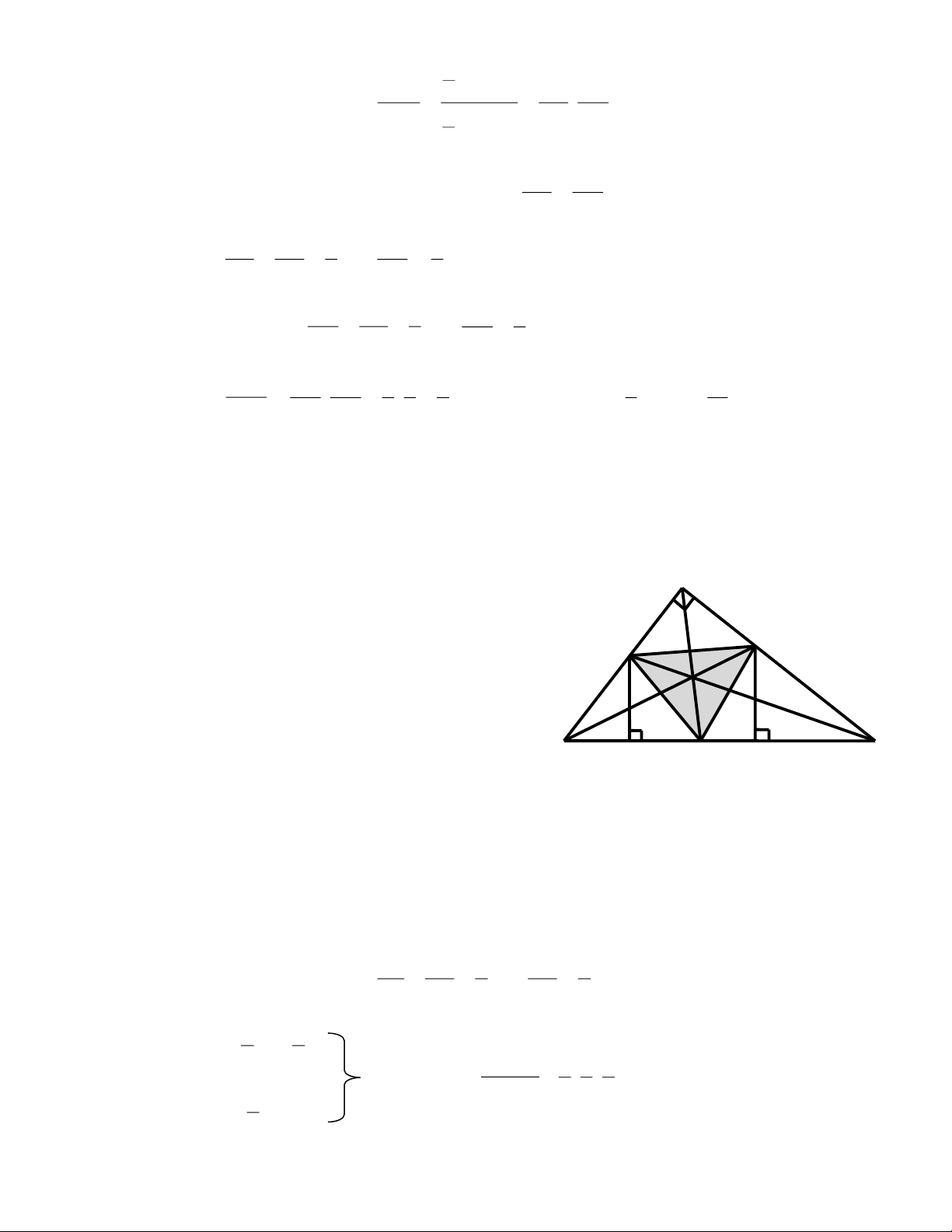
Ví dụ 5. Cho ABC có AB = 3; AC = 4, BC = 5. Vẽ các đường phân giác AD, BE, CF. Tính diện tích
tam giác DEF. (Đề thi học sinh giỏi quận Ba đình 1998 - 1999)
Tìm cách giải.
- Để tính được diện tích của  DEF thì ta phải đi A tính SABC, SAEF, SBFD, SDFC
Học sinh dễ dàng tính được SABC, SAEF vì đó là hai E F tam giác vuông.
- Để tính được SBFD, SDFC thì cần phải kẻ thêm
đường cao. Căn cứ thêm vào giả thiết : có phân giác của B H C D K
các góc nên từ đó suy ra kẻ đường cao FH và EK => FH = FA; EK = EA.
Trình bày lời giải
ABC có AB = 3, AC = 4, BC = 5.
Nên ddcm  ABC vuông tại A. FA CA 4 FA 4
Ta có CF là phân giác ACB => = = => = FB CB 5 AB 9 4 4 => FA = .3 = 9 3 AE.AF 1 3 4 => (*) SAEF = = . . = 1 3 2 2 2 3 Cmtt => AE = . 2 Trang 6 Hạ FH ⊥ BC ; EK ⊥ BC.
=> FH = FA ; EK = AE ( Tính chất tia pg của một góc) 15
Cmtt như trên ta tính được DB =
( Dựa vào định lí đường phân giác trong tam giác) 7 20 => DC = 7 FH.BD 1 4 15 10 (*) SBFD = = . . = 2 2 3 7 7 EK.DC 1 3 20 15 (*) SDFC = = . . = 2 2 2 7 7 AB.AC 3.4 (*) SABC = = = 6 2 2
=> SDEF = SABC - ( SAEF + SBFD + SDFC) 10 Vậy SDEF = . 7
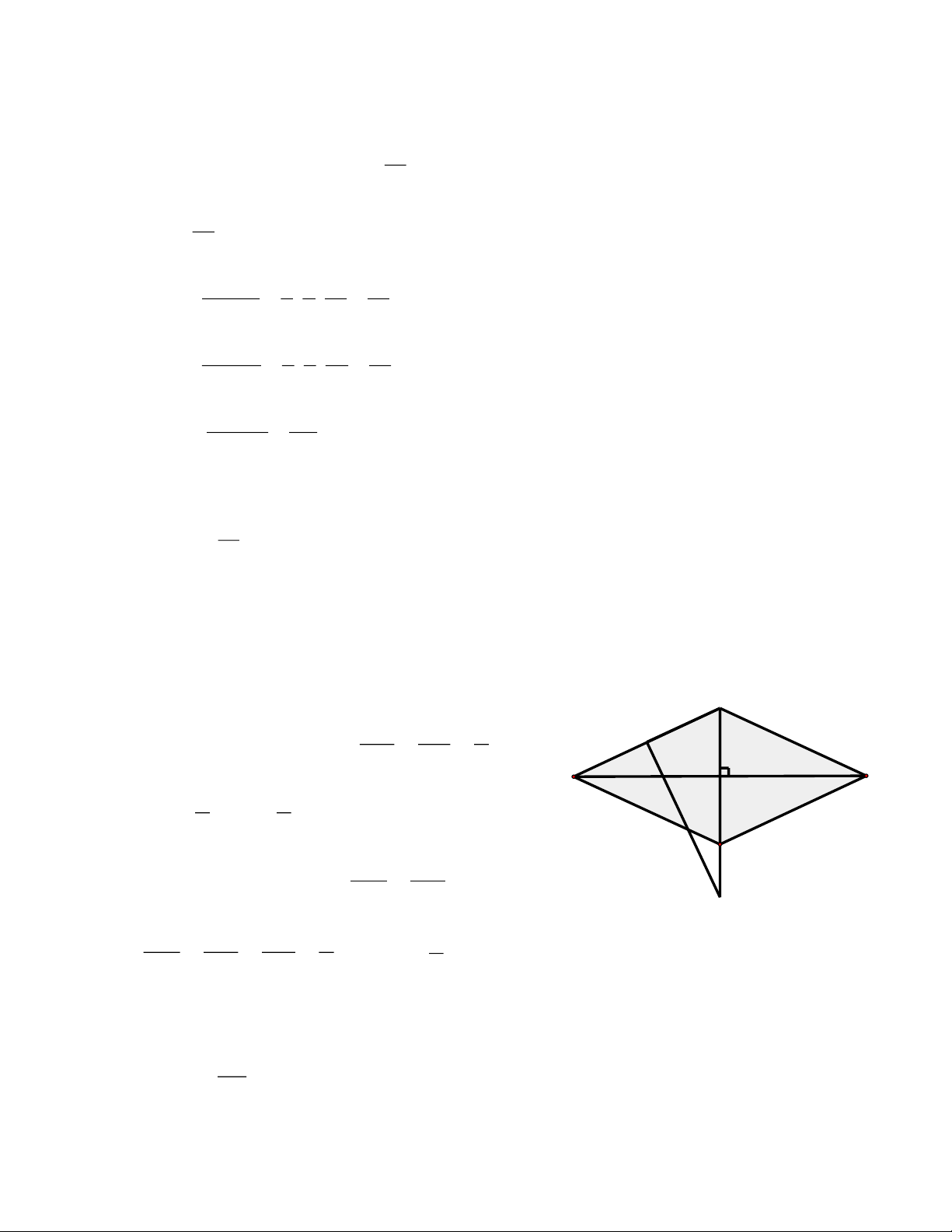
Ví dụ 6. Cho hình thoi ABCD, hai đường chéo AC, BD cắt nhau tại O. Đường trung trực của AB cắt
BD, AC tại M, N. Biết MB = a, NA = b. Tính diện tích hình thoi theo a và b. Bài giải
Gọi H là trung điểm của AB. Dễ dàng nhận thấy: B AN HN b H
*) AHN ∽ MHN ( g.g) => = = MB HB a N O A C b b => HN = HB . = HA . a a D AH HN
*) AHN ∽ AOB (g.g) => = AO OB M OB HN HN b b => = = = => OB = OA . OA AH HB a a
*) AHN vuông tại H => HN2 + HA2 = AN2 ( Theo định lí Pitago) 2 b
=> HA2(1 + 2 ) = b2 . a Trang 7 2 2 a b 2 2 4a b Do đó HA2 = => AB2 = 4HA2 = 2 2 a + b 2 2 a + b
*) AOB vuông => OA2 + OB2 = AB2 2 b 2 2 2 4a b => OA2 + OA . 2 = a 2 2 a + b 4 2 4a b 2 2a b 2 2a b Do đó OA2 = 2 2 2 => OA = và OB = (a + b ) 2 2 a + b 2 2 a + b Mà SABCD = 2.OA.OB 3 3 8a b Vậy SABCD = 2 2 2 (a + b )
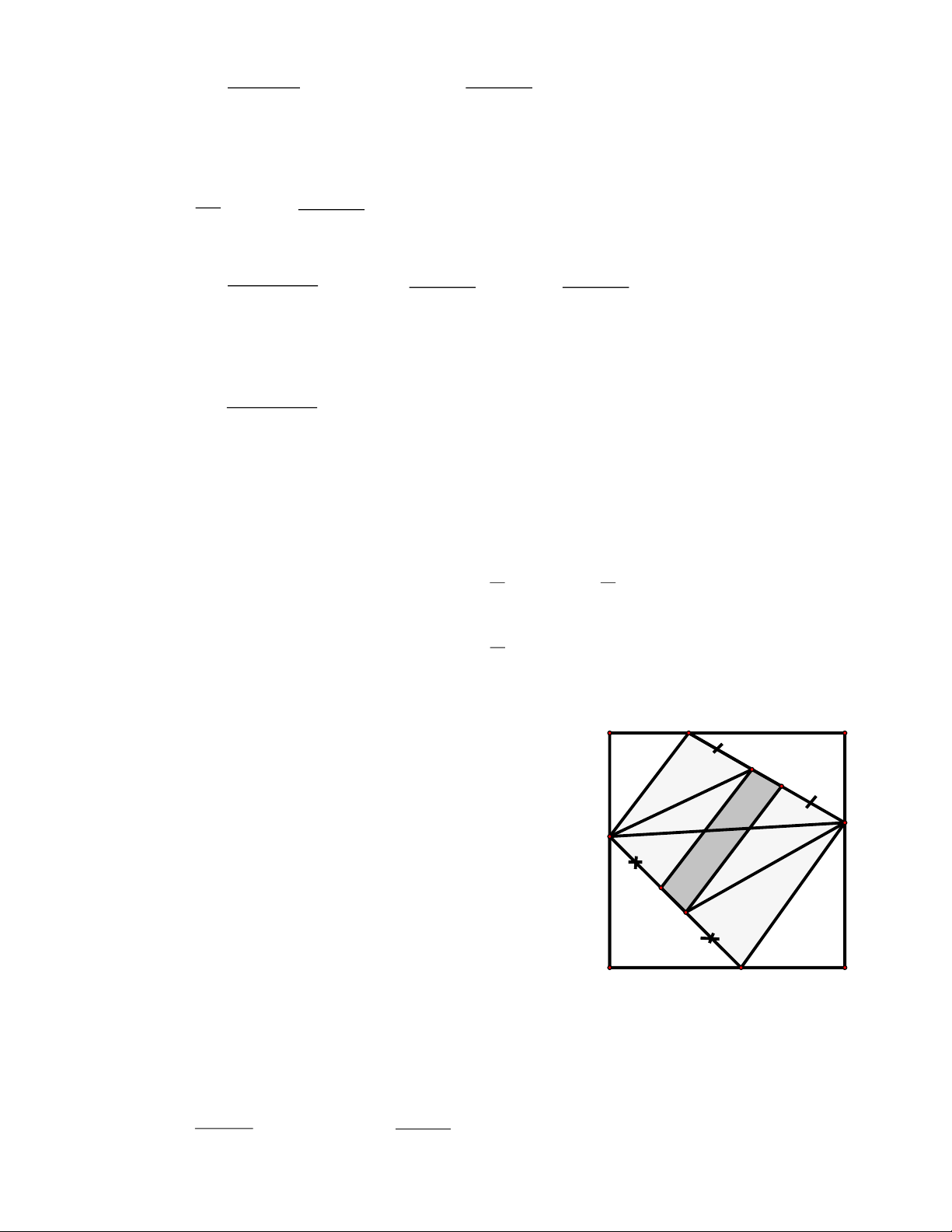
Ví dụ 7. Cho hình vuông ABCD có cạnh bằng 30cm. Trên các cạnh AB, BC, CD, DA thứ tự lấy các
điểm E, F, G, H: AE = 10cm; BF =12cm, CG = 14 cm, DH = 16cm. a) Tính SEFGH . 2 2
b) Trên EF lấy hai điểm M, N : sao cho EM = MF, FN= EN. 3 3 2
Trên cạnh HG lấy hai điểm P, Q : GP = HQ = MF. Tính SMNPQ . 5 Tìm cách giải. 10cm E
a) Ta nhận thấy để tính được S A B EFGH phải thông qua S M
ABCD, SAEH, SEBF, SFCG, SHGD là các hình tính được diện N 12cm
tích qua các công thức đã học. H F
b) Vì tứ giác MNPQ có các đỉnh nằm trên cạnh của
tứ giác EFGH ở những vị trí đặc biệt theo gt đã nêu. Do đó 16cm Q
ta cần tìm mối liên hệ giữa tứ giác MNPQ với EFGH. Từ P
đó tính được diện tích của tứ giác MNPQ. D C G 14cm
Trình bày lời giải
a) Từ gt => EB = 20cm, CF = 18cm, DG = 16cm, AH = 14cm. *) SABCD = 900 cm2. AE.AH EB.BF *) SAEH = = 70 cm2; SEBF = = 120cm2 2 2 Trang 8 FC.CG DH.DG SFCG = = 126cm2; SHGD = = 128 cm2. 2 2
=> SEFGH = 900 - ( 70 + 120 + 126 + 128) = 456 cm2 2 2 3
b) Vì EM = 2MF(gt) => EM = EF => SHEM = S => SHMF = SHFE 3 5 HEF 5 5 2 3 3
GP = HG (gt) => PH = HG => SHFP = SHFG 5 5 5 3 3
=> SHMF + SHFP = ( SHEF + SHFG) = SEFGH . 5 5 1 1 1 1
Dd chứng tỏ PQ = HP , MN = MF => SMQP = SMHP ; SPMN = SMPF. 3 3 3 3 1 1 3 1
=> SMQP + SPMN = ( SMHP + SMPF.) = . S S EFGH = EFGH 3 3 5 5 1 1
=> SMNPQ = SEFGH = .456 = 91,2 (cm2) 5 5
II/ BÀI TẬP VẬN DỤNG
Bài 1. Cho hình thoi ABCD có A 0
= 60 . Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC,
CD, DA. Chứng minh đa giác EBFGDH là lục giác đều.
Bài 2. Cho tam giác ABC, O là trọng tâm của tam giác. Gọi E, F, G lần lượt là các điểm đối xứng với
điểm O qua trung điểm của AB, BC, AC. Chứng minh lục giác AEBFCG là lục giác đều.
Bài 3. Cho ngũ giác ABCDE có các cạnh bằng nhau và A = B = C .
a) Chứng minh tứ giác ABCD là hình thang cân.
b) Chứng minh ngũ giác ABCDEF là ngũ giác đều.
Bài 4. Cho ngũ giác đều ABCDE. Gọi K là giao điểm của hai đường chéo AC và BE.
a) Tính số đo mỗi góc của ngũ giác.
b) Chứng minh CKED là hình thoi.
Bài 5. Cho hình chữ nhật ABCD. E là điểm bất kì nằm trên đường chéo AC. Đường thẳng qua E, song
song với AD cắt AB, DC lần lượt tại F, G. Đường thẳng qua E, song song với AB cắt AD, BC lần
lượt tại H, K. Chứng minh hai hình chữ nhật EFBK và EGDH có cùng diện tích.
Bài 6. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ BP ⊥ MN, CQ ⊥ MN (P, Q  MN).
a) Chứng minh tứ giác BPQC là hình chữ nhật. b) Chứng minh S = S . BPQC ABC
Bài 7. Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh các tứ giác
ADCM và ABCN có diện tích bằng nhau. Cho hình thang vuông ABCD ( A = D 0 = 90 ), AB = 3cm, AD = 4cm và ABC 0
= 135 . Tính diện tích của hình thang đó Trang 9 ĐS: S = cm2 20 . ABCD
Bài 8. Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Chứng minh S = S + S . BCHI ABDE ACFG
Bài 9. Diện tích hình bình hành bằng cm2 24
. Khoảng cách từ giao điểm của hai đường chéo đến các
đường thẳng chứa các cạnh hình bình hành bằng cm 2 và cm 3
. Tính chu vi của hình bình hành. ĐS: P = c 20 m. ABCD
Bài 10. Cho hình bình hành ABCD. Gọi K, O, E, N là trung điểm của AB, BC, CD, DA. Các đoạn
thẳng AO, BE, CN và DK cắt nhau tại L, M, R, P. Chứng minh S = S 5. . ABCD MLPR
Bài 11. Cho tam giác ABC. Gọi E, F lần lượt là trung điểm của BA, BC. Lấy điểm M trên đoạn thẳng
EF (M  E, M  F). Chứng minh S + S = S . AMB BMC MAC
Bài 12. Cho tam giác ABC cân tại A, điểm M thuộc đáy BC. Gọi BD là đường cao của tam giác
ABC; H và K chân đường vuông góc kẻ từ M đến AB và AC. Chứng minh: MH + MK = BD .
Bài 13. Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC.
Tính tỉ số diện tích của:
a) Các tam giác DAC và DCK.
b) Tam giác DAC và tứ giác ADLB.
c) Các tứ giác ABKD và ABLD. S S S ĐS: a) DAC 3 = b) DAC 3 = c) ABKD 4 = . S 2 S 5 S 5 DCK ADLB ABLD
Bài 14. Cho tam giác ABC, hai đường trung tuyến AM, BN cắt nhau tại G. Diện tích tam giác AGB bằng cm2 336
. Tính diện tích tam giác ABC. ĐS: S = cm2 1008 . ABC
Bài 15. Cho tam giác ABC. Trên cạnh AB lấy điểm D sao cho BD = 3DA, trên cạnh BC lấy điểm E
sao cho BE = 4EC. Gọi F là giao điểm của AE và CD. a) Chứng minh: FD = FC. b) Chứng minh: S = S 2 . ABC AFB
Bài 16. Cho tam giác đều ABC, đường cao AH và điểm M thuộc miền trong của tam giác. Gọi P, Q, R
lần lượt là chân đường vuông góc kẻ từ M đến BC, AC, AB. Chứng minh: MP + MQ + MR = AH.
Bài 17. Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AC, AB. Từ N kẻ đường
thẳng song song với BM cắt đwòng thẳng BC tại D. Biết diện tích tam giác ABC bằng a cm2 ( ) .
a) Tính diện tích hình thang CMND theo a. b) Cho a = cm2 128 và BC = c
32 m. Tính chiều cao của hình thang CMND. ĐS: a) S = a cm2 ( ) b) = . CMND h 4(cm)
Bài 18. Cho tứ giác ABCD. Kéo dài AB một đoạn BM = AB, kéo dài BC một đoạn CN = BC, kéo dài
CD một đoạn DP = CD và kéo dài DA một đoạn AQ = DA. Chứng minh S = S 5. MNPQ ABCD Trang 10 HD: Từ S = S 2 , S = S 2 , S = S 2 , S = S 2  đpcm PDQ DAC MNB ABC QAM DAB PNC DBC Trang 11