



































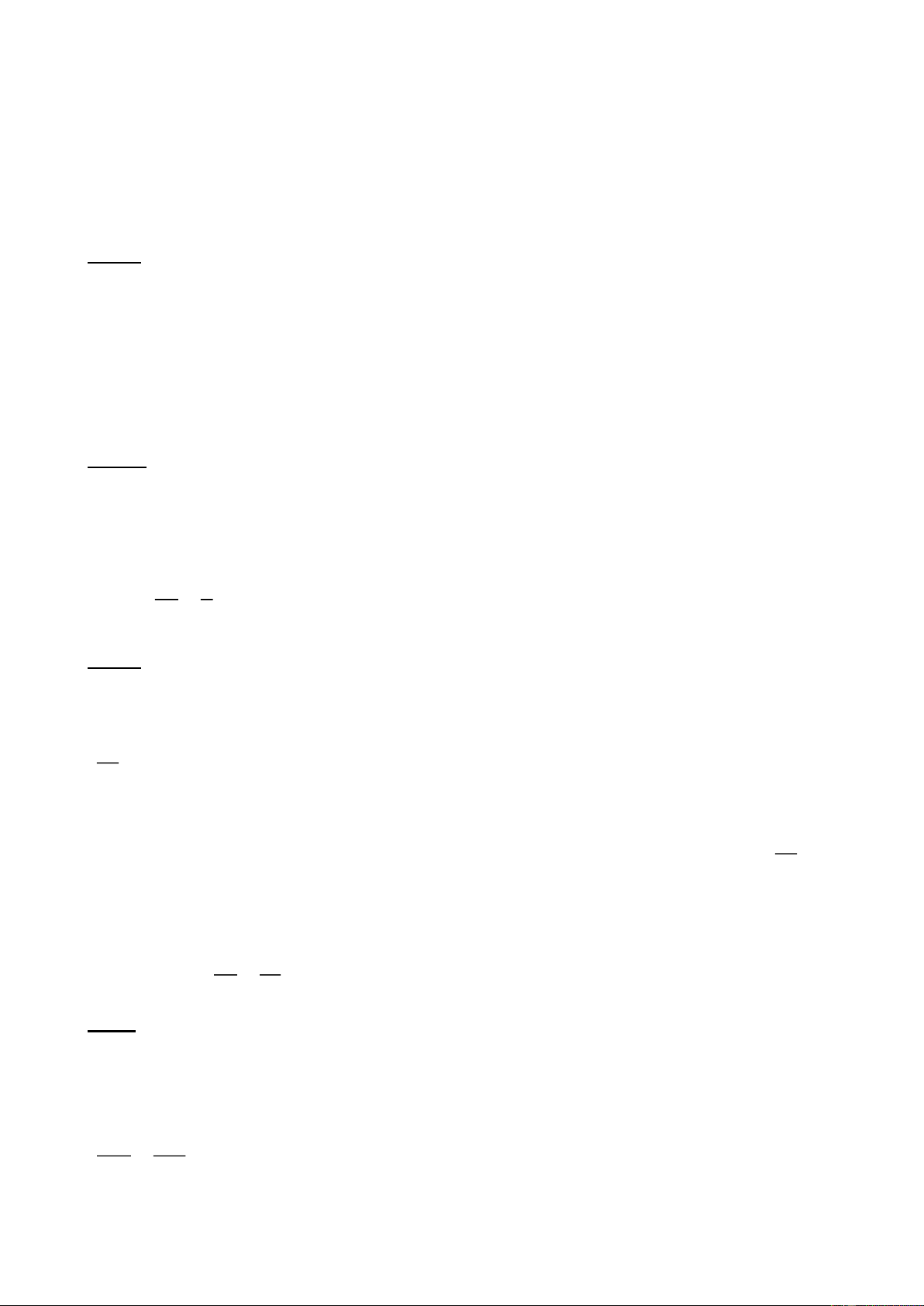

























Preview text:
1 Ngày soạn: / /20...
TIẾT 1+ 2+ 3. CHỦ ĐỀ 1. PHÂN THỨC ĐẠI SỐ. TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC ĐẠI SỐ. Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Nhận biết phân thức đại số, tử thức và mẫu thức của một phân thức.
- Viết điều kiện xác định của phân thức và tính giá trị của phân thức tại giá trị của
biến thỏa mãn điều kiện xác định.
- Nhận biết hai phân thức bằng nhau.
- Mô tả tính chất cơ bản của phân thức đại số.
- Biết quy đồng mẫu thức nhiều phân thức trong trường hợp thuận lợi. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Áp dụng tính chất của phân thức đại số để giải một số dạng bài tập. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức Bài 21, bài 22 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1: Nêu ĐN phân thức đại số?
Câu 2: Nêu quy tắc bằng nhau của hai phân thức ? 2
Câu 3.Nêu điều kiện xác định của phân thức ?
Câu 4: Nêu tính chất cơ bản của phân thức đại số?
Câu 5. Nêu các bước rút gọn phân thức đại số ?
Câu 6. Nêu các bước quy đồng các phân thức đại số?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 6 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học của bài 20, 21 để giải bài tập liên
quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1: Dùng định nghĩa hai phân thức bằng nhau chứng minh các phân thức sau bằng nhau. 3 4 4 xy 5x y 2 x .( x + 3) x a / = b / = 3 7 35x y . x ( x + 3)2 x + 3 2 2 − x x − 4x + 4 3 2 x − 9x −x − 3x c / = d / = 2 2 + x 4 − x 15 − 5x 5
Bài 2. Tính giá trị của biểu thức. (x + 2)( 2 2x + 2x ) ( với x = -1/2 x + ) 1 ( 3 4x − x )
Bài 3. Rút gọn phân thức 2 3 7x + 14x + 7 32(x − 2) a) b) 2 2 3x + 3x 64 − 64x +16x
Bài 4. Tìm điều kiện của biến để giá trị của mỗi biểu thức sau xác định: 5x + 3 2 2 x + x a, 4x + b, 6 (x −1)( y + 1) c) Sản phẩm: Bài 1: a/ Ta có: 3 xy3.35x3y = 35x4y4 = 7.5x4y4 3 4 4 do đó xy 5x y = 3 7 35x y
b/ Ta có: x2(x + 3)(x + 3) = x.x.(x + 3)2 2 x .( x + 3) do đó : x = . x ( x + 3)2 x + 3 c/ Ta có:
( 2 - x).(4 - x2) = (2 + x) (x2 - 4x + 4) 2
Do đó: 2 − x x − 4x + 4 = 2 2 + x 4 − x d/ Tương tự ta có:
5.(x3 - 9x) = (15 - 5x).( -x2 - 3x) 3 2 x − 9x −x − 3x Nên = 15 − 5x 5
Bài 2. Tính giá trị của biểu thức. (x + 2)( 2 2x + 2x ) ( với x = -1/2 x + ) 1 ( 3 4x − x ) Ta có: (x − 2)( 2
2x + 2x ) ( x − 2).2 . x (1+ x) ( = x + ) 1 ( 3 4x − x ) (x + ) 1 . . x ( 2 4 − x )
(x − 2).2 .x(1+ x) 2 − = ( = x + ) 1 . .
x (2 − x)( x + 2) x + 2 1 − 2 − 2 − 4 − Thay x =
vào biểu thức ta được: = = 2 x + 2 1 − 3 + 2 2 Bài 3. 2 2 7x +14x + 7 7(x +1) 7.(x +1) a) = = ) 2 3x + 3x 3x(x +1) 3x 3 3 32(x − 2) 32(x − 2) b) = = 2.(x − 2) 2 2 64 − 64x +16x 16.(2 − x) 5x + 3
Bài 4. a, 4x + xác định khi 4x+6 0 6 −3
2(2x +3) 0 2x -3 x 2 5x + 3 −3 Vậy biểu thức 4x + xác định khi x 6 2 2 2 x + x b, x − y + 0 (x −1)( y + xác định khi ( 1)( 1) 1) x 1 và y -1
d) Tổ chức thực hiện: 4
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3, 4 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 5,6,7
Bài 5: Tìm mẫu thức chung của các phân thức sau. 2 y −x a / ; ; 3 2 4 3 3 15x y 10x z 20 y z x z y b / ; ; 2 2 2 2
y − yz y + yz y − z 5 z 7 c / ; ;
2x − 4 3x − 9 50 − 25x
Bài 6. Quy đồng mẫu các phân số: 2 y −x a / ; ; 3 2 4 3 3 15x y 10x z 20 y z x z y b / ; ; 2 2 2 2
y − yz y + yz y − z 5 2 7 c / ; ;
2x − 4 3x − 9 50 − 25x
Bài 7. Tìm mẫu thức chung rồi quy đồng của các phân thức sau. 7x −1 3 − 2x 2x −1 x +1 a / ; b / ; 2 2 2x + 6x x − 9 2 2 x − x 2 − 4x + 2x x −1 2x 2 x 3 4x c / ; ; d) ; ; 3 2
x +1 x − x +1 x +1 2
2x + 4 2x − 4 x − 4 c) Sản phẩm: Bài 5. a/ MTC: 60x4y3z3. b/ Ta có: y2 - yz = y(y - z) y2 + yz = y(y + z) 5 y2 - z2 = (y + z)(y – z) Vậy MTC: y.(y + z)(y - z) c/ Ta có: 2x - 4 = 2( x - 2) 3x - 9 = 3(x - 3) 50 - 25x = 25(2 - x) Vậy MTC : 150(x - 2)(x - 3) Bài 6. 2 y −x a / ; ; 3 2 4 3 3 15x y 10x z 20 y z - MTC: 60x4y3z3 - NTP: 60x4y3z3 : 15x3y2 = 4xyz3 60x4y3z3 : 10x4z3 = 6y3 60x4y3z3 : 20y3z = 3x4z2 - Quy đồng. 3 4 5 2 2 8xyz y 24 y −x 3 − x z = ; = ; = 3 2 4 3 3 4 3 4 3 3 3 4 3 3 15x y 60x y z 10x z 60x y z 20 y z 60x y z b) MTC: y.(y + z)(y - z) x x x( y + z) = = 2 y − yz
y( y − z)
y( y − z).( y + z) z z
z.( y − z) = = 2 y + yz y( y + z)
y( y + z)( y − z) 2 y y y = = 2 2 y − z
( y − z)( y + z)
y( y + z)( y − z) c) MTC : 150(x - 2)(x – 3) 5 5 5.75.(x − 3) 375(x − 3) = = = 2x − 4 2.(x − 2)
150(x − 2)(x − 3)
150(x − 2)(x − 3) 2 2 2.50(x − 2) 100.(x − 2) = = = 3x − 9 3(x − 3)
150(x − 3)(x − 2)
150(x − 3)(x − 2) 7 7 − 42( − x − 3) = = 50 − 25x 25(x − 2)
150(x − 3)(x − 2) Bài 7. a/ MTC : 2.(x + 3)(x - 3) 7x −1 7x −1
(7x −1)(x − 3) = = 2 2x + 6x 2(x + 3)
2(x + 3)(x − 3) 3 − 2x 2(3 − 2x) = 2 x − 9
2(x + 3)(x − 3) b/ MTC : 2x(x - 1)2 2x −1
−(2x −1) −(2x −1)2(x −1) = = 2 2 x − x x(x −1) 2x(x −1) x +1 (x +1)x = − 2 2 2 − 4x + 2x 2x(x −1) 6 c/ MTC: x3 + 1=( x+1)( 2 x − x +1) x −1 x −1 = 3 2 x +1
(x +1)(x − x +1) 2x 2x(x +1) = 2 2 x − x +1
(x +1)(x − x +1) 2 2 2.(x − x +1) = 2 x +1
(x +1)(x − x +1) d) MTC: 2x.(x-2)(x+2) x x x(x − 2) = = 2x + 4 2(x + 2)
2(x + 2)(x − 2) 3 3 3(x + 2) = = 2x − 4 2(x − 2)
2(x + 2)(x − 2) 4x 4x 8x = = 2 x − 4 (x + 2)(x − 2)
2(x + 2)(x − 2)
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
4. Hướng dẫn về nhà:
- Ôn lại phân thức đại số và tính chất cơ bản của phân thức đại số.
- Làm lại các bài tập vào vở - Làm bài tập :
Bài 8. Rút gọn các phân thức sau: x2 −16 x2 + 4x + 3 1 x 5 (x + y 3 ) a)
(x 0, x 4) b) (x 3 − ) c)
(y + (x + y) 0) 4x − x2 2x + 6 y 5 (x + y 2 )
5(x − y) − 3(y − x) 2x + y 2 + x 5 + y 5 d) (x y) e) (x −y) 10(x − y) 2x + y 2 − x 5 − y 5 x2 − xy a 2 x2 − a 4 x + a 2 f)
(x y, y 0) g)
(b 0, x 1 ) x 3 y − y2 3 b 5 − b 5 x2 4x2 − 4xy h)
(x 0, x y) x3 5 − x2 5 y
Bài 9. Rút gọn các phân thức sau: 7
a3 + b3 + c3 − a 3 bc
x3 − y3 + z3 + x 3 yz a) b)
a2 + b2 + c2 − ab − bc − ca (x + y 2 ) + (y + z 2 ) + (z− x 2 )
x3 + y3 + z3 − x 3 yz
a2(b − c) + b2(c − a) + c2(a − b) c) d) (x − y 2 ) + (y − z 2 ) + (z− x 2 )
a4(b2 − c2) + b4(c2 − a2) + c4(a2 − b2)
a2(b − c) + b2(c − a) + c2(a − b)
x24 + x20 + x16 + ...+ x4 +1 e) f) .
ab2 − ac2 − b3 + bc2
x26 + x24 + x22 + ...+ x2 +1 Ngày soạn: / /20...
TIẾT 4+ 5+ 6. CHỦ ĐỀ 2. PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: 8 I. MỤC TIÊU 1. Kiến thức:
- Thực hiện phép cộng và trừ phân thức đại số
- Vận dụng các tính chất giao hoán, kết hợp của phép cộng phân thức và quy tắc dấu
ngoặc với phân thức trong tính toán. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Rèn luyện cộng, trừ các phân thức đại số. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 3. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức Bài 23 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1: Nêu quy tắc cộng hai phân thức cùng mẫu và khác mẫu ?
Câu 2: Nêu quy tắc trừ hai phân thức cùng mẫu và khác mẫu ?
Câu 3. Nêu quy tắc dấu ngoặc ?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét . 9
- Gv: Gọi HS trả lời từng câu hỏi ( 3 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học của bài 23 để giải bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Thực hiện phép tính sau : 2 x 10 x −10x 25 a) + ; b) + 2 2 x +10 x +10 x − 25 x − 25
Bài 2: Thực hiện phép tính : x + 1 2x + 3 x x 4xy a) + b) + + . 2x + 6 x 2 + 3x x − 2 y x + 2 y 2 2 4 y − x
Bài 3. Cộng các phân thức sau: 1 2 3 a) + +
(x −1)(x − 2)
(2 − x)(3 − x)
(1− x)(x − 3) 1 1 1 b) + + 3 x −1 1 2 − x x + x +1 x y z c) + +
(x − y)(x − z)
( y − z)( y − x)
(z − x)(z − y) 1 1 2 4 8 16 d) + + + + + 2 4 8 16 1 − x 1 + x 1 + x 1 + x 1 + x 1 + x c) Sản phẩm Bài 1: x 10 x +10 a) + = =1 x +10 x +10 x +10 x −10x 25 x −10x + 25 (x −5)2 2 2 x − 5 b) + = = = . 2 2 2 x − 25 x − 25 x − 25
(x +5)(x −5) x +5 Bài 2: x + 1 2x + 3 a) + 2x + 6 x 2 + 3x 2x + 6 = 2(x + 3) x2 + 3x =x(x +3) MTC: 2x(x + 3) x + 1 2x + 3 x(x +1) 2(2x + 3) + = + 2x + 6 x 2 + 3x 2x(x + 3) 2x(x + 3) 2
x + x + 4x + 6
(x +3)(x + 2) x + 2 = = = 2x(x + 3) 2x ( x + 3) 2x 10 x x 4xy b) + + . x − 2 y x + 2 y 2 2 4 y − x MTC: 4y2 - x2 x x 4xy + + x − 2 y x + 2 y 2 2 4 y − x
−x(x + 2y)
x (2y − x) 4xy = ( + +
2 y − x)(2y + x)
(x + 2 y) (2 y − x)
(2y − x)(2y + x) 2 2
−x − 2xy + 2xy − x + 4xy = (
2 y − x)(2y + x) 2 2 − x + 4xy 2x = ( =
2 y − x)(2y + x) 2 y + x Bài 3. 1 2 3 + +
a) (x −1)(x − 2) (2 − x)(3 − x) (1− x)(x − 3) 1 =
(x −1)(x − 2)(x − 3) 1 1 1 1 b) + + = 3 x −1 1 2 − x x + x +1 3 x −1 x y z c) + + =0
(x − y)(x − z)
( y − z)( y − x)
(z − x)(z − y) 1 1 2 4 8 16 32 d) + + + + + = 2 4 8 16 1 − x 1 + x 1 + x 1 + x 1 + x 1 + x 32 1 − x
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao. 11
b) Nội dung: HS làm bài 4, 5,6,7
Bài 4. Thực hiện phép tính 1 1 1 1 1 x − 5 A= ( + + ; B = + + x + 2)( x + 3) 2 x + 3 4x +15x +14 2 x x + 5 x + 5x
Bài 5. Cộng các phân thức cùng mẫu: 1− 2x 3 + 2 y 2x − 4 2 x − 2 2 − x a) + + b) + 3 3 3 6x y 6x y 6x y 2 2 x(x −1) x(x −1) 2 3x +1 x − 6x 2 2 x + 38x + 4 3x − 4x − 2 c) + d) + 2 2 x − 3x +1 x − 3x +1 2 2 2x +17x +1 2x +17x +1
Bài 6. Dùng quy tắc đổi dấu để tìm mẫu thức chung rồi thực hiện phép cộng: 2x +1 5 y + 2 y +1 4 2 5x − 6 a) + + b) + + x − 2 y 2 y − x x − 2 y 2 x + 2 x − 2 4 − x 1− 3x 3x − 2 3x − 2 c) + + 1 1 x d) + + 2 2x 2x −1 2x − 4x 2 2 2 x + 6x + 9 6x − x − 9 x − 9
Bài 7. Thực hiện phép tính − 2 2x x + 2 x − 2 y x + 3 y + 3 a + 1 ) b) + c) + x − 1
x − 1 2x(x + y) 2xy + 2 2x 2 x − 2 y
(y −x)(y + x) c) Sản phẩm: 1 1 1 Bài 4. a) A = ( + + x + 2)( x + 3) 2 x + 3 4x +15x +14 1 1 1 = ( + + x + 2)( x + 3) x + 3 (x + 2)(4x + 7)
4x + 7 + (x + 2)(4x + 7) + x + 3 =
(x + 2)(x + 3)(4x + 7) 2
4x + 7 + 4x +15x +14 + x + 3 =
(x + 2)(x + 3)(4x + 7) 2 4x + 20x + 24 4(x + 2)(x + 3) 4 = = =
(x + 2)(x + 3)(4x + 7)
(x + 2)(x + 3)(4x + 7) 4x + 7 1 1 x − 5 b) B = + + 2 x x + 5 x + 5x 1 1 x − 5
x + 5 + x + x − 5 3x 3 = + + = = = x x + 5 x(x + 5) x(x + 5) x(x + 5) x + 5 Bài 5. 1− 2x 3 + 2 y 2x − 4 a) + + 3 3 3 6x y 6x y 6x y
1− 2x + 3 + 2 y + 2x − 4 2 y 1 = = = 3 3 3 6x y 6x y 3x 2 x − 2 2 − x b) + 2 2 x(x −1) x(x −1) 2 2
x − 2 + 2 − x x − x x(x −1) 1 = = = = 2 2 2 x(x −1) x(x −1) x(x −1) (x −1) 12 2 3x +1 x − 6x c) + 2 2 x − 3x +1 x − 3x +1 2 2
3x +1+ x − 6x x − 3x +1 = = = 1 2 2 x − 3x +1 x − 3x +1 2 2 x + 38x + 4 3x − 4x − 2 d ) + 2 2 2x +17x +1 2x +17x +1 2 2
x + 38x + 4 + 3x − 4x − 2 = 2 2x +17x +1 2 2 4x + 34x + 2 2(2x +17x +1) = = = 2 2 2 2x +17x +1 2x +17x +1 Bài 6. 2x +1 5 y + 2 y +1 a) + + x − 2 y 2 y − x x − 2 y 2x +1 5 − y − 2 y +1 = + + x − 2 y x − 2 y x − 2 y
2x +1− 5 y − 2 + y +1 = x − 2 y 2x − 4 y 2 ( x − 2 y) = = = 2 x − 2 y x − 2 y 4 2 5x − 6 b) + + 2 x + 2 x − 2 4 − x 4 2 6 − 5x = + + 2 x + 2 x − 2 x − 4
4(x − 2) + 2(x + 2) + 6 − 5x = (x − 2)(x + 2) x + 2 1 = ... = = (x − 2)(x + 2) x − 2 1− 3x 3x − 2 3x − 2 c) + + 2 2x 2x −1 2x − 4x 1− 3x 3x − 2 2 − 3x = + + 2 2x 2x −1 4x − 2x
(1− 3x)(2x −1) + 2x(3x − 2) + 2 − 3x = 2x(2x −1) 1− 2x 1 − = ... = = 2x(2x −1) 2x 13 1 1 x d) + + 2 2 2 x + 6x + 9 6x − x − 9 x − 9 1 1 − x = + + 2 2 2 x + 6x + 9 x − 6x + 9 x − 9 1 1 − x = + + 2 2 (x + 3) (x − 3) (x − 3)(x + 3) 2 2
(x − 3) − (x + 3) + x(x − 3)(x + 3) = 2 2
(x − 3) (x + 3) 2 x − 21x = ... = 2 2
(x − 3) (x + 3) Bài 7. − 2 2x x + 1 −2x + 2 x + a + = 1 ) x−1 x−1 x − 1 (x−1)2 = = x − x − 1 1 2 x − 2 y x + 3 y + 3 b) c) + 2x (x y) + + 2xy + 2 2x 2 x − 2 y
(y −x)(y + x) 2 x − 2 x + 3 y + 3 x + 3 −y − = y = + = + 3 2x (x y) + +
2x (x + y) 2 x − 2 2 y y − 2 2 x x − 2 2 y x − 2 y 2
x + 3 − y − 3 x − x − 2 y
(x− y)(x+ y) x− y 1 = y = = = 2 x − 2 2 y x − 2 y x +
2x (x y) = 2x(x y) = + + 2x y
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
4. Hướng dẫn về nhà:
- Ôn lại tính chất của tỉ lệ thức, tính chất của dãy tỉ số bằng nhau.
- Làm lại các bài tập vào vở
- Làm bài tập : Bài 8: Thực hiện phép tính 2 12 x + 4 x − 2 2 x 2x 1 a/ + b) + c) + + + 1 2 x + 3 x − 9 2 2 2x + 4
x − 4 x + 1 x − 1 1− x LG: 14 2 12 2 12 a/ + = + 2 x + 3 x − 9 x + 3 (x −3)(x + 3) 2(x − 3) 12 = ( + x − 3)(x + 3) (x −3)(x + 3) 2x − 6 + 12 2x + 6 = ( = x − 3)(x + 3) (x −3)(x + 3) 2 = x −3 x + 4 x − 2 x + 4 x − + = 2 b) 2 2x 4 x − 4 2 (x 2) + + + (x+ 2)(x−2) (x+ 4)(x−2) 2 (x − 2) = 2(x 2)(x 2) + + −
2 (x + 2)(x − 2) 2
x − 2x + 4x − 8 + 2x − 2 4 x + 4x − 12
(x+6)(x−2) x+ = 6 (x+ 2)(x−2)
= (x+2)(x−2) = (x+2)(x−2) = x+2 2 x + 2x + 1 c) + x + 1 2 1 x − 1 1 − x 2 x 2x − = + 1 x ( 1 1
x − 1) ( x + 1) + + + x − 1 2 x ( x − 1) = 2x (x 1)(x 1) + − + (x −1)(x + 1) −1( x + 1) (x −1)(x + 1) + (x 1)(x 1) + − + (x −1)(x + 1) 3 x − 2
x + 2x − x − 1 + 2 x − 3 1 x + x − = 2 (x 1)(x 1) = − + (x −1)(x + 1) 2 x + x + = 2 x + 1 15 Ngày soạn: / /20...
TIẾT 7+ 8+ 9. CHỦ ĐỀ 3: PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ. Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Thực hiện phép nhân và phép chia hai phân thức đại số
-Vận dụng tính chất của phép nhân phân thức địa số trong tính toán. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Rèn luyện kí năng tính toán nhân và chia hai phân thức đại số. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 4. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức Bài 24 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1: Nêu Quy tắc nhân hai phân thức đại số?
Câu 2: Nêu Quy tắc chia hai phân thức đại số?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs 16
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 2 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học của bài 24 để giải bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Rút gọn phân thức 3 18y 2 15x 2 2 2x − 20x + 50 x −1 a) − . b) . 4 − 3
25x 9y 3 3x + 3 ( 4 x − ) 5
x + 3 8 −12x + 6 2 3 x − x x − 2 2 x − 2x − 3 c) . d) . 2 x − 4 9x + 27 x + 1 2 x − 5x + 6
Bài 2. Thực hiện phép tính 5x −10 2 x + x 3x + 3 a. : (2x − ) 4 b. : 2 x + 7 5 2
x −10x + 5 5x − 5
Bài 3. Tìm đa thức Q biết: x2 + 2x x2 − 4 Q . = x −1 x2 − x c) Sản phẩm: Bài 1. 3 18y 2 15x 3 2 18y 15 . x 6 a) − . = = 4 − 3
25x 9y 4 3 2 25x 9 . y 5x 2 2 2x − 20x + 50 x −1 x − 1 b) . = 3 3x + 3 ( 4 x − ) 5 6.(x − ) 5
x + 3 8 −12x + 6 2 3 x − x − (2 − x)2 c) . = 2 x − 4 9x + 27 ( 9 x + ) 2 x − 2 2 x − 2x − 3 d) . = 1. x + 1 2 x − 5x + 6 Bài 2. 5x −10 a) : (2x − ) 4 2 x + 7 ( 5 x − ) 2 1 5 = . = 2 x + 7 ( 2 x − ) 2 ( 3 x + ) 1 2 x + x 3x + 3 b) : 5 2
x −10x + 5 5x − 5 17 x(x + ) 1 ( 5 x − ) 1 x = . = ( 5 x − ) 1 2 ( 3 x + ) 1 ( 3 x + ) 1 Bài 3. x2 + 2x x2 − 4 Q . = x −1 x2 − x 2 x − 4 2 x + 2x x − 2 Q = : = 2 x − x x − 1 2 x
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6,7 2 x − 4x + 4
Bài 4 Cho phân thức A= x − 2
a. Tìm điều kiện x để phân thức có nghĩa b. Rút gọn phân thức
c. Tính giá trị của phân thức với x=4
Bài 5. Cho phân thức 3 2
x − 3x + 4x −1 B= x − 3
a. Tìm điều kiện xác định
b. Tìm giá trị nguyên của x để biểu thức nhận giá trị nguyên
Bài 6. Thực hiện phép tính 2 2 x y x + y 3x − 2 y 3x + 6 2x − 4 2 x − 36 x + 5 a) . b) .(x + y) c) . d) . 2 x + xy xy 2 2
x + 2xy + y 4x − 8 x + 2 2x +10 6 − x
Bài 7. Thực hiện phép tính: 1 2 3 x −14 2 + − − a) A= + + x 2x x 5 50 5x : b) B = + + 2
x − 9 3− x x + 3 x + 3 2(x + 5) x 2x(x + 5) 18 c) Sản phẩm: Bài 4
a. Phân thức xác định khi x-2 0 x 2 2 x − 4x + 4 b.Ta có A= x − 2 2 (x − 2) = = x − 2 x − 2 c. Khi x = 4 thì A= 4 - 2=2
Bài 5. a. Biểu thức xác định khi x-3 0 x 3 11 b. Ta có : B = x2+4 + x − 3
Ta thấy khi x lấy giá trị nguyên thì x2+4 nhận giá trị nguyên, để B nhận giá trị nguyên khi x-3 là ước của 11 x-3 = 11 hoặc x-3 = -11 x = 14 ( Thỏa mãn đk)
hoặc x = -9 ( thỏa mãn đk) 2 2 2 2 x y x + y
x y .(x + y) Bài 6. a) . = = y 2 x + xy xy
x(x + y).xy 3x − 2 y
(3x − 2 y)(x + y) 3x − 2 y b) .(x + y) = = 2 2 2
x + 2xy + y (x + y) x + y 3x + 6 2x − 4
3(x + 2) 2(x − 2) 3 c) . = . = 4x − 8 x + 2 4(x − 2) x + 2 2 2 x − 36 x + 5 (x − 6)(x + 6) x + 5 x + 5 d) . = . = − 2x +10 6 − x 2(x + 6) −(x − 6) 2 Bài 7. − a)A= 1 2 3 x 14 + + : = 2
x − 9 3− x x + 3 x + 3
1− 2 (x + 3) + 3(x − 3) x −14 : 2 x − 9 x + 3 x −14 x + 3 1 = ( = + )( − ) . x 3 x 3 x −14 x − 3 3 2 2 + + − + + − + + − + − b) x(x 2)x
2(x 5)(x 5) 50 5x x 2x 2x 50 50 5x B = = 2x(x + 5) 2x(x + 5) 3 2 2
x + 4x − 5x
x(x + 5x − x − 5)
x(x + 5)(x −1) x −1 = = = = 2x(x + 5) 2x(x + 5) 2x(x + 5) 2
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở 19
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
4. Hướng dẫn về nhà .
- Ôn lại phép nhân và phép chia hai phân thức đại số.
- Làm lại các bài tập vào vở. 3 2 x − 3x + 6
Bài 8. Cho biểu thức : P = 2 x − 3x
a. Tìm điều kiện xác định
b.Tính giá trị của P khi x = 2
c. Tìm giá trị nguyên của x để P nhận giá trị nguyên.
Bài 9. Xác định các giá trị của a, b, c để: 9 2
x −16x + 4 = a + b + c 3 x − 3 2 x + 2x x x −1 x − 2
Kết quả a = 2; b = 3; c = 4 1 1 1
Bài 10: a) C/m rằng − = x x + 1 x(x + ) 1 1 1 1 1 b.Tính + + +...+ x(x + ) 1 (x + )( 1 x + ) 2 (x + )( 2 x + ) 3 (x + )( 99 x + ) 100 1 1 1 1 c) Tính + + + 2 2 x + x x + 3x + 2 2 x + 5x + 6 2 x + 7x +12 Ngày soạn: / /20... 20
TIẾT 10+ 11+ 12. CHỦ ĐỀ 4: PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN. Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Hiểu khái niệm phương trình bậc nhất một ẩn và cách giải.
- Giải quyết một số vấn đề thực tiễn gắn với phương trình bậc nhất. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
-Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Vận dụng kiến thức của chương giải một số bài tập . 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 5. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 25 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu dạng tổng quát của phương trình bậc nhất một ẩn?
Câu 2. Nêu khái niệm nghiệm của phương trình?
Câu 3: Nêu dạng tổng quát của phương trình bậc nhất một ẩn và cách giải?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs 21
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 3 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 25 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1: Bằng quy tắc chuyển vế hãy giải các phương trình sau: a, x- 2,25 = 0,75. c, 4,2 = x + 2,1 b, 19,3 = 12 - x . d, 3,7 - x = 4.
Bài 2. Giải các phương trình sau: 5x − 4 16x +1 12x + 5 2x − 7 a. = b. = . 2 7 3 4
Bài 3. Giải các phương trình sau: a/ 7x - 8 = 4x + 7 b/ 2x + 5 = 20 - 3x c/ 5y + 12 = 8y + 27 d/ 13 - 2y = y - 2
e/ 3 + 2,25x + 2,6 = 2x + 5 + 0,4x
f/ 5x + 3,48 - 2,35x = 5,38 - 2,9x + 10,42 c) Sản phẩm: Bài 1.
a, x - 2,25 = 0,75 x = 0,75 + 2,25 x = 3.
b, 19,3 = 12 – x x = 12 - 19,3 x = - 7,3
c, 4,2 = x + 2,1 - x = 2,1 - 4,2 - x = - 2,1 x = 2,1.
d, 3,7 - x = 4 -x = 4 - 3,7 -x = 0,3 x = - 0,3 5x − 4 16x +1 7(5x − 4) 2(16x +1) Bài 2. a. = = 2 7 14 14
7( 5x – 4 ) = 2( 16x + 1 ) 35x – 28 = 32x + 2 35x – 32x = 2 + 28 3x = 30 x = 10. 12x + 5 2x − 7 4(12x + 5) 3(2x − 7) b. = = 3 4 12 12
4( 12x + 5 ) = 3 ( 2x – 7 ). 48x + 20 = 6x – 21 42x = - 41 22 − 41 x = 42
Bài 3. a/ 7x - 8 = 4x + 7 7x - 4x = 7 + 8 3x = 15 x = 5. Vậy S = { 5 }. b/ 2x + 5 = 20 - 3x 2x + 3x = 20 - 5 5x = 15 x = 3 Vậy S = { 3 }. c/ 5y + 12 = 8y + 27 5y - 8y = 27 - 12 -3y = 15 y = - 5 Vậy S = { -5 }. d/ 13 - 2y = y - 2 -2y - y = -2 - 13 -3y = -15 y = 5. Vậy S = { 5 }.
e/ 3 + 2,25x + 2,6 = 2x + 5 + 0,4x
2,25x - 2x - 0,4x = 5 - 3 - 2,6 -0,15x = -0,6 x = 4 Vậy S = { 4 }.
f/ 5x + 3,48 - 2,35x = 5,38 - 2,9x + 10,42
5x - 2,35x + 2,9x = 5,38 - 3,48 +10,42 5,55x = 12,32 x = 1232/555. Vậy S = { 1232/555}.
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày 23
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6
Bài 4. Giải phương trình sau:
a)(2x – 1)(3x + 2) – 6x(x+5) = 1
b)(4x – 1)2 – (8x + 1)(2x – 3) = 5
Bài 5. Xác định m để phương trình sau nhận x = -3 làm nghiệm: 3x + m = x - 1
Bài 6. Giải và biện luận phương trình có chứa tham số m.
( m2- 9 ) x – m2 – 3m = 0. c) Sản phẩm:
Bài 4. a)(2x – 1)(3x + 2) – 6x(x+5) = 1
6x2 + 4x – 3x – 2 – 6x2 – 30x = 1
6x2 – 6x2 + 4x – 3x – 30x = 1 + 2 - 29x = 3 x = - 3/29 Vậy x = - 3/29
b)(4x - 1)2 - (8x + 1)(2x - 3) = 5
16x2- 8x + 1-(16x2 -24x +2x –3) = 5
16x2- 8x+ 1 -16x2 + 24x- 2x +3 = 5
16x2 -16x2 -8x +24x -2x = 5 -1- 3 14x = 1 x = 1/14 Vậy x = 1/14 Bài 5:
Thay x = -3 vào phương trình ta được: 3.(-3) + m = -3 - 1 -9 + m = -4 m = 5
Vậy với m = 5 thì x = -3 làm nghiệm: 3x + m = x – 1
Bài 6. ( m2- 9 ) x – m2 – 3m = 0.
Nếu m2 – 9 0 , tức là m 3 phương trình đã cho là phương trình bậc nhất (với ẩn
số x) có nghiệm duy nhất: 2 m + 3m m x = = 2 m − 9 m − 3
Nếu m = 3 thì phương trình có dạng 0x – 18 = 0 phương trình này vô nghiệm. 24
Nếu m = - 3, phương trình có dạng 0x + 0 = 0. mọi số thực x R đều là nghiệm của phương trình.
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
4. Hướng dẫn về nhà .
- Ôn lại kiến thức về phương trình bậc nhất một ẩn.
- Làm lại các bài tập vào vở.
- Làm bài tập. Bài 7: Giải các phương trình sau
a) 3 – 4x(25 – 2x) = 8x2 + x – 300 2(1 − 3x) 2 + 3x 3(2x + 1) b) − = 7 − 5 10 4 5x + 2 8x −1 4x + 2 c) − = − 5 6 3 5
d) 13 - 6x = 5 e) 10 + 4x = 2x − 3 f) 7 − (2x+4) = −(x+4)
g) (x−1) −(2x−1) = 9 − x
Bài 8: Giải và biện luận phương trình với tham số m.
a. m( x – 1 ) = 5 – ( m – 1 )x. b. m( x + m ) = x + 1. Ngày soạn: / /20... 25
TIẾT 13+ 14+ 15. CHỦ ĐỀ 5. GIẢI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH. Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Học sinh củng cố các bước giải bài toán bằng cách lập phương trình.
- Giải quyết một số vấn đề thực tiên gắn với phương trình bậc nhất. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Vận dụng các bước giải bài toán bài toán bằng cách lập phương trình vào các bài tập . 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 6. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 26 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Nêu các bước giải bài toán bằng cách lập phương trình?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét . 26
- Gv: Gọi HS trả lời từng câu hỏi
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 26 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Một khu vườn hình chữ nhật có chiều dài gấp 2 lần chiều rộng. Nếu tăng chiều
rộng 4 mét và giảm chiều dài 6 mét thì diện tích của khu vườn không thay đổi. Tìm chu vi của khu vườn.
Bài 2. Một khu vườn hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu tăng chiều
rộng thêm 10m và giảm chiều dài đi 5m thì diện tích tăng thêm 450m2. Tính diện tích
của khu vườn lúc đầu.
Bài 3. Một người đi xe máy từ A đến B với vân tốc 40 km/h . Lúc về, người đó đi với
vận tốc 30 km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính quãng đường AB. c) Sản phẩm:
Bài 1. Gọi chiều rộng của khu vườn lúc đầu là x (m) (đk: x > 0)
=> Chiều dài của khu vườn lúc đầu là 2x (m)
Do đó diện tích của khu vườn lúc đầu là: x.2x = 2x2 (m2)
Chiều rộng sau khi tăng là: x + 4 (m)
Chiều dài sau khi giảm là: 2x - 6 (m)
Diện tích khu vườn lúc sau là: (x + 4)(2x - 6) (m2)
Theo bài ra ta có pt: 2x2 = (x + 4)(2x - 6) 2x2 = 2x2 + 2x - 24 x = 12 (Thỏa mãn đk)
Chiều rộng của khu vườn lúc đầu là: 12m
Chiều dài của khu vườn lúc đầu là: 2.12 = 24m
Chu vi của khu vườn lúc đầu là: 2(24 + 12) = 72m
Bài 2. Gọi chiều rộng là x ( m ) điều kiện: x 0
Chiều dài là 3x (cm)
Diện tích khu vườn ban đầu là: 2 3x (cm2)
Chiều rộng sau khi tăng thêm 10m là: x + 10 (m)
Chiều dài sau khi giảm đi 5m là: 3x - 5 (m)
Theo bài ta có phương trình: (x + )( x − ) 2 10 3 5 = 3x + 450 27
Giải phương trình ta được: x = 20 ( Thỏa mãn)
Bài 3. Gọi x (km) là quãng đường AB.( ĐK : x > 0) x x Thời gian đi: (giờ) ; thời gian về: (giờ) 40 30
Vì thời gian về nhiều hơn thời gian đi là 45 phút = 3 giờ nên ta có 4 phương trình: x x 3 – = 30 40 4 4x – 3x = 90
x = 90 (Thỏa mãn điều kiện)
Vậy quãng đường AB là: 90 km
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6
Bài 4. Hiện nay tuổi của bố gấp ba lần tuổi của Nam. Biết rằng 14 năm sau thì tuổi
của bố gấp hai lần tuổi Nam. Tìm số tuổi của Nam hiện nay.
Bài 5. Một người đi xe đạp từ A đến B với vận tốc 20km/h, rồi nghỉ lại 30 phút. Sau
đó đi từ B về A với vận tốc 15 km/h. Tính quãng đường AB, biết tổng thời gian cả đi
lẫn về và nghỉ tại B hết 4 giờ.
Bài 6. Một canô xuôi dòng từ bến A đến bến B mất 6 giờ và ngược dòng từ bến B về
bến A mất 8 giờ. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc của nước chảy là 2 km/h. 28
Bài 7. Một số tự nhiên có 4 chữ số. Nếu viết thêm vào bên trái và bên phải chữ số đó
cùng chữ số 1 thì được một số có sáu chữ số gấp 21 lần số ban đầu. Tìm số tự nhiên lúc ban đầu? c) Sản phẩm:
Bài 4. Gọi tuổi của nam hiện nay là x ( tuổi) ĐK: x N *
Tuổi của bố hiện nay là 3x
Tuổi của Nam 14 năm sau là x 14
Tuổi bố 14 năm sau là 3x 14
Theo bài ta có phương trình: 3x 14 2 x 14
Giải phương trình ta được x 14( thoả mãn )
Vậy tuổi của Nam hiện nay là 14 1
Bài 5. Đổi 30 phút = (h) 2
- Gọi độ dài quãng đường AB là x (km), ĐK x > 0. x
- Thời gian đi từ A đến B là (h) 20 x
- Thời gian đi từ B về A là (h) 15 x x 1 - Theo bài ra ta có PT: + + = 4 20 15 2
Giải phương trình ta được x = 30 ( thoả mãn)
-Vậy độ dài quãng đường AB là: 30 km.
Bài 6. Gọi x(km) là khoảng cách giữa hai bến sông A và B (x > 0) Khi đó: x
Vận tốc của ca nô khi đi từ A đến B là: (km/h) 6 x
Vận tốc của ca nô khi đi từ B về A là: (km/h) 8
Vì vận tốc xuôi – vận tốc ngược = 2 lần vận tốc nước x x Nên ta có pt: - = 2.2 6 8 4x − 3x 96 = x = 96 (t/m) 24 24
Vậy: Khoảng cách giữa hai bến sông A và B là 96 km. Bài 7.
Gọi số ban đầu là x (đk x N , x > 999 ) , ta viết được x = abcd , với a, b, c, d là các chữ số, a 0.
TA CÓ: abcd = 1000a + 100b + 10c + d.
Viết thêm vào bên trái và bên phải chữ số đó cùng chữ số 1 thì được một số: 1abc 1
d = 100 000 + 10 000a + 1000b + 100c + 10d + 1
= 100 001 + 10 ( 1000a + 100b + 10c + d ) = 100 001 + 10x. 29
Theo bài ra ta có phương trình : 100 001 + x = 21x
Giải phương trình ta được x = 9091 (tmđk) .
Vậy số tự nhiên ban đầu là 9091
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
4. Hướng dẫn về nhà.
- Ôn lại kiến thức về giải bài toán bằng cách lập phương trình.
- Làm lại các bài tập vào vở và làm bài tập
Bài 8. Một xe ôtô khách đi từ địa điểm A đến địa điểm B với vận tốc 60km/h. Sau
khi nghỉ tại địa điểm B 12 phút xe khách đó quay về A với vận tốc 50km/h, thời gian
tổng cộng (từ lúc xuất phát đến lúc quay trở về địa điểm A) là 9 giờ. Tính độ dài quãng đường AB.
Bài 9. Một khu vườn hình chữ nhật có chu vi 280 m. người ta làm một lối đi xung
quanh khu vườn đó, có chiều rộng 2 m. tính các kích thước của vườn, biết rằng phần
đất còn lại trong vườn để trồng trọt là 4256m2.
Bài 10. Một phân số có tử số bé hơn mẫu số là 11. nếu tăng tử số lên 3 đơn vị và 3
giảm mẫu số đi 4 đơn vị thì được một phân số bằng . tìm phân số ban đầu. 4 30 Ngày soạn: / /20...
TIẾT 16+ 17+ 18. CHỦ ĐỀ 6: HÀM SỐ BẬC NHẤT VÀ ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Thiết lập bảng giá trị của hàm số bậc nhất.
- Vẽ đồ thị của hàm số bậc nhất. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Vận dụng hàm số bậc nhất và đồ thị của hàm số bậc nhất vào giải quyết một số bài toán thực tiễn 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 27,28 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1: Nêu khái niệm hàm sô?
Câu 2. Nêu khái niệm mặt phẳng tọa độ ? Đồ thị hàm số?
Câu 3. Nêu khái niệm hàm số bậc nhất và đồ thị hàm số bậc nhất ?
Câu 4. Nêu các bước vẽ đồ thị hàm số bậc nhất ?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện: 31
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 4 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 27,28 để giải bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3,4
Bài 1. Trong các hàm số sau, hàm số nào là hàm số nhất? Đối với những hàm số bậc
nhất đó, xác định a,b lần lượt là hệ số của x, hệ số tự do. a) y= 2x-3 b) y= x+4 c) y= 0x- 1 d) y= 4x
Bài 2. Cho hàm số y= ax + 3. Tìm a biết rằng x= 1 thì y= 5.
Bài 3. Cho hàm số y= f(x)= 2
y = f (x) = x + 4 .Tính f(1), f(-1) , f(2) , f(-2)
Bài 4. Vẽ đồ thị hàm số a) y= 2x- 4 b) y= -x+3 c) Sản phẩm
Bài 1. a) Hàm số y=2x-3 là hàm số bậc nhất có a= 2; b= -3
b) Hàm sô y= x+4 là hàm số bậc nhất có a= 1; b= 4
c) Hàm số y= 0x – 1 không phải là hàm số bậc nhất
d) Hàm số y= 4x là hàm số bậc nhất có a=4 ; b= 0
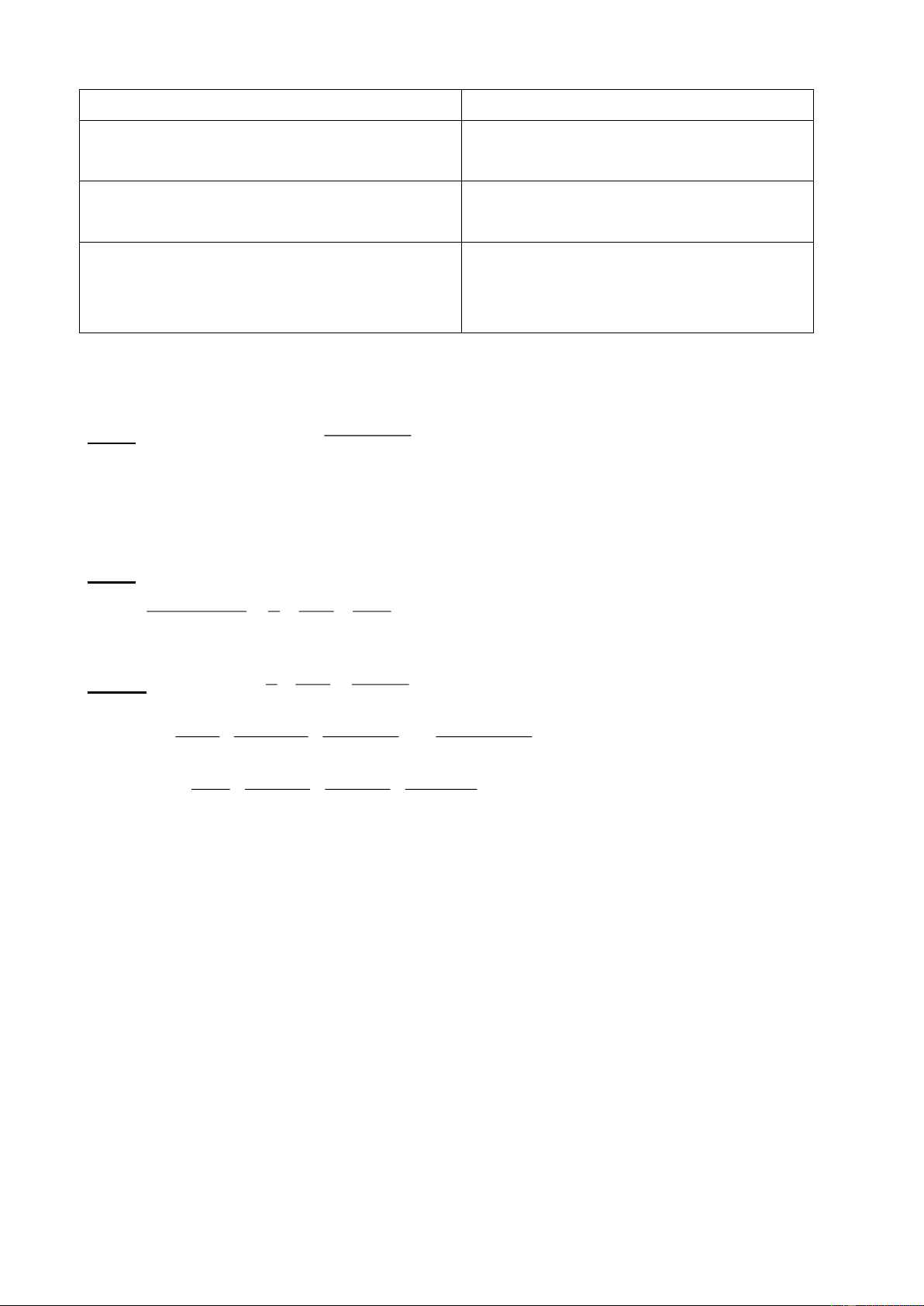
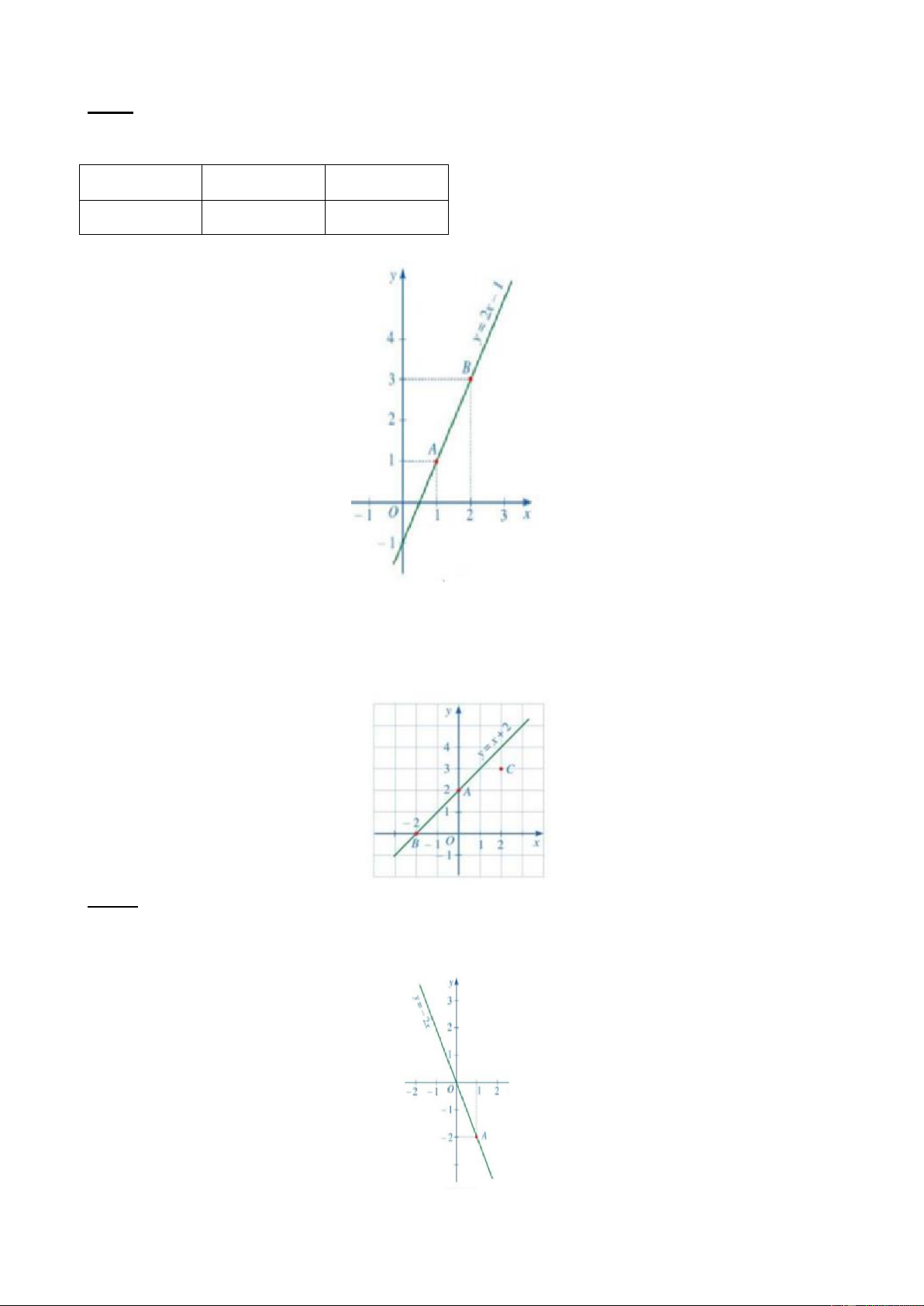
Bài 2. Với x=1 ; y= 5 ta có 5= a.1 +3 suy ra a= 2 Bài 3. Ta có f ( ) 2 1 = 1 +4=5 ; f (− ) 2 1 =(-1) +4= 5 , f (2) 2 =2 +4= 8 , f ( 2 − ) 2 = ( 2 − ) + 4 = 8 32 Bài 4. a) y= 2x- 4 Với x= 0 thì y= -4 Với y=0 thì x= 2
Đồ thị hàm số y= 2x- 4 là đường thẳng
đi qua 2 điểm M(0;-4) và N(2;0 )
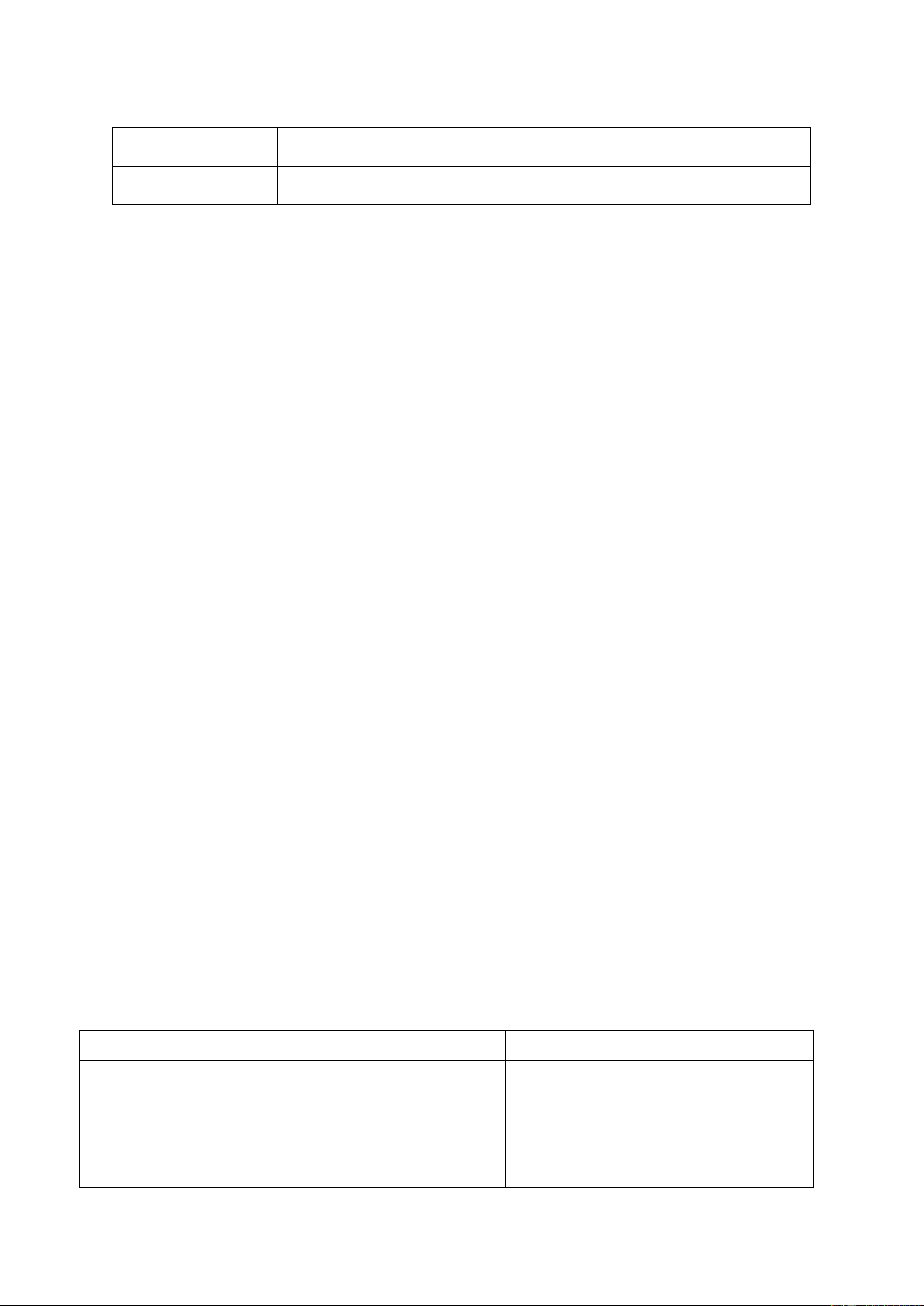
b) Với đồ thị hàm số y= -x +3 cho x=0 thì y= 3 cho y=0 thì x= 3
Đồ thị hàm số y= -x+ 3 là đường thẳng
đi qua hai điểm P(0;3) và Q(3:0)
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 5,6,7
Bài 5. Vẽ đồ thị hàm số sau: a) y= 2x- 3 b) y= -3x +4
Bài 6. a) Tìm giá trị của m để đồ thị hàm số y 3x m đi qua điểm ( A 1;2) .
b) Tìm giá trị của tham số m để đồ thị hàm số y x m đi qua điểm ( B 0;3)
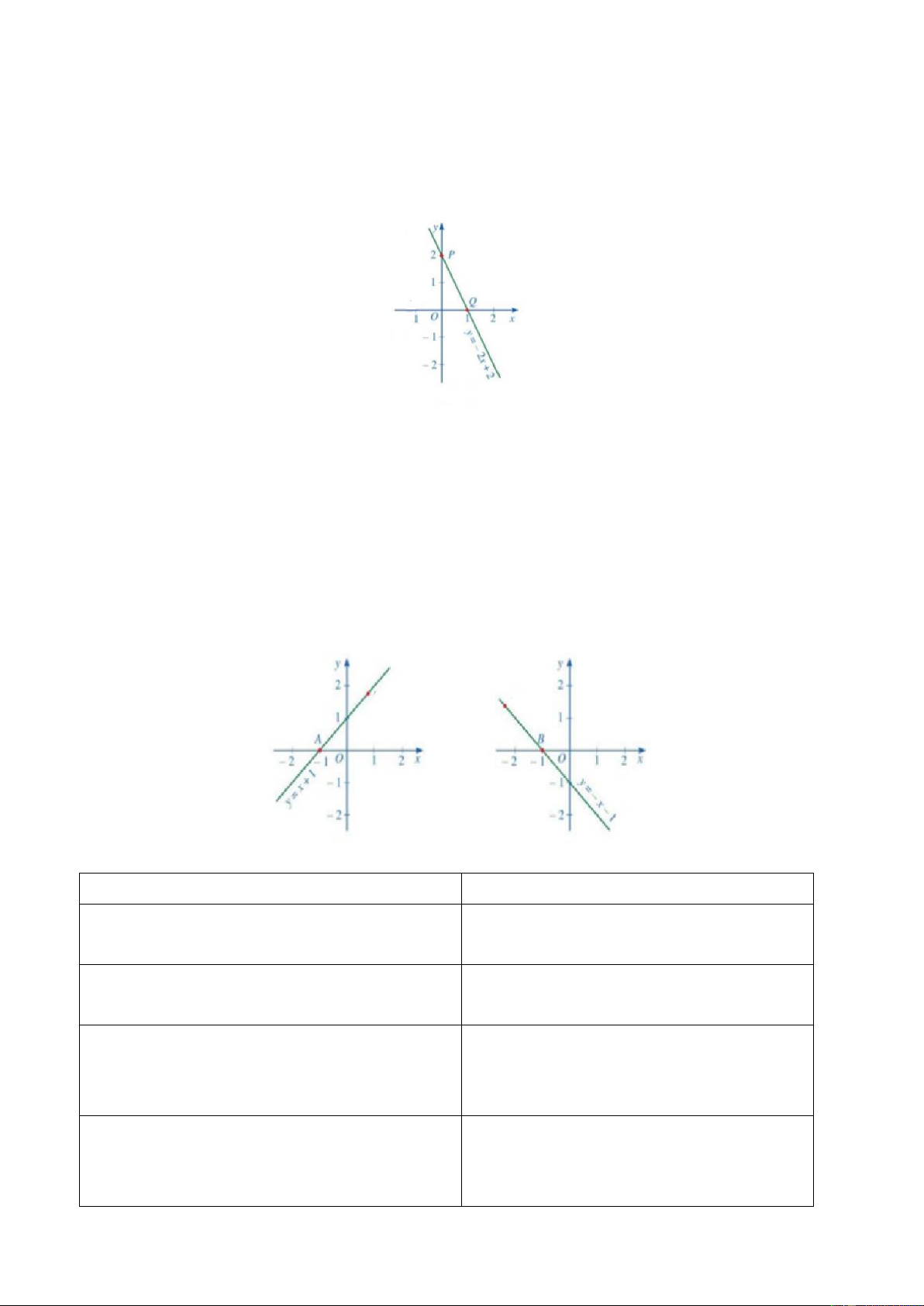
Bài 7. Vẽ đồ thị hàm số a) y= 2x-1 b) y= x+2 33
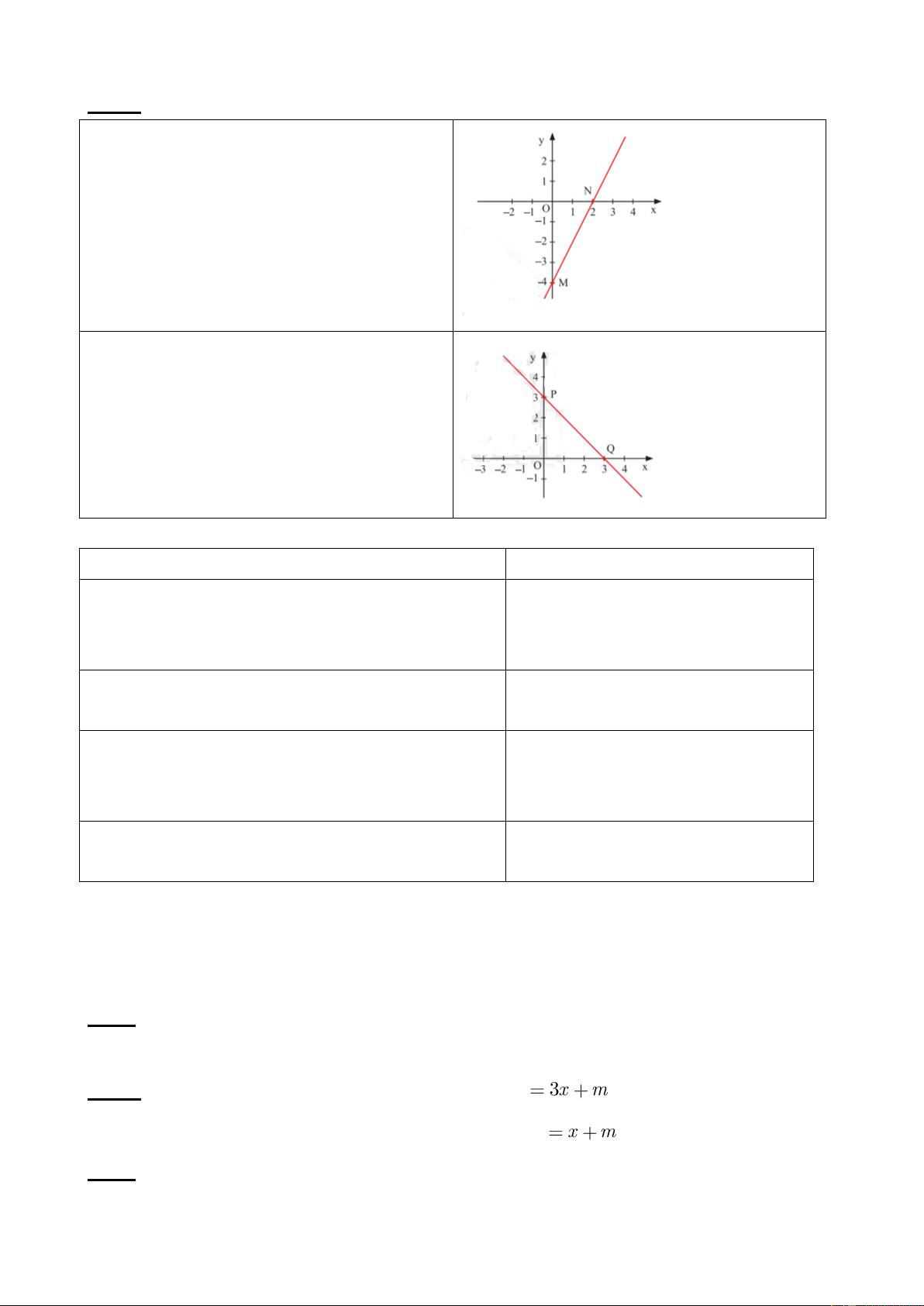
Bài 8.vẽ đồ thị các hàm số sau: a) y=-2x b) y= -2x+2 c) y=x+1 d) y= -x-1 c) Sản phẩm: Bài 5. a) 3 x 0 2 y 3 0 3 Đồ thị hàm số y 2x
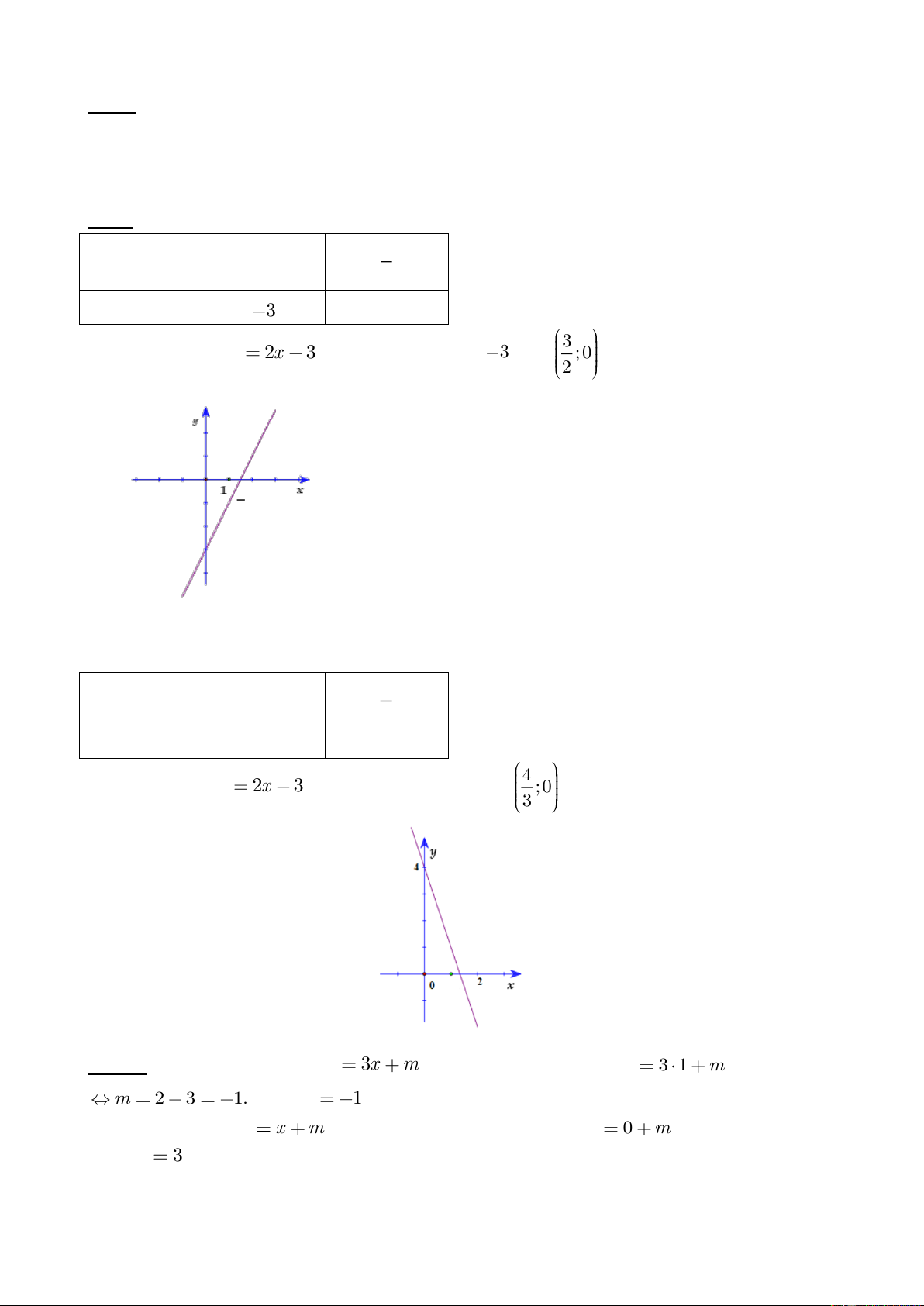
3 đi qua 2 điểm 0; 3 và ;0 2 3 0 2 -3 b) 4 x 0 3 y 4 0 Đồ 4 thị hàm số y 2x
3 đi qua 2 điểm 0;4 và ;0 3
Bài 6. a) Để đồ thị hàm số y 3x m đi qua điểm ( A 1;2) thì 2 3 1 m m 2 3 1. Vậy m 1.
b) Đồ thị hàm số y x m đi qua điểm ( B 0;3) nên ta có 3 0 m . Vậy m
3 là giá trị cần tìm. 34 Bài 7. a) Ta có bảng sau: x 1 2 y=2x-1 1 3 b) y=x+ 2 Với x= 0 thì y= 2 Với y=0 thì x= -2
Đồ thị hàm số y= x+2 là đường thẳng đi qua 2 điểm A(0;2) và B(-2;0) Bài 8.
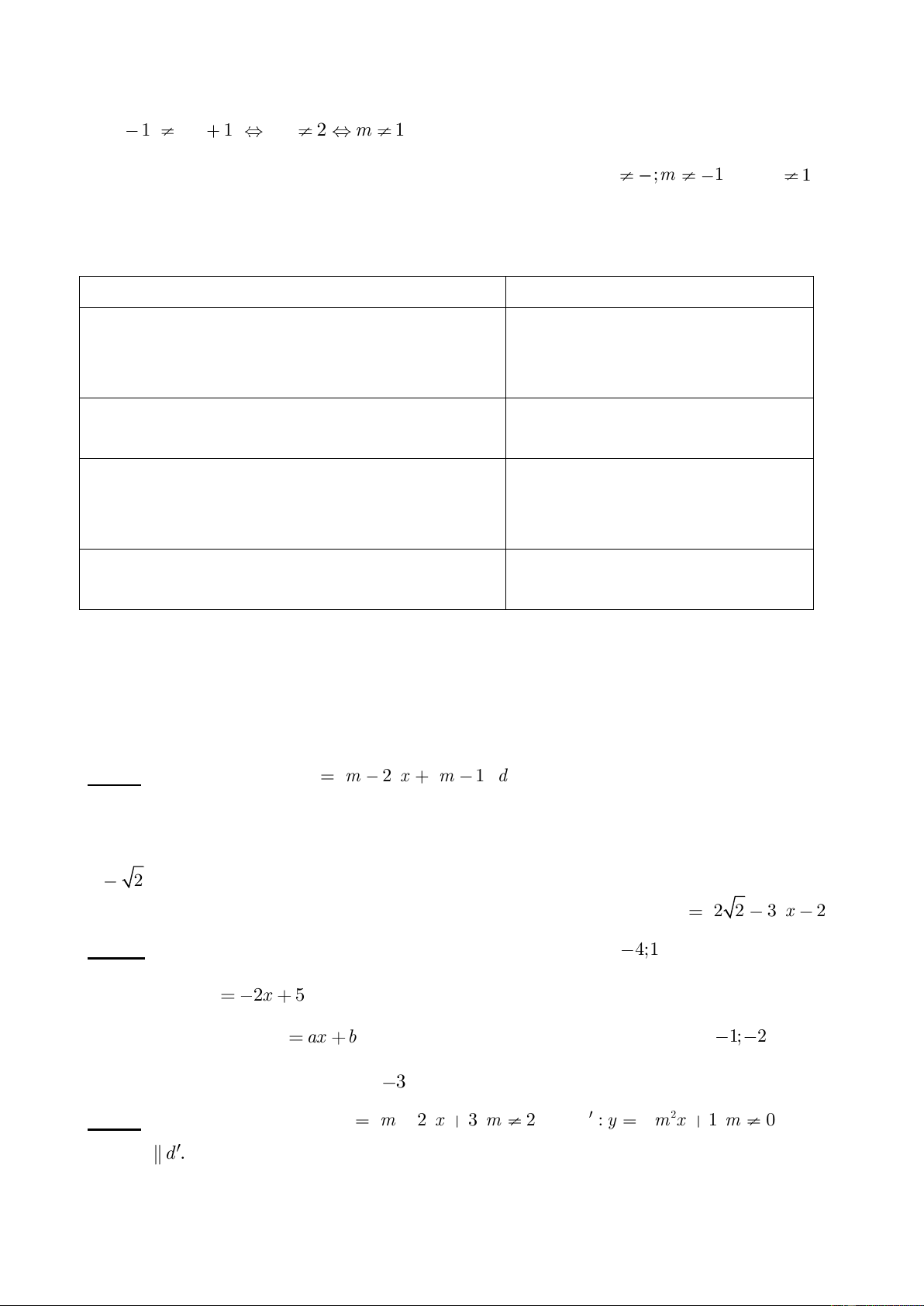
Với x= 0 thì y=0 Với x=1 thì y= -1
Đồ thị hàm số y= -2x là đường thẳng đi qua điểm O(0,0) và A(1,-2) 35 b) y= -2x +2 Với x= 0 thì y=2 Với y=0 thì x= 1
Đồ thị hàm số y= -2x +2 là đường thẳng đi qua hai điểm P(0;2) và Q(1;0) c) y= x+ 1 Với x=0 thì y=1 Với y=0 thì x=-1
Đồ thị hàm số y= x+1 là đường thẳng đi qua 2 điểm (0;1) và (-1;0) d) y= -x -1 Với x= 0 thì y= -1 Với y=0 thì x= -1
Đồ thị hàm số y= -x-1 là đường thẳng đi qua 2 điểm (0;-1) và (-1;0)
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 36 3. Hướng dẫn về nhà.
- Ôn lại kiến thức về hàm số bậc nhất và cách vẽ đồ thị hàm số bậc nhất.
- Làm lại các bài tập vào vở. - Làm bài tập :
Bài 9. Cho các hàm số sau, những hàm số nào là hàm số bậc nhất ? Hãy xác định hệ số a, b của chúng.
a) y= 0.x -5 b) y= 1-3x c) y= -0,6 x
d) y= 2.(x −1) + 3 e) y=2x2+1
Bài 10. Vẽ đồ thị các hàm số sau: a) y= -x+2 b) y= 2x+2 c) y= 3x -1 d) y= -x-2 37 Ngày soạn:
TIẾT 19+ 20+ 21. CHỦ ĐỀ 7: HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Nhận biết khái niệm hệ số góc của đường thẳng y= ax + b ( a 0 )
- Sử dụng hệ số góc của các đường thẳng để nhận biết và giải thích sự cắt nhau,
trùng nhau hoặc song song của hai đường thẳng cho trước. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Áp dụng kiến thức vào giải bài tập . 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 29 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu ĐN hệ số góc của đường thẳng ?
Câu 2. Dấu hiệu nhận biết hai đường thẳng cắt nhau, song song , trùng nhau?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ 38
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 2HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 29 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc a= 2 và đi qua điểm A(1;5)
Bài 2. Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là 3 và cắt trục
tung tại điểm có tung độ bằng -1
Bài 3. Tìm giá trị của m để đường thẳng y= (m-2)x + 2 ( m 2 ) song song với đường thẳng y= -2x+1
Bài 4. Cho hai hàm số y 3m 1 x 2 và y m 1 x 7 (với m là tham số).
Tìm giá trị của m để hai hàm số trên là hàm bậc nhất và đồ thị của chúng là hai đường thẳng cắt nhau. c) Sản phẩm
Bài 1. Hàm số bậc nhất cần tìm có dạng y= 2x+ b
Vì đường thẳng đi qua điểm A(1;5) nên ta có: 5= 2.1+b suy ra b= 3
Vậy hàm số cần tìm là y= 2x+3 Bài 2.
Vì a= 3 nên hàm số bậc nhất có dạng y= 3x+ b
Vì đường thẳng cắt trục tung tại điểm có tung độ bằng -1 nên x=0; y= -1 Ta có : 1= 3.0+b suy ra b= 1
Vây hàm số cần tìm là y= 3x+1
Bài 3. Hai đường thẳng đã cho song song với nhau khi m-2= -2 suy ra m=0 thỏa mã
điều kiện m 2 . Vậy giá trị m cần tìm là m= 0
Bài 4. Các hàm số đã cho là hàm số bậc nhất khi và chỉ khi: 1 3m 1 0 m 3 m 1 0 m 1 39
Đồ thị của hai hàm số đã cho là hai đường thẳng cắt nhau khi và chỉ khi: 3m 1 m 1 2m 2 m 1 1
Vậy các giá trị của m thoả mãn đồng thời các điều kiện m ;m 1 và m 1 là 3 giá trị cần tìm
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 5,6,7
Bài 5. Cho đường thẳng y m 2 x m 1 d
a) Tìm giá trị của m để đường thẳng d đi qua góc tọa độ.
b) Tìm giá trị của m để đường thẳng d cắt trục hoành tại điểm có tung độ bằng 3 2 .
c) Tìm giá trị của m để đường thẳng d song song với đường thẳng y 2 2 3 x 2 .
Bài 6. a) Viết phương trình đường thẳng đi qua điểm A 4;1 và song song với đường thẳng y 2x 5.
b) Xác định hàm số y ax b biết rằng đồ thị của nó đi qua điểm B 1; 2 và cắt
trục Oy tại điểm có tung độ bằng 3 .
Bài 7.Cho 2 đường thẳng d : y m 2 x 3 m 2 và 2 d : y m x 1 m 0 .Tìm m để d d . 40 c) Sản phẩm:
Bài 5. a) Đường thẳng d đi qua gốc tọa độ O khi m 1 0 hay m 1. Khi đó hàm số là y x
b) Để đường thẳng d cắt trục hoành tại điểm có tung độ bằng 3 2 thì m 1 3 2 hay m 4 2
c) Để đường thẳng d cắt trục hoành tại điểm có tung độ bằng 3 2 thì m 2 2 2 3 và m 1 2 m 2 2 1 và m 1 m 2 2 1 Khi đó hàm số y 2 2 3 x 2 2 2
Bài 6. a) Phương trình đường thẳng song song với đường thẳng y 2x 5 có dạng : y 2x b b 5 d .
Vì d đi qua điểm A 4;1 nên 2. 4 b 1 b
7 (thoã mãn điều kiện b 5).
Vậy phương trình đường thẳng cần tìm là y 2x 7 .
b) Vì đồ thị của hàm số y ax b luôn đi qua điểm B 1; 2 nên ta có : a b
2 (1). Vì đồ thị của hàm số y ax
b cắt trục Oy tại điểm có tung độ bằng 3 nên ta có : b 3 (2).
Từ (1) và (2) suy ra : a 1;b 3 y x 3 . Bài 7. 2 m 2 m d d 3 1 m 1 2 m m 2 0 . m 2
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 41
4. Hướng dẫn về nhà.- Ôn lại cách về hệ số góc của đường thẳng và dấu hiệu nhận
biết 2 đường thẳng cắt nhau, song song và trùng nhau.
- Làm lại các bài tập vào vở.
- Làm bài tập : Bài 8. Cho hàm số y m 1 x m 3 .
a) Tìm giá trị của m để đồ thị của hàm số song song với đồ thị hàm số y 2x 1 .
b) Tìm giá trị của m để đồ thị của hàm số đi qua điểm 1; 4 .
c) Tìm điểm cố định mà đồ thị của hàm số luôn đi qua với mọi m.
LG. a) Hàm số y m 1 x m
3 có đồ thị song song với đồ thị của hàm số m 1 2 y 2x 1 m 1 m 3 1 b) Hàm số y m 1 x m
3 có đồ thị đi qua điểm có tọa độ 1; 4 4 m 1 m 3 m 3
c) Gọi M x ;y là một điểm thuộc đồ thị của hàm số y m 1 x m 3 0 0 Điểm M cố định y m 1 x m 3 đúng với mọi m. 0 0 m x 1 x y 3 0 đúng với mọi m. 0 0 0 x 1 0 x 1 0 0 x y 3 0 y 4 0 0 0
Như vậy ta có điểm cố định cần tìm là M 1;4 . 1
Bài 9: Cho đường thẳng d : y 2m 1 x 2m 3 với m 1 2 d : y m 1 x m với m 1 2
Tìm giá trị của m để:
a) d cắt d b) d song song với d c) d vuông góc với d 1 2 1 2 1 2
Bài 10 : Viết phương trình đường thẳng d trong các trường hợp sau:
a) d đi qua điểm A nằm trên Ox có hoành độ bằng – 3 và song song với đường thẳng d : y 5x 4 1 1
b) d vuông góc với đường thẳng d : y x
2018 và đi qua giao điểm của 2 2 d : y x 3 với trục tung 3
Bài 11: Viết phương trình đường thẳng d trong các trường hợp sau: a) Cắt d : y x
4 tại một điểm nằm trên trục Ox và cắt d : y 5x 3 tại một điểm 1 2 nằm trên trục Oy
b) Đi qua điểm M 2; 3 và chắn trên hai trục tọa độ những đoạn bằng nhau.
Bài 12: Cho đường thẳng d có phương trình là y mx m 1 .
Chứng tỏ rằng khi m thay đổi thì đường thẳng d luôn đi qua một điểm cố định. Tìm điểm cố định ấy. 42 Ngày soạn: / /20...
TIẾT 22+ 23+ 24. CHỦ ĐỀ : 8 CÁCH TÍNH XÁC SUẤT CỦA BIẾN CỐ BẰNG TỈ SỐ Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Tính xác suất bằng tỉ số kết quả thuận lợi cho cho biến cố và số kết quả có thể trong
trường hợp các kết quả có thể là đồng khả năng. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Áp dụng kiến thức vào giải bài tập các bài tập thực tế. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm, ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 30,31 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu cách tính xác suất bằng tỉ số ?
Câu 2. Việc tính xác suất của một biến cố E trong một hành động hay thực nghiệm
đồng khả năng sẽ gồm những bước nào ?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà . 43
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 2HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 30,31 để giải bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Viết ngẫu nhiên một số tự nhiên có hai chữ số: a)
Tìm số phần tử của tập hợp D gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra. b)
Tìm xác suất của biến cố “Số tự nhiên được viết ra là bội của 9”
Bài 2. Một hộp có 52 cái thẻ cùng loại, mỗi thẻ được ghi một trong các số 1,2,3..,52
hai thẻ khác nhau thì ghi 2 số khác nhau. 44
Rút ngẫu nhiên một thẻ trong hộp . Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số có chữ số tận cùng bằng 5”
b) “Số xuất hiện trên thẻ được rút ra là số có hai chữ số”
c) “Số xuất hiện trên thẻ được rút ra là số có có 2 chữ số với tích các chữ số bằng 6”
Bài 3. Viết ngẫu nhiên một số tự nhiên có ba chữ số:
a) Có bao nhiêu cách viết ngẫu nhiên một số tự nhiên như vậy
b) Tính xác suất của mỗi biến cố sau:
- “Số tự nhiên được viết ra là lập phương của một số tự nhiên”
- “Số tự nhiên được viết ra là số chia hết cho 10” c) Sản phẩm
Bài 1. Tâp hợp gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là: D = 10;11;...;
99 số phần tử của D là 90
a) Các kết quả thuận lợi của biến cố “Số tự nhiên được viết ra là bội của 9” là:
18,27,...,99. Do đó có 10 kết quả thuận lợi của biến cố đó. Vì thế xác suất của biến 10 1 cố là: = 90 9 Bài 2.
a) Các kết quả thuận của biến cố “Số xuất hiện trên thẻ được rút ra là số có chữ số
tận cùng bằng 5” là: 5,15,25,35,45 có 5 kết quả thuận lợi .Xác suất của biến cố đó là 5 : 52
b) Các kết quả thuận của biến cố “Số xuất hiện trên thẻ được rút ra là số có hai chữ
số” là: 10, 11,12,13,...,52 có 43 kết quả thuận lợi .Xác suất của biến cố đó là : 43 52
c) Các kết quả thuận của biến cố “Số xuất hiện trên thẻ được rút ra là số có có 2 chữ
số với tích các chữ số bằng 6” là: 16, 61,23,32 có 4 kết quả thuận lợi .Xác suất của biến cố đó là : 4 1 = 52 13 Bài 3.
a) Các số tự nhiên có 3 chữ số là: 100,101,...999 có tất cả 900 số
b) Các kết quả thuận của biến cố “Số tự nhiên được viết ra là lập phương của một
số tự nhiên” là: 5,6 7,8,9 có 5 kết quả thuận lợi .Xác suất của biến cố đó là 5 1 : = 900 180 45
- Các kết quả thuận của biến cố “Số tự nhiên được viết ra là số chia hết cho 10” là:
100,110,120,...990 có 90 kết quả thuận lợi .Xác suất của biến cố đó là : 90 1 = 900 10
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6
Bài 4. Bạn An thực hiện gieo một con xúc xắc.
a) Liệt kê các kết quả có thể của thực nghiệm trên.
b) Liện kê các kết quả thuận lợi và tính xác suất cho các biến cố sau:
- A “ Số chấm xuất hiện trên con xúc xắc là số chẵn”
- B “ Số chấm xuất hiện trên con xúc xắc là số nguyên tố”
- C “ Số chấm xuất hiện trên con xúc xắc là số lớn hơn 3”
Bài 5. Một hộp đựng 20 tấm thẻ ghi số 1,2,..,20. Bạn Nam rút ngẫu nhiên một tấm thẻ
từ trong hộp .Tính xác suất của biến cố sau: a)
A “Rút được tấm thẻ ghi số chẵn” b)
B “Rút được tấm thẻ ghi số nguyên tố” c)
C “Rút được tấm thẻ ghi số chính phương”
Bài 6. Một túi đựng các viên bị giống hệt nhau chỉ khác màu, trong đó có 12 viên bi
màu xanh, 10 viên bi màu đỏ và 8 viên bi màu trắng. Bạn Nam lấy ngẫu nhiên một
viên bi trong túi. Tính xác suất của các biến cố sau:
a) A “ Nam lấy được viên bi màu xanh”
b) B “ Nam lấy được viên bi màu đỏ ” 46
c) C “ Nam lấy được viên bi màu trắng”
d) D “ Nam lấy được viên bi màu xanh hoặc màu đỏ”
e) E “ Nam không lấy được viên bi màu xanh” c) Sản phẩm: Bài 4.
a) Các kết quả của thực nghiệm là : 1,2,3,4,5,6 có 6 kết quả .
b) - Các kết quả thuận lợi của biến cố A “ Số chấm xuất hiện trên con xúc xắc là số
chẵn” là: 2,4,6 có 3 kết quả thận lợi .Do đó 3 1 P( ) A = = 6 2
- Các kết quả thuận lợi của biến cố B “ Số chấm xuất hiện trên con xúc xắc là số
nguyên tố” là: 2,3,5 có 3 kết quả thận lợi .Do đó 3 1 P(B) = = 6 2
-Các kết quả thuận lợi của biến C “ Số chấm xuất hiện trên con xúc xắc là số lớn hơn
2” là: 3, 4, 5, 6 có 4 kết quả thuận lợi .Do đó 4 2 P(C) = = 6 3 Bài 5. a.
Các kết quả thuận lợi của biến cố A “Rút được tấm thẻ ghi số chẵn” là: 2, 4, 10 1
6,...,20 có 10 kết quả thuận lợi . P( ) A = = 20 2 b.
Các kết quả thuận lợi của biến cố B “Rút được tấm thẻ ghi số nguyên tố” 7
là: 2,3,5,7,11,13,19 có 7 kết quả thuận lợi . P(B) = 20
c. Các kết quả thuận lợi của biến cố C “Rút được tấm thẻ ghi số chính phương” 4 1
là: 1,4,9,16 Có 4 kết quả thuận lợi . P(C) = = 20 5 12 2
Bài 6. a) Có 12 kết quả thuận lợi của biến cố A. Vậy P( ) A = = 30 5 10 1
b) Có 10 kết quả thuận lợi của biến cố B. Vậy P(B) = = 30 3 8 4
c) Có 8 kết quả thuận lợi của biến cố C. Vậy P(C) = = 30 15 22 11
d) Có 22 kết quả thuận lợi của biến cố D. Vậy P(D) = = 30 15 18 3
e) Có 18 kết quả thuận lợi của biến cố E. Vậy P(E) = = 30 5
d) Tổ chức thực hiện: 47
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
3. Hướng dẫn về nhà.
- Ôn lại cách tính xác suất bằng tỉ số.
- Làm lại các bài tập vào vở.
- Làm bài tập : Bài 7. Chọn ngẫu nhiên một số có hai chữ số. Tính xác xuất của các biến cố sau:
a) A “ Số được chọn nhỏ hơn 30”
b) B “ Số được chọn nhỏ hơn 30”
Bài 8. Trong một phòng có 20 bạn học sinh lớp 8A gồm 8 bạn nam, 12 bạn nữ và 20
bạn lớp 8B gồm 15 nữ , 5 nam. Chọn ngẫu nhiên 1 học sinh trong phòng. Tính xác
suất của các biến cố sau:
a) A “ Chọn một học sinh nam”
b) B “ Chọn một học sinh nam lớp 8B”
c) C “ Chọn một học sinh nữ lớp 8A” 48 Ngày soạn: / /20...
TIẾT 25+26+27. CHỦ ĐỀ 9: MỐI LIÊN HỆ GIỮA XÁC SUẤT THỰC
NGHIỆM VỚI XÁC SUẤT VÀ ỨNG DỤNG Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Tính xác suất thực nghiệm trong một số ví dụ có tình huống thực tế
- Ước lượng xác suất của một biến cố bằng xác suất thực nghiệm.
- Ứng dụng trong một số bài toán đơn giản. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm- Năng lực
giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Vận dụng kiến thức để giải bài tập. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 32 để giải toán thành thạo. 49
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu xác suất thực nghiệm của biến cố E?
Câu 2. Nêu mối quan hệ giữa xác suất thực nghiệm và xác suất ?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
Câu 1. Giả sử trong n lần thực nghiệm hoặc n lần theo dõi ( quan sát) một hiện
tượng ta thấy biến cố E xảy ra k lần. Khi đó xác xuất thực nghiệm của biến cố E bằng
k , tức là bằng tỉ số giữa số lần xuất hiện của biến cố E và số lần thực hiện thực n
nghiệm hoặc theo dõi hiện tượng đó.
Câu 2. Xác suất của biến cố E được ước lượng bằng xác suất thực nghiệm của k E: P(E)
trong đó n là số lần thực nghiệm hay theo dõi một hiện tượng, k là số lần n biến cố E xảy ra.
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 2 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 32 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Kiểm tra ngẫu nhiên 1000 chiếc ô tô do nhà máy X sản xuất thì có 2 chiếc
không đạt chất lượng. Hãy tính ước lượng xác suất của biến cố A: “một ô tô của nhà
máy X sản xuất không đạt chất lượng”
Bài 2. Trong 500 trẻ sơ sinh chào đời ở tỉnh X người ta thấy 240 bé gái. Hãy tính
ước lượng của xác xuất của biến cố E “Trẻ sơ sinh là bé trai”
Bài 3. Hai bạn An và Bình lần lượt thực hiện việc gieo đồng thời hai con xúc xắc và
mỗi lần gieo sẽ nhận được số điểm bằng tổng số chấm xuất hiện trên hai con xúc xắc. 50
An gieo 50 lần và Bình được gieo 60 lần. An gieo trước và ghi lại kết quả của mình như sau: Sổ điểm 1 2 3 4 5 6 7 8 9 10 11 12 Số lần 2 5 1 6 2 3 4 5 3 4 8 7
Trước khi Bình gieo, hãy dự đoán xem có bao nhiêu lần điểm của Bình nhận được là: a) Một số chẵn b) Một số nguyên tố c) Một số lớn hơn 8 c) Sản phẩm
Bài 1. Trong 1000 lần quan sát ta thấy biến cố A xảy ra 2 lần Do đó xác suấ 2
t thực nghiệm của biến cố A là: = 0,002 = 0,2% 1000
Vậy xác suất của biến cố A được ước lượng là 0,2%
Bài 2. Trong 500 trẻ sơ sinh có số bé trai là: 500-240= 260 bé trai 260
Xác suất thực nghiệm của biến cố E là: P(E) = = 0,52 = 52% 500
Xác suất của biến cố E được ước lượng là 52%.
Bài 3. a) Xác suất thực nghiệm của biến cố “ số điểm nhận được của An là một số chẵn” là :
5 + 6 + 3 + 5 + 4 + 7 = 0,6 = 60% 50
Dự đoán số lần điểm của Bình nhận được là một số chẵn: 60%.60= 36 ( lần)
b) Xác suất thực nghiệm của biến cố “ số điểm nhận được của An là một số nguyên tố” là :
5 +1+ 2 + 5 + 4 + 8 = 0,4 = 40% 50
Dự đoán số lần điểm của Bình nhận được là một số nguyên tố: 40%.60= 24 ( lần)
c) Xác suất thực nghiệm của biến cố “ số điểm nhận được của An là lớn hơn 8” là : 3 + 4 + 8 + 7 = 0,44 = 44% 50
Dự đoán số lần điểm của Bình nhận được là một số lớn hơn 8 là: 44%.60= 28 ( lần)
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc. 51
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5, 6, 7
Bài 4. Thống kê điểm kiểm tra học kì I môn toán của một nhóm 150 học sinh lớp 8
được chọn ngẫu nhiên tại 5 lớp của trường THCS A, thu được kết quả như bảng sau: Số điểm 1 2 3 4 5 6 7 8 9 10
Số học sinh 10 12 16 20 18 15 20 15 11 13
a) Chọn ngẫu nhiên một học sinh của trường A. Hãy tính xác suất thực nghiệm của các biến cố sau:
• A “ Học sinh đó có điểm nhỏ hơn hoặc bằng 5”
• B “ Học sinh đó có điểm từ 8 đến 10”
b) Hãy dự đoán trong nhóm 100 học sinh lớp 8 chọn ngẫu nhiên từu năm lớp khác nhau của trường A:
• Có bao nhiêu học sinh có điểm không vượt quá 5
• Có bao nhiêu học sinh có điểm từ 8 đến 10
Bài 5. Thống kê số vụ tai nạn giao thông trong hai tháng 3 và 4 của thành phố X
được cho kết quả như bảng sau: Số vụ tai nạn giao 0 1 2 3 4 5 6 7 8 thông xảy ra trong một ngày Số ngày 5 6 16 8 10 7 3 3 2
Từ bảng thống kê trên, hãy dự đoán xem trong bốn tháng 5,6,7 ,8 tới của Thành phố X:
a) Có bao nhiêu ngày có nhiều nhất 3 vụ tai nạn giao thông.
b) Có bao nhiêu ngày có ít nhất 5 vụ tai nạn giao thông 52 c) Sản phẩm:
Bài 4. a) Tổng số học sinh có điểm nhỏ hơn hoặc 5 là: 10+12+16+20+18= 56 (hs) 56
Xác suất thực nghiệm của biến cố A là P( ) A = 0,37(3) 37% 150
Tổng số học sinh có điểm từ 8 đến 10 là : 15+11+13=39 (hs) 39
Xác suất thực nghiệm của biến cố B là P(B) = 0, 26 = 26% 150
b) Số học sinh có điểm không vượt quá 5 là: 37%.100= 37 hs
Số học sinh có điểm từ 8 đến 10 là: 26%. 100= 26 ( học sinh) Bài 5.
a) Xác suất thực nghiệm của biến cố “ Số ngày có nhiều nhất 3 vụ tai nạn giao thông” (5 + 6 +16 + 8) 7 là: = 60 12
Trong bốn tháng 5, 6, 7, 8 tới Thành phố có số ngày nhiều nhất 3 vụ tai nạn giao 7 thông là: .120 = 70 (ngày) 12
b) Xác suất thực nghiệm của biến cố “ Số ngày có ít nhất 5 vụ tai nạn giao thông” là: (7 + 3 + 3 + 2) 1 = 60 4
Trong bốn tháng 5, 6, 7, 8 tới Thành phố X có số ngày nhiều nhất 3 vụ tai nạn giao 1
thông là: .120 = 30 (ngày ) 4
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 3. Hướng dẫn về nhà.
- Ôn lại cách Tính xác suất thực nghiệm trong một số ví dụ có tình huống thực tế
- Làm lại các bài tập vào vở. 53 - Làm bài tập :
Bài 6. Một nhà máy sản xuất laptop tiến hành kiểm tra chất lượng của 2000 chiếc
laptop được sản xuất và thấy có 10 chiếc bị lỗi . Trong một lô hàng 6000 chiếc
laptop . Hãy dự đoán xem có khoảng bao nhiêu chiếc laptop không bị lỗi .
Bài 7. Bảng sau đây thống kê kết quả khảo sát số người thích một bộ phim mới tại 5
quận A, B, C, D của thành phố X Số người khảo sát
Số người thích bộ phim mới Quận Nam Nữ Nam Nữ A 40 45 12 15 B 38 49 13 18 C 30 32 10 9 D 27 25 9 7 E 45 42 13 12 Tổng số 180 192 57 61
a) Chọn ngẫu nhiên một người ở quận A. Ước lượng xác suất của biến cố:
A: “Người được chọn thích bộ phim đó”
b) Chọn ngẫu nhiên một người ở quận E. Ước lượng xác suất của biến cố: B “Người
được chọn không thích bộ phim đó”
c) Chọn ngẫu nhiên 800 người ở thành phố X. Ước lượng trong đó có bao nhiêu
người thích bộ phim đó?
d) Chọn ngẫu nhiên 600 người nữ ở thành phố X. Ước lượng trong đó có bao nhiêu
người thích bộ phim đó? 54 Ngày soạn: / /20...
TIẾT 28+29+ 30. CHỦ ĐỀ 10: BA TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Nắm được ba trường hợp đồng dạng của tam giác
- Áp dụng ba trường hợp đồng dạng của tam giác để giải bài tập. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Áp dụng kiến thức để giải bài tập. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 33, 34 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu định nghĩa hai tam giác đồng dạng?
Câu 2. Nêu định lý trường hợp đặp biệt của hai tam giác?
Câu 3. Nêu ba trường hợp đồng dạng của tam giác ? 55
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 3 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 33,34 để giải bài tập liên quan
từ cơ bản đến nâng cao.
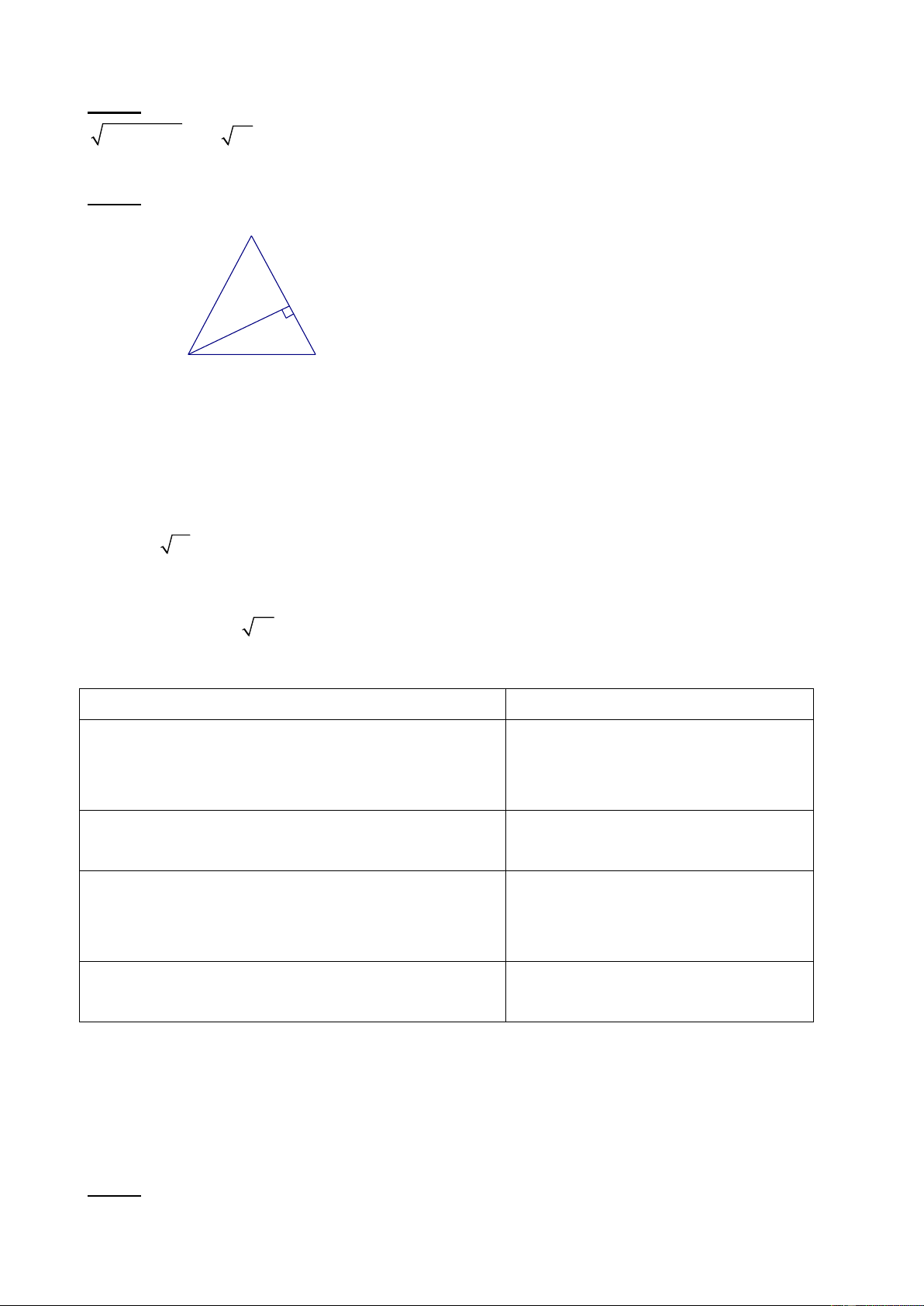
b) Nội dung: Làm bài tập 1,2,3 Bài 1: Cho hình vẽ A
a) ABC có đồng dạng với DEF hay D không? 9 6 4 6
b) Tính tỉ số chu vi của hai tam giác B 12 C E 8 F
Bài 2: Cho tam giác ABC có độ dài các A
cạnh tỉ lệ với 4, 5, 6. Cho biết: D D FE∽ A
CB và cạnh nhỏ nhất của D
EF là 0,8cm. Tính độ dài các cạnh B C E còn lại của F D EF .
Bài 3. Cho tam giác ABC đồng dạng với tam giác A' B 'C ' . Cho biết
AB = 6cm, BC =10cm CA =14cm và chu vi tam giác A' B 'C ' bằng 45cm. Tính độ dài
các cạnh của tam giác A' B 'C ' . c) Sản phẩm Bài 1. 56 AB AC BC 3 a) Ta có: = = = A BC∽ D
EF ( .c .cc) DF DE EF 2 C
AB + BC + CA 6 + 9 +12 27 3 b) ABC = = = = C
DE + EF + FD 4 + 6 + 8 18 2 DEF Bài 2. Vì D EF∽ A BC nên D
EF cũng có độ dài các cạnh tỉ lệ với 4, 5, 6
Giải sử DE EF DF DE = 0,8cm
Vì ba cạnh của tam giác ABC có độ dài tỉ lệ với 4, 5, 6 nên ta có: DE EF FD = =
= 0,2 EF =1(cm); FD =1,2(cm) 4 5 6 Bài 3. AB BC CA
AB + BC + CA 2 Ta có: A BC∽ A ' B 'C ' = = = = A' B ' B 'C ' C ' A'
A' B '+ B 'C '+ C ' A' 3
A'B' = 9c ,
m B 'C ' = 15c ,
m A'C ' = 21c . m
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6
Bài 4: Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi , P , Q R lần lượt
là trung điểm của các đoạn thẳng O , A O , B OC . a) Chứng minh: P QR∽ A BC
b) Cho biết ABC có chu vi bằng 543cm. Tính chu vi PQR 57
Bài 5. Cho tam giác ABC có các cạnh AB = 24cm AC = 28c .
m Đường phân giác góc A
cắt cạnh BC tại D . Gọi M , N lần lượt là hình chiếu của các điểm , B C trên đường thẳng AD . BM a) Tính tỉ số CN AM DM b) Chứng minh = AN DN
Bài 6. Cho tam giác ABC có AC = 8c ,
m AC =16cm . Gọi D và E là hai điểm lần lượt
trên cạnh AB và AC sao cho BD = 2c , m CE =13c . m Chứng minh rằng a. A EB∽ A DC
b. AED = ABC , cho DE = 5cm . Tính BC ? c. A . E AC = A . D AB
Bài 7. Cho hình vuông ABCD . Trên cạnh BC lấy điểm E , tia AE cắt đường thẳng
CD tại M , tia DE cắt đường thẳng AB tại N , Chứng minh rằng: a) N BC∽ B CM
b) BM ⊥ CN c) Sản phẩm: Bài 4. AB BC CA
AB + BC + CA 2 Ta có: A BC∽ A ' B 'C ' = = = = A' B ' B 'C ' C ' A'
A' B '+ B 'C '+ C ' A' 3
A'B' = 9c ,
m B 'C ' = 15c ,
m A'C ' = 21c . m Bài 5. BM BD AB a) Ta có: BM CN (⊥ AD) 6 / / B MD∽ C ND = = = CN CD AC 7 AM DN BM b) A BM ∽ A
CN ( .cg.c) = = AN DM CN Bài 6. A 3 1 6 13 2 B C 58 a. A EB∽ A DC( . c g.c) AE AB 1
b) Xét AED và ABC , có: = = và A: chung AD AC 2 AED ∽ ABC ( .
c g.c) AED = ABC AE AD c. Vì A ED∽ A BC =
AE.AC = A . B AD AB AC BN BE BN BE
Bài 7. a. Xét E
DC , có: BN / /CD = = (1) CD EC BC EC AB BE BC BE Xét E
CN , có: AB / /CM = = (2) CM EC CM EC BN BC Từ (1)(2) 0 =
; B = C = 90 NB C ∽ B CM ( . c g.c) BC CM b. 0 0 0 NBC ∽ B
CM C = M ,C + C = 90 C + M = 90 CHM = 90 1 1 2 2
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 3. Hướng dẫn về nhà.
- Ôn lại cách thực hiện phép cộng và phép trừ hai đa thức , tính chất của phép cộng đa thức
- Làm lại các bài tập vào vở. - Làm bài tập : 59
Bài 8: Cho tứ giác ABCD có AB = 3cm , A 3 B
BC =10cm , CD =12cm , AD = 5cm, đường
chéo BD = 6cm . Chứng minh rằng: 10 5 a. A BD∽ B CD 6
b. ABCD là hình thang. D 12 C
Bài 9: Cho tam giác ABC cân tại A và M là trung
điểm của cạnh đáy BC . Một điểm D thay đổi trên A
cạnh AB . Lấy một điểm E trên cạnh AC sao cho 2 MB CE = . Chứng minh: BD E a. D BM ∽ M CE I 2 D 1 2 b. D
ME đồng dạng với hai tam giác trên 1 H 2
c. DM là phân giác của BDE , EM là phân giác của 3 1 B M C CED
d. Khoảng cách từ M đến DE không đổi khi D thay đổi trên AB Lời giải 2 a) Ta có: MB CE MB CE MC CE = = =
; B = C D BM ∽ M CE( . c g.c) BD MB BD MB BD CM BD MB BD b) D BM ∽ M CE = = ME DM ME DM B = M 2 Xét D BM và D ME , có: D BM ∽ D ME( .
c g.c) D BM ∽ M CE∽ D ME BM BD = ME DM c. D BM ∽ D
ME D = D DM là phân giác BDE 1 2 DM E ∽ M
CE E = E EM là phân giác DEC 2 1
d. Từ M kẻ MH ⊥ AC, MI ⊥ DE 60
Ta có M nằm trên phân giác của CED MI = MH , mà MH không đổi.
Vậy MI không đổi khi D thay đổi trên AB . Ngày soạn: / /20...
TIẾT 31+32+33 . CHỦ ĐỀ 11: BA TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Củng cố kiến thức về ba trường hợp đồng dạng của tam giác. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Thực hiện các phép tính cộng, trừ hai đa thức
- Vận dụng các tính chất của phép cộng đa thức trong tính toán. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: Luyện tập 61
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 26 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1: Cho tam giác ABC có AB = 6c ,
m AC = 9cm , D A
thuộc AC sao cho ABD = C . Tính AD ? D B C
Bài 2: Cho tam giác ABC có AB AC . Đường phân A
giác AD . Lấy điểm E trên cạnh AC sao cho 2 1 CED = BAC E
a. Tìm tam giác đồng dạng với ABC
b. Chứng minh rằng DE = DB B D C
Bài 3: Cho ABC có AM là phân giác BAC (M BC ) . A
Kẻ tia Cx thuộc nửa mặt phẳng bờ BC không chứa A 1
sao cho BCx = BAC. Gọi N là giao điểm của Cx và 2 tia AM . Chứng minh: 2 a) BM.MC = MN.MA B 1 C M b) A BM ∽ A NC c) Tam giác BCN cân N c) Sản phẩm.
Bài 1. Xét ABD và AC , B có: A:chung AB BD AD ABD ∽ AC
B(g.g) = = AD = 4cm ABD = C AC CB AB DE DC
Bài 2. a) Ta có: A BC∽ D
EC(g.g) = (1) AB AC DC AC DC DB b. Xét ABC , có: A = A = = (2) 1 2 DB AB AC AB 62 DE DB Từ (1)(2) =
DE = DB (đpcm). AB AB Bài 3.
a) Xét BAM và NCM , có:
BAM = MCN; M = M BA M ∽ N
CM (g.g) BM.MC = MN.MA 1 2
b) Từ câu a ABM = CNM A BM ∽ A
NC (g.g ) BM MN c) Từ câu a ta lại có: = B MN ∽ A MC ( . c g.c) MA CA 1
NBM = CAM = BAC 2
Có: NBM = BCN đpcm.
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6
Bài 4: Cho hình chữ nhật ABCD , kẻ DH ⊥ AC H . A B N Gọi 1
M , N, K lần lượt là trung điểm của BC, AH, DH H
a. Tứ giác MNCK là hình gì? M 2 b. Chứng minh A DN∽ D CK K 1 c. DN ⊥ MN D C 63
Bài 5: Cho hình bình hành ABCD , qua D kẻ đường N
thẳng cắt AC, A ,
B BC lần lượt tại I , M , N . Chứng minh rằng: a. A ID∽ C IN b. A DM ∽ C ND A M B
c. AM.CN = A . B AC I 1 d. 2
DI = IN.IM (khó) D C
Bài 6: Cho tam giác ABC ( AB AC ) , phân giác AM . A
Ở miền ngoài tam giác vẽ tia Cx sao cho BCx = BAD .
Gọi N là giao điểm của Cx và AM . Chứng minh rằng: M B C a. BM.MC = MN.MA b. A BM ∽ A CN N c. B CN cân d. 2 AM = A . B AC − M . B MC c) Sản phẩm:
Bài 4. a) Ta có KN // MC, KN = MC M
NKC là hình bình hành AD AH b) Ta có A DH ∽ D
CH(g.g) = CD DH AD AN 1 1 = AN = NH =
AH , DK = HK = DH CD DK 2 2 A = D 1 1
c) Cách 1: Chứng minh H là trực tâm của tam giác
D = N (slt) N = C Cách 2: 2 1 1 1
DN ⊥ MN D = C
KNM = KCM (hbh) 2 1 Bài 5. a) ta có: A ID∽ C
IN(g.g) b) AD M ∽ C
ND(g.g)(DAN = CND, N = D) AI AM AI AD c) I
CD, có: AM / /CD = (Hệ quả ThaLes) mà: = ( A ID∽ CI N) IC CD IC CN 64 AD AM Vậy: =
AM.CN = A . D DC = A . B BC CN DC ID AD d) Xét C
IN , có: AD //CN = (3) IN CN IM AM AD AM Xét A
DM , có: AM // DC = (4) . Mà A DM ∽ CND = (5) ID CD CN CD ID IM Từ (3)(4)(5) 2 =
ID = IM.IN IN ID Bài 6. a. B AM ∽ N
CM(g − g) BM.MC = MN.MA
b) Từ câu a ABM = CNM ABM ∽ AN C(g.g) BM MN c. Từ câu a, có: = B MN ∽ A MC( . c g.c) MA CM BM MN 1 = B MN ∽ A MC( .
c g.c) NBM = CAM =
BAC NBM = BCN MA CM 2 AM AB d. A MB∽ A
CN(g − g) =
AM.AN = A . B AC(1) AC AN AM MB A MB∽ CM
N (g − g) =
AM.AN = M . B MC(2) CM MN
Trừ từng vế của (1) và (2) ta được: 2
AM(AN − NM) = AB.AC − MB.MC AM = AB.AC − MB.MC
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 3. Hướng dẫn về nhà.
- Ôn lại các trường hợp đồng dạng của tam giác .
- Làm lại các bài tập vào vở. 65 - Làm bài tập :
Bài 7: Cho tam giác ABC có các đường cao BE, CF. Chứng minh:
a) AB.AF = AC.AE b) AEF = ABC .
Bài 8. Cho tam giác ABC vuông tại A có AB > AC, M là điểm tùy ý trên cạnh BC.
Qua M kẻ Mx ⊥ BC và cắt đoạn AB tại I, cắt tia CA tại D a) Chứng minh ABC MDC. BI BC b) Chứng minh = BM BA
c) CI cắt BD tại K. Chứng minh BI.BA + CI.CK không phụ thuộc vị trí điểm M HD giải C M K D I A B x c) B
IC có IM và CA là 2 đường cao cắt nhau tại D do đó BD cũng là đường cao
mà BD cắt IC tại K do đó BK ⊥ IC nên 0 CKB = 90 Khi đó C IM C BK (g.g) CI CM = (2 cạnh t/ư) CB CK
CI.CK = CM.CB(2) Từ (1) và (2) BI.BA + CI.CK = BM.BC + CM.BC = BC.(BM + CM) = BC2
Vậy BI.BA + CI.CK không phụ thuộc vào vị trí của M 66 Ngày soạn: / /20...
TIẾT 34+35+36. CHỦ ĐỀ 12: ĐỊNH LÝ PYTATHAGORE VÀ ỨNG DỤNG Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Giải thích định lý Pythagore
- Củng cố kiến thức về Định lý Pythagore.
- Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lý Pythagore
- Giải quyết một số vấn đề trong thực tiễn gắn với việc vận dụng định lý Pythagore 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Vận dụng Định lý Pythagore để giải các bài tập. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT 67
a) Mục tiêu: Hs được củng cố kiến thức bài 24,25 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Phát biểu định lý Pythagore (thuận và đảo ) ?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời câu hỏi
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 35 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. a) cho tam giác ABC có hai cạnh góc vuông là AB= 4cm , AC= 3cm . Tính
độ dài cạnh huyền BC của tam giác vuông đó
b) Cho tam giác MNP vuông tại M có NP= 10cm, MN= 6cm. Tính MP
Bài 2. Một chiếc tivi màn hình phẳng có chiều rộng và chiều dài lần lượt là 72 cm và
120 cm. Tính độ dài đường chéo của ti vi theo đơn vị inch ( biết 1 inch 2, 54 cm)
Bài 3. Cho tam giác ABC cân ở A. Kẻ BH vuông góc với AC. Biết AH = 3cm, HC =
2cm. Tính độ dài cạnh BC. c) Sản phẩm Bài 1.
a) Áp dụng định lý Pythagore vào tam giác vuông ABC ta có: 2 2 2 2 2
BC = AB + AC = 4 + 3 = 25 Suy ra BC= 5 cm
b) Áp dụng định lý Pythagore vào tam giác MNP vuông ta có: 2 2 2
NP = MN + MP 2 2 2 2 2
MP = NP − MN =10 − 6 = 64 MP = 8cm 68
Bài 2. Áp dụng định lý Pythagore độ dài đường chéo của ti vi là: 2 2
120 + 72 = 24 34(cm) 55(inch) Bài 3. A 3 H 2 B C
Vì H AC nên AC = AH + HC = 3 + 2 = 5 (cm).
Tam giác ABC cân ở A (gt) nên AB = AC = 5 cm.
Áp dụng định lý Py-ta-go vào tam giác vuông AHB (vuông tại H), ta có: 2 2 2
AB = AH + HB 2 2 2 2 2
AH = AB − AH = 5 − 3 = 16 AH = 16 = 4(cm)
Áp dụng định lý Py-ta-go vào tam giác vuông BHC (vuông tại H), ta có: 2 2 2 2 2
BC = HC + HB = 2 + 4 = 20 BC = 20(cm)
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6,7
Bài 4: Cho tam giác ABC vuông ở A có AB = 6cm, AC = 8cm. 69
a) Tính độ dài cạnh BC;
b) Kẻ AH vuông góc với BC ( H BC ). Biết AH = 4,8 cm. Tính độ dài các đoạn BH, CH.
Bài 5. Cho tam giác ABC vuông ở A có AC = 20cm. Kẻ AH vuông góc với BC
( H BC ). Biết BH = 9cm, HC = 16cm. Tính AB, AH
Bài 6. Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC ( H BC ). Tính chu vi tam
giác ABC, biết AB = 5cm, AH = 4cm, HC = 12 cm.
Bài 7. Có tam giác nào là tam giác vuông trong số các tam giác có độ dài ba cạnh như sau không?
a) 15cm, 8cm, 18cm. b) 21dm, 20dm, 29dm. c) 5m, 6m, 8m. c) Sản phẩm: Bài 4. A 8 6 4,8 B H C
a) Vì tam giác ABC vuông ở A (gt) nên theo định lý Pythagore ta có: 2 2 2 2 2
BC = AB + AC = 6 + 8 = 100 BC = 100 =10(cm)
b) Vì AH ⊥ BC(gt) nên tam giác AHB vuông tại H. Theo định lý Pythagore, ta có: 2 2 2
AB = AH + BH 2 2 2 2 2
BH = AB − AH = 6 − 4,8 = 12,96
BH = 12,96 = 3,6(cm)
Vì H BC (gt) nên BC = BH + HC, do đó HC = BC – BH = 10 – 3,6 = 6,4 (cm) Bài 5. A 20 B 9 H 16 C
Vì H BC BC = BH + HC = 9 + 16 = 25 (cm).
Tam giác ABC vuông ở A (gt) nên theo định lý Py-ta-go, ta có: 2 2 2
BC = AB + AC 2 2 2 2 2
AB = BC − AC = 25 − 20 = 225 AB = 225 = 15(cm)
Áp dụng định lý Py-ta-go vào tam giác vuông AHC (vuông tại H), ta có: 2 2 2
AC = AH + HC 2 2 2 2 2
AH = AC − HC = 20 −16 = 144
AH = 144 = 12(cm) 70 Bài 6. A 5 4 H B 12 C
Tam giác AHB vuông ở H (gt) nên theo định lý Py-ta-go, ta có: 2 2 2
AB = AH + BH 2 2 2 2 2
BH = AB − AH = 5 − 4 = 9 BH = 9 = 3(cm)
Áp dụng định lý Py-ta-go vào tam giác vuông AHC (vuông tại H), ta có: 2 2 2 2 2
AC = AH + HC = 4 +12 = 160 AC = 160(cm)
Bài 7. a) Ta có: 182 = 324; 152 + 82 = 225 + 64 = 289 2 2 2
18 15 +8 (vì 324 289)
Nên tam giác đã cho không là tam giác vuông.
b) Ta có: 292 = 881; 212 + 202 = 441 + 400 = 881 2 2 2 29 = 21 + 20 (= 881)
Nên theo định lý Pythagore đảo thì tam giác đã cho là tam giác vuông. c) a) Ta có:
82 = 64; 52 + 62 = 25 + 36 = 61 2 2 2
8 5 + 6 (vì 64 61)
Nên tam giác đã cho không là tam giác vuông.
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 3. Hướng dẫn về nhà.
- Ôn lại Định lý Pythagore
- Làm lại các bài tập vào vở. - Làm bài tập : 71
Bài 8. Cho tam giác ABC vuông tại A
a) Tính độ dài BC nếu AB= 7cm, AC= 24 cm
b) Tính AB biết AC= 5 cm, BC= 13 m
c) Tính AC biết BC= 15 cm, AB= 9 cm
Bài 9. Chứng minh rằng tam giác ABC vuông trong các trường hợp sau
a) AB= 8cm, AC= 15 cm, BC= 17 cm
b) AB= 29 cm, AC= 21 cm, BC= 20 cm
c) AB= 12cm, AC= 37 cm, BC= 35 cm
Bài 10. Một con thuyền neo ở một điểm cách chân tháp hải đăng 180m. Cho biết
tháp hải đăng cao 25 m. hãy tính khoảng cách từ truyền đến ngọn hải đăng 72 Ngày soạn: / /20...
TIẾT 37+38+39. CHỦ ĐỀ 13: CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC VUÔNG. Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Giải thích các trường hợp đồng dạng của tam giác vuông
- Giải quyết một số vấn đề thực tiễn gắn với việc vận dụng các tam giác. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Vận dụng kiến thức để chứng minh hai tam giác đồng dạng. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 36 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu các trường hợp đồng dạng của tam giác ?
Câu 2. Nêu các trường hợp đồng dạng của tam giác vuông ? 73
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 2 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 26 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
bằng góc nhọn của tam giác vuông kia.
Bài 1: Cho tam giác ABC vuông tại A , đường cao AH a. Cho HB = 9c ,
m HC =16cm . Tính AH, A , B AC b. Chứng minh rằng: 2 AH = H . B HC ; 2 AB = B . C BH
Bài 2. Cho tam giác ABC vuông tại A (AB < AC), 0
ACB = 30 . Kẻ đường cao AD. a) Chứng minh B
AD đồng dạng với B
CA; từ đó suy ra 2 AB = B . D B . C
b) Cho BD = 2 cm; BC = 32 cm. Tính AD.
c) Tia phân giác của ABC cắt AC tại E. Chứng minh: 2 AB = A . E AC.
Bài 3. Cho tam giác ABC nhọn. Kẻ các đường cao BD và CE cắt nhau tại H .
a) Chứng minh AD AC = AE AB . b) Chứng minh A DE∽ A BC . c) Chứng minh 2
BH BD + CH CE = BC . c) Sản phẩm. Bài 1. A 20 15 12 B 9 H 16 C 74 a) Xét A HB và C HA, có: 0 H = H = 90 1 2 A HB∽ 2 C
HA AH = CH.BH AH =12(c ) m ABH = CAH b) Ta có: 2 A BH ∽ C B
A (g.g) AB = C . B CH Bài 2. A E C F D B
a) Xét BAD và BCA có: 0
BAC = BDA = 90 (gt) ABC là góc chung Suy ra: B AD∽ B CA (g-g) Do đó: AB BD 2 = AB = B .B D C BC AB
b) Ta có: BD = 2cm; BC = 32 cm 2 AB = B .B D C Theo phần a: 2 AB = 2.32 AB = 8(cm)
Áp dụng định lí Pythagore vào tam giác ABD 2 2 2
AB = BD + AD 2 2 AD = 8 − 2 AD = 60(cm)
Vậy AD = 60(cm) ABC c) 0 EBA = EBC = = 30 2 Xét BAE và CAB có: 0 EAB = BAC = 90 0 EBA = BCA = 30 75 Suy ra: B AE∽ C AB (g-g) Do đó: AB AC 2 =
AB = AC.AE AE AB Bài 3. A D E H B F C
a) Xét hai tam giác vuông ADB và AEC có A chung ABD
ACE ( cùng phụ với A) AD AB A DB∽ A EC (g.g), =
AD AC = AE AB . AE AC AD AE
b) Từ kết quả câu a) = AB AC
Xét hai tam goác ADE và ABC có A AD AE chung và = A DE∽ A BC (c.g.c). AB AC b)
Gọi H là giao của AH và BC. AH cắt BC tại F thì AF ⊥ BC . B HF và B
CD là hai tam giác vuông có chung DBC nên B HF∽ B CD (g.g),
tương tự ta cũng có C HF ∽ C
BE (g.g), từ đó ta có BH BD = BF BC và
CH CE = CF CB . Vậy 2
BH BD + CH CE = BC .
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động 76
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5
Bài 4. Cho tam giác ABC vuông tại A, có AH là đường cao.
a) Chứng minh ABC đồng dạng với HBA. 2 b) Chứng minh AH = BH.CH .
c) Gọi D và E thứ tự là trung điểm của AH và CH. Chứng minh S BH DAB = S CH ECA d) Chứng minh BD ⊥ AE.
Bài 5. Cho tam giác ABC vuông tại A . Đường cao AE, phân giác BD
(E BC, D AC) . F là giao điểm của AE và BD. Hãy chứng minh: a) A BC∽ A E C b) B .
D EF = BF.AD . c) Sản phẩm: Bài 4. A _ D _ B C // // H E
a) Xét ABC và HBA có: 0
BAC = BHA = 90 (gt) ABC là góc chung
Suy ra: ABC ∽ HBA(g-g)
b) Xét HBA và HAC có: 0
BHA = AHC = 90 ( AH là đường cao)
HBA = HAC (cùng phụ với góc ACB)
Suy ra: HBA ∽ HAC(g-g) 77 Do đó: AH BH 2 =
AH = BH.CH CH AH 2 2 S BH BH
c) Vì HBA ∽ HAC (cm ở câu b) => HAB = = . 2 S AH AH HCA 2 S BH BH
Theo câu b: AH2 = BH.CH => HAB = = S BH.CH CH HCA
Vì AD = DH (gt) => 2AD = AH => SABH = 2.SABD
Tương tự vì HE = CE => 2.SACE = SHCA => S BH DBA = (ĐPCM) S CH ECA
d) Có DBA ∽ EAC nên DBA = EAC Suy ra: 0
DBA + BAE = EAC + BAE = BAC = 90 Nên BD ⊥ AE Bài 5. B E F A C D a) Xét ABC và A E C có: 0 BAC = E A C = 90 C chung A BC∽ A E C ( g - g) b) Xét BAD và BEF có: 0 BAD = E B F = 90 A D B
= EBF ( vì BD là phân giác của B ) B D A ∽ E B F( g - g) D B AD = D
B .EF=AD.BF BF EF
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp. 78
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 3. Hướng dẫn về nhà.
- Ôn lại các trường hợp đồng dạng của tam giác vuông.
- Làm lại các bài tập vào vở và làm bài tập
Bài 6: Cho tam giác ABC vuông tại A N có AB = 6c , m AC = 8c .
m Lấy điểm M trên cạnh AC sao cho AM = A . B Kẻ ME ⊥ BC = . E
a) Chứng minh CM.CA = C . E C . B A
b) Tia BA và tia EM cắt nhau tại N ,
đường thẳng BM cắt CN tại F . Chứng F M minh A MB∽ F
MC và tam giác ACN B E C vuông cân.
c) Tính tỉ số diện tích của hai tam giác
BFN và tam giác MFC . Hướng dẫn b) Ta có A MB∽ F
MC (g.g ) , mà A
MB vuông cân F MC vuông cân 0 FCM = 45 A
NC vuông tại A có 0 ANC = 45 A NC vuông cân. 2 c) B NF ∽ F MC (gg) S BN BFN = = 49. S CM MFC 79 Ngày soạn: / /20...
TIẾT 40+41+42. CHỦ ĐỀ 14: CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC VUÔNG. Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Giải thích các trường hợp đồng dạng của tam giác vuông
- Giải quyết một số vấn đề thực tiễn gắn với việc vận dụng các tam giác. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Vận dụng kiến thức để chứng minh hai tam giác đồng dạng. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 26 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3 80
Bài 1. Cho ABC vuông tại A, có AB = 12 cm ; AC = 16 cm. Kẻ đường cao AH (HBC).
a) Chứng minh: HBA ∽ ABC
b) Tính độ dài các đoạn thẳng BC, AH.
c) Trong ABC kẻ phân giác AD (DBC). Trong ADB kẻ phân giác DE EA DB FC
(EAB); trong ADC kẻ phân giác DF (FAC). Chứng minh rằng: =1 EB DC FA
Bài 2. Cho tam giác ABC vuông tại A và có đường cao AH.
a) Chứng minh rằng: HBA ∽ ABC
b) Gọi M; N lần lượt là trung điểm của BC và AB. Qua B vẽ đường thẳng vuông góc
với BC cắt MN tại I. Chứng minh rằng: IB2 = IM.IN
c) Gọi O là giao điểm của IC và AH. Chứng minh rằng: O là trung điểm của AH C) Sản phẩm Bài 1. A F E B H D C
a) Xét HBA và ABC có: 0 AHB = BAC = 90 ; ABC chung
Suy ra : HBA ∽ ABC (g.g)
b) Áp dụng định lí Pytago trong tam giác ABC ta có: 2 2 2
BC = AB + AC = 2 2 2 12 +16 = 20 BC = 20 cm
Ta có HBA ∽ ABC (Câu a) AB AH = 12 AH = BC AC 20 16 12.16 AH = = 9,6 cm 20 EA DA c) =
(vì DE là tia phân giác của ADB ) EB DB FC DC =
(vì DF là tia phân giác của ADC ) FA DA EA FC DA DC DC = = (1) EB FA DB DA DB EA FC DB DC DB DB (1) = EA DB FC =1 (nhân 2 vế với ) EB FA DC DB DC EB DC FA DC Bài 2. 81 D A I O N C B H M
a) Xét ∆HBA và ∆ABC ta có: góc B chung góc BHA = góc BAC = 900
HBA ∽ ABC (g.g)
b) MN là đường trung bình của ∆ABC => MN // AC mà AB ⊥ AC=> MN ⊥ AB
Xét ∆NIB và ∆BIM ta có: BIM là góc chung 0 INB = IBM = 90
=> ∆NIB ∽∆BIM (g. g) IB IN => = => IB2 = IM.IN IM IB
c) Gọi D là giao điểm của BI và CA
∆BCD có MB = MC ; MI//CD => IB = ID (1) ∆CIB có OH//IB => OH CO = (2) IB CI ∆CID có OA//ID => OA CO = (3) ID CI
Từ (1), (2) và (3) suy ra OH = OA => O là trung điểm của AH
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
2. Hoạt động 2: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 3,4 82
Bài 3. Cho ABC vuông tại A, có AB = 15cm, AC = 20cm. Kẻ đường cao AH và trung tuyến AM. a) Tính BC, AH; b) Tính BH, CH;
c) Tính diện tích tam giác AHM.
Bài 4. Cho tam giác ABC vuông ở A, đường cao AH.
• Chứng minh: ABC đồng dạng với HBA.
• Cho AB = 6 cm, BC = 10 cm. Tính HB.
• Vẽ HE ⊥ AB (E AB), HF ⊥ AC (F AC). Chứng minh: AE.AB = AF.AC.
Bài 5: Cho hình chữ nhật ABCD . Kẻ D C
DE vuông góc với AC tại E . Gọi P
M , N, P lần lượt là trung điểm của
BC, AE và DE . Chứng minh: E M AD AE a. = N DC DE b. A ND∽ D PC A B c. ND ⊥ NM c) Sản phẩm: Bài 3. A B H M C
a) Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 152 + 202 = 625 Suy ra: BC = 25cm
Lại có: AH.BC = AB.AC = 2S ABC 83 AB.AC 15.20 Nên AH = = = 12(cm) BC 25
b)Xét hai tam giác ABH và CBA có góc B chung; 0 BAC = AHB = 90 BH AB nên ABH ∽ C BA (g.g), suy ra = BA BC 2 2 Do đó BH = AB 15 = = 9(cm) . BC 25
Vì vậy CH = BC – BH = 25 – 9 = 16 (cm). BC c) HM = BM – BH = - BH = 12,5 – 9 = 3,5(cm) 2 1 1 2 S
= AH.HM = .12.3,5 = 21(cm ) AHM 2 2 Bài 4. A F 6 E B C H 10 S
Chứng minh ABC ∽ HBA (g.g) Nên được AB2 = BH.BC 2 2 AB 6 HB = = = 3,6 (cm) BC 10
Nên được AH2 = AE.AB và AH2 = AF.BC AE.AB = AF.AC. Bài 5. A : chung a) Xét A DE và A CD, có: A DE∽ A
CD(g.g) 0
AED = ADC = 90 AE DE AE AD AN b) Ta có: A DE∽ A CD = = = AD CD DE DC DP
Chứng minh được: A ND∽ D NC( . c g. ) c
c) P là trực tâm tam giác CDN CP ⊥ DN(1)
Tứ giác MNPC là hình bình hành MN / /PC(2) MN ⊥ DN
d) Tổ chức thực hiện: 84
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 3. Hướng dẫn về nhà.
- Ôn lại cách thực hiện phép cộng và phép trừ hai đa thức , tính chất của phép cộng đa thức
- Làm lại các bài tập vào vở. - Làm bài tập :
Bài 6: Cho tam giác ABC cân tại A , A
gọi H là trung điểm của BC . Vẽ HE
vuông góc với AC , gọi O là trung điểm
của HE . Vẽ BK vuông góc với AC, BE K
cắt AO tại I I E a. Chứng minh: A HE∽ B CK O b. Chứng minh: A .
E EK = BK.OE B H C
c. Chứng minh: OA ⊥ BE Lời giải a) Xét A HE và B CK , có: 0
AEH = BKC = 90 ; HAE = CBK A
HE∽BCK ( g.g) AE HE OE b) Ta có: A HE∽ B
CK (g.g) = = BK CK EK AE BK = A EO∽ B KE ( . c g.c) EO KE c) Theo câu b, có: 85 0 A EO∽ B KE( .
c g.c) EBK = EAI ; KBE + EBK = 90 0
KEB + EAI = 90 Ngày soạn: / /20...
TIẾT 43+44+45. CHỦ ĐỀ 15: HÌNH CHÓP TAM GIÁC ĐỀU Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Mô tả đỉnh, cạnh bên, mặt bên, mặt đáy của hình chóp tam giác.
- Tạo lập hình chóp tam giác đều
- Tính diện tính xung quanh và thể tích của hình chóp tam giác đều.
- Giải quyết một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh
của hình chóp tam giác đều. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Tính thể tích, diện tích xung quanh của hình chóp tam giác đều. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 86 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 38 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu công thức tính diện tích xung quanh của hình chóp tam giác đều ?
Câu 2. Nêu công thức tính thể tích của hình hóp tam giác đều ?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà .
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 2 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 38 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Tính diện tích xung quanh của hình chóp tam giác đều S.ABC biết SH= 8cm, AC= 6cm 87
Bài 2. Tính diện tích xung quanh của hình chóp tam giác đều S.MNP biết SP= 13 cm, IP= 5 cm
Bài 3. Tính thể tích của hình chóp tam giác đều S.ABC, biết cạnh đáy bằng 8 cm, chiều cao 12 cm. c) Sản phẩm Bài 1.
Nửa chu vi đáy của hình chóp tam giác đều S.ABC là: 1 P= .(6 + 6 + 6) = 9 ( cm) 2
Trung đoạn của hình chóp tam giác đều là d= SH= 8cm
Diện tích xung quanh của hình chóp đều S.ABC là: S = 9.8 = 72 (cm2) xp Bài 2.
Tam giác SMP cân có SI ⊥ MP nên SI là đường trung tuyến của tam giác SMN suy ra MN= 2.MP= 2.5= 10 cm
Nửa chu vi đáy của hình chóp tam giác đều S.MNP là: 1 P= .(10 +10 +10) = 15 ( cm) 2
Áp dụng định lý Pythagore vào tam giác vuông SIP ta có: 2 2 2 2 SI =
SP − IP = 13 − 5 = 12 (cm)
Trung đoạn của hình chóp tam giác đều là d= SI= 12cm
Diện tích xung quanh của hình chóp đều S.MNP là: S = 15.12 = 180 (cm2) xp Bài 3.
Tam giác ABC cân có CH ⊥ nên CH là đường trung tuyến của tam giác ABC suy 1 1 ra HA = HB = AB = .8 = 4(cm) 2 2
Tam giác AHC vuông tại H nên 2 2 2
HA + HC = AC ( theo định lý Pythagore) Suy ra 2 2 2 4 + HC = 8 88 Suy ra HC= 48 6,92 cm 1 1 S = A . B CH = .8.6,9 = 27, 6 (cm2) ABC 2 2 1 1 3 V
= SH = .27,6.12 =110, 4(cm ) S . ABC 3 3
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6
Bài 4. Tính diện tích xung quanh của hình chóp tam giác đều có độ dài cạnh đáy là
10 cm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là 12cm.
Bài 5. Cho hình chóp tam giác đều S.ABC có độ dài cạnh đáy 4 cm và độ dài trung
đoạn bằng 10 cm. Tính diện tích xung quanh của hình chóp tam giác đều
Bài 6. Một kho chứa dạng hình chóp tam giác đều với độ dài cạnh đáy khoảng 12 m
và độ dài trung đoạn khoảng 8m. Người ta muốn sơn bên ngoài cả ba mặt xung quanh
của kho chứa đó và không sơn phần làm cửa có diện tích là 5 2 m . Biết mỗi 2 m sơn
trả 30000 đồng. Cần phải trả bao tiền để hoàn thành việc sơn phủ đó. 89 .
Bài 7. Tính thể tích khối rubik có dạng hình chóp đều . Biết khối rubik này có bốn
mặt là các tam giác đều bằng nhau cạnh 4,7 cm và chiều cao 4 cm; chiều cao của khối rubik bằng 3,9 cm c) Sản phẩm: Bài 4.
Diện tích cung quanh của hình chóp tam giác đều S.ABC là : 1 2 S = .
p d = .(10.3).12 = 180 (cm ) xq 2 Bài 5.
Diện tích cung quanh của hình chóp tam giác đều S.ABC là : 1 2 S = .
p d = .(4.3).10 = 60 (cm ) xq 2
Bài 6. Diện tích xung quanh của kho chứa đó là: 1 2 s = .
p d = .(12.3).8 = 144 (m ) xq 2
Diện tích cần sơn là : 144- 5= 139 ( 2 m )
Số tiền cần phải trả để hoàn thành việc sơn phủ đó là: 139.30000=4170000 đ 1 1 1
Bài 7. Thể tích của khối rubik là : 3
V = .S.h = .( .4,7.4).3,9 = 12, 25 (cm ) 3 3 2
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs 90
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
3. Hướng dẫn về nhà.
- Ôn lại kiến thức về hình chóp tam giác đều , công thức tính thể tích và diện tích
xung quanh của hình chóp tam giác đều. - Làm bài tập :
Bài 8. Tính diện tích xung quanh, diện tích toàn phần và thể tích của:
a) Hình chóp tam giác đều có chiều cao là 98,3 cm ; tam giác đáy có độ dài cạnh là
40 cm và chiều cao 34,6 cm; Chiều cao mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là 99 cm.
b) Hình chóp tam giác đều có độ dài cạnh đáy là 120 cm, chiều cao là 68 cm , chiều
cao mặt bên xuất phát từ đỉnh của hình chóp tam giác là 90 cm. Ngày soạn: / /20...
TIẾT 46+ 47+ 48. CHỦ ĐỀ 16: HÌNH CHÓP TỨ GIÁC ĐỀU. Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức:
- Mô tả đỉnh, cạnh bên, mặt bên, mặt đáy của hình chóp tứ giác đều.
- Tạo lập hình chóp tứ giác đều.
- Tính diện tính xung quanh và thể tích của hình chóp tứ giác đều.
- Giải quyết một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh
của hình chóp tứ giác đều. 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. 91 Năng lực riêng:
- Tính thể tích, diện tích xung quanh của hình chóp tứ giác đều. 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu
2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: ÔN TẬP LÝ THUYẾT
a) Mục tiêu: Hs được củng cố kiến thức bài 39 để giải toán thành thạo.
b) Nội dung: HS trả lời các câu hỏi
Câu 1. Nêu công thức tính diện tích xung quanh của hình chóp tứ giác đều ?
Câu 2. Nêu công thức tính thể tích của hình hóp tứ giác đều ?
c) Sản phẩm: Hs trả lời câu hỏi đã được chuẩn bị sẵn ở nhà . 92
d) Tổ chức thực hiện:
Hoạt động của GV
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các câu hỏi - Yêu cầu - Nhận nhiệm vụ
Bước 2: Thực hiện nhiệm vụ. Hs: HĐ cá nhân
- Gv: Theo dõi, đôn đốc, giúp hs
Bước 3: Báo cáo, Thảo luận.
- HS dưới lớp nhận xét .
- Gv: Gọi HS trả lời từng câu hỏi ( 2 HS)
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh vào vở học
- Gv: Nhận xét chốt kiến thức đã sử dụng để thêm chiều. giải bài
2. Hoạt động 2: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học bài 39 để giải bài tập liên quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
Bài 1. Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 6 cm và độ dài trung
đoạn bằng 7cm. Tính diện tích xung quanh của hình chóp tứ giác đó.
Bài 2. Một hộp quà lưu niệm có dạng hình chóp tứ giác đều , với độ dài cạnh đáy là
8 cm và chiều cao 9 cm. Tính thể tích của hộp quà đó. 93
Bài 3. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 7 cm và độ dài
trung đoạn bằng 10 cm. Tính diện tích xung quanh của hình chop tứ giác đó
Bài 4. Tính thể tích của hình chóp tứ giác đều có chiều cao 3 cm, độ dài cạnh của tứ giác là 5 cm. c. Sản phẩm
Bài 1. Diện tích xung quanh của hình chóp tứ giác đó là: 1 2 S
= .(6.4).7 = 84(cm ) Xq 2 1
Bài 2. Thể tích hộp quà lưu niệm đó là: 2 3
V = .8 .9 = 192(cm ) 3
Bài 3. Diện tích xung quanh của hình chóp tứ giác S.ABCD đó là: 1 2 S
= .(7.4).10 = 140(cm ) Xq 2
Bài 4. Thể tích của hình chóp tứ giác đều là: 1 1 2 3 V = S
.h = .5 .3 = 25(cm ) đáy 3 3
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân 94
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
3. Hoạt động 3: Vận dụng
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 5,6,7
Bài 5. Tính diện tích toàn phần và thể tích của hình chóp tứ giác đều có độ dài cạnh
đáy là 72 dm, chiều cao là 68 dm, chiều cao của mặt bên xuất phát từ đỉnh của hình
chóp tứ giác đều là 77 dm.
Bài 6. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 12 cm và độ dài
trung đoạn bằng 15 cm . Tính diện tích xung quanh của hình chóp tứ giác đều đó.
Bài 7. Kim tự tháp Giza nổi tiếng ở Ai Cập có dạng hình chóp tứ giác đều với chiều
cao khoảng 147 m và đáy là hình vuông cạnh khoảng 230 m a)
Tính thể tích của kim tự tháp. b)
Đường cao của mặt bên xuất phát từ đỉnh của kim tự thấp đo được dài 186,6 m.
Tính diện tích xung quanh của kim tự tháp Giza. c) Sản phẩm: 1 Bài 5. 2 2 S = S + S
= .(72.4).77 + 72 =16272 (cm ) tp Xq đáy 2 1 1 V= 2 3 V =
S.h = .72 .68 = 117504 (cm ) 3 3 1 Bài 6. 2 S = . p d =
.(12.4).15 = 360 (cm ) xq 2 Bài 7. 1 1
a) Thể tích của kim tự tháp Giza là: đáy 2 3 V = S
.h .230 .147 = 2592100(m ) đáy 3 3 1
b) Diện tích xung quanh của kim tự tháp Giza là: 2 S
4. .230 = 85836(m ) xq 2
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở 95
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài.
3. Hướng dẫn về nhà.
- Ôn lại công thức tính diện tích xung quanh và thể tích của hình chóp tứ giác đều.
- Làm lại các bài tập vào vở. - Làm bài tập :
Bài 8. Cho hình chóp tứ giác đều có độ dài cạnh đáy là 15 cm và chiều cao 8cm. Tính
thể tích của hình chóp tứ giác đều.
Bài 9: Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh như hình vẽ
a) Tính thể tích không khí trong chiếc lều.
b) Tính diện tích vải lều ( không tính các mép dán), biết chiều cao của mặt bên xuất
phát từ đỉnh của chiêc lều là 3,18 m. Ngày soạn: / /20...
TIẾT 49+ 50+ 51. CHỦ ĐỀ 17: ÔN TẬP HỌC KÌ II Ngày giảng Lớp: Sĩ số 8A1: 8A3: 8A4: I. MỤC TIÊU 1. Kiến thức: 96
- Củng cố kiến thức học kì II để chuẩn bị kiểm tra 2. Năng lực: Năng lực chung:
- Năng lực tự chủ và tự học trong tìm tòi khám phá
- Năng lực giao tiếp và hợp tác trong trình bày, thảo luận và làm việc nhóm
- Năng lực giải quyết vấn đề và sáng tạo trong thực hành, vận dụng. Năng lực riêng:
- Áp dụng kiến thức học kì II để giải bài tập 3. Phẩm chất:
- Bồi dưỡng hứng thú, say mê trong học tập; ý thức làm việc nhóm,ý thức tìm tòi,
khám phá và sáng tạo cho Hs.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU: 1. Giáo viên:
Giáo án, phiếu học tập, phấn các màu 2. Học sinh: Vở, nháp, bút
III. TIẾN TRÌNH DẠY HỌC:
1. Hoạt động 1: Luyện tập
a) Mục tiêu: Hs vận dụng được kiến thức đã học của học kì II để giải bài tập liên
quan từ cơ bản đến nâng cao.
b) Nội dung: Làm bài tập 1,2,3
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs.
Bước 1: Chuyển giao nhiệm vụ.
Hs: - Lắng nghe Gv giao việc.
Gv giao Hs lần lượt làm các bài tập 1,2,3 - Nhận nhiệm vụ
- Yêu cầu Hs hoạt động cá nhân
Bước 2: Thực hiện nhiệm vụ Hs: hoạt động
- Gv: Theo dõi, đôn đốc, giúp đỡ em
Bước 3: Báo cáo, Thảo luận.
Hs: Tại chỗ nhận xét bài của bạn
- Gọi HS lên bảng trình bày
- Gv: Yêu cầu cả lớp theo dõi và nhận xét.
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần
- Gv: Nhận xét sửa lỗi sai cho HS.
đáp án vào vở học thêm chiều.
2. Hoạt động 2: Vận dụng 97
a) Mục tiêu: Hs vận dung được kiến thức đã học để tự giải các dạng bài tập liên quan
từ cơ bản đến nâng cao.
b) Nội dung: HS làm bài 4, 5,6,7 c) Sản phẩm:
d) Tổ chức thực hiện:
Hoạt động của Gv.
Hoạt động của Hs
Bước 1: Chuyển giao nhiệm vụ. HS chép đề vào vở
Gv chiếu bài tập lên màn hình.
Bước 2: Thực hiện nhiệm vụ.
Hs: hoạt động cá nhân và giải ra nháp.
- Gv: Theo dõi, đôn đốc HS
Bước 3: Báo cáo, Thảo luận.
HS lên bảng trình bày , HS dưới lớp
- Gv: Yêu cầu học sinh lên bảng chữa nhận xét .
Bước 4: Kết luận, Nhận định.
- Hs: Ghi chép nhanh, đẹp phần đáp
- Gv: Nhận xét, chốt kiến thức trọng tâm án vào vở . của bài. 3. Hướng dẫn về nhà.
- Ôn lại kiến thức học kì II
- Làm lại các bài tập vào vở. - Làm bài tập :




